A Phase Map for Vertical Upflow of Slightly Cohesive Geldart A Powders Focused on High Solids Mass Flux

Featured Application

The findings of this article are significant to vertical upflow legs of Fluidized Dense phase Conveying (FDC) as well as to High Density Circulating Fluidized Bed (HD-CFB) risers.

Abstract

Flow regimes of vertical upflow for slightly cohesive Geldart A powders at high solids mass flux ($G_s$ $\gtrsim$ 500 kg/m²s) are not fully resolved. In particular, Dense Suspension Upflow (DSU) as a distinct flow regime and its transition boundaries are not broadly accepted. Furthermore, the locus of the pressure gradient minimum, which is the broadly accepted dense–dilute transition at low $G_s,$ requires validation at high $G_s$. In our recent work, by adapting the phase map of Wirth and by Eulerian modeling, DSU was defined as a distinct flow regime with gross upflow of solids and with granular temperature at the wall greater than that in the bulk. This study has further validated the definition of DSU and its transition boundaries by extending the modeling to areas not fully explored in the earlier work. Furthermore, this study has identified (a) the possibility of a phase of DSU between fast fluidization and turbulent regime at all $G_s$; and (b) the need to review the suitability of the locus of the pressure gradient minimum as the dense–dilute transition at high $G_s$. Additionally, our work has demonstrated (a) a new provisional correlation that the upper transport velocity for Geldart A powders is significantly greater than hitherto predicted; and (b) the slip velocity in the transport regimes increases with $G_s$ to peak within fast fluidization and falls thereafter to attain low multiples of the terminal settling velocity within DSU.

1. Introduction

Resolved phase maps are a means for a priori prediction of flow regimes from powder characteristics, enabling the selection of robust operating envelopes and facilitating numerical modeling. The regimes of vertical upflow in straight pipes of uniform circular cross-section under gas–solids two-phase flow for Slightly Cohesive Geldart A (SCA) powders (Hausner Ratio < 1.25) [1,2] are well resolved by fluidization research at lower solids mass flux ($G_s\lesssim$ 500 kg/m²s). However, high $G_s$ operations such as Fluidized Dense phase Conveying (FDC), typically 1000 $\lesssim$ $G_s$ $\lesssim$ 3000 kg/m²s [3], are uncommon, and there are knowledge gaps. Specifically, Dense Suspension Upflow (DSU) as a separate flow regime and its boundaries with Fast Fluidization (FF) and Core-Annular Flow (CAF) are not broadly accepted [4,5]; while the locus of the pressure minimum is broadly accepted as the dense–dilute transition at low $G_s$ [6,7], its suitability at high $G_s$ requires validation, too.

In our recent work focused on FDC [8,9,10], the Phase Map of Wirth [11] (PMW) was adapted to resolve the high $G_s$ regimes for SCA powders, including DSU and its transition boundaries, with inputs from published literature [3,4,6,7,12,13,14,15,16,17,18,19] and numerical modeling by the Eulerian–Eulerian Two-Fluid Model with constitutive relations based on the Granular Kinetic Theory (TFM). Based on a limited set of simulations, DSU was proposed as a unique dense flow regime, characterized by gross upflow of solids and with the granular temperature ($\mathsf{\Theta }$) in the bulk lower than that at the wall. The intent of this study is to further validate DSU and its transition boundaries with FF, CAF, and dilute phase flow by additional simulations to cover areas not fully explored in the earlier work.

This article is organized as follows: Section 1.1 includes a pertinent summary of our recent work, to provide background and to set this study in context; Section 1.2 gives an outline of this study and objectives; Section 2 covers the study methodology and methods; Section 3 presents the study results; Section 4 covers a critical evaluation of the results and discussions; and Section 5 concludes with the study findings and impact.

1.1. Pertinent Summary of the Recent Work

This summary covers (a) FDC, (b) vertical upflow patterns for SCA powders, (c) PMW adapted to FDC of SCA powders, (d) provisional correlation for the upper transport velocity ($V_{tr2}$) for Geldart A powders, (e) validation of DSU and its boundaries by Eulerian modeling, and (f) slip velocity for SCA powders in the transport regime.

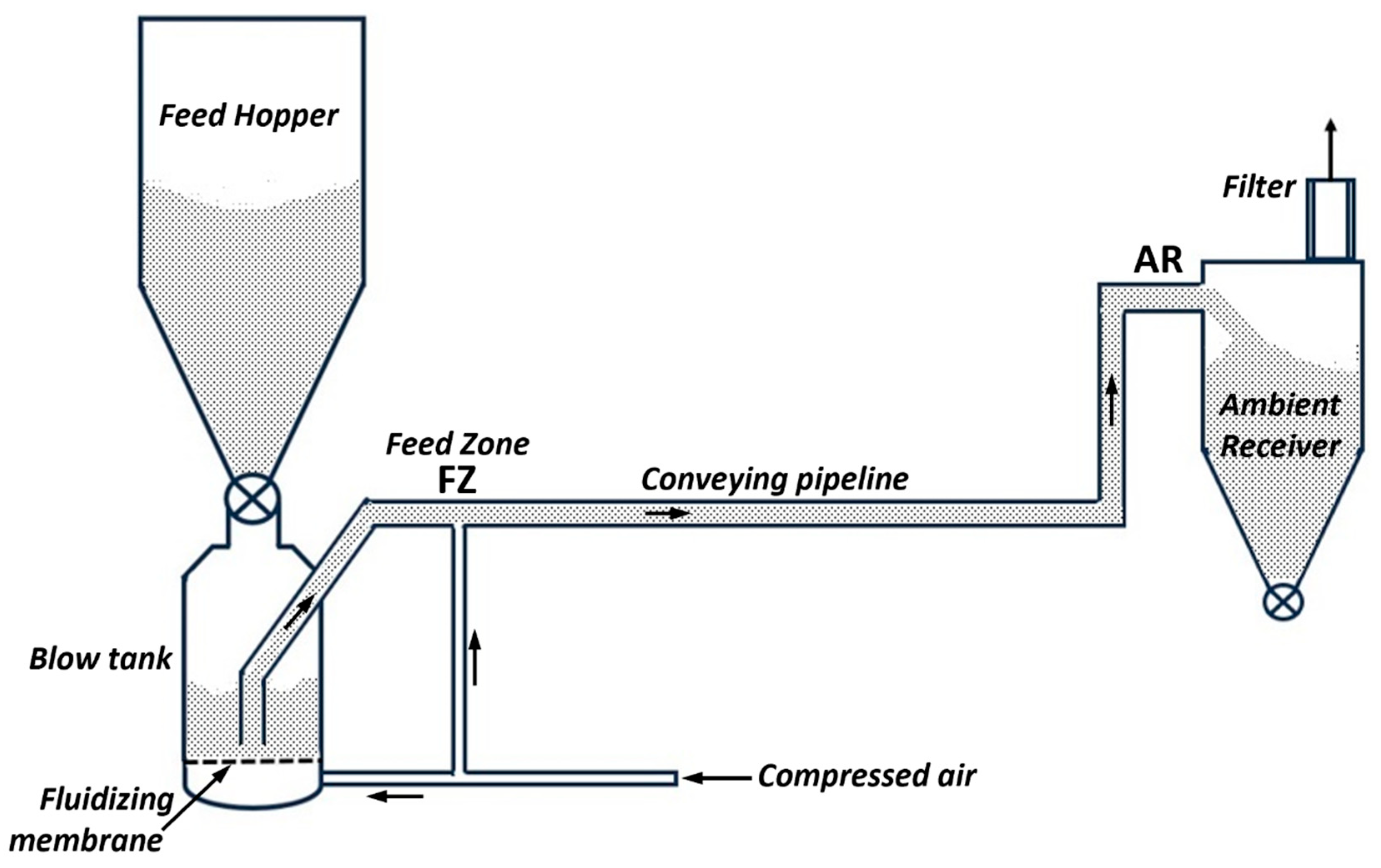
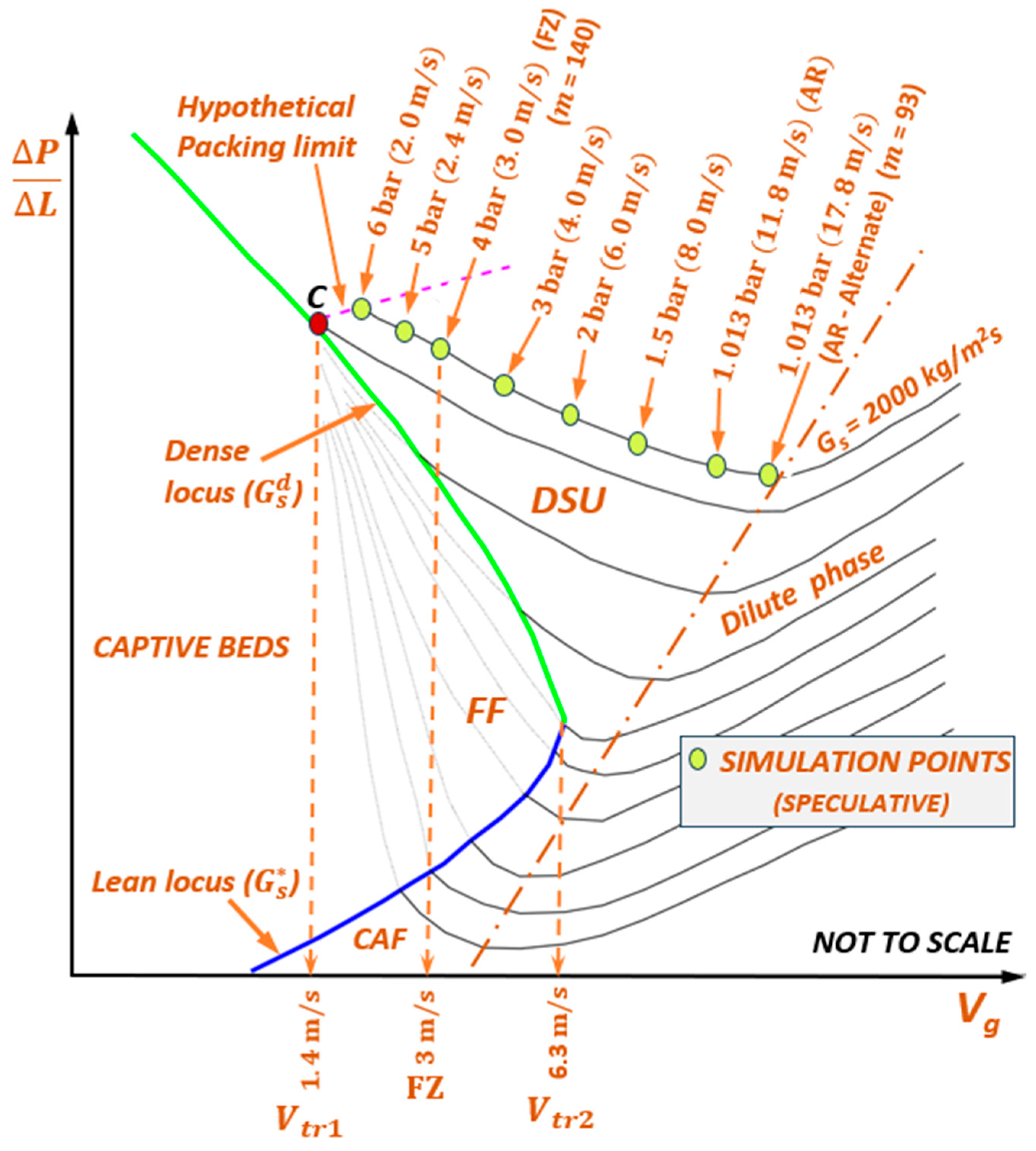
1.1.1. Fluidized Dense Phase Conveying

FDC is the dense conveying mode of fine powders [20] that are easily aeratable but deaerate slowly, typically Geldart C and A [21], with the Geldart A-B boundary at 4 bar per Grace [22] as a reasonable upper bound (Figure 1) [10]. The overlap of FDC and Dilute Phase Only (DPO) solids at the A-B boundary is largely attributed to the chart accounting only for the particle size ($d_p$) and not for the Particle Size Distribution (PSD) [3]; outlier FDC powders at high Archimedes numbers ($Ar$) are probably due to stronger mechanisms of cohesion [22]. Recall that the scope of this article is limited to SCA powders (Hausner Ratio < 1.25) and excludes Geldart C behavior; SCA powders can be slightly cohesive due to the ubiquitous van der Waals forces ($F_{vdW}$), but powder-specific mechanisms such as liquid bridges and electrostatic and magnetic forces are excluded too.

An example of an FDC system is included in Figure 2 [3]. The blow tank is essentially a fluidized bed feeder that enables high solids flux (1000 $\lesssim$ $G_s$ $\lesssim$ 3000 kg/m²s) and loading (150 $\lesssim$ $m$ $\lesssim$ 300). The Feed Zone (FZ) is typically at ~4 bar with superficial gas velocity ($V_{g,FZ}$) ~ 3 m/s; as the air expands along the conveying pipeline to the Ambient Receiver (AR), $V_g$ increases and the solids volume fraction (${\epsilon }_s$) decreases. Conveying pipelines are typically predominantly horizontal with some vertical upflow legs.

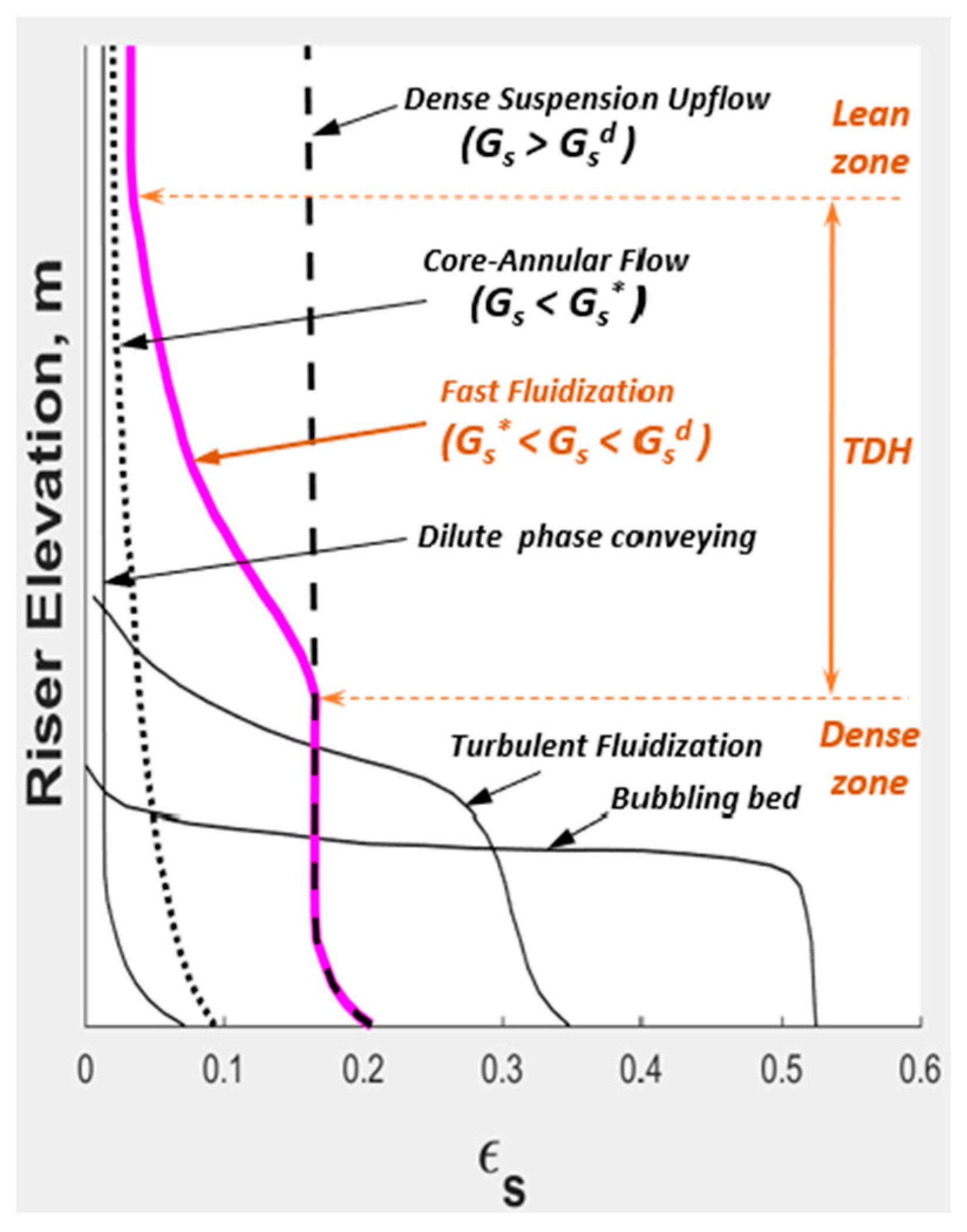
1.1.2. Vertical Upflow Patterns for SCA Powders

Flow patterns of vertical upflow for SCA powders are shown in Figure 3 [3,6,7,11,12,29,30,31,32,33,34,35,36]. Flow in the vertical upflow legs of FDC is referred to as ‘Non-Slugging dense phase Flow’ (NSF) [32], comprising DSU, FF, and CAF. Flow patterns in Figure 3 are further discussed below, together with the PMW.

It is important to recognize that the terminology used in pneumatic conveying and fluidization literature is often inconsistent, both within each field and across them. Definitions of the terms, as adopted in our work, are included in Appendix A.

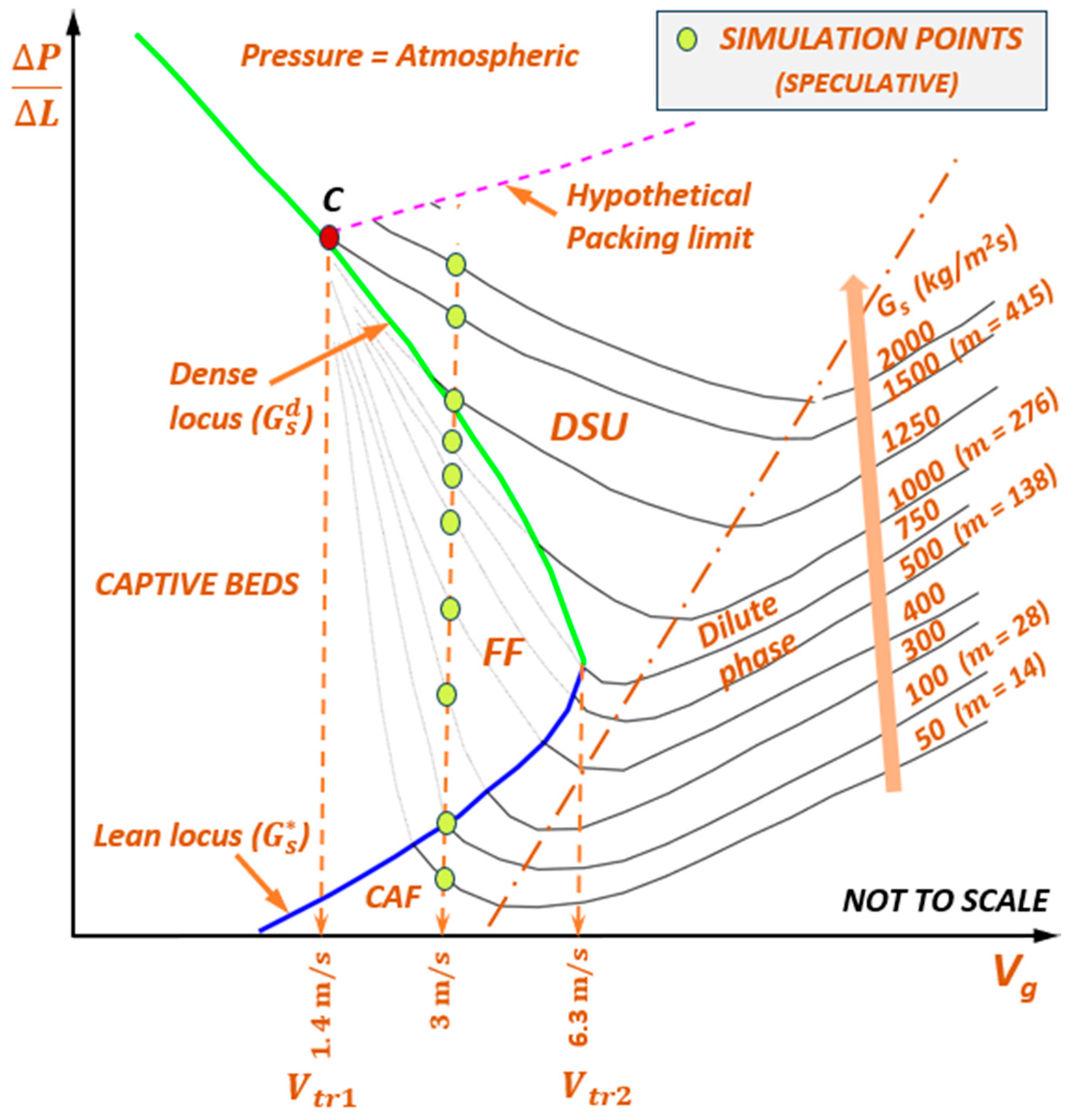
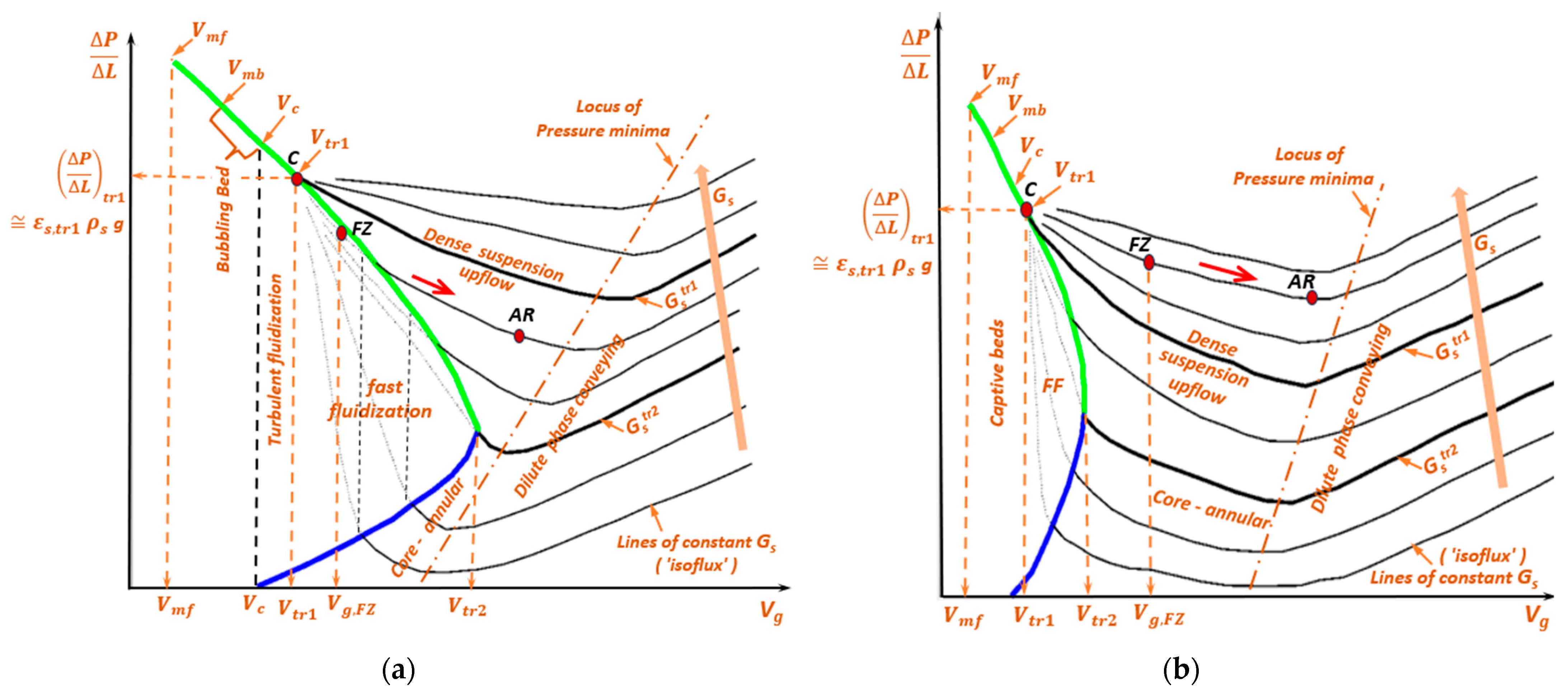
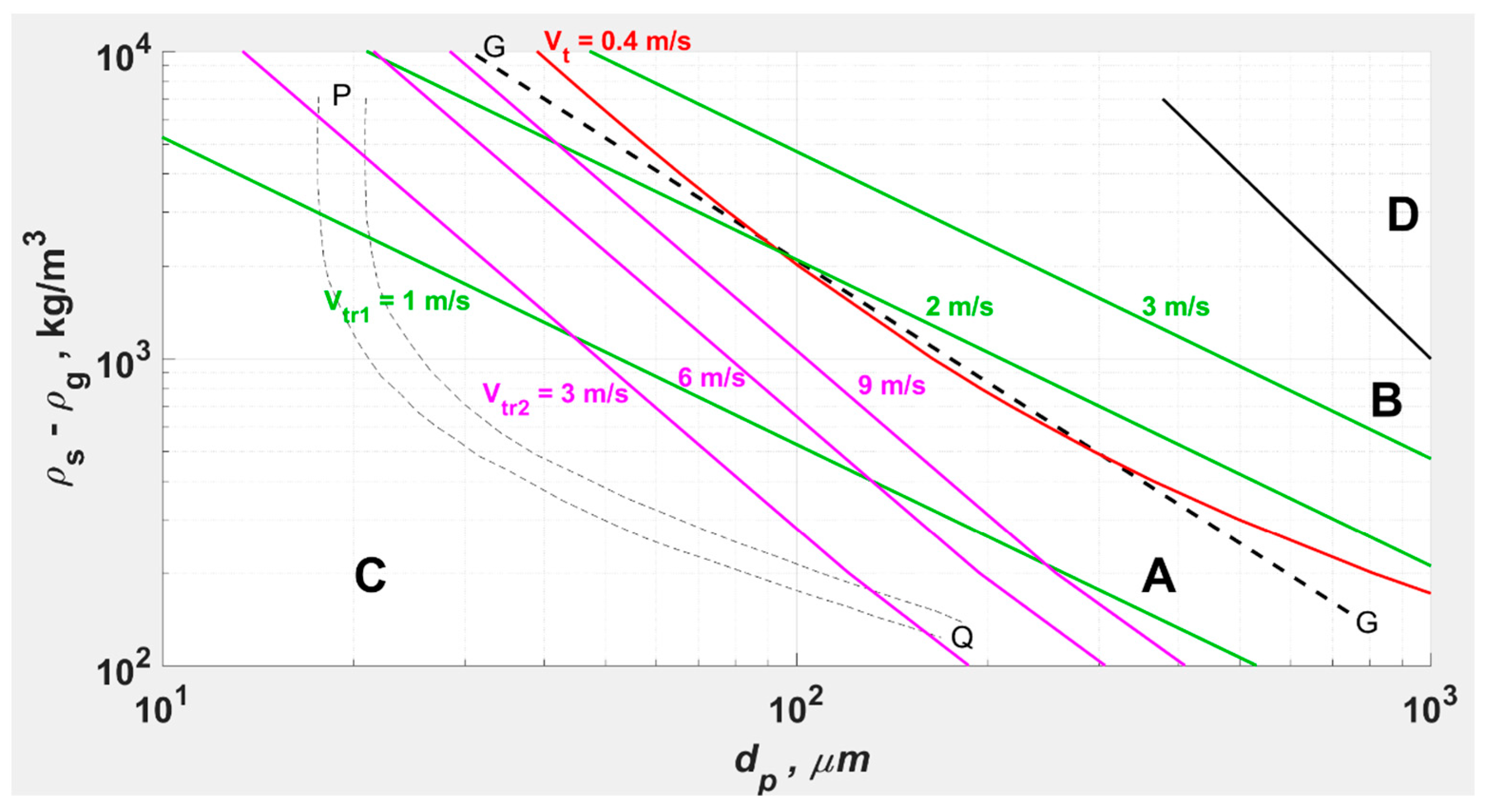
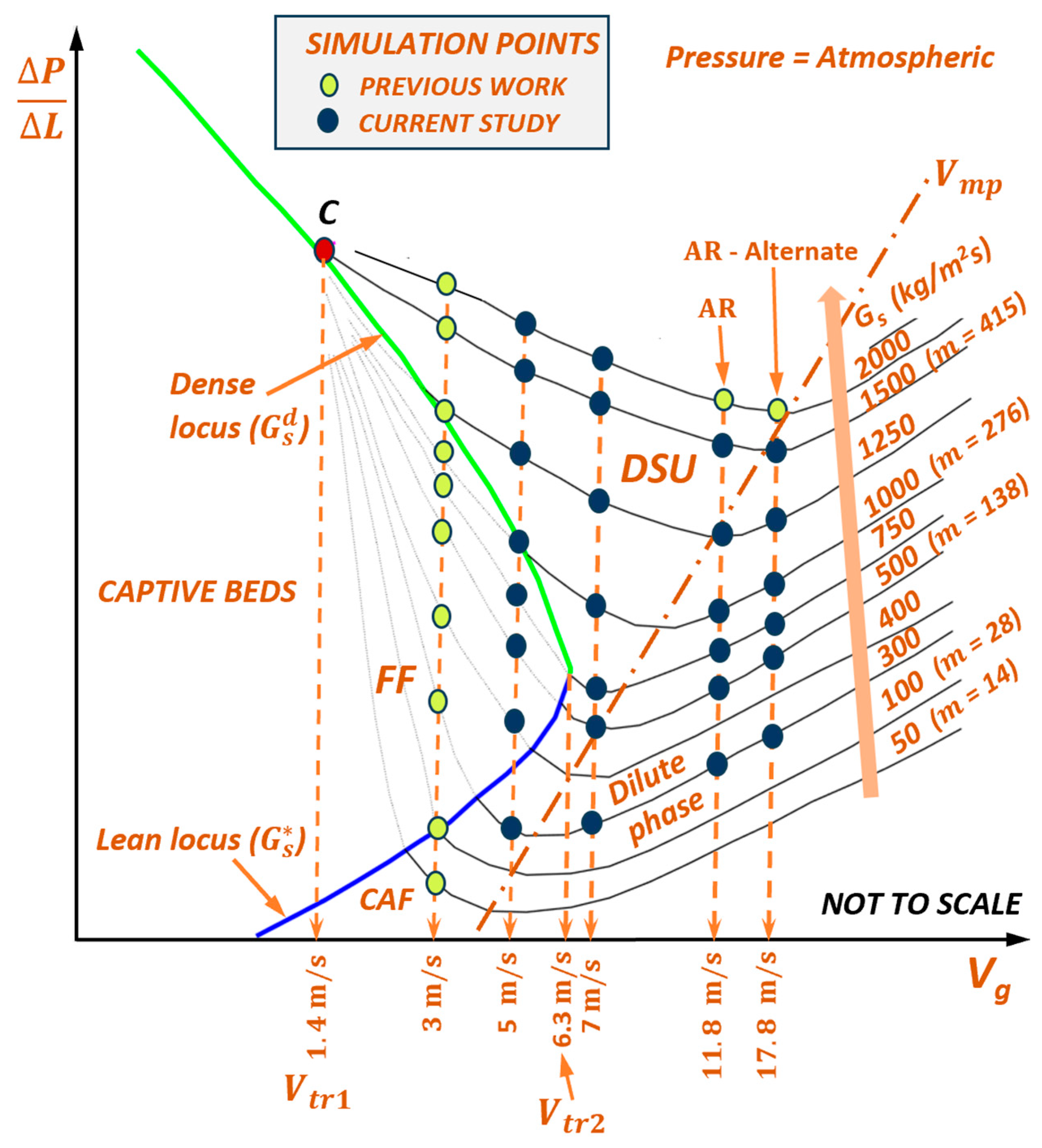
1.1.3. The Phase Map of Wirth

Figure 4 includes the PMW adapted to FDC, showing the typical operating ranges for coarser and finer SCA powders. The map is discussed below, referring to Figure 3 and Figure 4a, and considers a Circulating Fluidized Bed (CFB) riser equipped to separate the entrained solids and recirculate to the bottom. Starting from a fixed bed and increasing the $V_g$ gradually, the bed goes through the patterns of captive fluidized beds and transitions to the transport regimes at the lower transport velocity ($V_{tr1}$).

Regarding the captive fluidized beds: Increasing the $V_g$ gradually from a fixed bed, a phase of solid-like expansion ensues at the minimum fluidization velocity ($V_{mf}$), resulting in an expanded porous structure held together at the points of contact by weak $F_{vdW}$ [37] and/or frictional forces [35]; a phase of fluid-like particulate expansion may follow when the yield stress is overcome, for lighter powders (especially if harder), such as the fillites cenospheres reported by Geldart and Wong [38] (more details in [10]). Bubbling fluidization follows at the minimum bubbling velocity, and is characterized by gross circulation of the emulsion and rising bubbles [37]. Axial slugging, with fast-rising (${>V}_g$) round-nosed slugs and with the powder falling smoothly around the periphery, may follow only in narrow-diameter beds ($D<$ 100 mm), as the maximum stable bubble size (which increases with the terminal settling velocity of the particles, $V_t$) is limited for the powders [39]. Turbulent fluidization follows at the onset of turbulent fluidization ($V_c$), wherein the large rising bubbles disappear [40]. The bed finally transitions to transport regimes at $V_{tr1}$ (~10$V_t$ based on the mean particle size, due to clustering) [17]. Within the captive beds, the solids inventory is virtually constant, but for any entrainment in the turbulent fluidization regime, the relation between $V_g$ and ${\epsilon }_s$ ($\cong ∆P/∆L$/${\rho }_s g$) is essentially unique [18].

Regarding the transport regime: once past $V_{tr1}$, the entire column of powder starts to flow (although the solids velocity at the bottom can be significantly lower than that at the top), requiring recirculation of solids to maintain the inventory. The relation between $V_g$ and ${\epsilon }_s$ is now dependent on $G_s$: high $G_s$ leads to DSU (corresponds to HD-CFB, as defined in our work) and low $G_s$ to FF (corresponds to Low Density Circulating Fluidized Bed, LD-CFB). FF is characterized by an S-Shaped axial ${\epsilon }_s$ Profile (SSP), with a dense zone at the bottom, a lean zone at the top, and Transport Disengagement Height (TDH) in between [14,36] (Figure 5); DSU is characterized by gross upflow of solids with little backmixing. At $V_{tr1}<V_g<V_{tr2}$, DSU, FF, and CAF may all occur at a same $V_g$ but at decreasing $G_s$ (Figure 3): DSU at $G_s$ greater than the gross upflow flux ($G_s^d$), CAF at $G_s$ less than the saturation carrying capacity ($G_s^{*}$), and FF in between at $G_s^{*}<G_s<G_s^d$. CAF consists of at least some downflow in the denser annulus, with net upflow overall; at the transition to FF at $G_s^{*}$, the denser annulus turns to net downflow and the solids start to form a dense zone at the bottom, with CAF continuing on the top of it. With further increase in $G_s$, the bottom dense zone grows to occupy the entire riser at $G_s^d$ at the transition to DSU [13,41]. The locus of the minimum pressure velocity ($V_{mp}$) is broadly accepted as the dense–dilute transition at lower $G_s$ (typically at ${\epsilon }_s\lesssim$ 0.02) [6,7].

PMW captures the locus of $∆P/∆L$ versus $V_g$ for both the bottom dense zone (green in Figure 4) and the top lean zone (blue in Figure 4) of FF. Starting within FF, from an SSP corresponding to a given $V_g$ and $G_s$, holding the $G_s$ constant, and increasing the $V_g$ gradually, the bottom dense zone gets leaner and the top lean zone denser until the TDH disappears, resulting in essentially axially uniform ${\epsilon }_s$ (but for the change in pressure due to static head of solids; there can be significant radial gradients, though), with the ${\epsilon }_s$ coinciding with the lean or the dense locus based on the $G_s$. With a sufficiently tall CFB riser and an appropriate range of $V_g$ and $G_s$, the loci are fully traced and converge at the upper transport velocity ($V_{tr2}$), beyond which FF is not observed. Therefore, the PMW demarcates the boundaries of FF, with CAF at the locus of $G_s^{*}$ (‘onset of accumulative choking’, as defined in our work), with DSU at the locus of $G_s^d$, and its upper $V_g$ limit at $V_{tr2}$.

Key differences between the version of PMW proposed by Wirth [11] and that adapted to SCA powders in Figure 4 include the following: (a) locus of the top lean zone (i.e., entrainment), due to clustering of particles, only starts at $V_c$ (at a low multiple of $V_t$ based on the mean particle size) rather than at $V_t$ [12,17]; (b) lines of constant $G_s$ (‘isoflux’) converge at $\mathit{C}$($V_{tr1}$, ${\epsilon }_{s,tr1}$) (‘end of accumulative choking’, as defined in our work), wherein entrainment has virtually stopped and the particles have collapsed into a turbulent bed, to follow the essentially unique locus within the captive beds [36], rather than directly at $V_{mf}$; and (c) experimental data of Wang et al. [16] suggests that, with decreasing $V_g$, the isofluxes at $G_s^{tr1}<G_s<G_s^{tr2}$ may not sustain DSU but may slip into and traverse within FF towards $\mathit{C}$, as the bed gets denser overall.

The ‘other dense flow patterns’ in Figure 3, corresponding to captive fluidized beds, are generally not observed during FDC of SCA powders. The reported minimum $V_{g,FZ}$ of $\cong$2 m/s [3,27] is clearly greater than $V_{tr1}$ for SCA powders at the 4 bar corresponding to FZ (Figure 6), and $V_{tr1}$ corresponding to the A-B boundary is about 2 m/s, even at ambient conditions (Figure 7). Note that turbulent fluidized beds typically operate at 0.5 $< V_g<$ 1.5 m/s [40]. Furthermore, as discussed above, the characteristics of the transport regimes are clearly different from those of the captive beds. Even at the dense and axially uniform conditions of DSU, there are radial gradients in the solids’ velocity, and the slip velocity, as discussed below in Section 1.1.6, can be orders of magnitude greater than $V_{mf}$ and $V_{mb}$ due to clustering of particles to a larger effective $d_p$. Also, unlike in captive beds such as bubbling beds, segregation by size is insignificant in CFB risers for fine powders, especially at higher $G_s$ [6,37,42].

Impermeable Plug Flow (IPF), with plugs rendered essentially impermeable and separated by air gaps, the plug-1 of Kalman and Rawat [44], is indicated in Figure 3 as a part of FDC for the following reasons: (a) IPF is probable at $Ar <$ 100 [44,45], which covers the SCA powders (Figure 1); (b) in the FDC experiment of Cong et al. [46], IPF did not occur at a regime of its own but whenever the aeration in the blow tank became ineffective; (c) a flow that starts as IPF at the FZ may transition to FDC towards the AR due to the expansion of the interstitial air; (d) the concave up curves in the conveying characteristics of some of the FDC powders reported by Mills [3] were probably due to IPF, too [10]. However, IPF is probably appropriate as a separate conveying mode from FDC, for the following reasons: (a) conveying systems intended to operate under IPF (‘pulse phase’) are designed specifically with special ‘plug forming systems’ to enable the formation and to control the length of the plugs, and the plugs so formed remain separated for long conveying distances [3,32,47]; (b) an FDC system (inadvertently) designed based on IPF may not interchangeably operate under NSF at the same capacity [3,32,47]. Therefore, based on conceptual reasoning, IPF is not explored by numerical modeling in our work, which is focused primarily on NSF (DSU, FF, and CAF).

FDC for coarser SCA powders, towards the A-B boundary, may occur under DSU and/or FF (Figure 4a), and for finer SCA powders, towards the C-A boundary, predominantly under DSU (Figure 4b) due to the magnitudes of their $V_{tr2}$ relative to $V_{g,FZ}$. Furthermore, $G_s^{tr2}$, which is the $G_s$ corresponding to $V_{tr2}$ and the threshold $G_s$ for DSU, also scales significantly between finer and coarser powders. Published experimental data for a fine and a coarse SCA powder are compared in

Table 1. Dependence of $V_{tr2}$ and $G_s^{tr2}$ on powder characteristics and riser diameter.

${\mathit{d}}_{\mathit{p}}$ μm	${\mathit{\rho }}_{\mathit{s}}$ kg/m3	${\mathit{P}}_{45}$	${\mathit{V}}_{\mathit{t}}$ m/s	D m	L m	${\mathit{V}}_{\mathit{g}}$ m/s	${\mathit{G}}_{\mathit{s}}$ kg/m2s	${\mathit{V}}_{\mathit{t}\mathit{r}1}$ m/s	${\mathit{V}}_{\mathit{t}\mathit{r}2}$ m/s	${\mathit{G}}_{\mathit{s}}^{\mathit{t}\mathit{r}2}$ kg/m2s	Reference
(30) *	(1500) *	--	0.039	0.19	11.5	1–3	$\lesssim$38	~1.0	1.8	38	[11]
85	1500	~0.1	(0.33) *	0.08	18.0	5–9	800–1800	--	$\gtrsim$9.0	$\lesssim$1400	[16]
79	1490	0.08	(0.24) *	0.303	20.4	12.2	285–690	--	>12.8	--	[19]

* Values indicated within brackets are estimates; not reported in the references.

: while Wirth [11] observed $V_{tr2}$ and $G_s^{tr2}$ at just 1.8 m/s and 38 kg/m²s, respectively, for a fine powder, Wang et al. [16] observed them to be $\gtrsim$9.0 m/s and $\lesssim$1400 kg/m²s, respectively, for a coarse powder. The isoflux corresponding to $G_s^{tr2}$ is the hypothetical boundary between CAF and DSU at $V_{tr2}<V_g<V_{mp}$.

Furthermore, the magnitude of $V_{tr2}$ for a given Geldart A powder increases with $D$. Included in Table 1 is the powder of Issangya et al. [19], comparable to that of Wang et al. [16]. While Wang et al. approached $V_{tr2}$ at $V_g$ $\gtrsim$ 9.0 m/s in a riser of $D=$ 0.08 m, Issangya et al. have reported conspicuous SSPs at $V_g=$ 12.2 m/s (in their Figure 4) as well as net downflow in the annulus at $V_g=$ 12.8 m/s (and a $G_s$ as low as 368 kg/m²s) (in their Figure 13) in a riser of $D=$ 0.303 m. Occurrence of SSPs at increasingly higher $V_g$ with increasing $D$ has also been demonstrated numerically by Pita and Sundaresan [48]. Furthermore, the direct dependence of $G_s^{*}$ on $D$ for Geldart A powders, in the correlation of Breault and Weber [49], suggests the same, too.

FF is an established operating regime for industrial CFBs, although the solids inventory in the riser can be sensitive to changes in both $V_g$ and $G_s$ [15]. Vertical upflow legs of FDC may operate stably under this diffuse regime of accumulative choking, too, unlike the unstable zone of sharp ‘classical choking’ and slugging observed with larger particles.

That DSU corresponds to transport of fine powders at high $G_s$ has been suggested by some researchers, for example, [50]. Klinzing et al. [32] (p. 117, 123, 156, 158, 178) actually consider NSF to include FF as well as turbulent fluidization, flanked by ‘slugging dense phase’ and dilute phase; they [32] (p. 166) allude to DSU whilst discussing the work of Matsen [51], emphasizing the importance of $G_s$ on flow behavior. Note that the PMW is essentially the same as the empirical map proposed earlier by Matsen [51] in his Figure 10, with his ‘supercritical’ zone corresponding to DSU.

Limitations of PMW: (a) while the map is helpful in understanding the flow regimes at high $G_s$, it is specific to the experimental powder and also to the experimental $D$; and (b) a PMW plotted based on experimental data may incorporate a change in operating pressure for the $∆P/∆L$ along the isofluxes.

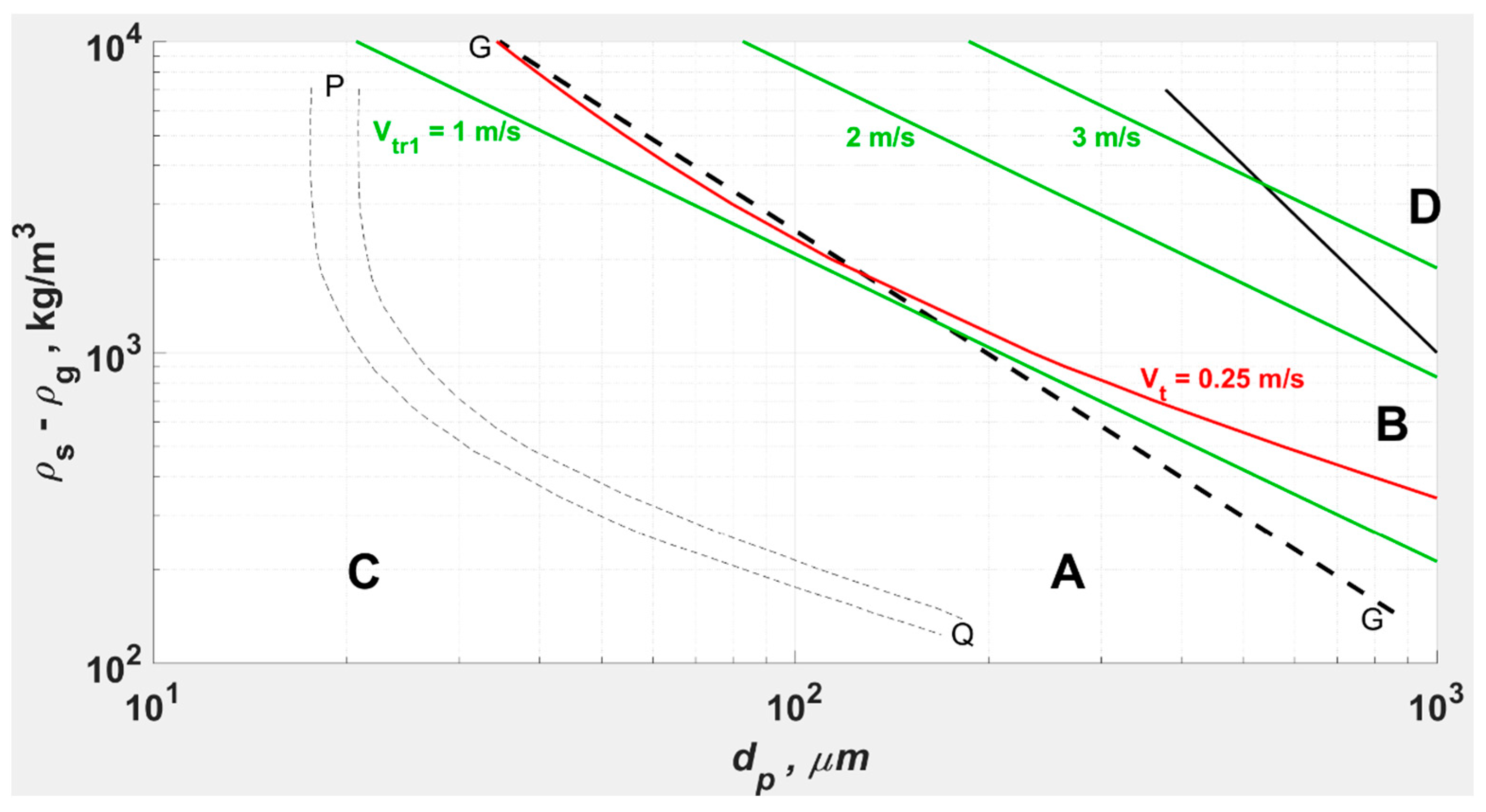
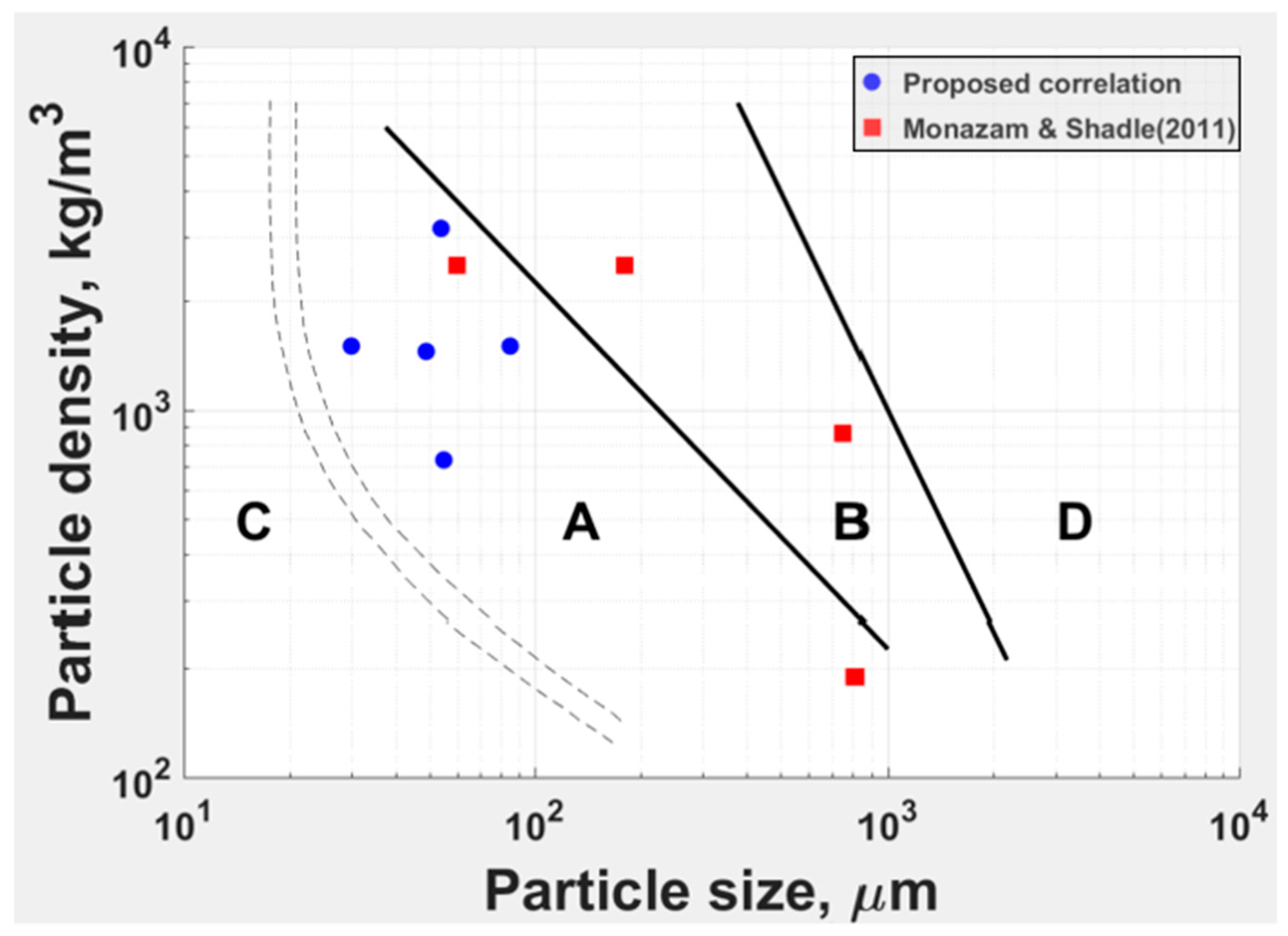
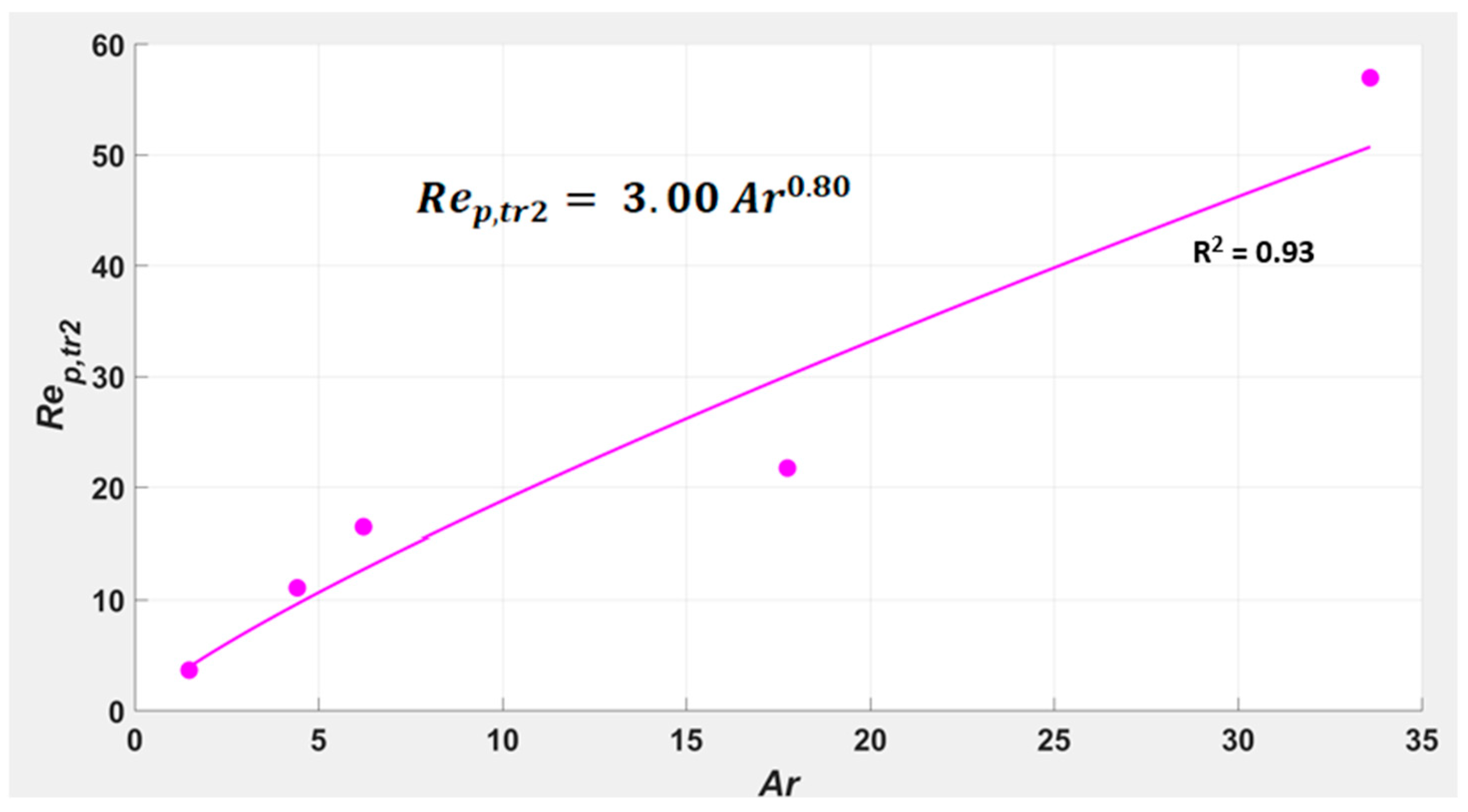
1.1.4. Provisional Correlation for Upper Transport Velocity

The only reported correlation for $V_{tr2}$, by Monazam and Shadle [15], underpredicts for Geldart A powders. It was based on a limited set of data, including Geldart B and atypical Geldart A solids (Figure 8), and on indirect measurements of $V_{tr2}$ by column emptying times.

A provisional correlation (1), shown in Figure 9, was proposed based on powders that clearly classify as Geldart A (Figure 8), for which direct measurements of $V_{tr2}$ in ambient CFBs are reported [11,14,16,36,52]; ${Re}_{p,tr2}$ is the particle Reynolds number corresponding to $V_{tr2}$. It is provisional because of the recognized uncertainties (recorded in [10]) in the limited set of imprecise data collated from disparate experiments, and as the dependence of $V_{tr2}$ on the fraction of fines ($P_{45}$) and $D$ are not incorporated. More details in [10] (pp. 146–150).

$${Re}_{p,tr2}=3.00 {Ar}^{0.8}$$

(1)

Although provisional, the correlation demonstrates that $V_{tr2}$ for Geldart A powders is significantly higher than hitherto predicted [10]. Notably, while $V_{tr2}$ per (1) for the simulated powder ($d_p$ = 70 $\mathsf{\mu }$ m and ${\rho }_s$ = 1400 kg/m³) is 6.3 m/s, Eulerian modeling predicts it to be between 5 and 7 m/s (Section 3).

1.1.5. Validation of DSU and Its Boundaries by Eulerian Modeling

DSU has only been an area of active research in the last 25 years. Whilst most of the reported high $G_s$ CFB experiments are at $G_s\lesssim$ 750 kg/m²s, in a recent experiment, Wang et al. (2022) [16] have achieved as high a $G_s$ as 1800 kg/m²s, comparable with typical FDC systems.

Although DSU and FF are the transport regimes most relevant to high $G_s$ operations such as FDC, DSU as a separate flow regime and its transition boundaries are not broadly accepted [4,5]. The following knowledge gaps (referring to Figure 4) were taken up for exploration/validation by Eulerian modeling:

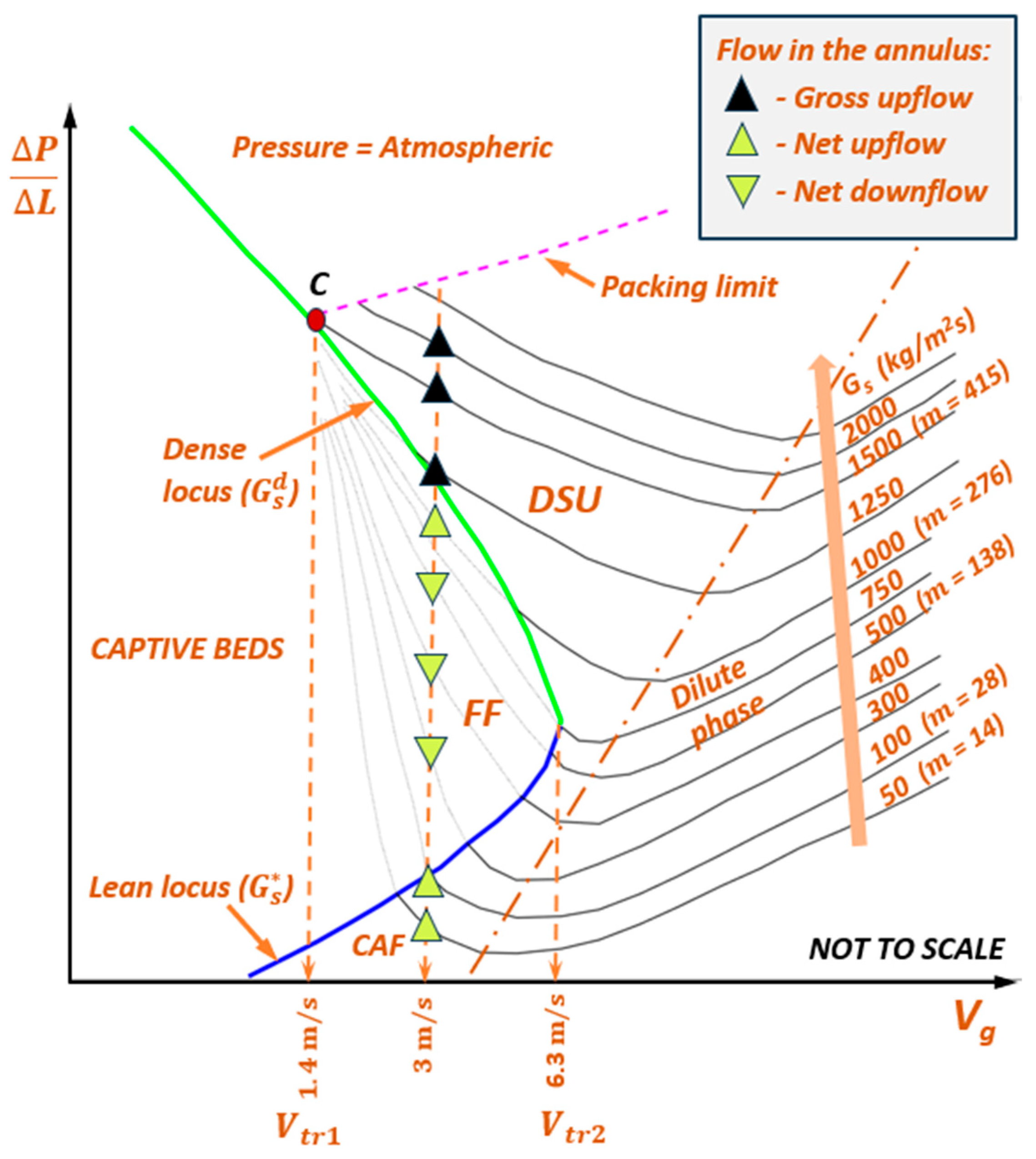
• Some researchers, for example, [4,53] do not recognize DSU as a separate flow regime, as it has not hitherto been defined based on clear transitions in the behavior of the flow field. Therefore, it was intended to explore whether the transitions to DSU can be perceived from the trend in any of the distributed parameters as the flow field changes.
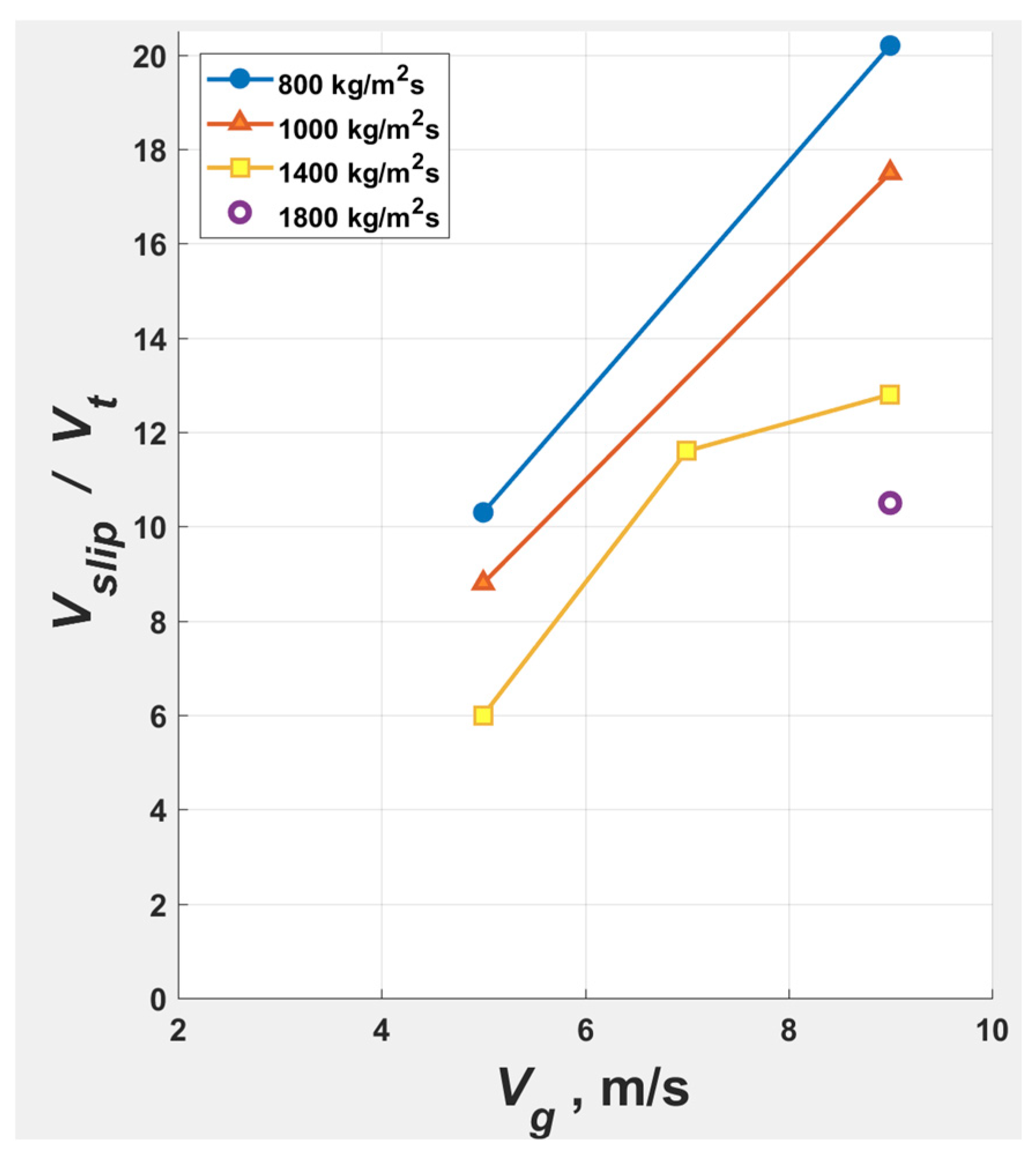
• The phase map in Figure 4 considers the criterion of Li and Kwauk [14] (based on vertical upflow experiments in straight pipes of uniform circular cross-section), which is the disappearance of SSP, for the transition from FF to DSU. The experiment of Wang et al. [16] suggests that, at $V_{tr1}<V_g<V_{tr2}$, SSP most probably disappears at $G_s^d$, when the riser attains gross upflow with little backmixing. However, there is some uncertainty in the axial ${\epsilon }_s$ profiles reported in [16] that needed clarification: the riser having attained $G_s^d$, for example, at $G_s$ = 1400 kg/m²s and $V_g$ = 9 m/s in the Figure 6(d) of [16], appeared to show backmixing at lower elevations at $G_s$ of 1800 kg/m²s; the backmixing was probably due to the riser being unable to sustain gross upflow with the increased feed of low-velocity solids that required acceleration.
• Locus of $V_{mp}$ is broadly accepted as the criterion for the dense–dilute transition at low $G_s$ [6,7] (wherein it is generally observed at ${\epsilon }_s\lesssim$ 0.02). This criterion may be suitable at the high $G_s$ of DSU, too, at $G_s>G_s^{tr2}$, considering that the static head of solids dominates at dense conditions (such as towards the FZ), and other losses take over at dilute conditions (such as near AR); however, this requires validation.
• That the isofluxes at high $G_s$ converge towards $\mathit{C}$ required validation, as the experimental results for a vertical upflow segment of a composite pipeline under FDC [3] indicated that they may possibly be diverging towards a ‘hypothetical packing limit’ instead (Figure 10).

Figure 10. Simulation runs of the previous work—VDU runs to study the transition from FF to DSU. Note that the simulation points were speculative regarding the flow regimes at the time of designing the runs. Indicated $V_{tr1}$ and $V_{tr2}$ are estimates per [43] and (1), respectively.

Figure 10. Simulation runs of the previous work—VDU runs to study the transition from FF to DSU. Note that the simulation points were speculative regarding the flow regimes at the time of designing the runs. Indicated $V_{tr1}$ and $V_{tr2}$ are estimates per [43] and (1), respectively.

The methodology and methods for the previous work, including the powder selected for modeling, were the same as those of the current study and are discussed in Section 2. Only the simulation runs, conditions, and findings of the previous work are discussed here.

Two sets of runs were carried out (Figure 10 and Figure 11), with a riser of $D$ = 0.04 m and height ($L$) = 10.0 m: (a) VDU (Vertical Dense Upflow) runs to study the transition from FF to DSU, at increasing $G_s$ from 50 to 2000 kg/m²s at a fixed $V_g$ of 3 m/s, with ambient pressure at the outlet of the riser; (b) VPND (Vertical Packing limit and Dilute phase) runs following an isoflux at $G_s$ = 2000 kg/m²s, from the conditions of the FZ at 4 bar and $V_g$ = 3 m/s, towards the AR at ambient pressure and $V_g$ = 11.8 m/s and towards the dense limit, up to 6 bar and $V_g$ = 2 m/s. A further VPND run was carried out for an alternate AR case at $V_g$ = 17.8 m/s, considering that the flow started at the FZ at 6 bar and $V_g$ = 3 m/s instead; this case required $L$ = 15 m to exclude the entrance flow development zone (in the numerical model results) at the higher $V_g$.

The results in Figure 12 validated that the transition from FF to DSU, defined as the disappearance of SSP, occurs at $G_s^d$. SSP persists in the axial profile with a net upflow of solids at $G_s$ = 1000 kg/m²s and only disappears with gross upflow at $G_s$ = 1250 kg/m²s $\cong G_s^d$; gross upflow is maintained at $G_s>G_s^d$ (Figure 10) as well as in the VPND runs at $G_s$ = 2000 kg/m²s (Figure 11). Therefore, the backmixing near the wall at lower elevations, observed by Wang et al. [16] at $G_s$ = 1800 kg/m²s and $V_g$ = 9 m/s, was probably due to solids entering the riser bottom at a lower velocity, although from a fluidized bed feeder, which requires acceleration. The fraction of downflowing cells was used in lieu of the fraction of downflowing particles, as only the averages over the cells are available in Eulerian modeling.

The transition from FF to DSU, as well as DSU as a separate flow regime, could also be perceived from the radial profiles in Figure 13: (a) pre-wall dip in the profiles of ${\epsilon }_s$ transition to pre-wall spike; (b) profiles of $\mathsf{\Theta }$ transition from being greater in the bulk than at the wall to vice versa.

Figure 14 shows that the flow in the annular region (which starts as gross upflow within the dilute phase) transitions to net upflow within CAF to net downflow at the transition to FF, but reverts within FF to net upflow with increasing $G_s$ and finally to gross upflow at the transition to DSU. Note that the transition from CAF to FF was only observed at $G_s$ = 300 kg/m²s, as against the speculative simulation points in Figure 10.

Probable reasons for the variation in ${\epsilon }_s$ at the pre-wall region are discussed in [10].

The reasoning for the transition in the radial profiles of $\mathsf{\Theta }$ is as follows: For downflow in the annular region, it is essential for $\mathsf{\Theta }$ to dissipate at the wall, so that the solids concentrate at the wall [54]. The radial gradient in solids velocity ($V_s$) is the source of $\mathsf{\Theta }$. Stronger radial gradients in $V_s$ at lower $G_s$ allow for the $\mathsf{\Theta }$ produced in the bulk to dissipate at the wall. With increasing $G_s$, as the production of $\mathsf{\Theta }$ decreases with diminishing gradients in $V_s$, and as the dissipation of $\mathsf{\Theta }$ in the bulk increases as the square of the increasing ${\epsilon }_s$, the radial profile of $\mathsf{\Theta }$ reverses from ${\mathsf{\Theta }}_{bulk}> {\mathsf{\Theta }}_{wall}$ to vice versa. This reversal in the radial profiles of $\mathsf{\Theta }$, with > 2 orders of magnitude drop in ${\mathsf{\Theta }}_{bulk}$, is a clear indicator of the transition.

The trend in $∆P/∆L$ for the VPND runs (Figure 15), from the FZ at $V_g$ = 3 m/s towards the dense limit at $V_g$ = 2 m/s, indicated that the isofluxes at high $G_s$ also converge towards $\mathit{C}$($V_{tr1}$, ${\epsilon }_{s,tr1}$) rather than diverging towards the hypothetical packing limit. This is because the static head of solids becomes increasingly dominant towards the dense limit, with the viscous losses diminishing and the frictional losses remaining insignificant at ${\epsilon }_s<$ 0.5 (Figure 16), the threshold for frictional losses (${\epsilon }_s^{min}$).

The trend in $∆P/∆L$ in Figure 15, from the FZ at $V_g$ = 3 m/s towards the AR at $V_g$ = 11.8 m/s, indicates that the pressure minimum is not attained at the AR for the conditions simulated. The pressure minimum is probably not attained at the alternate AR at $V_g$ = 17.8 m/s either, with the static head of solids still the major component. However, a change in the flow regime towards the dilute phase can be perceived in the radial profiles in Figure 16 at $V_g$ = 17.8 m/s, with $V_s$ attaining a clear parabolic profile, and more significantly, $\mathsf{\Theta }$ reverting towards ${\mathsf{\Theta }}_{bulk}>{\Theta }_{wall}$. This reversal in $\mathsf{\Theta }$ clearly preserves DSU as a transport regime at $V_{tr1}<V_g<V_{mp}$, with $G_s>G_s^d$ at ${V_{tr1}<V}_g<V_{tr2}$ or $G_s>G_s^{tr2}$ at $V_{tr2}<V_g<V_{mp}$, and with ${\mathsf{\Theta }}_{bulk}<{\Theta }_{wall}$ (Figure 4,

Table 2. Characteristics of the transport regimes for SCA powders. Reproduced from [10].

Regime	${\mathit{V}}_{\mathit{g}}$ (m/s)	${\mathit{G}}_{\mathit{s}}$ (kg/m2s)	$\mathsf{\Theta }$ (m2/s2)	Flow in the Annular Region
CAF	${V_{tr1}<V}_g<V_{mp}$	$G_s<G_s^{*}$$\mathrm{at} {V_{tr1}<V}_g<V_{tr2}$ $G_s<G_s^{tr2}$$\mathrm{at} {V_{tr2}<V}_g<V_{mp}$ #	${\mathsf{\Theta }}_{wall}<{\mathsf{\Theta }}_{bulk}$	Net upflow with (at least some) downflow.
FF	${V_{tr1}<V}_g<V_{tr2}$	$G_s^{*}<G_s<G_s^d$	${\mathsf{\Theta }}_{wall}<{\mathsf{\Theta }}_{bulk}$	$\mathrm{For} \mathrm{a} \mathrm{given} {V_{tr1}<V}_g<V_{tr2}$$, \mathrm{with} \mathrm{increasing} G_s$, the annulus transitions from net downflow to net upflow (Figure 14).
DSU	${V_{tr1}<V}_g<V_{mp}$	$G_s>G_s^d$$\mathrm{at} {V_{tr1}<V}_g<V_{tr2}$	${\mathsf{\Theta }}_{wall}>{\mathsf{\Theta }}_{bulk}$	Gross upflow.
		$G_s>G_s^{tr2}$$\mathrm{at} {V_{tr2}<V}_g<V_{mp}$ #
Dilute phase	$V_g>V_{mp}$	$\mathrm{All} G_s$ $	${\mathsf{\Theta }}_{wall}<{\mathsf{\Theta }}_{bulk}$	Gross upflow.

^# Isoflux of $G_s^{tr2}$ is a hypothetical boundary between CAF and DSU at ${V_{tr2}<V}_g<V_{mp}$. ^$ Suitability of $V_{mp}$ as the dense–dilute boundary at $G_s>G_s^{tr2}$ requires further validation.

).

A phase of ‘annular flow’, with upflowing annulus, is perceived in the radial profiles of $G_s$ in Figure 16 at high $V_g$, before the transition to the dilute phase. However, it may not be possible to clearly demarcate such a phase based on the changes in the flow field behavior, and it is probably appropriate as a part of DSU.

Identifying DSU as a distinct flow regime marked by gross upflow of solids, with ${\mathsf{\Theta }}_{wall}>{\Theta }_{bulk}$, is of practical importance to industrial CFBs. Recall that, as defined in our work, FF and DSU correspond to LD-CFB and HD-CFB, respectively (Figure 3). Downflow in the annulus significantly affects residence time distribution and interphase contacting [55], making HD-CFB the preferred configuration. As gross upflow flux ($G_s^d$) increases with $d_p$, ${\rho }_s$, and $D$, achieving this regime may require much higher $G_s$—for example, ≳1400 kg/m²s at a $V_g$ of 9 m/s, as observed by Wang et al. [16] (Table 1) with $d_p$ = 85 μm, ${\rho }_s$ = 1500 kg/m³, and $D$ = 0.08 m—than what is typical in industrial CFBs ($G_s$ ≲ 750 kg/m²s, larger $D$ and higher $V_g$ [6,19]). This suggests that a narrower $D$ can be helpful in attaining HD-CFB.

Kim et al. [13] proposed an alternate criterion for the transition from FF to DSU: the $G_s$ at which the net upflow of solids is achieved in the annulus. Experimental data, for example [16,19] show that this transition happens at a fraction of $G_s^d$, when SSP is still conspicuous and backmixing is substantial. Therefore, this criterion may lack practical relevance, and DSU might not be classifiable as a distinct flow regime based on flow field behavior. Furthermore, it may not be possible to distinguish between CAF and DSU using this criterion, either.

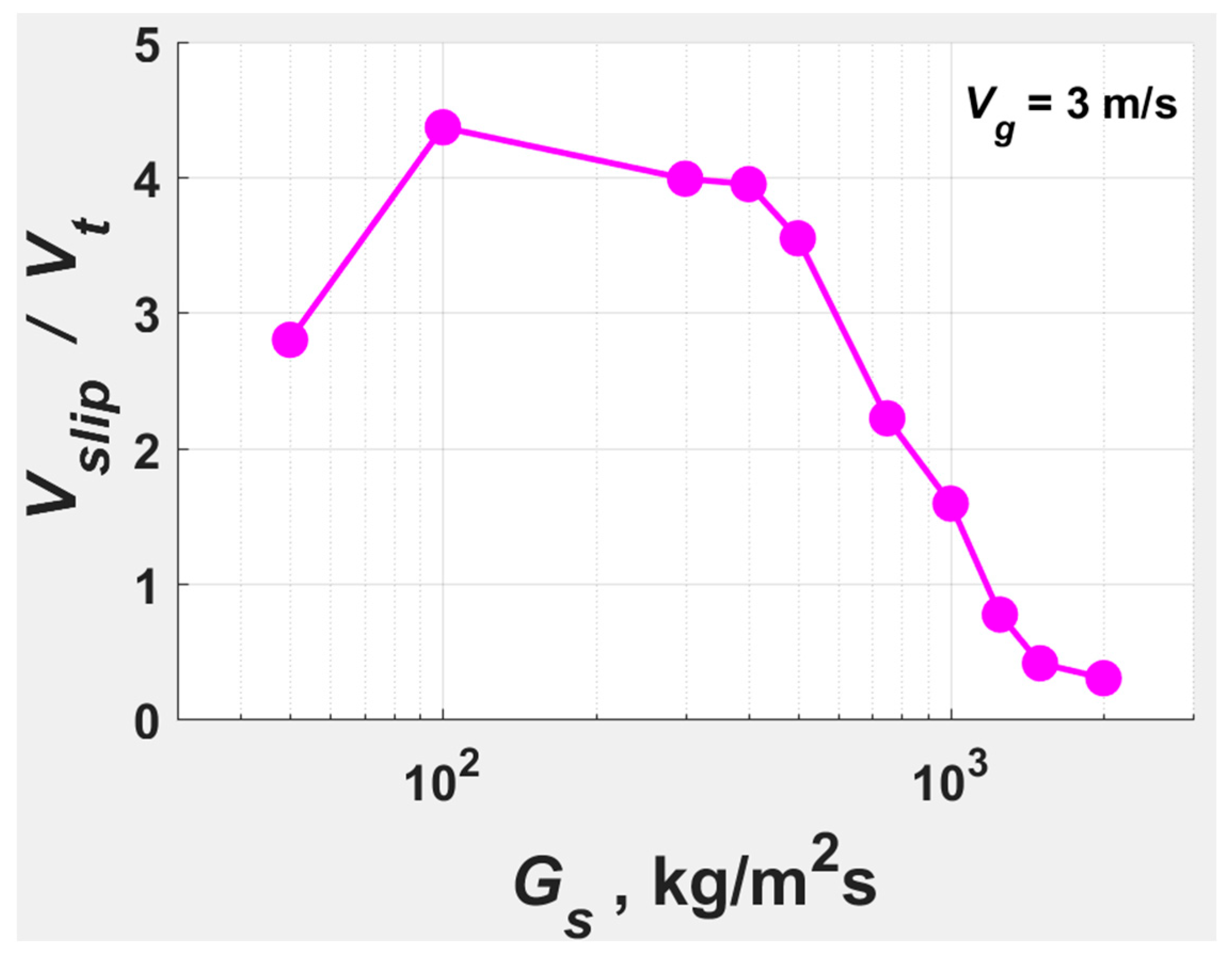
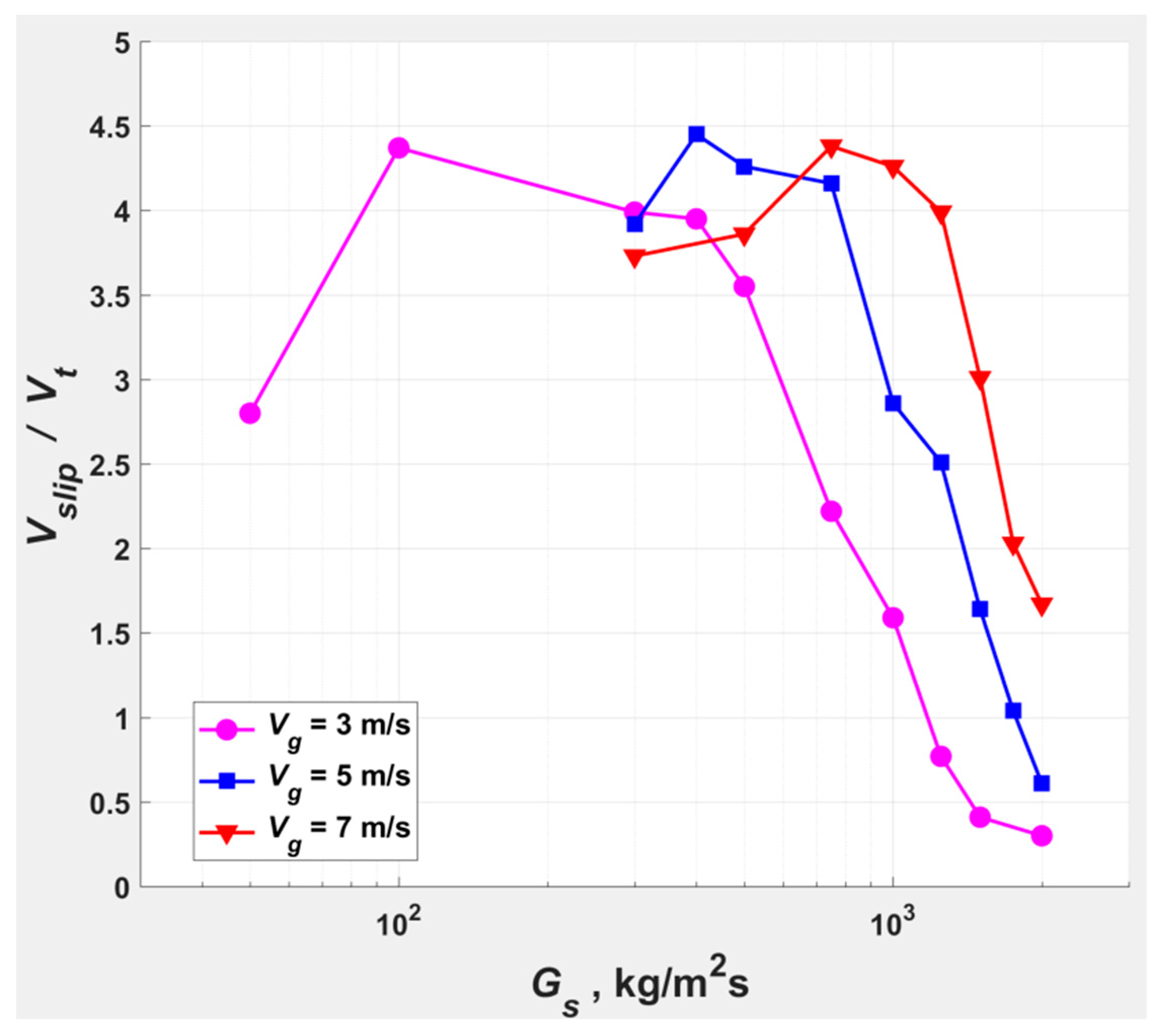
1.1.6. Slip Velocity

Yerushalmi and Cankurt [17] observed the slip velocity ($V_{slip}$) (2) to be a low multiple of $V_t$ at the transition to transport regimes at $V_{tr1}$, to increase within FF to peak at ~20$V_t$, and to drop thereafter within the CAF (‘transport riser’) to attain essentially $V_t$ as the particles approach unhindered flow conditions at the dilute phase.

$$V_{slip}=\left|V_g/\left(1-{\epsilon }_s\right)-G_s/{\rho }_s{\epsilon }_s\right|$$

(2)

The definition of $V_{slip}$ in Equation (2) assumes steady-state conditions, with the ${\epsilon }_s$ representing the average under statistically steady conditions. $V_{slip}$ is typically estimated (e.g., [56] (p. 5457); [10] (pp. 266–267)) as the average of the values calculated at various riser elevations using the prevalent $V_g$ (accounting for the compressibility of the gas) and cross-sectional average ${\epsilon }_s$.

Yerushalmi and coworkers [17,18], in their bed expansion experiments at $G_s\lesssim$ 150 kg/m²s, observed the peak $V_{slip}$ within FF to increase monotonously with increasing $G_s$. However, Figure 14 of Issangya et al. [56] indicates the $V_{slip}$ to be saturating at $G_s\lesssim$ 400 kg/m²s and to be at the cusp of decline. In fact, the experiments of Wang et al. [16] at $G_s\le$ 1800 kg/m²s indicate the $V_{slip}$ at high $G_s$ to be declining with increasing $G_s$ (Figure 17). Therefore, experimental results suggest that, with increasing $G_s$, peak $V_{slip}$ increases initially to attain a maximum within FF and decreases thereafter. Simulation results indicated a similar trend too, with $V_{slip}$ attaining a maximum within FF and dropping off thereafter to a fraction of $V_t$ within DSU (Figure 18); the maximum observed $V_{slip}\cong$ 4.4 $V_t$ is commensurate for the lower $V_g$ of 3 m/s used for the simulations.

1.2. Study Objectives and Outline

The objective of this study is to further validate the PMW in Figure 4 by TFM simulations, covering areas not fully explored in the earlier work:

• The transition from FF to DSU at $V_{tr1}<V_g<V_{tr2}$, at a higher $V_g$ of 5 m/s.
• The transition from CAF to DSU at $V_{tr2}<V_g<V_{mp}$, at a $V_g$ of 7 m/s.

This is also towards the validation that the isoflux at $G_s^{tr2}$ marks this transition. Furthermore, together with the runs at $V_g$ = 5 m/s, this helps towards the validation of the magnitude of $V_{tr2}$ as predicted by (1).

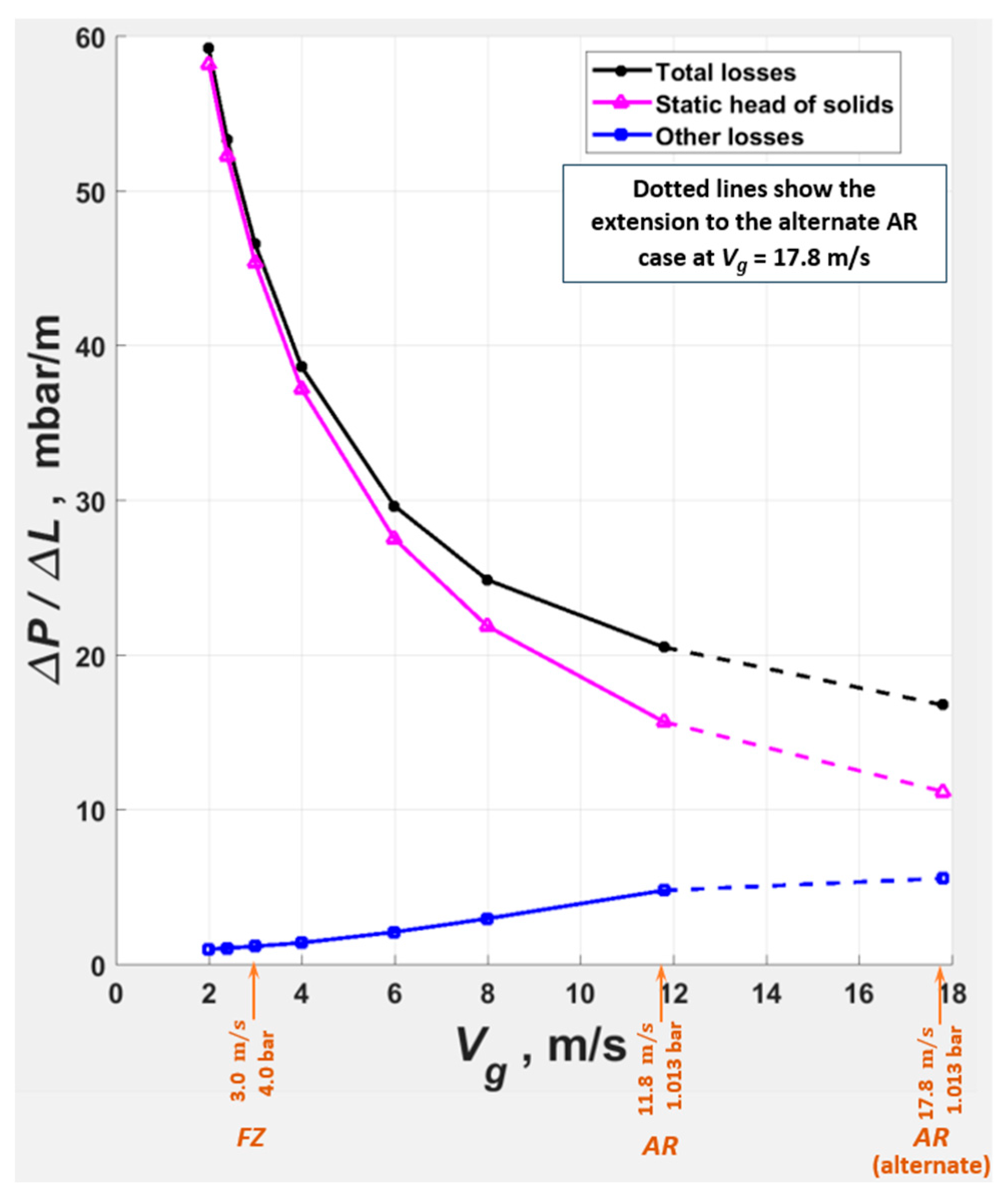
• The dense–dilute transition at $G_s>G_s^{tr2}$, at $V_g$ = 11.8 and 17.8 m/s (i.e., at the same $V_g$ as the AR and alternate AR of the earlier work), but at lower $G_s$.

With the intention of studying the dense limit at $G_s\gg G_s^{tr2}$, which is significant to finer SCA powders, a $G_s$ of 2000 kg/m²s was chosen for the earlier work. However, the corresponding $G_s/{\rho }_s$ ($G_s$ normalized by ${\rho }_s$) of 1.43 m³/m²s is higher than the typical $\lesssim$1.2 m³/m²s reported for FDC systems (Figure 2-59 of [10]), and $V_{mp}$ was not attained, even at the $V_g$ of 17.8 m/s, due to the higher ${\epsilon }_s$ (static head of solids). Therefore, it is intended to study the dense–dilute transition at lower $G_s$.

The criterion for the transition from FF/CAF to DSU is the attainment of gross upflow in the riser, with ${\mathsf{\Theta }}_{wall}>{\mathsf{\Theta }}_{bulk}$ (Table 2). Similarly, the criterion for the dense–dilute transition is also gross upflow, but with ${\mathsf{\Theta }}_{wall}<{\mathsf{\Theta }}_{bulk}$ (Table 2).

Additional simulation runs carried out for the current study are shown in Figure 19; simulation points are speculative with regard to the flow regime at the time of selection. All the runs were carried out with an ambient pressure outlet.

2. Materials and Methods

The methodology and methods adopted for this study are the same as the previous work and are discussed in greater detail in [10], which enables this work to be independently reproduced or adapted. Only the key items, such as the characteristics of the simulated powder, numerical modeling approach, model options, model scheme, simulation conditions, and model limitations, are summarized below. Items such as the reasoning behind the selection of the numerical modeling approach and model options, the full set of model equations, model validation details, and the computational system are available in [10].

Numerical modeling of gas–solids two-phase flow involves the prediction of solids distribution in the riser for the range of $V_g$ and $G_s$. Solids distribution can be highly nonuniform at all space and time scales [55,57], as reflected in the flow regimes in Figure 3. At high $V_g$, such as in the transport regimes, the nonuniformities appear as clusters—dynamic groupings of loosely bound particles surrounded by gas or dilute zones—while at low $V_g$, such as in the captive beds, as bubbles—gas pockets rising through the emulsion. Nonuniformities arise from the intrinsic instabilities due to particle–particle and particle–wall collisions, gravity, and other nonlinearities such as turbulence and drag. Modeling involves accounting for the interplay of these factors, as well as the complexities due to the characteristics of the powder.

The Eulerian–Eulerian Two-Fluid modeling approach with constitutive relations based on the Granular Kinetic Theory (TFM in short) was chosen for resolved models with distributed parameter solutions, at relatively low computational cost and with no practical limitation on the number of particles modeled. TFM uses the granular temperature ($\mathsf{\Theta }={\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}〈{\overrightarrow{C}}_s^2〉$, where $〈{\overrightarrow{C}}_s^2〉$ is the mean square of the peculiar velocity of the particles), a measure of the oscillating kinetic energy of the particles, for deriving the solids phase pressure and shear and bulk viscosities. TFM, including its Cartesian 2D slice through the axis version, is proven for the prediction of vertical upflow phenomena such as homogeneous bed expansion, bubble rise, clusters and streamers, CAF, and so forth. TFM is widely used for CFB [58], as well as FDC (e.g., [59,60,61,62]) research. Its mechanistic basis supports its application to areas such as DSU with limited experimental resolution. MFiX-TFM, the version of TFM available within the open-source MFiX code, was chosen for the modeling.

The model options (Table 3) were chosen from those available within the standard MFiX-TFM code, without non-trivial changes:

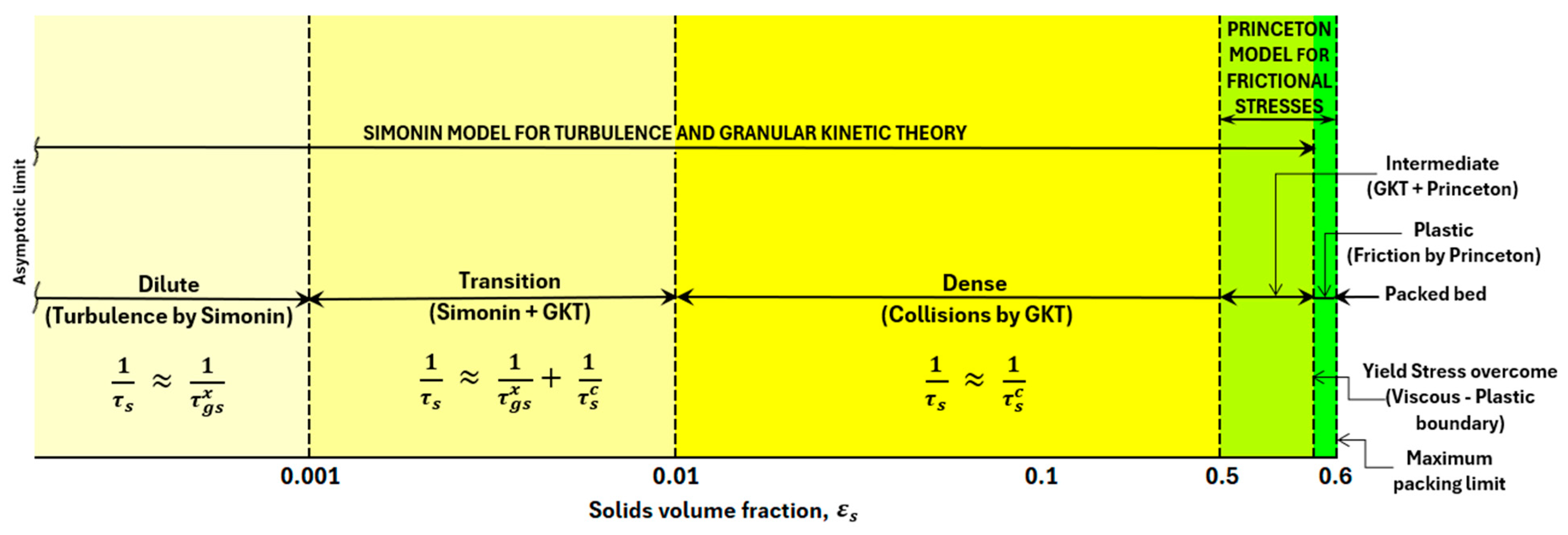
• The ‘Simonin, 1996’ viscous stress model [54,63,64,65] covers dilute turbulent through to the dense limit of the viscous regime by a dissipation time scale (${\tau }_s$), essentially a harmonic mean of collisional (${\tau }_s^c$) and particle relaxation (${\tau }_{gs}^x$) time scales; the turbulence model of Simonin and the Granular Kinetic Theory are recovered at the dilute and dense limits, respectively (Figure 20).
• The viscous stress model complemented by the Princeton model for frictional stresses [66] covers the full spectrum of ${\epsilon }_s$ (Figure 20).
• The $k_g-{ϵ}_g$ turbulence model is essential for the turbulence model of Simonin; the code automatically uses the turbulence wall functions for the gas phase wall Boundary Conditions (BC) when the $k_g-{ϵ}_g$ turbulence model is used.
• The Schiller and Naumann isolated sphere correlation used in the MFiX-TFM code for the Di Felice drag law was replaced with the Dalla Valle isolated sphere correlation, in line with Di Felice [67].
• The Di Felice drag law conforms well with Wen-Yu and Ergun drag laws in their respective ranges, without the steep transition between the Wen-Yu and Ergun laws at ${\epsilon }_s$ = 0.2 observed in the Gidaspow-blend drag law [8,10].
• Gas and solids flow rates specified for the mass inlet BC were steady and uniform across the inlet cross-section. $\mathsf{\Theta }$ was set at 1 × 10⁻⁸ m²/s² at the BC and $k_g$ and ${\in }_g$ at 0.01 m²/s² and 0.1 m²/s³, respectively.
• A constant pressure was specified for the pressure outlet BC.
• Free-slip wall BC with no applied granular temperature flux is used as a good approximation for the solids phase at rapid flow conditions of the transport regime [54,68,69].

The model was validated for (a) $∆P/∆L$ under gas-only flow, (b) CAF pattern, (c) trends in radial profiles for ${\epsilon }_s$ and $V_s$ (largely vis-à-vis [16]), (d) trend in $V_{slip}$ with increasing $G_s$ during NSF, and (e) $∆P/∆L$ under NSF; details in [10] (pp. 252–267).

Table 3. Model options.

Description	Option	Remarks
MFiX version	22.3.1	[70]
Viscous stress model	Simonin, 1996	[54,63,64,65]
Turbulence model	$k_g-{ϵ}_g$
Frictional stress model	Princeton	[66]
${\epsilon }_s^{min}$ for frictional stresses	0.5	Model default
Drag model	Di Felice	[67]
Radial distribution function	Carnahan—Starling	Code default
Conveying medium	Air at 20 °C
Air density	Ideal gas law
Inlet—Outlet BC	Mass Inlet—Pressure Outlet
Wall BC for gas phase	No-slip wall (Wall functions)
Wall BC for solids phase	Free-slip wall
Initial conditions	$\mathrm{Empty} \mathrm{pipe} ({\epsilon }_s$ and all velocities set to zero)

Table 3. Model options.

Description	Option	Remarks
MFiX version	22.3.1	[70]
Viscous stress model	Simonin, 1996	[54,63,64,65]
Turbulence model	$k_g-{ϵ}_g$
Frictional stress model	Princeton	[66]
${\epsilon }_s^{min}$ for frictional stresses	0.5	Model default
Drag model	Di Felice	[67]
Radial distribution function	Carnahan—Starling	Code default
Conveying medium	Air at 20 °C
Air density	Ideal gas law
Inlet—Outlet BC	Mass Inlet—Pressure Outlet
Wall BC for gas phase	No-slip wall (Wall functions)
Wall BC for solids phase	Free-slip wall
Initial conditions	$\mathrm{Empty} \mathrm{pipe} ({\epsilon }_s$ and all velocities set to zero)

Figure 20. Numerical modeling scheme. Reproduced from [8]. Key references include [54,63,65,66]. ${\tau }_s$ is the dissipation time scale (s), ${\tau }_{gs}^x$ is the particle relaxation time scale (s), and ${\tau }_s^c$ is the collisional time scale (s).

Figure 20. Numerical modeling scheme. Reproduced from [8]. Key references include [54,63,65,66]. ${\tau }_s$ is the dissipation time scale (s), ${\tau }_{gs}^x$ is the particle relaxation time scale (s), and ${\tau }_s^c$ is the collisional time scale (s).

A monodisperse powder of $d_p$ = 70 µm and ${\rho }_s$ = 1400 kg/m³ was chosen for modeling. Considerations in the selection of the powder [10] (pp. 231–233) are as follows:

• Although atypical, a monodisperse powder was chosen, as polydisperse powders, which are typically modeled as multiple solid phases of monodisperse powders, increase the computational load and model complexity.
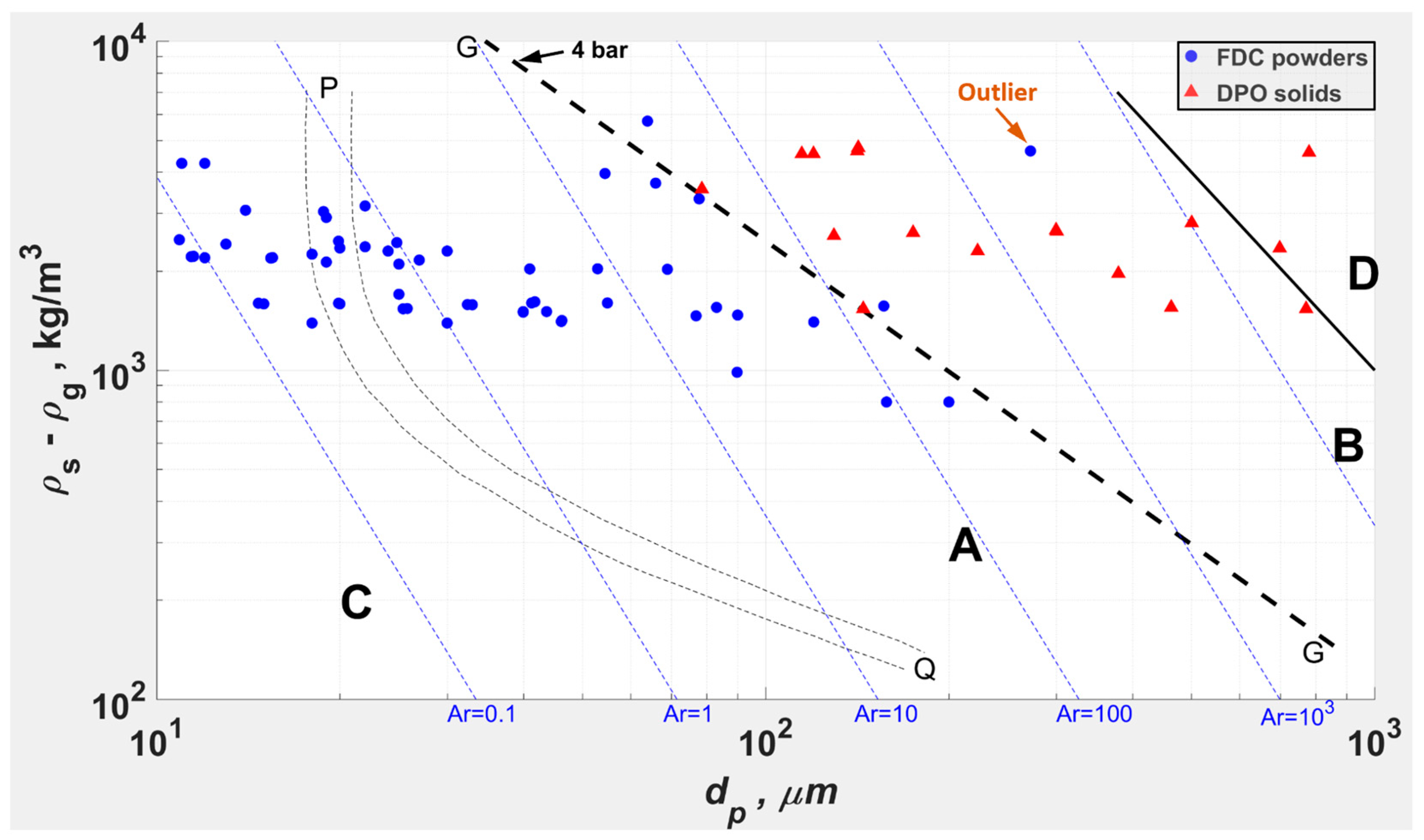
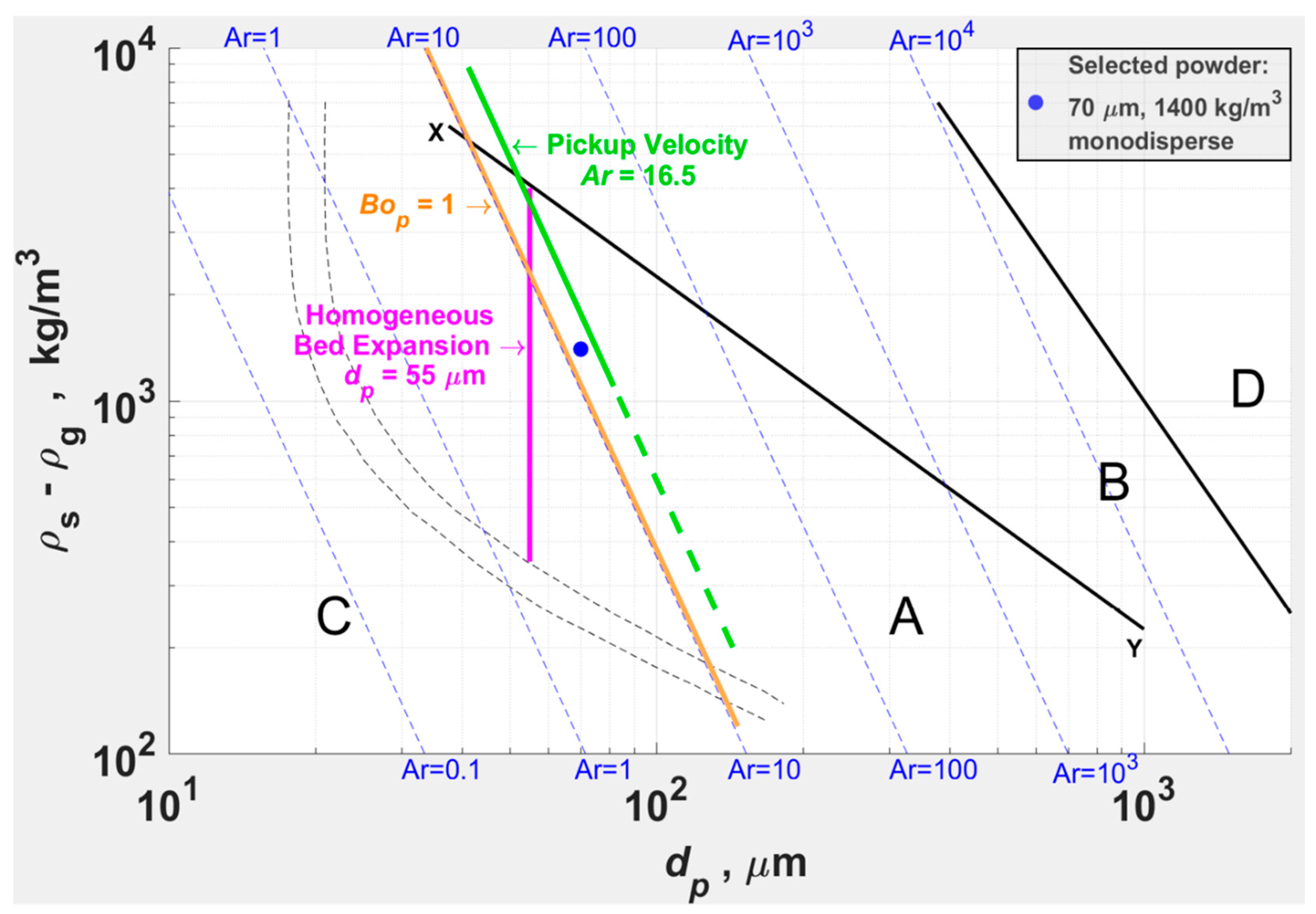
• Geldart A powders close to the A-B boundary may tend to Geldart B unless they are wide in PSD, including significant $P_{45}$ [3,71]. As it was opted to model a monodisperse powder with dominant gravity over $F_{vdW}$, the powder had to be low in $d_p$ and ${\rho }_s$ to be sufficiently away from the A-B boundary and to clearly classify as Geldart A.
• On the other hand, the powder had to be sufficiently high in $d_p$ and ${\rho }_s$, such that it is dominant in gravity over $F_{vdW}$. Cohesion models for $F_{vdW}$ for the TFM modeling approach had only started to emerge (e.g., [72,73]) and were not available in the standard MFiX-TFM code.
• Within the computing means, it may not have been possible to model a finer and/or polydisperse powder with significant $P_{45}$, even if a $F_{vdW}$ model had been readily available. With the requirement for the cell size ($∆x$) ~ 10$d_p$ for reliable predictions, computational load increases significantly with decreasing $d_p$.
• The selected $d_p$ and ${\rho }_s$ correspond to typical FCC powders for which resolved CFB data was widely reported, including those at high $G_s$ (e.g., [6,16,19]), to enable model validation. However, the model validation [10] (pp. 252–267) was based on the shapes and trends in the radial profiles of ${\epsilon }_s$ and $V_s$ since a one-to-one correspondence cannot be expected between the monodisperse powder modeled and the experimental powders (polydisperse with significant $P_{45}$), and the differences between the numerical modeling and the experimental conditions (in $V_g$, $G_s$ and $D$).

The properties of the hypothetical powder chosen for modeling are listed in

Table 4. Properties of the hypothetical powder at ambient conditions.

Property			Value	Remarks
Particle diameter	$d_p$	µm	70	Monodisperse spheres
Particle density	${\rho }_s$	kg/m3	1400
Archimedes number	$Ar$	--	17.5
Solids volume fraction—random loose-packed	${\epsilon }_s^{max}$	--	0.6	Maximum packing limit [33,76]
Particle–particle restitution	$e_p$	--	0.95
Particle–wall restitution	$e_w$	--	0.89	[77]
Angle of wall friction	${\phi }_w$	°	11.86	[77]
Angle of internal friction	$\phi$	°	30	[76]
Terminal settling velocity	$V_t$	m/s	0.186	Haider and Levenspiel [33]
Minimum fluidization velocity	$V_{mf}$	m/s	0.003	Baeyens’ equation [37]
Minimum bubbling velocity	$V_{mb}$	m/s	0.007	Abrahamsen and Geldart [78]
Lower transport velocity	$V_{tr1}$	m/s	1.4	Bi et al. [43]
Upper transport velocity	$V_{tr2}$	m/s	6.3	Equation (1)

, including the estimates for the key velocities. The powder is composed of monodisperse, hard, nearly elastic spheres. The powder clearly classifies as Geldart A, but with dominant gravity over $F_{vdW}$ (Figure 21). A cohesion model was not considered essential, as the powder lies above the thresholds for dominant $F_{vdW}$ per homogeneous bed expansion ($d_p$ = 55 µm) [35,74], as well as the granular Bond number (${Bo}_p$ = 1) [29] (${Bo}_p$ is the ratio between interparticle forces and the weight of the particle); furthermore, the powder lies close to the threshold based on pickup velocity studies ($Ar$ = 16.5), which was actually correlated, including polydisperse powders [75]. Experimental data for particle–particle restitution ($e_p$) is scarce; values between 0.9 and 0.95 are widely reported. The value of 0.95 was chosen during model validation [10]. The maximum packing limit was set at ${\epsilon }_s$ = 0.6 based on random loose-packed spheres [33,76].

Geometry and numerics are summarized in Table 5 (more details in [10]):

• Long-pipe models were used to capture the SSP of FF.
• Within the computing means, a Cartesian 2D slice through the axis models, with square cells of 29$d_p$ for nominal grid and 14$d_p$ for fine grid, were used.
• Nominal grid runs were used in general; confirmation runs at $V_g$ = 3 m/s were carried out with the fine grid.
• Tolerances for the nominal grid runs were the code defaults and were tightened by an order of magnitude for the fine grid runs.
• Simulation duration: Given the geometry and the relatively high $V_g$ and $G_s$, that is, with little chance for dead pockets, initial transients were generally overcome within 2 residence times, as was verified by solids hold up and axial profiles. Data was averaged thereafter at 100 Hz over 5 s for the current study and over several residence times in the previous work for statistically steady results.
• Underrelaxation factors in Table 6 were optimized for the conditions by statistical experiments [10]. The results indicated that the problem of backflow observed frequently with pressure outlet BC may be overcome by setting the factors for the axial (V) momentum and turbulent kinetic energy at 1.0. Reasoning is intuitive: backflow may occur if the axial momentum is throttled relative to other factors.
• Parallel processing by Distributed Memory Parallel (DMP) was with maximum axial decomposition and no radial decomposition, for the geometry. Simulations were carried out in the Google Cloud with the Command Line Interface. Visualization and post-processing were carried out on the desktop, largely by the open-source VisIt software (version 3.1.4) and MATLAB (version R2017a/R2023b).

Table 5. Geometry and numerics.

Description			Vertical Upflow—Nominal Grid	Vertical Upflow—Fine Grid
Pipeline (riser) diameter	$D$	m	0.04	0.04
Pipeline (riser) length:	$L$	m
$V_g$ = 3 m/s cases			10.0	9.999
$V_g$ > 3 m/s cases			15.0	--
Coordinates			Cartesian 2D	Cartesian 2D
Grid:
$V_g$ = 3 m/s cases			20 × 5000 × 1	40 × 9999 × 1
$V_g$ > 3 m/s cases			20 × 7500 × 1	--
Cell size	$\mathsf{\Delta }x$	m	0.0020	0.0010
Cell size in particle diameters			29	14
Time step, maximum	${∆t}_{max}$	s	1 × 10−5–3 × 10−5	1 × 10−5
Parallel processing
$V_g$ = 3 m/s cases			DMP (1-8-1)	DMP (1-16-1)
$V_g$ > 3 m/s cases			DMP (1-16-1)	--
Spatial discretization			Superbee	Superbee
Temporal discretization			Implicit Euler	Implicit Euler

Table 5. Geometry and numerics.

Description			Vertical Upflow—Nominal Grid	Vertical Upflow—Fine Grid
Pipeline (riser) diameter	$D$	m	0.04	0.04
Pipeline (riser) length:	$L$	m
$V_g$ = 3 m/s cases			10.0	9.999
$V_g$ > 3 m/s cases			15.0	--
Coordinates			Cartesian 2D	Cartesian 2D
Grid:
$V_g$ = 3 m/s cases			20 × 5000 × 1	40 × 9999 × 1
$V_g$ > 3 m/s cases			20 × 7500 × 1	--
Cell size	$\mathsf{\Delta }x$	m	0.0020	0.0010
Cell size in particle diameters			29	14
Time step, maximum	${∆t}_{max}$	s	1 × 10−5–3 × 10−5	1 × 10−5
Parallel processing
$V_g$ = 3 m/s cases			DMP (1-8-1)	DMP (1-16-1)
$V_g$ > 3 m/s cases			DMP (1-16-1)	--
Spatial discretization			Superbee	Superbee
Temporal discretization			Implicit Euler	Implicit Euler

Table 6. Underrelaxation factors.

Underrelaxation Factor		Code Default	Selected
UR_FAC(1)	Gas pressure	0.8	0.8
UR_FAC(2)	$\mathrm{Solids} \mathrm{volume} \mathrm{fraction} ({\epsilon }_s$)	0.5	1.0 #
UR_FAC(3 & 5)	Radial (U & W) momentums	0.5	0.5
UR_FAC(4)	Axial (V) momentum	0.5	1.0
UR_FAC(8)	$\mathrm{Granular} \mathrm{temperature} (\mathsf{\Theta }$)	0.5	0.5
UR_FAC(9)	$\mathrm{Turbulent} \mathrm{kinetic} \mathrm{energy} (k_g$ & ${\in }_g$)	0.8	1.0

^# A value of 0.5 (and not 0.8) was used in case of instabilities.

Table 6. Underrelaxation factors.

Underrelaxation Factor		Code Default	Selected
UR_FAC(1)	Gas pressure	0.8	0.8
UR_FAC(2)	$\mathrm{Solids} \mathrm{volume} \mathrm{fraction} ({\epsilon }_s$)	0.5	1.0 #
UR_FAC(3 & 5)	Radial (U & W) momentums	0.5	0.5
UR_FAC(4)	Axial (V) momentum	0.5	1.0
UR_FAC(8)	$\mathrm{Granular} \mathrm{temperature} (\mathsf{\Theta }$)	0.5	0.5
UR_FAC(9)	$\mathrm{Turbulent} \mathrm{kinetic} \mathrm{energy} (k_g$ & ${\in }_g$)	0.8	1.0

^# A value of 0.5 (and not 0.8) was used in case of instabilities.

The following are the key model limitations:

• Whereas typical SCA powders are polydisperse, containing significant $P_{45}$, the modeled powder is monodisperse.
  Potential effects of PSD are as follows:

  -

  Widening the PSD with increasing $P_{45}$ results in (a) increased homogeneous bed expansion ($V_{mb}$) [38,78]; (b) higher emulsion phase voidage [78] and smaller bubbles in bubbling beds [79]; and (c) lower $V_c$ [40] and $V_{tr1}$ [43]. While the influence of $P_{45}$ at higher ${\epsilon }_s$, that is, under homogeneous bed expansion and bubbling beds, may be attributed to increased interparticle forces due to the increased interparticle contacts [71], that at lower ${\epsilon }_s$, that is, the reduction in $V_c$ and $V_{tr1}$, may be attributed to lower ‘effective cluster terminal velocity’ and hence a higher entrainment rate [18].

  -

  Closer to the A-B boundary, when considering a powder of negligible $P_{45}$ such that gravity is dominant over $F_{vdW}$, widening the PSD, even without increasing $P_{45}$, enhances Geldart A behavior due to the suppression of bubbles for the decreasing $V_t$ (per the criterion of Harrison et al. (1961), cited in [29], for bubble stability in liquid fluidized beds).

The influence of PSD on the behavior of Geldart A powders is reviewed in [10] (pp. 71–72, 82–85).

• A cohesion model for $F_{vdW}$ is not included. As discussed above, the modeled powder has dominant gravity over $F_{vdW}$ and a cohesion model is not considered necessary. Note that a cohesion model is not available within the standard MFiX-TFM code, and it may not be possible to incorporate a finer or a polydisperse powder within the computing means.
• Other cohesion mechanisms, namely liquid bridges and electrostatic and magnetic forces, are excluded too, as they result in flow patterns that are significantly different from those of the powders affected by $F_{vdW}$ (and gravitational forces) alone (reviewed in [10] (pp. 66–71)) and may require specific cohesion models.

  -

  Electrostatic charging of dry dielectric powders in gas–solids systems occurs mainly by contact and friction (tribocharging). Significant charge transfer from the pipe wall, uneven charge distribution within the powder bulk, space charge effects, interactions with flow dynamics, and localized corona discharges can lead to a highly irregular distribution of electrostatic charges over time and space. This nonuniformity, often involving regions of opposite polarity, promotes powder sticking, agglomeration, or buildup along the pipe wall (e.g., [80,81]). Research is underway for incorporating electrostatic forces in numerical models [81].

  -

  Magnetic forces, depending on the degree of magnetization, can be much stronger and longer in range than $F_{vdW}$; however, the order of magnitude of weak magnetic materials such as magnetite is probably more relevant here [82], especially given that there is no applied external magnetic field [29]. Mills [3] has reported an iron powder that showed divergent constant pressure drop curves in the conveying characteristics, as against typical powders that show a pressure drop minimum.

  -

  Liquid bridges affect the flowability of powders in general, with progressive deterioration at relative humidity of the air (RH) > 50% [1,38]. Hydrophilic powders may be affected at an even lower RH due to ‘capillary condensation’, the formation of liquid menisci around surface asperities that are in (near) contact. A meniscus attracts the particles together due to ‘capillary force’, that is, surface tension and Laplace pressure; the force may magnify with a film of adsorbed moisture and in softer materials, also due to the plastic deformation of the surface asperities [83]. Research is underway for incorporating liquid bridges in numerical models (e.g., [84]).

• Interfacial forces other than drag (viz., virtual mass, history, spin lift, and slip–shear lift) are not incorporated. Amongst them, the slip–shear lift force can be notable under strong gradients in $V_g$.
• Cartesian 2D coordinates were used. Gas–solids two-phase flow is inherently 3D, and 2D models do not accurately represent the geometry [85,86]; however, Cartesian 2D TFM models are well established to predict vertical upflow phenomena at relatively low computational cost (enabling long pipe models within the computing means). They may not be suitable for asymmetric flows (such as side inlet and outlet) [87]; however, it is not a limitation for a project with a full-bore inlet and outlet. They may not accurately predict axial pressure and radial voidage profiles simultaneously [86].
• Resolved TFM models use homogeneous drag laws, which consider uniform distribution of particles, while the actual distribution can be highly inhomogeneous at all spatiotemporal scales. As the gas tends to bypass the clusters under inhomogeneous conditions, the predicted drag can be significantly higher than the actual. Therefore, fine grids with a cell size $∆x$ ~ 10$d_p$ are required for reliable predictions [54,85], and $∆x$ > 40$d_p$ may even produce qualitatively incorrect results [54].
• Within the computing means, $∆x$ ~ 29$d_p$ for nominal grid runs and ~14$d_p$ for fine grid confirmation runs were used for our work.
• Rigorous wall BC are not used for the solids phase; however, free-slip wall BC with no applied granular temperature flux is a good approximation under rapid flow conditions [54,68,69].

3. Results

Below are the processed results of the numerical simulations indicated in Figure 19 to support the discussions in Section 4. Results for the individual simulations are available in the Supplementary Material.

Figure 22 is the PMW based on the simulation results, plotted to scale. Points to note:

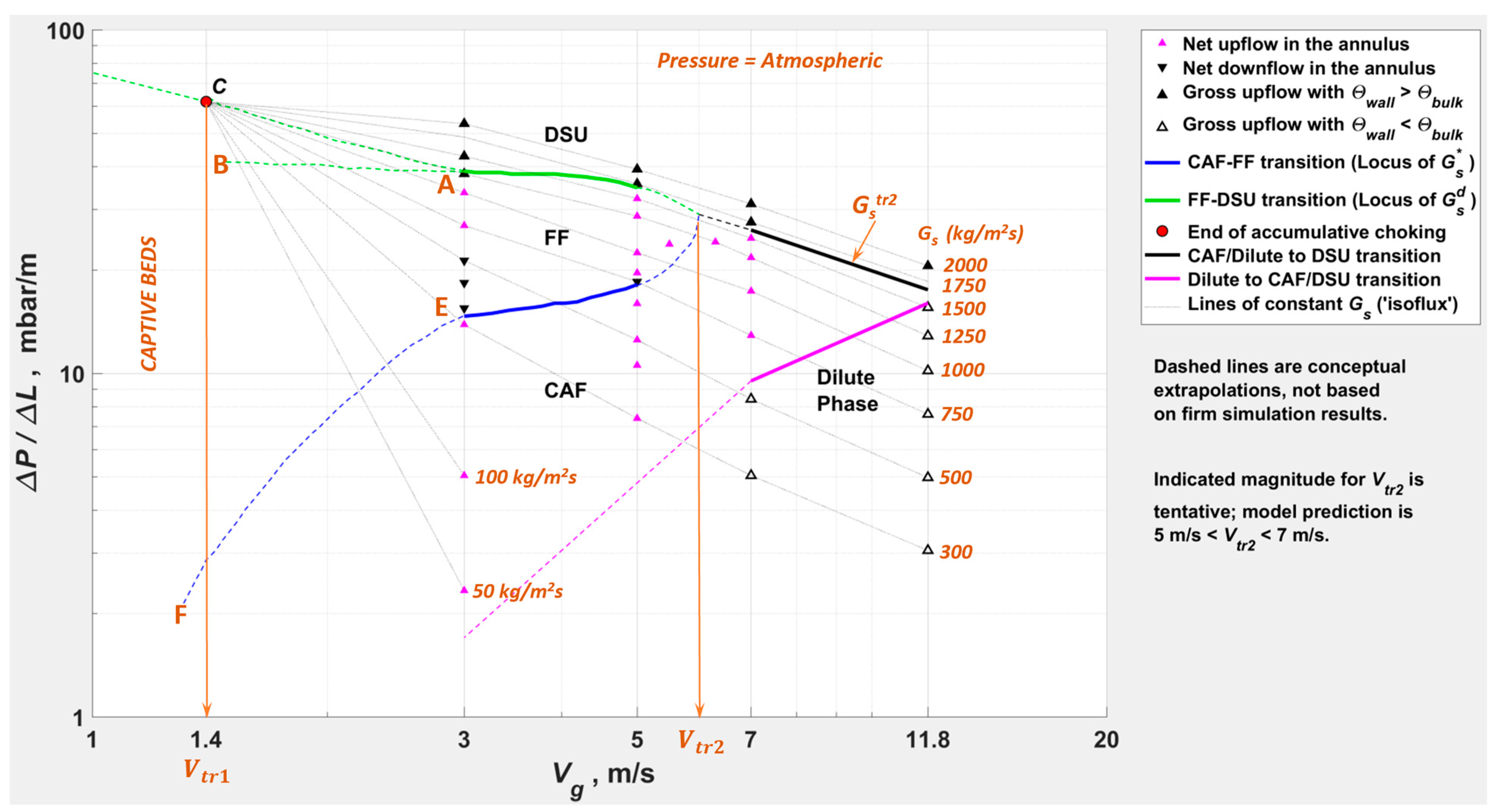
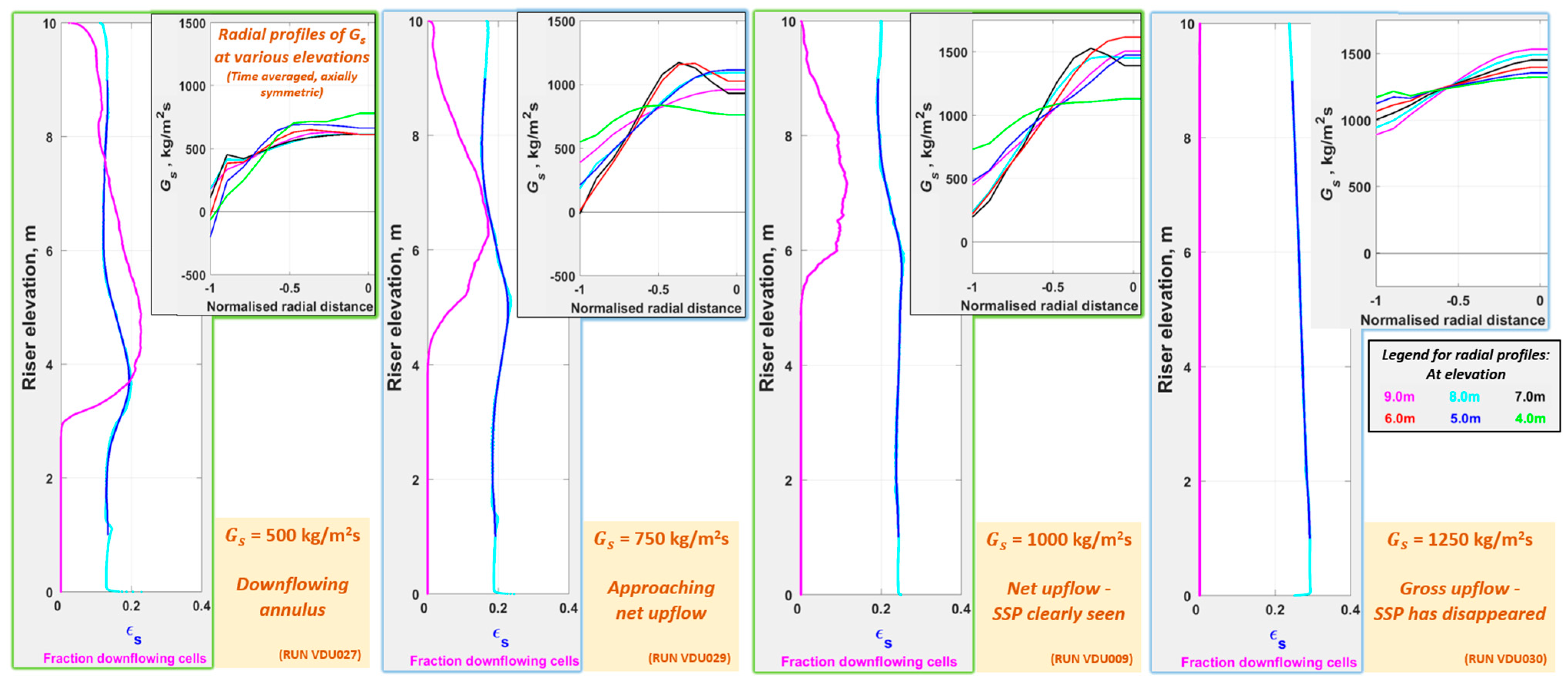
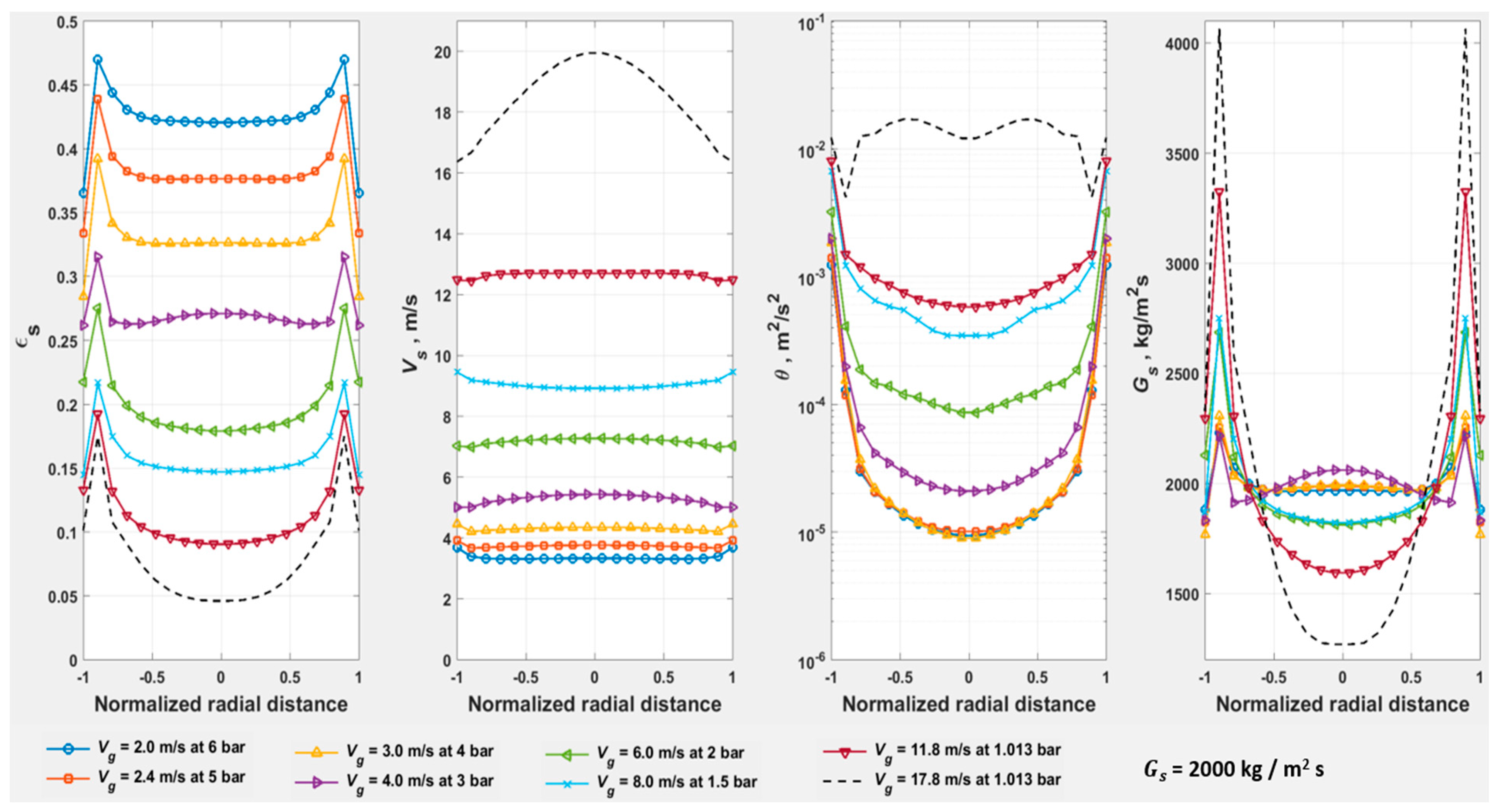
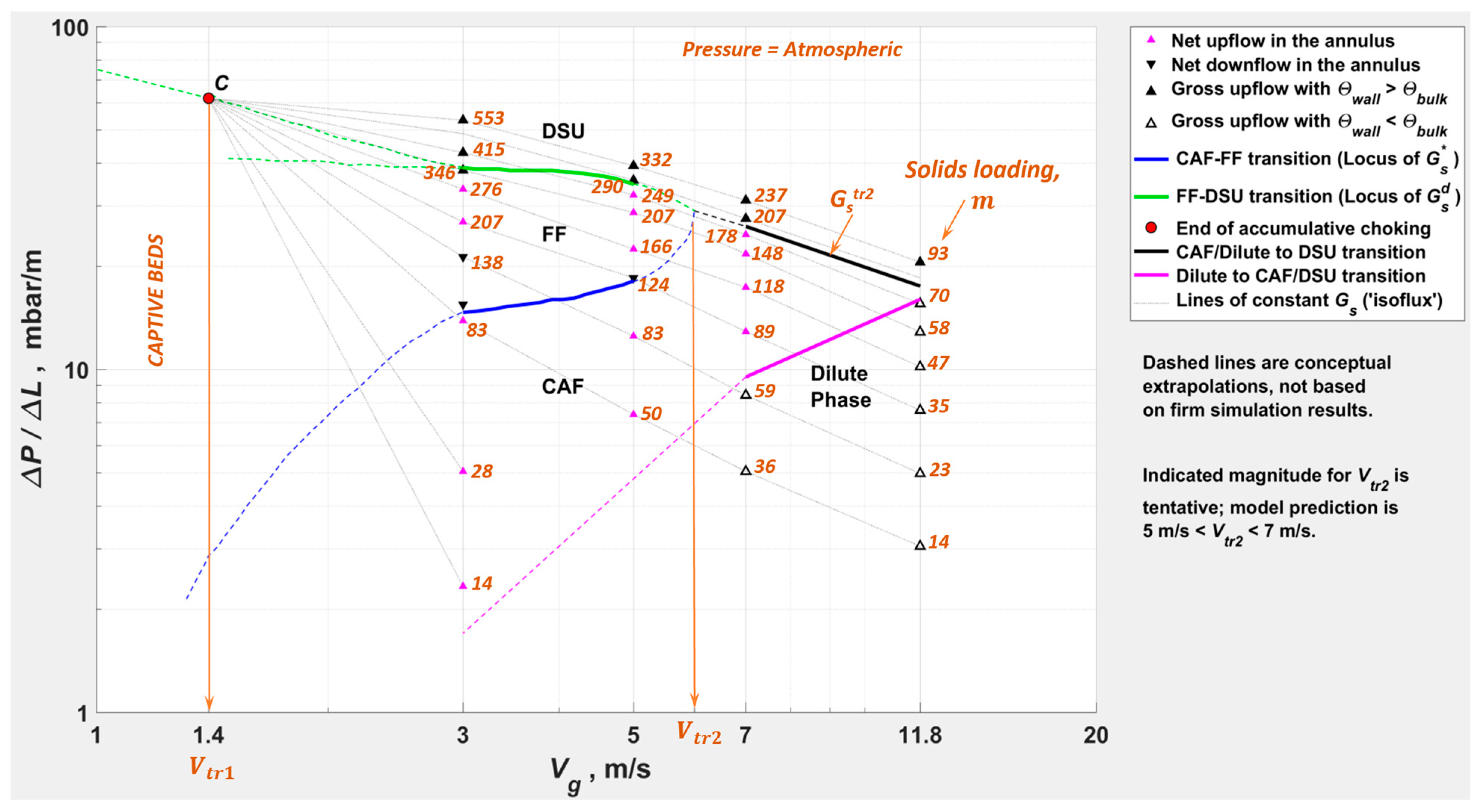
• DSU, FF, CAF, and dilute phase regimes are demarcated per the criteria in Table 2.
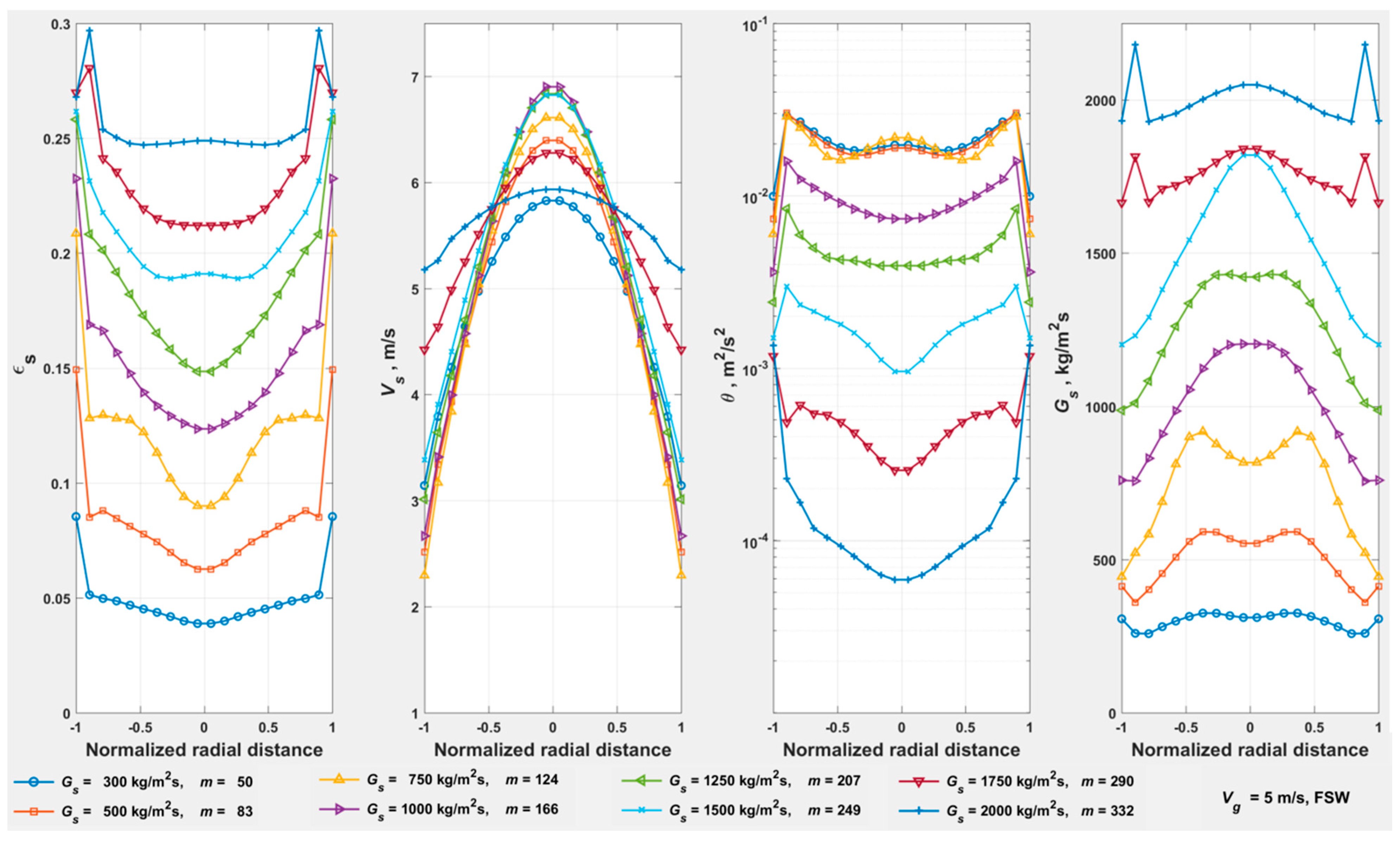
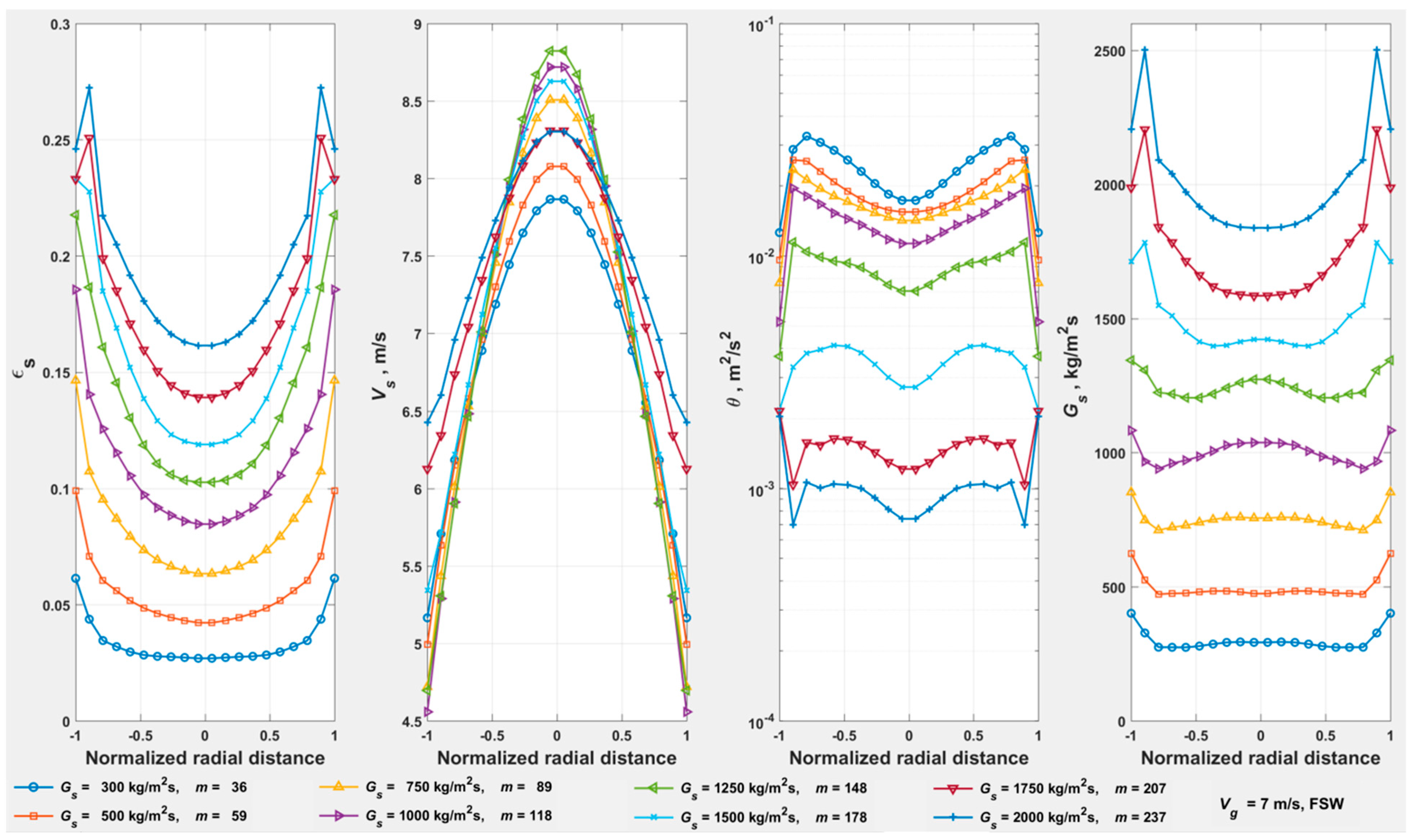
• The riser averaged radial profiles in Figure 23 and Figure 24 illustrate the transitions from FF to DSU at $V_g$ = 5.0 m/s and from CAF to DSU at $V_g$ = 7.0 m/s, respectively, based on the behavior of the flow field (in line with Table 2): (a) profiles of ${\epsilon }_s$ transition to show a pre-wall spike; (b) profiles of $\mathsf{\Theta }$ transition from ${\mathsf{\Theta }}_{wall}<{\mathsf{\Theta }}_{bulk}$ to vice versa.
• Results for the simulations at $V_g$ = 17.8 m/s are omitted, as the simulated $L$ of 15 m is probably inadequate at the higher $V_g$.
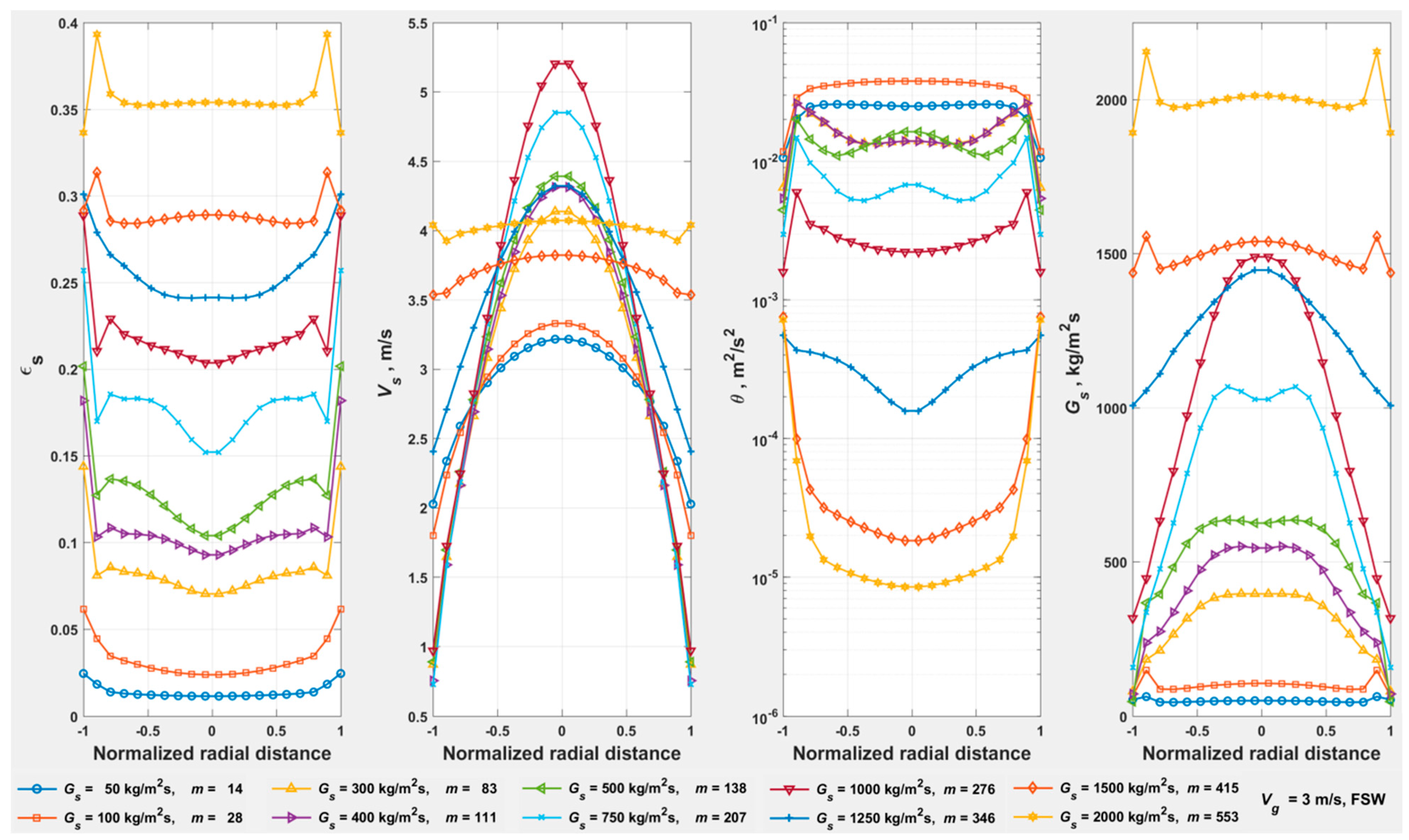
• The transition from DSU to dilute phase, perceived in Figure 16, in the radial profiles at $V_g$ = 17.8 m/s and $G_s$ of 2000 kg/m²s is also perceived at $G_s$ down to 1000 kg/m²s ($G_s/{\rho }_s$ of 0.71) towards the top of the riser. However, the profiles at $G_s$ < 1000 kg/m²s are clearly spurious, with the inlet zone of flow development (in the simulation) occupying the entire $L$ = 15 m. Therefore, all the results at $V_g$ = 17.8 m/s are omitted in Figure 22 to avoid any uncertainty.
• The extent of FF at 5 m/s < $V_g$ < 7 m/s is not fully resolved by simulations. The indicated magnitude of $V_{tr2}$ (and the corresponding $∆P/∆L$) is tentative, based on conceptual extrapolation of the loci of $G_s^{*}$ (green), $G_s^d$ (blue), and the boundary between CAF/Dilute phase and DSU (black).
• $\mathit{C}$($V_{tr1}$, ${(∆P/∆L)}_{tr1}$), the end of accumulative choking, is based on the estimated $V_{tr1}$ (Table 4), and the ${(∆P/∆L)}_{tr1}$ is considered to be at the dense limit in Figure 15.
• The extrapolation of the dense locus towards $\mathit{C}$, the line AC in Figure 22, is per the phase map conceived in Figure 4. The line AB shows a probable alternate trajectory for the locus; the reasoning is in Section 4.
• The line EF is the conceptual extrapolation of the lean locus towards the onset of turbulent fluidization at ($V_c$, ${(∆P/∆L)}_{V_c}$), with the $({∆P/∆L)}_{V_c}$ (~1 mbar/m) being essentially the gas-only pressure drop at $V_c$ (~1 m/s).
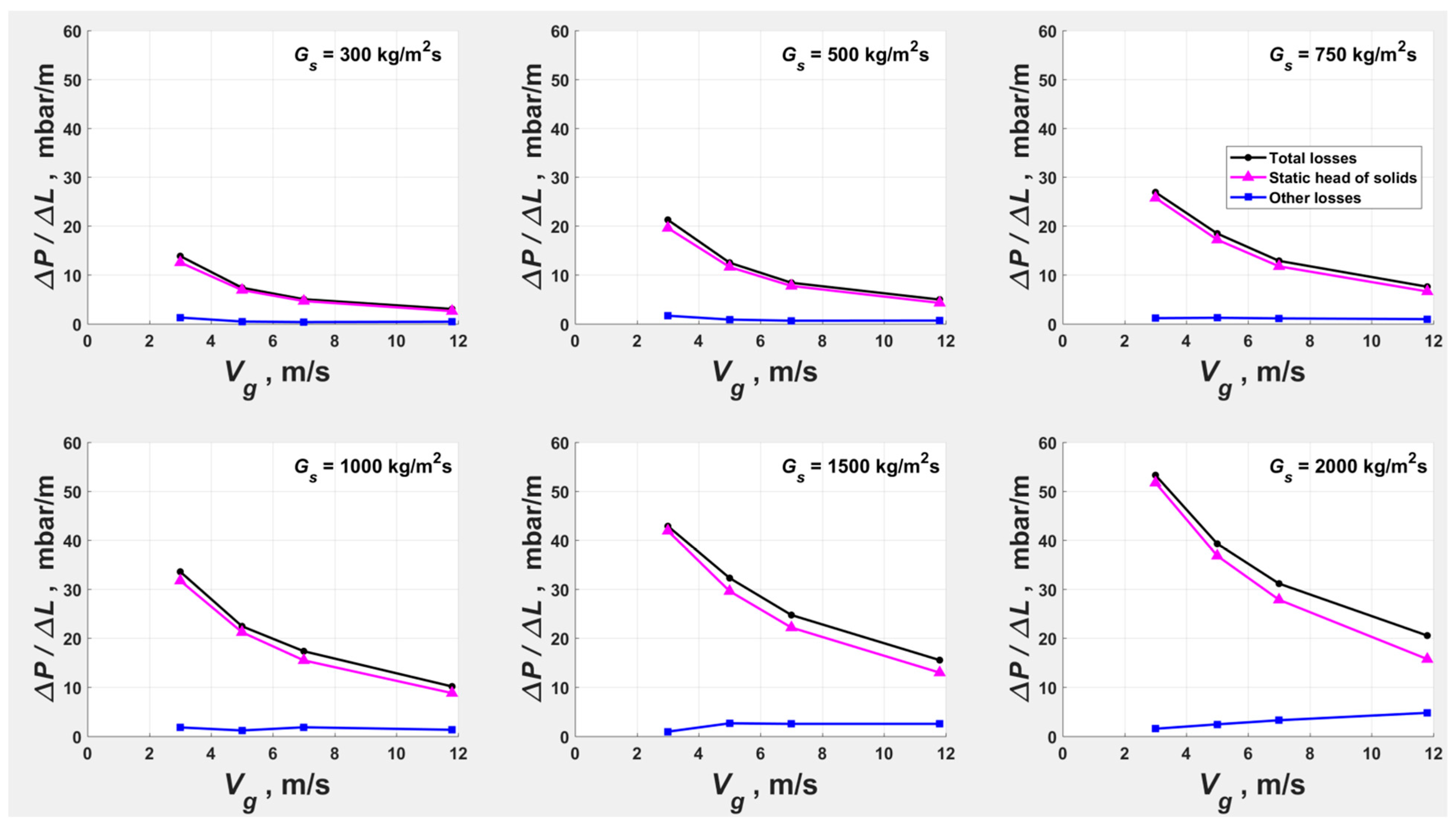
• The transitions from dilute to CAF/DSU for the isofluxes at 300 < $G_s$ < 1500 kg/m²s for the simulated powder do not coincide with the locus of $V_{mp}$.

Figure 22. PMW based on the simulation results.

Figure 22. PMW based on the simulation results.

Figure 23. Radial profiles averaged over the riser for the runs at $V_g$ = 5 m/s. A copy of the figure is enclosed in the Supplementary Material. Profiles were averaged over 6 to 14 m. The transition from FF to DSU, as well as DSU as a separate flow regime, can be perceived from the radial profiles: pre-wall dip in the profiles of ${\epsilon }_s$ transition to pre-wall spike; profiles of $\mathsf{\Theta }$ transition from ${\mathsf{\Theta }}_{wall}<{\mathsf{\Theta }}_{bulk}$ to vice versa.

Figure 23. Radial profiles averaged over the riser for the runs at $V_g$ = 5 m/s. A copy of the figure is enclosed in the Supplementary Material. Profiles were averaged over 6 to 14 m. The transition from FF to DSU, as well as DSU as a separate flow regime, can be perceived from the radial profiles: pre-wall dip in the profiles of ${\epsilon }_s$ transition to pre-wall spike; profiles of $\mathsf{\Theta }$ transition from ${\mathsf{\Theta }}_{wall}<{\mathsf{\Theta }}_{bulk}$ to vice versa.

Figure 24. Radial profiles averaged over the riser for the runs at $V_g$ = 7 m/s. A copy of the figure is enclosed in the Supplementary Material. Profiles were averaged over 6 to 14 m. The transition from CAF to DSU, as well as DSU as a separate flow regime, can be perceived from the radial profiles: the profiles of ${\epsilon }_s$ transition to show a pre-wall spike; profiles of $\mathsf{\Theta }$ transition from ${\mathsf{\Theta }}_{wall}<{\mathsf{\Theta }}_{bulk}$ to vice versa.

Figure 24. Radial profiles averaged over the riser for the runs at $V_g$ = 7 m/s. A copy of the figure is enclosed in the Supplementary Material. Profiles were averaged over 6 to 14 m. The transition from CAF to DSU, as well as DSU as a separate flow regime, can be perceived from the radial profiles: the profiles of ${\epsilon }_s$ transition to show a pre-wall spike; profiles of $\mathsf{\Theta }$ transition from ${\mathsf{\Theta }}_{wall}<{\mathsf{\Theta }}_{bulk}$ to vice versa.

Figure 25 indicates on the PMW the solids loading ($m$) at the simulation points. The transition from dilute phase to CAF/DSU occurs at increasing $m$ with increasing $V_g$. The transition from DSU to FF/CAF/dilute phase occurs at decreasing $m$ with increasing $V_g$. The transition from CAF to FF (the locus of $G_s^{*}$) occurs at increasing $m$ with increasing $V_g$. No further correlations are evident from the results.

Figure 26 shows the trend in $∆P/∆L$ versus $V_g$ at various $G_s$, with breakup between the static head of solids and other losses. The other losses are largely viscous, as the ${\epsilon }_s$ remains below the threshold (${\epsilon }_s^{min}$ = 0.5) for frictional stresses in Figure 13 (as well as at the dense limit of the high $G_s/{\rho }_s$ in Figure 16). Clearly, the static head of solids is the dominant loss across the conditions simulated, and the other losses are yet to take over at $V_g$ = 11.8 m/s.

Figure 27 is an update of Figure 18 to include the $V_{slip}$ at $V_g$ = 5 and 7 m/s. Trends at the higher $V_g$ are similar to those at 3 m/s.

4. Discussion

Simulation results show a clear transition between the flow regimes in accordance with Table 2, and the qualitative PMW conceived in Figure 4 can be traced in Figure 22, with the PMW plotted to scale. Detailed evaluation of the results is as follows.

A subtler manifestation of SSP is perceived during CAF, too, with $G_s<G_s^{*}$ at $V_g=$ 5 m/s, as well as with $G_s<G_s^{tr2}$ at $V_g=$ 7 m/s. However, as the classification of flow regimes per Table 2 is independent of SSP, there is no ambiguity.

While the results of the simulations at $V_g$ = 3, 5, 7, and 11.8 m/s are of appropriate accuracy, the results at $V_g$ = 17.8 m/s are omitted in the PMW (Figure 22), as the $L$ of 15 m is probably inadequate for simulating fully developed flow at the higher $V_g$. As the riser is expected to be under gross upflow at $V_g$ = 17.8 m/s, either under dilute phase or under DSU with essentially axially uniform conditions, simulations with axially periodic BC are probably a better option. Axially periodic vertical upflow simulations can be carried out very efficiently under pseudo-2D [54]. The preliminary results of such simulations are encouraging; however, selecting the appropriate initial conditions remains to be resolved.

A key difference between the PMW in Figure 4 and that in Figure 22 is the trajectory of the isofluxes. The isofluxes in Figure 4 are based on (limited) experimental results: (a) isofluxes at $G_s^{tr1}>G_s>G_s^{tr2}$, based on the experimental results of Wang et al. [16], are shown not to sustain DSU with decreasing $V_g$, as the bed gets denser overall, but to slip into and traverse within the FF zone towards $\mathit{C}$; and (b) isofluxes at $G_s<G_s^{tr2}$, based on the experimental results at low $G_s$ (e.g., [14,18]), are shown to traverse towards $\mathit{C}$ within the FF zone. However, the simulation results in Figure 22 suggest (a) isofluxes at $G_s>G_s^{tr2}$ (such as at 1750 and 2000 kg/m²s) sustain and traverse within DSU towards $\mathit{C}$ (akin to the results of Wirth [11]); and (b) isofluxes at $G_s<G_s^{tr2}$ (such as at 1250 < $G_s$ < 1500 kg/m²s) also attain DSU and traverse within DSU towards $\mathit{C}$. Therefore, the simulation results suggest the possibility of an alternate trajectory (AB in Figure 22, as against AC) for the locus of $G_s^d$, that is, a phase of DSU between FF and the transition to a turbulent bed at $\mathit{C}$, at all $G_s$. This requires further research, as the experimental evidence is limited and the numerical modeling is based on an atypical Geldart A powder.

The PMW in Figure 4 (b) identifies a particular isoflux, $G_s^{tr2}$, the one corresponding to $V_{tr2}$, as the boundary between CAF and DSU at $V_{tr2}<V_g<V_{mp}$. The boundary in Figure 22 (black color, at $G_s\cong$ 1700 kg/m²s) is shown accordingly, too, and is not fully resolved by the simulation data. Whether the boundary can be demarcated by the isoflux of $G_s^{tr2}$ or whether it traverses a range of $G_s$ requires further validation.

The magnitude of $V_{tr2}$ is not fully resolved by the simulations. However, the predicted range, at 5 m/s < $V_{tr2}$ < 7 m/s, covers the magnitude of 6.3 m/s predicted by (1).

Recall that dilute phase flow, as defined in Table 2, is characterized by gross upflow of solids with ${\mathsf{\Theta }}_{wall}<{\mathsf{\Theta }}_{bulk}$. Simulation results in Figure 25 indicate that the dense–dilute boundary occurs at $m\gg$ ~10 (and ${\epsilon }_s\gg$ ~0.02), widely reported for low $G_s$. Furthermore, simulation results in Figure 22 clearly indicate that the transition from dilute phase to CAF/DSU at 300 < $G_s$ < 1500 kg/m²s does not coincide with the locus of $V_{mp}$. Results for $∆P/∆L$ in Figure 26 suggest that $V_{mp}$ is not attained at $V_g$ = 11.8 m/s across the conditions simulated, with the component of other losses (largely viscous losses) yet to take over that due to the static head of solids. Hence, the suitability of the locus of $V_{mp}$ as the dense–dilute boundary at higher $G_s$ may require review (recognizing that typical SCA powders—polydisperse with significant $P_{45}$—may result in lower ${\epsilon }_s$ across the conditions studied than the simulated monodisperse powder).

As indicated in Section 3, the other losses for the simulated powder are largely viscous, as the ${\epsilon }_s$ remains below the threshold (${\epsilon }_s^{min}$ = 0.5) for frictional stresses (Figure 13 and Figure 16). With the frictional losses insignificant for the simulated atypical powder (monodisperse with dominant gravity), it is likely to be insignificant for typical SCA powders (polydisperse with significant $P_{45}$) too, as they are generally lower in ${\epsilon }_s$ in the transport regimes [16,33,88].

Profiles for $V_{slip}$ in Figure 27 clearly show the trend discussed in Section 1.1.6, increasing with $G_s$ initially to attain a maximum but falling off thereafter to a low multiple/fraction of $V_t$ within DSU. However, unlike the experimental results of Wang et al. [16] in Figure 17, $V_{slip}$ in the simulation results in Figure 27 peaks at ~4.5 $V_t$ for all three $V_g$, probably because the simulated powder is monodisperse with dominant gravity over $F_{vdW}$ as against the polydisperse powder with $P_{45}$ ~ 0.1 (Table 1) used in [16]. Note that the higher magnitudes of $V_{slip}$ within DSU suggest significant clustering of particles; the drag predicted for the $V_{slip}$, assuming a uniform distribution of primary particles, exceeds the static head of solids by orders of magnitude and is therefore not credible.

The following are the key limitations of the study:

• The powder chosen for numerical modeling—monodisperse spheres with dominant gravity over $F_{vdW}$—is atypical. Typical SCA powders can be non-spherical and polydisperse with significant $P_{45}$, often with dominant $F_{vdW}$ over gravity.
• Only one riser diameter ($D$) is modeled. As discussed in Section 1.1.3, key vertical upflow parameters such as $V_{tr2}$ and $G_s^{tr2}$ for SCA powders are dependent on $D$.

While the findings of the study are encouraging, further experimental and numerical validation with a range of SCA powders and various $D$ would be required.

5. Conclusions

Below are the key outcomes of the earlier work:

• Adapted the vertical upflow phase map of Wirth to SCA powders to (a) define DSU as a separate transport regime characterized by gross upflow of solids, with ${\mathsf{\Theta }}_{wall}>{\mathsf{\Theta }}_{bulk}$; and (b) identify that the operating regimes of vertical upflow at high $G_s$ for coarser powders occurs under DSU and/or FF, and for finer powders predominantly under DSU.
• Demonstrated that the upper transport velocity ($V_{tr2}$) for Geldart A powders can be significantly higher than hitherto predicted, by a new, provisional correlation (1).
• Demonstrated that at $V_{tr1}<V_g<V_{tr2}$ and when increasing the $G_s$ gradually from a low value, $V_{slip}$ increases initially to attain a maximum and falls thereafter to a low multiple of $V_t$ within DSU.

The findings of the current study validate the above classification of DSU and its transition boundaries. Furthermore, the current study has identified areas for further research within the phase map: (a) the possibility of a phase of DSU at all $G_s$, prior to the transition to the turbulent regime; and (b) the need to review the suitability of the locus of $V_{mp}$ as the transition boundary between the dilute phase and DSU/CAF at high $G_s$.

The impact of the findings is both practical and theoretical. They are relevant to high $G_s$ operations such as FDC systems and HD-CFBs. The demonstration that DSU can be characterized as a separate flow regime based on the transitions in the behavior of the flow field may lead to its broader acceptance as a unique transport regime. DSU as a unique high $G_s$ regime with gross upflow of solids is of practical significance to industrial HD-CFBs, wherein a narrow residence time distribution is desired. The demonstration that $V_{tr2}$ for Geldart A powders can be significantly greater than hitherto predicted will help towards accurate a priori mapping of phases for the powders.

Areas for further research include the following:

• Further experimental and numerical validation of the phase map with a range of SCA powders and various $D$:

  -

  Possibility of a phase of DSU between FF and the turbulent regime at all $G_s$.

  -

  Review of the suitability of the locus of $V_{mp}$ as the dense–dilute transition boundary at high $G_s$.

  -

  Investigation of the DSU–dilute transition at high $V_g$ with axially periodic BC, for example, by pseudo-2D models [54].

  -

  Suitability of $G_s^{tr2}$ as the boundary between CAF and DSU at ${V_g>V}_{tr2}$.

• Further validation of DSU as a unique transport regime, based on the behavior of the flow field, such as by analyses of higher order moments or deterministic chaos parameters [53].
• A robust correlation for $V_{tr2}$, incorporating $P_{45}$ and $D$ and based on CFB experiments with a range of Geldart A powders.
• While the PMW, a plot of $∆P/∆L$ versus $V_g$, is specific to the experimental powder and experimental $D$, a priori mapping of phases for untested powders may require a plot generalized by dimensionless groups [4,7,13].