Multi-Objective Robust Design of Segmented Thermoelectric–Thermal Protection Structures for Hypersonic Vehicles Using a High-Fidelity Thermal Network
Abstract
1. Introduction
2. Thermal Network Construction Methods
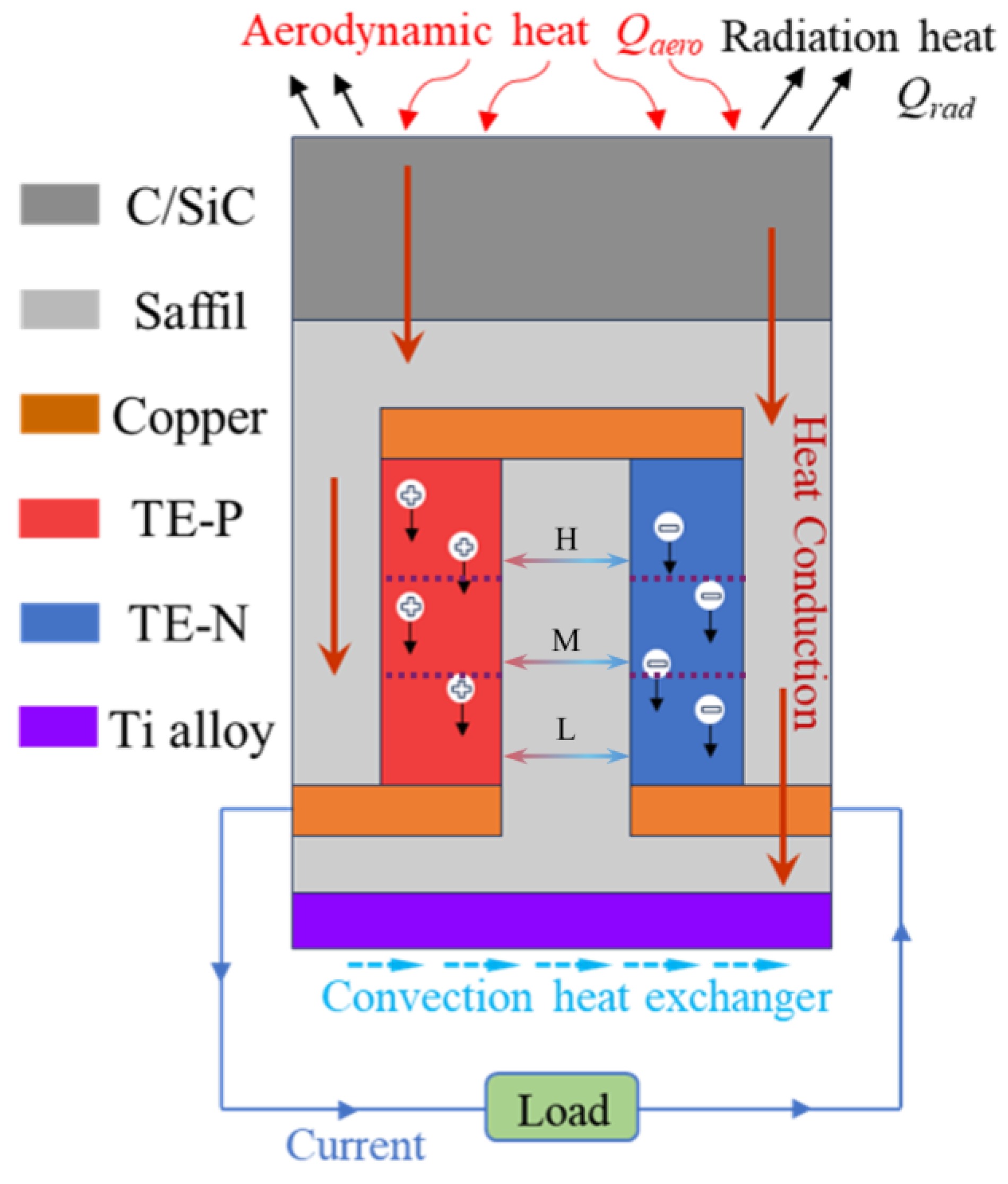
2.1. Segmented Thermoelectric-TPS Design
2.1.1. Geometry-Based Configuration
2.1.2. Three-Segment Thermoelectric Material System
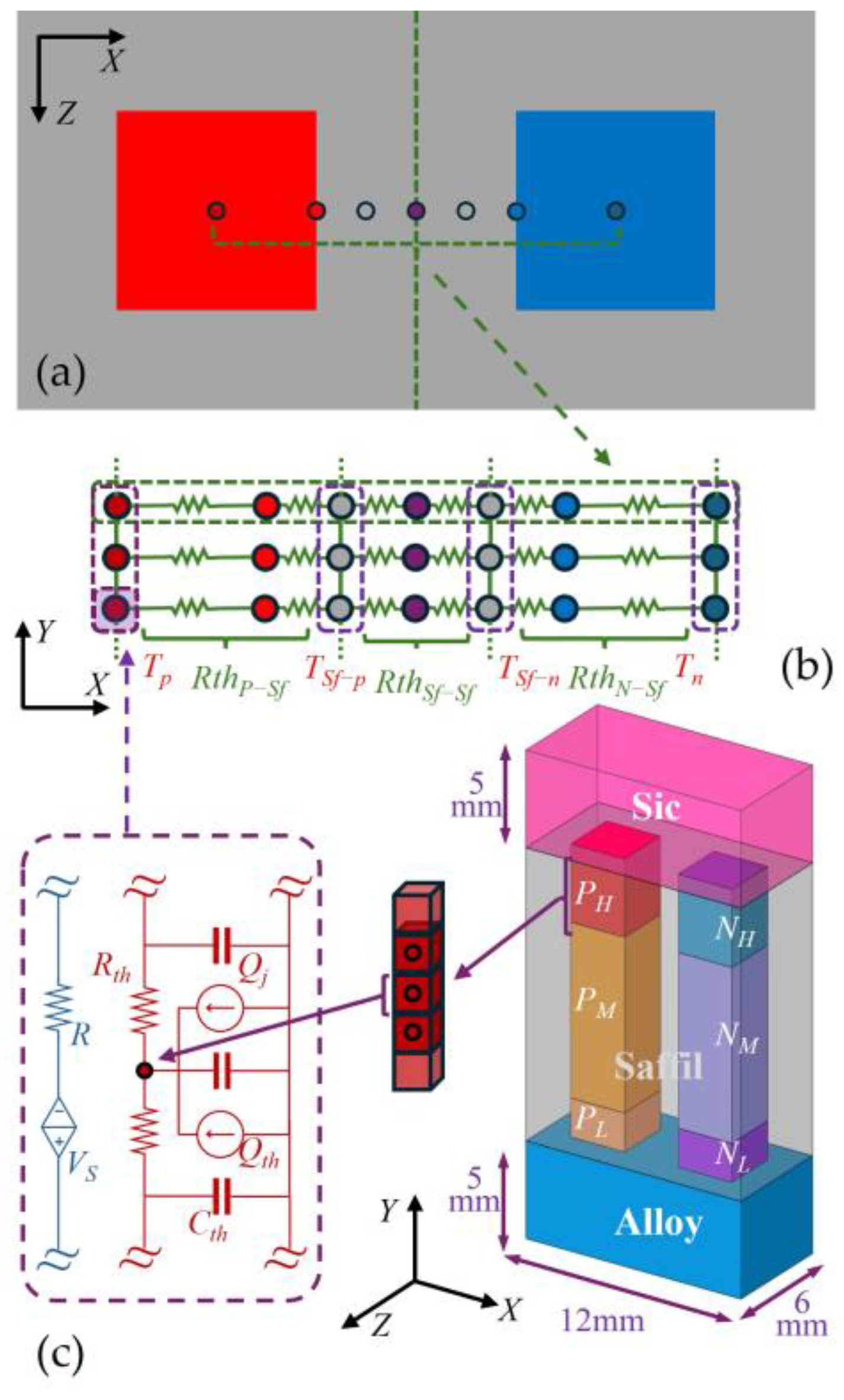
2.2. High-Fidelity Thermal Network Modeling Method
2.2.1. Quasi-Two-Dimensional Thermoelectric Coupled Model
2.2.2. Lateral Heat Transfer: Hybrid Equivalent Thermal-Resistance Network Model
2.2.3. Longitudinal Thermoelectric Coupling Model
- TE element: For control volumes within the thermoelectric materials (p- and n-type legs), the governing equation includes heat capacity, conduction, Joule heating, the Thomson effect, and lateral heat leakage:where ρ is the density, Cp is the specific heat capacity, λ is the thermal conductivity, ρe is the electrical resistivity, τ is the Thomson coefficient, J is the current density, and q′lateral(y) denotes the lateral heat-loss source term supplied by the lateral thermal network model in Section 2.2.2.
- Non-thermoelectric element: For non-thermoelectric materials (e.g., SiC layer, titanium alloy, Saffil Insulator), the equation reduces to the standard heat diffusion form, containing only heat capacity, conduction, and lateral heat leakage. Although the SiC and titanium alloy layers are homogeneous, retaining the parallel four-column nodal topology (Figure 4) reduces temperature error at the thermoelectric (TE) interfaces.
- Open-circuit voltage (Voc): obtained by summing the Seebeck electromotive forces generated by the P/N legs across all segments, as shown in Equation (9):
- Total internal resistance (Rin): the series sum of the bulk resistances of all material segments together with the Electrical Contact Resistances (ECRs) of all interfaces, as shown in Equation (10):
- Output power (Pload): when an external load resistance Rload is connected, the circuit current I and the output power Pload are given, respectively, by Equations (11) and (12):
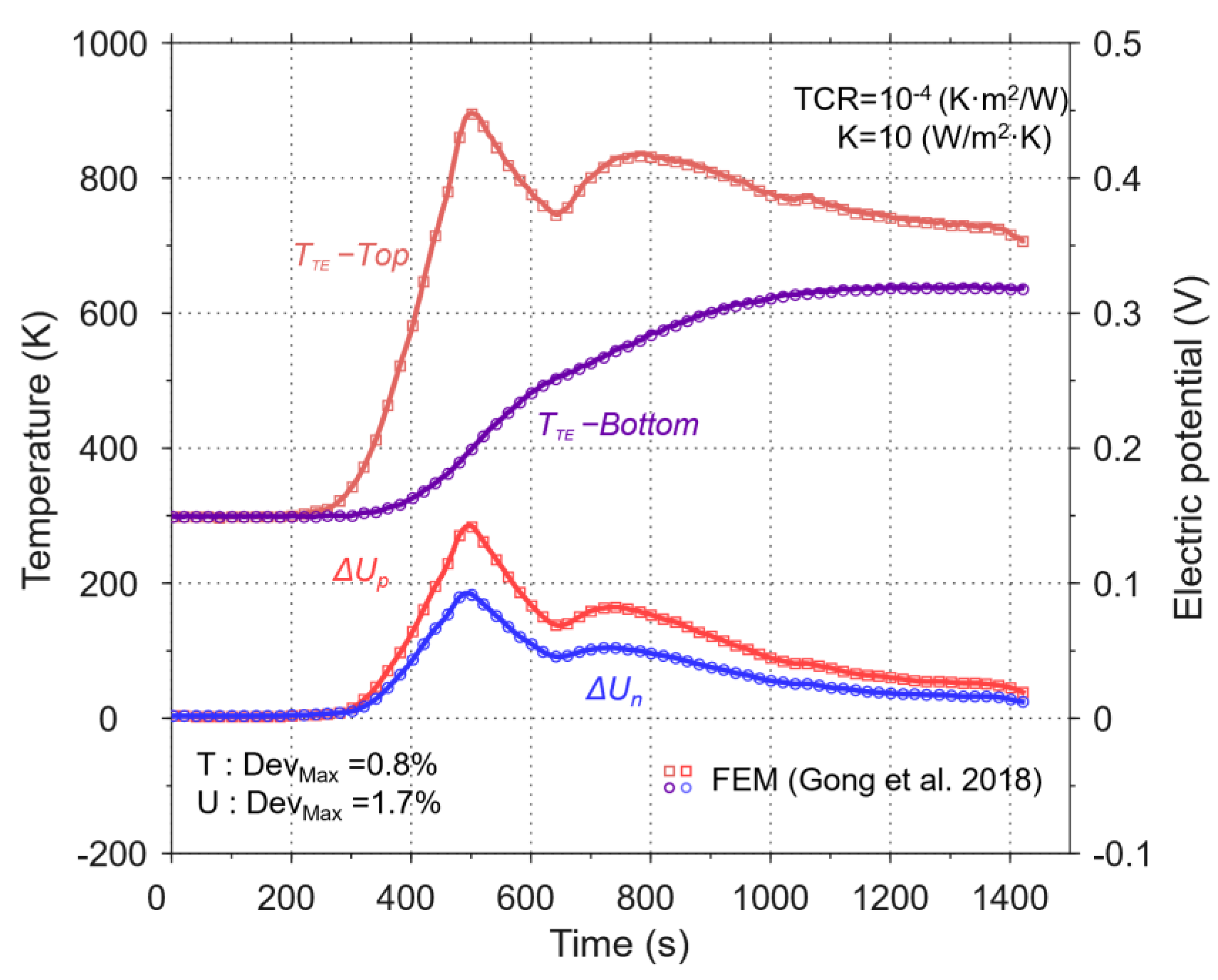
2.2.4. Baseline Model Validation
2.2.5. Integration of Interfacial Contact Effects
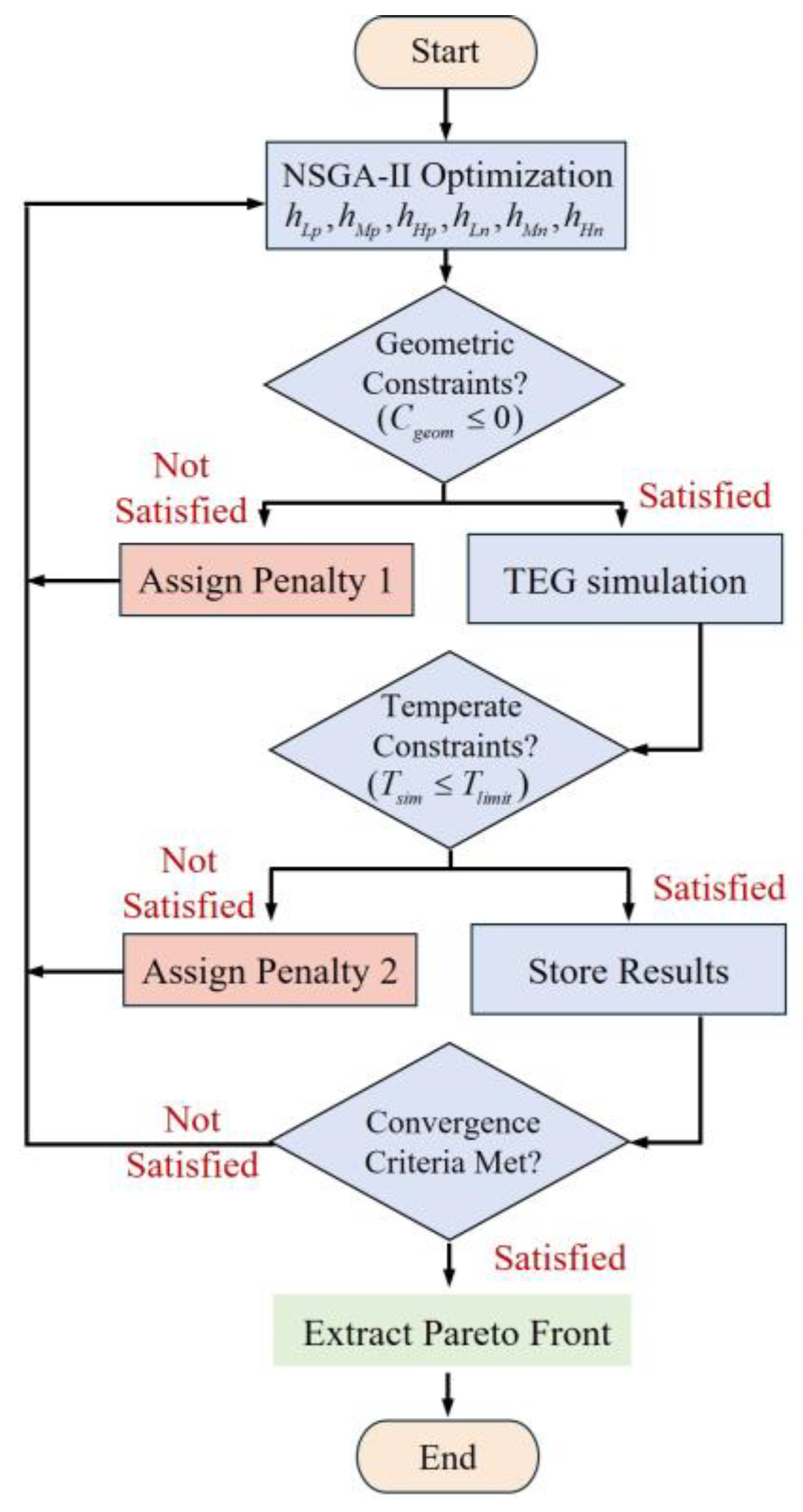
3. Structural Design Optimization
3.1. Problem Formulation
3.2. Design Variables and Constraints
3.2.1. Design Variables
3.2.2. Constraints
- Total stack height: the thermoelectric structural height HTEtotal must lie between 15 mm and 25 mm.
- P/N leg height consistency: to maintain a level structure, the total heights of the p- and n-type legs must be equal, i.e., HP = HN.
- Material temperature upper bound: for every material node k and any time t, the instantaneous temperature must satisfy Tk(t) ≤ Tlimit,k.
- Cabin-side temperature upper bound: To protect onboard electronic equipment, the temperature at the inner (cabin-side) surface of the structure must not exceed 440 K.
3.3. Objective Functions
- Objective: maximize the average ideal power per unit mass, a key indicator of the system’s power-to-mass ratio.where denotes full-cycle average ideal output power.f2: Maximum thermal expansion mismatch
- Objective: minimize the peak absolute difference, over the entire operating period, between the total thermal expansion lengths of the p-type and n-type legs.
- Objective: f3 is a composite thermal reliability metric. It first applies a large positive penalty term—the overtemperature integral—to strictly preclude any overtemperature anywhere in the system. Only when no overtemperature occurs over the entire spatiotemporal domain does the objective switch to a negative reward whose magnitude equals the minimum relative thermal safety margin sustained across space and time. Minimizing f3 thereby eliminates overtemperature risk and, conditional on safe operation, maximizes the robustness of the thermal design.where Tlimit,k is the specified maximum allowable temperature for the material used in element k; Δt is the time-step size.
4. Results and Discussion
4.1. Comparison of Optimization Results
4.2. Thermoelectric Characteristic Analysis
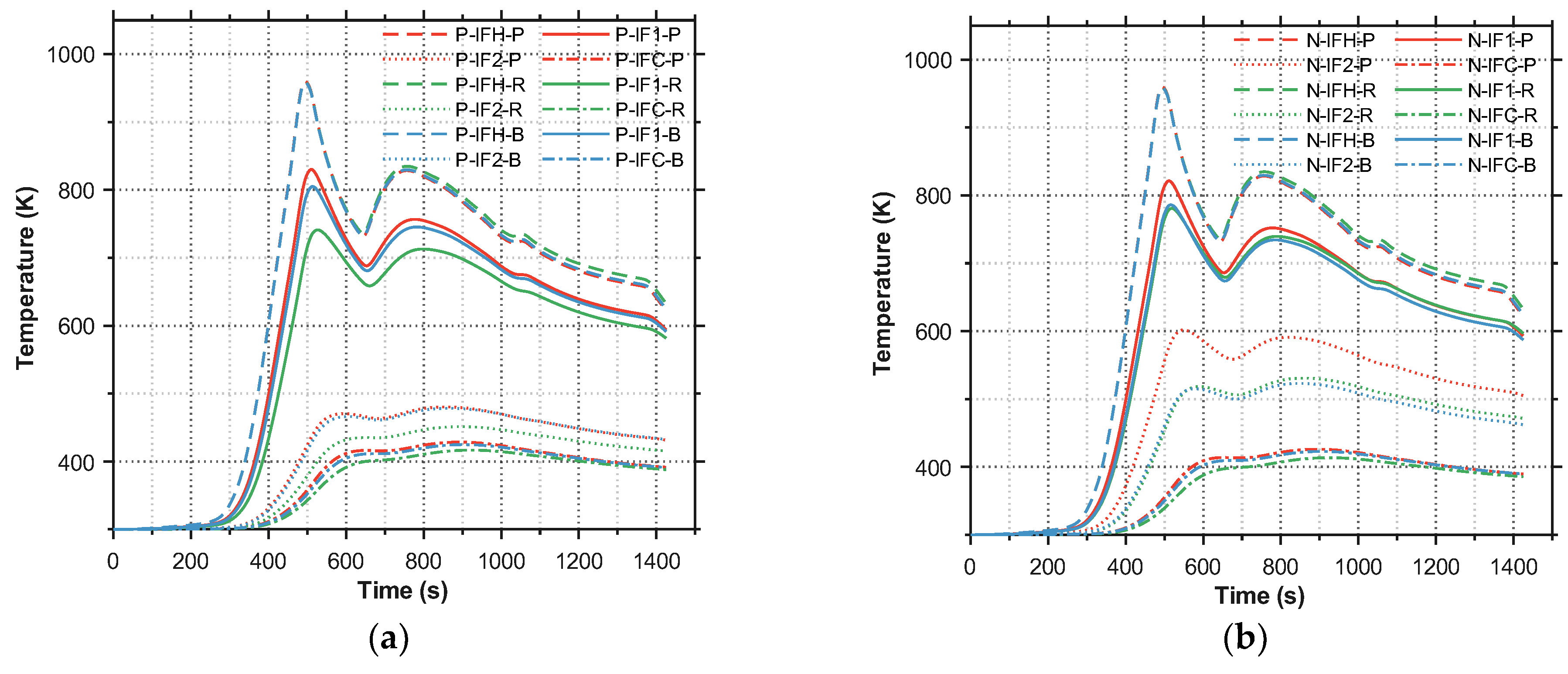
4.2.1. Temperature Characteristics
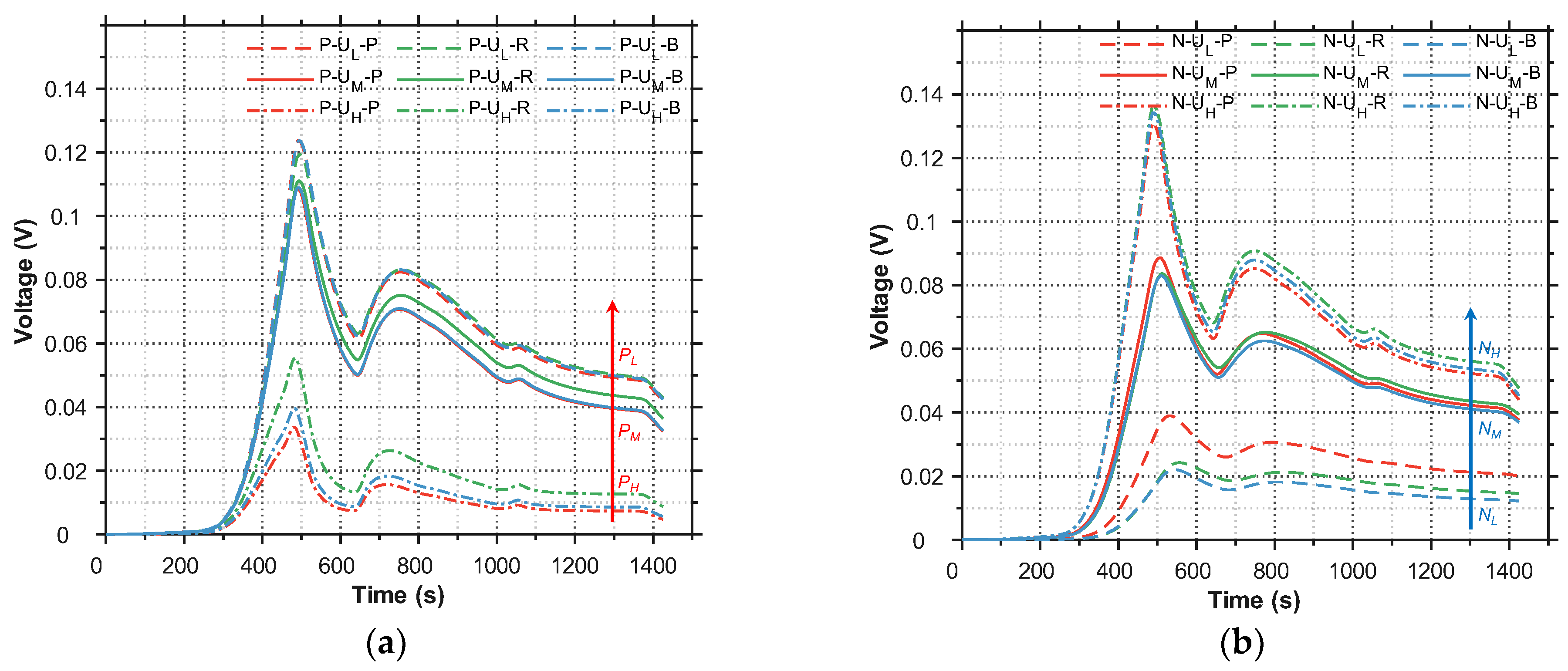
4.2.2. Electrical Characteristic
5. Conclusions
- The proposed quasi-2D thermal network model, which incorporates the hybrid equivalent resistance method and accounts for full transient thermoelectric effects (Seebeck, Peltier, Thomson, Joule), was verified to achieve high accuracy (relative error < 2%) against published 3D FEM results. This model reduced calculation time to on the order of seconds, making complex transient multi-objective optimization feasible. However, it is important to note that this efficiency relies on assumptions of periodic symmetry and uniform cross-sections. While valid for the unit-cell analysis performed here, these assumptions may limit direct applicability for asymmetric configurations or edge effects in finite arrays without recalibration.
- The multi-objective optimization revealed a severe conflict between specific power (f1) and normalized thermal margin (f3). Designs pursuing maximum power inherently favor a smaller total thickness, which reduces thermal resistance, raises cold-side temperatures, and drastically diminishes the thermal margin, leading to high risks of material failure by overheating.
- The effectiveness of the multi-objective optimization framework is demonstrated by the identified Balanced design (Design B). As shown by the quantitative results, compared to the Power-Priority design (Design P), Design B achieves a 61% reduction in thermal expansion mismatch (f2) and raises the minimum thermal margin (f3) from 0.8%to 5% throughout the entire flight envelope, while sacrificing only 6.8% of the maximum achievable specific power (f1).
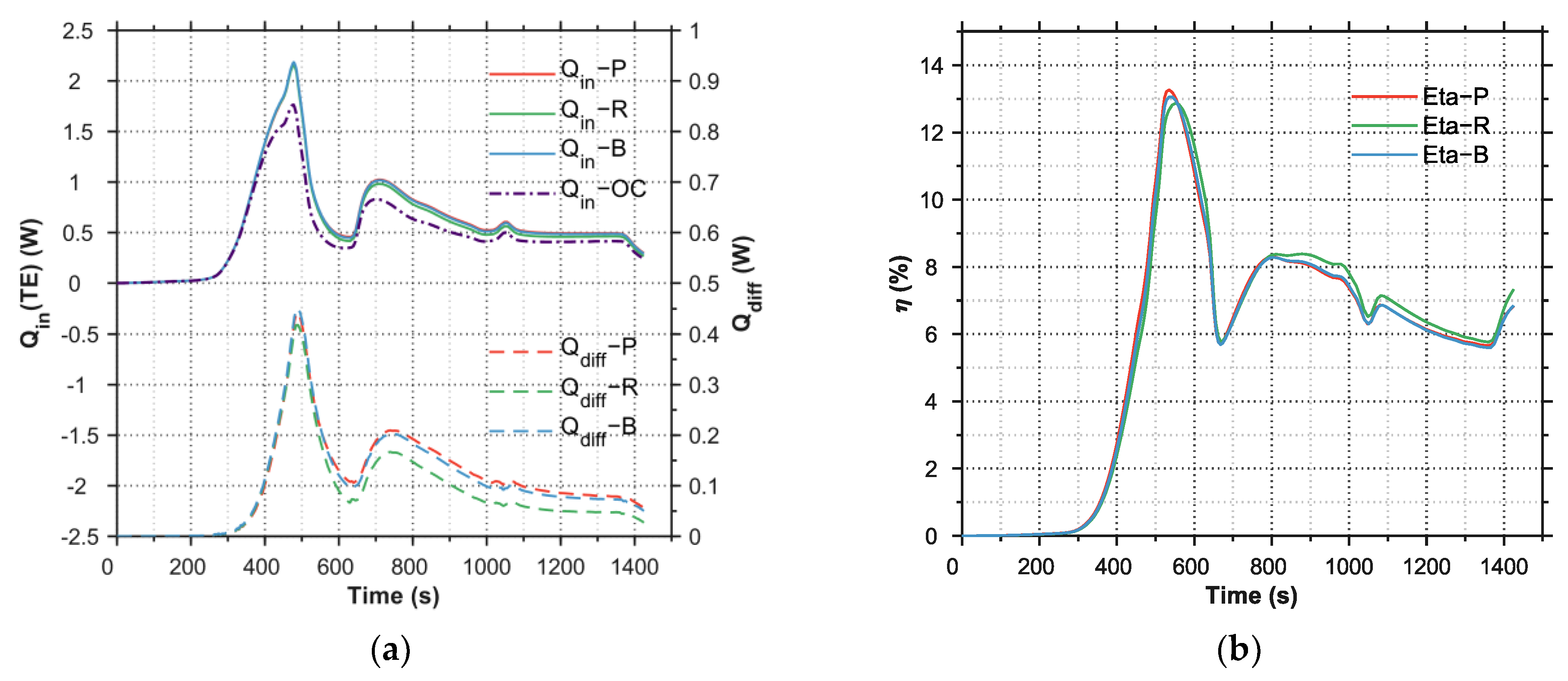
- Despite distinct geometric configurations among the optimized designs (P, R, B), the peak conversion efficiency consistently converges to approximately 13%. This indicates that, under the constraint of uniform cross-sectional legs, the efficiency ceiling is primarily governed by the ZT values of the material system. However, this value does not represent the absolute physical limit. Future research exploring variable cross-section architectures (e.g., hourglass or tapered legs) could potentially surpass this 13% threshold by more effectively matching the local thermal impedance to the material’s optimal temperature range.
- Translating optimized designs into flight-ready hardware entails substantial manufacturing and operational challenges. In particular, assembling multi-segment thermoelectric generator (TEG) structures demands precise control of interfacial quality, as thermal and electrical contact resistances can significantly degrade conversion efficiency. Moreover, the hypersonic flight environment—characterized by repeated thermal cycling, high-amplitude vibration, and shock loading—subjects the structure to risks of material fatigue and interfacial delamination over extended missions. Scaling to large-scale production introduces additional difficulties in maintaining consistent material properties and geometric tolerances. Therefore, future work must bridge the gap between theory and application through rigorous experimental validation under relevant flight conditions and the development of robust, high-yield manufacturing processes to ensure system reliability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- An, K.; Guo, Z.; Xu, X.; Huang, W. A framework of trajectory design and optimization for the hypersonic gliding vehicle. Aerosp. Sci. Technol. 2020, 106, 106110. [Google Scholar] [CrossRef]
- Gou, J.-J.; Yan, Z.-W.; Hu, J.-X.; Gao, G.; Gong, C.-L. The heat dissipation, transport and reuse management for hypersonic vehicles based on regenerative cooling and thermoelectric conversion. Aerosp. Sci. Technol. 2021, 108, 106373. [Google Scholar] [CrossRef]
- Behrens, B.; Müller, M. Technologies for thermal protection systems applied on re-usable launcher. Acta Astronaut. 2004, 55, 529–536. [Google Scholar] [CrossRef]
- Gori, F.; Corasaniti, S.; Worek, W.M.; Minkowycz, W.J. Theoretical prediction of thermal conductivity for thermal protection systems. Appl. Therm. Eng. 2012, 49, 124–130. [Google Scholar] [CrossRef]
- Gong, C.-L.; Gou, J.-J.; Hu, J.-X.; Gao, F. A novel TE-material based thermal protection structure and its performance evaluation for hypersonic flight vehicles. Aerosp. Sci. Technol. 2018, 77, 458–470. [Google Scholar] [CrossRef]
- Zhang, D.; Qin, J.; Feng, Y.; Ren, F.; Bao, W. Performance evaluation of power generation system with fuel vapor turbine onboard hydrocarbon fueled scramjets. Energy 2014, 77, 732–741. [Google Scholar] [CrossRef]
- Song, S.; Liu, W.; Peitsch, D.; Schaefer, U. Detailed design of a high speed switched reluctance starter/generator for more/all electric aircraft. Chin. J. Aeronaut. 2010, 23, 216–226. [Google Scholar] [CrossRef]
- Cheng, K.; Qin, J.; Zhang, D.; Bao, W.; Jing, W. Performance evaluation for a combined power generation system of closed-Brayton-cycle and thermoelectric generator with finite cold source at room temperature on hypersonic vehicles. Energy 2022, 254, 124444. [Google Scholar] [CrossRef]
- Surhone, L.M.; Tennoe, M.T.; Henssonow, S.F. Ram Air Turbine; Collins Aerospace: Wilson, NC, USA, 2010. [Google Scholar]
- Wang, Y.; Cheng, K.; Dang, C.; Wang, C.; Qin, J.; Huang, H. Performance and experimental investigation for a novel heat storage based thermoelectric harvester for hypersonic vehicles. Energy 2023, 263, 125885. [Google Scholar] [CrossRef]
- Bell, L.E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems. Science 2008, 321, 1457–1461. [Google Scholar] [CrossRef]
- Chen, W.-H.; Chiou, Y.-B. Geometry design for maximizing output power of segmented skutterudite thermoelectric generator by evolutionary computation. Appl. Energy 2020, 274, 115296. [Google Scholar] [CrossRef]
- Gao, G.; Gou, J.-J.; Gong, C.-L.; Hu, J.-X.; Gao, R.-C. A novel mechanical-thermal-electrical thermal protection system concept and its multi-scale performance evaluation for hypersonic launch vehicles. Compos. Struct. 2021, 268, 113962. [Google Scholar] [CrossRef]
- Cheng, K.; Zhang, D.; Qin, J.; Zhang, S.; Bao, W. Performance evaluation and comparison of electricity generation systems based on single- and two-stage thermoelectric generator for hypersonic vehicles. Acta Astronaut. 2018, 151, 15–21. [Google Scholar] [CrossRef]
- Cheng, K.; Qin, J.; Jiang, Y.; Lv, C.; Zhang, S.; Bao, W. Performance assessment of multi-stage thermoelectric generators on hypersonic vehicles at a large temperature difference. Appl. Therm. Eng. 2018, 130, 1598–1609. [Google Scholar] [CrossRef]
- Cheng, K.; Qin, J.; Sun, H.; Dang, C.; Zhang, S.; Liu, X.; Bao, W. Performance assessment of an integrated power generation and refrigeration system on hypersonic vehicles. Aerosp. Sci. Technol. 2019, 89, 192–203. [Google Scholar] [CrossRef]
- Cheng, K.; Qin, J.; Jiang, Y.; Zhang, S.; Bao, W. Performance comparison of single- and multi-stage onboard thermoelectric generators and stage number optimization at a large temperature difference. Appl. Therm. Eng. 2018, 141, 456–466. [Google Scholar] [CrossRef]
- Chen, L.; Li, J.; Sun, F.; Wu, C. Performance optimization of a two-stage semiconductor thermoelectric-generator. Appl. Energy 2005, 82, 300–312. [Google Scholar] [CrossRef]
- Gao, G.; Li, D.; Gou, J.-J.; Gong, C.-L.; Li, S.-M. A study of interfacial electrical contact resistances of thermoelectric generators for hypersonic vehicles by experimental measurements and two-scale numerical simulations. Aerosp. Sci. Technol. 2022, 131, 107966. [Google Scholar] [CrossRef]
- Gou, J.-J.; Hu, J.-X.; Yan, Z.-W.; Gao, G.; Gong, C.-L. Effects of physical dimensions, temperature ranges and interfacial thermal contacts on the multi-stage thermoelectric generators for a hypersonic vehicle. Int. J. Energy Res. 2022, 46, 20021–20038. [Google Scholar] [CrossRef]
- Shittu, S.; Li, G.; Zhao, X.; Ma, X.; Akhlaghi, Y.G.; Fan, Y. Comprehensive study and optimization of concentrated photovoltaic-thermoelectric considering all contact resistances. Energy Convers. Manag. 2020, 205, 112422. [Google Scholar] [CrossRef]
- Zhang, A.B.; Wang, B.L.; Pang, D.D.; Chen, J.B.; Wang, J.; Du, J.K. Influence of leg geometry configuration and contact resistance on the performance of annular thermoelectric generators. Energy Convers. Manag. 2018, 166, 337–342. [Google Scholar] [CrossRef]
- Piggott, A. Detailed Transient Multiphysics Model for Fast and Accurate Design, Simulation and Optimization of a Thermoelectric Generator (TEG) or Thermal Energy Harvesting Device. J. Electron. Mater. 2019, 48, 5442–5452. [Google Scholar] [CrossRef]
- Gou, J.J.; Gong, C.L.; Tao, W.Q. Appropriate utilization of the unit cell method in thermal calculation of composites. Appl. Therm. Eng. 2018, 139, 295–306. [Google Scholar] [CrossRef]
- Chen, M.; Rosendahl, L.A.; Condra, T.J.; Pedersen, J.K. Numerical modeling of thermoelectric generators with varying material properties in a circuit simulator. IEEE Trans. Energy Convers. 2009, 24, 112–124. [Google Scholar] [CrossRef]
- Chavez, J.A.; Ortega, J.A.; Salazar, J.; Turo, A.; Garcia, M.J. SPICE model of thermoelectric elements including thermal effects. In Proceedings of the 17th IEEE Instrumentation and Measurement Technology Conference, Baltimore, MD, USA, 1–4 May 2000; IEEE: Piscataway, NJ, USA, 2000; Volume 2, pp. 1019–1023. [Google Scholar] [CrossRef]
- Nickolay, M.; Fischer, L.; Martin, H. Shape factors for conductive heat flow in circular and quadratic cross-sections. Int. J. Heat Mass Transf. 1998, 41, 1437–1444. [Google Scholar] [CrossRef]
- Bai, F.X.; Yu, H.; Peng, Y.K.; Li, S.; Yin, L.; Huang, G.; Chen, X.J. Electronic topological transition as a route to improve thermoelectric performance in Bi0.5Sb1.5Te3. Adv. Sci. 2022, 9, 2105709. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Li, X.; Sun, C.; Song, W.; Zhao, W.; Zhang, Q. Robust Room Temperature Thermoelectric Performance of Mg3(Sb, Bi)2-Based Alloys via Multivalent Mn Doping. Adv. Funct. Mater. 2024, 34, 2315886. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, Q.; Chen, L.; Goto, T.; Hirai, T. Synthesis and thermoelectric properties of p-type- and n-type-filled skutterudite RyMxCo4−xSb12 (R: Ce, Ba, Y, M: Fe, Ni). J. Appl. Phys. 2005, 97, 093712. [Google Scholar] [CrossRef]
- Rogl, G.; Grytsiv, A.; Yubuta, K.; Puchegger, S.; Bauer, E.; Raju, C. In-doped multifilled n-type skutterudites with ZT = 1.8. Acta Mater. 2015, 95, 201–211. [Google Scholar] [CrossRef]
- Joshi, G.; Lee, H.; Lan, Y.; Wang, X.; Zhu, G.; Wang, D.; Ren, Z. Enhanced thermoelectric figure-of-merit in nanostructured p-type silicon germanium bulk alloys. Nano Lett. 2008, 8, 4670–4674. [Google Scholar] [CrossRef]
- Kallel, A.C.; Roux, G.; Martin, C.L. Thermoelectric and mechanical properties of a hot pressed nanostructured n-type Si80Ge20 alloy. Mater. Sci. Eng. A 2013, 564, 65–70. [Google Scholar] [CrossRef]
- Wen, L.; Yin, L.; Li, X.; Chen, S.; Zhang, T.; Cheng, J.; Ma, B.; Ren, Y.; Xiao, L.; Cao, F.; et al. Unified contact layers design for highly efficient segmented PbTe/Bi2Te3 thermoelectric devices. Energy Environ. Sci. 2025, 18, 9939–9948. [Google Scholar] [CrossRef]
- Wojciechowski, K.T.; Zybala, R.; Mania, R. High temperature CoSb3–Cu junctions. Microelectron. Reliab. 2011, 51, 1198–1202. [Google Scholar] [CrossRef]
- Yoo, C.Y.; Yeon, C.; Jin, Y.; Kim, Y.; Song, J.; Yoon, H.; Min, G. Determination of the thermoelectric properties of a skutterudite-based device at practical operating temperatures by impedance spectroscopy. Appl. Energy 2019, 251, 113341. [Google Scholar] [CrossRef]
- Zhang, Q.; Liao, J.; Tang, Y.; Gu, M.; Ming, C.; Qiu, P.; Chen, L. Realizing a thermoelectric conversion efficiency of 12% in bismuth telluride/skutterudite segmented modules through full-parameter optimization and energy-loss minimized integration. Energy Environ. Sci. 2017, 10, 956–963. [Google Scholar] [CrossRef]
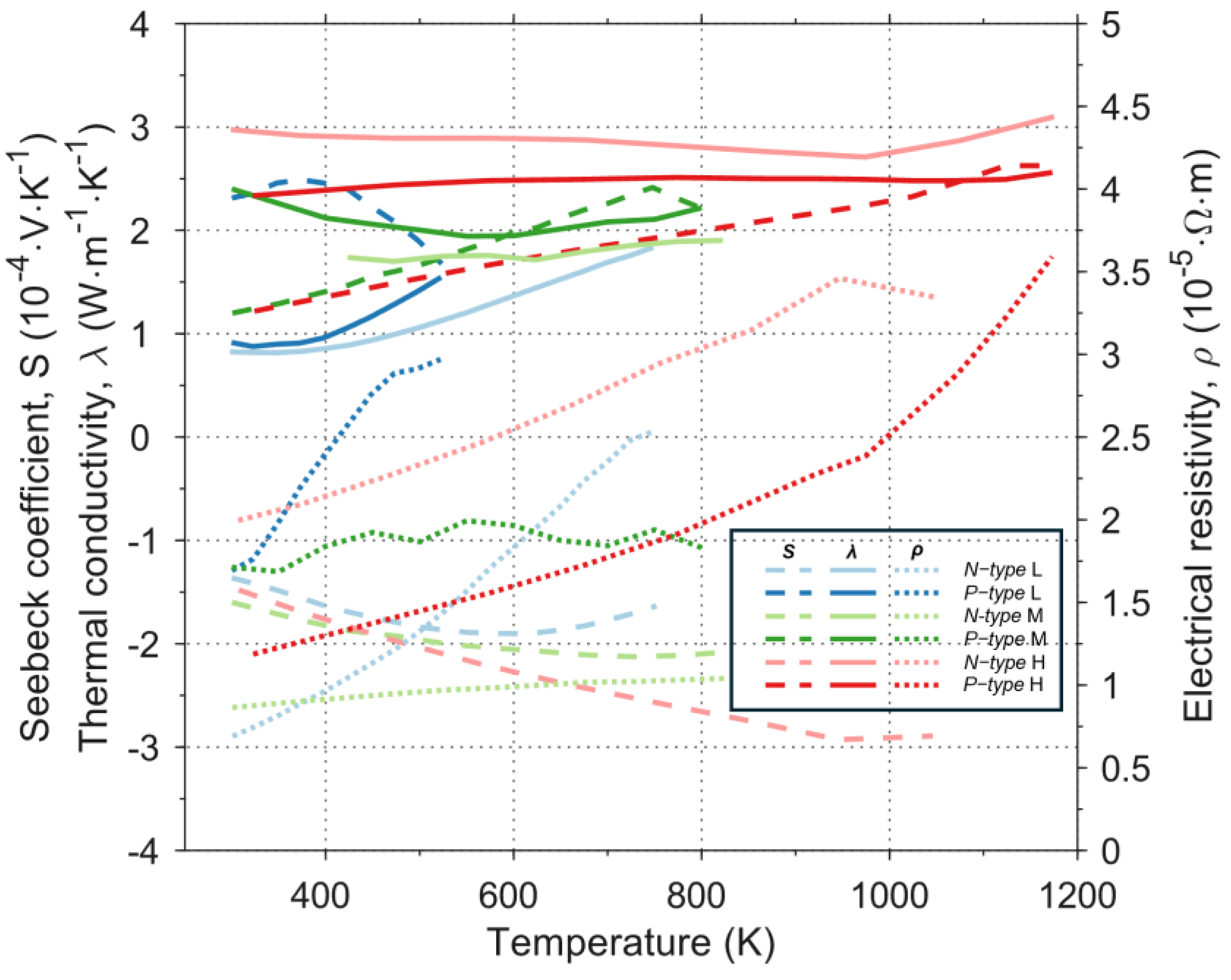





| Categories | P-Type | Tlimit | CTE | N-Type | Tlimit | CTE |
|---|---|---|---|---|---|---|
| LTE | Bi0.5Sb1.5Te3 [28] | <520 K | 1.65 × 10−5 | Mg3.17Mn0.03Bi1.49 Sb0.5Te0.01 [29] | <740 K | 2.23 × 10−5 |
| MTE | Ba0.30Ni0.05Co3.95Sb12 [30] | <850 K | 9.5 × 10−6 | (Sr0.080Ba0.043Yb0.054 In0.008)Co4Sb12 [31] | <850 K | 9.5 × 10−6 |
| HTE | Si80Ge20 [32] | <1200 K | 4.2 × 10−6 | Si80Ge20 [33] | <1200 K | 4.2 × 10−6 |
| Interface | TCR (K·m2/W) | ECR (Ω·m2) |
|---|---|---|
| HTE-Electrode | 2 × 10−5 | 5 × 10−9 |
| HTE-MTE | 3 × 10−5 | 2 × 10−9 |
| MTE-LTE | 4 × 10−5 | 1 × 10−9 |
| LTE-Electrode | 1 × 10−5 | 5 × 10−10 |
| Design | f1 (W/kg) | f2 (μm) | f3 (%) |
|---|---|---|---|
| P (Max specific power) | 28.1 | 12.5 | 0.8 |
| R (Reliability-prioritized) | 22.7 | 11.3 | 8.9 |
| B (Balanced) | 24.5 | 3.6 | 5.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Dong, H.; Cheng, K.; Zhu, K.; Xia, T. Multi-Objective Robust Design of Segmented Thermoelectric–Thermal Protection Structures for Hypersonic Vehicles Using a High-Fidelity Thermal Network. Appl. Sci. 2025, 15, 12482. https://doi.org/10.3390/app152312482
Zhao Y, Dong H, Cheng K, Zhu K, Xia T. Multi-Objective Robust Design of Segmented Thermoelectric–Thermal Protection Structures for Hypersonic Vehicles Using a High-Fidelity Thermal Network. Applied Sciences. 2025; 15(23):12482. https://doi.org/10.3390/app152312482
Chicago/Turabian StyleZhao, Yidi, Hao Dong, Keming Cheng, Kongjun Zhu, and Tianyu Xia. 2025. "Multi-Objective Robust Design of Segmented Thermoelectric–Thermal Protection Structures for Hypersonic Vehicles Using a High-Fidelity Thermal Network" Applied Sciences 15, no. 23: 12482. https://doi.org/10.3390/app152312482
APA StyleZhao, Y., Dong, H., Cheng, K., Zhu, K., & Xia, T. (2025). Multi-Objective Robust Design of Segmented Thermoelectric–Thermal Protection Structures for Hypersonic Vehicles Using a High-Fidelity Thermal Network. Applied Sciences, 15(23), 12482. https://doi.org/10.3390/app152312482








