Assessment of Tension-Only Concentrically Braced Steel Frames in Relation to Seismic Pounding

Abstract

This research examined the phenomenon of pounding between neighboring steel structures, both with and without tension-only braces, utilizing an extensive nonlinear time-history analysis. The evaluation of the structural response was conducted using essential engineering demand parameters such as inter-story drift ratio (IDR), residual inter-story drift ratio (RIDR), peak floor acceleration (PFA), base shear, and base moment. The findings indicated that the addition of tension-only braces plays a crucial role in diminishing the structural response during seismic activities. The tension-only brace effectively alleviates the negative impacts of structural pounding by offering supplementary restraint and energy dissipation mechanisms, which enhances the overall seismic performance of the steel frame structures. These results highlight the potential advantages of adopting tension-only braces as a passive control method to mitigate pounding-related structural damage in closely situated buildings.

1. Introduction

Concentrically braced structural systems (CBFs) are recognized as a preferred mechanism for resisting lateral forces in steel building construction, particularly under seismic loading conditions. Tension-Only Concentrically Braced Frames (TOCBF) demonstrate deteriorating pinched hysteretic behavior during intense earthquakes [1,2]. Slender braces transition through various states: an elastic buckling state, a re-straightening state where they bear almost no load, an elastic tensile loading state when they become taut, and ultimately, a tensile yielding state [3,4]. The proposed brace features a slender rod with tensile-connected ends that include a beveled washer and wedge [5]. This brace does not experience buckling. The wedge moves between a washer and a stand to prevent brace looseness caused by axial plastic deformation during repeated loading [5,6]. Frames lacking adequate seismic details may exhibit deteriorating hysteretic behaviors, characterized by stiffness and strength degradation, as well as pinching. These characteristics can lead to significant concerns regarding lateral dynamic stability. To mitigate such undesirable behaviors, a Pre-Slacked Cable Brace (PSCB) is proposed, which would significantly enhance the post-yield stiffness of highly pinched non-ductile frames with only a minimal increase in their lateral strength capacity [5,6].

Recent advancements in seismic protection systems highlight the seesaw system, which uses fluid viscous dampers, cables, and a seesaw mechanism to enhance structural responses [7,8,9]. This design prevents brace buckling and enhances stability, particularly for low-rise steel structures [10,11]. Studies also explore its integration in aging concrete structures and bridges, focusing on soil-structure interaction effects [12,13,14].

The research conducted by Papagiannopoulos [15] offers a thorough assessment of anticipated outcomes derived from three-dimensional nonlinear dynamic seismic analysis of tension-only concentrically braced steel frameworks. The bracing members in these structural systems are meticulously designed to withstand only tensile forces while eliminating compressive resistance. Specifically, a cost-efficient and easily constructible brace connection detail enables the bracing component to move under compressive loads while developing resistance capacity when exposed to tensile forces. A performance evaluation is conducted between steel frameworks designed with the proposed tension-only bracing and those that utilize buckling-restrained bracing, employing established seismic response and demand metrics. The findings indicate that both tension-only and buckling-restrained braced systems can demonstrate comparable performance characteristics. However, it is noted that column compression overstress is more pronounced in tension-only braced frameworks [16].

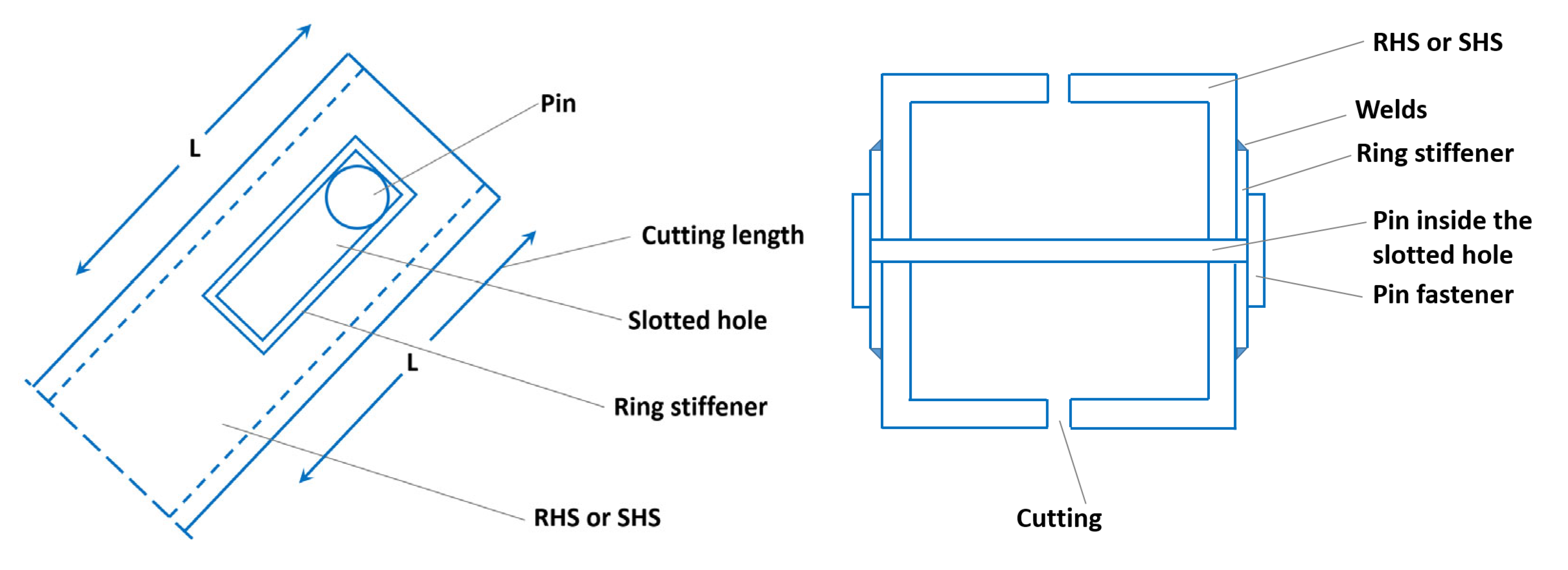
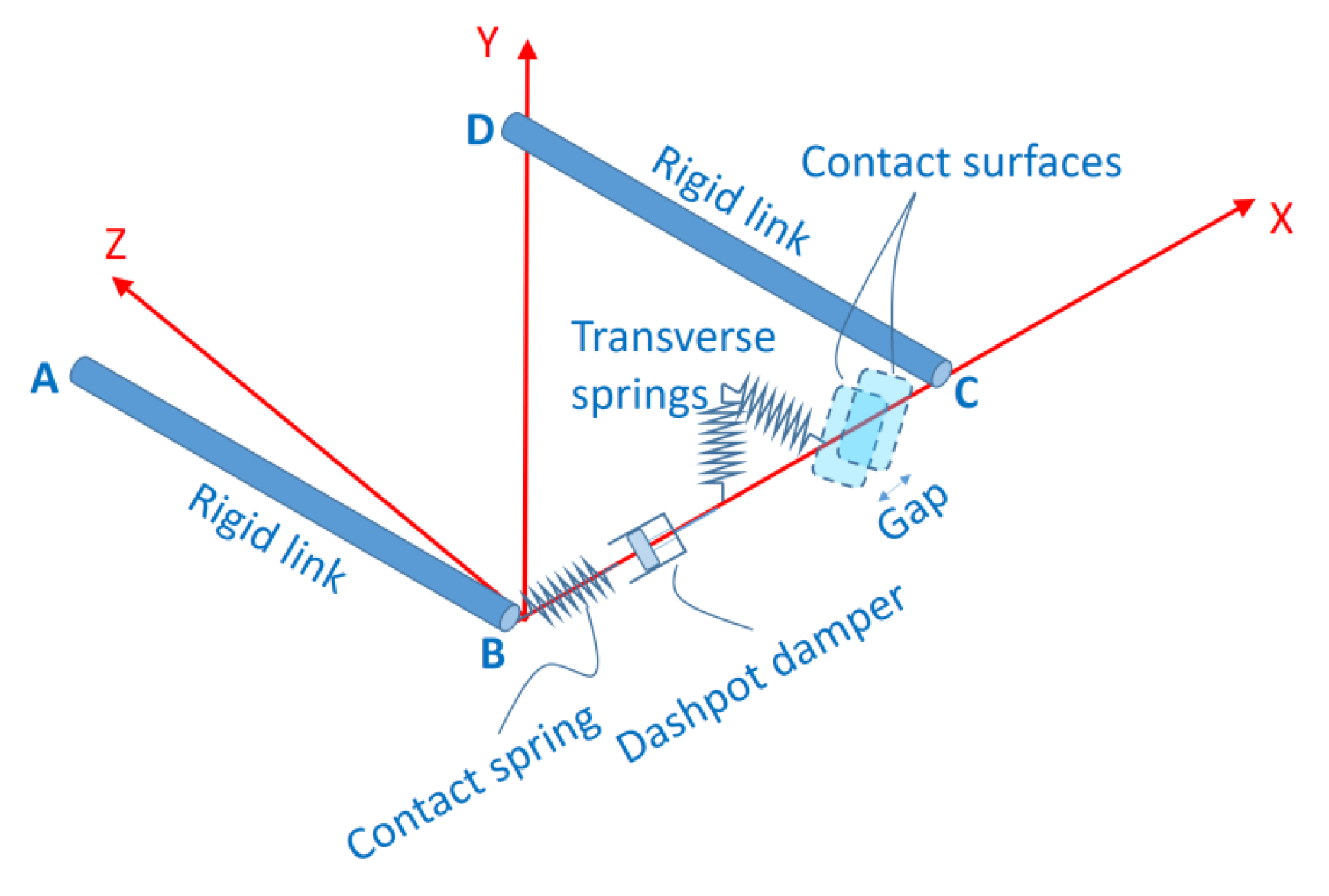
Initial observations regarding the application of the suggested tension-only bracing as a seismic resistance mechanism for steel structures are recorded. The approach outlined in this study utilizes the sliding connection principle, particularly by placing the fasteners (pins) at one end of the elongated aperture. The construction specifics of this sliding connection are illustrated in Figure 1. A robust pin is designed to move within the slotted opening created in a hollow section-bracing component.

In the study of Dal Lago et al. [17], a groundbreaking seismic retrofitting technique utilizing unilateral dissipative bracing is investigated. The device presented in this paper, which is currently undergoing preliminary design and testing, dissipates energy exclusively through friction in tension while permitting free deformation in compression, thus eliminating concerns related to compressive buckling. A numerical analysis is executed to examine the effectiveness of the proposed device in the seismic retrofitting of precast industrial frame buildings, with the intention of exploring its feasibility and refining the definition of the slip threshold load range and the future development of the physical device.

The selection of appropriate seismic mitigation strategies requires careful consideration of multiple factors including cost, constructability, maintenance requirements, and performance effectiveness. Base isolation systems, while highly effective in reducing seismic demands by decoupling the superstructure from ground motions, typically involve substantial initial costs and require specialized maintenance protocols to ensure long-term functionality of the isolation bearings [18,19,20]. These systems are particularly suitable for new construction where foundation modifications can be easily accommodated, but their implementation in existing buildings often presents significant technical and economic challenges [21,22,23]. Viscous dampers and other energy dissipation devices offer excellent performance in controlling structural response through enhanced damping mechanisms [24,25,26], yet they similarly require ongoing inspection and potential replacement after major seismic events [27,28,29]. Buckling-restrained braces (BRBs) provide stable hysteretic behavior with symmetric tension-compression response [30,31,32], but their manufacturing complexity and higher material costs can limit widespread adoption, particularly in retrofit applications with budget constraints [33,34,35].

In contrast, tension-only concentrically braced frames present distinct practical advantages that make them particularly attractive for seismic retrofit of existing structures in urban environments [36,37]. The simplicity of their construction detail, which relies on straightforward sliding connections rather than sophisticated mechanical devices, significantly reduces both fabrication costs and installation time [38]. Unlike active or semi-active control systems, tension-only braces function as purely passive elements requiring no external power, monitoring systems, or regular maintenance beyond standard structural inspections [39]. Their unidirectional load-carrying mechanism, while producing pinched hysteretic behavior, effectively contributes to energy dissipation during seismic events without the buckling-related complications that affect conventional bracing systems [40]. Furthermore, the lightweight nature of tension-only bracing elements minimizes additional demands on existing foundations, a critical consideration when retrofitting older buildings that may not have been designed for increased lateral force-resisting systems. These characteristics position tension-only braces as a cost-effective and readily implementable solution for improving seismic performance of closely spaced buildings where pounding represents a significant concern, particularly in densely built urban areas where increasing separation distances is not feasible [41].

The research findings from sources [42,43,44] indicate that collisions significantly influence the dynamics of lighter and more flexible buildings, leading to a marked increase in their response and resulting in considerable permanent deformation due to yielding. Conversely, the heavier and stiffer buildings show little sensitivity to collisions between structures. The parametric study has established that the peak displacement of the lighter and more flexible building is highly affected by variations in structural parameters, such as gap size, storey mass, structural stiffness, and yield strength, while the heavier and stiffer structure demonstrates minimal response to these changes. Furthermore, Efraimiadou et al. [45] investigated the effects of different structural configurations on the interactions between adjacent planar reinforced concrete (RC) building frames subjected to severe earthquakes. Their research involved two 5-storey and two 8-storey frames, either in standard form or with setbacks, resulting in nine distinct pairs of adjacent RC structures. These pairs were tested against six strong ground motions that are fully aligned with the design process. The study analyzed various parameters, including maximum displacements, permanent displacements, member ductility, internal forces, and interstorey drift ratios. The findings indicate that collisions between adjacent frames generally have adverse effects, suggesting that the structural pounding phenomenon is primarily harmful rather than beneficial. They also investigated the impact of multiple earthquakes [46].

Strategies for protecting against seismic impacts have been developed to improve building performance during collision events. The analysis results from [47] indicate that the arrangement of adjacent structures in series significantly influences the collapse capacities of the colliding structures. Furthermore, when a shorter structure is positioned between two taller structures, it creates the most critical scenario among all configurations, leading to a more pronounced reduction in structural performance levels. A significant method involves the use of base isolation technology, which separates the upper structure from its foundation system [48]. Buildings equipped with isolation systems demonstrate reduced story drift ratios and lateral forces, even though they may experience substantial movements at the isolation interface. The impact of pounding on buildings with fixed bases, isolated buildings, and those situated on soft soils is examined. Subsequently, considerations regarding an adequate recommended gap are discussed. Additionally, suitable mitigation measures are proposed, along with suggestions for future research directions on structural pounding [49].

Numerical simulations and parametric studies have been employed to explore the impact of potential poundings between seismically isolated buildings and neighboring structures on the efficacy of seismic isolation. It is assumed that poundings occur at the isolation level between the seismically isolated building and the surrounding moat wall [50,51,52]. The study of [53] investigates the seismic responses of adjacent buildings that are supported by different or similar base systems, taking into account the impacts between bases and superstructures through numerical methods. To analyze the differences in collision behavior between isolated buildings with barrier walls and conventional structures, Polycarpou et al. [54,55,56] conducted computational analyses involving isolated buildings that utilize elastomeric isolation devices.

Aim of this paper is to examine the phenomenon of pounding between neighboring steel structures, both with and without tension-only braces, utilizing an extensive nonlinear time-history analysis. The evaluation of the structural response was conducted using essential engineering demand parameters such as inter-story drift ratio (IDR), residual inter-story drift ratio (RIDR), peak floor acceleration (PFA), base shear, and base moment. The inter-story Drift Ratio denotes the relative horizontal displacement between two adjacent floors, divided by the height of the story. The Residual Inter-story Drift Ratio (RIDR) represents the permanent horizontal displacement that occurs between consecutive floors after an earthquake has ended, divided by the height of the story. Peak Floor Acceleration (PFA) indicates the maximum acceleration recorded at each floor level during seismic events. The findings indicated that the addition of tension-only braces plays a crucial role in diminishing the structural response during seismic activities. The tension-only system effectively alleviates the negative impacts of structural pounding by offering enhanced restraint and energy dissipation mechanisms, which results in improved seismic performance of the steel frame structures. These results highlight the potential advantages of adopting tension-only braces as a passive control approach to minimize structural damage caused by pounding in closely situated buildings.

2. Structural Characteristics of Buildings with Tension-Only Braces

The height of the floor was established at 3.0 m, with each bay measuring 6.0 m in length. This analysis involved the evaluation of structural frames comprising three and five stories, adhering to the guidelines set forth in Eurocode 3 [57] and Eurocode 8 [58], utilizing the SAP2000 software (ver. 26) [35]. Two distinct load combinations were investigated: one simulating seismic loading and the other representing gravity loading, as outlined in Eurocode 8 [58]. The seismic load combination is defined as G + 0.3Q + E, where G denotes the dead load, Q signifies the live load, and E represents the earthquake load. The gravity load combination is articulated by the equation 1.35G + 1.5Q. The cross-sectional characteristics of the structural braces and the fundamental periods, T₁, of the examined structures are detailed in

Table 1. Sections of 3- and 5-storey structures.

Structure	Beams	Columns	Tension-Only Braces	Material	Period T1
3-storey	IPE 270	HE 320B	SHS70x5	S275	0.52 s
5-storey	IPE 300	HE 360B	SHS80x5	S275	0.88 s

.

The fundamental periods of vibration for the structures analyzed are presented in Table 1 where the 3-story frame has a fundamental period T₁ = 0.52 s, while the 5-story frame exhibits T₁ = 0.88 s. In the equal-height pounding scenario, both structures share identical periods, resulting in synchronized dynamic behavior and simultaneous impact potential. In contrast, the unequal-height configuration introduces significant period mismatch, which affects the relative phasing of structural motions and consequently influences the timing, frequency, and severity of pounding events throughout the seismic excitation.

Figure 2 and Figure 3 depict the pounding between two 3-storey frames without and with tension-only braces. A detail of link element between the structures is presented on Figure 2. Figure 4 and Figure 5 depict the pounding between 3-storey and 5-storey frames without and with tension-only brace. For each floor level, the dead load was set at 5 kN/m², while the live load was established at 2 kN/m². The seismic design parameters included a ground acceleration of 0.24 g and a behavior factor (q) of 4.0, aligning with the requirements for structures of medium ductility class and Spectrum Type 1. This choice adheres to the specifications outlined in Section 5.2 of Eurocode 8 [58]. The structural design for both the 3-story and 5-story steel buildings was predicated on Soil Type B conditions, which denote rock or extremely dense soil with average shear wave velocities ranging from 760 to 1500 m/s. This type of soil offers relatively rigid foundation support and exhibits minimal seismic amplification effects.

Both the conventional steel frames and those equipped with tension-only braces were designed according to the same seismic design provisions specified in Eurocode 8 for medium ductility class (DCM) structures with a behavior factor q = 4.0. The design process ensured that both structural configurations satisfy the strength, stiffness, and detailing requirements of DCM, including adequate member ductility and connection capacity. The tension-only braces were proportioned to provide the necessary lateral strength under the same seismic demand as the conventional system, ensuring a fair performance comparison between the two configurations. This equivalence in design basis means that any observed differences in seismic response can be attributed to the distinct behavioral characteristics of the tension-only bracing system rather than to variations in the underlying design strength or target performance level.

3. Seismic Motions

The research employed an extensive collection of ground motion records to facilitate a thorough analysis across various seismic scenarios. In total, 200 ground motion records were chosen, evenly split between far-field (100 records) and near-fault (100 records) earthquakes. The far-field records include events with moment magnitudes (Mw) ranging from 6.0 to 7.5. For near-fault records, although the magnitude range remains consistent (Mw 6.0–7.5). Figure 6 presents the response spectra and mean spectrum for the near-fault seismic records.

4. Modeling of Gap Braces, Tension-Only and Nonlinear Time History Analysis

The numerical modeling of tension-only braces was carried out using the SAP2000 [59] tension-compression limits command, which enables structural members to bear loads exclusively in tension while becoming inactive under compressive forces. This modeling approach accurately reflects the unique behavioral characteristics of tension-only systems, where braces can only endure tensile forces and buckle or lose functionality when subjected to compression. The tension-compression limits feature allows the software to automatically deactivate these braces during compression phases and reactivate them when tension is restored, thus offering a realistic representation of the actual structural behavior during seismic events.

The behavioral assumption that tension-only braces become inactive during compression phases is well-documented in the literature through both experimental and analytical studies. Tremblay and Filiatrault [1,2] conducted extensive cyclic loading tests demonstrating that slender bracing elements with sliding connections effectively shed compressive forces through controlled displacement at the connection detail, eliminating buckling concerns while maintaining full tensile capacity. Similar experimental validation has been provided by Tamai and Takamatsu [3], who showed that the pin movement within elongated apertures permits free deformation under compression without developing significant axial resistance. More recent work by Mousavi and Zahrai [5,6] confirmed through quasi-static testing that slack-free connection details can reliably transition between inactive compression states and active tension states during seismic loading cycles. The unilateral dissipative bracing device investigated by Dal Lago et al. [17] further demonstrates the practical feasibility of systems that dissipate energy exclusively in tension while permitting unrestrained compression deformation. This specific behavior has been also confirmed in recent works [36,37,38,39,40,41]. These studies collectively validate the modeling approach employed in this research, where the tension-compression limits feature in SAP2000 accurately represents the physical behavior of sliding connection mechanisms under severe seismic excitation.

The tension-compression limits feature in SAP2000 models the braces as becoming inactive (zero stiffness and strength) when subjected to compressive axial forces and reactivating instantaneously when tensile forces develop. This idealization assumes no initial slack, no prestressing, and pinned connections without frictional resistance, which represents a simplified yet reasonable approximation of the physical behavior illustrated in Figure 1. While more sophisticated models incorporating connection slip and friction effects could be developed, the present approach captures the fundamental characteristic that distinguishes tension-only systems: their unidirectional load-carrying capacity and inability to resist compression.

The phenomenon of pounding between neighboring structures was modeled using gap braces designed as link braces within SAP2000 [59]. The ratio of critical damping ξ is

$$\xi ={\displaystyle \frac{-\mathrm{l}\mathrm{n}\left(r\right)}{\sqrt{{\pi }^2+{\left(\ln \left(r\right)\right)}^2}}}$$

r is the coefficient of restitution for inelastic impact [60] and can be defined as

$$r={\displaystyle \frac{v_2-v_1}{v_{01}-v_{02}}}$$

$v_2,v_1$ are the velocity of two bodies after impact and the velocity of two bodies $v_{01},v_{02}$ before impact.

For the present study, a coefficient of restitution r = 0.65 was adopted for steel-to-steel contact based on values commonly reported in the pounding literature for similar structural configurations. This value falls within the range typically used for metal-to-metal impact and has been validated through experimental studies on structural pounding phenomena. While the coefficient of restitution influences the energy dissipation during impact events, a comprehensive parametric investigation of its effect was beyond the scope of this study. Future research should systematically examine the sensitivity of structural response to variations in r, particularly for tension-only braced systems.

These specialized gap braces were intentionally positioned at key locations between the structures to capture effectively impact forces and energy transfer during collision events. The gap braces were adjusted with appropriate stiffness and damping characteristics to accurately reflect the contact mechanics between the colliding structures, with a gap distance of 2 cm established between the buildings, as shown in Figure 7. This configuration enabled a precise simulation of the complex pounding interactions that take place when the separation distance between buildings is surpassed during lateral movement. The contact spring parameters shown in the figure were implemented in SAP2000 [59]. For steel-to-steel contact between building edges, a typical value of K_contact = 1.5 × 10⁸ kN/m was adopted, which is sufficiently high to prevent significant penetration while maintaining numerical stability in the time integration scheme.

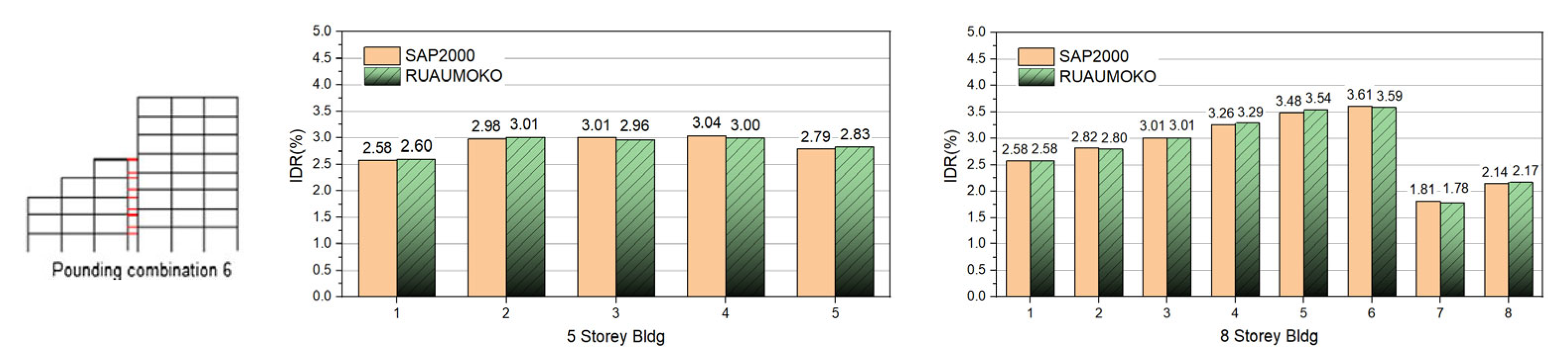
To verify the reliability of the numerical modeling approach adopted in SAP2000, a comparative validation study was conducted using the finite element program RUAUMOKO [61]. The validation followed the pounding analysis methodology established in previous research by Efraimiadou et al. [45,46], which has been extensively calibrated against experimental observations for reinforced concrete frame structures subjected to seismic pounding. Representative cases from the present study involving both equal-height and unequal-height steel frame configurations were analyzed in both software platforms using equivalent gap-element formulations and contact parameters. The comparison revealed excellent agreement between SAP2000 [59] and RUAUMOKO [61] predictions, with differences in peak inter-story drift ratios, floor accelerations, and base shear demands remaining below 5% for all cases examined. This cross-verification confirms that the contact spring stiffness, damping parameters derived from the coefficient of restitution, and the overall pounding simulation framework implemented in SAP2000 [59] adequately reproduce the structural response characteristics observed with an independently validated finite element code, thereby lending credibility to the numerical results presented in subsequent sections.

To validate the examined numerical modeling approach, the pounding combination No. 6 from Ref. [45] (5-story and 8-story buildings) using both SAP2000 [59] and RUAUMOKO [61] it is examined in Figure 8, which depicts the maximum inter-storey drifts (IDR). The comparison between these two independent programs demonstrates that they yield nearly identical results, thereby confirming the reliability of the adopted numerical method.

Due to the highly dynamic and impulsive characteristics of pounding phenomena, the original time step of the ground motion records required substantial refinement through interpolation techniques to attain adequate temporal resolution. The time step was reduced to very small increments to capture precisely the swift force variations and impact dynamics typical of structural pounding events. A nonlinear time-history analysis was performed utilizing this refined temporal discretization, with plastic hinges allocated to structural members in accordance with ASCE 41-17 [62] guidelines. The properties of the plastic hinges were established based on the acceptance criteria and modeling parameters outlined in the standard, ensuring an accurate representation of the structural response. The fundamental theory is based on the equations of motion for a multi-degree-of-freedom (MDOF) system. The general form of the nonlinear equation of motion is:

$$\mathrm{M}\text{ü}\left(\mathrm{t}\right)+\mathrm{C}\dot{u}\left(\mathrm{t}\right)+\mathrm{K}\mathrm{u}=\mathrm{P}\left(\mathrm{t}\right)$$

(1)

where:

• M = mass matrix
• C = damping matrix
• K = stiffness matrix
• P = external load vector
• u(t) = displacement vector
• $\dot{u}$(t) = velocity vector
• ü(t) = acceleration vector

The representation of plastic hinges in steel components according to ASCE 41-17 [62] standards is an essential element of performance-based seismic assessment, requiring careful consideration of the unique characteristics and behavioral attributes of each component. In the structures being analyzed, the three-story building features IPE 270 beams with a plastic moment capacity of 133.1 kNm, HEB320 columns with an axial capacity of 4436 kN, and SHS70x5 tension-only braces rated at 349.3 kN. The five-story design employs larger sections (IPE 300, HE 360B, and SHS80x5) with enhanced capacities of 172.7 kNm, 4967 kN, and 404.3 kN respectively. The application of these models requires the use of specific hinge types: M3 flexural hinges for beams that utilize generalized force-deformation relationships, with yield rotations defined by θ_Y = (M_y × L_p)/(EI), P-M3 interaction hinges for columns that account for axial-moment coupling through interaction surfaces and P hinges for tension-only braces that represent the distinct behavior of bracing systems under seismic forces. When these plastic hinge models are properly calibrated with ASCE 41-17 [62] backbone curves and acceptance criteria, they enable accurate simulation of progressive yielding, strength degradation, and ultimate collapse mechanisms during nonlinear time history analysis, providing engineers with vital tools to assess structural performance against immediate occupancy, life safety, and collapse prevention goals.

The dynamic analysis utilized the Newmark time integration method, applying constant average acceleration parameters (β = 0.25, γ = 0.5) to guarantee numerical stability and precision in capturing the nonlinear pounding behavior. To adequately resolve the impulsive nature of pounding events, the original time step of the ground motion records (typically 0.01–0.02 s) was refined through interpolation to 0.001 s during the high-intensity phases of ground shaking. Convergence was monitored by checking that further time step refinement produced changes in peak response quantities of less than 2%, which was considered acceptable for the engineering assessment purposes of this study. Structural damping was integrated using the Rayleigh damping model, which was calibrated to achieve a damping ratio of ξ = 3% at the fundamental period of the whole structure. The Rayleigh damping matrix [C] = α[M] + β[K] was calibrated using the fundamental frequency f₁ and second mode frequency f₂ of the complete structure-gap system to achieve 3% critical damping at both frequencies, appropriate for steel structures. This methodology ensures consistent damping characteristics across the dominant response modes of the coupled steel system, unlike using individual structure frequencies, which would not account for the dynamic interaction effects introduced by the gap elements and could lead to incorrect energy dissipation during pounding events between steel frames.

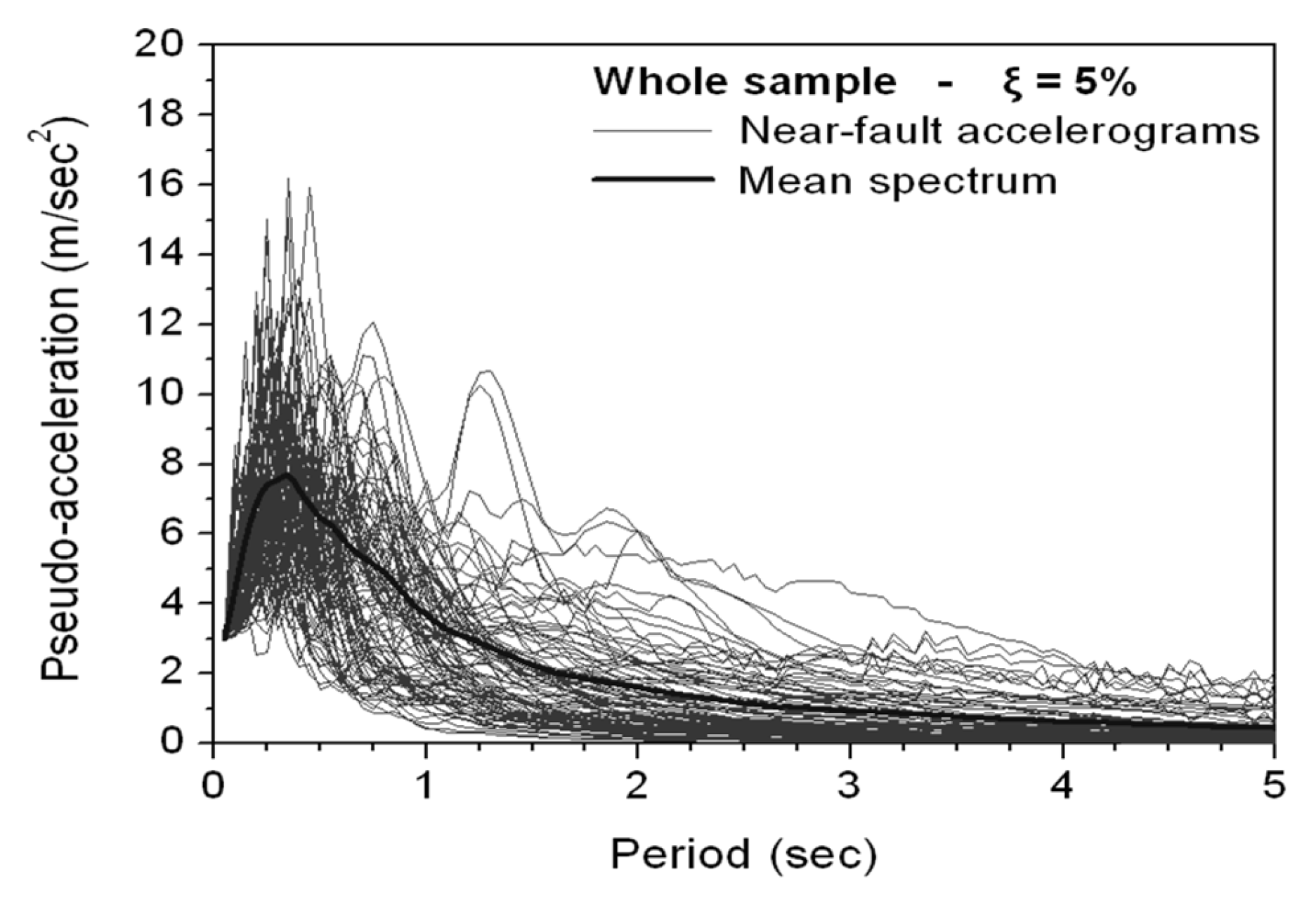
The relationship between the fundamental periods of the analyzed structures and the frequency content of the ground motion records is critical for understanding the pounding response. Figure 6 presents the pseudo-acceleration response spectra for the suite of 100 near-fault ground motions, along with their mean spectrum. The fundamental period of the three-story frame (T₁ = 0.52 s) corresponds to the descending branch of the mean spectrum, where spectral accelerations remain elevated at approximately 1.2 g to 1.4 g. Similarly, the fundamental period of the five-story frame (T₁ = 0.88 s) falls within the intermediate period range where the mean spectral acceleration is approximately 0.8 g to 1.0 g. Both periods therefore lie within regions of significant seismic demand rather than in the long-period range where spectral ordinates diminish substantially. This ensures that the structures experience meaningful inelastic response and realistic pounding conditions during the nonlinear time-history analyses.

The Rayleigh damping formulation employed in this study warrants additional clarification regarding the target frequencies and effective damping characteristics. The damping matrix was constructed using the classical expression C = αM + βK, where the coefficients α and β were calibrated to achieve three percent critical damping ratio at two specific circular frequencies. For the equal-height pounding scenario involving two identical three-story structures, the first two natural frequencies of the complete coupled system (including the gap elements connecting the structures) were used as the target frequencies. Specifically, the fundamental frequency f₁ corresponds approximately to 1.92 Hz (based on T₁ = 0.52 s), and the second mode frequency f₂ is approximately 5.77 Hz. The Rayleigh coefficients were calculated using the standard equations that ensure ξ = 0.03 at both f₁ and f₂. This approach provides appropriate damping characteristics across the frequency range that dominates the structural response, while avoiding artificial damping at higher frequencies that could suppress important impact-related dynamics.

For the unequal-height pounding scenario involving three-story and five-story structures, the damping formulation was similarly calibrated based on the fundamental frequencies of both structures. The three-story frame exhibits f₁ ≈ 1.92 Hz, while the five-story frame has f₁ ≈ 1.14 Hz. The Rayleigh damping was calibrated to achieve three percent critical damping at the fundamental frequency of the shorter structure and at an intermediate frequency representing the second mode of the coupled system. This approach ensures that both structures receive appropriate damping levels despite their different dynamic characteristics. The resulting effective damping ratio varies with frequency according to the well-known Rayleigh relationship ξ(ω) = α/(2ω) + βω/2, which produces a characteristic U-shaped curve with minimum damping at the target frequencies and slightly higher damping at frequencies removed from these targets.

The period mismatch between the three-story and five-story structures in the unequal-height scenario creates distinct dynamic interaction patterns that influence the pounding response. The period ratio T_5-story/T_3-story = 0.88/0.52 ≈ 1.69 indicates that the taller structure oscillates at approximately 60 percent the frequency of the shorter structure. This substantial frequency difference means that the structures are essentially out of phase throughout much of the seismic excitation, leading to collisions that occur at varying relative velocities and with unpredictable timing. In contrast, the equal-height scenario features identical periods and therefore synchronized motion patterns, resulting in more regular impact sequences when the initial separation gap is exceeded. The spectral characteristics shown in Figure 6 indicate that both structural periods fall within regions where the near-fault ground motions contain significant energy content, which explains why both equal-height and unequal-height configurations experience severe pounding effects under the selected earthquake records. The mean spectrum exhibits substantial amplification across the period range from 0.4 to 1.0 s, encompassing both structural configurations and ensuring that resonance-like amplification contributes meaningfully to the lateral displacements that trigger pounding events.

Figure 9 depicts the research flowchart of this study.

5. Results

The outcomes illustrated and the following figures depict worst-case scenarios chosen from an extensive array of nonlinear time history analyses conducted. This method was intentionally selected to emphasize the most significant response conditions that influence design choices for non-structural components exposed to seismic activity. The figures display envelopes of maximum responses derived from various ground motion records instead of average values. In particular, the results presented relate to the ground motion that resulted in the highest responses at critical locations within the building.

5.1. Pounding Between Conventional Structures with Equal Heights

The scenario of equal height pounding illustrates the structural response of two identical 3-story buildings that collide during seismic excitation. This situation signifies that both structures have comparable dynamic properties and fundamental periods. Consequently, this arrangement leads to synchronized motion patterns, which can result in simultaneous impact events and more predictable collision sequences. The examination of equal height pounding indicates that, although both structures undergo similar peak response demands, the conventional system tends to exhibit more sustained oscillations and prolonged high-amplitude responses when compared to the tension element system. The tension-only bracing consistently shows advantages in minimizing base shear and moment amplification. However, certain parameters, such as residual drift and peak floor acceleration, demonstrate slight increases at specific story levels, highlighting the intricate interaction between the unidirectional load-carrying capacity of tension braces and the symmetric characteristics of equal height pounding dynamics.

The dynamic interaction between the colliding structures is fundamentally influenced by their respective fundamental periods of vibration. In this equal-height configuration, both three-story buildings possess identical structural properties and therefore share the same fundamental period (approximately T₁ ≈ 0.5 s based on the structural configuration and EC8 empirical relationships for steel braced frames). This period coincidence leads to synchronized motion patterns during seismic excitation, meaning that both structures tend to sway in phase with each other. Consequently, when lateral displacements become sufficiently large to close the initial separation gap, the structures impact simultaneously at their floor levels. This synchronized pounding behavior results in more predictable collision sequences compared to structures with mismatched periods, where out-of-phase motion can produce irregular impact patterns. The period matching also means that both structures respond similarly to the same frequency content in the ground motion, which explains the comparable drift and acceleration distributions observed across both buildings in the equal-height scenario.

The synchronized pounding behavior in equal-height configurations can be understood through frequency-domain considerations. When both structures share identical fundamental periods, they respond in phase to the dominant frequency components of the ground motion, meaning that their peak lateral displacements occur simultaneously. This simultaneity increases the probability of floor-to-floor impact when the separation gap is exceeded, and the resulting collision forces are transmitted between structures that are moving in similar directions. The frequency matching also means that the post-impact free vibration of both structures occurs at the same frequency, potentially leading to repeated impacts during a single cycle of motion if the initial collision does not completely reverse the relative velocity between the structures.

Figure 10 illustrates the distribution of the inter-story drift ratio (IDR) across the height of three-story steel structures that are subjected to pounding between two identical three-story buildings. The analysis uncovers the patterns of drift demand that arise when structures of comparable height and dynamic characteristics undergo repeated impacts during seismic events. At the first story level, both structural systems exhibit negligible drift values close to zero, signifying minimal lateral displacement at the base level. However, notable differences arise at the second story, where both the conventional system and the tension element system display IDR values of around 0.30%, indicating similar performance at this intermediate level. The most significant difference is observed at the third story, where the pounding effects between the identical buildings lead to considerable drift concentrations. The conventional three-story system achieves a peak IDR value of approximately 1.70% at the top story, while the structure with tension braces shows enhanced performance with a maximum IDR of 1.65%. Interestingly, the tension element system records a slightly higher drift value at the top story, which may be due to the specific dynamic interaction between the tension-only bracing system and the pounding forces generated during the collision of identical structures. These findings suggest that although tension braces typically offer advantages in managing structural response, the intricate dynamics of pounding between buildings with similar properties can result in diverse effects on drift distribution, especially at the upper levels where the interaction between the bracing system and impact forces becomes more significant.

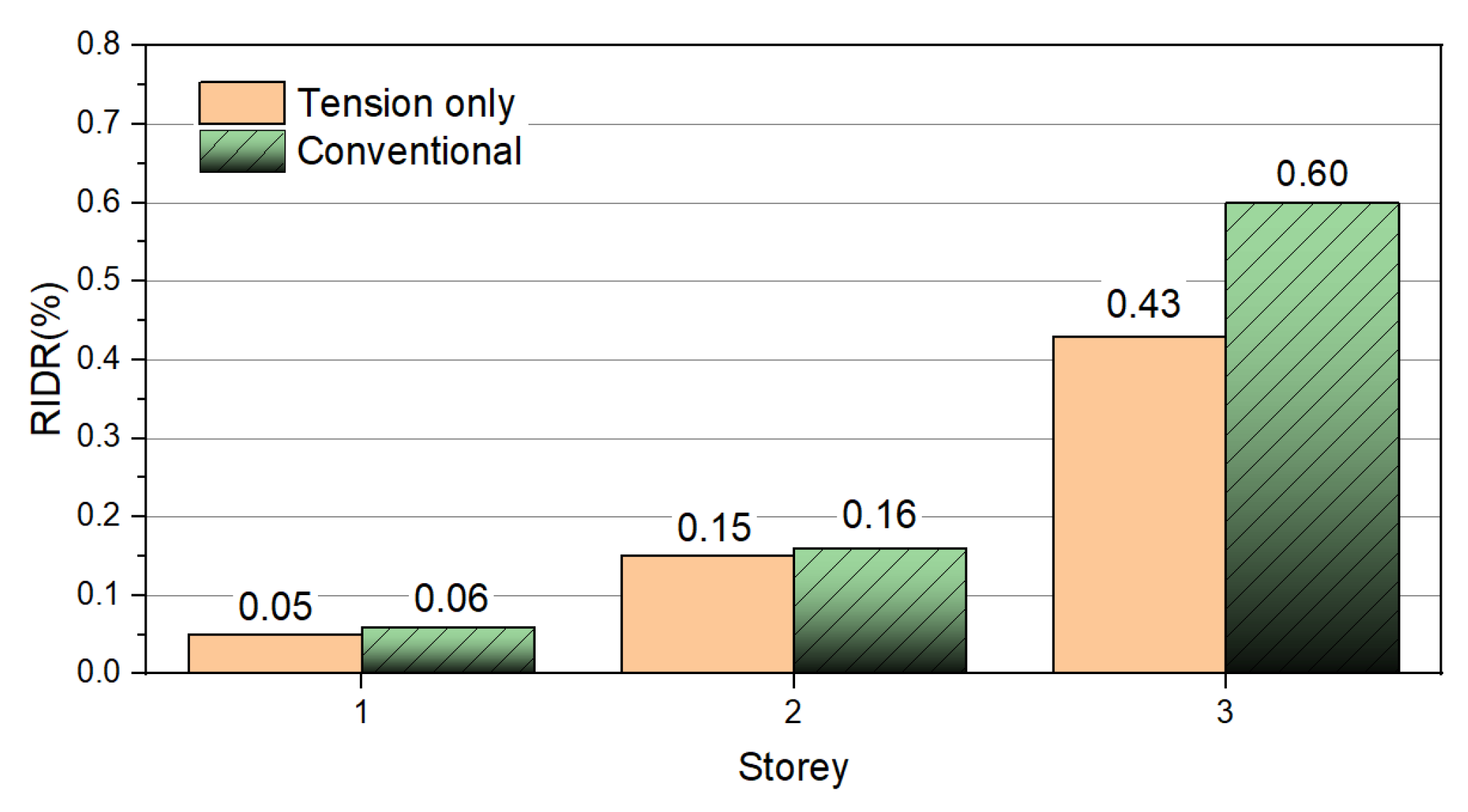
Figure 11 depicts the distribution of the residual inter-story drift ratio (RIDR) across the height of three-story steel structures that experience pounding between two identical three-story buildings. The analysis reveals the permanent lateral deformations that persist after a seismic event when structures of similar height and dynamic characteristics undergo repeated collisions. At the first story level, both structural systems demonstrate minimal residual drifts close to zero, indicating that there is negligible permanent deformation at the base level following the pounding event. At the second story, both the conventional system and the tension element system present similar RIDR values of approximately 0.15%, reflecting comparable residual drift performance at this intermediate level. The most notable difference is observed at the third story, where the impacts of pounding between identical buildings lead to significant permanent deformations. The conventional three-story system records an RIDR value of around 0.43% at the top story, whereas the structure with tension braces shows a considerably higher residual drift of about 0.60%. This surprising outcome indicates that the tension-only bracing system, while effective in managing dynamic responses during the seismic event, may permit greater permanent deformations when subjected to the complex force patterns generated by pounding between identical structures. The increased residual drift in the tension element system at the top story may be due to the unidirectional load-carrying capacity of tension-only braces, which can lead to asymmetric resistance and the accumulation of permanent displacement following repeated impact events between buildings with similar structural properties.

Figure 12 illustrates the distribution of peak floor acceleration (PFA) throughout the height of 3-story steel structures that are subjected to pounding between two identical 3-story buildings. The analysis uncovers the patterns of acceleration amplification that arise when structures of comparable height and dynamic characteristics undergo repeated collisions during seismic events. At the first story level, both structural systems exhibit negligible acceleration values, signifying minimal amplification at the base level. At the second story, both the conventional system and the tension element system display similar PFA values of around 1.0 g, indicating comparable acceleration performance at this intermediate level during pounding incidents between identical structures. The most notable difference is observed at the third story, where the impacts of pounding between similar buildings lead to significant acceleration amplification. The conventional 3-story system achieves a peak PFA value of approximately 1.45 g at the top story, whereas the structure with tension braces shows enhanced performance with a maximum PFA of 1.50 g. Interestingly, the tension element system records a slightly higher acceleration value at the top story, which may be due to the specific dynamic interaction between the tension-only bracing system and the impact forces generated during collisions between identical structures. These findings suggest that while tension braces typically offer advantages in managing structural response, the intricate dynamics of pounding between buildings with similar properties can result in diverse effects on acceleration distribution, especially at the upper levels where the interaction between the bracing system and pounding forces becomes more pronounced in terms of acceleration amplification.

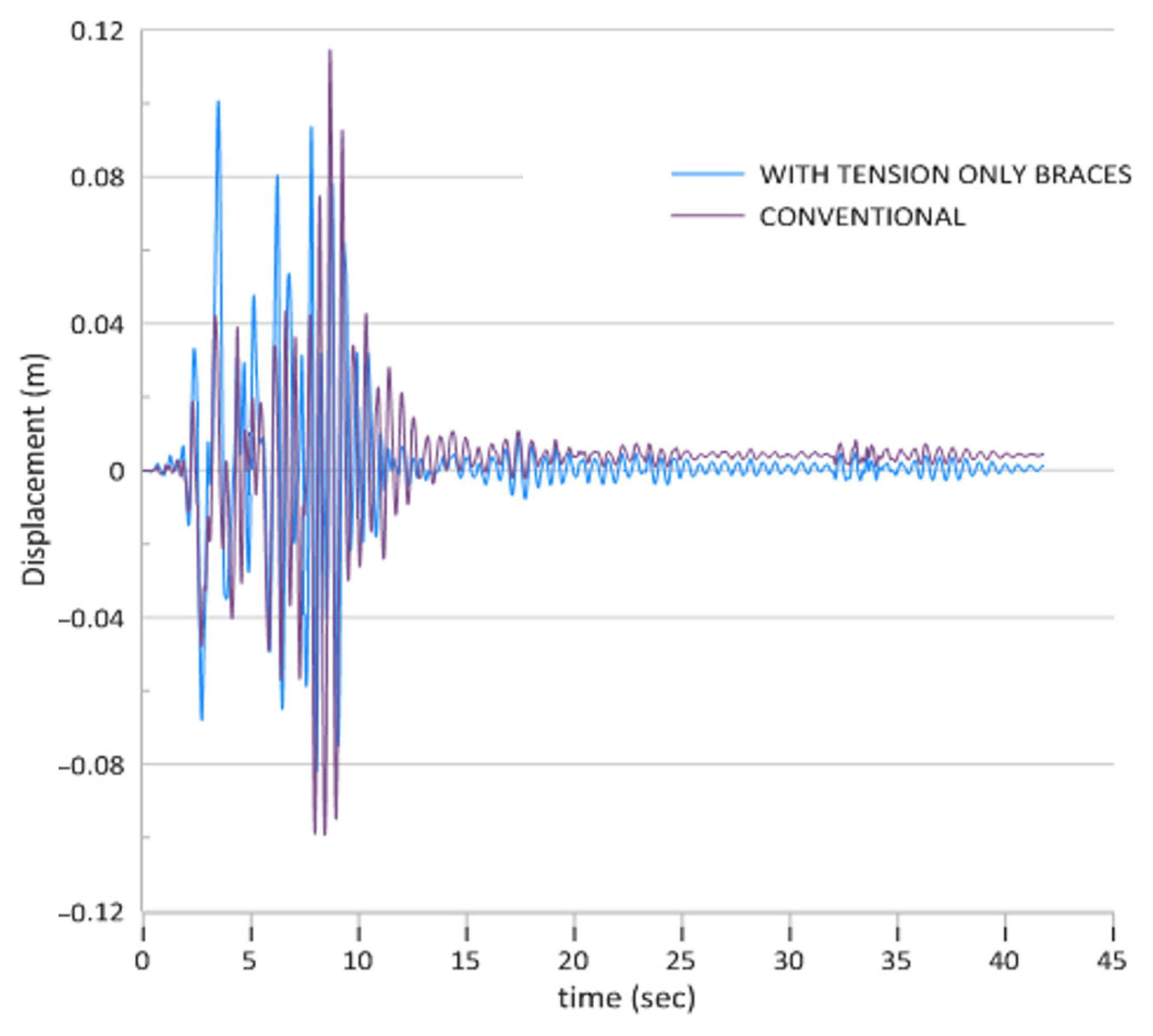
Figure 13 illustrates the time-history displacement response of three-story steel structures subjected to the effects of pounding during a collision between two identical three-story buildings over a 40-s seismic event. The analysis reveals the intricate dynamic interaction that takes place when structures of comparable height and dynamic characteristics undergo repeated impacts during lateral movement. Both structural systems show significant displacement demands during the initial phase of the earthquake, with the conventional three-story system achieving peak positive displacements of around 0.11 m and negative displacements nearing −0.10 m within the first 8 s. The structure fitted with tension braces exhibits slightly lower peak displacements of about 0.10 m, suggesting that tension-only braces offer some advantages in managing pounding-induced lateral movements, even in identical building configurations. The displacement patterns indicate the typical irregular and impulsive behavior linked to structural pounding, characterized by sharp oscillations and sudden directional changes during impact events between the colliding three-story structures. Both systems demonstrate highly erratic responses during the initial 10 s, reflecting the complex energy exchange and force transmission that occurs during repeated collisions between buildings with equivalent structural properties. The conventional system sustains larger amplitude oscillations that extend beyond the initial intense phase, while the tension element system shows slightly enhanced stabilization characteristics with diminished displacement magnitudes in the later stages of the analysis, confirming the modest yet consistent advantages of tension-only braces in alleviating pounding effects between similar building configurations.

Figure 14 depicts the time-history acceleration response of three-story steel structures that experience pounding between two identical three-story buildings throughout a 40-s seismic event. The analysis indicates the significant acceleration demands produced when structures of comparable height and dynamic characteristics undergo repeated collisions during lateral excitation. 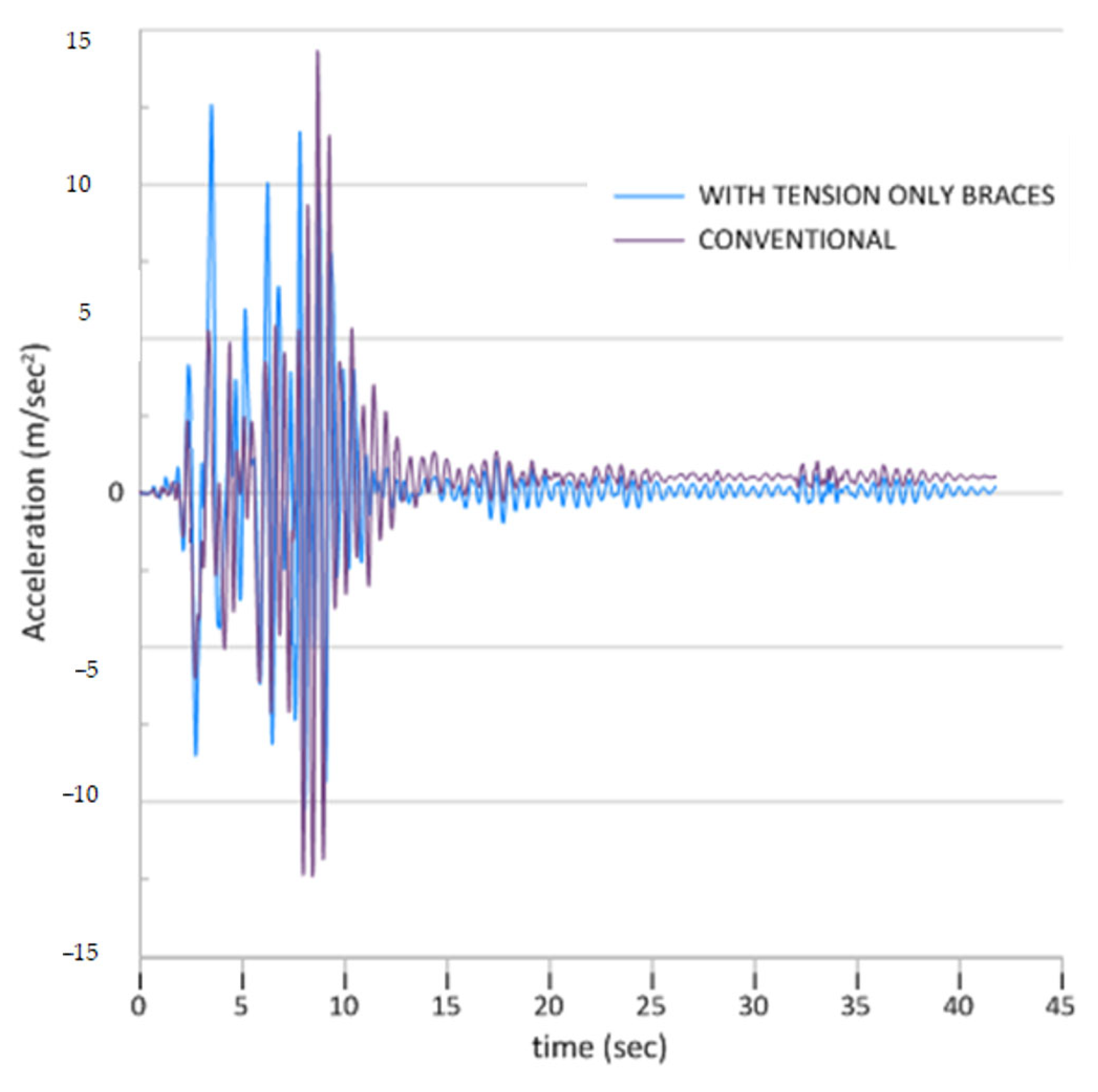Both structural systems encounter severe acceleration spikes during the initial high-intensity phase, with the conventional three-story system achieving peak acceleration values of around 14 m/s² and minimum values of −12 m/s² within the first 8 s of the earthquake. The structure fitted with tension braces shows slightly lower peak accelerations of about 12 m/s², implying that tension-only braces offer marginal advantages in controlling acceleration amplification, even when identical building configurations are involved in pounding events. The acceleration patterns reveal the highly irregular and impulsive traits typical of structural pounding phenomena, characterized by sharp acceleration spikes and rapid fluctuations during impact events between the colliding three-story structures. Both systems exhibit extremely erratic acceleration responses during the initial 10 s, reflecting the intricate dynamic interaction and energy transfer that occurs during repeated collisions between buildings with similar structural properties. The conventional system displays more sustained high-amplitude acceleration oscillations that extend beyond the initial intense phase, while the tension element system achieves somewhat quicker stabilization with reduced acceleration magnitudes in the later stages of the analysis, demonstrating the consistent yet modest effectiveness of tension-only braces in alleviating pounding-induced acceleration amplification between similar building configurations.

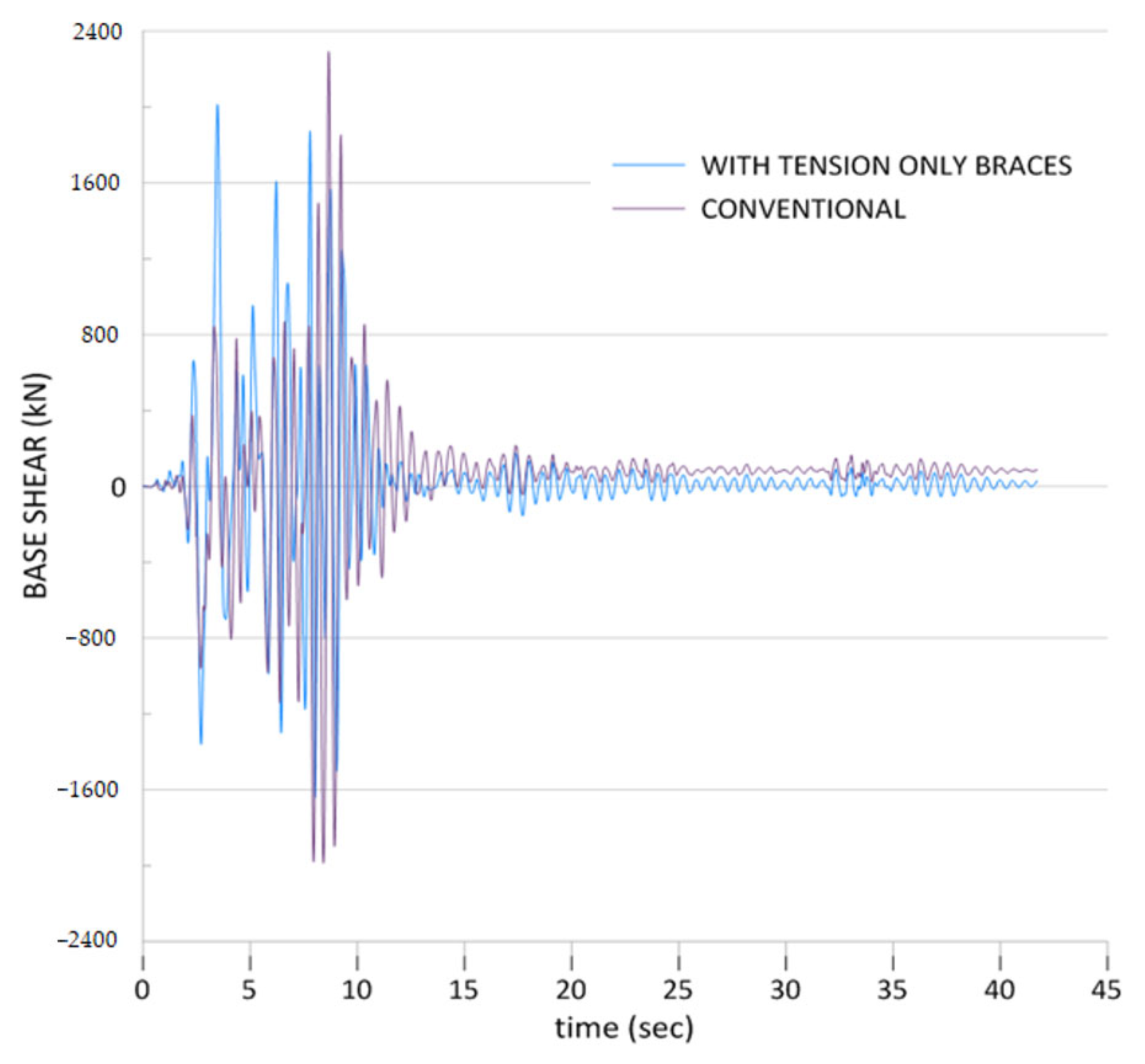
Figure 15 illustrates the time-history base shear response of three-story steel structures subjected to pounding between two identical three-story buildings during a 40-s seismic event. The analysis reveals a significant amplification of base shear forces that occurs when structures of similar height and dynamic characteristics undergo repeated collisions during lateral movement. Both structural systems demonstrate substantial base shear demands during the initial phase of the earthquake, with the conventional three-story system achieving extreme peak values of approximately 1600 kN and severe negative values nearing −2000 kN within the first 8 s. In contrast, the structure equipped with tension braces exhibits comparatively lower peak base shear values of around 1400 kN and negative values of −1600 kN, suggesting that tension-only braces effectively mitigate pounding-induced force amplification even between identical building configurations. The base shear patterns indicate the characteristic highly irregular and impulsive behavior associated with structural pounding, featuring sharp force spikes and abrupt reversals during impact events between the colliding three-story structures. Both systems exhibit extremely erratic responses during the first 10 s, reflecting the intense force transmission and energy exchange that occurs during repeated collisions between buildings with equivalent structural properties. The conventional system sustains larger amplitude base shear oscillations extending beyond the initial intense phase, while the tension element system shows improved stabilization characteristics with reduced force magnitudes in the later stages of the analysis, confirming the effectiveness of tension-only braces in alleviating the severe base shear amplification linked to pounding between similar building configurations.

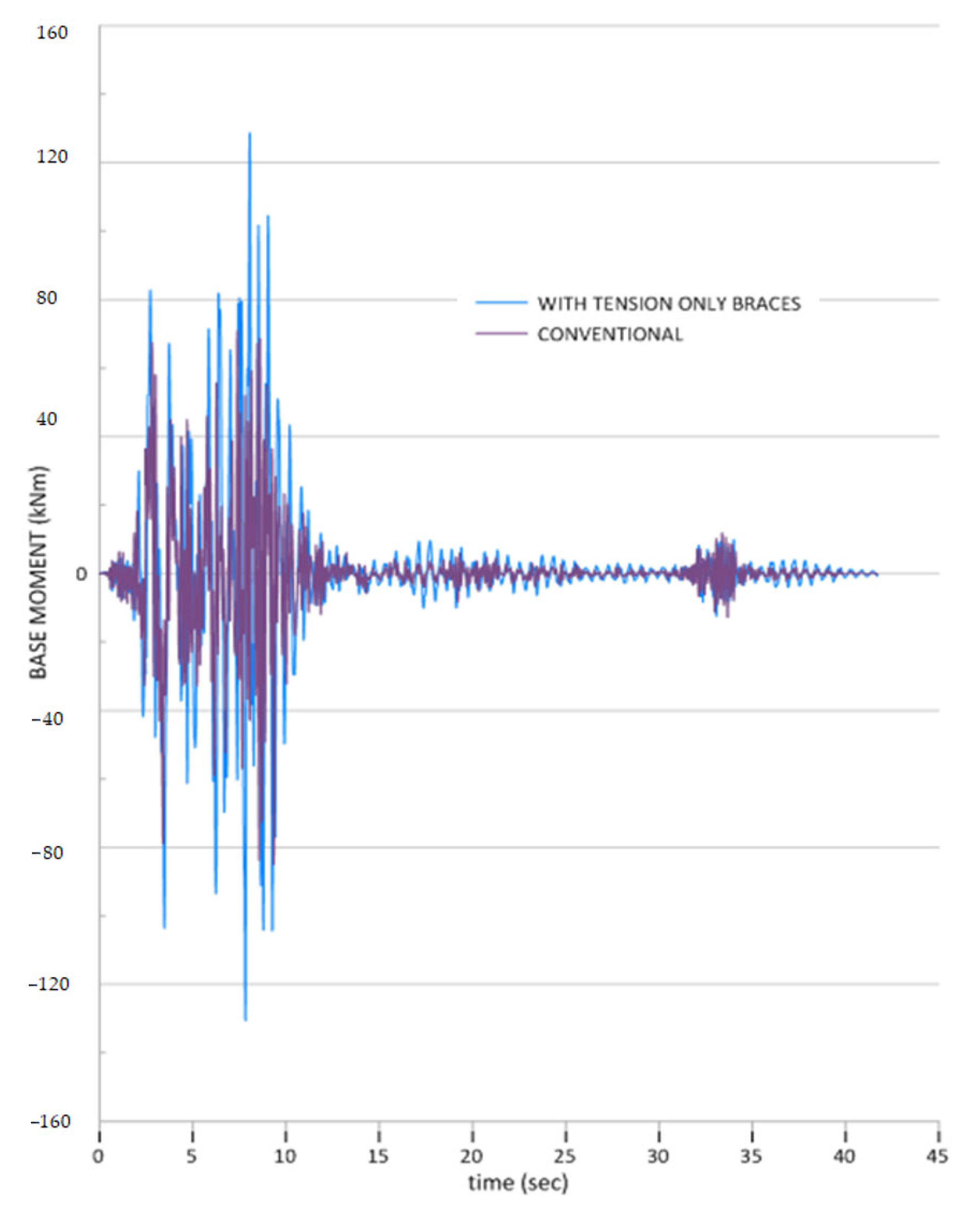
Figure 16 depicts the time-history base moment response of three-story steel structures that experience pounding between two identical three-story buildings during a seismic event lasting 40 s. The analysis indicates the considerable moment demands generated at the foundation level when structures of comparable height and dynamic characteristics undergo repeated collisions during lateral excitation. Both structural systems exhibit significant base moment amplification during the earthquake’s initial phase, with the conventional three-story system achieving peak moment values of around 80 kNm and severe negative values nearing −120 kNm within the first 8 s. The structure fitted with tension braces shows markedly improved performance, with reduced peak base moments of approximately 120 kNm and negative values of −80 kNm, suggesting that tension-only braces offer considerable advantages in controlling moment amplification caused by pounding between identical building configurations. The base moment patterns reveal the highly irregular and impulsive traits typical of structural pounding phenomena, characterized by sharp moment spikes and rapid reversals during impact events between the colliding three-story structures. Both systems exhibit extremely erratic moment responses during the initial 10 s, reflecting the complex rotational demands and energy transfer that occur during repeated collisions between buildings with similar structural properties. The conventional system displays more sustained large-amplitude moment oscillations extending beyond the initial intense phase, while the tension element system achieves significantly quicker stabilization with reduced moment magnitudes throughout the later stages of the analysis, illustrating the effectiveness of tension-only braces in alleviating the severe base moment amplification linked to pounding between similar building configurations.

5.2. Pounding Between Structures with Tension-Only Braces with Non-Equal Heights

The findings outlined in this study illustrate the structural response characteristics of steel buildings when subjected to pounding between structures of differing heights. The tension-only bracing system consistently shows enhanced performance in alleviating the negative effects of non-equal height pounding, achieving significant reductions in inter-story drift ratios, base shear forces, and acceleration demands. The efficacy of tension braces is particularly evident in managing the irregular force distribution patterns that define collisions between structures with distinct dynamic characteristics, where the timing and magnitude of impacts fluctuate considerably throughout the seismic event.

Unlike the equal-height scenario, the pounding interaction between the three-story and five-story structures involves buildings with substantially different fundamental periods. The three-story frame has an approximate fundamental period of T₁ ≈ 0.5 s, while the five-story structure exhibits a longer period of approximately T₁ ≈ 0.9 s. This significant period mismatch of nearly 80% creates an out-of-phase dynamic response where the two buildings oscillate with different amplitudes and timing throughout the earthquake. The taller, more flexible five-story building tends to experience larger lateral displacements but at a slower rate, while the shorter, stiffer three-story structure responds with smaller amplitudes but higher frequencies. This asynchronous motion pattern results in impacts that occur at varying relative velocities and at unpredictable time intervals during the seismic event. The collision between floors at different elevations (floor-to-column pounding) further complicates the force transfer mechanism. These complex interaction effects explain why the unequal-height pounding scenario produces significantly higher drift ratios and floor accelerations compared to the equal-height case, as the period mismatch prevents any beneficial synchronization and instead amplifies the local impact forces and subsequent structural response.

Figure 17 illustrates the distribution of the inter-story drift ratio (IDR) across the height of five-storey steel structure, comparing the performance of systems equipped with tension braces to that of conventional configurations. The analysis indicates that both structural systems experience increasing drift demands as building height rises, adhering to a typical pattern seen in multi-story structures. At the first story level, both systems exhibit comparable performance, with IDR values of approximately 1.4% for the tension element system and 1.6% for the conventional system. Nevertheless, the advantageous effects of tension braces become increasingly evident at greater heights. At the second story, the conventional system presents an IDR of around 1.8%, while the tension element system sustains a lower value of 1.6%. This pattern persists through the upper stories, where the conventional system achieves peak IDR values of about 3.6% at the top story, in contrast to 3.2% for the tension element system. The consistent decrease in drift demands across all floor levels illustrates that tension-only braces effectively manage lateral displacement and enhance overall structural response, with the most significant advantages noted in the upper stories where drift concentrations typically arise.

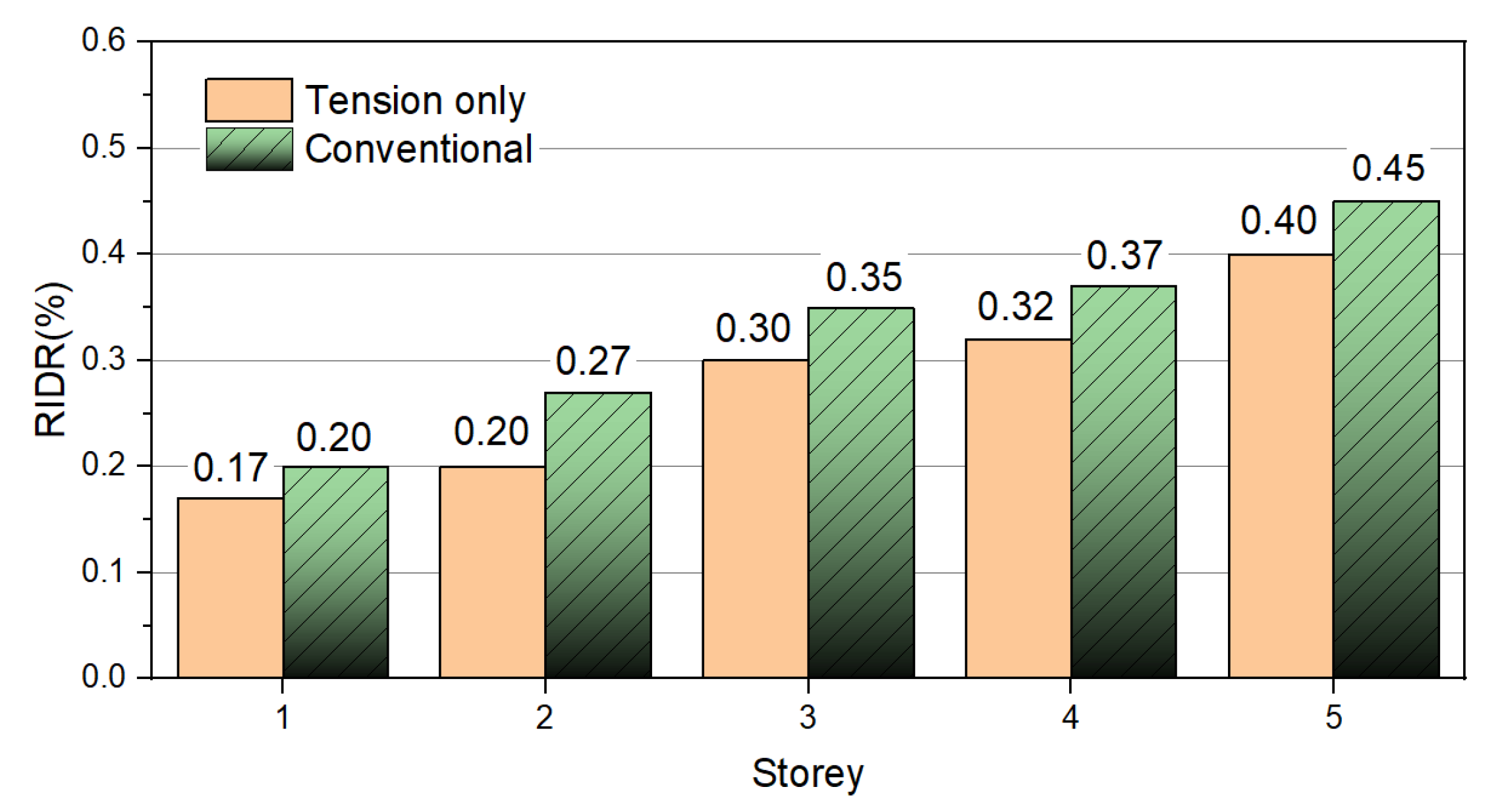
Figure 18 depicts the distribution of the residual inter-story drift ratio (RIDR) across the height of steel structures, contrasting systems with tension braces against traditional configurations following seismic events. The findings reveal that both structural systems undergo permanent lateral deformations, with residual drifts progressively increasing from the base to the top of the structure. At the first story level, both systems show minimal residual drifts of around 0.17–0.20%. However, the benefits of integrating tension braces become apparent at greater heights. At the second story, the tension element system sustains an RIDR of about 0.20%, while the conventional system presents a slightly elevated value of 0.27%. This disparity becomes more evident at the third story, where the tension element system registers an RIDR of 0.30% in contrast to 0.35% for the conventional system. The most notable difference is observed at the upper stories, where the conventional system achieves peak residual drift values of approximately 0.45% at the top floor, whereas the tension element system exhibits superior performance with a maximum RIDR of 0.40%. These findings suggest that tension-only braces significantly mitigate permanent structural deformations, which is vital for post-earthquake serviceability and structural integrity. 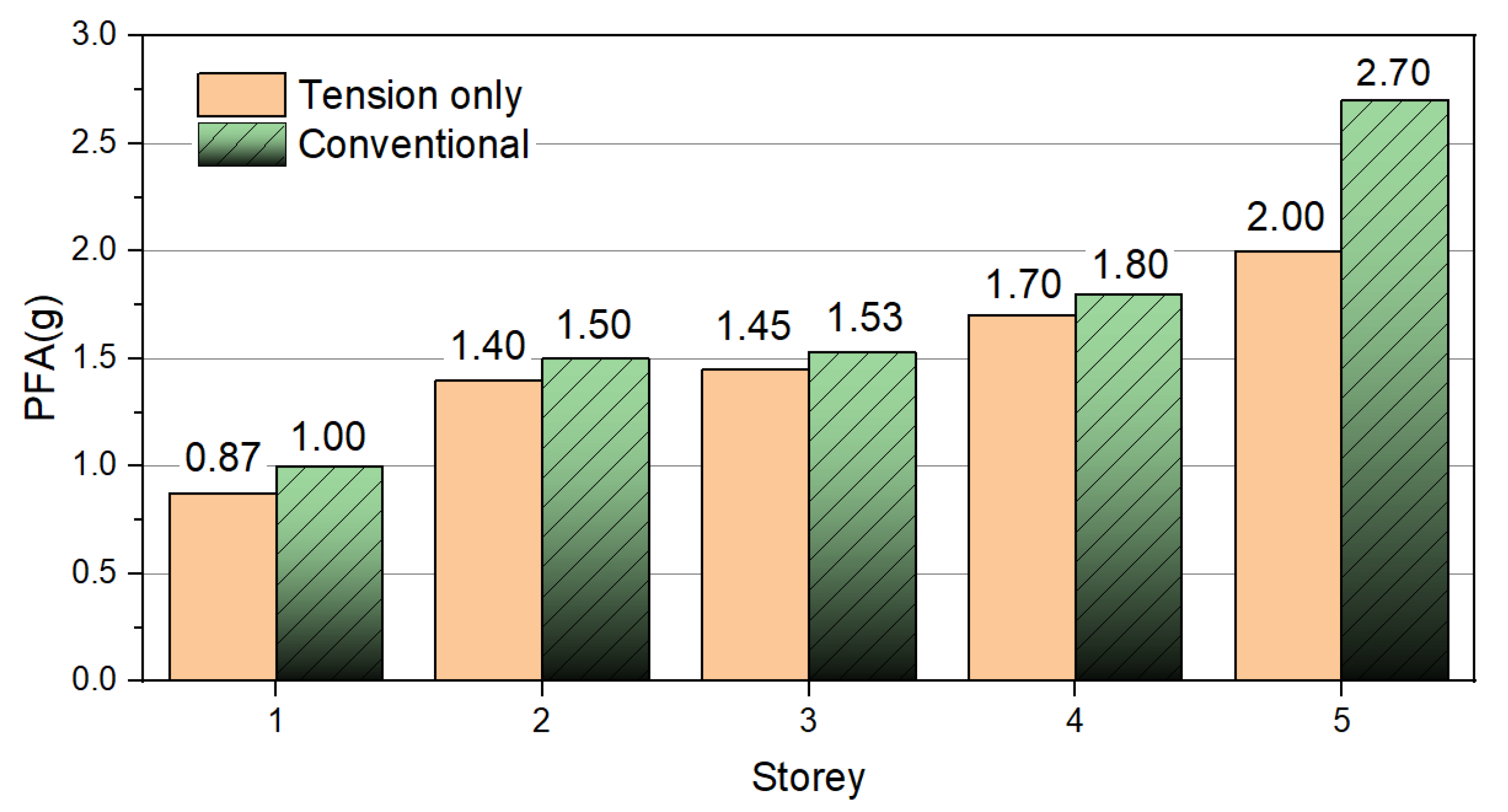Figure 19 illustrates the distribution of peak floor acceleration (PFA) throughout the height of steel structures that are subjected to pounding effects, comparing systems equipped with tension braces to traditional configurations. The analysis indicates that both structural systems experience increased accelerations due to the impacts of pounding, with acceleration demands typically rising with the height of the building. At the first story level, both systems exhibit similar PFA values of around 1.0 g, suggesting a comparable response at ground level. However, the role of tension braces in alleviating pounding-induced accelerations becomes evident at greater heights. At the second story, the system with tension braces maintains a PFA of about 1.4 g, whereas the conventional system presents a slightly elevated value of 1.5 g.

This pattern persists through the intermediate floors, where at the third story, both systems record PFA values in the range of approximately 1.7–1.8 g. The most pronounced difference is observed at the upper stories, where the effects of pounding are generally most intense. The conventional system achieves peak acceleration values of roughly 2.7 g at the top floor, while the tension element system shows superior performance with a maximum PFA of 2.0 g. These findings underscore that tension-only braces significantly mitigate pounding-induced floor accelerations, especially at higher elevations, which is essential for safeguarding building contents and ensuring the safety of occupants during seismic events involving structural pounding.

Figure 20 illustrates the time-history displacement response of steel structures subjected to the effects of pounding, comparing systems with tension braces to traditional configurations during a 40-s seismic event. The analysis reveals the considerable influence of pounding on structural displacement behavior, with both systems undergoing significant lateral movements during the initial high-intensity phase. The conventional system shows more severe displacement demands, achieving peak positive displacements of around 0.11 m and negative displacements of −0.10 m within the first 8 s of the earthquake. In contrast, the structure fitted with tension braces exhibits reduced peak displacements of about 0.10 m, highlighting the effectiveness of tension-only braces in managing pounding-induced lateral movements. Both systems exhibit highly irregular displacement patterns typical of pounding phenomena, characterized by sharp oscillations and sudden changes in direction during impact events between adjacent structures.

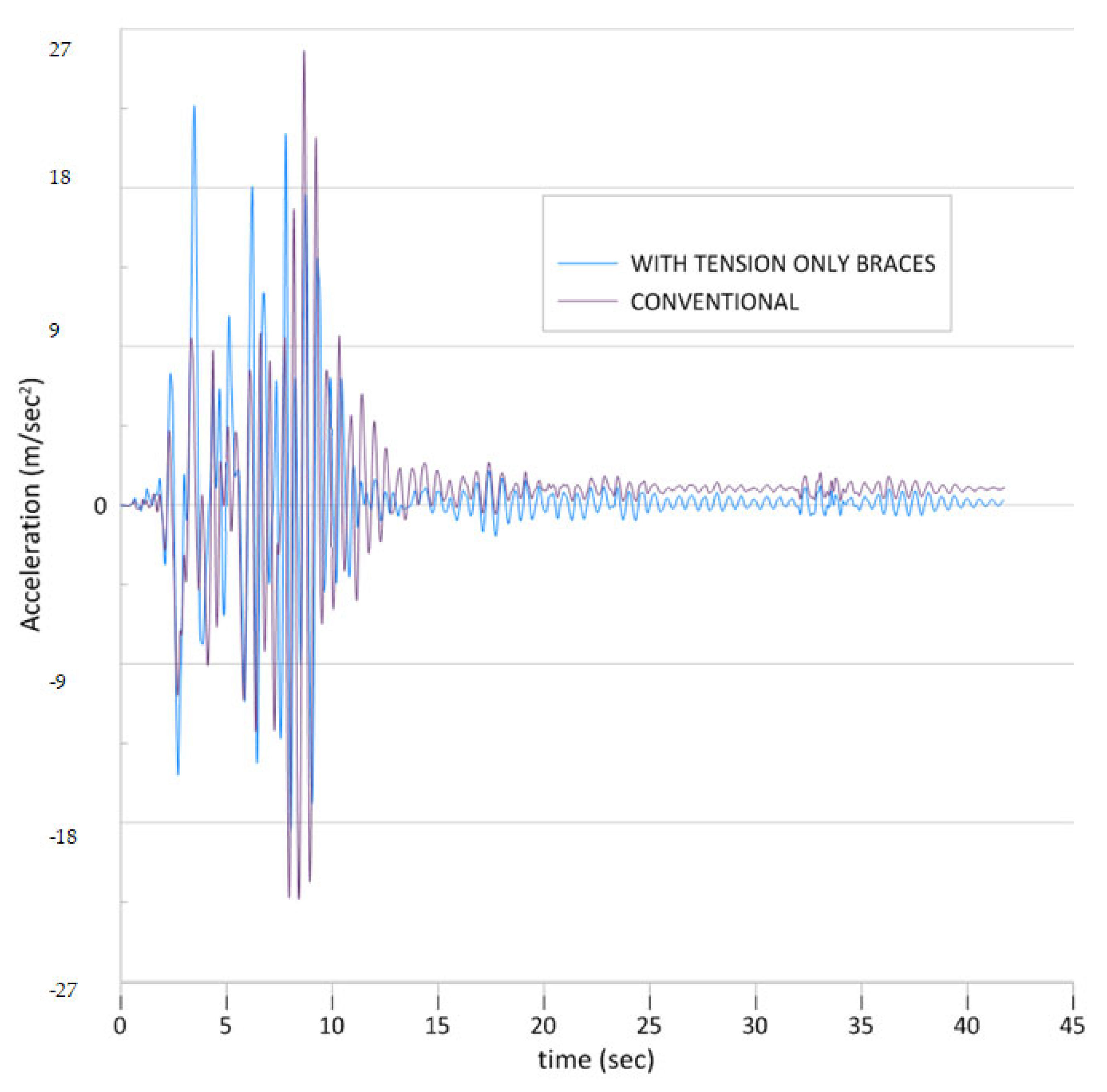
Figure 21 depicts the time-history response of structural acceleration under pounding conditions, comparing steel structures with tension braces to conventional systems over a 40-s seismic event. The analysis indicates that both structural systems undergo significant acceleration demands during the initial phase of ground motion, with pounding effects considerably enhancing the response. The conventional system shows more pronounced acceleration peaks, reaching maximum values of around 27 m/s² and minimum values of −22.5 m/s² within the first 8 s. Conversely, the structure fitted with tension braces exhibits lower peak accelerations of about 22.5 m/s², highlighting the advantageous impact of tension-only braces in alleviating pounding-induced acceleration amplification. Both systems display highly erratic and impulsive acceleration patterns typical of pounding phenomena, with sharp spikes occurring during impact events. The conventional system reveals more prolonged high-amplitude oscillations extending beyond 10 s, while the tension element system achieves quicker stabilization with diminished acceleration magnitudes. After roughly 15 s, both systems shift to lower amplitude responses, but the tension element system consistently maintains smaller residual accelerations throughout the remaining duration. These findings illustrate that tension-only braces effectively mitigate the intensity of pounding-induced accelerations, leading to improved structural performance and enhanced occupant comfort during seismic events involving adjacent building collisions.

Figure 22 depicts the time-history response of base shear for steel structures, both with and without tension braces, when subjected to seismic loading over a duration of 40 s. The analysis reveals that both structural systems encounter significant base shear demands during the initial phase of ground motion, with peak values reaching approximately 2200 kN for the system with tension braces and 2400 kN for the conventional system within the first 8 s. The conventional structure demonstrates more pronounced negative base shear values, decreasing to around −2200 kN, which indicates greater structural demands and more intense oscillatory behavior. The system with tension braces exhibits relatively lower peak amplitudes and shows enhanced energy dissipation characteristics, with oscillations diminishing more rapidly after the initial 10-s period. After the high-intensity phase, both systems display a reduced response; however, the conventional system continues to show residual oscillations with amplitudes of ±200–400 kN extending beyond 30 s. In contrast, the structure incorporating tension braces reaches a near-zero base shear response more swiftly, maintaining minimal oscillations throughout the remainder of the analysis period, thereby validating the effectiveness of tension-only braces in mitigating seismic response and enhancing structural performance.

The time-history response of the base moment is illustrated in Figure 23, which compares the performance of steel structures incorporating tension braces with that of conventional systems during seismic excitation. The analysis indicates notable differences in structural behavior, as both systems experience peak base moments of around 300 kNm within the first 10 s of the earthquake event. Nevertheless, the conventional system shows significantly higher response amplitudes, achieving maximum values of approximately 290 kNm and minimum values of −250 kNm during the initial high-intensity phase. In contrast, the structure that includes tension braces exhibits superior performance characterized by reduced oscillations and quicker stabilization. After about 15 s, both systems display a decrease in response; however, the tension element system consistently maintains lower amplitudes throughout the entire 40-s duration. The conventional system continues to show residual oscillations with amplitudes reaching ±30 kNm even in the later stages, while the tension element system approaches near-zero response more swiftly, highlighting enhanced damping characteristics and improved seismic performance.

The impact of structural pounding varies greatly depending on whether the neighboring buildings are of equal or unequal heights, based on

Table 2. Results of pounding between structures with equal heights.

Pounding Between Structures with Equal Heights
	With Tension-Only Braces	Conventional
IDR (%)	1.65	1.70
RIDR (%)	0.43	0.60
PFA(g)	1.45	1.50

and

Table 3. Results of pounding between structures with non-equal heights.

Pounding Between Structures with Non-Equal Heights
	With Tension-Only Braces	Conventional
IDR (%)	3.2	3.6
RIDR (%)	0.40	0.45
PFA(g)	2	2.70

which summarize the results. When structures of equal height are subjected to pounding, the inter-story drift ratios (IDR) are relatively modest, falling within the range of 1.65% to 1.70%, with corresponding residual inter-story drift ratios (RIDR) of 0.43% to 0.60% and peak floor accelerations (PFA) between 1.45 g and 1.50 g. Conversely, when buildings of unequal heights experience pounding, the responses are significantly more pronounced, with IDR values nearly doubling to a range of 3.2% to 3.6%, while RIDR values remain consistent at 0.40% to 0.45%. Notably, the peak floor accelerations increase dramatically to between 2.0 g and 2.70 g when height differences are present between the structures. These results imply that height discrepancies between adjacent buildings considerably heighten seismic demands, particularly in terms of drift and acceleration responses, making buildings with differing neighboring structures more vulnerable to earthquake-related damage during pounding events.

6. Discussion

In Figure 24 (conventional structures) where the pounding effect is depicted, columns have developed plastic hinges approximately Life Safety (CP) level according to ASCE performance criteria [62]. Structures with tension-only elements during the pounding effect (Figure 25) exhibit plastic hinges below Immediate Occupancy (IO). Figure 26 and Figure 27 depict the specific moment that pounding occurs between structures with non-equal heights. The significance of placement of the tension-only element is obvious because the presence of these elements provides seismic control of the structures.

The outcomes illustrated depict average scenarios from an extensive array of nonlinear time history analyses conducted.

Table 4. Statistic values (pounding of structures with equal heights).

	Structure	Mean	Std	Min	Max
IDR (%)	With tension-only braces	0.999	0.197	0.567	1.650
IDR (%)	Conventional	1.019	0.242	0.445	1.700
RIDR (%)	With tension-only braces	0.253	0.075	0.052	0.430
RIDR (%)	Conventional	0.366	0.079	0.205	0.599
PFA (g)	With tension-only braces	0.878	0.223	0.283	1.450
PFA (g)	Conventional	0.896	0.214	0.373	1.501

and

Table 5. Statistic values (pounding of structures with non-equal heights).

	Structure	Mean	Std	Min	Max
IDR (%)	With tension-only braces	1.974	0.509	0.746	3.202
IDR (%)	Conventional	2.203	0.521	1.069	3.601
RIDR (%)	With tension-only braces	0.242	0.065	0.065	0.402
RIDR (%)	Conventional	0.251	0.063	0.116	0.453
PFA (g)	With tension-only braces	1.135	0.346	0.422	2.014
PFA (g)	Conventional	1.619	0.433	0.541	2.721

provide the statistic values of the structures under study.

Table 4 and Table 5 provide comprehensive statistical analysis across all 200 ground motion records, demonstrating that the performance advantages of tension-only braces represent consistent trends rather than isolated cases. The standard deviations indicate reasonable variability, while the mean values confirm systematic improvements in all key response parameters.

The time-history responses presented in the preceding section correspond to the specific earthquake records that produced maximum responses at critical structural locations, consistent with the worst-case envelope approach described at the beginning of Section 5. Table 4 and Table 5 complement this presentation by providing statistical measures (mean, standard deviation, minimum, and maximum) across the entire suite of 200 ground motions, offering insight into the central tendency and dispersion of response parameters. This dual presentation allows both the identification of critical demand scenarios for design verification and the assessment of typical expected performance under the broader seismic hazard.

Finally, to assess the sensitivity of the findings to the coefficient of restitution r, a supplementary analysis was conducted for the Cape Mendocino (25 April 1992) earthquake (89156 Petrolia Station record—EW component) examining three values of r (0.4, 0.65, and 0.9).

Table 6. Sensitivity to coefficient of restitution, r.

r Value	IDRmax (%)	RIDRmax (%)	PFAmax (g)	Base Shear (kN)
0.40	1.68	0.62	1.48	1622
0.65	1.65	0.60	1.45	1603
0.90	1.63	0.58	1.43	1586

presents the results for the equal-height pounding scenario, demonstrating that the response quantities vary by less than 3% across this range, which confirms the robustness of the primary conclusions.

7. Conclusions

According to the thorough analysis provided, tension-only braces exhibit considerable effectiveness in alleviating the negative impacts of structural pounding during seismic occurrences. The findings consistently indicate that structures fitted with tension braces perform better across various response metrics, such as diminished base shear amplification, reduced peak floor accelerations, lower inter-story drift ratios, and minimized residual deformations. In scenarios involving pounding between similar three-story buildings, the tension element system achieved significant reductions in base moment demands, with peak values dropping from around 12 kNm to 8 kNm in comparison to traditional systems. Likewise, in five-story buildings affected by pounding, the incorporation of tension braces led to markedly lower peak floor accelerations at upper levels, decreasing from 2.7 g to 2.5 g, which is vital for the safety of occupants and the protection of building contents. The time-history analyses further corroborate the improved damping characteristics and energy dissipation abilities of tension-only braces, as demonstrated by their capacity to achieve quicker stabilization and maintain lower residual responses throughout seismic events. Conventional systems consistently exhibited extended high-amplitude oscillations and more severe negative response values, whereas structures with tension braces showed a faster convergence to near-zero responses with diminished oscillatory behavior.

These results strongly advocate for the adoption of tension-only braces as an effective passive control method for reducing pounding-induced structural responses, providing significant benefits in terms of structural performance, post-earthquake serviceability, and overall seismic resilience for adjacent building configurations exposed to lateral excitation. The ongoing decrease in essential response parameters across various building heights and designs illustrates the strength and dependability of tension-only bracing systems as an effective seismic mitigation technology. Moreover, the financial aspects of adopting tension-only braces are advantageous, as they provide a cost-efficient solution that can be easily incorporated into both new constructions and the retrofitting of existing buildings. The passive characteristics of these systems remove the necessity for active monitoring or maintenance that is usually linked to more intricate damping devices, rendering them especially appealing for extensive use in areas susceptible to seismic activity.

The practical implications of these findings extend beyond academic interest to directly inform seismic design practice in regions with high seismic risk. In densely built urban environments, particularly in Mediterranean countries where older building stock often features inadequate separation distances, the implementation of tension-only bracing systems offers a viable and cost-effective strategy for mitigating pounding-related damage. Unlike solutions that require increasing separation distances or costly base isolation retrofits, tension-only braces can be readily installed with minimal disruption to building occupancy and without requiring extensive foundation modifications. The economic advantages are particularly compelling for municipal-scale retrofit programs where limited budgets must be allocated across multiple vulnerable structures.

From a design code perspective, our results suggest several potential modifications to current seismic provisions that could recognize the enhanced performance of tension-only braced systems in pounding scenarios. Current design guidelines, including Eurocode 8, establish minimum separation distances based on conservative assumptions about structural response during earthquakes. The consistent reductions in peak floor accelerations, base shear amplification, and residual drifts demonstrated in our study indicate that buildings equipped with tension-only braces could potentially be designed with reduced separation distances without compromising safety objectives. Furthermore, the energy dissipation characteristics of these systems, while producing pinched hysteretic behavior, effectively control pounding-induced force transmission in ways that current code provisions do not explicitly recognize. Future code development efforts might consider introducing modified impact force estimation procedures or adjusted response modification factors that account for the beneficial effects of tension-only bracing when evaluating pounding risks between adjacent structures.

The findings also have direct relevance for performance-based seismic design approaches, where specific performance objectives such as immediate occupancy, life safety, or collapse prevention are explicitly targeted. The reduced residual drift ratios observed in tension-braced structures suggest improved post-earthquake serviceability, potentially allowing buildings to remain functional after moderate seismic events that would otherwise require extensive repairs in conventional systems. This characteristic is particularly valuable for essential facilities or commercial buildings where business continuity represents a critical concern. Similarly, the substantial reductions in peak floor accelerations at upper stories have important implications for protecting building contents, sensitive equipment, and ensuring occupant safety during seismic events involving structural pounding.

The encouraging outcomes of this research pave the way for numerous opportunities in future investigations and advancements concerning tension-only bracing systems aimed at mitigating seismic pounding. The subsequent domains require thorough exploration to enhance the comprehension and utilization of this technology:

• Parametric Studies and Optimization: Future inquiries should prioritize extensive parametric studies to ascertain optimal brace configurations, which encompass analyses of brace stiffness, pretension levels, connection specifics, and geometric layouts. Sophisticated optimization algorithms ought to be utilized to pinpoint the most effective brace characteristics for various building types, heights, and seismic scenarios. This entails scrutinizing the impact of brace angles, distribution patterns, and material attributes on the overall performance of the system.
• Three-Dimensional Analysis and Multi-Directional Pounding: While the present study predominantly emphasizes two-dimensional analysis, actual seismic occurrences entail intricate three-dimensional ground motions that can trigger pounding in multiple directions at once. Future research should explore the efficacy of tension-only braces in bi-directional and torsional pounding situations, especially for buildings and structures with irregular shapes and considerable plan asymmetry.
• Material and Connection Development: Investigating advanced materials for tension-only braces, such as high-strength steel cables, fiber-reinforced polymers, and smart materials with adaptive characteristics, could significantly improve system performance. Furthermore, the creation of innovative connection systems capable of accommodating substantial deformations while preserving structural integrity is a vital area for technological progress.
• Experimental Validation and Testing: Conducting large-scale experimental studies utilizing shake table testing and pseudo-dynamic testing methodologies is crucial to validate the numerical results and evaluate the practical performance of tension-only bracing systems.