A Fuzzy Rule-Based Decision Support in Process Mining: Turning Diagnostics into Prescriptions
Abstract
1. Introduction
- Baseline performance indicators are established through statistical analysis.
- Diagnostic insight into bottlenecks, inefficiencies, and deviations is supplied through process mining.
- Actionable prescriptions for managerial decision-making are produced through fuzzy rule-based reasoning.
2. Literature Review
- IF ticket waiting time has more than 8 h and resource utilization is above 95 percent, then assign more service agents.
- IF there is a high process deviation and a low level of throughput rate THEN develop a re-assessment of the workflow.
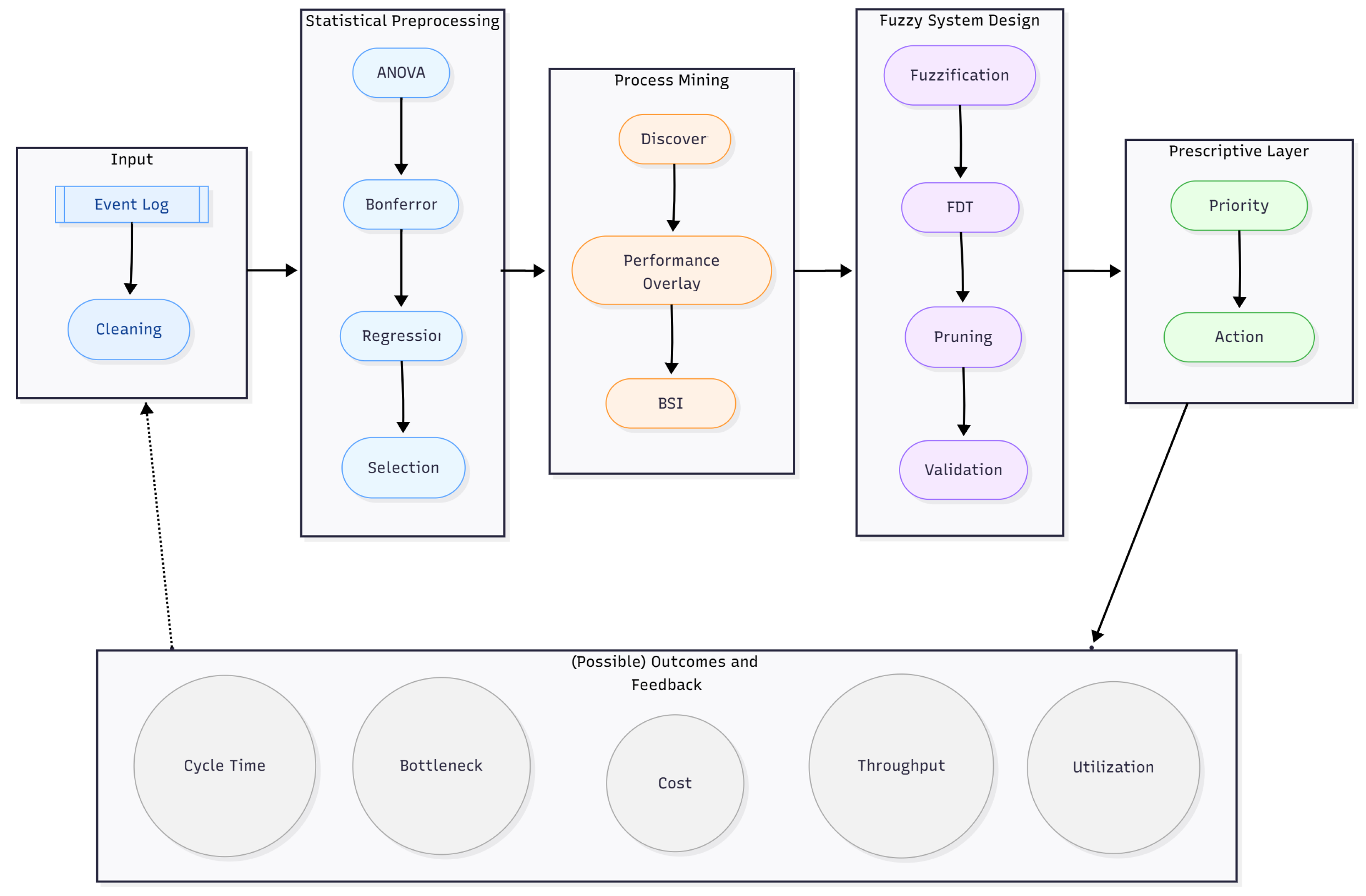
3. Methodological Framework
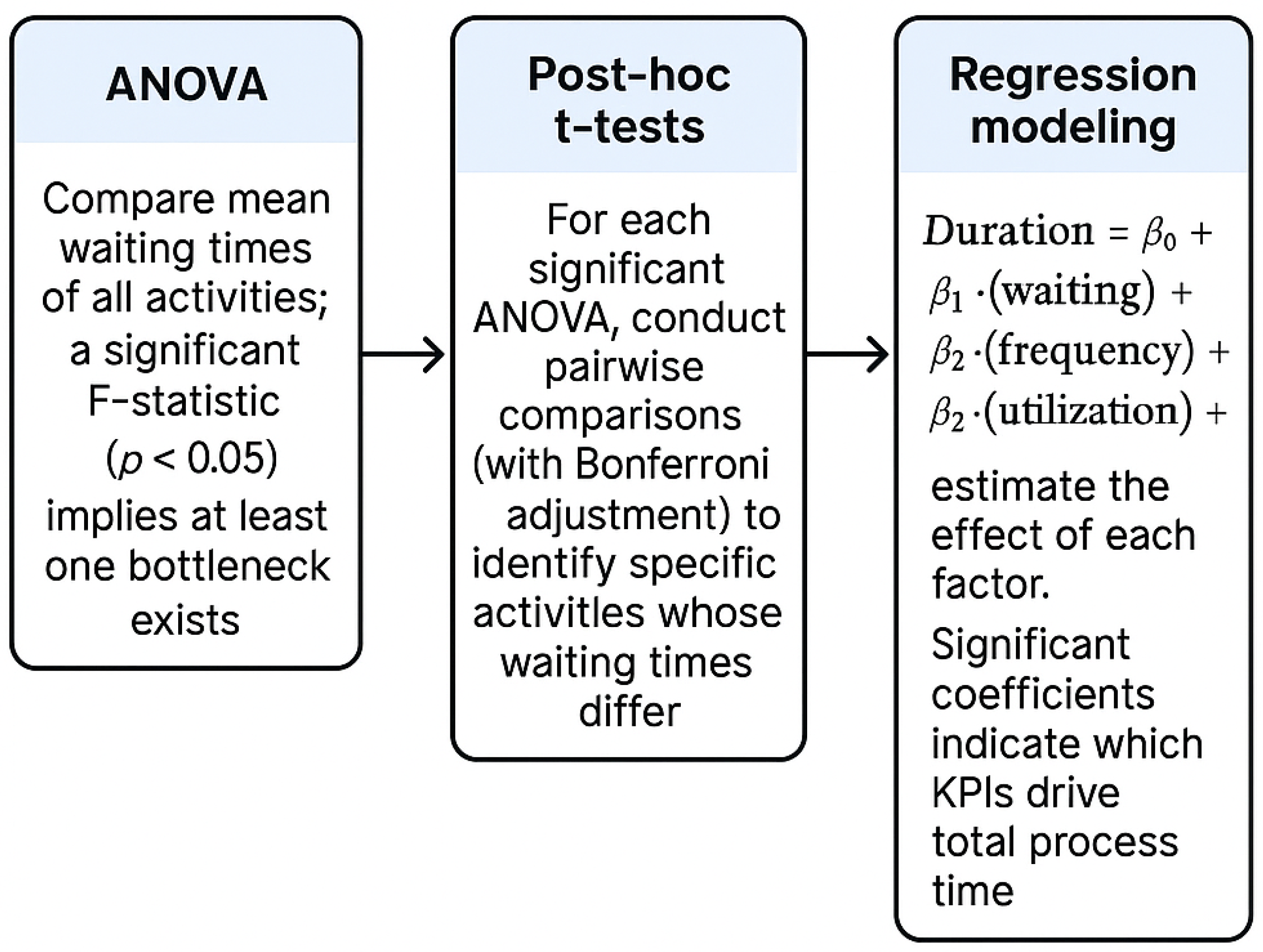
3.1. Statistical Preprocessing
3.2. Process Mining for Bottleneck Detection
3.3. Fuzzy System Design
3.3.1. Variable Definition
3.3.2. Rule Base Construction Using Fuzzy Decision Trees
4. Experimental Evaluation
4.1. Dataset and Experimental Setup
4.2. Statistical Preprocessing and Analysis
4.2.1. ANOVA and Significance Testing
4.2.2. Multiple Linear Regression Analysis
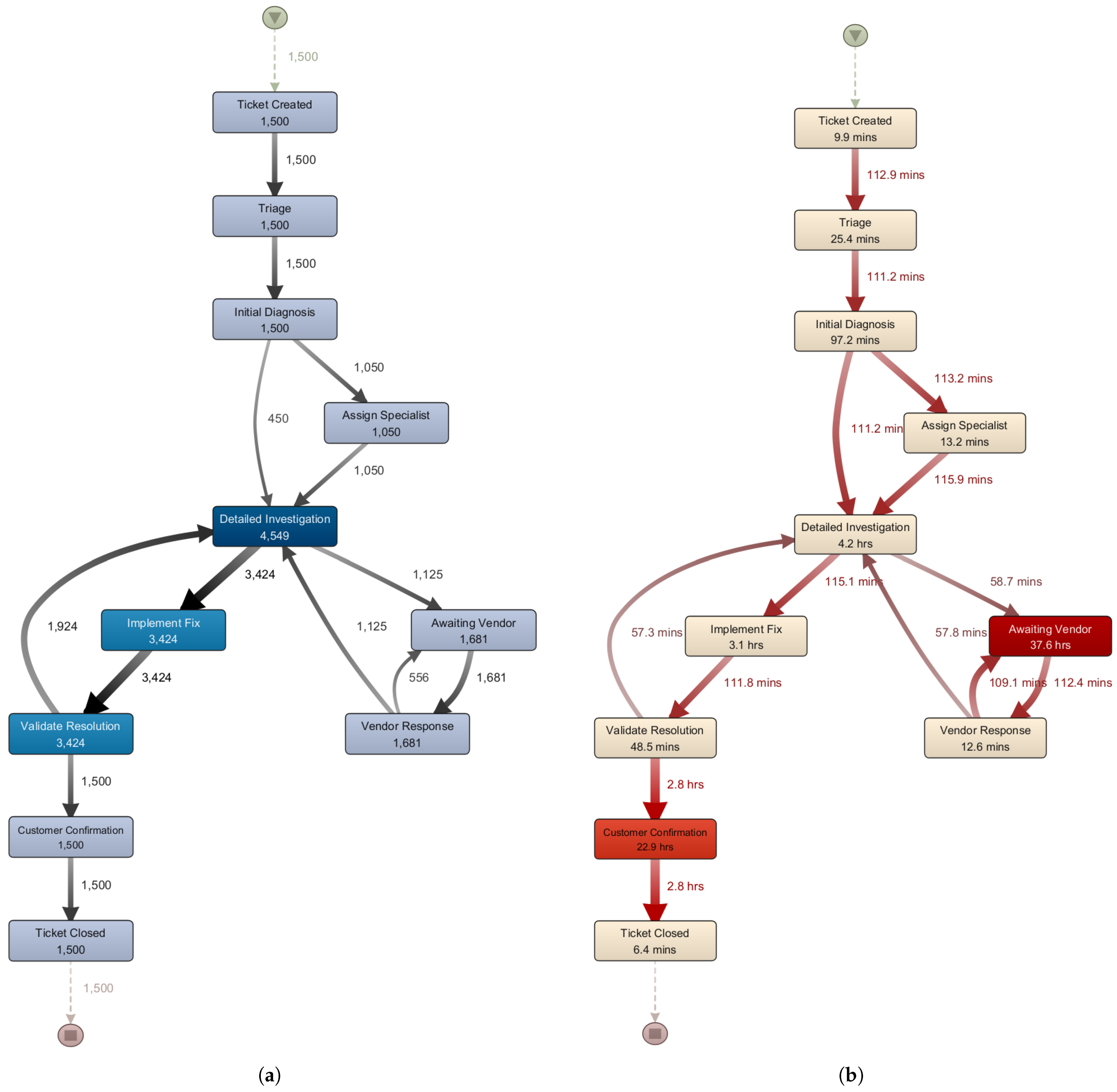
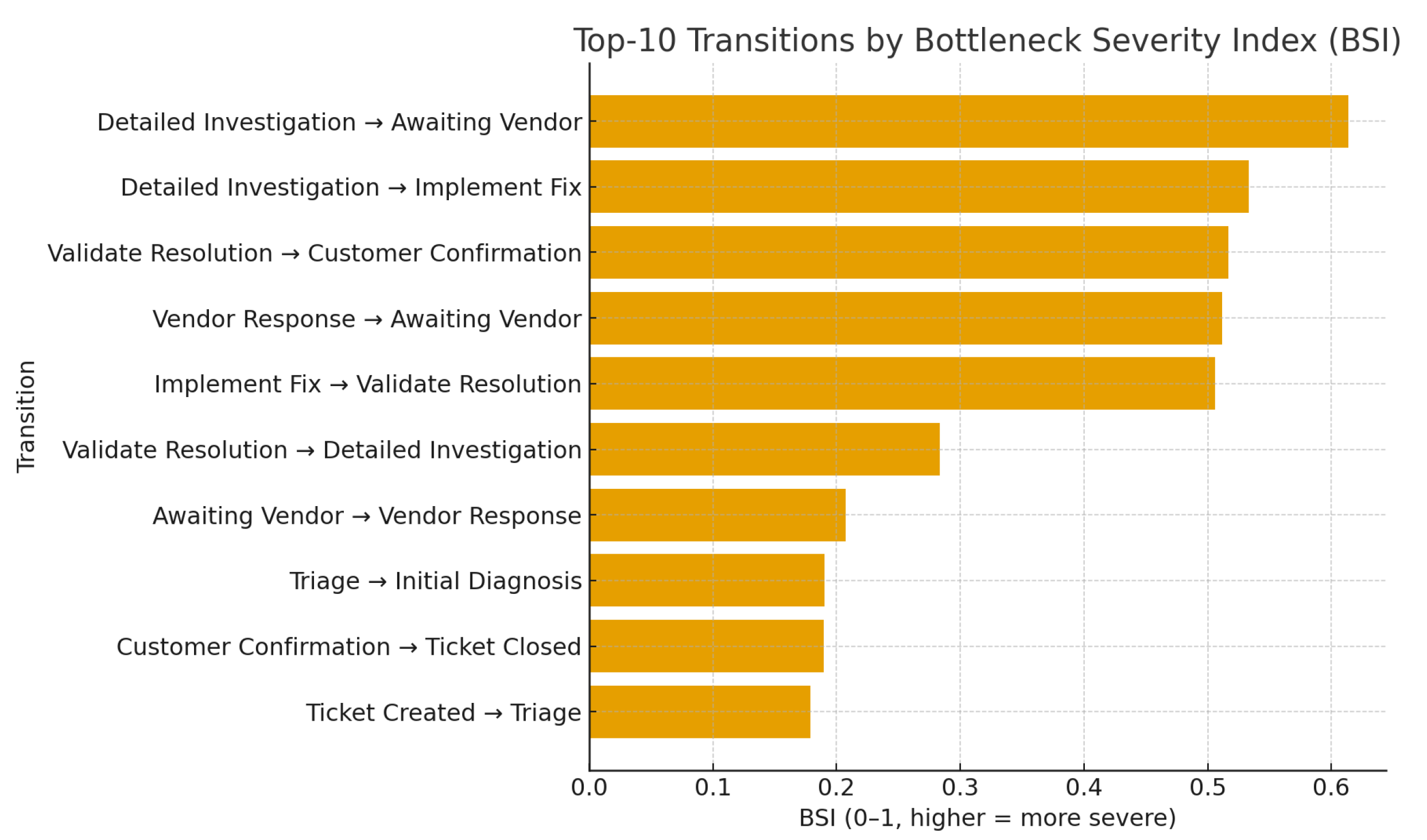
4.3. Process Mining and Bottleneck Visualization
4.4. Fuzzy Rule Analysis and Interpretability
4.5. Intervention Scenario Analysis
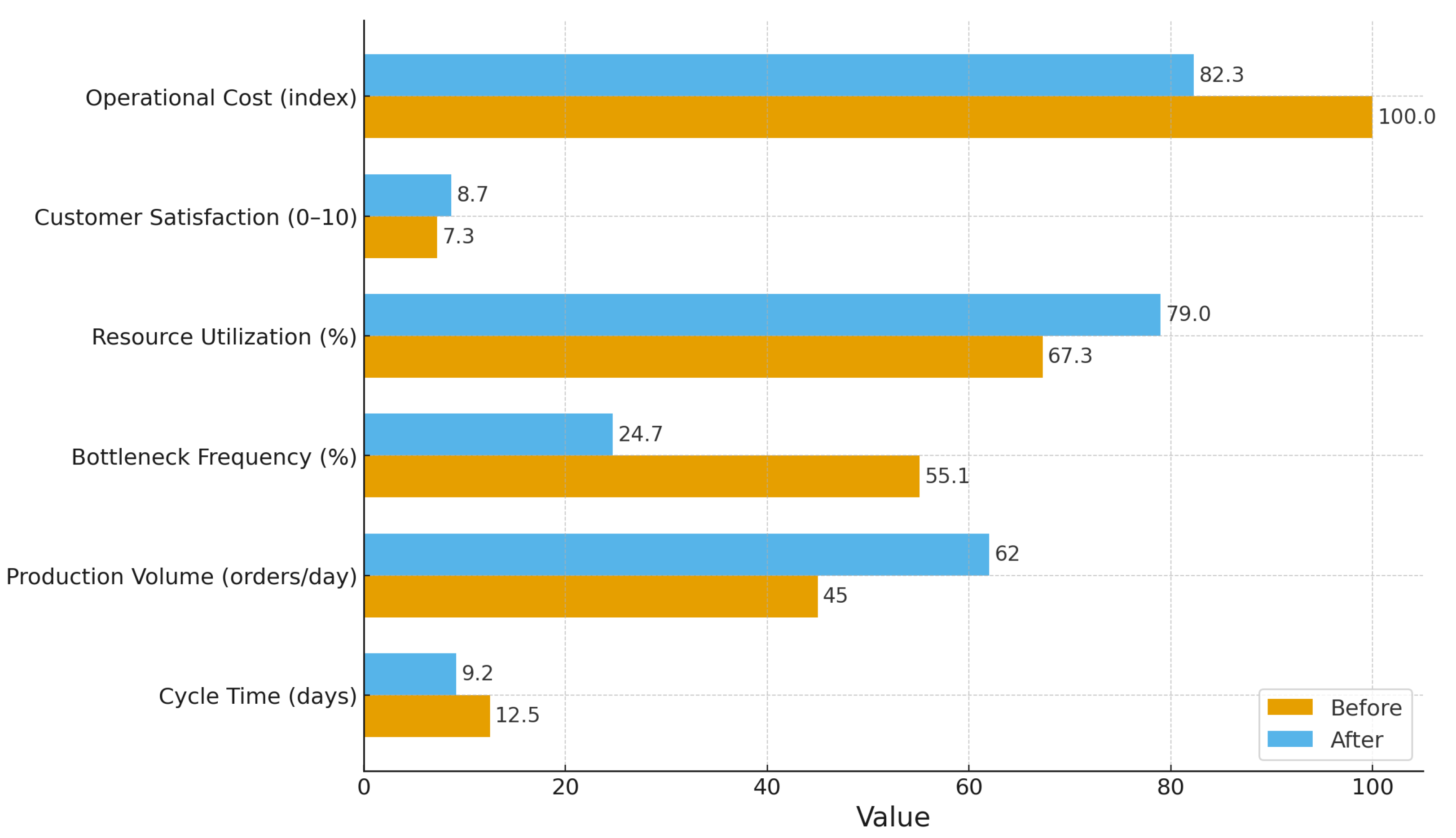
- Incident Resolution bottleneck: When long waiting (14.1 h context) coincided with high resolver utilization (95%), the rule above was activated and the assignment of an additional backup resolver was recommended. Waiting time was reduced by 57.1% (4.2 h → 1.8 h), indicating that capacity augmentation at a highly utilized support tier can directly and substantially shorten ticket queues.
- Service Desk overload: Under high load, redistribution of tickets to available agents in other queues was prescribed. A 57.4% reduction in waiting (6.8 h → 2.9 h) was achieved, suggesting that horizontal load balancing can be as effective as adding staff when multiple support groups exist.
- Vendor delay: Activation of an early escalation protocol yielded a 52.9% improvement (5.1 h → 2.4 h), implying that delays caused by external vendor dependencies respond well to proactive coordination rather than internal rescheduling.
4.6. Fuzzy Decision Tree Performance Evaluation
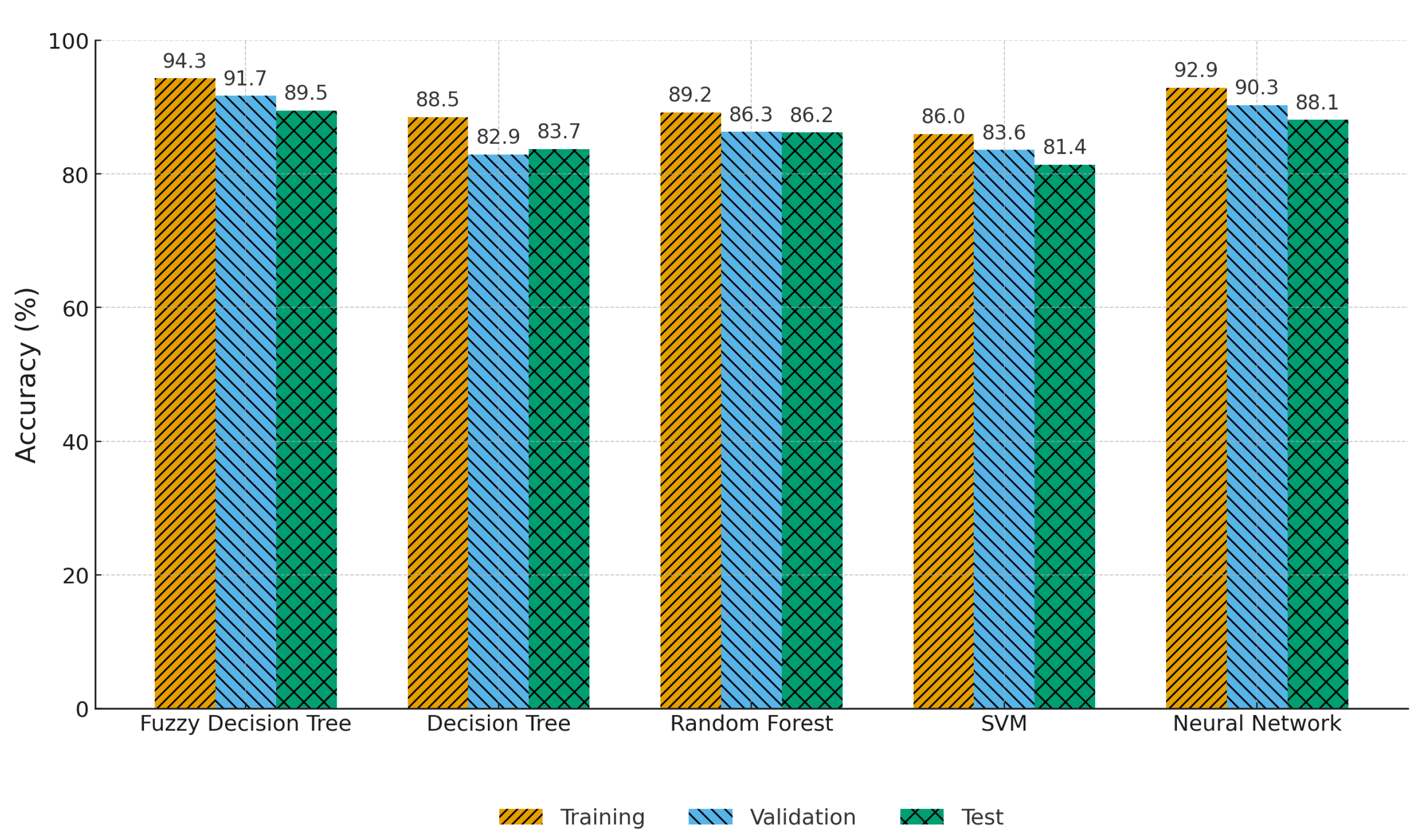
4.6.1. Model Comparison and Accuracy Assessment
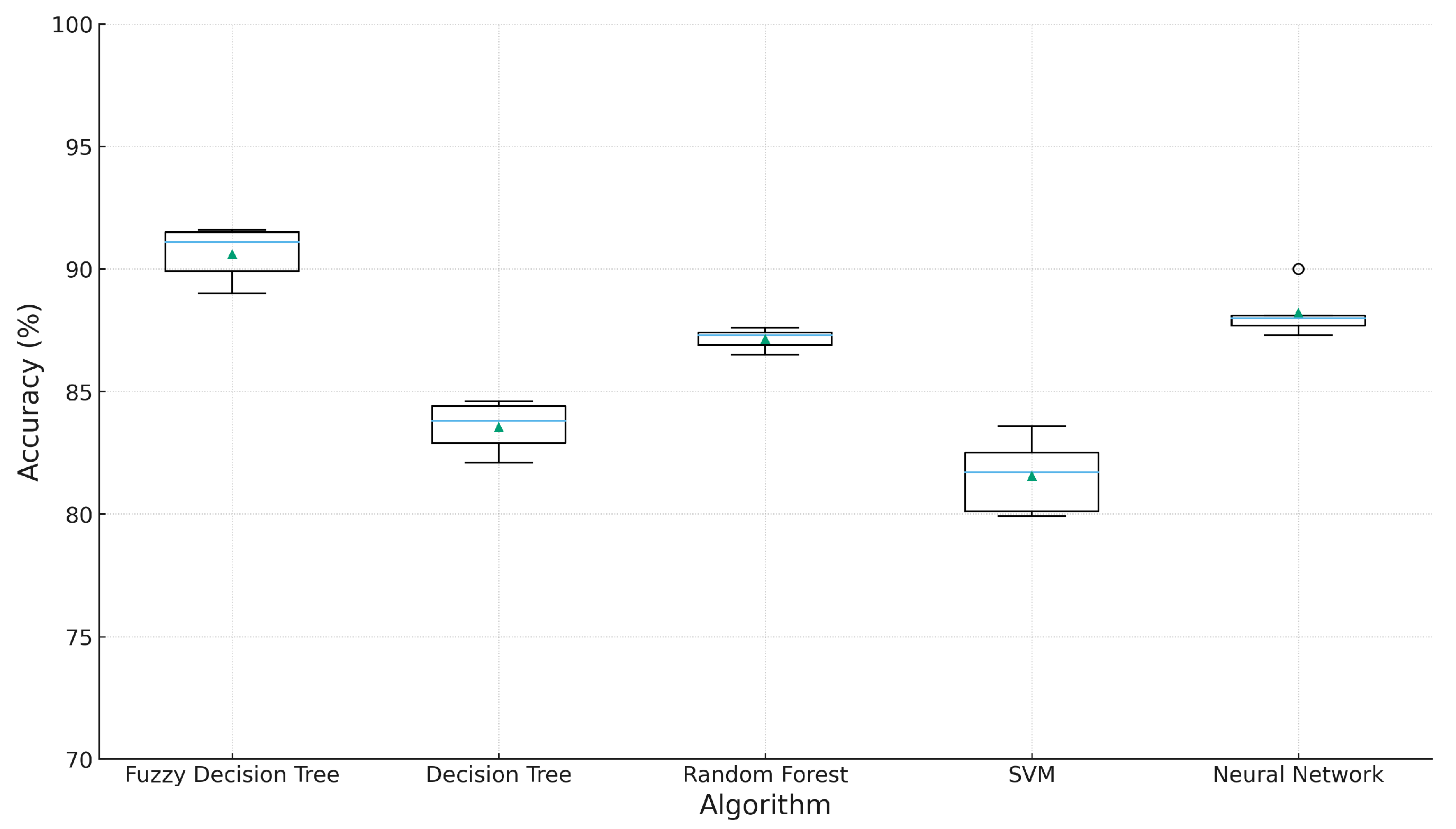
4.6.2. Cross-Validation and Model Robustness
4.6.3. Performance Improvements
4.7. Validation and Significance Testing
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Muñoz-Gama, J.; Martin, N.; Fernandez-Llatas, C.; Johnson, O.A.; Sepúlveda, M.; Helm, E.; Gálvez-Yanjari, V.; Rojas, E.; Martinez-Millana, A.; Aloini, D.; et al. Process Mining for Healthcare: Characteristics and Challenges. J. Biomed. Inform. 2022, 127, 103994. [Google Scholar] [CrossRef] [PubMed]
- Dogan, O.; Oztaysi, B. Genders prediction from indoor customer paths by Levenshtein-based fuzzy kNN. Expert Syst. Appl. 2019, 136, 42–49. [Google Scholar] [CrossRef]
- Özdağoğlu, G.; Damar, M.; Erenay, F.S.; Turhan Damar, H.; Himmetoğlu, O.; Pinto, A.D. Monitoring patient pathways at a secondary healthcare services through process mining via Fuzzy Miner. BMC Med. Inform. Decis. Mak. 2025, 25, 199. [Google Scholar] [CrossRef] [PubMed]
- Navin, K.; Krishnan, M.B. Mukesh Fuzzy rule based classifier model for evidence based clinical decision support systems. Intell. Syst. Appl. 2024, 22, 200393. [Google Scholar]
- Reinhard, P.; Li, M.M.; Peters, C.; Leimeister, J.M. Enhancing IT Service Management Through Process Mining—A Digital Analytics Perspective on Documented Customer Interactions. In Digital Analytics im Dienstleistungsmanagement: Customer Insights, Prozesse der Künstlichen Intelligenz, Digitale Geschäftsmodelle; Springer: Berlin/Heidelberg, Germany, 2025; pp. 327–360. [Google Scholar]
- Kubrak, K.; Milani, F.; Nolte, A.; Dumas, M. Prescriptive process monitoring: Quo vadis? PeerJ Comput. Sci. 2022, 8, e1097. [Google Scholar] [CrossRef]
- Khamis, M.; Al-Mashat, K.; El-Ghonemy, H. A Hybrid Decision Support System Integrating Machine Learning and Operations Research for Supply Chain Optimization. Comput. Ind. Eng. 2025, 190, 109987. [Google Scholar]
- Orošnjak, M.; Saretzky, F.; Kedziora, S. Prescriptive Maintenance: A Systematic Literature Review and Exploratory Meta-Synthesis. Appl. Sci. 2025, 15, 8507. [Google Scholar] [CrossRef]
- Suh, J.; Kim, S.; Cho, M.; Kang, H.W. A Hybrid Decision Support System for Predicting Treatment Order Outcomes in Psychiatry. J. Med. Internet Res. 2025, 27, e45678. [Google Scholar]
- Cao, J.; Zhou, T.; Zhi, S.; Lam, S.; Ren, G.; Zhang, Y.; Wang, Y.; Dong, Y.; Cai, J. Fuzzy inference system with interpretable fuzzy rules: Advancing explainable artificial intelligence for disease diagnosis—A comprehensive review. Inf. Sci. 2024, 662, 120212. [Google Scholar] [CrossRef]
- Kostopoulos, G.; Davrazos, G.; Kotsiantis, S. Explainable artificial intelligence-based decision support systems: A recent review. Electronics 2024, 13, 2842. [Google Scholar] [CrossRef]
- van der Aalst, W.M.P. Process Mining: Data Science in Action; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Reinkemeyer, L. Process mining in action. Process Min. Action Princ. Use Cases Outlook 2020, 11, 116–128. [Google Scholar]
- Chen, J.; Li, P.; Fang, W.; Zhou, N.; Yin, Y.; Xu, H.; Zheng, H. Fuzzy association rules mining based on type-2 fuzzy sets over data stream. Procedia Comput. Sci. 2022, 199, 456–462. [Google Scholar] [CrossRef]
- Novak, C.; Pfahlsberger, L.; Bala, S.; Revoredo, K.; Mendling, J. Enhancing decision-making of IT demand management with process mining. Bus. Process Manag. J. 2023, 29, 230–259. [Google Scholar] [CrossRef]
- Vázquez-Barreiros, B.; Chapela, D.; Mucientes, M.; Lama, M.; Berea, D. Process Mining in IT Service Management: A Case Study. In Proceedings of the ATAED@ Petri Nets/ACSD, Torun, Poland, 19–20 June 2016; pp. 16–30. [Google Scholar]
- Eggert, M.; Dyong, J. Applying process mining in small and medium sized it enterprises–challenges and guidelines. In Proceedings of the International Conference on Business Process Management, Münster, Germany, 11–16 September 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 125–142. [Google Scholar]
- Donadello, I.; Di Francescomarino, C.; Maggi, F.M.; Ricci, F.; Shikhizada, A. Outcome-oriented prescriptive process monitoring based on temporal logic patterns. Eng. Appl. Artif. Intell. 2023, 126, 106899. [Google Scholar] [CrossRef]
- Porouhan, P. Process mining analysis to enhance systematic workflow of an IT company. Int. J. Simul. Process Model. 2022, 19, 148–181. [Google Scholar] [CrossRef]
- Bozorgi, Z.D.; Teinemaa, I.; Dumas, M.; La Rosa, M.; Polyvyanyy, A. Prescriptive process monitoring for cost-aware cycle time reduction. In Proceedings of the 2021 3rd International Conference on Process Mining (ICPM), Eindhoven, The Netherlands, 31 October–4 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 96–103. [Google Scholar]
- Bozorgi, Z.D.; Teinemaa, I.; Dumas, M.; La Rosa, M.; Polyvyanyy, A. Prescriptive process monitoring based on causal effect estimation. Inf. Syst. 2023, 116, 102198. [Google Scholar] [CrossRef]
- Verhoef, B.J.; Dumas, M.; Teinemaa, I.; Maggi, F.M. Using Reinforcement Learning to Optimize Responses in Care Processes: A Prescriptive Process Mining Approach. In Proceedings of the Business Process Management Workshops, Utrecht, The Netherlands, 11–16 September 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 57–69. [Google Scholar]
- Su, Z.; Polyvyanyy, A.; Lipovetzky, N.; Sardiña, S.; van Beest, N. Adaptive goal recognition using process mining techniques. Eng. Appl. Artif. Intell. 2024, 133, 108189. [Google Scholar] [CrossRef]
- De Moor, J.; Weytjens, H.; De Smedt, J.; De Weerdt, J. Simbank: From simulation to solution in prescriptive process monitoring. In Proceedings of the International Conference on Business Process Management, Vienna, Austria, 1–5 September 2025; Springer: Berlin/Heidelberg, Germany, 2025; pp. 165–182. [Google Scholar]
- Chen, Z.; McClean, S.; Tariq, Z.; Georgalas, N.; Adefila, A. Integrating IT Infrastructure Metrics into Business Process Mining: A Telecommunications Industry Case Study. In Proceedings of the 2025 12th International Conference on Information Technology (ICIT), Delhi, India, 17–19 December 2025; IEEE: Piscataway, NJ, USA, 2025; pp. 665–670. [Google Scholar]
- Chvirova, D.; Egger, A.; Fehrer, T.; Kratsch, W.; Röglinger, M.; Wittmann, J.; Wördehoff, N. A multimedia dataset for object-centric business process mining in IT asset management. Data Brief 2024, 55, 110716. [Google Scholar] [CrossRef]
- Bouacha, M.; Sbai, H. Business-IT Alignment in Cloud environment: Survey on the use of process mining. In Proceedings of the 2023 14th International Conference on Intelligent Systems: Theories and Applications (SITA), Rabat, Morocco, 19–20 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Caizaguano, C.O.C.; Fonseca, E.R.; Caizaguano, C.S.; Vega, M.D.; Bazán, P. Modelo de Gestión de Residuos de Equipos de Informática y Telecomunicaciones (REIT) mediante la Minería de Procesos; Technical Report E45; Associação Ibérica de Sistemas e Tecnologias de Informacao: Lisbon, Portugal, 2021. [Google Scholar]
- Phasom, P.; Chum-Im, N.; Kungcharoen, K.; Premchaiswadi, N.; Premchaiswadi, W. Process mining for improvement of IT service in automobile industry. In Proceedings of the 2021 19th International Conference on ICT and Knowledge Engineering (ICT&KE), Bangkok, Thailand, 24–26 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–7. [Google Scholar]
- Magnus, H.; Silva, J.; Fialho, J.; Wanzeller, C. Process Mining–case study in a process of IT incident management. In Proceedings of the CAPSI 2020 Proceedings, Lisbon, Portugal, 12–13 November 2020; p. 25. [Google Scholar]
- Sundararaj, A.; Knittl, S.; Grossklags, J. Challenges in IT Security Processes and Solution Approaches with Process Mining. In Proceedings of the International Workshop on Security and Trust Management, Guildford, UK, 14–18 September 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 123–138. [Google Scholar]
- Sakchaikun, J.; Tumswadi, S.; Palangsantikul, P.; Porouhan, P.; Premchaiswadi, W. IT help desk service workflow relationship with process mining. In Proceedings of the 2018 16th International Conference on ICT and Knowledge Engineering (ICT&KE), Phuket, Thailand, 21–23 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Kang, C.J.; Kang, Y.S.; Lee, Y.S.; Noh, S.; Kim, H.C.; Lim, W.C.; Kim, J.; Hong, R. Process Mining-based Understanding and Analysis of Volvo IT’s Incident and Problem Management Processes. In Proceedings of the BPIC@ BPM, Beijing, China, 26 August 2013; Volume 85. [Google Scholar]
- Paszkiewicz, Z.; Picard, W. Analysis of the Volvo IT Incident and Problem Handling Processes using Process Mining and Social Network Analysis. In Proceedings of the BPIC@ BPM, Beijing, China, 26 August 2013. [Google Scholar]
- Edgington, T.M.; Raghu, T.; Vinze, A.S. Using process mining to identify coordination patterns in IT service management. Decis. Support Syst. 2010, 49, 175–186. [Google Scholar] [CrossRef]
- Gerke, K.; Tamm, G. Continuous quality improvement of IT processes based on reference models and process mining. In Proceedings of the 15th Americas Conference on Information Systems, San Francisco, CA, USA, 6–9 August 2009; Springer: Berlin/Heidelberg, Germany, 2009; p. 786. [Google Scholar]
- Wang, J.; Gui, L.; Zhu, H. Incremental fuzzy temporal association rule mining using fuzzy grid tables. Appl. Intell. 2021, 52, 1389–1405. [Google Scholar] [CrossRef]
- Saatchi, R. Fuzzy logic concepts, developments and implementation. Information 2024, 15, 656. [Google Scholar] [CrossRef]
- Dogan, O.; Avvad, H. Fuzzy Clustering Based on Activity Sequence and Cycle Time in Process Mining. Axioms 2025, 14, 351. [Google Scholar] [CrossRef]
- Alateeq, M.; Pedrycz, W. Logic-oriented fuzzy neural networks: A survey. Expert Syst. Appl. 2024, 257, 125120. [Google Scholar] [CrossRef]
- Oleksii, D.; Zoia, S.; Gegov, A.; Arabikhan, F. Application of fuzzy decision support systems in IT industry functioning. In Proceedings of the International Conference on Information and Knowledge Systems, Kharkiv, Ukraine, 4–6 October 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 283–295. [Google Scholar]
- SS Júnior, J.; Mendes, J.; Souza, F.; Premebida, C. Survey on deep fuzzy systems in regression applications: A view on interpretability. Int. J. Fuzzy Syst. 2023, 25, 2568–2589. [Google Scholar] [CrossRef]
- Wang, T.; Gault, R.; Greer, D. Data Informed Initialization of Fuzzy Membership Functions. Int. J. Fuzzy Syst. 2025, 1–12. [Google Scholar] [CrossRef]
- Janikow, C.Z. Fuzzy decision trees: Issues and methods. IEEE Trans. Syst. Man, Cybern. 1998, 28, 1–14. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Niu, J.; Chen, D.; Li, J.; Wang, H. Fuzzy Rule Based Classification Method for Incremental Rule Learning. IEEE Trans. Fuzzy Syst. 2022, 30, 3748–3761. [Google Scholar] [CrossRef]
- Pascual-Fontanilles, J.; Valls, A.; Moreno, A.; Romero-Aroca, P. Continuous Dynamic Update of Fuzzy Random Forests. Int. J. Comput. Intell. Syst. 2022, 15, 1–17. [Google Scholar] [CrossRef]
- Tavares, E.; Moita, G.F.; Silva, A.M. eFC–Evolving Fuzzy Classifier with Incremental Clustering Algorithm Based on Samples Mean Value. Big Data Cogn. Comput. 2024, 8, 183. [Google Scholar] [CrossRef]
- Mehmood, H.; Kostakos, P.; Cortes, M.; Anagnostopoulos, T.; Pirttikangas, S.; Gilman, E. Concept Drift Adaptation Techniques in Distributed Environment for Real-World Data Streams. Smart Cities 2021, 4, 349–371. [Google Scholar] [CrossRef]
| Study | Method Used | Diagnosis Provided | Prescription Mechanism | Limitations |
|---|---|---|---|---|
| [25] | Case study integrating IT metrics with process mining in telecom operations | Identifies performance bottlenecks and misalignments between IT resources and business processes | Combines IT logs with event data to recommend resource allocation improvements | Limited to one telecom case; lacks cross-industry validation |
| [26] | Dataset construction and validation for object-centric process mining | Reveals fragmented event data and lack of object-level process visibility in IT asset systems | Provides an annotated dataset enabling event correlation across IT assets | Dataset is synthetic; limited testing on real IT environments |
| [27] | Conceptual framework and survey analysis on business–IT alignment in cloud environments | Highlights lack of automation and weak formalization in Business–IT alignment | Proposes process mining for dynamic resource allocation and alignment in cloud-based BPaaS | Conceptual; not empirically validated or implemented |
| [15] | Action research integrating process mining with IT demand management | Diagnoses inefficiencies and lack of visibility in IT change processes | Uses process mining to support operational decision-making and risk identification | Evaluated on limited insurance cases; lacks generalization |
| [17] | Case study on process mining adoption in an IT SME | Identifies challenges such as data quality issues, resource scarcity, and low process maturity | Provides practical guidelines for SMEs to implement process mining effectively | Focused on one IT SME; results not broadly generalizable |
| [28] | Process mining framework for IT and telecommunication equipment waste management (REIT model) | Identifies inefficiencies in recycling and disposal workflows for IT assets | Applies process mining to monitor compliance and improve e-waste process control | Focused on simulation and conceptual validation; lacks large-scale industrial testing |
| [29] | Fuzzy Miner and Social Network Miner applied to IT help-desk event logs | Detects excessive service-time violations and unbalanced workload among IT staff | Suggests workload redistribution and SLA re-definition through social-network analysis | Limited to one IT service department; no automation or predictive component |
| [30] | Case study of process mining in IT incident-management process | Diagnoses bottlenecks and delays in IT incident resolution workflows | Uses discovered process models to enhance incident-management efficiency and transparency | Applied in a single organization; lacks quantitative evaluation of improvement results |
| [31] | Experimental case study using conformance checking for Identity and Access Management (IAM) processes | Detects deviations and anomalous user-access behaviors in IAM workflows | Proposes conformance-based detection integrated with threat analysis for cybersecurity monitoring | Demonstrated on simulated IAM data; limited coverage of real-world security complexity |
| [32] | Correlational analysis of IT help-desk workflow using process mining techniques | Reveals relationships between IT service activities, highlighting repetitive inefficiencies | Implements relationship mapping to improve coordination and streamline service delivery | Restricted to internal IT workflow; no generalization beyond case study environment |
| [16] | Case study of process mining in IT service management (ITSM) | Identifies inefficiencies, redundant steps, and SLA violations in IT support processes | Suggests SLA redesign and improved workflow automation based on discovered event logs | Limited to a single IT service provider; lacks statistical generalization |
| [33] | Event log analysis of IT help-desk processes using ProM tools (BPI Challenge 2013 dataset) | Reveals service bottlenecks and suboptimal escalation patterns in IT problem management | Applies performance analysis to enhance process transparency and issue resolution speed | Focuses only on Volvo IT dataset; lacks predictive or adaptive modeling |
| [34] | Combined process mining and social network analysis for IT incident handling | Detects coordination gaps between IT service agents and departments | Integrates social network mapping with process models to improve collaboration efficiency | Limited dataset; analysis scope restricted to incident coordination only |
| [35] | Structural equation modeling (SEM) integrated with process mining on IT service data | Identifies hidden coordination constructs (Observe, Discover, Produce, Context) within IT service outsourcing processes | Recommends SLA refinements and governance mechanisms for aligning provider and client objectives | Focused on one U.S. government outsourcing case; no validation across other industries |
| [36] | ITIL-based reference modeling combined with process mining for continuous quality improvement | Diagnoses deviations between designed (to-be) and executed (as-is) IT service processes | Implements ITIL KPIs with process mining for monitoring compliance and detecting inefficiencies | Demonstrated on CRM support process; lacks multi-organizational validation |
| [37] | Incremental fuzzy temporal association rule mining | Efficient discovery of evolving temporal patterns and frequent itemsets | Not explicit (focuses on mining efficiency, no direct prescriptive rules) | Needs efficiency improvements; limited to temporal association mining |
| Transition | Frequency | P90 Wait (h) | BSI |
|---|---|---|---|
| Detailed Investigation–Awaiting Vendor | 1125 | 66.51 | 0.613 |
| Detailed Investigation–Implement Fix | 3424 | 7.93 | 0.533 |
| Validate Resolution–Customer Confirmation | 1500 | 46.46 | 0.517 |
| Vendor Response–Awaiting Vendor | 556 | 65.72 | 0.512 |
| Implement Fix–Validate Resolution | 3424 | 4.46 | 0.506 |
| Validate Resolution–Detailed Investigation | 1924 | 8.25 | 0.284 |
| Awaiting Vendor–Vendor Response | 1681 | 3.81 | 0.208 |
| Triage–Initial Diagnosis | 1500 | 5.49 | 0.19 |
| Customer Confirmation–Ticket Closed | 1500 | 5.4 | 0.19 |
| Ticket Created–Triage | 1500 | 4.05 | 0.179 |
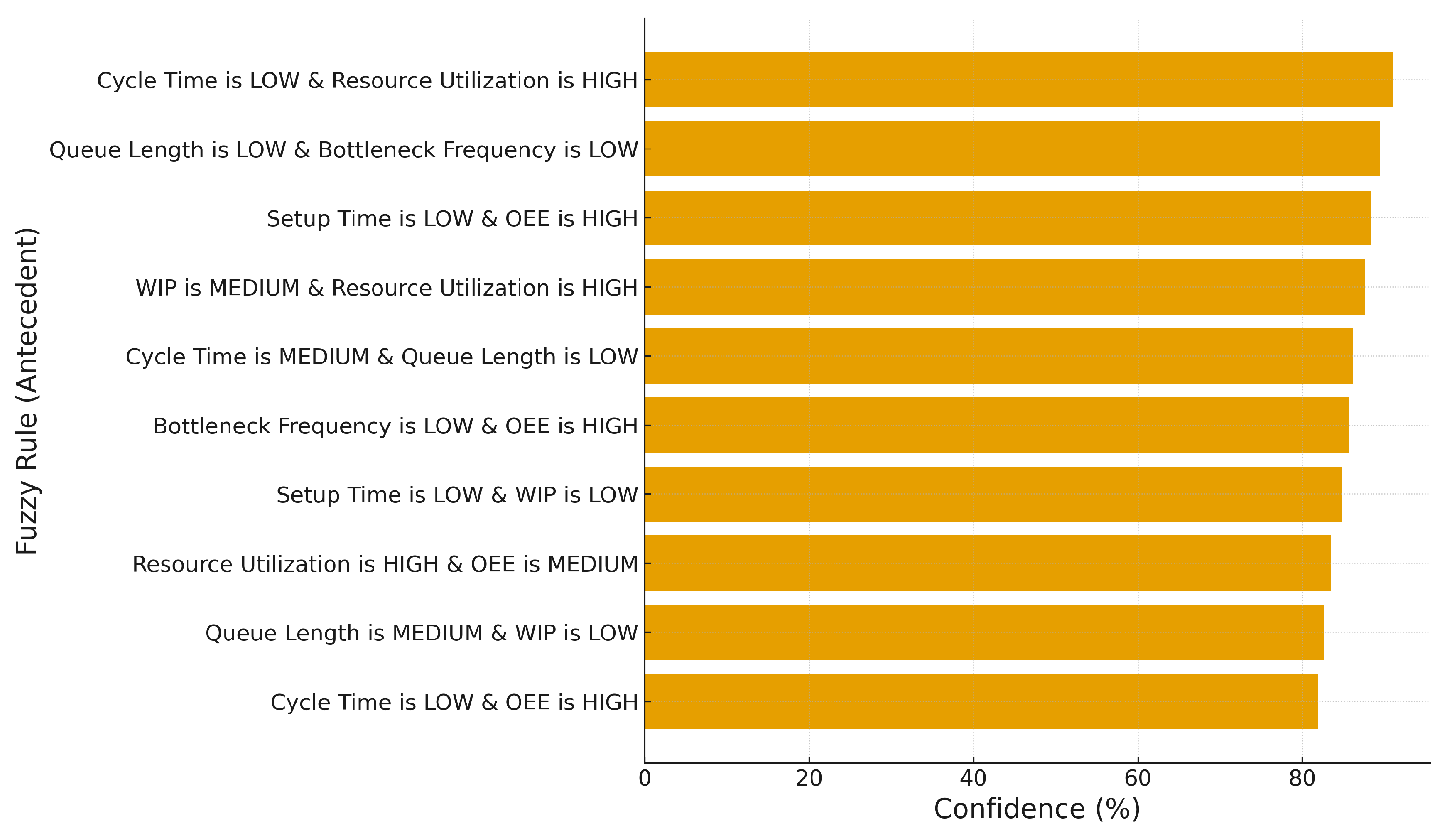
| Antecedent (IF…) | Consequent (THEN…) | Support (%) | Confidence (%) | Lift |
|---|---|---|---|---|
| Cycle Time is LOW & Resource Utilization is HIGH | Throughput is HIGH | 12.4 | 91.0 | 1.31 |
| Queue Length is LOW & Bottleneck Frequency is LOW | Delay Risk is LOW | 10.8 | 89.5 | 1.27 |
| Setup Time is LOW & OEE is HIGH | Operational Cost is LOW | 9.9 | 88.4 | 1.22 |
| WIP is MEDIUM & Resource Utilization is HIGH | Production Volume is HIGH | 11.2 | 87.6 | 1.18 |
| Cycle Time is MEDIUM & Queue Length is LOW | Customer Satisfaction is HIGH | 8.7 | 86.2 | 1.15 |
| Bottleneck Frequency is LOW & OEE is HIGH | Cycle Time is LOW | 7.5 | 85.7 | 1.14 |
| Setup Time is LOW & WIP is LOW | Throughput is HIGH | 6.9 | 84.9 | 1.12 |
| Resource Utilization is HIGH & OEE is MEDIUM | Operational Cost is LOW | 5.8 | 83.5 | 1.10 |
| Scenario | Action | Before | After |
|---|---|---|---|
| Incident Resolution bottleneck | Assign backup resolver (rule-triggered) | 4.2 h | 1.8 h |
| Service Desk overload | Redistribute tickets across agents | 6.8 h | 2.9 h |
| Vendor delay | Trigger early escalation protocol | 5.1 h | 2.4 h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dogan, O.; Avvad, H. A Fuzzy Rule-Based Decision Support in Process Mining: Turning Diagnostics into Prescriptions. Appl. Sci. 2025, 15, 12402. https://doi.org/10.3390/app152312402
Dogan O, Avvad H. A Fuzzy Rule-Based Decision Support in Process Mining: Turning Diagnostics into Prescriptions. Applied Sciences. 2025; 15(23):12402. https://doi.org/10.3390/app152312402
Chicago/Turabian StyleDogan, Onur, and Hunaıda Avvad. 2025. "A Fuzzy Rule-Based Decision Support in Process Mining: Turning Diagnostics into Prescriptions" Applied Sciences 15, no. 23: 12402. https://doi.org/10.3390/app152312402
APA StyleDogan, O., & Avvad, H. (2025). A Fuzzy Rule-Based Decision Support in Process Mining: Turning Diagnostics into Prescriptions. Applied Sciences, 15(23), 12402. https://doi.org/10.3390/app152312402








