Comparison of Point Measurement Strategies and Mathematical Algorithms for Evaluation in Contact Measurement of a Spherical Surface on a CMM
Abstract
1. Introduction
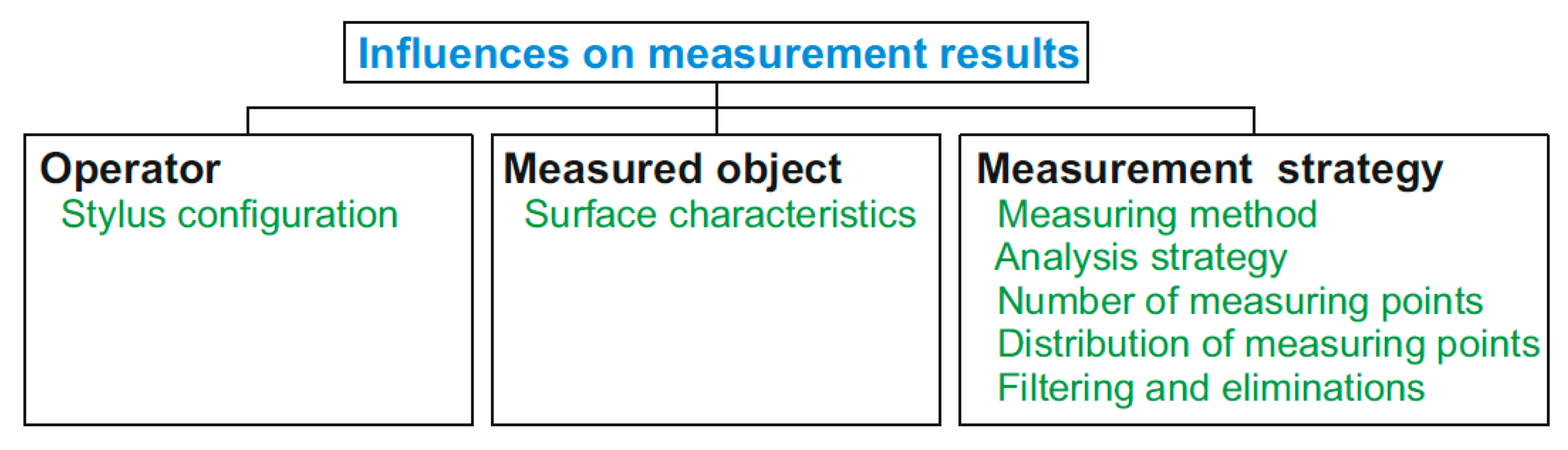
- The most significant influence on the measurement result comes from the measuring strategy, the operator, and the inspection task, which together account for more than 50 percent of the effect [8]. Sadaoui [9] examines the impact of component placement, its orientation on measurement planning, and the optimization of the measurement approach in the paper.
- From the perspective of experimental design, the stylus configuration plays a critical role in the measurement result. Different materials used for the stylus shaft, tip diameter, stylus length, extension, stiffness, and mass can affect the measurement result. The thermal expansion of carbon fiber is , while for tungsten carbide it is [10]. Therefore, it is essential to calibrate the stylus under the actual measurement conditions.
- It is recommended to use the shortest possible stylus system (stylus without/with extension) within the specifications given by the manufacturer. Increasing stylus length causes the stylus to bend or deflect, which increases the error and reduces accuracy [11].
- The elastic modulus E (GPa) is a material property describing the relationship between stress and strain when a solid body is deformed. A higher elastic modulus indicates greater resistance to deformation. The elastic modulus is ≥450 GPa for carbon fiber and 620 GPa for tungsten carbide. Styli with a tip diameter smaller than 2 mm typically have tungsten carbide shafts, while those with tip diameters larger than 2 mm may use either tungsten carbide or carbon fiber shafts, with the shaft diameter increasing proportionally with the probe diameter [12,13]. As the shaft diameter increases, the stiffness of the stylus and its resistance to bending also increase.
- The probe tip diameter has a fundamental impact on distortions caused by the tip’s mechanical filtration effect. Lou et al. [14] investigated the effect of probe tip diameter on the measurement of additively manufactured parts. Their results show that probe diameter has a significant influence on the measurement result. The role of probe diameter as a mechanical filter is further confirmed by other studies [15,16].
- Salah [17] studied the influence of the stylus, combined with scanning speed, on roundness and measurement uncertainty using a calibration ring. The impact of stylus tip radius on the mean form error at different probing speeds is approximately 1 m.
- Woźniak and Dobosz [18] investigated the influence of surface shape (flat, convex, concave), object stiffness, and surface roughness on touch trigger probe accuracy and measurement uncertainty.
2. Materials and Methods
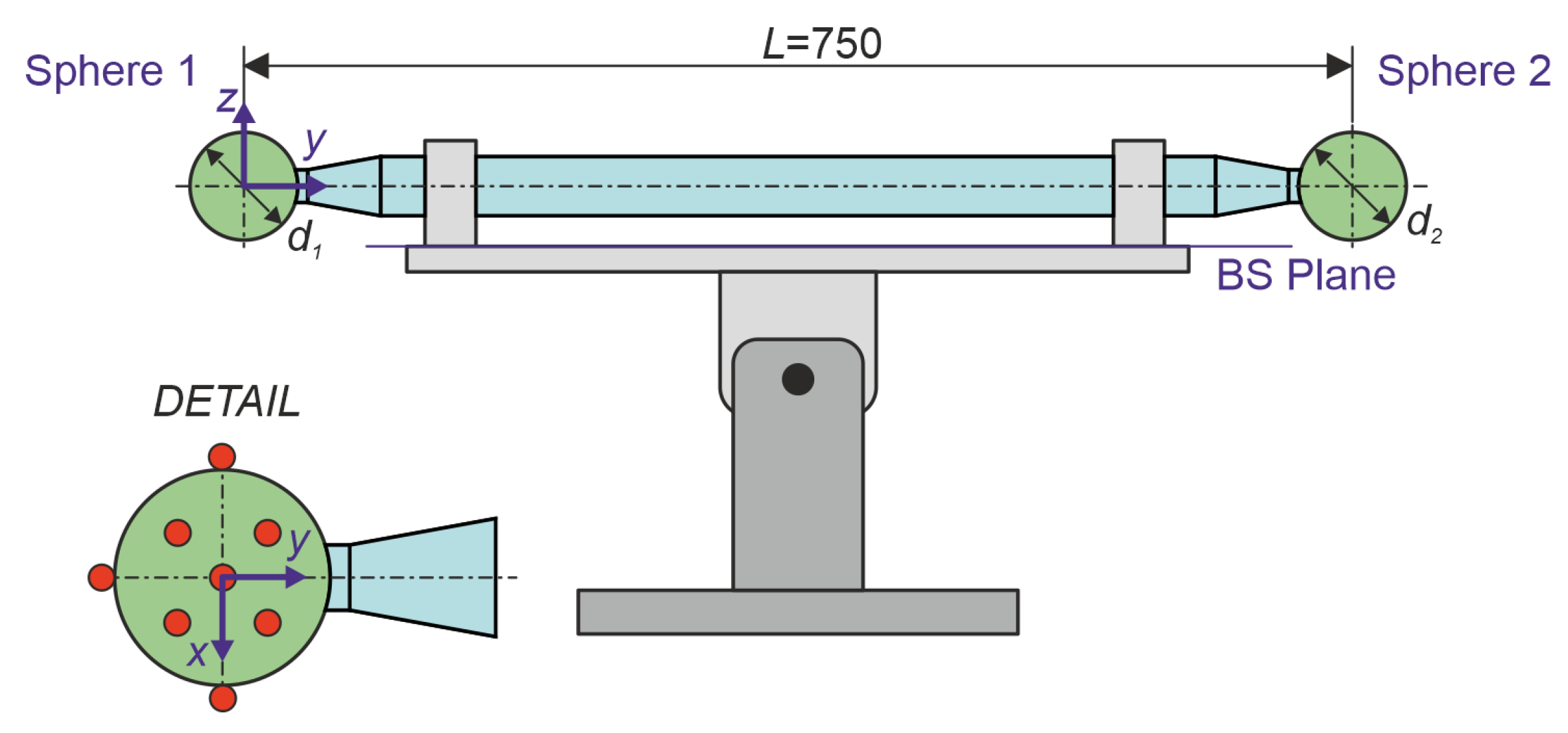
2.1. Experimental Setup
- Sphere—Within the Sphere feature, points from the first measurement were used with coordinates adjusted according to the change in probe tip diameter , while preserving the normal vectors , . The Sphere feature was created using the LSQ evaluation method.
- Mid Point (MP)—Within the Point feature, points were measured as Mid Points; the point coordinates and their direction vectors are the same as for the Sphere feature, but they are measured as individual points.
- Space Point (SP)—Within the Point feature, points were measured as Space Points with the option Plane measurement always. Points to determine the normal vector are measured along the direction of the largest component of the normal vector, after which the point is measured at the specified coordinates using the obtained normal vector.
- Touch Point (TP)—Within the Point feature, points were measured as Touch Points along the direction of the largest component of the normal vector.
- Circle—Within the Circle feature, the measurement was performed by scanning 8 circles with a 2 mm spacing and a step width of 0.2 mm between points.
2.2. Used Spheres Fitting Methods
2.2.1. Octave Code for the Kåsa Method
01 % Kasa LSQ method 02 phi=[x ones(N,1)]; 03 s=-(x(:,1).^2+x(:,2).^2+x(:,3).^2); 04 coeff=pinv(phi)*s; 05 % Center 06 CK=-coeff(1:3)’/2; 07 disp([’CK: ’,num2str(CK,12)]) 08 % Radius 09 RK=sqrt(sum(CK.^2)-coeff(4)); 10 disp([’rK: ’,num2str(RK,12)])
2.2.2. Octave Code for the Minimum Sphere’s Shell Width Method
01 options=optimset(’TolFun’,1.e-12,’TolX’,1.e-12); 02 [CM,w_fmin]=fminsearch(’width’,CN,options) % Newton initial guess CN 03 rvM=x-CM; % radius vectors - CM - Midpoint Center 04 for k=1:N, 05 rrM(k)=norm(rvM(k,:)); % radii 06 end 07 rM=(max(rrM)+min(rrM))/2; % Midpoint radius 08 wM=max(rrM)-min(rrM); % shell width - the same as w_fmin 01 function [w]=width(p) % Sphere center p 02 global x; % x - matrix [xi,yi,zi] of size N x 3 03 N=size(x,1); % Points number 04 rv=x-p; 05 for k=1:N 06 r(k)=norm(rv(k,:)); % radii 07 endfor 08 w=max(r)-min(r); % width of a shell
3. Results
| Calypso Form | Kåsa | Mid | Kåsa | Mid | |||
|---|---|---|---|---|---|---|---|
| Option | (mm) | All | Newton | Range | Newton | Range | |
| Half-Width (μm) | RMSE (μm) | ||||||
| 0.750844 | 0.433 | 0.409 | 0.498 | 0.433 | 0.233 | 0.240 | |
| Sphere | 1.500736 | 0.453 | 0.371 | 0.521 | 0.453 | 0.212 | 0.238 |
| 2.500557 | 2.144 | 0.430 | 2.341 | 2.146 | 0.527 | 1.203 | |
| 0.750844 | 0.436 | 0.384 | 0.473 | 0.436 | 0.217 | 0.227 | |
| Mid Point | 1.500736 | 0.605 | 0.489 | 0.727 | 0.605 | 0.270 | 0.301 |
| 2.500557 | 2.225 | 0.561 | 2.470 | 2.225 | 0.574 | 1.350 | |
| 0.750844 | 0.500 | 0.463 | 0.546 | 0.500 | 0.250 | 0.270 | |
| Space Point | 1.500736 | 0.696 | 0.604 | 0.822 | 0.696 | 0.332 | 0.353 |
| 2.500557 | 1.639 | 0.487 | 1.958 | 1.639 | 0.472 | 1.079 | |
| 0.750844 | 0.532 | 0.404 | 0.627 | 0.532 | 0.236 | 0.263 | |
| Touch Point | 1.500736 | 1.215 | 0.563 | 1.449 | 1.249 * | 0.381 | 0.737 |
| 2.500557 | 0.423 | 0.387 | 0.481 | 0.423 | 0.224 | 0.235 | |
| 0.750844 | 1.663 | 0.678 | 1.662 | 1.564 | 0.270 | 0.849 | |
| Circle Scan | 1.500736 | 1.438 | 0.805 | 1.438 | 1.242 | 0.311 | 0.492 |
| 2.500557 | 2.885 | 0.785 | 4.078 | 2.885 | 0.333 | 1.505 | |
4. Discussion
- 1.
- The differences between the results obtained by the Kåsa and Newton methods are presented in Table 6, Table 9 and Table 12. The maximum difference for the diameter d was pm (for mm and the Sphere feature). For the center coordinates, the maximum differences were pm, pm, and pm, obtained for mm and the features Sphere, Mid Point, and Sphere, respectively (see Table 12). These results indicate that the LSQ solutions obtained by the Kåsa and Newton methods can be considered “identical” at the nanometer scale. Given the minimal differences in diameter and position, computation time may play a more significant role. For Circle measurements with 2200 points, the computation time was at most 0.3 ms for the Kåsa method and 1.2 ms for the Newton method. Comparing the results, rounded to 1 nm, obtained by the Calypso software and the Kåsa/Newton methods (Table 4, Table 5, Table 7, Table 8, Table 10 and Table 11) shows that for the Circle Scan measurement strategy, the diameter differences are less than or equal to 3 nm, and the coordinate differences are less than or equal to 2 nm. For all other strategies/options, the results and values are identical, with the only exceptions being nm for the Sphere option at mm, nm for the Mid Point option, and nm for the Space Point option at mm. Finally, the absolute values are always less than 1.388 m (for LSQ methods Calypso/Kåsa/Newton), which is below the maximum permissible error of length measurement of the device for —1.885 m calculated in (1) above (Table 5, Table 8 and Table 11). Hence, each of the applied strategies can be considered suitable for measurement.
- 2.
- In the experiment, new touch probes and an adapter plate were used to eliminate the effect of wear. The air temperature near the measured object varied by no more than 0.3 K during touch probe calibration and measurement. The differences for the individual probes and strategies are small. The smallest deviations were observed for the probe with mm using the Mid Point, Sphere, and Circle Scan strategies (see Table 5, Table 8 and Table 11, and Figure 7). The Touch Point strategy shows the smallest variance for the touch probes used (Figure 7).The differences are probably due to the influence of the stiffness of the sensing systems. The probe extensions are made of the same material and have the same thickness (diameter). The probe with mm has a shorter metallic shaft (diameter 1 mm), the probe with mm has a shaft with a diameter of 3.5 mm, and the probe with mm has a shaft with a diameter of 2 mm.
- 3.
- 4.
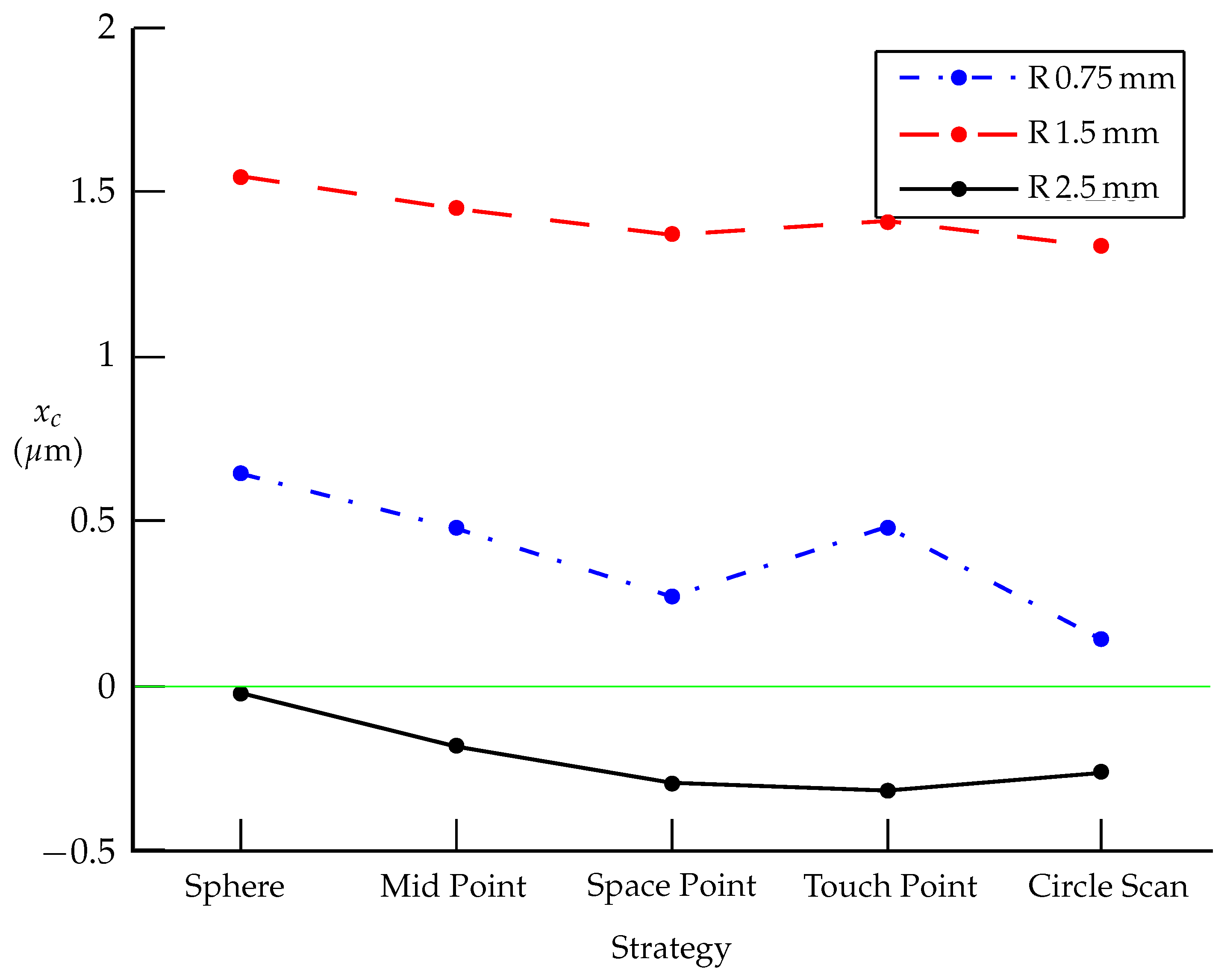
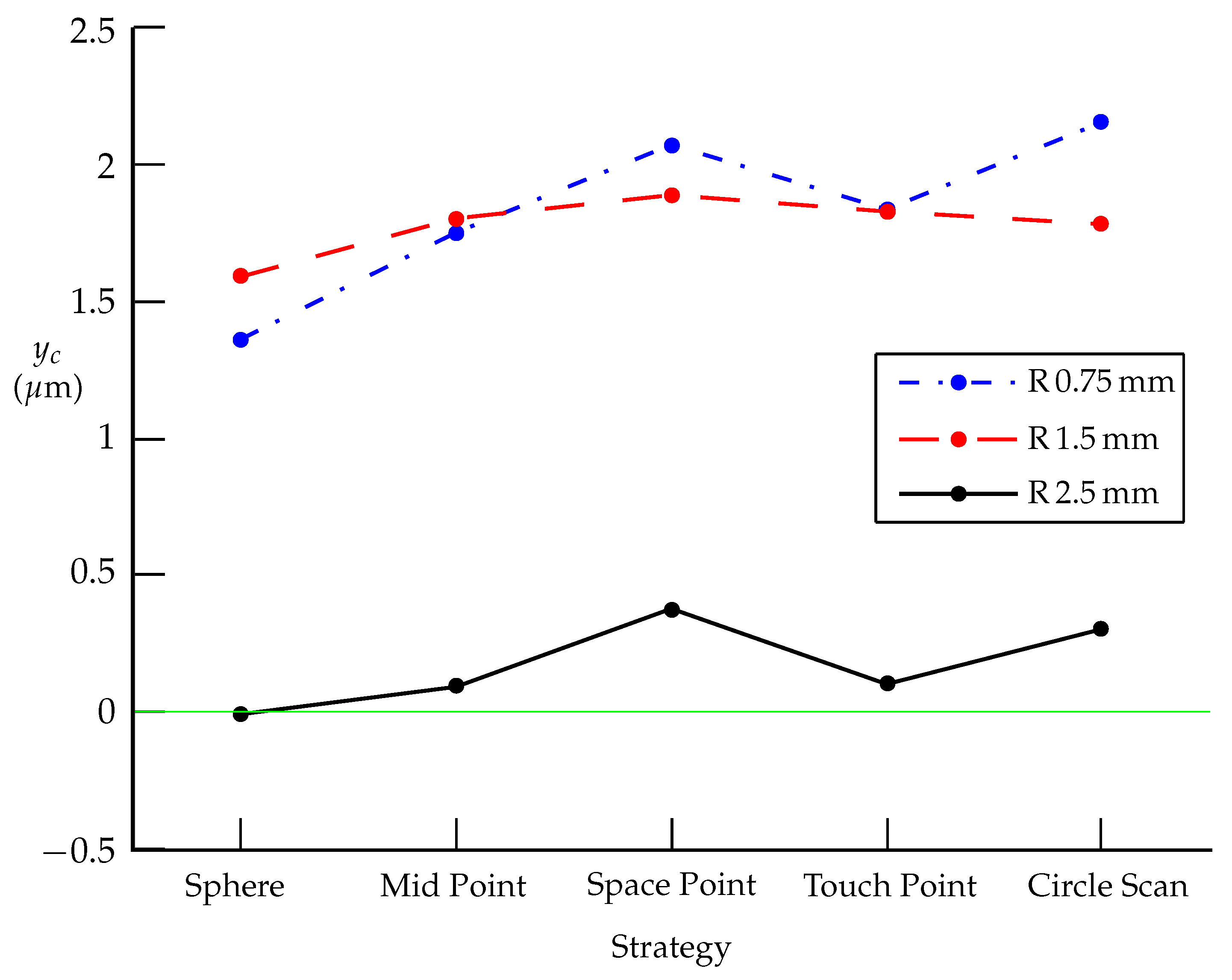
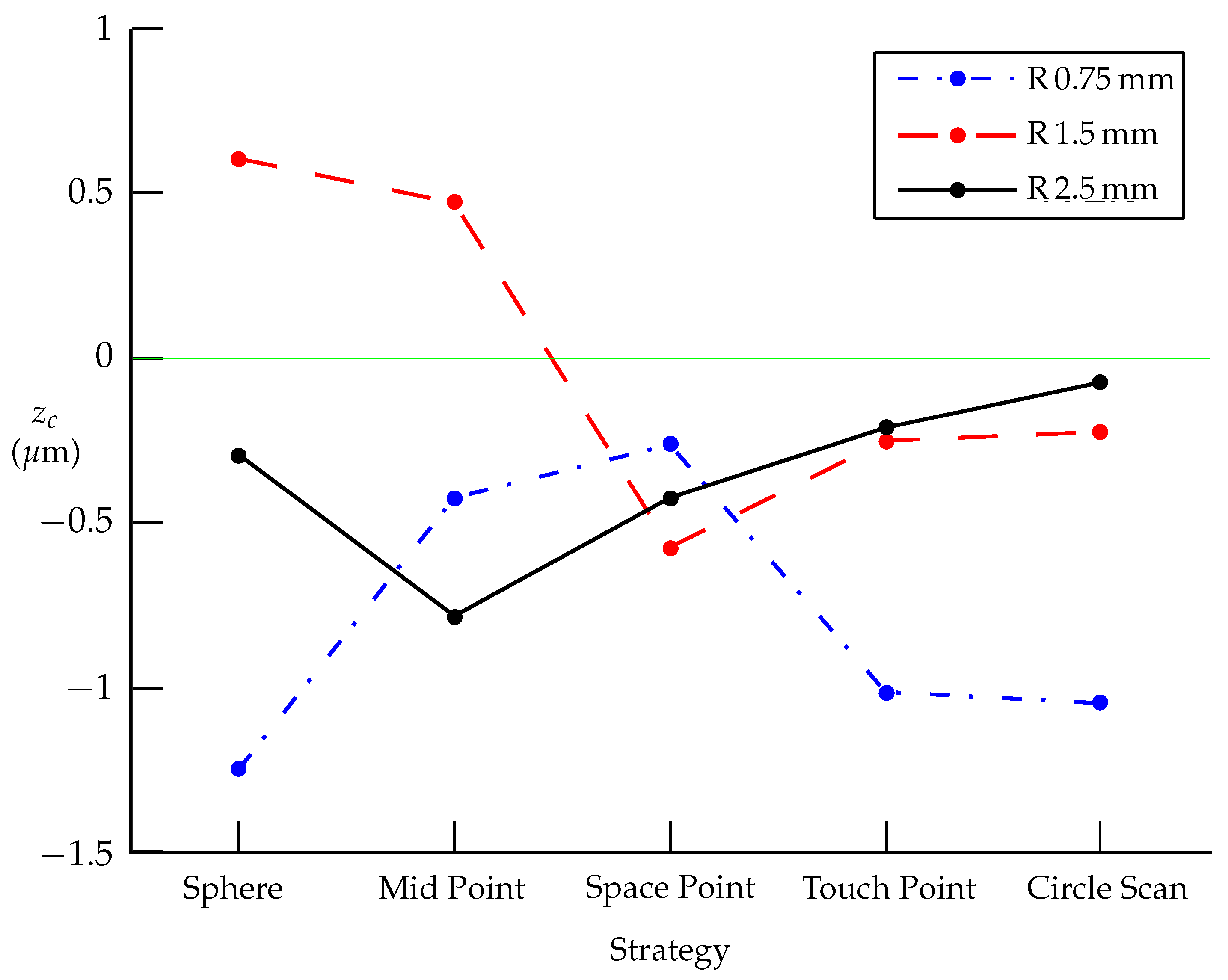
- The centers of spheres created from individual measurements depend on the evaluation method (LSQ, minimum feature) (see Table 4, Table 7 and Table 10), as well as on the elimination of outliers and data filtering. Figure 8, Figure 9 and Figure 10 show the position of the evaluated center for different probe radii and strategies. It is evident that for measuring the diameter and center of the sphere, the probe with a radius of mm provides the best results for all coordinates, while the mm probe gives better results for the and coordinates than the mm probe. The results are consistent with [14,15].
- 5.
- Form values in Calypso for a Feature and the values obtained using the geometric tolerance Form may not be identical. In the experiment, the Sphere features were created using the LSQ evaluation method, which corresponds to the Kåsa/Newton method. The geometric tolerance Form value in Calypso corresponds to the Minimum Feature evaluation method and to the Midrange method. Differences are present in both the diameters of the Spheres and their centers. The differences between the Form of the Sphere feature and Kåsa/Newton and between Form and Midrange are on the order of picometers. From the definitions of LSQ and Minimum Feature, and from the mathematical computation of RMSE, it follows that the geometric tolerance values from Minimum Feature (Midrange) will always be smaller than those from LSQ. Zaimovic-Uzunovic [13] recommends using a stylus tip with the smallest possible diameter for measuring shape deviations to limit mechanical filtering during surface measurement.
- 6.
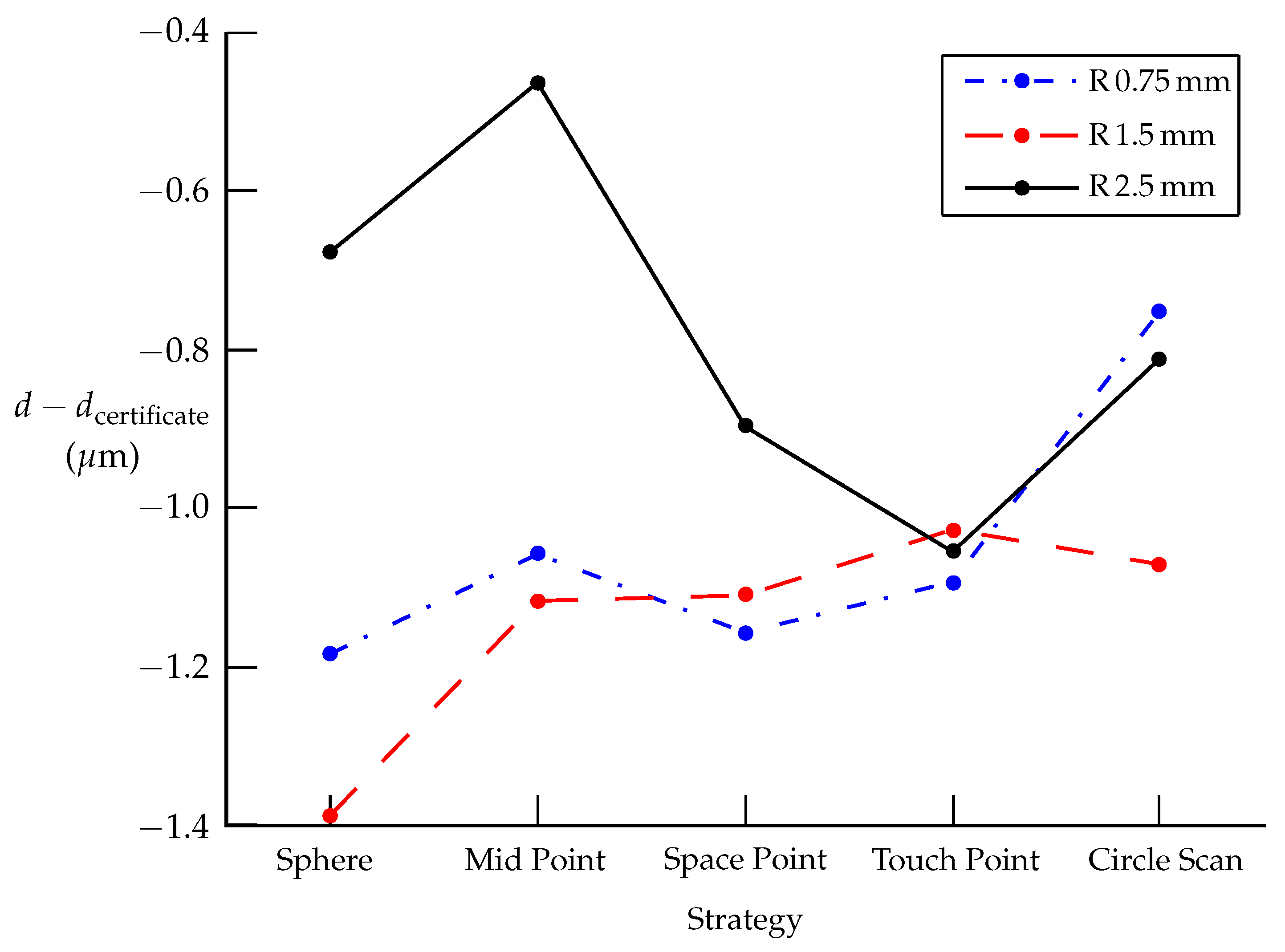
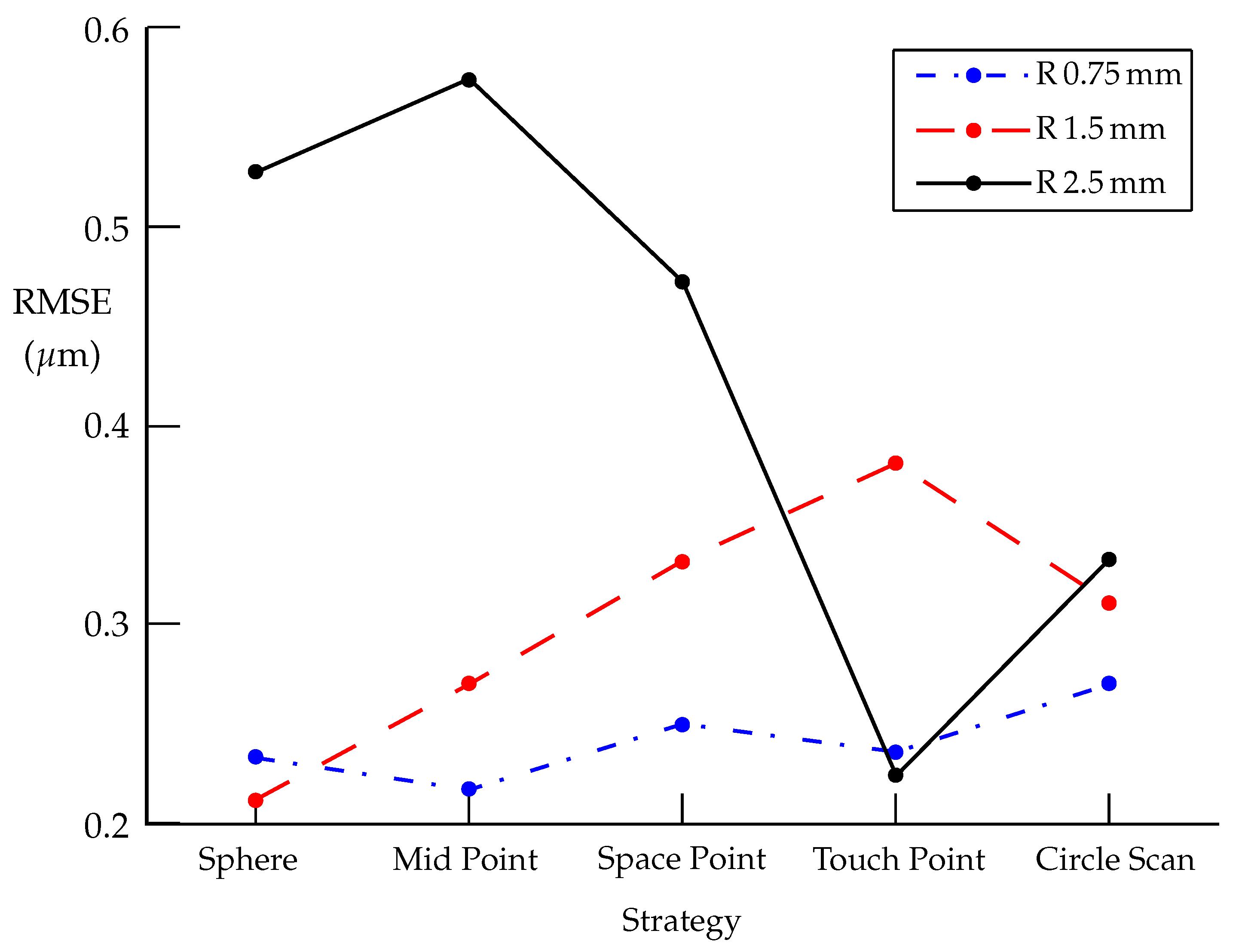
- The smallest RMSE values (Table 3 and Figure 11) and their variation ranges (VR) for the strategies Sphere, Mid Point, Space Point, and Touch Point were achieved for the probe mm, where the RMSE was at most 0.25 m and the variation range was 0.033 m. For the Kåsa/Newton method, RMSE values are always less than 0.575 m ( mm, Mid Point). These results also correspond to the half-width values from Calypso (maximum 0.532 m, VR 0.099 m) and Form 2 (maximum 0.463 m, VR 0.079 m).
- 7.
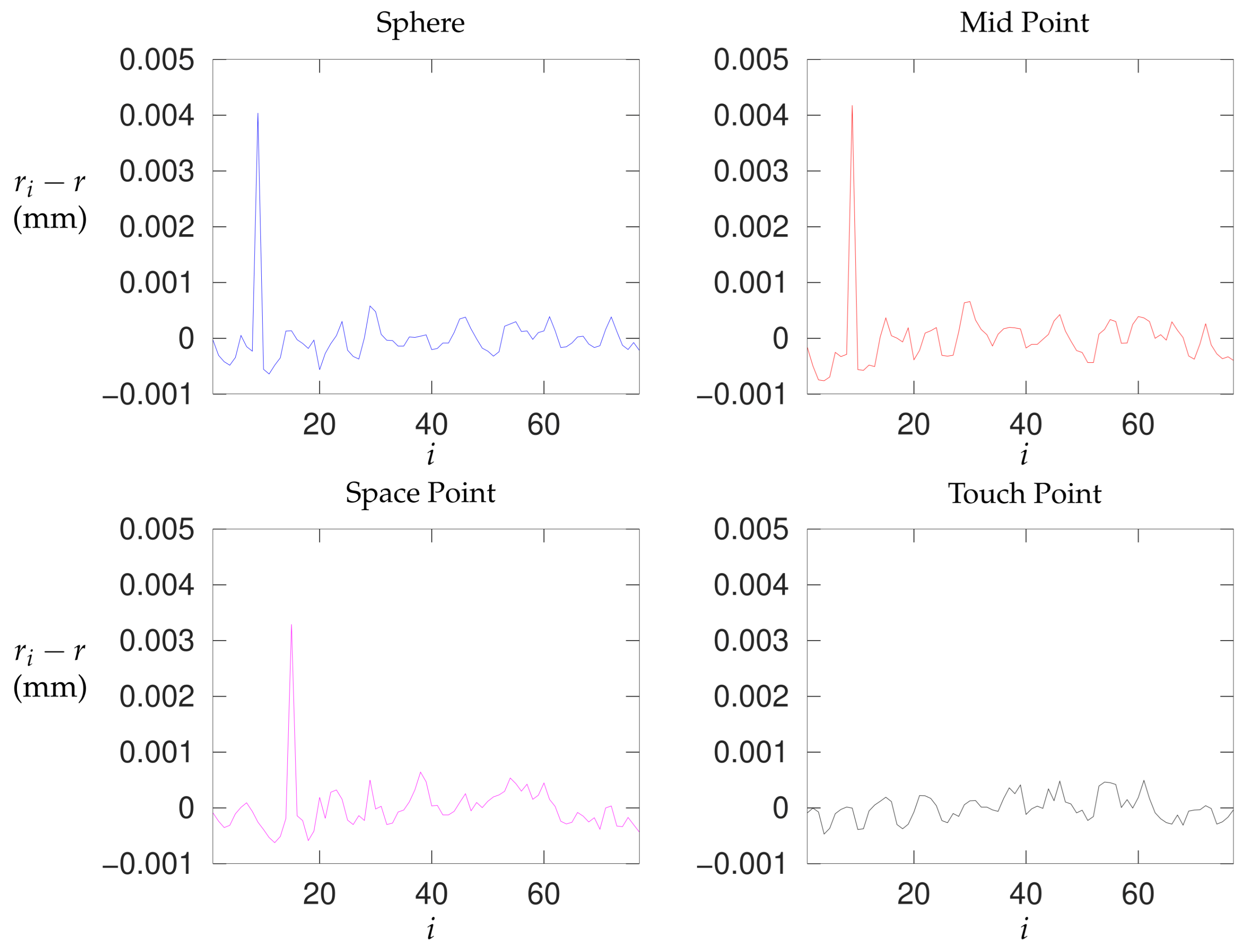
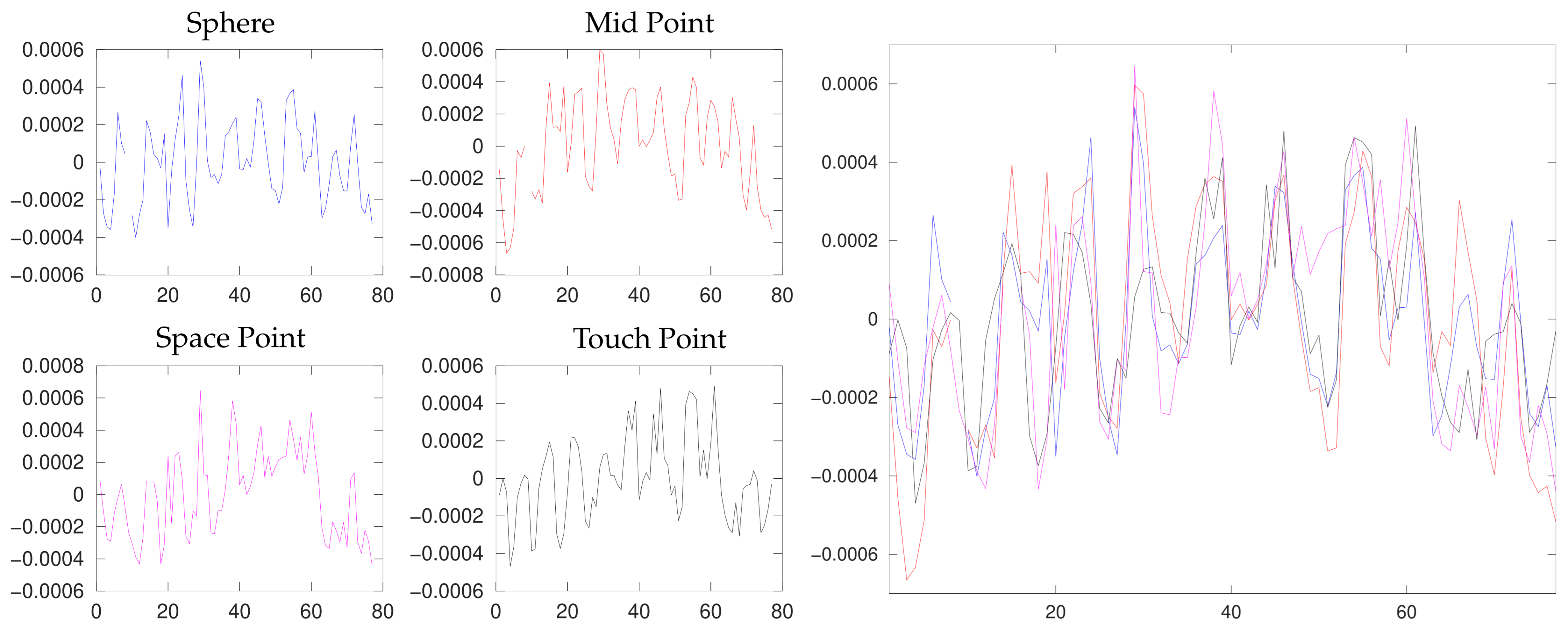
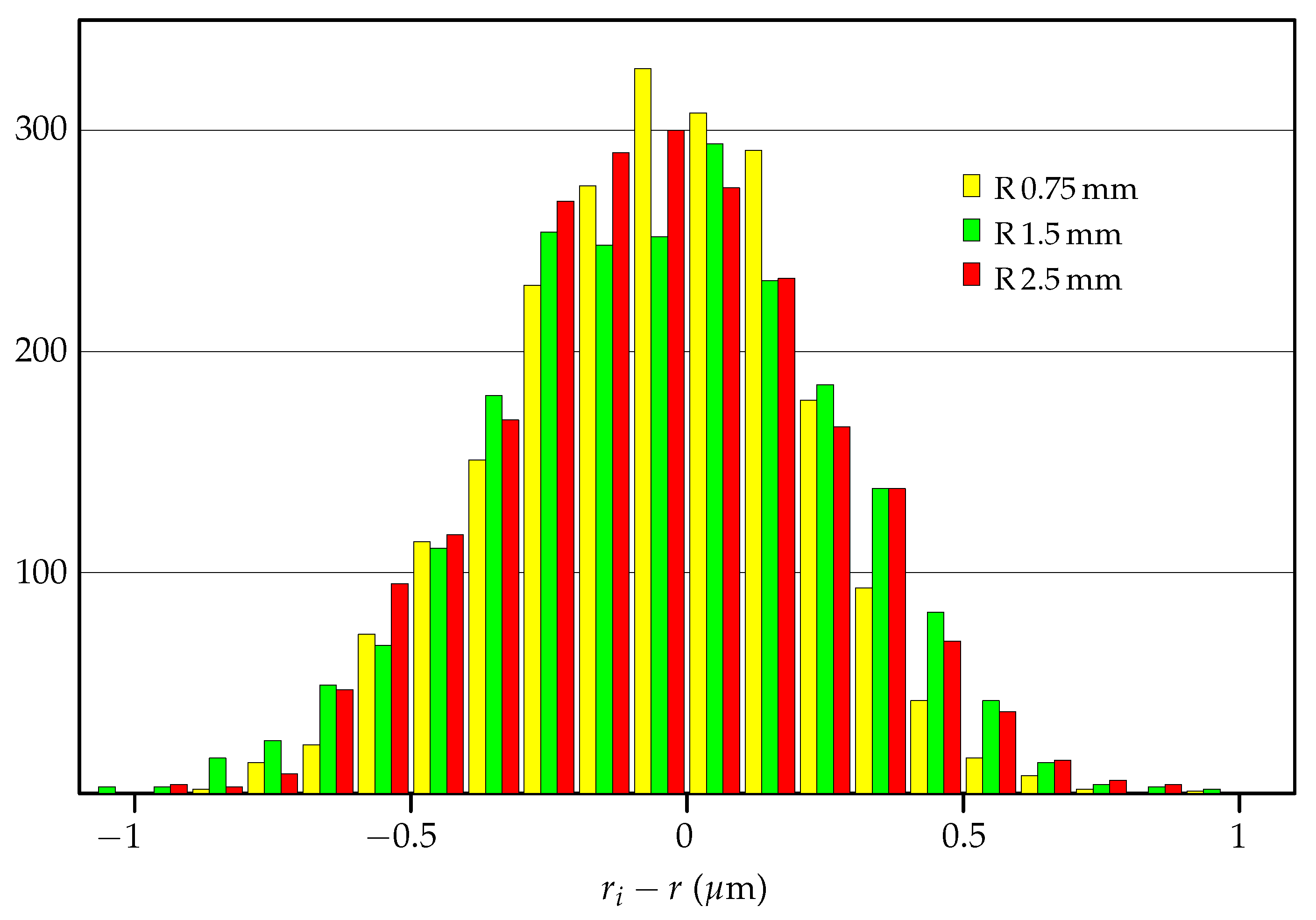
- Figure 12 shows the differences between the radii defined in (4) and the calculated radius r, for , …, 77, for four measurement options for mm. The Sphere and Mid Point datasets contain the extreme point , and the Space Point dataset contains the extreme point —so only one point in each of these cases causes the large half-width values in the corresponding rows of Table 3. Removing this point leads to smaller RMSE values; however, and become larger (see Figure 13 and Table 11 and Table 13). Figure 14 shows a histogram of the differences for the Circle Scan option for all three probe radii. Several extreme values for each radius have been ignored; the number of points has been 2147 of 2151, 2203 of 2205, and 2244 of 2253, respectively, for probe radii , , and mm. We believe that the difference between the three distributions is insignificant.
| Option | Form | Kåsa Newton | Mid Range | Kåsa Newton | Mid Range | Kåsa Newton |
|---|---|---|---|---|---|---|
| Half-Width (μm) | RMSE (μm) | |||||
| Sphere | 0.430 | 0.471 | 0.430 | 0.219 | 0.232 | |
| Mid Point | 0.561 | 0.631 | 0.564 | 0.292 | 0.320 | |
| Space Point | 0.487 | 0.543 | 0.487 | 0.266 | 0.288 | |
| Touch Point | 0.423 | 0.481 | 0.423 | 0.224 | 0.235 | |
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Varga, J.; Tóth, T.; Frankovský, P.; Dulebová, Ľ.; Spišák, E.; Zajačko, I.; Živčák, J. The Influence of Automated Machining Strategy on Geometric Deviations of Machined Surfaces. Appl. Sci. 2021, 11, 2353. [Google Scholar] [CrossRef]
- Mian, S.H.; Al-Ahmari, A. New developments in coordinate measuring machines for manufacturing industries. Int. J. Metrol. Qual. Eng. 2014, 5, 101. [Google Scholar] [CrossRef]
- Boeckmans, B.; Vlaeyen, M.; Probst, G.; Dewulf, W.; Haitjema, H.; Kruth, J.-P. CMM tactile probe performance evaluation according to ISO/DIS 10360-5:2018. In Proceedings of the Laser Metrology and Machine Performance XIII—13th International Conference and Exhibition on Laser Metrology, Machine Tool, CMM and Robotic Performance (LAM|DAMAP 2019), Aachen, Germany, 9–12 June 2019; pp. 111–119. Available online: https://www.euspen.eu/knowledge-base/LAM19121.pdf (accessed on 6 November 2025).
- Flack, D. Measurement Good Practice Guide No. 42. CMM Verification; National Physical Laboratory. Queen’s Printer and Controller of HMSO: Teddington, UK, 2011; ISSN 1368-6550. Available online: https://eprintspublications.npl.co.uk/2045/1/mgpg42.pdf (accessed on 6 November 2025).
- Lee, M.; Cho, N.-G. Surface normal estimation of freeform surface using efficient neighborhood selection method in point cloud data. Meas. Sci. Technol. 2013, 24, 095001. [Google Scholar] [CrossRef]
- Shen, Y.; Ren, J.; Huang, N.; Zhang, Y.; Zhang, X.; Zhu, L. Surface form inspection with contact coordinate measurement: A review. Int. J. Extrem. Manuf. 2023, 5, 022006. [Google Scholar] [CrossRef]
- Weckenmann, A.; Estler, T.; Peggs, G.; McMurtry, D. Probing Systems in Dimensional Metrology. CIRP Ann. 2004, 53, 657–684. [Google Scholar] [CrossRef]
- Carl Zeiss Industrielle Messtechnik GmbH. Influences on Measuring Results, EN_60_023_014I, Printed in Germany, CZ-II/2014; Carl Zeiss Industrielle Messtechnik GmbH: Oberkochen, Germany, 2014. [Google Scholar]
- Sadaoui, S.E.; Phan, N.D.M. Touch Probe Measurement in Dimensional Metrology: A Review. Int. J. Automot. Mech. Eng. 2021, 18, 8647–8657. [Google Scholar] [CrossRef]
- Renishaw User Guide: Precision Styli, Part Number: H-1000-3304. Available online: https://www.renishaw.com/resourcecentre/en/details/--130708?lang=en (accessed on 23 July 2025).
- What Is a CMM Stylus? Available online: https://hexagon.com/resources/resource-library/what-is-a-cmm-stylus (accessed on 23 July 2025).
- Zeiss Metrology Shop. Available online: https://shop.metrology.zeiss.co.uk/ (accessed on 23 July 2025).
- Zaimovic-Uzunovic, N.; Lemes, S. Cylindricity Measurement on a Coordinate Measuring Machine. In Advances in Manufacturing; Hamrol, A., Ciszak, O., Legutko, S., Jurczyk, M., Eds.; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Lou, S.; Brown, S.B.; Sun, W.; Zeng, W.; Jiang, X.; Scott, P.J. An investigation of the mechanical filtering effect of tactile CMM in the measurement of additively manufactured parts. Measurement 2019, 144, 173–182. [Google Scholar] [CrossRef]
- Miguel, P.C.; King, T.; Abackerli, Á. A review on methods for probe performance verification. Measurement 1998, 23, 15–33. [Google Scholar] [CrossRef]
- Johnson, R.P.; Yang, Q.; Butler, C. Dynamic error characteristics of touch trigger probes fitted to coordinate measuring machines. IEEE Trans. Instrum. Meas. 1998, 47, 1168–1172. [Google Scholar] [CrossRef]
- Ali, S. Probing System Characteristics in Coordinate Metrology. Meas. Sci. Rev. 2010, 10, 120–129. [Google Scholar] [CrossRef]
- Woźniak, A.; Dobosz, M. Influence of Measured Objects Parameters on CMM Touch Trigger Probe Accuracy of Probing. Precis. Eng. 2005, 29, 290–297. [Google Scholar] [CrossRef]
- Flack, D. Measurement Good Practice Guide No. 41. CMM Measurement Strategies; National Physical Laboratory. Queen’s Printer and Controller of HMSO: Teddington, UK, 2014; ISSN 1368-6550. Available online: https://www.npl.co.uk/resources/gpgs/cmm-measurement-strategies (accessed on 6 November 2025).
- ZEISS Measuring Strategies Cookbook—English Edition, 11th ed.; Carl Zeiss Industrial Metrology: Oberkochen, Germany, 2019.
- Zeng, L.; Chen, Y. Measurement point layout strategy of free-form surface based on gridding using coordinate measuring machine. Int. J. Metrol. Qual. Eng. 2023, 14, 7. [Google Scholar] [CrossRef]
- Bastas, A. Comparing the probing systems of coordinate measurement machine: Scanning probe versus touch-trigger probe. Measurement 2020, 156, 107604. [Google Scholar] [CrossRef]
- Swornowski, P.; Rucki, M. The errors occurring in the CMM fitting method. Meas. Sci. Rev. 2003, 3, 135–138. Available online: https://www.measurement.sk/2003/S3/Swornowski.pdf (accessed on 6 November 2025).
- Ali, S.H.R. The influence of fitting algorithm and scanning speed on roundness error for 50 mm standard ring measurement using CMM. Metrol. Meas. Syst. 2008, 15, 33–53. [Google Scholar]
- Calvo, R.; D’Amato, R.; Gómez, E.; Domingo, R. A Comparative Experimental Study of an Alternative CMM Error Model under Least-Squares and Minimum Zone Fittings for Industrial Measuring. Procedia Eng. 2015, 132, 780–787. [Google Scholar] [CrossRef]
- Calypso Networks Association. Calypso Basics—Operating Instructions; Version 2016; Zeiss: Oberkochen, Germany, 2016. [Google Scholar]
- Tóth, T.; Dovica, M.; Buša, J.; Buša, J. Verification of Coordinate Measuring Machine Using a Gauge Block. Meas. Sci. Rev. 2024, 24, 226–233. [Google Scholar] [CrossRef]
- Mazur, T.; Szymanski, T.; Samociuk, W.; Rucki, M.; Ryba, T. The Impact of Probe Angle and Swivel Length on Contact Point Identification in Coordinate Measuring Machine Measurements: A Case Study. Sensors 2025, 25, 2008. [Google Scholar] [CrossRef]
- Mazur, T.; Rucki, M.; Jakubowicz, M.; Cepova, L. Analysis of the Direction-Dependent Point Identification Accuracy in CMM Measurement. In Advances in Manufacturing III. MANUFACTURING 2022; Diering, M., Wieczorowski, M., Harugade, M., Pereira, A., Eds.; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Mazur, T.; Cepova, L.; Szymanski, T.; Rucki, M. Analysis of the Planar Point Identification Accuracy in CMM Measurements. Sensors 2022, 22, 7005. [Google Scholar] [CrossRef] [PubMed]
- Intro to Coordinate Metrology. Available online: https://hexagon.com/resources/resource-library/intro-coordinate-metrology (accessed on 24 September 2025).
- Giganto, S.; Martínez-Pellitero, S.; Meana, V.; Cuesta, E.; Barreiro, J. Influence of point cloud filtering on optical inspection of additive manufactured metal parts. Precis. Eng. 2024, 90, 12–20. [Google Scholar] [CrossRef]
- Mohaghegh, K.; Roncevic, V.; Andreasen, J.L.; De Chiffre, L. Investigation on the effect of filtering and plane creation on differences between XCT and CMM measurements on a miniature step gauge. In Proceedings of the 19th European Conference on Non-Destructive Testing, Göteborg, Sweden, 11–15 October 2020. [Google Scholar] [CrossRef]
- Raja, J.; Muralikrishnan, B.; Fu, S. Recent advances in separation of roughness, waviness and form. Precis. Eng. 2002, 26, 222–235. [Google Scholar] [CrossRef]
- Muralikrishnan, B.; Ren, W.; Stanfield, E.; Everett, D.; Zheng, A.; Doiron, T. Applications of profile filtering in the dimensional metrology of fuel cell plates. Meas. Sci. Technol. 2013, 24, 065003. [Google Scholar] [CrossRef]
- ISO 10360-2:2009; Geometrical Product Specifications (GPS)—Acceptance and Reverification Tests for Coordinate Measuring Machines (CMM), Part 2: CMMs Used for Measuring Linear Dimensions. ISO: Geneva, Switzerland, 2009.
- Carl Zeiss Contura G2 Specification, Version: October 2016, EN_60_022_335II Printed in Germany MAC-CZ-I/2014 Uoo; Carl Zeiss Industrielle Messtechnik GmbH: Oberkochen, Germany, 2014; Available online: https://5.imimg.com/data5/SELLER/Doc/2020/10/IO/QE/OS/50240193/7-zeiss-contura-g2-coordinate-measuring-machine.pdf (accessed on 6 November 2025).
- Delonge, P. Computer optimization of Deschamps’ method and error cancellation in reflectometry. In Proceedings of the IMEKO Symposium on Microwave Measurement, Budapest, Hungary, 10–13 May 1972; pp. 117–123. [Google Scholar]
- Kåsa, I. A circle fitting procedure and its error analysis. IEEE Trans. Inst. Meas. 1976, 25, 8–14. [Google Scholar] [CrossRef]
- Chernov, N. Circular and Linear Regression: Fitting Circles and Lines by Least Squares; CRC Press, Taylor & Francis Group, A CHAPMAN & HALL BOOK: Boca Raton, FL, USA, 2010; Available online: https://web.archive.org/web/20130512154618id_/http://people.cas.uab.edu:80/~mosya/cl/book.pdf (accessed on 6 November 2025).
- Zhang, X.; Zhang, H.; He, X.; Xu, M.; Jiang, X. Chebyshev fitting of complex surfaces for precision metrology. Measurement 2013, 46, 3720–3724. [Google Scholar] [CrossRef]
- Nievergelt, Y. A finite algorithm to fit geometrically all midrange lines, circles, planes, spheres, hyperplanes, and hyperspheres. Numer. Math. 2002, 91, 257–303. [Google Scholar] [CrossRef]
- Eaton, J.W.; Bateman, D.; Hauberg, S.; Wehbring, R. GNU Octave Version 10.3.0 Manual: A High-Level Interactive Language for Numerical Computations. 2025. Available online: https://octave.org/doc/v10.3.0/ (accessed on 6 November 2025).
- Matlab, R2025b; The MathWorks, Inc.: Natick, MA, USA, 2025. Available online: https://ch.mathworks.com/products/matlab.html (accessed on 10 April 2025).
- Shakarji, C.M. Least-Squares Fitting Algorithms of the NIST Algorithm Testing System. J. Res. NIST 1998, 103, 633–641. [Google Scholar] [CrossRef] [PubMed]
- Gander, W.; Golub, G.H.; Strebel, R. Least-squares fitting of circles and ellipses. BIT 1994, 34, 558–578. [Google Scholar] [CrossRef]
- Pratt, V. Direct least-squares fitting of algebraic surfaces. Comput. Graph. 1987, 21, 145–152. Available online: http://boole.stanford.edu/pub/fit.pdf (accessed on 6 November 2025). [CrossRef]




| Category | Items in Category |
|---|---|
| Feature | Sphere, Point, Plane, Cylinder, Line, Circle, etc. |
| Point strategies/Point mode | Touch Point, Space Point, Mid Point, Plane Point, etc. |
| Circle strategies | Single Points, Four Point Cirle Macro, Circle Path, etc. |
| Sphere strategies | Single Points, Sphere Macro, Circle Path, etc. |
| Feature evaluation method | LSQ (Gauss), Minimum Feature, Maximum inscribed element, Minimum circumscribed element, etc. |
| Form and position | Form, Flatness, Roundness, Cylindricity, etc. |
| Outlier elimination | Standard deviation multiplicator, Undulation per revolution, wavelength |
| Characteristic | Dimension, Position , Geometric tolerance, etc. |
| Probe Name | (mm) | (mm) | (mm) | (mm) | (mm) |
|---|---|---|---|---|---|
| R 0.75 | .51.5 | 20 | 1 | 60 | 0.750844 |
| R 1.55 | 3 | 33 | 2 | 50 | 1.500736 |
| R 2.55 | 5 | 30 | .53.5 | 50 | 2.500557 |
| Option | Calypso | Kåsa Newton | Midrange | |
|---|---|---|---|---|
| 0.000646 | 0.000645 | 0.000730 | ||
| Sphere | 0.001361 | 0.001361 | 0.001414 | |
| 0.000478 | 0.000478 | 0.000502 | ||
| Mid Point | 0.001750 | 0.001750 | 0.001815 | |
| 0.000271 | 0.000271 | 0.000329 | ||
| Space Point | 0.002071 | 0.002071 | 0.002197 | |
| 0.000483 | 0.000483 | 0.000547 | ||
| Touch Point | 0.001835 | 0.001835 | 0.001751 | |
| 0.000140 | 0.000139 | |||
| Circle Scan | 0.002151 | 0.002153 | 0.001800 | |
| Option | Calypso | Kåsa Newton | Midrange | |
|---|---|---|---|---|
| d | 25.399070 | 25.399070 | 25.399197 | |
| Sphere | ||||
| d | 25.399196 | 25.399196 | 25.399259 | |
| Mid Point | ||||
| d | 25.399097 | 25.399097 | 25.399260 | |
| Space Point | ||||
| d | 25.399161 | 25.399161 | 25.398889 | |
| Touch Point | ||||
| d | 25.399503 | 25.399506 | 25.399049 | |
| Circle Scan | ||||
| Option | ||||
|---|---|---|---|---|
| Sphere | 12.0 | |||
| Mid Point | 12.5 | |||
| Space Point | 22.6 | |||
| Touch Point | 12.1 | |||
| Circle Scan | 19.6 |
| Option | Calypso | Kåsa Newton | Midrange | |
|---|---|---|---|---|
| 0.001549 | 0.001549 | 0.001759 | ||
| Sphere | 0.001589 | 0.001589 | 0.001568 | |
| 0.000606 | 0.000606 | 0.000604 | ||
| 0.001450 | 0.001450 | 0.001741 | ||
| Mid Point | 0.001803 | 0.001802 | 0.001953 | |
| 0.000471 | 0.000471 | 0.000497 | ||
| 0.001371 | 0.001371 | 0.001643 | ||
| Space Point | 0.001887 | 0.001887 | 0.002033 | |
| 0.001413 | 0.001413 | 0.001097 | ||
| Touch Point | 0.001827 | 0.001827 | 0.002754 | |
| 0.000601 | ||||
| 0.001335 | 0.001334 | 0.000814 | ||
| Circle Scan | 0.001779 | 0.001781 | 0.002076 | |
| 0.000125 |
| Option | Calypso | Kåsa Newton | Midrange | |
|---|---|---|---|---|
| d | 25.398866 | 25.398866 | 25.398936 | |
| Sphere | ||||
| d | 25.399137 | 25.399137 | 25.399212 | |
| Mid Point | ||||
| d | 25.399144 | 25.399144 | 25.399207 | |
| Space Point | ||||
| d | 25.399227 | 25.399227 | 25.399063 | |
| Touch Point | ||||
| d | 25.399183 | 25.399185 | 25.399100 | |
| Circle Scan | ||||
| Option | ||||
|---|---|---|---|---|
| Sphere | 12.4 | |||
| Mid Point | 17.9 | |||
| Space Point | 24.0 | |||
| Touch Point | 7.4 | 24.0 | ||
| Circle Scan | 30.3 |
| Option | Calypso | Kåsa Newton | Midrange | |
|---|---|---|---|---|
| 0.000460 | ||||
| Sphere | ||||
| 0.000414 | ||||
| Mid Point | 0.000093 | 0.000093 | ||
| 0.000128 | ||||
| Space Point | 0.000378 | 0.000378 | 0.001886 | |
| 0.000355 | ||||
| Touch Point | 0.000103 | 0.000103 | 0.000130 | |
| Circle Scan | 0.000302 | 0.000304 | ||
| 0.000769 |
| Option | Calypso | Kåsa Newton | Midrange | |
|---|---|---|---|---|
| d | 25.399577 | 25.399577 | 25.399676 | |
| Sphere | ||||
| d | 25.399791 | 25.399791 | 25.399863 | |
| Mid Point | ||||
| d | 25.399357 | 25.399357 | 25.399582 | |
| Space Point | ||||
| d | 25.399199 | 25.399199 | 25.399197 | |
| Touch Point | ||||
| d | 25.399443 | 25.399446 | 25.399729 | |
| Circle Scan | ||||
| Option | ||||
|---|---|---|---|---|
| Sphere | 23.7 | 21.3 | ||
| Mid Point | 21.0 | 20.7 | ||
| Space Point | 20.9 | 31.2 | 13.6 | 11.7 |
| Touch Point | 0.6 | 11.7 | ||
| Circle Scan | 27.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buša, J.; Dovica, M.; Tóth, T. Comparison of Point Measurement Strategies and Mathematical Algorithms for Evaluation in Contact Measurement of a Spherical Surface on a CMM. Appl. Sci. 2025, 15, 12392. https://doi.org/10.3390/app152312392
Buša J, Dovica M, Tóth T. Comparison of Point Measurement Strategies and Mathematical Algorithms for Evaluation in Contact Measurement of a Spherical Surface on a CMM. Applied Sciences. 2025; 15(23):12392. https://doi.org/10.3390/app152312392
Chicago/Turabian StyleBuša, Ján, Miroslav Dovica, and Teodor Tóth. 2025. "Comparison of Point Measurement Strategies and Mathematical Algorithms for Evaluation in Contact Measurement of a Spherical Surface on a CMM" Applied Sciences 15, no. 23: 12392. https://doi.org/10.3390/app152312392
APA StyleBuša, J., Dovica, M., & Tóth, T. (2025). Comparison of Point Measurement Strategies and Mathematical Algorithms for Evaluation in Contact Measurement of a Spherical Surface on a CMM. Applied Sciences, 15(23), 12392. https://doi.org/10.3390/app152312392







