Robust Path-Tracking Control for Autonomous Vehicles: A Model-Reference-Adaptive-Control-Based Integrated Chassis Control Strategy
Abstract
1. Introduction
- Adding actuators or applying basic coordination strategies alone may not adequately address model uncertainties or external disturbances. For instance, determining front and rear steering angles in 4 WS vehicles based on nominal models has been criticized for underutilizing the system’s capabilities, resulting in limited performance gains [24].
- An Adaptive Framework for Integrated Chassis Control: A new hierarchical control architecture is proposed that fundamentally integrates a high-level Model Reference Adaptive Control (MRAC) strategy with a low-level Integrated Chassis Control (ICC) layer. This architecture is designed to overcome the critical limitation of traditional ICC, which relies on a fixed nominal model. The MRAC framework actively compensates for severe uncertainties (e.g., modeling errors from LTI assumptions, parameter variations in mass and friction, and external disturbances), which cause nominal controllers to degrade.
- Stability for a Safety-Critical Adaptive System: The practical stability and reliability of the proposed adaptive controller are ensured by incorporating a -modification term into the MRAC adaptation laws. While standard adaptive laws can suffer from parameter drift and high-frequency chattering, this modification guarantees the Uniformly Ultimately Bounded (UUB) stability of all closed-loop signals, making the adaptive strategy robust and suitable for a safety-critical application like autonomous driving.
- Optimal Coordination of Adaptive Commands under Actuator Constraints: The gap between high-level adaptive control theory and practical multi-actuator implementation is bridged. A constrained weighted least-squares torque allocator is designed to translate the adaptive yaw moment command into optimal, coordinated commands for the four in-wheel motors. This allocator robustly handles the over-actuated system while respecting critical, real-world actuator limitations, including static torque-speed (T-N) maps and dynamic torque-rate constraints.
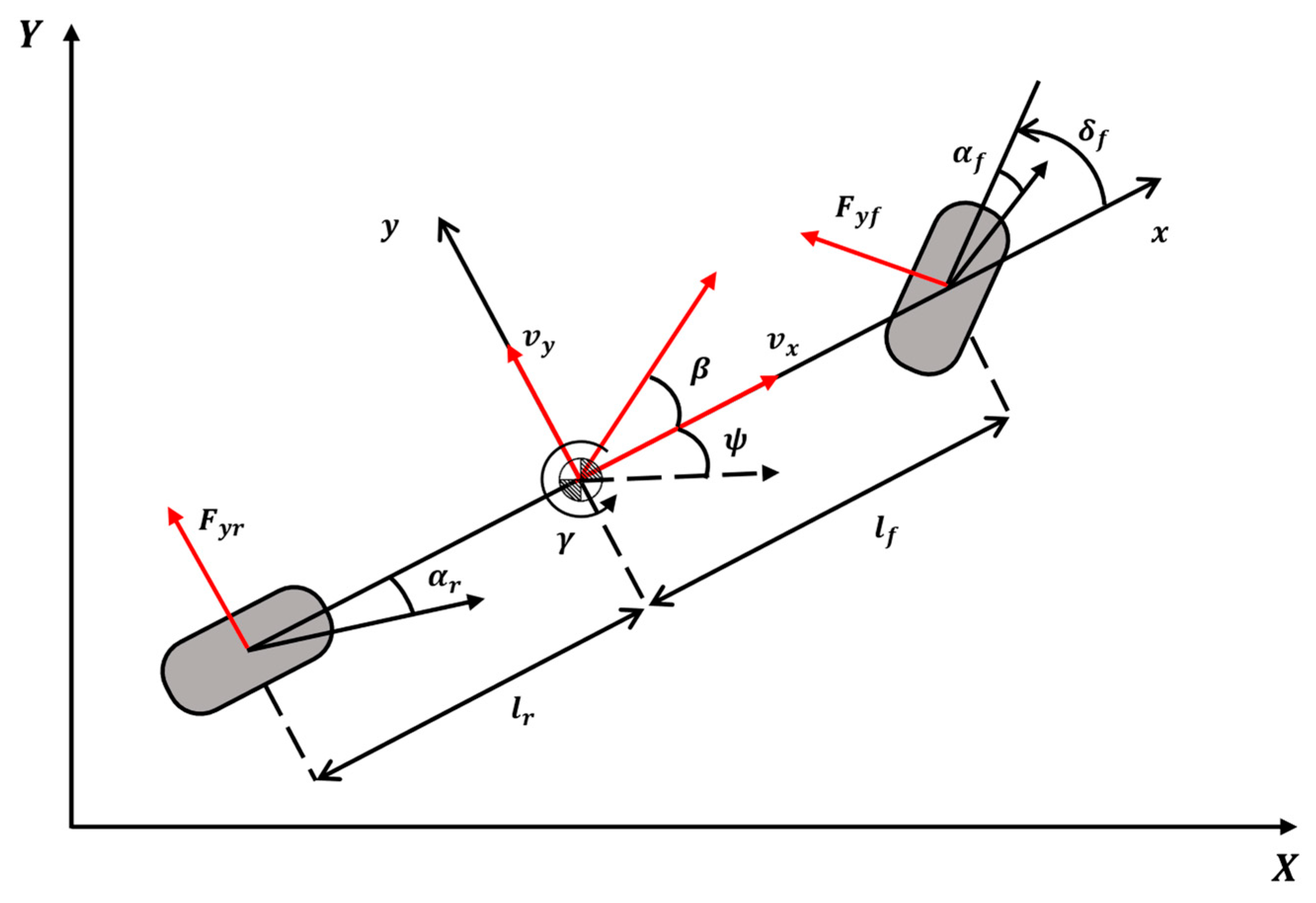
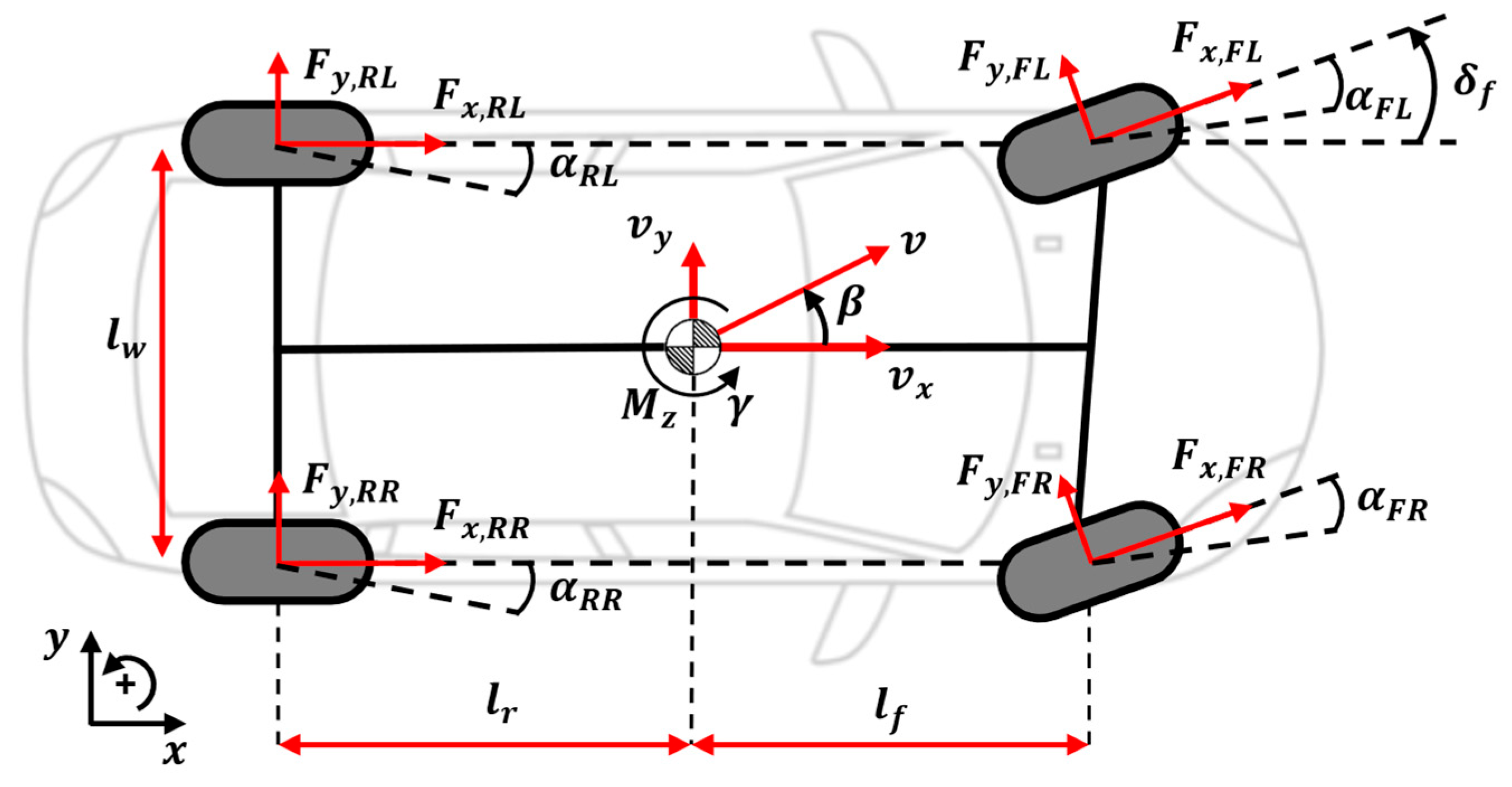
2. Vehicle Dynamics Model
2.1. Path-Following Model
2.2. Torque-Vectoring Model
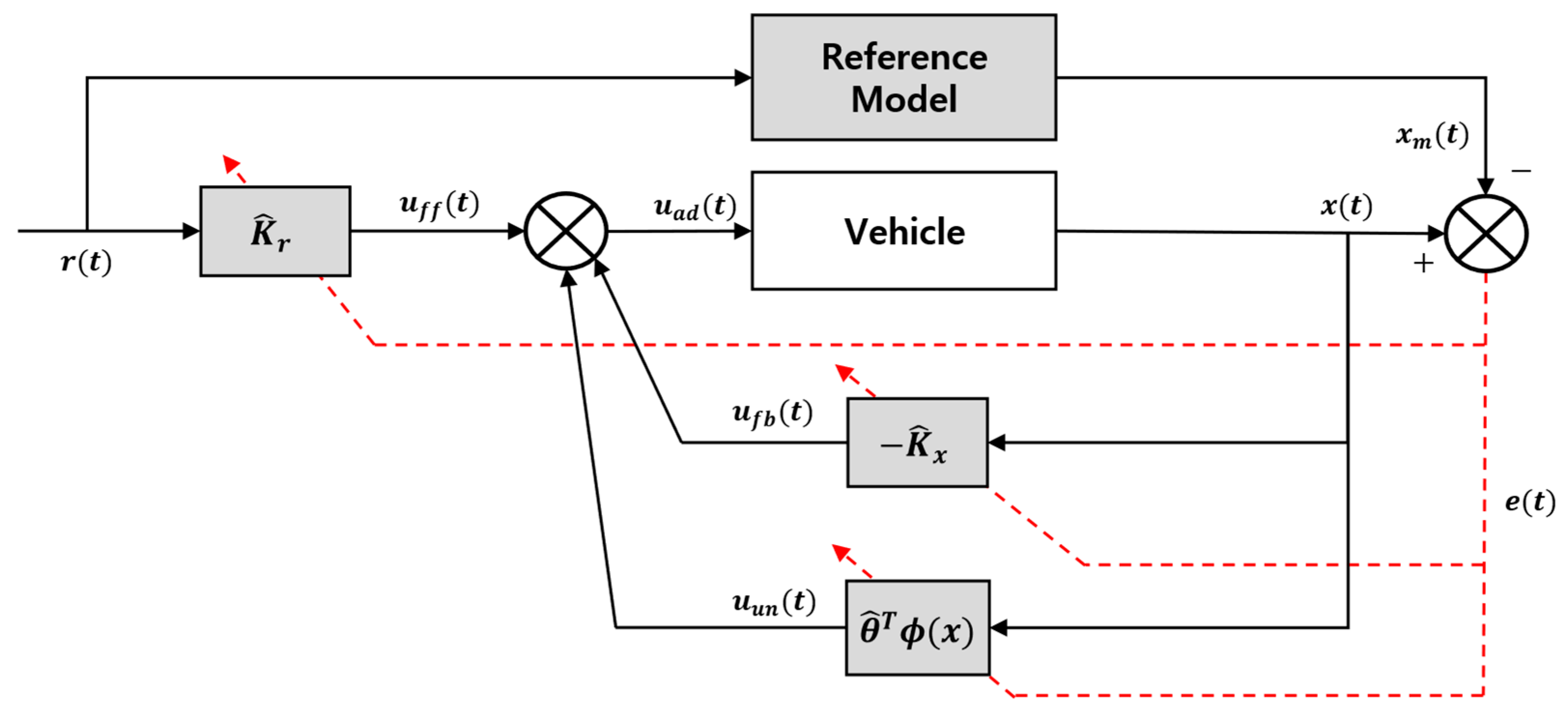
3. MRAC
3.1. Standard MRAC Framework
3.2. σ-Modification
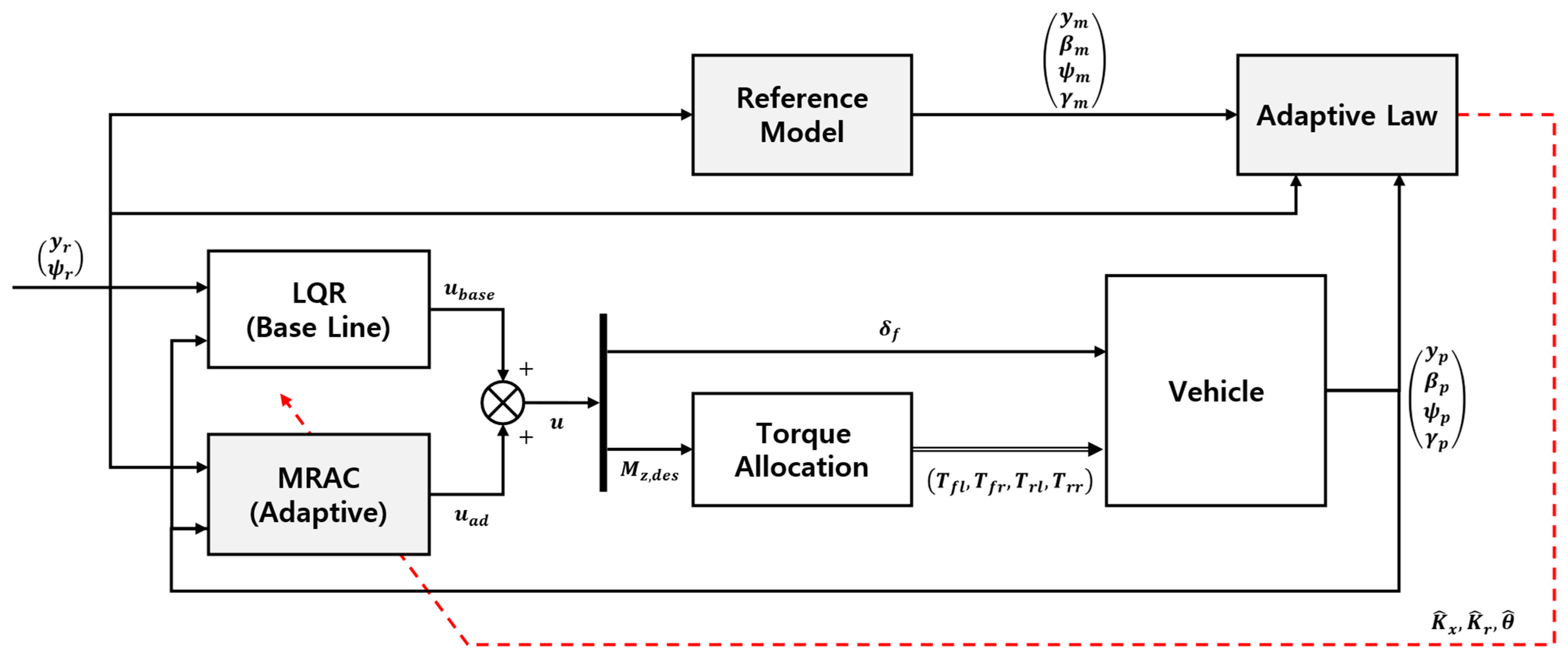
4. Design of the Proposed Adaptive Integrated Chassis Controller
4.1. Design of the Lateral Controller
4.2. Design of the Chassis Controller
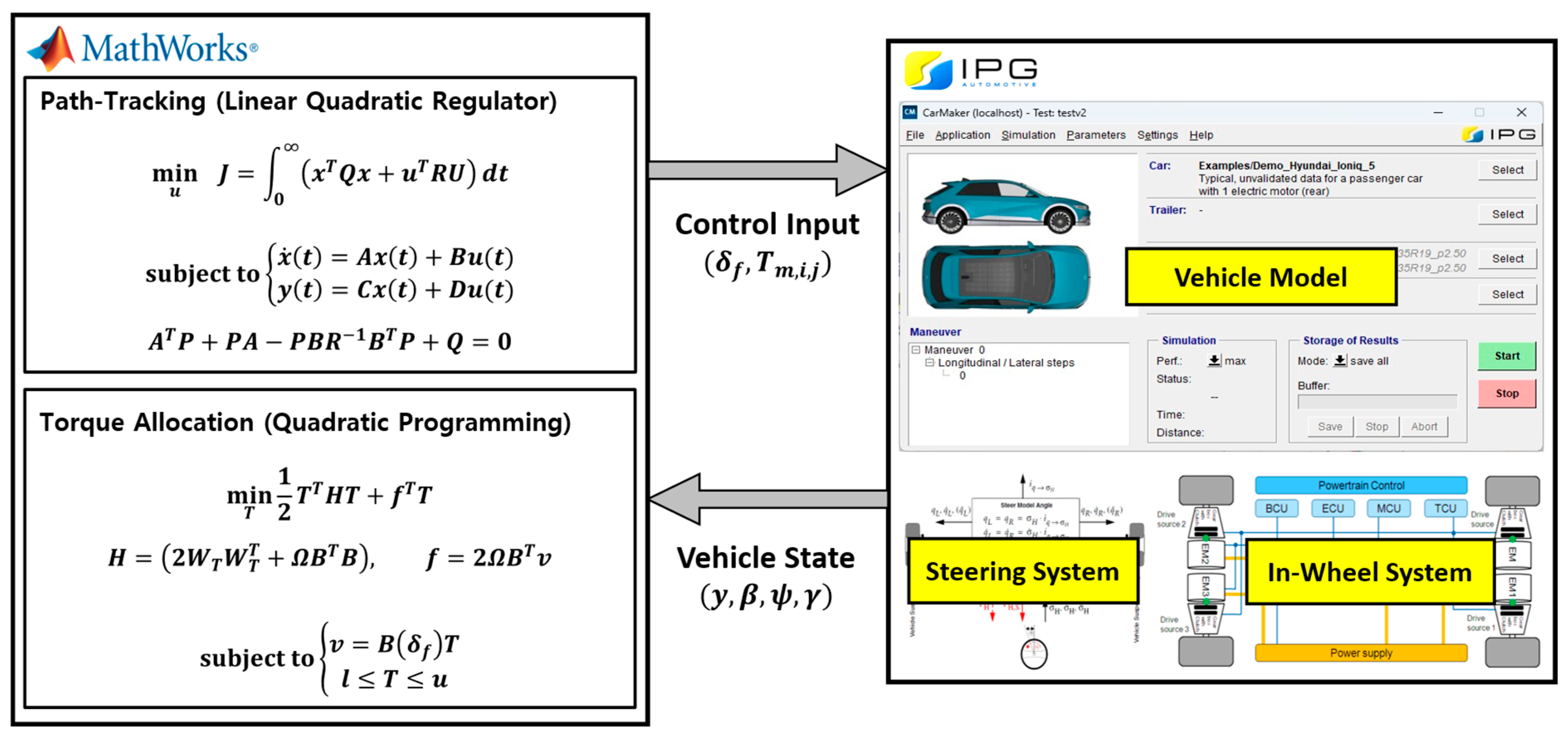
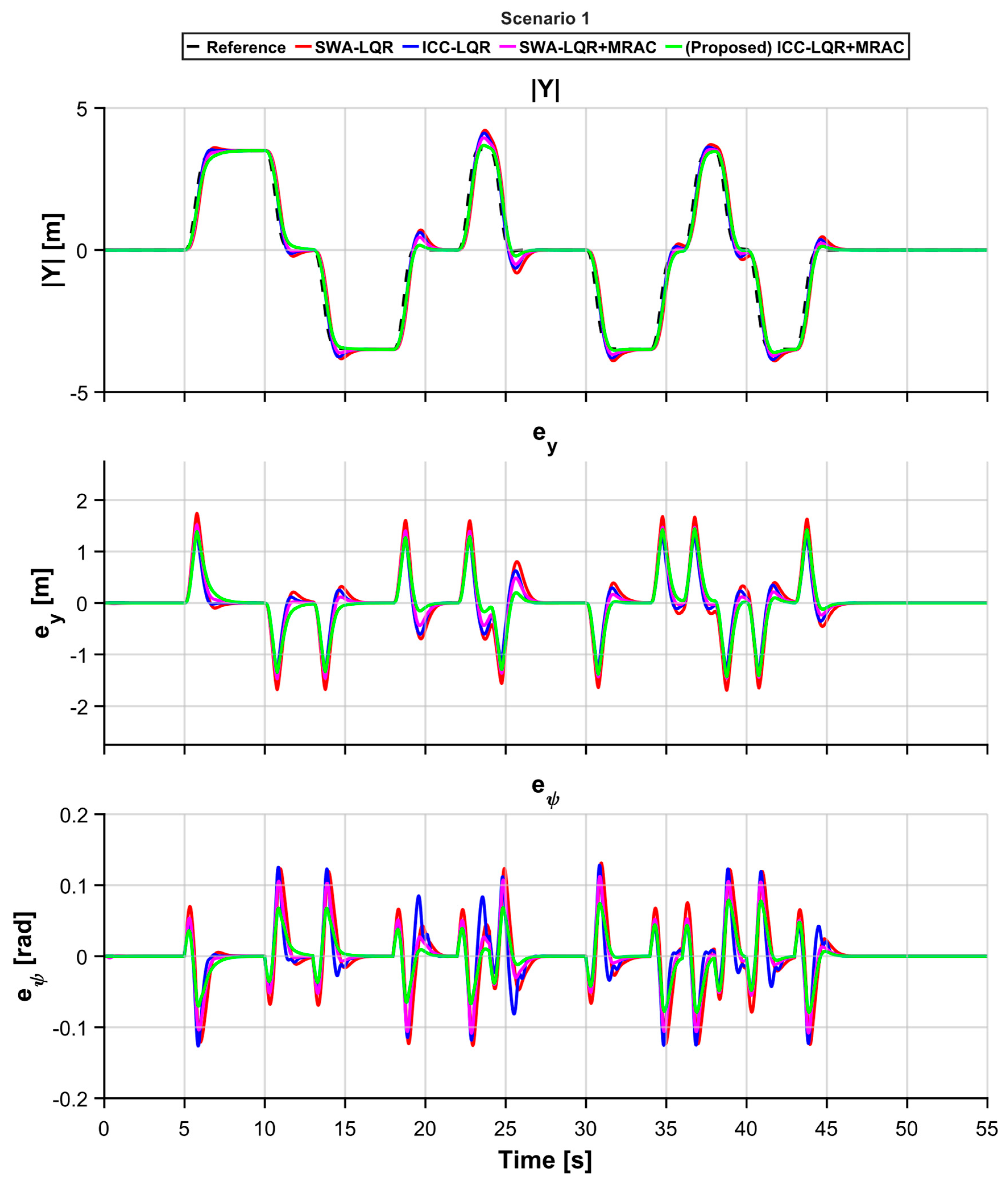
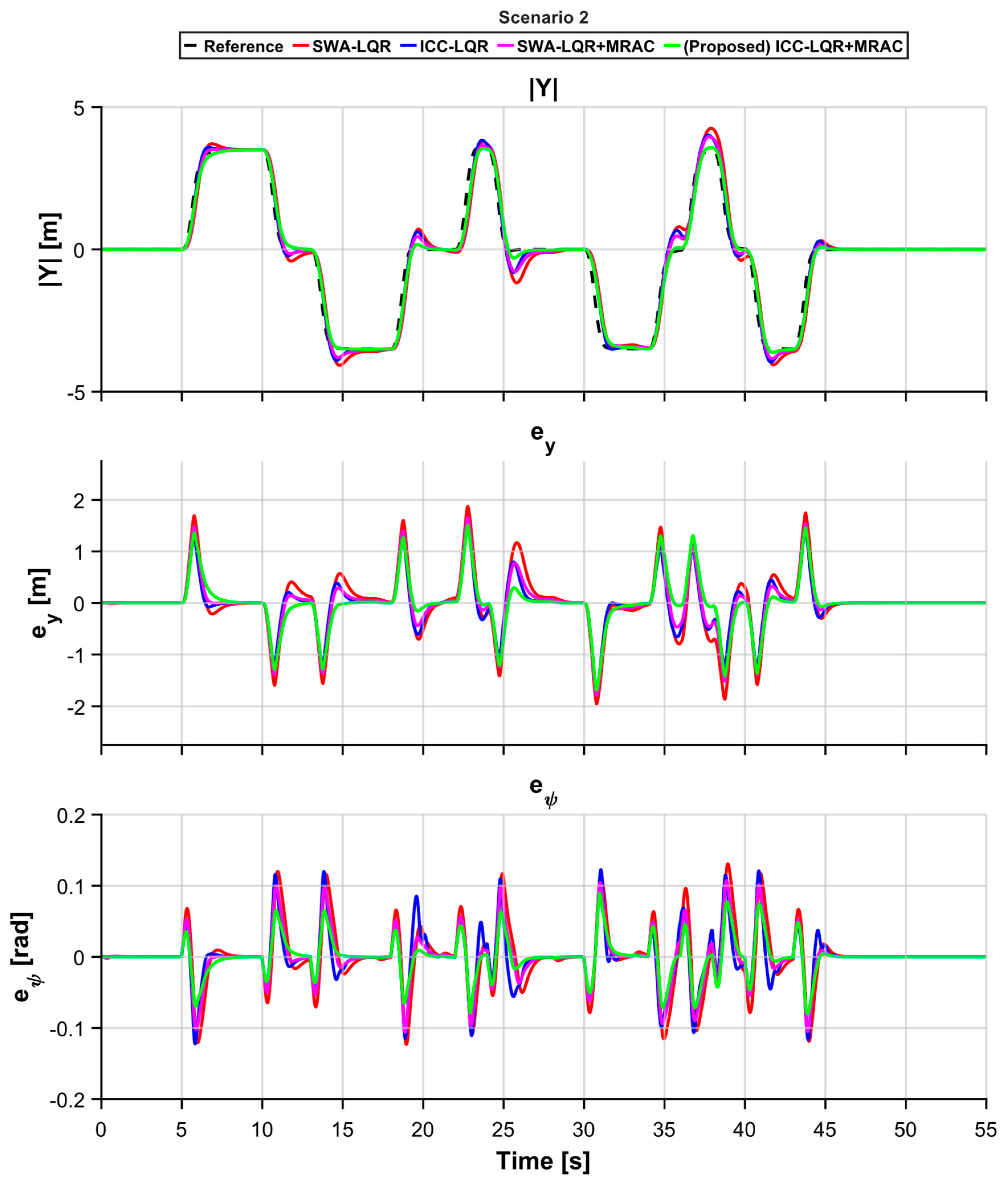
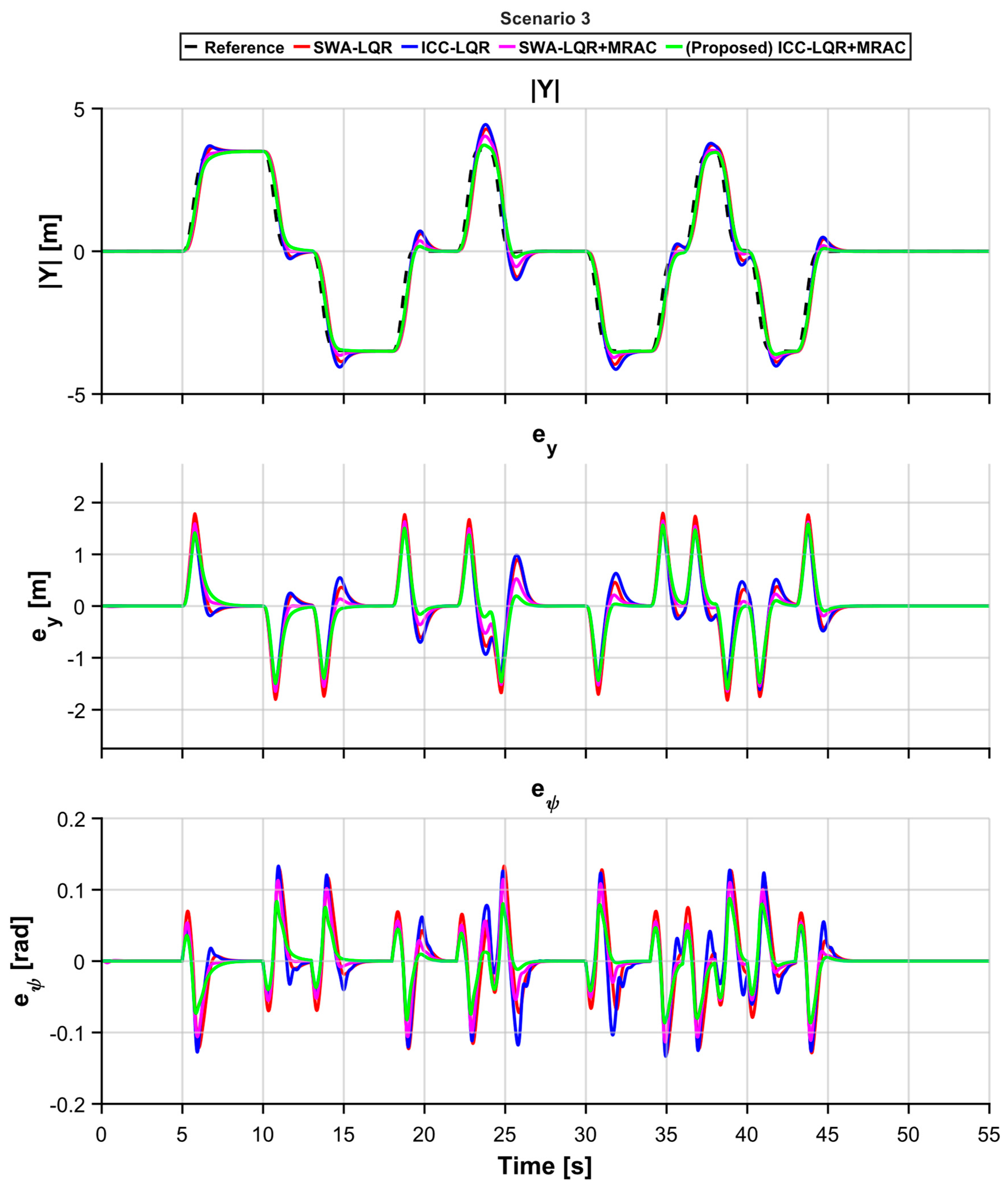
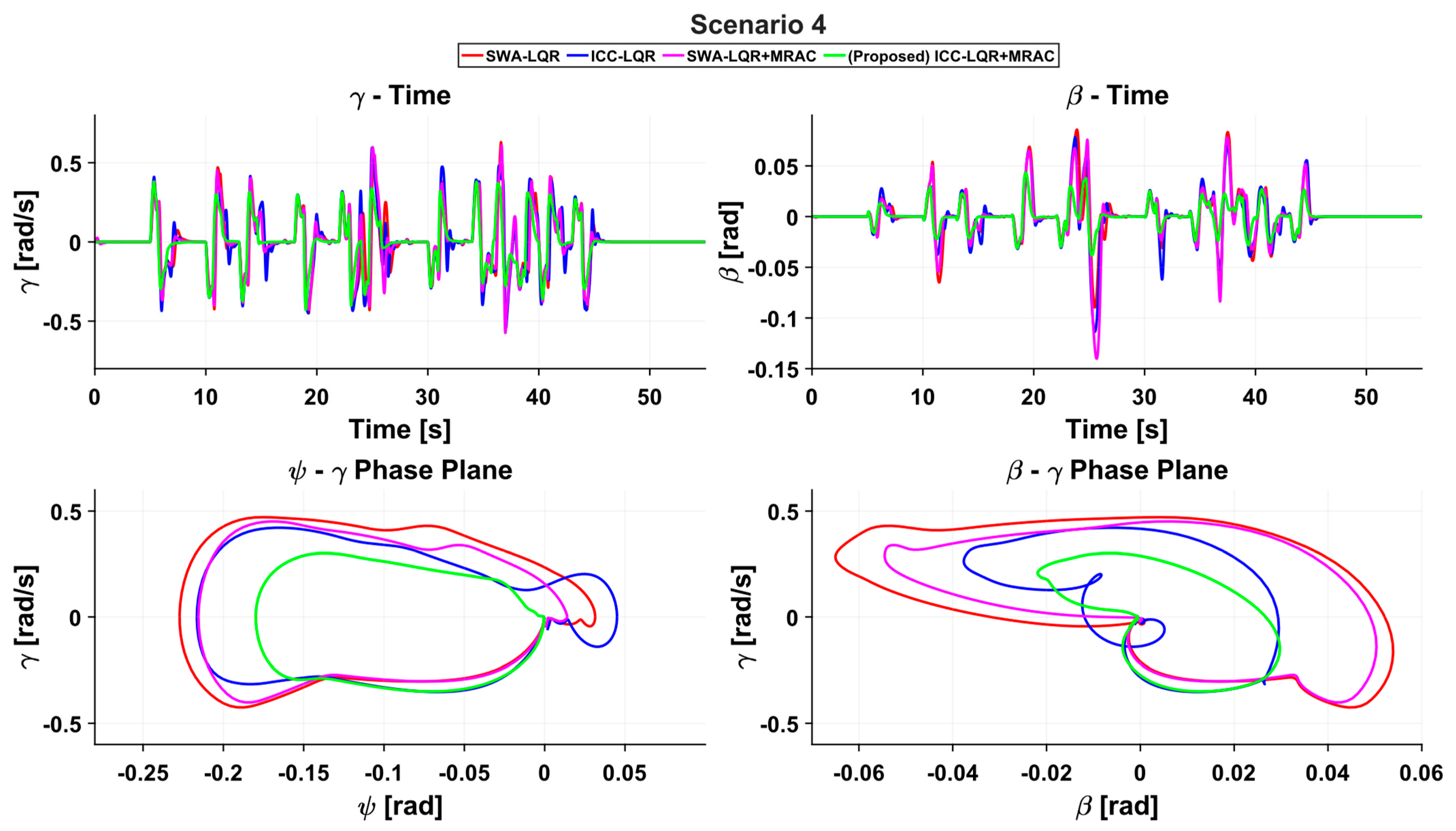
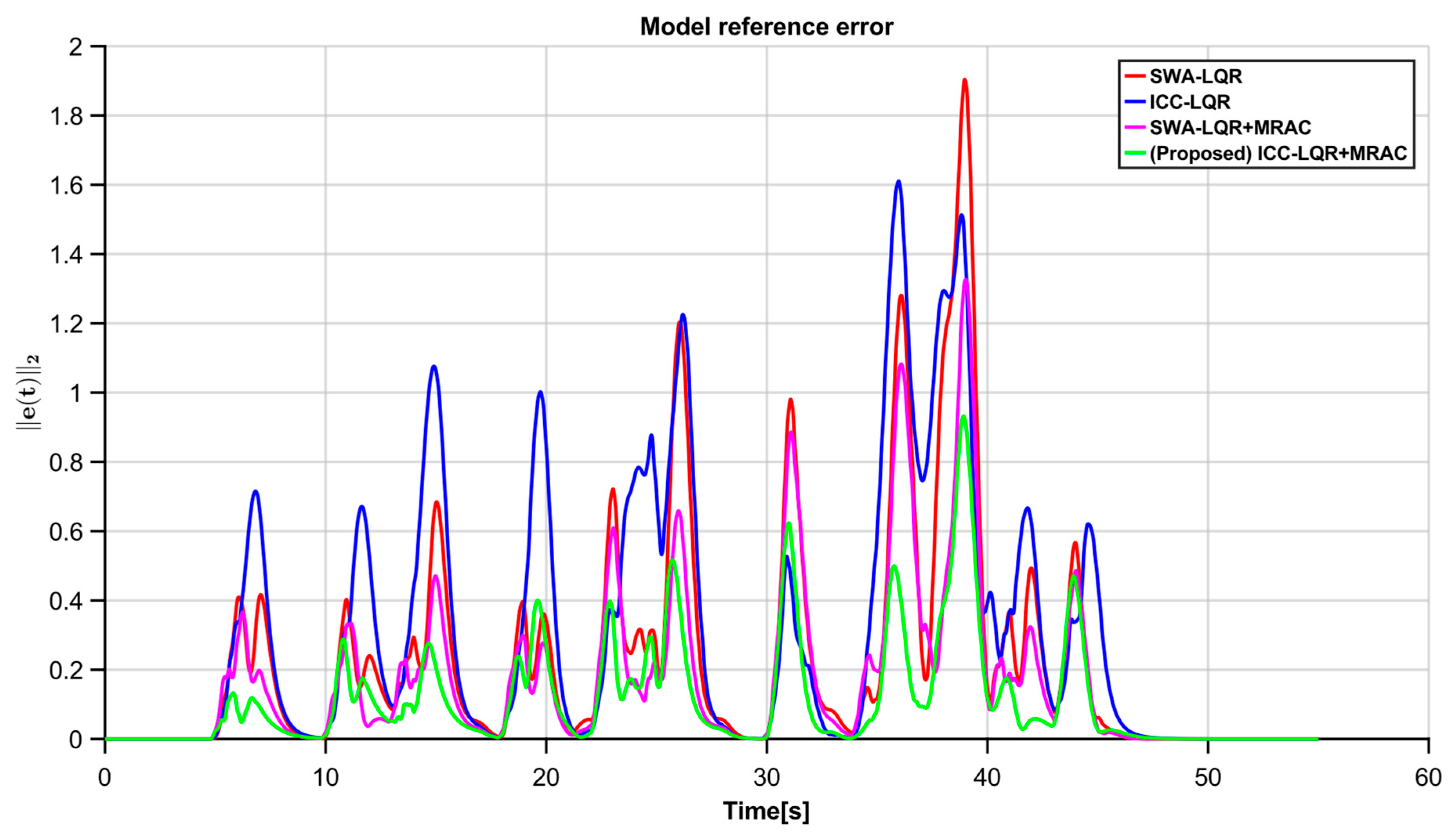
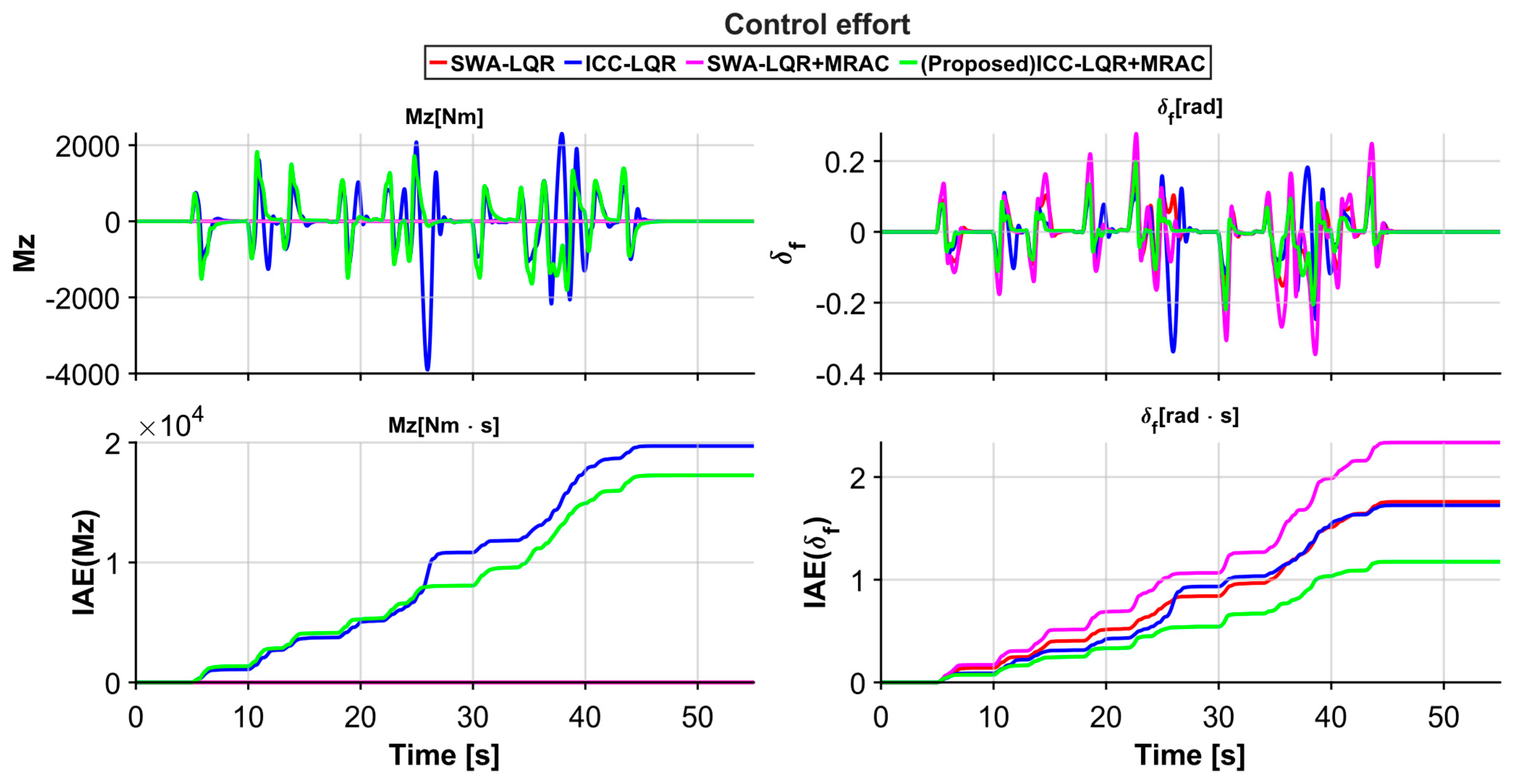
5. Simulation and Results
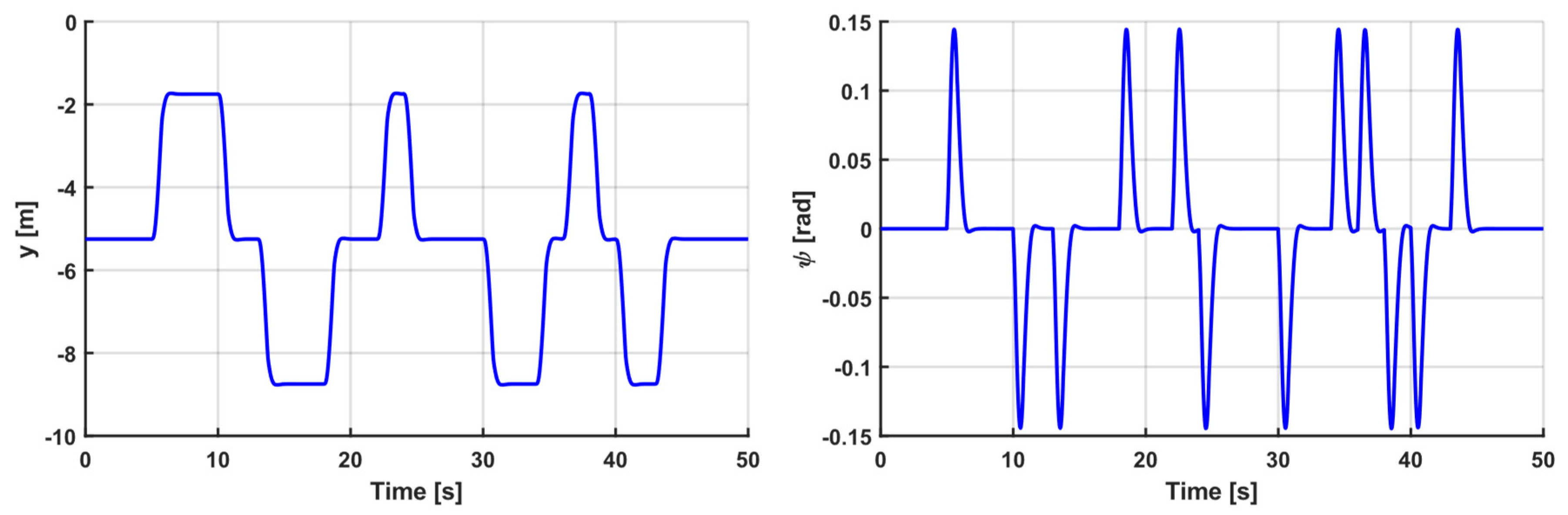
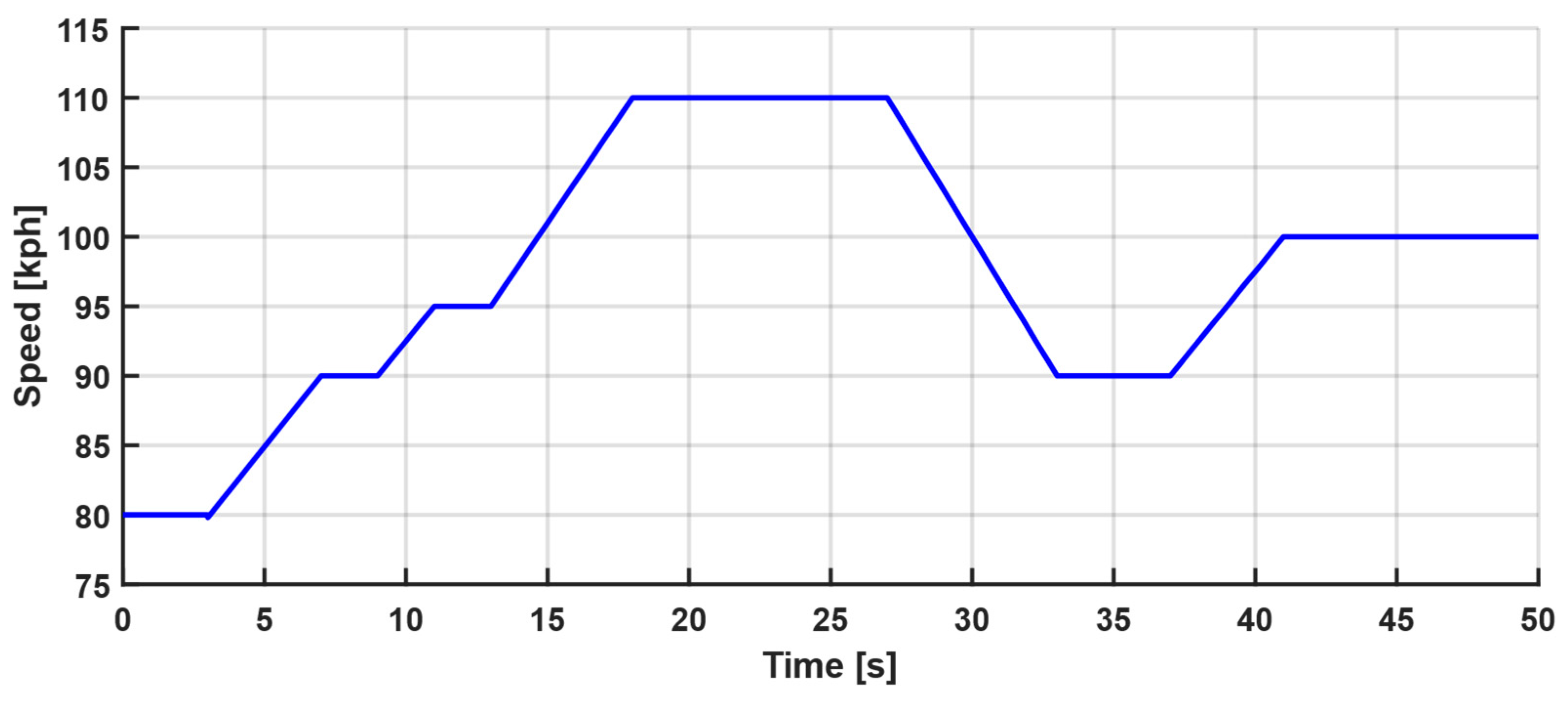
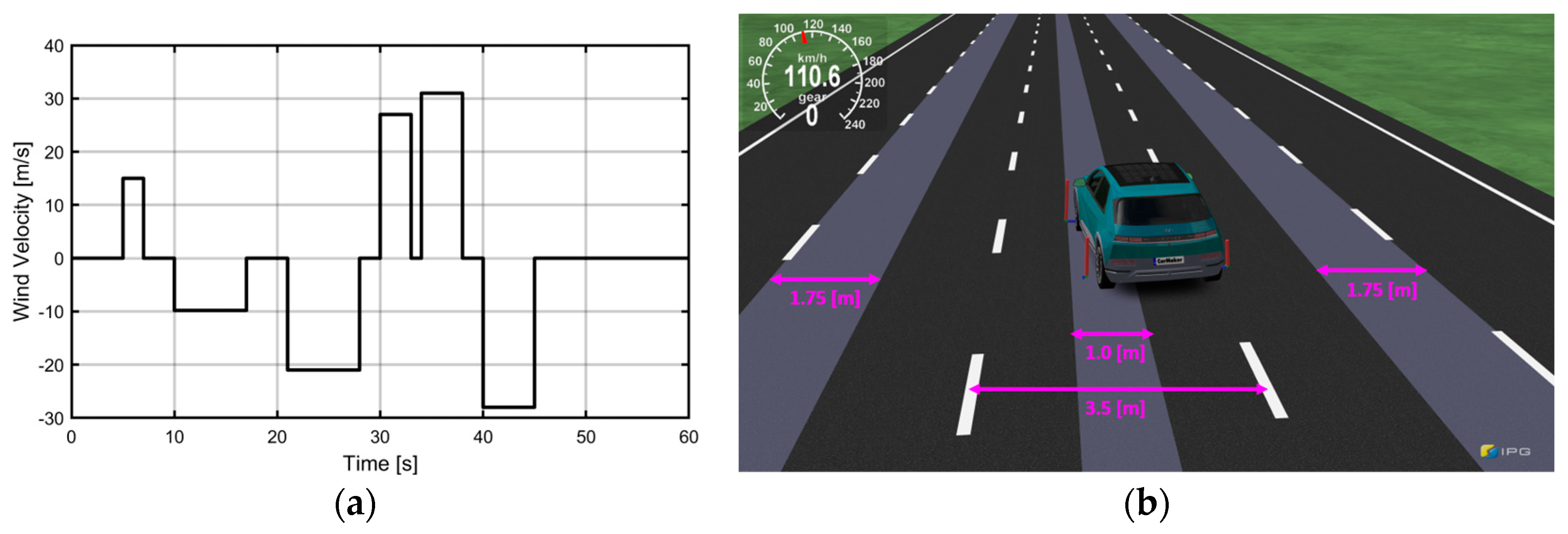
5.1. Simulation Setup
5.2. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stano, P.; Montanaro, U.; Tavernini, D.; Tufo, M.; Fiengo, G.; Novella, L.; Sorniotti, A. Model predictive path tracking control for automated road vehicles: A review. Annu. Rev. Control 2023, 55, 194–236. [Google Scholar] [CrossRef]
- Olofsson, B.; Nielsen, L. Using crash databases to predict effectiveness of new autonomous vehicle maneuvers for lane-departure injury reduction. IEEE Trans. Intell. Transp. Syst. 2021, 22, 3479–3490. [Google Scholar] [CrossRef]
- Chen, M.; Ren, Y.; Ou, M. Adaptive robust path tracking control for autonomous vehicles considering multi-dimensional system uncertainty. World Electr. Veh. J. 2023, 14, 11. [Google Scholar] [CrossRef]
- Jeong, Y.; Yim, S. Integrated path tracking and lateral stability control with four-wheel independent steering for autonomous electric vehicles on low friction roads. Machines 2022, 10, 650. [Google Scholar] [CrossRef]
- Liu, H.; Liu, C.; Hao, L.; Zhang, D. Stability analysis of lane-keeping assistance system for trucks under crosswind conditions. Appl. Sci. 2023, 13, 9891. [Google Scholar] [CrossRef]
- Singh, A.S.P.; Nishihara, O. Trajectory tracking and integrated chassis control for obstacle avoidance with minimum jerk. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4625–4641. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, L.; Wang, J.; Ren, C. Cooperative control of path tracking and driving stability for intelligent vehicles on potholed road. IEEE Trans. Intell. Veh. 2023, 9, 2499–2508. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Liu, C.-Z.; Wu, X.; Fang, S.-N.; Yong, J.-W. Robust LMI-based H ∞ controller integrating AFS and DYC of autonomous vehicles with parametric uncertainties. IEEE Trans. Syst. Man. Cybern. Syst. 2021, 51, 6901–6910. [Google Scholar] [CrossRef]
- Dai, Y.; Wang, D. A tube model predictive control method for autonomous lateral vehicle control based on sliding mode control. Sensors 2023, 23, 3844. [Google Scholar] [CrossRef]
- Yang, S.; Xu, J.; Qian, Y.; Chen, L.; Yin, G. Adaptive MPC-based lateral path-tracking control for automatic vehicles. World Electr. Veh. J. 2024, 15, 95. [Google Scholar] [CrossRef]
- Skrickij, V.; Kojis, P.; Šabanovič, E.; Shyrokau, B.; Ivanov, V. Review of integrated chassis control techniques for automated ground vehicles. Sensors 2024, 24, 600. [Google Scholar] [CrossRef]
- Potluri, R.; Singh, A.K. Path-tracking control of an autonomous 4WS4WD electric vehicle using its natural feedback loops. IEEE Trans. Control Syst. Technol. 2015, 23, 2053–2062. [Google Scholar] [CrossRef]
- Hang, P.; Chen, X.; Luo, F. LPV/H∞ controller design for path tracking of autonomous ground vehicles through four-wheel steering and direct yaw-moment control. Int. J. Automot. Technol. 2019, 20, 679–691. [Google Scholar] [CrossRef]
- Sun, P.; Stensson Trigell, A.; Drugge, L.; Jerrelind, J. Energy-efficient direct yaw moment control for in-wheel motor electric vehicles utilising motor efficiency maps. Energies 2020, 13, 593. [Google Scholar] [CrossRef]
- Jeong, Y.; Yim, S. Path tracking control with four-wheel independent steering, driving and braking systems for autonomous electric vehicles. IEEE Access 2022, 10, 74733–74746. [Google Scholar] [CrossRef]
- Ren, Y.; Zheng, L.; Khajepour, A. Integrated model predictive and torque vectoring control for path tracking of 4-wheel-driven autonomous vehicles. IET Intell. Transp. Syst. 2019, 13, 98–107. [Google Scholar] [CrossRef]
- Tan, Q.; Dai, P.; Zhang, Z.; Katupitiya, J. MPC and PSO based control methodology for path tracking of 4WS4WD vehicles. Appl. Sci. 2018, 8, 1000. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, L.; Li, Y.; Li, S.; Liang, Y. Cooperative strategy of trajectory tracking and stability control for 4WID autonomous vehicles under extreme conditions. IEEE Trans. Veh. Technol. 2023, 72, 3105–3118. [Google Scholar] [CrossRef]
- Na, J.; Yang, J.; Gao, G. Reinforcing transient response of adaptive control systems using modified command and reference model. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 2071–2084. [Google Scholar] [CrossRef]
- Liang, Y.; Li, Y.; Khajepour, A.; Zheng, L. Holistic Adaptive Multi-Model Predictive Control for the Path Following of 4WID Autonomous Vehicles. IEEE Trans. Veh. Technol. 2021, 70, 69–81. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, J.; Yin, X. Adaptive sliding mode control for yaw stability of four-wheel independent-drive EV based on the phase plane. World Electr. Veh. J. 2023, 14, 116. [Google Scholar] [CrossRef]
- Lee, J.E.; Kim, B.W. A novel adaptive non-singular fast terminal sliding mode control for direct yaw moment control in 4WID electric vehicles. Sensors 2025, 25, 941. [Google Scholar] [CrossRef]
- Meléndez-Useros, M.; Viadero-Monasterio, F.; Jiménez-Salas, M.; López-Boada, M.J. Static Output-Feedback Path-Tracking Controller Tolerant to Steering Actuator Faults for Distributed Driven Electric Vehicles. World Electr. Veh. J. 2025, 16, 40. [Google Scholar] [CrossRef]
- Tan, X.; Liu, D.; Xiong, H. Optimal control method of path tracking for four-wheel steering vehicles. Actuators 2022, 11, 61. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, K.; Zhang, P.; Yan, F. Direct yaw moment control for distributed drive electric vehicles based on hierarchical optimization control framework. Math 2024, 12, 1715. [Google Scholar] [CrossRef]
- Nguyen, K.-D. A Predictor-Based Model Reference Adaptive Controller for Time-Delay Systems. IEEE Trans. Autom. Control 2018, 63, 4375–4382. [Google Scholar] [CrossRef]
- Narendra, K.S.; Annaswamy, A.M. Stable Adaptive Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1989; ISBN 978-0138399948. [Google Scholar]
- Ioannou, P.A.; Kokotović, P.V. Instability analysis and improvement of robustness of adaptive control. Automatica 1984, 20, 583–594. [Google Scholar] [CrossRef]
- Lavretsky, E.; Wise, K.A. Robust and Adaptive Control: With Aerospace Applications; Springer: London, UK, 2013; ISBN 978-1-4471-4395-6. [Google Scholar]
- Lavretsky, E.; Gadient, R.; Gregory, I.M. Predictor-based model reference adaptive control. J. Guid. Control Dyn. 2010, 33, 1195–1200. [Google Scholar] [CrossRef]
- Byrne, R.H.; Abdallah, C.T. Design of a model reference adaptive controller for vehicle road following. Math. Comput. Model. 1995, 22, 343–354. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Z.; Shen, H.; Wang, J. Yaw-rate-tracking-based automated vehicle path following: An MRAC methodology with a closed-loop reference model. ASME Lett. Dyn. Syst. Control 2021, 2, 021010. [Google Scholar] [CrossRef]
- Lee, D.; Jang, K.; Lee, S.; Kim, L.; Bang, H. Closed-Loop MRAC Augmented LQR with Integral Action for Quadrotor UAV under the Uncertainties. In Advances in Aerospace Guidance, Navigation and Control: Proceedings of the 2022 CEAS EuroGNC Conference; Springer: Cham, Switzerland, 2022; pp. 30–45. [Google Scholar]
- Yang, G.; Yao, J. Multilayer neurocontrol of high-order uncertain nonlinear systems with active disturbance rejection. Int. J. Robust Nonlinear Control 2024, 34, 2972–2987. [Google Scholar] [CrossRef]
- Dixit, S.; Montanaro, U.; Dianati, M.; Oxtoby, D.; Mizutani, T.; Mouzakitis, A.; Fallah, S. Integral MRAC with bounded switching gain for vehicle lateral tracking. IEEE Trans. Control Syst. Technol. 2021, 29, 1711–1722. [Google Scholar] [CrossRef]
- Montanaro, U.; Chen, C.; Rizzo, A.; Sorniotti, A. Output-Based Enhanced Closed-Loop Model Reference Adaptive Control and Its Application to Direct Yaw Moment Control. Int. J. Robust Nonlinear Control 2024, 34, 9471–9500. [Google Scholar] [CrossRef]
- Park, M.; Yim, S. Design of static output feedback integrated path tracking controller for autonomous vehicles. Processes 2025, 13, 1335. [Google Scholar] [CrossRef]
- Yin, D.; Wang, J.; Du, J.; Chen, G.; Hu, J.-S. A new torque distribution control for four-wheel independent-drive electric vehicles. Actuators 2021, 10, 122. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control, 3rd ed.; Springer: New York, NY, USA, 2012. [Google Scholar]
- Wang, W.; Ma, T.; Yang, C.; Zhang, Y.; Li, Y.; Qie, T. A path-following lateral control scheme for four-wheel independent drive autonomous vehicle using sliding mode prediction control. IEEE Trans. Transp. Electrific. 2022, 8, 3192–3207. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002; ISBN 978-0-13-067389-3. [Google Scholar]
- Ioannou, P.A.; Sun, J. Robust Adaptive Control; Prentice Hall: Upper Saddle River, NJ, USA, 1996; ISBN 978-0-13-439100-7. [Google Scholar]
- Naqvi, S.S.A.; Jamil, H.; Iqbal, N.; Khan, S.; Khan, M.; Qayyum, F.; Kim, D.-H. Evolving electric mobility: In-depth analysis of integrated electronic control unit development in electric vehicles. IEEE Access 2024, 12, 15957–15983. [Google Scholar] [CrossRef]
- Li, B.; Ahmadi, J.; Lin, C.; Siampis, E.; Longo, S.; Velenis, E. Integrated path-tracking and control allocation controller for autonomous electric vehicle under limit handling condition. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; IEEE: Las Vegas, NV, USA, 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Johansen, T.A.; Fossen, T.I. Control allocation—A survey. Automatica 2013, 49, 1087–1103. [Google Scholar] [CrossRef]
- Yong, J.; Gao, F.; Ding, N.; He, Y. An integrated algorithm for vehicle stability improvement with the coordination of direct yaw moment and four-wheel steering control. Int. J. Veh. Des. 2017, 74, 231–256. [Google Scholar] [CrossRef]
- Anderson, B.D.O.; Moore, J.B. Optimal Control: Linear Quadratic Methods; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989; ISBN 978-0-13-638560-8. [Google Scholar]
- Kang, J.; Yi, K.; Heo, H. Control allocation–based optimal torque vectoring for 4WD electric vehicle. In Proceedings of the 2012 SAE World Congress & Exhibit; SAE Technical Paper 2012-01-0246; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Lee, S.; Kim, K.; Moon, S.; Kim, B.; Ahn, J.; Hwang, J.; Kim, D.; Woo, S.; Yoo, J. A novel lateral dynamics control strategy of in-wheel motor vehicle to improve agility and straight-line driving stability. IEEE Trans. Veh. Technol. 2024, 73, 9849–9864. [Google Scholar] [CrossRef]

| Symbol | Value | Unit |
|---|---|---|
| 25 | ||
| 2065.03 | ||
| 3637.526 | ||
| 1.801 | ||
| 1.169 | ||
| 1.638 | ||
| 149,744 | ||
| 93,678 |
| No. | Mass Increase [+180 kg] | Road Friction [0.4, 0.8] | Cross Winds [15, 30 m/s] |
|---|---|---|---|
| SCENARIO 1 | O | X | X |
| SCENARIO 2 | O | X | O |
| SCENARIO 3 | O | O | X |
| SCENARIO 4 | O | O | O |
| Symbol | Value |
|---|---|
| 0.01 |
| Scenario 1 | Lateral Deviation [] | Heading Error [] | ||||
|---|---|---|---|---|---|---|
| RMSE [m] | PE [m] | IAE [ms] | RMSE [rad] | PE [rad] | IAE [rad·s] | |
| SWA-LQR | 0.54037 | 1.74177 | 16.2169 | 0.0414205 | 0.131308 | 1.29172 |
| SWA-LQR+MRAC | 0.408807 | 1.36952 | 11.6688 | 0.0349666 | 0.128338 | 0.997914 |
| ICC-LQR | 0.454319 | 1.52195 | 12.6861 | 0.0327833 | 0.112221 | 0.952673 |
| Proposed | 0.402558 | 1.34112 | 11.5777 | 0.0246866 | 0.0791489 | 0.740466 |
| Scenario 2 | Lateral Deviation [] | Heading Error [] | ||||
| RMSE [] | PE [] | IAE [] | RMSE [] | PE [] | IAE [] | |
| SWA-LQR | 0.567065 | 1.95018 | 18.3311 | 0.0416151 | 0.130601 | 1.34098 |
| SWA-LQR+MRAC | 0.442667 | 1.72329 | 12.5813 | 0.0343042 | 0.12257 | 1.02393 |
| ICC-LQR | 0.467075 | 1.7871 | 13.9467 | 0.0327486 | 0.107025 | 0.995802 |
| Proposed | 0.439688 | 1.68548 | 12.0913 | 0.0244142 | 0.0893403 | 0.735768 |
| Scenario 3 | Lateral Deviation [] | Heading Error [] | ||||
| RMSE [] | PE [] | IAE [] | RMSE [] | PE [] | IAE [] | |
| SWA-LQR | 0.582372 | 1.8152 | 17.51 | 0.0425816 | 0.133144 | 1.34851 |
| SWA-LQR+MRAC | 0.499045 | 1.61238 | 15.4794 | 0.0398713 | 0.133374 | 1.24944 |
| ICC-LQR | 0.505308 | 1.64634 | 14.2031 | 0.0336265 | 0.114554 | 0.994984 |
| Proposed | 0.477097 | 1.59648 | 13.1411 | 0.0262197 | 0.0877509 | 0.781502 |
| Scenario 4 | Lateral Deviation [] | Heading Error [] | ||||
| RMSE [] | PE [] | IAE [] | RMSE [] | PE [] | IAE [] | |
| SWA-LQR | 0.65285 | 2.66333 | 21.0876 | 0.0438557 | 0.153238 | 1.4379 |
| SWA-LQR+MRAC | 0.569221 | 2.26809 | 18.3778 | 0.0423506 | 0.15992 | 1.3676 |
| ICC-LQR | 0.581271 | 2.70021 | 17.5042 | 0.0359311 | 0.141737 | 1.13054 |
| Proposed | 0.48856 | 1.77022 | 13.7968 | 0.0270436 | 0.0949164 | 0.834595 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.; Oh, T.; Kim, J.; Yoo, J. Robust Path-Tracking Control for Autonomous Vehicles: A Model-Reference-Adaptive-Control-Based Integrated Chassis Control Strategy. Appl. Sci. 2025, 15, 12387. https://doi.org/10.3390/app152312387
Park S, Oh T, Kim J, Yoo J. Robust Path-Tracking Control for Autonomous Vehicles: A Model-Reference-Adaptive-Control-Based Integrated Chassis Control Strategy. Applied Sciences. 2025; 15(23):12387. https://doi.org/10.3390/app152312387
Chicago/Turabian StylePark, Siyeong, Taeyoung Oh, Jeesu Kim, and Jinwoo Yoo. 2025. "Robust Path-Tracking Control for Autonomous Vehicles: A Model-Reference-Adaptive-Control-Based Integrated Chassis Control Strategy" Applied Sciences 15, no. 23: 12387. https://doi.org/10.3390/app152312387
APA StylePark, S., Oh, T., Kim, J., & Yoo, J. (2025). Robust Path-Tracking Control for Autonomous Vehicles: A Model-Reference-Adaptive-Control-Based Integrated Chassis Control Strategy. Applied Sciences, 15(23), 12387. https://doi.org/10.3390/app152312387







