Grouting Power Prediction Method Based on CEEMDAN-CNN-BiLSTM
Abstract
1. Introduction
2. Grouting Process and Experimental Data Acquisition
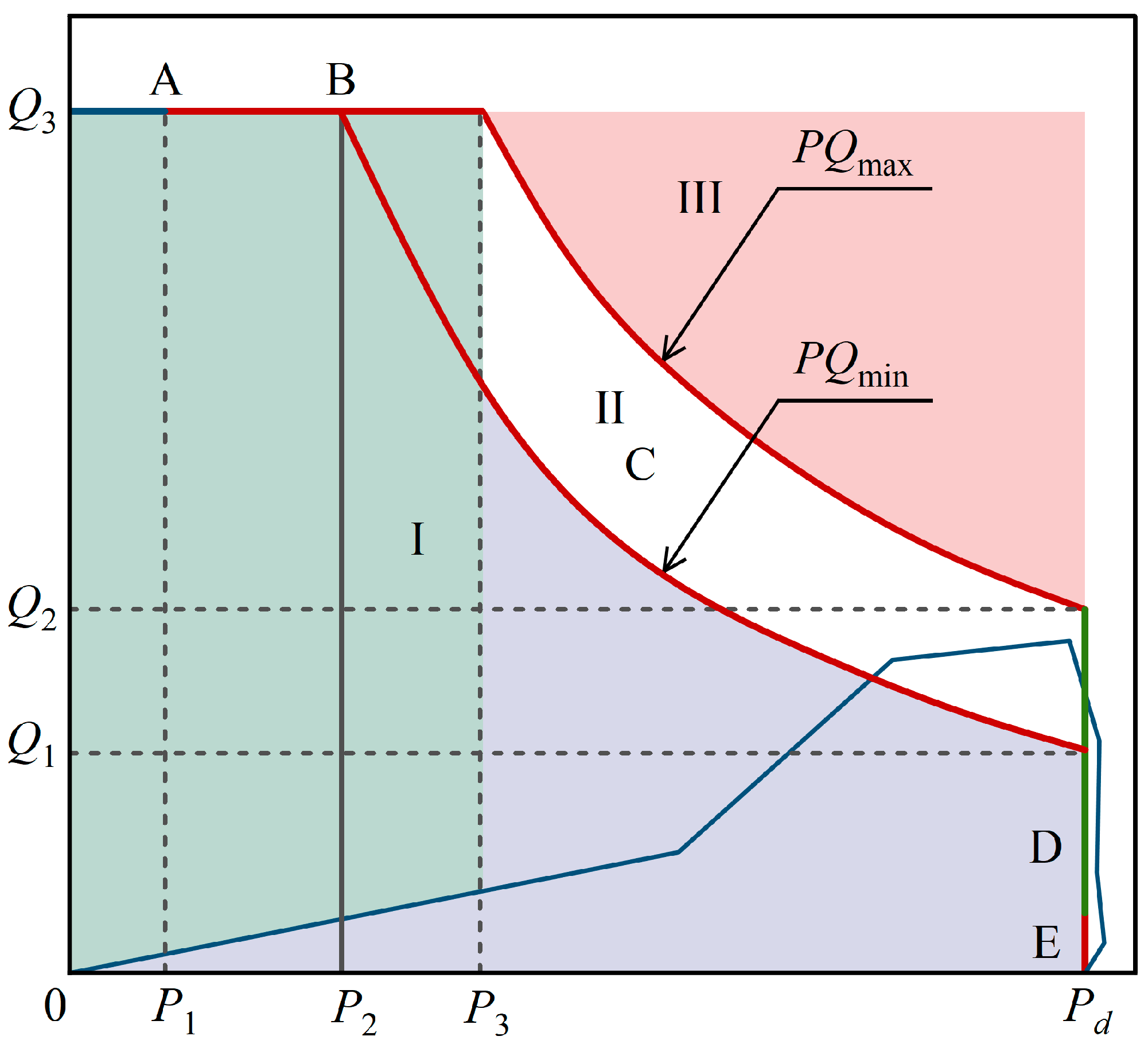
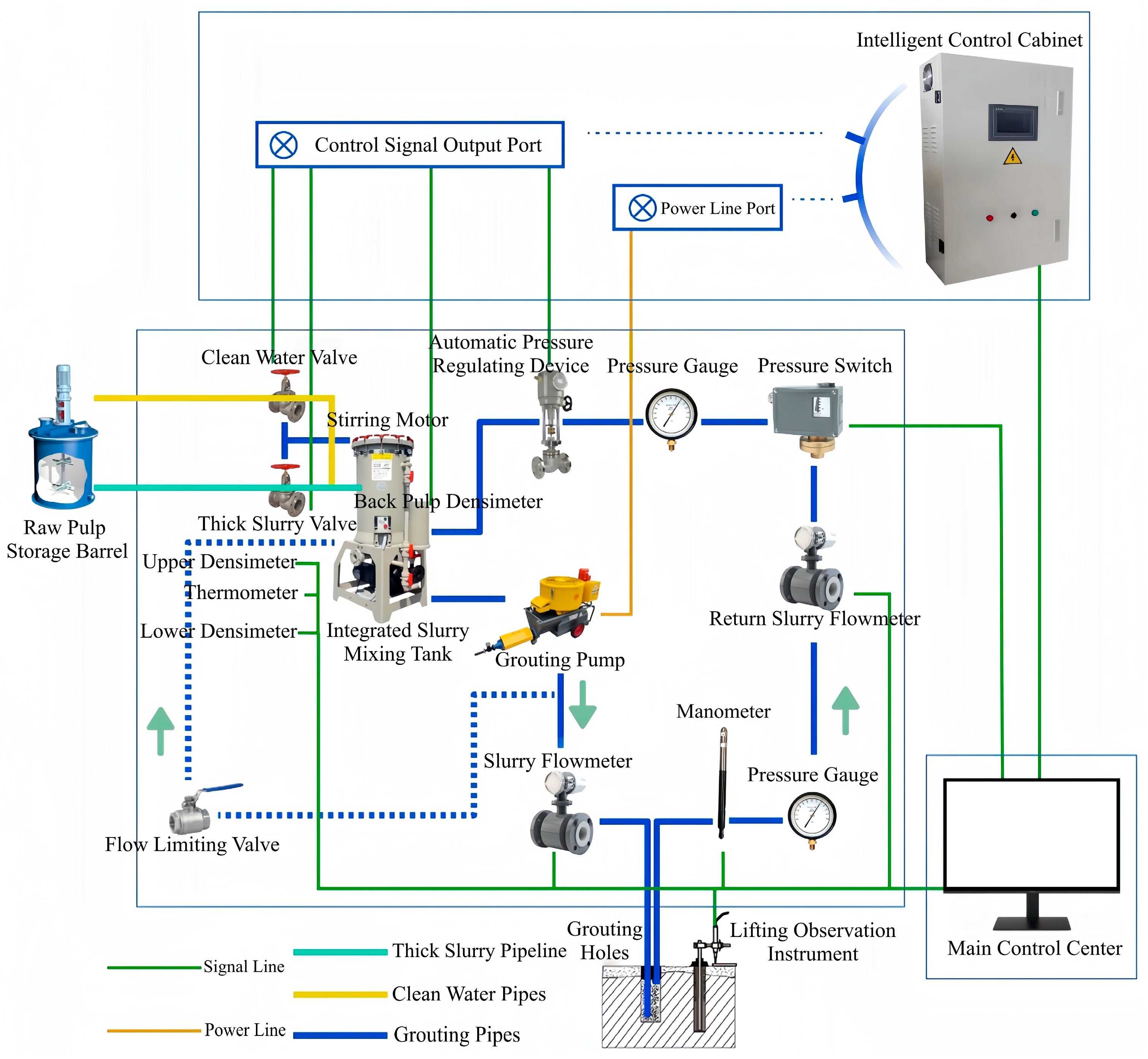
2.1. Grouting Process
2.2. Grouting Experimental Data Acquisition
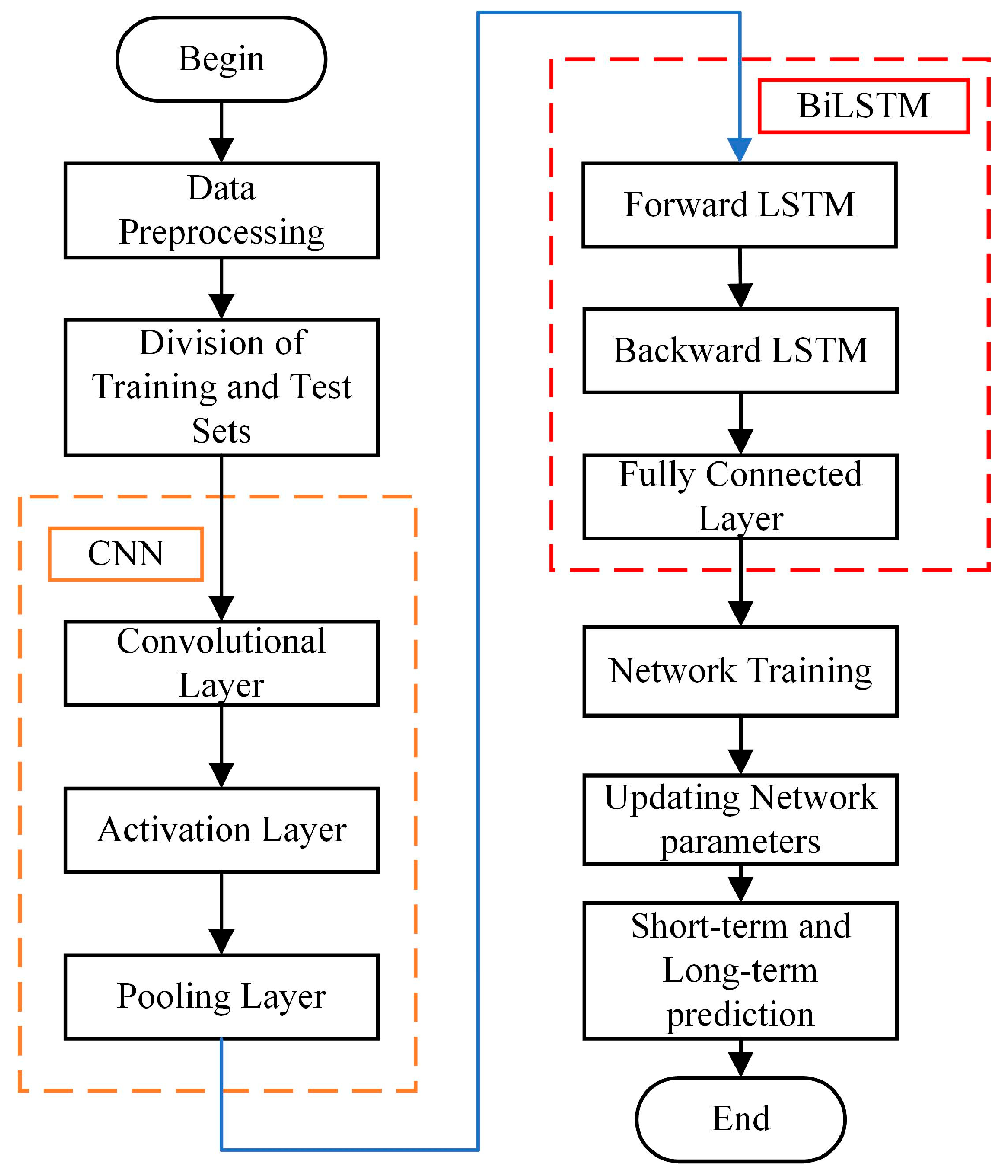
3. Methodology for Grouting Power Prediction
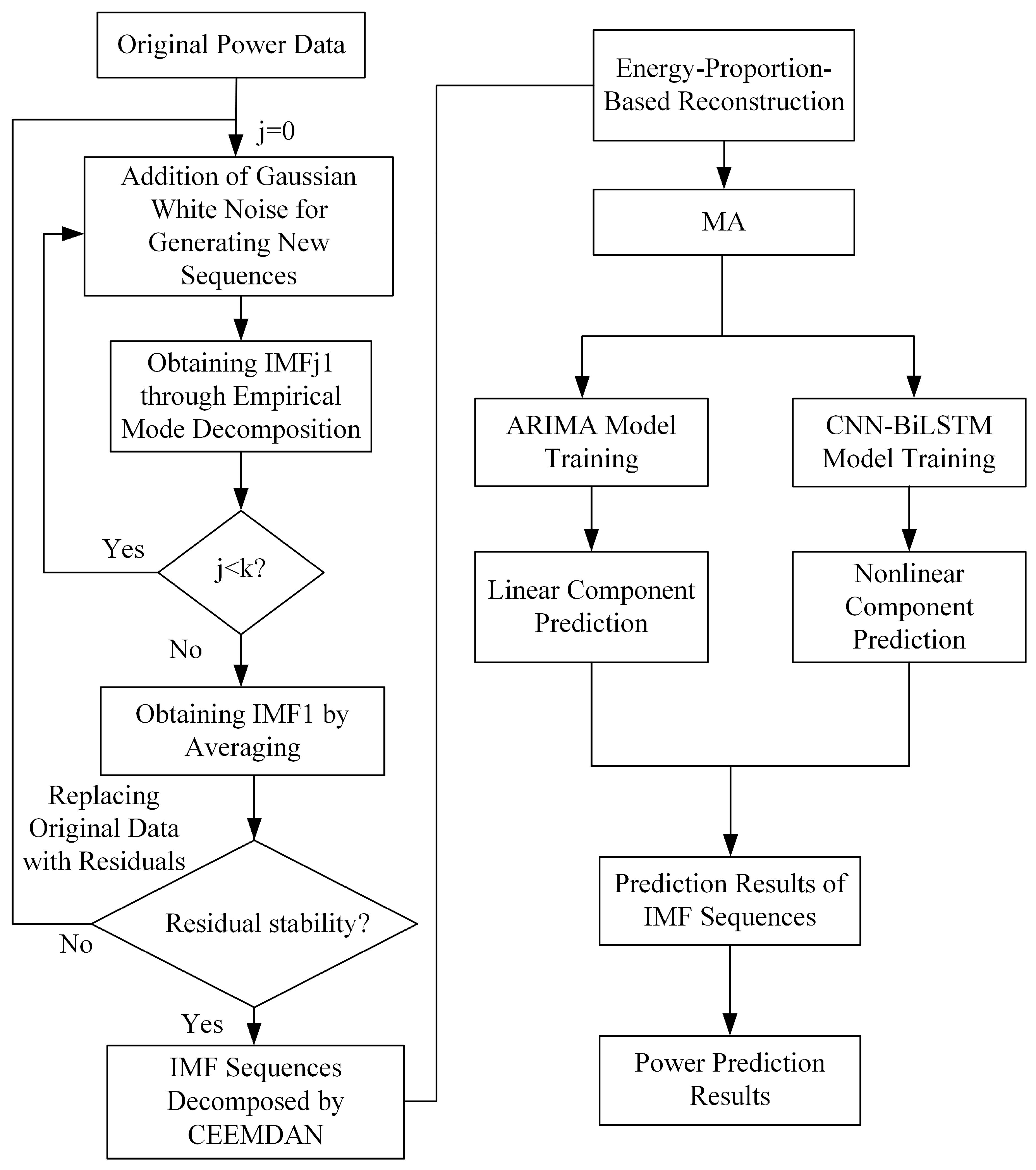
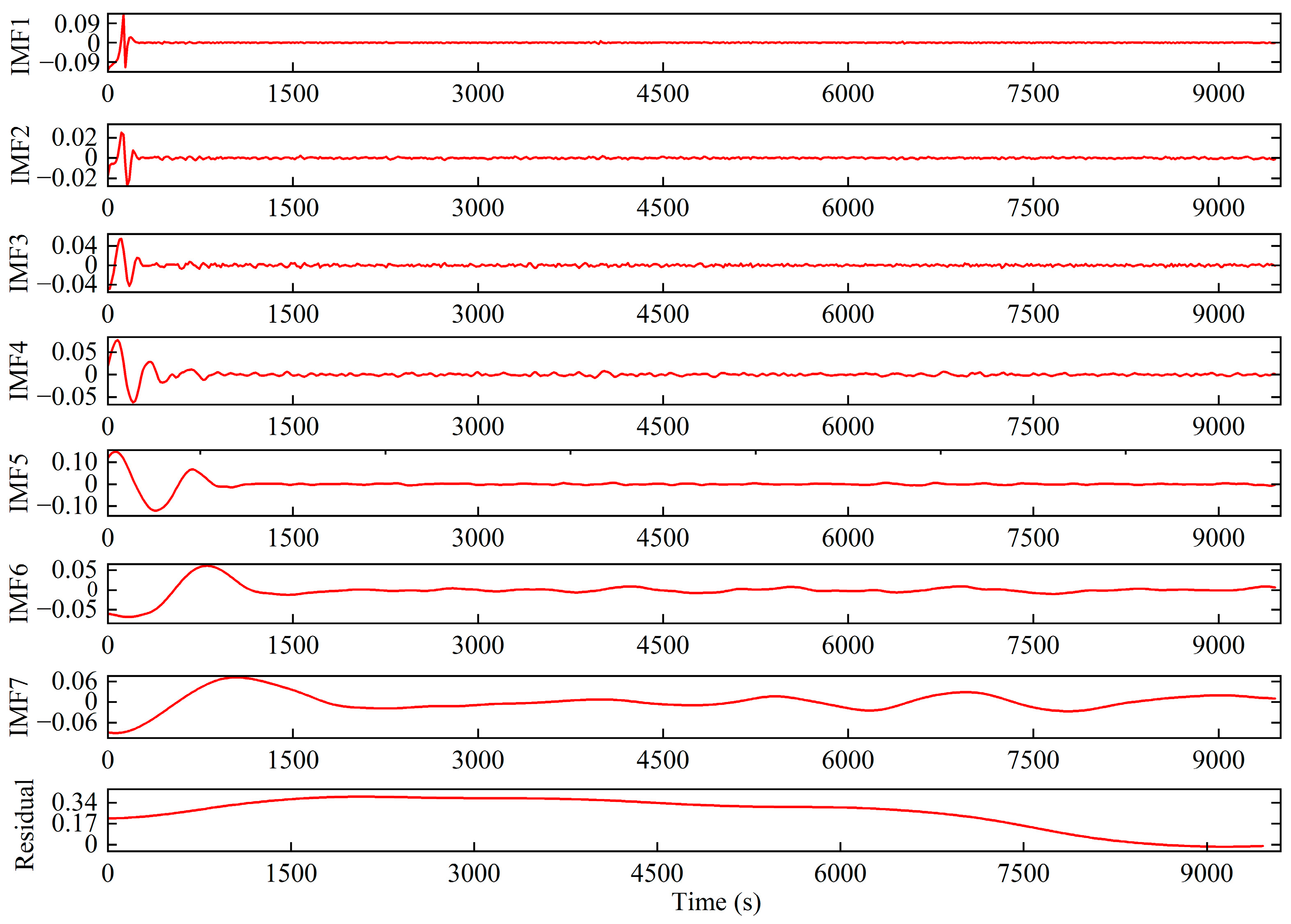
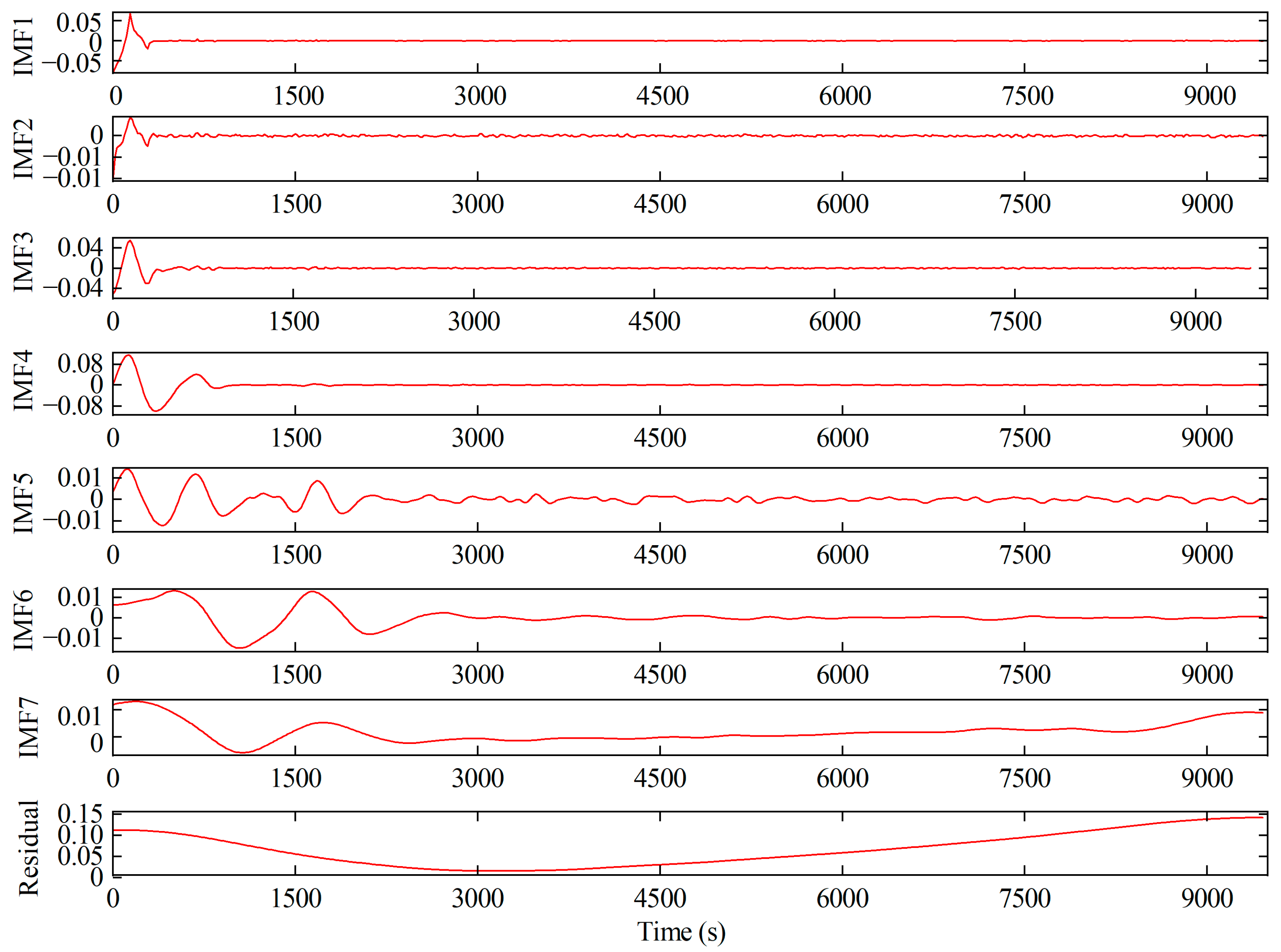
3.1. Principle of the CEEMDAN Method
3.2. ARIMA Model
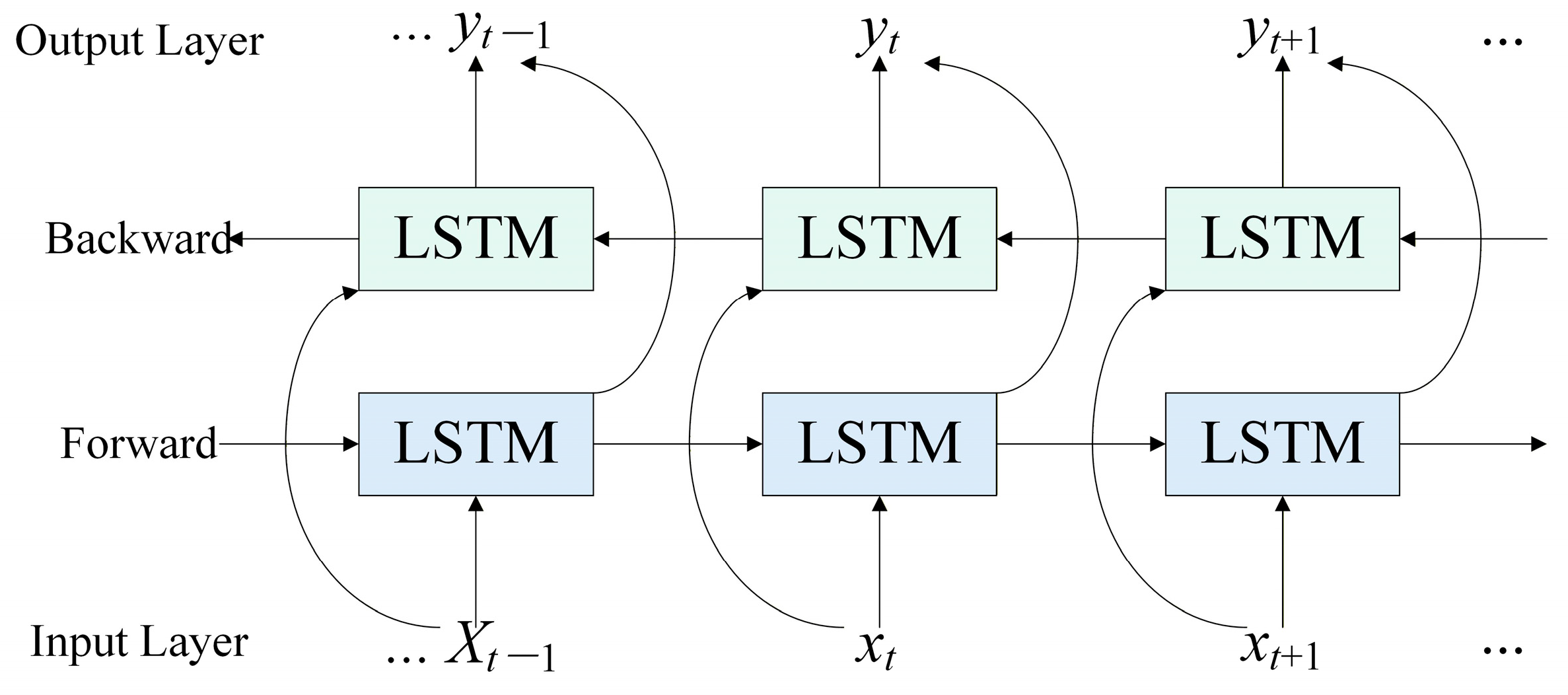
3.3. Principle of the CNN-BiLSTM Method
4. Experimental Results and Discussion
4.1. Evaluation Metrics for Prediction Performance
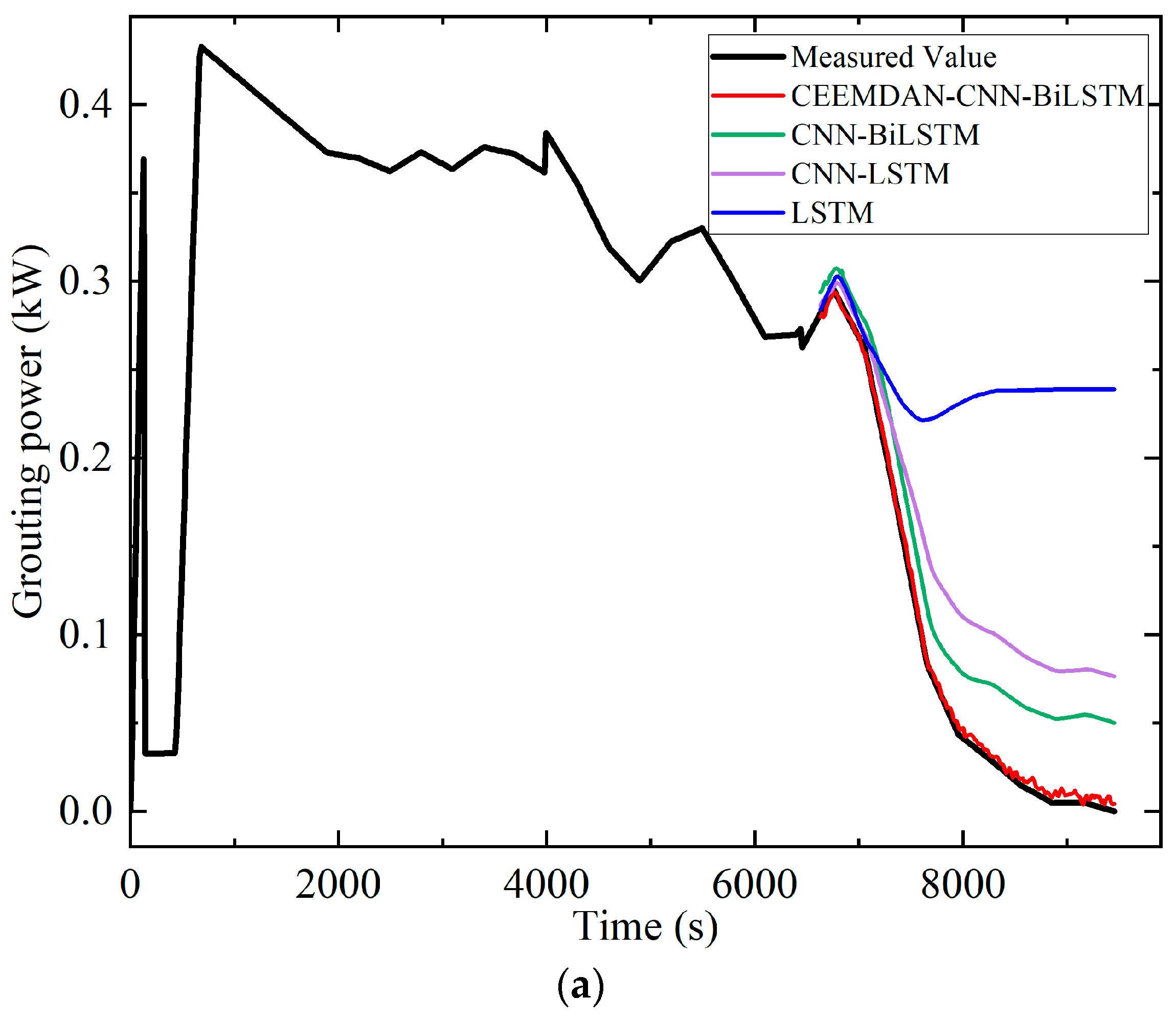
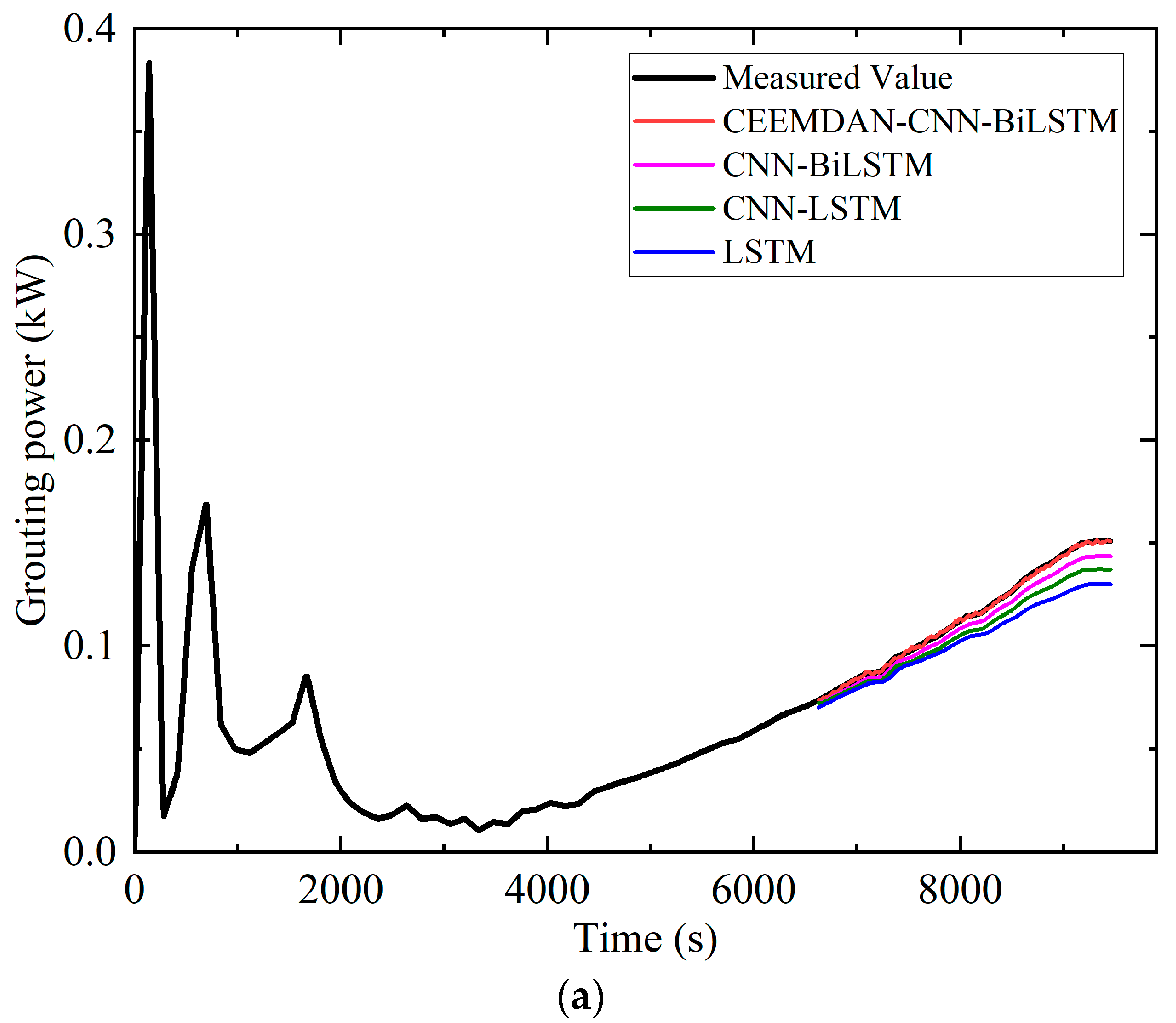
4.2. Grouting Power Prediction Under Normal Conditions
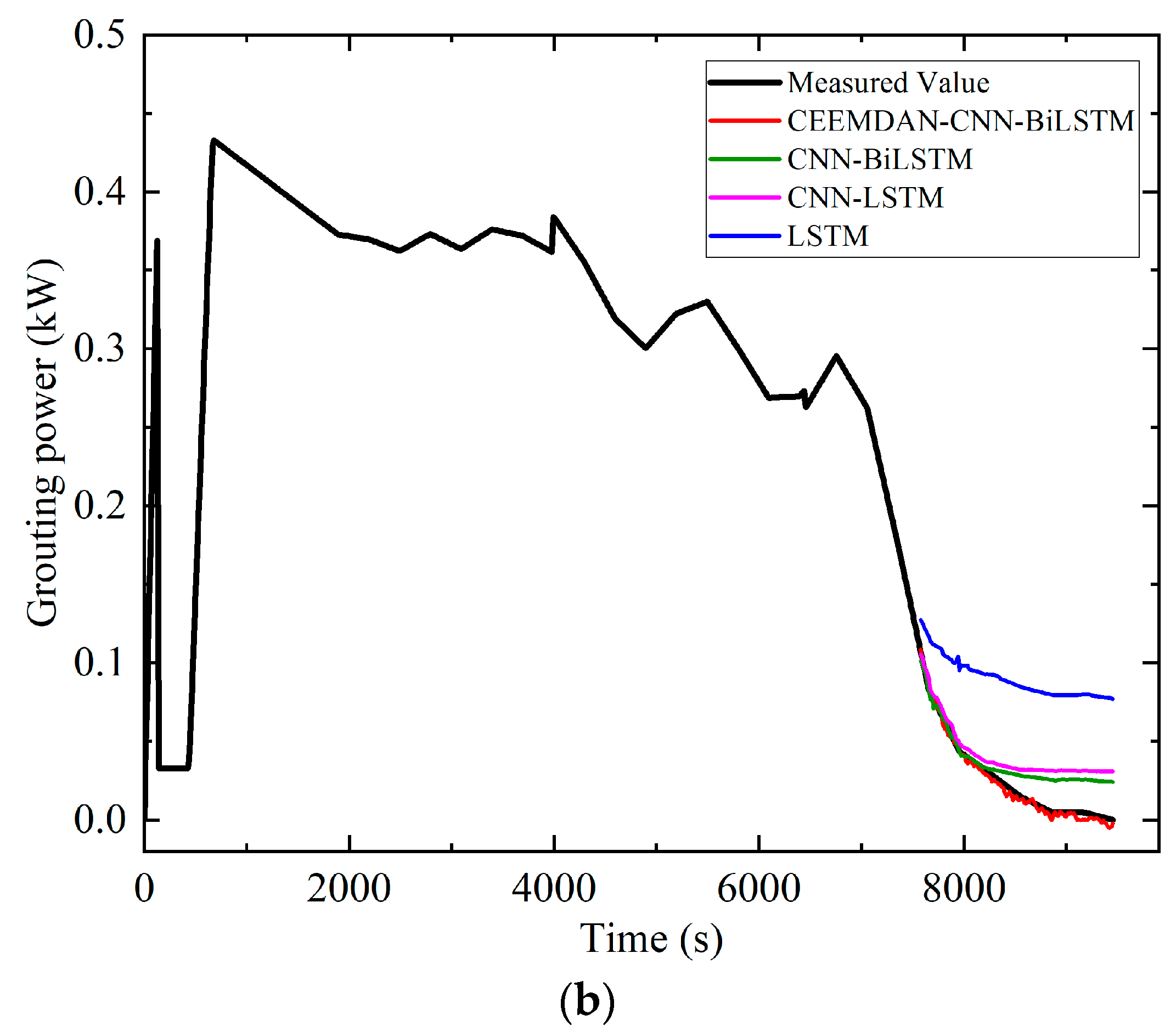
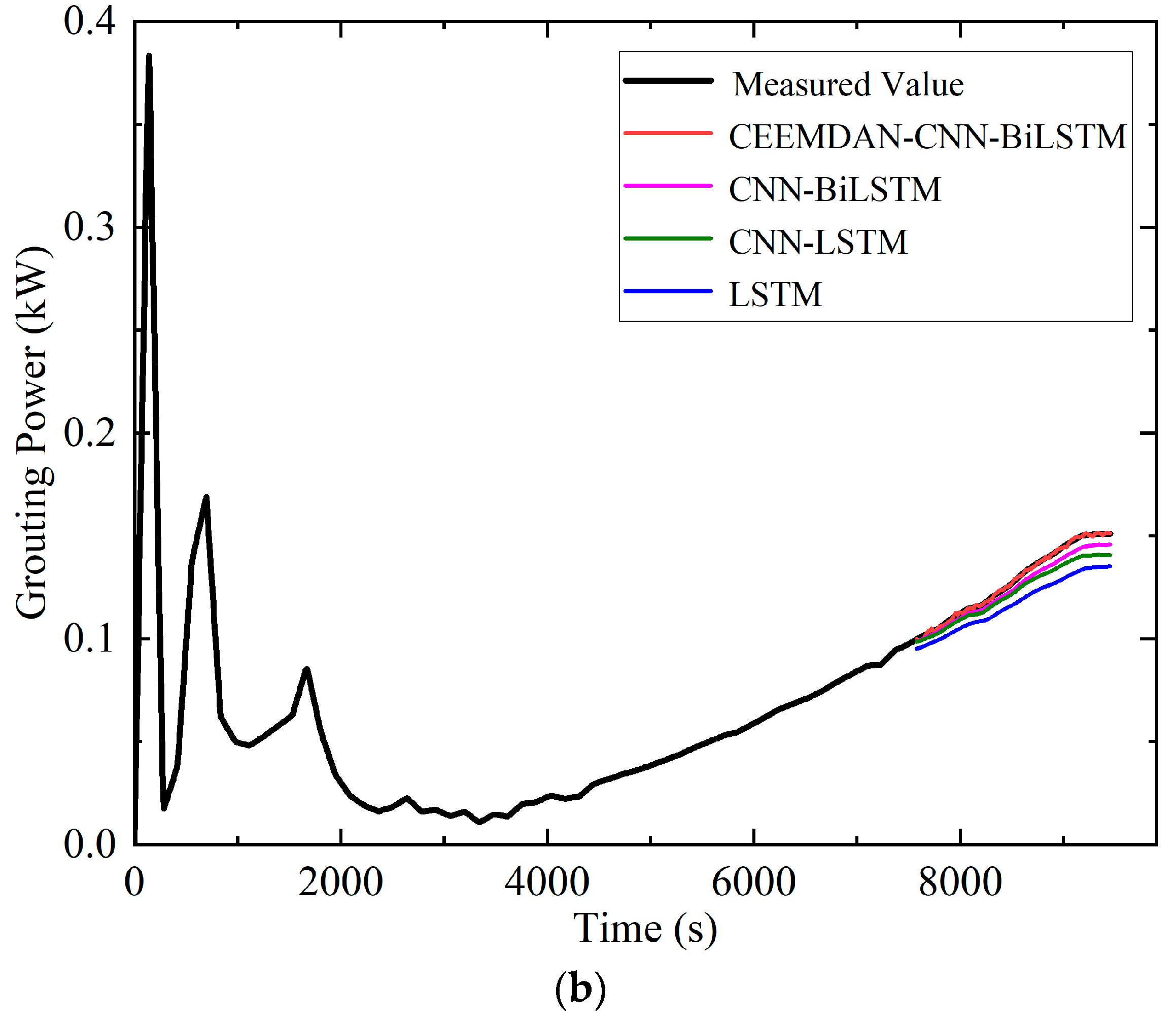
4.3. Grouting Power Prediction Under Heaving Conditions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Maximum allowable grouting power threshold | |
| Minimum allowable grouting power threshold | |
| Original grouting power data | |
| New sequence with Gaussian white noise added | |
| Gaussian white noise added at the j-th iteration | |
| First IMF obtained by CEEMDAN decomposition | |
| Normal velocity First IMF obtained by EMD | |
| Residual sequence after the first decomposition step | |
| Final residual sequence | |
| Linear component | |
| Nonlinear fluctuation component | |
| Moving average step size | |
| Grouting power value at current time step | |
| Grouting power value at previous time step | |
| Measurement error | |
| Differencing order | |
| Predicted grouting power value | |
| Measured grouting power value | |
| Root Mean Square Error | |
| Mean Absolute Error | |
| Coefficient of determination |
References
- Xu, X.; Wu, Z.; Weng, L.; Chu, Z.; Liu, Q.; Wang, Z. Investigating the impacts of reinforcement range and grouting timing on grouting reinforcement effectiveness for tunnels in fault rupture zones using a numerical manifold method. Eng. Geol. 2024, 330, 107423. [Google Scholar] [CrossRef]
- Peng, L.; Xiong, J.; Liu, Y. A self-control and visual grouting model test system and measurement method. Measurement 2020, 154, 107481. [Google Scholar] [CrossRef]
- Fan, Q.; Jiang, X.; Wang, K.; Huang, C.; Li, G.; Wei, P. Cement grouting online monitoring and intelligent control for dam foundations. J. Intell. Constr. 2023, 1, 1–15. [Google Scholar] [CrossRef]
- Ismail, F.B.; Al-Faiz, H.; Hasini, H.; Al-Bazi, A.; Kazem, H.A. A comprehensive review of the dynamic applications of the digital twin technology across diverse energy sectors. Energy Strategy Rev. 2024, 52, 101334. [Google Scholar] [CrossRef]
- Moshood, T.D.; Rotimi, J.O.; Shahzad, W.; Bamgbade, J.A. Infrastructure digital twin technology: A new paradigm for future construction industry. Technol. Soc. 2024, 77, 102519. [Google Scholar] [CrossRef]
- Wang, K.; Chen, P.; Xu, K.; Yang, C.; Li, Y.; Zong, H. A forchheimer-based fluid-solid coupling model for nonlinear flow of power-law grouts in fractured rock grouting. Sci. Rep. 2025, 15, 29445. [Google Scholar] [CrossRef]
- Wu, Y.; Ren, G.; Zhang, X.; Zhao, C.; Zhao, C. Spherical permeation grouting model of a power-law fluid considering the soil unloading effect. Int. J. Geomech. 2024, 24, 04023266. [Google Scholar] [CrossRef]
- Ye, F.; Qin, N.; Han, X.; Liang, X.; Gao, X.; Ying, K. Displacement infiltration diffusion model of power-law grout as backfill grouting of a shield tunnel. Eur. J. Environ. Civ. Eng. 2022, 26, 1820–1833. [Google Scholar] [CrossRef]
- Zhao, L.; Qi, X.; Tan, F.; Chen, Y. A new prediction model of the jet grouting column diameter for three jet grouting systems. Comput. Geotech. 2023, 163, 105753. [Google Scholar] [CrossRef]
- Gaspar, G.; Budjac, R.; Sedivy, S.; Stremy, M.; Benka, D.; Nemlaha, E.; Elias, R. Innovative Grouting Process Monitoring: Design and Implementation of a Measurement Device with Datalogger Function. IEEE Access 2025, 13, 19340–19352. [Google Scholar] [CrossRef]
- Xue, L.; Zhu, Y.; Guan, T.; Ren, B.; Tong, D.; Wu, B. Grouting Power Prediction Using a Hybrid Model Based on Support Vector Regression Optimized by an Improved Jaya Algorithm. Appl. Sci. 2020, 10, 7273. [Google Scholar] [CrossRef]
- Li, X.; Zhong, D.; Ren, B.; Fan, G.; Cui, B. Prediction of curtain grouting efficiency based on ANFIS. Bull. Eng. Geol. Environ. 2019, 78, 281–309. [Google Scholar] [CrossRef]
- Zhao, W.; Feng, S.; Liu, J.; Sun, B. An explainable intelligent algorithm for the multiple performance prediction of cement-based grouting materials. Constr. Build. Mater. 2023, 366, 130146. [Google Scholar] [CrossRef]
- Zhe, Y.; Hou, K.; Wang, Z.; Yang, S.; Sun, H. Prediction model for grouting volume using borehole image features and explainable artificial intelligence. Constr. Build. Mater. 2025, 470, 140626. [Google Scholar] [CrossRef]
- Hu, M.; Xie, H.; Lu, J. Prediction of Grouting Volume for Shield Tunnel Construction Based on Integrated Learning Model. In Proceedings of the 2025 IEEE 8th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 14–16 March 2025; IEEE: New York City, NY, USA, 2025; pp. 1311–1315. [Google Scholar]
- Zhong, D.; Liu, Z.; Su, Z.; Li, K.; Li, X. Predicting and controlling the cement intake during curtain grouting of dam foundations. Eur. J. Environ. Civ. Eng. 2022, 26, 4237–4262. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, X.; Wang, J.; Xue, L.; Yu, J.; Chen, W. A hybrid interval prediction model for the PQ index using a lower upper bound estimation-based extreme learning machine. Soft Comput. 2021, 25, 11551–11571. [Google Scholar] [CrossRef]
- Chen, X.; Deng, L.; Xie, T.; Liang, J. Research on Dam Grouting Efficiency Based on Dynamic Detection and Prediction of Cement Slurry Rheology. In Proceedings of the 2024 14th Asian Control Conference (ASCC), Dalian, China, 5–8 July 2024; IEEE: New York City, NY, USA, 2024; pp. 1710–1716. [Google Scholar]
- Niu, J.; Wang, B.; Wang, H.; Deng, Z.; Liu, J.; Li, Z.; Chen, G.; Zhang, B. An intelligent prediction method of the karst curtain grouting volume based on support vector machine. Geofluids 2020, 2020, 8892106. [Google Scholar] [CrossRef]
- Spampinato, C.; Valastro, S.; Calogero, G.; Smecca, E.; Mannino, G.; Arena, V.; Balestrini, R.; Sillo, F.; Ciná, L.; La Magna, A.; et al. Improved radicchio seedling growth under CsPbI3 perovskite rooftop in a laboratory-scale greenhouse for Agrivoltaics application. Nat. Commun. 2025, 16, 2190. [Google Scholar] [CrossRef]
- Arena, V.; Smecca, E.; Valastro, S.; Bongiorno, C.; Fisicaro, G.; Deretzis, I.; Spampinato, C.; Mannino, G.; Dattilo, S.; Scamporrino, A.A.; et al. Lead Detection in a Gig-Lox TiO2 Sponge by X-ray Reflectivity. Nanomaterials 2023, 13, 1397. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Yin, Z.; Liu, Y.; Laouafa, F. Multiphysics modelling of backfill grouting in sandy soils during TBM tunnelling. Acta Geotech. 2023, 18, 553–571. [Google Scholar] [CrossRef]
- Li, G.; Cao, H.; Wu, J.; Wang, B.; Zhou, X.; Zhao, W.; Cai, X. Multiphase flow coupling analysis of shield synchronous grouting filling law with time-dependent viscosity. Aip Adv. 2023, 13, 125126. [Google Scholar] [CrossRef]
- Jayaraman, P.; Nagarajan, K.K.; Partheeban, P.; Krishnamurthy, V. Critical review on water quality analysis using IoT and machine learning models. Int. J. Inf. Manag. Data Insights 2024, 4, 100210. [Google Scholar] [CrossRef]
- Cui, X. A comprehensive study on damage prediction of pile foundations of inclined high rise buildings and the effect of compaction grouting. Sci. Rep. 2025, 15, 31813. [Google Scholar] [CrossRef] [PubMed]
- Sui, X.; Leng, Z.; Wang, S.; Cai, X.; Gong, M.; Zhang, L. In-situ grouting rate prediction of semi-flexible pavement based on a novel composite dielectric constant model and ground-penetrating radar. Constr. Build. Mater. 2024, 438, 137209. [Google Scholar] [CrossRef]
- Wang, F.; Tadele, M.; Chen, X. Bi-directional long short-term memory recurrent neural network with attention for stack voltage degradation from proton exchange membrane fuel cells. J. Power Sources 2020, 461, 228170. [Google Scholar] [CrossRef]
- Sun, B.; Liu, X.; Wang, J.; Wei, X.; Yuan, H.; Dai, H. Short-term performance degradation prediction of a commercial vehicle fuel cell system based on CNN and LSTM hybrid neural network. Int. J. Hydrog. Energy 2023, 48, 8613–8628. [Google Scholar] [CrossRef]
- Peng, Y.; Chen, T.; Xiao, F.; Zhang, S. Remaining useful lifetime prediction methods of proton exchange membrane fuel cell based on convolutional neural network-long short-term memory and convolutional neural network-bidirectional long short-term memory. Fuel Cells 2023, 23, 75–87. [Google Scholar] [CrossRef]
- Jiang, H.; Qiu, X. Performance assessment of a newly developed and highly stable grouting material for a completely weathered granite dam foundation. Constr. Build. Mater. 2021, 299, 123956. [Google Scholar] [CrossRef]
- Ren, Z.; Zhang, C.; Wang, Y.; Lan, S.; Liu, S. Stability analysis and grouting treatment of inclined shaft lining structure in water-rich strata: A case study. Geohazard Mech. 2023, 1, 308–318. [Google Scholar] [CrossRef]
- Kang, H.; Li, W.; Gao, F.; Yang, J. Grouting theories and technologies for the reinforcement of fractured rocks surrounding deep roadways. Deep. Undergr. Sci. Eng. 2023, 2, 2–19. [Google Scholar] [CrossRef]
- Liang, X.; Feng, K.; Hu, Z.; Wang, C.; He, C. Study on grout ratio and performance of backfill grouting in water-rich strata. Constr. Build. Mater. 2024, 443, 137766. [Google Scholar] [CrossRef]
- Peng, P.; Peng, F.; Sun, Z.; Zhang, D. Grouting for tunnel stability control and inadequate grouting section recognition: A case study of countermeasure of giant karst cave. Appl. Sci. 2022, 12, 11895. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, J.; Li, R.; He, L.; Liu, C. Effects of elevated ground temperatures on properties of cement grouts for deep rock grouting. Deep. Undergr. Sci. Eng. 2025, 4, 171–188. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, G.; Guo, Y.; Feng, Z.; Gupta, R.; Liu, W.V. Development of a novel cement-based grout with enhanced thermal and sealing performance for borehole heat exchangers. Energy Build. 2024, 302, 113754. [Google Scholar] [CrossRef]
- Cheng, X.; Sheng, L.; Xia, Z.; Liu, Y.; Ma, X.; Pan, J.; Zheng, G.; Wang, R. Grouting theory and strategy of simultaneous control of the horizontal and vertical deformations of tunnels. Int. J. Geomech. 2024, 24, 04023267. [Google Scholar] [CrossRef]
- Cao, C.; Xie, Z.; Zhang, N.; Han, C.; Yan, G.; Mu, F.; Zhang, W. Differential roof cutting for roadway support in dual gob-side entry retention on a single working face− Multilevel continuous anchor-grouting control technology: A case study. Eng. Fail. Anal. 2024, 163, 108475. [Google Scholar] [CrossRef]
- Wu, S.; Guo, H.; Zhang, X.; Wang, F. Short-Term Photovoltaic Power Prediction Based on CEEMDAN and Hybrid Neural Networks. IEEE J. Photovolt. 2024, 14, 960–969. [Google Scholar] [CrossRef]
- Karijadi, I.; Chou, S. A hybrid RF-LSTM based on CEEMDAN for improving the accuracy of building energy consumption prediction. Energy Build. 2022, 259, 111908. [Google Scholar] [CrossRef]
- Zhang, J.; Ye, L.; Lai, Y. Stock price prediction using CNN-BiLSTM-Attention model. Mathematics 2023, 11, 1985. [Google Scholar] [CrossRef]
- Song, B.; Liu, Y.; Fang, J.; Liu, W.; Zhong, M.; Liu, X. An optimized CNN-BiLSTM network for bearing fault diagnosis under multiple working conditions with limited training samples. Neurocomputing 2024, 574, 127284. [Google Scholar] [CrossRef]
| Parameter | Range | Resolution | Context |
|---|---|---|---|
| Average Pressure | 0–10 MPa | ±0.1% FS | Measured by a pressure transducer at the grouting line. The key variable for power calculation and control. |
| Injection Rate | 0–100 L/min | ±0.5% of reading | Measured by an electromagnetic flowmeter. Determines the grout delivery speed. |
| Slurry Density | 1.0–2.0 g/cm3 | ±0.01 g/cm3 | Measured in-line by a nuclear density meter. Used to calculate and control the water-cement ratio in real-time. |
| Grouting Power | / | Calculated | The primary control parameter. Represents the real-time energy input. |
| Cumulative Heaving | 0–50 mm | ±0.1 mm | Measured by a high-precision displacement sensor to monitor formation lift-off, a critical safety indicator. |
| Return Flow Rate | 0–30 L/min | ±0.5% of reading | Measured to assess grout loss and detect anomalies like heaving or fracturing. |
| Training Set Ratio | Model | RMSE | MAE | R2 | Confidence Interval (95%) |
|---|---|---|---|---|---|
| 70% | CEEMDAN-CNN-BiLSTM | 0.0037 | 0.0035 | 0.9893 | [0.0035, 0.0040] |
| CNN-BiLSTM | 0.0379 | 0.0359 | 0.9619 | [0.0364, 0.0395] | |
| CNN-LSTM | 0.0605 | 0.0545 | 0.8754 | [0.0578, 0.0632] | |
| LSTM | 0.1744 | 0.1504 | 0.7264 | [0.1650, 0.1838] | |
| 80% | CEEMDAN-CNN-BiLSTM | 0.0028 | 0.0023 | 0.9889 | [0.0025, 0.0031] |
| CNN-BiLSTM | 0.0144 | 0.0114 | 0.9658 | [0.0132, 0.0157] | |
| CNN-LSTM | 0.0188 | 0.0159 | 0.8915 | [0.0173, 0.0204] | |
| LSTM | 0.0651 | 0.0635 | 0.5123 | [0.0629, 0.0672] |
| Training Set Ratio | Model | RMSE | MAE | R2 | Confidence Interval (95%) |
|---|---|---|---|---|---|
| 70% | CEEMDAN-CNN-BiLSTM | 0.0006 | 0.0005 | 0.9989 | [0.0006, 0.0007] |
| CNN-BiLSTM | 0.0047 | 0.0044 | 0.9619 | [0.0045, 0.0050] | |
| CNN-LSTM | 0.0085 | 0.0078 | 0.8754 | [0.0081, 0.0091] | |
| LSTM | 0.0127 | 0.0113 | 0.7264 | [0.0120, 0.0136] | |
| 80% | CEEMDAN-CNN-BiLSTM | 0.0006 | 0.0005 | 0.9986 | [0.0005, 0.0007] |
| CNN-BiLSTM | 0.0039 | 0.0036 | 0.9658 | [0.0037, 0.0042] | |
| CNN-LSTM | 0.0065 | 0.0058 | 0.8915 | [0.0060, 0.0070] | |
| LSTM | 0.0118 | 0.0110 | 0.5123 | [0.0111, 0.0124] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Y.; Huang, F.; Cao, Z.; Yang, Y. Grouting Power Prediction Method Based on CEEMDAN-CNN-BiLSTM. Appl. Sci. 2025, 15, 12382. https://doi.org/10.3390/app152312382
Ding Y, Huang F, Cao Z, Yang Y. Grouting Power Prediction Method Based on CEEMDAN-CNN-BiLSTM. Applied Sciences. 2025; 15(23):12382. https://doi.org/10.3390/app152312382
Chicago/Turabian StyleDing, Ye, Fan Huang, Zhi Cao, and Yang Yang. 2025. "Grouting Power Prediction Method Based on CEEMDAN-CNN-BiLSTM" Applied Sciences 15, no. 23: 12382. https://doi.org/10.3390/app152312382
APA StyleDing, Y., Huang, F., Cao, Z., & Yang, Y. (2025). Grouting Power Prediction Method Based on CEEMDAN-CNN-BiLSTM. Applied Sciences, 15(23), 12382. https://doi.org/10.3390/app152312382





