One More Thing on the Subject: Prediction of Chaos in a Josephson Junction with Quadratic Damping by the Melnikov Technique, Possible Probabilistic Control over Oscillations
Abstract
1. Introduction
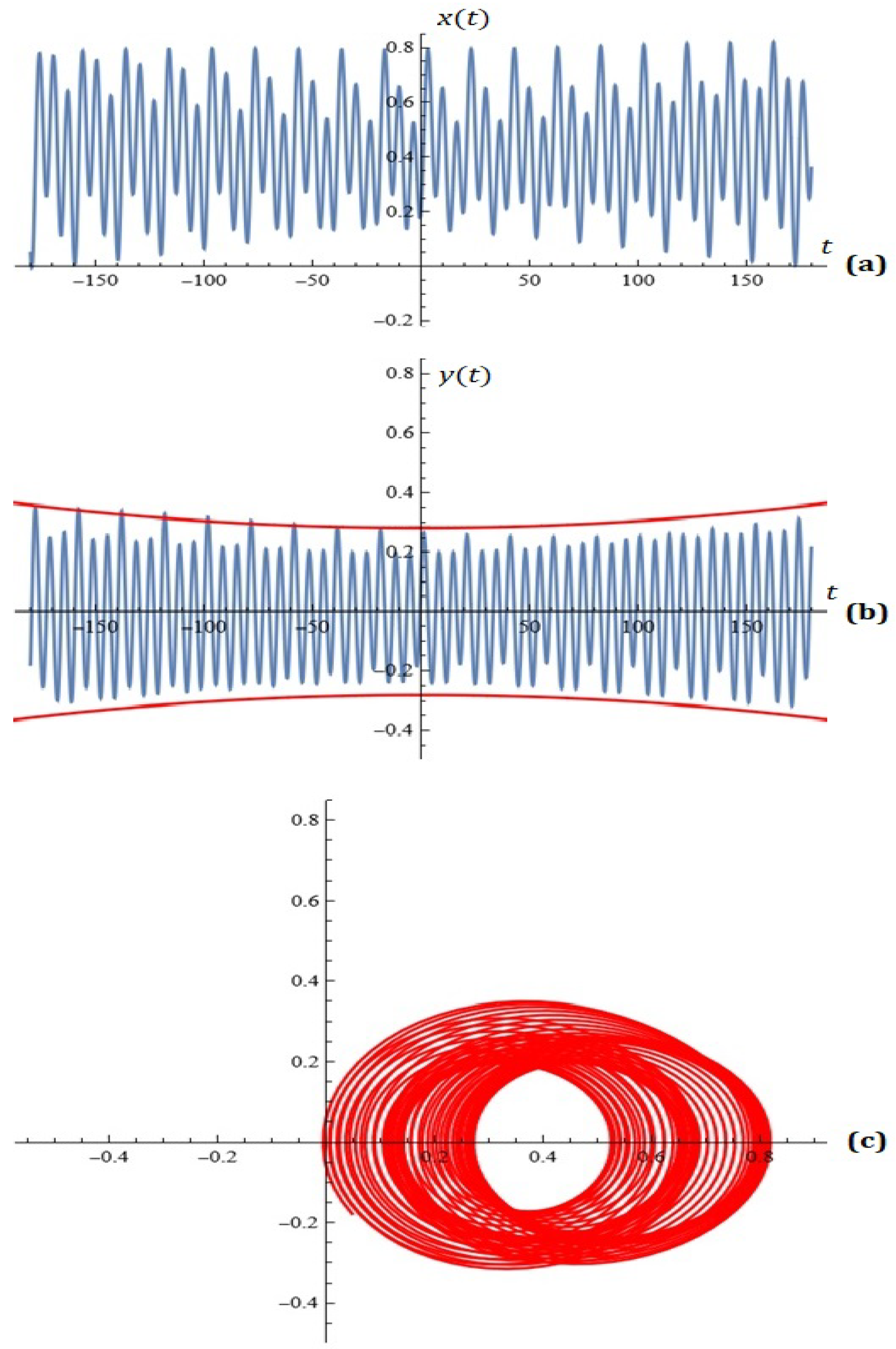
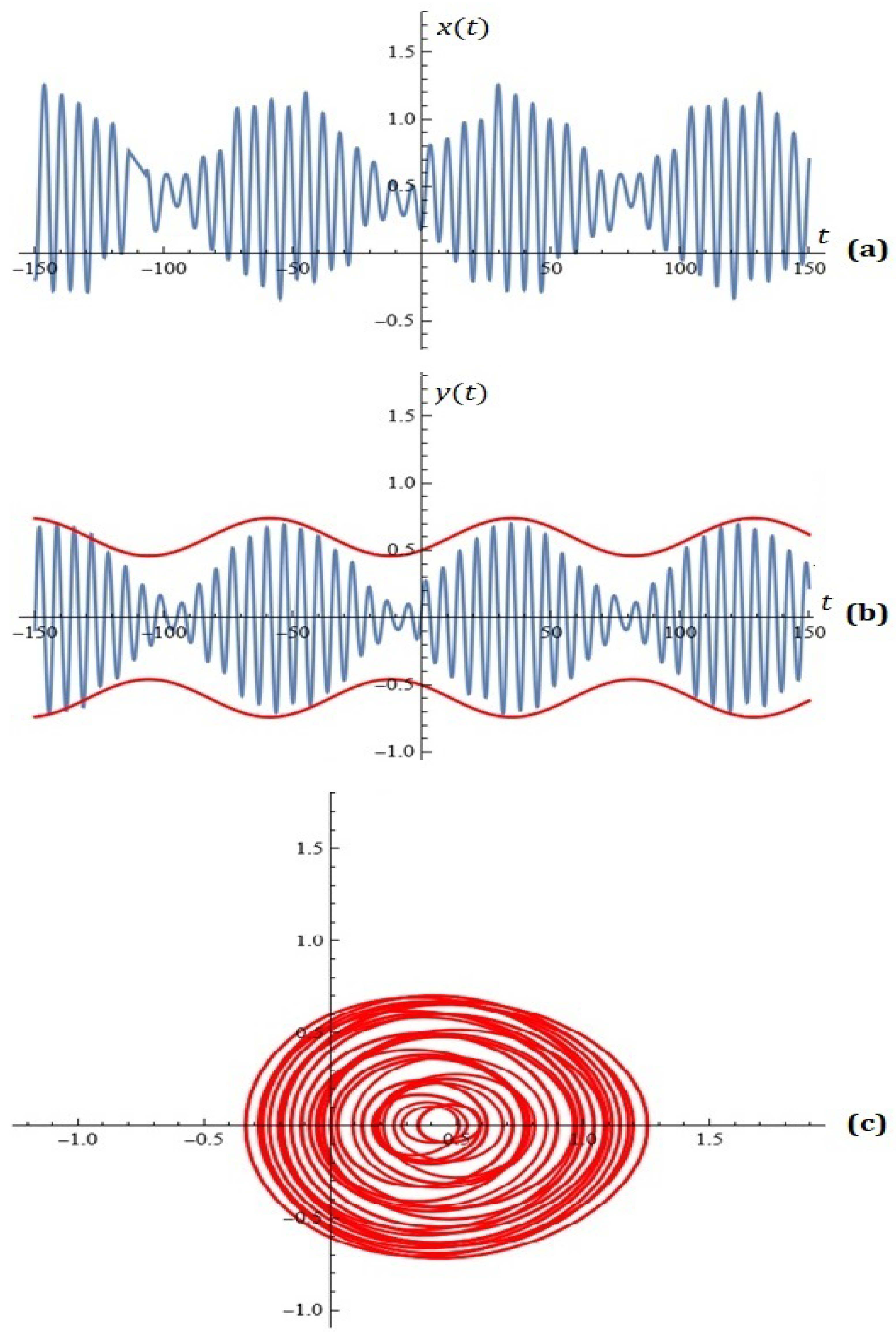
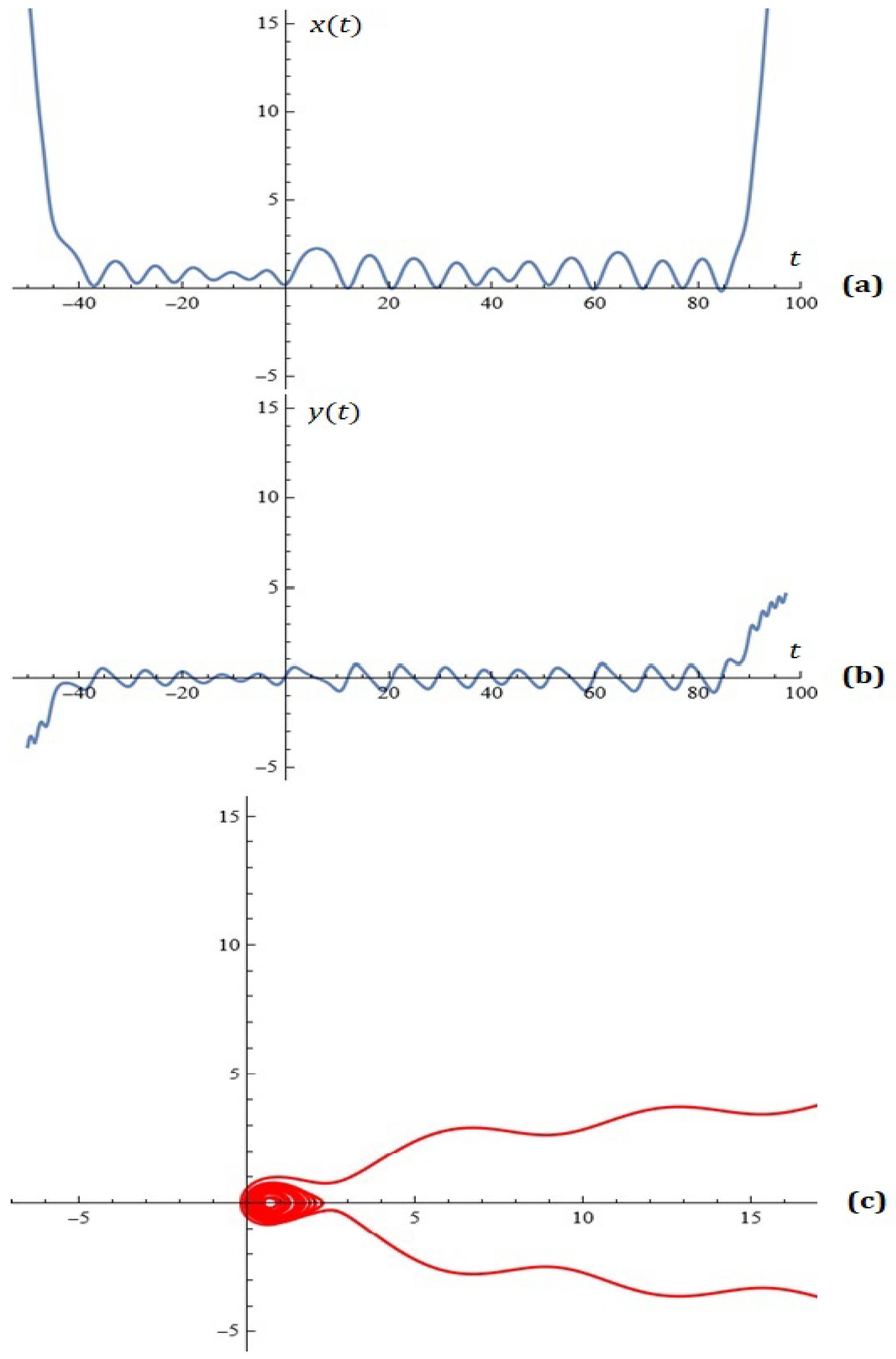
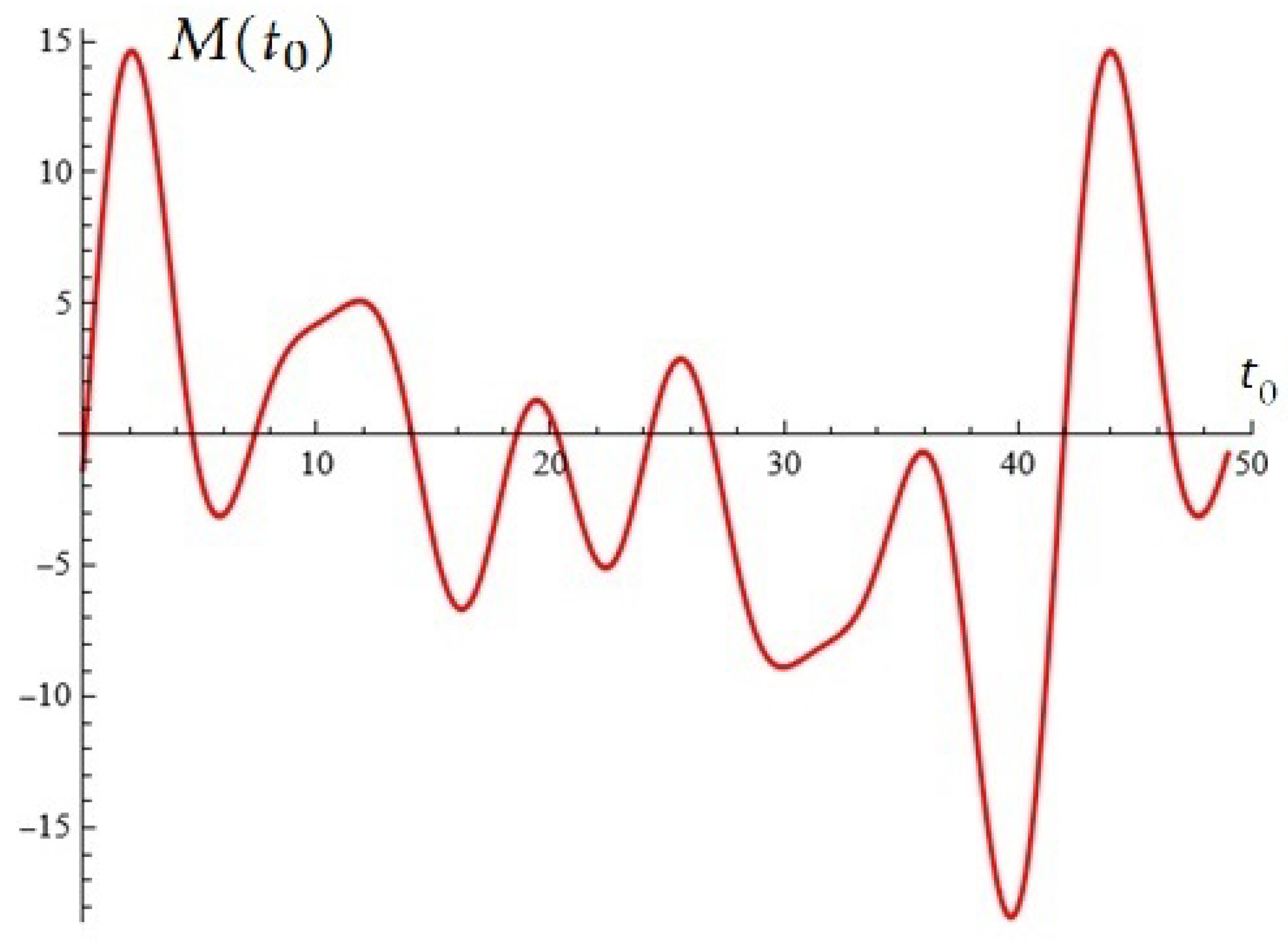
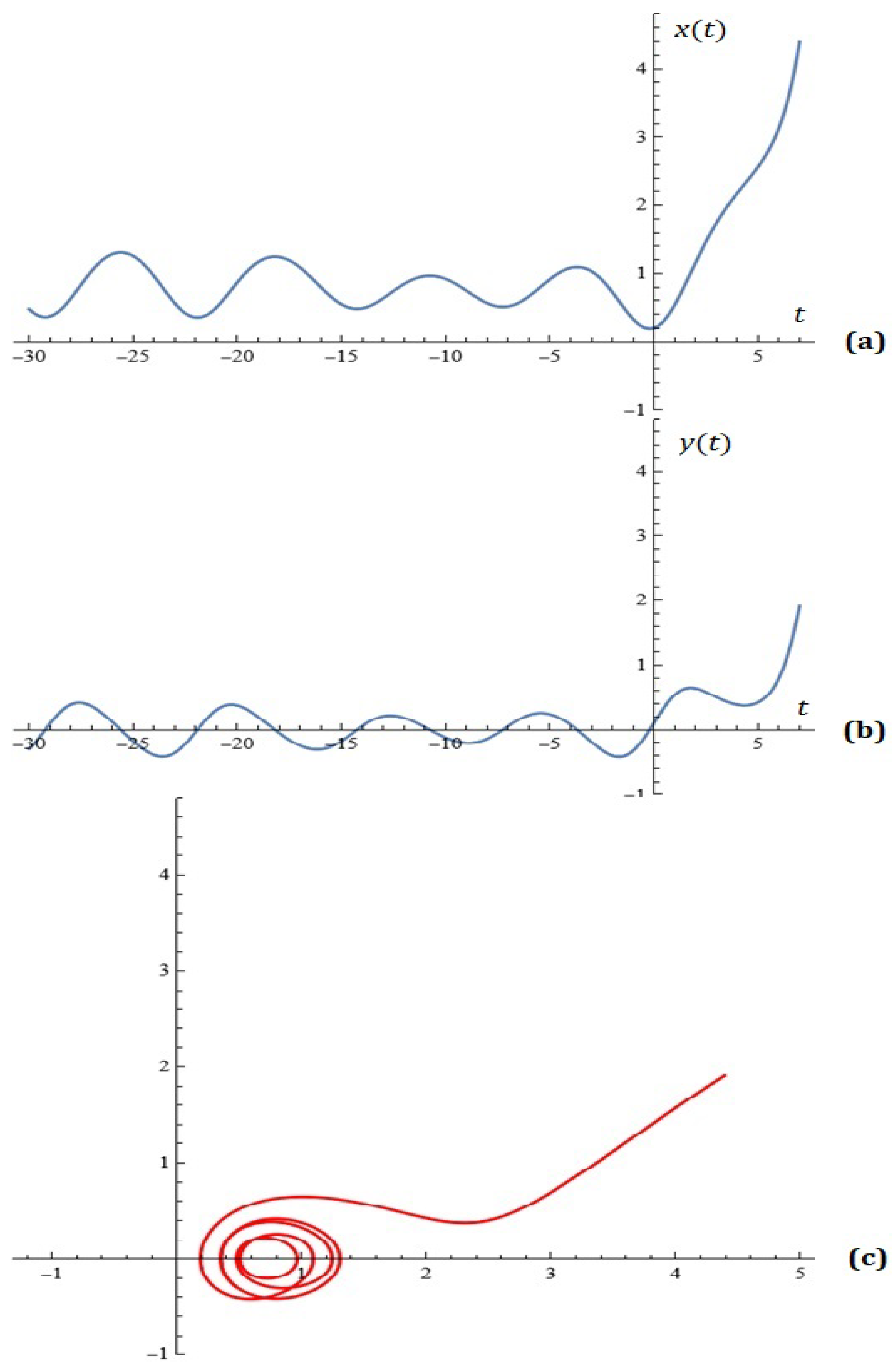
2. A New Model— Some Simulations
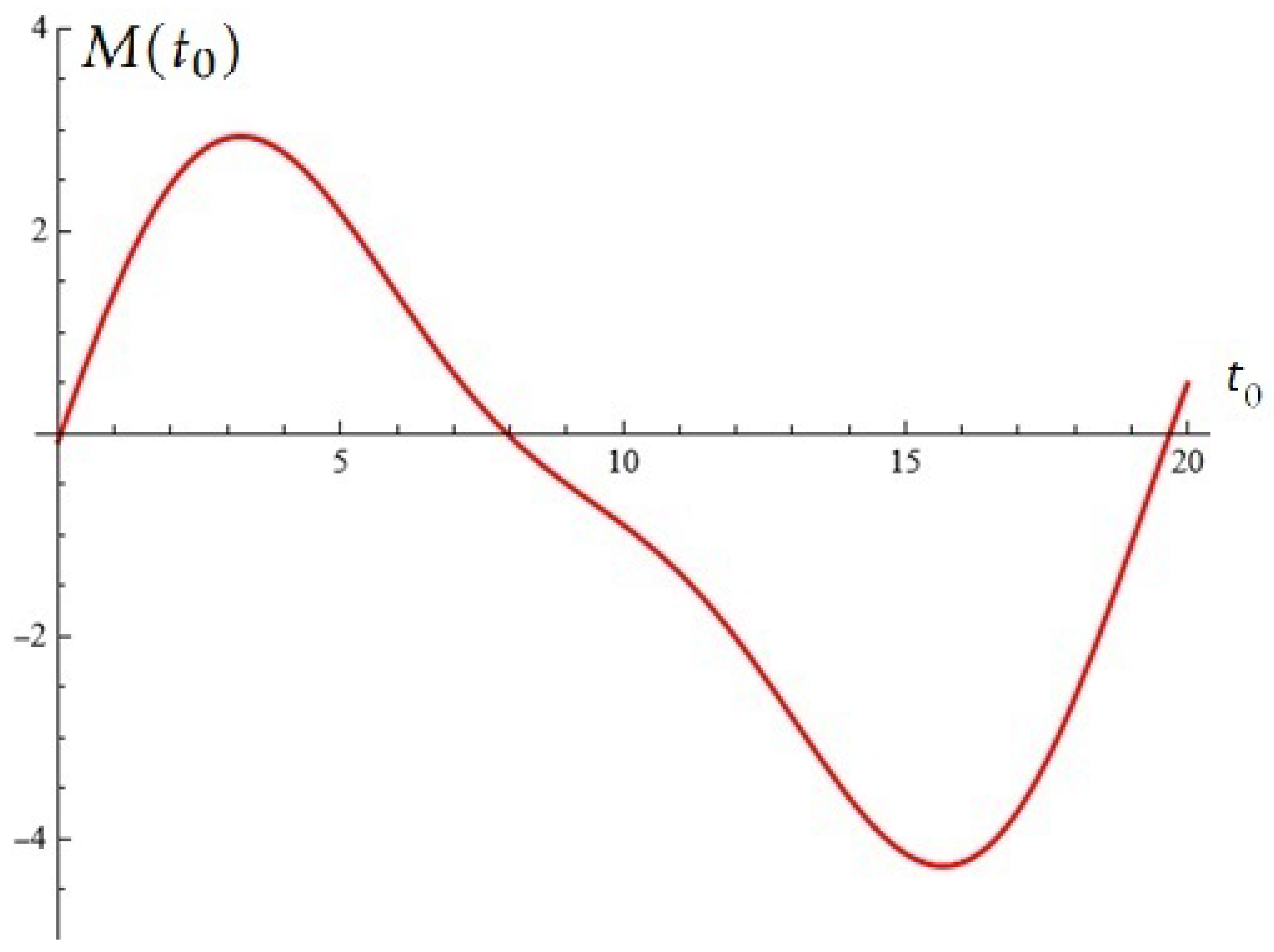
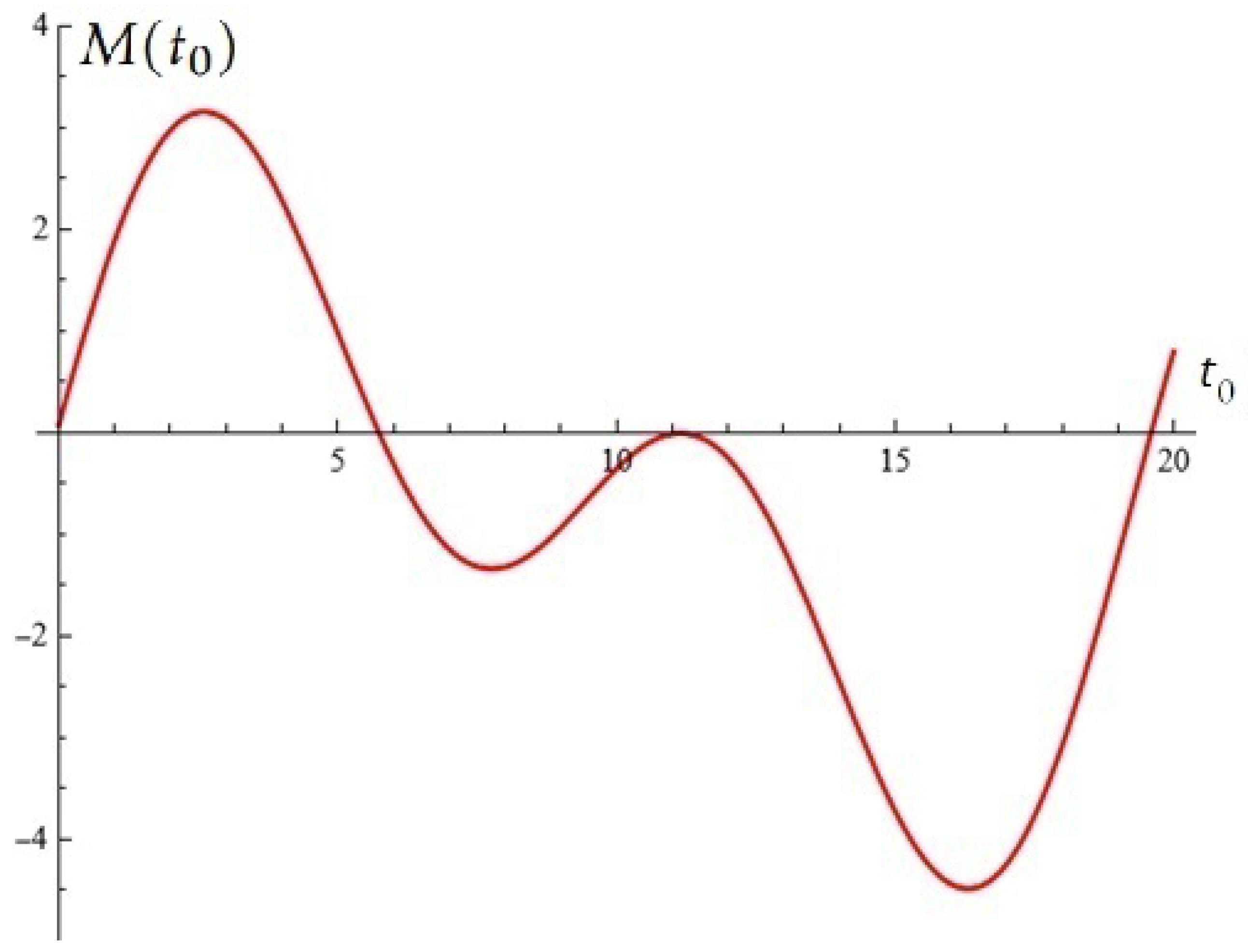
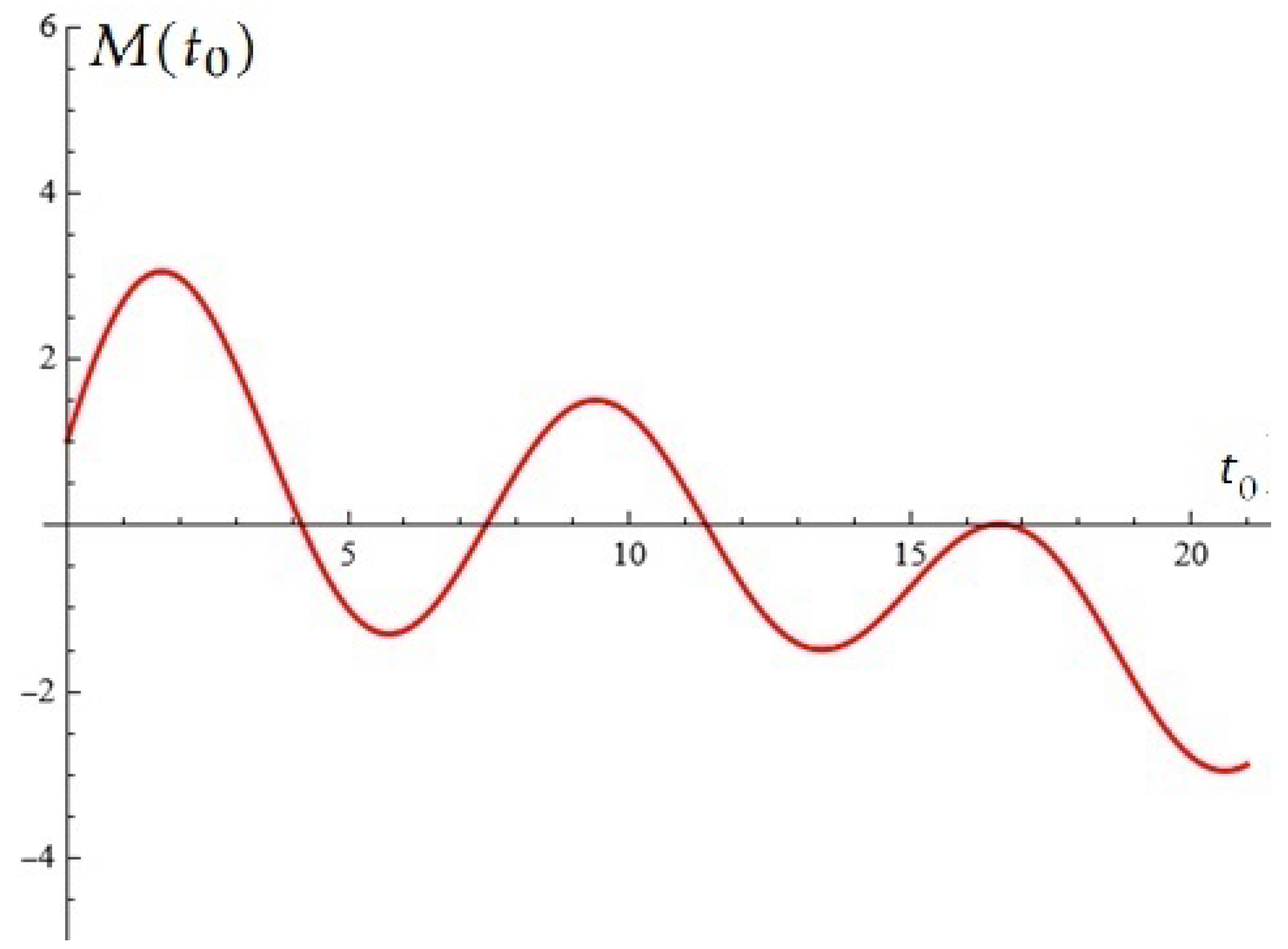
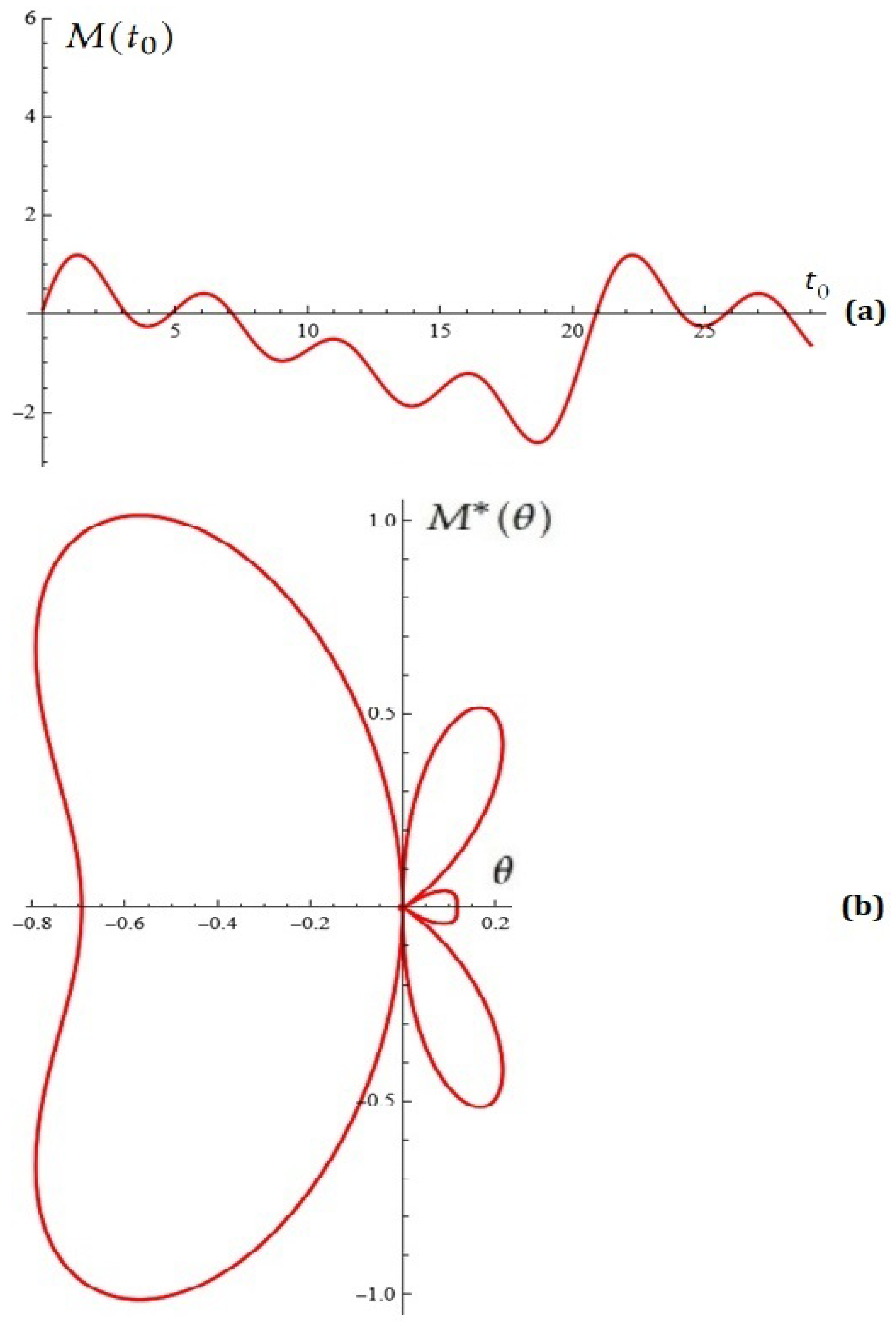
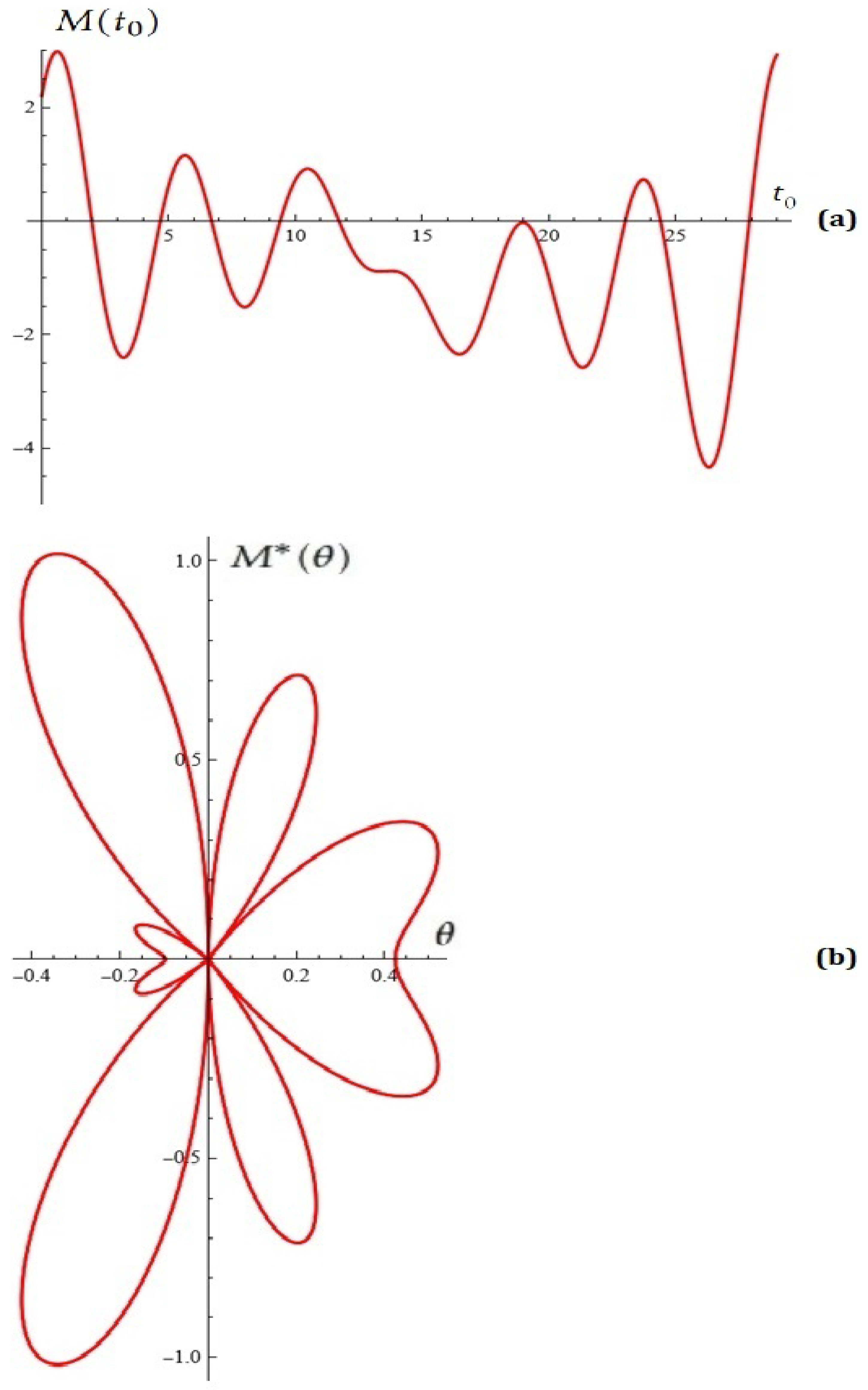
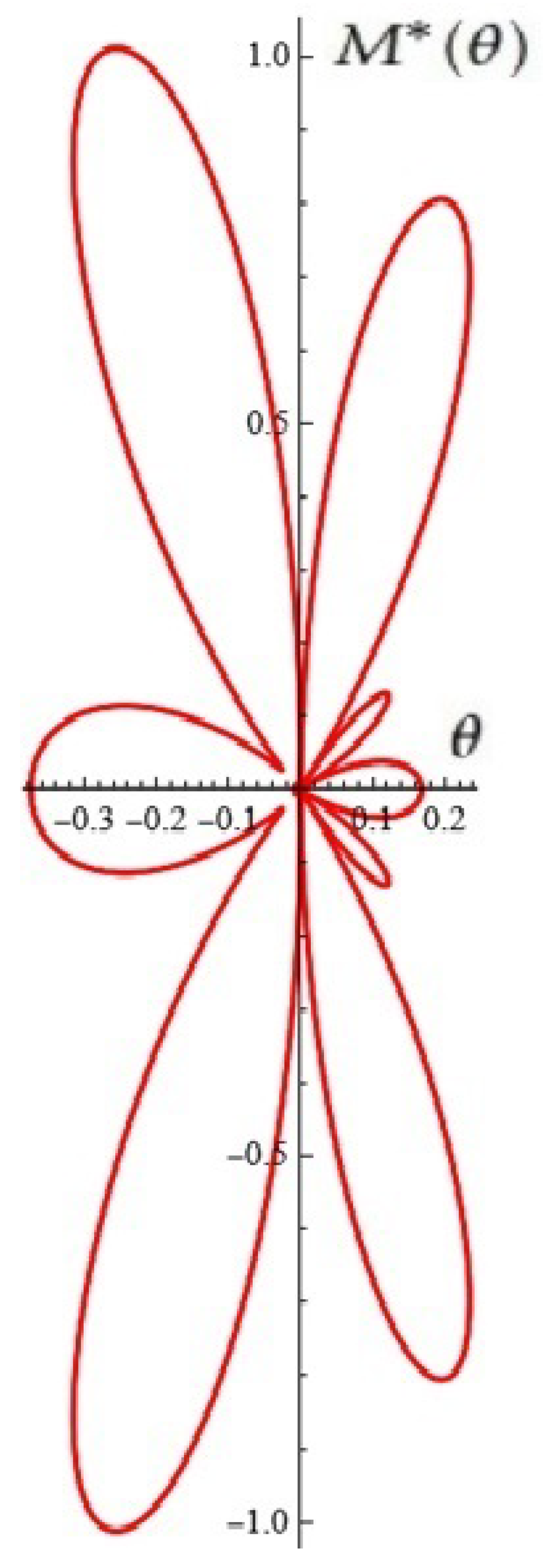
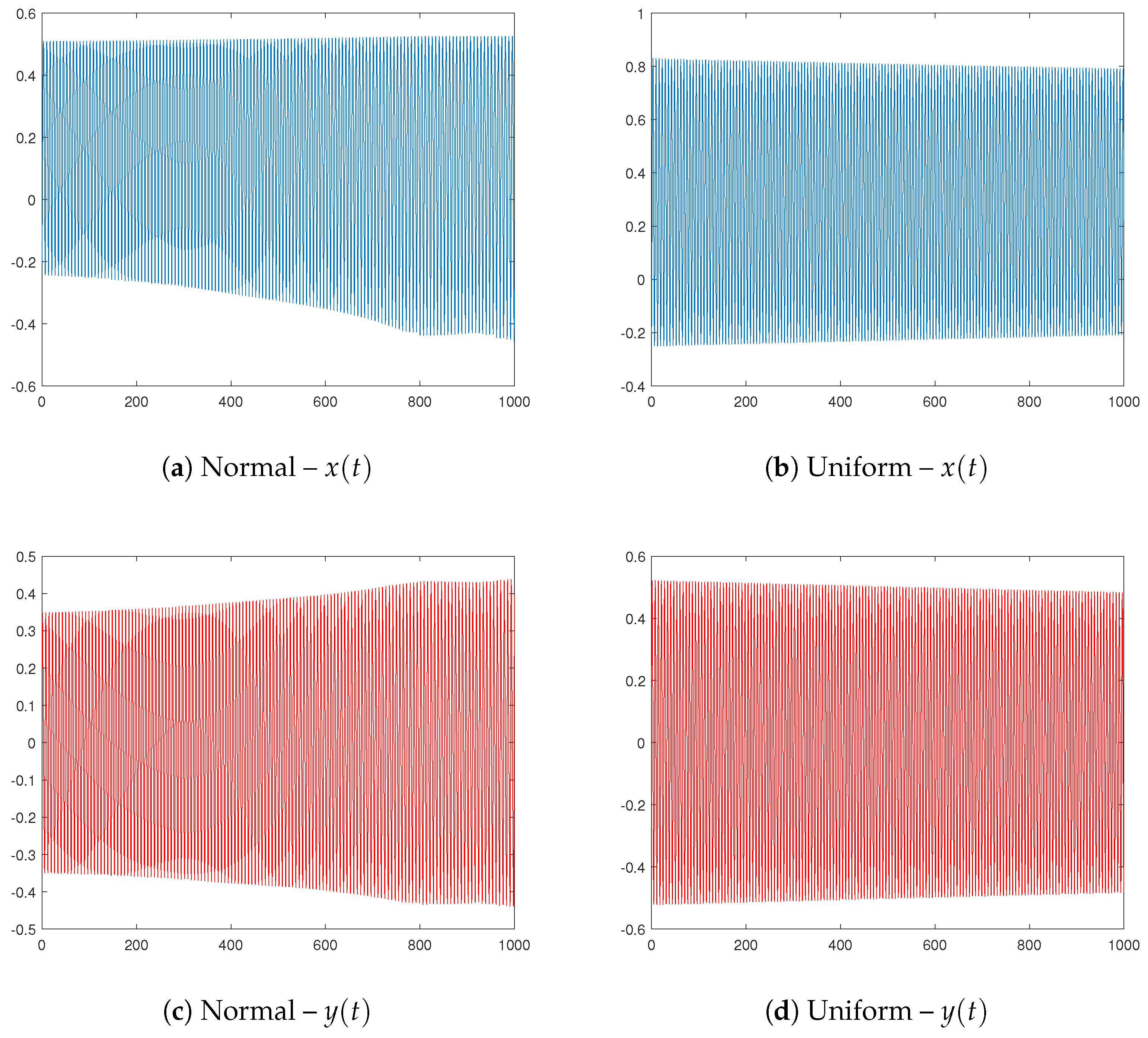
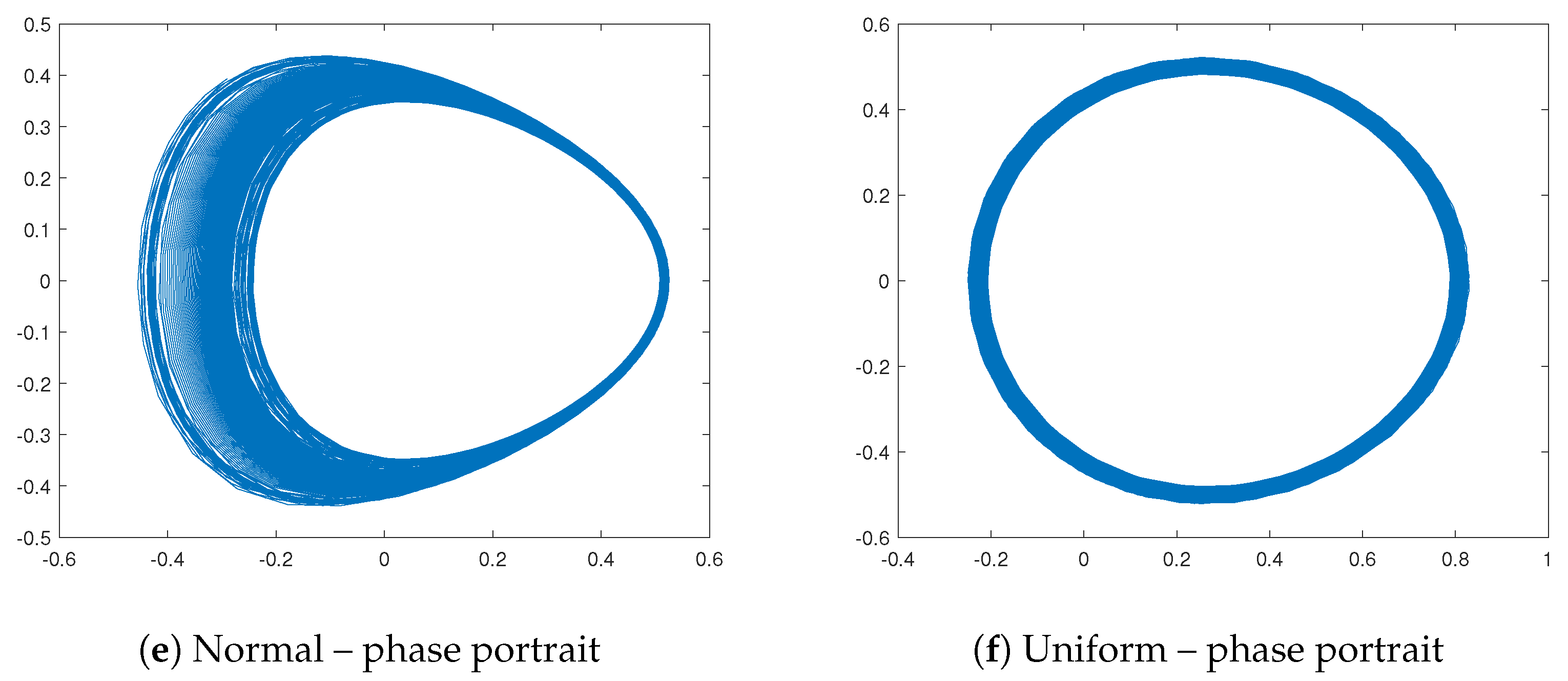
3. Using Stochastic Construction to Potentially Control Oscillations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jaklevic, R.C.; Lambe, J.; Silver, A.H.; Mercereau, J.E. Quantum Interference Effects in Josephson Tunneling. Phys. Rev. Lett. 1964, 12, 159–160. [Google Scholar] [CrossRef]
- Clarke, J.; Braginski, A.I. (Eds.) The SQUID Handbook: Fundamentals and Technology of SQUIDs and SQUID Systems; Wiley-VCH: Weinheim, Germany, 2004; Volume 1. [Google Scholar]
- Clarke, J.; Braginski, A.I. (Eds.) The SQUID Handbook: Applications of SQUIDs and SQUID Systems; Wiley-VCH: Weinheim, Germany, 2006; Volume 2. [Google Scholar]
- Ritala, R.K.; Salomaa, M.M. Odd and even subharmonics and chaos in RF SQUIDS. J. Phys. C Solid State Phys. 1983, 16, 477–484. [Google Scholar] [CrossRef]
- Ritala, R.K.; Salomaa, M.M. Chaotic dynamics of periodically driven rf superconducting quantum interference devices. Phys. Rev. B 1984, 29, 6143–6154. [Google Scholar] [CrossRef]
- Fesser, K.; Bishop, A.R.; Kumar, P. Chaos in rf SQUID’s. Appl. Phys. Lett. 1983, 43, 123–124. [Google Scholar] [CrossRef]
- Schieve, W.C.; Bulsara, A.R.; Jacobs, E.W. Homoclinic chaos in the rf superconducting quantum-interference device. Phys. Rev. A 1988, 37, 3541–3552. [Google Scholar] [CrossRef] [PubMed]
- Ling, F.H.; Bao, G. A numerical implementation of Melnikov’s method. Phys. Lett. A 1987, 122, 413–417. [Google Scholar] [CrossRef]
- Salam, F.M.A. The Mel’nikov technique for highly dissipative systems. SIAM J. Appl. Math. 1987, 47, 232–243. [Google Scholar] [CrossRef]
- Schecter, S. Melnikov’s method at a saddle–node and the dynamics of the forced Josephson junction. SIAM J. Math. Anal. 1987, 18, 1699–1715. [Google Scholar] [CrossRef]
- Grebogi, C.; Ott, E.; Yorke, J.A. Basin boundary metamorphoses: Changes in accessible boundary orbits. Phys. D 1987, 24, 243–262. [Google Scholar] [CrossRef]
- Bruhn, B.; Koch, B. Homoclinic and Heteroclinic Bifurcations in rf SQUIDs. Z. Naturforsch. A 1988, 43, 930–938. [Google Scholar] [CrossRef]
- Kyurkchiev, N.; Zaevski, T.; Iliev, A.; Branzov, T. A Note on the Dynamics of Modified rf-SQUIDs: Simulations and Possible Control over Oscillations. Mathematics 2025, 13, 722. [Google Scholar] [CrossRef]
- Falko, C.; Parker, W. Operating characteristics of thin-film rf-biased SQUID’s. J. Appl. Phys. 1975, 46, 3238–3243. [Google Scholar] [CrossRef]
- Zhang, Y.; Muck, M.; Braginski, A.I.; Topfer, H. High-sensitivity microwave rf SQUID operating at 77 K. Supercond. Sci. Technol. 1994, 7, 269–272. [Google Scholar] [CrossRef]
- Zhang, Y.; Muck, M.; Herrmann, K.; Schubert, J.; Zander, W.; Braginski, A.I.; Heiden, C. Sensitive rf SQUIDs and magnetometers operating at 77 K. IEEE Trans. Appl. Supercond. 1993, 3, 2465–2468. [Google Scholar] [CrossRef]
- Il’ichev, E.; Zakosarenko, V.; Ijsselsteijn, R.P.; Schultze, V. Inductive reply of high-Tc rf SQUID in the presence of large thermal fluctuations. J. Low Temp. Phys. 1997, 106, 503–508. [Google Scholar] [CrossRef]
- Chesca, B. On the theoretical study of an rf-SQUID operation taking into account the noise influence. J. Low Temp. Phys. 1994, 94, 515–538. [Google Scholar] [CrossRef]
- Greenberg, Y. Signal characteristics for high Tc rf SQUID from its small signal voltage-frequency characteristics. J. Low Temp. Phys. 1998, 114, 297–316. [Google Scholar] [CrossRef]
- Jeanneret, B.; Benz, S.P. Application of the Josephson effect in electrical metrology. Eur. Phys. J. Spec. Top. 2009, 172, 181–206. [Google Scholar] [CrossRef]
- Martínez-Pérez, M.J.; Koelle, D. NanoSQUIDs: Basics and recent advances. Phys. Sci. Rev. 2017, 2, 20175001. [Google Scholar] [CrossRef]
- Tarte, E.J.; Moseley, R.W.; Kölbl, M.R.; Booij, W.E.; Burnell, G.; Blamire, M.G. Asymmetry modulated SQUIDS. Supercond. Sci. Technol. 2000, 13, 983–988. [Google Scholar] [CrossRef]
- Likharev, K.K.; Semenov, V.K. RSFQ logic/memory family: A new Josephson-junction technology for sub-terahertz-clock-frequency digital systems. IEEE Trans. Appl. Supercond. 1991, 1, 3–28. [Google Scholar] [CrossRef]
- Soloviev, I.I.; Klenov, N.V.; Bakurskiy, S.V.; Kupriyanov, M.Y.; Gudkov, A.L.; Sidorenko, A.S. Beyond Moore’s technologies: Operation principle of a superconductor alternative. Beilstein J. Nanotechnol. 2017, 8, 2689–2710. [Google Scholar] [CrossRef] [PubMed]
- Vitanov, N.; Martinov, N. On the solitary waves in the sine-Gordon model of the two-dimensional Josephson junction. Z. Phys. B Condens. Matter 1996, 100, 129–135. [Google Scholar] [CrossRef]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar]
- Wiggins, S. Global Bifurcations and Chaos; Springer: New York, NY, USA, 1988. [Google Scholar]
- Chacon, R. Control of Homoclinic Chaos by Weak Periodic Perturbations; World Scientific Series of Nonlinear Science; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2005; Volume 55. [Google Scholar]
- Braiman, Y.; Goldhirsch, I. Taming chaotic dynamics with weak periodic perturbations. Phys. Rev. Lett. 1991, 66, 2545–2548. [Google Scholar] [CrossRef]
- Ostrovskii, V.; Karimov, A.; Rybin, V.; Kopets, E.; Butusov, D. Comparing the Finite-Difference Schemes in the Simulation of Shunted Josephson Junctions. In Proceedings of the 23rd Conference of Open Innovations Association (FRUCT), Bologna, Italy, 13–16 November 2018; pp. 300–305. [Google Scholar]
- Salam, F.M.A.; Sastry, S.S. The complete dynamics of the forced Josephson junction circuit-The regions of chaos. In Chaos in Nonlinear Dynamical Systems; Chandra, J., Ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1984; pp. 43–55. [Google Scholar]
- Cveticanin, L.; Herisanu, N.; Ninkov, I.; Jovanovic, M. New Closed-Form Solution for Quadratic Damped and Forced Nonlinear Oscillator with Position-Dependent Mass: Application in Grafted Skin Modeling. Mathematics 2022, 10, 2706. [Google Scholar] [CrossRef]
- Bartuccelli, M.; Christiansen, P.L.; Pedersen, N.F.; Sørensen, M.P. Prediction of chaos in a Josephson junction by the Melnikov-function technique. Phys. Rev. B 1986, 33, 4686–4691. [Google Scholar] [CrossRef]
- Melnikov, V.K. On the stability of the center for time periodic perturbations. Trans. Mosc. Math. Soc. 1963, 12, 3–52. [Google Scholar]
- Pedersen, N.F.; Saermark, K. Analytical solution for a Josephson-Junction model with capacitance. Physica 1973, 69, 572–578. [Google Scholar] [CrossRef]
- Makrelov, I.; Kyurkchiev, N.; Tamburov, S. Two two-sided methods for simultaneous determination of all roots of trigonometric and exponential polynomials. Trav. Sci. Univ. Plovdiv Math. 1985, 23, 289–298. [Google Scholar]
- Proinov, P.; Cholakov, S.; Vasileva, M. Fully Computable Convergence Analysis of a Fourth Order Iterative Method for Finding Polynomial Roots. J. Appl. Math. Comput. 2025, 71, 6365–6380. [Google Scholar] [CrossRef]
- Marcheva, P.I.; Ivanov, I.K.; Ivanov, S.I. On the Q-Convergence and Dynamics of a Modified Weierstrass Method for the Simultaneous Extraction of Polynomial Zeros. Algorithms 2025, 18, 205. [Google Scholar] [CrossRef]
- Sendov, B.; Andreev, A.; Kyurkchiev, N. Numerical solution of polynomial equations. In Handbook of Numerical Analysis; Ciarlet, P.G., Lions, J.L., Eds.; Elsevier Science Publ.: Amsterdam, The Netherlands, 1994; Volume III, pp. 625–778. [Google Scholar]
- Golev, A.; Terzieva, T.; Iliev, A.; Rahnev, A.; Kyurkchiev, N. Simulation on a Generalized Oscillator Model: Web-Based Application. Comptes Rendus Acad. Bulg. Sci. 2024, 77, 230–237. [Google Scholar] [CrossRef]
- Georgieva, M.; Grozdev, S. Morphodynamics for the Development of Noospheric Intelligence; East-West Publishing House: Sofia, Bulgaria, 2016. (In Bulgarian) [Google Scholar]
- Dolph, C.L. A Current Distribution for Broadside Arrays which Optimizes the Relationship between Beam Width and Side-Lobe Level. Proc. IRE 1946, 34, 335–348. [Google Scholar] [CrossRef]
- Tu, L.; Ng, B.P. Exponential and generalized Dolph - Chebyshev functions for flat-top array beam pattern synthesis. Multidimens. Syst. Signal Process. 2013, 25, 541–561. [Google Scholar] [CrossRef]
- Hutu, F.; Cauet, S.; Coirault, P. Antenna Arrays Principle and Solutions: Robust Control Approach. Int. J. Comput. Commun. Control 2008, 3, 161–171. [Google Scholar] [CrossRef]
- Iordache, M.; Paillot, J.M.; Dumitrescu, I.; Ionita, M. Analysis of Coupled Oscillators Applied to Antenna Arrays. Ann. Univ. Craiova Electr. Eng. Ser. 2010, 34, 1–10. [Google Scholar]
- Kyurkchiev, N.; Zaevski, T.; Iliev, A.; Kyurkchiev, V.; Rahnev, A. Studying homoclinic chaos in a class of piecewise smooth oscillators: Melnikov’s approach, symmetry results, simulations and applications to generating antenna factors using approximation and optimization techniques. Symmetry 2025, 17, 1144. [Google Scholar] [CrossRef]
- Apostolov, P.; Valchev, D.G. Closed-Form Expressions for Half Power Beam Width and Steering of Two-Dimensional Rectangular Binomial Array Antenna. In Proceedings of the 2024 15th National Conference with International Participation (ELECTRONICA), Sofia, Bulgaria, 16–17 May 2024; pp. 1–4. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kyurkchiev, N.; Zaevski, T.; Iliev, A.; Kyurkchiev, V.; Rahnev, A. One More Thing on the Subject: Prediction of Chaos in a Josephson Junction with Quadratic Damping by the Melnikov Technique, Possible Probabilistic Control over Oscillations. Appl. Sci. 2025, 15, 12359. https://doi.org/10.3390/app152312359
Kyurkchiev N, Zaevski T, Iliev A, Kyurkchiev V, Rahnev A. One More Thing on the Subject: Prediction of Chaos in a Josephson Junction with Quadratic Damping by the Melnikov Technique, Possible Probabilistic Control over Oscillations. Applied Sciences. 2025; 15(23):12359. https://doi.org/10.3390/app152312359
Chicago/Turabian StyleKyurkchiev, Nikolay, Tsvetelin Zaevski, Anton Iliev, Vesselin Kyurkchiev, and Asen Rahnev. 2025. "One More Thing on the Subject: Prediction of Chaos in a Josephson Junction with Quadratic Damping by the Melnikov Technique, Possible Probabilistic Control over Oscillations" Applied Sciences 15, no. 23: 12359. https://doi.org/10.3390/app152312359
APA StyleKyurkchiev, N., Zaevski, T., Iliev, A., Kyurkchiev, V., & Rahnev, A. (2025). One More Thing on the Subject: Prediction of Chaos in a Josephson Junction with Quadratic Damping by the Melnikov Technique, Possible Probabilistic Control over Oscillations. Applied Sciences, 15(23), 12359. https://doi.org/10.3390/app152312359








