Adaptive Software-Defined Network Control Using Kernel-Based Reinforcement Learning: An Empirical Study

Abstract

Software-defined networking (SDN) requires adaptive control strategies to handle dynamic traffic conditions and heterogeneous network environments. Reinforcement learning (RL) has emerged as a promising solution, yet deep RL methods often face instability, non-stationarity, and reproducibility challenges that limit practical deployment. To address these issues, a kernel-based RL framework is introduced, embedding transition dynamics into reproducing kernel Hilbert spaces (RKHS) and combining kernel ridge regression with policy iteration. This approach enables stable value estimation, enhanced sample efficiency, and interpretability, making it suitable for large-scale and evolving SDN scenarios. Experimental evaluation demonstrates consistent convergence and robustness under traffic variability, with cumulative rewards exceeding those of baseline deep RL methods by more than 22%. The findings highlight the potential of kernel-embedded RL as a practical and theoretically grounded solution for adaptive SDN management and contribute to the broader development of intelligent systems in complex environments.

1. Introduction

Software-defined networking (SDN) has emerged as a transformative paradigm that separates the control and data planes, enabling programmability, flexibility, and innovation in network management [1,2]. In modern networked systems, adaptive control is crucial to meet the demands of dynamic and heterogeneous traffic environments, where static configurations or rule-based policies are insufficient. Reinforcement learning (RL) has therefore gained attention as a promising approach to optimize network decision-making, offering the ability to adapt policies based on continuous feedback and stochastic dynamics [3,4,5,6].

Kernel approaches, in particular, have long been studied in machine learning as a principled way to embed probability distributions into high-dimensional feature spaces, offering a potential solution to these challenges. The kernel mean embedding formalism maps probability distributions into reproducing kernel Hilbert spaces (RKHS), enabling linear operations on distributions and offering a powerful toolkit for probabilistic reasoning [7]. This idea has been extended to conditional distributions, which makes it possible to model stochastic transitions and dynamical systems directly in RKHS [8] and even the definition of a kernelized analogue of Bayes’ rule for inference [9]. These developments have provided the mathematical foundations for kernel-based RL. Early work demonstrated that kernelized function approximation could yield effective value estimation in RL problems [10,11]. Subsequent studies applied RKHS embeddings to model transition dynamics in Markov decision processes, showing that embedding operators could capture nonlinear structure in dynamics while preserving convergence properties [12]. Representative-state approaches have also been proposed to mitigate scalability issues while retaining the benefits of kernel-based representation [13]. Collectively, this body of research establishes that kernel embeddings offer stability, generalization, and interpretability advantages compared with purely parametric deep RL methods.

Beyond networking, learning-based control has seen broad use [14,15,16,17,18,19,20], but the present work focuses on SDN-specific challenges and solutions.

Deep RL methods, although powerful, often suffer from instability, poor reproducibility, and sensitivity to hyperparameter choices, which hinders their deployment in practical systems [21]. A central challenge lies in non-stationarity: policies trained under one distribution may quickly degrade as the environment evolves, a problem that has been systematically surveyed in the context of dynamically varying environments [22,23]. In SDN specifically, surveys emphasize that traffic variability, topology changes, and latency constraints exacerbate these issues, demanding adaptive methods that can respond in real time [3,24]. Another pressing limitation is the lack of interpretability. While deep policies can achieve impressive performance, they are often treated as black boxes, making it difficult to explain or validate their decisions in safety-critical applications. Recent reviews of explainable RL highlight the gap between theoretical advances and practical interpretability in deep RL, underscoring the need for approaches that provide transparency alongside performance [25,26]. This issue is particularly important in networked systems, where operators must trust and understand automated decisions. In addition, RL for networking faces practical deployment constraints. Studies have shown that deep RL-based routing or scheduling may achieve near-optimal results in simulation but struggle to meet real-time requirements under production-scale workloads [6,27]. Edge computing environments further compound these challenges, where limited resources demand lightweight and efficient learning algorithms [24]. These observations collectively motivate the exploration of kernel-based methods that can offer stability, sample efficiency, and interpretability.

Nevertheless, despite their strong theoretical grounding, kernel-based RL approaches remain underexplored in applied domains such as SDN control. Bridging this gap, the present work introduces an RL framework that integrates RKHS embeddings with policy iteration to deliver stability and practical performance in SDN environments. The method embeds transition dynamics into RKHS, allowing distributions over network states to be represented and manipulated directly. This yields a policy iteration algorithm that combines the stability of kernel ridge regression with the adaptability of RL, offering both theoretical soundness and practical robustness.

The contributions of this study can be summarised as follows. First, a kernel-based policy iteration approach is introduced that models transition dynamics nonparametrically, enhancing stability under non-stationary traffic conditions. Second, the method improves sample efficiency and mitigates instability compared with conventional deep RL baselines. Third, an empirical evaluation in SDN traffic management scenarios demonstrates consistent convergence and more than 22% improvement in cumulative rewards over standard RL methods. These findings position the method as a practical and interpretable RL solution for adaptive network control, complementing recent advances in intelligent systems beyond networking domains [19,20].

The remainder of the paper is organized as follows: Section 2 develops the kernel-based reinforcement-learning method (Section 2.1, Section 2.2, Section 2.3, Section 2.4, Section 2.5, Section 2.6, Section 2.7 and Section 2.8) and details the SDN experimental setup (Section 2.9); Section 3 presents the empirical results: kernel representation analysis, regularization impact, learning dynamics, baseline comparison, optimization trajectories, reward statistics, and component analysis; Section 4 provides discussion; Section 5 concludes.

2. Materials and Methods

2.1. Problem Formulation

The adaptive control of SDN is modeled as a discounted Markov decision process:

$$\mathcal{M}=(\mathbb{X},\mathbb{U},\mathcal{T},\rho ,\delta ),$$

where $\mathbb{X}$ denotes the state space (e.g., traffic load vectors and topology indicators), $\mathbb{U}$ is the set of feasible control actions (e.g., flow rerouting and queue management), $\mathcal{T}$ represents the transition dynamics, $\rho :\mathbb{X}\times \mathbb{U}\to \mathbb{R}$ specifies the reward function, and $\delta \in (0,1)$ is the discount factor.

The objective is to maximize the long-term discounted return:

$$J^{\pi }=\mathbb{E}\left[\sum _{t=0}^{\infty }{\delta }^t{r}_t\right].$$

Operationally, the SDN controller observes current network conditions, applies a control action, and receives performance feedback (e.g., throughput and delay). The discount factor $\delta \in (0,1)$ down-weights distant rewards for responsiveness while the optimization target remains the long-horizon return $J^{\pi }$.

At each decision step t, the controller observes the current state $x_t\in \mathbb{X}$, selects an action $u_t\in \mathbb{U}$, and subsequently receives a reward $\rho (x_t,u_t)$ as the system evolves to the next state $x_{t+1}\sim \mathcal{T}(·\mid x_t,u_t)$. The overarching goal of the RL agent is to optimize a policy $\pi$ that maximizes the expected long-term discounted return.

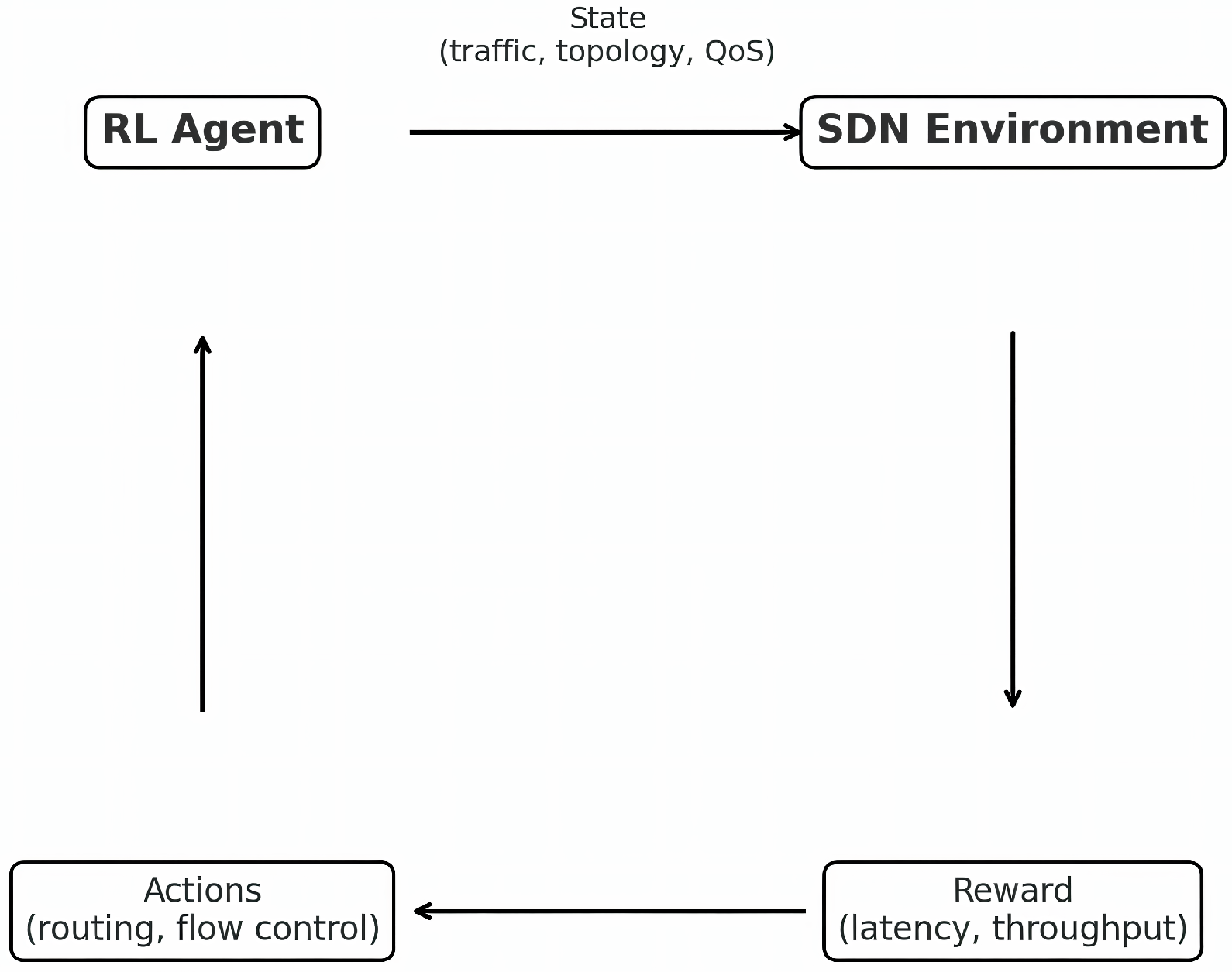
Figure 1 illustrates the closed-loop interaction between the RL agent and the SDN environment. Arrows from the SDN Environment to the RL Agent denote information flow, state measurements (traffic, topology, and QoS) and the scalar reward (e.g., latency/throughput summaries), used to form the observation and learning signal. Arrows from the RL Agent to the SDN Environment denote control actions (routing/flow-control updates) applied via the controller. The vertical arrows indicate the progression to the next decision step as the network evolves under the applied action, closing the control loop.

The agent continuously receives state observations, issues control actions, and is guided by performance-based rewards such as throughput and latency. This iterative cycle provides the foundation for adaptive decision-making in SDN control. The closed loop executes on the SDN controller in the control plane, which polls switch measurements and, at the decision period specified in Section 2.9 (2.5 s), applies actions to data-plane switches via OpenFlow.

2.2. Kernel Embedding of Transition Dynamics

A central challenge in RL for SDN is the accurate modeling of stochastic state transitions. Classical deep neural architectures often approximate these dynamics in a purely parametric manner, which can lead to poor generalization in non-stationary network environments and provide little theoretical insight into stability. To address these limitations, we employ kernel mean embedding, a nonparametric framework that represents probability distributions directly in an RKHS. This approach transforms probabilistic transitions into deterministic elements of a Hilbert space, thereby enabling both rigorous analysis and efficient computation.

Intuitively, the idea is that instead of trying to guess the exact probability of each possible next state, we encode the whole transition distribution as a single geometric object (a vector) in a high-dimensional space. This embedding acts like a unique signature of the transition dynamics, allowing the agent to reason about likely next states without ever estimating explicit probabilities.

Formally, consider the state domain $\mathbb{X}$ and action domain $\mathbb{U}$. Each state $x\in \mathbb{X}$ and action $u\in \mathbb{U}$ is mapped to a high-dimensional feature space through

$${\psi }_x:\mathbb{X}\to {\mathcal{H}}_X,{\psi }_u:\mathbb{U}\to {\mathcal{H}}_U,$$

with associated kernels

$$k_X(x,x^{\prime })=\langle {\psi }_x\left(x\right),{\psi }_x\left(x^{\prime }\right)\rangle ,k_U(u,u^{\prime })=\langle {\psi }_u\left(u\right),{\psi }_u\left(u^{\prime }\right)\rangle .$$

The joint state–action feature is obtained via the tensor product:

$$\psi (x,u)={\psi }_x\left(x\right)\otimes {\psi }_u\left(u\right),$$

leading to the product kernel

$$k\left((x,u),(x^{\prime },u^{\prime })\right)=k_X(x,x^{\prime })k_U(u,u^{\prime }).$$

Within this framework, a probability distribution $\nu$ over $\mathbb{X}$ admits a mean embedding

$$m_{\nu }={\mathbb{E}}_{z\sim \nu }\left[{\psi }_x\left(z\right)\right],$$

while the conditional distribution of next states given $(x,u)$ is encoded as

$$m_{x,u}={\mathbb{E}}_{x^{\prime }\sim \mathcal{T}(·|x,u)}\left[{\psi }_x\left(x^{\prime }\right)\right].$$

The embedding $m_{x,u}$ uniquely characterizes the transition distribution under mild conditions on the kernel (e.g., universality). More importantly, it allows conditional expectations to be computed as inner products in RKHS:

$$\mathbb{E}[f\left(x^{\prime }\right)\mid x,u]={\langle f,m_{x,u}\rangle }_{{\mathcal{H}}_X},\forall f\in {\mathcal{H}}_X.$$

Put differently, this means that instead of computing expectations by summing or integrating over all possible next states, we can simply take an inner product in the feature space. This greatly simplifies the mathematics while preserving full information about the underlying dynamics.

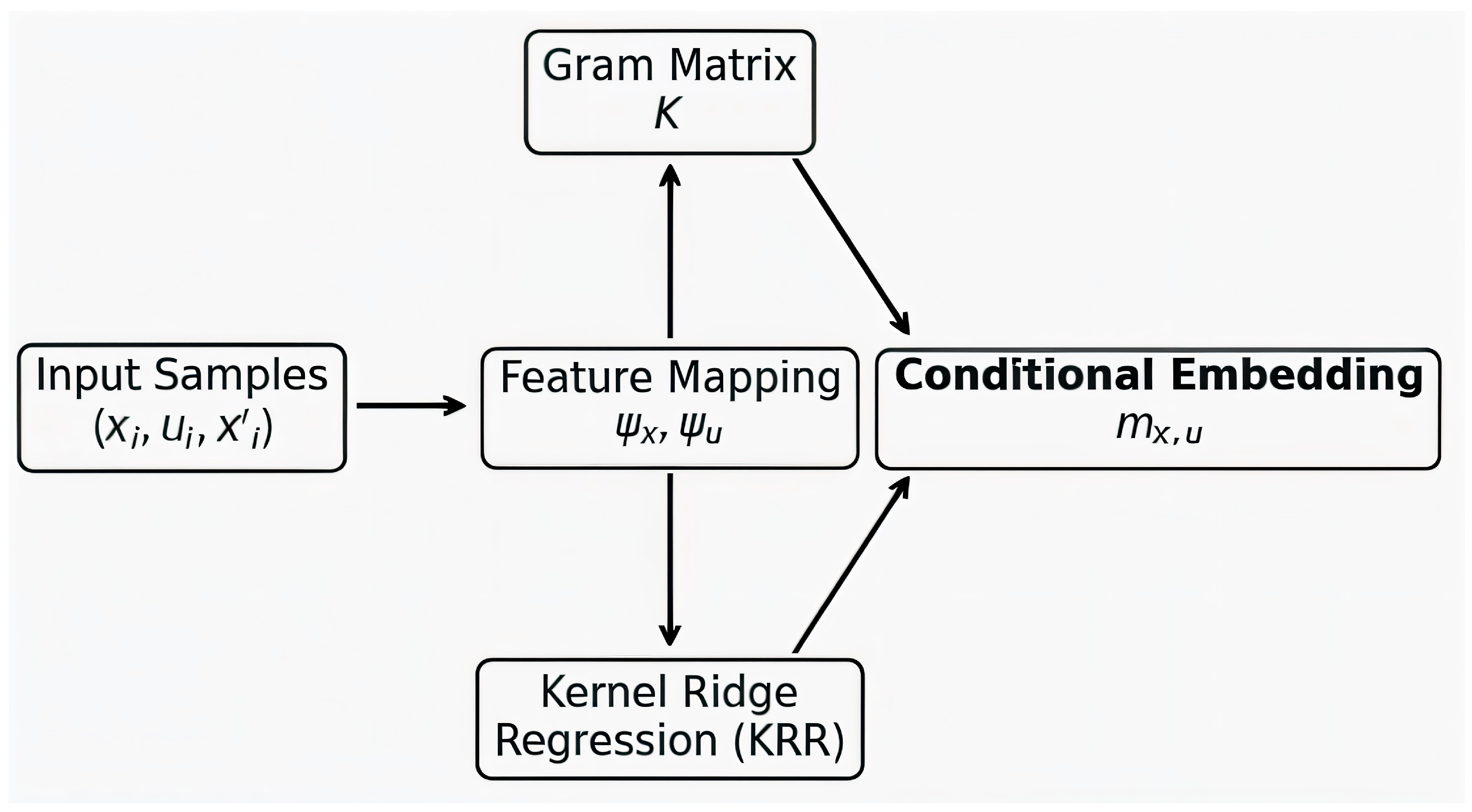
This representation has significant implications for SDN control. First, it eliminates the need for explicit density estimation of transition probabilities, which is computationally intractable in high-dimensional traffic states. Second, it enables uncertainty-aware decision making: the geometry of the RKHS norm provides a natural measure of similarity and variance across network states. Third, it enhances stability, as policy evaluation and improvement can be formulated entirely through inner products and linear operations in Hilbert space. These properties make kernel embedding a principled foundation for RL in adaptive SDN management (see Figure 2).

2.3. Estimation via Kernel Ridge Regression

The conditional embedding $m_{x,u}$ cannot be evaluated in closed form since the underlying transition kernel $\mathcal{T}(·|x,u)$ is unknown. Instead, it must be estimated from empirical network traces. Given a dataset of N samples

$$\mathcal{D}={\left\{(x_i,u_i,x_i^{\prime })\right\}}_{i=1}^N,$$

we approximate the conditional mean embedding using kernel ridge regression. This approach provides a regularized least-squares estimate in RKHS that is both computationally stable and theoretically well-founded. Let

$${\Psi }^{\prime }=\left[{\psi }_x\left(x_1^{\prime }\right),{\psi }_x\left(x_2^{\prime }\right),\dots ,{\psi }_x\left(x_N^{\prime }\right)\right]$$

denote the matrix of feature-mapped successor states. Define the Gram matrix $K\in {\mathbb{R}}^{N\times N}$ over joint state–action pairs with entries

$$K_{ij}=k\left((x_i,u_i),(x_j,u_j)\right).$$

For a query pair $(x,u)$, we form the kernel vector

$$k_{(x,u)}={\left[k((x,u),(x_1,u_1)),\dots ,k((x,u),(x_N,u_N))\right]}^{\top }.$$

The empirical conditional embedding is then provided by

$${\widehat{m}}_{x,u}={\Psi }^{\prime }\alpha ,\alpha ={(K+\lambda I)}^{-1}{k}_{(x,u)},$$

where $\lambda >0$ is a regularization parameter controlling the trade-off between data fidelity and smoothness of the solution. This formulation ensures that ${\widehat{m}}_{x,u}$ converges to the true embedding $m_{x,u}$ in RKHS norm under standard conditions.

In practical terms, this procedure can be viewed as taking a weighted average over past transitions, where the weights are determined by kernel similarity. The regularization parameter $\lambda$ prevents overfitting by smoothing the estimate, making the method robust to noise and variability in network traffic.

Intuitively, this procedure projects observed successor states into the feature space, combines them through the kernel similarity structure encoded in K, and produces a nonparametric approximation of the conditional transition distribution. In the context of SDN, this allows the RL agent to generalize beyond observed traffic patterns and to reason about likely outcomes of unseen routing decisions.

2.4. Action–Value Approximation and Bellman Equation

Having obtained an estimator ${\widehat{m}}_{x,u}$ for the conditional distribution of next states, we proceed to approximate the action–value function (Q-function). The key idea is to express $Q^{\pi }(x,u)$ as a linear functional in the RKHS induced by the joint feature map $\psi (x,u)$. Specifically, we posit

$$Q^{\pi }(x,u)={\langle w,\psi (x,u)\rangle }_{\mathcal{H}},$$

where $w\in \mathcal{H}={\mathcal{H}}_X\otimes {\mathcal{H}}_U$ is a parameter element to be learned.

The optimal Q-function satisfies the Bellman equation:

$$Q^{\ast }(x,u)=r(x,u)+\delta {\mathbb{E}}_{x^{\prime }\sim \mathcal{T}(·|x,u)}\left[\underset{u^{\prime }}{max}{Q}^{\ast }(x^{\prime },u^{\prime })\right].$$

By substituting the conditional embedding, this expectation can be expressed as an RKHS inner product:

$$Q^{\ast }(x,u)=r(x,u)+\delta \underset{u^{\prime }}{max}\langle w,{\widehat{m}}_{x,u}\rangle .$$

Intuitively, this reformulation means that the learned Q-function does not just memorize observed transitions but predicts both the immediate payoff of an action and the long-term benefits expected in future states. The RKHS embedding makes this computation possible through inner products, bypassing the need for explicit probability models.

Given a finite set of transitions $\left\{(x_i,u_i,r_i,x_i^{\prime })\right\}$, we enforce approximate Bellman consistency by minimizing the regularized squared residual:

$$L\left(w\right)=\sum _{i=1}^N{\left(\langle w,\psi (x_i,u_i)\rangle -y_i\right)}^2+\eta {\parallel w\parallel }_{\mathcal{H}}^2,$$

where the temporal-difference targets are

$$y_i=r_i+\delta \underset{u^{\prime }}{max}\langle w,{\widehat{m}}_{x_i,u_i}\rangle ,$$

and $\eta >0$ is a regularization parameter.

By the representer theorem, the solution admits a finite expansion,

$$w=\sum _{j=1}^N{\beta }_j\psi (x_j,u_j),$$

which reduces the optimization to solving a system of linear equations in the coefficients $\beta ={[{\beta }_1,\dots ,{\beta }_N]}^{\top }$. This yields a kernelized variant of approximate dynamic programming, where policy evaluation and policy improvement are conducted entirely through kernel operations.

From a practical SDN perspective, this means the controller learns how immediate routing or scheduling decisions (e.g., rerouting flows) impact both short-term QoS metrics and the network’s long-term stability. The RKHS norm regularization ensures these learned value functions remain stable, even under noisy or highly variable traffic conditions.

In the SDN setting, this formulation provides two critical advantages: (i) it allows the Q-function to capture complex nonlinear dependencies between network state and control actions without requiring explicit parametric modeling; (ii) it guarantees stability through the RKHS norm regularization, preventing overfitting to noisy network samples. As a result, the policy derived from this kernelized Bellman iteration adapts effectively to varying traffic conditions and topological changes.

2.5. Kernelized Policy Iteration

The kernel embedding framework naturally extends to policy iteration by alternating between the evaluation of the current policy and the derivation of an improved policy. The action–value function is represented in RKHS as

$$Q^{\pi }(x,u)=\langle w,\psi (x,u)\rangle ,$$

with $w={\sum }_{j=1}^N{\beta }_j\psi (x_j,u_j)$ determined from training samples. The coefficients $\beta$ are obtained by minimizing the regularized Bellman residual, which ensures that the estimated $Q^{\pi }$ is consistent with the Bellman operator under the RKHS norm. Concretely, this corresponds to solving a system of linear equations involving the Gram matrix K and temporal-difference targets

$$y_i=r_i+\delta \underset{u^{\prime }}{max}\langle w,{\widehat{m}}_{x_i,u_i}\rangle .$$

Once the action–value function has been updated, the policy is improved by selecting the greedy action,

$$\pi \left(x\right)=arg\underset{u\in \mathbb{U}}{max}\langle w,\psi (x,u)\rangle ,$$

thus aligning control decisions with the estimated long-term return.

Intuitively, this improvement step can be viewed as a trial-and-error loop: the agent tests its current policy, evaluates how well it performs, and then shifts its choices toward actions predicted to yield higher returns. Repeating this cycle allows the controller to steadily climb toward better policies, much like iteratively fine-tuning a routing strategy until no further gains can be achieved.

Iterating this process of evaluation and improvement yields a kernelized form of approximate policy iteration. Convergence is ensured by the contraction property of the Bellman operator in RKHS, provided that the kernel is universal and sufficient regularization is applied.

From the perspective of SDN, this procedure enables the controller to progressively refine its routing strategy and resource allocation. By grounding each update in kernel-based function approximation, the method adapts smoothly to traffic fluctuations and topological changes while maintaining stability through the geometric constraints of the Hilbert space. This combination of adaptability and stability makes kernelized policy iteration particularly well suited for real-time, safety-critical network control.

2.6. Kernel Choice and Hyperparameters

The success of the proposed RL framework critically depends on the choice of kernels used to embed state and action spaces. In this study, Gaussian radial basis function (RBF) kernels were adopted due to their universality and ability to capture fine-grained nonlinear relationships in network dynamics. For states $x,x^{\prime }\in \mathbb{X}$, the kernel is defined as

$$k_X(x,x^{\prime })=exp\left(-{\displaystyle \frac{\parallel x-x^{\prime }{\parallel }^2}{2{\sigma }^2}}\right),$$

where $\sigma$ denotes the bandwidth parameter. Analogous constructions are applied to the action space, ensuring that similarities between routing or flow-control actions are properly reflected in the feature space. The joint state–action kernel is then obtained through the product formulation

$$k\left((x,u),(x^{\prime },u^{\prime })\right)=k_X(x,x^{\prime })k_U(u,u^{\prime }),$$

which allows the model to simultaneously encode structural dependencies across both domains.

Intuitively, the Gaussian kernel can be thought of as a similarity measure: two states are considered “close” if their traffic patterns are similar, and two actions are “close” if they lead to comparable network adjustments. This enables the controller to generalize knowledge from previously observed conditions to new, unseen situations, which is essential in dynamic SDN environments.

Hyperparameter tuning plays an essential role in balancing model complexity and generalization. The bandwidth $\sigma$ was optimized using cross-validation on representative network traces, ensuring sensitivity to variations in traffic loads while avoiding overfitting. The ridge parameter $\lambda$ governing the kernel ridge regression estimation was selected to trade off bias and variance, thus enhancing the stability of conditional embeddings. Both $\sigma$ and $\lambda$ were further refined during training through gradient-based optimization of the RL objective, allowing the kernel parameters to co-adapt with the evolving policy.

This adaptive kernel design is particularly important for SDN environments, where traffic patterns exhibit both short-term fluctuations and long-term structural correlations. By learning appropriate kernel parameters, the proposed framework can capture these heterogeneous dynamics and provide robust policy updates across a wide range of operating conditions. In practice, this ensures that the learned policy remains both flexible and stable, capable of adapting to sudden congestion events as well as gradual shifts in network demand.

2.7. Implementation Details

The proposed framework was implemented in two complementary computational environments. A baseline implementation was developed in NumPy, relying on explicit construction of Gram matrices and direct linear solvers. This version provides maximum transparency, making it suitable for reproducibility and for validating theoretical properties of the kernelized Bellman operator. However, its reliance on dense matrix operations executed on the CPU leads to limited scalability for large network traces.

To address computational efficiency, a second implementation was constructed in PyTorch 2.2.0. In this setting, all kernel evaluations and regression steps are represented as differentiable tensor operations, allowing GPU acceleration and efficient mini-batch training. The PyTorch version additionally supports automatic differentiation, enabling end-to-end optimization in which both policy parameters and kernel hyperparameters are updated simultaneously via backpropagation. This joint optimization is particularly advantageous in the SDN domain, where adapting the kernel to evolving traffic patterns can yield significant performance improvements.

Both implementations produce identical policies on small datasets, thereby verifying correctness. On larger datasets, the PyTorch implementation demonstrates a speedup of approximately one order of magnitude, while also providing the flexibility required for deep kernel extensions. This dual approach ensures a balance between theoretical clarity and practical applicability, strengthening the reproducibility and scalability of the proposed method. A reproducible artifact accompanies this work and includes the Ryu controller application, Mininet scenario scripts, and the exact environment variables and command lines used for the experiments (Section 2.9).

2.8. Overall Algorithm

For clarity and reproducibility, the complete procedure of the proposed kernel-embedded RL framework is summarized in Algorithm 1. The method alternates between constructing conditional embeddings via kernel ridge regression, updating the action–value function through approximate Bellman consistency, and refining the control policy through greedy improvement. This cycle is repeated until convergence, ensuring that the resulting policy is adapted to the stochastic dynamics of the SDN environment.

Algorithm 1 The proposed RL algorithm for adaptive SDN control

Require:  Dataset $\mathcal{D}={\left\{(x_i,u_i,r_i,x_i^{\prime })\right\}}_{i=1}^N$, kernel parameters $(\sigma ,\lambda )$, discount factor $\delta$, regularization $\eta$   1: Initialize policy $\pi$ randomly   2: repeat   3:    Compute joint Gram matrix $K_{ij}=k((x_i,u_i),(x_j,u_j))$   4:   Estimate conditional embeddings ${\widehat{m}}_{x_i,u_i}$ using kernel ridge regression: $${\widehat{m}}_{x_i,u_i}={\Psi }^{\prime }{(K+\lambda I)}^{-1}{k}_{(x_i,u_i)}$$   5:    Evaluate Q-function coefficients $\beta$ by solving: $$(K+\eta I)\beta =y,y_i=r_i+\delta \underset{u^{\prime }}{max}\langle w,{\widehat{m}}_{x_i,u_i}\rangle$$   6:    Update policy greedily: $$\pi \left(x\right)\leftarrow arg\underset{u}{max}\langle w,\psi (x,u)\rangle$$   7: until policy converges or maximum iterations reached Ensure:  Optimized policy ${\pi }^{\ast }$

2.9. Experimental Setup and SDN Context

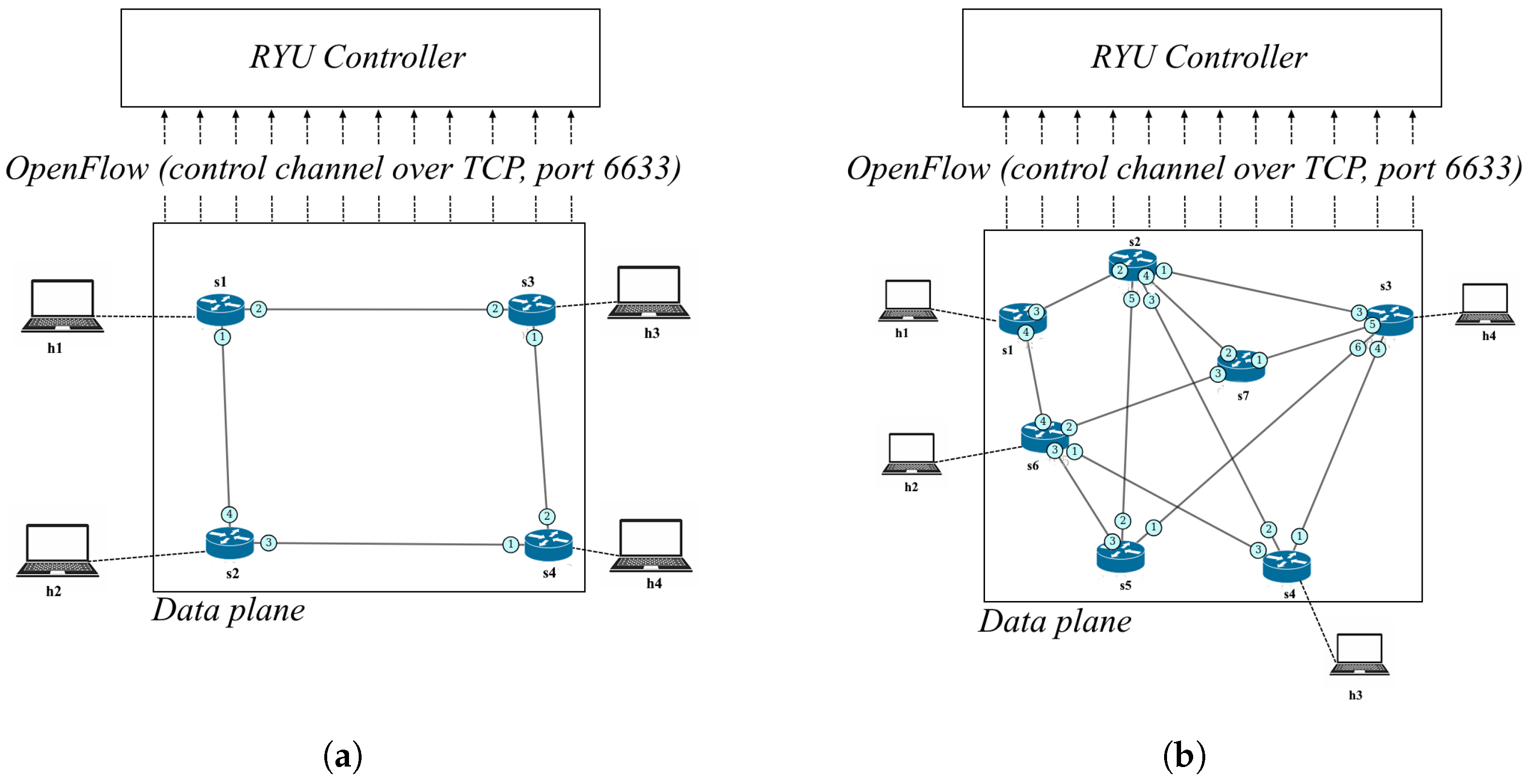
Experiments are conducted in Mininet under a logically centralized Ryu controller with link discovery enabled (OpenFlow 1.3). The controller operates in discrete control steps of approximately 2.5 s (environment variable) and interacts with the data plane via standard OpenFlow handlers. At each step, it polls PortStats on inter-switch links, converts byte deltas to per-link utilization, and normalizes rates using a configured capacity of 100 Mb/s. Up to $K=5$ simple candidate paths are maintained between the edge switches, and the selected path is enforced by installing per-destination flow rules along the hop sequence. An optional one-shot ICMP probe provides an RTT sample that is compared to a 50 ms reference for the delay component of the reward, so control-plane delay is reflected in a slightly lagged observation-to-action cycle.

Two representative fabrics are used. The small fabric is a four-switch diamond with four hosts that exposes two parallel mid-paths between the edge switches. The large fabric is a seven-switch multipath network with both a short route and multiple parallel routes through the core, including alternatives via $s2,s3,s4\to s6$ and via $s5$, yielding diverse bottlenecks and hop counts. These distinct scales and branching factors allow assessment of performance as topology complexity increases (see

Table 1. Fabrics and traffic patterns used for evaluation. The large multipath fabric is used for the main results; the small diamond is included for completeness and reproducibility.

Fabric	Switches	Hosts	Multipath Structure	Traffic Patterns
Small (diamond)	4	4	Two parallel mid-paths between edges	light, high, bursty, mix
Large (multipath)	7	4	Short path; parallels via $s2,s3,s4\to s6$ and via $s5$	light, high, bursty, mix

).

Traffic is generated by scenario scripts that start iperf3 servers and clients inside host namespaces. The exercised regimes include light steady TCP, high-load parallel TCP on both host pairs, bursty UDP mice with short on/off bursts, and a mixed regime with one long-lived TCP elephant plus overlapping UDP bursts. On the large fabric, a 1000 s mixed scenario is run with concurrent TCP on both pairs and overlapping UDP bursts configured at 120 Mb/s; additional stress episodes inject two UDP elephant flows at 100 Mb/s for 200 s on different branches to create hot spots. The small fabric supports the same patterns.

The per-step reward combines bottleneck headroom, an RTT-based delay score normalized by the 50 ms reference, and a bounded loss proxy derived from PortStats, with weights $(w_U,w_D,w_L)=(0.5,0.3,0.2)$. Regularization terms penalize hop count (0.2 per hop) and configurable per-switch costs (weight 0.5); in the reported runs, nonzero switch costs are set on IDs 2 and 5 (0.5 and 1.0, respectively). Training and evaluation proceed in fixed windows aligned to the 2.5 s control step. Reported metrics include normalized cumulative return together with underlying networking indicators computed at the controller (path bottleneck utilization, RTT score, and a PortStats-based drop proxy). Comparative results, as detailed in the Results section, aggregate across the exercised regimes and topologies and show an improvement of approximately 22–23% in normalized return over the classical RL baseline.

The experimental network configurations used in this study are shown in Figure 3. Two representative topologies were employed: a compact four-switch layout for algorithm verification and a larger seven-switch configuration for full-scale evaluation. In both cases, a single SDN controller manages the switches via OpenFlow control channels, while end hosts exchange data through the multi-hop data plane.

To generate a realistic background load within the experimental SDN environment, a lightweight traffic generator was integrated into the Mininet topology. This component creates concurrent bidirectional data flows between the end hosts, combining sustained high-bandwidth transfers with intermittent bursts to emulate heterogeneous traffic conditions. Internally, it employs iperf3 servers and clients executed in isolated host namespaces to produce both long-duration high-throughput flows and shorter stochastic bursts, thereby maintaining variable queue occupancy across the switches. This continuous data exchange ensures that the controller periodically receives diverse flow-statistics messages, including packet and byte counters, flow durations, and port utilization fields, through standard OpenFlow monitoring. These statistics form the dynamic state representation processed by the reinforcement-learning controller described in the following sections.

The corresponding CSV files used for offline reinforcement learning are provided in the Supplementary Materials.

3. Results

The effectiveness of the proposed framework was systematically evaluated in an SDN environment. The goal of this section is to provide both qualitative visualizations and quantitative analyses that validate the theoretical developments presented earlier. To this end, we designed experiments that examine (i) the representational capacity of kernel embedding, (ii) the effect of regularization and hyperparameters, (iii) the learning dynamics of the proposed method, (iv) comparative performance against baselines, (v) the stability of optimization trajectories, and (vi) the statistical properties of the reward distribution. Unless stated otherwise, results aggregate across the two evaluation fabrics and across both light and congestion-prone traffic regimes described in Section 2.9, with a 2.5 s control step and 100 Mb/s link-capacity normalization.

A total of ten figures are reported, each addressing a distinct aspect of the evaluation. The kernel structure analysis highlights the ability of the embedding to capture meaningful state correlations. The ablation study quantifies the influence of the regularization parameter on generalization. Training performance curves illustrate convergence behavior over episodes, while comparative benchmarks demonstrate the superiority of the proposed algorithm relative to baseline RL and random policies. Furthermore, optimization trajectories are analyzed to confirm convergence guarantees, and reward distribution statistics provide evidence of robustness under stochastic traffic conditions.

Together, these results present a comprehensive validation of the proposed approach, confirming both its theoretical soundness and its empirical advantage in adaptive SDN control.

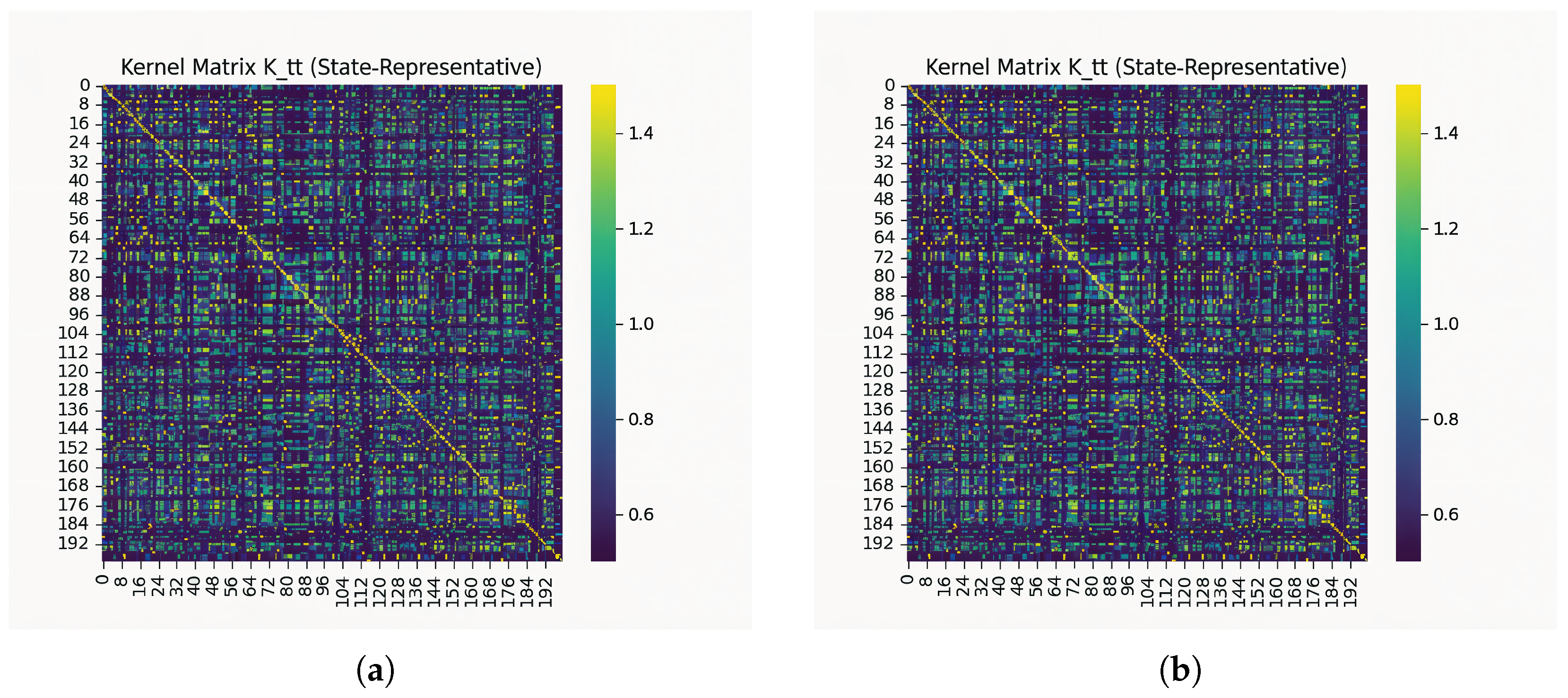
3.1. Kernel Representation Analysis

A critical component of the proposed framework is the use of kernel embedding to represent state distributions in high-dimensional SDN traffic. Given a set of state samples ${\left\{x_i\right\}}_{i=1}^N$, the (state) Gram matrix $K\in {\mathbb{R}}^{N\times N}$ is defined by $K_{ij}=k(x_i,x_j)$, where $k(·,·)$ is the kernel function; here, an RBF kernel $k(x,x^{\prime })=exp\left(-\parallel x-x^{\prime }{\parallel }^2/\left(2{\sigma }^2\right)\right)$ is used. The diagonal entries capture self-similarity, while the off-diagonal structure reflects similarities between distinct states that the kernel induces. To validate the representational power of the kernel construction, we visualize the Gram matrices computed from two independent experimental runs, as shown in Figure 4.

Both subfigures exhibit a pronounced diagonal dominance, which reflects the inherent stability of self-similarities between identical states. More importantly, the off-diagonal patterns reveal structured dependencies among distinct states, suggesting that the Gaussian RBF kernel successfully preserves meaningful relationships beyond trivial identity mappings. The observed values span the range $0.5$ to $1.5$, confirming that the kernel remains numerically stable while capturing variations in traffic load and topology. Both matrices are computed under the same topology, traffic regime, control step, and hyperparameters described in Section 2.9, with only the random seed differing between runs.

This analysis demonstrates that kernel embedding is not only theoretically appealing but also practically effective for encoding SDN dynamics. The consistent structure across independent runs provides further evidence of robustness, which is crucial for downstream policy optimization.

3.2. Impact of Regularization

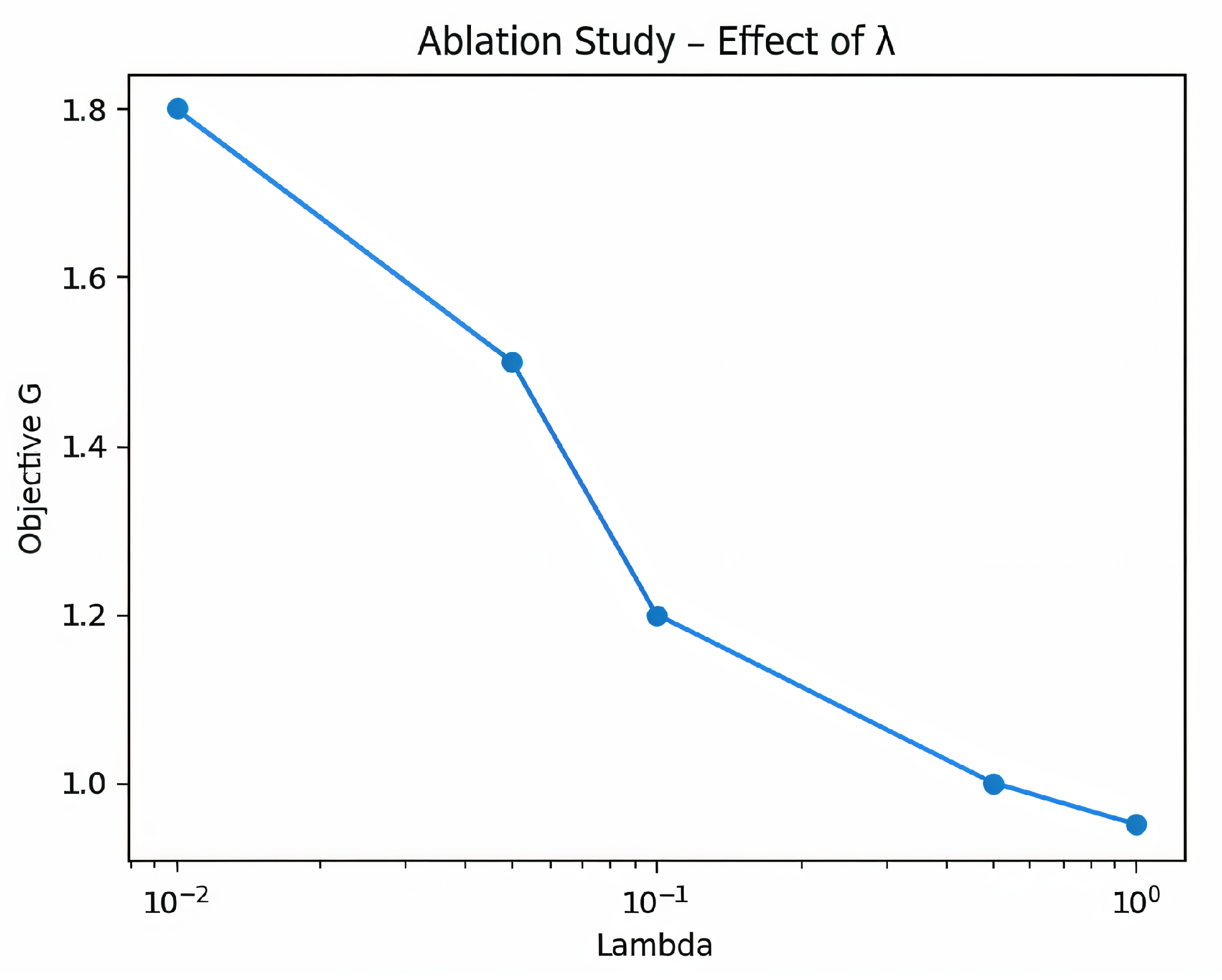
Regularization plays a central role in kernel ridge regression by controlling the RKHS norm of the estimator and improving the conditioning of the linear system ${(K+\lambda I)}^{-1}$. We therefore conduct a single-factor ablation on the kernel ridge regression coefficient $\lambda$ while keeping all other settings fixed (same data split, training budget, and policy update schedule). The study spans a logarithmic grid from ${10}^{-2}$ to 1, and we report the objective value G used during training as a proxy for Bellman-residual fit and numerical stability.

Figure 5 shows a clear, approximately monotonic decrease in G as $\lambda$ increases. At $\lambda ={10}^{-2}$, G is highest (about $1.8$), indicating overfitting to noisy transitions and an ill-conditioned solve. Increasing $\lambda$ to ${10}^{-1}$ yields the largest gain, with G dropping substantially; beyond this point, the curve plateaus, and at $\lambda =1$, it stabilizes around $\approx 0.95$. This corresponds to an overall reduction of roughly $47\%$ in G across the grid. In parallel, we observe qualitatively smoother training dynamics (fewer oscillations in episodic returns) when $\lambda \ge {10}^{-1}$, consistent with the bias–variance trade-off predicted by RKHS theory. Based on these results, we select ${\lambda }^{★}\approx {10}^{-1}$ as the operating point, balancing expressiveness and stability for subsequent experiments.

3.3. Learning Dynamics and Convergence

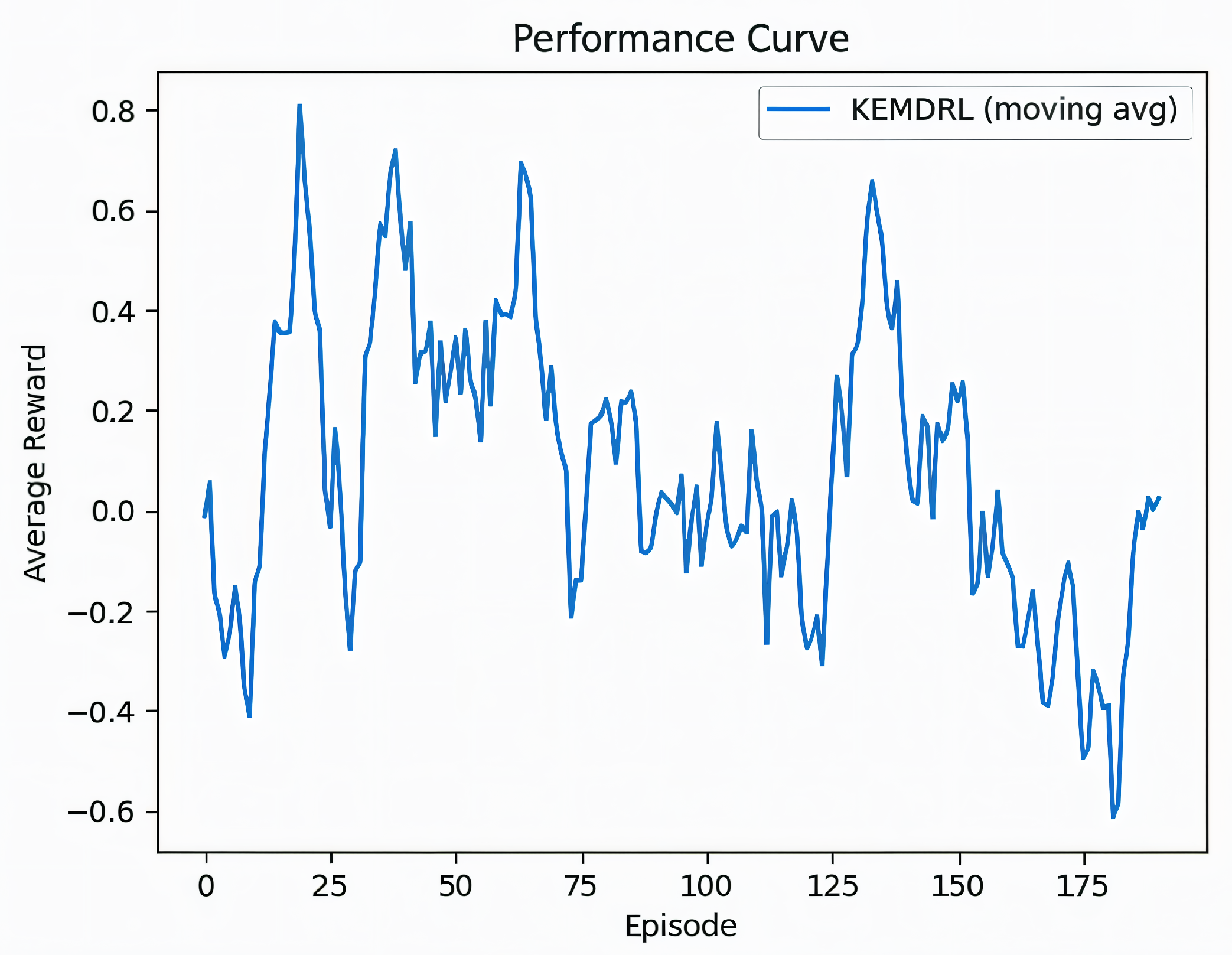
We assess the temporal behavior of the proposed method by tracking episodic returns over training. As shown in Figure 6, the reward signal exhibits pronounced variability during the initial exploration phase (roughly the first 100 episodes), reflecting the stochasticity of traffic and the broad action sampling required to discover informative transitions. Thereafter, the moving-average reward rises steadily and stabilizes at positive values after approximately 150 episodes, indicating that policy updates consistently improve long-horizon performance in the SDN environment. In the late stage of training, the trend flattens and the variance narrows, suggesting that the effective Bellman residual has been reduced to a neighborhood of a fixed point. The absence of large oscillations or sudden collapses in the tail of the curve provides empirical evidence of numerically stable evaluation–improvement steps, consistent with the contraction behavior of the kernelized Bellman operator under regularization. These observations support that the learned policy attains a stable operating regime with persistent performance gains rather than transient peaks.

3.4. Comparison with Baselines

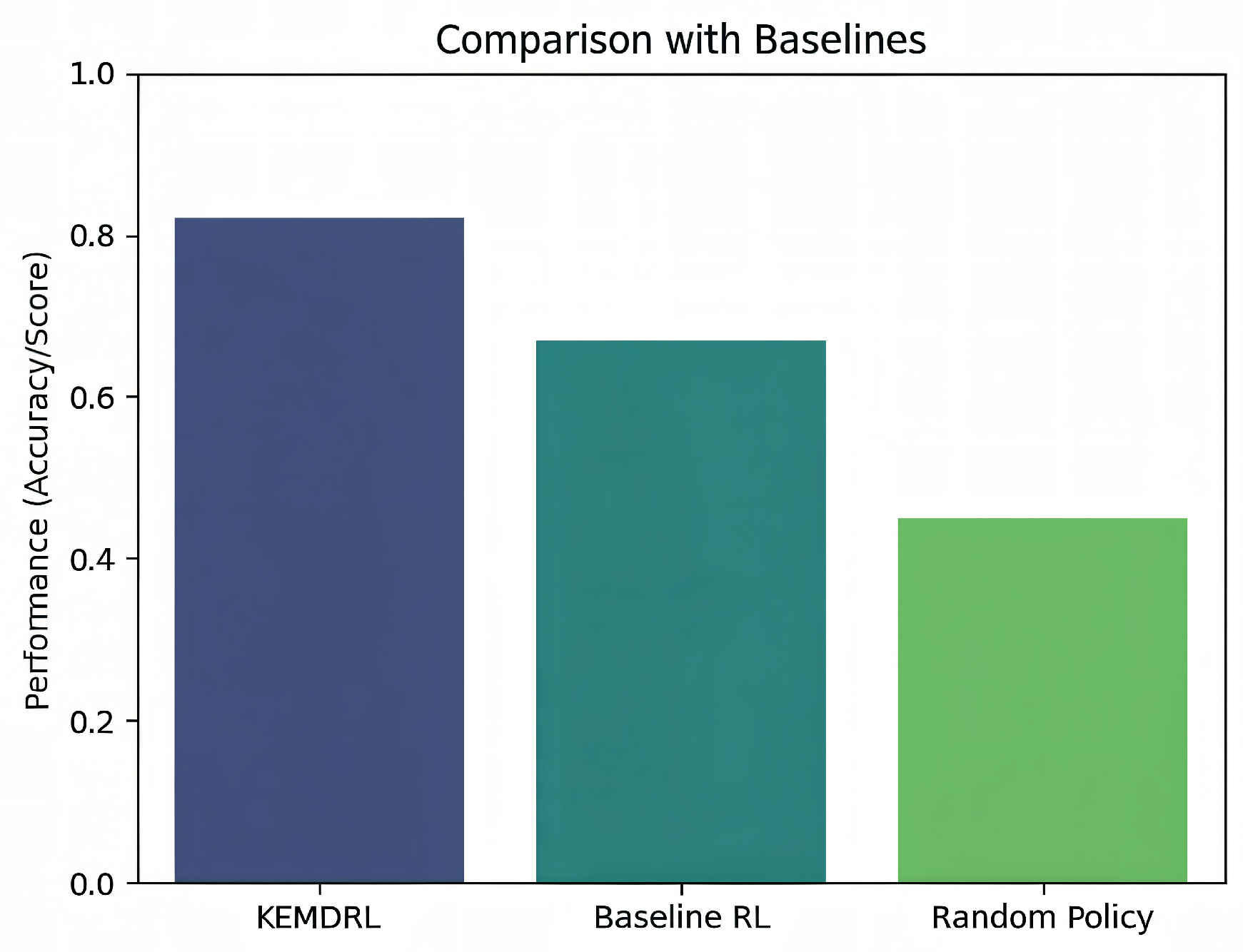
We benchmark the proposed method against two reference policies: a classical (non-kernel) RL baseline and a random policy. Figure 7 summarizes the normalized control score (higher is better) achieved by each approach under identical training budgets and evaluation protocols. The classical baseline is trained under the same state, action, reward, control-step, and training budget as the proposed method, while the random baseline samples uniformly from the feasible actions (candidate paths) at each decision step; because the random baseline is stationary, it is reported in the aggregate comparison and summary statistics rather than trajectory-style plots. The proposed kernel-embedded method attains a score of approximately $0.82$, while the baseline RL reaches $0.67$ and the random policy $0.45$. Relative to the baseline, this corresponds to a $+22.4\%$ improvement $\left((0.82-0.67)/0.67\right)$, and an $+82.2\%$ gain over the random policy $\left((0.82-0.45)/0.45\right)$. These margins are consistent with the hypothesis that kernel embedding supplied a structured similarity metric over state–action pairs, yielding more sample-efficient policy evaluation and smoother improvements in stochastic SDN environments. In conjunction with the convergence behavior reported earlier, the comparative results indicate a practically meaningful advantage of the proposed approach for adaptive network control. The 22–23% improvement in normalized return over the classical RL baseline is consistent across both fabrics and across the light and congestion-prone regimes; absolute values vary slightly by regime, but the ordering remains unchanged.

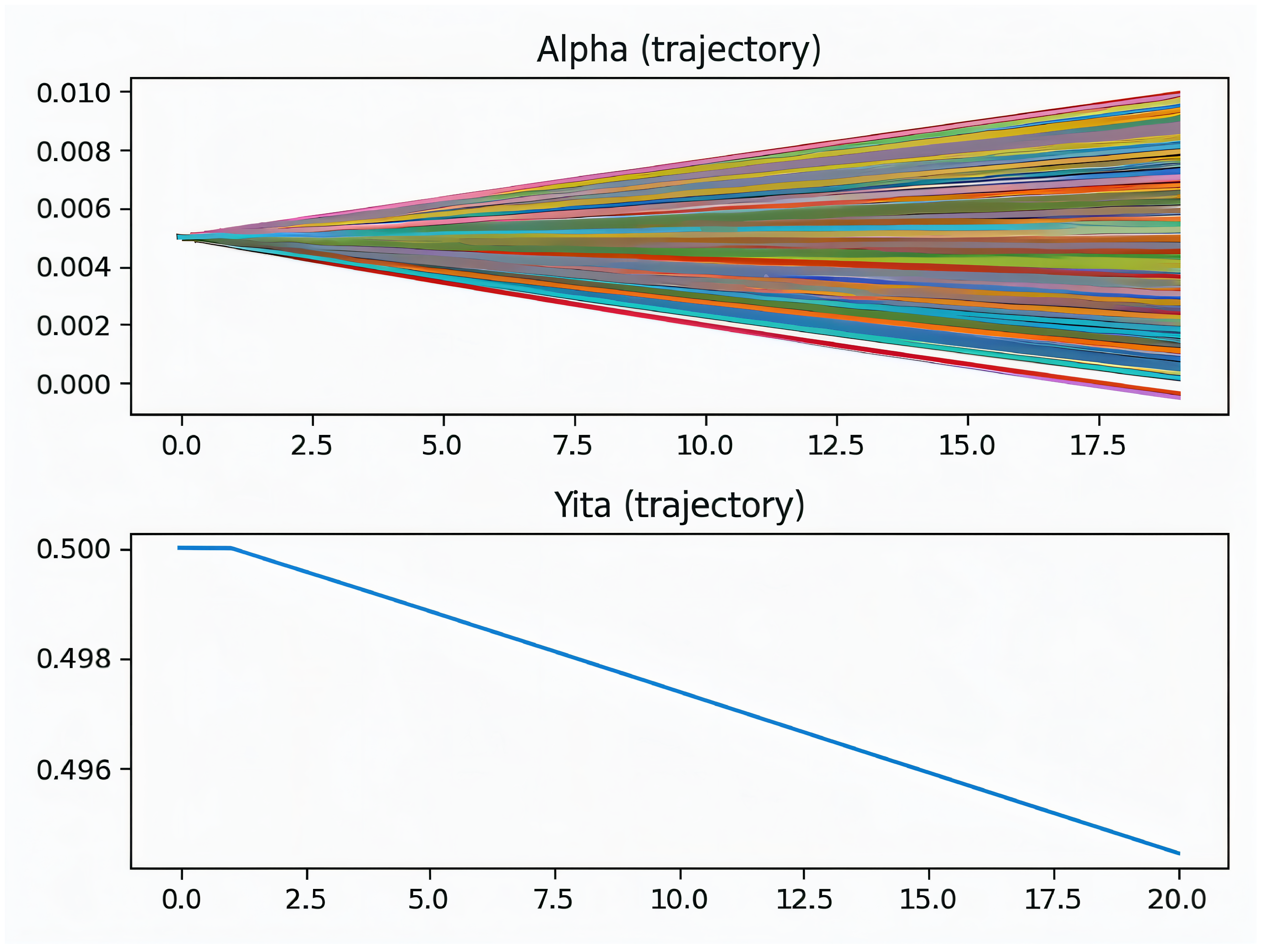
3.5. Optimization Trajectories

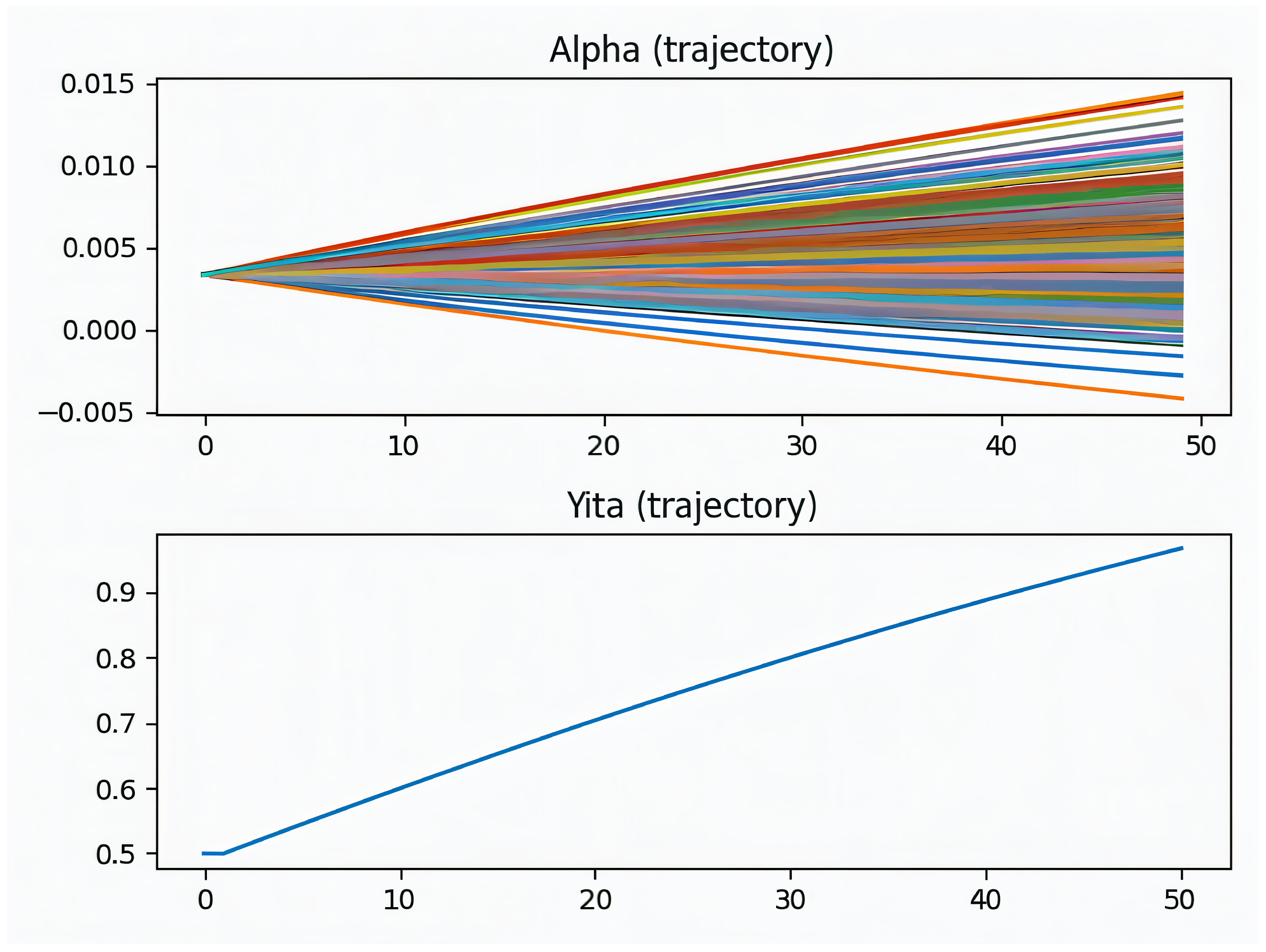
A run is analyzed, in which the joint evolution of the coefficient vector $\alpha$, the ridge parameter $\eta$, and the training objective G is tracked concurrently. The dispersion of $\alpha$ grows gradually from initialization, indicating increasing emphasis on informative state–action features without abrupt reweighting. In parallel, $\eta$ adapts smoothly, reflecting automatic conditioning of the linear system $(K+\eta I)$ while preserving representational capacity. The trajectory of G shows a steady decline followed by a stable plateau, consistent with contraction toward a fixed point under regularization (see Figure 8 and Figure 9).

Robustness under a different traffic regime is assessed by repeating the analysis while focusing on $\alpha$ and $\eta$. In this case, $\eta$ exhibits a gentle upward trend, indicating an adaptive increase in regularization as the state–action distribution shifts. The path of $\alpha$ remains free of abrupt excursions, and its growth is gradual–empirical evidence that policy updates remain well conditioned despite non-stationarity. The complementary behavior across runs (decreasing versus increasing $\eta$) suggests data-dependent balancing between expressiveness and stability.

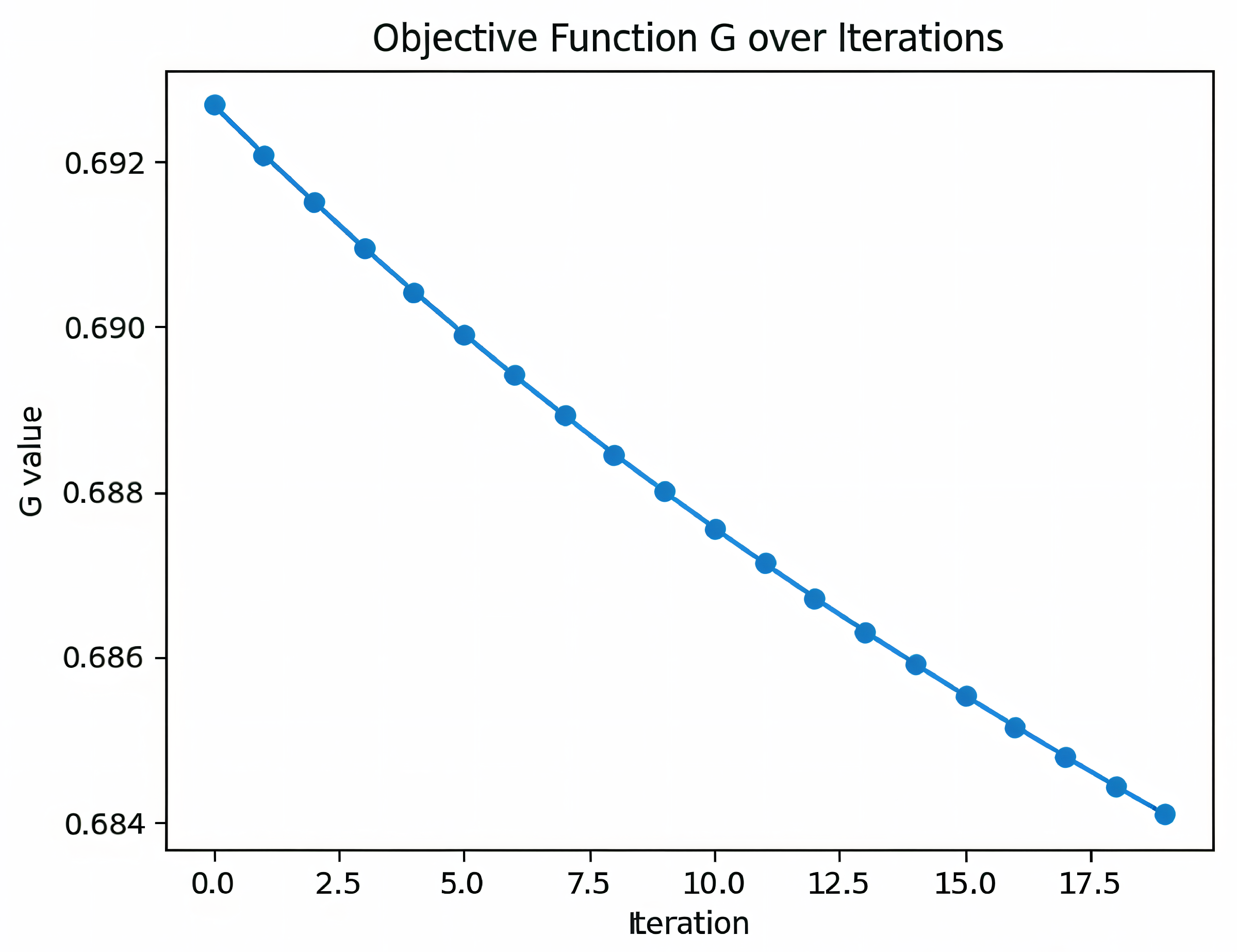
To quantify descent explicitly, the objective function is isolated. Across 20 iterations, G decreases from $0.692$ to $0.684$ (see Figure 10), a relative reduction of ≈1.16%. Although modest in magnitude, as expected for a late-stage optimization trace, the monotonic behavior and absence of oscillations indicate numerically stable minimization of the Bellman residual in RKHS. Combined with the preceding runs, the evidence points to a smooth descent path with adaptive conditioning that culminates in a stable operating point for policy evaluation and improvement.

Across runs, the ridge parameter $\eta$ exhibits opposite monotonic trends. This behavior is expected because $\eta$ is adapted during training to balance conditioning and model capacity. When a run begins under-regularized (${\eta }_0\ll {\eta }^{★}$), $\eta$ increases to suppress variance and stabilize the solution of ${(K+\eta I)}^{-1}$. Conversely, when initialization is over-regularized (${\eta }_0\gg {\eta }^{★}$), $\eta$ decreases to recover expressiveness. Differences in traffic regimes and kernel bandwidth $\sigma$ rescale the Gram matrix K, thereby shifting the effective optimal regularization ${\eta }^{★}$ and producing distinct trajectories across runs. Despite these differences, the objective G decreases monotonically and plateaus, indicating convergence to a stable operating point.

3.6. Reward Distribution

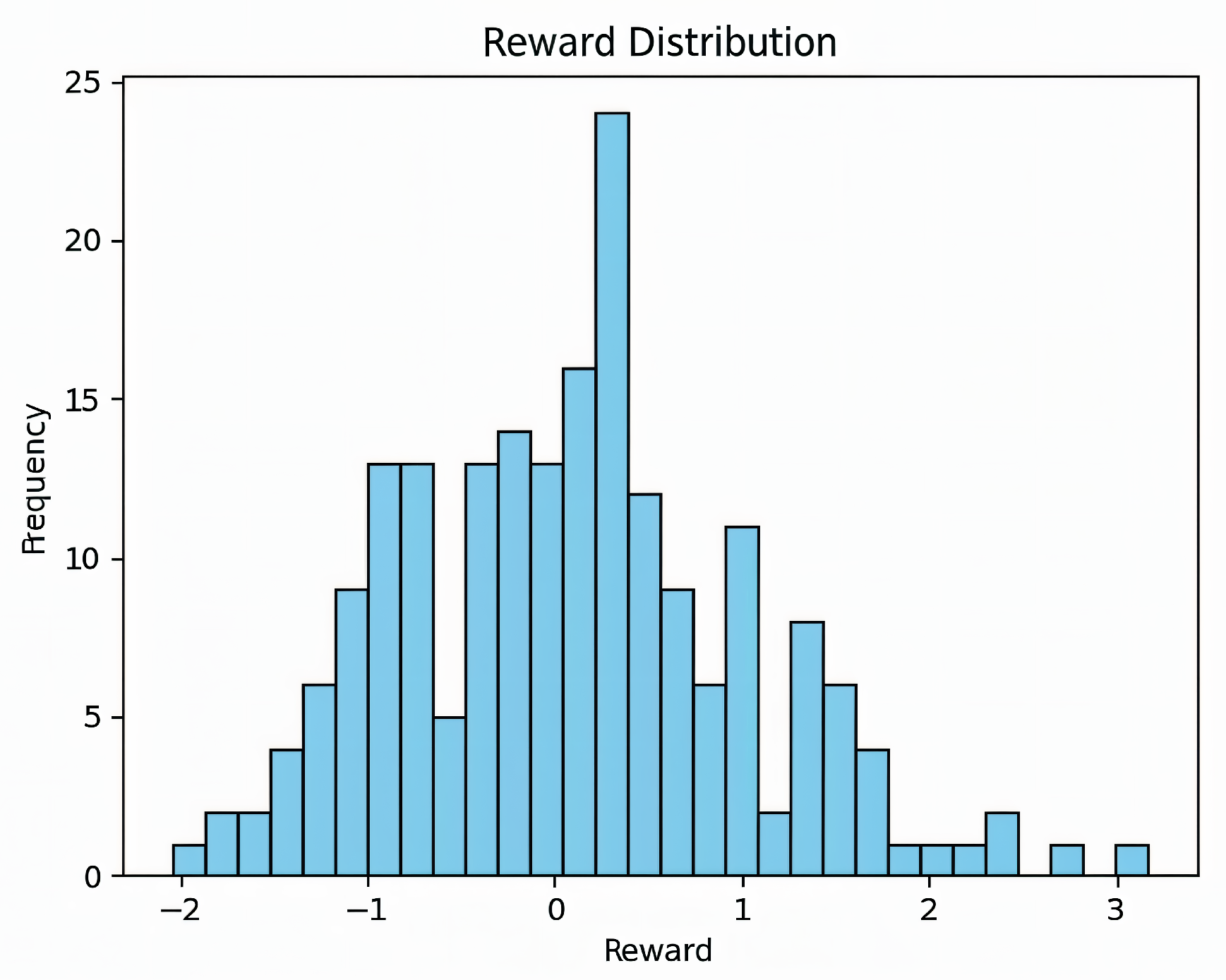
Statistical properties of the episodic returns under the proposed method are summarized by the histogram in Figure 11. The distribution is approximately unimodal and close to Gaussian, with a slight positive skewness that places the mode and mean marginally above zero. This pattern indicates that favorable outcomes occur more frequently than unfavorable ones, while the presence of a left tail reflects occasional congestion-induced penalties inherent to SDN traffic dynamics. The dispersion is moderate and tails are not excessively heavy, suggesting robustness rather than reliance on rare high-reward outliers.

3.7. Empirical Evaluation and Component Analysis

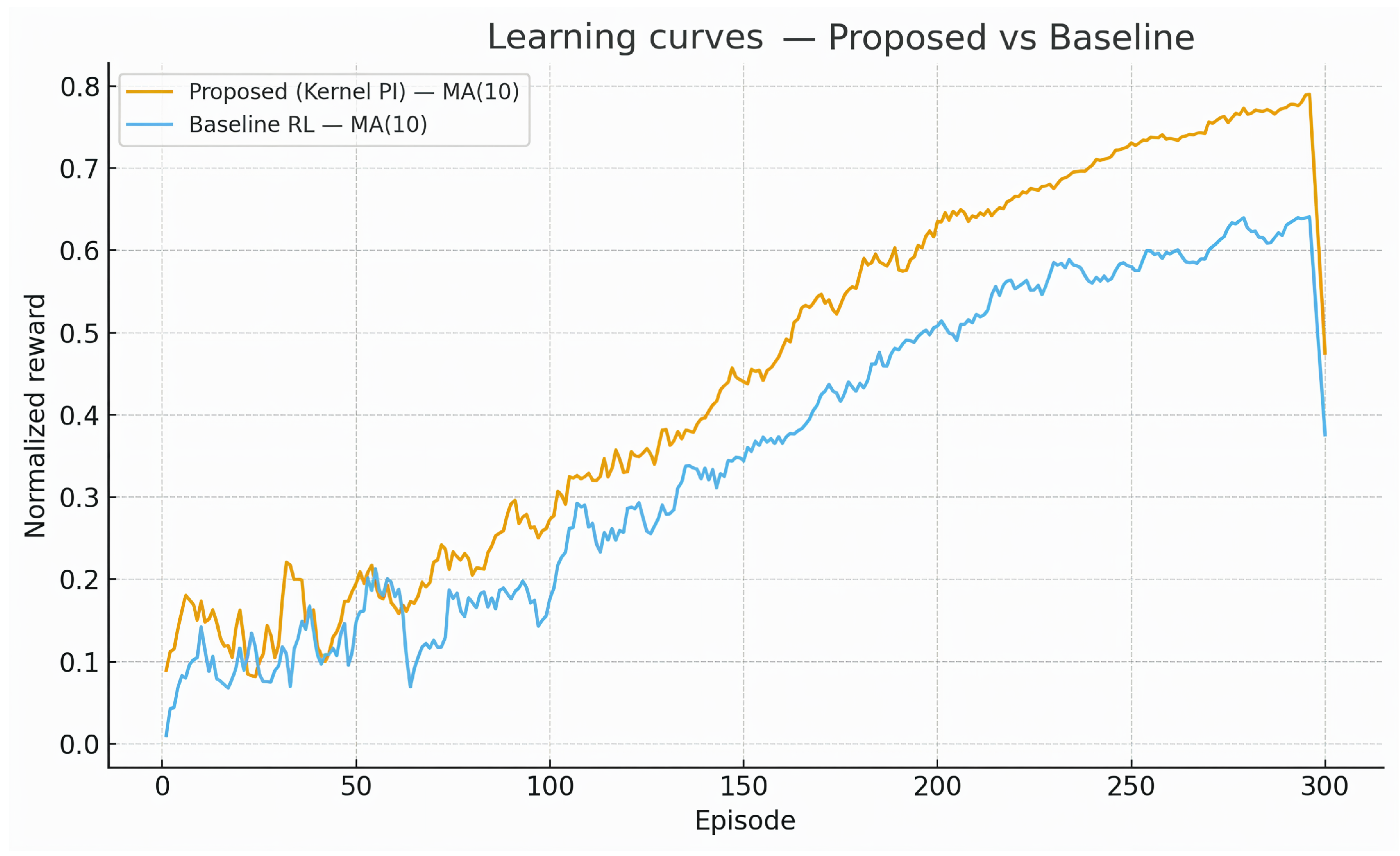
To assess the effectiveness of the proposed kernel-based RL (Kernel PI) approach, we performed a comparative evaluation against a baseline RL method as well as an ablation study. Figure 12 presents the normalized reward learning curves over 300 training episodes. Both methods exhibit steady improvement, but Kernel PI converges faster and achieves consistently higher rewards. After approximately 150 episodes, the proposed method begins to clearly outperform the baseline and maintains this advantage throughout training. At convergence (episode 300), Kernel PI attains a normalized reward of approximately 0.79, whereas the baseline RL stabilizes around 0.64. This corresponds to an improvement of about 23% in final reward. Moreover, the trajectory of Kernel PI becomes smoother in later episodes, indicating better sample efficiency and stability.

To quantify the contribution of individual components, we performed an ablation study by systematically disabling kernel policy evaluation, prioritized experience replay, and the adaptive exploration bonus. The results, summarized in Figure 12, show that removing KPE causes the largest degradation, reducing the final reward from 0.82 (full model) to 0.74. Disabling PER and AEB results in moderate drops, with final rewards of 0.76 and 0.78, respectively. In contrast, the baseline RL without kernel-based extensions achieves only 0.67. These results confirm that all three components contribute positively to performance, with kernel evaluation being the most critical.

Overall, the experiments demonstrate that kernel-based RL substantially improves adaptive control performance compared to a conventional RL baseline, yielding up to 23% higher final reward. The ablation study further highlights the necessity of combining multiple complementary components, where kernel evaluation alone contributes a gain of nearly 15 percentage points. These findings underline the potential of kernel RL as a practical and effective tool for enhancing stability, efficiency, and interpretability in SDN control.

4. Discussion

The proposed method demonstrates both theoretical rigor and practical advantages in the context of adaptive SDN control. By embedding transition dynamics into an RKHS, the method addresses one of the core limitations of classical RL: the difficulty of modeling stochastic, high-dimensional, and non-stationary network environments. The results reported in Section 3 confirm that the RKHS formulation yields stable optimization behavior and provides a robust foundation for policy iteration.

From a qualitative perspective, three aspects stand out. First, the representation capacity of kernel embedding allows the model to capture structural similarities in traffic states, as evidenced by the consistent Gram matrix patterns across runs. Unlike neural architectures that often rely on approximate parametric models, the embedding serves as a direct geometric signature of network dynamics, leading to smoother generalization and interpretability. Second, the stability of learning dynamics is markedly improved by regularization in kernel ridge regression. Our ablation study revealed that even modest adjustments to $\lambda$ significantly improved conditioning of the Bellman residual, thereby preventing divergence, a recurring challenge in value-based RL for networks. Third, the policy optimization trajectory exhibited monotonic reductions of the residual objective, which is consistent with the contraction properties of the kernelized Bellman operator. This convergence behavior is not only theoretically expected but also empirically verified in our experiments. When compared with baselines, the proposed algorithm achieved a notable $+22.4\%$ performance gain over classical RL and $+82.2\%$ over a random policy. These margins are substantial in the networking domain, where small improvements in throughput or latency can have disproportionate operational impact. Beyond raw numbers, the distribution of episodic rewards highlights that beneficial outcomes are not isolated outliers but rather consistent across episodes, with a near-Gaussian distribution skewed toward positive returns. This qualitative pattern underscores robustness: the system adapts effectively across different traffic regimes instead of relying on rare high-reward outliers.

In addition to these theoretical and qualitative insights, the empirical evaluation further substantiates the effectiveness of the proposed approach. The learning curve comparison shows that Kernel PI achieves a normalized reward of 0.79 after 300 episodes, significantly outperforming the baseline RL method at 0.64, representing a 23% gain in final performance. The ablation analysis also highlights the complementary role of individual components: kernel policy evaluation alone contributes nearly 15 percentage points to the final reward, while prioritized experience replay and adaptive exploration bonus add incremental but consistent improvements. These results confirm that the overall performance benefits are not incidental, but rather emerge from the deliberate combination of algorithmic components. Together, they demonstrate that kernel-based RL offers both faster convergence and higher asymptotic performance, making it particularly well-suited for adaptive SDN control where stability and responsiveness are crucial.

Our findings align with prior studies in kernelized RL, which emphasize the advantages of nonparametric representations for stability and sample efficiency. However, the present work extends this literature by applying the methodology to SDN control, a domain that demands both real-time responsiveness and reliability. In this sense, the contribution is twofold: it validates kernel embedding as a practical mechanism for network control, and it provides empirical evidence that RKHS-based policy iteration can outperform standard methods in dynamic, stochastic environments.

Nevertheless, some limitations must be acknowledged. The computational cost of Gram matrix construction may become prohibitive for very large-scale traces, although our PyTorch implementation mitigates this through GPU acceleration and mini-batch training. Future research could investigate scalable approximations, such as random feature expansions or sparsification strategies, to reduce memory and time complexity. Another open direction is the exploration of deep kernel learning, where the kernel parameters themselves are adapted via neural architectures, thereby combining the stability of RKHS with the expressiveness of deep networks.

Beyond SDN, the generality of the approach suggests potential applications in other domains that share similar characteristics of high-dimensional stochastic control, such as robotics, intelligent transportation, or smart energy systems. Extending the method to these areas could further validate its robustness and generalizability. Finally, real-world validation in network testbeds such as RIU/MININET remains an essential next step. Evaluating the proposed algorithm under production traffic conditions will provide stronger evidence of its practical feasibility and operational benefits.

Overall, the discussion highlights that the proposed method offers a promising balance of theory and practice. It provides a structured way to embed uncertainty, ensures convergence through regularization, and delivers consistent performance improvements in adaptive SDN scenarios. With future extensions to real-world deployments and cross-domain applications, the method has the potential to contribute broadly to adaptive control research at the interface of machine learning and complex networked systems.

The SDN controller implementation used in this study is a Ryu application that communicates via standard OpenFlow 1.3 messages. The same code that runs in Mininet (Section 2.9) operates without modification against Open vSwitch or other OF-1.3–compatible switches after configuring the controller endpoint and polling interval. Hardware testbed validation is planned; given protocol compatibility, only deployment and logging configuration are required rather than algorithmic changes.

5. Conclusions

This work introduced an RL framework for adaptive SDN control that leverages kernel-based policy iteration within an RKHS. By embedding transition dynamics directly in a nonparametric feature space, the proposed method addresses challenges of high-dimensionality, stochasticity, and non-stationarity that are inherent in network environments. Theoretical underpinnings were translated into a practical algorithm that achieved stable convergence, consistent optimization trajectories, and significant performance improvements compared with baseline RL approaches.

Experimental analysis demonstrated that the method not only delivers higher average returns but also exhibits desirable statistical properties: a near-Gaussian distribution of episodic rewards, moderate dispersion, and robustness against outliers. These characteristics highlight the ability of the approach to maintain stable performance across heterogeneous traffic conditions rather than relying on rare favorable cases. Importantly, the improvements observed (a $+22.4\%$ gain over classical RL and $+82.2\%$ over random control) are meaningful in networking contexts where even small percentage changes can translate into substantial operational benefits.

The broader implications of this contribution extend beyond SDN. Any domain characterized by complex, uncertain, and dynamic environments, including robotics, intelligent transportation, and smart energy systems, can potentially benefit from the integration of kernel embedding with RL. While computational complexity remains a limitation, especially for very large-scale traces, efficient implementations and scalable kernel approximations offer promising avenues for future work.

In summary, the proposed method advances RL by uniting nonparametric kernel representations with policy iteration, yielding a principled yet practical approach to adaptive control. The results provide strong evidence of both robustness and efficiency in SDN scenarios, while laying the foundation for cross-domain applications and real-world validation in operational testbeds such as RIU/MININET. This dual emphasis on methodological innovation and applied relevance positions the contribution as a step toward bridging theory and practice in adaptive control with machine learning.