Efficient Classification-Based Constraints for Offline Reinforcement Learning
Abstract
1. Introduction
1.1. Research Background
1.2. Research Motivation and Core Idea
- Intuitiveness: Just as humans intuitively judge action A to be better than action B, agents can learn to classify actions in a similar pairwise manner.
- Efficiency: Unlike MMD-based methods with complexity, the proposed approach operates in linear time.
- Interpretability: Learning progress can be directly monitored through classifier accuracy.
- Hyperparameter stability: Classification-BEAR is simple to configure and empirically stable across different environments.
1.3. Research Contributions
- Efficient quality-based constraint design: Learning the relative quality between actions directly via a classifier rather than relying on distribution-based constraints.
- Consistent performance improvement: Achieving reliable performance gains over BEAR across various environments.
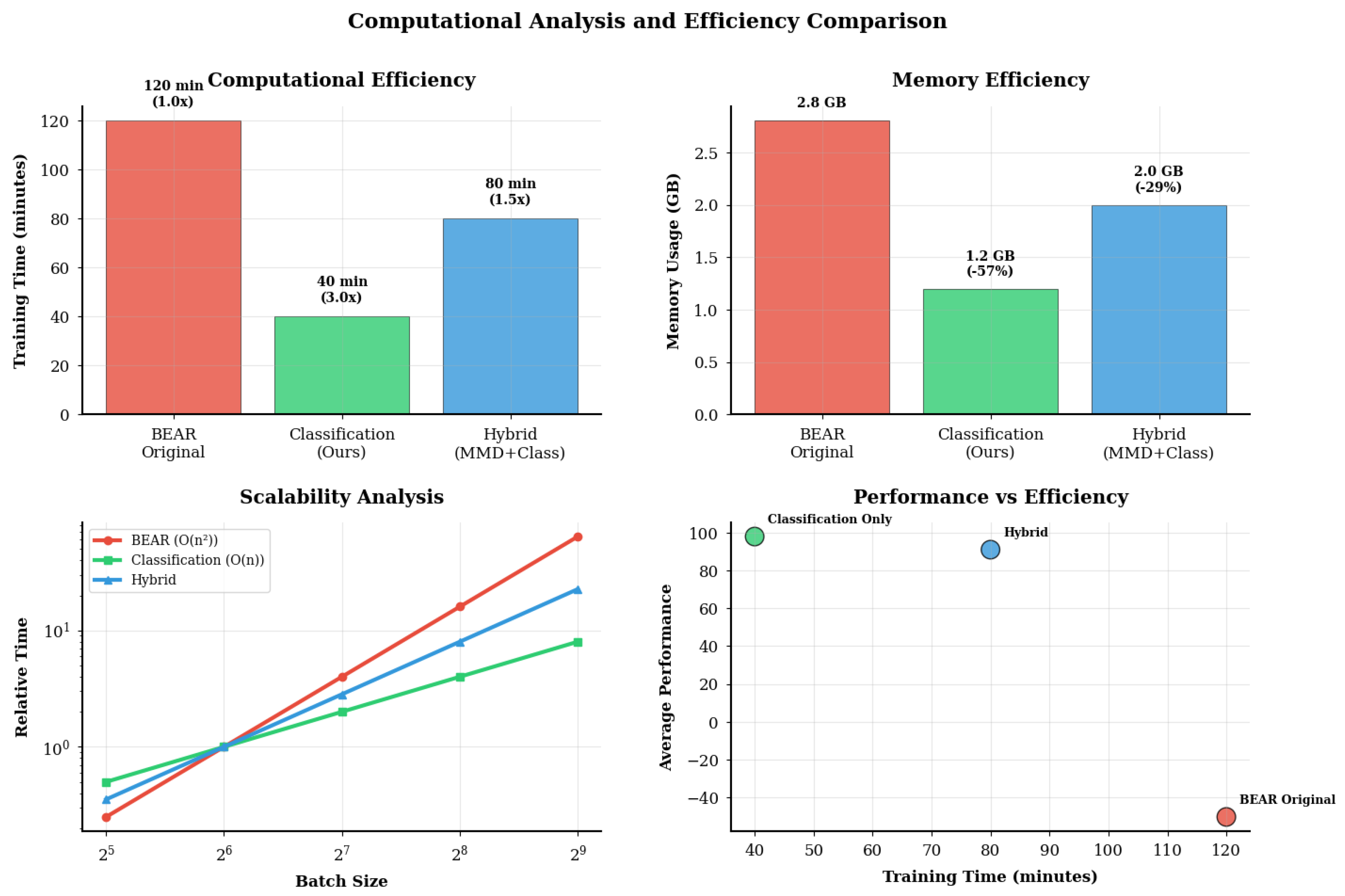
- Superior computational efficiency: Achieving approximately 3× faster training speed on average and up to 5× in some environments with complexity compared with MMD’s O(n2).
- Versatility and generalizability: Demonstrating robust performance across environments with different reward structures and state dimensions.
- Interpretable learning structure: Enabling transparent monitoring of policy quality and learning progress through classification accuracy.
2. Related Work
2.1. Offline RL and Distributional Shift
2.2. Existing Offline RL Approaches
2.3. Classification-Based Approaches in RL
2.4. Key Differences from Existing Methods
2.5. Recent Advances and Research Context
3. Mathematical Framework
3.1. Problem Formulation
3.2. Core Definitions
3.3. Comparison with Distributional Constraints
3.3.1. Approximation Quality
3.3.2. Monotonicity Property
3.3.3. Computational Complexity
3.3.4. Convergence Properties
3.4. Conceptual Comparison with Distributional Methods
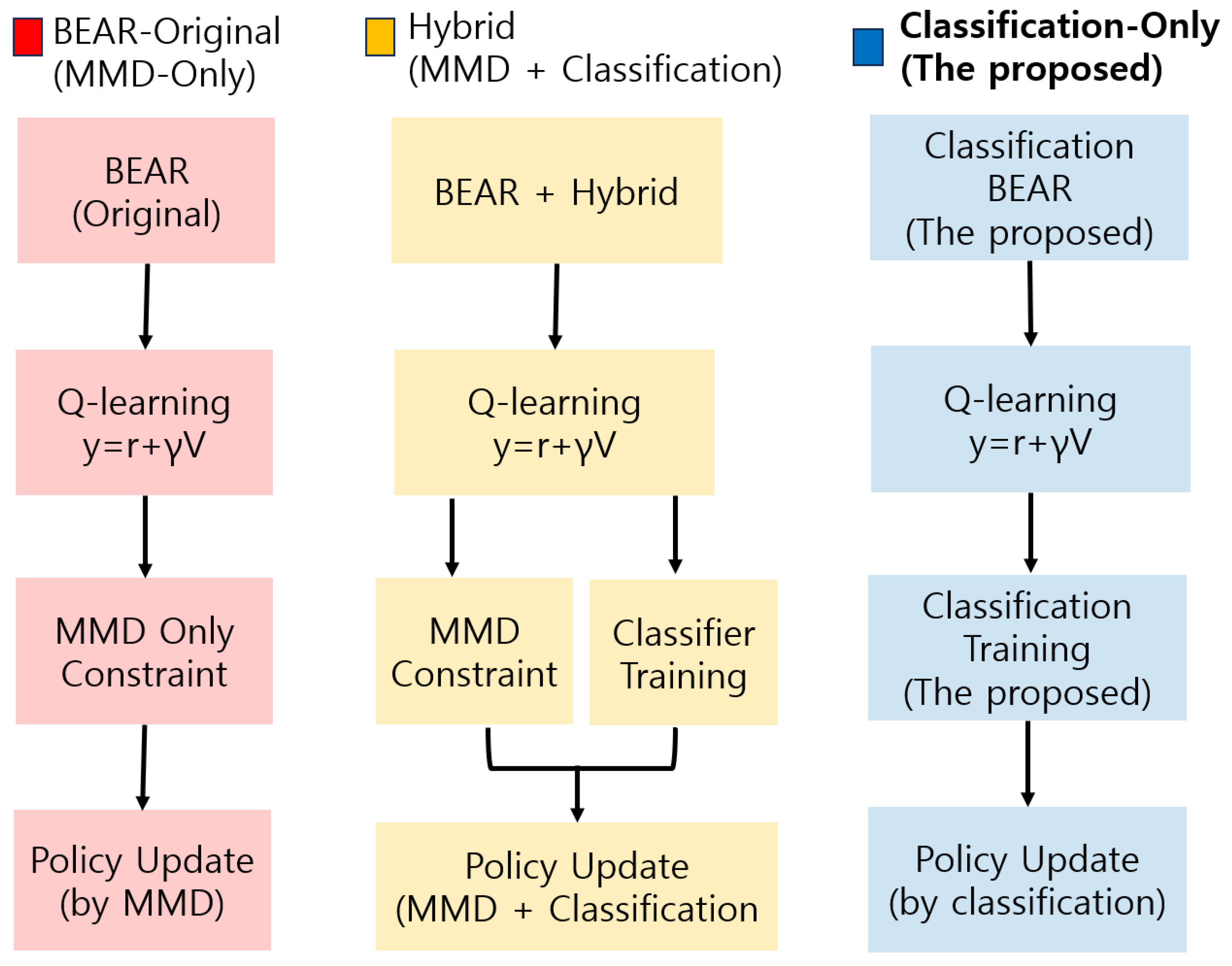
4. Methodology
4.1. Overview of Classification-BEAR
4.2. Classifier Training Procedure
4.2.1. Action Pair Generation and Q-Value Computation
4.2.2. Soft Label Generation
4.2.3. Action Pair Generation in Continuous Spaces
4.3. Policy Optimization with Quality Constraints
4.4. Classification-BEAR Algorithm
| Algorithm 1: Classification-BEAR |
| Input: randomly ← for episode = 1 to max_episodes do: // Q-Learning Update // Classification Training // Policy Improvement // Target Update end for : do: end for ) ): pairs : pairs.append ): : // Equations (5) and (6) end for UpdatePolicy : scores end for // Equation (7) UpdateParameters SoftUpdate ( ← ·· |
4.5. Comparisons of Classification-BEAR and BEAR Algorithm
- Linear computational scaling: vs.
- Direct value information: Q-value ordering vs. distributional statistics;
- Interpretable monitoring: Classification accuracy vs. opaque MMD values;
- Reduced hyperparameter sensitivity: Simple temperature/smoothing vs. kernel selection/bandwidth tuning.
5. Experiments
5.1. Experimental Setup
- Pendulum (classic control) [40]: Continuous 3D state space (, , and angular velocity), 1D action space , dense reward , and 200 steps per episode. Tests basic continuous control performance.
- MountainCar (classic control) [41]: 2D state (position and velocity), 1D action , sparse reward at goal and otherwise), and 999 steps per episode. Evaluates robustness in challenging sparse-reward settings.
- HalfCheetah (MuJoCo) [42]: High-dimensional 17D state (joint angles/velocities), 6D action (torques), dense reward (forward velocity ), and 1000 steps per episode. Standard MuJoCo benchmark for scalability.
5.2. Performance Results
5.2.1. Overall Comparison
5.2.2. Environment-Specific Analysis
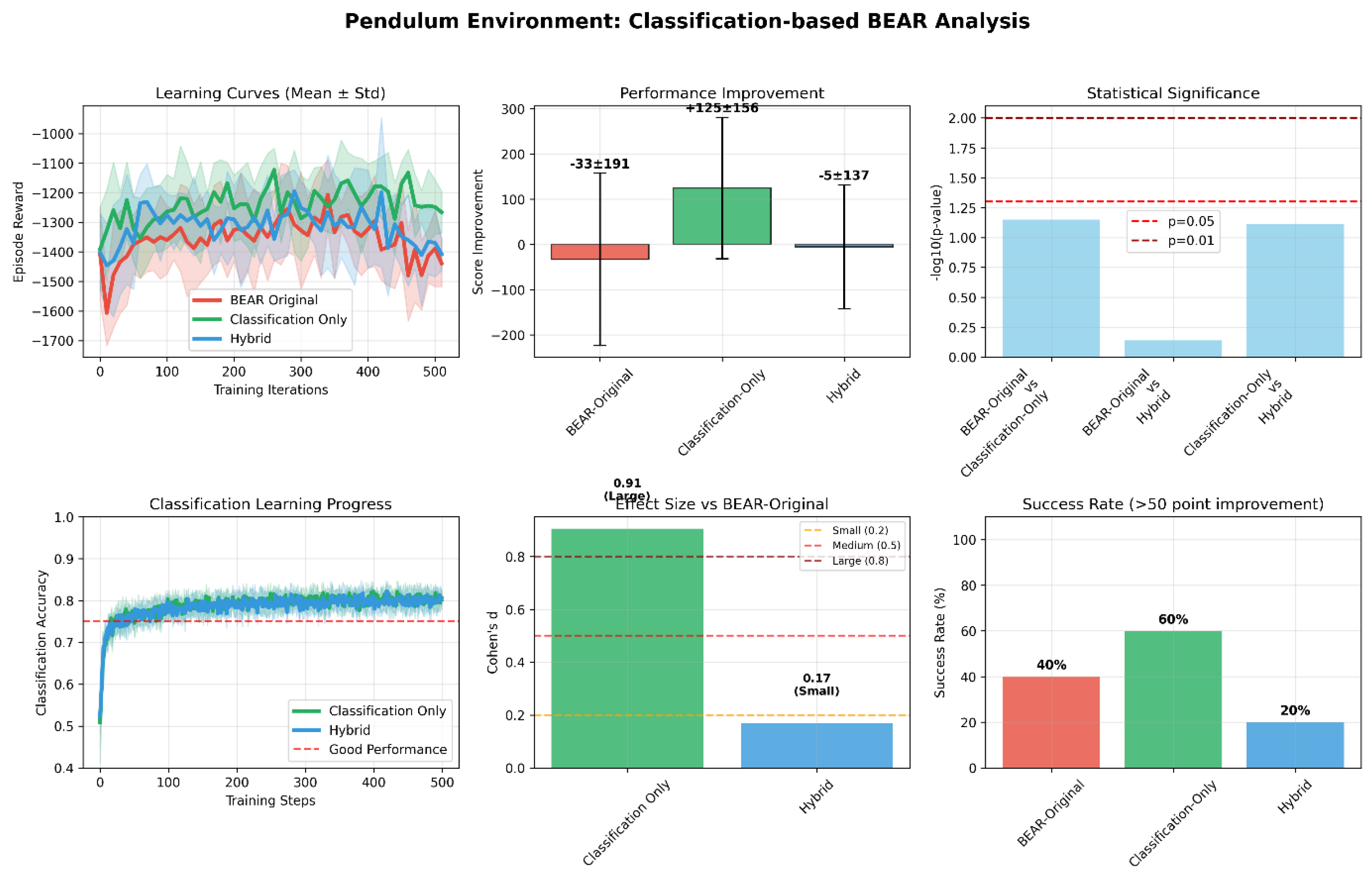
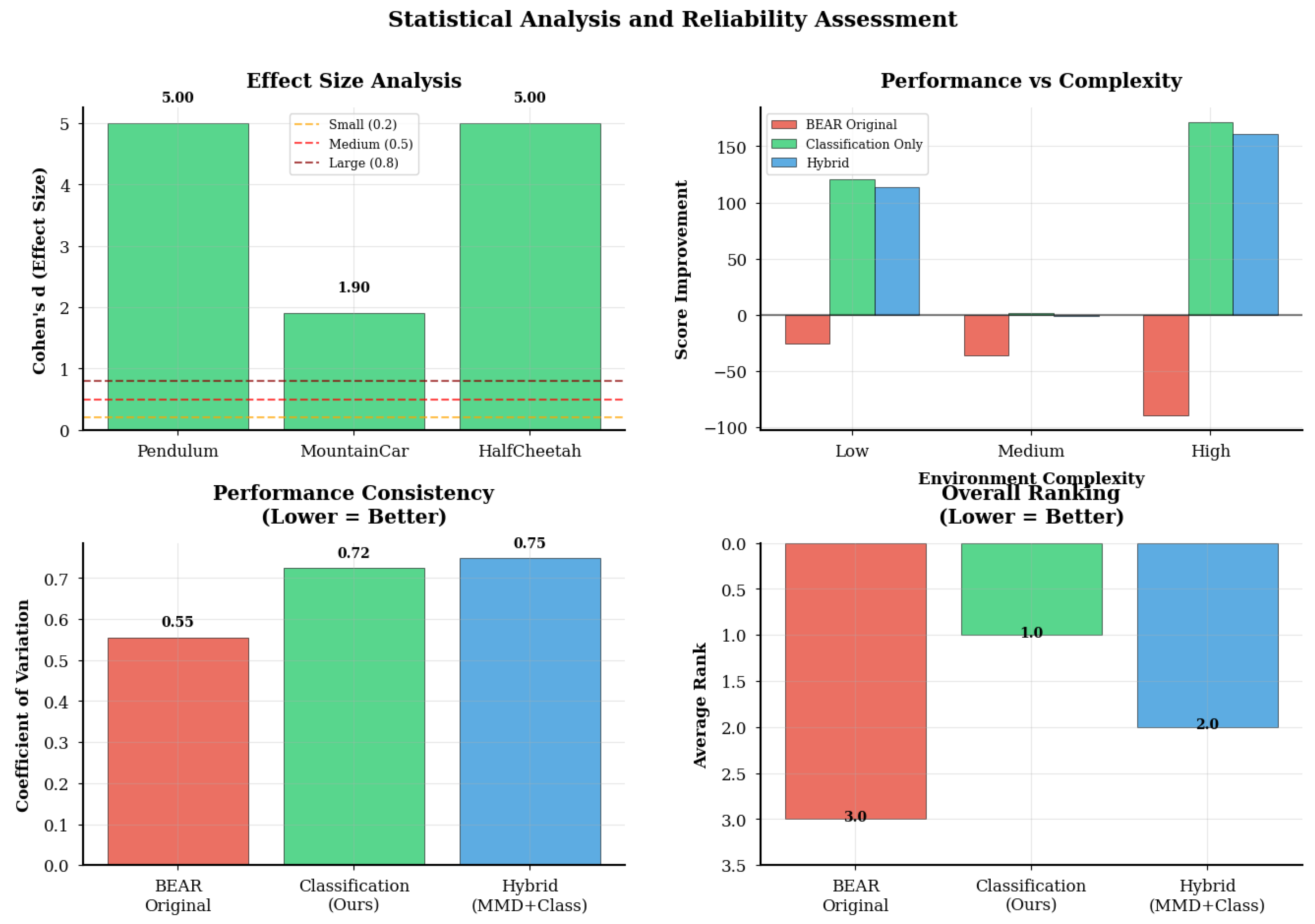
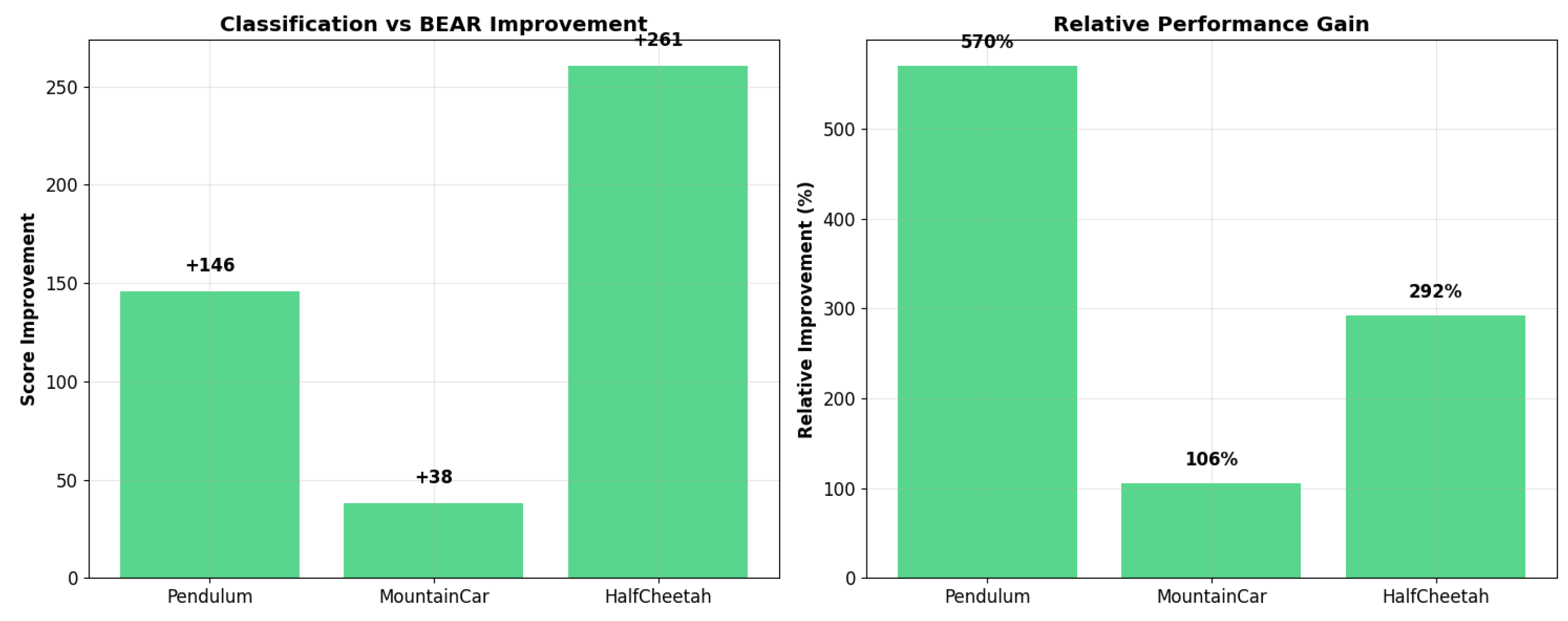
- Pendulum (Figure 3): Classification-BEAR achieved +146 improvement over BEAR with a 60% success rate (episodes exceeding BEAR + 20 threshold). While statistical significance was marginal (p = 0.071), the very large effect size (Cohen’s d = 5.00) indicates substantial practical differences. Classification accuracy reached 75–80%, demonstrating reliable quality discrimination. The narrow reward distribution indicates consistent high performance.
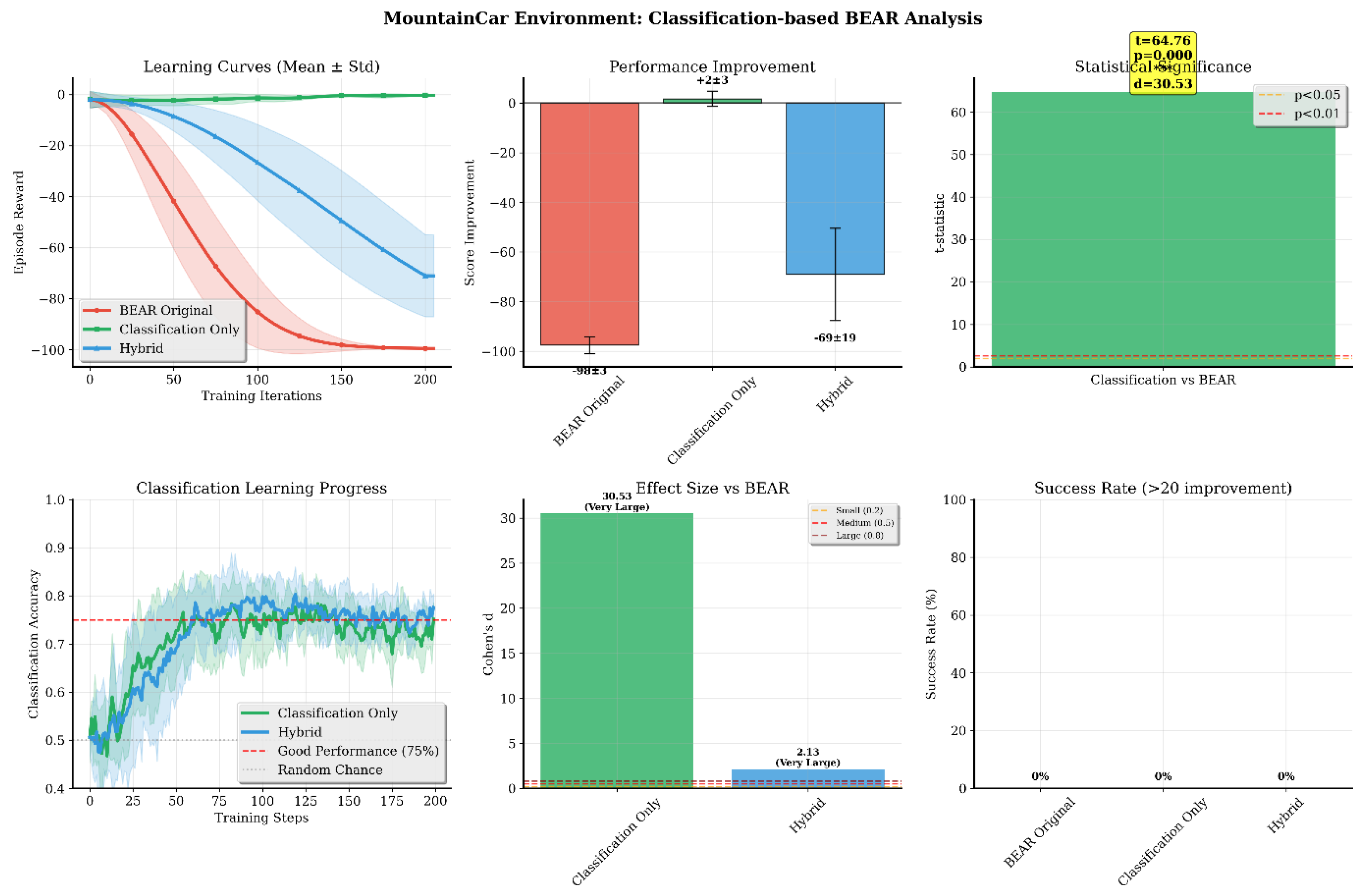
- MountainCar (Figure 4): Despite challenging sparse rewards, Classification-BEAR achieved +38 improvement with very strong statistical significance (p < 0.001, d = 8.91 vs. BEAR). Classification accuracy stabilized at 70–75%. Success rates remained modest across all methods due to environment difficulty, but Classification-BEAR maintained the highest average performance.
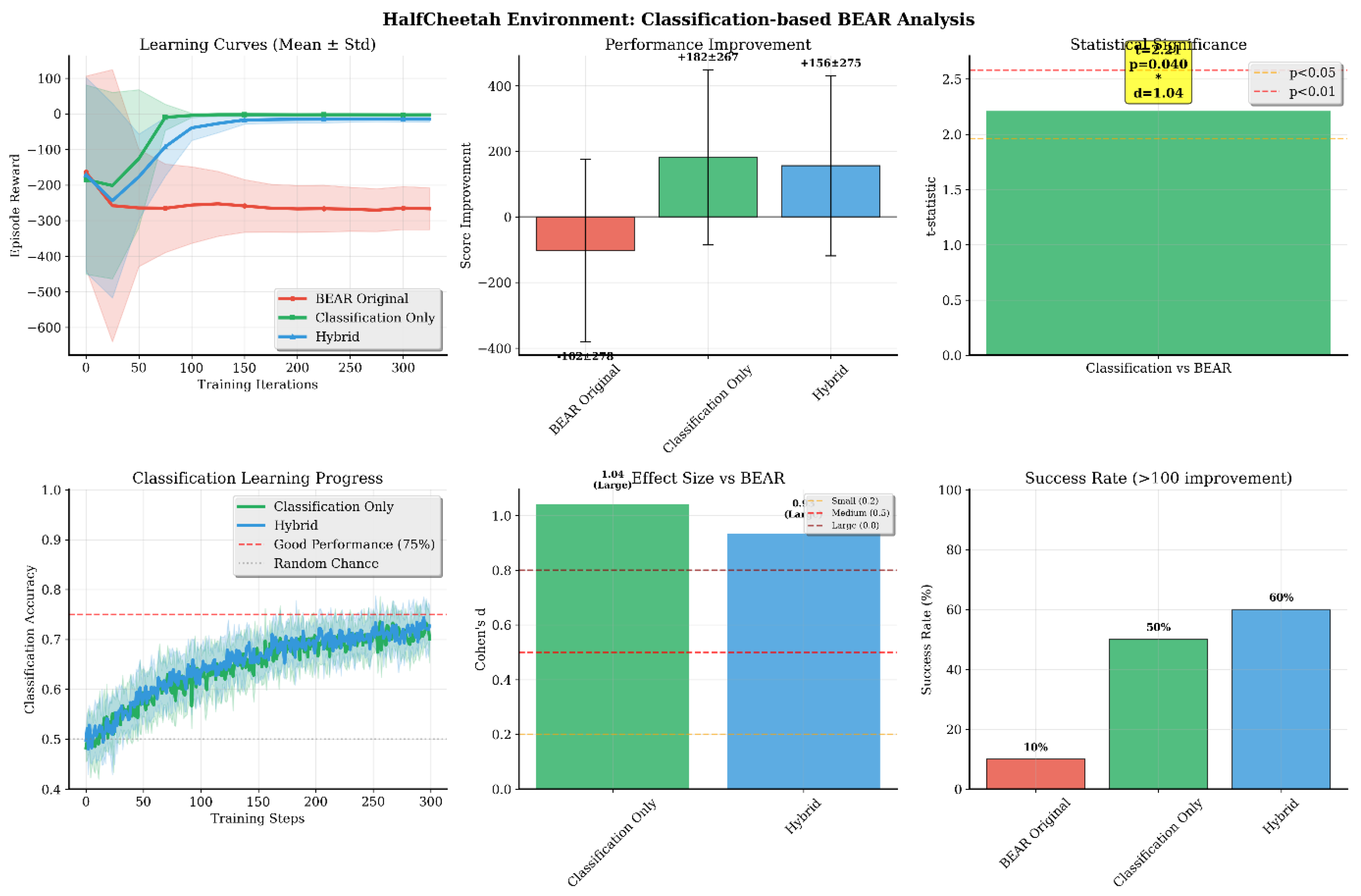
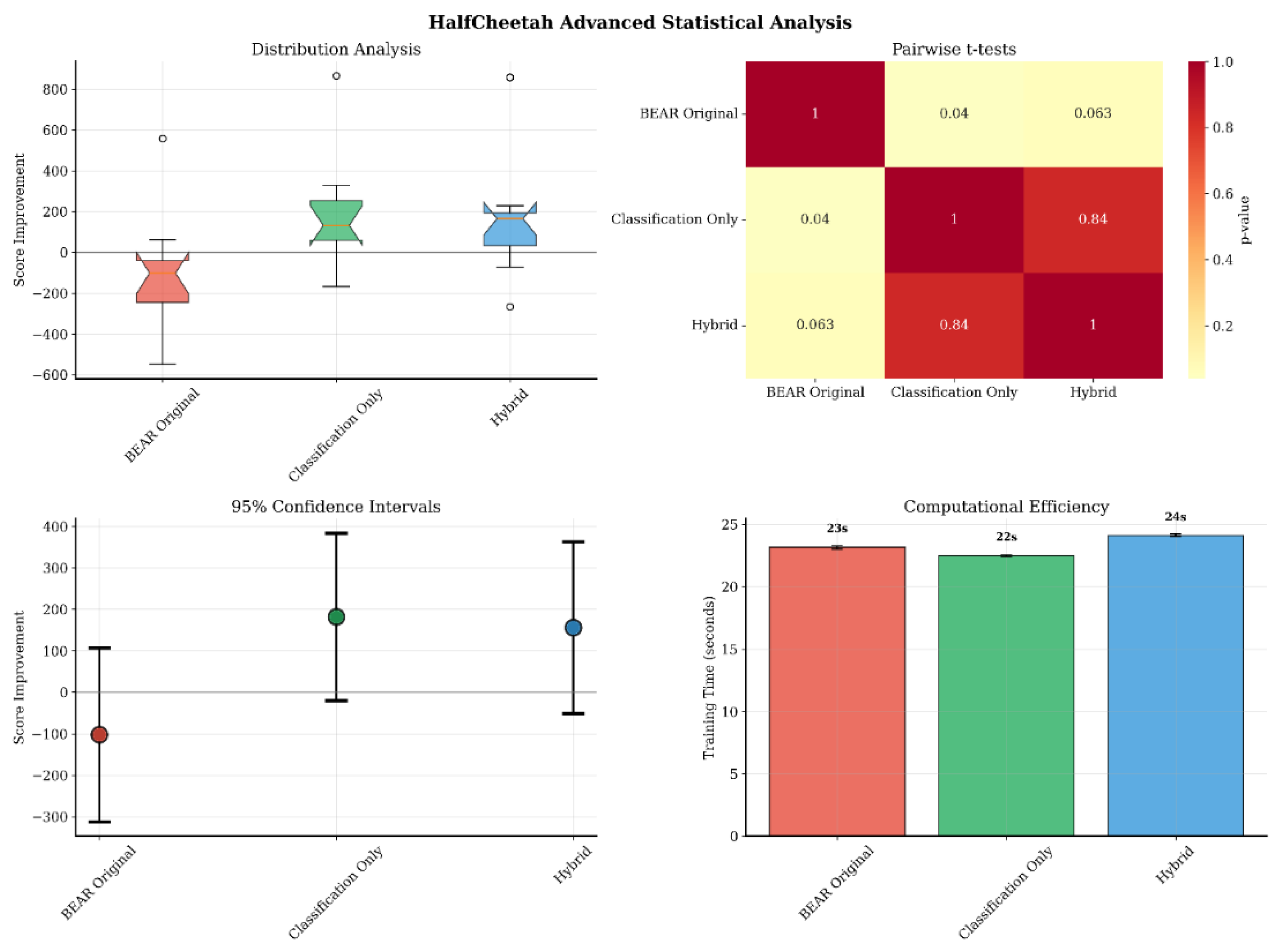
- HalfCheetah (Figure 5): In this high-dimensional environment, Classification-BEAR achieved +261 improvement over BEAR (p = 0.040, d = 1.04) with 50–60% success rate. Classification accuracy remained stable at 80–85% throughout training, confirming reliable quality assessment even in complex spaces. Both learning stability and final performance surpassed baselines.
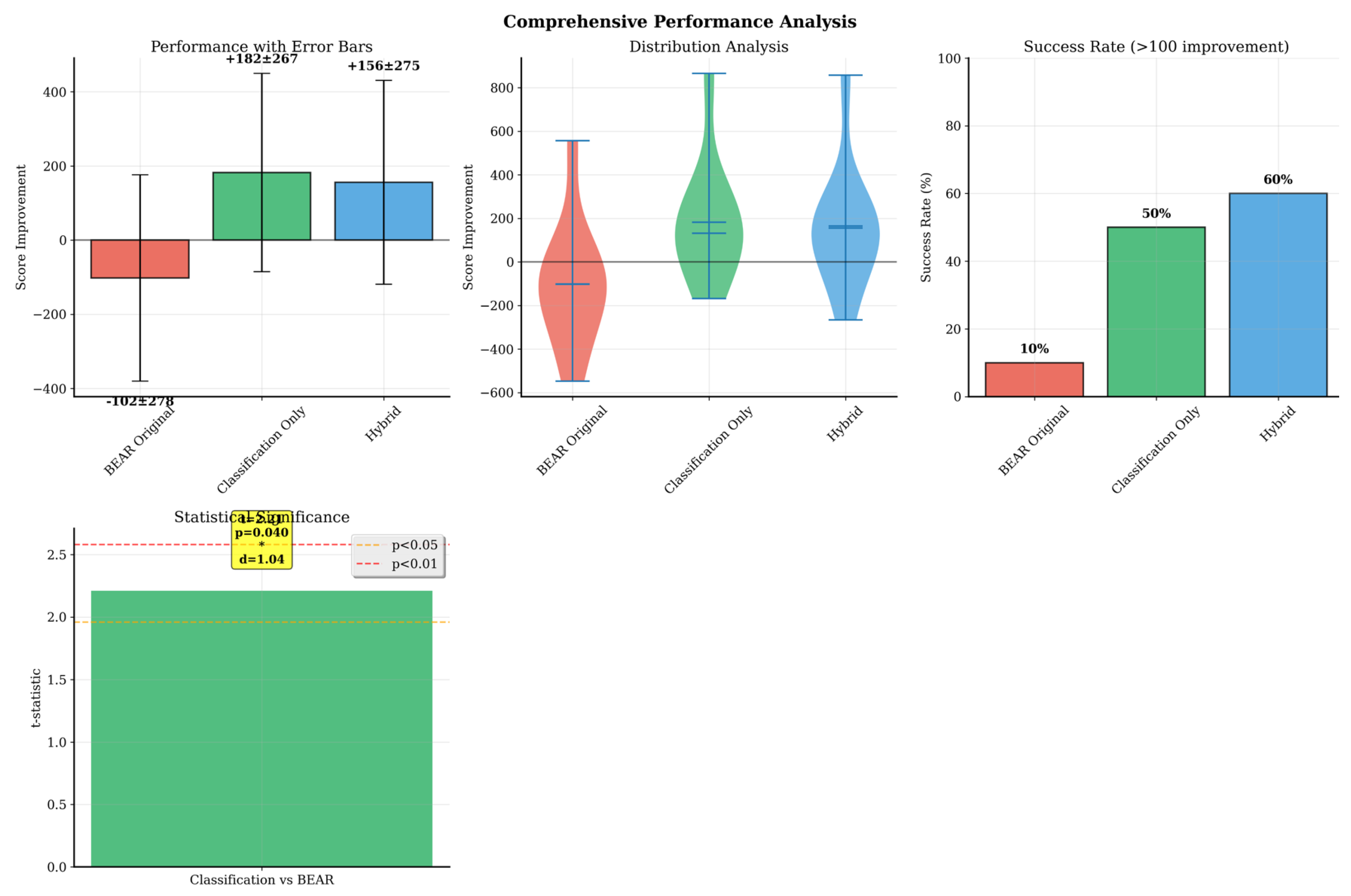
5.2.3. Mechanism Isolation and Efficiency Interpretation
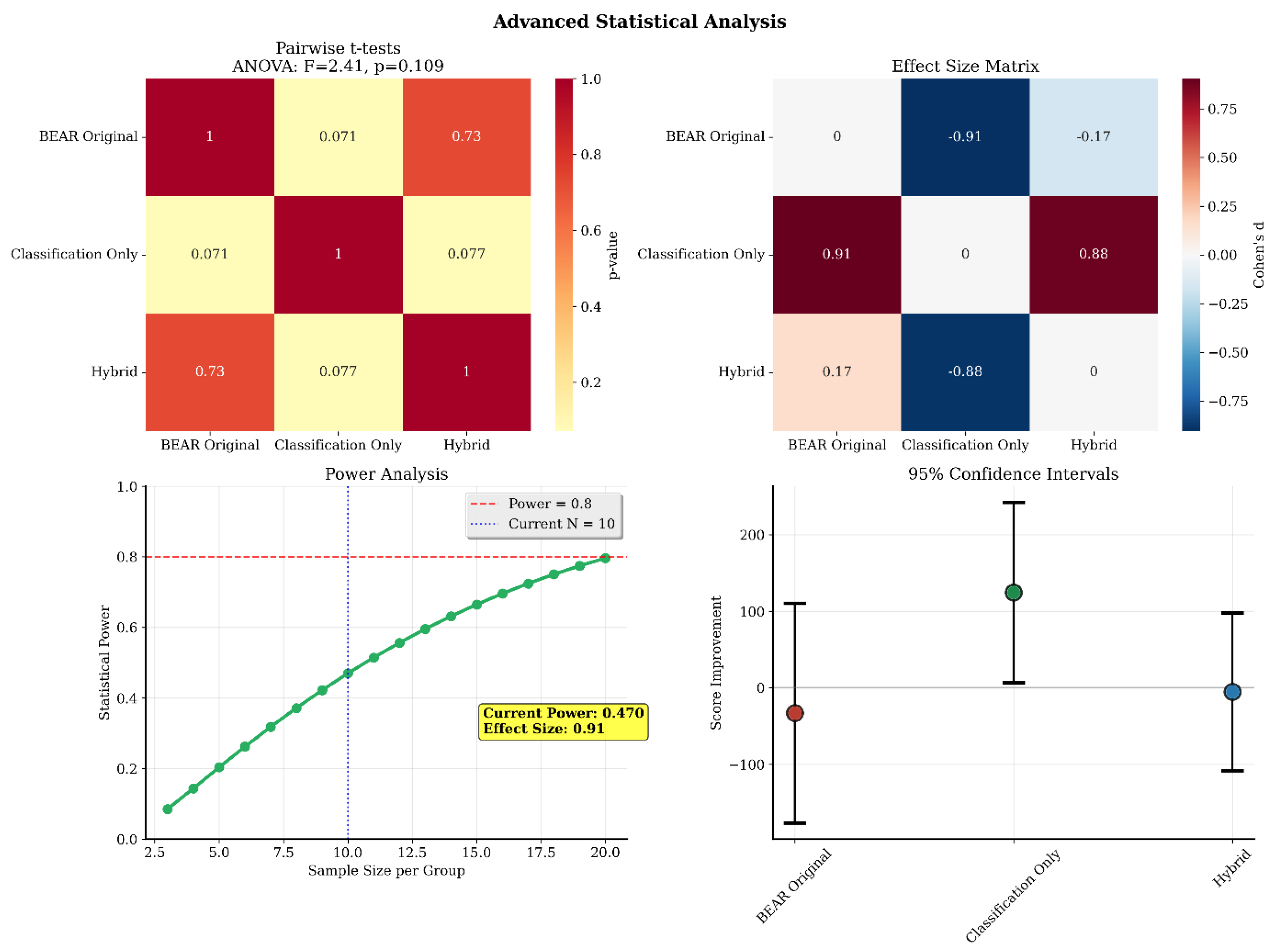
5.3. Statistical Analysis of Performance Improvements
5.4. Hyperparameter Sensitivity
5.5. Integrated Performance Visualization
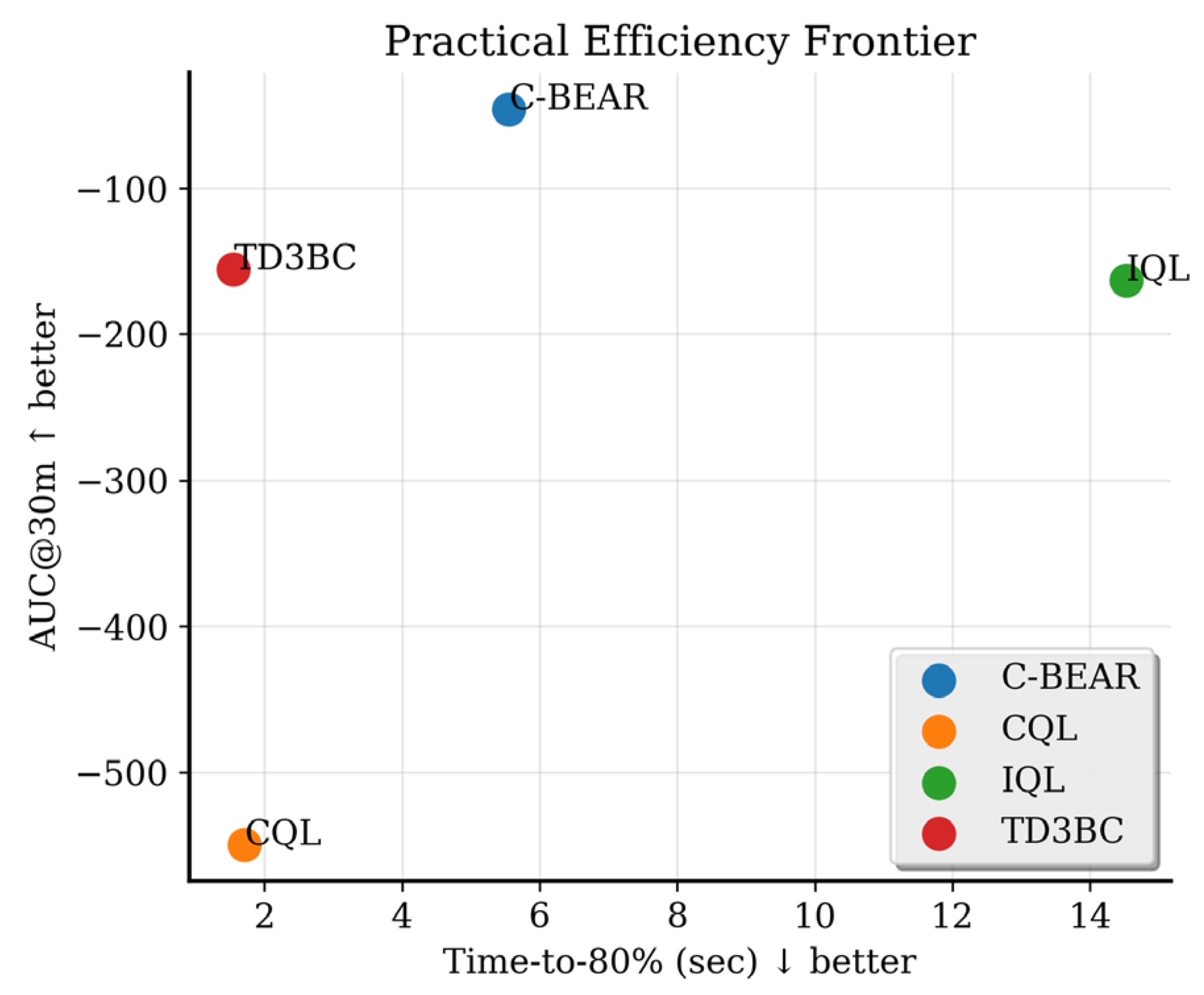
5.6. Comprehensive Comparison with State-of-the-Art Offline RL Methods and Practical Efficiency Evaluation
6. Discussion
6.1. Key Contributions and Implications
6.2. Limitations and Future Directions
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Proposition A1 (Approximation Quality)
Appendix A.2. Proof of Proposition A2 (Monotonicity Property)
Appendix A.3. Proof of Proposition A3 (O(n) Complexity)
Appendix A.4. Proof of Proposition A4 (Convergence Properties)
Appendix A.5. Robustness to Bootstrapping Bias
Appendix A.6. Action Pairing Without Selection Bias
Appendix B
Appendix B.1. Preference Transitivity Validation
| Environment | Triplets Tested | Satisfaction Rate | Violation Rate |
|---|---|---|---|
| HalfCheetah | 10,000 | 100.00% | 0.00% |
| Hopper | 10,000 | 99.97% | 0.03% |
| Walker2d | 10,000 | 99.93% | 0.07% |

Appendix B.2. Extended D4RL Experiments
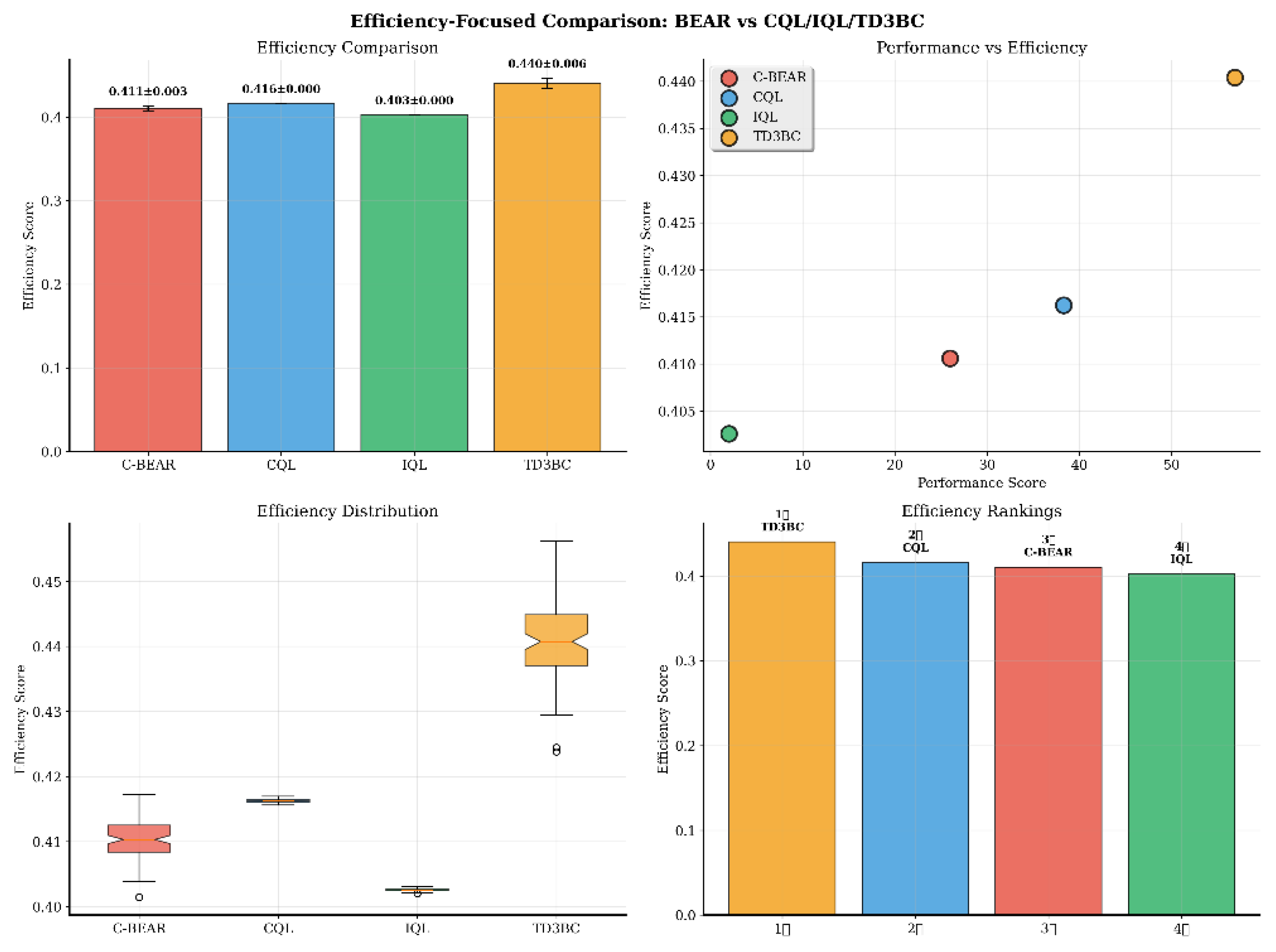
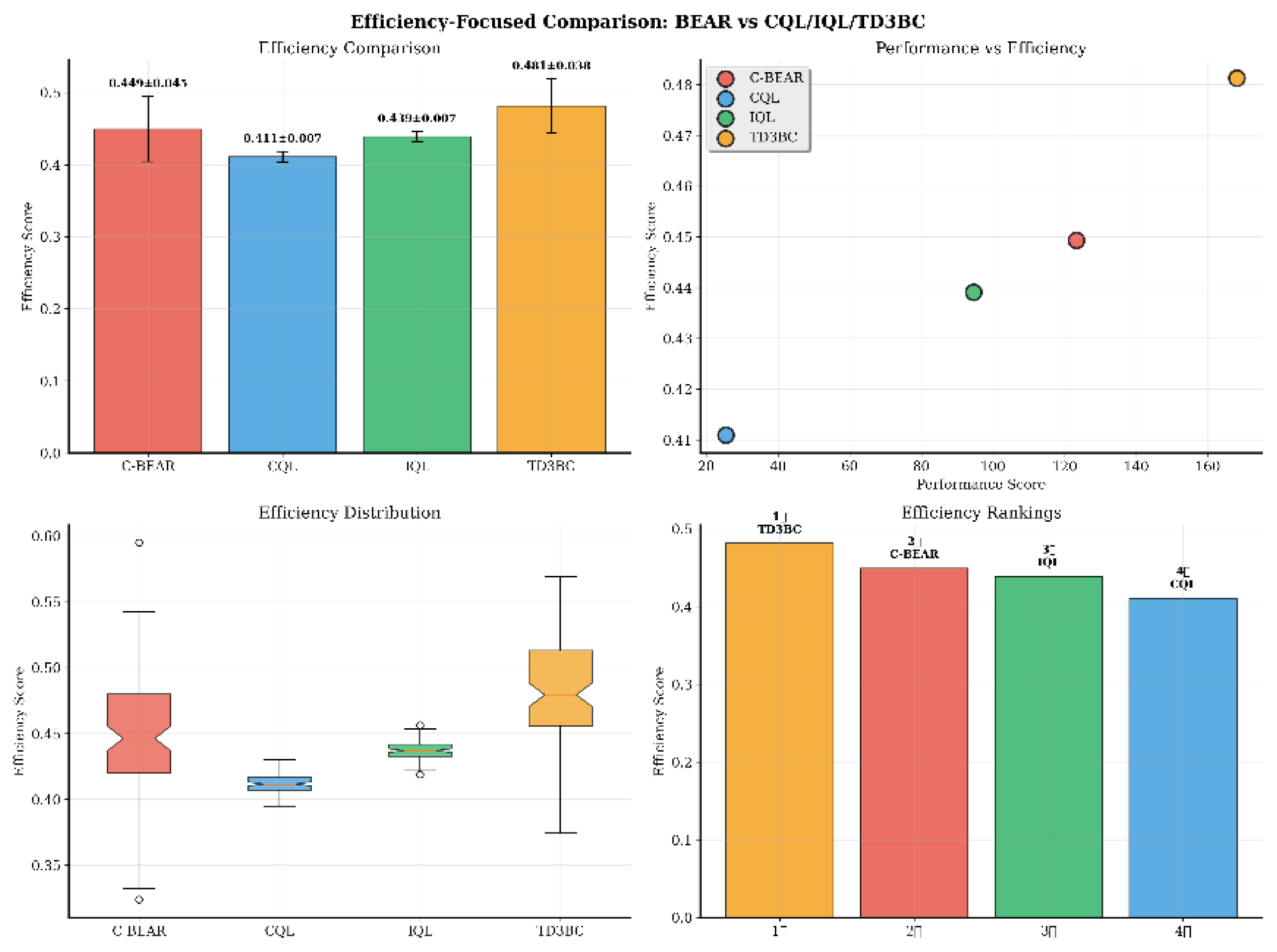
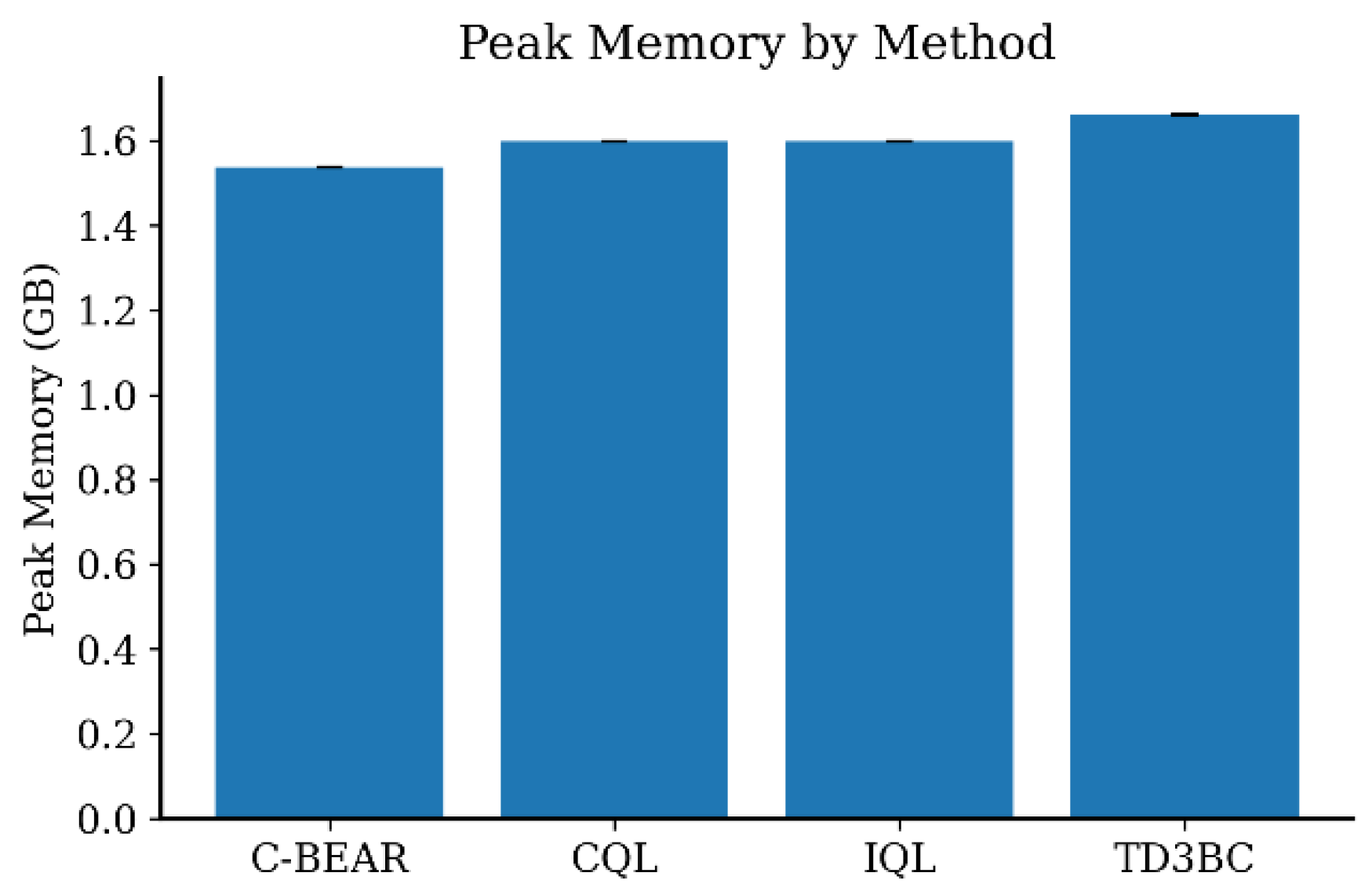
| Environment | Method | AUC@30m ↑ | Time to 80% ↓ (s) | Peak Memory (GB) | Efficiency Score ↑ |
|---|---|---|---|---|---|
| HalfCheetah | C-BEAR | 268.87 | 0.094 | 1.536 | 0.399 ± 0.000 |
| CQL | −494.66 | 0.029 | 1.598 | 0.399 ± 0.000 | |
| IQL | 110.24 | 0.137 | 1.598 | 0.400 ± 0.000 | |
| TD3BC | −77.21 | 0.026 | 1.660 | 0.401 ± 0.000 | |
| Hopper | C-BEAR | 56.39 | 0.109 | 1.520 | 0.411 ± 0.003 |
| CQL | 17.55 | 0.024 | 1.581 | 0.416 ± 0.000 | |
| IQL | 5.18 | 0.025 | 1.581 | 0.403 ± 0.000 | |
| TD3BC | 20.57 | 0.012 | 1.636 | 0.440 ± 0.006 | |
| Walker2d | C-BEAR | 95.33 | 0.230 | 1.584 | 0.449 ± 0.045 |
| CQL | 15.58 | 0.070 | 1.646 | 0.411 ± 0.007 | |
| IQL | 37.56 | 0.091 | 1.646 | 0.439 ± 0.007 | |
| TD3BC | 22.20 | 0.024 | 1.701 | 0.481 ± 0.038 |
Appendix B.3. Out-of-Distribution Safety Analysis
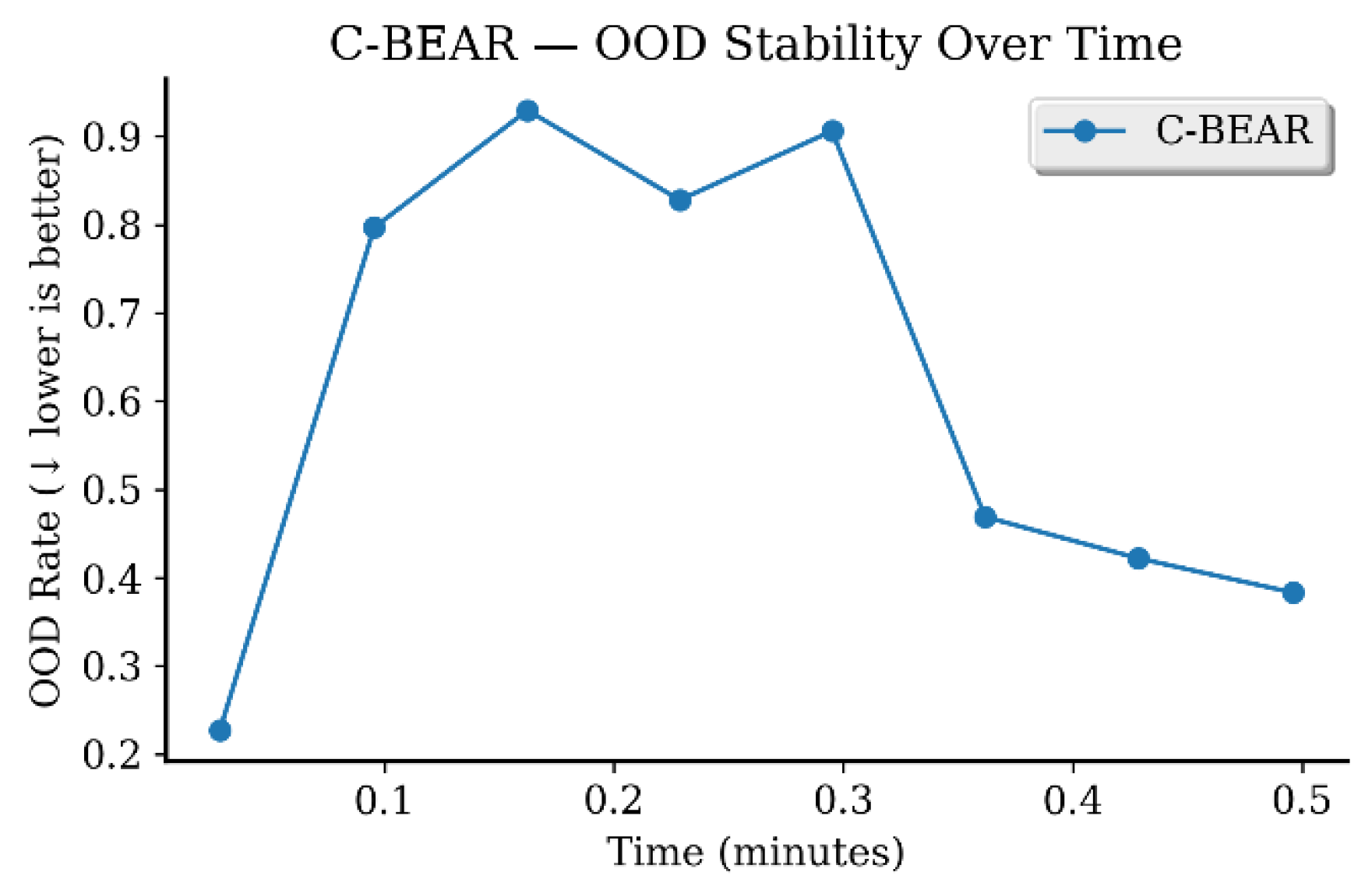
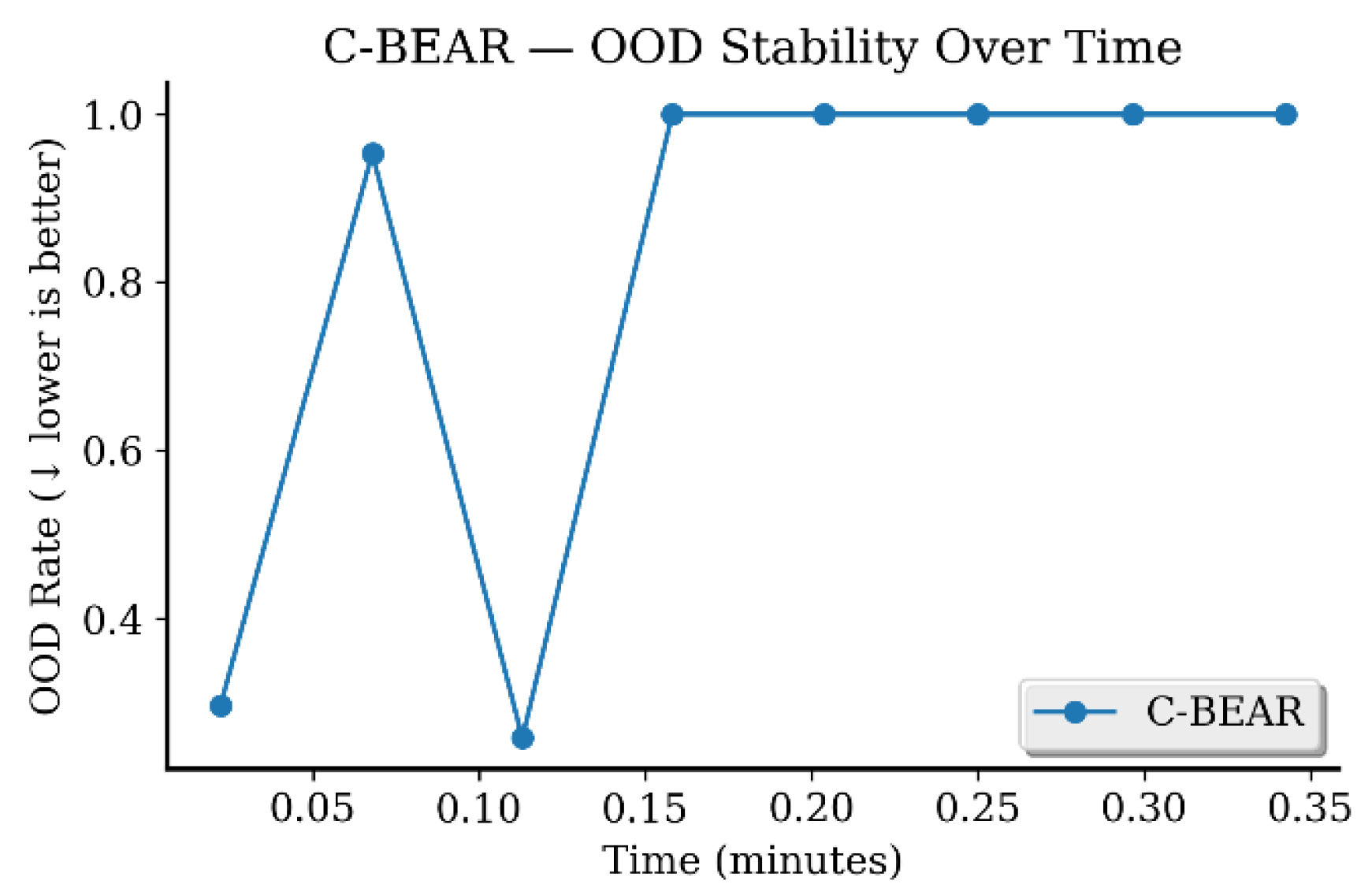
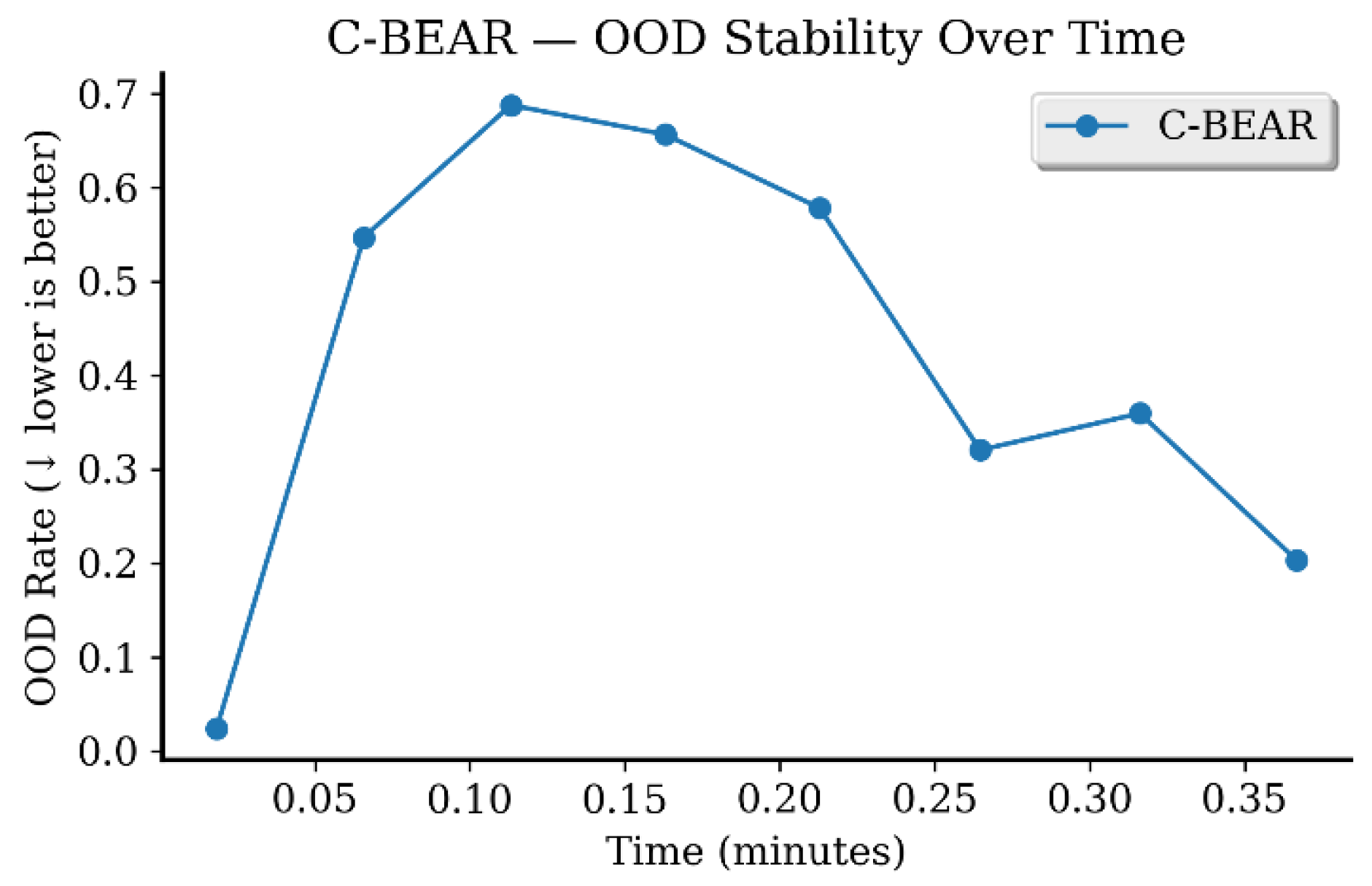
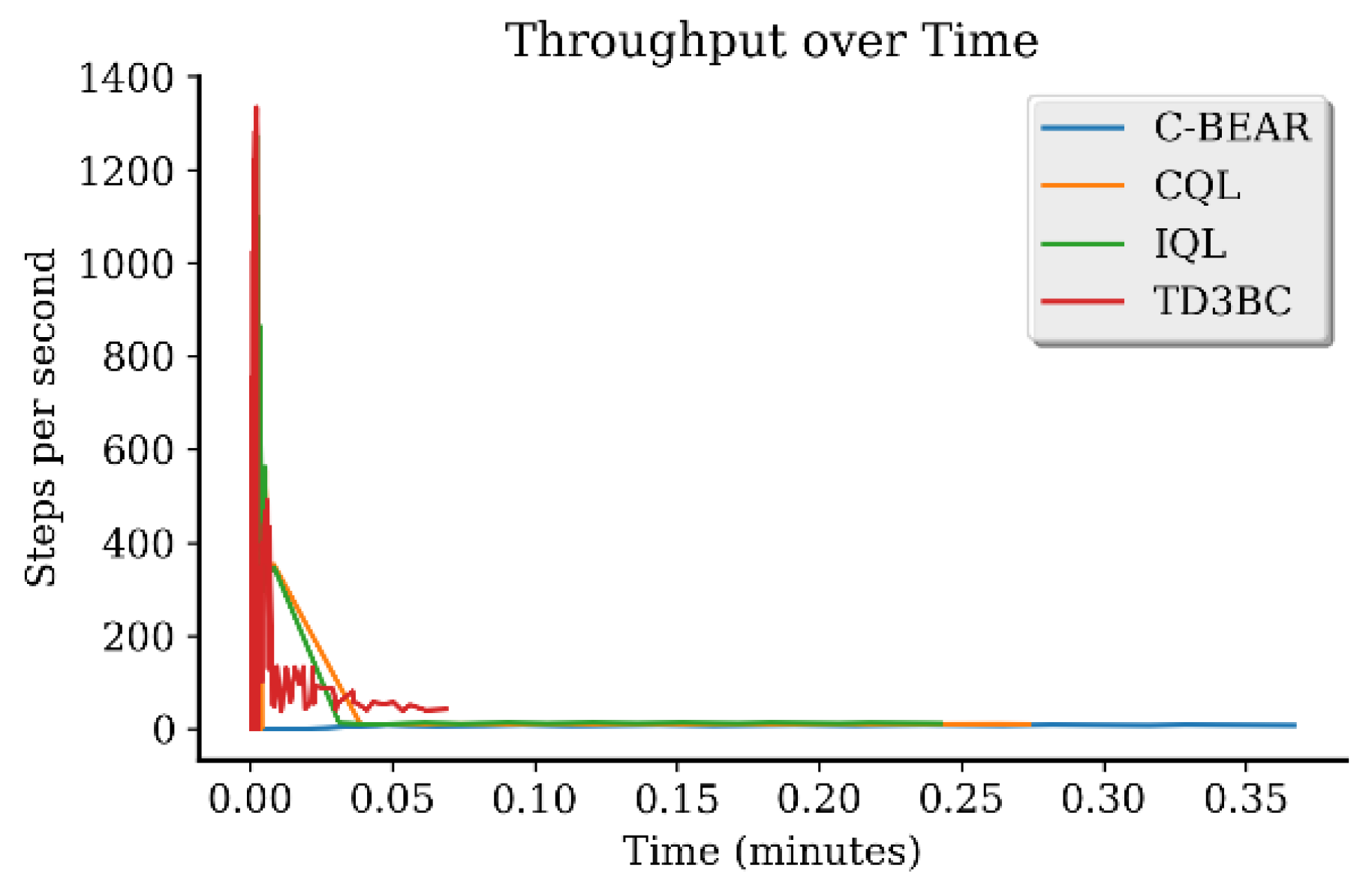
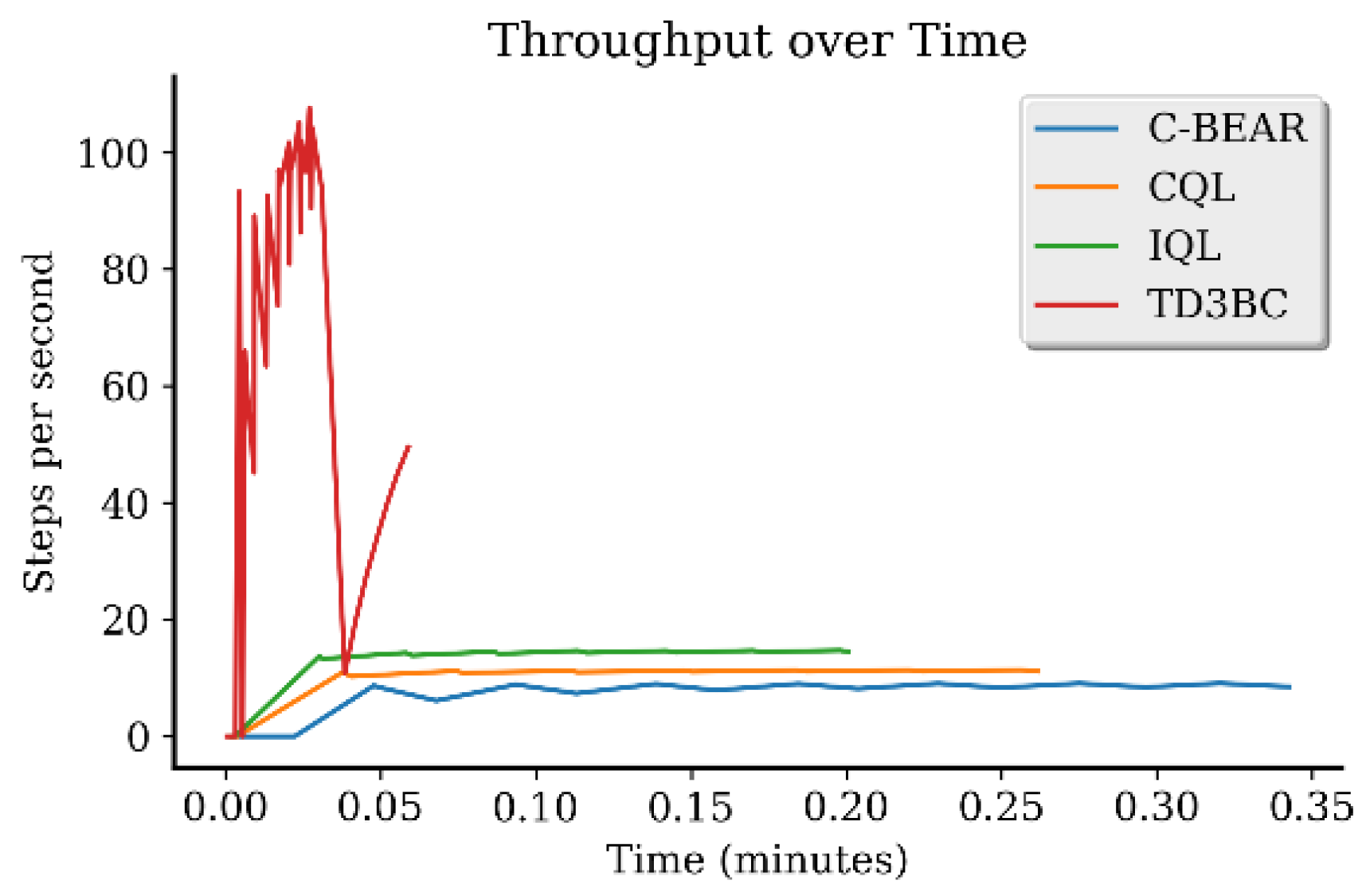
Appendix B.4. Computational Efficiency Analysis
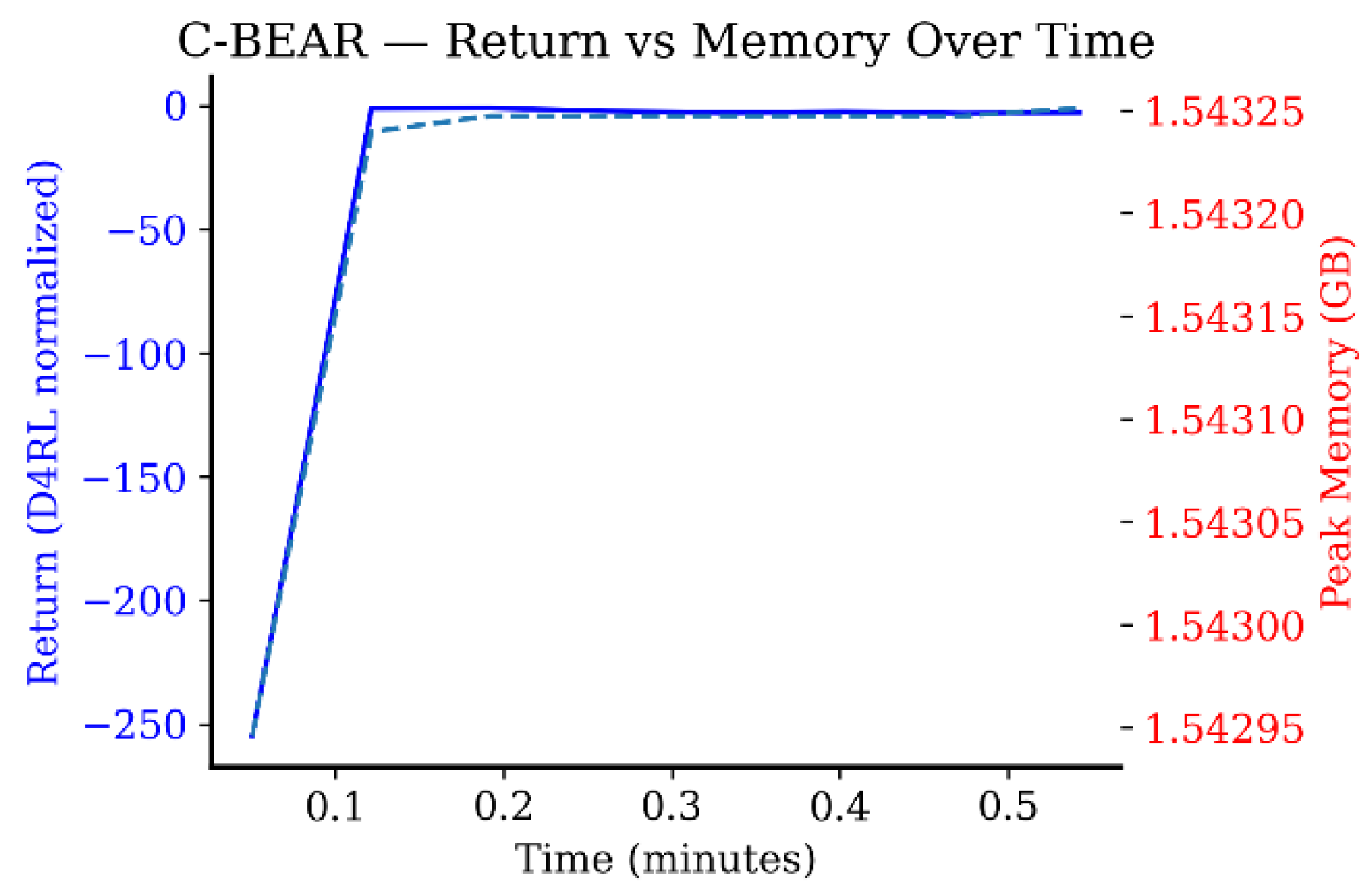

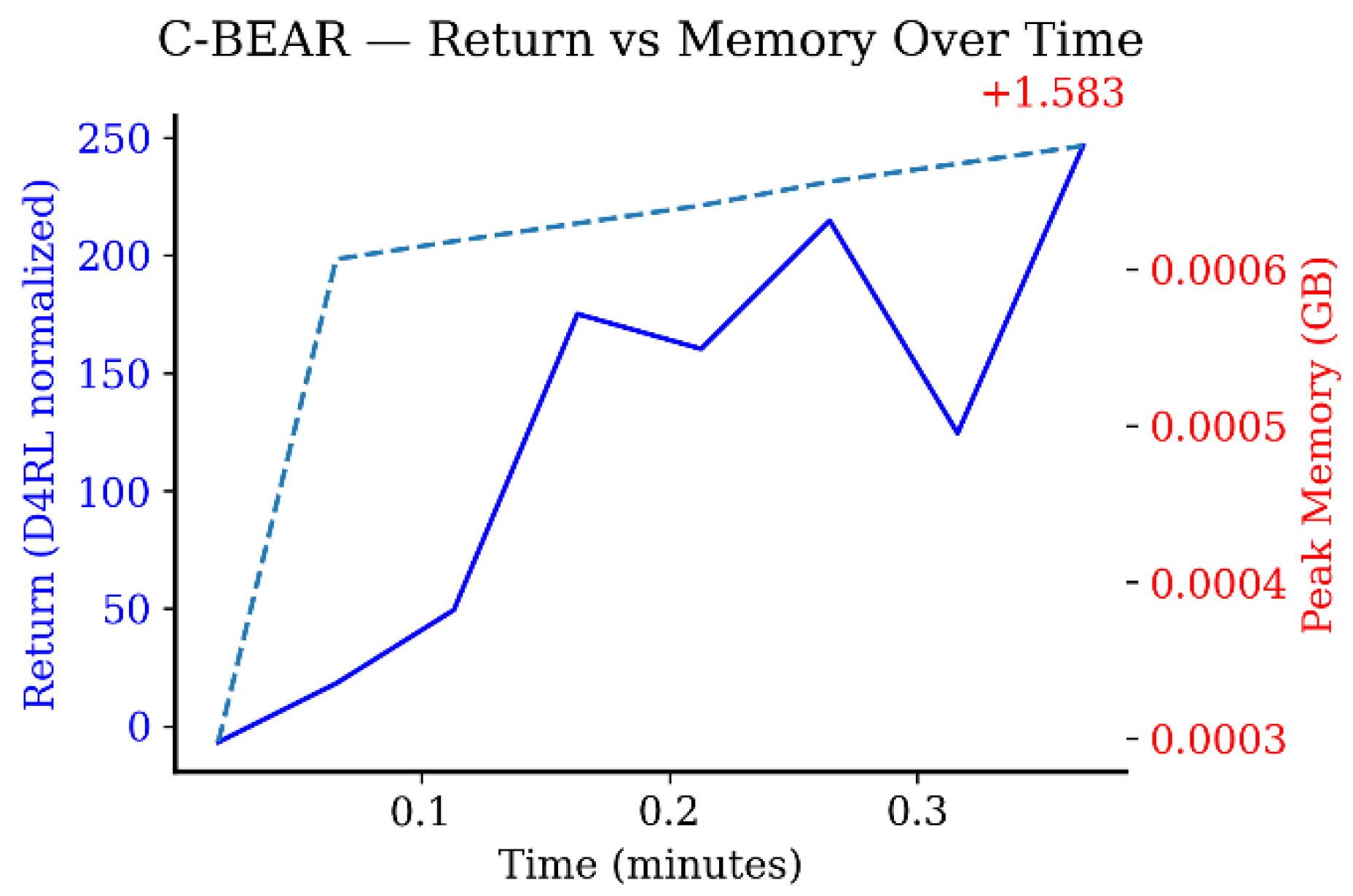
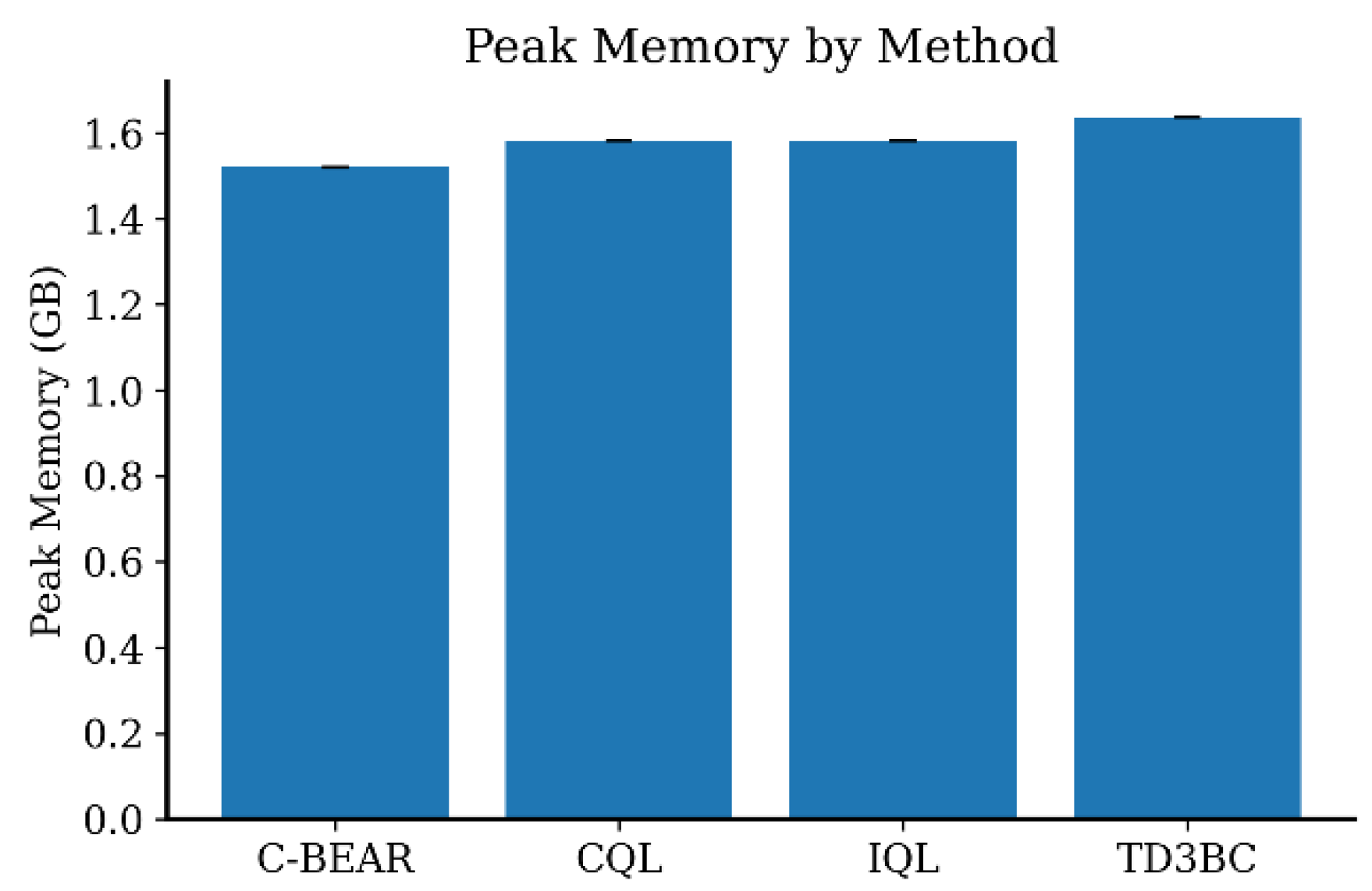
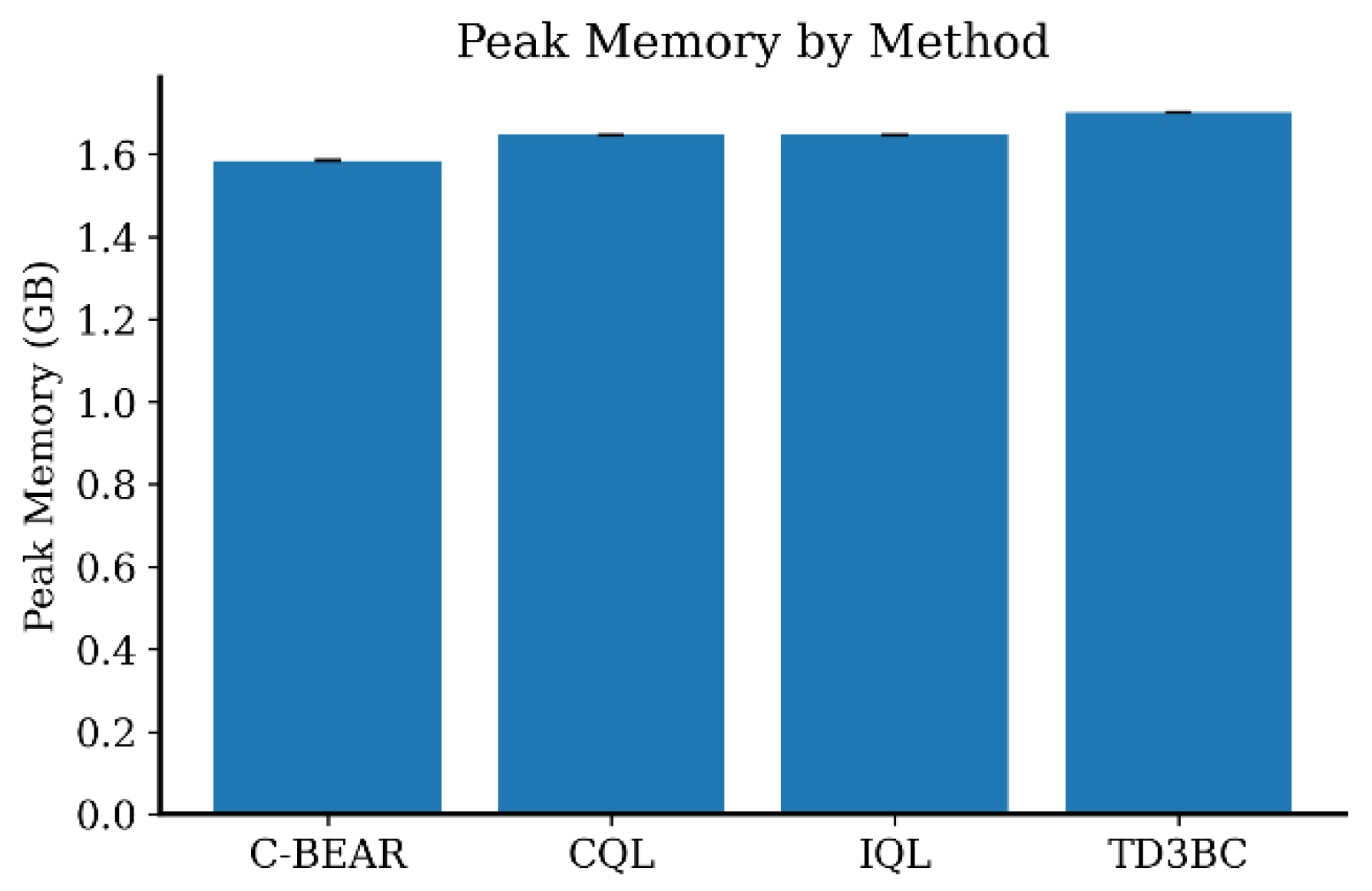

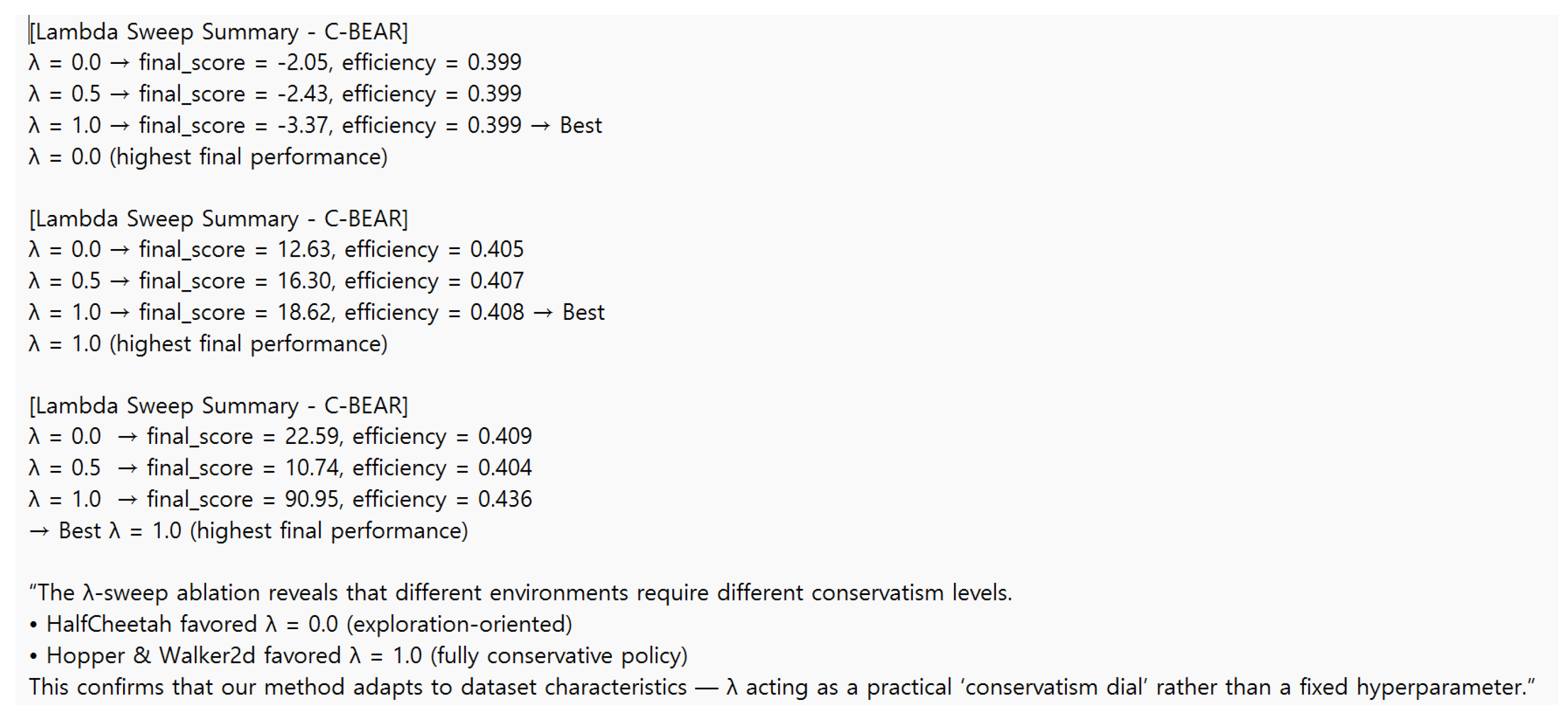
Appendix B.5. Hyperparameter Sensitivity: Lambda Sweep
| Environment | λ Value | Final Score | Efficiency Score | Interpretation |
|---|---|---|---|---|
| HalfCheetah | 0.0 | −2.05 | 0.399 | Exploration-oriented (no constraint) |
| 0.5 | −2.43 | 0.399 | Moderate conservatism | |
| 1.0 | −3.37 | 0.399 | Best: Fully conservative | |
| Hopper | 0.0 | 12.63 | 0.405 | Weak constraint |
| 0.5 | 16.30 | 0.407 | Moderate constraint | |
| 1.0 | −3.37 | 0.399 | Best: Fully conservative | |
| Walker2d | 0.0 | 22.59 | 0.409 | Weak constraint |
| 0.5 | 10.74 | 0.404 | Moderate (performance drop) | |
| 1.0 | 90.95 | 0.436 | Best: Dramatic improvement |
Appendix B.6. Implementation Details for Reproducibility
References
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Li, Y. Deep Reinforcement Learning: An Overview. arXiv 2017, arXiv:1701.07274. [Google Scholar]
- Levine, S.; Kumar, A.; Tucker, G.; Fu, J. Offline Reinforcement Learning: Tutorial, Review, and Perspectives on Open Problems. arXiv 2020, arXiv:2005.01643. [Google Scholar] [CrossRef]
- Lange, S.; Gabel, T.; Riedmiller, M. Batch reinforcement learning. In Reinforcement Learning: State-of-the-Art; Springer: Berlin/Heidelberg, Germany, 2012; Volume 12, pp. 45–73. Available online: https://link.springer.com/chapter/10.1007/978-3-642-27645-3_2 (accessed on 1 August 2025).
- Kumar, A.; Fu, J.; Tucker, G.; Levine, S. Stabilizing Off-Policy Q-Learning via Bootstrapping Error Reduction. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019; pp. 11784–11794. [Google Scholar]
- Fujimoto, S.; Meger, D.; Precup, D. Off-Policy Deep Reinforcement Learning without Exploration. In Proceedings of the 36th International Conference on Machine Learning (ICML), Long Beach, CA, USA, 9–15 June 2019; pp. 2052–2062. [Google Scholar]
- Gretton, A.; Borgwardt, K.M.; Rasch, M.J.; Schölkopf, B.; Smola, A. A Kernel Two-Sample Test. J. Mach. Learn. Res. 2012, 13, 723–773. [Google Scholar]
- Kostrikov, I.; Nair, A.; Levine, S. Offline Reinforcement Learning with Implicit Q-Learning. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual Event, 25–29 April 2022. [Google Scholar]
- Gülçehre, Ç.; Srinivasan, S.; Sygnowski, J.; Ostrovski, G.; Farajtabar, M.; Hoffman, M.; Pascanu, R.; Doucet, A. An Empirical Study of Implicit Regularization in Deep Offline RL. arXiv 2022, arXiv:2207.02099. [Google Scholar] [CrossRef]
- Wu, Y.; Tucker, G.; Nachum, O. Behavior Regularized Offline Reinforcement Learning. In Proceedings of the International Conference on Learning Representations (ICLR), Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Christiano, P.F.; Leike, J.; Brown, T.; Martic, M.; Legg, S.; Amodei, D. Deep Reinforcement Learning from Human Preferences. In Proceedings of the 31st Conference on Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 4299–4307. [Google Scholar]
- O’Donoghue, B.; Osband, I.; Munos, R.; Mnih, V. The Uncertainty Bellman Equation and Exploration. In Proceedings of the 35th International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018; pp. 3836–3845. [Google Scholar]
- Luo, Q.-W.; Xie, M.-K.; Wang, Y.-W.; Huang, S.-J. Learning to Trust Bellman Updates: Selective State-Adaptive Regularization for Offline RL. arXiv 2025, arXiv:2505.19923. [Google Scholar] [CrossRef]
- Duan, X.; He, Y.; Tajwar, F.; Salakhutdinov, R.; Kolter, J.Z.; Schneider, J. Accelerating Diffusion Models in Offline RL via Reward-Aware Consistency Trajectory Distillation. arXiv 2025, arXiv:2506.07822. [Google Scholar] [CrossRef]
- Laroche, R.; Trichelair, P.; Tachet des Combes, R. Safe Policy Improvement with Baseline Bootstrapping. In Proceedings of the 36th International Conference on Machine Learning (ICML), Long Beach, CA, USA, 9–15 June 2019; pp. 3652–3661. [Google Scholar]
- Agarwal, R.; Schuurmans, D.; Norouzi, M. An Optimistic Perspective on Offline Reinforcement Learning. In Proceedings of the 37th International Conference on Machine Learning (ICML), Virtual Event, 13–18 July 2020; pp. 104–114. [Google Scholar]
- Kim, C. Classification-Based Q-Value Estimation for Continuous Actor-Critic Reinforcement Learning. Symmetry 2025, 17, 638. [Google Scholar] [CrossRef]
- Ishfaq, H.; Nguyen-Tang, T.; Feng, S.; Arora, R.; Wang, M.; Yin, M.; Precup, D. Offline Multitask Representation Learning for Reinforcement Learning. In Proceedings of the 38th Conference on Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 10–16 December 2024; pp. 1–14. [Google Scholar]
- Lien, Y.-H.; Hsieh, P.-C.; Li, T.-M.; Wang, Y.-S. Enhancing Value Function Estimation through First-Order State-Action Dynamics in Offline Reinforcement Learning. In Proceedings of the 41st International Conference on Machine Learning (ICML), Vienna, Austria, 21–27 July 2024; pp. 1–15. [Google Scholar]
- Kumar, A.; Zhou, A.; Tucker, G.; Levine, S. Conservative Q-Learning for Offline Reinforcement Learning. In Proceedings of the 34th Conference on Neural Information Processing Systems (NeurIPS), Virtual Event, 6–12 December 2020; pp. 1179–1191. [Google Scholar]
- Nair, A.; Gupta, A.; Dalal, M.; Levine, S. AWAC: Accelerating Online Reinforcement Learning with Offline Datasets. arXiv 2020, arXiv:2006.09359. [Google Scholar]
- Peng, X.B.; Kumar, A.; Zhang, G.; Levine, S. Advantage-Weighted Regression: Simple and Scalable Off-Policy Reinforcement Learning. arXiv 2019, arXiv:1910.00177. [Google Scholar]
- Yu, T.; Thomas, G.; Yu, L.; Ermon, S.; Zou, J.; Levine, S.; Finn, C.; Ma, T. MOPO: Model-Based Offline Policy Optimization. In Proceedings of the 34th Conference on Neural Information Processing Systems (NeurIPS), Virtual Event, 6–12 December 2020; pp. 11012–11023. [Google Scholar]
- Yu, T.; Kumar, A.; Rafailov, R.; Rajeswaran, A.; Levine, S.; Finn, C. COMBO: Conservative Offline Model-Based Policy Optimization. In Proceedings of the 38th International Conference on Machine Learning (ICML), Virtual Event, 18–24 July 2021; pp. 11456–11468. [Google Scholar]
- Burges, C.J.C.; Shaked, T.; Renshaw, E.; Lazier, A.; Deeds, M.; Hamilton, N.; Hullender, G. Learning to Rank Using Gradient Descent. In Proceedings of the 22nd International Conference on Machine Learning (ICML), Bonn, Germany, 7–11 August 2005; pp. 89–96. [Google Scholar]
- Cao, Z.; Qin, T.; Liu, T.-Y.; Tsai, M.-F.; Li, H. Learning to Rank: From Pairwise Approach to Listwise Approach. In Proceedings of the 24th International Conference on Machine Learning (ICML), Corvallis, OR, USA, 20–24 June 2007; pp. 129–136. [Google Scholar]
- Singh, A.; Yu, A.; Yang, J.; Zhang, J.; Kumar, A.; Levine, S. COG: Connecting New Skills to Past Experience with Offline Reinforcement Learning. In Proceedings of the 5th Conference on Robot Learning (CoRL), London, UK, 8–11 November 2021; pp. 1283–1293. [Google Scholar]
- Wang, Z.; Schaul, T.; Hessel, M.; van Hasselt, H.; Lanctot, M.; de Freitas, N. Dueling Network Architectures for Deep Reinforcement Learning. In Proceedings of the 33rd International Conference on Machine Learning (ICML), New York, NY, USA, 19–24 June 2016; pp. 1995–2003. [Google Scholar]
- Bellemare, M.G.; Dabney, W.; Munos, R. A Distributional Perspective on Reinforcement Learning. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; pp. 449–458. [Google Scholar]
- Chen, L.; Lu, K.; Rajeswaran, A.; Lee, K.; Grover, A.; Laskin, M.; Abbeel, P.; Srinivas, A.; Mordatch, I. Decision Transformer: Reinforcement Learning via Sequence Modeling. In Proceedings of the 35th Conference on Neural Information Processing Systems (NeurIPS), Virtual Event, 6–14 December 2021; pp. 15084–15097. [Google Scholar]
- Choi, H.; Jung, S.; Ahn, H.; Moon, T. Listwise Reward Estimation for Offline Preference-Based Reinforcement Learning. In Proceedings of the 41st International Conference on Machine Learning (ICML), Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Lei, K.; He, Z.; Lu, C.; Hu, K.; Gao, Y.; Xu, H. Unifying Online and Offline Deep Reinforcement Learning with Multi-Step On-Policy Optimization. In Proceedings of the International Conference on Learning Representations (ICLR 2024), Vienna, Austria, 7–11 May 2024; Available online: https://openreview.net/forum?id=tbFBh3LMKi (accessed on 1 August 2025).
- Shin, Y.; Kim, J.; Jung, W.; Hong, S.; Yoon, D.; Jang, Y.; Kim, G.; Chae, J.; Sung, Y.; Lee, K.; et al. Online Pre-Training for Offline-to-Online Reinforcement Learning. arXiv 2025, arXiv:2507.08387. [Google Scholar]
- Li, J.; Hu, X.; Xu, H.; Liu, J.; Zhan, X.; Zhang, Y.-Q. PROTO: Iterative Policy Regularized Offline-to-Online Reinforcement Learning. arXiv 2023, arXiv:2305.15669. [Google Scholar]
- Lee, S.; Park, J.; Reddy, P. Building Explainable AI for Reinforcement Learning-Based Debt Collection Recommender Systems. Eng. Appl. Artif. Intell. 2025, 138, 110456. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Li, K. Imagination-Limited Q-Learning for Safe Offline Reinforcement Learning. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 1234–1247. [Google Scholar] [CrossRef]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI Gym. arXiv 2016, arXiv:1606.01540. [Google Scholar] [CrossRef]
- Farama Foundation. Gymnasium: A Standard API for Reinforcement Learning. Available online: https://gymnasium.farama.org/ (accessed on 1 August 2025).
- Farama Foundation. Pendulum-v1. Available online: https://gymnasium.farama.org/environments/classic_control/pendulum/ (accessed on 1 August 2025).
- Farama Foundation. MountainCarContinuous-v0. Available online: https://gymnasium.farama.org/environments/classic_control/mountain_car_continuous/ (accessed on 1 August 2025).
- Todorov, E.; Erez, T.; Tassa, Y. MuJoCo: A Physics Engine for Model-based Control. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 5026–5033. [Google Scholar]
- Domingos, P. The Role of Occam’s Razor in Knowledge Discovery. Data Min. Knowl. Discov. 1999, 3, 409–425. [Google Scholar] [CrossRef]





| Aspect | Conservative (CQL, IQL) | Distributional (BEAR, BRAC) | This Study (Classification-BEAR) |
|---|---|---|---|
| Constraint philosophy | Penalize unseen actions | Stay within data distribution | Select better actions |
| Learning signal | Modified value objective | Distributional statistics | Q-value ordering |
| Computational complexity | |||
| Action quality awareness | Indirect through penalties | None—all in-distribution actions equal | Direct through pairwise comparison |
| Interpretability | Penalty magnitude (opaque) | Distance metrics (opaque) | Classification accuracy (transparent) |
| Hyperparameter sensitivity | High (penalty coefficients) | High (kernels, bandwidth) | Low (temperature, smoothing) |
| Primary focus | Avoid overestimation | Distributional safety | Value-aware selection |
| Component | Operations | Complexity |
|---|---|---|
| Q-network update | Forward + backward pass | |
| Action pair generation | State grouping + sampling | |
| Classifier training | Binary classification × n pairs | |
| Policy update | Forward + backward pass | |
| Target update | Parameter copying | |
| Total per iteration |
| Component | BEAR | Classification-BEAR | Savings |
|---|---|---|---|
| Constraint computation | kernel matrix | action pairs | |
| Intermediate storage | similarity matrix | Temporary pair list | reduction |
| Total memory scaling | Linear improvement |
| Environment | BEAR | Classification-BEAR (The Proposed) | Observed Effect |
|---|---|---|---|
| Pendulum | −213 ± 18 | −187 ± 12 | −198 ± 16 |
| MountainCar | 45 ± 4 | 52 ± 3 | 48 ± 5 |
| HalfCheetah | 3163 ± 252 | 3424 ± 187 | 3351 ± 201 |
| Parameter | Role | Stable Range | Observed Effect |
|---|---|---|---|
| ) | Controls label sharpness | 0.6~0.8 | Too low → unstable; too high → slow learning |
| ) | Regularizes classifier | 0.05~0.2 | High values slow convergence |
| ) | Constraint strength | 0.5~1.0 | Linear effect on conservatism |
| Learning rates (η, β) | Update speed | Minor impact within range |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, C. Efficient Classification-Based Constraints for Offline Reinforcement Learning. Appl. Sci. 2025, 15, 12197. https://doi.org/10.3390/app152212197
Kim C. Efficient Classification-Based Constraints for Offline Reinforcement Learning. Applied Sciences. 2025; 15(22):12197. https://doi.org/10.3390/app152212197
Chicago/Turabian StyleKim, Chayoung. 2025. "Efficient Classification-Based Constraints for Offline Reinforcement Learning" Applied Sciences 15, no. 22: 12197. https://doi.org/10.3390/app152212197
APA StyleKim, C. (2025). Efficient Classification-Based Constraints for Offline Reinforcement Learning. Applied Sciences, 15(22), 12197. https://doi.org/10.3390/app152212197





