A Review of Theoretical, Experimental and Numerical Advances on Strain Localization in Geotechnical Materials
Abstract
1. Introduction
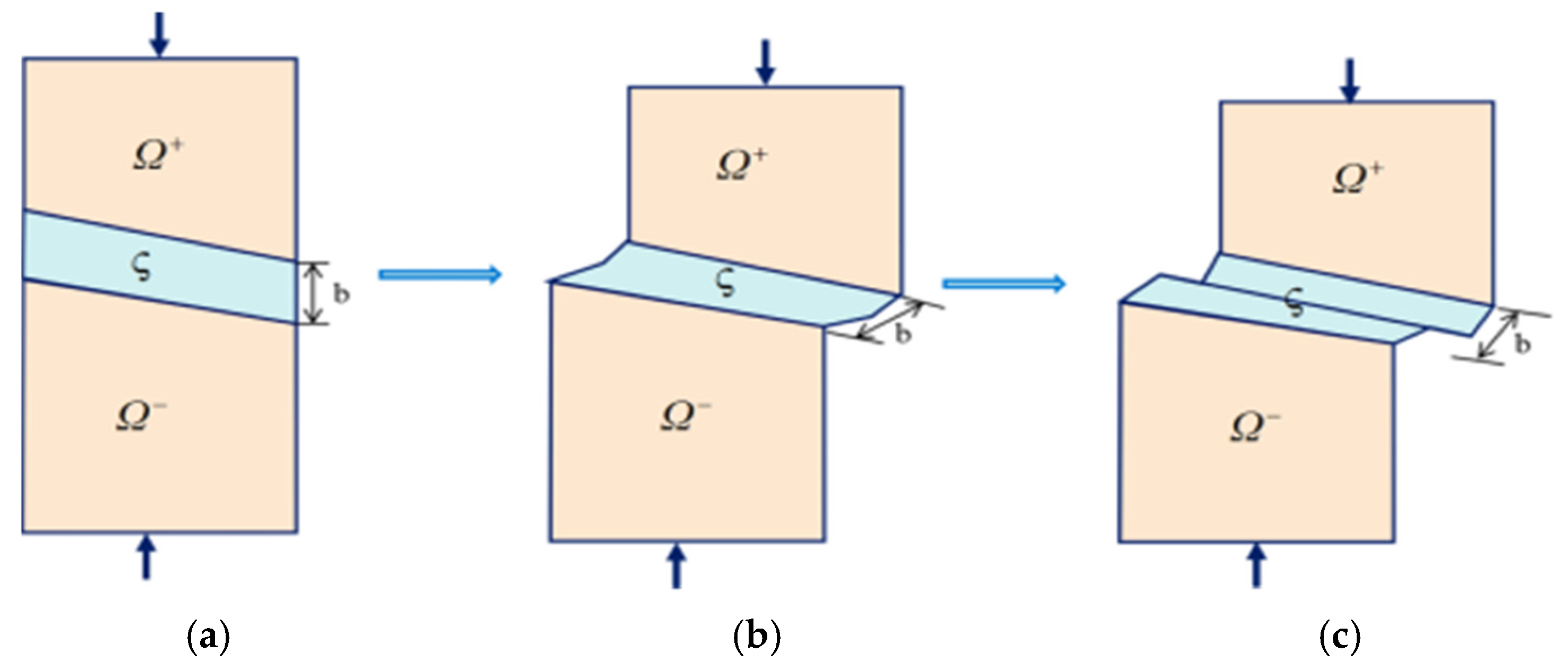
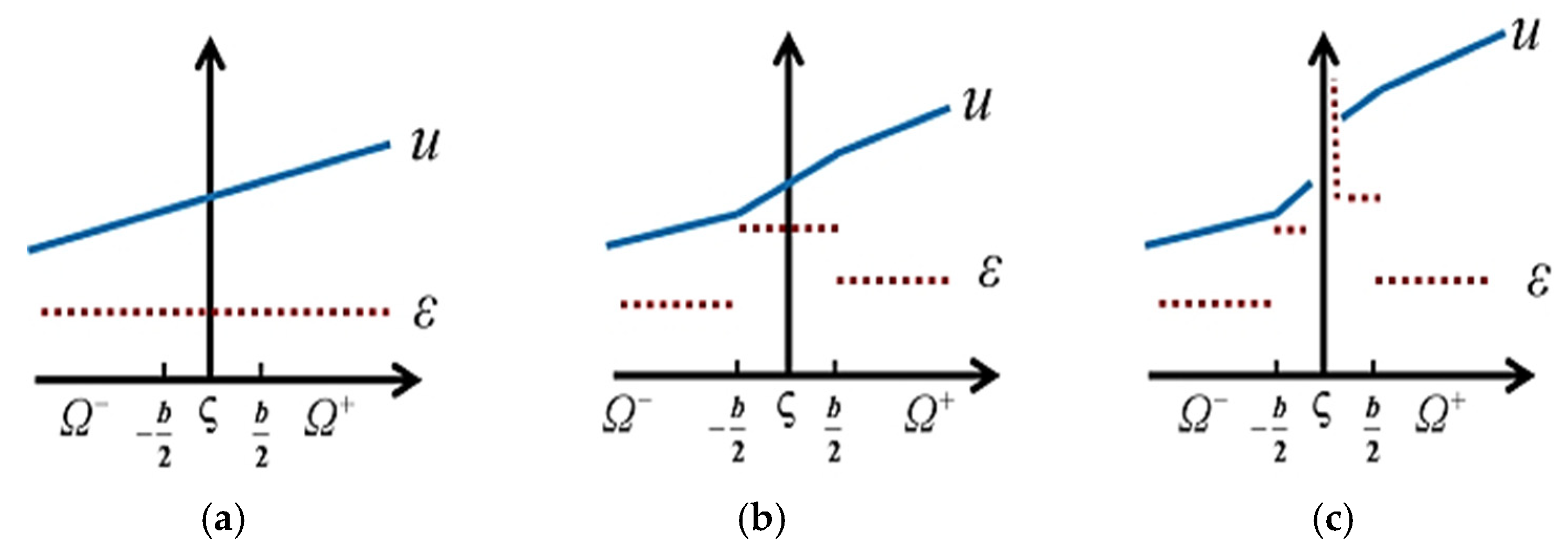
- (a)
- Continuum stage (where displacement and strain fields are continuous): During the initial loading or deformation stage, when external forces are applied to geotechnical materials, strain within the material gradually develops as the external forces increase. However, the relative displacement between different parts of the material remains small, and deformation continues to exhibit continuous characteristics. This stage typically manifests as linear elastic or nonlinear elastoplastic behavior.
- (b)
- Weak discontinuity stage (where the displacement field is continuous, but the strain field is discontinuous): As external forces increase or loading continues, localized failure or strain concentration becomes evident in the mechanical response of the geotechnical material. This is usually caused by the deterioration of the material’s internal microstructure or displacement instability. During this stage, strain begins to exhibit discontinuities, such as the formation and development of shear bands. Such strain discontinuities can lead to stress redistribution and a reduction in local load-bearing capacity.
- (c)
- Strong discontinuity stage (where both displacement and strain fields are discontinuous): When external forces or strains continue to increase, shear bands and slip surfaces within the geotechnical material further propagate, ultimately leading to discontinuous displacement across the entire material. This stage is typically characterized by the formation of distinct failure zones or faults, accompanied by significant displacements and unstable behavior. The discontinuous displacement stage is commonly observed in geohazards (such as landslides and collapses) or during the failure processes of engineering structures.
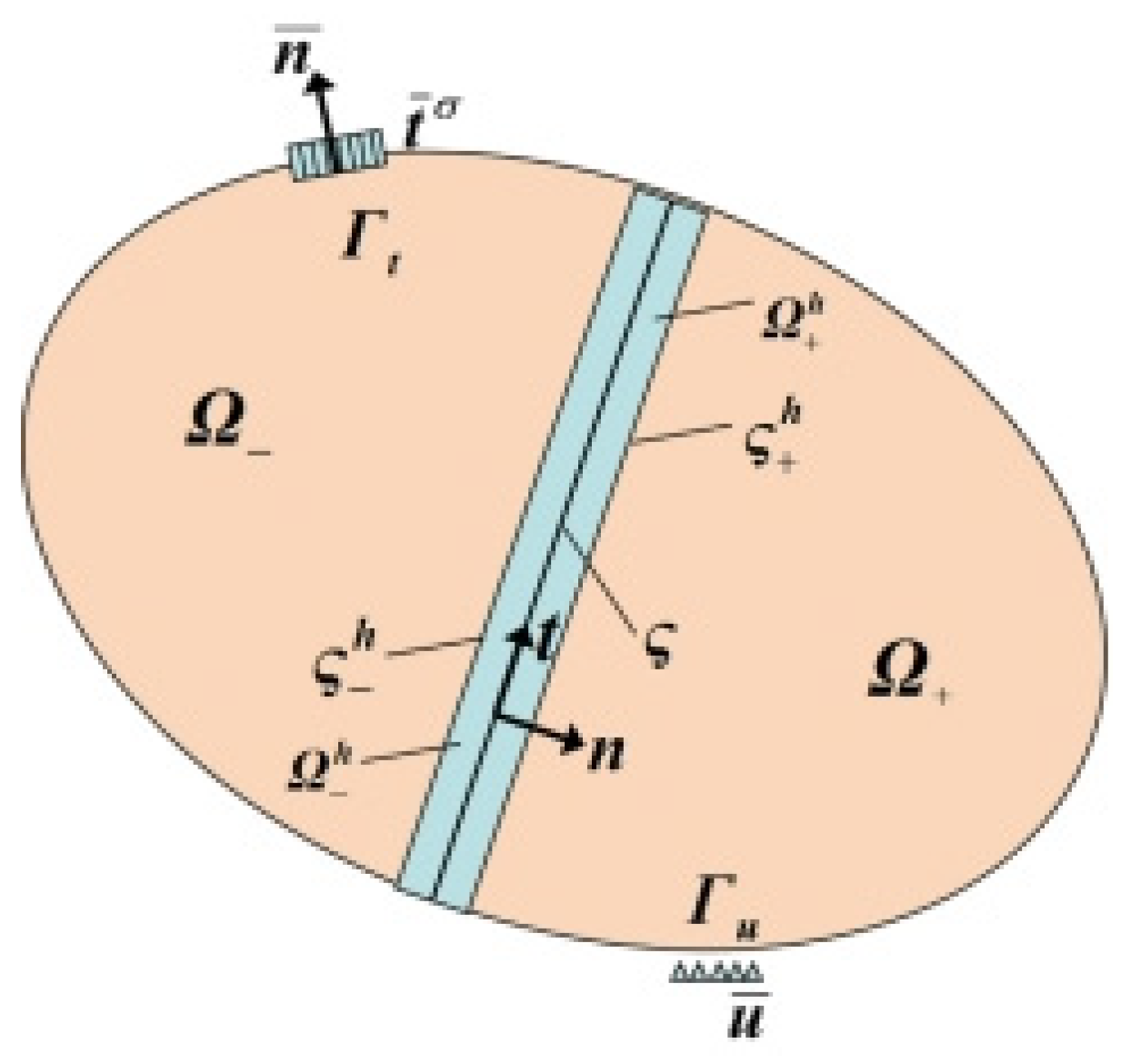
2. Theoretical Modeling
2.1. Classical Geotechnical Mechanics Modeling
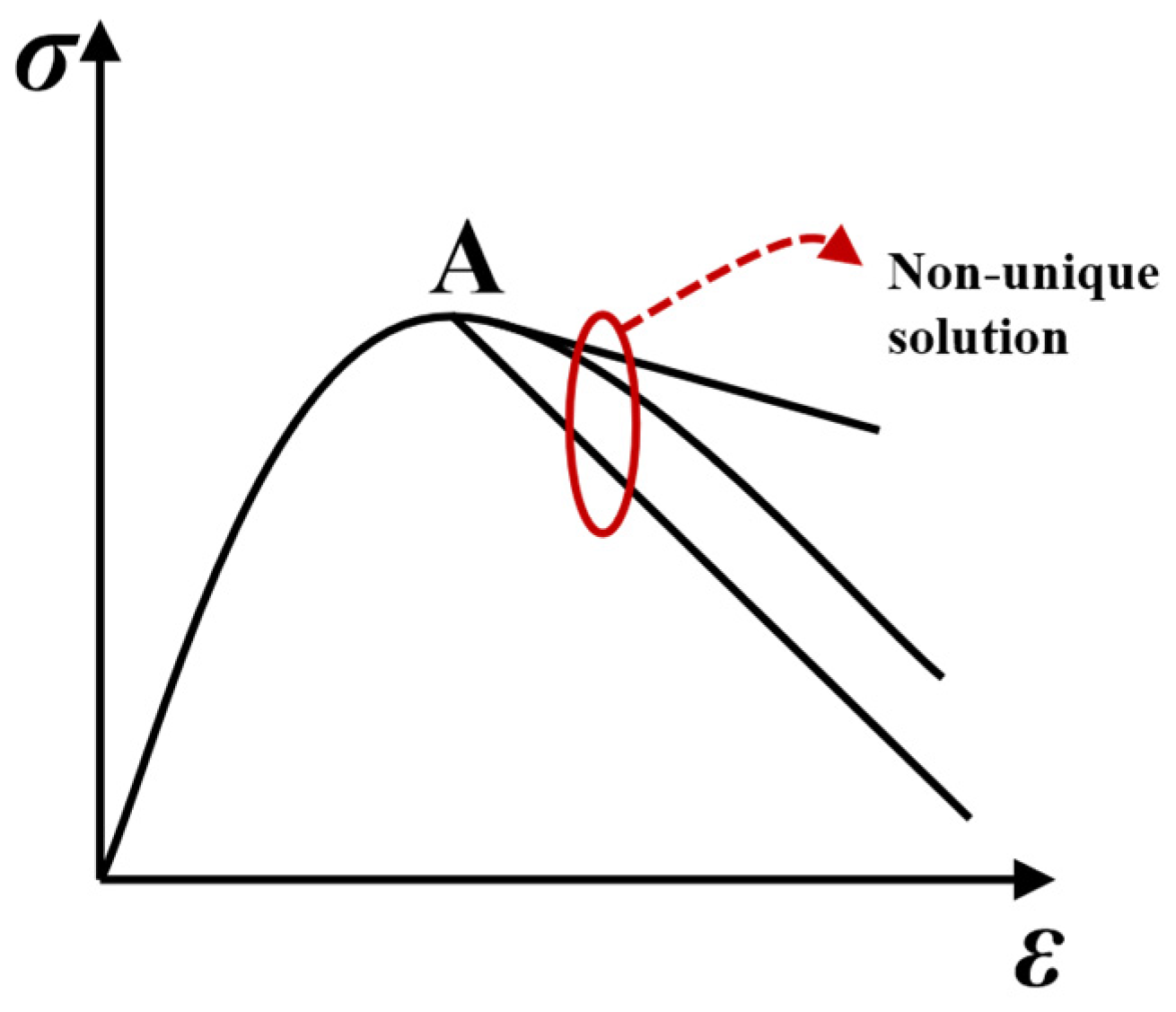
2.2. Bifurcation Theory Modeling
3. Experimental Observations
4. Numerical Simulation
4.1. Classical Finite Element Method Numerical Simulation
4.2. Weak Discontinuity Method Numerical Simulation
4.3. Strong Discontinuity Method Numerical Simulation
4.4. Discrete Lattice Models for Strain Localization
4.5. Innovative Research on Weak–Strong Discontinuous Coupling Numerical Methods
4.6. Spectral Analysis of the Regularization Effect of Numerical Methods
5. Conclusions and Discussions
5.1. Conclusions
- (1)
- Numerical simulation has become an indispensable tool for studying strain localization. While the classical Finite Element Method (FEM) is powerful, it suffers from pathological mesh dependency when modeling strain softening due to the lack of an internal length scale. To address this, various regularization techniques have been developed.
- (2)
- Weak discontinuity methods, such as the Cosserat continuum theory, introduce an internal length scale (e.g., via rotational degrees of freedom and couple stresses), enabling the simulation of shear bands with finite thickness and obtaining mesh-independent results for materials exhibiting weak discontinuities.
- (3)
- Strong discontinuity methods, like the Strong Discontinuity Approach (SDA) and the (Extended Finite Element Method (XFEM), embed displacement jumps within elements. They are highly effective for modeling strong discontinuities (e.g., cracks) but typically assume zero-thickness localization zones, making them less suitable for materials where the finite thickness of shear bands plays a crucial role.
- (4)
- Innovative coupled methods, particularly the Cos-SDA model, represent a significant breakthrough. By integrating Cosserat continuum theory for the continuous phase and SDA for the discontinuity line, this approach successfully bridges the gap between weak and strong discontinuity modeling. It allows for the simulation of the entire progressive failure process—from diffuse strain localization (weak discontinuity) to the formation of distinct slip surfaces (strong discontinuity)—in semi-brittle geomaterials like soft rocks and cohesive–frictional soils.
5.2. Discussions and Future Perspectives
- (1)
- From 2D to 3D Modeling: Many advanced numerical models, including the promising Cos-SDA framework, have been primarily developed and validated under 2D plane strain conditions. Extending these models to fully three-dimensional scenarios is crucial for tackling real-world geotechnical problems, such as the stability of tunnels, slopes, and foundations under complex loading conditions.
- (2)
- Model Validation and Parameter Determination: While numerical models are becoming increasingly sophisticated, determining their internal parameters (e.g., the internal length scale in Cosserat models) from standard laboratory tests remains challenging. There is a need for more comprehensive experimental data, particularly from true triaxial and hollow cylinder tests, to calibrate and validate these complex constitutive models under a wider range of stress paths.
- (3)
- Multi-Field Coupling: Although not covered in this review, it is important to note that multi-field coupling (e.g., hydro-mechanical, thermo-hydro-mechanical) has been successfully incorporated into strain localization models for porous media. Future work could further integrate such coupled processes into the advanced mechanical localization frameworks discussed herein, particularly for applications involving unsaturated soils, energy geostructures, or nuclear waste disposal.
- (4)
- Cyclic and Dynamic Loading: This review has primarily focused on monotonic loading conditions. However, many engineering applications involve cyclic (e.g., earthquake, wave) or dynamic loads. Investigating the evolution of strain localization under such loading conditions is an important and complex area for future research.
- (5)
- Transition to Large-Scale Engineering Applications: A key challenge lies in scaling up these advanced, often computationally intensive, models for analyzing large-scale geotechnical structures. Developing efficient computational strategies and simplified engineering models that retain the essential physics of localization will be vital for practical application.
- (6)
- Integration of Data-Driven Methods: The rise of artificial intelligence and machine learning offers new possibilities. These techniques could be used for model calibration, uncertainty quantification, and even developing surrogate models to accelerate simulations involving strain localization.
- (7)
- Advancement in Experimental and Multi-Scale Computational Techniques: Emerging technologies are revolutionizing the study of strain localization. The integration of X-ray computed tomography (X-ray CT) with Digital Image Correlation (DIC) provides unprecedented, four-dimensional insights into the evolution of internal microstructures and strain fields within geotechnical specimens during deformation. Concurrently, multi-scale coupling techniques, such as DEM-FEM coupling, bridge the gap between particle-scale mechanics and continuum-scale responses, offering a more fundamental understanding of localization initiation and propagation. Furthermore, Machine Learning (ML) and other data-driven approaches are opening new frontiers for constitutive model discovery, uncertainty quantification, and the development of efficient surrogate models, potentially bypassing traditional limitations of phenomenological modeling.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kuhl, E.; Ramm, E.; Willam, K. Failure Analysis of Elasto-Plastic Material Models on Different Levels of Observation. Int. J. Solids Struct. 2000, 37, 7259–7280. [Google Scholar] [CrossRef]
- Mosler, J. Numerical Analyses of Discontinuous Material Bifurcation: Strong and Weak Discontinuities. Comput. Methods Appl. Mech. Eng. 2005, 194, 979–1000. [Google Scholar] [CrossRef]
- Oliver, J.; Cervera, M.; Manzoli, O. Strong Discontinuities and Continuum Plasticity Models: The Strong Discontinuity Approach. Int. J. Plast. 1999, 15, 319–351. [Google Scholar] [CrossRef]
- Arthur, J.R.F.; Dunstan, T.; Al-Ani, Q.A.J.L.; Assadi, A. Plastic Deformation and Failure in Granular Media. Geotechnique 1978, 28, 125–128. [Google Scholar] [CrossRef]
- Bardet, J.P. A Comprehensive Review of Strain Localization in Elastoplastic Soils. Comput. Geotech. 1990, 10, 163–188. [Google Scholar] [CrossRef]
- Euler, L. Methodus Inveniendi Lineas Curvas Maximi Minimive Proprietate Gaudentes, Sive Solutio Problematis Isoperimetrici Latissimo Sensu Accepti, Additamentum {II}; Marcum-Michaelem Bousquet: Lausanne, Switzerland, 1744. [Google Scholar]
- Poincaré, H. Sur l’équilibre d’une Masse Fluide Animée d’un Mouvement de Rotation. Acta Math. 1885, 7, 259–380. [Google Scholar] [CrossRef]
- Hadamard, J. Lecons Sur La Propagation Des Ondes et Les Equations de 1’hydrodynamicque; A. Hermann: Paris, France, 1903. [Google Scholar]
- Hill, R. A General Theory of Uniqueness and Stability in Elastic-Plastic Solids. J. Mech. Phys. Solids 1958, 6, 236–249. [Google Scholar] [CrossRef]
- Tracy, Y.T. Plastic Flow and Fracture in Solids; Elsevier: Amsterdam, The Netherlands, 1961. [Google Scholar]
- Hill, R. Acceleration Waves in Solids. J. Mech. Phys. Solids 1962, 10, 1–16. [Google Scholar] [CrossRef]
- Mandel, J. Conditions de Stabilité et Postulat de Drucker; Springer: Berlin/Heidelberg, Germany, 1966. [Google Scholar]
- Rice, J.R. The Localization of Plastic Deformation. In Proceedings of the 14th International Congress of Theoratical Applied Mechanics, Delf, The Netherlands, 30 August–4 September 1976; pp. 207–220. [Google Scholar]
- Rudnicki, J.W.; Rice, J.R. Conditions for the Localization of Deformation in Pressure-Sensitive Dilatant Materials. J. Mech. Phys. Solids 1975, 23, 371–394. [Google Scholar] [CrossRef]
- Runesson, K.; Saabye Ottosen, N.; Dunja, P. Discontinuous Bifurcations of Elastic-Plastic Solutions at Plane Stress and Plane Strain. Int. J. Plast. 1991, 7, 99–121. [Google Scholar] [CrossRef]
- Ottosen, N.S.; Runesson, K. Properties of Discontinuous Bifurcation Solutions in Elasto-Plasticity. Int. J. Solids Struct. 1991, 27, 401–421. [Google Scholar] [CrossRef]
- Mechanics, E. Bifurcations in Elastic-Plastic. Int. J. Solids Struct. 1993, 30, 521–544. [Google Scholar]
- De Borst, R.; Sluys, L.J.; Mühlhaus, H.B.; Pamin, J. Fundamental Issues in Finite Element Analyses of Localization of Deformation. Eng. Comput. 1993, 10, 99–121. [Google Scholar] [CrossRef]
- Tomita, Y. Simulations of Plastic Instabilities in Solid Mechanics. Appl. Mech. Rev. 1994, 47, 171–205. [Google Scholar] [CrossRef]
- Drucker, D.C. On Uniqueness in the Theory of Plasticity. Q. Appl. Math. 1956, 14, 35–42. [Google Scholar] [CrossRef]
- Valanis, K.C. Banding and Stability in Plastic Materials. Acta Mech. 1989, 79, 113–141. [Google Scholar] [CrossRef]
- Morgenstern, N.R.; Tchalenko, J. S Microscopic Structures in Kaolin Subjected to Direct Shear. Géotechnique 1967, 17, 309–328. [Google Scholar] [CrossRef]
- Roscoe, K.H. The Influence of Strains in Soil Mechanics. Geotechnique 1970, 20, 129–170. [Google Scholar] [CrossRef]
- Scarpelli, G.; Wood, D.M. Experimental Observation of Shear Band Pattern in Direct Shear Tests. In Proceedings of the IUTAM: Conference on Deformation and Failure of Granular Materials, Delft, The Netherlands, 31 August–3 September 1982. [Google Scholar]
- Bishop, A.W.; Henkel, D.J. The Measurement of Soil Properties in the Triaxial Test; E. Arnold: London, UK, 1957. [Google Scholar]
- Arthur, J.R.F.; Dunstan, T. Rupture Layers in Granular Media. Deform. Fail. Granul. Mater. IUTAM Symp. Delft 1982.
- Lade, P.V.; Tsai, J. Effects of Localization in Triaxial Tests on Clay. In Proceedings of the 11th International Conference on Soil Mechanics and Foundation Engineering, San Francisco, CA, USA, 12–16 August 1985. [Google Scholar]
- Vardoulakis, I. Bifurcation Analysis of the Triaxial Test on Sand Samples. Acta Mech. 1979, 32, 35–54. [Google Scholar] [CrossRef]
- Hettler, A.; Vardoulakis, I. Behaviour of Dry Sand Tested in a Large Triaxial Apparatus. Geotechnique 1984, 34, 183–197. [Google Scholar] [CrossRef]
- Desrues, J.; Chambon, R.; Mokni, M.; Mazerolle, F. Void Ratio Evolution inside Shear Bands in Triaxial Sand Specimens Studied by Computed Tomography. Geotechnique 1996, 46, 529–546. [Google Scholar] [CrossRef]
- Alshibli, K.A.; Batiste, S.N.; Sture, S. Strain Localization in Sand: Plane Strain versus Triaxial Compression. J. Geotech. Geoenvironmental Eng. 2003, 129, 483–494. [Google Scholar] [CrossRef]
- Meng, L.; Li, T.; Jiang, L.; Ma, H. Experimental Study on the Influence of Temperature on Shale Mechanical Properties under Conventional Triaxial Compression. Adv. Mater. Res. 2011, 250–253, 1452–1455. [Google Scholar] [CrossRef]
- Vardoulakis, I. Shear Band Inclination and Shear Modulus of Sand in Biaxial Tests. Int. J. Numer. Anal. Methods Geomech. 1980, 4, 103–119. [Google Scholar] [CrossRef]
- Vardoulakis, I.; Graf, B. Calibration of Constitutive Models for Granular Materials Using Data from Biaxial Experiments. Geotechnique 1985, 35, 299–317. [Google Scholar] [CrossRef]
- Vermeer, P.A. The Orientation of Shear Bands in Biaxial Tests. Geotechnique 1990, 40, 223–236. [Google Scholar] [CrossRef]
- Han, C.; Vardoulakis, I.G. Plane-Strain Compression Experiments on Water-Saturated Fine-Grained Sand. Geotechnique 1991, 41, 49–78. [Google Scholar] [CrossRef]
- Han, C.; Drescher, A. Shear Bands in Biaxial Tests on Dry Coarse Sand. Soils Found. 1993, 33, 118–132. [Google Scholar] [CrossRef]
- Labuz, J.F.; Dai, S.T.; Papamichos, E. Plane-Strain Compression of Rock-like Materials. Int. J. Rock Mech. Min. Sci. Geomech. 1996, 33, 573–584. [Google Scholar] [CrossRef]
- Finno, R.J.; Harris, W.W.; Mooney, M.A.; Viggiani, G. Shear Bands in Plane Strain Compression of Loose Sand. Geotechnique 1997, 47, 149–165. [Google Scholar] [CrossRef]
- Alshibli, K.A.; Sture, S. Shear Band Formation in Plane Strain Experiments of Sand. J. Geotech. Geoenvironmental Eng. 2000, 126, 20000069798. [Google Scholar] [CrossRef]
- Chu, J.; Lo, S.C.R.; Lee, I.K. Strain Softening and Shear Band Formation of Sand in Multi-Axial Testing. Geotechnique 1996, 46, 63–82. [Google Scholar] [CrossRef]
- Wang, Q.; Lade, P.V. Shear Banding in True Triaxial Tests and Its Effect on Failure in Sand. J. Eng. Mech. 2001, 127, 754–761. [Google Scholar] [CrossRef]
- Rodriguez, N.M.; Lade, P.V. True Triaxial Tests on Cross-Anisotropic Deposits of Fine Nevada Sand. Int. J. Geomech. 2013, 13, 779–793. [Google Scholar] [CrossRef]
- Minaeian, V.; Dewhurst, D.N.; Rasouli, V. An Investigation on Failure Behaviour of a Porous Sandstone Using Single-Stage and Multi-Stage True Triaxial Stress Tests. Rock Mech. Rock Eng. 2020, 53, 3543–3562. [Google Scholar] [CrossRef]
- Dimitri, R.; Rinaldi, M.; Trullo, M.; Tornabene, F.; Fidelibus, C. FEM/XFEM Modeling of the 3D Fracturing Process in Transversely Isotropic Geomaterials. Compos. Struct. 2021, 276, 114502. [Google Scholar] [CrossRef]
- Trädegård, A.; Nilsson, F.; Östlund, S. FEM-Remeshing Technique Applied to Crack Growth Problems. Comput. Methods Appl. Mech. Eng. 1998, 160, 115–131. [Google Scholar] [CrossRef]
- Bordas, S.P.A.; Rabczuk, T.; Hung, N.X.; Nguyen, V.P.; Natarajan, S.; Bog, T.; Quan, D.M.; Hiep, N.V. Strain Smoothing in FEM and XFEM. Comput. Struct. 2010, 88, 1419–1443. [Google Scholar] [CrossRef]
- Anderssohn, R.; Hofmann, M.; Bahr, H.A. FEM-Bifurcation Analysis for 3D Crack Patterns. Eng. Fract. Mech. 2018, 202, 363–374. [Google Scholar] [CrossRef]
- Lambert, C.; Buzzi, O.; Giacomini, A. Influence of Calcium Leaching on the Mechanical Behavior of a Rock-Mortar Interface: A DEM Analysis. Comput. Geotech. 2010, 37, 258–266. [Google Scholar] [CrossRef]
- Wang, R.; Dafalias, Y.F.; Fu, P.; Zhang, J.M. Fabric Evolution and Dilatancy within Anisotropic Critical State Theory Guided and Validated by DEM. Int. J. Solids Struct. 2020, 188–189, 210–222. [Google Scholar] [CrossRef]
- Schöpfer, M.P.J.; Abe, S.; Childs, C.; Walsh, J.J. The Impact of Porosity and Crack Density on the Elasticity, Strength and Friction of Cohesive Granular Materials: Insights from DEM Modelling. Int. J. Rock Mech. Min. Sci. 2009, 46, 250–261. [Google Scholar] [CrossRef]
- Mendonça, T.S.; Peixoto, R.G.; Ribeiro, G.O. Crack Propagation Using the Continuum Strong Discontinuity Approach by the BEM: Some Numerical Remarks. J. Brazilian Soc. Mech. Sci. Eng. 2018, 40, 520. [Google Scholar] [CrossRef]
- Giannopoulos, G.I.; Anifantis, N.K. A BEM Analysis for Thermomechanical Closure of Interfacial Cracks Incorporating Friction and Thermal Resistance. Comput. Methods Appl. Mech. Eng. 2007, 196, 1018–1029. [Google Scholar] [CrossRef]
- Peixoto, R.G.; Ribeiro, G.O.; Pitangueira, R.L.S.; Penna, S.S. The Strong Discontinuity Approach as a Limit Case of Strain Localization in the Implicit BEM Formulation. Eng. Anal. Bound. Elem. 2017, 80, 127–141. [Google Scholar] [CrossRef]
- Panique Lazcano, D.R.; Galindo Aires, R.; Patiño Nieto, H. Bearing Capacity of Shallow Foundation under Cyclic Load on Cohesive Soil. Comput. Geotech. 2020, 123, 103556. [Google Scholar] [CrossRef]
- Zhang, J.; Li, L.; Sun, D. Similarity Solution for Undrained Cylindrical Cavity Contraction in Anisotropic Modified Cam-Clay Model Soils. Comput. Geotech. 2020, 120, 103405. [Google Scholar] [CrossRef]
- Yan, L.; Xu, W.; Wang, R.; Meng, Q. Numerical Simulation of the Anisotropic Properties of a Columnar Jointed Rock Mass under Triaxial Compression. Eng. Comput. 2018, 35, 1788–1804. [Google Scholar] [CrossRef]
- Menon, S.; Song, X. A Computational Periporomechanics Model for Localized Failure in Unsaturated Porous Media. Comput. Methods Appl. Mech. Eng. 2021, 384, 113932. [Google Scholar] [CrossRef]
- Tao, S.; Tang, X.; Rutqvist, J.; Hu, M.; Liu, Q. Simulating Three Dimensional Thermal Cracking with TOUGH-FEMM. Comput. Geotech. 2020, 124, 103654. [Google Scholar] [CrossRef]
- Li, S.; Liu, W.K. Meshfree and Particle Methods and Their Applications. Appl. Mech. Rev. 2002, 55, 1–34. [Google Scholar] [CrossRef]
- Lu, M.; Zhang, H.; Zheng, Y.; Zhang, L. A Multiscale Finite Element Method with Embedded Strong Discontinuity Model for the Simulation of Cohesive Cracks in Solids. Comput. Methods Appl. Mech. Eng. 2016, 311, 576–598. [Google Scholar] [CrossRef]
- Andrade, J.E.; Avila, C.F. Multiscale Modeling of Granular Matter: A Hierarchical Scheme. In Multiscale and Multiphysics Processes in Geomechanics, Borja, R.I., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 9783642196294. [Google Scholar]
- Chen, Q.; Andrade, J.E.; Samaniego, E. AES for Multiscale Localization Modeling in Granular Media. Comput. Methods Appl. Mech. Eng. 2011, 200, 2473–2482. [Google Scholar] [CrossRef]
- Sun, Y.; Roubin, E.; Shao, J.; Colliat, J.B. FE Modeling of Concrete with Strong Discontinuities for 3D Shear Fractures and Comparison with Experimental Results. Eng. Fract. Mech. 2021, 251, 107752. [Google Scholar] [CrossRef]
- Tang, H.; Dong, Y.; Wang, T.; Dong, Y. Simulation of strain localization with discrete element-Cosserat continuum finite element two scale method for granular materials. J. Mech. Phys. Solids 2019, 122, 450–471. [Google Scholar] [CrossRef]
- Arslan, H.; Sture, S. Finite Element Simulation of Localization in Granular Materials by Micropolar Continuum Approach. Comput. Geotech. 2008, 35, 548–562. [Google Scholar] [CrossRef]
- Radulovic, R. Numerical Modeling of Localized Material Failure by Means of Strong Discontinuities at Finite Strains. Ph.D. Thesis, Ruhr University Bochum, Bochum, Germany, 2010. [Google Scholar]
- Wei, W.; Tang, H.; Liu, Y.; Chen, H. Cosserat model incorporating anisotropy evolution and its application in numerical analysis of strain localization in clay. Acta Geotech. 2025, 20, 365–385. [Google Scholar] [CrossRef]
- Ebrahimian, B. Evolution of Shear Localization in an Elasto-Plastic Cosserat Material under Shearing. Key Eng. Mater. 2014, 577–578, 21–24. [Google Scholar] [CrossRef]
- de Borst, R. A Generalisation of J2-Flow Theory for Polar Continua. Comput. Methods Appl. Mech. Eng. 1993, 103, 347–362. [Google Scholar] [CrossRef]
- Iordache, M.M.; Willam, K. Localized Failure Analysis in Elastoplastic Cosserat Continua. Comput. Methods Appl. Mech. Eng. 1998, 151, 559–586. [Google Scholar] [CrossRef]
- De Borst, R. Simulation of Strain Localization: A Reappraisal of the Cosserat Continuum. Eng. Comput. 1991, 8, 317–332. [Google Scholar] [CrossRef]
- Chen, J.S.; Zhang, X.; Belytschko, T. An Implicit Gradient Model by a Reproducing Kernel Strain Regularization in Strain Localization Problems. Comput. Methods Appl. Mech. Eng. 2004, 193, 2827–2844. [Google Scholar] [CrossRef]
- Tvergaard, V.; Needleman, A. Effects of Nonlocal Damage in Porous Plastic Solids. Int. J. Solids Struct. 1995, 32, 1063–1077. [Google Scholar] [CrossRef]
- Lu, X.; Bardet, J.P.; Huang, M. Numerical Solutions of Strain Localization with Nonlocal Softening Plasticity. Comput. Methods Appl. Mech. Eng. 2009, 198, 3702–3711. [Google Scholar] [CrossRef]
- Mánica, M.A.; Gens, A.; Vaunat, J.; Ruiz, D.F. Nonlocal Plasticity Modelling of Strain Localisation in Stiff Clays. Comput. Geotech. 2018, 103, 138–150. [Google Scholar] [CrossRef]
- Eringen, A.C.; Edelen, D.G.B. On Nonlocal Elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Zervos, A.; Papanastasiou, P.; Vardoulakis, I. A Finite Element Displacement Formulation for Gradient Elastoplasticity. Int. J. Numer. Methods Eng. 2001, 50, 1369–1388. [Google Scholar] [CrossRef]
- Zervos, A.; Papanastasiou, P.; Vardoulakis, I. Shear Localisation in Thick-Walled Cylinders Under Internal Pressure Based on Gradient. J. Theor. Appl. Mech. 2008, 38, 81–100. [Google Scholar]
- De Borst, R.; Mühlhaus, H.-B. Gradient-dependent Plasticity: Formulation and Algorithmic Aspects. Int. J. Numer. Methods Eng. 1992, 35, 521–539. [Google Scholar] [CrossRef]
- Chiricotto, M.; Giacomelli, L.; Tomassetti, G. Dissipative Scale Effects in Strain-Gradient Plasticity: The Case of Simple Shear. SIAM J. Appl. Math. 2016, 76, 688–704. [Google Scholar] [CrossRef]
- Zervos, A.; Vardoulakis, I.; Papanastasiou, P. Influence of Nonassociativity on Localization and Failure in Geomechanics Based on Gradient Elastoplasticity. Int. J. Geomech. 2007, 7, 63–74. [Google Scholar] [CrossRef]
- Niazi, M.S.; Wisselink, H.H.; Meinders, T. Viscoplastic Regularization of Local Damage Models: A Latent Solution. Key Eng. Mater. 2012, 504–506, 845–850. [Google Scholar] [CrossRef]
- Simons, E.C.; Weerheijm, J.; Sluys, L.J. A Viscosity Regularized Plasticity Model for Ceramics. Eur. J. Mech. A/Solids 2018, 72, 310–328. [Google Scholar] [CrossRef]
- Cosserat, E.; Cosserat, F. Théorie Des Corps Déformables; Herman et Fils: Paris, France, 1909. [Google Scholar]
- Mindlin, R.D. Influence of Couple-Stresses on Stress Concentrations. Exp. Mech. 1963, 3, 1–7. [Google Scholar] [CrossRef]
- Sternberg, E.; Muki, R. The Effect of Couple-Stresses on the Stress Concentration around a Crack. Int. J. Solids Struct. 1967, 3, 69–95. [Google Scholar] [CrossRef]
- Mühlhaus, H.B.; Vardoulakis, I. The Thickness of Shear Bands in Granular Materials. Geotechnique 1987, 37, 271–283. [Google Scholar] [CrossRef]
- Papanastasiou, P.C.; Vardoulakis, I.G. Numerical Treatment of Progressive Localization in Relation to Borehole Stability. Int. J. Numer. Anal. Methods Geomech. 1992, 16, 389–424. [Google Scholar] [CrossRef]
- Oda, M.; Iwashita, K.; Kazama, H. Micro-Structure Developed in Shear Bands of Dense Granular Soils and Its Computer Simulation—Mechanism of Dilatancy and Failure. In IUTAM Symposium on Mechanics of Granular and Porous Materials; Solid Mechanics and its Applications; Fleck, N.A., Cocks, A.C.F., Eds.; Springer: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Papanastasiou, P.; Zervos, A. Wellbore Stability Analysis: From Linear Elasticity to Postbifurcation Modeling. Int. J. Geomech. 2004, 4, 2–12. [Google Scholar] [CrossRef]
- Khoei, A.R.; Karimi, K. An Enriched-FEM Model for Simulation of Localization Phenomenon in Cosserat Continuum Theory. Comput. Mater. Sci. 2008, 44, 733–749. [Google Scholar] [CrossRef]
- Li, X.; Tang, H. A Consistent Return Mapping Algorithm for Pressure-Dependent Elastoplastic Cosserat Continua and Modelling of Strain Localisation. Comput. Struct. 2005, 83, 1–10. [Google Scholar] [CrossRef]
- Zhang, H.W.; Wang, H.; Chen, B.S.; Xie, Z.Q. Analysis of Cosserat Materials with Voronoi Cell Finite Element Method and Parametric Variational Principle. Comput. Methods Appl. Mech. Eng. 2008, 197, 741–755. [Google Scholar] [CrossRef]
- Chen, K.; Zou, D.; Tang, H.; Liu, J.; Zhuo, Y. Scaled Boundary Polygon Formula for Cosserat Continuum and Its Verification. Eng. Anal. Bound. Elem. 2021, 126, 136–150. [Google Scholar] [CrossRef]
- Tang, H.; Guan, Y.; Zhang, X.; Zou, D. Low-Order Mixed Finite Element Analysis of Progressive Failure in Pressure-Dependent Materials within the Framework of the Cosserat Continuum. Eng. Comput. 2017, 34, 251–271. [Google Scholar] [CrossRef]
- Tang, H.; Zhu, F.; Yang, D.; Papazafeiropoulos, G. Numerical Simulation of Strain Localization Based on Cosserat Continuum Theory and Isogeometric Analysis. Comput. Geotech. 2021, 129, 103874. [Google Scholar] [CrossRef]
- Tang, H.; Wei, W.; Liu, F.; Chen, G. Elastoplastic Cosserat Continuum Model Considering Strength Anisotropy and Its Application to the Analysis of Slope Stability. Comput. Geotech. 2020, 117, 103235. [Google Scholar] [CrossRef]
- Tang, H.; Sun, F.; Zhang, Y.; Dong, Y. Elastoplastic Axisymmetric Cosserat Continua and Modelling of Strain Localization. Comput. Geotech. 2018, 101, 159–167. [Google Scholar] [CrossRef]
- Jirásek, M.; Zimmermann, T. Rotating Crack Model with Transition to Scalar Damage. J. Eng. Mech. 1998, 124, 277–284. [Google Scholar] [CrossRef]
- Jirásek, M.; Zimmermann, T. Analysis of Rotating Crack Model. J. Eng. Mech. 1998, 124, 842–851. [Google Scholar] [CrossRef]
- Tejchman, J.; Bauer, E. Numerical Simulation of Shear Band Formation with a Polar Hypoplastic Constitutive Model. Comput. Geotech. 1996, 19, 221–244. [Google Scholar] [CrossRef]
- Xie, D.; Waas, A.M. Discrete Cohesive Zone Model for Mixed-Mode Fracture Using Finite Element Analysis. Eng. Fract. Mech. 2006, 73, 1783–1796. [Google Scholar] [CrossRef]
- Aymerich, F.; Dore, F.; Priolo, P. Prediction of Impact-Induced Delamination in Cross-Ply Composite Laminates Using Cohesive Interface Elements. Compos. Sci. Technol. 2008, 68, 2383–2390. [Google Scholar] [CrossRef]
- Turon, A.; Dávila, C.G.; Camanho, P.P.; Costa, J. An Engineering Solution for Mesh Size Effects in the Simulation of Delamination Using Cohesive Zone Models. Eng. Fract. Mech. 2007, 74, 1665–1682. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Nguyen, C.T.; Bordas, S.; Heidarpour, A. Modelling Interfacial Cracking with Non-Matching Cohesive Interface Elements. Comput. Mech. 2016, 58, 731–746. [Google Scholar] [CrossRef]
- Kawashita, L.F.; Hallett, S.R. A Crack Tip Tracking Algorithm for Cohesive Interface Element Analysis of Fatigue Delamination Propagation in Composite Materials. Int. J. Solids Struct. 2012, 49, 2898–2913. [Google Scholar] [CrossRef]
- Paulino, G.H.; Celes, W.; Espinha, R.; Zhang, Z.J. A General Topology-Based Framework for Adaptive Insertion of Cohesive Elements in Finite Element Meshes. Eng. Comput. 2008, 24, 59–78. [Google Scholar] [CrossRef]
- Samimi, M.; Van Dommelen, J.A.W.; Geers, M.G.D. A Self-Adaptive Finite Element Approach for Simulation of Mixed-Mode Delamination Using Cohesive Zone Models. Eng. Fract. Mech. 2011, 78, 2202–2219. [Google Scholar] [CrossRef]
- Schrefler, B.A.; Secchi, S.; Simoni, L. On Adaptive Refinement Techniques in Multi-Field Problems Including Cohesive Fracture. Comput. Methods Appl. Mech. Eng. 2006, 195, 444–461. [Google Scholar] [CrossRef]
- Armero, F.; Garikipati, K. An Analysis of Strong Discontinuities in Multiplicative Finite Strain Plasticity and Their Relation with the Numerical Simulation of Strain Localization in Solids. Int. J. Solids Struct. 1996, 33, 2863–2885. [Google Scholar] [CrossRef]
- Oliver, J. Modelling Strong Discontinuities in Solid Mechanics via Strain Softening Constitutive Equations. Part 1: Fundamentals. Int. J. Numer. Methods Eng. 1996, 39, 3575–3600. [Google Scholar] [CrossRef]
- Fan, Z.; Zheng, H.; Nie, Z.; Wang, Y.; Han, C. Influence of Soil Non-Homogeneity on Shear Band Evolution Investigated by the Numerical Manifold Method Combined with the Assumed Enhanced Strain Method. Eng. Anal. Bound. Elem. 2021, 127, 1–7. [Google Scholar] [CrossRef]
- Borja, R.I. Finite Element Model for Strain Localization Analysis of Strongly Discontinuous Fields Based on Standard Galerkin Approximation. Comput. Methods Appl. Mech. Eng. 2000, 190, 1529–1549. [Google Scholar] [CrossRef]
- Simo, J.C.; Oliver, J.; Armero, F. An Analysis of Strong Discontinuities Induced by Strain-Softening in Rate-Independent Inelastic Solids. Comput. Mech. 1993, 12, 277–296. [Google Scholar] [CrossRef]
- Nagashima, T.; Wang, C. XFEM Analyses Using Two-Dimensional Quadrilateral Elements Enriched with Only the Heaviside Step Function. Int. J. Comput. Methods 2022, 19, 2150063. [Google Scholar] [CrossRef]
- Belytschko, T.; Moës, N.; Usui, S.; Parimi, C. Arbitrary Discontinuities in Finite Elements. Int. J. Numer. Methods Eng. 2001, 50, 993–1013. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic Crack Growth in Finite Elements with Minimal Remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Liu, Z.L.; Menouillard, T.; Belytschko, T. An XFEM/Spectral Element Method for Dynamic Crack Propagation. Int. J. Fract. 2011, 169, 183–198. [Google Scholar] [CrossRef]
- Oliver, J.; Huespe, A.E.; Sánchez, P.J. A Comparative Study on Finite Elements for Capturing Strong Discontinuities: E-FEM vs X-FEM. Comput. Methods Appl. Mech. Eng. 2006, 195, 4732–4752. [Google Scholar] [CrossRef]
- Dvorkin, E.N.; Cuitiño, A.M.; Gioia, G. Finite Elements with Displacement Interpolated Embedded Localization Lines Insensitive to Mesh Size and Distortions. Int. J. Numer. Methods Eng. 1990, 30, 541–564. [Google Scholar] [CrossRef]
- Klisinski, M.; Runesson, K.; Sture, S. Finite Element with Inner Softening Band. J. Eng. Mech. 1991, 117, 575–587. [Google Scholar] [CrossRef]
- Reza, H. Finite Element Analysis of Fracture of Concrete and Masonry Structures. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 1992. [Google Scholar]
- Oliver, J. Modelling Strong Discontinuities in Solid: Part 2. Int. J. Numer. Method Eng. 1996, 39, 3601–3623. [Google Scholar] [CrossRef]
- Regueiro, R.A.; Borja, R.I. Plane Strain Finite Element Analysis of Pressure Sensitive Plasticity with Strong Discontinuity. Int. J. Solids Struct. 2001, 38, 3647–3672. [Google Scholar] [CrossRef]
- Regueiro, R.A.; Borja, R.I. A Finite Element Model of Localized Deformation in Frictional Materials Taking a Strong Discontinuity Approach. Finite Elem. Anal. Des. 1999, 33, 283–315. [Google Scholar] [CrossRef]
- Oliver, J.; Huespe, A.E.; Pulido, M.D.G.; Chaves, E. From Continuum Mechanics to Fracture Mechanics: The Strong Discontinuity Approach. Eng. Fract. Mech. 2001, 69, 113–136. [Google Scholar] [CrossRef]
- Armero, F.; Ehrlich, D. Finite Element Methods for the Multi-Scale Modeling of Softening Hinge Lines in Plates at Failure. Comput. Methods Appl. Mech. Eng. 2006, 195, 1283–1324. [Google Scholar] [CrossRef]
- Ehrlich, D.; Armero, F. Finite Element Methods for the Analysis of Softening Plastic Hinges in Beams and Frames. Comput. Mech. 2005, 35, 237–264. [Google Scholar] [CrossRef]
- Alfaiate, J.; Moonen, P.; Sluys, L.J.; Carmeliet, J. On the Use of Strong Discontinuity Formulations for the Modeling of Preferential Moisture Uptake in Fractured Porous Media. Comput. Methods Appl. Mech. Eng. 2010, 199, 2828–2839. [Google Scholar] [CrossRef]
- Foster, C.D.; Borja, R.I.; Regueiro, R.A. Embedded Strong Discontinuity Finite Elements for Fractured Geomaterials with Variable Friction. Int. J. Numer. Meth. Eng. 2007, 72, 549–581. [Google Scholar] [CrossRef]
- Lu, M.; Zhang, H.; Zheng, Y.; Zhang, L. A Multiscale Finite Element Method for the Localization Analysis of Homogeneous and Heterogeneous Saturated Porous Media with Embedded Strong Discontinuity Model. Int. J. Numer. Methods Eng. 2017, 112, 1439–1472. [Google Scholar] [CrossRef]
- Benkemoun, N.; Gelet, R.; Roubin, E.; Colliat, J.B. Poroelastic Two-Phase Material Modeling: Theoretical Formulation and Embedded Finite Element Method Implementation. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 1255–1275. [Google Scholar] [CrossRef]
- Čarija, J.; Nikolić, M.; Ibrahimbegovic, A.; Nikolić, Ž. Discrete Softening-Damage Model for Fracture Process Representation with Embedded Strong Discontinuities. Eng. Fract. Mech. 2020, 236, 107211. [Google Scholar] [CrossRef]
- Fagerström, M.; Larsson, R. Theory and Numerics for Finite Deformation Fracture Modelling Using Strong Discontinuities. Int. J. Numer. Methods Eng. 2006, 66, 911–948. [Google Scholar] [CrossRef]
- Alfaiate, J.; Simone, A.; Sluys, L.J. Non-Homogeneous Displacement Jumps in Strong Embedded Discontinuities. Int. J. Solids Struct. 2003, 40, 5799–5817. [Google Scholar] [CrossRef]
- Motamedi, M.H.; Weed, D.A.; Foster, C.D. Numerical Simulation of Mixed Mode (I and II) Fracture Behavior of Pre-Cracked Rock Using the Strong Discontinuity Approach. Int. J. Solids Struct. 2016, 85–86, 44–56. [Google Scholar] [CrossRef]
- Hadzalic, E.; Ibrahimbegovic, A.; Dolarevic, S. Failure Mechanisms in Coupled Soil-Foundation Systems. Coupled Syst. Mech. 2018, 7, 27–42. [Google Scholar] [CrossRef]
- Nikolic, M.; Ibrahimbegovic, A. Rock Mechanics Model Capable of Representing Initial Heterogeneities and Full Set of 3D Failure Mechanisms. Comput. Methods Appl. Mech. Eng. 2015, 290, 209–227. [Google Scholar] [CrossRef]
- Tang, H.; Li, Y.; Hu, Z.; Song, X. Numerical Simulation of Strain Localization through an Integrated Cosserat Continuum Theory and Strong Discontinuity Approach. Comput. Geotech. 2022, 151, 104951. [Google Scholar] [CrossRef]
- Li, Y.; Tang, H.; Song, X.; Hu, Z. Regularization Analysis of the Strong Discontinuity-Cosserat Finite Element Method for Modeling Strain Localization in Cohesive-Frictional Materials by Spectral Theory. Comput. Geotech. 2023, 162, 105640. [Google Scholar] [CrossRef]
- Li, Y.; Tang, H.; Zhu, F.; Hu, Z. An Anisotropic Elastoplastic Strong Discontinuity Model for Shear Failure in Anisotropic Rock Masses. Comput. Geotech. 2024, 176, 106762. [Google Scholar] [CrossRef]
- Borja, R.I.; Regueiro, R.A. Strain Localization in Frictional Materials Exhibiting Displacement Jumps. Comput. Methods Appl. Mech. Eng. 2001, 190, 2555–2580. [Google Scholar] [CrossRef]
- Di Luzio, G. Spectral Localization Analysis in Nonlocal Softening Materials. In Proceedings of the 9th International Conference on Fracture Mechanics of Concrete and Concrete Structures (FraMCoS-9), Berkeley, CA, USA, 29 May–1 June 2016. [Google Scholar] [CrossRef]
- Bardet, J.P. Finite Element Analysis of Rockburst as Surface Instability. Comput. Geotech. 1989, 8, 177–193. [Google Scholar] [CrossRef]
- Bardet, J.P. Finite Element Analysis of Plane Strain Bifurcation within Compressible Solids. Comput. Struct. 1990, 36, 993–1007. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures; Stenquist, W., Ed.; Prentice Hall: New Jersey, NJ, USA, 1996; ISBN 0133014584. [Google Scholar]
- Van der Veen, H.; Vuik, C.; De Borst, R. Eigenvalue Analysis of Nonassociated Plasticity. Comput. Math. Appl. 1999, 38, 107–115. [Google Scholar] [CrossRef]
- Di Luzio, G.; Bažant, Z.P. Spectral Analysis of Localization in Nonlocal and Over-Nonlocal Materials with Softening Plasticity or Damage. Int. J. Solids Struct. 2005, 42, 6071–6100. [Google Scholar] [CrossRef]
- Lu, X.; Bardet, J.P.; Huang, M. Spectral Analysis of Nonlocal Regularization in Two-Dimensional Finite Element Models. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 219–235. [Google Scholar] [CrossRef]



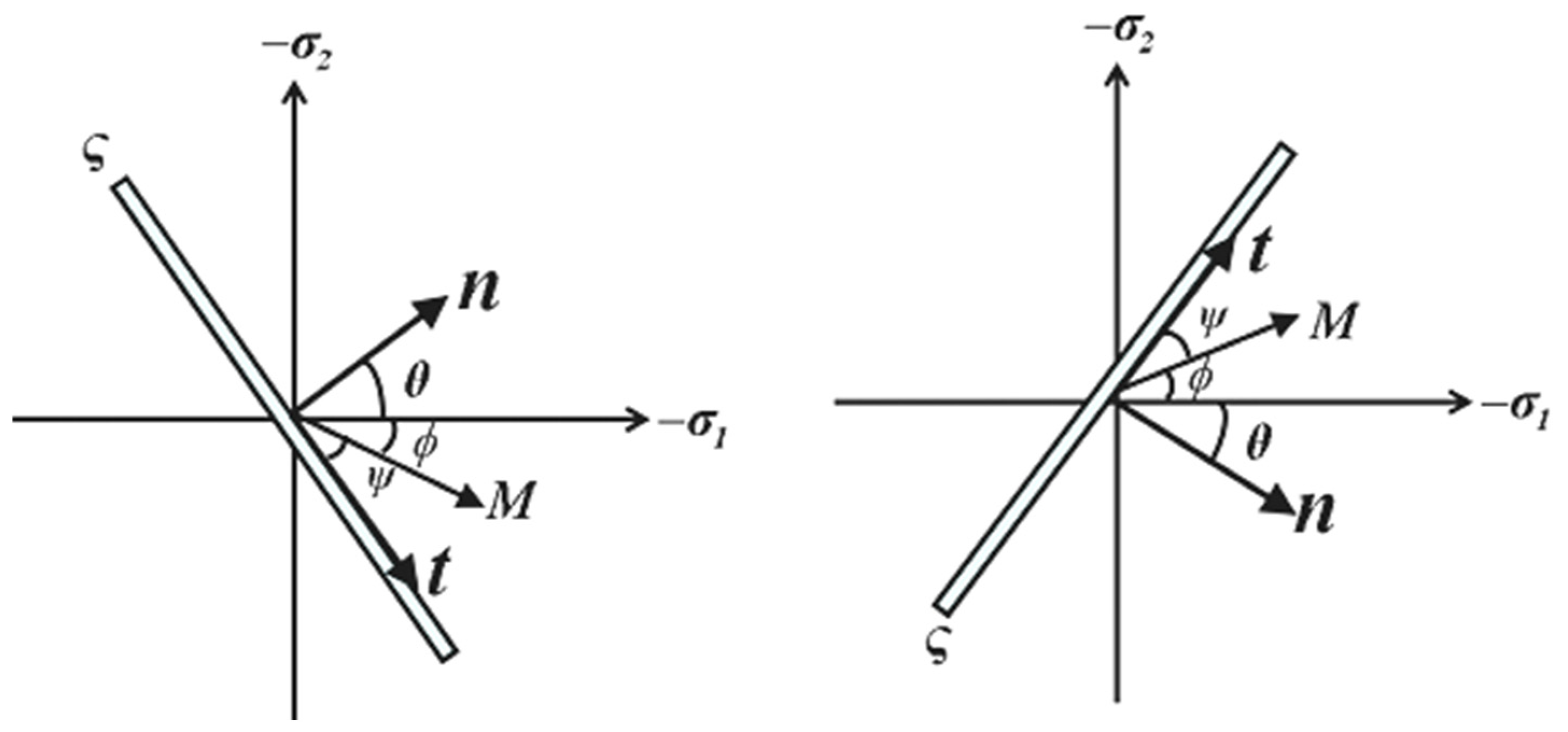

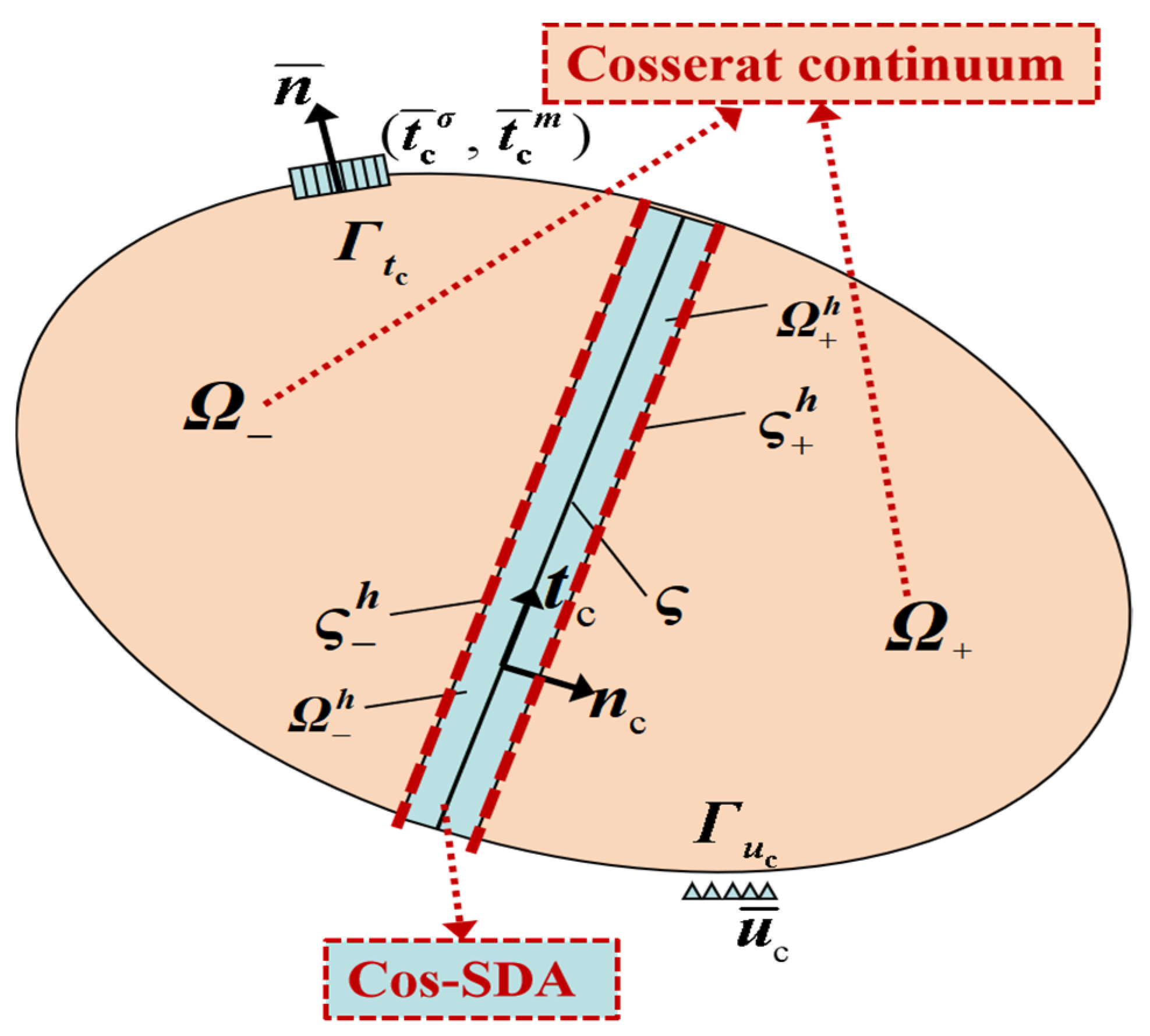

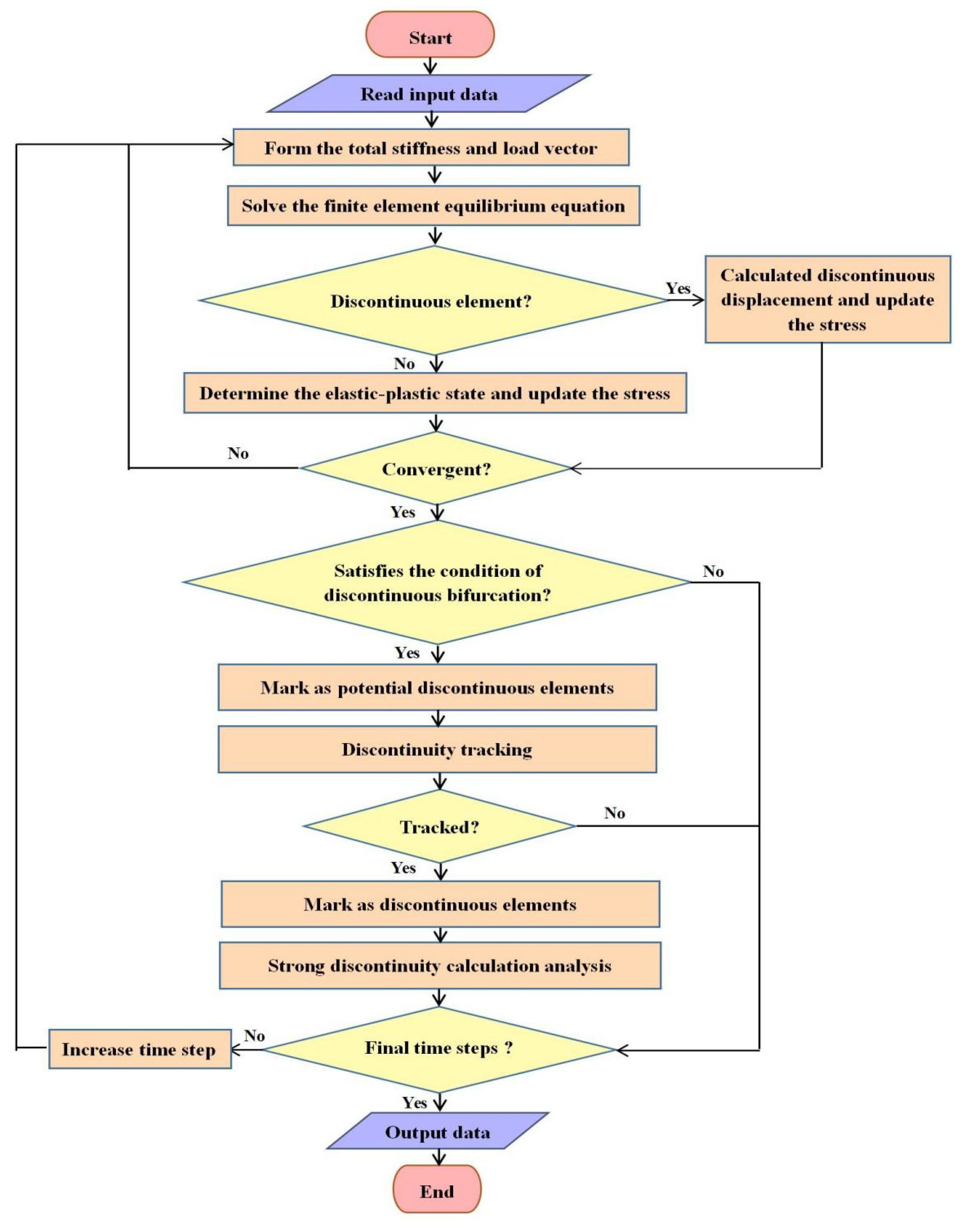
| Test Method | Measurement Techniques | Typical Shear Band Thickness | Typical Shear Band Inclination | Remarks |
|---|---|---|---|---|
| Direct Shear Test | Microscopy, X-ray | 10 × average grain size | Fixed to 0° by apparatus (Not a material property) | Simple operation; stress rotation; confined shear plane |
| Plane Strain Test | X-ray, Stereophotogrammetry, Digital Image Correlation | 10–30 × grain size | Close to Arthur’s solution | Easy to observe localization; widely used for 2D analysis |
| Conventional Triaxial Test | CT, Digital Imaging, Acoustic Emission | Correlated with particle size; Slope: Minimal impact from average effective stress level and particle shape | Varies with density and confinement | Axisymmetric stress; difficult to observe localization process |
| True Triaxial Test | Digital Imaging, Strain Gauges | Depends on intermediate stress ratio | Aligns with Arthur’s solution for certain sands | Complex setup; captures full 3D stress effects |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Sun, A.; Zhu, F. A Review of Theoretical, Experimental and Numerical Advances on Strain Localization in Geotechnical Materials. Appl. Sci. 2025, 15, 12154. https://doi.org/10.3390/app152212154
Li Y, Sun A, Zhu F. A Review of Theoretical, Experimental and Numerical Advances on Strain Localization in Geotechnical Materials. Applied Sciences. 2025; 15(22):12154. https://doi.org/10.3390/app152212154
Chicago/Turabian StyleLi, Yonghui, Anyuan Sun, and Feng Zhu. 2025. "A Review of Theoretical, Experimental and Numerical Advances on Strain Localization in Geotechnical Materials" Applied Sciences 15, no. 22: 12154. https://doi.org/10.3390/app152212154
APA StyleLi, Y., Sun, A., & Zhu, F. (2025). A Review of Theoretical, Experimental and Numerical Advances on Strain Localization in Geotechnical Materials. Applied Sciences, 15(22), 12154. https://doi.org/10.3390/app152212154





