Interpretable Ensemble Learning Models for Credit Card Fraud Detection

Abstract

With the growing advantages and conveniences provided by digital transactions, the financial sectors also face a loss of billions of dollars each year. While the use of credit cards has made life easier and convenient, it has also become a significant threat. Detecting fraudulent transactions in financial sectors, such as banking, is a major issue because existing fraud detection methods are rule-based and unable to detect unknown patterns. The tactics and techniques used by fraudsters are far more advanced than they are, making machine learning (ML) a valuable approach to improve detection efficiency. While numerous studies have explored machine learning models for credit card fraud detection, most have prioritized accuracy metrics alone, offering little attention to how or why models make decisions. This lack of interpretability creates barriers for financial institutions, where regulatory compliance and user trust are critical. In particular, the systematic application of explainable AI (XAI) techniques such as SHAP and LIME to fraud detection remains scarce. This study addresses this gap by combining high-performing ensemble models (Random Forest and XGBoost) with advanced interpretability methods (SHAP and LIME), providing both strong predictive performance and transparent feature-level explanations. Such integration not only improves fraud detection but also strengthens the trustworthiness and deployability of AI systems in real-world financial contexts. A real-world credit card dataset is used to evaluate both models, and experimental results show that Random Forest achieved higher precision (89.09%) and F1 score (0.9159), while XGBoost yielded better recall (95.56%) and ROC AUC (0.9997). To address the crucial need for interpretability, SHAP and LIME analyses were applied, revealing the most influential features behind model predictions and enhancing transparency in decision-making. Overall, this study demonstrates the potential of integrating explainable artificial intelligence (XAI) into fraud detection systems, thereby enhancing trust and reliability in financial institutions.

1. Introduction

In today’s digital economy, online payments have become integral to everyday life, offering convenience and efficiency in activities such as bill payments, shopping, and money transfers. However, these advances have also introduced critical challenges, particularly credit card fraud, financial loss, and privacy risks. Fraudsters often exploit stolen card information in online transactions, where the absence of a physical card makes detection more difficult. Traditional fraud detection methods are largely rule-based and limited to identifying known fraud patterns. As fraudulent techniques continue to evolve, there is a pressing need for machine learning approaches capable of detecting previously unseen and sophisticated fraud strategies. Without effective solutions, users’ trust in digital payment systems may be severely undermined. Machine learning can play a vital role in this because it allows the ability to learn and understand complex, unknown patterns, which are crucial for detecting fraudulent activities. A wide range of ML techniques, including logistic regression, support vector machines, Random Forest, and gradient boosting methods, have been applied to credit card fraud detection with notable success in improving predictive accuracy and among them, ensemble methods such as Random Forest (RF) and Extreme Gradient Boosting (XGBoost) [1] are particularly effective for handling numerical features and complex data distributions [2]. Although prior studies [3] have compared the predictive performance of RF and XGBoost and acknowledged the importance of interpretability, most have focused primarily on classification outcomes, with limited exploration of explainability. The interpretability of these models using XAI techniques remains underexplored, with existing research largely centered on XGBoost alone. The lack of interpretability, as highlighted by [4], remains a major gap to the practical deployment of ML models in financial systems, as it is often unclear why a given transaction is classified as legitimate or fraudulent. In high-stakes domains such as banking, interpretability and explainability are not optional features but regulatory and ethical requirements. Financial institutions must be able to justify automated decisions to stakeholders, auditors, and end users. The ability to explain model predictions not only enhances trust but also facilitates troubleshooting and supports informed decision-making. Explainable AI (XAI) techniques such as SHAP and LIME provide valuable insights into feature contributions at both the global and individual level, enabling domain experts to validate outcomes and detect potential biases. Incorporating interpretability into fraud detection models, therefore, strengthens technical performance while improving transparency, accountability, and usability in financial institutions.

This paper addresses this gap by implementing and comparing Random Forest and XGBoost on a real-world credit card fraud dataset, evaluated using standard metrics such as accuracy, precision, recall, and interpretability. Unlike prior studies that have primarily focused on predictive performance or examined interpretability in isolation, this study provides a systematic comparison of both models by integrating two leading XAI techniques, SHAP and LIME. The analysis not only identifies which features drive fraudulent classifications but also contrasts how each model communicates its decisions to end users. This dual evaluation of performance and interpretability offers novel insights into the trade-offs between accuracy, recall, and explainability. The findings provide practical guidance for selecting models based on deployment requirements and contribute to the design of fraud detection systems that are both reliable and transparent.

The remainder of this paper is organized as follows: Section 2 reviews the Related Work on fraud detection and explainable machine learning. Section 3 describes the Materials and Methods, including the implementation details of the proposed techniques with SHAP and LIME. Section 4 presents the Results. Section 5 provides a Comparative Analysis of the proposed models. Section 6 presents the conclusion, summarizing the key findings of the study and laying out future research directions for scholars.

2. Related Work

2.1. Traditional Methods for Credit Card Fraud Detection

Credit card fraud is a growing challenge in financial transactions, particularly in the context of online payment systems, as it has become a mode of payment. Online transaction fraud is hard to detect, as the card is not physically available. Many traditional fraud detection systems are available, such as rule-based, statistical methods, and blacklist whitelist. These methods heavily rely on known patterns, making them not suitable for such types of fraud because the techniques used for fraud are now more advanced than these methods. Researchers [5] have developed fraud detection systems using both traditional statistical methods and machine learning techniques. However, traditional approaches are often limited in adapting to evolving fraud patterns, leading to financial losses and reputational risks for institutions. Consequently, recent work has shifted toward machine learning (ML) models, which can learn from historical transaction data and adapt to emerging fraudulent behaviors.

Another study [6] concludes that traditional rule-based systems are increasingly ineffective in detecting modern fraud attacks because these can be reversed and often generate high false positives and false negatives, which directly causes missing real threats. The rule-based systems are too rigid and unsuitable to tackle modern fraud [7] as they are not adaptable. These works emphasize the necessity of ML-based techniques that leverage data-driven learning to detect both known and novel fraud behaviors.

2.2. Machine Learning Approaches for Credit Card Fraud Detection

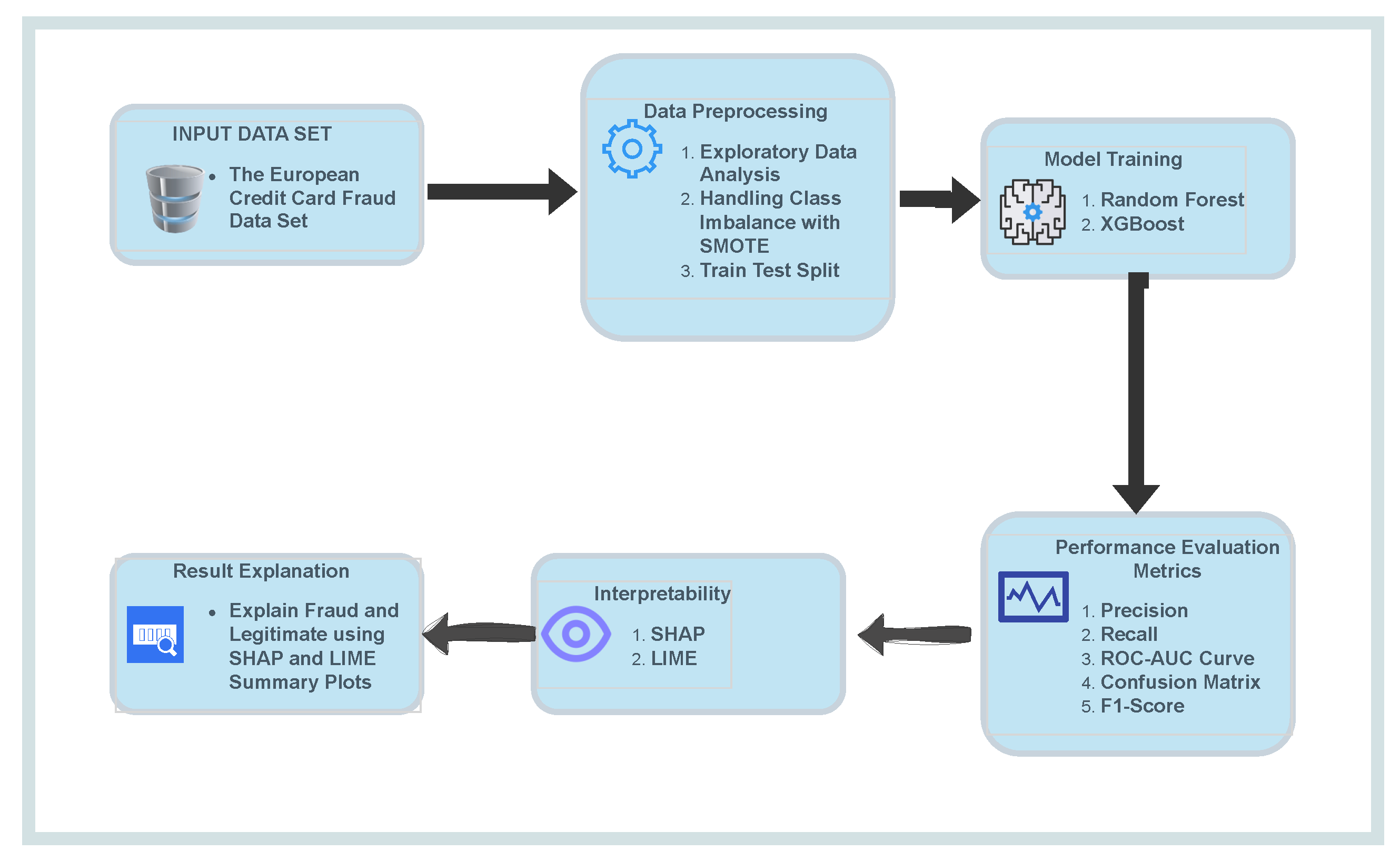
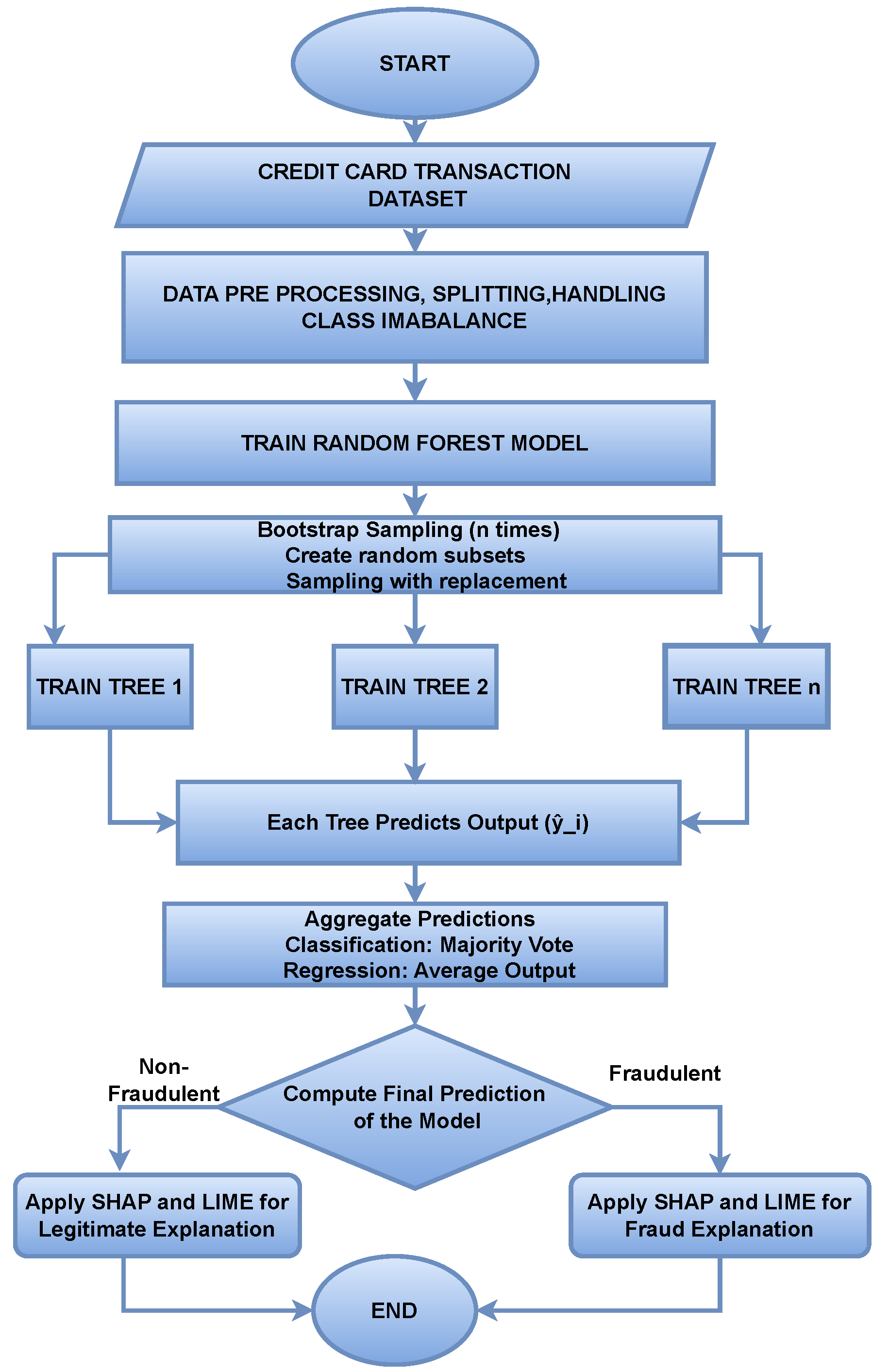
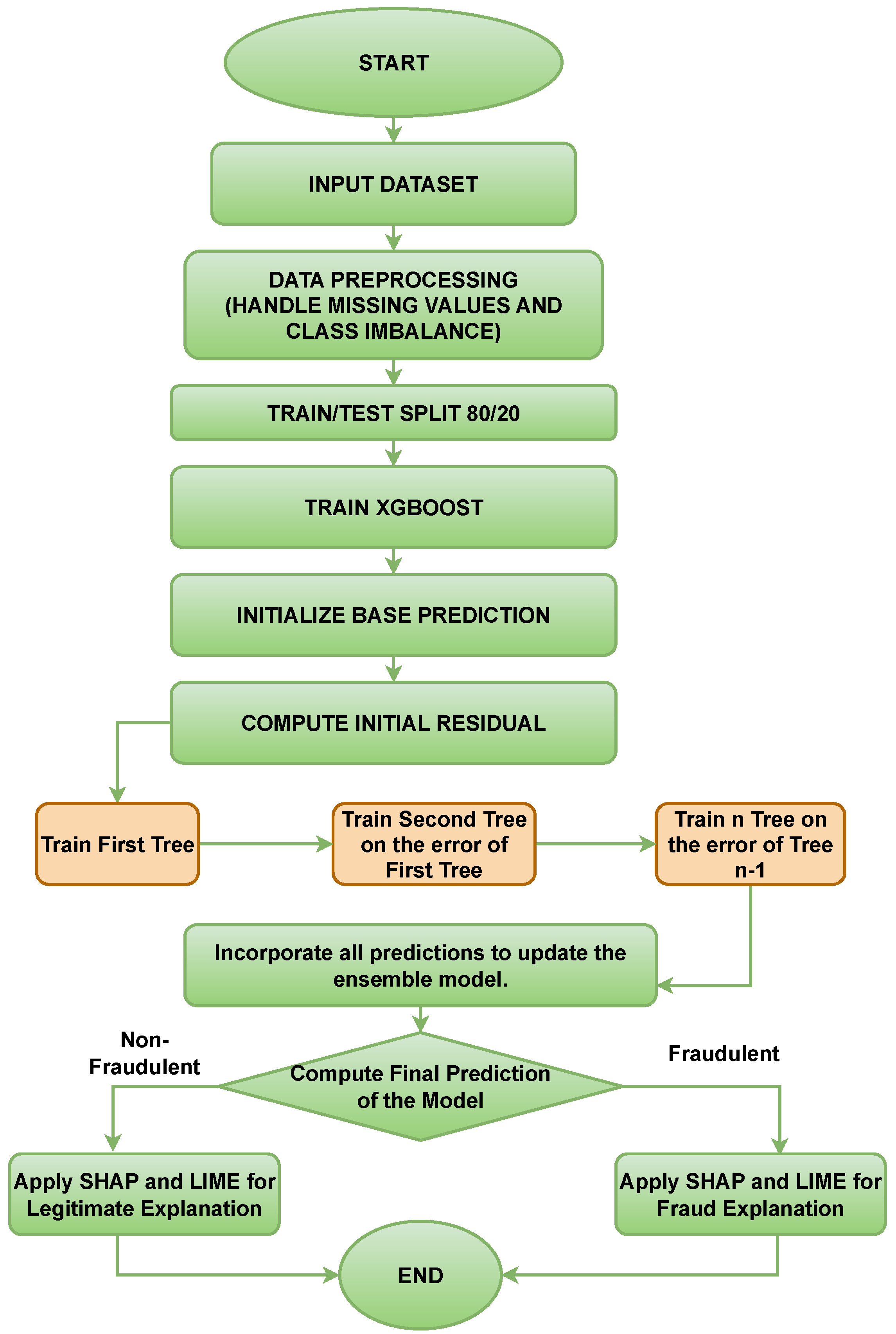
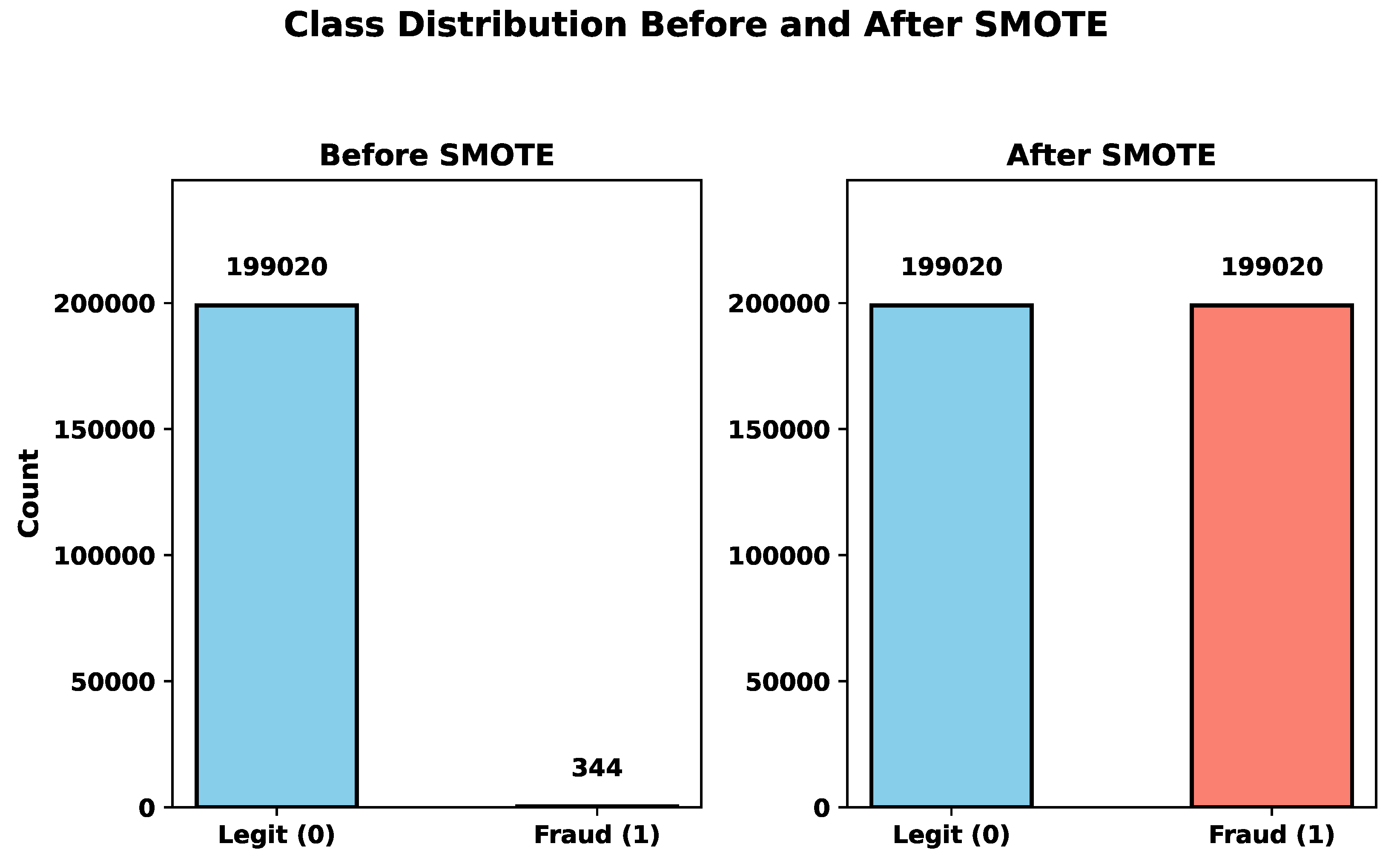
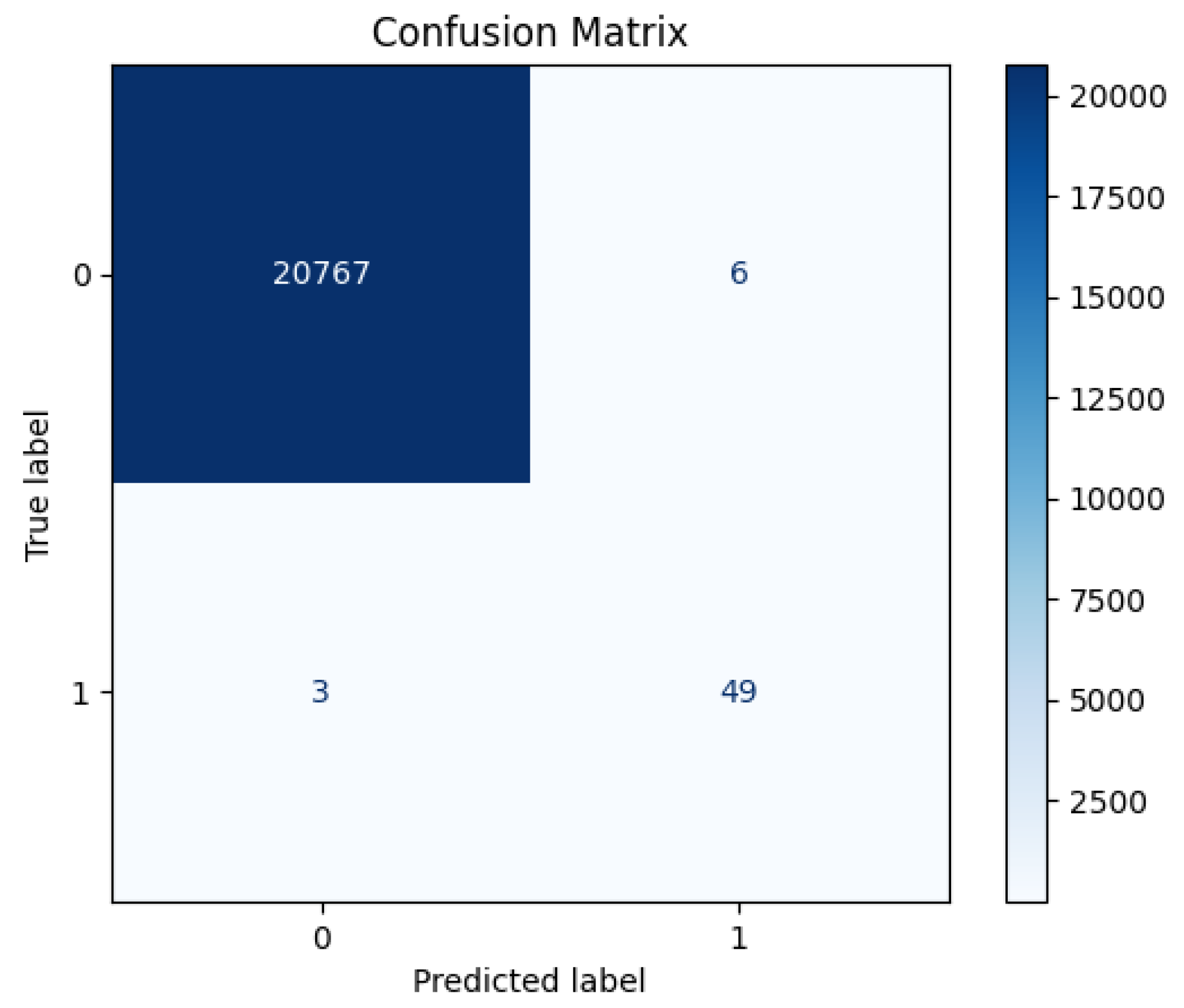
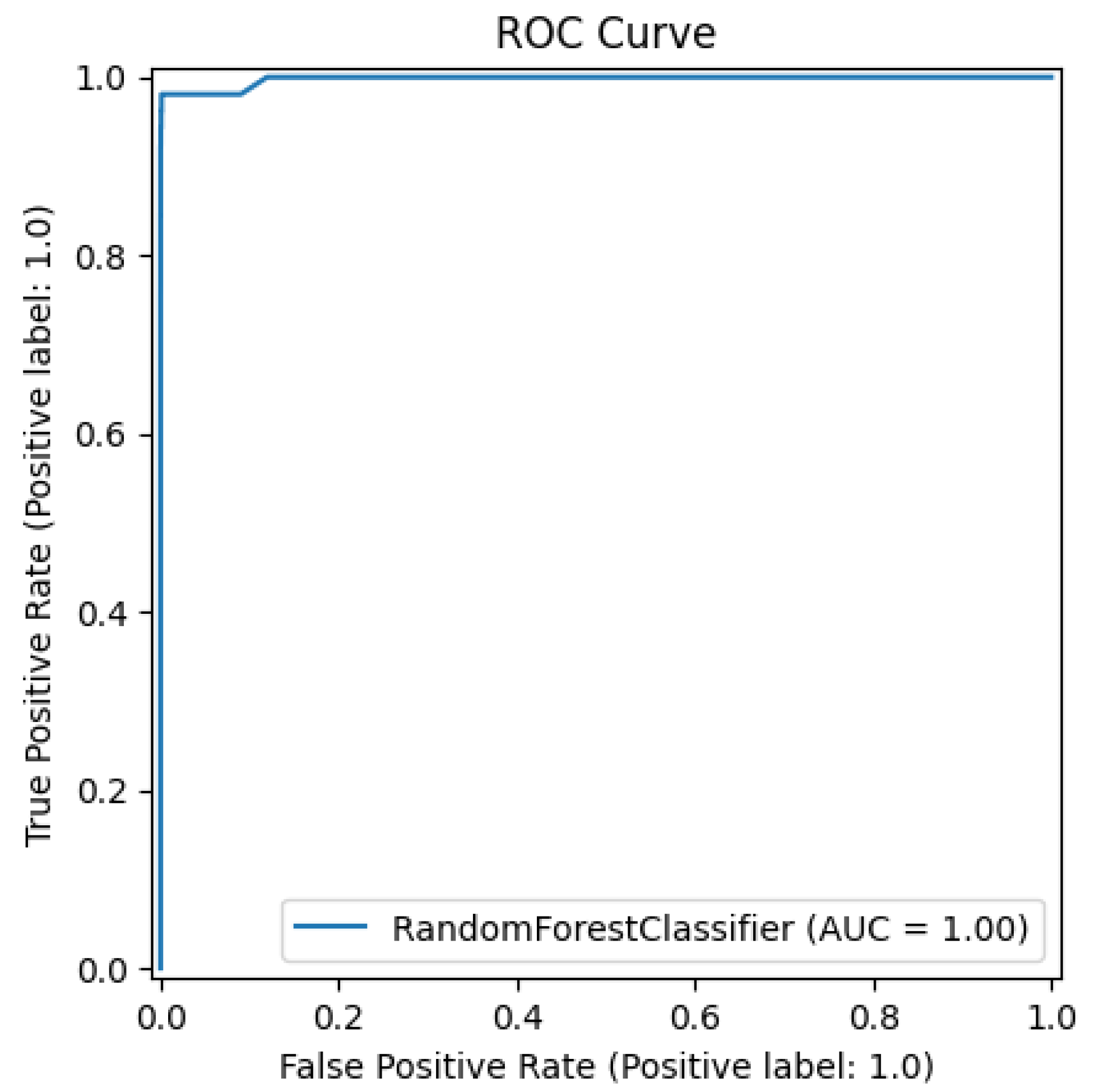
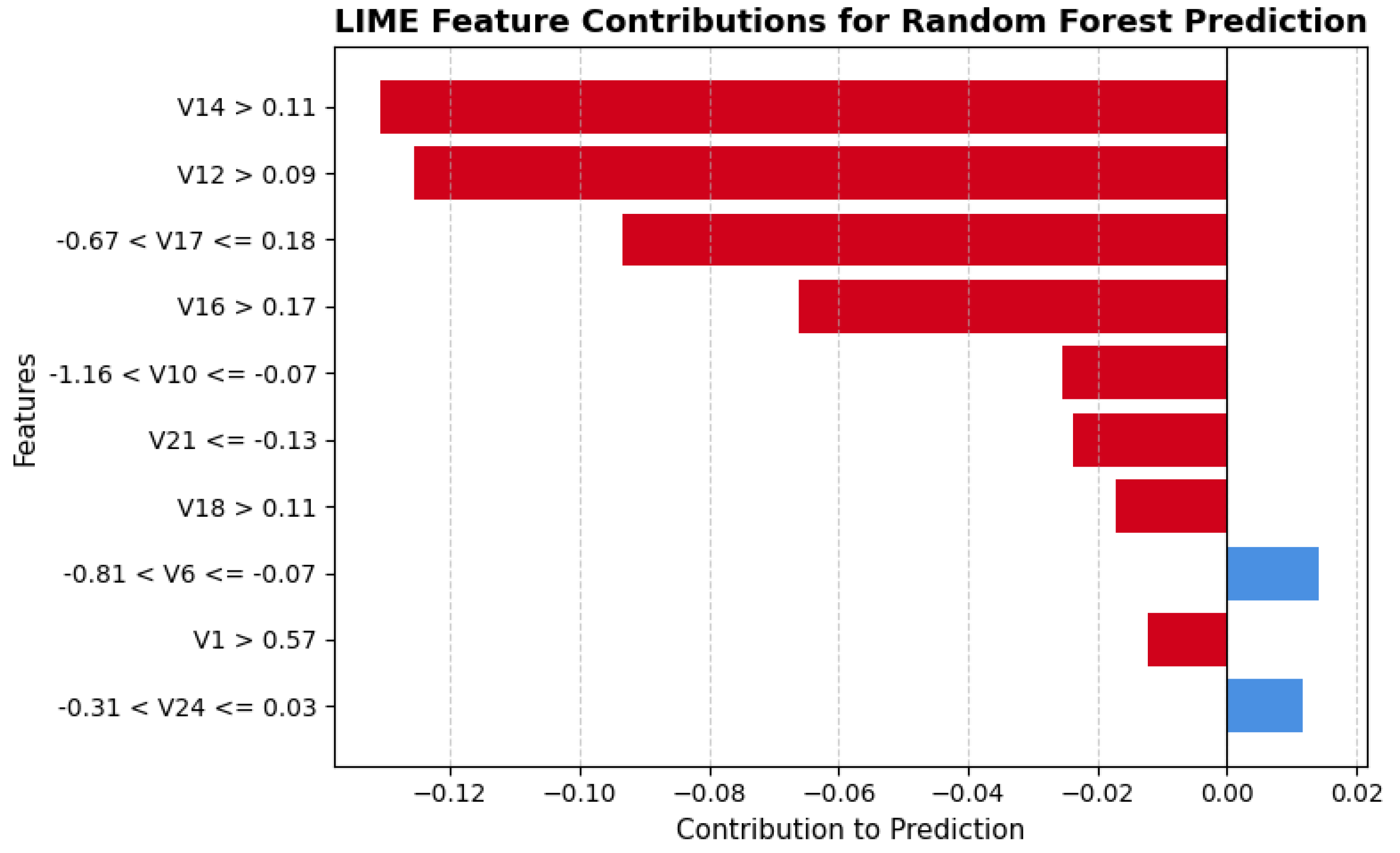
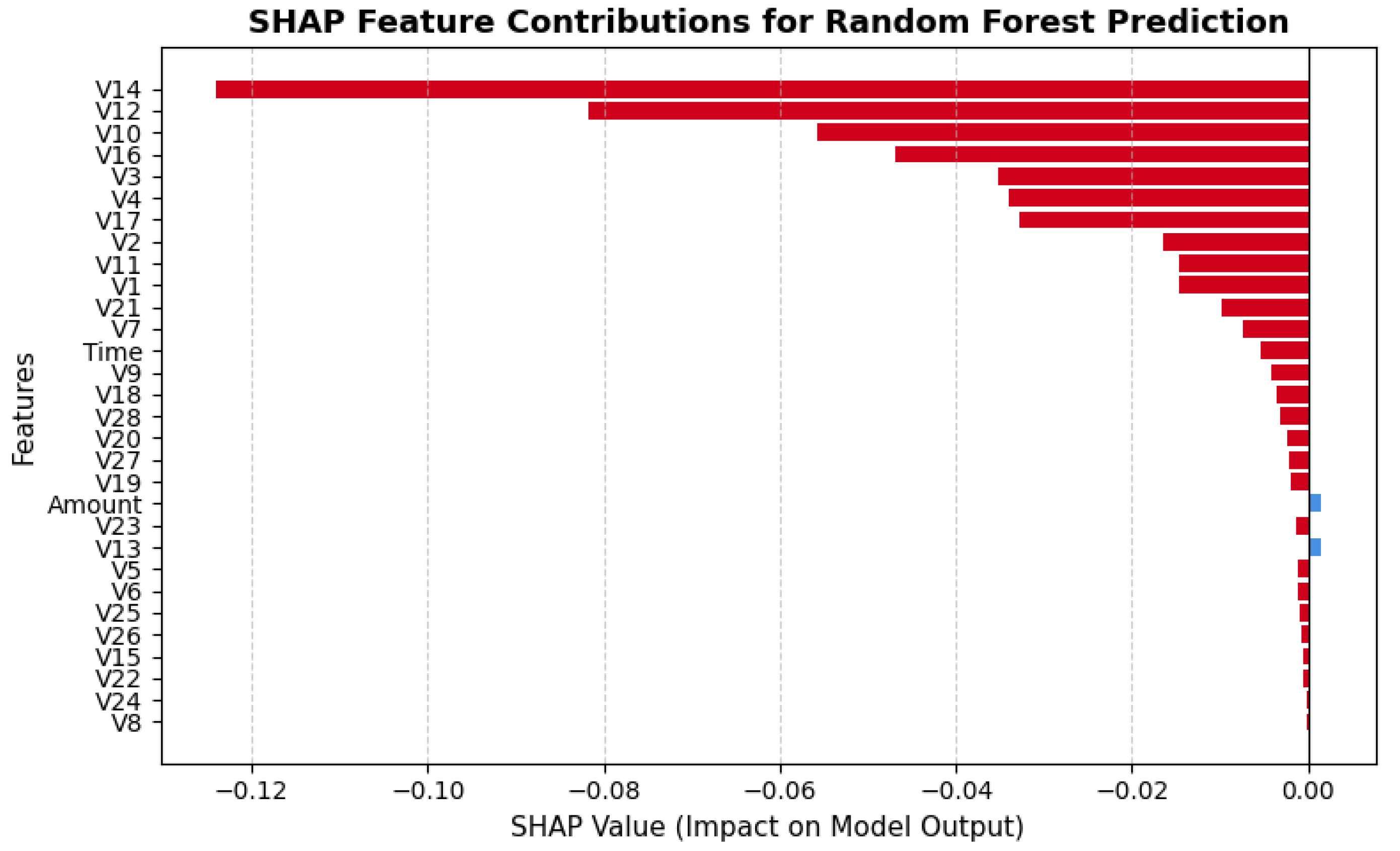
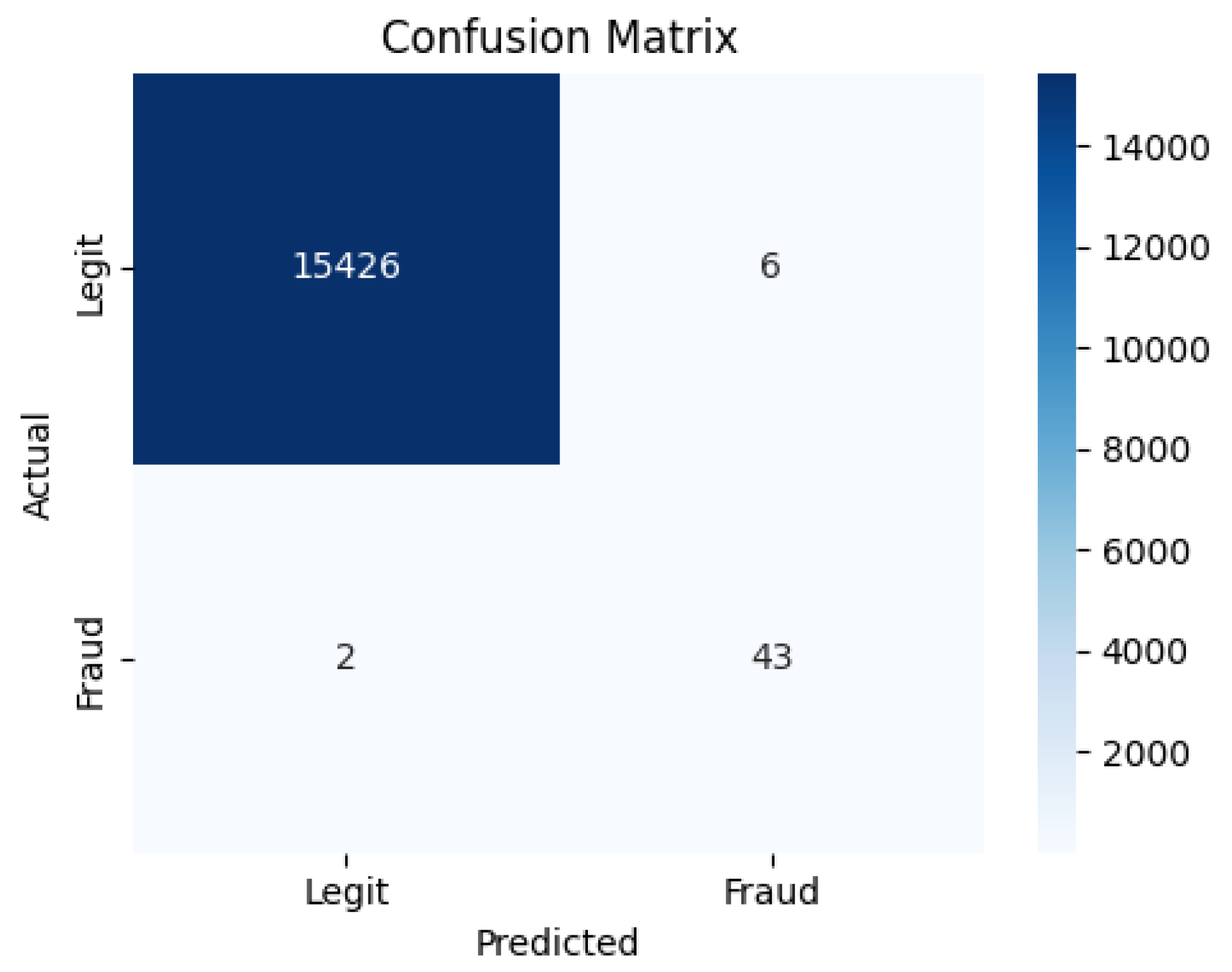
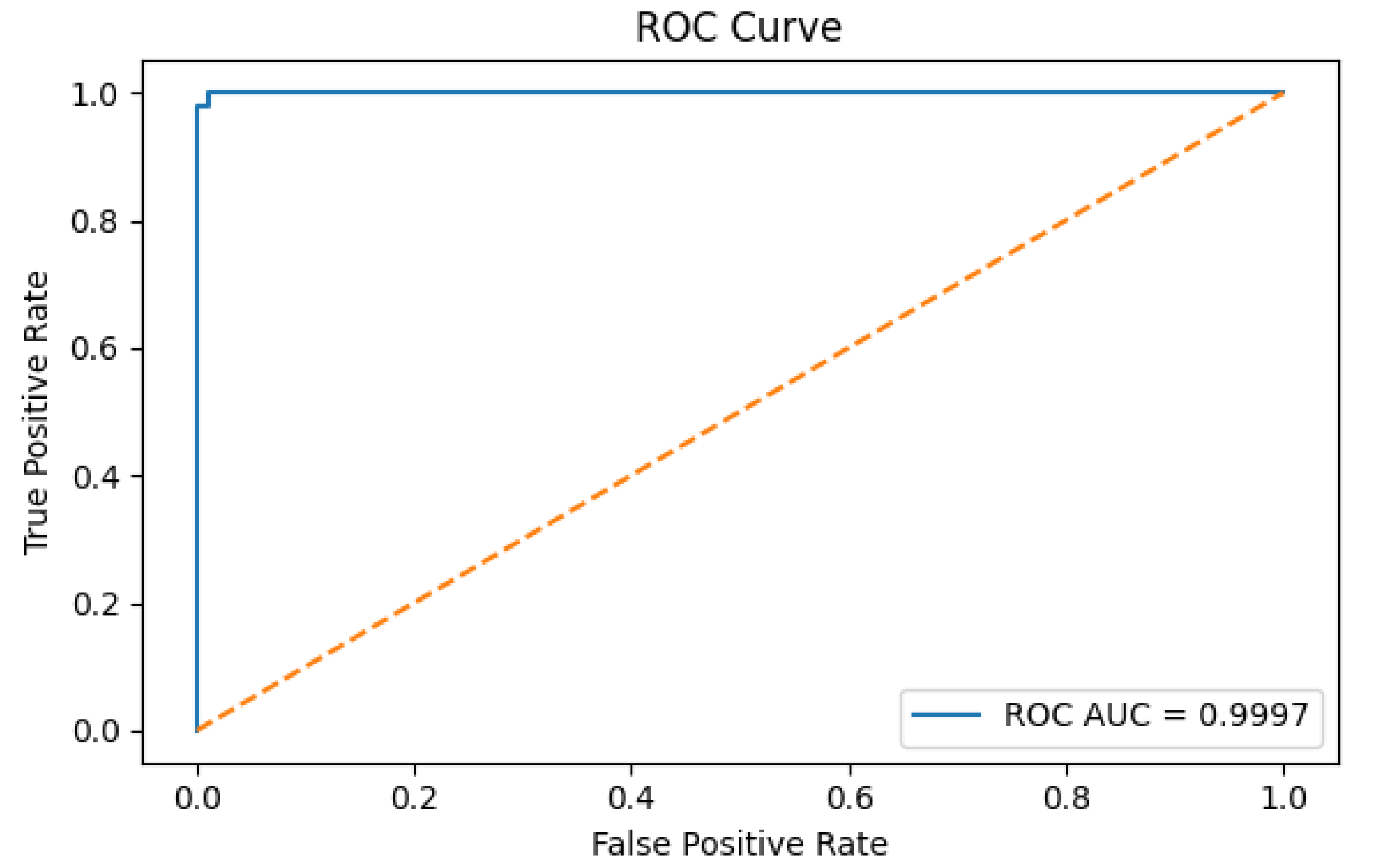
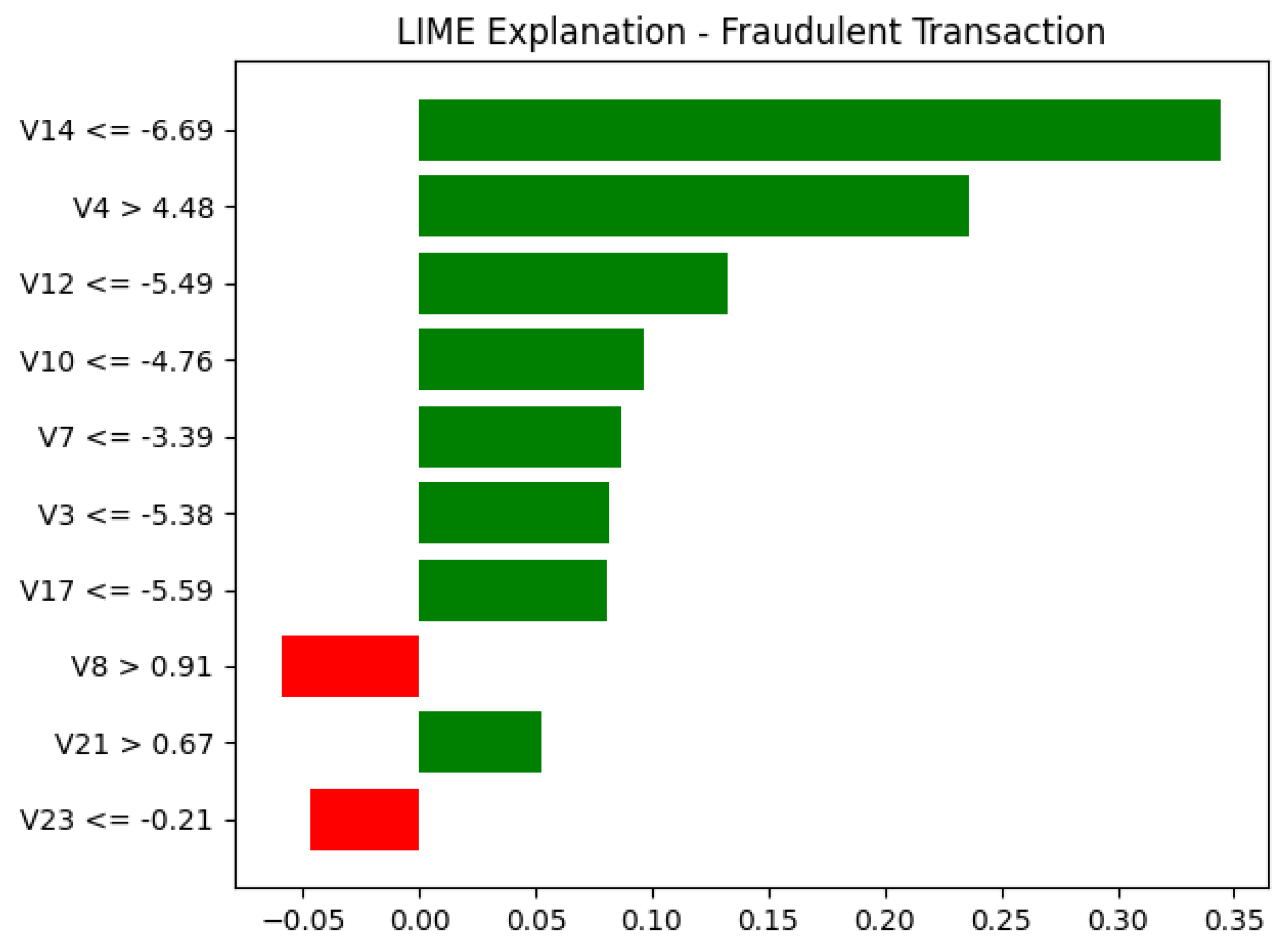
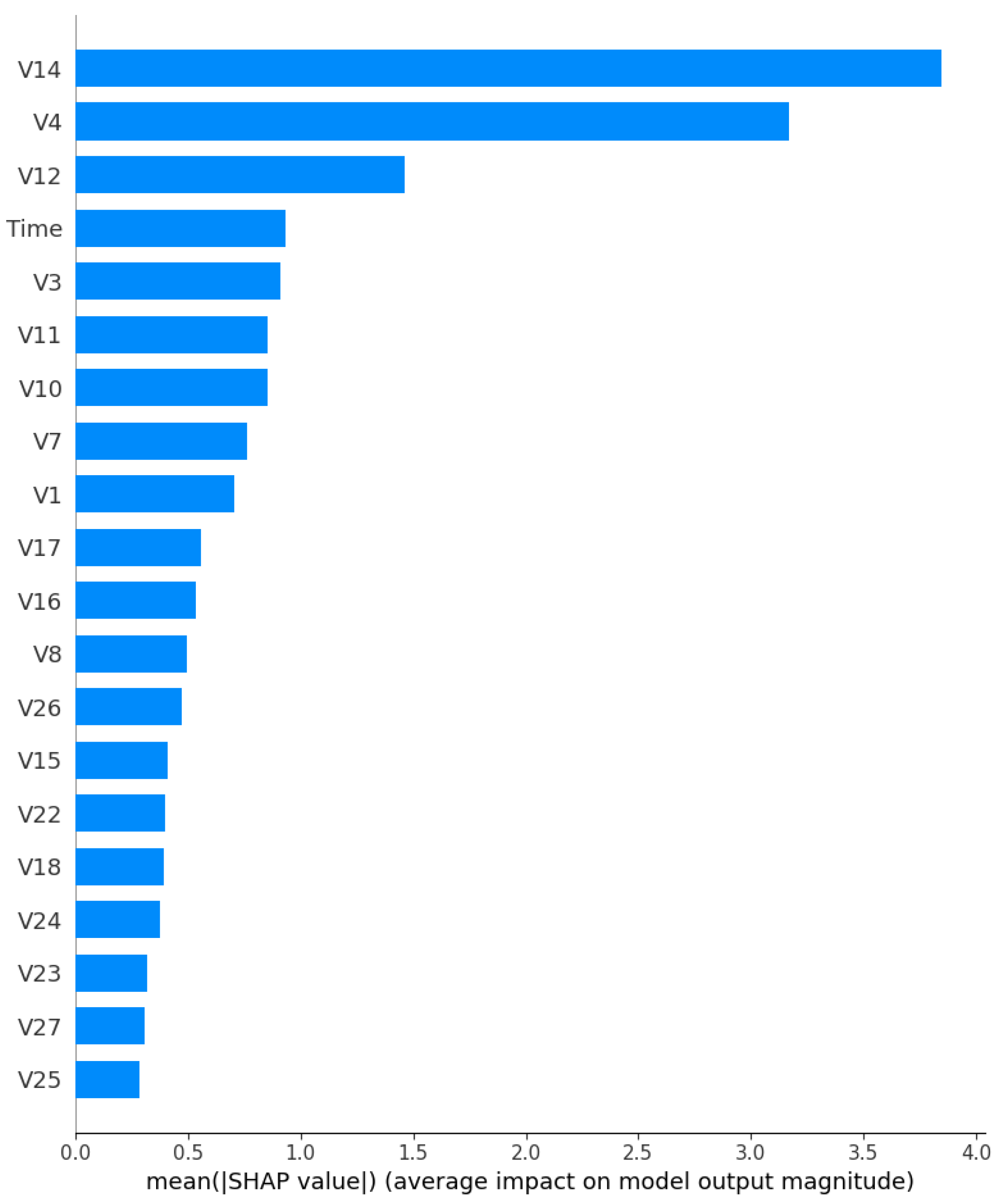
Machine learning models have shown strong potential in handling imbalanced fraud detection datasets, where class distributions are highly skewed. Imbalanced datasets pose a significant challenge in credit card fraud detection, as the small proportion of fraudulent transactions often leads to biased models with poor generalization. Researchers in [8] conducted a comprehensive survey of ML methods and highlighted both the limitations caused by data imbalance and the importance of incorporating explainable systems to improve reliability. They further suggested that hybrid approaches could enhance performance. However, despite these advances, a key challenge remains in understanding model decisions, particularly in regulatory-compliant industries such as banking, where explainability is essential for accountability and trust. The study [9] compared various ML algorithms and data balancing techniques, including SMOTE, ADASYN, and NCR, for handling highly imbalanced fraud detection datasets. Their results showed that XGBoost with Random Oversampling achieved the highest F1-score (92.43%), followed closely by Random Forest. While these findings confirm the strong predictive power of ensemble models, they also underscore the need for explainability, as high performance alone does not satisfy regulatory and operational requirements in fraud detection. Unsupervised methods have also been explored to overcome challenges such as data imbalance, privacy concerns, and limited availability of labeled fraud data. For example, Kennedy et al. [10] proposed a framework that combines SHAP-based feature selection with an autoencoder for label generation. Their approach demonstrated that unsupervised learning can be effective for numerical transaction data. However, the framework relied only on SHAP for global feature ranking, which limited interpretability at the individual decision level. This highlights the need for approaches that incorporate both global and local explainability, a gap this study addresses by systematically applying SHAP and LIME to ensemble models. Unsupervised anomaly detection has also been combined with explainability techniques. Hancock et al. [11] integrated SHAP with Isolation Forest to identify the most informative features without relying on labeled data. Their results showed that models trained on the top 15 SHAP-ranked features achieved performance comparable to, and in some cases better than, those trained on the full feature set, as measured by AUPRC and AUC. While effective for feature selection, this approach primarily emphasized global importance and did not provide deeper insights into instance-level interpretability, which is essential for decision justification in financial applications.

2.2.1. Deep Learning and Hybrid Approaches

Deep learning models such as ResNeXt and Gated Recurrent Units (GRU) for fraud detection were explored by [12] and compared their results with traditional machine learning models. Despite their success in performance metrics, these deep learning models lacked interpretability, which makes it difficult to understand the model. Similarly, in [13], they integrate Graph Neural Networks (GNN) and Autoencoders for fraud detection, and their results declared high performances, but the inherent complexity of these models raised concerns about their transparency and real-world deployment in banking systems. Another significant contribution to credit card fraud detection is presented by authors who developed a hybrid deep learning framework integrating Generative Adversarial Networks (GANs) with Recurrent Neural Networks (RNNs) [14]. In this approach, the GAN component generates realistic synthetic fraudulent transactions to mitigate class imbalance, while the discriminator, implemented using architectures such as Simple RNN, Long Short-Term Memory (LSTM), and Gated Recurrent Units (GRU), learns to differentiate between real and generated transactions. The model achieved outstanding performance, with the GAN-GRU configuration attaining a sensitivity of 0.992 and a specificity of 1.000 on the European credit card dataset. While this method effectively enhances detection accuracy and data diversity, it primarily focuses on deep neural modeling without offering interpretability. In contrast, the present work leverages ensemble learning models (Random Forest and XGBoost) alongside explainable AI (SHAP and LIME) to ensure both predictive strength and model transparency, facilitating better understanding and trust in financial decision-making systems. Yang et al. [15] proposed an advanced framework that integrates a Mixture of Experts (MoE) architecture with a Deep Neural Network-based Synthetic Minority Over-sampling Technique (DNN-SMOTE) to address the severe class imbalance in credit card fraud detection. Their approach combines multiple specialized expert networks trained to detect specific fraud patterns, while the DNN-SMOTE component generates synthetic samples to improve data balance and overall classification performance. Although their model achieved outstanding accuracy (99.93%) and robustness, it primarily focuses on deep neural network optimization without providing interpretability into decision-making processes. In contrast, the present study employs ensemble learning methods, Random Forest and XGBoost, augmented with explainable AI (XAI) techniques such as SHAP and LIME. This combination not only enhances detection performance on imbalanced datasets but also provides transparent, interpretable explanations for each model prediction, making the framework more suitable for real-world financial applications where interpretability and regulatory compliance are critical.

2.2.2. Ensemble Learning Techniques for Fraud Detection

Ensemble learning techniques are well-suited for numerical features because they provide high accuracy and improve classification. These methods have been widely used in fraud detection systems. In [16], the authors explored RF and XGBoost against deep learning models. Their study revealed that while deep networks can capture complex fraud patterns, RF and XGBoost remain preferable for real-time fraud detection due to their computational efficiency and interpretability. The study [17] compared RF and XGBoost under varying class imbalance conditions and concluded that hyperparameter-tuned XGBoost consistently outperformed Random Forest in F1-score and precision. Despite these advantages, their study did not investigate the interpretability of these ensemble models, which leaves a critical gap in understanding how these models make decisions. The study [18] demonstrated that ensemble techniques perform better than other ML models as they are simple, require less data, and work well with explainability tools. Jiang et al. [19] proposed an Unsupervised Attentional Anomaly Detection Network (UAAD-FDNet) for credit card fraud detection, where fraudulent transactions were treated as anomalies instead of being handled through traditional supervised classification. Their model integrates an autoencoder with feature attention and a generative adversarial network (GAN) to enhance representation learning and mitigate the effects of class imbalance. While this unsupervised approach effectively detects anomalies without relying on labeled data, it lacks interpretability and fails to explain the reasoning behind its predictions. In contrast, the present study employs supervised ensemble learning models, Random Forest and XGBoost, combined with explainable AI (XAI) techniques such as SHAP and LIME, thereby achieving both strong predictive performance and transparent model interpretability in financial fraud detection. Mosa et al. [20] proposed the CCFD framework, which integrates meta-heuristic optimization (MHO) techniques with traditional machine learning algorithms such as Random Forest and SVM to enhance feature selection and classification efficiency in credit card fraud detection. Their study focused on mitigating the data imbalance problem and optimizing computational performance through intelligent feature subset selection. In contrast, the current research emphasizes interpretability and ensemble learning by combining Random Forest and XGBoost models with explainable AI (XAI) techniques, including SHAP and LIME, to achieve both high predictive accuracy and model transparency, providing more interpretable and trustworthy fraud detection outcomes.

2.2.3. Explainable AI in Fraud Detection

Regulatory bodies such as finance and banking are often required to demonstrate the results to their stakeholders and end-users, explaining why a certain transaction was labeled as fraudulent by the model. Machine learning models perform very well in detecting complex patterns of fraud, but they often lack explainability and interpretability, which are crucial for real-life systems. Systematic reviews have also emphasized the strengths and limitations of existing fraud detection approaches. Ali et al. [4] found that credit card fraud is the most extensively studied area, with ensemble methods such as Random Forest frequently applied due to their robustness in handling imbalanced data. However, the review also underscored the persistent lack of interpretability in these models, calling for the integration of XAI techniques to enhance transparency. This aligns directly with the focus of the present study, which applies SHAP and LIME to bridge this gap in ensemble-based fraud detection. Recent work has begun to incorporate explainability into fraud detection frameworks. For instance, Nobel et al. [21] applied SHAP and LIME across multiple machine learning models and demonstrated that these tools enhance transparency, improve feature attribution, and provide actionable insights for financial analysts. However, the study excluded Random Forest, a widely used ensemble method in fraud detection, and did not systematically compare interpretability between models. This gap motivates our focus on evaluating both Random Forest and XGBoost with SHAP and LIME to provide a more comprehensive analysis of explainability in fraud detection. Aljunaid et al. [22] applied XGBoost with SHAP and LIME to improve interpretability in financial fraud detection, demonstrating that these tools can help explain model predictions and support decision-making. However, their analysis was limited to a single ensemble method (XGBoost) and did not compare interpretability across different models. Building on this, our study evaluates both Random Forest and XGBoost to provide a broader perspective on how ensemble methods balance predictive performance with explainability. Another study [23] explored the use of SHAP for anomaly detection in financial systems, showing that SHAP can enhance model interpretability by identifying influential features. While this work demonstrated the value of explainability in unsupervised settings, it focused only on SHAP and did not incorporate complementary tools such as LIME, which provide local, instance-level explanations. Our study extends this direction by systematically applying both SHAP and LIME to ensemble models, enabling a more comprehensive evaluation of interpretability in fraud detection. The study [24] demonstrated the use of SHAP and LIME for enhancing interpretability in machine learning models, applying them in the context of urban remote sensing for land class mapping. Their findings showed that while XGBoost achieved higher accuracy, Random Forest provided clearer explanations, making it more suitable for applications where regulatory compliance and transparency are critical. Although conducted in a different domain, this work underscores the broader importance of balancing accuracy with interpretability, a trade-off that this study investigates specifically in the context of financial fraud detection.

Similarly, Caelen, O. [25] reviewed machine learning approaches to fraud detection, categorizing them into supervised, unsupervised, and hybrid models. The study found that supervised methods such as Random Forest, XGBoost, SVM, and Logistic Regression perform well when sufficient labeled data are available but struggle with severe class imbalance. To mitigate this, the authors emphasized relying on precision, recall, F1-score, and AUC-ROC rather than overall accuracy. In contrast, unsupervised models like K-Means and DBSCAN are better suited for unlabeled datasets but are limited to detecting unusual patterns. These findings reinforce the importance of choosing models and evaluation metrics carefully, particularly in imbalanced fraud detection settings, a consideration central to this study.

A separate investigation [26] compares the performance of several classifiers, including Random Forest, Decision Tree, Naive Bayes, Logistic Regression, K-Nearest Neighbors, and SVM, using a real-world dataset characterized by a significant class imbalance. Random Forest exhibits effective results, achieving precision and recall rates of 0.98 and 0.93, respectively. The study noted potential drawbacks such as limited model interpretability and challenges in adapting to new types of fraud.

XGBoost has been shown to outperform traditional models such as logistic regression in fraud detection. For example, Dichev et al. [27] demonstrated that XGBoost reduces both false positives and false negatives, thereby improving accuracy, operational efficiency, and regulatory compliance. However, the study also emphasized the dependence on feature engineering and noted that interpretability remains a challenge.

Building on this, Tursunalieva et al. [28] highlighted the role of XAI tools in enhancing transparency, trust, and accountability in fraud detection systems. At the same time, the authors cautioned that balancing predictive accuracy with interpretability and ethical considerations remains difficult, calling for standardized, user-centric XAI frameworks. These insights underscore the need for comparative studies, such as the present work, that evaluate both performance and interpretability in ensemble models.

Machine learning techniques, particularly ensemble models such as Random Forest and XGBoost, have demonstrated strong potential in fraud detection due to their ability to analyze large-scale numerical data and uncover hidden patterns. While these models achieve high accuracy, their lack of interpretability remains a major limitation. For example, Btoush et al. [29] applied Random Forest and XGBoost to credit card fraud detection, reporting F1-scores of 85.71% (RF: precision 97.40%, recall 76.53%) and 85.3% (XGBoost: precision 95.00%, recall 77.55%). Although a hybrid model outperformed both, the study did not incorporate interpretability techniques such as SHAP or LIME. Similarly, Khalid et al. [30] proposed an ensemble framework combining SVM, KNN, Random Forest, Bagging, and Boosting to address challenges of data imbalance, computational efficiency, and real-time detection, yet interpretability was not considered.

In summary, prior studies have demonstrated the effectiveness of Random Forest and XGBoost for fraud detection but have largely overlooked interpretability, with SHAP and LIME rarely applied systematically. This study addresses that gap by comparing both models on a real-world dataset and integrating SHAP and LIME to evaluate interpretability alongside predictive performance. In doing so, it contributes practical guidance for building transparent and reliable fraud detection systems.

3. Materials and Methods

This study aims to implement and compare the performance of two popular machine learning models, Random Forest (RF) and XGBoost, for the detection of credit card fraud in online transactions. Additionally, to enhance the interpretability of these models, SHAP (SHapley Additive Explanations) and LIME (Local Interpretable Model-Agnostic Explanations) were used, which are XAI tools. The chosen approach will allow us to assess not only the accuracy and efficiency of the models but also their transparency, which is crucial for deploying machine learning solutions in financial sectors. The first step was the preprocessing of the credit card fraud detection dataset, followed by training the Random Forest and XGBoost models. The models will be evaluated using common standard classification metrics such as accuracy, precision, recall, F1 score, and ROC-AUC, and the key metric is interpretability. To ensure that the results are interpretable, SHAP and LIME will be utilized to explain the models’ predictions and to understand which features most influence the classification decisions. Comparison of these models will help identify the most effective approach for online transaction fraud detection while maintaining transparency and interoperability. This will also helps in gaining and maintaining end user trust in these digital payment methods, but also helps explain the model’s prediction to stakeholders and end users. As shown in Figure 1, the figure demonstrates the complete proposed methodology of the research.

3.1. Data Set

The study uses the European Credit Card Fraud Detection Dataset from Kaggle, which contains anonymized real-world transactions. This dataset has become a standard benchmark in fraud detection research due to its highly imbalanced nature, anonymized transaction features, and widespread acceptance in the literature. Its use ensures that our results can be compared fairly with prior studies.The dataset comprises 284,807 transactions with 492 fraudulent cases, resulting in a highly imbalanced class distribution. Features are numerical due to a Principal Component Analysis (PCA) transformation, with the class column in

Table 1. Example transactions from the credit card fraud detection dataset.

Time	V1	V2	V3	Amount	Class
406	−1.3598	−0.0728	2.5363	149.62	Legitimate
472	1.1919	0.2660	0.1664	0.00	Fraudulent

indicating fraud (1) or legitimate (0) transactions. Features V1–V28 are anonymized principal components, and their original meanings are undisclosed to preserve confidentiality. Consequently, SHAP and LIME explanations in this study are expressed in terms of PCA components rather than the original economic variables. While this limits direct interpretability, the PCA features still capture meaningful variance and relationships within the data. To mitigate this limitation, our interpretability analysis focuses on identifying which components (e.g., V4, V12) consistently drive model predictions, highlighting the latent dimensions most associated with fraudulent behavior.

This approach ensures compliance with dataset constraints while still enabling a valuable comparison of explainability methods applied to fraud detection models. Table 1 illustrates two representative sample, one legitimate and one fraudulent, highlighting structural differences in feature distributions and reflecting the dataset’s imbalance characteristics.

3.2. Data Processing

The selected dataset needs to pass through some steps before training the models on it. These steps help in organizing the features and making efficient predictions. The steps are:

3.2.1. Oversampling

The dataset was highly imbalanced, with fraudulent transactions representing less than 0.2% of all records. To address this, the Synthetic Minority Oversampling Technique (SMOTE) was applied. SMOTE was chosen over alternative oversampling approaches such as ADASYN and Borderline-SMOTE. Unlike ADASYN, which adaptively generates more synthetic samples for difficult cases (potentially amplifying noise), or Borderline-SMOTE, which focuses only on borderline instances (risking class overlap), SMOTE produces a balanced set of synthetic samples by interpolating between existing minority class neighbors. This approach provides a stable and general representation of the minority class, ensuring that the model achieves improved recall without overfitting to noisy or ambiguous cases. Given the highly imbalanced nature of fraud detection, SMOTE offered the best balance between effectiveness and reliability for this study.

While SMOTE was applied only to the training set, SHAP and LIME explanations were generated on the untouched test data, providing transparent insights into the model’s decision-making process. The consistency of feature importance across both models demonstrates that SMOTE enhanced recall without altering interpretability, highlighting the robustness of SHAP and LIME in explaining real-world fraud predictions. The mathematical formulation of the oversampling process is provided in Appendix A.2.

3.2.2. Data Splitting

The dataset is divided into 80% training and 20% testing. This is the balanced division of the dataset, as the model will get trained on enough data and learn complex patterns, and also enough data for evaluation. The mathematical equations described in Appendix A.1 demonstrate the splitting of the dataset.

3.3. Machine Learning Models

In this study, we employ Random Forest (RF) and XGBoost (XGB), two of the most widely used and high-performing ensemble learning methods for structured data problems. These models perform very well for numerical features, handle imbalance, and avoid overfitting.

3.3.1. Random Forest (RF)

Random Forest (RF) was selected for this study due to its robustness in handling noisy and imbalanced datasets, as well as its ability to provide straightforward feature importance measures. Since the credit card fraud dataset consists of highly imbalanced classes and numerous numerical features, RF is suitable because it reduces overfitting through bootstrapping and aggregation of multiple decision trees. Hyperparameter tuning was performed using GridSearchCV with 3-fold cross-validation. The following ranges were explored: n_estimators $\in \{100,200,500\}$, max_depth$\in \{\mathrm{None},5,10,15\}$, and class_weight$\in \{\mathrm{None},\mathrm{balanced}\}$. The final model was selected with n_estimators = 500, max_depth = None, and class_weight = “None”, as this configuration achieved the highest F1 score (0.9998) during 3-fold cross-validation. Additionally, RF provides distributed feature importance scores, which were later compared against SHAP and LIME explanations to evaluate the model’s interpretability in fraud detection. The mathematical formulations of Random Forest, SHAP, and LIME are included in Appendix B. The overall workflow of the Random Forest model, integrated with SHAP and LIME for both global and local interpretability, is illustrated in Figure 2.

3.3.2. XGBoost (XGB)

In this study, XGBoost was selected because of its effectiveness in handling highly imbalanced fraud detection datasets and its ability to capture nonlinear interactions among transaction features. Hyperparameter tuning was conducted using a grid search with cross-validation. The final model was configured with learning_rate = 0.05, n_estimators = 300, max_depth = 6, and scale_pos_weight = 10, which provided the best trade-off between recall and precision while improving minority-class recall without significantly increasing false positives. To further enhance interpretability, SHAP and LIME were applied to the final tuned model. SHAP was used to compute both global feature importance and local feature contributions for individual predictions, while LIME provided case-specific explanations for fraud detection decisions. The integration of these methods improved the transparency of the XGBoost classifier, helping to identify which transaction features contributed most to detecting fraudulent activities. The mathematical details of the XGBoost learning objective and regularization are provided in Appendix B.7, and the workflow of the tuned model integrated with SHAP and LIME is presented in Figure 3.

3.4. Performance Metrics

Standard key evaluation metrics will be used to evaluate the performance of each model. These metrics will help to compare and select the best model for a real-world scenario among them. The following are the key metrics used by the present study:

3.4.1. Accuracy

Accuracy measures the proportion of correctly classified transactions (fraudulent and legitimate). However, in fraud detection, where data is highly imbalanced, accuracy alone can be misleading, as a model predicting all transactions as legitimate would still achieve high accuracy. The exact formulation is provided in Appendix C.

3.4.2. Precision

Precision evaluates how many of the transactions flagged as fraud are actually fraudulent. In this study, high precision ensures that customers are not falsely accused of fraud. The mathematical formula is presented in Appendix C.

3.4.3. Recall

Recall measures how many of the actual fraudulent transactions are successfully detected. For fraud detection, recall is critical since missing fraudulent activity (false negatives) can lead to significant financial loss. The formula is given in Appendix C.

3.4.4. F1-Score

The F1-score balances precision and recall, ensuring that the model performs well in both detecting fraud and avoiding false alarms. This makes it especially suitable for highly imbalanced datasets. The equation is provided in Appendix C.

3.4.5. ROC-AUC

The ROC-AUC score evaluates the model’s ability to distinguish between fraudulent and legitimate transactions across different threshold settings. A higher AUC indicates better discrimination ability. Its mathematical definition is given in Appendix C.

3.5. Model Interpretability Using SHAP and LIME

While model performance metrics provide an overall evaluation, they do not explain why a prediction was made. To address this, SHAP (SHapley Additive exPlanations) and LIME (Local Interpretable Model-Agnostic Explanations) are used in this study. SHAP values help identify which features (such as transaction amount, time, or frequency) contribute most to distinguishing between fraudulent and legitimate transactions. This provides both a global understanding of model behavior and local explanations for individual predictions. LIME is applied to explain single predictions in detail by approximating the model locally with an interpretable one. This is particularly useful for fraud detection, where investigating why a specific transaction was flagged as fraud can increase trust in the model.

It is important to note that the dataset used in this study is the publicly available European credit card fraud dataset, where the original financial attributes were anonymized using Principal Component Analysis (PCA). As a result, the features (V1–V28) are principal components rather than raw economic variables. This transformation limits the direct interpretability of individual features in economic terms. However, applying SHAP and LIME in this context remains valuable for two reasons: first, it ensures transparency by showing which components drive model predictions, thereby helping to identify the most influential latent patterns in the data; second, it allows a fair comparison of how different models (Random Forest and XGBoost) rely on these components, providing insights into model reliability and robustness even when the raw variables are unavailable. Thus, the use of SHAP and LIME contributes not only to model interpretability but also to methodological transparency in fraud detection research, where sensitive data constraints necessitate the use of anonymized features. The mathematical formulations of SHAP and LIME are presented in Appendix D.

3.6. Implementation

In this study, the implementation of credit card fraud detection using machine learning algorithms is carried out by focusing on two widely used models: Random Forest and XGBoost. The overall workflow begins with data pre-processing, which includes cleaning the dataset, handling missing values, and addressing class imbalance through the Synthetic Minority Over-sampling Technique (SMOTE). After preprocessing, the dataset is divided into training and testing subsets to evaluate generalization. The Random Forest and XGBoost models are then trained on the training data and evaluated on the testing data. Their performance is assessed using standard classification metrics such as precision, recall, F1-score, and the AUC-ROC curve, which are particularly important in imbalanced classification problems such as fraud detection.

In addition to predictive performance, model interpretability is considered a key evaluation aspect. Explainable AI (XAI) tools such as SHAP and LIME are applied to both models to analyze feature contributions at the global and local levels. This allows the study not only to compare the predictive accuracy of the models but also to evaluate their transparency in decision-making, which is crucial in high-stakes domains such as financial fraud detection.

The following subsections provide a detailed description of the steps taken to implement the proposed methodology.

3.6.1. Environment Setup

The implementation of the credit card fraud detection system was carried out in Python, utilizing several machine learning libraries and tools for data manipulation, model training, and evaluation. All experiments were implemented in open source software, likewise Python (Version 3.10) within a JupyterLab (Version 4.4.10) environment, using Anaconda for package management. The following provides an overview of the environment setup used for this research:

3.6.2. Software and Libraries

The implementation was carried out in Python using widely adopted machine learning and data analysis libraries. Specifically, scikit-learn (Version 1.7.2) was used for preprocessing, evaluation, and the Random Forest model. XGBoost (Version 3.1.1) was employed for gradient boosting classification; and imbalanced-learn (Version 0.14.0) was applied for handling class imbalance through SMOTE. Data manipulation and visualization were performed using pandas (Version 2.3.3) and standard plotting libraries.

3.6.3. Hardware Requirements

• The implementation was conducted on a standard desktop system with 8 GB of RAM and a 2.6 GHz Intel i5 processor. This configuration was sufficient to process the dataset and train the models within reasonable time limits.

3.6.4. Tools for Model Evaluation

Model evaluation was carried out using scikit-learn (Version 1.7.2), where performance metrics such as accuracy, precision, recall, F1-score, and AUC-ROC were calculated. Visualization libraries such as seaborn (Version 0.13.0) were used to present results through plots, including confusion matrices and ROC curves, ensuring clarity and interpretability.

3.6.5. Data Loading and Preprocessing

The Credit Card Fraud Detection Dataset was loaded into the Python environment using pandas (Version 3.14). Exploratory Data Analysis (EDA) was first conducted to verify dataset integrity and visualize class distribution, confirming the severe imbalance between fraudulent and legitimate transactions. To address this imbalance, the Synthetic Minority Over-sampling Technique (SMOTE) was applied, generating synthetic fraudulent samples and producing a balanced dataset. The feature variables (X) and the target label (y) were separated, and after applying SMOTE, balanced sets ($X_{res}, y_{res}$) were used for model training. Finally, the dataset was split into training (80%) and testing (20%) sets to evaluate the models on unseen data.

3.6.6. Random Forest Implementation

The Random Forest model was trained on the preprocessed dataset following these steps:

• Initialization: The classifier was instantiated with 500 decision trees (n_estimators = 500), no restriction on tree depth (max_depth = None), and class weights set to “None.” These hyperparameters were selected using GridSearchCV with 3-fold cross-validation, optimizing for the F1 score to achieve the best balance between precision and recall.
• Training: The model was trained on the SMOTE-balanced training dataset using bootstrap sampling.
• Prediction and Evaluation: Predictions were generated on the test set, and performance was measured using accuracy, precision, recall, F1-score, and AUC-ROC.

3.6.7. XGBoost Implementation

The XGBoost classifier was implemented as follows:

• Initialization: The model was initialized with hyperparameters optimized using grid search and 3-fold cross-validation. The search space included learning_rate $\in \{0.01,0.05,0.1\}$, n_estimators$\in \{100,200,300\}$, max_depth$\in \{3,5,7\}$, and scale_pos_weight$\in \{1,10,50\}$. The optimal configuration obtained was learning_rate = 0.05, n_estimators = 300, max_depth = 5, and scale_pos_weight = 10.
• Training: The XGBoost model was trained on the SMOTE-balanced dataset using gradient boosting, where each subsequent tree learned to correct the residual errors from previous iterations.
• Prediction and Evaluation: Predictions were made on the held-out test set, and model performance was assessed using accuracy, precision, recall, F1-score, and AUC-ROC, consistent with the evaluation of Random Forest.

3.7. Model Interpretability with SHAP and LIME

To address the black-box nature of ensemble models, this study applied SHAP (SHapley Additive exPlanations) and LIME (Local Interpretable Model-agnostic Explanations). These methods were chosen because they complement each other: SHAP provides a game-theoretic framework for consistent global and local feature attributions, while LIME generates intuitive surrogate models for instance-level explanations. Together, they enhance the transparency of fraud detection models.

3.7.1. SHAP

SHAP is grounded in cooperative game theory, where each feature’s contribution is quantified using Shapley values, ensuring consistent and fair attribution of feature importance. SHAP values were computed using the shap library. Summary plots were generated to identify the most influential features across the dataset, while force plots illustrated how individual features shaped specific predictions.

3.7.2. LIME

LIME perturbs the input data and fits an interpretable surrogate model in the local neighborhood of an instance, capturing the decision boundary of the black-box model at that point. The lime package was used to generate local explanations for selected transactions. LIME visualizations highlighted the features most responsible for the classification of individual transactions, offering case-level interpretability that complements SHAP’s global perspective.

4. Results

In this section, the performance results of the Random Forest and XGBoost models for detecting credit card fraud in online transactions are evaluated on a real-world dataset. The evaluation metrics used include Accuracy, Precision, Recall, F1-Score, ROC-AUC, and interoperability plots.

4.1. Data Balancing with SMOTE

The original dataset suffered from a significant class imbalance, as the fraudulent transactions are very rare. This imbalance can negatively impact the model’s ability to learn fraud patterns and make accurate predictions. To address this, the Synthetic Minority Oversampling Technique (SMOTE) was applied to oversample the minority class in the training dataset. As shown in Figure 4, the comparison illustrates the model performance before and after applying SMOTE to handle class imbalance.

4.2. Random Forest Evaluation Results

The Random Forest model demonstrated exceptional performance, as shown in

Table 2. Evaluation metrics of Random Forest for credit card fraud detection.

Metric	Value
Accuracy	0.9996
Precision	0.8909
Recall	0.9423
F1 Score	0.9159
ROC AUC	0.9979

, with an ROC AUC of 0.9979, indicating a very high ability to discriminate between legitimate and fraudulent transactions. Although the overall accuracy of 99.96% appears impressive, it should be interpreted cautiously due to the dataset’s class imbalance; accuracy alone may not fully capture the model’s effectiveness in identifying fraud.

More importantly, the model achieved a precision of 89.09% and a recall of 94.23% for fraud detection. This strong balance between precision and recall suggests that the model not only identifies the vast majority of fraudulent cases but also maintains a relatively low rate of false positives. The resulting F1 score of 0.9159 confirms this balanced and robust performance. In practical terms, this means that the model is highly effective at detecting fraud while minimizing the number of legitimate transactions incorrectly flagged as fraudulent.

Table 3. Classification report of Random Forest.

Class	Precision	Recall	F1-Score	Support
0 (Legit)	1.00	1.00	1.00	85,295
1 (Fraud)	0.89	0.94	0.92	148
Accuracy	0.9996 (on 85,443 instances)
Macro Avg	0.95	0.97	0.96	85,443
Weighted Avg	1.00	1.00	1.00	85,443

further details the classification performance. For the majority (legitimate) class, the model achieved near-perfect precision, recall, and F1-score, an expected outcome given the large volume of legitimate transactions. More importantly, for the minority (fraudulent) class, the model’s precision of 0.89 and recall of 0.94 translate to a very strong F1-score of 0.92. These results highlight the model’s capability to capture nearly all fraudulent activities while keeping false alarms manageable, making it highly suitable for real-world fraud detection scenarios.

4.2.1. Confusion Matrix for Random Forest

The confusion matrix in Figure 5 illustrates the classification performance of the Random Forest model. Out of all transactions in the test set, 20,767 legitimate transactions were correctly identified as non-fraudulent (true negatives), while only 6 legitimate cases were incorrectly flagged as fraud (false positives). For the fraudulent class, the model successfully detected 49 fraudulent transactions (true positives) and missed only 3, which were incorrectly classified as legitimate (false negatives). These results demonstrate the model’s remarkable precision and recall in identifying fraudulent behavior. The very low number of false negatives indicates that the Random Forest model rarely fails to detect fraud, minimizing potential financial risk. Similarly, the small number of false positives shows that few legitimate transactions are incorrectly flagged, maintaining a practical balance between security and customer convenience. Overall, the confusion matrix confirms the robustness and reliability of the Random Forest model in distinguishing between legitimate and fraudulent transactions.

4.2.2. ROC Curve for Random Forest

The ROC curve in Figure 6 demonstrates the trade-off between the true positive rate and the false positive rate across various classification thresholds. For the Random Forest model, the area under the curve (AUC) reached 1.00, indicating an almost perfect ability to distinguish between fraudulent and legitimate transactions. This exceptional performance means that the model maintains both high sensitivity (ability to detect fraud) and high specificity (ability to correctly identify legitimate transactions) across a wide range of thresholds. In practical terms, such a high AUC value implies that the Random Forest model can be effectively tuned to meet different operational goals, for instance, prioritizing recall to detect even the rarest fraudulent activities or emphasizing precision to reduce false alarms. Overall, the ROC curve confirms the robustness and reliability of the model in handling highly imbalanced fraud detection data.

4.2.3. Cross-Validation vs. Test Performance for Random Forest

To evaluate the generalization capability of the Random Forest classifier and ensure that overfitting did not occur, 3-fold cross-validation was performed in addition to testing the model on an independent dataset. The updated results are summarized in

Table 4. Random Forest Cross-Validation vs. Test Set Results.

Metric	Cross-Validation (CV = 3)	Test Set
F1 Score	0.9998	0.9159
Accuracy	–	0.9996
Precision	–	0.8909
Recall	–	0.9423
ROC AUC	–	0.9979

.

As shown, the Random Forest model achieved an exceptionally high F1 score of 0.9998 during 3-fold cross-validation, reflecting excellent consistency across the training folds and confirming that the model effectively captured the underlying data patterns without signs of overfitting.

When evaluated on the independent test set, the model maintained strong performance with an F1 score of 0.9159, accuracy of 99.96%, and ROC AUC of 0.9979. These results indicate that the Random Forest classifier generalizes effectively to unseen data, demonstrating both high recall (0.9423) for detecting fraudulent transactions and strong precision (0.8909) for minimizing false positives. Overall, the close agreement between cross-validation and test performance highlights the robustness and reliability of the Random Forest model for credit card fraud detection.

4.3. Interpretability Results Using SHAP and LIME

The following section describes the result of SHAP and LIME. It is important to note that these features are anonymized PCA components, and while their semantic meaning is unavailable, SHAP and LIME allow us to quantify and compare their relative importance, thereby improving interpretability despite this limitation. Since PCA inherently produces variance-scaled components, the feature values are already on comparable scales. Therefore, removing additional preprocessing steps such as normalization or standardization did not alter the Random Forest performance or the SHAP/LIME explanations, which explains the consistency observed in our results.

LIME Explanation for Random Forest

LIME was employed to generate instance-level explanations for the Random Forest model, offering insights into how individual feature values influenced the model’s decision for a specific transaction. In the LIME plot, negative feature contributions indicate that a feature increases the likelihood of the transaction being classified as fraud, while positive contributions shift the prediction toward the legitimate class. This interpretability allows us to understand how feature-level variations shape the model’s reasoning.

As shown in Figure 7, features such as V14, V12, V17, and V16 contributed most strongly toward predicting the transaction as fraudulent, with higher or specific threshold values (e.g., V14 > 0.11 and V12 > 0.09) pushing the prediction in that direction. Conversely, features like V1 and V24 had positive contributions, supporting the classification of the transaction as legitimate. Intermediate features such as V10, V21, V18, and V6 exerted smaller yet meaningful influences on the outcome.

These findings indicate that the Random Forest model’s decision is shaped by a combination of multiple influential variables rather than being dominated by a single factor. This diversity of contributing features enhances model interpretability and reliability. From a practical standpoint, the LIME explanations help fraud analysts understand why certain transactions are labeled as fraudulent or legitimate, providing transparency and confidence in the Random Forest model’s predictive behavior.

4.4. SHAP Analysis for Random Forest

To interpret the Random Forest model, SHAP was employed to quantify the contribution of each feature to the model’s output. The local SHAP explanation in Figure 8 illustrates the magnitude and direction of feature influence for an individual transaction. The analysis reveals that V14, V12, and V10 exert the strongest negative SHAP values, indicating that their lower or abnormal values significantly drive the model toward predicting a fraudulent transaction.

Other features such as V16, V3, and V4 also contribute notably but to a lesser extent, refining the model’s decision boundary by capturing subtle irregularities in transaction behavior. The predominance of negative SHAP values in this explanation suggests that the identified instance exhibits patterns typically associated with fraudulent activity, particularly within the dimensions encoded by V14 and V12. Overall, the SHAP analysis provides a transparent understanding of the Random Forest decision process. It highlights which features most strongly influenced the model toward labeling the transaction as fraud and confirms that the model’s predictions are based on interpretable, behaviorally meaningful variables rather than random noise. Such explainability is crucial for increasing trust and accountability in automated fraud detection systems used by financial institutions.

4.5. Results for XGBoost Model

The performance of the XGBoost model was evaluated using several evaluation metrics, as shown in

Table 5. XGBoost Model Evaluation Metrics.

Metric	Score
Accuracy	0.9995
Precision	0.8776
Recall	0.9556
F1 Score	0.9149
ROC AUC	0.9997

. The model achieved a high accuracy of 99.95%, with a precision score of 87.76%, recall of 95.56%, and an F1-score of 91.49%, demonstrating strong fraud detection capability. Additionally, the ROC AUC value of 0.9997 confirms the model’s excellent ability to discriminate between legitimate and fraudulent transactions. These results indicate that XGBoost is a highly effective model for credit card fraud detection in imbalanced datasets.

The classification report for the XGBoost model is presented in

Table 6. XGBoost Model Classification Report.

Class	Precision	Recall	F1-Score	Support
0 (Legit)	1.00	1.00	1.00	15,432
1 (Fraud)	0.88	0.96	0.91	45
Accuracy: 0.9995
Macro Avg	0.94	0.98	0.96	15,477
Weighted Avg	1.00	1.00	1.00	15,477

, which provides detailed performance metrics including precision, recall, and F1-score for each class (fraud and legitimate transactions).

4.5.1. Confusion Matrix for XGBoost

The confusion matrix in Figure 9 illustrates the classification performance of the XGBoost model on the test set. The matrix shows 15,426 legitimate transactions correctly classified (true negatives) and 43 fraudulent transactions correctly detected (true positives), with 6 false positives and 2 false negatives.

From these counts, the specificity (true negative rate) is $\mathrm{Specificity}={\displaystyle \frac{\mathrm{15,426}}{\mathrm{15,426}+6}}\approx 0.99961$ (99.96%), and the recall (sensitivity) for the fraud class is ${\mathrm{Recall}}_{\mathrm{fraud}}={\displaystyle \frac{43}{43+2}}\approx 0.95556$ (95.56%). These results indicate XGBoost very rarely misclassifies legitimate transactions while still detecting the vast majority of fraudulent cases.

4.5.2. ROC Curve for XGBoost

The Receiver Operating Characteristic (ROC) curve for the XGBoost classifier, shown in Figure 10, rises steeply toward the top-left corner, reflecting the model’s ability to achieve a high true positive rate while keeping the false positive rate extremely low. The Area Under the Curve (AUC) of 0.9997 further confirms the outstanding discriminative capacity of XGBoost in distinguishing fraudulent from legitimate transactions.

While the ROC curve demonstrates near-perfect performance, it is important to note that in the context of fraud detection, a very high AUC does not automatically guarantee optimal real-world effectiveness. Even with such excellent separation, the operating threshold must be carefully chosen to balance the cost of false positives, such as unnecessary customer alerts, with the risk of false negatives, i.e., undetected fraud. Thus, the ROC analysis highlights the superior capability of XGBoost while also emphasizing the importance of threshold calibration for practical deployment in fraud detection systems.

4.5.3. Cross-Validation vs. Test Performance

To further evaluate the generalization ability of the XGBoost classifier, we compared the performance obtained from cross-validation with that on the independent test set.

Table 7. XGBoost Cross-Validation vs. Test Set Results.

Metric	Cross-Validation (CV = 3)	Test Set
F1 Score	0.9998	0.9149
Accuracy	–	0.9995
Precision	–	0.8776
Recall	–	0.9556
ROC AUC	–	0.9997

summarizes the results.

As shown, cross-validation yielded an almost perfect F1 score (0.9998), indicating that the model fit the training folds extremely well. However, when evaluated on the unseen test set, the F1 score dropped to 0.9149, with precision of 0.8776 and recall of 0.9556. This discrepancy highlights the slight overfitting of XGBoost during training, despite maintaining an excellent ROC AUC of 0.9997 on the test set. Overall, these results demonstrate that while XGBoost generalizes well, careful threshold selection and regularization remain important for deployment in fraud detection systems.

4.5.4. LIME Explanation for XGBoost

To enhance the interpretability of the XGBoost model, Local Interpretable Model-agnostic Explanations (LIME) were applied. As illustrated in Figure 11, the local explanation highlights how individual feature values influenced the prediction of a fraudulent transaction.

In this case, features such as V14, V4, and V12 provided the strongest positive contributions (green bars), pushing the model toward a fraud classification. Additional features including V10, V7, V3, and V17 also reinforced this decision, though with smaller magnitudes. Conversely, features like V8 and V23 contributed negatively (red bars), pulling the prediction slightly toward the legitimate class.

Overall, the positive signals dominated, resulting in the transaction being classified as fraud. In the LIME plots, positive feature contributions indicate that the feature value increases the likelihood of fraud, while negative contributions suggest that the feature value decreases this likelihood (i.e., favors the legitimate class). This localized explanation helps demonstrate that the model’s classification is driven by a combination of multiple influential features rather than a single factor, thereby offering transparency in fraud detection.

4.6. SHAP Explanation for XGBoost

To further interpret the predictions of the XGBoost classifier, SHapley Additive exPlanations (SHAP) were applied. The summary plot in Figure 12 not only ranks features by their overall importance but also illustrates the distribution of their impact across transactions. Among the most influential features were V14, V12, and V10, which showed both high average contributions and wide variability. For instance, high values of V14 strongly increased the likelihood of a fraud prediction, whereas lower values of V12 tended to push predictions in the same direction. This pattern suggests that these features capture transaction behaviors that sharply distinguish fraudulent from legitimate cases. The distributional nature of the SHAP plot also reveals heterogeneity: while some features (e.g., V10) consistently exert a moderate effect, others (V14) show highly variable contributions depending on the transaction, indicating that they are context-dependent signals of fraud. Such insights are critical in fraud detection, where not all features contribute uniformly across instances. In addition, a SHAP force plot was generated for a single fraud case to visualize how individual feature values combined to produce the final prediction. In this example, features such as V14 and V12 exerted strong positive “pushes” toward the fraud class, while others (e.g., V17) provided smaller counteracting influences. The interplay of these forces demonstrates that XGBoost integrates multiple signals—both supportive and contradictory, before flagging a transaction as fraudulent. This level of transparency is valuable in financial applications, as it allows analysts to validate model outputs, identify the dominant risk drivers in each case, and better understand the trade-offs underlying automated fraud detection.

5. Comparative Analysis of Random Forest and XGBoost Models

This section presents a comparative analysis of the Random Forest (RF) and XGBoost (XGB) models based on key performance metrics for credit card fraud detection. The evaluation considers Accuracy, Precision, Recall, F1-score, and ROC AUC, while also reflecting on the implications of these results in the context of imbalanced data.

5.1. Performance Analysis of Random Forest and XGBoost

As summarized in

Table 8. Performance Comparison of Random Forest and XGBoost.

Metric	Random Forest	XGBoost
Accuracy	0.9996	0.9995
Precision	0.8909	0.8776
Recall	0.9423	0.9556
F1-Score	0.9159	0.9149
ROC AUC	0.9979	0.9997

, both models achieved exceptionally high overall accuracies (≈99.95%), demonstrating strong performance on the credit card fraud detection task. However, given the highly imbalanced nature of the dataset, accuracy alone is not a sufficient indicator of model quality; therefore, metrics such as precision, recall, F1-score, and ROC AUC offer deeper insights into model behavior.

The Random Forest model achieved a slightly higher precision (0.8909), indicating that when it classified a transaction as fraudulent, it was more likely to be correct. This aligns with Random Forest’s ensemble bagging approach, which effectively reduces variance and minimizes false positives. Such high precision is beneficial for financial institutions, as it helps limit unnecessary manual reviews and operational costs associated with incorrectly flagged transactions.

Conversely, XGBoost demonstrated a higher recall (0.9556), reflecting its superior ability to identify fraudulent transactions. This improvement stems from XGBoost’s boosting mechanism, which iteratively focuses on misclassified samples, enabling it to capture subtle fraud patterns that might be overlooked by Random Forest. High recall is especially important in fraud detection, where undetected frauds (false negatives) can result in significant financial losses.

In terms of overall balance, both models performed competitively, with Random Forest achieving an F1-score of 0.9159 and XGBoost closely matching it at 0.9149. However, XGBoost exhibited a slightly higher ROC AUC (0.9997 vs. 0.9979), indicating marginally stronger discriminative capability across varying classification thresholds.

Overall, the comparison reveals that while Random Forest offers excellent precision and robust overall accuracy, XGBoost provides slightly better recall and overall discriminative power. The choice between the two should therefore depend on organizational priorities: Random Forest may be preferred in scenarios emphasizing precision and reduction of false alarms, whereas XGBoost is more suitable for applications prioritizing maximum fraud detection coverage.

5.2. Interpretability Analysis Using SHAP and LIME

To gain deeper insight into how the Random Forest (RF) and XGBoost (XGB) models make fraud predictions, both global (SHAP) and local (LIME) explanation techniques were applied.

Table 9. Key Interpretability Results for Random Forest and XGBoost Models.

Aspect	Random Forest	XGBoost
Top SHAP Features	V14, V12, V10 (strongest influence)V16, V3, V4 (moderate impact)	V14, V12, V10 (most influential)V4, V7, V3, V17 (moderate impact)
SHAP Insights	Negative SHAP values for V14, V12, and V10 drive fraud predictions;lower or abnormal feature values indicate fraudulent behavior;model relies on multiple meaningful attributes.	High values of V14 and low values of V12 increase fraud likelihood;heterogeneous contributions across transactions;features show context-dependent influence on fraud classification.
Top LIME Indicators	V14 > 0.11, V12 > 0.09, V17 and V16 > 0.17 contribute most to fraud predictions;V1 and V24 show positive (legitimate) influence.	V14, V4, and V12 show strongest positive (fraud) contributions;V10, V7, V3, and V17 reinforce fraud decision;V8 and V23 contribute negatively (legitimate).
Additional LIME Patterns	Intermediate features (V10, V21, V18, V6) provide smaller but consistent influence;model decisions shaped by multiple interacting variables.	Positive contributions dominate, indicating strong fraud signal;combination of supportive and opposing features drives classification.
Model Sensitivity	Balanced and interpretable;decisions distributed across several strong predictors;less prone to single-feature dominance.	Highly responsive to top predictors (V14, V12);captures fine-grained fraud signals but slightly more sensitive to noise.

summarizes the top features and key interpretability findings.

5.2.1. Global Explanations (SHAP)

Both Random Forest and XGBoost identified V14, V12, and V10 as the most influential features in distinguishing fraudulent from legitimate transactions. However, the magnitude and distribution of SHAP values differ between the two models, reflecting their distinct learning behaviors.

For the Random Forest model, negative SHAP values for V14, V12, and V10 indicate that lower or abnormal feature values strongly drive predictions toward the fraud class. The model distributes importance across several moderately influential variables, such as V16, V3, and V4, suggesting that its decisions are shaped by a balanced combination of multiple behavioral indicators rather than a few dominant ones.

In contrast, XGBoost exhibits more concentrated and variable SHAP contributions. Features such as V14 and V12 show strong and sometimes highly polarized effects, indicating sharper sensitivity to certain transaction patterns. Meanwhile, V10, V4, V7, and V17 provide additional but smaller contributions that refine the model’s classification boundary. This heterogeneity in SHAP distributions suggests that XGBoost captures a broader range of nuanced patterns across transactions, albeit with greater dependence on its most impactful features.

Overall, SHAP analysis demonstrates that Random Forest achieves interpretability through distributed feature influence, while XGBoost achieves higher discriminative precision by emphasizing a smaller subset of highly informative variables.

5.2.2. Local Explanations (LIME)

At the transaction level, the LIME analyses provide a detailed understanding of how individual feature values influence model predictions. For the Random Forest model, features such as V14, V12, V17, and V16 exert the strongest positive contributions toward predicting fraudulent transactions. In contrast, features like V1 and V24 contribute positively toward classifying the transaction as legitimate, reflecting their stabilizing influence on the model’s decision. These results demonstrate that Random Forest bases its classification on a combination of multiple influential variables, rather than relying on a single dominant feature, which enhances interpretability and robustness.

For the XGBoost model, LIME explanations reveal more fine-grained local patterns. The features such as V14, V4, and V12 provide the strongest positive contributions (pushing the model toward a fraud classification), supported by smaller yet meaningful effects from V10, V7, V3, and V17. Conversely, features such as V8 and V23 exhibit negative contributions, slightly favoring the legitimate class.

Overall, while both models identify similar key predictors, XGBoost exhibits greater sensitivity to localized variations in feature values, capturing subtle behavioral anomalies that may only occur in rare or complex fraud cases. Random Forest, by comparison, emphasizes broader and more stable decision patterns, yielding consistent yet slightly less granular explanations.

5.2.3. Comparative Insights

• Feature Focus: Both models emphasize similar key predictors (V14, V12, and V4), but XGBoost’s sharper SHAP distributions indicate stronger dependence on a smaller set of dominant features. In contrast, Random Forest distributes importance more evenly across several moderately influential variables, contributing to its stability.
• Temporal Dynamics: XGBoost effectively captures temporal and sequential patterns, such as transactions occurring at unusual times—while Random Forest shows minimal sensitivity to such temporal variations.
• Pattern Complexity: XGBoost uncovers more intricate feature interactions and narrower decision boundaries, enhancing its ability to detect subtle or rare anomalies. However, this increased complexity may introduce a higher risk of overfitting. Random Forest maintains broader and more interpretable decision rules that generalize well across unseen data.
• Robustness vs. Sensitivity: Random Forest demonstrates higher precision, minimizing false positives and ensuring consistent reliability in deployment. XGBoost, on the other hand, achieves higher recall and stronger discriminative power, making it better suited for high-risk scenarios where missing even a few fraud cases is unacceptable.

5.3. Comprehensive Metric-Based Comparison of Random Forest and XGBoost Models

As summarized in Table 8, both models achieved exceptionally high overall accuracies (above 99.9%), demonstrating strong discriminative capability for the fraud detection task. However, accuracy alone is not sufficient in imbalanced datasets; therefore, precision, recall, F1-score, and ROC AUC provide more meaningful insights into real-world performance as presented in

Table 10. Comparison Between Random Forest and XGBoost.

Category	Metric	Random Forest	XGBoost	Winner
Performance	Accuracy	0.9996	0.9995	RF
	Precision	0.8909	0.8776	RF
	Recall	0.9423	0.9556	XGB
	F1 Score	0.9159	0.9149	RF (slightly)
	ROC AUC	0.9979	0.9997	XGB
Interpretability	SHAP Focus	Balanced across top 8–10 features (V14, V12, V10)	Concentrated on dominant few (V14, V12, V10)	Tie
	LIME Clarity	Stable, broad thresholds (V14 > 0.11, V12 > 0.09)	More detailed local rules (V14, V4, V12, V8)	XGB
Imbalance	SHAP Shift Stability	Stable under resampling	More variable feature magnitudes	RF
Efficiency	Training Speed	Moderate (bagging ensemble)	Faster convergence (boosting)	XGB

.

The Random Forest model achieved slightly higher precision (0.8909), meaning that when it predicted a transaction as fraudulent, it was more often correct. This aligns with the ensemble’s bagging nature, which emphasizes variance reduction and robustness, thereby minimizing false positives. Such characteristics make Random Forest particularly useful in operational settings where reducing unnecessary manual investigations is crucial.

On the other hand, XGBoost exhibited a marginally higher recall (0.9556) and a comparable F1-score (0.9149 vs. 0.9159), reflecting its superior sensitivity in identifying fraudulent transactions. This advantage arises from XGBoost’s boosting framework, which incrementally corrects previous errors and effectively captures complex, subtle relationships within the data. High recall is especially valuable in domains where missing fraudulent activity carries significant financial and reputational costs.

Both models displayed near-perfect ROC AUC values, 0.9979 for Random Forest and 0.9997 for XGBoost, indicating excellent discriminative power across varying decision thresholds. This confirms that each classifier maintains a strong ability to separate legitimate from fraudulent transactions under different operating conditions.

Overall, while Random Forest provides greater stability and precision (reducing false alarms), XGBoost offers slightly enhanced recall and sensitivity, making it better suited for environments prioritizing maximum fraud detection coverage. The choice between the two models should thus depend on the operational trade-off between minimizing false positives and maximizing detection completeness.

6. Conclusions

This study presented a comprehensive comparison of Random Forest (RF) and XGBoost (XGB) models for credit card fraud detection, focusing on achieving an optimal balance between predictive accuracy and interpretability. Experimental results demonstrated that both models achieved exceptional performance, with overall accuracies exceeding 99.95%. The RF model yielded higher precision (0.8909), effectively reducing false positives and unnecessary manual reviews, while XGB achieved superior recall (0.9556) and ROC AUC (0.9997), enhancing the detection of fraudulent cases with greater coverage. Both models produced nearly identical F1-scores (approximately 0.915), confirming strong consistency between precision and recall.

Through interpretability analysis using SHAP and LIME, the study identified V14, V12, and V10 as the most influential features across both models. SHAP results indicated that RF distributed influence more evenly across a broader set of variables, reflecting model stability and robustness, whereas XGB exhibited sharper, more concentrated feature impacts, suggesting stronger sensitivity to dominant predictors. Similarly, LIME analyses revealed that RF relied on stable, generalizable thresholds, while XGB captured more granular, context-dependent feature interactions. These complementary insights provide transparency into how each model arrives at its predictions, which is critical for building user trust in financial decision-making systems.

The practical implication of these findings is clear: effective fraud detection requires not only high predictive performance but also interpretability to support regulatory compliance, model validation, and stakeholder confidence. The comparative analysis shows that RF is better suited for precision-driven contexts that demand reliability and fewer false alarms, while XGB excels in recall-oriented applications where capturing all potential frauds is the priority.

Nevertheless, the study acknowledges several limitations. The analysis was conducted using a single benchmark dataset, which may not fully capture the variability of real-world fraud behavior. Additionally, evaluations were performed in an offline environment, without addressing deployment factors such as latency, adaptability, and model drift.

Future research directions include:

• Extending validation across diverse datasets and financial domains to ensure generalizability.
• Developing hybrid or ensemble frameworks that integrate the precision of RF with the recall strength of XGB.
• Exploring advanced explainability tools beyond SHAP and LIME, such as counterfactual and causal interpretability methods.
• Implementing adaptive, real-time fraud detection pipelines with continuous retraining and monitoring capabilities.

In conclusion, this work contributes to advancing fraud detection systems that are not only accurate but also interpretable and trustworthy. By bridging the gap between performance excellence and model transparency, the study provides actionable guidance for designing explainable AI solutions in high-stakes financial applications.