Realization of Efficient Exploration by Self-Generating Evaluation Considering Curiosity and Fear Indices Based on Prediction Error

Abstract

In this paper, we propose a reinforcement-learning method in which an agent generates intrinsic rewards by evaluating its environment based on sensor data. The evaluation is perormed from three perspectives, one of which concerns the predictability of sensor inputs. This perspective focuses on the magnitude of the prediction error: a large error suggests environment uncertainty and leads to a low evaluation. However, prediction errors can arise from two distinct causes that previous method fail to distinguish. The first is the intrinsic unpredictability of a situation, where high prediction error persists even after sufficient learning. Such states are likely to be dangerous and should be assigned low evaluations to discourage the agent from entering them. The second is insufficient learning of the predictor itself, where high prediction error simply reflects the need for further exploration. These states should be assigned high evaluations to encourage learning. To address these cases this study introduced a method that evaluates environmental states by jointly considering the degree of danger and the necessity of further predictor learning with the learning progress for each sensor input. Two complimentary evaluation indices were proposed curiosity, which promotes exploration of insufficiently learned states, and fear, which discourages entry into unpredictable or hazardous states. The effectiveness of the proposed method was demonstrated through simulation experiments in a two-dimensional discrete environment.

1. Introduction

In recent years, robots have been expected to play an active role in a variety of situations [1,2,3] and adapt to a wide variety of environments. Therefore, studies [4,5,6,7] using reinforcement-learning (RL) [8,9,10] have attempted to enable robots to adapt to various environments [11,12,13]. In reinforcement learning, an agent receives a reward as an evaluation of its behavior in the environment. Additionally, the agent learns based on the reward through trial and error. Rewards are generated by a reward function that considers tasks and environments in advance.

In RL, there is a field of study termed intrinsic reward [14,15,16] in which an agent creates the reward itself. In basic RL, the agent learns the behavior depending on the external rewards given by the environment. Therefore, if the environment and task change or the setting of external rewards is inadequate, the agent can not learn suitable behaviors [17,18]. Thus, methods for assisting with action learning without depending on external rewards have been investigated [19,20,21]. As method using intrinsic reward was proposed as one of these methods. Conventional methods using intrinsic rewards include the intrinsic curiosity module (ICM) [22,23] and random network distillation (RND) [24,25]. The ICM generates an intrinsic reward based on the prediction error of the states and promotes exploration. The ICM consists of feature extraction layers, a forward model, and an inverse model. The forward model predicts the next state based on the current state and action. In contrast, the inverse model predicts the next action based on the current and subsequent states. The larger the prediction error, which is calculated by the prediction from the forward or inverse model, the higher the value of the intrinsic reward. The RND generates an intrinsic reward based on the novelty of the states and promotes exploration. An RND comprises of two similar neural networks. One of these, termed the prediction network, learns the information of states in the environment. The other network, termed the target network, has random weights and does not learn the state information in the environment. As the learning of the prediction network progresses, the weights of the two networks differ significantly. In this case, low intrinsic rewards are generated. However, when the weights of two networks are similar, they are likely to be in a state of novelty. Therefore, high intrinsic rewards are generated, which prompt exploration.

We have proposed a “self-generating evaluation (SGE)” method [26,27], which uses sensor data to generate internal rewards. In conventional methods, internal rewards are designed to promote exploratory behavior that aids task completion. In contrast, SGE generates internal rewards as pleasurable or unpleasant signals based on the behavioral petterns of the sensor inputs. We posit that the agent in the robot can evaluate the environmental stimulus based on the tendency of the sensor input, if the robot is equipped with a suitable sensor for the robot’s body. Therefore, many perspectives have been designed to evaluate the dangers of environmental stimuli. The agent generates an evaluation for the environmental stimulus based on these perspectives when the agent receives it. The internal reward is calculated from the evaluation and applied to RL. Thus, the agent recognizes the physical features of the robot based on the internal reward and learns a behavior that is suitable for the robot.

One aspect of the SGE is the predictability of the sensor input, which is used to evaluate the environmental stimulus based on the absolute value of the prediction error. The prediction error is the difference between the values calculated by the predictor and actual input value. The larger the absolute value of the prediction error, the more unpredictable the state. In this situation, the robot introducing the agent can be damaged unexpectedly, because the agent can not select a suitable action for the environment and task. Therefore, when the prediction error of the input is large, the predictability evaluation indicator calculates a low evaluation value and prompts an avoidance behavior. However, as a factor in the large prediction error, the learning of the predictor may be insufficient because of the small number of searches for states with large prediction errors. In the previous method, only cases of unpredictable and dangerous stimuli in the environment were considered for large prediction errors, because they focused on the degree of danger. Therefore, the previous method did not consider cases in which the predictor did not sufficiently learn environmental stimuli. Even if the reason for the high prediction error is the lack of predictor learning for a learnable stimulus, the agent in the previous method avoided this because it considered the stimulus to be dangerous. Therefore, the predictor could not receive an insufficiently learned stimulus, and the learning of the predictor for the stimulus did not progress. Consequently, the agent could not determine the most suitable behavior for its environment or capacity.

To address this problem, the predictability of sensor inputs by considering both the predictor’s learning progress and the degree of environmental danger was evaluated. Accordingly, an evaluation index was proposed that encourages exploratory behavior when learning progress is insufficient and avoidance behaivor when prediction errors indicate danger. One of the evaluation inidices focuses on the stimuli that the predictor has not yet learned. Therefore, this evaluation index prompts exploratory behaviors to learn for these stimuli. This evaluation index is defined as “the evaluation index of curiosity”, whereas the other foucuses on stimuli that the predictor can not predict. Therefore, this evaluation index indicates discomfort and avoidance behaviors for these stimuli. This evaluation index is defined as “the evaluation index of fear.” Both evaluation indices calculated the evaluation value by considering the magnitude and changes in the prediction error. This magnitude was used to evaluate whether a critical stimulus could be predicted. The change in the prediction error was used to evaluate its tendency to increase or decrease. Considering these factors, it is posited that the agent exhibits exploratory behavior while improving its avoidance performance.

This study aims to improve the exploration efficiency by introducing two new evaluation indices—curiosity and fear—to replace the conventional evaluation index based on the predictability of sensor inputs. In addition, the performance of the proposed method was compared with those of previous studies in a two-dimensional simulation environment to demonstrate its usefulness.

2. Algorithm of Self-Generated Evaluations

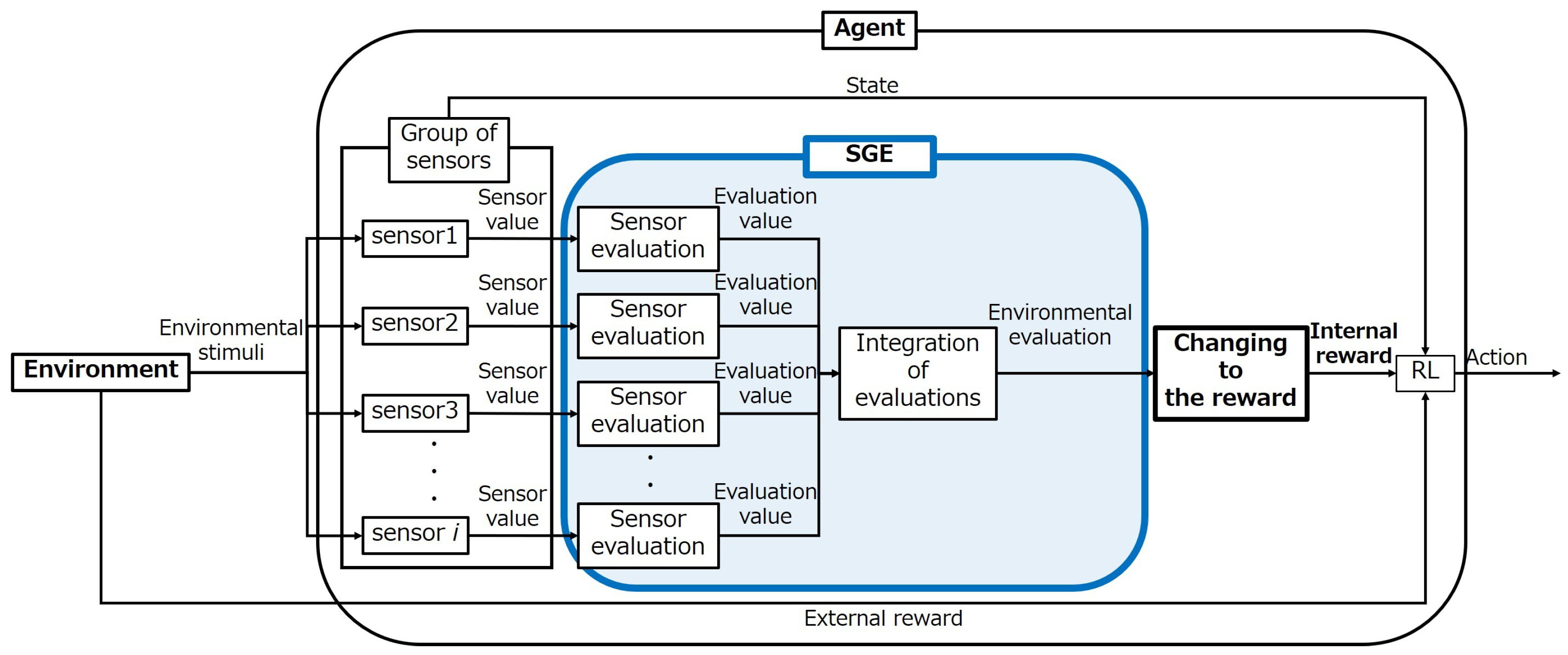
In the SGE, the agent evaluates the sensor data and calculates the reward from the evaluation. The reward function in reinforcement learning must be pre-designed by the designer by considering the environment and task. Therefore, the reward function must be redesigned when the environment and tasks change. Therefore, it is difficult for RL agents in reinforcement learning to adapt autonomously to dynamic environments. To solve this problem, we proposed the SGE method. It is posited that, by receiving stimuli from the environment as sensor information, the agent can evaluate whether the current state is good or bad based on the differences in the stimuli within each state. By converting the evaluations generated by the agent into rewards, the agent can learn behaviors independent of the reward function and adapt autonomously to a wide variety of environments. A flowchart of the RL using SGE is shown in Figure 1.

In SGE, an agent evaluates the stimuli from an environment based on three perspectives that are designed to avoid damage to or failure of the robot. The first factor was the magnitude of the sensor input. This perspective provided an evaluation index for the magnitude of sensor inputs. The magnitude of the input was considered because a large stimulus to the robot can cause damage or machine failure. Therefore, the magnitude of the sensor input was considered. The second perspective concerned the predictability of sensor inputs. This perspective provided an evaluation index for the predictability of sensor inputs. The reasons for the difficulty in prediction may include a lack of experience and the characteristics of the stimuli. If an agent cannot predict the status of a state, it cannot select the appropriate behavior in that state. In such cases, the agent may experience sudden environmental damage. Therefore, the predictability of the sensor input was considered. The third perspective concerned the time variation of the sensor input. This perspective had an evaluation index for the time variation of the sensor inputs. In a real environment, a certain type of stimulus is always emitted, and the characteristics of the stimulus change with location and time. The agent can distinguish each state based on the differences in the characteristics of the stimuli. If the input does not vibrate for a long time, there is a high probability of an abnormality occurring inside or outside the agent. The agent is unable to learn effectively because it perceives that the state has not changed despite performing numerous actions. Therefore, temporal variation in the sensor input was considered.

Evaluation indices were designed to evaluate the environment based on these three perspectives. All the evaluation values calculated from the evaluation index were between zero and one. The evaluation value is defined such that values closer to zero correspond to stronger avoidance of stimuli. Finally, the evaluation values for each evaluation index were integrated into a single evaluation value for a single sensor input. The details of each evaluation index and integration of the evaluation values are explained in Section 2.1 and Section 2.2. A flowchart of the generated sensor evaluation values for SGE is shown in Figure 2.

2.1. Calculation Method of the Evaluation Values by Each Evaluation Index in SGE

First, the evaluation index was explained from the perspective of the magnitude of the sensor input. The evaluation value for the magnitude $E_{S_i}\left(n_t\right)$ of the nth input to sensor i during an action at time t is defined by Equation (1) using the mean value of sensor input ${\mu }_i\left(n_t\right)$, maximum value $ma{x}_i$ in the input value range, constant $N_i$, and variable ${\delta }_i\left(n_t\right)$. In Equation ( refeqn:magnitude), if the mean value of the input values ${\mu }_i\left(n_t\right)$ becomes too large, the evaluation value $E_{S_i}\left(n_t\right)$ will be low. This design was intended to prompt the robot to avoid damage from stimuli. The sensor input values for the stimuli tended to be high when the robot was damaged by it. Therefore, calculating the low evaluation values for the mean of the large input values can prompt the agent to avoid damaging the robot.

$$E_{S_i}\left(n_t\right)={\left[1+exp\left\{{\displaystyle \frac{{\mu }_i\left(n_t\right)-\frac{ma{x}_i+{\delta }_i\left(n_t\right)}{2}}{N_i(ma{x}_i-{\delta }_i\left(n_t\right))}}\right\}\right]}^{-1}$$

(1)

$${\mu }_i\left(n_t\right)={\displaystyle \frac{1}{n}}\sum _{j=0}^n{\psi }_i\left(n_t\right)$$

(2)

The mean value ${\mu }_i\left(n_t\right)$ of the input value ${\psi }_i\left(n_t\right)$ and the variable ${\delta }_i\left(n_t\right)$ used in Equation (1) is explained. The magnitude of the sensor input used to generate the evaluation was calculated as the average value of the input within a certain period, using Equation (2). The mean of the input values is used to obtain receive numerous input formations in a single action. If the mean value of the input values ${\mu }_i\left(n_t\right)$ becomes too large, the evaluation value $E_{S_i}\left(n_t\right)$ will be low. The variable ${\delta }_i\left(n_t\right)$ called “habituation for the magnitude of the input” is updated each time data is input by the Equation (3) using constant ${\beta }_i$. Thus, the evaluation value of the magnitude of the input fluctuates, and the agent can easily adapt to the current environment.

$${\delta }_i\left(n_t\right)={\delta }_i\left(n_{t-1}\right)+{\beta }_i\{{\mu }_i\left(n_t\right)-{\delta }_i\left(n_{t-1}\right)\}$$

(3)

Next, the evaluation index is explained from the perspective of the predictability of the sensor input. The evaluation value for the magnitude $E_{S_i}\left(n_t\right)$ of the nth input to sensor i during an action at time t is defined by Equation (4) using the prediction error $D_i\left(n_t\right)$ and constant $S_i$. The evaluation value $E_{P_i}\left(n_t\right)$ is higher when the prediction error $D_i\left(n_t\right)$ is smaller when the prediction error $D_i\left(n_t\right)$ is larger. This design was intended to prompt the robot to avoid unpredictable sensor inputs that were difficult for the agent to handle. It can be considered that the prediction errors between the actual sensor input and the prediction sensor input tend to be large when the actually sensor input is unpredictable. Therefore, calculating low evaluation values for large prediction errors can prompt the agent to avoid unpredictable sensor inputs. The value of constant $S_i$ determines the change in the evaluation value.

$$E_{P_i}\left(n_t\right)=exp\left\{{\displaystyle \frac{-D_i{\left(n_t\right)}^2}{S_i}}\right\}$$

(4)

The prediction error $D_i\left(n_t\right)$, calculated using Equation (4) is as fllows: the prediction error $D_i\left(n_t\right)$ was calculated by Equation (5) using the prediction value $f_i\left(n_t\right)$ and the input value ${\psi }_i\left(n_t\right)$. The prediction value $f_i\left(n_t\right)$ is calculated using (6), which is a predictor with a constant number of inputs up to the $n_t$th input.

$$D_i\left(n_t\right)={\psi }_i\left(n_t\right)-f_i\left(n_t\right)$$

(5)

$$f_i\left(n_t\right)={\omega }^T\varphi \left(n_t\right)+b$$

(6)

In this study, the support vector regression (SVR) [28,29] is used as a predictor. The radial basis function kernel [30] was used as the mapping function $\varphi$.

Finally, the evaluation index is explained from the perspective of the time variation of the sensor input. The evaluation value for the time variation $E_{S_i}\left(n_t\right)$ of the nth input to sensor i during an action at time t is defined by Equation (7) using the variable $d_i\left(n_t\right)$ and constant $k_i$. The variable $d_i\left(n_t\right)$ is a function that measures the time of no change in the input values over time and is defined by Equation (8). If there is no change in the sensor input over time, then there is a high probability of abnormalities occurring outside or inside the agent. Therefore, if the time of no change in sensor input over time is long, the value of $d_i\left(n_t\right)$ is large owing to the attenuation rate ${\gamma }_i$ and the evaluation value $E_{T_i}\left(n_t\right)$ is low.

$$E_{T_i}\left(n_t\right)=\exp \left\{{\displaystyle \frac{-d_i\left(n_t\right)}{k_i}}\right\}$$

(7)

$$d_i\left(n_t\right)=\left\{\begin{array}{c}{\gamma }_i{d}_i(n_t-1)\left(\right|{\psi }_i(n_t-1)-{\psi }_i\left(n_t\right)|\ne 0)\hfill \\ d_i(n_t-1)+1\left(\right|{\psi }_i(n_t-1)-{\psi }_i\left(n_t\right)|=0)\hfill \end{array}\right.$$

(8)

2.2. Integrating Evaluations

Then, the integration of the evaluation values is explained. The evaluation values from each perspective were calculated based on the sensor input. These three evaluation values are integrated into one evaluation value $E_i\left(n_t\right)$, for the nth input value of sensor i at time t. The sensor evaluation value is defined in Equation (9) as the geometric mean of the evaluation value based on Equations (1), (4) and (7).

$$E_i\left(n_t\right)=\sqrt[3]{E_{S_i}\left(n_t\right)·E_{P_i}\left(n_t\right)·E_{T_i}\left(n_t\right)}$$

(9)

2.3. Converting to the Reward

The method for calculating the reward was also explained. The evaluation values were generated for each input. However, the rewards were calculated for each action. Therefore, all evaluations of sensor i during an action were averaged, and the evaluation value for one action was calculated. The updated formula for the mean of the evaluation value ${\mu }_{E_i}$ is defined by Equation (10) using the discount rate ${\gamma }_e$.

$${\mu }_{E_i}\leftarrow (1-{\gamma }_e){\mu }_{E_i}+{\gamma }_e{E}_i\left(n_t\right)$$

(10)

In this case, the evaluation value with a value range of 0–1 is normalized from $-1$ to 1 for the calculation of a suitable reward for the evaluation value. The formula for calculating the reward is defined in Equation (11).

$$R=2{\mu }_{E_i}-1$$

(11)

3. Proposal Method: Calculating the Evaluation of Curiosity and Fear Considering the Time Variation of the Prediction Error

This study aims to improve exploration efficiency while avoiding great danger. Therefore, we propose introducing an evaluation index of curiosity to prompt exploratory behavior, and an evaluation index of fear to avoid danger based on prediction errors. The curiosity evaluation index considers cases in which the factors that result in larger prediction errors are due to a lack of learning. The prediction error was approximately zero. To achieve this, the predictor that calculates the predicted value must learn the stimuli. Therefore, the evaluation index of curiosity has a high value when the magnitude of the prediction error is medium, considering the stimulus to be predictable and lacking learning for the predictor. Calculating a high evaluation value also prompts exploratory behavior in response to similar stimuli. The curiosity evaluation index considers variations in the prediction error. If the prediction error does not change over several inputs, the learning of the predictor is considered complete; otherwise, no further learning can occur. In this case, the agent must prioritize the archiving task or avoid the danger of exploratory behavior for a similar stimulus. Therefore, exploratory behavior is restrained by calculating a low evaluation value based on the variation in the prediction error. The evaluation index of fear considers cases in which factors that result in larger prediction errors are caused by unpredictable and dangerous stimuli. A large prediction error indicates that the stimulus was unpredictable for the predictor. In this case, the agent cannot select the appropriate behavior and unexpectedly receives dangerous stimuli. Therefore, the evaluation index of fear had a low value when the magnitude of the prediction error was large, considering the stimulus to be unpredictable and dangerous. Calculating a low evaluation value also prompted avoidance behavior in response to similar stimuli. The fear evaluation index also considers variations in the prediction error. If the prediction error in the current stimulus is small, and the prediction error has an increasing trend, the evaluation value is higher if based solely on the magnitude of the prediction error. However, the prediction error was large because it exhibited an increasing trend. In this case, the agent should consider avoiding this behavior in the near future. Therefore, the avoidance behavior is prompted by calculating a low evaluation value based on the variation in the prediction error.

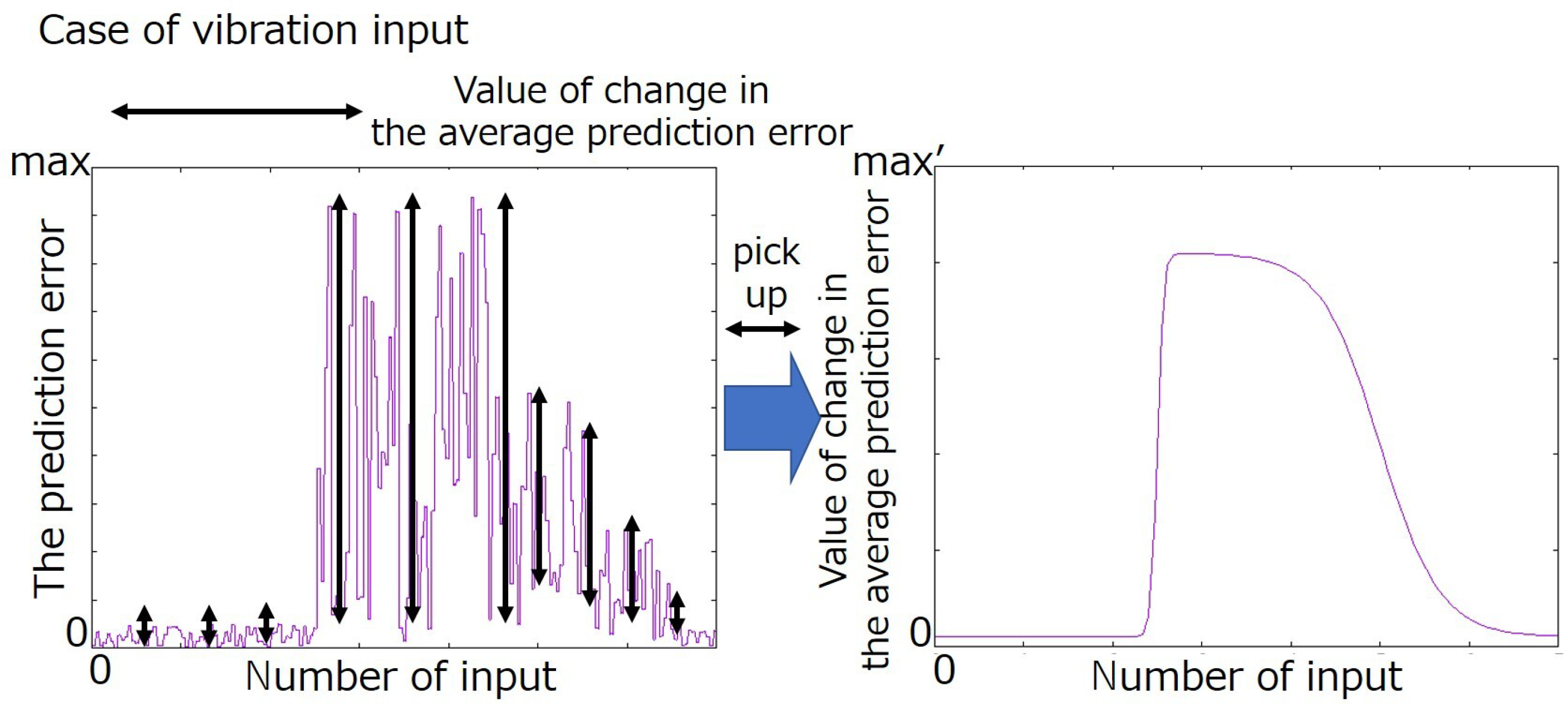
The proposed method focuses on the change in the prediction error to account for time variation in the prediction error. If the change in the prediction error is small, the predictor is likely to have completed the learning for inputs that tend to be close to the current input. However, if the change error is large, learning the inputs that tend to be close to the current input is difficult. By changing the state and accounting for changes in the prediction error, it is possible to evaluate the learning progress of a predictor or comprehend the changing trend in the prediction error. The proposed method considered the prediction error trend over a certain period. This is because the prediction accuracy of the predictor was calculated using the prediction error between the number of inputs. In this study, the accuracy of prediction in the predictor is defined as “the average prediction error.” The average prediction error is calculated using the weighted average of the prediction errors between the number of inputs. 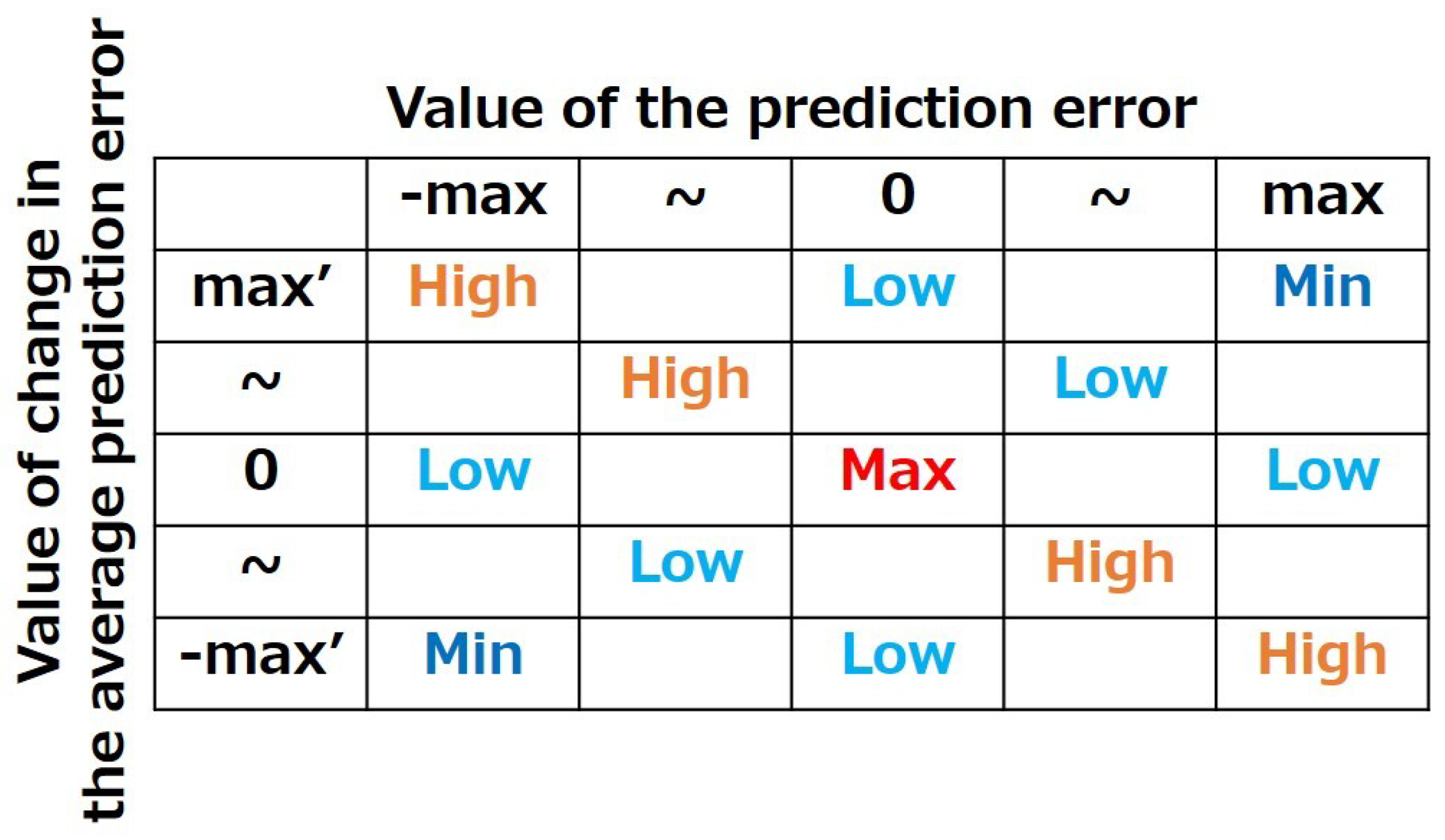Figure 3 shows the relationship between the change in the average prediction error and the transition in the prediction error.

The formula to calculate the amount of change $\Delta P$ in the average prediction error of the nth input to sensor i during action at time t is defined by Equations (12) and (13), using prediction error D. In Equation (12), the average prediction error $P\left(n_t\right)$ is calculated using the weighted average of the prediction error between the past b inputs. The newer the prediction error for the input, the greater the weighted average weight on the prediction error of the past input. Equation (13) calculates the difference between the current average prediction error $P\left(n_t\right)$ and the average prediction error $P(n_t-1)$ for one input.

$$P_i\left(n_t\right)={\displaystyle \frac{{\sum }_{j=1}^b{w}_j·D_i\left(t_{n+(j-1-b) }\right)}{{\sum }_{j=1}^b{w}_j}}$$

(12)

$$\Delta P_i\left(n_t\right)=P_i\left(n_t\right)-P_i(n_t-1)$$

(13)

3.1. Method to Calculate the Evaluation Value of Curiosity

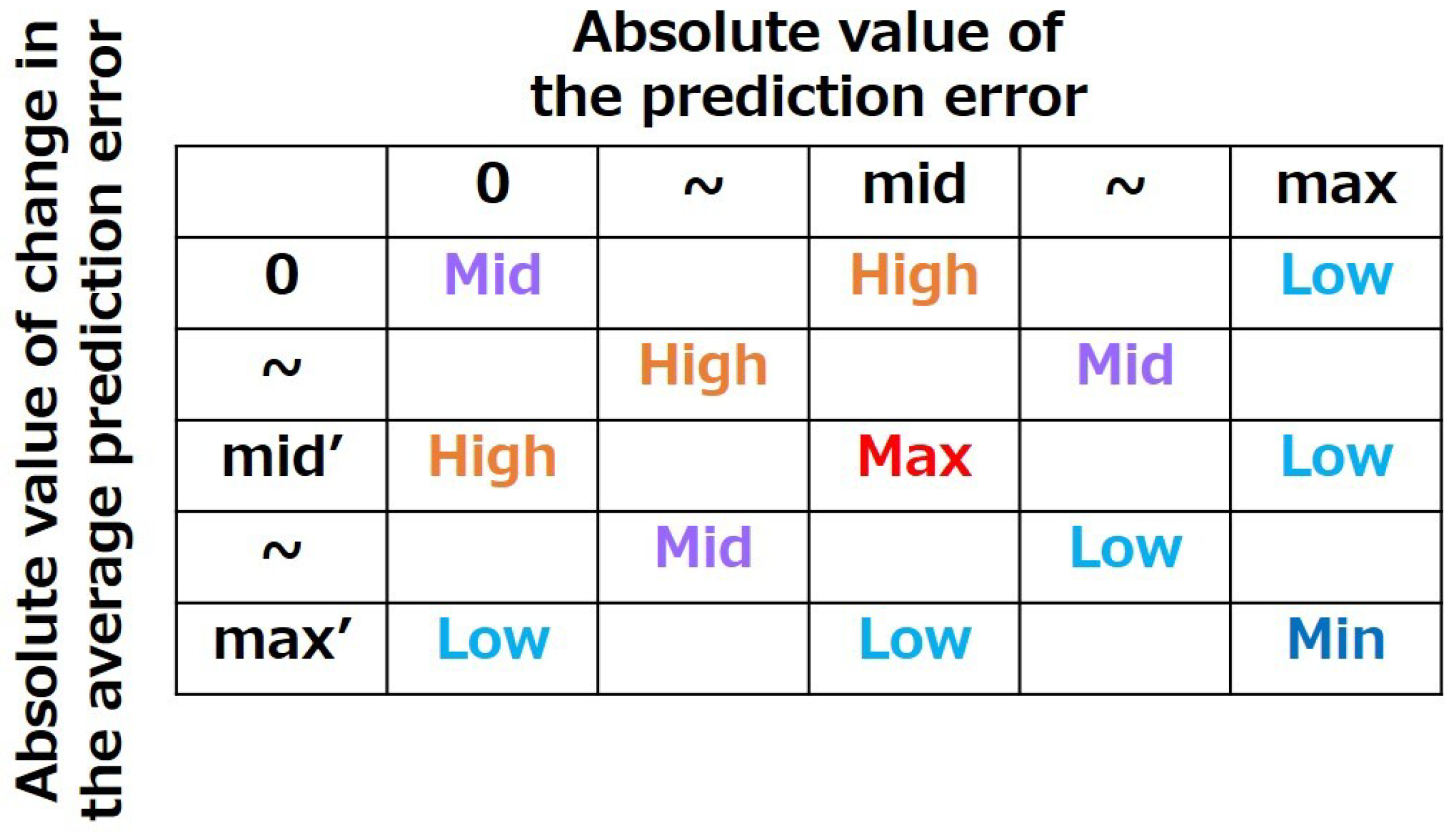
In the proposed method, the curiosity evaluation index calculates the evaluation value based on the magnitude of the prediction error and amount of change in the average prediction error. If the magnitude of the prediction error and amount of change in the average prediction error are moderate, the evaluation index of curiosity is close to the highest evaluation value, prompting the agent to explore the learning of the predictor. However, if both the magnitude of the prediction error and the amount of change in the average prediction error are small, the evaluation index of curiosity is close to the lowest evaluation value and restrains the agent’s exploration behavior for the predictor’s learning, assuming that the predictor’s learning is complete. If both the magnitude of the prediction error and the amount of change in the average prediction error are large, the evaluation index of curiosity is calculated to be close to the lowest evaluation value and restrains the agent’s exploration behavior for the predictor’s learning, assuming that the predictor’s learning is difficult. Figure 4 shows a schematic of the evaluation differences based on the relationship between the magnitude of the prediction error and change in the average prediction error of the curiosity evaluation index.

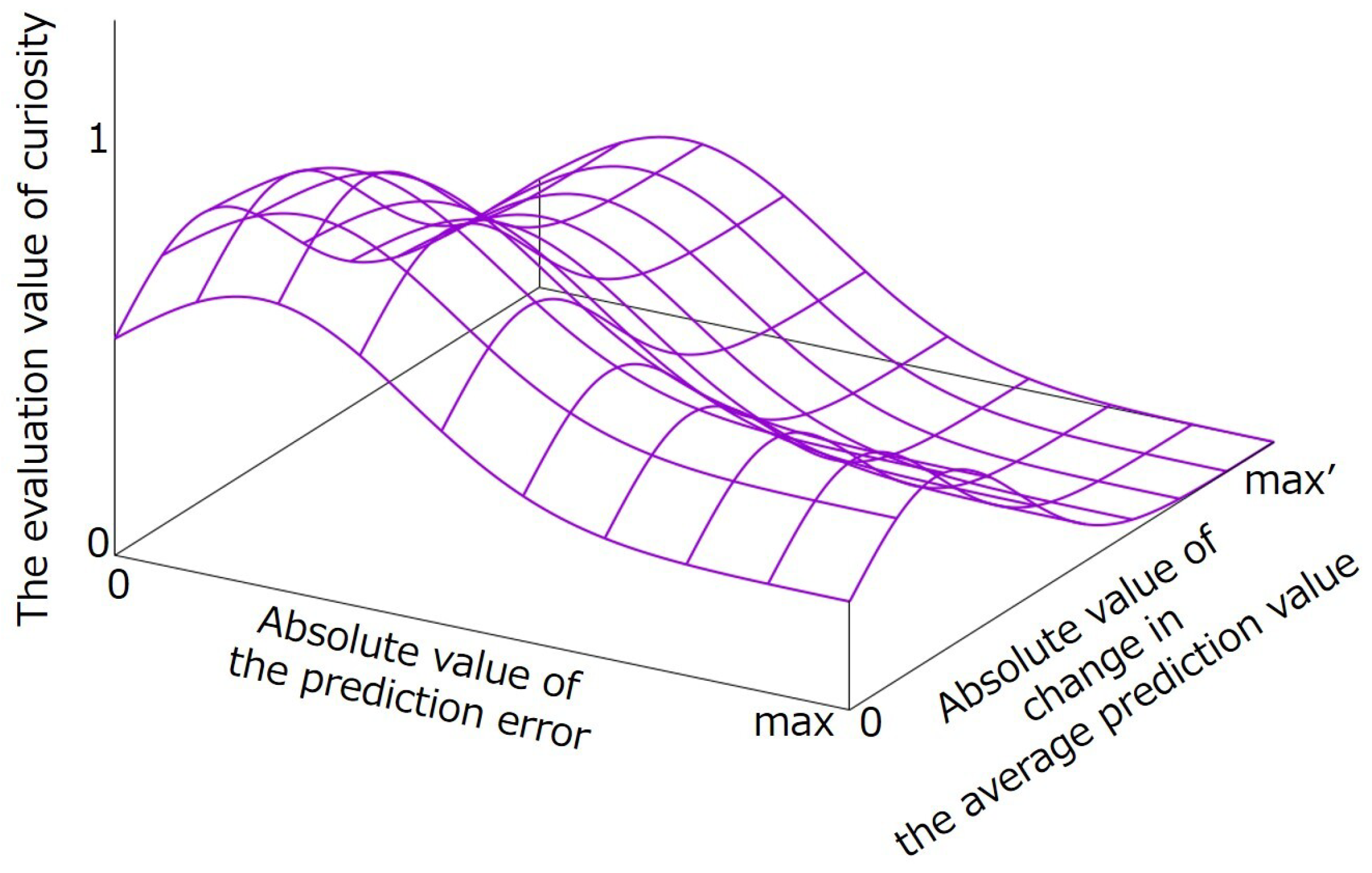
The evaluation value for the curiosity $E_{C_i}\left(n_t\right)$ of the nth input to sensor i during an action at time t is defined by Equation (14) using the absolute value of the prediction error $|D_i\left(n_t\right)|$, the amount of change in the average prediction error $\Delta G\left(n_t\right)$, and the constants $p_{C_1},p_{C_2}$ and $m_C$. Equation (14) is illustrated in Figure 5. Equation (14) yields a value between 0 and 1: the first half of Equation (14) considers the magnitude of the prediction error. The second half of Equation (14) considers the change in the average prediction error. Equation (14) is designed by combining the two Gaussian functions. The purpose of this is to calculate higher evaluation values as the values of $|D_i\left(n_t\right)|$ and $|\Delta G_i\left(n_t\right)|$ approach a medium value, as shown in Figure 4. Additionally, this enabled the calculation of a high or medium evaluation value when the values of $|D_i\left(n_t\right)|$ and $|\Delta G_i\left(n_t\right)|$ were close to zero. This enabled the calculation of a low evaluation value when the values of $|D_i\left(n_t\right)|$ and $|\Delta G_i\left(n_t\right)|$ were close to the maximum value.

$$E_{C_i}\left(n_t\right)={\displaystyle \frac{1}{2}}exp\left\{-{\displaystyle \frac{\left(\right|D_i\left(n_t\right){|-p_{C_1})}^2}{2{m_C}^2}}\right\}+{\displaystyle \frac{1}{2}}exp\left\{-{\displaystyle \frac{\left(\right|\Delta G_i\left(n_t\right){|-p_{C_2})}^2}{2{m_C}^2}}\right\}$$

(14)

Table 1. Sample of the calculated evaluation values of curiosity.

		Absolute Value of the Prediction Error $|{\mathit{D}}_{\mathit{i}}\left({\mathit{n}}_{\mathit{t}}\right)|$
		$|{\mathit{D}}_{\mathit{i}}\left({\mathit{n}}_{\mathit{t}}\right)|$= 0.00	$|{\mathit{D}}_{\mathit{i}}\left({\mathit{n}}_{\mathit{t}}\right)|$= 1.00	$|{\mathit{D}}_{\mathit{i}}\left({\mathit{n}}_{\mathit{t}}\right)|$= 3.00	$|{\mathit{D}}_{\mathit{i}}\left({\mathit{n}}_{\mathit{t}}\right)|$= 6.00
Absolute value of change in the average prediction error $|\Delta G_i\left(n_t\right)|$	$|\Delta G_i\left(n_t\right)|$ = 0.00	$0.61$	$0.80$	$0.37$	$0.30$
	$|\Delta G_i\left(n_t\right)|$ = 1.00	$0.80$	$1.00$	$0.57$	$0.50$
	$|\Delta G_i\left(n_t\right)|$ = 3.00	$0.37$	$0.57$	$0.14$	$0.07$
	$|\Delta G_i\left(n_t\right)|$ = 6.00	$0.30$	$0.50$	$0.07$	$0.00$

shows the sample of the calculated evaluation values of curiosity based on Figure 5. In Table 1, the values of $p_{C_1}, p_{C_2}, m_C, max$ and $ma{x}^{\prime }$, which are the constants of Equation (14), are set to 1.00, 1.00, 1.00, 1.00, 6.00 and 6.00, respectively.

In Table 1, the evaluation value of curiosity is the highest when $|D_i\left(n_t\right)|$ and $|\Delta G_i\left(n_t\right)|$ are 1.00 and 1.00. The closer $|D_i\left(n_t\right)|$ and $|\Delta G_i\left(n_t\right)|$ get to 1.00 and 1.00, the higher the evaluation values of curiosity become. This shows that the values of $p_{C_1}$ and $p_{C_2}$ in Equation (14) are the determining constants for the values of $|D_i\left(n_t\right)|$ and $|\Delta G_i\left(n_t\right)|$ when the evaluation is the highest.

3.2. Method to Calculate the Evaluation Value of Fear

In the proposed method, the fear evaluation index calculates the evaluation value based on the relationship between the magnitude of the prediction error and change in the average prediction error. When the prediction error is small and the change in the average prediction error is large, the prediction error can increase. In this case, the evaluation index of fear calculates a low value to predict avoidance behavior. When the prediction error is large, the evaluation index of fear calculates the evaluation value considering the plus and minus of the change in the average prediction error and the plus and minus of the magnitude of the prediction error. If the positive and negative values of the prediction error are the same as the change in the average prediction error, then the prediction error can be expanded. In this case, the evaluation index for fear is close to the lowest eigenvalue. However, if the positive and negative values of the prediction error differ, then the positive and negative values of the changes in the average prediction error are believed to reduce the error. In this case, the evaluation index for fear was close to its highest value. By calculating the evaluation value, the decrease in the prediction error was prompted, whereas the increase in the prediction error was restrained. Figure 6 shows a schematic of the evaluation differences based on the relationship between the magnitude of the prediction error and amount of change in the average prediction error in the evaluation index of fear.

The evaluation value for the fear $E_{F_i}\left(n_t\right)$ of the nth input to sensor i during an action at time t is defined by Equation (15) using the prediction error $D_i\left(n_t\right)$, the amount of change in the average prediction error $\Delta G\left(n_t\right)$, and the constants $p_F,m_{F_1},$ and $m_{F_2}$. Equation (15) is illustrated in Figure 7. Equation (15) yields a value between 0 and 1: the first half of Equation (15) considers the case in which the positive and negative values of the prediction error, and the negative values in the amount of change in the average prediction error are different. The second half of Equation (15) considers a case in which the positive and negative values of the prediction error and the amount of change in the average prediction error are the same. Equation (15) is designed by combining the two Gaussian functions. The purpose of this was to calculate the lower evaluation values as the distance increased from the center to zero, in accordance with Figure 6. Additionally, this enables different evaluation calculation tendencies for when the same sign in $D_i\left(n_t\right)$ and $\Delta G_i\left(n_t\right)$ occurs, and when different sign in $D_i\left(n_t\right)$ and $\Delta G_i\left(n_t\right)$ occur.

$$E_{F_i}\left(n_t\right)=\left[p_F\times exp\left\{-{\displaystyle \frac{{(D_i\left(n_t\right)-\Delta G_i\left(n_t\right))}^2}{m_{F_1}}}\right\}+(1-p_F)\right]\times exp\left\{-{\displaystyle \frac{{(D_i\left(n_t\right)+\Delta G_i\left(n_t\right))}^2}{m_{F_2}}}\right\}$$

(15)

Table 2. Sample of the calculated evaluation values for fear.

Value of the Prediction Error $|{\mathit{D}}_{\mathit{i}}\left({\mathit{n}}_{\mathit{t}}\right)|$
		${\mathit{D}}_{\mathit{i}}\left({\mathit{n}}_{\mathit{t}}\right)$= −6.00	${\mathit{D}}_{\mathit{i}}\left({\mathit{n}}_{\mathit{t}}\right)$= −3.00	${\mathit{D}}_{\mathit{i}}\left({\mathit{n}}_{\mathit{t}}\right)$= 0.00	${\mathit{D}}_{\mathit{i}}\left({\mathit{n}}_{\mathit{t}}\right)$= 3.00	${\mathit{D}}_{\mathit{i}}\left({\mathit{n}}_{\mathit{t}}\right)$= 6.00
Value of changein the average prediction error $|\Delta G_i\left(n_t\right)|$	$\Delta G_i\left(n_t\right)$ = −6.00	$0.00$	$0.00$	$0.03$	$0.14$	$0.25$
	$\Delta G_i\left(n_t\right)$ = −3.00	$0.00$	$0.09$	$0.36$	$0.32$	$0.14$
	$\Delta G_i\left(n_t\right)$ = 0.00	$0.03$	$0.36$	$1.00$	$0.36$	$0.03$
	$\Delta G_i\left(n_t\right)$ = 3.00	$0.14$	$0.32$	$0.36$	$0.09$	$0.00$
	$\Delta G_i\left(n_t\right)$ = 6.00	$0.25$	$0.14$	$0.03$	$0.00$	$0.00$

shows a sample of the calculated evaluation values of fear, based on Figure 7. In Table 2, the values of $p_F,m_{F_1},m_{F_2},max$, and $ma{x}^{\prime }$, which are the constants of Equation (15), were set to 0.75, 15.00, 15.00, 6.00, and 6.00 respectively.

In Table 2, the evaluation value of fear is highest when $D_i\left(n_t\right)$ and $\Delta G_i\left(n_t\right)$ are 0.00 and 0.00. When the sign of $D_i\left(n_t\right)$ and sign of $\Delta G_i\left(n_t\right)$ are different, the father $D_i\left(n_t\right)$ and $\Delta G_i\left(n_t\right)$ are from 0.00, and the closer evaluation values of fear are 0.25. The value of $1-p_F$ is 0.25 in settings of Table 2. This shows that the value of $p_F$ in Equation (15) determines the upper limit evaluation value of fear when both $D_i\left(n_t\right)$ and $\Delta G_i\left(n_t\right)$ are the maximum values and their signs are different.

3.3. Integration of Curiosity and Fear as the Predictability Perspective of the Sensor Input

Finally, the integration of the evaluation values of curiosity and fear based on prediction errors is explained. The evaluation indices of curiosity and the evaluation index of fear were designed as evaluation indices the predictability of the sensor input. Therefore, to calculate a single evaluation value from a single evaluation perspective, curiosity and fear evaluation values were integrated. The formula for the evaluation value $E_{P_i}\left(n_t\right)$, which integrates the evaluation values of curiosity $E_{C_i}\left(n_t\right)$ and fear $E_{F_i}\left(n_t\right)$, is defined in Equation (16). To set the computed evaluation values between 0 and 1, they were integrated using the arithmetic mean.

$$E_{F_i}\left(n_t\right)={\displaystyle \frac{1}{2}}(E_C\left(n_t\right)+E_F\left(n_t\right))$$

(16)

4. Experiments

Simulation experiments were conducted to compare the performance of the proposed method with that of previous studies. Experiments in one-dimensional environments compared the differences in ratings calculated for various inputs. Experiments in a two-dimensional environment compared learning using different methods to calculate the input ratings.

In this experiments, the performances of three methods were compared: a previous method using the evaluation index of predictability, the proposed method using the evaluation index of curiosity and fear, and a method that did not consider the time variation of the prediction error in the evaluation index of curiosity and fear. In this experiment, a method that did not consider the time variation of the prediction error in the evaluation index of curiosity and fear was called the proposed prototype method. The reason for including the proposed prototype method for comparison is that the evaluation index of predictability, which was the previous method, does not consider the time variation of the prediction error. Therefore, one comparison was used to test whether establishing an evaluation index for curiosity and fear was useful. Equations (17) and (18) show the calculation method for the evaluation value, which does not consider the time variation of the prediction error in the evaluation indices of curiosity and fear. Equation (17) shows the calculation method for the evaluation value in the evaluation index of curiosity using the absolute value of the prediction error $|D_i\left(n_t\right)|$ and the constants $p_C$, and $m_C$. This equation consists only of the part that considers the magnitude of the prediction error in Equation (14).

$$E_{C_i}\left(n_t\right)=exp\left\{-{\displaystyle \frac{\left(\right|D_i\left(n_t\right){|-p_C)}^2}{2{m_C}^2}}\right\}$$

(17)

Equation (18) shows the calculation method for the evaluation value in the fear evaluation index using the absolute value of the prediction error $|D_i\left(n_t\right)|$ and constants $m_F$, and $p_F$. This equation deffers from Equation (4). This is because a sigmoid function base, such as that in Equation (18), is considered more sensitive to the magnitude of the prediction error than in Equation (4), which is a Gaussian function-based expression.

$$E_{F_i}\left(n_t\right)=1-{\displaystyle \frac{1}{1+exp\left\{m_F\left(\right|D_i\left(n_t\right)|-p_F)\right\}}}$$

(18)

4.1. Simulation Experiment in One-Dimensional Environment

This experiment aimed to validate that the proposed method could calculate a high evaluation value when the magnitude of the prediction error and amount of change in the average prediction error were moderate. The aim of this experiment was to compare the evaluation values of each method. Therefore, in this experiment, the evaluation values relative to the number of inputs were compared between the proposed, prototype and previous methods.

4.1.1. Experiment Settings

The experimental settings are listed in

Table 3. Settings for the experiment.

Settings	Definition
Number of experiments	Each 1 time
End condition of the experiment	Reaching the goal
Maximum of accelerometer $[\mathrm{m}/{\mathrm{s}}^2]$	10.0
Minimum of accelerometer $[\mathrm{m}/{\mathrm{s}}^2]$	−10.0

. The settings of the agents used in the experiment are listed in

Table 4. Settings of the agent in this experiment.

Agent Constants	The Set Values
The constant $S_i$ for Equation (4) in previous method	20.00
The constant b for Equation (12) in proposed prototype method and proposed method	50
The constant of curiosity $p_C, m_C$ for Equation (17) in proposed prototype method	1.00, 1.00
The constant of fear $p_F, m_F$ for Equation (18) in proposed prototype method	2.00, 3.00
The constant of curiosity $p_{C_1}, p_{C_2}, m_C$ for Equation (14) in proposed method	1.00, 1.00, 0.05, 0.05
The constant of fear $p_F, m_{F_1}, m_{F_2}$ for Equation (15) in proposed method	0.35, 20.00, 25.00

.

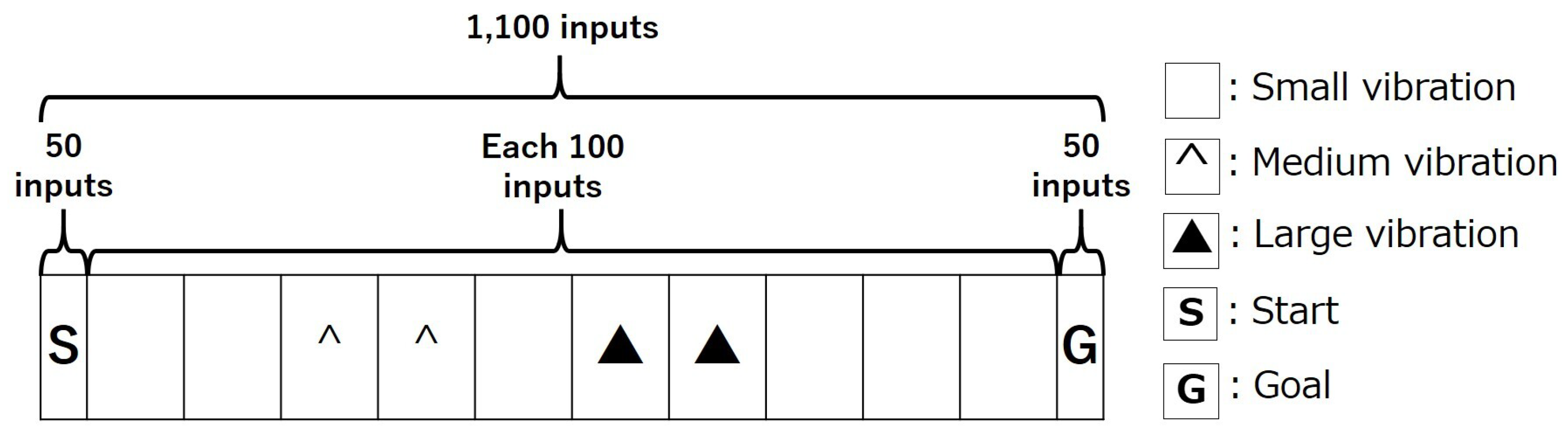
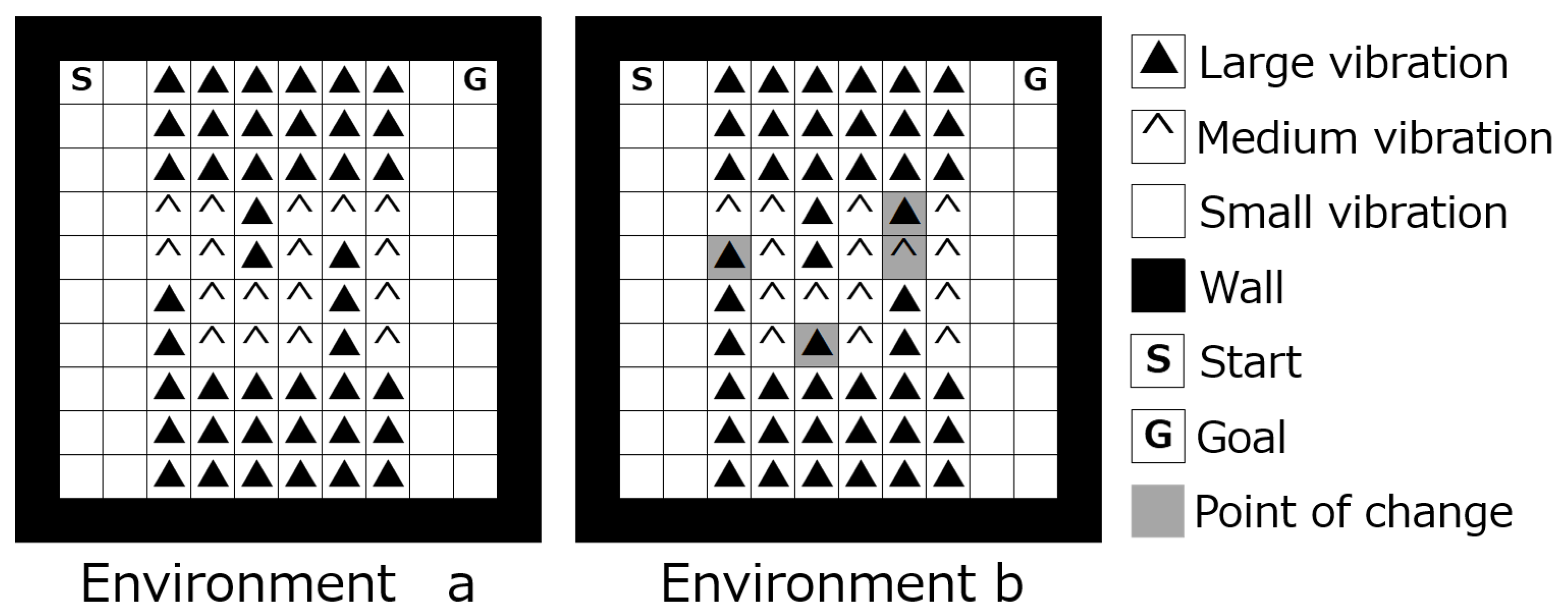
The end condition for each trial was when the agent reached the goal or had executed 100 actions. In this experiment, the performance of the robot introducing the agent using the previous method, the robot introducing the agent using the proposed prototype method, and the robot introducing the agent using the proposed method were compared in a virtual environment. All robots can select only the right ones, which is the goal direction for each state. All the robots were loaded with acceleration sensors. In this experiment, the acceleration sensor received 100 inputs for each action considering the continuum state. In this experiment, SVR was predicted for the short-term. Therefore, SVR can hold up to 100 data inputs for the current behavior, and it resets training every time it starts a new behavior. The simulation experiment was conducted in a one-dimensional environment that included three types of vibration inputs, as shown in Figure 8.

The input value $\psi$ is generated by Equation (19). The range of random values U in Equation (19) ranges from $-1$ to 1. A random value U was generated for 100 inputs when the agent started an action.

$$\psi =\left\{\begin{array}{c}9.5U\left(Largevibration\right)\hfill \\ 2.5U\left(Mediumvibration\right)\hfill \\ 0.5U\left(Smallvibration\right)\hfill \end{array}\right.$$

(19)

4.1.2. Experiment Results

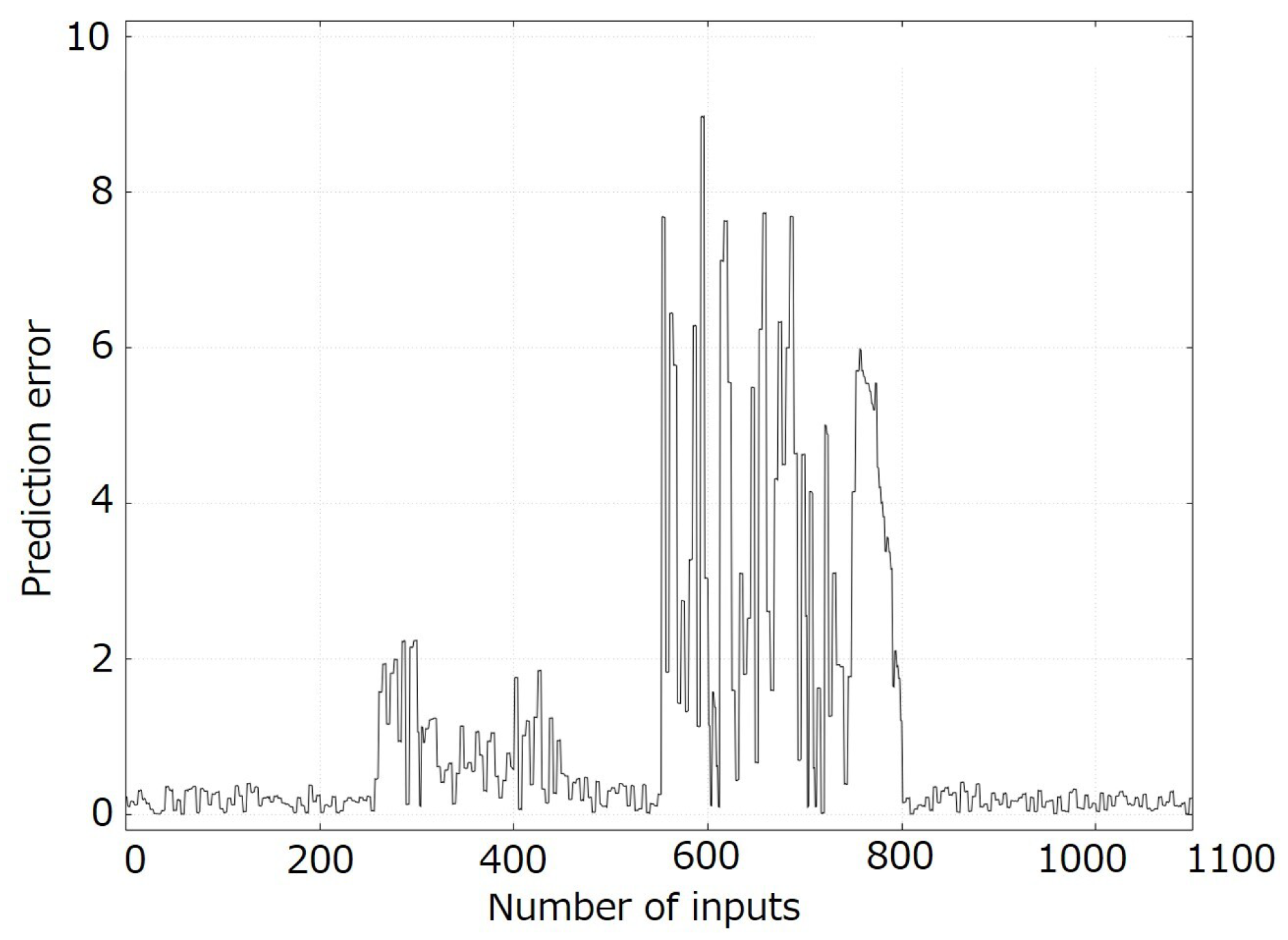
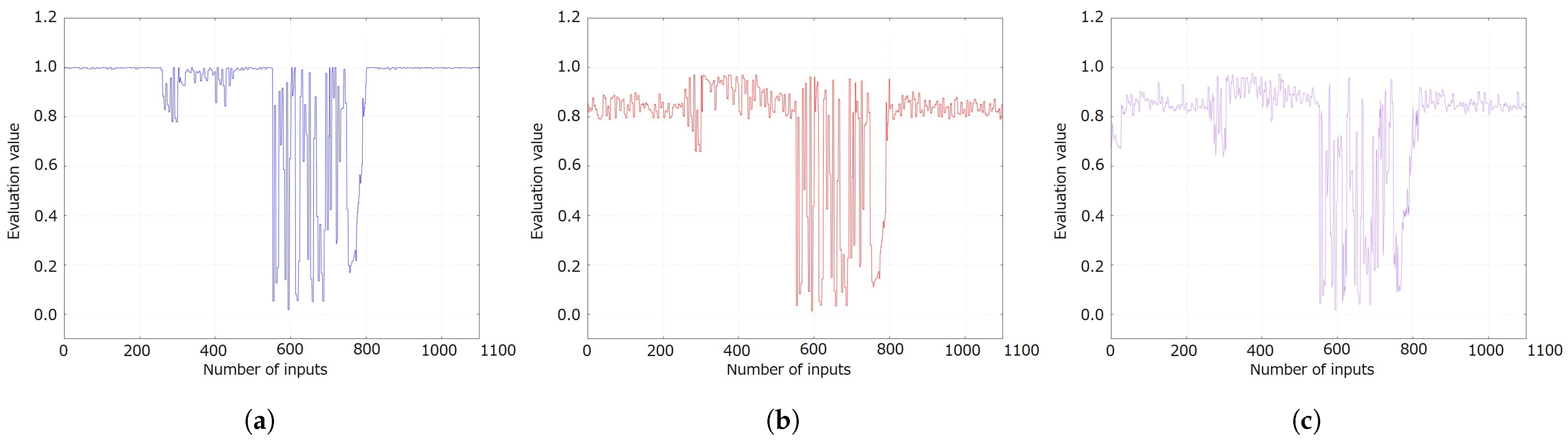
Figure 9 shows the transition of the prediction error in the experiment. Figure 10 shows the transition of the evaluation values for each method.

Table 5. Average and standard deviation of the evaluation values for each method.

	Small Vibration		Medium Vibration		Large Vibration
	Average	Standard Deviation	Average	Standard Deviation	Average	Standard Deviation
previous	$0.9717$	$0.0732$	$0.9448$	$0.0620$	$0.5797$	$0.3483$
prototype	$0.8219$	$0.0890$	$0.8911$	$0.0836$	$0.5028$	$0.3506$
proposed	$0.8330$	$0.0881$	$0.8836$	$0.0809$	$0.4630$	$0.2974$

presents the mean and standard deviation of the evaluation values for each method.

Based on the averaged figure and table, it was confirmed that the proposed method calculates the evaluation value according to the design concept. It was also confirmed that the transition of the evaluation values differed between the methods. In Figure 10, the evaluation values of the previous method are close to 1, which is the highest evaluation value in situations where the vibration and prediction errors are small. However, the evaluation values of the proposed prototype method and the proposed method are 0.8–0.9 in those situations. Therefore, by considering the evaluation index for curiosity, the evaluation values were reduced in situations where the vibration and prediction errors were small. In situations where the vibration and prediction errors were moderate, the evaluation value of the previous method fluctuated between 0.8 and 1.0. However, the evaluation values of the proposed prototype method and the proposed method tended to be higher than those in situations where the vibration and prediction errors were small. In this case, the evaluation value of the proposed prototype method was slightly higher than that of the proposed method. In situations where the vibration and prediction errors are large, the evaluation values of the proposed method are less likely to exceed 0.8. In Table 5, the mean and standard deviation of the evaluation value in the proposed method are also the lowest of all the methods.

4.1.3. Discussion

First, the transition of the evaluation value in the previous method was significantly different from that in the other methods. In the proposed prototype and the proposed method, the evaluation value of the predictability of the sensor input is calculated by the mean value of the evaluation value for curiosity and fear. Therefore, it is believed that the transition in the evaluation value changed by integrating the evaluation of curiosity with that of fear, which was not considered in the previous method. Next, the trend of the evaluation value in the proposed method was significantly different from that of the other methods in situations where the vibration and prediction errors were large. Only the proposed method considered time variation in the prediction error. The prediction error changed significantly for every few inputs in a state of large vibrations. Therefore, the average prediction error, which was used to consider the temporal variation in the prediction error in the proposed method, changed significantly. This suggests that the evaluation values for curiosity and fear in the proposed method were low. Consequently only the evaluation values of the proposed method tended to be difficult to exceed 0.8 in the states of large vibration.

4.2. Simulation Experiment in Two-Dimensional Dynamic Environment

This experiment aimed to validate the proposed method considering that the evaluation indices of curiosity and fear were more efficient than the exploration behavior of the previous method in a dynamic environment. Therefore, in this experiment, the number of actions relative to the number of trials and the cumulative number of actions were compared between the proposed, proposed prototype and previous methods.

4.2.1. Experiment Settings

The experimental settings are listed in

Table 6. Settings of this experiment.

Settings	Definition
Number of experiments	Each 5 times
Number of trials per experiment	800 trials
Trial	Executing 100 actions or reaching the goal
Reward for goal	2.0
Reward for one action	−1.0
Reward for wall collision	−10.0
Maximum of accelerometer $[\mathrm{m}/{\mathrm{s}}^2]$	10.0
Minimum of accelerometer $[\mathrm{m}/{\mathrm{s}}^2]$	−10.0
The environment before 400 trial	Environment a
The environment after 401 trial	Environment b

. The settings common to all agents are listed in

Table 7. Settings common to all agents in this experiment.

Agent Constants	The Set Values
The learning rate $\alpha$ in Q-learning	0.3
The discount rate $\gamma$ in Q-learning	0.9
The value of $ϵ$ in $ϵ$-greedy method	0.01
The constant $N_i$ for Equation (1) in SGE	0.08
Intial value of the variable ${\delta }_i$ for Equation (1) in SGE	5.0
The constant ${\beta }_i$ for Equation (3) in SGE	0.001
The constant $k_i$ for Equation (7) in SGE	250.0
The constant ${\gamma }_i$ for Equation (8) in SGE	0.99

. The settings that differ by agent are listed in

Table 8. Settings that differ by agent in this experiment.

Agent Constants	The Set Values
The constant $S_i$ for Equation (4) in previous method	20.00
The constant b for Equation (12) in proposed prototype method and proposed method	50
The constant of curiosity $p_C,m_C$ for Equation (17) in proposed prototype method	1.00, 1.00
The constant of fear $p_F,m_F$ for Equation (18) in proposed prototype method	2.00, 3.00
The constant of curiosity $p_{C_1},p_{C_2},m_C$ for Equation (14) in proposed method	1.00, 1.00, 0.05, 0.05
The constant of fear $p_F,m_{F_1},m_{F_2}$ for Equation (15) in proposed method	0.35, 20.00, 25.00

.

Each experiment comprised 800 trials. The end condition for each trial was when the agent reached the goal or executed the 100 actions.

In this experiment, the performance of the robot introducing the agent using the previous method, the robot introducing the agent using the proposed prototype method and the robot introducing the agent using the proposed method were compared in a virtual environment. The previous and proposed methods were tested each ten times. Both robots can select up, down, left, or right in each state. Both robots were loaded with acceleration sensors. In the experiment, the acceleration sensor received 100 inputs for each action considering the continuum state. The learning method for both agents was Q-learning, and the strategy for both agents was $\epsilon$-greedy. The simulation experiment was executed a two-dimensional dynamic environment that included three types of vibration inputs, as shown in Figure 11. This environment is surrouncded by walls on all sides. If the agent collides witha a wall, the agent returns to the state from one step prior.

The input value $\psi$ is generated using Equation (19) in Section 4.1. The random value U in Equation (19) ranges from $-1$ to 1. A random value U was generated for 100 inputs when the agent started an action. In this experiment, the state of the environment changed after 400 and 401 trials. The agent learns in the environment until the end of the 400th trial and in environment b from the start of the 401st trial. The minimum number of actions in both environments was 19.

4.2.2. Experiment Results

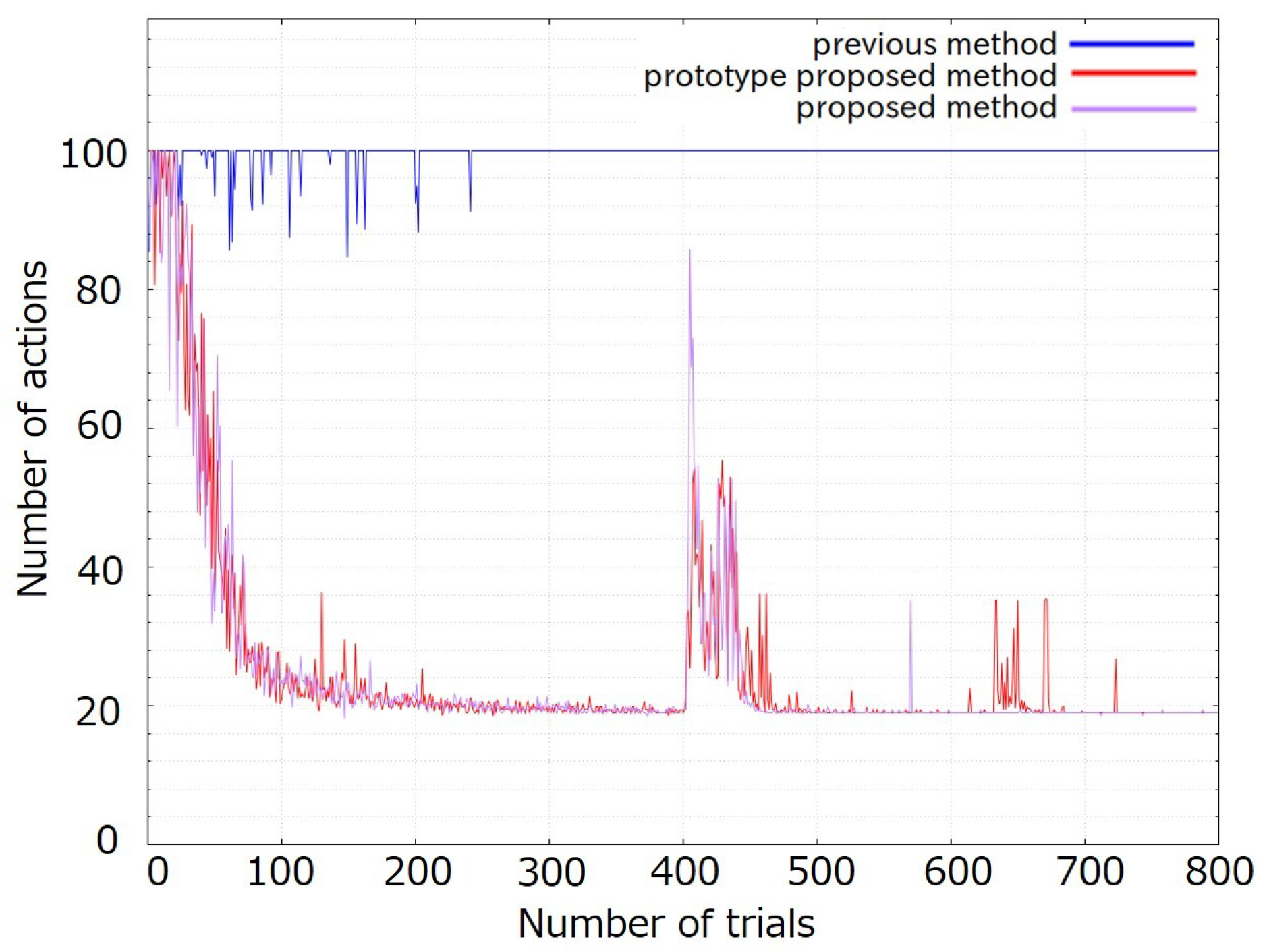
Figure 12 shows the transition of the average number of actions for each trial in the 5 times experiments.

Table 9. Average and standard deviation of the total number of actions for each method.

	Previous	Proposed Prototype	Proposed
Average	79,794.8	20,205.6	20,069.6
Standard deviation	$93.7$	$884.8$	$462.5$

lists the average in number of actions for each trial in the 5 times experiments.

The results of this experiment demonstrated the usefulness of considering the evaluation index of curiosity. As shown in Figure 12, there was a significant difference in the transition before the environmental change between the previous method and other methods. In the previous method, the number of actions fluctuated during the initial stages of the experiment. However, the number of actions was always 100, which was the maximum number of actions in this experiment after the middle stage. As shown in Table 9, the average was significantly larger than that of the others, and the standard deviation was also significantly smaller. Therefore, it can be said that the number of actions in the previous method did not converge. However, the number of actions in the proposed prototype method and the proposed method tended to converge both before and after the environmental change. Before the environmental change, no significant differences were observed between the proposed prototype method and the proposed method. After the environmental change, the number of actions in the proposed prototype method increased rapidly immediately following the environmental change and 700 trials. However, immediately following the environmental change, the number of actions in the proposed method increased more rapidly than in the proposed prototype method. However, only one rapid increase in the number of actions was observed. From Table 9, the average and the standard deviation in the proposed method is smaller than in the proposed prototype method.

4.2.3. Discussion

First, the number of actions in the previous method does not converge. In this experiment, the input tendency was changed at least twice from the start to the goal. Therefore, the prediction error increased by at least twofold. In the previous method, the larger the prediction error, the lower is the evaluation value. Therefore, in this experiment, when the prediction error increased temporarily, the previous method calculated a lower evaluation value. Consequently, it is believed that the number of actions in the previous method did not converge, because the robot introduced in the previous method turned around the start and did not reach the goal. However, the proposed prototype method and the proposed method calculated high evaluation values for moderate prediction errors. Therefore, when the prediction error temporarily increased, both methods can visit the state of the new input tendency. Consequently, it is believed that the number of actions in both methods converge. Finally, the average and standard deviation of the total number of actions in the proposed method were lower than those in the proposed prototype method. The proposed method considers the average prediction errors. Therefore, when the robot continues to receive the similar inputs, the evaluation value of the proposed method decreases because it is difficult to change the prediction error. Consequently, the robot that introduced the proposed method prioritized obtaining the goal reward and could learn the path faster and more consistently than the proposed prototype method in this experiment. However, it is believed that the robot that introduced the proposed prototype method relied on the state of the middle vibration input, such that a moderate prediction error was calculated. This is because the proposed prototype method always calculated high evaluation values for moderate prediction errors.

5. Conclusions and Future Works

This study enabls efficient excitation behavior by considering the curiosity evaluation index. The previous method has a problem in that the predictor cannot progress to learn the input, that the agent has only encountered a few times, using the evaluation index of predictability. Therefore, we propose introducing an evaluation index of curiosity that considers the learning progress of the predictor and the evaluation index of fear that considers the danger of unpredictable inputs. In the proposed method, the magnitude and time variation of the prediction error are used to calculate the evaluation error. Therefore, the average prediction error, which was calculated using that between several inputs, was defined to evaluate the time variation of this error. This study aims to improve exploration efficiency using the proposed method.

In future work, experiments should be conducted to compare the performance of the proposed method with those of the conventional method, ICM, and RND. This study aimed to achieve a more efficient exploration of the proposed method than previous methods by considering curiosity and fear. Therefore, the proposed method was based only on the method described in this study. However, a comparison with the previous method alone was insufficient to demonstrate the usefulness of the proposed method’s exploration performance in the method for efficient exploration. To further demonstrate the usefulness of the proposed method, it should be compared with ICM and RND, which are conventional method that use curiosity in standard reinforcement-learning benchmark environments. As another future work, curiosity, which is an immediate reaction to new stimuli, is enumerated. In this study, curiosity was induced based on prediction errors. Therefore, curiosity is affected by the progress of the predictor’s learning of the stimuli. Conversely, immediate responses to new stimuli can lead in to the discovery of new states and environments, thereby making them more applicable to the environment. Therefore, we considered introducing curiosity to induce short-term exploratory behavior toward new stimuli.