Research on Multi-Beam Interference Competition Suppression Algorithms for Laser Doppler Vibrometry
Abstract
1. Introduction
2. Principle
- (1)
- If the stray light power is zero, as discussed, , . The IQ demodulation method can accurately extract the instantaneous velocity.
- (2)
- If the target surface exhibits only small-amplitude, high-frequency vibration (with an amplitude much smaller than the wavelength), and can be regarded as a stable value. The IQ demodulation result exhibits a linear scaling relationship with the target’s vibrational motion, and no spurious signals are generated.
- (3)
- If the target undergoes large-amplitude, low-frequency motion with non-negligible stray light power. The variable is guaranteed to traverse every value within the interval with a sweep frequency of . Due to the nonlinearity of function , spurious signals emerge at frequency . The frequency of these artifacts varies proportionally with the target’s velocity, generating the characteristic chirp signal in the system.
- (4)
- Specifically, if and , , leading to severe signal distortion. However, this degenerate case requires exceptionally stringent conditions to manifest in practice.
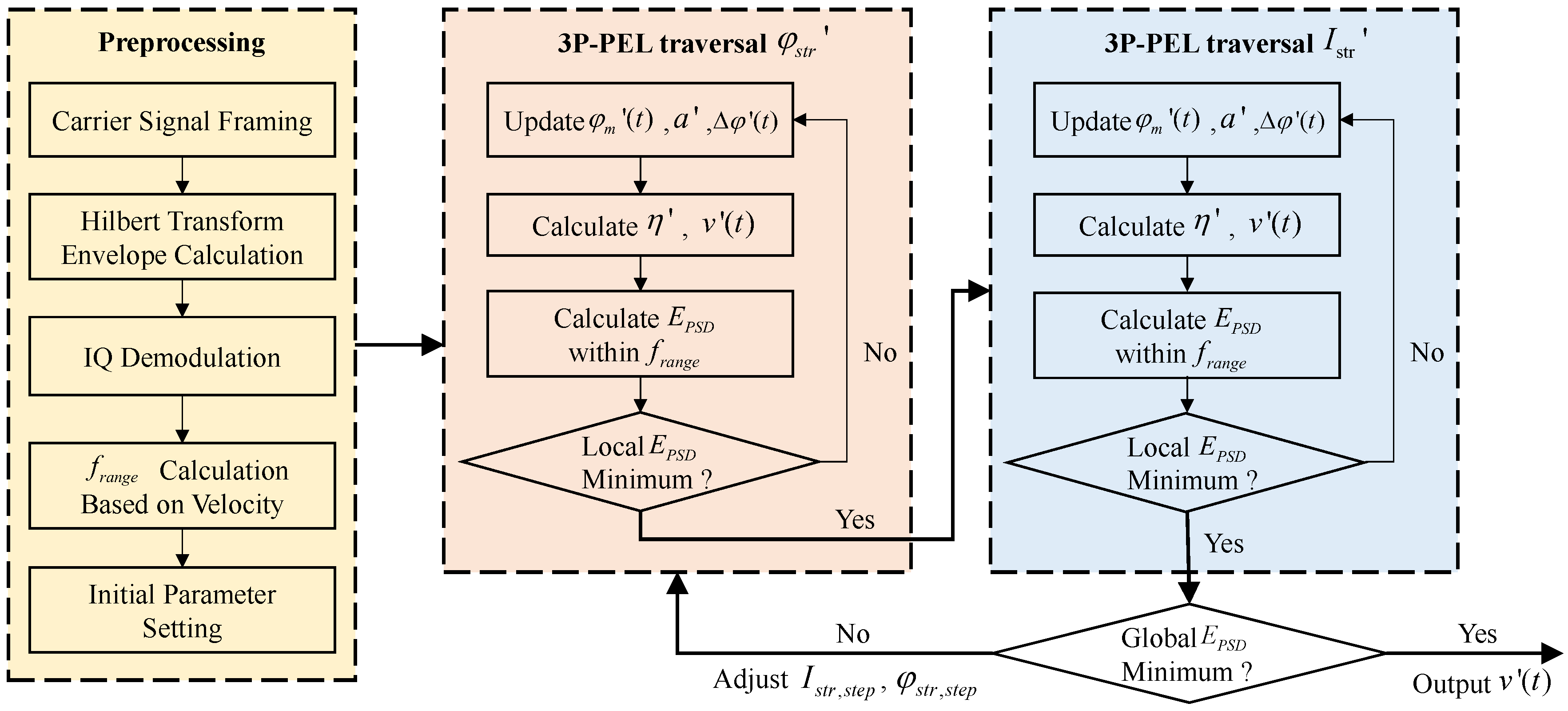
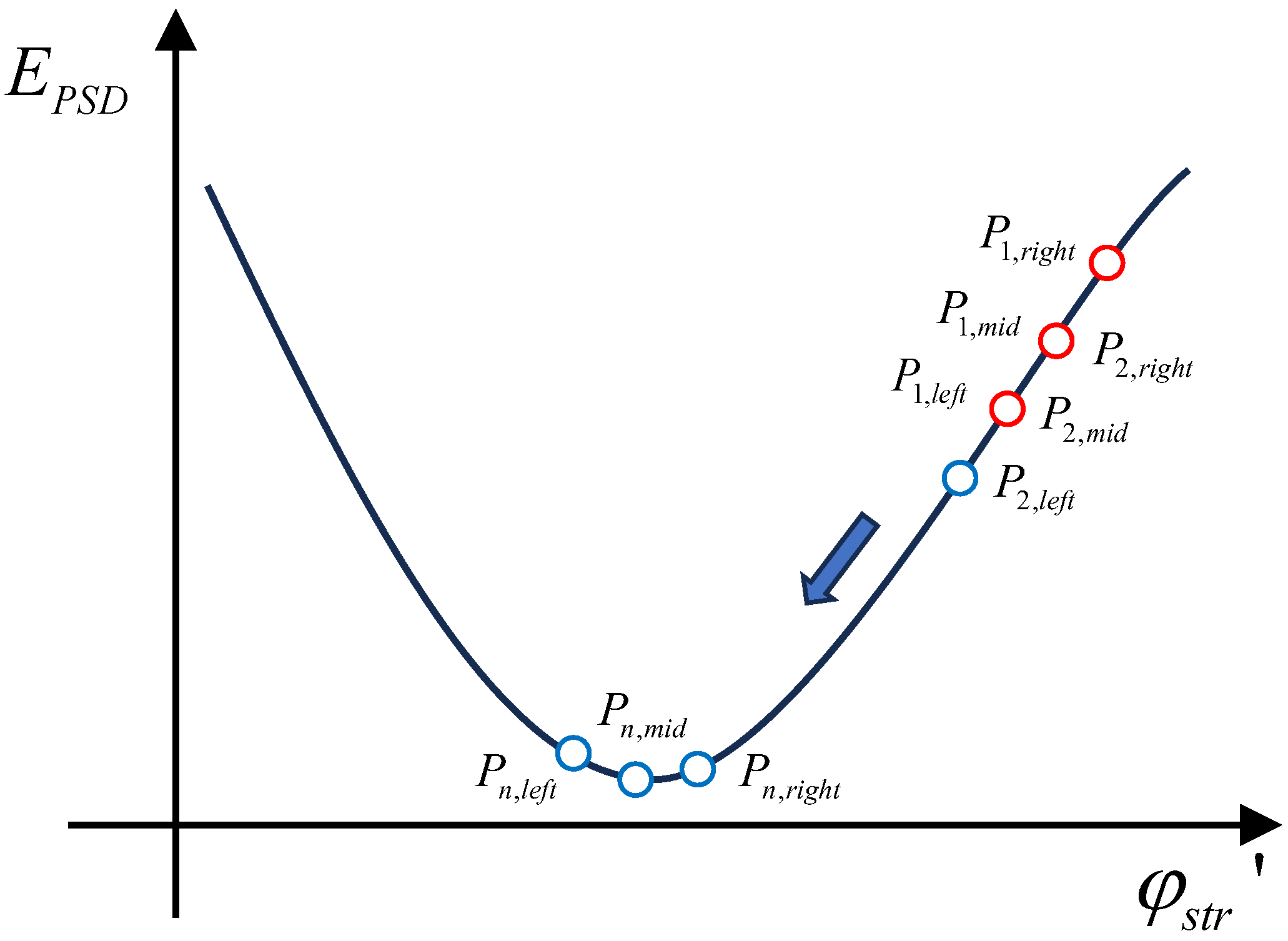
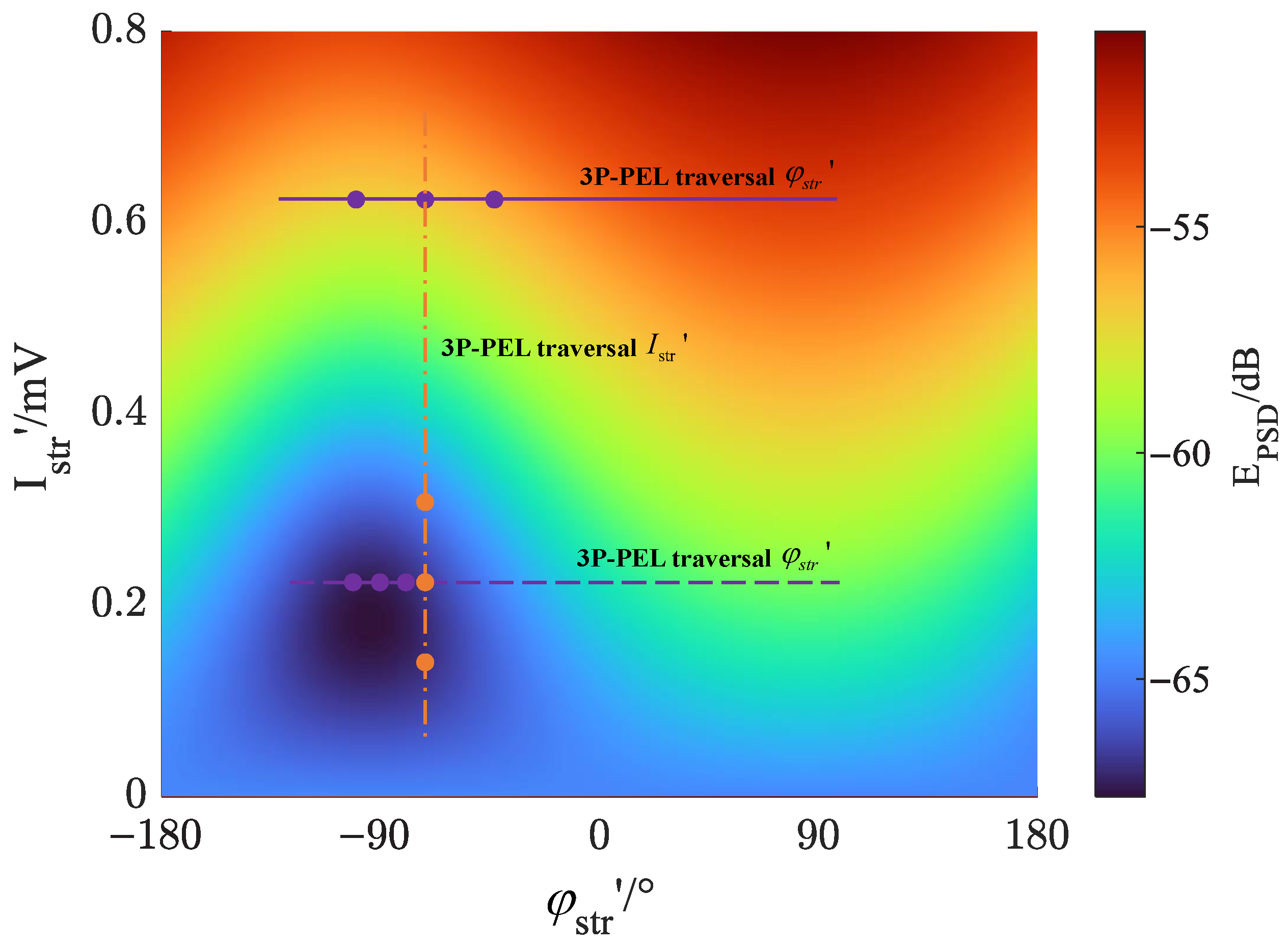
3. Correction Algorithm
4. Simulation
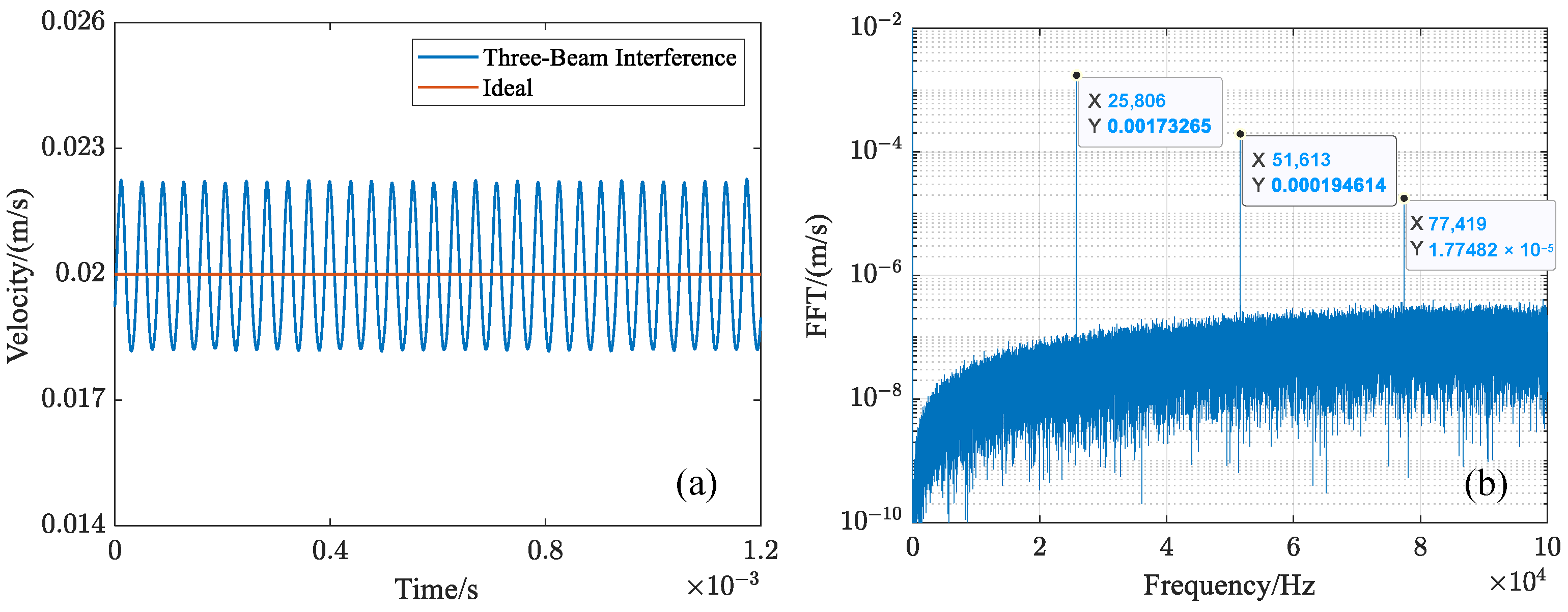
4.1. Uniform Motion
4.2. Uniform Motion + Micro-Vibrations
4.3. Non-Uniform Motion + Micro-Vibrations
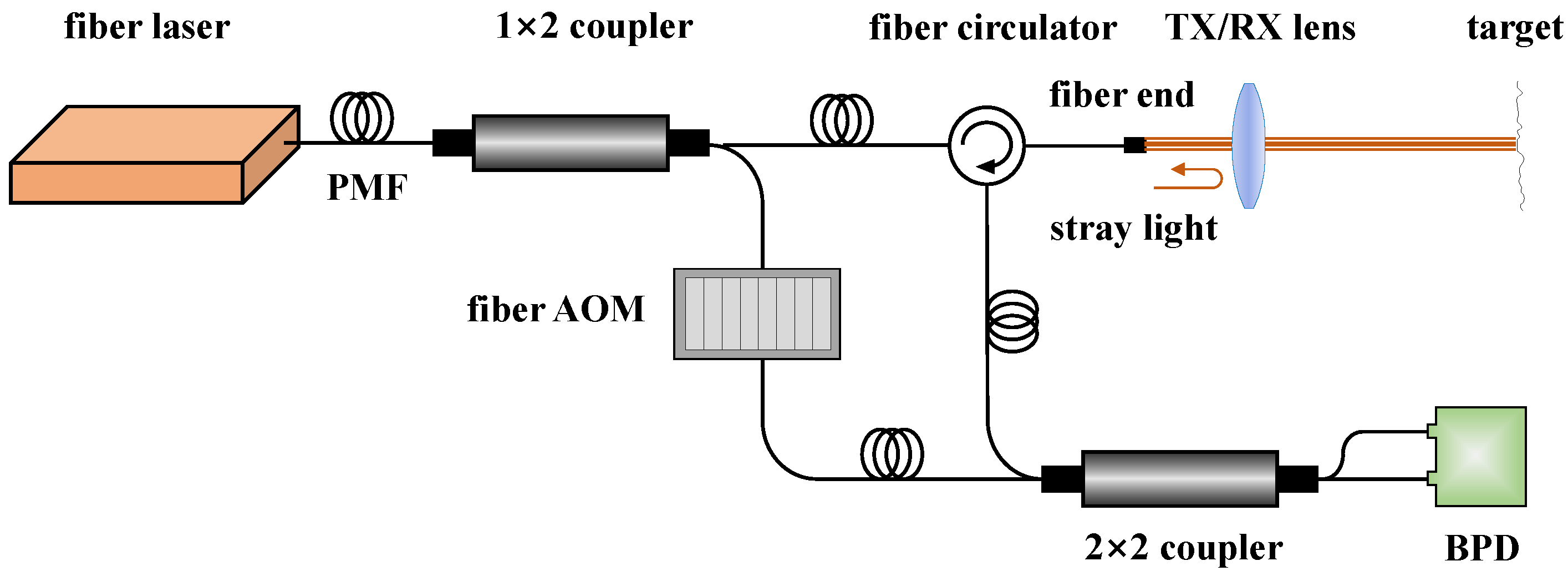
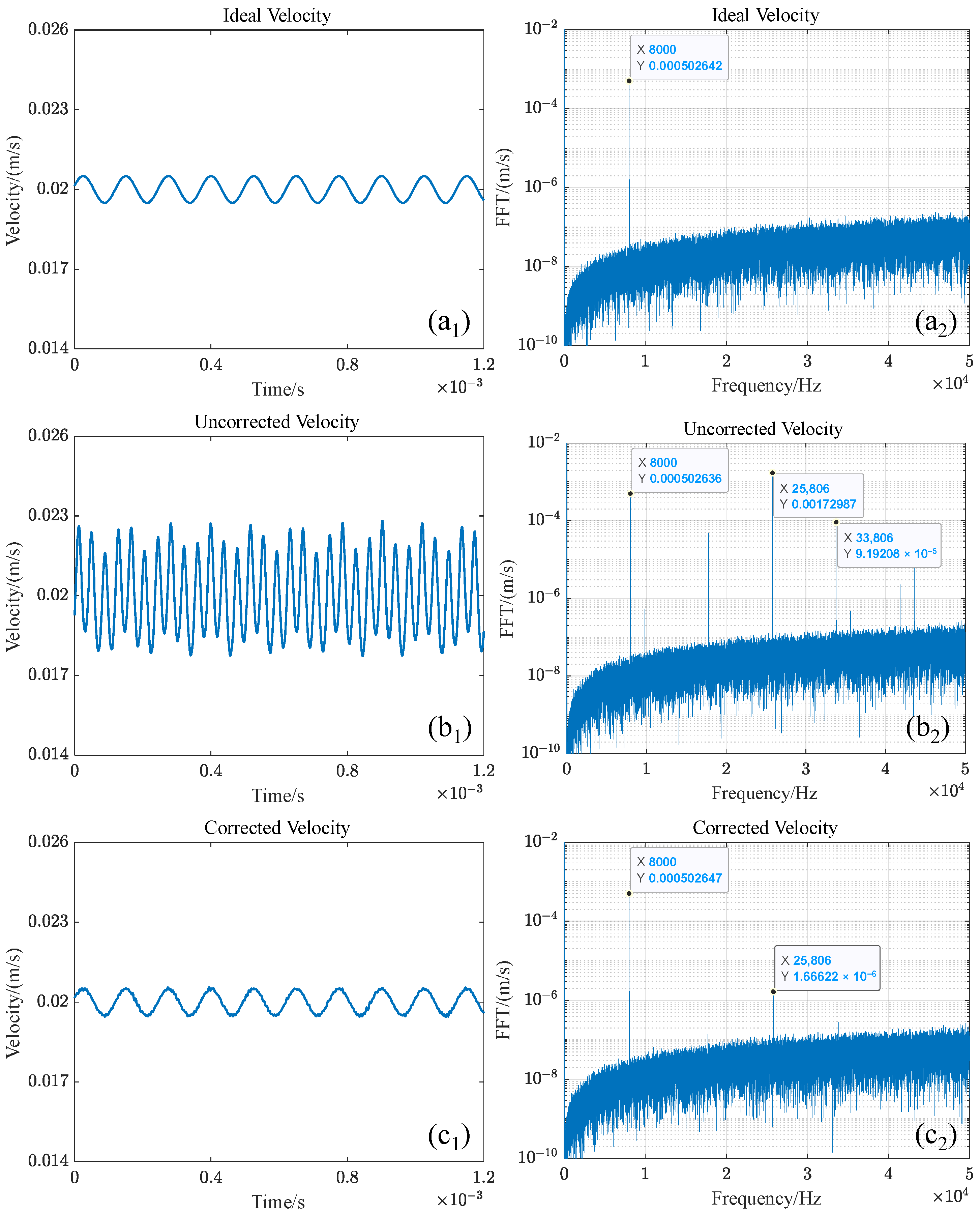
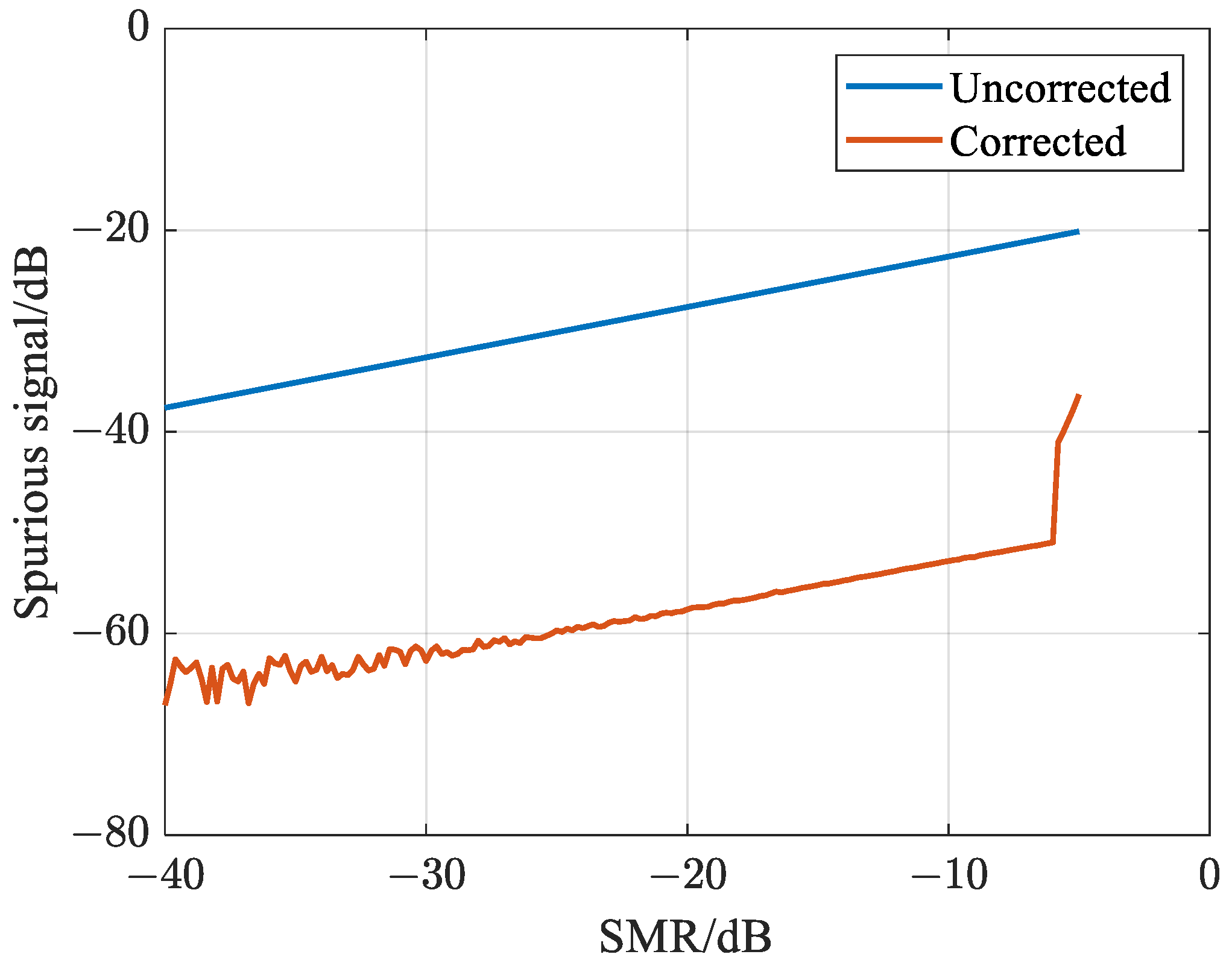
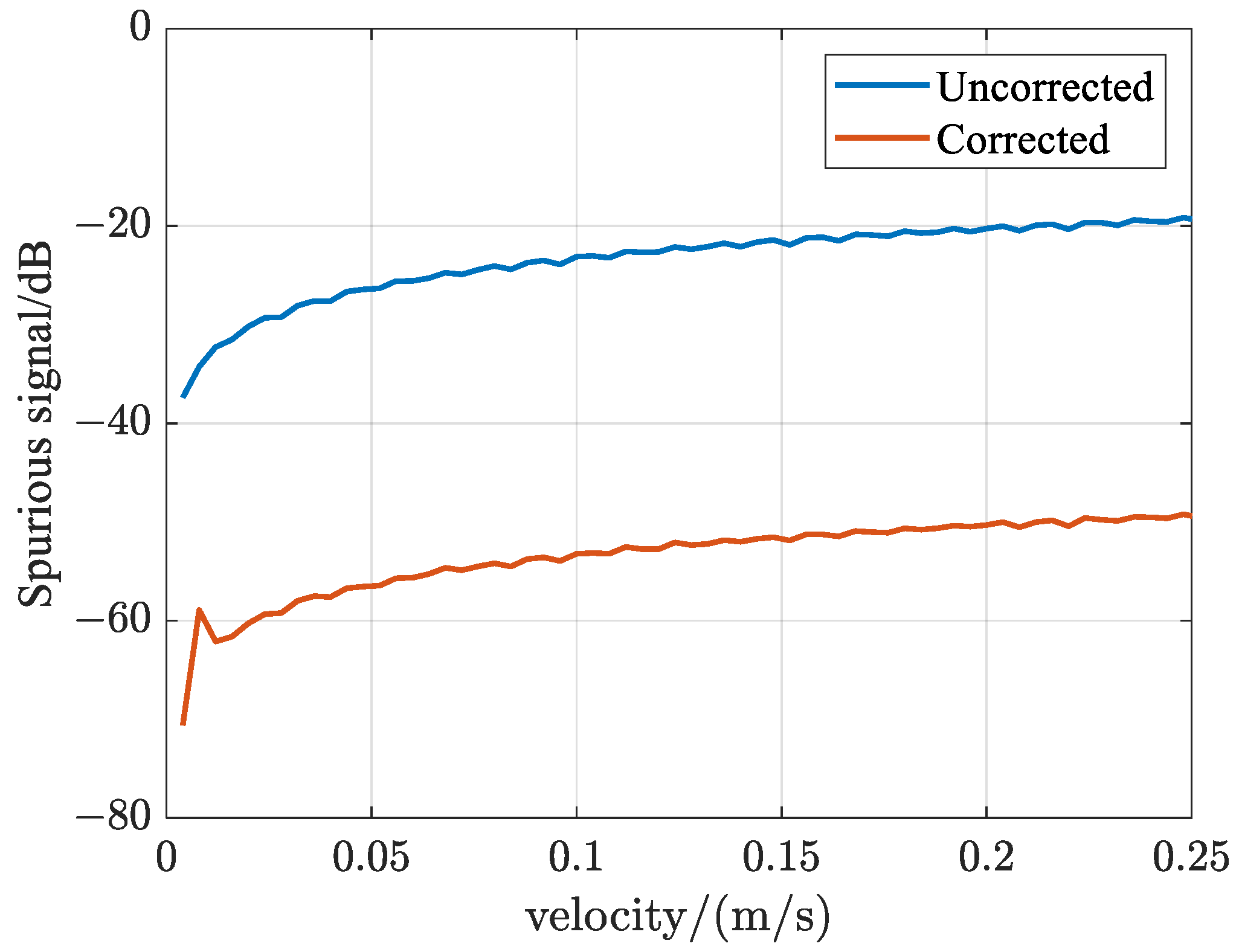
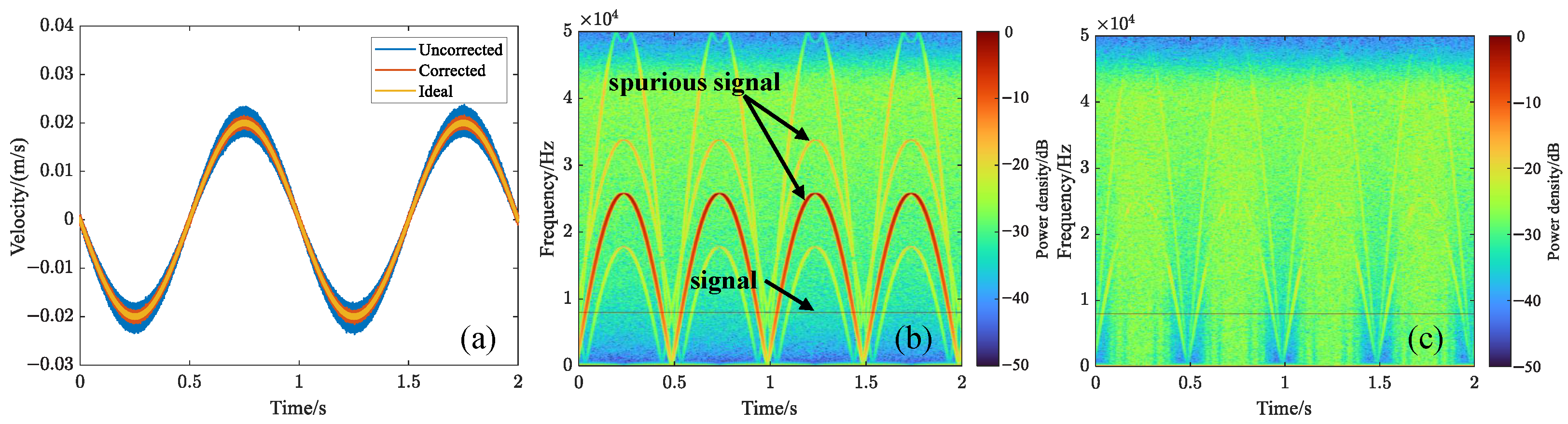
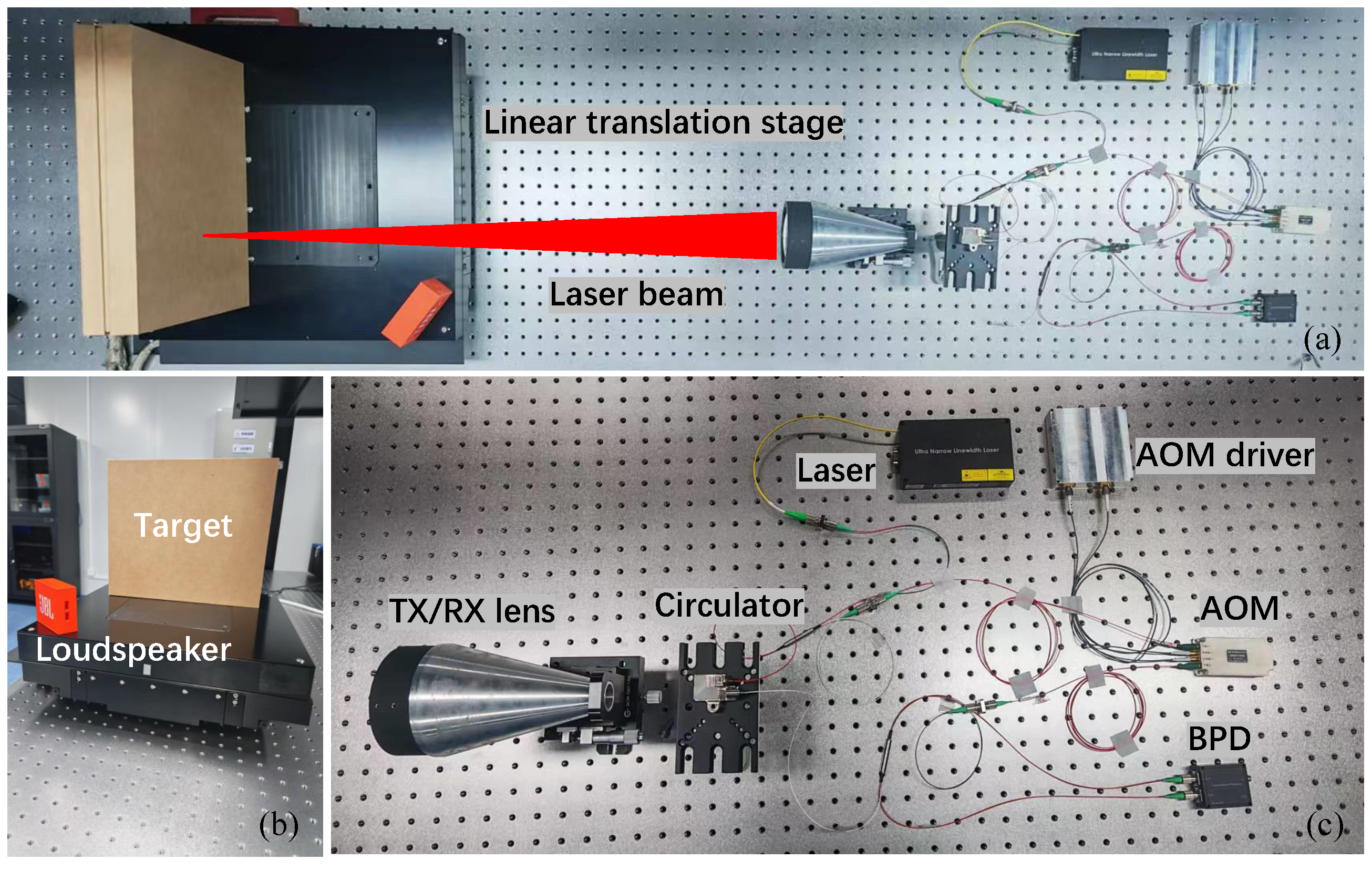
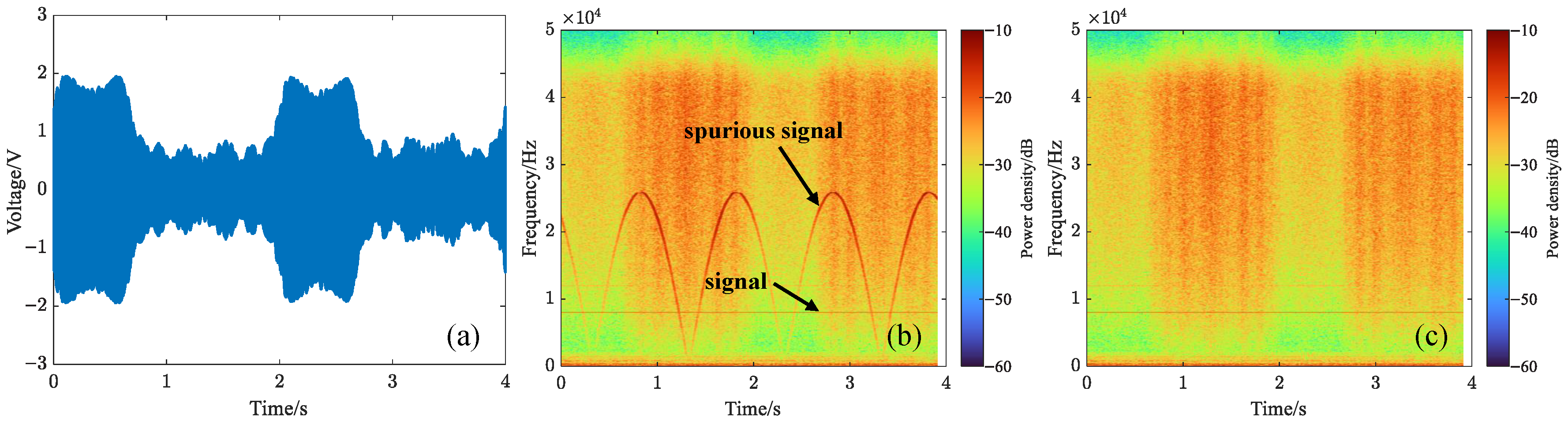
5. Experiments
5.1. Uniform Motion + Micro-Vibrations
5.2. Non-Uniform Motion + Micro-Vibrations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khalil, H.; Kim, D.; Nam, J.; Park, K. Accuracy and Noise Analyses of 3D Vibration Measurements Using Laser Doppler Vibrometer. Measurement 2016, 94, 883–892. [Google Scholar] [CrossRef]
- Liu, H.; Ji, D.; Lin, J.; Liu, Z.; Li, H. Residual Angular Speed Analysis Based on Laser Doppler Vibrometer and Its Application in Planetary Gearbox Diagnosis. Measurement 2025, 250, 116987. [Google Scholar] [CrossRef]
- Yuan, K.; Zhu, W. Identification of Modal Parameters of a Model Turbine Blade with a Curved Surface under Random Excitation with a Three-Dimensional Continuously Scanning Laser Doppler Vibrometer System. Measurement 2023, 214, 112759. [Google Scholar] [CrossRef]
- Hagara, M.; Pástor, M.; Lengvarský, P.; Palička, P.; Huňady, R. Modal Parameters Estimation of Circular Plates Manufactured by FDM Technique Using Vibrometry: A Comparative Study. Appl. Sci. 2024, 14, 10609. [Google Scholar] [CrossRef]
- Rzasa, J.R.; Cho, K.; Davis, C.C. Long-Range Vibration Detection System Using Heterodyne Interferometry. Appl. Opt. 2015, 54, 6230–6236. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; He, Y.; Shang, J.; Chen, W. Experimental Study on the 1550 Nm All Fiber Heterodyne Laser Range Finder. Appl. Opt. 2009, 48, 6575–6582. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Shen, Y.; Wang, Y.; Kong, X.; Zhang, W. Research on the Speckle Effect Suppression Technology of a Laser Vibrometer Based on the Dual-Wavelength Detection Principle. Appl. Sci. 2025, 15, 4858. [Google Scholar] [CrossRef]
- Rembe, C.; Halkon, B.J.; Ismail, M.A.A. Measuring Vibrations in Large Structures with Laser-Doppler Vibrometry and Unmanned Aerial Systems: A Review and Outlook. Adv. Devices Instrum. 2025, 6, 103. [Google Scholar] [CrossRef]
- Pasch, S.; Leister, R.; Gatti, D.; Örlü, R.; Frohnapfel, B.; Kriegseis, J. Measurements in a Turbulent Channel Flow by Means of an LDV Profile Sensor. Flow Turbul. Combust. 2024, 113, 195–213. [Google Scholar] [CrossRef]
- O’Brien, C.; Falagán, N.; Kourmpetli, S.; Landahl, S.; Terry, L.A.; Alamar, M.C. Non-Destructive Methods for Mango Ripening Prediction: Visible and near-Infrared Spectroscopy (visNIRS) and Laser Doppler Vibrometry (LDV). Postharvest Biol. Technol. 2024, 212, 112878. [Google Scholar] [CrossRef]
- Yu, T.; Tang, Q.; Vinayaka, S. Identifying Structural Properties of a Steel Railway Bridge for Structural Health Monitoring Using Laser Doppler Vibrometry. Autom. Constr. 2024, 160, 105320. [Google Scholar] [CrossRef]
- Tao, S.; Zhen, S.; Fang, J.; Chen, X.; Yu, B. Analysis of Multi-Beam Interference in Heterodyne Detection System. In Proceedings of the Fourth International Conference on Optoelectronic Science and Materials (ICOSM 2022), Hefei, China, 16–18 September 2022; SPIE: Bellingham, DC, USA, 2023; Volume 12553, pp. 152–159. [Google Scholar] [CrossRef]
- Kong, X.X.; Zhang, W.X.; Cai, Q.S.; Wu, Z.; Dai, Y.; Xiang, L.B. Multi beam hybrid heterodyne interferometry based phase enhancement technology. Acta Phys. Sin. 2020, 69, 190601. [Google Scholar] [CrossRef]
- Yarovoi, L.; Siegmund, G. The Effect of Three-Wave Interference in Laser Doppler Vibrometry. Meas. Sci. Technol. 2004, 15, 2150–2156. [Google Scholar] [CrossRef]
- Hao, Y.; Kong, X.; Cai, Q.; Zhang, W.; Wu, Z.; Dai, Y.; Wang, Y. Analysis of Effect of Circulator Noise on Laser Interferometry System. Acta Opt. Sin. 2021, 41, 0912003. [Google Scholar] [CrossRef]
- Wu, S.s.; Lü, T.; Li, Y.y.; Wang, T.f.; Guo, J. Multi-Beam Interference Competition in Heterodyne Detection. Optoelectron. Lett. 2019, 15, 213–216. [Google Scholar] [CrossRef]
- Kong, X.; Xiangli, B.; Zhang, W.; Wu, Z.; Zhang, D. Research on LDV Stray Light Suppression Technology Based on Four-Wave Hybrid Interference. In Proceedings of the Electro-Optical Remote Sensing XIII, Strasbourg, France, 9–12 September 2019; SPIE: Bellingham, DC, USA, 2019; Volume 11160, pp. 98–104. [Google Scholar] [CrossRef]
- Wang, Y.; Shen, Y.; Kong, X.; Zhang, W. Chirp Noise Analysis in Laser Doppler Vibration Measurement and Its Suppression Methods. Acta Opt. Sin. 2024, 44, 0507001. [Google Scholar] [CrossRef]
- Arahira, S.; Ono, H.; Onawa, Y.; Itoh, M.; Shimura, D.; Fujii, A.; Murai, H. Silicon Photonics-Based Laser Doppler Vibrometer with an Integrated Phase Modulator. Opt. Express 2025, 33, 40703–40714. [Google Scholar] [CrossRef] [PubMed]
- Volkers, H. On the Calibration of Laser Doppler Vibrometers Using Simulated Excitation. Meas. Sens. 2025, 38, 101748. [Google Scholar] [CrossRef]

| Author | Strategy | System Complexity | Processing Effectiveness | Data Continuity |
|---|---|---|---|---|
| Wu | optical system design | ++ | +++ | − 1 |
| Kong | optical system design | +++ | + | − |
| Wang | data post-processing | + | ++ | + |
| Shen | data post-processing | + | +++ | + |
| Component | Item | Parameter | Unit |
|---|---|---|---|
| Laser | wavelength | 1550 | nm |
| Laser | output power | 25 | mW |
| AOM | driver frequency | 250 | kHz |
| AOM | output power | 0.2 | mW |
| TX/RX lens | emission power | 20 | mW |
| TX/RX lens | alignment distance | 5 | m |
| BPD | bandwidth | 1 | MHz |
| BPD | gain | 5 | V/W |
| data aquisition card | sampling rate | 2 | MHz |
| data aquisition card | input range | ±5 | V |
| data aquisition card | quantization bits | 16 | bit |
| cardboard box | size | 40 × 30 | cm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Kong, X.; Zhang, R.; Wang, Y.; Zhang, W. Research on Multi-Beam Interference Competition Suppression Algorithms for Laser Doppler Vibrometry. Appl. Sci. 2025, 15, 12020. https://doi.org/10.3390/app152212020
Shen Y, Kong X, Zhang R, Wang Y, Zhang W. Research on Multi-Beam Interference Competition Suppression Algorithms for Laser Doppler Vibrometry. Applied Sciences. 2025; 15(22):12020. https://doi.org/10.3390/app152212020
Chicago/Turabian StyleShen, Yangyi, Xinxin Kong, Rui Zhang, Yahao Wang, and Wenxi Zhang. 2025. "Research on Multi-Beam Interference Competition Suppression Algorithms for Laser Doppler Vibrometry" Applied Sciences 15, no. 22: 12020. https://doi.org/10.3390/app152212020
APA StyleShen, Y., Kong, X., Zhang, R., Wang, Y., & Zhang, W. (2025). Research on Multi-Beam Interference Competition Suppression Algorithms for Laser Doppler Vibrometry. Applied Sciences, 15(22), 12020. https://doi.org/10.3390/app152212020






