Resonant Soft X-Ray Scattering Reveals Chromophore Domains in Polymer Doped with Disperse Orange 11 Dye
Featured Application
Abstract
1. Introduction
1.1. Background
1.2. Approach
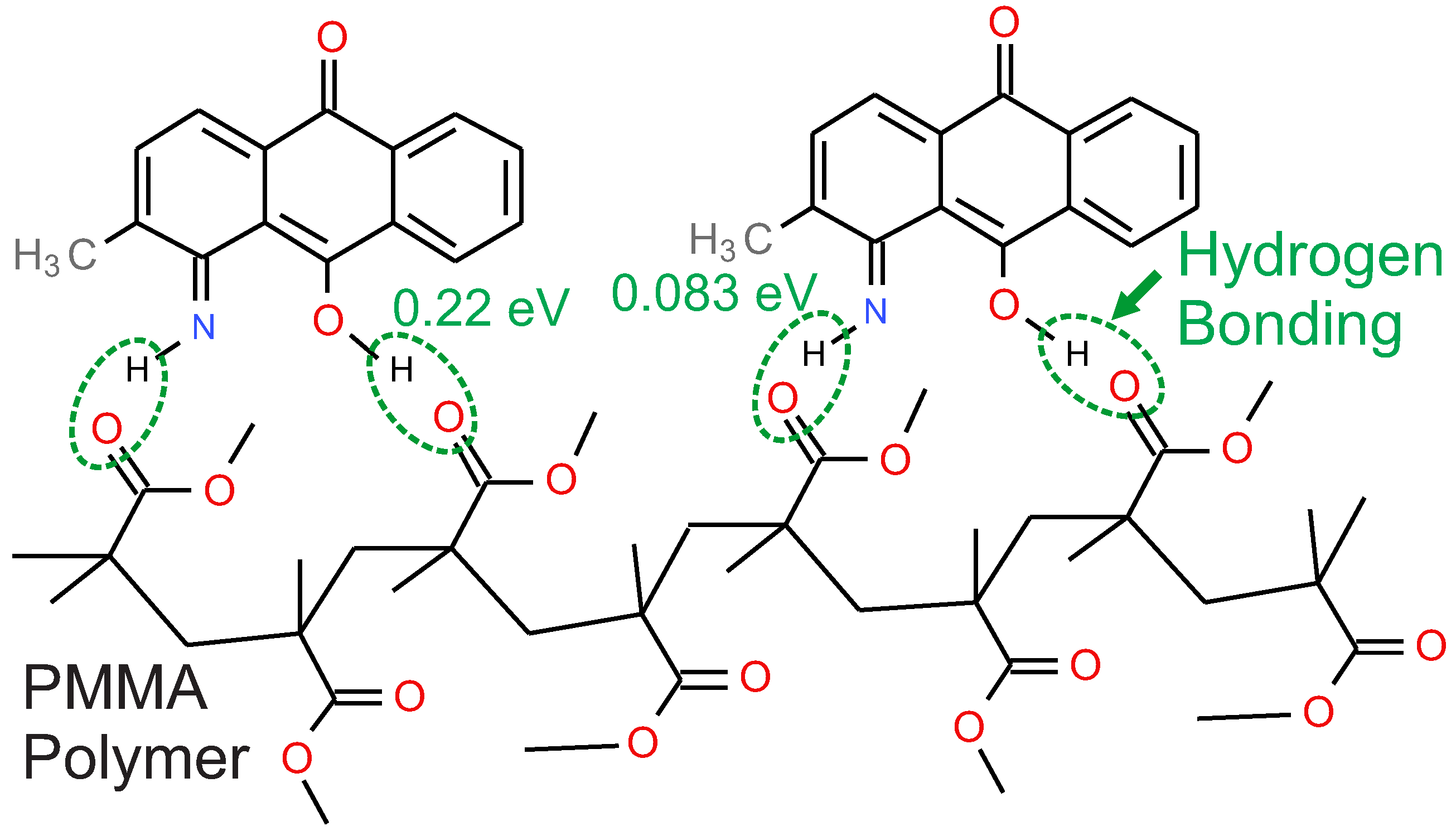
1.3. Motivation
1.3.1. Ruling out Mechanisms
1.3.2. Observed Behavior
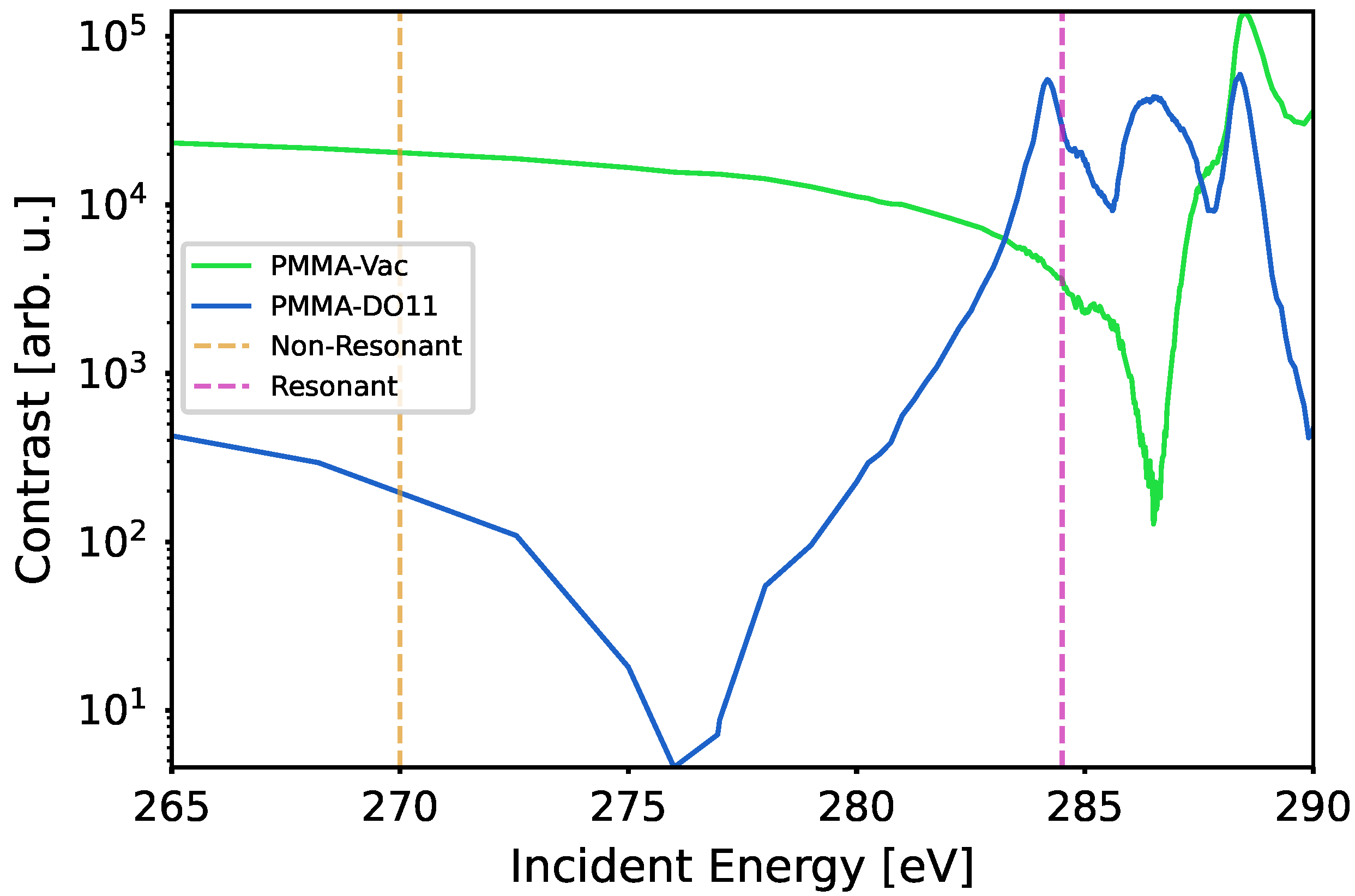
1.3.3. Scattering
2. Materials and Methods
2.1. Sample Preparation
2.2. Resonant Soft X-Ray Scattering
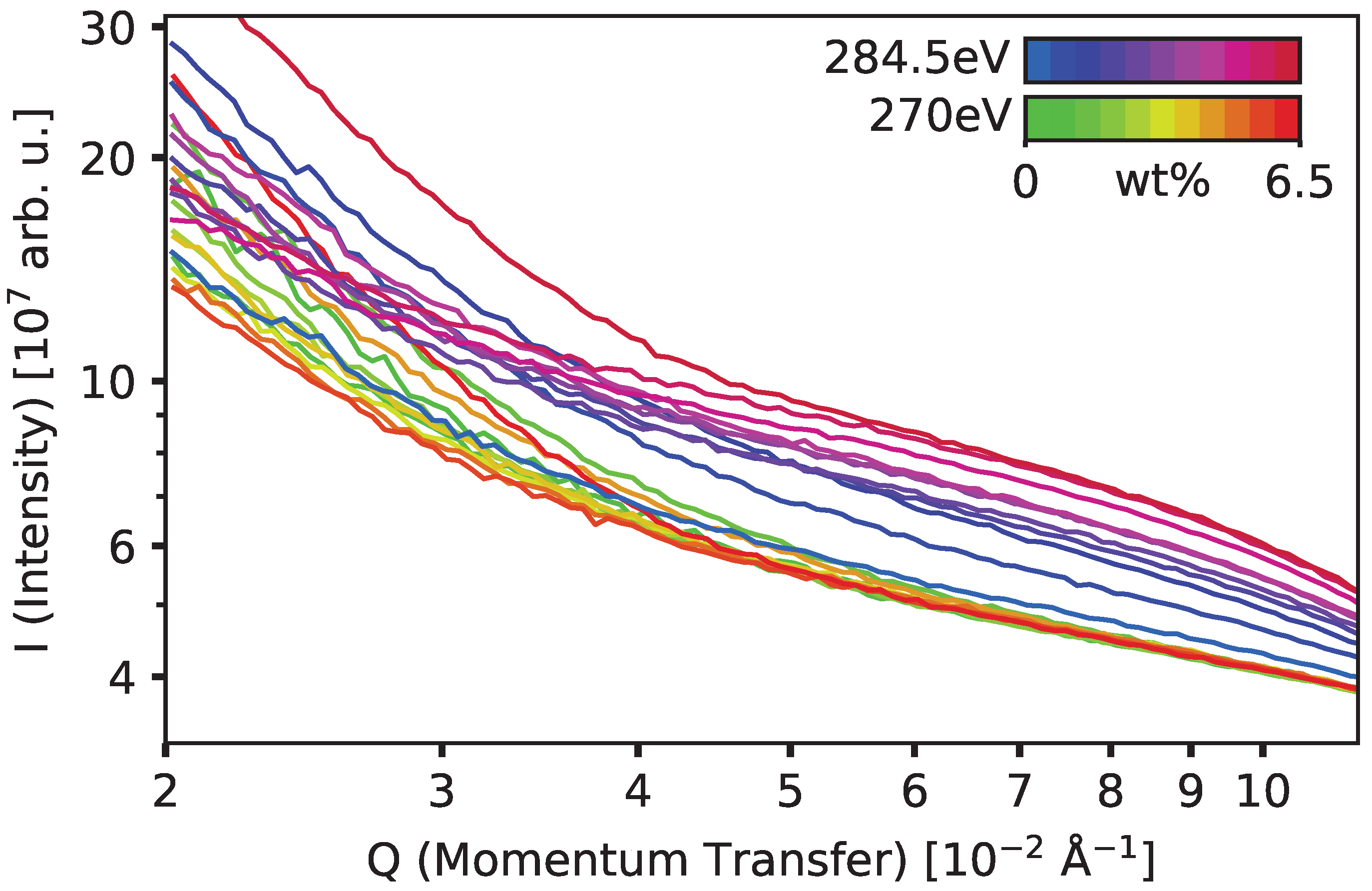
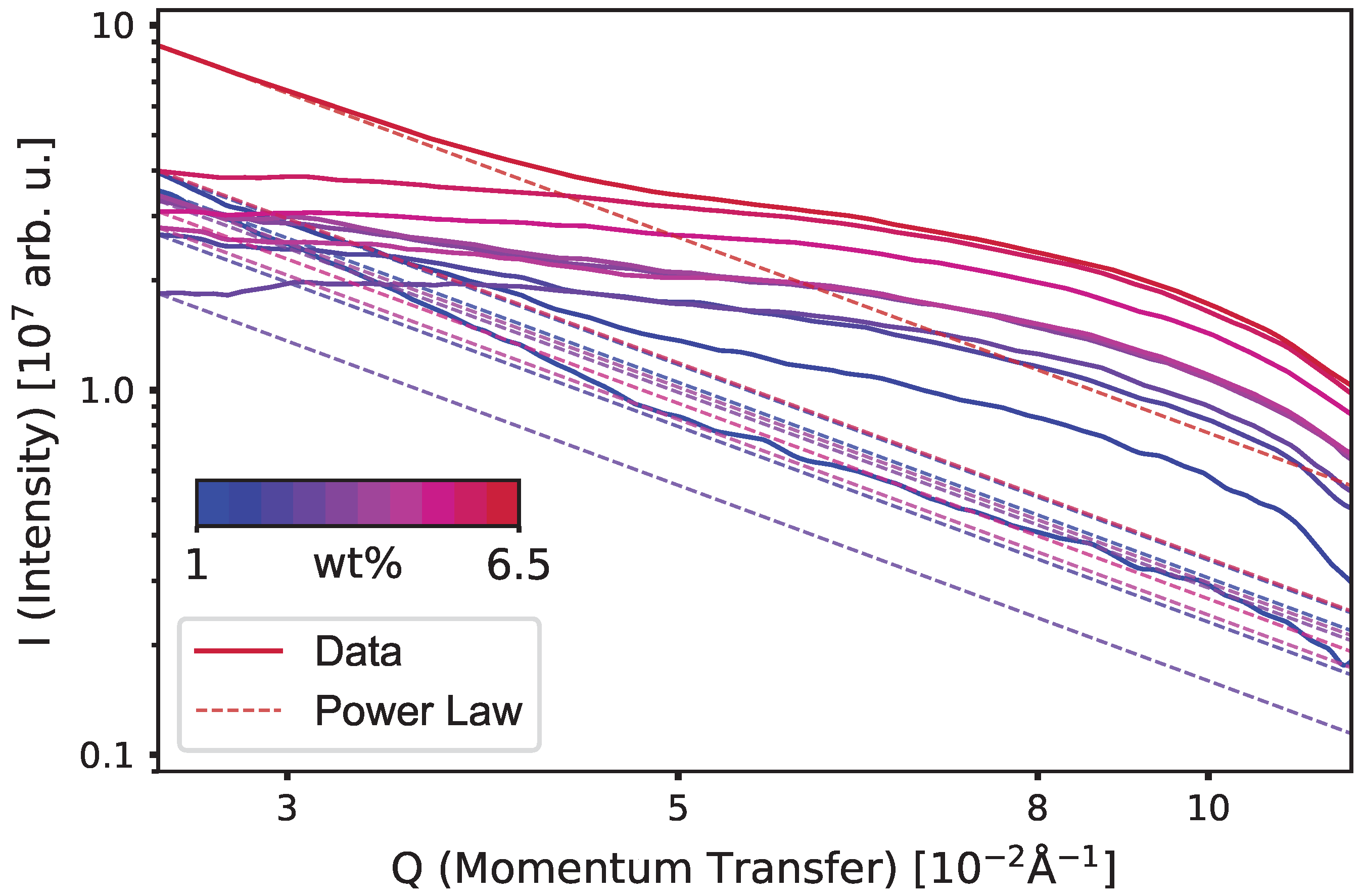
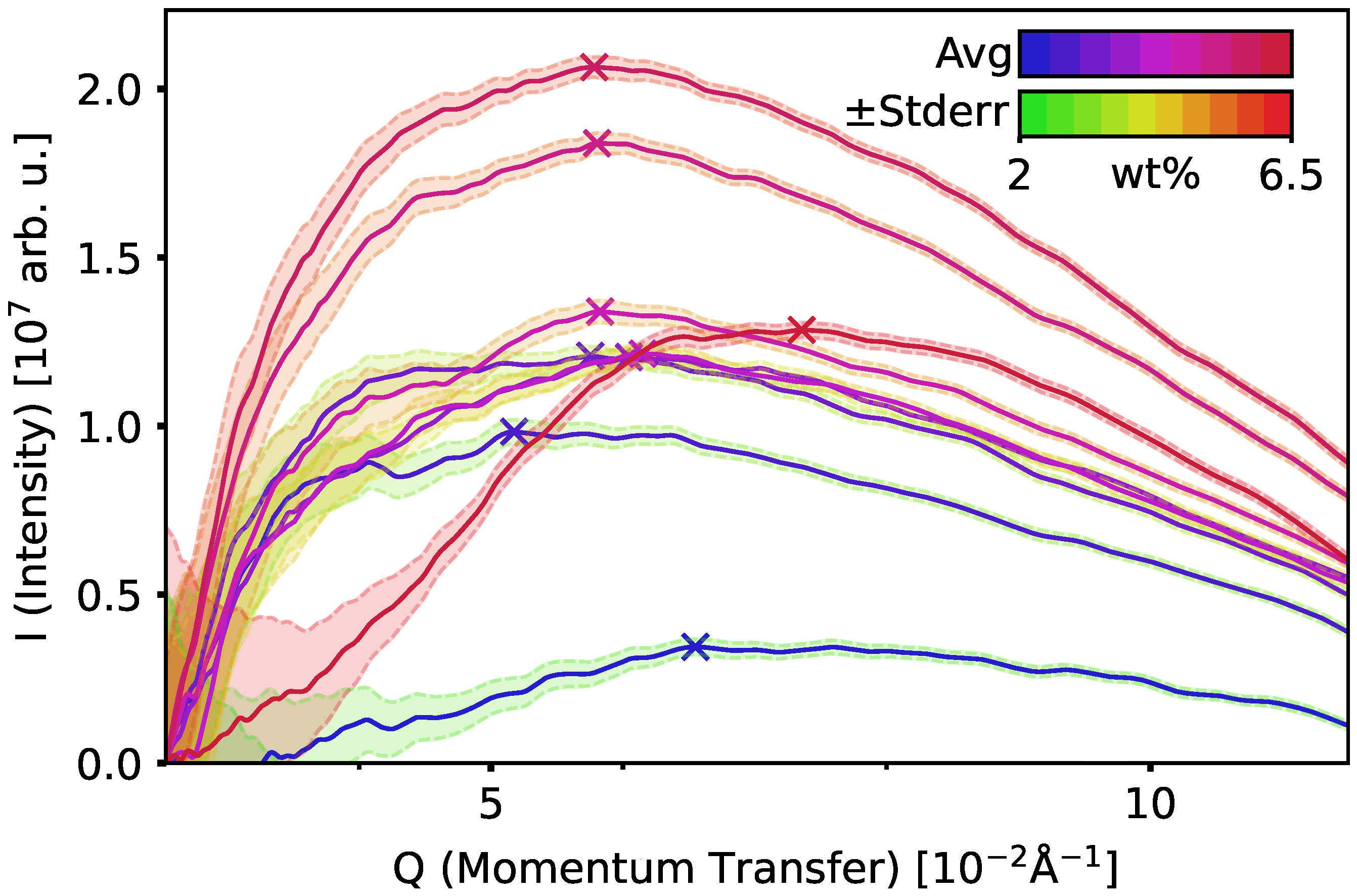
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Singer, K.D.; Kuzyk, M.G.; Sohn, J.E. Second-order Nonlinear-optical Processes in Orientationally Ordered Materials: Relationship Between Molecular and Macroscopic Properties. J. Opt. Soc. Am. B 1987, 4, 968–976. [Google Scholar] [CrossRef]
- Howell, B.; Kuzyk, M.G. Lasing Action and Photodegradation of Disperse Orange 11 Dye in Liquid Solution. Appl. Phys. Lett. 2004, 85, 1901–1903. [Google Scholar] [CrossRef]
- Dhakal, P.; Kuzyk, M.G. Molecular structure and reversible photodegradation in anthraquinone dyes. J. Photochem. Photobiol. A 2016, 328, 66–76. [Google Scholar] [CrossRef]
- Dhakal, P.P.; Kuzyk, M.G. Self-Healing Properties of 1-Amino,2,4-Dibromoanthraquinone Dye Doped in PMMA Polymer. J. Phys. Chem. C 2017, 121, 351. [Google Scholar] [CrossRef]
- Duarte, F.J. Organic Lasers and Organic Photonics, 2nd ed.; IOP Publishing: Bristol, UK, 2024. [Google Scholar]
- Sorokin, P.P.; Lankard, J.R.; Hammond, E.C.; Moruzzi, V.L. Laser-pumped Stimulated Emission from Organic Dyes: Experimental Studies and Analytical Comparisons. IBM J. Res. Dev. 1967, 11, 130–148. [Google Scholar] [CrossRef][Green Version]
- Farmer, G.I.; Huth, B.G.; Taylor, L.M.; Kagan, M.R. Time-Resolved Stimulated Emission Spectra of an Organic Dye Laser. Appl. Phys. Lett. 1968, 12, 136–138. [Google Scholar] [CrossRef]
- Fletcher, A.N. FY 1980 Report on Dye Laser Materials; Defense Technical Information Center: Fort Belvoir, VA, USA, 1981. [CrossRef]
- Daughton, W.J.; Givens, F.L. An Investigation of the Thickness Variation of Spun-on Thin Films Commonly Associated with the Semiconductor Industry. J. Electrochem. Soc. 1982, 129, 173. [Google Scholar] [CrossRef]
- Peng, G.D.; Ji, P.; Chu, P. Electro-optic polymer optical fibers and their device applications. Proc. SPIE 2002, 4459, 101–117. [Google Scholar] [CrossRef]
- Lu, Y.; Lowther, Z.; Christianson, N.D.; Li, Z.; Baer, E.; Kuzyk, M.G.; Dawson, N.J. Demonstration of a self-healing all-polymer distributed Bragg reflector laser. Appl. Phys. Lett. 2020, 116, 103301. [Google Scholar] [CrossRef]
- Li, S.; Tu, Y.; Bai, H.; Hibi, Y.; Wiesner, L.W.; Pan, W.; Wang, K.; Giannelis, E.P.; Shepherd, R.F. Simple Synthesis of Elastomeric Photomechanical Switches That Self-Heal. Macromol. Rapid Commun. 2019, 40, 1800815. [Google Scholar] [CrossRef]
- Karothu, D.P.; Weston, J.; Desta, I.T.; Naumov, P. Shape-Memory and Self-Healing Effects in Mechanosalient Molecular Crystals. J. Am. Chem. Soc. 2016, 138, 13298–13306. [Google Scholar] [CrossRef]
- Habault, D.; Zhang, H.; Zhao, Y. Light-triggered self-healing and shape-memory polymers. Chem. Soc. Rev. 2013, 42, 7244–7256. [Google Scholar] [CrossRef]
- Stubbs, N.; Bridgewater, M.; Stubbs, M.; Crescimanno, M.; Kuzyk, M.G.; Dawson, N.J. Polylactic acid promotes healing of photodegraded disperse orange 11 molecules. Opt. Mater. 2018, 76, 11–15. [Google Scholar] [CrossRef]
- Zhang, J.; Huo, M.; Li, M.; Li, T.; Li, N.; Zhou, J.; Jiang, J. Shape memory and self-healing materials from supramolecular block polymers. Polymer 2018, 134, 35–43. [Google Scholar] [CrossRef]
- White, S.; Sottos, N.; Geubelle, P.; Moore, J.; Kessler, M.; Sriram, S.; Brown, E.; Viswanathan, S. Autonomic healing of polymer composites. Nature 2001, 409, 794–797. [Google Scholar] [CrossRef] [PubMed]
- Westfall, N.J.; Dirk, C.W. The photochemistry of the self-healing chromophore Disperse Orange 11. J. Phys. Organ. Chem. 2012, 25, 704–712. [Google Scholar] [CrossRef]
- Anderson, B.; Ramini, S.K.; Kuzyk, M.G. Imaging studies of photodamage and self-healing of anthraquinone derivative dye doped polymers. In SPIE Laser Damage Symposium Proceedings; Exarhos, G., Ed.; SPIE: Boulder, CO, USA, 2011; Number 16. [Google Scholar]
- Anderson, B.R.; Gunawidjaja, R.; Eilers, H. Photodegradation and self-healing in a Rhodamine 6G dye and Y2O3 nanoparticle-doped polyurethane random laser. Appl. Phys. B 2015, 120, 1–12. [Google Scholar] [CrossRef]
- Braunlich, P.; Schmid, A. Contributions of Multiphoton Absorption to Laser-Induced Intrinsic Damage in NaCl. Appl. Phys. Lett. 1975, 26, 150–153. [Google Scholar] [CrossRef]
- Brawer, S. Phenomenological Theory of Laser Damage in Insulators. Phys. Rev. B 1979, 20, 3422–3444. [Google Scholar] [CrossRef]
- Chan, C.L.; Mazumder, J. The Effect of Radiative Heat Lost on Laser Material Damage. J. Appl. Phys. 1988, 63, 5890–5892. [Google Scholar] [CrossRef]
- Chase, L.L.; Lee, H.W.H.; Hughes, R.S. Investigation of Laser-Surface Interactions and Optical Damage Mechanisms Using Excitation by Pairs of Picosecond Laser Pulses. Appl. Phys. Lett. 1990, 57, 443–455. [Google Scholar] [CrossRef]
- Chen, C.L.; Mazumder, J. One-dimensional Steady-state Model for Damage by Vaporization and Liquid Expulsion Due to Laser-material Interaction. J. Appl. Phys. 1987, 62, 4579–4586. [Google Scholar] [CrossRef]
- Estler, R.C.; Nogar, N.S. Chemical Precursor to Optical Damage Detected by Laser Ionization Mass Spectrometry. Appl. Phys. Lett. 1988, 52, 2205–2207. [Google Scholar] [CrossRef]
- Exarhos, G.J.; Guenther, A.H.; Kozlowski, M.R.; Soileau, M.J. Laser-Induced Damage in Optical Materials; SPIE: Bellevue, WA, USA, 1998. [Google Scholar]
- Felix, M.P.; Nachbar, W. A Closer Look at Laser Damage in PMMA. Appl. Phys. Lett. 1974, 25, 25–27. [Google Scholar] [CrossRef]
- Jones, S.C.; Braunlich, P.; Casper, R.T.; Shen, X.A. Recent Progress on Laser-Induced Modifications and Intrinsic Bulk Damage of Wide Gap Optical Materials. Opt. Eng. 1989, 28, 1039–1068. [Google Scholar] [CrossRef]
- Kim, H.; Postlwaite, J.C.; Zyung, T.; Dlott, D.D. Ultrafast Imaging of Optical Damage Dynamics and Laser-Produced Wave Propagation in Polymethyl Methacrylate. J. Appl. Phys. 1988, 64, 2955–2958. [Google Scholar] [CrossRef]
- Milam, D. Laser-Induced Damage at 1064 nm, 125 psec. Appl. Opt. 1977, 16, 1204–1213. [Google Scholar] [CrossRef]
- Nechitailo, S. Mechanisms of Laser Damage to Transparent Polymer Materials. Bull. Acad. Sci. USSR, Phys. Ser. 1982, 46, 159–163. [Google Scholar]
- O’Connell, R.M.; Deaton, T.F.; Saito, T.T. Single- and Multiple-shot Laser-damage Properties of Commercial Grade PMMA. Appl. Opt. 1984, 23, 682–688. [Google Scholar] [CrossRef]
- Petzoldt, S.; Elg, A.P.; Reichling, M.; Reif, J.; Matthias, E. Surface Laser Damage Thresholds Determined by photoacoustic Deflection. Appl. Phys. Lett. 1988, 53, 2005–2007. [Google Scholar] [CrossRef]
- Summers, A.M.; Ramm, A.S.; Paneru, G.; Kling, M.E.; Flander, B.N.; Trallero-Herrero. Optical damage threshold of Au nanowires in strong femtosecond laser fields. Opt. Express 2014, 22, 4235. [Google Scholar] [CrossRef]
- Wood, R.M. Laser-Induced Damage of Optical Materials; Series in Optics and Optoelectronics; Taylor & Francis: Boca Raton, FL, USA, 2003. [Google Scholar]
- Zhang, Q.; Canva, M.; Stegeman, G. Wavelength dependence of 4-dimethylamino-4-nitrostilbene polymer thin film photodegradation. Appl. Phys. Lett. 1998, 73, 912. [Google Scholar] [CrossRef]
- Corbertt, J.W. Radiation Damage, Defects and Surfaces. Surf. Sci. 1979, 90, 205–239. [Google Scholar] [CrossRef]
- Fersman, I.; Khazov, L.D. Mechanism of Damage of the Surface of a Transparent Dielectric during Illumination with Short Light Pulse. Sov. J. Quantum Electron. 1973, 2, 319–323. [Google Scholar] [CrossRef]
- Kuznetsova, N.A.; Kaliya, O.L.; Solodar, S.L. The role of singlet oxygen in photodegradation of aminophenalenones. J. Appl. Spectrosc. 1985, 43, 901–904. [Google Scholar] [CrossRef]
- Howell, B.; Kuzyk, M.G. Amplified Spontaneous Emission and Recoverable Photodegradation in Disperse-Orange-11-Doped-Polymer. J. Opt. Soc. Am. B 2002, 19, 1790. [Google Scholar] [CrossRef]
- Anderson, B.; Kuzyk, M.G. Generalizing the correlated chromophore domain model of reversible photodegradation to include the effects of an applied electric field. Phys. Rev. E 2014, 89, 032601. [Google Scholar] [CrossRef][Green Version]
- Ramini, S.; Kuzyk, M. A self healing model based on polymer-mediated chromophore correlations. J. Chem. Phys. 2012, 137, 054705. [Google Scholar] [CrossRef]
- Ramini, S.K.; Anderson, B.; Hung, S.T.; Kuzyk, M.G. Experimental tests of a new correlated chromophore domain model of self-healing in a dye-doped polymer. Polym. Chem. 2013, 4, 4948–4954. [Google Scholar] [CrossRef]
- Anderson, B.; Ramini, S.; Kuzyk, M. Imaging studies of photodamage and self-healing in disperse orange 11 dye-doped PMMA. J. Opt. Soc. Am. B 2011, 28, 528–532. [Google Scholar] [CrossRef]
- Anderson, B.R.; Hung, S.T.; Kuzyk, M.G. Imaging studies of temperature dependent photodegradation and self-healing in disperse orange 11 dye-doped polymers. J. Chem. Phys. 2016, 145, 024901. [Google Scholar] [CrossRef]
- Anderson, B.; Bernhardt, E.; Kuzyk, M.G. A White Light Interferometric Microscope for Measuring Dose-Dependent Reversible Photodegradation. J. Appl. Phys. 2013, 114, 123103. [Google Scholar] [CrossRef]
- Zhang, M.Q.; Rong, M.Z. Extrinsic and Intrinsic Approaches to Self-Healing Polymers and Polymer Composites; Wiley: Hoboken, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Mangialetto, J.; Cuvellier, A.; Verhelle, R.; Brancart, J.; Rahier, H.; Van Assche, G.; Van den Brande, N.; Van Mele, B. Diffusion- and Mobility-Controlled Self-Healing Polymer Networks with Dynamic Covalent Bonding. Macromolecules 2019, 52, 8440–8452. [Google Scholar] [CrossRef]
- Stukalin, E.B.; Cai, L.H.; Kumar, N.A.; Leibler, L.; Rubinstein, M. Self-Healing of Unentangled Polymer Networks with Reversible Bonds. Macromolecules 2013, 46, 7525–7541. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.Y.; Meure, S.; Solomon, D. Self-healing polymeric materials: A review of recent developments. Prog. Polym. Sci. 2008, 33, 479–522. [Google Scholar] [CrossRef]
- Van Keuren, E.; Schrof, W. Fluorescence Recovery after Two-Photon Bleaching for the Study of Dye Diffusion in Polymer Systems. Macromolecules 2003, 36, 5002–5007. [Google Scholar] [CrossRef]
- Ramini, S.; Dawson, N.; Kuzyk, M. Testing the diffusion hypothesis as a mechanism of self-healing in Disperse Orange 11 doped in poly(methyl methacrylate). J. Opt. Soc. Am. B 2011, 28, 2408–2412. [Google Scholar] [CrossRef]
- Embaye, N.; Ramini, S.K.; Kuzyk, M.G. Mechanisms of reversible photodegradation in disperse orange 11 dye doped in PMMA polymer. J. Chem. Phys. 2008, 129, 054504. [Google Scholar] [CrossRef]
- Abbas, B.; Khalil, M.A. Dichroism of Poly(Methyl Methacrylate) Thin Films Doped with Disperse Orange 11 Molecules. Acta Phys. Pol. A 2009, 115, 857–863. [Google Scholar] [CrossRef]
- Hestand, N.J.; Spano, F.C. Expanded Theory of H- and J-Molecular Aggregates: The Effects of Vibronic Coupling and Intermolecular Charge Transfer. Chem. Rev. 2018, 118, 7069–7163. [Google Scholar] [CrossRef] [PubMed]
- Kobrin, P.; Fisher, R.; Gurrola, A. Reversible photodegradation of organic light-emitting diodes. Appl. Phys. Lett. 2004, 85, 2385–2387. [Google Scholar] [CrossRef]
- Howell, B. Transient Absorption and Stimulated Emission of the Organic Dye Disperse Orange 11. Ph.D. Thesis, Washington State University, Pullman, WA, USA, 2001. [Google Scholar]
- Anderson, B.R.; Gunawidjaja, R.; Eilers, H. Self-healing organic-dye-based random lasers. Opt. Lett. 2015, 40, 577–580. [Google Scholar] [CrossRef]
- Anderson, B.R.; Gunawidjaja, R.; Eilers, H. Random lasing and reversible photodegradation in disperse orange 11 dye-doped PMMA with dispersed ZrO2 nanoparticles. J. Opt. 2015, 18, 015403. [Google Scholar] [CrossRef]
- Christianson, N.D.; Lu, Y.; Dawson, N.J. Recovery of photodegraded rhodamine 6g in ester-containing polymer matrices. RSC Photochem. Photobiol. Sci. 2019, 18, 2865–2874. [Google Scholar] [CrossRef] [PubMed]
- Roe, R.J. Methods of X-Ray and Neutron Scattering in Polymer Science; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Magnussen, O.M.; Drnec, J.; Qiu, C.; Martens, I.; Huang, J.J.; Chattot, R.; Singer, A. In Situ and Operando X-ray Scattering Methods in Electrochemistry and Electrocatalysis. Chem. Rev. 2024, 124, 629–721. [Google Scholar] [CrossRef] [PubMed]
- van Franeker, J.J.; Hermida-Merino, D.; Gommes, C.; Arapov, K.; Michels, J.J.; Janssen, R.A.J.; Portale, G. Sub-Micrometer Structure Formation during Spin Coating Revealed by Time-Resolved In Situ Laser and X-Ray Scattering. Adv. Funct. Mater. 2017, 27, 1702516. [Google Scholar] [CrossRef]
- Freychet, G.; Cordova, I.; McAfee, T.R.; Kumar, G.; Pandolfi, R.; Anderson, C.; Dhuey, S.; Naulleau, P.; Wang, C.; Hexemer, A. Reconstructing the three-dimensional latent image of extreme ultraviolet resists with resonant soft X-ray scattering. J. Micro 2019, 18, 024003. [Google Scholar] [CrossRef]
- Nakamoto, A.; Yamakawa, S.; Harada, T.; Watanabe, T. Grazing-Incidence Soft-X-ray Scattering for the Chemical Structure Size Distribution Analysis in EUV Resist. J. Photopolym. Sci. Technol. 2022, 35, 61–65. [Google Scholar] [CrossRef]
- Henke, B.L.; Gullikson, E.M.; Davis, J.C. X-Ray Interactions: Photoabsorption, Scattering, Transmission, and Reflection at E = 50–30,000 eV, Z = 1–92. At. Data Nucl. Data Tables 1993, 54, 181–342. [Google Scholar] [CrossRef]
- Center for X-ray Optics and Advanced Light Source. X-Ray Data Booklet. Available online: https://xdb.lbl.gov/ (accessed on 17 September 2025).
- Ingham, B.; Kirby, N.; Wang, C.; Brady, M.; Carr, A. Elemental fingerprinting of mineral species in iron-fortified milk: Anomalous small-angle X-ray scattering and resonant soft X-ray scattering studies. J. Synchrotron Radiat. 2018, 25, 1106–1112. [Google Scholar] [CrossRef]
- Collins, B.A.; Gann, E. Resonant soft X-ray scattering in polymer science. J. Polym. Sci. 2022, 60, 1199–1243. [Google Scholar] [CrossRef]
- Swaraj, S.; Wang, C.; Araki, T.; Mitchell, G.; Liu, L.; Gaynor, S.; Deshmukh, B.; Yan, H.; McNeill, C.R.; Ade, H. The utility of resonant soft x-ray scattering and reflectivity for the nanoscale characterization of polymers. Eur. Phys. J. Spec. Top. 2009, 167, 121–126. [Google Scholar] [CrossRef]
- Linder, V.; Gates, B.D.; Ryan, D.; Parviz, B.A.; Whitesides, G.M. Water-Soluble Sacrificial Layers for Surface Micromachining. Small 2005, 1, 730–736. [Google Scholar] [CrossRef] [PubMed]
- Barbour, A.; Cai, Y.Q.; Fluerasu, A.; Freychet, G.; Fukuto, M.; Gang, O.; Gann, E.; Laasch, R.; Li, R.; Ocko, B.M.; et al. X-Ray Scattering for Soft Matter Research at NSLS-II. Synchrotron Radiat. News 2023, 36, 24–30. [Google Scholar] [CrossRef] [PubMed]
- Ilavsky, J. Nika: Software for two-dimensional data reduction. J. Appl. Crystallogr. 2012, 45, 324–328. [Google Scholar] [CrossRef]
- Dudenas, P.J.; Flagg, L.Q.; Goetz, K.; Shapturenka, P.; Fagan, J.A.; Gann, E.; DeLongchamp, D.M. How to RSoXS. J. Chem. Phys. 2025, 163, 061501. [Google Scholar] [CrossRef]
- Ade, H.; Hitchcock, A.P. NEXAFS microscopy and resonant scattering: Composition and orientation probed in real and reciprocal space. Polymer 2008, 49, 643–675. [Google Scholar] [CrossRef]
- Ferri, F.; Bertolotti, F.; Guagliardi, A.; Masciocchi, N. Nanoparticle size distribution from inversion of wide angle X-ray total scattering data. Sci. Rep. 2020, 10, 12759. [Google Scholar] [CrossRef]
- Anitas, E.M. Small-Angle Scattering from Fractals: Differentiating between Various Types of Structures. Symmetry 2020, 12, 65. [Google Scholar] [CrossRef]
- Kim, B.; Kim, W.; Kim, T.; Ko, B.; Hong, S.; Lee, K.; Kim, J.; Song, S.; Lee, S. Hydrogen-Bonding-Mediated Molecular Vibrational Suppression for Enhancing the Fluorescence Quantum Yield Applicable for Visual Phenol Detection. ACS Appl. Mater. Interfaces 2021, 13, 54339–54347. [Google Scholar] [CrossRef]
- Kalogeras, I.M.; Vassilikou-Dova, A. Dielectric Probe of Intermolecular Interactions in Poly(methyl methacrylate) (PMMA) and PMMA + SiO2 Matrixes Doped with Luminescent Organics. J. Phys. Chem. B 2001, 105, 7651–7662. [Google Scholar] [CrossRef]
- Moldoveanu, S.C.; David, V. Selection of the HPLC Method in Chemical Analysis; Elsevier: Chantilly, VA, USA, 2016; pp. 510–511. [Google Scholar]
- Hung, S.T.; Bhuyan, A.; Schademan, K.; Steverlynck, J.; McCluskey, M.D.; Koeckelberghs, G.; Clays, K.; Kuzyk, M.G. Spectroscopic studies of the mechanism of reversible photodegradation of 1-substituted aminoanthraquinone-doped polymers. J. Chem. Phys. 2016, 144, 114902. [Google Scholar] [CrossRef]
- Sampedro, D.; Sampedro Ruiz, D. Photoisomerization: Causes, Behavior and Effects; Chemistry research and applications; Nova Science Publishers: New York, NY, USA, 2019. [Google Scholar]
- Keefer, D.; Aleotti, F.; Rouxel, J.R.; Segatta, F.; Gu, B.; Nenov, A.; Garavelli, M.; Mukamel, S. Imaging conical intersection dynamics during azobenzene photoisomerization by ultrafast X-ray diffraction. Proc. Natl. Acad. Sci. USA 2021, 118, e2022037118. [Google Scholar] [CrossRef] [PubMed]
- Zolgharnein, J.; Asanjrani, N.; Bagtash, M.; Azimi, G. Multi-response optimization using Taguchi design and principle component analysis for removing binary mixture of alizarin red and alizarin yellow from aqueous solution by nano γ-alumina. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2014, 126, 291–300. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Egelhaaf, H.; Mack, H.; Azimi, H.; Brabec, C.J.; Meixner, A.J.; Zhang, D. Morphology Related Photodegradation of Low-Band-Gap Polymer Blends. Adv. Energy Mater. 2014, 4, 1400497. [Google Scholar] [CrossRef]
- Saurabh, K.; Dudenas, P.J.; Gann, E.; Reynolds, V.G.; Mukherjee, S.; Sunday, D.; Martin, T.B.; Beaucage, P.A.; Chabinyc, M.L.; DeLongchamp, D.M.; et al. CyRSoXS: A GPU-accelerated virtual instrument for polarized resonant soft X-ray scattering. J. Appl. Crystallogr. 2023, 56, 868–883. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steissberg, E.; Patterson, A.; Beyers, C.; Santiago, M.; Kuzyk, M.G.; Collins, B.A. Resonant Soft X-Ray Scattering Reveals Chromophore Domains in Polymer Doped with Disperse Orange 11 Dye. Appl. Sci. 2025, 15, 12006. https://doi.org/10.3390/app152212006
Steissberg E, Patterson A, Beyers C, Santiago M, Kuzyk MG, Collins BA. Resonant Soft X-Ray Scattering Reveals Chromophore Domains in Polymer Doped with Disperse Orange 11 Dye. Applied Sciences. 2025; 15(22):12006. https://doi.org/10.3390/app152212006
Chicago/Turabian StyleSteissberg, Elliot, Acacia Patterson, Carson Beyers, Melanie Santiago, Mark G. Kuzyk, and Brian A. Collins. 2025. "Resonant Soft X-Ray Scattering Reveals Chromophore Domains in Polymer Doped with Disperse Orange 11 Dye" Applied Sciences 15, no. 22: 12006. https://doi.org/10.3390/app152212006
APA StyleSteissberg, E., Patterson, A., Beyers, C., Santiago, M., Kuzyk, M. G., & Collins, B. A. (2025). Resonant Soft X-Ray Scattering Reveals Chromophore Domains in Polymer Doped with Disperse Orange 11 Dye. Applied Sciences, 15(22), 12006. https://doi.org/10.3390/app152212006






