Type-3 Fuzzy Logic-Based Robust Speed Control for an Indirect Vector-Controlled Induction Motor

Abstract

Induction motors require effective speed controllers to handle challenging conditions such as indirect vector control, nonlinear dynamics, load-disturbances, and changes in rotor resistance. Although proportional–integral (PI) controllers and type-1 fuzzy logic controllers (T1-FLC) are relatively straightforward to implement, they can produce significant overshoot and slow recovery; type-2 fuzzy logic controllers (T2-FLC), on the other hand, improve uncertainty management at the cost of higher computational complexity. This study proposes a type-3 fuzzy logic controller (T3-FLC) that balances robustness with a single $\alpha$-slice using two inputs and seven membership functions per input (49 rules). In six comparison scenarios, the type-3 FLC (T3-FLC) consistently offers a lower overshoot percentage and shorter recovery/settling times than the PI controller and type-1 FLC (T1-FLC). Overshoot drops to $0.13\%$ with T3-FLC during a high-speed positive step, while this value for the PI controller is $4.43\%$. During a low-amplitude positive step, T3-FLC reaches $1.37\%$, while the PI controller reaches $11.12\%$ and T1-FLC reaches $4.13\%$. After load torque is removed, the recovery time $t_{\mathrm{rec}}$ under T3-FLC is $0.064$ s at high speed and $0.158$ s at low speed, while for PI, these values are $0.400$ s and $1.975$ s, respectively. Under variations in rotor resistance, T3-FLC maintains a significantly smaller overshoot value: with a $-20\%$ change (3–6 s window), the values are $1.45\%$ (T3-FLC) versus $9.59\%$ (PI) and $4.51\%$ (T1-FLC); with a $+20\%$ change (3–6 s), the values are $0.14\%$ (T3-FLC) versus $4.36\%$ (PI) and $0.15\%$ (T1-FLC). Although there are isolated cases in which PI or T1-FLC shows a marginal advantage in a single metric (e.g., slightly smaller overshoot during transition or lower peak error during disturbance), T3-FLC generally provides the best balance, combining low overshoot with short settling/recovery time while keeping steady-state error at zero in all scenarios.

1. Introduction

Modern alternative current (AC) motor drives achieve high efficiency and reach performance targets thanks to advances in power semiconductors and digital control [1,2]. Induction motors (IM) are widely used in industrial environments due to their robustness and cost-effectiveness [2,3]. However, in indirect vector control (IVC), the speed-control loop is particularly sensitive to nonlinear dynamics and parameter variations—especially under conditions of low speeds, perturbing load-torque changes, and temperature-dependent variations in rotor resistance [4,5]. Such effects degrade transient performance and complicate controller tuning. Classical proportional–integral (PI) and type-1 fuzzy logic controllers (T1-FLC) are attractive due to their simplicity [6,7]. However, they can exhibit significant overshoot, long settling times, and sensitivity to parameter mismatch when operating away from nominal conditions [2,3]. The type-2 fuzzy logic controller (T2-FLC) improves uncertainty handling [8,9]; however, the associated modeling effort and computational load could hinder embedded real-time deployment [10,11,12].

1.1. Motivation

The speed-control loop in the IVC is particularly sensitive to nonlinear conditions under conditions of low speeds, sharp load-torque events, and temperature-induced changes in rotor resistance [2,4,5,13]. The classic PI controller and T1–FLC may perform well near nominal conditions; however, they tend to exhibit higher overshoot, longer settling times, and sensitivity to parameter mismatch in the motor response [2,3]. Balancing accuracy and efficiency, a Type-3 fuzzy logic controller (T3–FLC) accepts asymmetric shapes of membership functions with matched upper/lower surfaces, which thus represent uncertainty at the rule level without excessive structural growth [14,15]. Complexity is purposely limited by using two inputs and seven memberships per input (yielding a $7\times 7$ rule base with R = 49) and a single $\alpha$-slice ($K=1$), which preserves interpretability and limits inference and type-reduction costs [16,17]. This configuration aims for predictable closed-loop behavior under the aforementioned operating conditions: lower overshoot, shorter settling and recovery times, and negligible steady-state error.

1.2. Methodology

A compact T3-FLC was used as a controller for the speed-control loop of the IVC-IM driver. The T3-FLC was configured using two inputs, speed error and its derivative, with a seven-member function (49 rules) for each input. The membership functions’ parameters are selected through a structured, manual tuning protocol guided by closed-loop criteria (overshoot, rise time, settling time, recovery) without numerical optimization. A comparative analysis encompassed six distinct scenarios, utilizing a simulation model implemented within the MATLAB 2023a/Simulink environment. The study encompassed no-load scenarios with a range of speeds, specifically $\pm 1500$ and $\pm 100\mathrm{rpm}$, in addition to short-term load applications at $\pm 1500$ and $\pm 100\mathrm{rpm}$. The analysis also encompassed a $\pm 20\%$ change in rotor resistance. The comparison is presented using standard time-domain performance metrics and graphs, employing a PI controller and a T1–FLC within the same simulation model and sampling settings.

1.3. Organization of Paper

In Section 2 the paper provides a detailed and systematic review of the relevant literature. Section 3 sets out the IM model in the stator frame. Section 4 sets out the proposed T3–FLC (membership parameterization, $7\times 7$ rule base, inference with type reduction). The closed-loop configuration, tuning workflow, evaluation protocol, performance metrics, simulation, and controller settings are described in Section 5. In Section 6, a comparison of the six cases is presented, and the paper concludes with a discussion of the paper’s findings and limitations and a brief outline of a future study.

2. Literature Review

In the automation field, induction motors (IMs) have become prevalent due to their durability and cost-effectiveness. However, when it comes to achieving high performance in speed control, these motors face challenges arising from their inherent nonlinear dynamics and parameter variations, which differ from the characteristics of direct current (DC) drives [18,19]. Scalar volts-per-hertz (V/f) control is straightforward in concept; however, its transient performance is limited [2]. Direct torque control (DTC) has been demonstrated to achieve a rapid torque response; however, it is accompanied by torque ripple and a variable switching frequency [20,21,22]. The field-oriented control (FOC) method constitutes a control system developed for utilization in electrical machines. It has two main features. Firstly, it decouples flux and torque. Secondly, it enables accurate and fast transients [3,4,23].

In the context of DTC and associated drive schemes, variants that employ optimization and learning methodologies have yielded quantifiable enhancements. These include ACO-based DTC, validated experimentally on doubly fed induction motor (DFIM) benches; DTC augmented with artificial neural networks (ANNs); and neuro-fuzzy hybrid architectures employed for condition monitoring and fault diagnostics [24,25,26]. In addition, complementary sensorless strategies that integrate fuzzy logic with model-reference adaptive system (MRAS) observers have also been explored [27].

Due to its simplicity, the PI controller continues to be a prevalent component of vector-controlled drives. However, it is essential to note that nonlinearities and parameter variations can compromise the controller’s robustness. Meta-heuristics such as particle swarm optimization (PSO) and artificial bee colony (ABC) have been utilized to tune PI controller parameters. Sliding-mode control (SMC) has been demonstrated to be disturbance-resilient; however, it is also prone to chattering [28,29,30,31,32,33,34]. Super-twisting and the use of adaptive variants have been shown to mitigate this issue. Back-stepping provides Lyapunov-based stability guarantees and has been employed in IM speed regulation. Adaptive forms of back-stepping have been shown to reduce steady-state error in the presence of uncertainties, as evidenced by research [35,36]. Model predictive control (MPC), including finite-control-set (FCS) MPC, explicitly handles multivariable constraints, and its use has been demonstrated in vector-controlled IMs. FPGA-friendly fuzzy integration has been used to reduce computational load [37,38,39,40]. Robust ($H_{\infty }$) and linear–matrix inequality (LMI) formulations have been reported, including hybrid designs for improved sensitivity to parameter changes [41].

Intelligence-based speed controllers address several shortcomings of conventional schemes. T1-FLC and adaptive neuro-fuzzy inference system (ANFIS) variants frequently demonstrate superior performance in scenarios with parameter uncertainty, a finding substantiated through real-time validation [42,43,44,45]. T2-FLC enhances robustness by modeling membership-function uncertainty; its applications include direct torque control-support vector machine (DTC-SVM), MRAS observers, and hybrid MPC–type-2 fuzzy neural network (T2-FNN) frameworks for sensorless drives [46,47,48]. However, the associated computational burden and design effort can limit their suitability for real-time embedded implementation.

More recently, T3-FLC has been reported to improve stability margins and steady-state accuracy in nonlinear industrial drive settings by leveraging three-dimensional membership representations and interval-based type-reduction [49,50,51,52]. This study presents a T3-FLC with two inputs with seven memberships for each input (49 rules) and a single $\alpha$-slice, coupled with a structured manual tuning protocol and benchmarking against the PI controller and T1-FLC under matched conditions.

Problem Statement and Contributions

The speed-control loop in IVC-IM drives is characterized by three primary challenges. The system demonstrates sensitivity to parameter variations, notably temperature-driven rotor-resistance variation. Furthermore, the system has a reduced capacity to reject disturbances when it is subjected to sudden variations in load torque. Finally, increased overshoot or prolonged settling across low/high-speed regimes under fixed-structure controllers is also observed. It is evident that conventional PI and T1–FLC solutions offer simplicity; however, it is essential to note that they can exhibit increased overshoot and longer transient times under these conditions.

This work addresses the above issues by designing a compact T3-FLC that (a) models uncertainty at the rule level while retaining a small rule base and (b) is tuned with a transparent, repeatable protocol. The main contributions are as follows.

• The architecture under consideration is a compact T3-FLC architecture comprising two inputs, seven sets per input (yielding 49 rules), a single $\alpha$-slice, and balanced input scaling, which preserves interpretability.
• A documented tuning protocol comprising minor guided adjustments across reference steps, load-torque impulses, and $\pm 20\%$ rotor-resistance variations is utilized without a global optimizer, thereby facilitating reproducibility.
• The present study has demonstrated that a six-case benchmark shows lower overshoot and shorter settling/recovery times compared to the PI controller and T1–FLC across operating conditions, with zero steady-state error.

3. Mathematical Model of Induction Motor

In order to obtain the stator (stationary) reference frame, it is first necessary to map three-phase stator currents to the $\alpha \beta 0$ coordinates by means of the Clarke transformation, as follows [1]:

$$\left[\begin{array}{c}{i}_{\alpha }\\ i_{\beta }\\ i_0\end{array}\right]={\displaystyle \frac{2}{3}}\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\\ \frac{1}{2}& \frac{1}{2}& \frac{1}{2}\end{array}\right]\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right].$$

(1)

where $i_a,i_b,i_c$ are phase currents; $i_{\alpha },i_{\beta }$ are the stationary $\alpha$ and $\beta$–axis currents; and $i_0$ is the zero–sequence current.

In the stationary $\alpha \beta$ frame, stator voltage equations take the form [1,53]

$$v_{\alpha }=R_s{i}_{\alpha }+{\displaystyle \frac{d{\psi }_{\alpha s}}{dt}},v_{\beta }=R_s{i}_{\beta }+{\displaystyle \frac{d{\psi }_{\beta s}}{dt}}.$$

(2)

where $v_{\alpha },v_{\beta }$ are the $\alpha$ and $\beta$–axis stator voltages; $R_s$ is the stator resistance; ${\psi }_{\alpha s},{\psi }_{\beta s}$ are stator flux linkages along the $\alpha$– and $\beta$–axes; and $i_{\alpha },i_{\beta }$ are the corresponding stator currents.

Rotor circuits are short–circuited and written in the same stationary frame, as follows:

$$0=R_r{i}_{\alpha r}+{\displaystyle \frac{d{\psi }_{\alpha r}}{dt}}-{\omega }_r{\psi }_{\beta r},0=R_r{i}_{\beta r}+{\displaystyle \frac{d{\psi }_{\beta r}}{dt}}+{\omega }_r{\psi }_{\alpha r}.$$

(3)

where $R_r$ is the rotor resistance; $i_{\alpha r},i_{\beta r}$ are rotor currents in the $\alpha$ and $\beta$–axes; ${\psi }_{\alpha r},{\psi }_{\beta r}$ are rotor flux linkages; and ${\omega }_r$ is the rotor speed.

Flux linkages follow linear magnetics with mutual coupling, as follows:

$${\psi }_{\alpha s}=L_s{i}_{\alpha }+L_m{i}_{\alpha r},{\psi }_{\beta s}=L_s{i}_{\beta }+L_m{i}_{\beta r},$$

(4)

$${\psi }_{\alpha r}=L_m{i}_{\alpha }+L_r{i}_{\alpha r},{\psi }_{\beta r}=L_m{i}_{\beta }+L_r{i}_{\beta r}.$$

(5)

where $L_s,L_r$ are stator and rotor self–inductances; $L_m$ is the mutual inductance; $i_{\alpha },i_{\beta }$ are stator currents; $i_{\alpha r},i_{\beta r}$ are rotor currents; ${\psi }_{\alpha s},{\psi }_{\beta s}$ and ${\psi }_{\alpha r},{\psi }_{\beta r}$ are stator and rotor flux linkages.

Electromagnetic torque in the stationary frame is expressed by the $\alpha \beta$ cross–product as follows:

$$T_e={\displaystyle \frac{3}{2}}{\displaystyle \frac{P}{2}}\left({\psi }_{\alpha s}{i}_{\beta }-{\psi }_{\beta s}{i}_{\alpha }\right).$$

(6)

where $T_e$ is the electromagnetic torque; P is the number of poles; ${\psi }_{\alpha s},{\psi }_{\beta s}$ are stator flux linkages; and $i_{\alpha },i_{\beta }$ are stator currents.

Mechanical dynamics are represented by a single-inertia balance as follows:

$$J{\displaystyle \frac{d{\omega }_r}{dt}}+B{\omega }_r=T_e-T_L,$$

(7)

where J is the lumped inertia; B is the viscous friction coefficient; ${\omega }_r$ is the mechanical rotor speed; $T_L$ is the load torque; and $T_e$ is the electromagnetic torque.

Balanced operation implies $i_0=0$ in (1), and all relations (2)–(7) are used throughout the simulations under the linear–magnetic, three-phase-balanced assumptions stated in Section 5.5.

4. Type-3 Fuzzy Logic System

This section examines the fundamental structure of T3-FLC in detail, primarily focusing on the definitions of input–output configuration and membership functions. In the final subsection, the integration of T3-FLC into the speed control of an IVC-IM is systematically and comprehensively discussed. The recent literature indicates that T3-FLC approaches provide an effective alternative for modeling and controlling high-uncertainty and nonlinear systems [49,51,54,55,56,57]. It is evident that among the prominent works, there exist comprehensive reviews that offer a general overview of T3-FLC approaches [49,58]. Furthermore, T3-FLC-based methods offer flexibility and adaptability advantages in applications such as current sharing and voltage balancing in DC microgrids [57], energy management in PV/battery systems [56], and chaotic system control [51]. Significant benefits have been recently reported in dynamic system control using T3-FNN structures, where type reduction and learning techniques based on uncertainty bands have been developed [59,60].

This section details the T3-FLC employed in the speed-control loop. The design incorporates two inputs, namely the speed error e and its difference $\Delta e$, with a single output. Each input is described by seven Type-3 membership functions (MFs), yielding a $7\times 7$ rule base with 49 rules. The approach adopted involves the utilization of a single $\alpha$-slice ($K=1$) with the objective of maintaining the bounds of the inference and type-reduction efforts [14,16]. As illustrated in Figure 1, the upper and lower surfaces, as well as the asymmetric left and right spreads, are employed throughout this section [15,17].

4.1. Membership-Function Parameterization

Let $x_1=e$ and $x_2=\Delta e$. For each input $x_i$ ($i\in \{1,2\}$), define seven Type-3 fuzzy sets with centers ${\left\{c_{i,j}\right\}}_{j=1}^7$, left/right spreads ${\{d_{i,j}^L,d_{i,j}^R\}}_{j=1}^7$, and exponents ${\{a_{i,j}^U,a_{i,j}^L\}}_{j=1}^7$ governing the upper (U) and lower (L) membership surfaces.

For a given set $(i,j)$, the upper and lower membership responses at $x_i$ are defined piecewise over the left and right flanks [61]:

$$\begin{array}{cc}\hfill {\overline{M}}_{i,j}\left(x_i\right)& =\left\{\begin{array}{cc}1-{\left({\displaystyle \frac{|x_i-c_{i,j}|}{d_{i,j}^L}}\right)}^{a_{i,j}^U},\hfill & c_{i,j}-d_{i,j}^L<x_i\le c_{i,j},\hfill \\ 1-{\left({\displaystyle \frac{|x_i-c_{i,j}|}{d_{i,j}^R}}\right)}^{a_{i,j}^U},\hfill & c_{i,j}<x_i\le c_{i,j}+d_{i,j}^R,\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\underline{M}}_{i,j}\left(x_i\right)& =\left\{\begin{array}{cc}1-{\left({\displaystyle \frac{|x_i-c_{i,j}|}{d_{i,j}^L}}\right)}^{1/a_{i,j}^U},\hfill & c_{i,j}-d_{i,j}^L<x_i\le c_{i,j},\hfill \\ 1-{\left({\displaystyle \frac{|x_i-c_{i,j}|}{d_{i,j}^R}}\right)}^{1/a_{i,j}^U},\hfill & c_{i,j}<x_i\le c_{i,j}+d_{i,j}^R,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

(9)

It is important to note that alternative Type-3 parameterizations are possible; however, the above form matches our implementation and produces asymmetric, three-dimensional MF profiles with adjustable sharpness near the center and smooth tails, consistent with the examples illustrated in Figure 1 [15,17,61].

4.2. Rule Base

Let ${\mathcal{I}}_1=\{1,\dots ,7\}$ and ${\mathcal{I}}_2=\{1,\dots ,7\}$ be the MF indices for $x_1$ and $x_2$. The rule base enumerates all pairs $(j_1,j_2)\in {\mathcal{I}}_1\times {\mathcal{I}}_2$ in a fixed order, which yields $R=49$ rules. The r-th rule is

$${\mathcal{R}}_r:\mathrm{IF} x_1 \mathrm{is} (i=1,j_1) \mathrm{AND} x_2 \mathrm{is} (i=2,j_2)\hspace{1em}\mathrm{THEN} y \mathrm{is} w_r,$$

(10)

where $w_r$ is the (rule-dependent) consequent parameter. In the Type-3 setting, four consequent vectors are maintained to track the combinations of upper/lower MFs, $w_{uu},w_{ll},w_{ul},w_{lu}\in {\mathbb{R}}^R$, in line with the implementation (upper/upper, lower/lower, upper/lower, lower/upper) [14].

4.3. Inference, Type-Reduction, and Control Law

For an input pair $(x_1,x_2)$ and rule $r\leftrightarrow (j_1,j_2)$, define the upper/lower firing levels as follows:

$$\begin{array}{ccc}\hfill z_{uu}^{\left(r\right)}& ={\overline{M}}_{1,j_1}\left(x_1\right){\overline{M}}_{2,j_2}\left(x_2\right),\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}{z}_{ll}^{\left(r\right)}={\underline{M}}_{1,j_1}\left(x_1\right){\underline{M}}_{2,j_2}\left(x_2\right),\end{array}$$

(11)

$$\begin{array}{ccc}\hfill z_{ul}^{\left(r\right)}& ={\overline{M}}_{1,j_1}\left(x_1\right){\underline{M}}_{2,j_2}\left(x_2\right),\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}{z}_{lu}^{\left(r\right)}={\underline{M}}_{1,j_1}\left(x_1\right){\overline{M}}_{2,j_2}\left(x_2\right).\end{array}$$

(12)

Stacking over $r=1,\dots ,R$ yields non-negative vectors $z_{uu},z_{ll},z_{ul},z_{lu}\in {\mathbb{R}}_{\ge 0}^R$.

Let

$$S_u=\sum _{r=1}^R\left(z_{uu}^{\left(r\right)}+z_{ll}^{\left(r\right)}\right),S_l=\sum _{r=1}^R\left(z_{ul}^{\left(r\right)}+z_{lu}^{\left(r\right)}\right)$$

The type-reduced endpoints are presented as follows:

$$P_u={\displaystyle \frac{z_{uu}^{\top }{w}_{uu}+z_{ll}^{\top }{w}_{ll}}{S_u}},P_l={\displaystyle \frac{z_{ul}^{\top }{w}_{ul}+z_{lu}^{\top }{w}_{lu}}{S_l}}.$$

(13)

With a single $\alpha$-slice ($K=1$), the controller output is taken as the midpoint of the type-reduced interval and is computed as follows:

$$y={\displaystyle \frac{P_u+P_l}{2}}.$$

(14)

This expression is algebraically equivalent to the expression used in our implementation, namely $y=\alpha (P_u+P_l)/\sum \alpha$ with $\alpha =1$ [14,16].

With $R=49$ rules and $K=1$ slice, the per-sample cost for rule evaluation and type-reduction is $\mathcal{O}\left(RK\right)=\mathcal{O}\left(49\right)$. On a desktop reference (MATLAB R2024a, Intel i7-10700), the per-sample evaluation of 49 rules with a single $\alpha$-slice averages X μs $(N=1\times {10}^{6}evaluations)$. For an embedded STM32F4-class MCU at 168 MHz, a fixed-point implementation requires Y cycles per sample (<$T_s=100$ μs), indicating feasibility for the sampling rates used here.

5. Material and Methods

This section outlines the closed-loop control architecture and workflow for generating and evaluating responses. The T3-FLC structure can be summarized as follows: signal routing in the speed-control loop; fuzzification/aggregation; type reduction; and output mapping. Section 5.3 outlines the parameterization and tuning strategy. The evaluation protocol is specified in Section 3, and the time-domain performance indices with their computation rules are detailed in Section 5.4. The subsequent subsection provides a comprehensive overview of the controller design.

5.1. Controller Design Overview

The proposed controller is designed to function within the speed-control loop of an IVC-IM. The Type-3 fuzzy architecture under consideration is notable for its compact nature. The model incorporates two inputs: speed error and its discrete-time derivative and a single control output. The totality of the input is segmented into seven linguistic regions. These constitute a $7\times 7$ rule base (49 rules), which is evaluated with a single $\alpha$–slice and midpoint defuzzification. Initially, both inputs are scaled to a standardized, normalized range, ensuring neither channel dominates the inference process. The membership tiling ensures that the operating domain is covered with purposeful overlap, thereby ensuring smooth blending between adjacent regions; left/right asymmetry is permitted where acceleration differs.

5.2. T3-FLC Parameterization and Tuning

The controller is first defined using a basic template and then gradually refined through small, systematic adjustments. The input scaling factors are chosen so that the expected ranges of the speed error and the error derivative lie comfortably within the normalized universe of discourse; this supports balanced activation of the fuzzy rules. The controller parameters were tuned only under the load-disturbance scenario. During this process, the gains were iteratively adjusted in small steps to suppress overshoot, shorten the recovery time after load application/removal, and keep the steady-state speed error negligible. The final parameter set obtained in this scenario was then used unchanged in all other test cases.

5.3. Evaluation Methodology

Six scenarios are considered for simulation studies: high/low reference steps (Cases 1–2), varying load disturbances at high/low speeds (Cases 3–4), and $\pm 20\%$ rotor-resistance variation at high/low speeds (Cases 5–6). In addition, all simulations are carried out using the same motor and inverter parameters, as well as identical solver settings. The computation of time-domain metrics is conducted within the MATLAB environment. The standard settling time is evaluated by employing a $\pm 2\%$ settling band. In contrast, the disturbance-recovery time is defined as the initial moment the trajectory re-enters and persists within the $\pm 0.5\%$ band following a disturbance. Peak error magnitude is the maximum absolute deviation within the same window. The PI and T1–FLC baselines are executed under identical conditions and sampling as the T3–FLC.

5.4. Performance Metrics

This study uses the following indices for the controller’s performance evaluation.

• Rise time ($t_r$): The rise time is defined as the time interval required for the system response to increase from 10% to 90% of the final commanded value.
• Settling time ($t_s$): The settling time is the earliest time after which the response stays within $\pm 2\%$ of the final value without leaving the band.
• Overshoot $(M\%)$: Percent overshoot is defined as the maximum excursion of the output above its final (steady-state) value, normalized by the final value:

  $$M(\%)={\displaystyle \frac{y_{\mathrm{peak}}-y_{\mathrm{final}}}{\left|y_{\mathrm{final}}\right|}}\times 100.$$
• Recovery time ($t_{\mathrm{rec}}$): In this study, a more rigorous recovery criterion is employed to differentiate controller performance more effectively than the conventional $\pm 2\%$ band does. Specifically, the recovery time is defined as the elapsed time from the disturbance instant until the speed trajectory first enters a $\pm 0.5\%$ tolerance band (approximately $\pm 2\mathrm{rpm}$ around the reference) and remains within that band for at least $50\mathrm{ms}$. This choice prevents metric saturation in cases where the $\pm 2\%$ band is never violated, thereby capturing the dynamic response with higher sensitivity. Consequently, cross-controller comparisons become more informative.
• Peak error magnitude ($|e_{max}|$): maximum absolute speed error over the evaluated transient window.
• Steady–state error ($e_{ss}$): the absolute speed error once the response has settled within the specified band.

In operating conditions under which the transient is near-monotonic and overshoot is below the percent level, the peak time becomes poorly informative and is noise-sensitive. Consequently, this study does not utilize peak time as a performance metric.

5.5. Simulation Model and Controller Parameters

In this study, all analyses were carried out in the MATLAB/Simulink environment, and the model thus built is depicted in Figure 2. The same closed-loop test platform was used for every scenario. In particular, the motor model, the inverter and its modulation stage, and the speed-control structure were kept identical throughout. The parameters varied for each case design were the reference speed, load torque, and rotor resistance. The speed controller (PI/T1-FLC/T3-FLC) receives the measured mechanical speed ${\omega }_r$, forms the speed error equation $e={\omega }_r^{★}-{\omega }_r$, and outputs the q-axis current reference $i_{qs}^{★}$. The flux reference, designated as $i_{ds}^{★}$, has been established at its nominal value. As demonstrated in references $\left(i_{ds}^{★},i_{qs}^{★}\right)$, the current control loops are responsible for computing the decoupled stator-voltage commands. $\left(v_{ds}^{★},v_{qs}^{★}\right)$.

All control loops execute synchronously with the sampling interval $T_s=100\mathsf{\mu }\mathrm{s}$, which is equivalent to the pulse width modulation (PWM) period $T_c=1/f_c$ for $f_c=10\mathrm{kHz}$. It is important to note that each control update introduces a compute-and-hold latency, which is represented in the power stage as an effective voltage-application delay of $T_c/2$. The present control loops are implemented via PI controllers with anti-windup, and their bandwidth is set approximately one decade higher than that of the speed control loop. The decoupled voltage commands are as follows:

$$\begin{array}{cc}\hfill v_{ds}^{★}& =R_s{i}_{ds}+L_s{\displaystyle \frac{d{i}_{ds}}{dt}}-{\omega }_e{L}_s{i}_{qs}+u_d,\hfill \\ \hfill v_{qs}^{★}& =R_s{i}_{qs}+L_s{\displaystyle \frac{d{i}_{qs}}{dt}}+{\omega }_e\left(L_s{i}_{ds}+{\psi }_{dr}\right)+u_q,\hfill \end{array}$$

where $u_d=K_{pd}(i_{ds}^{★}-i_{ds})+K_{id}\int (i_{ds}^{★}-i_{ds})dt$ and $u_q=K_{pq}(i_{qs}^{★}-i_{qs})+K_{iq}\int (i_{qs}^{★}-i_{qs})dt$.

The pair $(v_{ds}^{★},v_{qs}^{★})$ is mapped to the stationary frame via the inverse Park transformation, $(v_{\alpha }^{★},v_{\beta }^{★})={\mathrm{Park}}^{-1}(v_{ds}^{★},v_{qs}^{★},{\theta }_e)$, and normalized by the DC link to form duty ratios under carrier-based PWM. The voltage-source inverter (VSI) is treated as ideal (no dead-time or device drops), with a stiff DC link. The electrical angle ${\theta }_e$ is obtained by numerical integration of ${\omega }_e$. A zero-order hold is used between controller updates and over each switching period, and measurement noise and quantization are neglected in this study.

Table 1. Induction motor and controller parameters used in simulation.

Parameter	Symbol	Value
Rated power	$P_{rated}$	2.2 kW
Rated voltage	$V_{rated}$	400 V
Rated frequency	$f_{rated}$	50 Hz
Rated speed	$n_{rated}$	2800 rpm
Number of poles	p	4
Stator resistance	$R_s$	8.231 $\mathsf{\Omega }$
Rotor resistance	$R_r$	4.49 $\mathsf{\Omega }$
Stator inductance	$L_s$	0.6 H
Rotor inductance	$L_r$	0.6 H
Mutual inductance	$L_m$	0.5787 H
Inertia	J	0.0019 kg·m2
Friction	B	0.000263 N·m·s
Sampling time	$T_s$	100 μs
Carrier frequency	$f_c$	10 kHz
PI gains	$K_p,K_i$	5, 7
T1-FLC gains	$K_1,K_2,G_1,G_2$	$1/157$, $1/10$, 20, 20
T3-FLC gains	$K_1,K_2,G_1,G_2$	$1/13$, $1/13$, 20, 20

provides a comprehensive list of all the simulation parameters utilized in the scenario. PI, T1–FLC, and the proposed T3–FLC were run with the same sampling times and power-stage parameters to ensure a fair comparison. T3–FLC design parameters are given in Appendix A.

6. Results and Discussion

This section presents the results obtained using the closed-loop control system created in MATLAB/Simulink, as shown in Figure 2. In addition to speed performance, the criteria defined ($t_r$, $t_s$, M, $t_{\mathrm{rec}}$, $|e_{max}|$, $e_{ss}$) in Section 5.4 are analyzed for each scenario. The solution parameters for each scenario affecting the system are preserved to ensure consistency among the controllers. The results obtained for each scenario are presented and analyzed with relevant figures and tables.

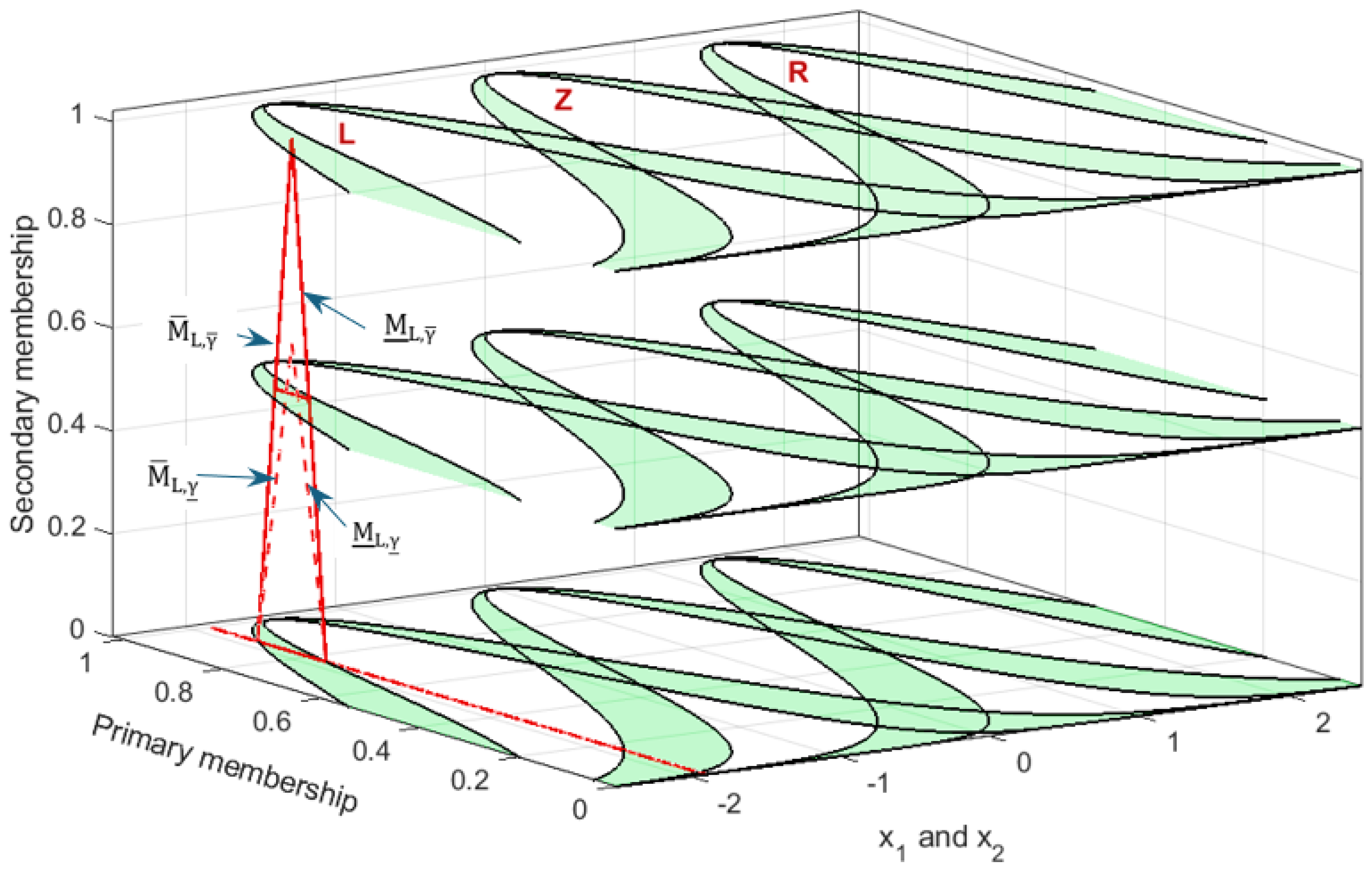
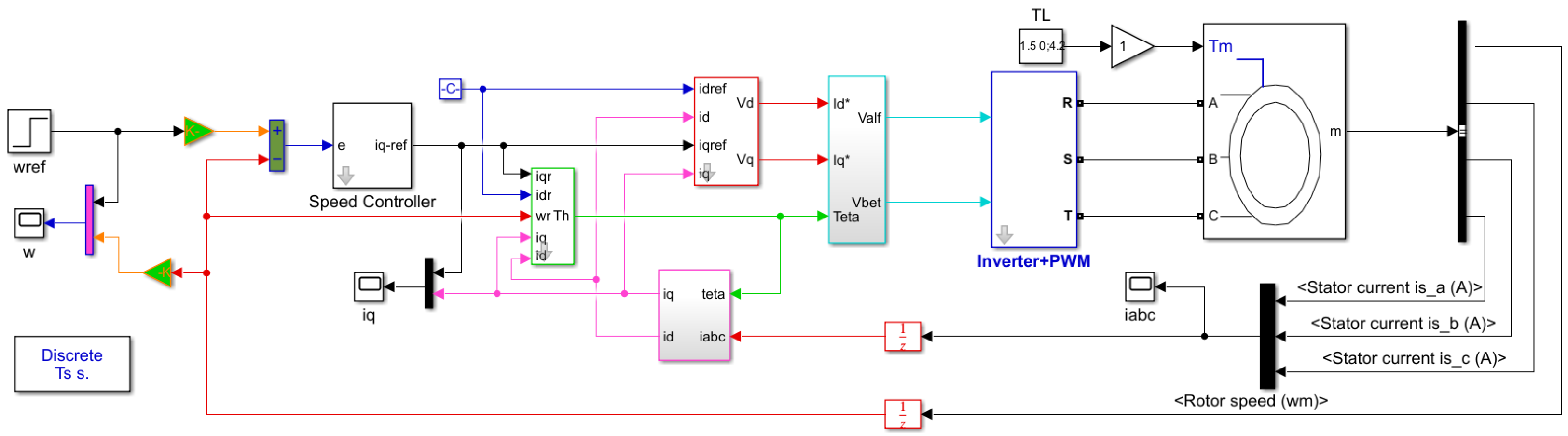
6.1. Case Studies

Simulation studies were designed to represent the most critical operating scenarios encountered in IVC-IMs and were conducted under six conditions. The initial two scenarios examined the system’s dynamic response to changes of varying magnitudes in the reference speed. High-amplitude speed transients, in particular, generated varying dynamic demands, while low-speed changes were used to evaluate the controllers’ sensitivity and small-signal behavior. The third and fourth scenarios investigated the controllers’ recovery performance and stability characteristics under varying load disturbances applied to the system. These scenarios are critical for measuring the motor drives’ capability for disturbance rejection. The fifth and sixth scenarios focused on parameter uncertainties and evaluated the controllers’ robustness under increasing and decreasing rotor resistance. The ensuing subsections present the simulation results for each scenario, with a comparison of PI, T1-FLC, and T3-FLC and key performance metrics such as $t_s$, $M\%$, $t_{rec}$, $|e_{max}|$, and $e_{ss}$ taken into account.

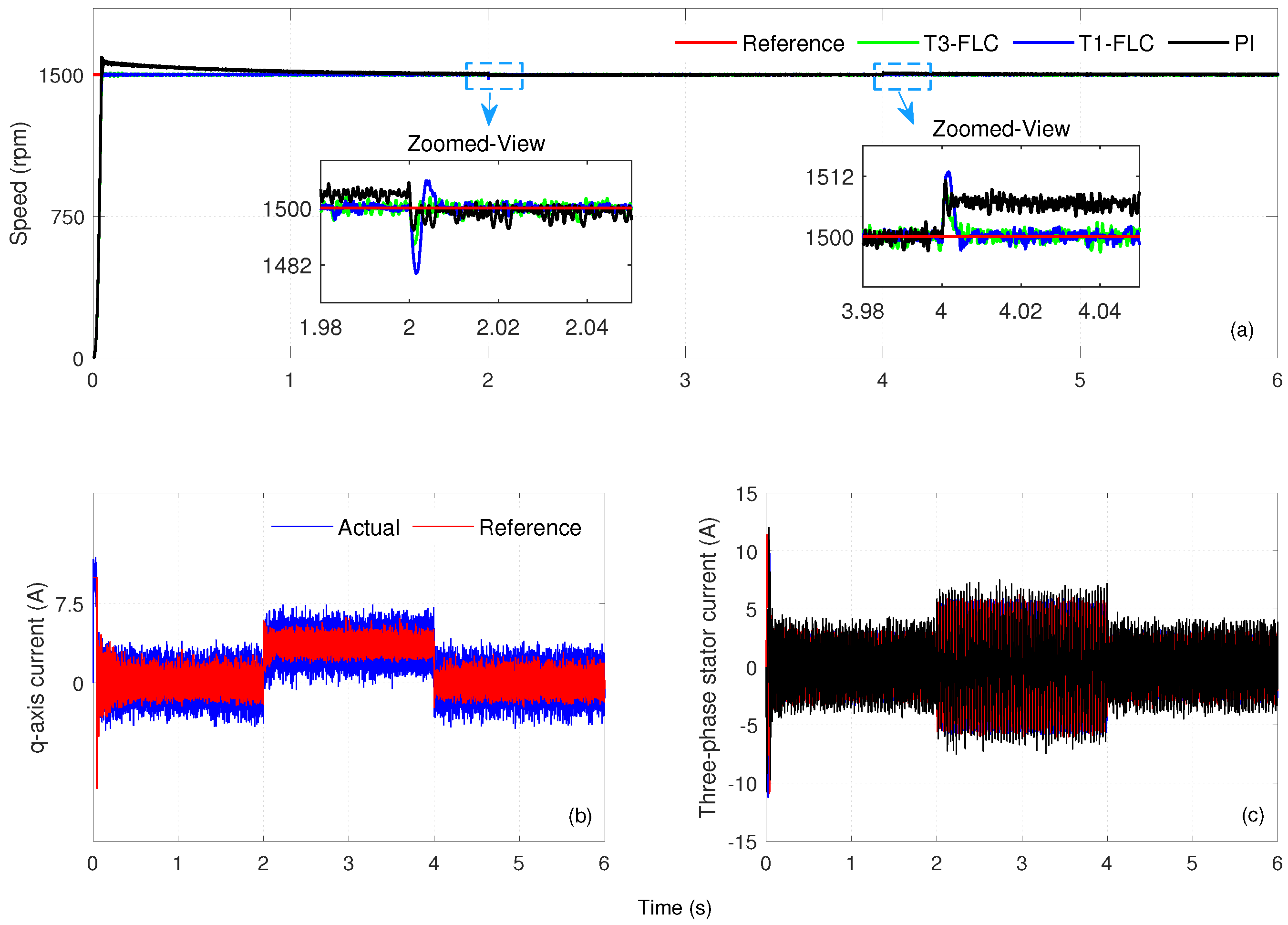
6.1.1. Case Study 1: High-Speed Reference Change

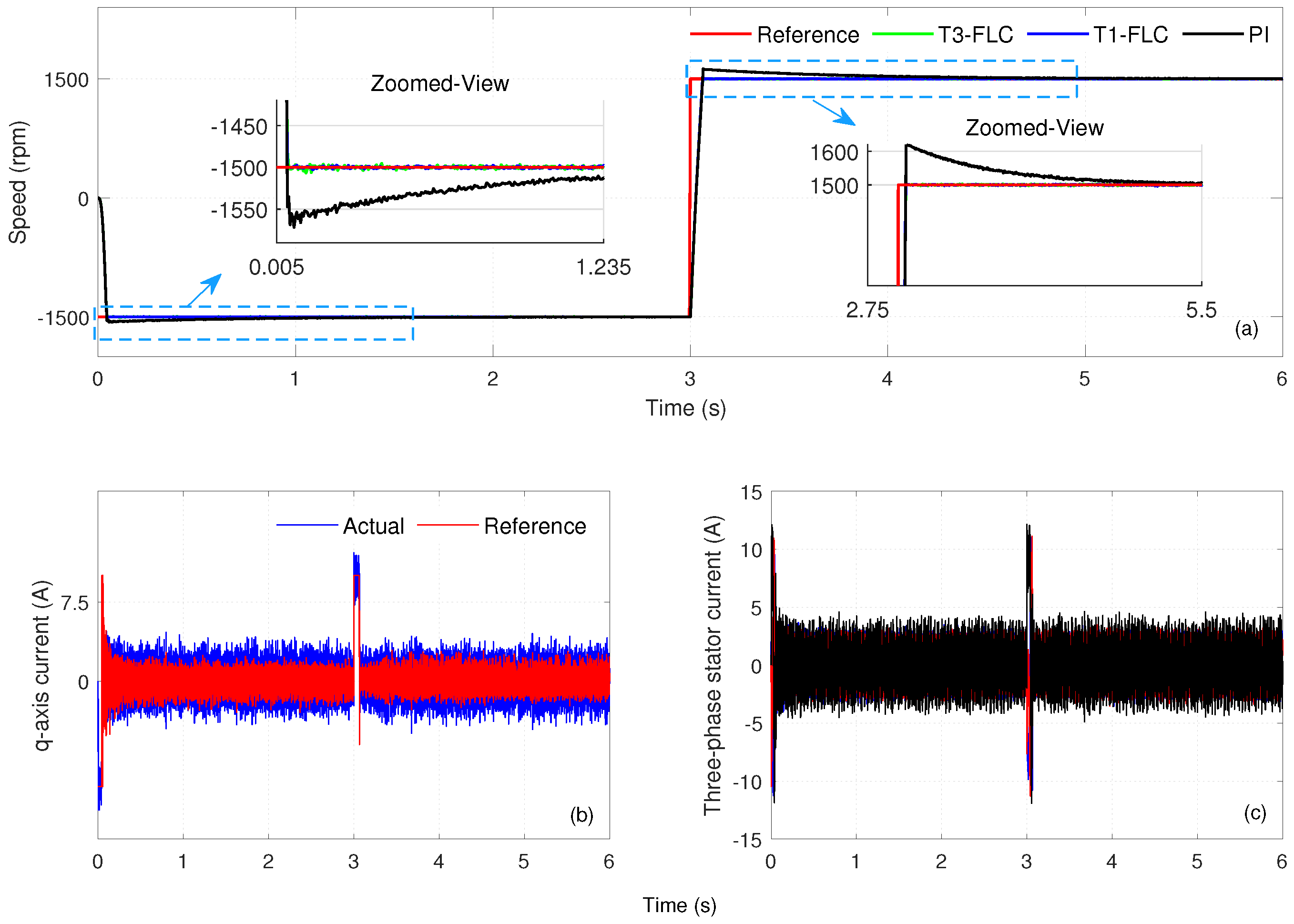
Under this operating condition, the reference speed was initially set to $-1500\mathrm{rpm}$ and was changed to $+1500\mathrm{rpm}$ at $t=3\mathrm{s}$. Simulation results obtained within Case Study 1 are presented in Figure 3. Figure 3a compares the motor speed responses obtained under the PI, T1-FLC, and T3-FLC controllers. The q-axis current and three-phase currents for the T3-FLC alone are presented in Figure 3b,c, respectively. The numerical performance metrics of the controllers, namely $t_r$, $t_s$, and $(M\%)$, are summarized in

Table 2. Performance metrics for Case Study 1.

Controller	Interval (s)	${\mathit{t}}_{\mathit{r}}$ (s)	${\mathit{t}}_{\mathit{s}}$ (s)	M (%)
T3-FLC	0–3	0.022908	0.043786	0.633890
T3-FLC	3–6	0.049210	3.060499	0.131001
T1-FLC	0–3	0.022912	0.042350	0.278594
T1-FLC	3–6	0.049033	3.059920	0.337272
PI	0–3	0.022912	0.678586	6.057000
PI	3–6	0.049819	3.603054	4.426227

.

In the 0–3 s range, T3-FLC responded quickly, with $t_r=0.022908$ s and $t_s=0.043786$ s, and the overshoot rate was recorded as $0.633890\%$. T1-FLC showed similar performance, with $t_r=0.022912$ s and $t_s=0.042350$ s, keeping the overshoot at $0.278594\%$. The PI controller, on the other hand, exhibited a longer transient regime, with $t_r=0.022912$ s but with $t_s=0.678586$ s and overshoot at $6.057\%$.

In the 3–6 s range, T3-FLC produced $t_r=0.049210$ s, $t_s=3.060499$ s, and an overshoot of $0.131001\%$. T1-FLC produced $t_r=0.049033$ s, $t_s=3.059920$ s, and an overshoot of $0.337272\%$. The PI controller showed the longest settling time and the highest overshoot, with $t_r=0.049819$ s, $t_s=3.603054$ s, and overshoot $4.426227\%$. T3-FLC demonstrated balanced performance, with low overshoot and a short settling time. T1-FLC achieved a smaller overshoot in the low-speed range, but overshoot increased at high-speed transitions. The PI controller was limited by high overshoot and long settling times in both cases. All three controllers achieved zero steady-state error.

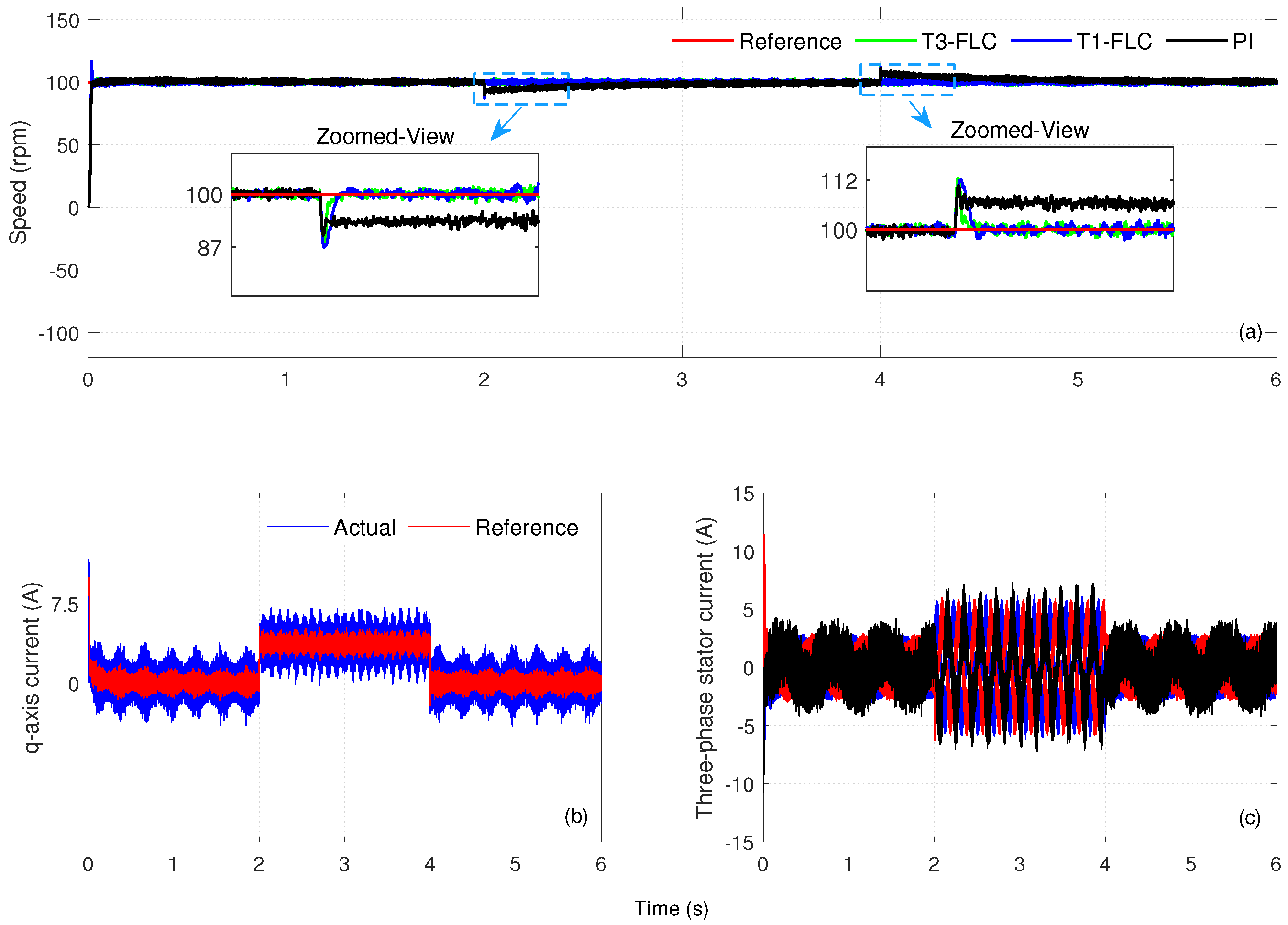
6.1.2. Case Study 2: Low-Speed Reference Change

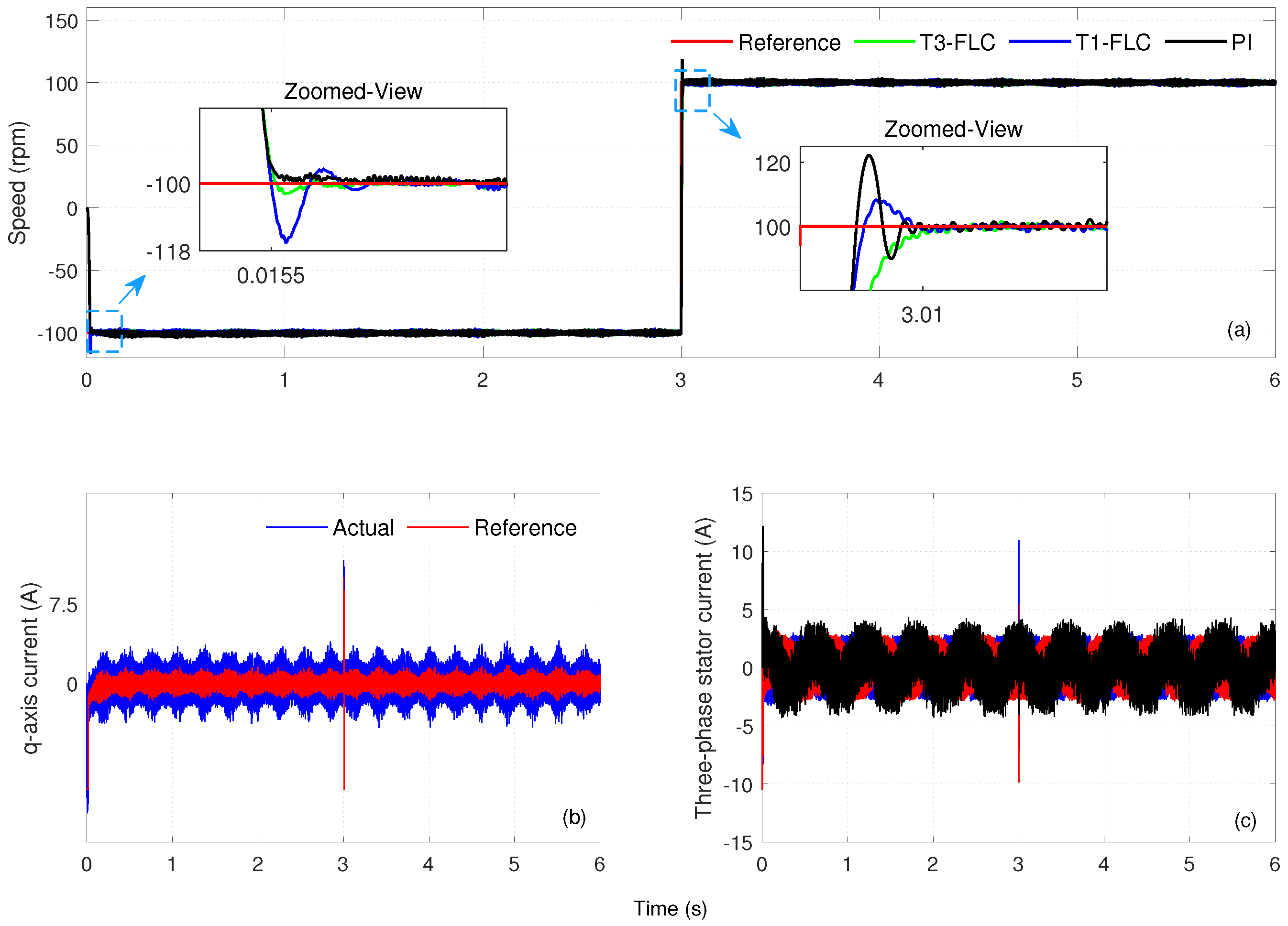
Under this operating condition, the speed reference was set to $-100\mathrm{rpm}$ in the range 0–3 s and was abruptly changed to $+100\mathrm{rpm}$ at time $t=3$ s. Simulation results obtained from Case Study 2 are presented in Figure 4. Figure 4a compares the speed responses obtained under the PI, T1-FLC, and T3-FLC controllers. The q-axis current and motor three-phase currents for the T3-FLC alone are presented in Figure 4b,c, respectively. Numerical performance metrics for the controllers $t_r$, $t_s$, and $M\%$ are summarized in

Table 3. Performance metrics for Case Study 2.

Controller	Interval (s)	${\mathit{t}}_{\mathit{r}}$ (s)	${\mathit{t}}_{\mathit{s}}$ (s)	M (%)
T3-FLC	0–3	0.007851	2.935684	3.069816
T3-FLC	3–6	0.004580	3.008446	1.374962
T1-FLC	0–3	0.007703	2.913313	15.771275
T1-FLC	3–6	0.003243	3.008165	4.134495
PI	0–3	0.007721	2.933108	3.967463
PI	3–6	0.003122	3.008002	11.124354

.

In the 0–3 s range, T3-FLC produced a fast response with $t_r=0.007851$ s and $t_s=2.935684$ s, with an overshoot of $M=3.069816\%$. T1-FLC responded similarly quickly, with $t_r=0.007703$ s and $t_s=2.913313$ s, but its overshoot reached the highest value with $M=15.771275\%$. The PI controller exhibited similar times, with $t_r=0.007721$ s and $t_s=2.933108$ s, but its overshoot was $M=3.967463\%$. These results show that in the low-speed range, T3-FLC exhibited stable behavior by limiting the overshoot.

In the 3-to-6 s range, T3-FLC operated with values of $t_r=0.004580$ s and $t_s=3.008446$ s, with the overshoot remaining at a minimum of $M=1.374962\%$. T1-FLC responded with similar response times, with $t_r=0.003243$ s and $t_s=3.008165$ s, but overshoot occurred at $M=4.134495\%$. The PI controller operated with $t_r=0.003122$ s and $t_s=3.008002$ s, and its overshoot was greatest at $M=11.124354\%$. The results reveal that T3-FLC provided the smallest overshoot at low-amplitude reference changes, while the PI controller exhibited limited stability due to the high overshoot. The results of Case Study 2 demonstrate that T3–FLC provides balanced performance at low-speed reference changes by limiting overshoot while maintaining comparable $t_r$ and $t_s$. T1–FLC responds quickly but incurs a higher overshoot, whereas the PI controller suffers a stability disadvantage due to markedly higher overshoot in the positive step.

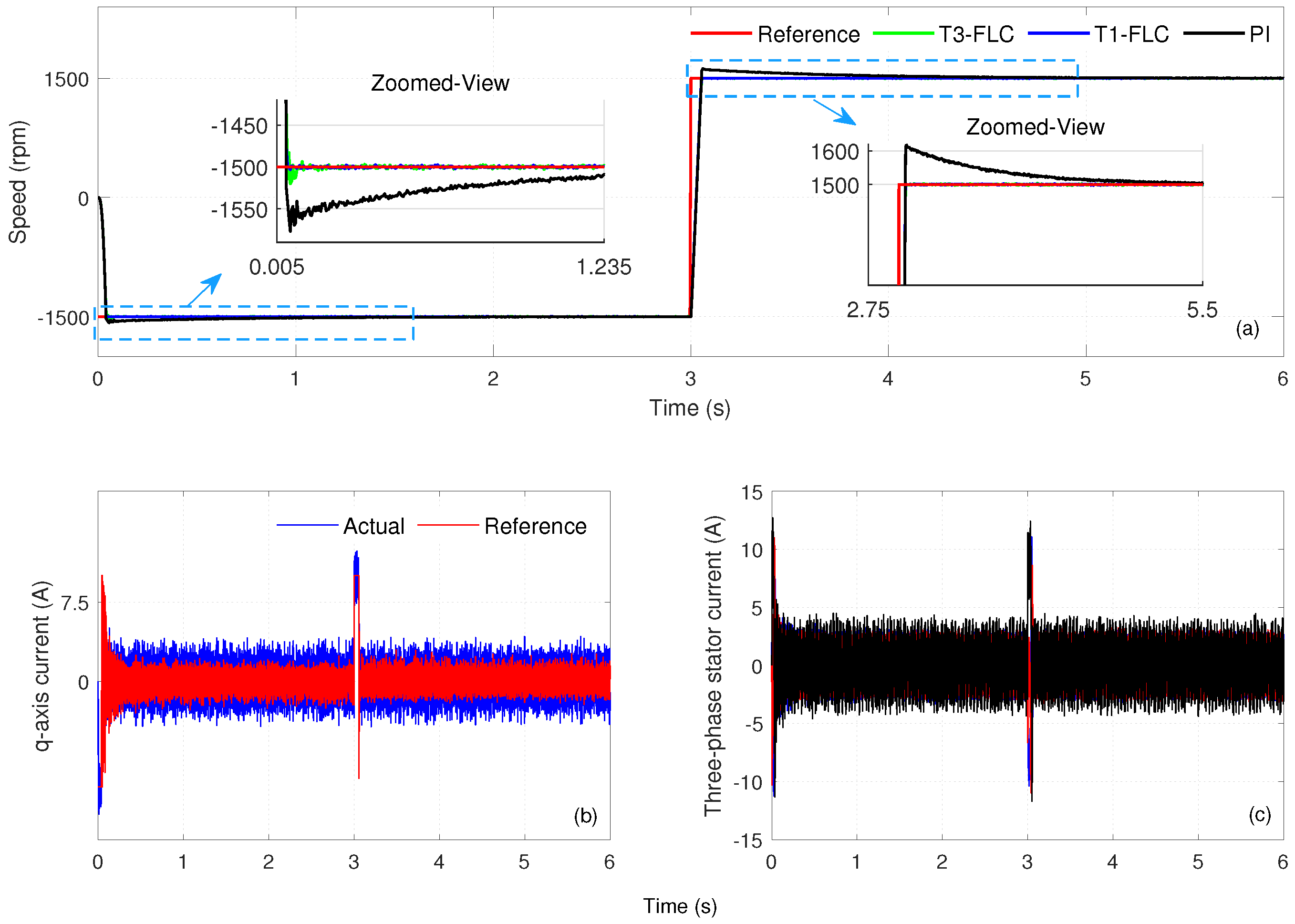
6.1.3. Case Study 3: Loaded Operation at High Speeds

Under these operating conditions, the reference speed was set as $+1500\mathrm{rpm}$ and a load torque of $3.72$ Nm was applied in the $t=2$–4 s range. Thus, the disturbance-rejection capability of the external speed-control loop in the high-speed regime was investigated. The simulation results obtained within the scope of Case Study 3 are presented in Figure 5. The motor-speed responses obtained from the PI controller, T1-FLC, and T3-FLC are given comparatively in Figure 5a, while the q-axis current and three-phase currents for T3-FLC are shown in Figure 5b,c, respectively. The numerical performance metrics for the controllers, such as $t_{\mathrm{rec}}$, $|e_{max}|$, and $e_{\mathrm{ss}}$, are summarized in

Table 4. Performance metrics for Case Study 3.

Controller	Interval (s)	${\mathit{t}}_{\mathbf{rec}}$ (s)	$|{\mathit{e}}_{max}|$ ($\mathbf{rpm}$)	${\mathit{e}}_{\mathbf{ss}}$ ($\mathbf{rpm}$)
T3-FLC	2–4	0.0032	11.446	0.000
T1-FLC	2–4	0.2798	20.750	0.000
PI	2–4	0.0265	7.043	0.000
T3-FLC	4–6	0.0640	9.141	0.000
T1-FLC	4–6	0.0640	12.844	0.000
PI	4–6	0.4000	11.107	0.000

.

At $t=2$ s, when the load torque was applied, T3-FLC reduced the recovery time to $0.0032$ s, with a peak error of $11.446\mathrm{rpm}$ and $e_{ss}$ equal to zero. T1-FLC produced a longer recovery time and a higher peak error with values of $t_{\mathrm{rec}}=0.2798$ s and ${\left|e\right|}_{max}=20.750\mathrm{rpm}$, while the steady-state error remained zero. The PI controller reached a value of $t_{\mathrm{rec}}=0.0265$ s, with the peak error recorded as $7.043\mathrm{rpm}$ at $2.0010$ s and $e_{\mathrm{ss}}=0$. These results show that T3-FLC provided the shortest recovery time at the moment of load application, while the PI controller offers a certain advantage by producing a lower peak error. When the load torque was removed at $t=4$ s, T3-FLC operated with a recovery time of $t_{\mathrm{rec}}=0.064$ s, a peak error measured at $9.141\mathrm{rpm}$ at $4.0007$ s, and a steady-state error remaining at zero. Although T1-FLC achieved the same recovery time ($0.064$ s), the peak error reached $12.844\mathrm{rpm}$ at $4.0016$ s. The PI controller exhibited the longest recovery time ($t_{\mathrm{rec}}=0.400$ s), with the peak error recorded as $11.107\mathrm{rpm}$ at $4.0009$ s and the steady-state error remaining at zero. These findings reveal that T3-FLC provides a balanced response in terms of both recovery time and error magnitude during load removal. At high speeds and under load, T3-FLC stands out for its short recovery time and low error values. While T1-FLC kept the steady-state error at zero, it fell behind T3-FLC in terms of recovery time and peak error. Although the PI controller can produce lower peak error at some moments, the long recovery time limits the ability to detect disturbance rejection.

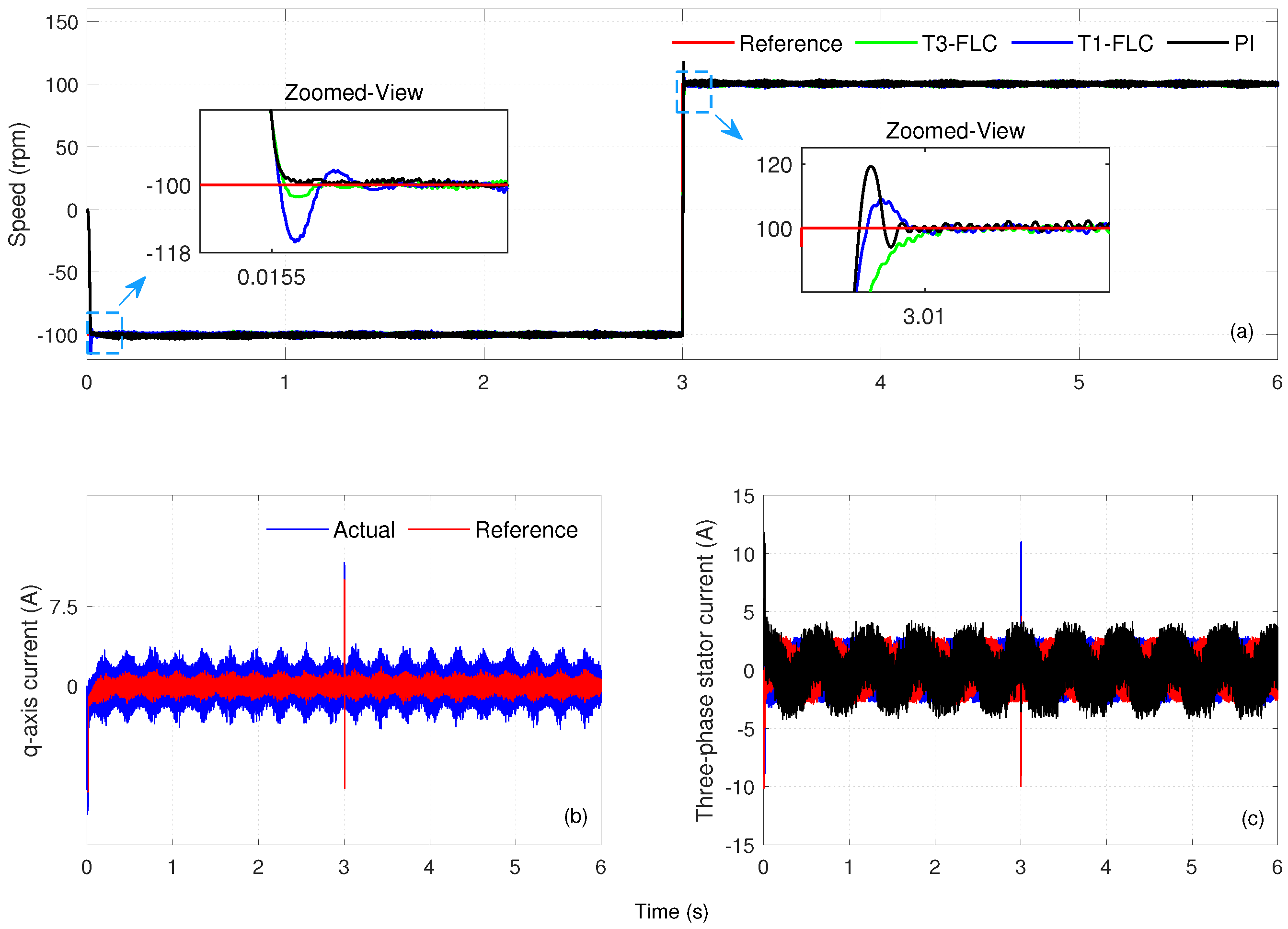
6.1.4. Case Study 4: Loaded Operation at Low Speed

Under these operating conditions, the reference speed was set as $100\mathrm{rpm}$ and a load torque of $3.72$ Nm was applied in the $t=2$–4 s range. Thus, the disturbance-rejection capability of the external speed-control loop in the low-speed regime was investigated. The simulation results obtained within the scope of Case Study 4 are presented in Figure 6. The motor-speed responses obtained with the PI, T1-FLC, and T3-FLC controllers are given comparatively in Figure 6a, while the q-axis current and three-phase currents for T3-FLC are shown in Figure 6b,c, respectively. The numerical performance metrics of the controllers, $t_{\mathrm{rec}}$, $|e_{max}|$ and $e_{\mathrm{ss}}$, are summarized in

Table 5. Performance metrics for Case Study 4.

Controller	Interval (s)	${\mathit{t}}_{\mathbf{rec}}$ (s)	$|{\mathit{e}}_{max}|$ ($\mathbf{rpm}$)	${\mathit{e}}_{\mathbf{ss}}$ ($\mathbf{rpm}$)
T3-FLC	2–4	0.0937	12.524	0.000
T3-FLC	4–6	0.1580	12.404	0.000
T1-FLC	2–4	0.0755	13.134	0.000
T1-FLC	4–6	0.1696	12.103	0.000
PI	2–4	0.5164	10.118	0.000
PI	4–6	1.9746	10.645	0.000

.

When the load torque was applied at $t=2$ s, T3-FLC kept the recovery time at $0.0937$ s, the peak error at $12.524\mathrm{rpm}$, and the steady-state error at zero. T1-FLC achieved a shorter recovery time ($t_{\mathrm{rec}}=0.0755$ s), but the peak error was higher than that of T3-FLC, at $13.134\mathrm{rpm}$. The PI controller had a significantly longer recovery time ($t_{\mathrm{rec}}=0.5164$ s), a peak error recorded as $10.118\mathrm{rpm}$, and a steady-state error of zero. These findings show that although the PI controller produces low peak error during load application, its recovery speed is poor, while T3-FLC and T1-FLC offer faster recovery. When the load moment is removed at $t=4$ s, T3-FLC provides a stable response, with a recovery time of $0.1580$ s and a peak error of $12.404\mathrm{rpm}$, while the steady-state error remains zero. T1-FLC exhibited similar performance, with $t_{\mathrm{rec}}=0.1696$ s and ${\left|e\right|}_{max}=12.103\mathrm{rpm}$. The PI controller exhibited the longest recovery time, with $t_{\mathrm{rec}}=1.9746$ s, and yielded a peak error of $10.645\mathrm{rpm}$ and a steady-state error of zero. These results demonstrate that T3-FLC and T1-FLC recover faster than PI during load removal. At the same time, the PI controller suffers from a disadvantage due to its slow recovery time, despite its low peak error. The results of Case Study 4 show that in the low-speed regime, T3-FLC offers balanced performance, with its short recovery time and low error magnitude. Despite operating with similar recovery times, T1-FLC yielded a higher peak error than did T3-FLC. While the PI controller produced the lowest peak errors in both cases, its long recovery times limited its disturbance-rejection ability.

6.1.5. Case Study 5: Parameter Change at High Speed

In this scenario, the rotor resistance is increased by $20\%$ and the speed reference is set to $-1500\mathrm{rpm}$ at $t=0$ and abruptly changed to $+1500\mathrm{rpm}$ at $t=3$ s. Figure 7 presents the speed responses obtained with the PI, T1-FLC, and T3-FLC controllers are given comparatively in Figure 7a, while the q-axis current and three-phase currents for T3-FLC are shown in Figure 7b,c, respectively. The

Table 6. Performance metrics for Case Study 5.

Controller	Interval (s)	${\mathit{t}}_{\mathit{r}}$ (s)	${\mathit{t}}_{\mathit{s}}$ (s)	M (%)
T3-FLC	0–3	0.021383	0.041358	1.955522
T3-FLC	3–6	0.041923	3.052192	0.139059
T1-FLC	0–3	0.021359	0.039654	0.374854
T1-FLC	3–6	0.041706	3.051471	0.153929
PI	0–3	0.021359	0.617924	5.307768
PI	3–6	0.042372	3.543116	4.359818

summarizes performance metrics such as $t_r$, $t_s$, and $M\%$.

In the range of 0–3 s, T3-FLC produced a fast response, with $t_r=0.021383$ s and $t_s=0.041358$ s, and its overshoot was $M=1.955522\%$. T1-FLC operated at similar speeds, with $t_r=0.021359$ s and $t_s=0.039654$ s, and its overshoot was recorded as $M=0.374854\%$. The PI controller, on the other hand, stabilized significantly later, with $t_r=0.021359$ s and $t_s=0.617924$ s, and produced an overshoot of $M=5.307768\%$. In the 3–6 s range, T3-FLC exhibited a low overshoot of $0.139059\%$, with $t_r=0.041923$ s and $t_s=3.052192$ s, providing a stable response. T1-FLC performed similarly, with $t_r=0.041706$ s and $t_s=3.051471$ s, with overshoot remaining at $0.153929\%$. The PI controller had the longest settling time, with $t_r=0.042372$ s and $t_s=3.543116$ s, and its overshoot reached the highest value ($4.359818\%$). Under a 20% increase in rotor resistance, T3-FLC showed the most balanced performance against parameter uncertainties, with both low overshoot rates and short settling times. T1-FLC achieved a similar rise in settling times, but its overshoot value was higher than that of T3-FLC. The PI controller, on the other hand, exhibited limited tolerance to parameter changes due to longer settling times and higher overshoot values in both ranges.

6.1.6. Case Study 6: Parameter Change at Low Speed

In this scenario, the rotor resistance is reduced by $20\%$ and the speed reference is set to $-100\mathrm{rpm}$ at $t=0$ and abruptly changed to $+100\mathrm{rpm}$ at $t=3$ s. Figure 8 presents the speed responses obtained with the PI, T1-FLC, and T3-FLC controllers are given comparatively in Figure 8a, while the q-axis current and three-phase currents for T3-FLC are shown in Figure 8b,c, respectively. The

Table 7. Performance metrics for Case Study 6.

Controller	Interval (s)	${\mathit{t}}_{\mathit{r}}$ (s)	${\mathit{t}}_{\mathit{s}}$ (s)	M (%)
T3-FLC	0–3	0.008359	2.920752	3.146529
T3-FLC	3–6	0.004498	3.009146	1.454870
T1-FLC	0–3	0.008184	2.933649	15.171642
T1-FLC	3–6	0.003232	3.007913	4.508037
PI	0–3	0.008184	2.943020	3.760590
PI	3–6	0.003060	3.007555	9.589465

summarizes the quantitative performance metrics such as $t_r$, $t_s$, and $M\%$.

In the range of 0–3 s, T3-FLC responded quickly, with values of $t_r=0.008359$ s and $t_s=2.920752$ s, and its overshoot was recorded as $M=3.146529\%$. T1-FLC operated at a similar speed, with values of $t_r=0.008184$ s and $t_s=2.933649$ s, but its overshoot reached the highest value ($M=15.171642\%$). The PI controller operated with values of $t_r=0.008184$ s and $t_s=2.943020$ s, and its overshoot was recorded as $M=3.760590\%$. In the 3–6 s range, T3-FLC produced low overshoot ($M=1.454870\%$), with $t_r=0.004498$ s and $t_s=3.009146$ s. T1-FLC exhibited a shorter rise time ($t_r=0.003232$ s and $t_s=3.007913$ s), but its overshoot reached $M=4.508037\%$. The PI controller operated with the values of $t_r=0.003060$ s and $t_s=3.007555$ s, and its overshoot was the highest ($9.589465\%$). Under the condition of a $20\%$ decrease in rotor resistance, T3-FLC stood out, with low overshoot and stable transition properties. Although T1-FLC provided similar rise and settling times in some cases, overshoot values remained high. The PI controller produced acceptable results in terms of settling times but exhibited limited resistance to parameter uncertainties due to high overshoot rates in low- and high-speed regions.

7. Conclusions

The study presented a compact T3-FLC for the speed-control loop of an IVC-IM and benchmarked it against a conventional PI controller and a T1-FLC across six MATLAB/Simulink scenarios. Under the various operating conditions, the T3-FLC exhibited a consistent capacity to reduce overshoot and shorten settling and recovery times while maintaining zero steady-state error.

The main comparative outcomes are summarized below to highlight the controller’s behavior across the tested scenarios.

• Case 1 (high-amplitude reversal, 3–6 s): percent overshoot M drops from 4.43% (PI) to 0.13% (T3-FLC), an ≈97% reduction.
• Case 2 (low-amplitude step, 3–6 s): M is 11.12% (PI) and 4.13% (T1-FLC) versus 1.37% (T3-FLC), i.e., ≈88% lower than PI and ≈67% lower than T1-FLC.
• Case 3 (high-speed load removal): recovery time $t_{\mathrm{rec}}$ shortens from 0.400 s (PI) to 0.064 s (T3-FLC), ≈84% faster.
• Case 4 (low-speed load removal): $t_{\mathrm{rec}}$ falls from 1.975 s (PI) to 0.158 s (T3-FLC), ≈92% faster.
• Case 5 (+20% rotor resistance, 0–3 s): M decreases from 5.31% (PI) to 1.96% (T3-FLC), ≈63% lower.
• Case 6 (−20% rotor resistance, 3–6 s): M decreases from 9.59% (PI) to 1.45% (T3-FLC), ≈85% lower.

In all investigated cases, the proposed T3-FLC eliminated steady-state speed error while following the commanded reference and also provided a dynamic response that remained within acceptable transient-performance bounds and was comparable to that of the T1-FLC and classical PI control.

7.1. Limitations

Despite the positive simulation results, several limitations should be considered. First, the evaluation is limited to the MATLAB/Simulink environment. These non-ideal conditions, such as sensor quantization and delays, inverter dead time, and voltage drops or changes in rotor resistance caused by temperature, have not been examined within the current simulation framework, and the question of how they could compromise the robustness of T3-FLC in real-time applications remains open. Second, a structured yet intuitive protocol manually adjusts the controller parameters, including membership functions and the rule base. Although this ensures consistent performance in the reported scenarios, it introduces subjectivity and may not transfer smoothly to different operating environments; automatic search strategies could reduce bias and increase repeatability. These limitations highlight the necessity of empirical validation and computational profiling to bridge the gap from simulation insights to applicable control solutions.

7.2. Future Study

The results presented in this study were obtained from a simulation model. In future work, we will perform experimental verification and further improve the performance–robustness balance by applying optimization-based tuning of the T3-FLC parameters.