PrivRewrite: Differentially Private Text Rewriting Under Black-Box Access with Refined Sensitivity Guarantees

Abstract

Text data is indispensable for modern machine learning and natural language processing but often contains sensitive information that must be protected before sharing or release. Differential privacy (DP) provides rigorous guarantees for privacy preservation, yet applying DP to text rewriting poses unique challenges. Existing approaches frequently assume white-box access to large language models (LLMs), relying on internal signals such as logits or gradients. These assumptions limit practicality, since real-world users typically interact with LLMs only through black-box APIs. We introduce PrivRewrite, a framework for differentially private text rewriting that operates entirely under black-box access. PrivRewrite constructs a diverse pool of candidate rewrites through randomized prompting and pruning and then employs the exponential mechanism to select a single release with end-to-end $ϵ$-DP. A key contribution is our refined sensitivity analysis of the utility function, which yields tighter bounds than naive estimates and thereby strengthens the accuracy guarantees of the exponential mechanism. The framework requires no fine-tuning, internal model access, or local inference, making it lightweight and deployable in practical API-based settings. Experimental results on benchmark datasets demonstrate that PrivRewrite achieves strong privacy–utility trade-offs, producing fluent and semantically faithful outputs while upholding formal privacy guarantees. These results highlight the feasibility of black-box DP text rewriting and show how refined sensitivity analysis can further improve utility under strict privacy constraints.

1. Introduction

With the rapid advancement of machine learning and deep learning technologies, the demand for large-scale datasets has steadily increased. In particular, free-text data are widely used in natural language processing tasks, making them an important resource for model training and evaluation. However, in sensitive domains such as healthcare, law, and finance, text data often contain private and sensitive information [1,2,3,4,5]. Thus, sharing such data, even for legitimate research or application development, raises serious privacy concerns and may violate legal regulations such as HIPAA [6] or GDPR [7]. This creates a fundamental challenge: how to make use of valuable textual data while preserving individual privacy.

To address the privacy risks associated with text data sharing, differential privacy (DP) [8,9,10] has been explored as a formal mechanism to prevent the original input text from revealing sensitive content. Existing approaches have applied DP at the token level, for example by injecting noise into word embeddings or substituting tokens with randomly selected alternatives according to DP-calibrated probabilities [11,12,13]. While these methods provide theoretical privacy guarantees, they often yield ungrammatical or semantically distorted outputs, which limits their practical utility. Sentence-level approaches apply DP to entire sequences, aiming to preserve both meaning and fluency while enforcing privacy constraints [14]. Nevertheless, these methods can still suffer from degraded semantic accuracy under stricter privacy budgets, and their utility often varies considerably across different downstream tasks.

With the widespread adoption of large language models (LLMs) [15,16], increasing efforts have focused on combining LLMs with DP to sanitize sensitive text data. Recent approaches typically leverage the generative or rewriting capabilities of LLMs to produce paraphrased outputs that satisfy formal DP constraints. These methods generally assume white-box access to the underlying model, including visibility into internal components such as logits or attention weights [17,18,19]. Such access enables fine-grained control over the generation process and facilitates DP mechanisms that depend on token-level scores. Although effective in controlled environments, these approaches require running and managing the model locally, which can be impractical in resource-constrained or deployment-sensitive scenarios.

While white-box methods provide fine-grained control over text generation, they rely on access to internal model components such as logits or attention weights. This typically requires running the model locally, which is often infeasible in practical scenarios. In contrast, most real-world users interact with LLMs through commercial APIs that only support input–output access, without exposing internal computations [20,21,22]. Under this constraint, it is important to design DP mechanisms that function entirely in a black-box setting, without depending on internal access, fine-tuning, or local inference. Such approaches would enable wider adoption of DP-based text rewriting, particularly in resource-limited or tightly regulated environments.

Thus, in this paper, we propose PrivRewrite, a text rewriting framework that provides formal DP guarantees using only black-box access to LLMs. The method requires no internal model access, fine-tuning, or local inference, making it lightweight and practical for real-world deployment. PrivRewrite consists of two key components: (i) sanitized candidate generation via an LLM and (ii) a DP selection mechanism applied to the candidate outputs. This design achieves end-to-end $ϵ$-DP while preserving semantic fidelity and fluency, even in scenarios where only API-based LLM access is available.

Unlike prior methods that assume internal access to LLMs, PrivRewrite demonstrates that formal DP can be achieved entirely under black-box access, enabling practical deployment in API-based and enterprise environments. This design aligns with the dominant deployment paradigm of contemporary LLM applications, where models are accessed through hosted APIs rather than locally operated white-box systems. By removing the need for access to model internals such as logits, gradients, or parameters, PrivRewrite extends formal DP protection to realistic and compliance-sensitive settings where white-box approaches cannot be applied. The contributions of this paper can be summarized as follows:

• We propose PrivRewrite, a novel method for DP text rewriting that achieves formal $ϵ$-DP guarantees using only black-box access to LLMs. The approach is lightweight, practical, and avoids reliance on model internals, fine-tuning, or local inference.
• We formally define the selection utility for the exponential mechanism in the text-rewriting setting and derive its global sensitivity. Our analysis yields a tighter sensitivity bound than naive estimates, enabling improved utility at the same privacy level.
• We conduct extensive experiments to assess the privacy–utility trade-off of PrivRewrite. Results demonstrate that our method achieves high semantic quality while maintaining formal DP guarantees and remains effective even in constrained API-only access scenarios.

The remainder of this paper is organized as follows. Section 2 reviews related work, and Section 3 provides necessary background and formally defines the problem addressed in this paper. Section 4 details the proposed PrivRewrite framework. Section 5 evaluates the proposed approach through experiments conducted on real-world datasets, and Section 6 presents the conclusions of the paper.

2. Related Work

Early efforts to apply DP to text focused on perturbing individual words using word embeddings. Feyisetan et al. [11] introduce a mechanism based on dχ-privacy, where each word is mapped into a vector space using a pre-trained embedding model, followed by nearest-neighbor decoding. Xu et al. [12] propose a differentially private text perturbation method based on a regularized Mahalanobis metric, which injects elliptical noise into word embeddings to improve privacy guarantees. Carvalho et al. [13] propose the truncated exponential mechanism, a general metric-DP method that privatizes words by selecting from nearby candidates using the exponential mechanism. Zhou et al. [23] propose TextObfuscator, a method that obfuscates word embeddings via random cluster-based perturbation to protect privacy. Yue et al. [24] propose SANTEXT and SANTEXT+, token-wise local DP mechanisms that sanitize raw text into readable output using embedding-based distance metrics. Chen et al. [25] extend this line of work by introducing CusText, a token-level sanitization method that avoids metric assumptions and instead privatizes each token using a customized candidate set and the exponential mechanism.

In contrast to word-level approaches, sentence-level DP methods aim to rewrite entire sentences to preserve global coherence. Meehan et al. [14] propose SentDP, a sentence-level local DP framework for document embeddings, which guarantees that any sentence in a document can be substituted without significantly changing the embedding. Bollegala et al. [26] propose CMAG, a metric DP mechanism for sentence embeddings that adapts Mahalanobis noise to local embedding geometry for improved privacy-utility tradeoff.

Recently, several methods have leveraged LLMs for sentence-level text rewriting under DP. Mattern et al. [17] propose a sentence-level anonymization approach based on paraphrasing with fine-tuned transformer models, offering formal DP guarantees while addressing the semantic and syntactic limitations of word-level methods. Utpala et al. [18] propose DP-Prompt, a sentence-level privacy mechanism that applies local DP using zero-shot prompting with LLMs. Meisenbacher et al. [19] propose DP-MLM, a sentence-level differentially private text rewriting method that leverages white-box access to masked language models to perform token-wise privatization via temperature-controlled sampling under a formal exponential mechanism. In contrast to these methods, our approach is fully black-box and operates solely through input-output interaction with LLM APIs, without requiring access to model internals or gradient information.

Another line of work applying DP in these days focuses on protecting private information in LLM prompting workflows, including both the user prompts and the data used to generate them. InferDPT [20] introduces a black-box framework that ensures DP by perturbing user prompts before submitting them to LLM APIs, aiming to prevent sensitive information leakage during inference. DP-GTR [27] introduces a local DP framework that protects sensitive prompts submitted to LLMs by combining group text rewriting and in-context learning to balance privacy and utility. EmojiPrompt [28] obfuscates sensitive prompts via symbolic transformations (e.g., emojis) using generative LLMs. While not formally DP, it adopts DP-inspired constraints to mitigate inference-time leakage. Split-and-Denoise [29] applies local DP to protect sensitive prompts by perturbing their token embeddings before sending them to the LLM. A local denoising model is then used to recover utility, achieving a privacy-utility tradeoff in black-box LLM inference. Cape [30] introduces a context-aware prompt perturbation mechanism using local DP, which enhances semantic coherence by combining token embedding distance and contextual logits in its utility function. To mitigate the long-tail sampling problem over large vocabularies, Cape adopts a bucketized exponential mechanism. DP-OPT [31] focuses on protecting sensitive training data used for prompt tuning. It uses a DP ensemble method to generate discrete prompts entirely on the client side, which are then deployed to black-box LLMs for inference. While DP-OPT does not obfuscate the prompt itself, it ensures that no private data can be reconstructed from the prompt, thus preventing leakage during prompt tuning.

Beyond DP, recent studies have extensively explored security and trust issues in LLMs. Zhou et al. [32] provide a comprehensive survey of backdoor threats in LLMs, categorizing attacks across the pre-training, fine-tuning, and inference phases, and summarizing existing defenses and evaluation methodologies. Wang et al. [33] review LLM-assisted program analysis, outlining static, dynamic, and hybrid pipelines for tasks such as vulnerability detection, malware analysis, and verification. Jaffal et al. [34] survey cybersecurity applications of LLMs, highlighting vulnerabilities such as data poisoning, backdoors, and prompt injection, along with emerging defense strategies. Choi et al. [35] analyze whether ChatGPT-style code transformations can evade authorship attribution and demonstrate that a feature-based method retains strong attribution accuracy. Lin and Mohaisen [36] conduct a comparative evaluation of multiple LLM families for vulnerability detection, examining how model size, quantization, and context window affect performance across programming languages. Alghamdi and Mohaisen [37] employ BERT-based models to assess the transparency of AR/VR application privacy policies. Lin and Mohaisen [38] evaluate LLM robustness in vulnerability detection, showing that performance strongly depends on tokenized input length and context window configuration.

3. Preliminary and Problem Definition

In this section, we present the necessary preliminaries, formally define the problem, and describe the threat model and assumptions considered in this work.

3.1. Preliminary

DP is a rigorous framework ensuring that the output of a randomized algorithm does not significantly change when a single individual’s data is modified. As a result, an adversary, even with arbitrary external knowledge, cannot confidently determine whether a specific individual’s data was included in the computation [8]. A randomized mechanism $\mathcal{A}$ satisfies $\epsilon$-DP if, for any two neighboring inputs x and $x^{\prime }$, and any subset $S\subseteq \mathcal{X}$, the following condition holds:

$$Pr[\mathcal{A}\left(x\right)\in S]\le e^{\epsilon }·Pr[\mathcal{A}\left(x^{\prime }\right)\in S].$$

Here, neighboring inputs refer to input datasets x and $x^{\prime }$ that differ in at most one individual’s data record. In the context of text rewriting, this typically means that the two inputs differ by a single sentence, document, or token, depending on the granularity of the privacy guarantee. This ensures that the presence or absence of a single data point has a limited influence on the output, thereby protecting individual privacy.

The parameter $\epsilon$, known as the privacy budget, quantifies the strength of the privacy guarantee. A smaller value of $\epsilon$ implies stronger privacy, as it forces the output distributions under x and $x^{\prime }$ to be nearly indistinguishable. However, this typically requires injecting more randomness, which can reduce output utility. On the other hands, a larger $\epsilon$ permits weaker privacy, but allows the mechanism to preserve more useful information with less noise. Thus, selecting $\epsilon$ involves a trade-off between privacy and utility.

The exponential mechanism is a general-purpose DP mechanism that selects an output from a discrete set based on a utility function, while preserving $\epsilon$-DP. It is particularly useful when the output space is non-numeric and standard noise-addition methods, such as the Laplace or Gaussian mechanisms, are not applicable.

Let $\mathcal{C}$ be a finite set of possible outputs, and let $u(x,c)$ be a utility function that evaluates the quality of each candidate $c\in \mathcal{C}$ with respect to the input x. The exponential mechanism selects an output c with probability proportional to:

$$Pr[\mathcal{A}\left(x\right)=c]\propto exp\left({\displaystyle \frac{\epsilon ·u(x,c)}{2\Delta u}}\right),$$

where $\Delta u$ is the sensitivity of the utility function, defined as:

$$\Delta u=\underset{c\in \mathcal{C}}{max}\underset{x,x^{\prime }}{max}|u(x,c)-u(x^{\prime },c)|,$$

for all neighboring inputs x and $x^{\prime }$. As long as the sensitivity $\Delta u$ is bounded, the exponential mechanism ensures $\epsilon$-DP. It is particularly suited for tasks like text rewriting, where the goal is to select a high-utility output from a set of candidates generated by a language model.

3.2. Problem Definition

In this paper, we consider the task of privatized text rewriting. Given a sensitive input sequence $x=(x_1,x_2,\dots ,x_T)$ consisting of T tokens, our objective is to design a randomized mechanism $\mathcal{M}$ that outputs a rewritten text $\tilde{x}$ while meeting three requirements:

• Utility: $\tilde{x}$ should preserve the semantic content of x and remain fluent and coherent.
• Privacy: $\mathcal{M}$ must satisfy $\epsilon$-DP with respect to x.
• Practicality: The mechanism should operate with only black-box access to a language model, without relying on internal components such as logits, gradients, or model weights.

To formalize the privacy requirement, we first specify the notion of neighboring inputs. We adopt a token-level definition: two sequences $x=(x_1,\dots ,x_T)$ and $x^{\prime }=(x_1^{\prime },\dots ,x_T^{\prime })$ are neighbors, written $x\sim x^{\prime }$, if they differ in at most one token position, i.e.,

$$d_H(x,x^{\prime })=\left|\{j\in \{1,\dots ,T\}:x_j\ne x_j^{\prime }\}\right|\le 1.$$

With this definition of neighbors, a randomized mechanism $\mathcal{M}$ satisfies $\epsilon$-DP if, for all $x\sim x^{\prime }$ and all measurable subsets S of outputs,

$$Pr[\mathcal{M}\left(x\right)\in S]\le e^{\epsilon }Pr[\mathcal{M}\left(x^{\prime }\right)\in S].$$

In summary, the problem studied in this paper is to design a mechanism $\mathcal{M}$ that maps each sensitive text x to a privatized rewrite $\tilde{x}$, ensuring semantic fidelity, $\epsilon$-DP at the token level, and deployability under black-box LLM access.

3.3. Threat Model and Assumptions

We consider two adversaries in the privatized text rewriting setting. The first is the provider-side adversary $A_{\mathrm{prov}}$, representing the external LLM provider that receives all queries through the API. Since each input $x=(x_1,\dots ,x_T)$ is first processed by a local ${\epsilon }_1$-DP sanitizer, the provider does not see the raw text but only a sanitized version that already satisfies DP. The second is the output-side adversary $A_{\mathrm{out}}$, which observes only the final rewrite $\tilde{x}=\mathcal{M}\left(x\right)$. This output is produced through an additional ${\epsilon }_2$-DP selection step, ensuring that even with arbitrary auxiliary information, $A_{\mathrm{out}}$ cannot reliably distinguish neighboring inputs.

This model reflects realistic deployment conditions. Major LLM providers offer enterprise configurations with contractual assurances that submitted prompts are not stored or reused for training. Although such assurances are operational rather than formal guarantees, our mechanism provides provable protection: the provider sees only locally privatized queries, while the external observer sees only the final DP-protected output.

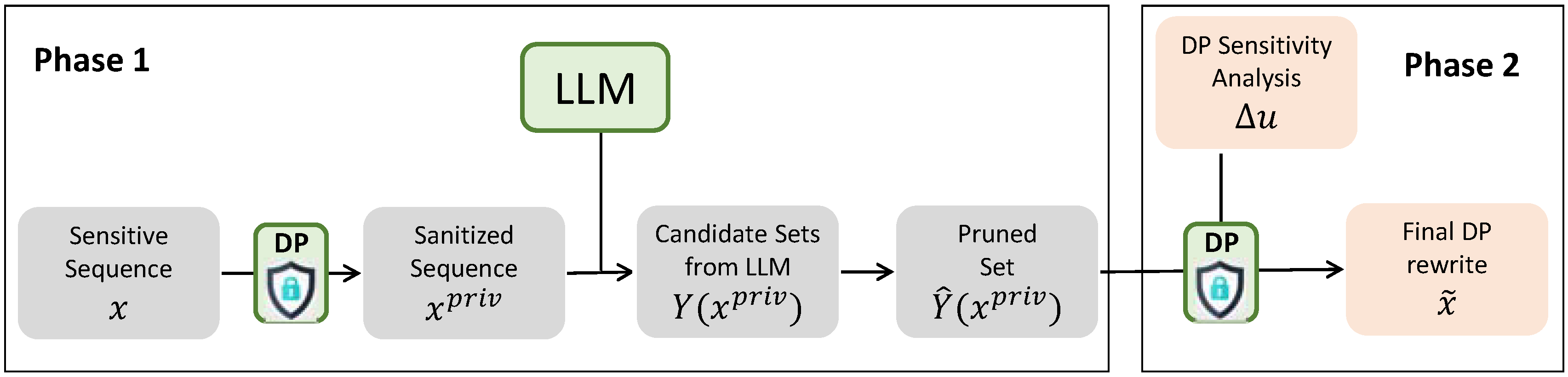
4. Proposed Method

In this section, we present PrivRewrite, a black-box text rewriting mechanism that satisfies $\epsilon$-DP. The proposed method converts each input sentence into a single privatized rewrite through two phases, illustrated in Figure 1.

• Phase 1 (Sanitized candidate generation): Given an input sequence, we construct a privatized view using a per-token DP sanitizer. The sanitized text is then submitted to the black-box LLM, which produces a set of k rewrite candidates. To reduce redundancy, near-duplicate candidates are pruned based on candidate-to-candidate similarity.
• Phase 2 (Differentially private selection): From the candidate set, we choose a single rewrite using the exponential mechanism. This mechanism samples according to a bounded similarity score with respect to the input, so that the final output preserves meaning while incorporating randomized noise for privacy.

In the following subsections, we describe each phase in detail.

4.1. Phase 1 (Sanitized Candidate Generation)

Let $\mathcal{V}$ denote a fixed vocabulary and $x=(x_1,\dots ,x_T)\in {\mathcal{V}}^T$ an input sequence. Phase 1 constructs a pruned candidate multiset in three steps: (i) sanitize x into a privatized view $x^{\mathrm{priv}}$, (ii) generate candidate rewrites from a black-box LLM using $x^{\mathrm{priv}}$, and (iii) remove near-duplicates based solely on candidate-to-candidate similarity.

4.1.1. Token-Level Sanitization

Given an input sequence $x=(x_1,\dots ,x_T)\in {\mathcal{V}}^T$, we generate its privatized counterpart $x^{\mathrm{priv}}=(x_1^{\mathrm{priv}},\dots ,x_T^{\mathrm{priv}})\in {\mathcal{V}}^T$ using the token-level exponential mechanism, a standard local-DP approach widely applied to text rewriting. For each position $i\in \left[T\right]$, we define a bounded utility function $u(t;x_i)\in [0,1]$ that measures the suitability of replacing the original token $x_i$ with $t\in \mathcal{V}$ (for example, a clipped cosine similarity between public unit-norm embeddings). Because $u(·;x_i)$ is bounded, its global sensitivity is 1.

The mechanism samples the privatized token according to

$$Pr\left[x_i^{\mathrm{priv}}=t|x_i\right]={\displaystyle \frac{exp\left(\frac{{\epsilon }_1}{2}u(t;x_i)\right)}{{\sum }_{t^{\prime }\in \mathcal{V}}exp\left(\frac{{\epsilon }_1}{2}u(t^{\prime };x_i)\right)}}.$$

Since the adjacency relation $x\sim x^{\prime }$ is defined by a single-token difference and the mechanism operates independently across positions, the sanitizer $x\mapsto x^{\mathrm{priv}}$ satisfies ${\epsilon }_1$-DP under parallel composition.

4.1.2. Candidate Generation Using LLM

In the second step, we query an LLM with the sanitized input $x^{\mathrm{priv}}$ to obtain multiple rewrite candidates. Formally, let ${\mathrm{LLM}}_k(·)$ denote a black-box API that generates k text completions in response to a given prompt. We denote the resulting candidate multiset as

$$Y\left(x^{\mathrm{priv}}\right)=\{y^{\left(1\right)},\dots ,y^{\left(k\right)}\}={\mathrm{LLM}}_k\left(x^{\mathrm{priv}}\right).$$

Since the query depends only on $x^{\mathrm{priv}}$, this step is a randomized post-processing of the privatized sequence and does not affect the privacy guarantee.

The motivation for generating k candidates, rather than directly releasing $x^{\mathrm{priv}}$, is to improve utility. Although $x^{\mathrm{priv}}$ already satisfies ${\epsilon }_1$-DP, it may deviate substantially from the semantics of the original input due to per-token noise. This loss of semantic fidelity is a well-known limitation of token- and word-level approaches [11,12,13,23]. By using $x^{\mathrm{priv}}$ only as a prompt to the LLM, we can leverage the model’s generative capacity to produce fluent and coherent rewrites. Sampling multiple candidates increases the probability that at least one candidate aligns well with the intended meaning of x. In Phase 2, a differentially private selection mechanism chooses a single output from $Y\left(x^{\mathrm{priv}}\right)$, ensuring that the final release preserves DP while improving semantic fidelity compared to directly publishing $x^{\mathrm{priv}}$.

4.1.3. Near-Duplicate Pruning

LLMs are known to produce highly similar or even near-duplicate outputs across different generations. As a result, the candidate set $Y\left(x^{\mathrm{priv}}\right)$ may contain substantial redundancy. To mitigate this, we apply a pruning step that relies only on pairwise similarity among candidates. Let $\psi :\mathrm{Text}\to {\mathbb{R}}^d$ be a fixed sentence encoder with ${\parallel \psi \left(y\right)\parallel }_2\le 1$ for all y, and define the cosine-based similarity

$$s(y,y^{\prime })=\frac{1}{2}\left(1+\langle \psi \left(y\right),\psi \left(y^{\prime }\right)\rangle \right)\in [0,1].$$

Here, $\langle \psi \left(y\right),\psi \left(y^{\prime }\right)\rangle$ denotes the inner product of the normalized embeddings, which equals their cosine similarity in $[-1,1]$. The transformation $\frac{1}{2}(1+·)$ simply shifts and rescales this range to $[0,1]$.

Given a similarity threshold ${\tau }_{\mathrm{dup}}\in (0,1)$ and a fixed public order $\pi$ over $\{1,\dots ,k\}$, we prune candidates using the following greedy procedure:

• Initialize $\widehat{Y}\leftarrow \mathsf{\varnothing }$.
• For each j in order $\pi$, add $y^{\left(j\right)}$ to $\widehat{Y}$ if $s(y^{\left(j\right)},y)<{\tau }_{\mathrm{dup}}$ for every $y\in \widehat{Y}$.

By construction, every pair of retained candidates is guaranteed to satisfy

$$s(y,y^{\prime })<{\tau }_{\mathrm{dup}}\mathrm{for}\mathrm{all}y\ne y^{\prime }\in \widehat{Y},$$

which ensures that $\widehat{Y}$ forms a set of mutually dissimilar rewrites. Equivalently, the procedure selects a maximal ${\tau }_{\mathrm{dup}}$-separated subset of $Y\left(x^{\mathrm{priv}}\right)$ under the similarity measure s. The parameter ${\tau }_{\mathrm{dup}}$ directly controls the degree of enforced diversity: larger values impose stricter separation and result in fewer but more distinct candidates, while smaller values allow more candidates at the cost of potential redundancy.

4.2. Phase 2 (Differentially Private Selection)

Given the pruned candidate multiset $\widehat{Y}=\{y^{\left(1\right)},\dots ,y^{\left(m\right)}\}$ obtained in Phase 1, the goal of Phase 2 is to select a single rewrite that balances semantic fidelity with formal privacy protection. We achieve this using the exponential mechanism, which favors candidates that are semantically closer to the input while ensuring that the selection procedure itself satisfies DP.

4.2.1. Utility Function

To apply the exponential mechanism, we first need to specify a utility function that measures the semantic alignment between the original sequence x and any candidate $y\in \widehat{Y}$, and then establish its global sensitivity. Let $v:\mathcal{V}\to {\mathbb{R}}^d$ be a token embedding map satisfying ${\parallel v\left(t\right)\parallel }_2\le 1$ for all $t\in \mathcal{V}$. For a sequence $x=(x_1,\dots ,x_T)$, we define its average embedding as

$$\varphi \left(x\right):={\displaystyle \frac{1}{T}}\sum _{i=1}^{T}v\left(x_i\right)\in {\mathbb{R}}^d.$$

Since the Euclidean norm is convex, the average of vectors with norm at most one also has norm at most one. Hence, ${\left|\varphi \left(x\right)\right|}_2\le 1$ for all sequences x.

Given the sensitive input x and a candidate $y\in \widehat{Y}$, we define the utility function

$$u_x\left(y\right):={\mathrm{clip}}_{[0,1]}\left(\frac{1}{2}+{\displaystyle \frac{1}{\rho }}\langle \varphi \left(x\right),\varphi \left(y\right)\rangle \right),$$

where $\rho >0$ is a smoothing parameter. The term $\langle \varphi \left(x\right),\varphi \left(y\right)\rangle$ is the Euclidean inner product between the normalized average embeddings of x and y, which lies in $[-1,1]$ and coincides with their cosine similarity. The operator ${\mathrm{clip}}_{[0,1]}$ truncates its argument into the unit interval, ensuring that $u_x\left(y\right)$ remains bounded in $[0,1]$. The parameter $\rho$ controls the trade-off between expressiveness and sensitivity: larger values yield a flatter utility landscape with lower sensitivity, while smaller values make the utility more responsive to semantic differences at the cost of higher sensitivity.

Given the utility function $u_x(·)$, the next step is to quantify its global sensitivity, which determines the noise level used by the exponential mechanism. While the trivial bound $\Delta u=1$ follows from $u_x(·)\in [0,1]$, it is overly conservative and would inject unnecessary noise, harming utility. Instead, we bound how much $u_x\left(y\right)$ can change when x and $x^{\prime }$ differ in a single token, yielding the following result.

Lemma 1 

(Global sensitivity of $u_x$). Under the neighboring relation $x\sim x^{\prime }$ (differing in at most one token),

$$\Delta u:=\underset{x\sim x^{\prime }}{sup}\underset{y\in \widehat{Y}}{sup}|u_x\left(y\right)-u_{x^{\prime }}\left(y\right)|\le {\displaystyle \frac{2}{T\rho }}.$$

Here, sup denotes the supremum, i.e., the worst-case value over all neighboring inputs and all candidates.

Proof. 

Let $x,x^{\prime }$ be neighboring sequences that differ only at position j. By definition, their average embeddings are

$$\varphi \left(x\right)={\displaystyle \frac{1}{T}}\sum _{i=1}^{T}v\left(x_i\right),\varphi \left(x^{\prime }\right)={\displaystyle \frac{1}{T}}\sum _{i=1}^{T}v\left(x_i^{\prime }\right).$$

Since all terms cancel except at index j, the difference reduces to

$$\varphi \left(x\right)-\varphi \left(x^{\prime }\right)={\displaystyle \frac{1}{T}}\left(v\left(x_j\right)-v\left(x_j^{\prime }\right)\right).$$

By taking the Euclidean norm and applying the triangle inequality, we obtain

$$\parallel \varphi \left(x\right)-\varphi \left(x^{\prime }\right){\parallel }_2={\displaystyle \frac{1}{T}}{\parallel v\left(x_j\right)-v\left(x_j^{\prime }\right)\parallel }_2\le {\displaystyle \frac{1}{T}}\left(\parallel v\left(x_j\right){\parallel }_2+{\parallel v\left(x_j^{\prime }\right)\parallel }_2\right)\le {\displaystyle \frac{2}{T}}.$$

For any fixed $y\in \widehat{Y}$, define

$$s:=\langle \varphi \left(x\right),\varphi \left(y\right)\rangle ,s^{\prime }:=\langle \varphi \left(x^{\prime }\right),\varphi \left(y\right)\rangle .$$

Then, by Cauchy–Schwarz,

$$\begin{array}{cc}\hfill |s-s^{\prime }|& =|\langle \varphi \left(x\right),\varphi \left(y\right)\rangle -\langle \varphi \left(x^{\prime }\right),\varphi \left(y\right)\rangle |\hfill \\ \hfill & =|\langle \varphi \left(x\right)-\varphi \left(x^{\prime }\right),\varphi \left(y\right)\rangle |\le \parallel \varphi \left(x\right)-\varphi \left(x^{\prime }\right){\parallel }_2{\parallel \varphi \left(y\right)\parallel }_2\le \frac{2}{T}.\hfill \end{array}$$

Define $h\left(t\right):={\mathrm{clip}}_{[0,1]}\left(\frac{1}{2}+\frac{1}{\rho }t\right)$ with $\rho >0$. Write $f\left(t\right)=\frac{1}{2}+\frac{1}{\rho }t$ and $g\left(z\right)={\mathrm{clip}}_{[0,1]}\left(z\right)$; then $h=g\circ f$. The map f is $(1/\rho )$-Lipschitz and the projection g is 1-Lipschitz, hence h is $(1/\rho )$-Lipschitz:

$$|h\left(a\right)-h\left(b\right)|\le \frac{1}{\rho }|a-b|\mathrm{for}\mathrm{all}a,b\in \mathbb{R}.$$

Applying this with $a=s$, $b=s^{\prime }$ yields

$$|u_x\left(y\right)-u_{x^{\prime }}\left(y\right)|=|h\left(s\right)-h\left(s^{\prime }\right)|\le \frac{1}{\rho }|s-s^{\prime }|\le \frac{1}{\rho }·\frac{2}{T}=\frac{2}{T\rho }.$$

Taking the supremum over all neighboring $x\sim x^{\prime }$ and all $y\in \widehat{Y}$ gives $\Delta u\le 2/\left(T\rho \right)$. This completes the proof. □

The trivial bound $\Delta u\le 1$ holds because $u_x\left(y\right)\in [0,1]$. However, Lemma 1 provides the sharper estimate $\Delta u\le {\displaystyle \frac{2}{T\rho }}$. Thus, in general, we obtain

$$\Delta u\le min\left\{1,\frac{2}{T\rho }\right\}.$$

In typical settings with $T>2$ and $\rho \ge 2$ (avoiding clipping), this simplifies to $\Delta u\le {\displaystyle \frac{1}{T}}<1$. Thus, the exponential mechanism can operate with a tighter sensitivity bound, leading to stronger concentration on high-utility candidates and improved semantic fidelity at the same privacy budget.

4.2.2. Exponential-Mechanism Selection

Given the pruned candidate set $\widehat{Y}=\{y^{\left(1\right)},\dots ,y^{\left(m\right)}\}$, the final output is selected using the exponential mechanism with privacy budget ${\epsilon }_2$. By Lemma 1, the global sensitivity of the utility function is bounded as

$$\Delta u=min\left\{1,\frac{2}{T\rho }\right\}.$$

The exponential mechanism defines a probability distribution over $\widehat{Y}$ that favors candidates with higher utility while ensuring ${\epsilon }_2$-DP. Specifically, the probability of selecting candidate $y\in \widehat{Y}$ is

$$Pr\left[\tilde{x}=y|x,\widehat{Y}\right]={\displaystyle \frac{exp\left(\frac{{\epsilon }_2}{2\Delta u}{u}_x\left(y\right)\right)}{{\sum }_{y^{\prime }\in \widehat{Y}}exp\left(\frac{{\epsilon }_2}{2\Delta u}{u}_x\left(y^{\prime }\right)\right)}}.$$

The released privatized rewrite $\tilde{x}$ is then drawn according to this distribution. By construction, the mechanism satisfies ${\epsilon }_2$-DP with respect to the input x, and the tighter bound on $\Delta u$ directly reduces the amount of randomness required, thereby improving the fidelity of the selected output.

4.3. Privacy Guarantee and Utility Analysis

This subsection provides the theoretical analysis of the proposed mechanism, addressing both its DP guarantee and the utility of the selection step.

4.3.1. Privacy Guarantee

The overall privacy follows directly from the composition of the two phases.

Theorem 1 

(End-to-End Privacy). Let ${\epsilon }_1$ and ${\epsilon }_2$ be the privacy budgets used in Phase 1 and Phase 2, respectively. Under the token-level neighboring relation, the mechanism that outputs the final rewrite $\tilde{x}$ satisfies $({\epsilon }_1+{\epsilon }_2)$-DP.

Proof. 

Phase 1 (sanitization). Each token $x_i$ is privatized independently using an ${\epsilon }_1$-DP mechanism. Under token-level adjacency, parallel composition implies that the entire sanitized sequence $x^{\mathrm{priv}}$ is ${\epsilon }_1$-DP.

Phase 2 (selection). Conditioned on the pruned candidate set $\widehat{Y}$, the exponential mechanism with privacy budget ${\epsilon }_2$ and sensitivity bound $\Delta u$ (Lemma 1) satisfies ${\epsilon }_2$-DP with respect to the original input x.

Composition. The final output $\tilde{x}$ is obtained by applying Phase 2 to the output of Phase 1. By the sequential composition theorem, the overall mechanism is $({\epsilon }_1+{\epsilon }_2)$-DP. □

4.3.2. Utility Analysis and Fallback Under Post-Processing

The exponential mechanism employed in Phase 2 provides a standard utility guarantee. With probability at least $1-\delta$, the selected candidate $\tilde{x}\in \widehat{Y}$ achieves utility close to that of the best element in $\widehat{Y}$ [39]:

$$u_x\left(\tilde{x}\right)\ge \underset{y\in \widehat{Y}}{max}{u}_x\left(y\right)-{\displaystyle \frac{2\Delta u}{{\epsilon }_2}}\left(lnm+ln\frac{1}{\delta }\right),m=\left|\widehat{Y}\right|.$$

Here, $u_x\left(\tilde{x}\right)$ denotes the utility of the selected candidate with respect to the input x, and ${max}_{y\in \widehat{Y}}{u}_x\left(y\right)$ is the maximum achievable utility among all candidates in the pruned set $\widehat{Y}$. The parameter m is the size of the candidate set, and $\delta$ is a confidence parameter that quantifies the probability of failure. In other words, with probability at least $1-\delta$, the selected output is nearly as good as the best available candidate.

Lemma 1 shows that the sensitivity decreases as $\Delta u\le 2/\left(T\rho \right)$, so the additive error term in the exponential-mechanism bound, $\frac{2\Delta u}{{\epsilon }_2}\left(lnm+ln(1/\delta )\right)$, scales as $O(1/T)$ for fixed ${\epsilon }_2$ and m. Pruning further decreases m, which in turn reduces the $lnm$ penalty in the bound. Together, these factors strengthen the utility of Phase 2 without altering the DP guarantee. However, Phase 1 may become more difficult as T increases, since maintaining semantic fidelity becomes harder for longer inputs. Token-level perturbations accumulate in the sanitized prompt, reducing the likelihood that a fixed candidate budget k yields a high-fidelity rewrite. Hence, while larger T theoretically improves the privacy–utility trade-off in Phase 2, the overall performance may vary due to these Phase 1 effects rather than the DP mechanism itself.

In deployment, some inputs may be heavily corrupted, resulting in incoherent or low-quality candidate rewrites. To maintain stable system behavior in such cases, the framework can incorporate simple fallback procedures that operate entirely as post-processing. When all generated candidates fail to produce a coherent rewrite, the system can either return the sanitized input generated in Phase 1, which already satisfies ${\epsilon }_1$-DP, or abstain from releasing a rewrite. Because these operations occur after the differentially private mechanism, they preserve the end-to-end $({\epsilon }_1+{\epsilon }_2)$-DP guarantee while preventing the release of meaningless outputs in practice.

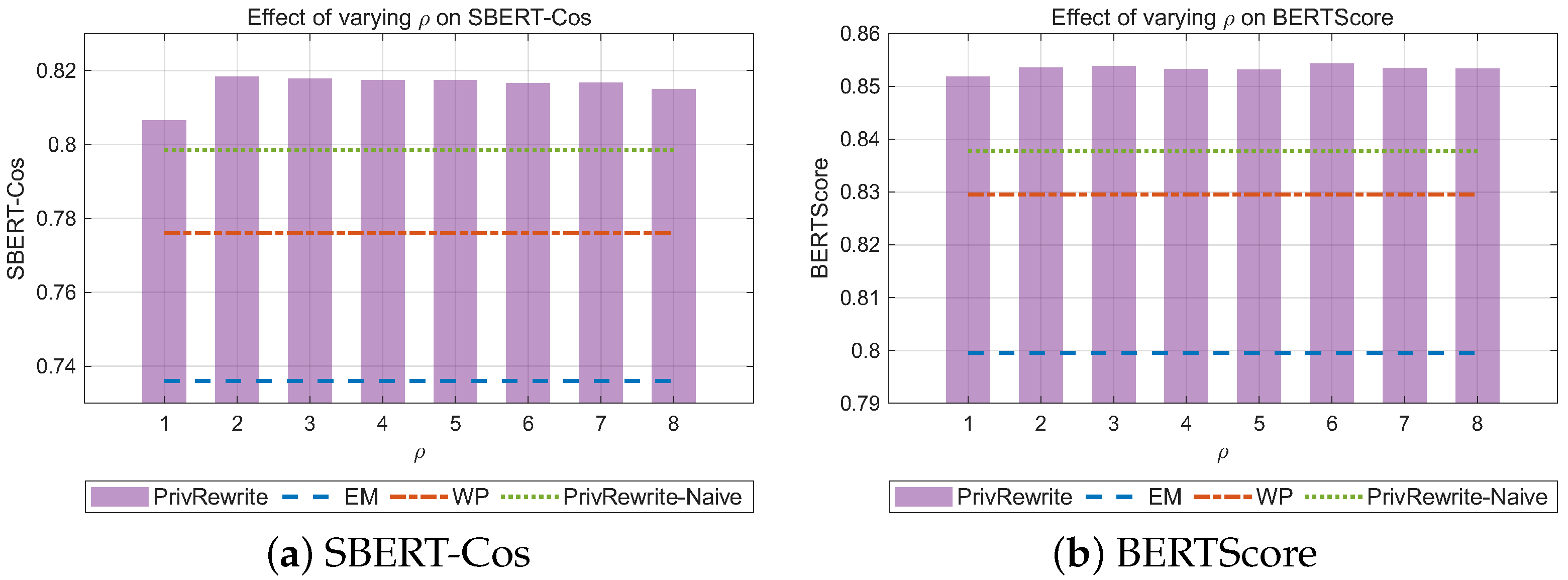
5. Experiments

In this section, we evaluate the proposed scheme using real datasets. We first describe the experimental setup and then present a discussion of the results.

5.1. Experimental Setup

Datasets: We evaluate the performance of the proposed method using real-world datasets to demonstrate its practical applicability. We use the MedQuAD dataset [40], which contains consumer health questions paired with authoritative answers from trusted sources, and randomly sample 500 question–answer pairs for evaluation. This dataset allows us to assess performance on specialized text. We also use the IMDB Movie Reviews dataset [41], a sentiment analysis corpus consisting of movie reviews labeled as positive or negative, from which we randomly sample 1000 reviews for evaluation. This dataset represents opinionated, more stylistically varied text, which helps evaluate the robustness of our method across different writing styles.

Baselines: We evaluate the performance of our method against the following alternatives:

• WordPerturb (WP) [11]: A word-level privatization approach based on $d_{\chi }$-privacy, a metric-based relaxation of DP. Each word embedding is perturbed with calibrated noise in the vector space and then mapped back to the nearest vocabulary word. This provides metric-DP guarantees while aiming to preserve semantic meaning.
• Exponential mechanism-based text rewriting (EM): An approach that applies the exponential mechanism [39] to rewrite each token independently. This corresponds to directly releasing the token-level sanitized text produced in Phase 1.
• PrivRewrite with naive sensitivity (PrivRewrite-Naive): A variant of our method where the global sensitivity in Phase 2 is conservatively set to $\Delta u=1$. This baseline isolates the effect of our proposed tight sensitivity analysis.
• PrivRewrite: The proposed approach introduced in this paper, which combines token-level sanitization (Phase 1) with tight-sensitivity exponential selection (Phase 2).

We emphasize that EM, PrivRewrite-Naive, and PrivRewrite all satisfy standard $\epsilon$-DP, whereas WP is based on the relaxed notion of $d_{\chi }$-privacy. Therefore, the numeric privacy parameter used by WP is not directly comparable to $\epsilon$ under our token-level adjacency. In this study, WP is included only as a metric-DP reference to illustrate relative utility trends under a weaker privacy notion. All quantitative performance statements and comparisons are made among the $\epsilon$-DP methods (EM, PrivRewrite-Naive, and PrivRewrite), while WP is discussed qualitatively for contextual reference.

Evaluation metrics and implementation: Given an input sequence x and its privatized rewrite $\tilde{x}$, we assess utility using two complementary measures of semantic preservation. First, we compute cosine similarity between Sentence-BERT embeddings of x and $\tilde{x}$ [42]; we refer to this measure as SBERT-Cos for brevity. Formally, let $f(·)$ denote the Sentence-BERT encoder. Then, SBERT-Cos is defined as

$$\mathrm{SBERT}\text{-}\mathrm{Cos}(x,\tilde{x})={\displaystyle \frac{\langle f\left(x\right),f\left(\tilde{x}\right)\rangle }{\parallel f\left(x\right)\parallel \parallel f\left(\tilde{x}\right)\parallel }}.$$

Second, we report BERTScore [43], a widely used metric for evaluating semantic overlap based on contextualized token embeddings from pretrained transformers. Together, these metrics capture both coarse-grained text similarity and fine-grained semantic alignment.

For implementation, we use the Gemini-2.0-Flash model accessed via API to generate candidate rewrites. The model is configured with temperature = 0.75 and a maximum generation length of 6000 tokens. The privacy budget $\epsilon$ is varied over $\{0.25, 0.5, 1.0, 2.0, 4.0\}$ and is evenly split between Phase 1 and Phase 2, i.e., ${\epsilon }_1={\epsilon }_2=\epsilon /2$. In Phase 1, the number of candidates generated by the LLM is varied in the range $[10, 50]$, with a default value of $k=50$ when not specified explicitly. The threshold for near-duplicate pruning ${\tau }_{\mathrm{dup}}$ is varied in the range $[0.6, 1.0]$, with a default value of ${\tau }_{\mathrm{dup}}=0.8$. In Phase 2, the scaling parameter $\rho$ is varied in the range $[1.0, 8.0]$, with a default value of $\rho =2$ when not specified explicitly.

5.2. Experimental Results

Before evaluating the final released privatized rewrite $\tilde{x}$, we first assess the utility of Phase 1 under varying privacy budgets $\epsilon$. To this end, we measure two types of semantic similarity. First, we compute the average SBERT-Cos between each input x and its privatized view $x^{\mathrm{priv}}$, which quantifies the direct utility loss introduced by the token-level DP sanitizer. Second, we compute the average SBERT-Cos between x and all candidates in $Y\left(x^{\mathrm{priv}}\right)$, which reflects how much semantic fidelity is recovered through LLM-based candidate generation.

As shown in

Table 1. Average SBERT-Cos under varying privacy budgets $\epsilon$. We report similarity between the input x and its privatized view $x^{\mathrm{priv}}$, as well as between x and the Phase 1 candidates $Y\left(x^{\mathrm{priv}}\right)$.

	$\mathit{x}$ vs. ${\mathit{x}}^{\mathbf{priv}}$					$\mathit{x}$ vs. Phase 1 Candidates
Dataset	$\mathit{\epsilon }=\mathbf{0}.\mathbf{25}$	$\mathit{\epsilon }=\mathbf{0}.\mathbf{5}$	$\mathit{\epsilon }=\mathbf{1}.\mathbf{0}$	$\mathit{\epsilon }=\mathbf{2}.\mathbf{0}$	$\mathit{\epsilon }=\mathbf{4}.\mathbf{0}$	$\mathit{\epsilon }=\mathbf{0}.\mathbf{25}$	$\mathit{\epsilon }=\mathbf{0}.\mathbf{5}$	$\mathit{\epsilon }=\mathbf{1}.\mathbf{0}$	$\mathit{\epsilon }=\mathbf{2}.\mathbf{0}$	$\mathit{\epsilon }=\mathbf{4}.\mathbf{0}$
MedQuAD	0.708	0.725	0.737	0.736	0.746	0.798	0.801	0.802	0.806	0.809
IMDB	0.679	0.689	0.696	0.713	0.722	0.772	0.778	0.788	0.792	0.798

, the similarities between x and $x^{\mathrm{priv}}$ are significantly lower, but the candidate scores remain substantially higher and relatively stable across different $\epsilon$ values. This gap highlights the recovery ability of the LLM. Even when the input is heavily perturbed, candidate generation restores much of the lost semantic content. Maintaining strong utility at this stage is crucial, as it allows Phase 2 to focus on differentially private selection without being constrained by low-quality candidates.

Figure 2 compares the utility of the final privatized rewrites across privacy budgets $\epsilon \in \{0.25, 0.5, 1.0, 2.0, 4.0\}$, using both SBERT-Cos and BERTScore on MedQuAD and IMDB. These two measures capture complementary aspects of semantic preservation, with SBERT-Cos reflecting overall sentence-level similarity and BERTScore providing a more fine-grained token-level alignment.

Across both datasets and metrics, PrivRewrite consistently achieves the strongest utility. Even under small privacy budgets where the injected noise is most severe, the privatized rewrites produced by PrivRewrite remain semantically close to the original inputs. This shows that the combination of token-level sanitization in Phase 1 and tight-sensitivity exponential selection in Phase 2 effectively balances the trade-off between privacy and utility. Importantly, the LLM plays a key role in this pipeline. Although Phase 1 inevitably reduces semantic fidelity by injecting noise, the candidate generation step leverages the LLM’s expressive capacity to recover much of the lost utility, as we showed in the results of Table 1. The tight sensitivity calibration in Phase 2 then ensures that the exponential mechanism can reliably favor these high-quality candidates, assigning higher probability to semantically faithful outputs without exceeding the privacy budget. This explains the steady improvement over the naive baseline.

PrivRewrite-Naive follows similar trends but does not match the performance of PrivRewrite. By fixing the global sensitivity conservatively at $\Delta u=1$, it avoids privacy risks but sacrifices semantic quality. The performance gap between the two variants illustrates the value of our proposed sensitivity analysis. Rather than adopting a worst-case bound, calibrating the exponential mechanism with a tighter estimate leads to measurable gains across all privacy budgets.

WP, which perturbs word embeddings under $d_{\chi }$-privacy, provides moderate utility. As a metric-DP method, its numeric privacy parameter is not directly comparable to $\epsilon$ under our framework, and its results are included only for contextual reference. WP performs better than the direct exponential-mechanism baseline but remains below both PrivRewrite variants. While metric-DP perturbation can retain some semantic content, it lacks the structured candidate-selection process of PrivRewrite, whose two-phase design enables LLM-generated candidates to recover much of the utility lost in the initial sanitization step. Finally, the exponential mechanism alone shows the weakest performance. This implies that directly perturbing tokens without LLM-based rewriting produces outputs that are differentially private but poorly aligned with the original input.

A comparison between SBERT-Cos and BERTScore reveals that the absolute values of BERTScore are higher, reflecting its sensitivity to fine-grained contextual token overlaps. Nevertheless, both metrics produce consistent trends: utility improves steadily as $\epsilon$ increases, all methods benefit from relaxed privacy constraints, and PrivRewrite maintains a clear advantage across settings. Together, these findings confirm that our framework adapts robustly to DP levels while preserving strong semantic fidelity.

Figure 3 shows the effect of varying $\rho$ on utility scores with privacy budget $\epsilon =2.0$ on the MedQuAD dataset. We note that although the results for $\epsilon =2.0$ are presented here, similar trends were consistently observed across other privacy budgets. EM, WP, and PrivRewrite-Naive are plotted as reference baselines. These methods are unaffected by $\rho$ since their mechanisms do not depend on this parameter. In contrast, PrivRewrite varies with $\rho$, reflecting its role in the Phase 2 utility function. The results reveal a non-monotonic pattern. Performance improves when moving from small to moderate values of $\rho$, reaching its peak around $\rho =2$, but then gradually saturates and shows a slight decline for larger values. This behavior matches the theoretical insight that increasing $\rho$ tightens the sensitivity bound and initially enhances selection quality, but excessive smoothing flattens the utility landscape and reduces the mechanism’s ability to discriminate among candidates. Both SBERT-Cos and BERTScore exhibit this trend, with BERTScore reporting slightly higher absolute values due to its token-level granularity. The consistency across metrics confirms that PrivRewrite achieves the best utility at moderate values of $\rho$ while remaining robust across a broad range.

Figure 4 illustrates the impact of the near-duplicate pruning threshold ${\tau }_{\mathrm{dup}}$ on utility for $\epsilon =2.0$ using the MedQuAD dataset. EM and WP are included as reference baselines since they are unaffected by ${\tau }_{\mathrm{dup}}$. The case ${\tau }_{\mathrm{dup}}=1$ corresponds to no pruning. As ${\tau }_{\mathrm{dup}}$ decreases from 1.0 to approximately 0.7–0.8, the utility improves, indicating that removing highly similar candidates enhances diversity and provides the exponential-mechanism selector with a more informative candidate pool. When ${\tau }_{\mathrm{dup}}$ becomes too small, however, performance declines because excessive pruning limits coverage and removes semantically relevant alternatives. This behavior reflects the inherent trade-off between candidate diversity and completeness: moderate pruning reduces redundancy and improves Phase 2 selection, whereas overly aggressive pruning constrains the mechanism’s ability to identify high-utility rewrites.

Figure 5 presents the effect of different allocations of the total privacy budget $\epsilon$ between Phase 1 and Phase 2, evaluated using the MedQuAD dataset. In this experiment, $\epsilon$ is fixed to 2.0, and the allocation ratios $({\epsilon }_1:{\epsilon }_2)$ are varied over $1:9$, $3:7$, $5:5$, $7:3$, and $9:1$. EM and WP are plotted as horizontal reference baselines since their performance is unaffected by the split. For the two-phase methods, PrivRewrite and PrivRewrite-Naive, performance remains stable across moderate variations but reaches its best value under a balanced split. When the allocation of the privacy budget becomes highly unbalanced, the overall utility declines. This occurs because an insufficient budget in Phase 1 limits the generation of semantically meaningful rewrite candidates, while an inadequate budget in Phase 2 reduces the ability of the exponential mechanism to reliably select the highest-utility candidate. These results indicate that an even allocation of the privacy budget across the two phases provides the most stable performance.

Figure 6 illustrates the impact of the candidate size k on (a) SBERT-Cos and (b) the runtime required to generate k candidates using the LLM on the MedQuAD dataset. In this experiment, the total privacy budget is fixed at $\epsilon =2.0$, while k varies from 10 to 50. EM and WP are included as horizontal reference baselines since their performance remains constant regardless of k. As shown in Figure 6a, increasing k consistently enhances the performance of PrivRewrite and PrivRewrite-Naive. This improvement arises because a larger candidate pool allows the selection of rewrites that better preserve the semantics of the original text. However, as depicted in Figure 6b, the runtime also increases with k, which is expected since generating more candidates entails greater computational and communication overhead for the LLM.

Even with a small candidate size (e.g., $k=10$), PrivRewrite already outperforms both EM and WP, demonstrating the robustness of the proposed approach with respect to k. Moreover, since PrivRewrite targets offline text publishing scenarios for privacy-preserving rewriting, the increased runtime with larger k does not impact real-time performance. In practice, the choice of k can be adjusted according to deployment needs: smaller k values are suitable for lightweight or latency-sensitive scenarios, whereas larger k values are recommended for applications requiring higher semantic quality.

Table 2. Representative output excerpts from EM, PrivRewrite-Naive, and PrivRewrite on MedQuAD.

Sample 1
Method	Text
Original	Pilomatrixoma is a benign (non-cancerous) skin tumor of the hair follicle (structure in the skin that makes hair). They tend to develop in the head and neck area and are usually not associated with any other signs and symptoms (isolated).
EM	Pilomatrixoma is a impervious (basis-carcinoma) plastic nerve of the wear pineal (includes in the yellowish that always bones). They get to establishing in the over and neck situated and are usually not possible with any no real and infection (remain).
PrivRewrite-Naive	Pilomatrixoma is a benign skin tumor that originates from hair follicle cells and often contains calcifications, giving it a firm texture. These tumors commonly appear in the head and neck region, typically presenting as painless, slow-growing masses without signs of inflammation.
PrivRewrite	Pilomatrixoma is a benign skin tumor, sometimes confused with more concerning conditions. These growths tend to occur on the head and neck and typically present without pain or signs of infection.
Sample 2
Original	Autoimmune hepatitis is a chronicor long lastingdisease in which the body’s immune system attacks the normal components, or cells, of the liver and causes inflammation and liver damage. The immune system normally protects people from infection by identifying and destroying bacteria, viruses, and other potentially harmful foreign substances.
EM	Autoimmune hepatitis is a chronicor in which the similar’s inhibiting provide arson the life aircraft, or bacterial, of the virus and chronic rashes and treat threatening. The protects provide if protect wanted from malignancy by diagnosing and tearing micro-organisms, viruses, and known cause deleterious foreigners toxin.
PrivRewrite-Naive	Autoimmune hepatitis is a chronic inflammatory liver disease where the body’s defense system mistakenly attacks the liver. This can cause prolonged liver damage, potentially leading to severe health risks and even life-threatening complications if left untreated.
PrivRewrite	Autoimmune hepatitis is a chronic inflammatory condition affecting the liver, where the body’s immune system mistakenly attacks its own liver cells. This can result in ongoing inflammation and damage to the liver, potentially leading to severe health problems and even life-threatening complications if left untreated.

presents example outputs from the $\epsilon$-DP approaches (EM, PrivRewrite-Naive, and PrivRewrite) on MedQuAD. These examples are included for illustration purposes only. EM often produces broken or semantically inconsistent sentences, whereas PrivRewrite-Naive improves readability but sometimes introduces additional details that are not present in the original text. In contrast, PrivRewrite maintains a more stable tone, preserves source meaning more faithfully, and produces fluent, coherent sentences. These examples show that PrivRewrite achieves clearer and more faithful outputs than both EM and PrivRewrite-Naive.

6. Conclusions

In this paper, we introduced PrivRewrite, a two-phase mechanism for differentially private text rewriting. The first phase privatizes the input through token-level sanitization, and the second phase applies the exponential mechanism with a tight sensitivity bound to select among candidates. A key novelty of PrivRewrite is the integration of an LLM in a black-box fashion together with a tightly bounded exponential mechanism. The LLM receives a privatized input and generates diverse candidate rewrites without requiring access to its internal parameters or training data. PrivRewrite then applies the exponential mechanism with the sharper sensitivity bound, which reduces unnecessary noise and allows the selection process to favor semantically faithful candidates. Experimental results on MedQuAD and IMDB demonstrated that PrivRewrite consistently outperforms existing baselines. By combining local sanitization with LLM-based generation and carefully calibrated DP selection, PrivRewrite provides a practical approach for privatized text rewriting with rigorous DP guarantees and robust utility.