CFD Analysis of Natural Convection Performance of a MMRTG Model Under Martian Atmospheric Conditions
Abstract
1. Introduction
2. Theoretical Background
2.1. Natural Convection
2.2. Governing Equations
- The Reynolds number quantifies the relative importance of inertial to viscous forces in a fluid flow. It is defined as follows:
- The Prandtl number is the ratio between the kinematic viscosity and the thermal diffusivity (). Both of them are intrinsic properties of a fluid.
- The Rayleigh number is the product of the Grashof and Prandtl numbers:
- The Nusselt number expresses the relationship between the heat flow exchanged by convection and the heat flow exchanged by conduction. This parameter can be defined as follows:
2.3. Martian Atmosphere
2.4. Radiative and Convective Heat Transfer Under Martian Conditions
2.5. MMRTG Model
- Central cylindrical core: representing the heat source region of the MMRTG.
- Eight radial fins: uniformly distributed around the cylindrical surface, functioning as extended surfaces that increase the effective heat dissipation area.
2.6. Study Cases
- Ambient temperature of Mars (), chosen within the representative diurnal and seasonal range observed on the planet (from 173 K during cold nights to 273 K during daytime conditions) [14].
- Surface temperature of the MMRTG () which typically ranges between 323 K and 473 K, depending on the heat generation and electrical load demand [27].
3. CFD Setup
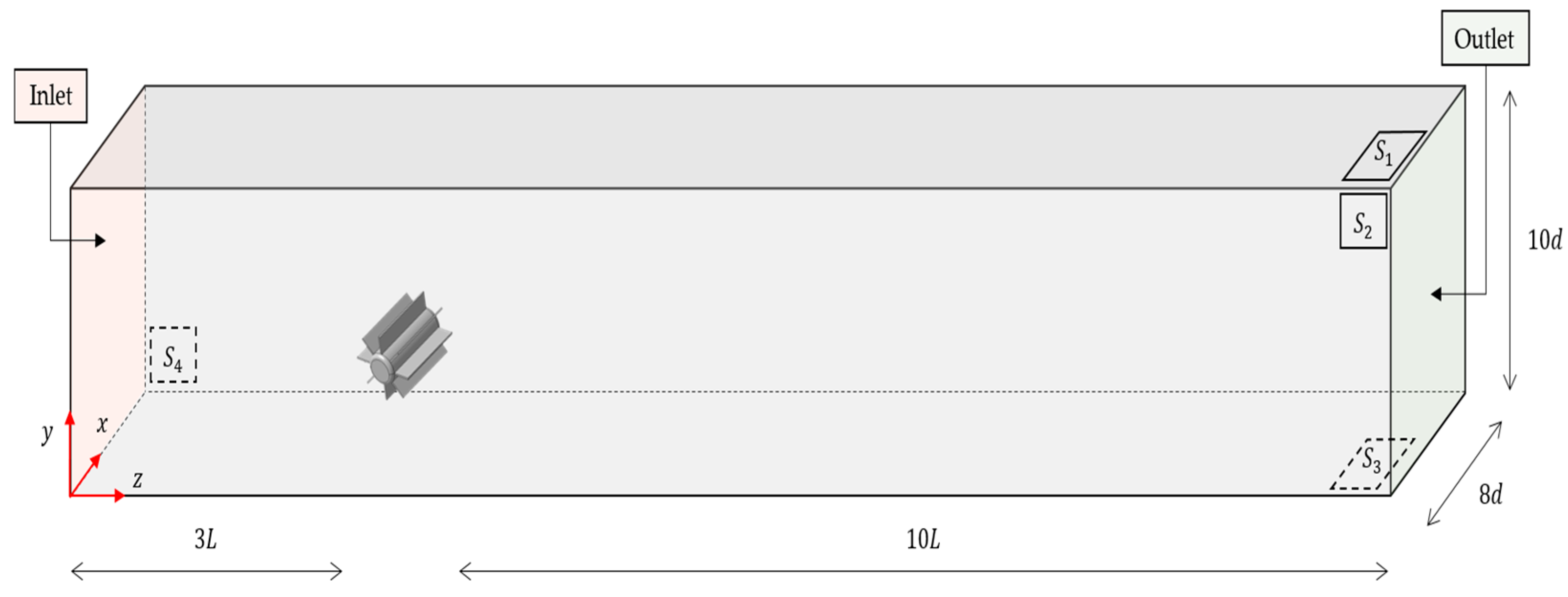
3.1. Computational Domain
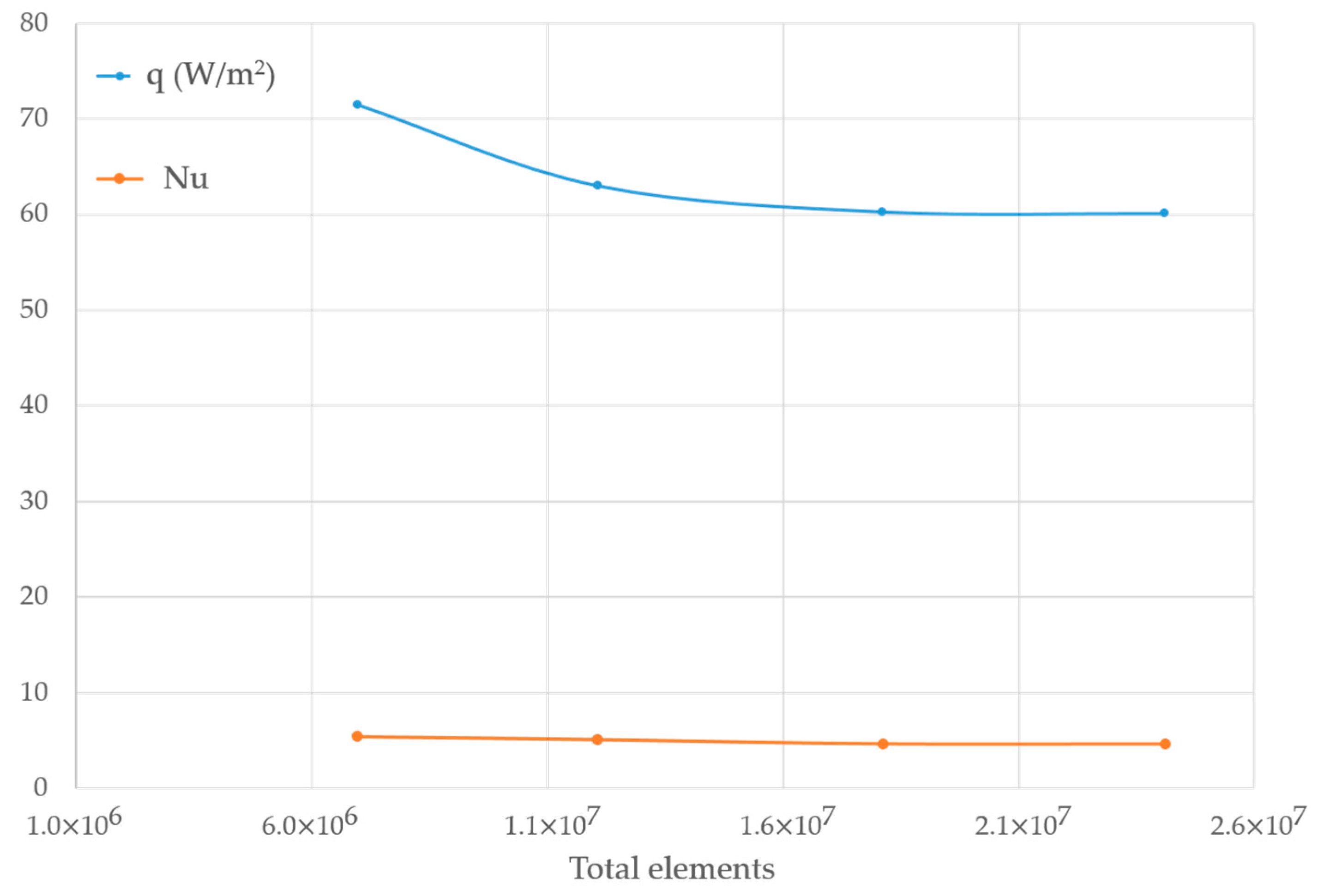
3.2. Mesh Strategy
3.3. Solver
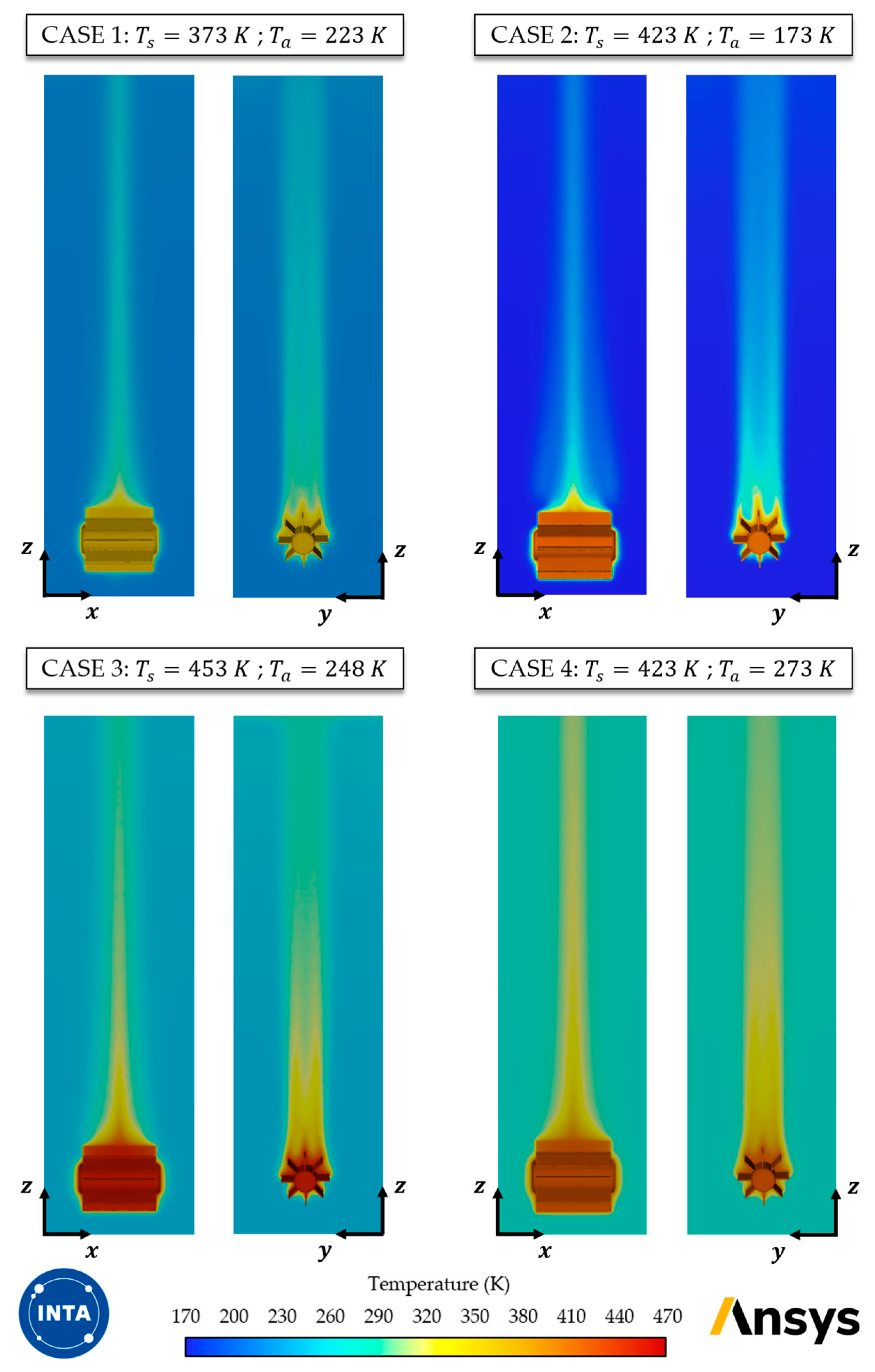
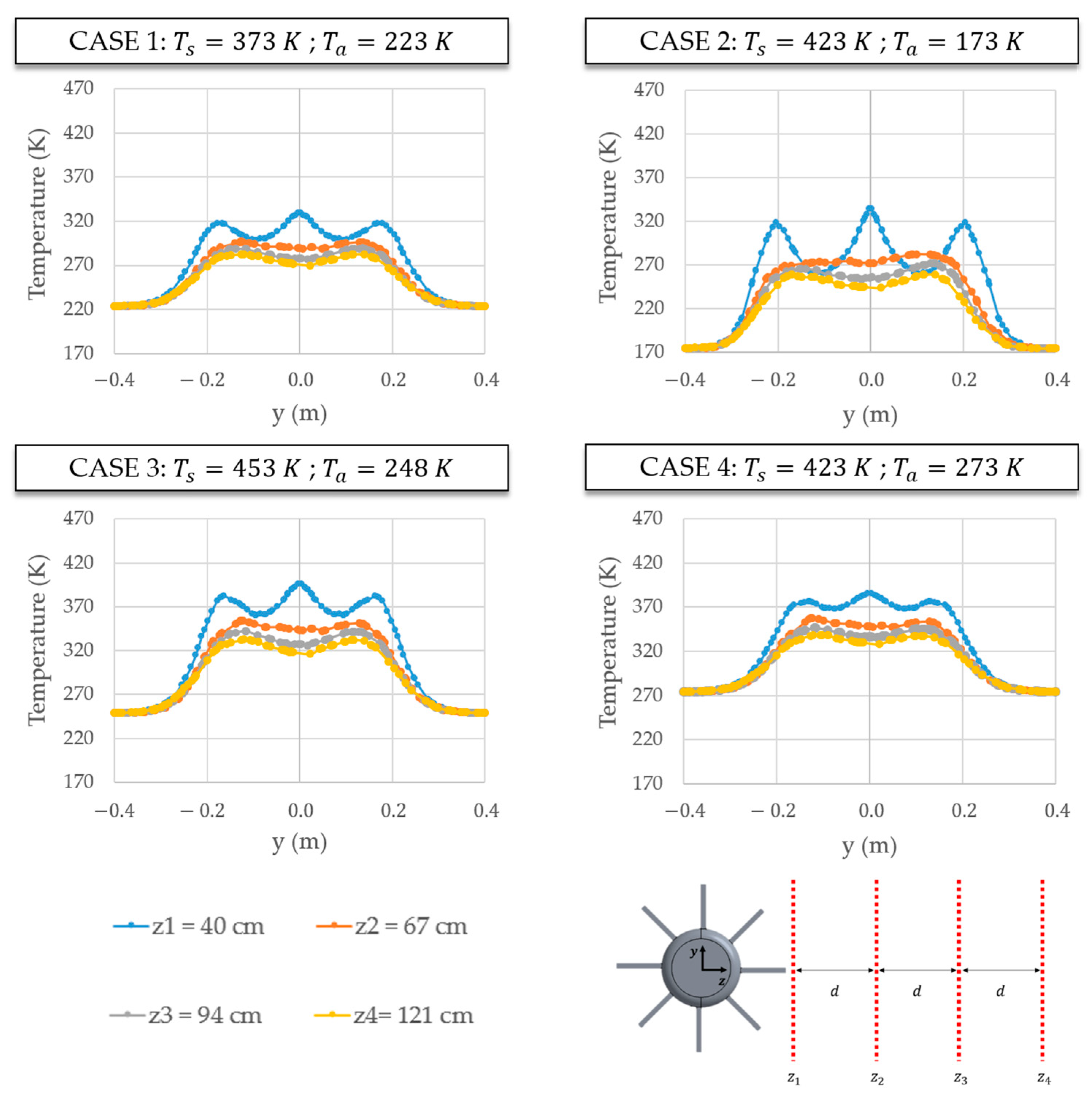
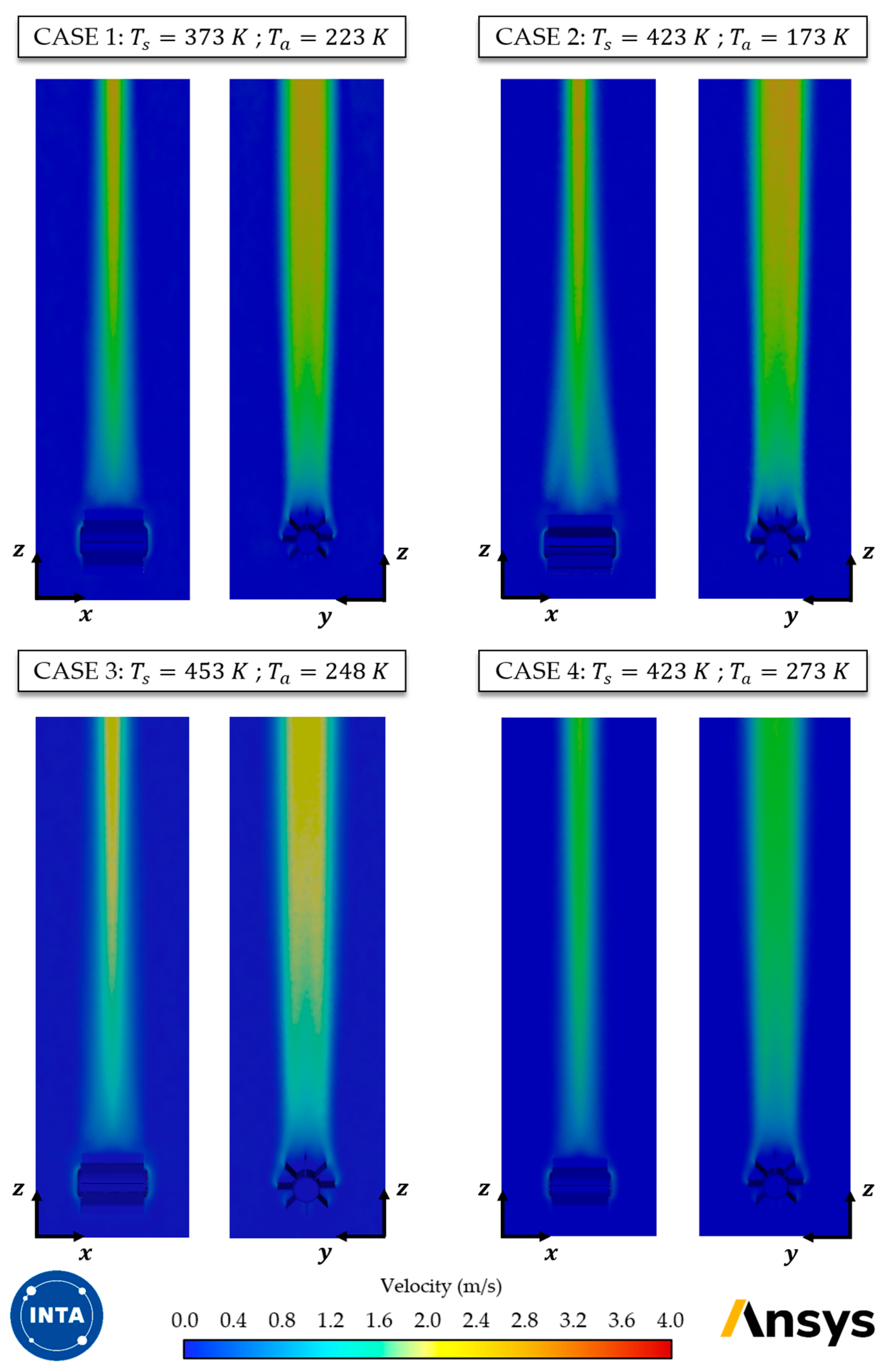
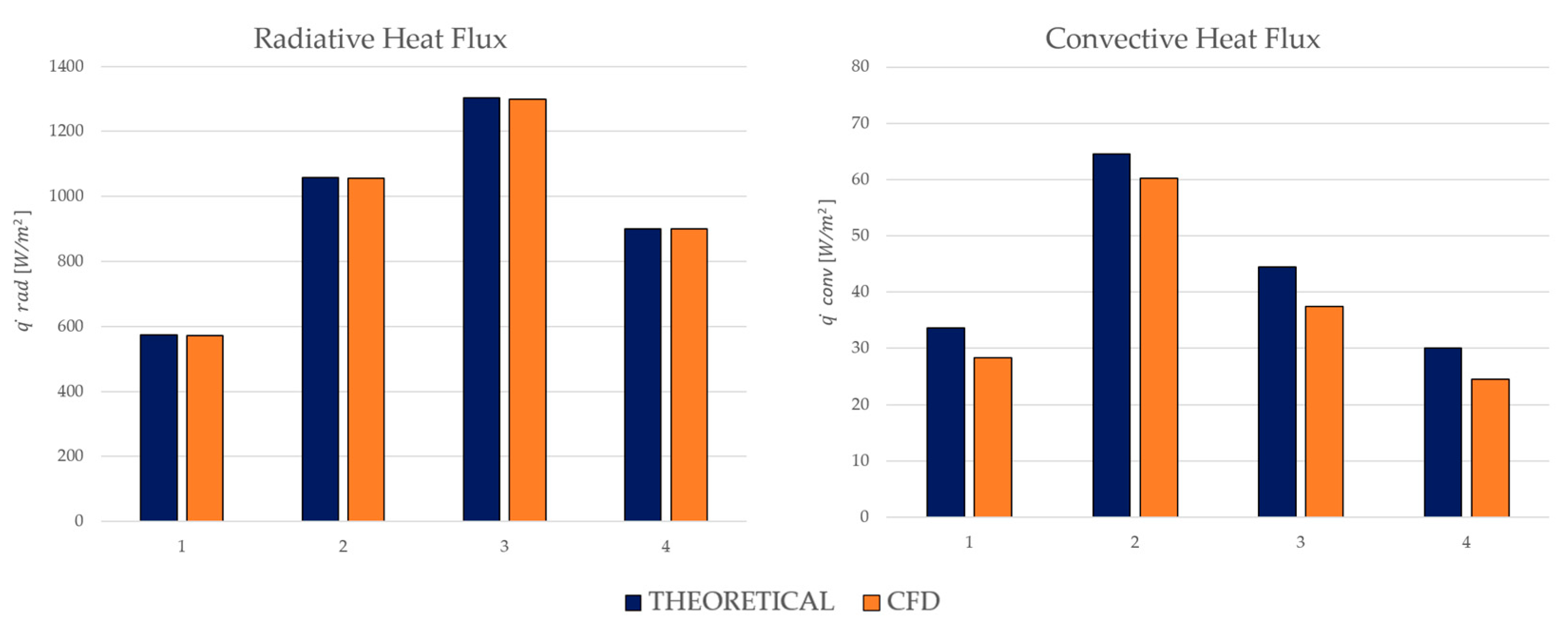
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| CO2 | Carbon Dioxide |
| INTA | Instituto Nacional de Técnica Aeroespacial |
| MMRTG | Multi-Mission Radioisotope Thermoelectric Generator |
| Ra | Rayleigh Number |
| Re | Reynolds Number |
| Gr | Grashof Number |
| Pr | Prandtl Number |
| Nu | Nusselt Number |
| Kn | Knudsen Number |
| Bi | Biot Number |
| SST k–ω | Shear Stress Transport k–omega turbulence model |
| Reactor surface temperature | |
| Ambient temperature | |
| ΔT | Temperature difference |
| Average wall heat flux | |
| Convective heat-transfer coefficient | |
| Reactor diameter | |
| Reactor length | |
| Fin height | |
| Fin thickness | |
| Fin length | |
| Density | |
| Dynamic viscosity | |
| Gravity acceleration | |
| Kinematic viscosity | |
| Thermal conductivity | |
| Thermal diffusivity | |
| Thermal expansion coefficient | |
| Characteristic velocity | |
| Gravitational acceleration |
References
- Klein, H.P. The Viking mission and the search for life on Mars. Rev. Geophys. 1979, 17, 1655–1662. [Google Scholar] [CrossRef]
- Taylor, E.J.; Jackson, G.S. Perseverance Rover Lands on Mars. Electrochem. Soc. Interface 2021, 30, 79–83. [Google Scholar] [CrossRef]
- Bell, J.F.; Maki, J.N.; Mehall, G.L.; Ravine, M.A.; Caplinger, M.A.; Bailey, Z.J.; Schaffner, J.A.; Cisneros, R.R.; Cloutis, E.A.; Gazis, P.R.; et al. The Mars 2020 Perseverance Rover Mast Camera Zoom (Mastcam-Z) Multi-spectral, Stereoscopic Imaging Investigation. Space Sci. Rev. 2021, 217, 24. [Google Scholar] [CrossRef]
- Huang, J.; Huang, D.; Chen, T.; Li, H. Numerical Investigation on Aerodynamics of a Rectangular Blade Rotor under Mars Air Conditions Using Large Eddy Simulation. Appl. Sci. 2023, 13, 5058. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, B.; Zhang, H.; Xiang, C.; Fan, W.; Zhao, Z. Analysis of Aerodynamic Characteristics of Propeller Systems Based on Martian Atmospheric Environment. Drones 2023, 7, 397. [Google Scholar] [CrossRef]
- Rodríguez-Sevillano, Á.A.; Casati-Calzada, M.J.; Bardera-Mora, R.; Feliz-Huidobro, A.; Calle-González, C.; Fernández-Antón, J. Flow Study on the Anemometers of the Perseverance Based on Towing Tank Visualization. Appl. Mech. 2022, 3, 1385–1398. [Google Scholar] [CrossRef]
- Garcia-Magariño, A.; Sor, S.; Bardera, R.; Muñoz, J. Mars 2020 Wind Velocity Measurement Interferences at High Reynolds Numbers. J. Spacecr. Rocket. 2020, 57, 354–363. [Google Scholar] [CrossRef]
- Ritz, F.; Peterson, C.E. Multi-Mission Radioisotope Thermoelectric Generator (MMRTG) Program Overview. In Proceedings of the 2004 IEEE Aerospace Conference, Big Sky, MT, USA, 6–13 March 2004; Volume 5, pp. 2950–2957. [Google Scholar] [CrossRef]
- Werner, J.; Lively, K.; Kirkham, D. A multi-mission radioisotope thermoelectric generator (MMRTG) for Mars 2020. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Lorenz, R.D.; Clarke, E.S. Influence of the Multi-Mission Radioisotope Thermoelectric Generator (MMRTG) on the local atmospheric environment. Planet. Space Sci. 2020, 193, 105075. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Z.; Zhen, Q.; Lu, W. Theoretical investigation of natural convection heat transfer in inclined and fully divided CO2 enclosures with partitions on Mars. Int. J. Heat Mass Transf. 2018, 126, 1113–1122. [Google Scholar] [CrossRef]
- Sun, Y.; Lin, G.; Bu, X.; Bai, L.; Xiao, C.; Wen, D. A Numerical Study of Fluid Flow and Heat Transfer in Carbon Dioxide Enclosures on Mars. Energies 2018, 11, 756. [Google Scholar] [CrossRef]
- Bardera, R.; Rodríguez-Sevillano, Á.A.; Barroso, E.; Matías, J.C.; López-Cuervo Alcaraz, A. Numerical analysis of the thermal convection through a flat plate in Martian conditions. Results Eng. 2024, 21, 102029. [Google Scholar] [CrossRef]
- Catling, D.C. Atmospheric evolution, Mars. In Encyclopedia of Paleoclimatology and Ancient Environments; Springer: Dordrecht, The Netherlands, 2009; pp. 66–75. [Google Scholar] [CrossRef]
- Bejan, A. Convection Heat Transfer, 4th ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 7th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Piqueux, S.; Kass, D.M.; Kleinböhl, A.; Slipski, M.; Hayne, P.O.; McCleese, D.J.; Schofield, J.T.; Heavens, N. Mars thermal inertia and surface temperatures by the Mars Climate Sounder. Icarus 2024, 419, 115851. [Google Scholar] [CrossRef]
- Ruzicka, M.C. On dimensionless numbers. Chem. Eng. Res. Des. 2008, 86, 835–868. [Google Scholar] [CrossRef]
- Huber, M.L.; Sykioti, E.A.; Assael, M.J.; Perkins, R.A. Reference Correlation of the Thermal Conductivity of Carbon Dioxide from the Triple Point to 1100 K and up to 200 MPa. J. Phys. Chem. Ref. Data 2016, 45, 013102. [Google Scholar] [CrossRef] [PubMed]
- Petrosyan, A.; Galperin, B.; Larsen, S.E.; Lewis, S.R.; Määttänen, A.; Read, P.L.; Renno, N.; Rogberg, L.P.H.T.; Savijärvi, H.; Siili, T.; et al. The Martian atmospheric boundary layer. Rev. Geophys. 2011, 49, RG3005. [Google Scholar] [CrossRef]
- Zurek, R.W. Martian great dust storms: An update. Icarus 1982, 50, 288–310. [Google Scholar] [CrossRef]
- Çengel, Y.A.; Ghajar, A.J. Heat and Mass Transfer: Fundamentals and Applications, 6th ed.; McGraw-Hill: New York, NY, USA, 2020. [Google Scholar]
- Modest, M.F.; Mazumder, S. Radiative Heat Transfer; Academic Press: Cambridge, MA, USA, 2021. [Google Scholar]
- Soria-Salinas, Á.T.; Zorzano, M.P.; Martín-Torres, F.J. Convective Heat Transfer Measurements at the Martian Surface. In 1st Symposium on Space Educational Activities; European Space Agency (ESA): Padova, Italy, 2015. [Google Scholar]
- Rodríguez-Sevillano, Á.A.; Casati-Calzada, M.J.; Bardera-Mora, R.; Matías-García, J.C.; Barroso-Barderas, E.; Fernández-Rivero, E. Image Analysis of the Influence of the Multi-Mission Radioisotope Thermoelectric Generator (MMRTG) on the Mars Environmental Dynamics Analyzer at Extremely Low Reynolds Number. Appl. Sci. 2025, 15, 220. [Google Scholar] [CrossRef]
- Churchill, S.W.; Chu, H.H.S. A comprehensive correlating equation for laminar, assisting, forced and free convection. AIChE J. 1977, 23, 10–16. [Google Scholar] [CrossRef]
- Otting, W.; Gard, L.; Hammel, T.; Bennett, R. Preparation of the MMRTG for the Mars Science Laboratory mission. In Proceedings of the 10th International Energy Conversion Engineering Conference, Ho Chi Minh City, Vietnam, 12–14 December 2012; p. 4062. [Google Scholar]
- Matsson, J.E. An Introduction to ANSYS Fluent 2022; Sdc Publications: Mission, KS, USA, 2022. [Google Scholar]
- Lintermann, A. Computational Meshing for CFD Simulations. In Clinical and Biomedical Engineering in the Human Nose; Inthavong, K., Singh, N., Wong, E., Tu, J., Eds.; Biological and Medical Physics, Biomedical Engineering; Springer: Singapore, 2021. [Google Scholar] [CrossRef]
- Wilcox, D.C. Formulation of the kw turbulence model revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef]
- Hellsten, A.; Laine, S.; Hellsten, A.; Laine, S. Extension of the k-omega-SST turbulence model for flows over rough surfaces. In Proceedings of the 22nd Atmospheric Flight Mechanics Conference, New Orleans, LA, USA, 11–13 August 1997; p. 3577. [Google Scholar]
- Miroshnichenko, I.; Sheremet, M. Comparative study of standard k–ε and k–ω turbulence models by giving an analysis of turbulent natural convection in an enclosure. EPJ Web Conf. 2015, 82, 01057. [Google Scholar] [CrossRef]
- Choi, S.K.; Kim, S.O. Turbulence modeling of natural convection in enclosures: A review. J. Mech. Sci. Technol. 2012, 26, 283–297. [Google Scholar] [CrossRef]
- Stern, F.; Wilson, R.V.; Coleman, H.W.; Paterson, E.G. Verification and Validation of CFD Simulations; IIHR Report No. 407 1999; Iowa Institute of Hydraulic Research: Iowa City, IA, USA, 1999. [Google Scholar]
- Peinado, L.; Muntean, V.; Perez-Grande, I. A free convection heat transfer correlation for very thin horizontal wires in rarefied atmospheres. Exp. Therm. Fluid Sci. 2021, 122, 110295. [Google Scholar] [CrossRef]



| Parameter | Approximate Value |
|---|---|
| Surface pressure | ~600 Pa |
| Surface temperature | 173 to 273 K |
| Atmospheric composition | ~95.3% CO2, 2.7% N2, 1.6% Ar, traces of O2, CO, H2O |
| Density at surface () | 0.011–0.018 kg/m3 |
| Dynamic viscosity () | ~1.0–1.2 × 10−5 Pa·s |
| Thermal conductivity () | ~0.01–0.02 W/(m·K) |
| Gravity acceleration () | 3.71 m/s2 |
| Dimensionless Number | Typical Range of Values on Mars |
|---|---|
| Reynolds () | 102–103 |
| Prandtl () | ∼0.7 |
| Grashof () | 102–106 |
| Rayleigh () | 102–106 |
| Nusselt () | 3–5 |
| Parameter | Symbol | Value (m) |
|---|---|---|
| Cylinder Diameter | d | 0.27 |
| Cylinder length | L | 0.68 |
| Fin length | 0.66 | |
| Fin height | 0.20 | |
| Fin thickness | 0.01 |
| Case | (MMRTG) | (Ambient) | Conditions | |
|---|---|---|---|---|
| 1 | 373 K | 223 K | 150 | Sunset conditions at mid-latitudes |
| 2 | 423 K | 173 K | 250 | Large thermal contrast in a nocturnal scenario |
| 3 | 453 K | 248 K | 205 | Peak reactor performance, warmer daytime atmosphere |
| 4 | 423 K | 273 K | 150 | High ambient temperature and reactor at elevated load |
| Mesh ID | Total Elements | Max. Skewness | Min. Orthogonal Quality | Max. Aspect Ratio | Min. Element Quality |
|---|---|---|---|---|---|
| 1 | 0.255 | 0.745 | 1.93 | 0.817 | |
| 2 | 0.243 | 0.757 | 1.88 | 0.825 | |
| 3 | 0.238 | 0.761 | 1.87 | 0.829 | |
| 4 | 0.239 | 0.760 | 1.86 | 0.828 |
| Case | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 373 | 223 | 298 | 1.13 | 0.74 | 4.63 × 105 | 681 | 3.45 × 105 |
| 2 | 423 | 173 | 298 | 1.46 | 0.74 | 7.72 × 105 | 879 | 5.75 × 105 |
| 3 | 453 | 248 | 351 | 1.21 | 0.77 | 3.89 × 105 | 624 | 3.00 × 105 |
| 4 | 423 | 273 | 348 | 1.04 | 0.77 | 2.91 × 105 | 539 | 2.24 × 105 |
| Case | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 373 | 223 | 150 | 28.293 | 0.189 | 3.642 | 3.638 |
| 2 | 423 | 173 | 250 | 60.235 | 0.241 | 4.653 | 4.647 |
| 3 | 453 | 248 | 205 | 37.443 | 0.183 | 3.527 | 3.523 |
| 4 | 423 | 273 | 150 | 24.392 | 0.163 | 3.140 | 3.136 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bardera-Mora, R.; Rodríguez-Sevillano, Á.; Matías-García, J.C.; Barroso-Barderas, E.; Fernández-Antón, J. CFD Analysis of Natural Convection Performance of a MMRTG Model Under Martian Atmospheric Conditions. Appl. Sci. 2025, 15, 11825. https://doi.org/10.3390/app152111825
Bardera-Mora R, Rodríguez-Sevillano Á, Matías-García JC, Barroso-Barderas E, Fernández-Antón J. CFD Analysis of Natural Convection Performance of a MMRTG Model Under Martian Atmospheric Conditions. Applied Sciences. 2025; 15(21):11825. https://doi.org/10.3390/app152111825
Chicago/Turabian StyleBardera-Mora, Rafael, Ángel Rodríguez-Sevillano, Juan Carlos Matías-García, Estela Barroso-Barderas, and Jaime Fernández-Antón. 2025. "CFD Analysis of Natural Convection Performance of a MMRTG Model Under Martian Atmospheric Conditions" Applied Sciences 15, no. 21: 11825. https://doi.org/10.3390/app152111825
APA StyleBardera-Mora, R., Rodríguez-Sevillano, Á., Matías-García, J. C., Barroso-Barderas, E., & Fernández-Antón, J. (2025). CFD Analysis of Natural Convection Performance of a MMRTG Model Under Martian Atmospheric Conditions. Applied Sciences, 15(21), 11825. https://doi.org/10.3390/app152111825






