Superior Performance of Extreme Gradient Boosting Model Combined with Affinity Propagation Clustering for Reliable Prediction of Permissible Exposure Limits of Hydrocarbons and Their Oxygen-Containing Derivatives
Abstract
1. Introduction
2. Fundamental Principles
2.1. Affinity Propagation Clustering Algorithm
2.2. Extreme Gradient Boosting
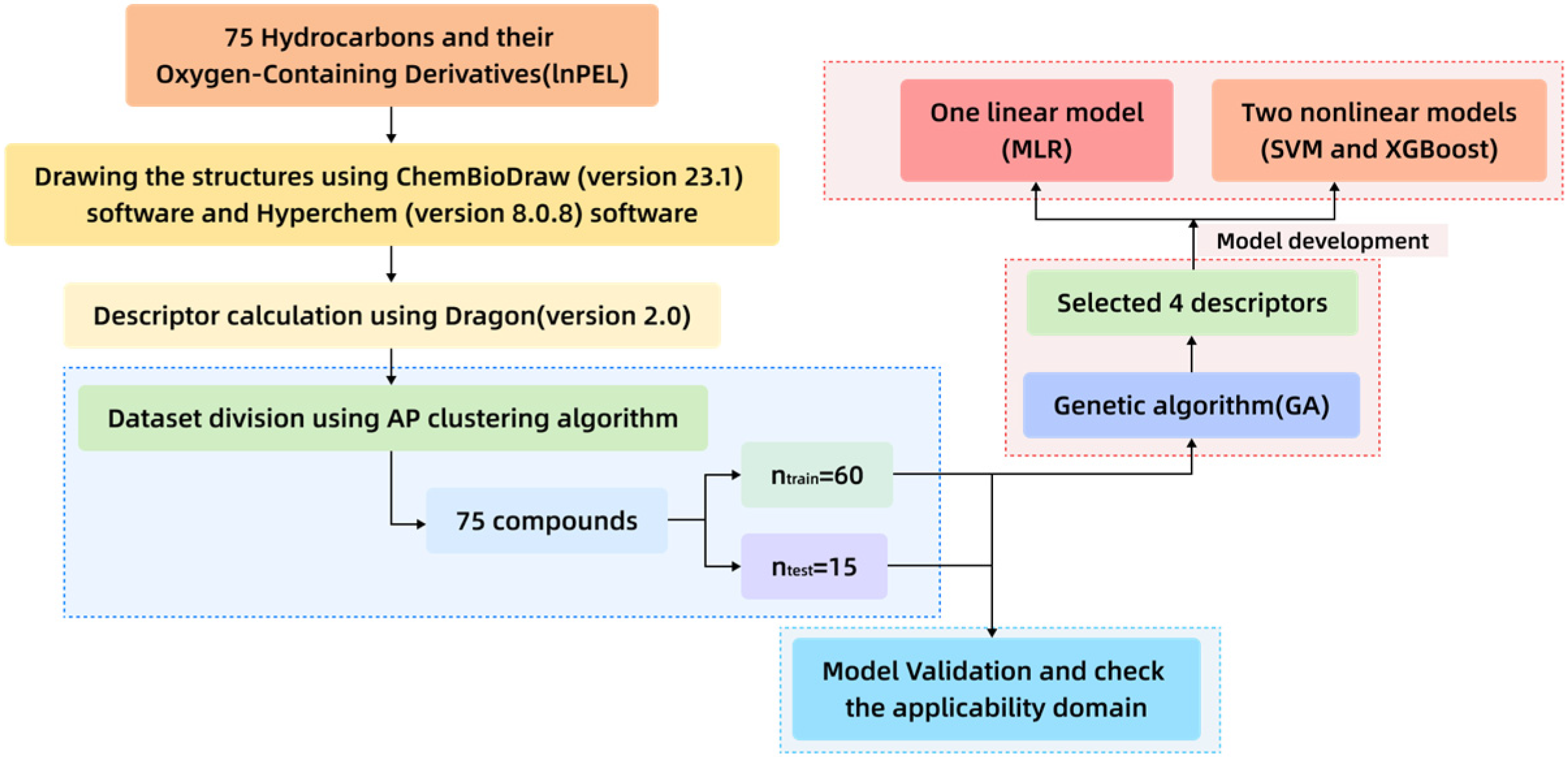
3. Sample and Methodology
3.1. Origin and Composition of the Sample Dataset
3.2. Selection of Characteristic Molecular Descriptors
3.3. Model Establishment
3.3.1. MLR Model
3.3.2. SVM Model
3.3.3. XGBoost Model
3.4. Model Validation and Evaluation
4. Results and Discussion
4.1. Performance of Models
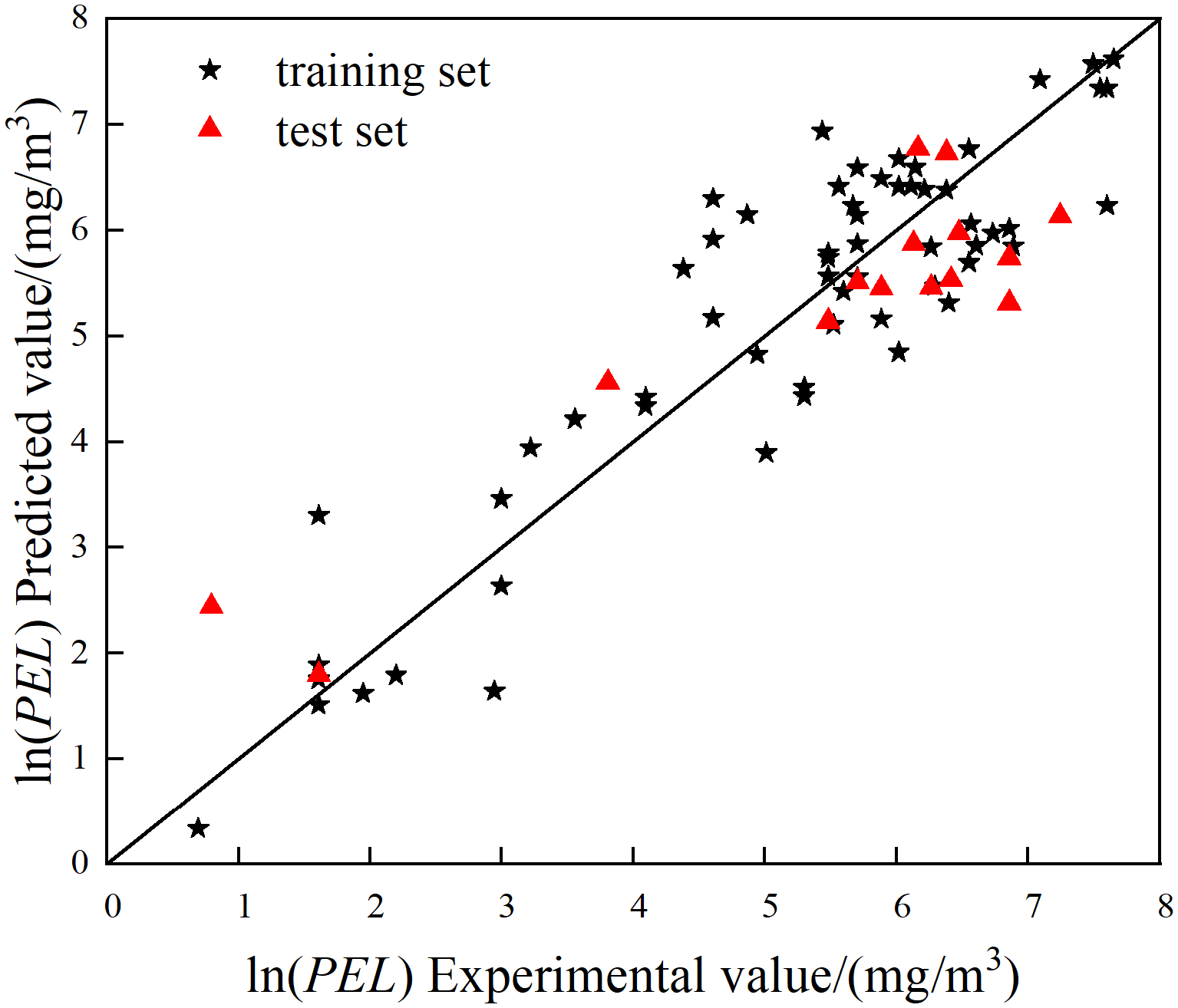
4.1.1. Results and Evaluation of the MLR Model
4.1.2. Results and Evaluation of the SVM Model
4.1.3. Results and Evaluation of the XGBoost Model
4.2. Model Evaluation and Validation
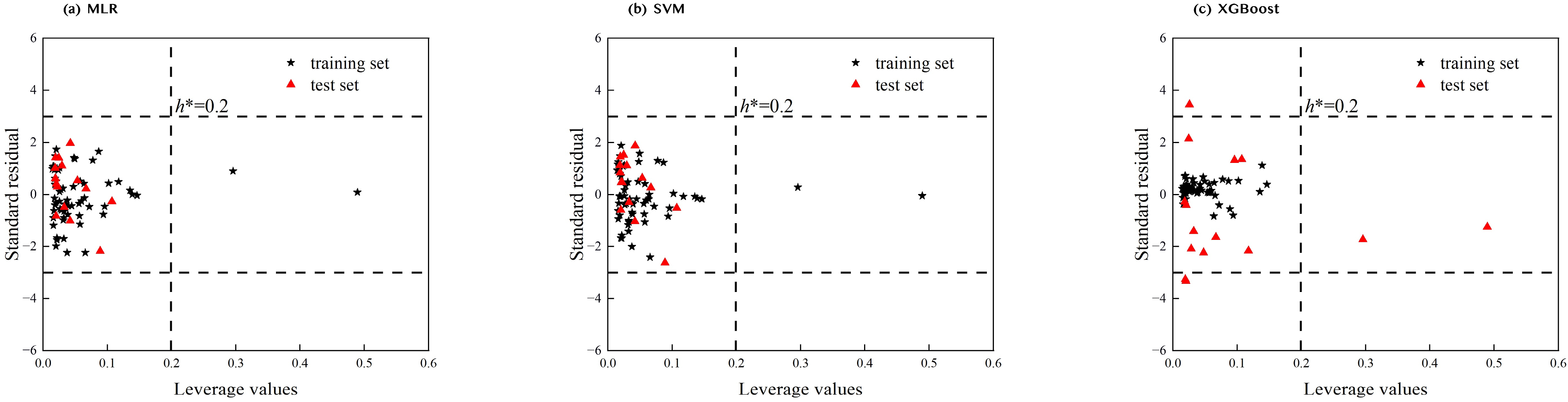
4.3. Evaluation of the Models’ Applicability Domain
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shen, Z.; Hu, Y.; Li, B.; Zou, Y.; Li, S.; Busser, G.W.; Wang, X.; Zhao, G.; Muhler, M. State-of-the-art progress in the selective photo-oxidation of alcohols. J. Energy Chem. 2021, 62, 338–350. [Google Scholar] [CrossRef]
- Yan, B.; Wu, J.; Deng, J.; Chen, D.; Ye, X.; Yao, Q. Recent progress in light-driven direct dehydroxylation and derivation of alcohols. Chin. J. Org. Chem. 2023, 43, 3055–3066. [Google Scholar] [CrossRef]
- Wei, D.; Bu, J.; Zhang, S.; Chen, S.; Yue, L.; Li, X.; Liang, K.; Xia, C. Light-driven stepwise reduction of aliphatic carboxylic esters to aldehydes and alcohols. Angew. Chem. Int. Ed. 2025, 64, e202420084. [Google Scholar] [CrossRef]
- McDonough, D.; Bezold, E.L.; Wuest, W.M.; Minbiole, K.P.C. The versatile synthesis and biological evaluation of all-alkyl biscationic quaternary phosphonium compounds: Atom-economical and potent disinfectants. RSC Med. Chem. 2025. [Google Scholar] [CrossRef] [PubMed]
- Tzouras, N.V.; Zorba, L.P.; Kaplanai, E.; Tsoureas, N.; Nelson, D.J.; Nolan, S.P.; Vougioukalakis, G.C. Hexafluoroisopropanol (HFIP) as a multifunctional agent in gold-catalyzed cycloisomerizations and sequential transformations. ACS Catal. 2023, 13, 8845–8860. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, R. Critical review of microbial degradation of aromatic compounds and exploring potential aspects of furfuryl alcohol degradation. J. Polym. Environ. 2019, 27, 901–916. [Google Scholar] [CrossRef]
- Bouzidi, H.; Laversin, H.; Tomas, A.; Coddeville, P.; Fittschen, C.; El Dib, G.; Roth, E.; Chakir, A. Reactivity of 3-hydroxy-3-methyl-2-butanone: Photolysis and OH reaction kinetics. Atmos. Environ. 2014, 98, 540–548. [Google Scholar] [CrossRef]
- Gugumus, F. Contribution to the role of aldehydes and peracids in polyolefin oxidation1. Photolysis and photooxidation of aldehydes in polyethylene. Polym. Degrad. Stab. 1999, 65, 259–269. [Google Scholar] [CrossRef]
- Shen, M.; Almallahi, R.; Rizvi, Z.; Gonzalez-Martinez, E.; Yang, G.; Robertson, M.L. Accelerated hydrolytic degradation of ester-containing biobased epoxy resins. Polym. Chem. 2019, 10, 3217–3229. [Google Scholar] [CrossRef]
- Zhang, S.; Jia, C.; Gao, H.; Huang, T.; Bai, X.; Suo, H.; Pu, G.; Wang, C.; Chen, H.; Ma, J. Pollution characteristics and potential sources of Peroxyacetyl Nitrate in a petrochemical industrialized city, Northwest China. Chemosphere 2025, 372, 144104. [Google Scholar] [CrossRef]
- Zhang, S.; Li, H.; He, R.; Deng, W.; Ma, S.; Zhang, X.; Li, G.; An, T. Spatial distribution, source identification, and human health risk assessment of PAHs and their derivatives in soils nearby the coke plants. Sci. Total Environ. 2023, 861, 160588. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.; Che, Y.; Li, T.; Yan, Z.; Zhao, W.; Lv, S.; Zhang, F.; Zhou, M.; Zhou, Y.; Zhu, Z.; et al. Exploring the mechanisms underlying effects of oxygenated polycyclic aromatic hydrocarbons exposure on inflammatory bowel disease. Ecotoxicol. Environ. Saf. 2025, 304, 119153. [Google Scholar] [CrossRef]
- Liu, R.; Liu, Z.; Liu, H.C.; Shi, H. An improved alternative queuing method for occupational health and safety risk assessment and its application to construction excavation. Autom. Constr. 2021, 126, 103672. [Google Scholar] [CrossRef]
- Fata, C.M.L.; Giallanza, A.; Micale, R.; Scalia, G.L. Ranking of occupational health and safety risks by a multi-criteria perspective: Inclusion of human factors and application of VIKOR. Saf. Sci. 2021, 138, 105234. [Google Scholar] [CrossRef]
- Dizdar, E.N.; Ünver, M. The assessment of occupational safety and health in Turkey by applying a decision-making method: MULTIMOORA. Hum. Ecol. Risk Assess. 2020, 26, 1693–1704. [Google Scholar] [CrossRef]
- Caraballo-Ay, Y. Occupational safety and health in Venezuela. Ann. Glob. Health 2015, 81, 512–521. [Google Scholar] [CrossRef]
- Boom, Y.J.; Enfrin, M.; Grist, S.; Giustozzi, F. Analysis of possible carcinogenic compounds in recycled plastic modified asphalt. Sci. Total Environ. 2023, 858, 159910. [Google Scholar] [CrossRef]
- Rappaport, S.M. The rules of the game: An analysis of Osha’s enforcement strategy. Am. J. Ind. Med. 1984, 6, 291–303. [Google Scholar] [CrossRef]
- Tang, S.H.; Zhang, C.; Zhou, L.L.; Li, Y.Q.; Xu, S.X.; Wang, Z. An investigation and analysis of an acute occupational methyl acetate poisoning. Chin. J. Ind. Hyg. Occup. Dis. 2021, 39, 943–946. [Google Scholar]
- Shen, H.; Xu, S.; Fei, X.; Song, X.; Chang, Q.; Zhu, B. Investigation and Analysis of an Acute Occupational Methanol Poisoning Accident. J. Environ. Occup. Med. 2020, 37, 818–820. [Google Scholar]
- Sayapathi, B.S.; Su, A.T.; Koh, D. The impact of different permissible exposure limits on hearing threshold levels beyond 25 dBA. Iran. Red Crescent Med. J. 2014, 16, e15520. [Google Scholar] [CrossRef] [PubMed]
- Jou, J.; Chen, J.; Lin, J.; Cheng, M. An easy-to-apply method for determining permissible exposure limit of retina to light. Heliyon 2022, 8, e10927. [Google Scholar] [CrossRef]
- Uhlemeier, K.V.; Wood, T.B. Laboratory evaluation of permissible exposure limits for men in hot environments. Am. J. Ind. Med. 1979, 40, 1097–1103. [Google Scholar]
- Wu, M. Discussion on the setting of emergency rescue isolation areas based on simulation of benzene tower leakage scenarios. Occup. Health Emerg. Rescue 2017, 35, 558–560. [Google Scholar]
- Yu, L.; Shen, X.; Yang, M.; Xiu, G.; Qian, F.; Wang, J. Simulation study on benzene leakage and exposure risk in the isomerization unit of the aromatic hydrocarbon plant. Chin. J. Saf. Sci. 2017, 27, 79–84. [Google Scholar]
- Szczesna, D.; Kupczewska-Dobecka, M.; Konieczko, K.; Jurewicz, J. P19-08 New values of occupational exposure limits (OELs) of inhalation anesthetics: Enflurane, isoflurane, sevoflurane and desflurane in Poland. Toxicol. Lett. 2022, 368, S213. [Google Scholar] [CrossRef]
- Tustin, A.W.; Cannon, D.L. Analysis of biomonitoring data to assess employer compliance with OSHA’s permissible exposure limits for air contaminants. Am. J. Ind. Med. 2021, 65, 81–91. [Google Scholar] [CrossRef]
- Kostoff, R.N.; Aschner, M.; Goumenou, M.; Tsatsakis, A. Setting safer exposure limits for toxic substance combinations. Food Chem. Toxicol. 2020, 140, 111346. [Google Scholar] [CrossRef]
- Occupational Safety and Health Administration. OSHA History. Available online: https://www.osha.gov/history (accessed on 24 October 2025).
- Zheng, Y. Occupational Exposure Assessment and Genetic Damage Study of Vinyl Chloride Workers. Master’s Thesis, Fudan University, Shanghai, China, 2009. [Google Scholar] [CrossRef]
- Pamies, D.; Estevan, C.; Vilanova, E.; Sogorb, M.A. Chapter 7-Alternative methods to animal experimentation for testing developmental toxicity. In Reproductive and Developmental Toxicology, 3rd ed.; Academic Press: Lausanne, Switzerland; Elche, Spain, 2022; pp. 107–125. [Google Scholar]
- DeSesso, J.M. Future of developmental toxicity testing. Curr. Opin. Toxicol. 2017, 3, 1–5. [Google Scholar] [CrossRef]
- Manganelli, S.; Schilter, B.; Scholz, G.; Benfenati, E.; Piparo, E.L. Value and limitation of structure-based profilers to characterize developmental and reproductive toxicity potential. Arch. Toxicol. 2020, 94, 939–954. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.; Rogers, W.J.; Sam, M.M. Experimental measurement and numerical analysis of binary hydrocarbon mixture flammability limits. Process Saf. Environ. Prot. 2009, 87, 94–104. [Google Scholar] [CrossRef]
- Rappaport, S.M. Threshold limit values, permissible exposure limits, and feasibility: The bases for exposure limits in the United States. Am. J. Ind. Med. 1993, 23, 683–694. [Google Scholar] [CrossRef]
- Tropsha, A.; Gramatica, P.; Gombar, V.K. The importance of being earnest: Validation is the absolute essential for successful application and interpretation of QSPR models. QSAR Comb. Sci. 2003, 22, 69–77. [Google Scholar] [CrossRef]
- Gissi, A.; Tcheremenskaia, O.; Bossa, C.; Battistelli, C.L.; Browne, P. The OECD (Q)SAR Assessment Framework: A tool for increasing regulatory uptake of computational approaches. Comput. Toxicol. 2024, 31, 100326. [Google Scholar] [CrossRef]
- Otto, M.A.; Martin, N.J.; Rous, J.S.; Stevens, M.E. Determination of airborne concentrations of dichlorvos over a range of temperatures when using commercially available pesticide strips in a simulated military guard post. J. Occup. Environ. Hyg. 2017, 14, D54–D61. [Google Scholar] [CrossRef] [PubMed]
- Habschied, K.; Šarić, G.K.; Krstanović, V.; Mastanjević, K. Biomonitoring and human exposure. Toxins 2021, 13, 113. [Google Scholar] [CrossRef] [PubMed]
- Storsjö, T.; Tinnerberg, H.; Sun, J.; Chen, R.; Farbrot, A. Elemental carbon—An efficient method to measure occupational exposure from materials in the graphene family. NanoImpact 2024, 33, 100499. [Google Scholar] [CrossRef]
- Cai, N.; Zhao, Y.; Xu, F.; Jiang, M.; Han, L.; Zhu, B.; Wang, B. Integrated internal and external exposure models for dimethylformamide risk assessment and health risk monetization. Ecotoxicol. Environ. Saf. 2025, 291, 117890. [Google Scholar] [CrossRef]
- Golalipour, K.; Akbari, E.; Hamidi, S.S.; Lee, M.; Enayatifar, R. From clustering to clustering ensemble selection: A review. Eng. Appl. Artif. Intell. 2021, 104, 104388. [Google Scholar] [CrossRef]
- Frey, B.J.; Dueck, D. Response to comment on clustering by passing messages between data points. Science 2008, 319, 726–727. [Google Scholar] [CrossRef]
- Bejar, J.; Paternina, M.R.A.; Mendez, A.Z.; Lugnani, L.; Tellez, E. Power system coherency assessment by the affinity propagation algorithm and distance correlation. Sustain. Energy Grids Netw. 2022, 30, 100658. [Google Scholar] [CrossRef]
- Fang, X.; Luo, C.; Zhang, D.; Zhang, H.; Qian, J.; Zhao, C.; Hou, Z.; Zhang, Y. Pre-selection of monitoring stations for marine water quality using affinity propagation: A case study of Xincun Lagoon, hainan, China. J. Environ. Manag. 2022, 325, 116666. [Google Scholar] [CrossRef]
- Reddy, V.S.; Kinnicutt, P.; Lee, R. Text document clustering: The application of cluster analysis to textual document. In Proceedings of the 2016 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 15–17 December 2016; IEEE: Las Vegas, NV, USA, 2016; pp. 1174–1179. [Google Scholar]
- Marc, M. Where Are the Exemplars? Science 2007, 315, 949–951. [Google Scholar] [CrossRef]
- The National Institute for Occupational Safety and Health (NIOSH). NIOSH Pocket Guide to Chemical Hazards; Centers for Disease Control and Prevention: Atlanta, GA, USA, 2020. Available online: https://www.cdc.gov/niosh/npg/npgdcas.html (accessed on 24 October 2025).
- Lin, M.; Yang, K.; Yu, Z.; Shi, Y.; Chen, C.L.P. Hybrid ensemble broad learning system for network intrusion detection. IEEE Trans. Ind. Inform. 2023, 20, 5622–5633. [Google Scholar] [CrossRef]
- Yu, Z.; Dong, Z.; Yu, C.; Yang, K.; Fan, Z.; Chen, C.L.P. A review on multi-view learning. Front. Comput. Sci. 2025, 19, 197334. [Google Scholar] [CrossRef]
- Kang, S.W.; Park, C.H. Effective federated XGBoost learning for multi-class classification in Non-IID environments. J. Supercomput. 2025, 81, 777. [Google Scholar] [CrossRef]
- Bauer, E.; Kohavi, R. An empirical comparison of voting classification algorithms: Bagging, boosting, and variants. Mach. Learn. 1999, 36, 105–139. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Mienye, I.D.; Sun, Y. A survey of ensemble learning: Concepts, algorithms, applications, and prospects. IEEE Access 2022, 10, 99129–99149. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- De, P.; Kar, S.; Ambure, P.; Roy, K. Prediction reliability of QSAR models: An overview of various validation tools. Arch Toxicol 2022, 96, 1279–1295. [Google Scholar] [CrossRef] [PubMed]
- Gutman, I. Degree-based topological indices. Croat. Chem. Acta 2013, 86, 351–361. [Google Scholar] [CrossRef]
- Coleman, W.F.; Arumainayagam, C.R. HyperChem 5 (by Hypercube, Inc.). J. Chem. Educ. 1998, 75, 416. [Google Scholar] [CrossRef]
- Hutter, M.C. Molecular descriptors for chemoinformatics (2nd ed.). ChemMedChem 2010, 5, 306–307. [Google Scholar] [CrossRef]
- Mauri, A.; Consonni, V.; Pavan, M.; Todeschini, R. Dragon software: An easy approach to molecular descriptor calculations. MATCH Commun. Math. Comput. Chem. 2006, 56, 237–248. [Google Scholar]
- Rogers, D.; Hopfinger, A.J. Application of genetic function approximation to quantitative structure-activity relationships and quantitative structure-property relationships. J. Chem. Inf. Comput. Sci. 1994, 34, 854–866. [Google Scholar] [CrossRef]
- Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors; Wiley-VCH: Weinheim, Germany, 2000. [Google Scholar]
- Cheng, J.; Sun, J.; Yao, K.; Xu, M.; Cao, Y. A variable selection method based on mutual information and variance inflation factor. Spectrochim. Acta Part A 2022, 268, 120652. [Google Scholar] [CrossRef] [PubMed]
- Peng, F.; Lu, L.; Wang, Y.; Yang, L.; Yang, Z.; Li, H. Predicting the formation of disinfection by-products using multiple linear and machine learning regression. J. Environ. Chem. Eng. 2023, 11, 110612. [Google Scholar] [CrossRef]
- Wainer, J.; Fonseca, P. How to tune the RBF SVM hyperparameters? An empirical evaluation of 18 search algorithms. Artif. Intell. Rev. 2021, 54, 4771–4797. [Google Scholar] [CrossRef]
- Lv, C.X.; An, S.; Qiao, B.; Wu, W. Time series analysis of hemorrhagic fever with renal syndrome in mainland China by using an XGBoost forecasting model. BMC Infect. Dis. 2021, 21, 839. [Google Scholar] [CrossRef]
- Rahman, M.S.; Chowdhury, A.H.; Amrin, M. Accuracy comparison of ARIMA and XGBoost forecasting models in predicting the incidence of COVID-19 in Bangladesh. PLoS Glob. Public Health 2022, 2, e0000495. [Google Scholar] [CrossRef]
- Pore, S.; Pelloux, A.; Chatterjee, M.; Banerjee, A.; Roy, K. Machine learning-based q-RASAR predictions of the bioconcentration factor of organic molecules estimated following the organisation for economic co-operation and development guideline 305. J. Hazard. Mater. 2024, 479, 135725. [Google Scholar] [CrossRef] [PubMed]
- Organisation for Economic Co-operation and Development (OECD). Guidance Document on the Validation of (Quantitative) Structure-Activity Relationship [(Q)SAR] Models; OECD Series on Testing and Assessment, No. 69; OECD Publishing: Paris, France, 2014. [Google Scholar]
- Gramatica, P. Principles of QSAR models validation: Internal and external. QSAR Comb. Sci 2007, 26, 694–701. [Google Scholar] [CrossRef]
- Wang, D.; Yuan, Y.; Duan, S.; Liu, R.; Gu, S.; Zhao, S.; Liu, L.; Xu, J. QSPR study on melting point of carbocyclic nitroaromatic compounds by multiple linear regression and artificial neural network. Chemom. Intell. Lab. Syst. 2015, 143, 7–15. [Google Scholar] [CrossRef]



| Nomenclature | Classification | Definition | VIF |
|---|---|---|---|
| X0Av | WHIM descriptors | The average connectivity index chi-0 serves as a quantitative descriptor of molecular branching | 1.422 |
| SIC4 | topological descriptors | The structural information content at the 4th-order neighborhood symmetry level serves as an indicator of molecular complexity | 1.408 |
| RDF010e | RDF descriptors | When weighted by atomic Sanderson electronegativity, the three-dimensional spatial structure reflects the molecular radial distribution | 1.240 |
| Dv | topological descriptors | When weighted by atomic van der Waals volume, the total feasibility index D serves as a descriptor of molecular size | 1.412 |
| Key Inspection Parameters | R2 | RMSE | SD | p | F |
|---|---|---|---|---|---|
| Result | 0.8202 | 0.7441 | 0.972 | <0.001 | 48.319 |
| Standard | >0.6 | A smaller value indicates a more favorable outcome. | A smaller value indicates a more favorable outcome. | <0.05 | >Ftheory |
| Characteristic Molecular Descriptors | Regression Coefficient | Standardized Coefficient | Standard Error | t-Value | Sig |
|---|---|---|---|---|---|
| Constant | 16.139 | 1.911 | −8.466 | <0.001 | |
| X0Av | 21.918 | 0.836 | 1.956 | 11.204 | <0.001 |
| RDF010e | −0.568 | −0.452 | 0.088 | −6.485 | <0.001 |
| Dv | 18.089 | 0.427 | 3.148 | 5.746 | <0.001 |
| SIC4 | 4.652 | 0.325 | 1.064 | 4.373 | <0.001 |
| Performance Parameters | Models | |||||
|---|---|---|---|---|---|---|
| MLR | SVM | XGBoost | ||||
| Training Set | Test Set | Training Set | Test Set | Training Set | Test Set | |
| R2 | 0.8202 | 0.8427 | 0.8229 | 0.843 | 0.9962 | 0.8892 |
| RMSE | 0.7441 | 0.8479 | 0.7243 | 0.9324 | 0.1012 | 0.6623 |
| MAE | 0.6034 | 0.7163 | 0.562 | 0.7906 | 0.0102 | 0.4386 |
| Q2loo | 0.8127 | 0.8225 | 0.9964 | |||
| Q2ext | 0.7936 | 0.7505 | 0.8921 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Zhang, Z.; Wei, Y.; Zhao, W.; Yuan, X. Superior Performance of Extreme Gradient Boosting Model Combined with Affinity Propagation Clustering for Reliable Prediction of Permissible Exposure Limits of Hydrocarbons and Their Oxygen-Containing Derivatives. Appl. Sci. 2025, 15, 11642. https://doi.org/10.3390/app152111642
Shi J, Zhang Z, Wei Y, Zhao W, Yuan X. Superior Performance of Extreme Gradient Boosting Model Combined with Affinity Propagation Clustering for Reliable Prediction of Permissible Exposure Limits of Hydrocarbons and Their Oxygen-Containing Derivatives. Applied Sciences. 2025; 15(21):11642. https://doi.org/10.3390/app152111642
Chicago/Turabian StyleShi, Jingjie, Zixiang Zhang, Yongde Wei, Wei Zhao, and Xiongjun Yuan. 2025. "Superior Performance of Extreme Gradient Boosting Model Combined with Affinity Propagation Clustering for Reliable Prediction of Permissible Exposure Limits of Hydrocarbons and Their Oxygen-Containing Derivatives" Applied Sciences 15, no. 21: 11642. https://doi.org/10.3390/app152111642
APA StyleShi, J., Zhang, Z., Wei, Y., Zhao, W., & Yuan, X. (2025). Superior Performance of Extreme Gradient Boosting Model Combined with Affinity Propagation Clustering for Reliable Prediction of Permissible Exposure Limits of Hydrocarbons and Their Oxygen-Containing Derivatives. Applied Sciences, 15(21), 11642. https://doi.org/10.3390/app152111642





