Enhanced Single-Point Mass Dynamic Model of Urban Trains for Automatic Train Operation (ATO) Systems

Abstract

The accurate prediction of train acceleration is an essential requirement for Automatic Train Operation (ATO) in urban railways. While traditional single-point mass models fail to capture the distributed dynamics of coupled vehicles, multi-point models are rarely practical due to their computational cost. In this paper, we propose an enhanced single-point mass model based on Long Short-Term Memory (LSTM) networks. The model is trained on Train Control and Monitoring System (TCMS) data from Busan Metro Line 3. By averaging the coupled dynamics of sequence-cars, we obtain a realistic single-point representation. The input data undergoes kinematic preprocessing and feature engineering, including lagging, cross, and statistical measurements. The key innovation of this paper is the physics-based feedback loop mechanism, which is built into the LSTM. This mechanism uses the predicted train acceleration at each time step to update systematically the acceleration-dependent features and make new predictions. This maintains physical consistency and causal relationships without requiring future measurements, reflecting the real-world ATO operational limits. Results demonstrate very high accuracy (R² = 0.9993, MAE = 0.0083 km/h²) without error accumulation, suggesting benefits for both ATO control accuracy and energy efficiency.

1. Introduction

Automatic train operation (ATO) systems play an important role for the modern urban trains as this can automatically execute driving sequences such as acceleration and deceleration, from station departure to precise stopping at the next station [1]. The ATO system continuously analyzes the current power status and determines the required compensatory power commands, which are executed through the Train Control and Monitoring System (TCMS). The TCMS generates the corresponding traction and braking forces through the coordinated operation of the traction motors, the regenerative braking systems, and the friction braking systems, directly influencing the final acceleration and speed profiles of the urban trains [2]. Therefore, the precise control of the motion of the urban trains fundamentally requires that accurate dynamic models are capable of predicting the train acceleration response under diverse operational conditions [3,4].

However, the forces acting on the urban trains exhibit extreme complexity, arising from the multiple interacting factors, including air resistance, rolling resistance, gradient resistance, and curve resistance [5]. Even with the theoretically complete dynamic models, the characteristics and responses of the system can inevitably vary with the vehicle aging, mechanical wear, and environmental conditions [6]. The actual train resistance can diverge significantly from the generalized train resistance due to various factors, such as operational disturbances [7], mechanical tolerances, and seasonal variations in temperature and humidity [8]. These discrepancies between theoretical predictions and actual operational behavior reveal the fundamental limitations of the conventional dynamic models applied to the design of the ATO system.

Traditional methods use either single-point or multi-point mass models to predict the dynamics of train systems. Single-point mass models simplify the dynamics by considering the entire train system as a concentrated mass and combining force balance equations. However, this approach leaves out the important distributed effects that occur along the train, such as the forces between connected vehicles, differences in braking behavior, and the resulting longitudinal vibrations [9]. Therefore, this simplified approach fails to capture the complex dynamic interactions that occur among sequence-cars. This limitation can be addressed by using the multi-point mass models, which represent individual cars with coupling dynamics and achieve a higher prediction fidelity [10,11,12]. However, the computation cost still limits these models in real-time ATO systems [13,14]. To address these limitations, recent research has increasingly adopted deep learning and AI approaches to capture and model complex train dynamics, while preserving computational efficiency [15,16,17,18].

Deep learning and artificial intelligence (AI) represent the main influential topics of recent research in the field of urban trains. Short-Term Memory (LSTM) networks have demonstrated particular effectiveness for time series prediction tasks involving temporal dependencies [19,20]. Several studies have investigated the data-driven approaches for the applications of the urban trains, including trajectory prediction [21,22], fault detection applications [23], virtual coupling [24], and comfort prediction [25]. However, existing approaches either lack physical rules [26] or require explicit dynamic model formulations, which limit their ability to capture the unmodeled disturbances across different operational scenarios and track characteristics [27,28]. Moreover, they needed to achieve prediction fidelity while maintaining computational efficiency, which is suitable for real-time ATO applications [29].

This paper presents an enhanced single-point mass dynamic model for the prediction of train acceleration, based on Long Short-Term Memory (LSTM), which incorporates physics-based feedback mechanisms. The model is trained using the operational data from 16 track sections covering 17 stations on Busan Metro Line 3. This data represents a realistic single-point by averaging the coupled dynamics of sequence-cars and also includes a variety of operational scenarios under real-world ATO conditions, such as varying track geometries, environmental factors, and disturbances. Firstly, the input data are prepared using a kinematic-based preprocessing methodology that ensures physical consistency through acceleration derivation, followed by a moving average filter. Then, the comprehensive feature engineering framework is implemented to create temporal representations through lagging, cross, and statistical features to provide accuracy in the prediction of the proposed model. The LSTM-based train dynamic model is strategically built in two phases: the training phase and the evaluation phase. The novel physics-based feedback mechanism is implemented into the LSTM to inform the predicted acceleration value for subsequent predictions, reflecting real-world operational constraints. The comprehensive validation across 16 diverse track sections demonstrates robust generalization and exceptional accuracy (R² = 0.9993, MAE = 0.0083 km/h²). Therefore, the proposed model can address the practical requirements of ATO systems, such as disturbance mitigation and precise automatic driving control in urban rail system automation.

This paper is organized into five sections. The next section briefly reviews the theoretical background of parametric dynamic models and introduces the definition of a dynamic model based on artificial intelligence (AI). Section 3 describes the implementation of the proposed enhanced single-point mass model based on LSTM and explains the design of the underlying train dynamics model. Section 4 presents the evaluation results of the proposed model. Finally, Section 5 concludes this paper.

2. Methodology

2.1. Problem Statement

The design of the ATO algorithm requires not only various characteristics affecting the movement of the train, but also a very high-precision dynamic modeling that reflects the unique characteristics of the braking system, considering the stopping function at the designated location on the platform [30].

A second problem is that even when modeling incorporates external disturbances to the greatest extent possible, errors in the electrical and mechanical characteristics of components from the same manufacturer can still occur, requiring operators to individually tune each train to match the original standard design values. This increases management costs. To address this issue, urban rail operators are demanding a system that enables automatic operation (ATO) for all trains based on their own dynamic modeling.

Railway vehicle dynamics is the analysis of various dynamic characteristics that appear due to friction adhesion between wheels and rails, various mechanical friction, traction characteristics, braking characteristics, the weight of each vehicle, various vibrations that occur during operation, and the gradient and curve of the track. The dynamic characteristics of a train can be divided into lateral dynamics in the left–right direction, longitudinal dynamics in the track direction, and vertical models for up-and-down movement, depending on the phenomenon [31]. In addition, in terms of the parametric approach, it is divided into a single-mass model and a multi-mass model that separately consider each parameter of a connected vehicle.

The single-mass model for the center of mass is considered to be in the middle of the vehicle. This model facilitates an understanding of acceleration/deceleration motion along the longitudinal track and mathematically expresses the forces acting on the train along the direction of motion, making it easy to capture transient motion [32]. Therefore, it has the advantage of simplifying calculations and increasing the possibility of system implementation, and is widely used in urban railway automatic train operation (ATO) research [33]. However, it has the problem of omitting the effects of various forces acting on each vehicle when starting, stopping, passing a slope, or passing a curve. Therefore, we attempted to reflect these characteristics in the point mass model by using the operational records of actual connected urban trains. This is because, in the actual vehicle driving record, a result includes all individual data of all sequence-cars. Recent research on automatic train operation (ATO) for urban trains heavily relies on single-point mass models, and the multi-point models can be viewed as an optimized or extended version of this model. This model is expressed as follows [28]:

$$x\left(t\right) = v$$

(1)

$$M\stackrel{.}{v}={ \alpha }_v^{a}F\left(t\right)-{\alpha }_v^{b}B\left(t\right)-\rho \left(v\right)-{ g}_v\left(x\right)-c_v\left(x\right)$$

(2)

$$\rho \left(v\right)=M(a{v}^2+\mathit{bv}+c)$$

(3)

where $M$ represents the total mass of the train, $F\left(t\right)$ and $B\left(t\right)$ denote the train traction force and the train braking force, ${\alpha }_v^a$ and ${\alpha }_v^b$ refer to the relative acceleration and braking coefficients, respectively. $g_v\left(x\right)$ and $c_v\left(x\right)$ represent the gradient resistance, and the curve resistance, respectively. $\rho \left(v\right)$ is the Davis formula, which represents the relationship between train speed and air resistance, and $a$, $b$, and $c$ represent resistance parameters. The typical parameters of Busan Metro in the Davis equation are as follows [34]: $a = 0.000745, b = 0.0359, \text{and} c = 1.867$.

2.2. Train Dynamics Model Based on LSTM

This study aims to develop a dynamic model using actual data from the automated operation (ATO) of Busan Metro Line 3. This ATO data contains a variety of resistance values (disturbances) that cannot be captured by parametric train dynamic models, allowing for transformation into the most complete dynamic model. Artificial Intelligence (AI) is a field of technology that enables computer systems to perform various advanced functions by mimicking human learning, reasoning, and perception. Rapid computer advancements are shaping AI technology as a core technology driving a new industrial era, and it is being widely utilized in areas such as autonomous driving, medical diagnosis, object recognition and classification, and finance [35,36]. In the railway industry, AI is emerging in the form of reinforcement learning-based automatic operation (ATO) control [37] and deep learning-based driving pattern learning model development [38], and is expected to become a new driving force for future railway development.

The data provided in this study are operational records related to autonomous train operation, containing a wide range of information. However, structuring the data is challenging. Therefore, applying machine learning models is challenging, requiring consideration of the field of deep learning. Machine learning models are designed to learn from structured data to make accurate predictions and decisions. However, if the data is not accurately labeled, the model cannot accurately understand the data. This problem can be solved by deep learning [39]. Deep learning models utilize multilayer artificial neural networks that mimic the neural network structure of the human brain to process data, automatically extract features, and enable learning and prediction [21]. Therefore, they are considered highly useful for building dynamic models.

The next consideration is the characteristics of the data. The chronological nature characterizes the operational data of urban trains, which is recorded sequentially from the start to the stop of each process. In this paper, the goal of this data is to nonparametrically explore, learn, and predict dynamic changes during driving, which will make it possible to create a dynamic model. Therefore, we utilized a Long Short-Term Memory (LSTM) neural network over alternative machine learning approaches according to the following characteristics. The LSTM network is an enhanced version of a recurrent neural network (RNN) that can retain information (long-term memory) from previous inputs through its unique gating mechanisms. LSTM has demonstrated excellent performance and its reliability in addressing time-series or sequential problems across multiple fields, such as natural language processing [40,41], financial forecasting [42,43], and energy demand prediction [44,45]. Additionally, LSTM-based approaches have been used in the research field of the railway industry and urban trains on dynamic modeling and speed prediction tasks (as mentioned in Section 1). Therefore, these characteristics prove that the LSTM-based approach is a good choice for implementing our proposed train dynamic model. Although LSTM was selected to capture temporal dependencies in sequential data, alternative machine learning approaches such as Gated Recurrent Units (GRU), Transformer-based architectures, and other methods may provide similar or additional advantages. Future work will explore using these alternative methods to implement or evaluate the performance of the train dynamic model. In this paper, static elements were excluded from the train dataset used for dynamic model extraction, while dynamic elements defined within the parametric model were selected and used as inputs.

3. Implementation of the Proposed Train Dynamic Model

3.1. Architecture of LSTM Network

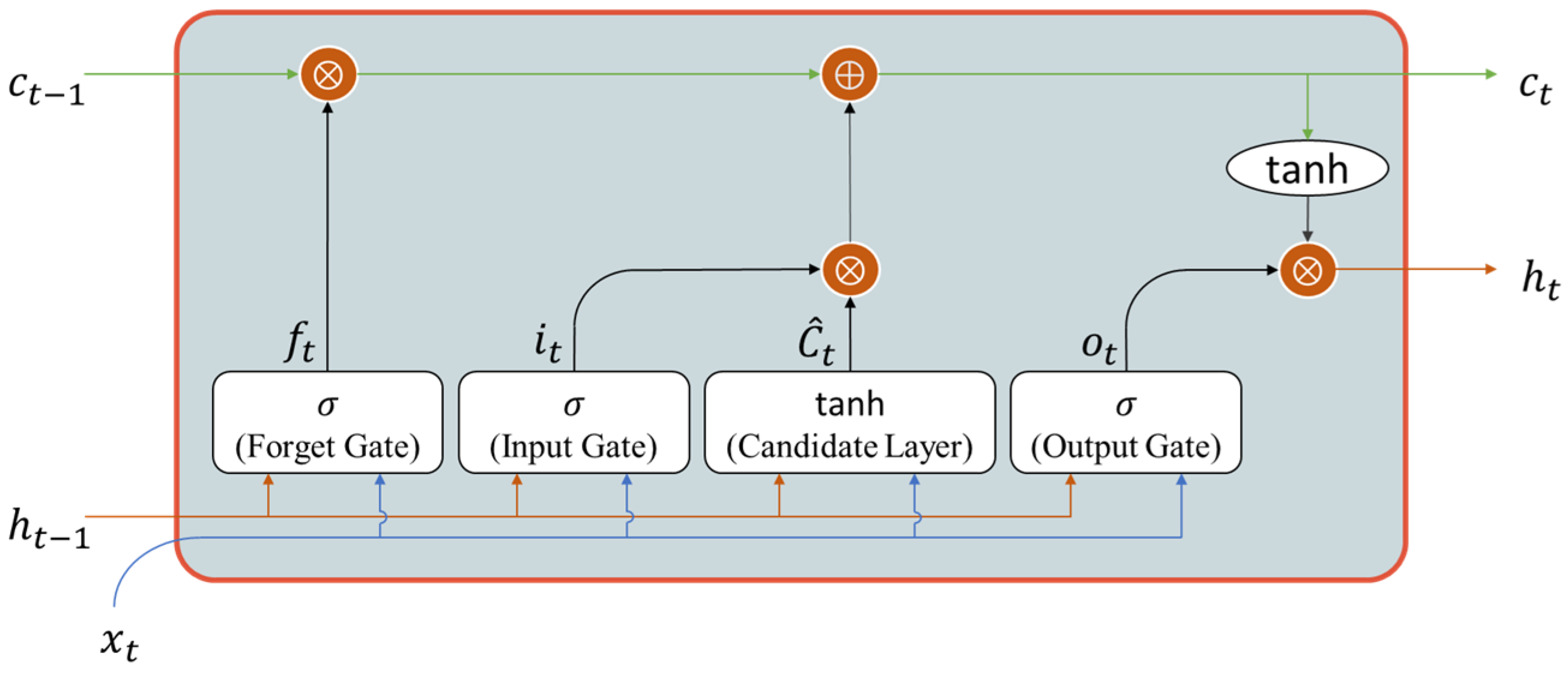
In 1997, Hochreiter and Schmidhuber first introduced Long Short-Term Memory (LSTM) [46], which is an improved version of the recurrent neural network (RNN). A single hidden state in traditional RNNs can make information disappear in the long term. LSTM can address this problem by introducing a memory cell to hold information for an extended period. Therefore, LSTM architectures are capable of learning long-term dependencies in sequential data, which is valuable for applications of time series analysis and other temporal pattern recognition tasks.

For train acceleration prediction, LSTM demonstrates particular effectiveness due to its ability to capture long-term temporal dependencies inherent in railway operational dynamics, where current acceleration states depend on historical speed profiles, track conditions, and control inputs. The LSTM architecture is shown in Figure 1 as follows:

The forget gate calculates values between 0 and 1 to decide what information should be erased or kept for future use from the previous cell state:

$$f_t = \sigma \left(W_f . [h_{t-1}, x_t] + b_f\right)$$

(4)

Using a sigmoid activation function, the input gate decides what new information should be saved from the current input ($x_t$) and the previous hidden state ($h_{t-1}$) (indicated by the blue arrow and orange arrow respectively in Figure 1) in the cell state:

$$i_t = \sigma \left(W_i . [h_{t-1}, x_t] +{ b}_i\right)$$

(5)

where the sigmoid activation function is

$$\sigma \left(x\right)={\displaystyle \frac{1}{1 +e^{-x}}}$$

(6)

The candidate memory cell creates a vector of new candidate values using a hyperbolic tangent activation function, which is as follows:

$${\widehat{C}}_t = \mathit{tanh}\left(W_c . [h_{t-1}, x_t] +{ b}_c\right)$$

(7)

where the tanh activation function is

$$\mathit{tanh}\left(x\right)={\displaystyle \frac{e^x-e^{-x}}{e^x+e^{-x}}}$$

(8)

The new cell state (indicated by the green arrow in Figure 1) is the combination of information from the forget gate and the new candidate memory cell:

$$C_t = {f_t \odot C}_{t-1} + i_t{ \odot \widehat{C}}_t$$

(9)

The output gate determines which parts of the cell state should result as the hidden state:

$$o_t = \sigma \left(W_o . [h_{t-1}, x_t] +{ b}_o\right)$$

(10)

Finally, the hidden state (indicated by the orange arrow in Figure 1) is the cell state to serve as both the current output and input for the next time step:

$$h_t ={{ o}_t \odot \mathit{tanh}(C}_t)$$

(11)

3.2. Preparation of Data

3.2.1. Data Collection

In this study, we collected the comprehensive datasets of actual in-field data, which were gathered through the “Train Control and Monitoring System (TCMS)” from Busan Metro Line 3 with a total of 16 track sections of all 17 stations from April 2020 and December 2022. Each track section has 21 datasets, which are randomly collected at different times, under different weather conditions, and with different external disturbances to provide high-resolution operational insights and reflect real-world operational diversity. The ATO data from the Train Control and Monitoring System (TCMS) provides aggregated traction and braking forces across four sequence cars, although each operates independently [47]. The resulting acceleration data averages across four sequence cars, which reflects multi-point mass dynamics, offering greater accuracy than a single-point mass model.

Busan Metro Line 3 consists of four sequence-cars. This paper utilizes the train’s operational data to derive dynamics. Traction and braking forces in the operational data affect the representative speed, which is the average speed that incorporates all speed variations in the sequence cars. Therefore, it is possible to reproduce macroscopic, observable physical behavior. This averaging approach can ensure the physical consistency based on the principles of the center of mass dynamics, which is the basis for the enhanced single-point mass model proposed in this paper. The TCMS data captures the total system behavior where force data (F) represents the sum of all traction and braking forces from the four sequence cars, while the mass varies at each station stop as passenger gets on and off, which reflects the actual weight changes in the entire train. For velocity and distance measurements, we apply averaging that corresponds to the motion of the train’s center of mass, which is consistent with traditional single-point mass modeling assumptions. Importantly, we systematically collected detailed track characteristics for every time step k, including track grade information (g), which affects the gravitational forces and curve information (c) that influences lateral dynamics and speed restrictions. These characteristics can cover potential information loss from the averaging process. This comprehensive data collection strategy can provide our proposed model to be more than the traditional single-point mass model. While some detailed information about forces between sequence-cars and the oscillations of the individual car is averaged out, the resulting enhanced single-point mass model retains the primary dynamics, which is important for ATO control. This approach balances the model between complexity and practical applicability, providing sufficient accuracy for ATO predictions while maintaining computational efficiency suitable for real-time operations. The dataset architecture divides the data into training and testing datasets. In the training sets, there are two divisions, namely train data and validation data according to “Time Series Split” function, which was mentioned in Section 3.3.

3.2.2. Data Preprocessing

In the real-world workspace, failures, faults, and noise in sensors or actuators can lead to missing data. LSTM-based algorithms may result in poor performance of regression and prediction due to the model bias and fitting effect. Therefore, the missing value in deep learning neural networks is still a challenging problem to obtain a more robust, optimized predictive dynamic train model. In this paper, the missing value treatment follows a sequential strategy, which begins with the forward fill to maintain temporal continuity and is followed by the backward fill to address remaining gaps. For completely missing information, we drop the rows.

The next phase of data preprocessing entails the computation of the acceleration, followed by the moving average filter, relating velocity change to displacement:

$$a = {\displaystyle \frac{v_2^2 - v_1^2}{2 \times ∆x}}$$

(12)

where $v_1$ and $v_2$ are consecutive velocity measurements and $∆x$ is the displacement. This equation can possible to introduce the error accumulation in the presence of the measurement noise. To mitigate the measurement noise and prevent error accumulation, we apply the moving average filter in two stages. Before acceleration calculation, velocity measurements are pre-filtered to remove the measurement noise using the moving average filter as follows:

$$v_f\left(k\right) = {\displaystyle \frac{1}{\omega }}\sum _{j = 0}^{\omega -1}v(k + j)$$

(13)

where ω is the window size. In this paper, the selection of window size (ω = 3) is based on the consideration aligned with the 0.25 s sampling interval. After computing acceleration using Equation (12), a second moving average filter is applied to prevent error accumulation as follows:

$$a_f\left(k\right) = {\displaystyle \frac{1}{\omega }}\sum _{j = 0}^{\omega -1}a(k + j)$$

(14)

These two stages of pre and post moving average filters ensures to compensate the error propagation issues through comprehensive evaluation, which was mentioned in Section 4. This physics-based approach ensures that the derived acceleration values accurately reflect the underlying train dynamics while maintaining consistency across different operational scenarios.

3.2.3. Feature Engineering

In this paper, a robust characterization of temporal dynamics and complex nonlinear relationships based on the input data features is constructed through feature engineering. This can help improve the quality of the results of regression and prediction of the LSTM neural network through short-term dynamics and long-term patterns [48]. In this paper, considering the accurate prediction for the next time step $k + 1$, more relationships and descriptions of the features from the previous data should be provided to be precise in prediction. Therefore, the feature selection criteria were established based on following three principles: (1) capturing the temporal dependencies inherent in train motion dynamics, (2) representing the physical characteristics of acceleration, deceleration, and momentum changes, and (3) maintaining computational efficiency while maximizing model performance. There are three types of features in the set: lagged features, crossed features, and statistical features, which are taken as the reference from [21]. Lagging features are provided to capture historical context or patterns by incorporating previous time steps:

$$X_{l_k}\left(t\right) = X(t-k)$$

(15)

where $k$ represents the lag step, ranging from 1 to 5. This approach can provide the historical influences on the current train behavior. Then, the cross features capture the complex relationships and dependencies between consecutive time steps:

$$X_{c_k}\left(t\right) = \prod _{\left\{i = 0\right\}}^{k}X(t - i)$$

(16)

These multiplicative features were introduced to model the nonlinear interactions, which are critical in representing train dynamics. Statistical features provide temporal information about the characteristics of the data through rolling window calculations:

$$X_{m_k}\left(t\right) = {\displaystyle \frac{1}{k}}\sum _{i = 0}^{k-1}X(t-i)$$

(17)

$$X_{s_k}\left(t\right)=\sqrt{ {\displaystyle \frac{1}{k}}\sum _{i=0}^{k-1}{\left(X\left(t-i\right)-X_{m_k}\left(t\right)\right)}^2}$$

(18)

where $k$ represents the window size (5, 10, or 20 time steps). First–last difference features capture trend information:

$$X_{d_k}\left(t\right) = X\left(t\right) - X(t-k)$$

(19)

This feature gives the overall change in state variables over the rolling window, providing acceleration trends, which can help in predicting future train states.

3.2.4. Data Normalization

After finishing the feature engineering procedure and before training the LSTM train dynamic model, data normalization is also a critical step in a data-driven model in order to prevent unbalanced input features, which can lead to uneven weight distribution and affect training performance. In this paper, the “MinMaxScaler” function is used to transform all input features to the range [0, 1], ensuring an equal contribution during model training:

$$x_n = {\displaystyle \frac{ x - x_{\mathit{min}}}{x_{\mathit{max}} - x_{\mathit{min}}}}$$

(20)

3.2.5. Loss Function and Evaluation Metrics

The model optimization employs “Mean Absolute Error” (MAE) as the primary loss function in this paper:

$$\mathrm{L} = {\displaystyle \frac{1}{N}}\sum _{i = 1}^N\left|a_{{k+1}_i}-{\widehat{a}}_{{k+1}_i}\right|$$

(21)

where $a_{{k+1}_i}$ represents actual acceleration values and ${\widehat{a}}_{{k+1}_i}$ denotes predicted acceleration values. Model performance is evaluated by using root mean squared error (RMSE) and R-squared (R²) as key metrics. Root mean square error (RMSE) emphasizes larger prediction errors:

$$\mathrm{RMSE} =\sqrt{ {\displaystyle \frac{1}{N}}\sum _{i = 1}^N{\left(a_{{k+1}_i}-{\widehat{a}}_{{k+1}_i}\right)}^2}$$

(22)

The coefficient of determination (R²) quantifies the proportion of variance explained by the model:

$$R^2 = 1 - {\displaystyle \frac{\sum _{i = 1}^N{\left(a_{{k+1}_i} - {\widehat{a}}_{{k+1}_i}\right)}^2}{\sum _{i = 1}^N{\left(a_{{k+1}_i} - {\stackrel{\_}{a}}_{{k+1}_i}\right)}^2}}$$

(23)

where ${\stackrel{\_}{a}}_{{k+1}_i}$ is the mean of actual values.

3.2.6. Hyperparameters

The hyperparameters impact the quality and accuracy of the predicted results. Therefore, the tuning of the hyperparameters is also important [49]. The hidden units per layer provide the capacity of the model to capture the temporal patterns in the acceleration data and balance the complexity of the model with the computational efficiency. When the hidden size is small, such as 16 and 32, the model cannot capture the complex patterns, leading to an underfit problem. If the hidden size further increases (128 and 256), the computation time unnecessarily grows, and there will be an overfitting problem. Therefore, we selected the hidden size of 64 to provide sufficient representational capacity while preventing the overfitting problem.

Then, the number of LSTM layers is needed to decide whether to capture more complex patterns. While the single layer cannot capture the hierarchical temporal features adequately, three or more layers cause an increase in the training time, higher overfitting risk, and diminishing returns. Therefore, in this paper, the two-LSTM layer structure is set up. The first layer captures the temporal dependencies, while the subsequent layer models the higher-order interaction patterns. To prevent overfitting, dropout regularization is also crucial for the LSTM network architecture. If the dropout regularization is insufficient (0.1–0.2), the model overfits to the training data. On the other hand, excessive regularization (0.4–0.5) can lead underfitting and loss of information. In this paper, dropout regularization at a rate of 0.3 is implemented to prevent overfitting by random neuron suppression.

The parameters of the proposed model are optimized using the “Adaptive Moment Estimation” (Adam) optimizer with the specified learning rate. The learning rate sets the step sizes during the optimization process called gradient descent. If the learning rate is too high (0.005–0.01), the process of training becomes less stable, overshooting minima, and exhibiting oscillations. Conversely, when the learning rate is too low (0.0001–0.0005), it could make convergence slow, which causes the model to get stuck in local minima.

The definition of batch size is the number of samples processed before the weight of the model is updated. When the batch size is small, ranging from 32 to 64, the training may produce noisy gradients, unstable learning, and slower performance per epoch. However, the larger the batch size, the less frequently the updates, leading to poor generalization. In this paper, a batch size of 128 samples is used to provide better gradient estimates while maintaining computational feasibility. The training process spans up to 500 epochs with an early stopping mechanism monitoring validation loss with a patience of 30 epochs to prevent the local minima and overfitting. Furthermore, our proposed model achieved the best performance by using the optimized hyperparameters, as shown in

Table 1. Tuning of hyperparameters.

Name of Types	Quantity
Hidden size	64
Number of LSTM layers	2
Dropout rate	0.3
Learning rate	0.001
Batch size	128
Number of epochs	500
Number of patience epochs	30

.

3.3. Design Architecture of the LSTM-Based Train Dynamic Model

The architecture of the proposed model, based on LSTM, is specifically engineered to capture the complex time series-based relationships in the Busan Metro Line 3’s operational data. It focuses on the physics-based constraints to make the prediction of the train acceleration more accurate. The core of the proposed model is composed of the hierarchical structure of dual-LSTM layers. The first LSTM layer is configured to pass through to the next layers with the full sequence of hidden states for temporal feature extraction. The mathematical operation of each LSTM layer processes the input sequence $X = \left[x_1, x_2, x_3, \dots , x_n\right]$, which passes through the gate mechanisms to create the hidden state sequences $H = \left[h_1, h_2, h_3, \dots , h_n\right]$. Then, the final LSTM layer gives only the final hidden state $h_n$ as the output, containing higher-order temporal interactions and long-term dependencies, which can help for accurate acceleration prediction.

Dropout regularization layers are placed after LSTM layers to specifically address the overfitting problem. This regularization method is critical for time-series applications where the model must generalize across diverse temporal patterns while avoiding the memorization of specific sequences. During training, the dropout layer randomly deactivates a fraction of the input neurons to zero. The mathematical expression of the dropout layer is as follows:

$$h_d = {\displaystyle \frac{h \odot m}{1 - p}}$$

(24)

where $h$ is the input hidden state, $m$ is a binary mask, which is sampled from a Bernoulli distribution with a probability $(1 - p)$ where $p$ is the dropout rate of 0.3, and $\odot$ denotes element-wise multiplication. The dropout is not used during inference, such as testing or evaluation, and the outputs are scaled by $(1 - p)$ to keep the activation values without dropout.

The Rectified Linear Unit (ReLU) activation layer introduces the nonlinearity after the final LSTM layer. The ReLU activation function is defined as follows:

$$\mathrm{f}\left(\mathrm{x}\right) =\left\{ \begin{array}{c}0, if x \le 0\\ x, if x > 0\end{array}\right.$$

(25)

The activation functions, such as sigmoid and tanh, before ReLU, were saturated. High values are given to 1.0, and small values snap to 0 or −1. This resulted in the vanishing gradient problem. The ReLU activation can address this problem by maintaining gradient flow for positive activations, introducing sparsity in the network representation.

Finally, we add a dense output layer to wrap up the model. This single dense layer takes all the temporal features and then converts them into a prediction of train acceleration at $k+1$ time step. For model compilation, mean absolute error (MAE) is used as a loss function along with the Adam optimizer and the tuned learning rate.

Cross-validation is critical for verifying model accuracy in data-driven models. We used “Time Series Split” function that keeps the data in chronological order. This function is only used in training datasets (which is explained in Section 3.2.1), not in testing datasets, as training datasets should be split into training datasets and validation datasets in order to build a robust trained model. The working principle of “Time Series Split” function is for each fold, we train on all data up to a certain point, then validate on the next chunk of data:

$$\mathit{For} \mathit{fold} k: \mathit{Train} = \left[ 0: n_{k }\right], \mathit{Validation} = [ n_{k }: n_{k-1 }]$$

(26)

Each fold gets more training data than the previous one, but we always check the performance of the model through validation datasets. In this paper, we used 30 folds to maintain sufficient training datasets in each fold and obtain a robust performance in terms of cross-validation. After this process, the testing procedure is performed on the testing dataset.

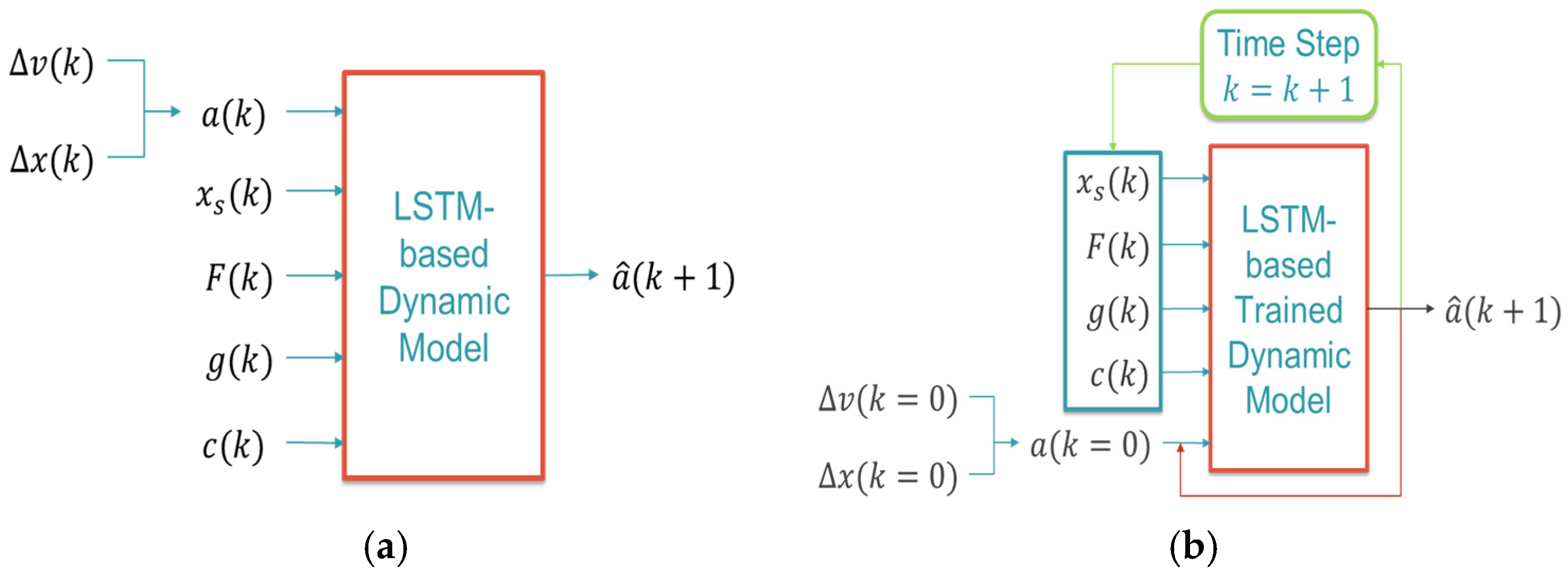
The proposed LSTM-based train dynamic model is designed in two distinct phases: the training phase, where the model learns from the real-world operation data of Busan Metro Line 3, and the evaluation phase, where the model operates with a physics-based feedback mechanism. During the training phase (as shown in Figure 2a), the model receives comprehensive input features representing the complete state of the train system, such as the rate of change in speed between the consecutive time steps ($∆v$), the position change along the track ($∆x$), the current position between two stations ($x_s$), the force-related parameter, which is provided by “Train Control and Monitoring System: (TCMS)”; representing powering and braking ($F$), the track grade information affecting gravitational forces ($g$), and the curve information influencing the lateral dynamics and speed restrictions ($c$). The ATO systems automatically adjust TCMS parameters according to the mass of the train, which represents the weight of passengers, changing from station to station. Therefore, the mass parameter is not explicitly considered in this paper as the TCMS parameter already includes the effects of the system mass. Additionally, the model also receives acceleration information ($a$) at time step $k$ as a part of the input features. Therefore, this complete information enables the model to learn complex mapping between the current operational states and future acceleration values. The output $\widehat{a}$ represents the predicted acceleration at the next time step $k+1$. During the training of the model, this predicted value is compared with the actual acceleration value through the MAE loss function (mentioned in Section 3.2.5) to adjust the internal parameters inside the model.

Novel Physics-Based Feedback Loop Mechanism

In this section, the novel physics-based feedback loop mechanism is presented. Once we have trained the model, it needs to work differently in a real-world train system. In the practical applications, only the initial state of the parameters, such as the position change, the velocity change, or the acceleration value, is available. Therefore, the model must use its own predictions as input to make the next prediction of the acceleration value, employing a feedback approach. The input features in the evaluation phase (indicated by the cyan arrow in Figure 2b) include the same operational parameters, except for acceleration only. In the evaluation phase (as shown in Figure 2b), initial values ${∆v}_0$ and ${∆x}_0$ are used to compute the initial acceleration $a_0$ at time step $k$, which serves as the starting point for the prediction sequence. For all subsequent time steps, the model receives the previously predicted acceleration $\widehat{a}$ at time step $k$ (indicated by the red arrow in Figure 2b), creating a closed-loop feedback system. This physics-based feedback mechanism can be mathematically expressed as follows:

$${\widehat{a}}_{k+1} = f (x_s, F, g, c, {\widehat{a}}_k)$$

(27)

where $f$ represents the trained LSTM model function and the green arrow in Figure 2b shows the changing of time step $k+1$. Therefore, this novel approach implements the feedback loop (indicated by the red arrow in Figure 2b) to create the recursive prediction structure, reflecting the real-world operational condition where the train control system has to make predictions about the future time step based on current measurements and past predictions.

The proposed physics-based feedback loop mechanism differs from the conventional approaches because it is in direct alignment with practical ATO control requirements and physical laws. In the predictive models, velocity is the common variable, which is used in control systems. However, in real ATO systems, acceleration can be directly used by converting to TCMS powering/ braking percentage (TCMS P/B%), which is the actual control input. This direct applicability motivates our approach of dynamic model to predict acceleration as the output. Following Newton’s second law of motion, we derive acceleration from the kinematic relationship between the change in velocity and distance, also applying a moving average filter to remove the measurement noise. The feedback mechanism maintains consistency with Newton’s laws that each predicted acceleration effects the estimates of the velocity and position for the next time step $k+1$, reflecting how the actual train dynamics evolve.

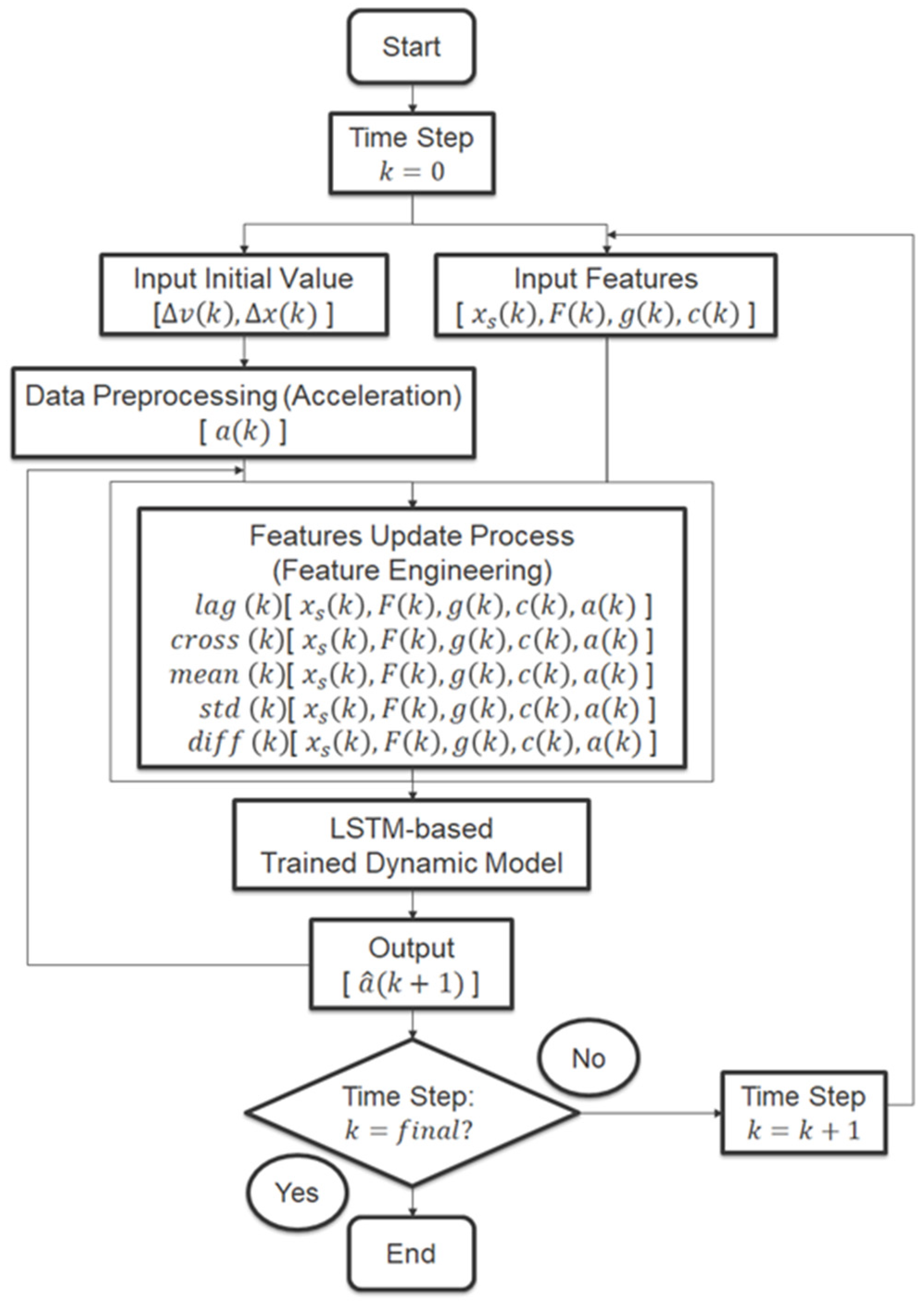
This approach of the physics-based feedback loop mechanism reflects the actual ATO controllers, where the control actions are continuously adjusted to achieve the desired future states based on the current system states. Figure 3 provides a detailed flowchart of this mechanism, showing how the feedback loop operates and updates features at each time step. The input initial values ($∆v, ∆x$) are provided only at the time step $k=0$ in order to implement data preprocessing for initial acceleration. Then, the feature update process is continuously performed and finally, all these input features enter into the LSTM-based trained dynamic model, which is already trained and loaded this trained model. The predicted output is for the next time step $k=k+1$ and the predicted acceleration at time step $k+1$ is the final output. This output will feedback to the input of acceleration for the next prediction cycle. An important detail we need to handle is the feature engineering of the acceleration predicted value. Since predicted accelerations are used through the feedback system, the model must update all acceleration-dependent features (feature engineering), such as lagging features, cross features, and statistical features of the predicted acceleration, to maintain physical consistency across the prediction horizon. This closed-loop architecture is simple but effective, ensuring that the model’s sequential predictions remain physically consistent and can be used directly in the real-world ATO control systems. Therefore, this architecture of the proposed LSTM-based train dynamic model ensures that, firstly, the model can learn effectively from historical data and then operate reliably in predictive control scenarios within a realistic operational environment.

4. Evaluation of the Proposed Enhanced Single-Point Mass Dynamic Model

The Busan Metro Line 3 dataset comprises 16 track sections, each with 21 records that share the same track geometries and operational profiles but vary by time, operational procedures, weather conditions, and external environments. All these data constitute the training set and the validation set according to Time Series Split cross-validation. For the test set, we randomly choose the dataset for each station to prove the robustness and effectiveness of the proposed model. The proposed model employs the best-performing fold and is evaluated on each station’s dataset, considering zero initial values for velocity change, position change, and acceleration at the beginning station at time 0.

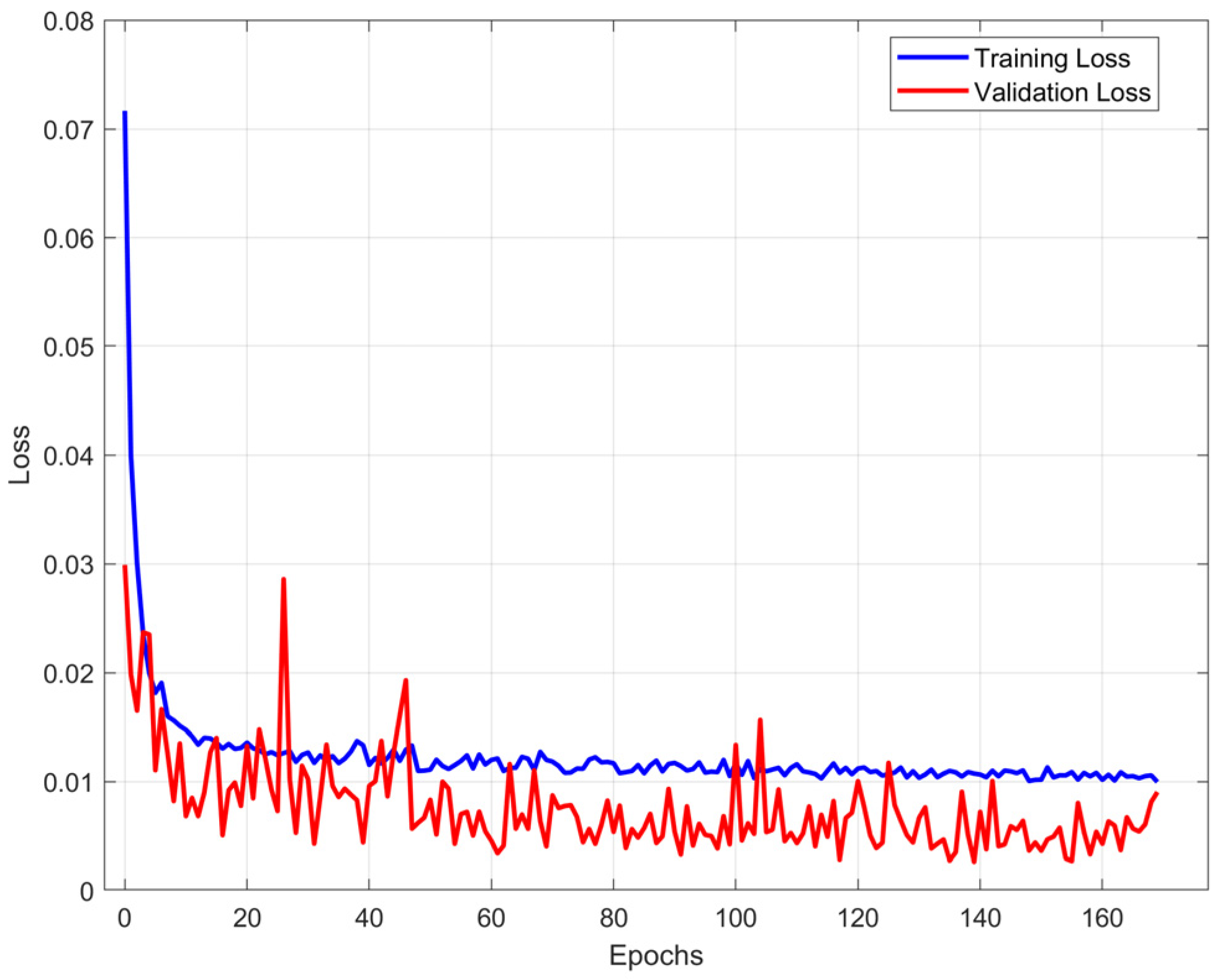
Figure 4 presents the training and validation loss curve for the proposed model during the training process for one-step ahead prediction. This figure shows that our proposed model has a fast convergence ability after 10 epochs and also proves that no overfitting was detected, that the validation loss (red line) is consistently lower than or comparable to the training loss (blue line) throughout the training period.

Figure 5, Figure 6, Figure 7 and Figure 8 illustrate the performance analysis of the model in terms of train acceleration across stations. Stations 1 and 3 demonstrate accurate prediction over sequences (500 time steps) with the complex multi-phase profiles, including rapid acceleration/deceleration transitions, where the proposed model can predict close alignment with the actual values. But the small differences seen during high-frequency oscillations at these stations are probably due to either the measurement noise or calculation of the single point mass model, as the actual data is based on the averaging of the multi-point mass model system of sequence cars, rather than fundamental prediction errors. Stations 2 and 4 also showcase the successful prediction over 400-time steps without error accumulation. Across all four stations, the model demonstrates strong capability in prediction through only the initial acceleration from rest, maintaining stability during operational transitions, and the precise tracking of both acceleration and deceleration phases.

Stations 5–8 provide the generalization of the model across varying acceleration magnitudes and temporal patterns. Station 5 displays aggressive train dynamics with initial acceleration exceeding 1.0 km/h², followed by complex oscillations, while the prediction of the model can follow throughout the challenging sequences. Station 6 demonstrates accurate prediction across the moderate magnitude operation with the successful capture of both powering and braking phase transitions. Station 7 presents a clear operation from cruising to braking conditions, where predictions show exceptional accuracy throughout either zero or non-zero acceleration periods. Station 8 shows the dynamics between the powering and braking conditions in about 0–150-time steps, with accurate predictions. Therefore, the model successfully passes the robustness of the prediction consistency across varying operational conditions.

Station 9 presents the longest operational distance with about 1000 time steps, followed by a long period of near-zero cruising (time steps 400~800), where the model accurately maintains stability without drift. Even though Station 10 exhibits significant oscillations, the model can predict precisely every sequence across the transition from powering to braking. Stations 11 and 12 display different dynamics and multiple-phase transition, where predictions demonstrate strong accuracy, proving the robustness of the model.

Stations 13 and 14 present complex deceleration patterns reaching about −1.5 km/h², where the prediction of the model maintains close alignment throughout the rapid transitions. Station 15 starts with the initial acceleration peaks around 1.2 km/h² and is then followed by the gradual deceleration and sustained negative acceleration phases. The model can demonstrate strong fidelity across the complete operation. Station 16 concludes the analysis with moderate acceleration dynamics with several transition phases. This confirms that the predictions of the model are consistent across all 16 track sections.

According to

Table 2. Performance metrics across all 16 track sections.

Track Section No.	MAE	RMSE	R2	Mean Error	Standard Deviation Error	Minimum Error	Maximum Error	Percentile 95th Absolute Error
1	0.0223	0.0291	0.9952	0.0167	0.0238	−0.0628	0.0851	0.0563
2	0.0128	0.0180	0.9989	0.0006	0.0180	−0.1103	0.0587	0.0374
3	0.0221	0.0289	0.9953	0.0151	0.0247	−0.0925	0.0793	0.0578
4	0.0107	0.0154	0.9990	0.0058	0.0142	−0.0602	0.0630	0.0336
5	0.0142	0.0273	0.9974	0.0046	0.0270	−0.0967	0.2702	0.0425
6	0.0102	0.0143	0.9993	0.0030	0.0140	−0.0557	0.0429	0.0323
7	0.0108	0.0181	0.9989	0.0021	0.0180	−0.0846	0.0752	0.0379
8	0.0144	0.0211	0.9976	0.0092	0.0190	−0.0616	0.0724	0.0454
9	0.0083	0.0162	0.9972	0.0065	0.0149	−0.0437	0.0824	0.0410
10	0.0113	0.0167	0.9987	−0.0007	0.0168	−0.0799	0.0459	0.0371
11	0.0150	0.0221	0.9984	−0.0003	0.0222	−0.0995	0.0598	0.0445
12	0.0139	0.0190	0.9990	−0.0008	0.0190	−0.0816	0.0491	0.0384
13	0.0103	0.0162	0.9984	0.0057	0.0152	−0.1134	0.0576	0.0351
14	0.0111	0.0188	0.9977	−0.0039	0.0184	−0.0834	0.1567	0.0403
15	0.0138	0.0199	0.9987	0.0016	0.0199	−0.0927	0.0652	0.0392
16	0.0128	0.0202	0.9986	−0.0020	0.0201	−0.0890	0.0450	0.0445

and

Table 3. Summary of regression evaluation metrics across all 16 track sections.

Regression Evaluation Metrics	MAE	RMSE	R2
Mean	0.0134	0.0201	0.9980
Standard deviation	0.0039	0.0047	0.0013
Minimum	0.0083	0.0143	0.9952
Maximum	0.0223	0.0291	0.9993

, the comprehensive statistical evaluation across all 16 track sections proves that the proposed enhanced single-point mass dynamic model is robust and provides a precise prediction. The mean absolute error (MAE) across all stations averages 0.0134 km/h² with a standard deviation of 0.0039. This points out the accurate prediction, achieving the lowest MAE of 0.0083 km/h² at station 9 and the highest MAE of 0.0223 km/h² at station 1. Root Mean Square Error (RMSE) averages 0.0201 km/h² with a standard deviation of 0.0047, proving that the larger prediction errors remain minimal across all different operational conditions. The coefficient of determination (R²) demonstrates robust performance with a mean value of 0.9980 and a significantly low standard deviation of 0.0013, ranging from 0.9952 at station 1 to 0.9993 at station 6. The error statistics show near-zero across all stations through mean errors. The 95th percentile absolute errors range from 0.0323 to 0.0578, which shows that even extreme prediction deviations still remain within acceptable operational bounds. Therefore, the station-by-station evaluation across all 16 diverse operational environments conclusively demonstrates that the proposed enhanced single-point mass dynamic model can perform precise predictions with the effectiveness of the feature-engineering approach for train acceleration dynamics in different operational contexts, while still following the physical rules. Moreover, the proposed model with the minimal error and high predictive accuracy can effectively support control systems in real-world urban train operations, particularly within automatic train operation (ATO) systems.

5. Conclusions

This paper successfully develops and validates an enhanced single-point mass dynamic model for train acceleration prediction using an AI approach alongside physics-based operational limitations. This paper surely addresses a critical gap in the intelligent urban train systems by providing the ability to accurately predict train acceleration, achieving prediction fidelity comparable to multi-point mass models, in real-time for optimized train control, energy management, and passenger comfort enhancement.

The methodological innovation addresses a fundamental challenge in the railway dynamics model, in which traditional single-point mass models lack accuracy for computational purposes by neglecting distributed dynamics. The kinematic-based preprocessing approach ensures physical consistency, along with the calculation of train speed from distance-to-go changes, and uses the fundamental kinematic equation to derive the acceleration, which then passes through the moving average filter. The comprehensive feature engineering framework provides the short-term operational variations and longer-term patterns, which are essential for accurate prediction, through lagging features to capture the historical context, cross features to model nonlinear interactions between consecutive states, and statistical features to give aggregated temporal information.

The design architecture of the proposed model strategically balances the model complexity with computational efficiency and also maintains the gradient flow by introducing nonlinearity, while it prevents overfitting. The Time Series Split cross-validation strategy with 30 folds ensures the temporal order preservation during model evaluation and prevents the information leakage from future observation, which is critical for time series forecasting. The training phase utilizes the complete operational data for supervised learning, while the evaluation phase implements a physics-based feedback mechanism, where it only uses the initial acceleration for predicting the train acceleration value, and later these predicted acceleration values inform subsequent predictions. Therefore, this mechanism accurately reflects real-world operational scenarios in urban trains for automatic train operation (ATO) systems.

A thorough statistical assessment conducted across all 16 track sections demonstrates the robustness of the proposed approach, yielding a minimum MAE of 0.0083 km/h² and RMSE of 0.0143 km/h². In addition, the coefficient of determination (R² = 0.9993) confirms that 99.93% of the variability in acceleration can be accounted for under diverse operational conditions. The feedback mechanism ensures stable predictions over sequences extending to 1000 time steps, without error accumulation, thereby validating its long-horizon forecasting capability. Therefore, this LSTM approach of an enhanced single-point mass dynamic model achieves significantly higher accuracy by capturing distributed dynamics, while it reduces computational costs compared to multi-point mass models. Moreover, the results of this paper can be applied not only to Busan Subway Line 3, but also to all urban railway trains for which operational data is available. Furthermore, they are expected to be useful in future acceleration/deceleration control of ATO.

The proposed LSTM-based train dynamic model offers a kind of simpler tool to facilitate ATO management by creating a dynamic model without requiring complex physical testing or extensive parameter calculations, typically needed in traditional approaches. The proposed model shows reasonable computational efficiency for real-time prediction, which can be later converted into TCMS powering or braking percentage (P/B%). This approach can help to integrate into existing ATO controller designs.

However, there are still some limitations in the proposed method. Firstly, collecting comprehensive data remains challenging, particularly for capturing the various weather conditions (rain, snow), varying passenger loads during station stops, and different external disturbances. Secondly, the data of raw on-board data from urban trains requires systematic preprocessing before use, and direct application is not feasible. Finally, the model depends on continuous input streams, including force from TCMS, and distance to go. Therefore, sensor failures or communication interruptions are a major concern. Although the algorithm for handling missing data is included in the data preprocessing stage, this area needs further improvement in future work to ensure reliable performance under sensor degradation or network disruptions. These limitations and boundary conditions highlight directions for future research.

In conclusion, the proposed model achieves reliable performance with minimal error, indicating its strong applicability to real-world ATO control systems for urban rail operations. Future research directions can be extended from this proposed model to multi-point mass modeling frameworks, which represent individual sequence car dynamics, achieving even higher prediction fidelity by directly modeling inter-vehicle coupling forces, differential braking effects, and longitudinal oscillations.