Comparing Multiple Machine Learning Models to Investigate Thermal Drivers in an Arid-Oasis Urban Park and Its Surroundings Using Mobile Monitoring
Abstract
1. Introduction
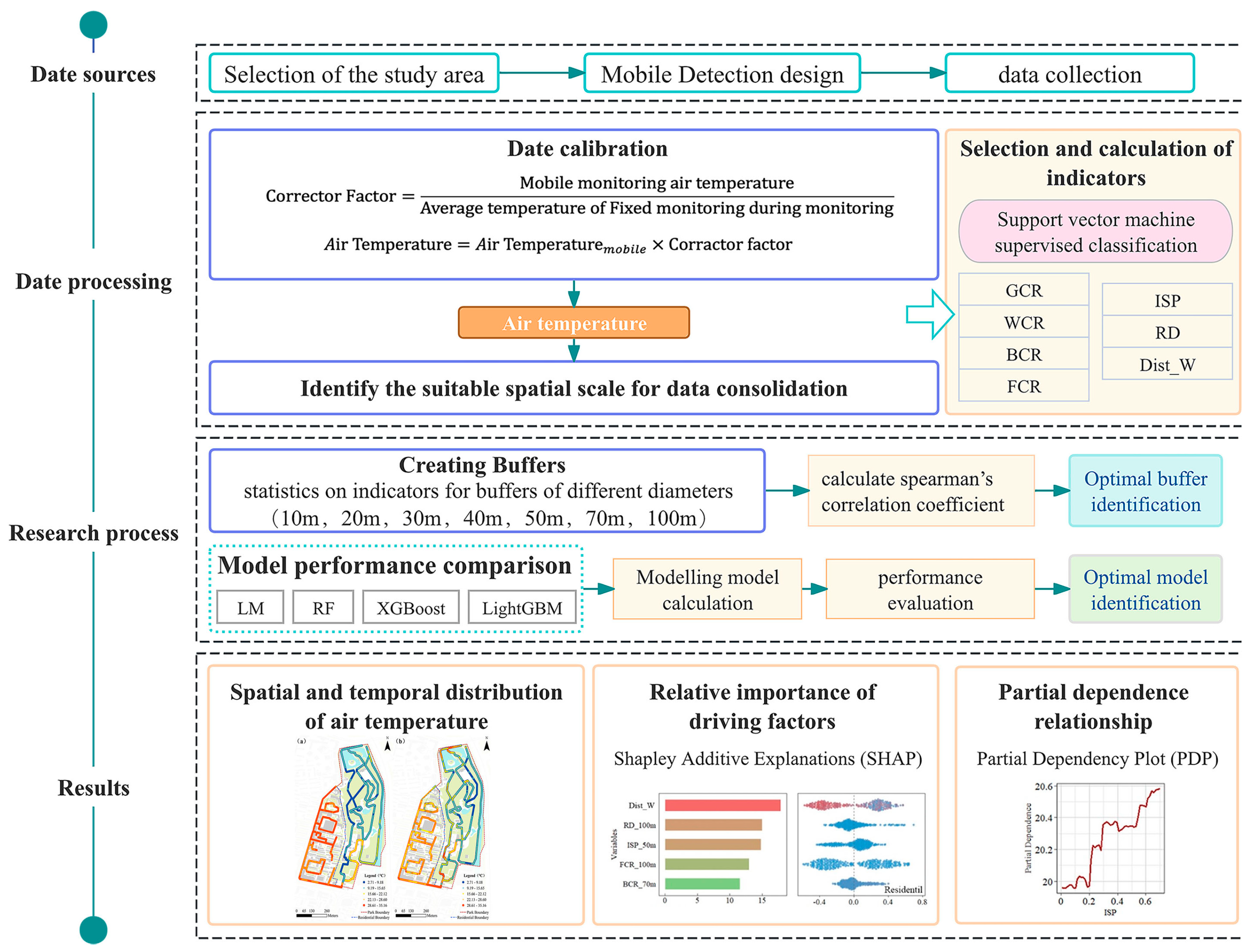
2. Materials and Methods
2.1. Study Area
2.2. Experimental Design and Data Collection
2.3. Selection and Calculation of Indicators
2.4. Identify the Suitable Spatial Scale for Data Consolidation
2.5. Model Construction
2.5.1. Multiple Linear Regression
2.5.2. Machine Learning Models
3. Results
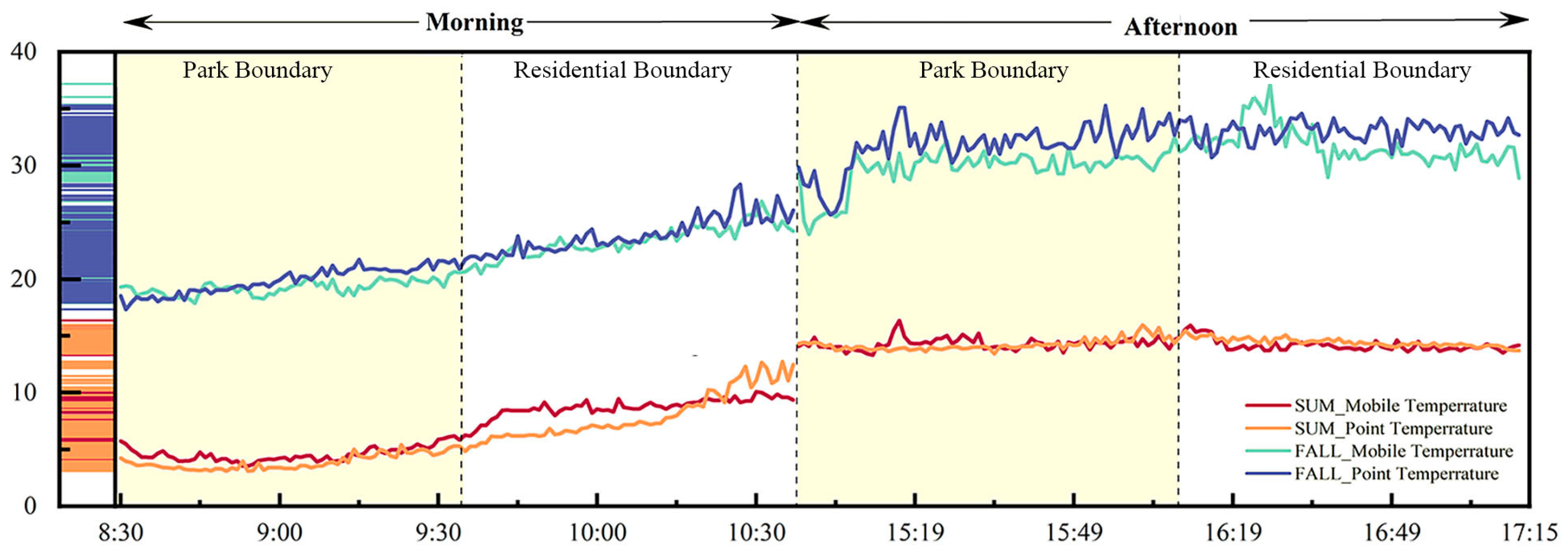
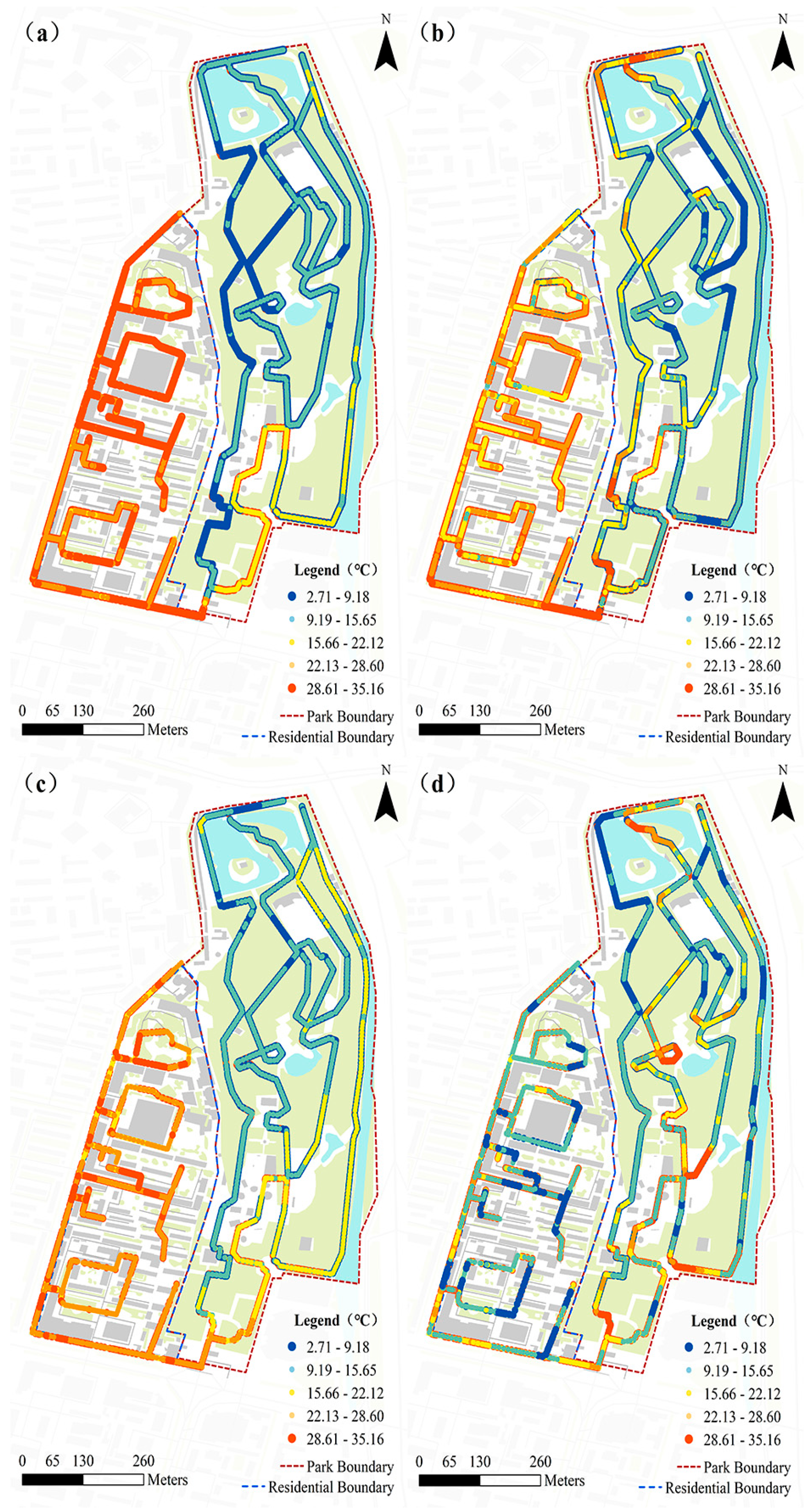
3.1. Spatial and Temporal Distribution of Air Temperature
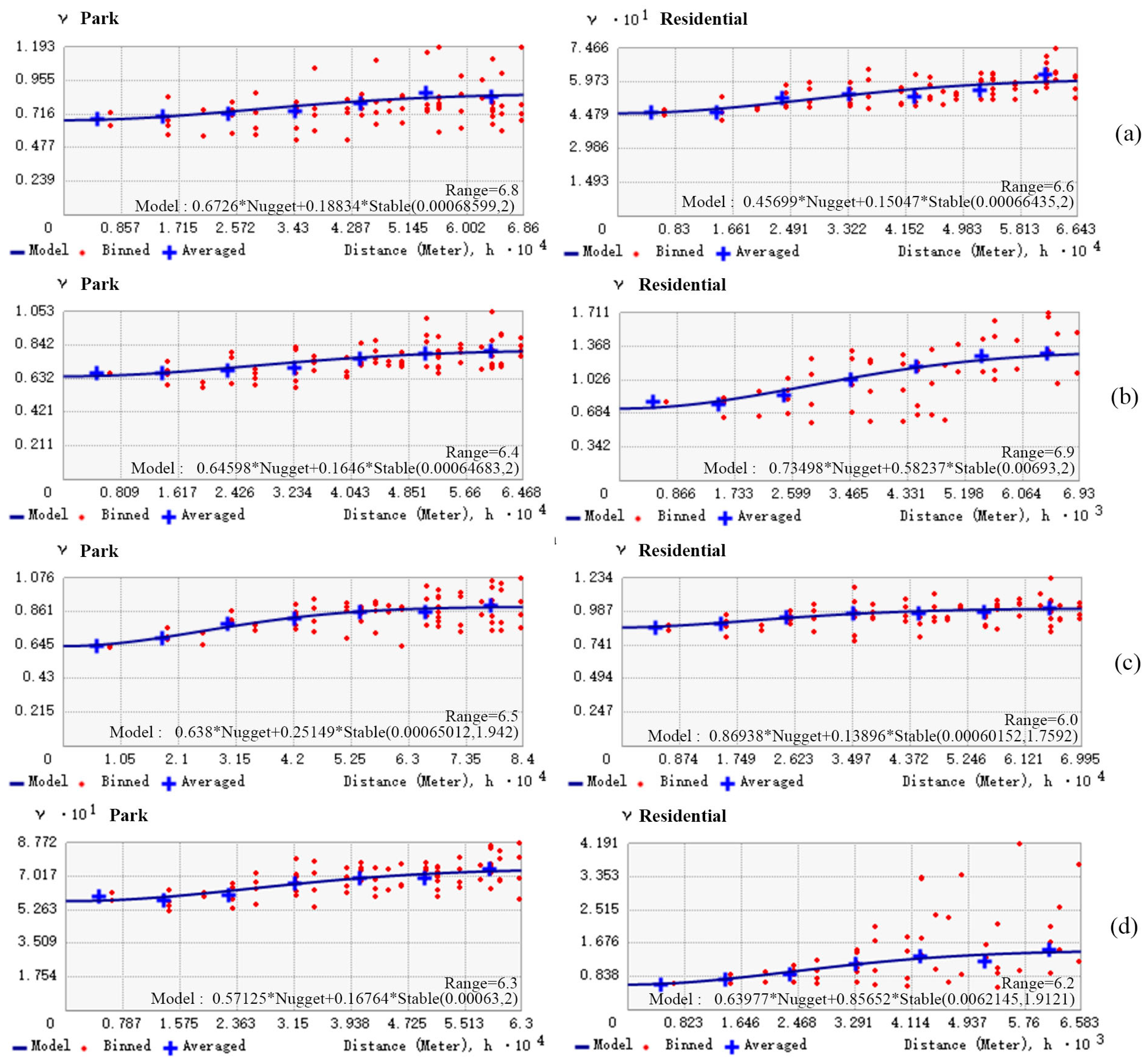
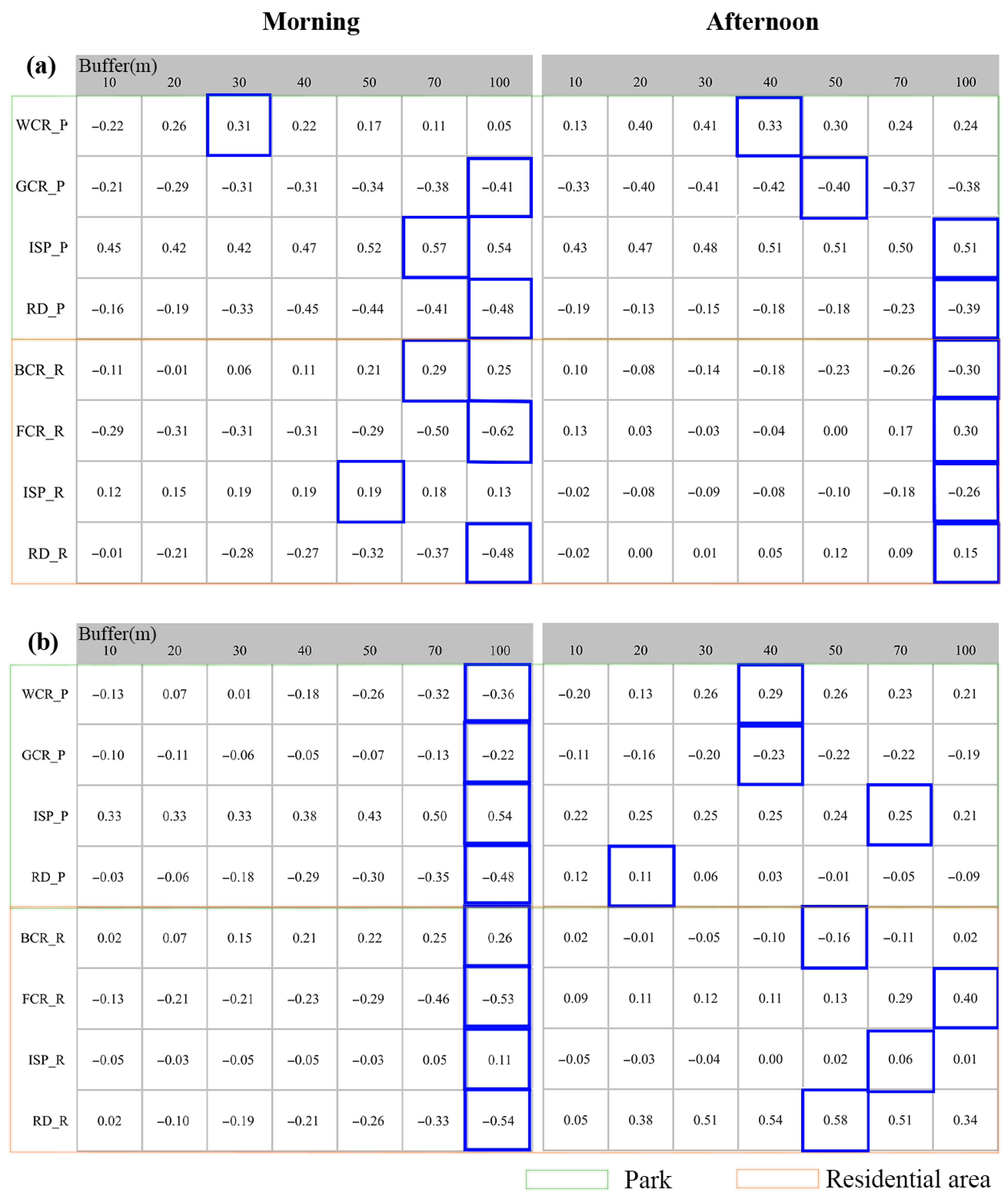
3.2. Optimal Buffer
3.3. Model Performance Comparison
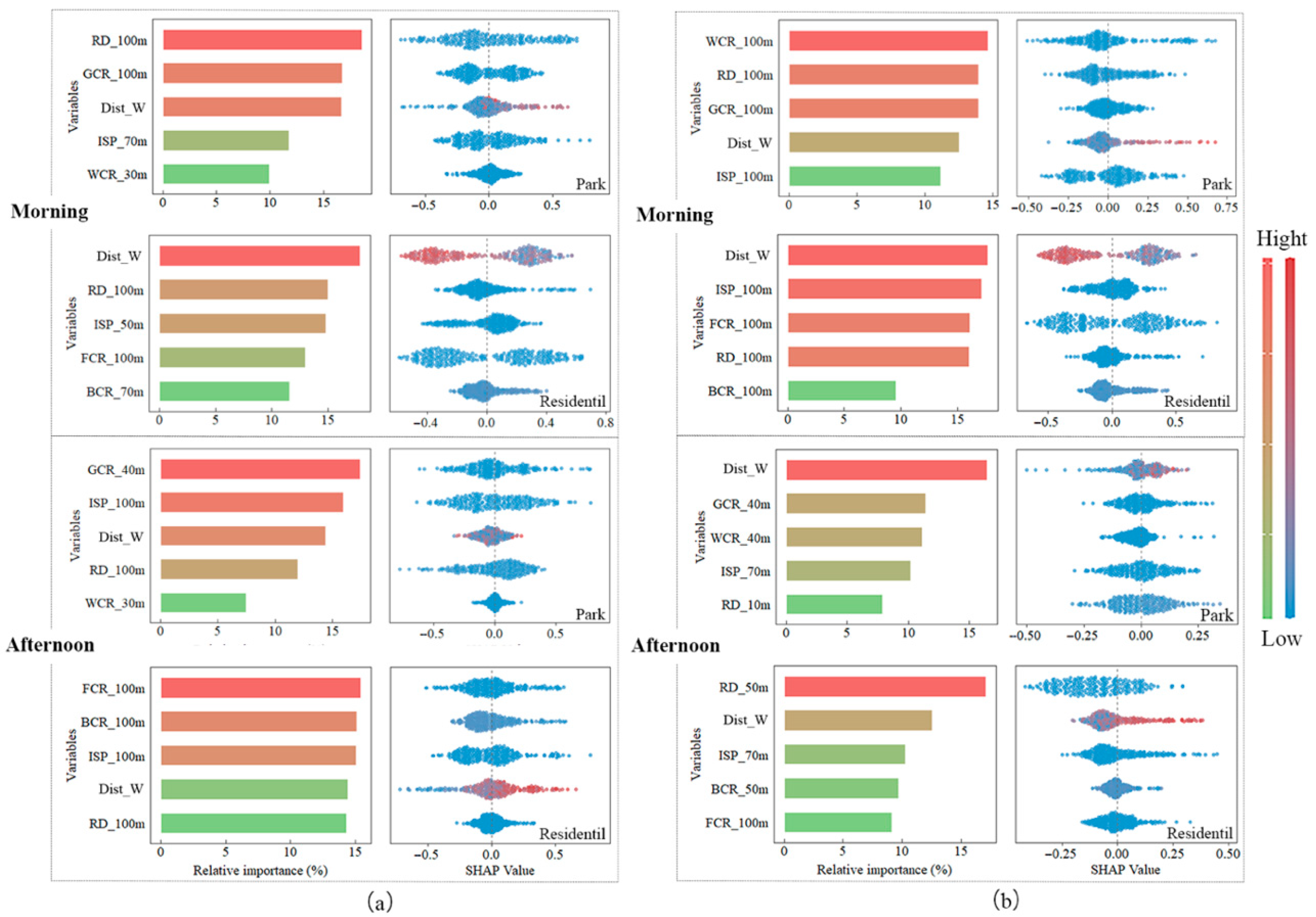
3.4. Identification of Dominant Driving Factors
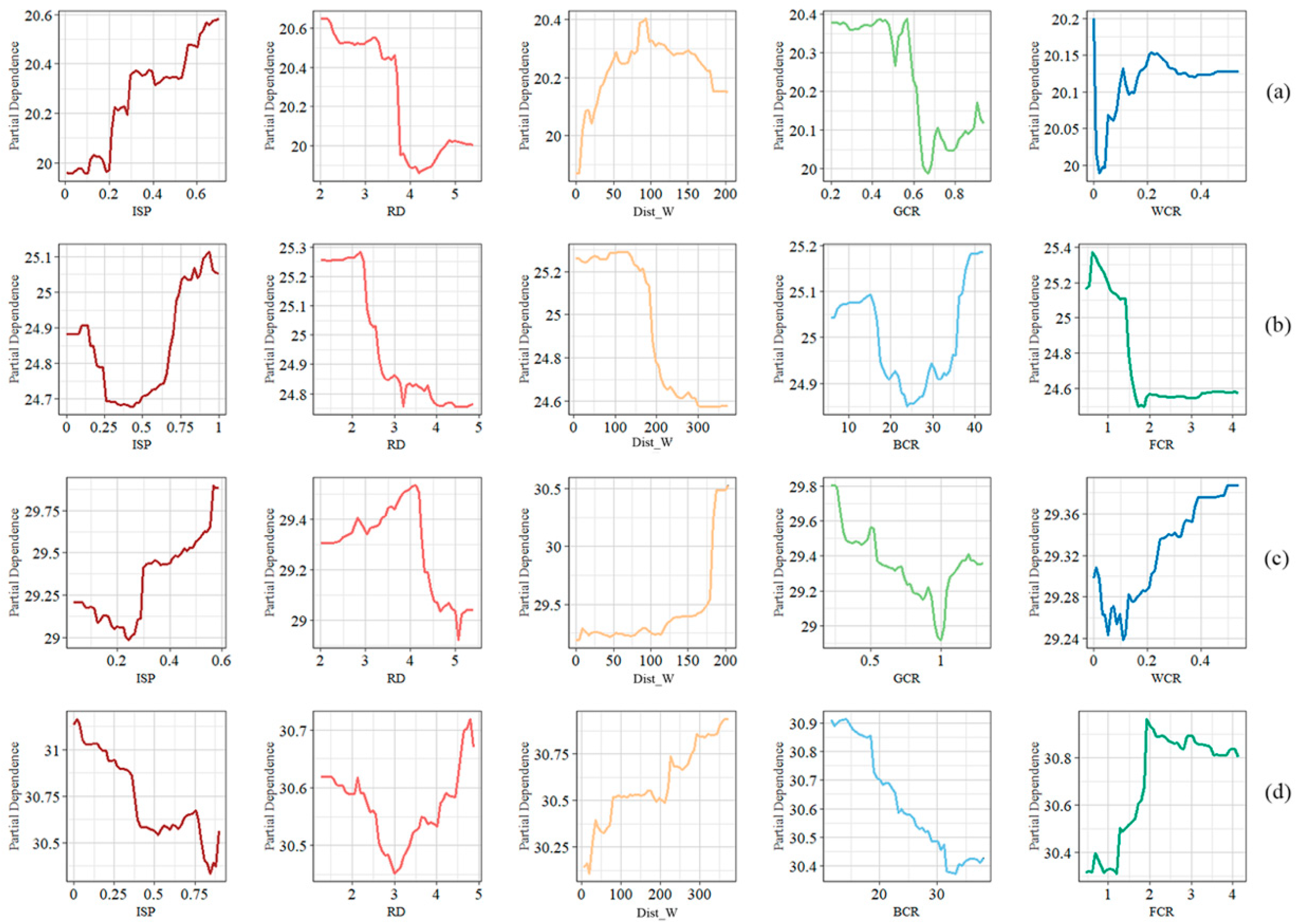
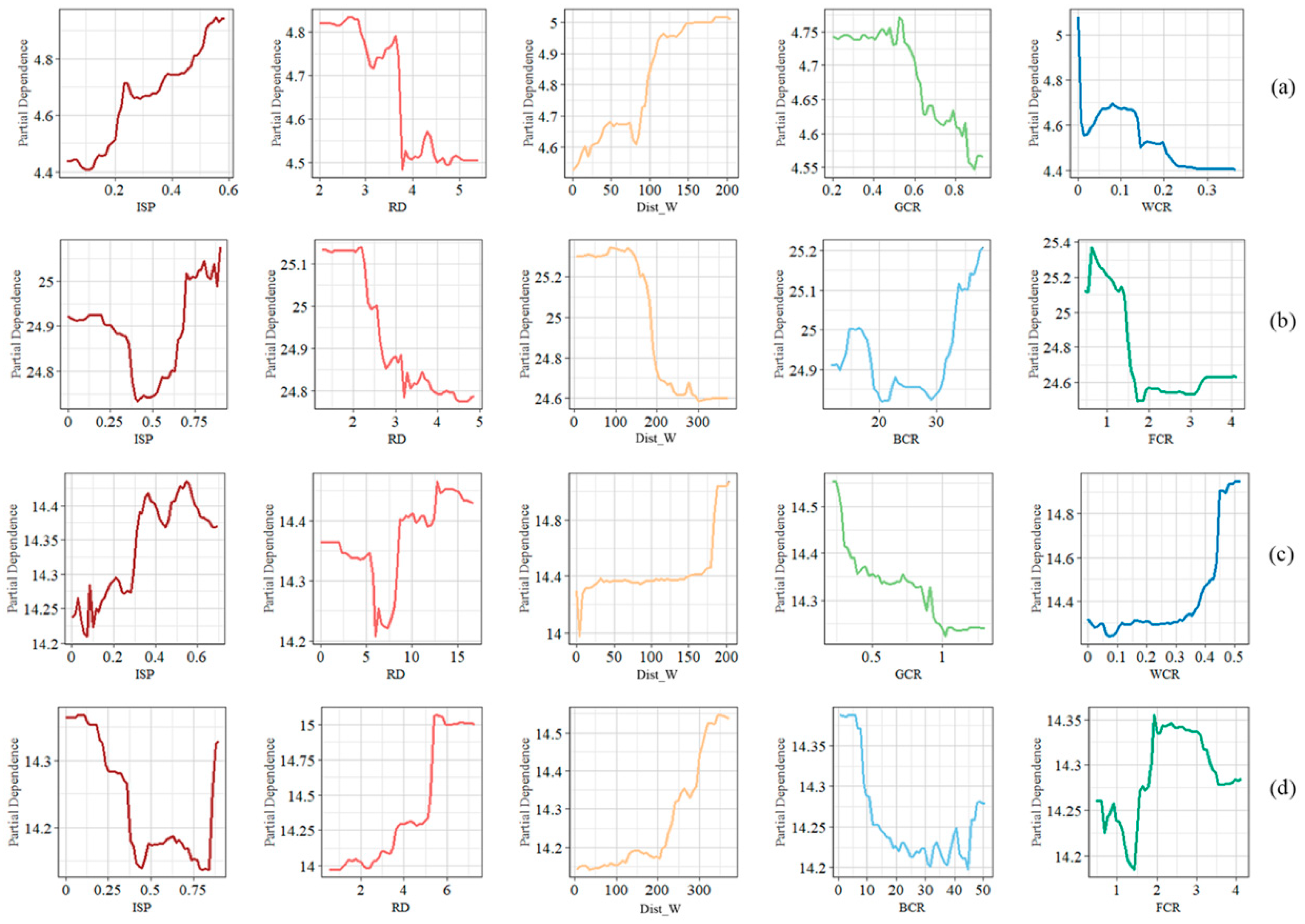
3.5. Partial Dependence and Threshold Effects of Driving Factors
4. Discussion
4.1. Differences in Optimal Spatial Scales and Variations in Ideal Spatial Scales
4.2. Comparison of Models
4.3. Divergent Dominant Factors Across Regions
4.4. Practical Implications for the Planning of Areas Adjacent to Urban Parks
4.5. Prospects and Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- United Nations Sustainable Development Goals Report. Available online: https://www.un.org/sustainabledevelopment/es/cities/ (accessed on 25 July 2025).
- Tuholske, C.; Caylor, K.; Funk, C.; Verdin, A.; Sweeney, S.; Grace, K.; Peterson, P.; Evans, T. Global urban population exposure to extreme heat. Proc. Natl. Acad. Sci. USA 2021, 118, e2024792118. [Google Scholar] [CrossRef]
- Zhang, X.; Estoque, R.C.; Murayama, Y. An urban heat island study in Nanchang City, China based on land surface temperature and social-ecological variables. Sustain. Cities Soc. 2017, 32, 557–568. [Google Scholar] [CrossRef]
- Arnett, E.B.; Hein, C.D.; Schirmacher, M.R.; Huso, M.M.; Szewczak, J.M. Evaluating the Effectiveness of an Ultrasonic Acoustic Deterrent for Reducing Bat Fatalities at Wind Turbines. PLoS ONE 2013, 8, e65794. [Google Scholar] [CrossRef]
- Nasrollahpour, R.; Skorobogatov, A.; He, J.; Valeo, C.; Chu, A.; van Duin, B. The impact of vegetation and media on evapotranspiration in bioretention systems. Urban For. Urban Green. 2022, 74, 127680. [Google Scholar] [CrossRef]
- Jiacheng, F.; Yupeng, W.; Dian, Z.; Shi-Jie, C. Impact of Urban Park Design on Microclimate in Cold Regions using newly developped prediction method. Sustain. Cities Soc. 2022, 80, 103781. [Google Scholar] [CrossRef]
- Wang, L.; Wang, W.; Tang, F.; Xu, H. Optimizing urban park cooling effects requires balancing morphological design and landscape structure. Sci. Rep. 2025, 15, 15435. [Google Scholar] [CrossRef]
- Kousis, I.; Pigliautile, I.; Pisello, A.L. Intra-urban microclimate investigation in urban heat island through a novel mobile monitoring system. Sci. Rep. 2021, 11, 9732. [Google Scholar] [CrossRef] [PubMed]
- Martins Gnecco, V.; Pigliautile, I.; Pisello, A.L. Long-Term Thermal Comfort Monitoring via Wearable Sensing Techniques: Correlation between Environmental Metrics and Subjective Perception. Sensors 2023, 23, 576. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Chen, H.; Zhou, X.; Wu, Y.; Liu, Y. Research on the relationship between urban morphology and air temperature based on mobile measurement: A case study in Wuhan, China. Urban Clim. 2020, 34, 100671. [Google Scholar] [CrossRef]
- García-Santos, V.; Sánchez, J.; Cuxart, J. Evapotranspiration Acquired with Remote Sensing Thermal-Based Algorithms: A State-of-the-Art Review. Remote Sens. 2022, 14, 3440. [Google Scholar] [CrossRef]
- Wang, X.; Rahman, M.A.; Mokroš, M.; Rötzer, T.; Pattnaik, N.; Pang, Y.; Zhang, Y.; Da, L.; Song, K. The influence of vertical canopy structure on the cooling and humidifying urban microclimate during hot summer days. Landsc. Urban Plan. 2023, 238, 104841. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, R.; Rui, J.; Yu, Y. Revealing the impact of urban spatial morphology on land surface temperature in plain and plateau cities using explainable machine learning. Sustain. Cities Soc. 2025, 118, 106046. [Google Scholar] [CrossRef]
- Anqi, Z.; Chang, X.; Weifeng, L. Relationships between 3D urban form and ground-level fine particulate matter at street block level: Evidence from fifteen metropolises in China. Build. Environ. 2022, 211, 108745. [Google Scholar] [CrossRef]
- Gongbo, C.; Shanshan, L.; Luke, D.K.; Hamm, N.A.S.; Wei, C.; Tiantian, L.; Jianping, G.; Hongyan, R.; Michael, J.A.; Yuming, G. A machine learning method to estimate PM2.5 concentrations across China with remote sensing, meteorological and land use information. Sci. Total Environ. 2018, 636, 52–60. [Google Scholar]
- Komeh, Z.; Hamzeh, S.; Memarian, H.; Attarchi, S.; Alavipanah, S.K. A Remote Sensing Approach to Spatiotemporal Analysis of Land Surface Temperature in Response to Land Use/Land Cover Change via Cloud Base and Machine Learning Methods, Case Study: Sari Metropolis, Iran. Int. J. Environ. Res. 2025, 19, 98. [Google Scholar] [CrossRef]
- Tanoori, G.; Soltani, A.; Modiri, A. Machine Learning for Urban Heat Island (UHI) Analysis: Predicting Land Surface Temperature (LST) in Urban Environments. Urban Clim. 2024, 55, 101962. [Google Scholar] [CrossRef]
- McCarty, D.; Lee, J.; Kim, H.W. Machine Learning Simulation of Land Cover Impact on Surface Urban Heat Island Surrounding Park Areas. Sustainability 2021, 13, 12678. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, C.; Li, J.; Gao, M.; Ma, R. Assessing the cooling efficiency of urban parks using data envelopment analysis and remote sensing data. Theor. Appl. Climatol. 2021, 145, 903–916. [Google Scholar] [CrossRef]
- ElTaweel, M.H.; Alfaro, S.C.; Siour, G.; Coman, A.; Robaa, S.M.; Wahab, M.M.A. Prediction and forecast of surface wind using ML tree-based algorithms. Meteorol. Atmos. Phys. 2023, 136, 1. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, J. Green and grey cooling: Mitigating pedestrians perceived temperature via urban shades. Build. Environ. 2025, 285, 113585. [Google Scholar] [CrossRef]
- Tsin, P.K.; Knudby, A.; Krayenhoff, E.S.; Ho, H.C.; Brauer, M.; Henderson, S.B. Microscale mobile monitoring of urban air temperature. Urban Clim. 2016, 18, 58–72. [Google Scholar] [CrossRef]
- Lam, C.K.C.; Alnaqshabandy, H.; Lewin, S.; Morewood, J.; Xie, X.; Goodhew, S. Making intra-urban monitoring ‘a walk in the park’: A mobile monitoring approach for assessing pedestrians’ environmental conditions. Build. Environ. 2025, 284, 113487. [Google Scholar] [CrossRef]
- Kousis, I.; Pigliautile, I.; Pisello, A.L. Investigating the intra-urban thermal and air quality environment: New transect sensing methodology and measurements. Measurement 2023, 219, 113210. [Google Scholar] [CrossRef]
- Huang, C.; Hu, T.; Duan, Y.; Li, Q.; Chen, N.; Wang, Q.; Zhou, M.; Rao, P. Effect of urban morphology on air pollution distribution in high-density urban blocks based on mobile monitoring and machine learning. Build. Environ. 2022, 219, 109173. [Google Scholar] [CrossRef]
- Rivera, M.; Basagaña, X.; Aguilera, I.; Agis, D.; Bouso, L.; Foraster, M.; Medina-Ramón, M.; Pey, J.; Künzli, N.; Hoek, G. Spatial distribution of ultrafine particles in urban settings: A land use regression model. Atmos. Environ. 2012, 54, 657–666. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, J.; Xie, S.; Chen, X. Study on the Spatial and Temporal Distribution of Thermal Comfort and Its Influencing Factors in Urban Parks. Atmosphere 2024, 15, 183. [Google Scholar] [CrossRef]
- Ferreira, L.S.; Duarte, D.H.S. Exploring the relationship between urban form, land surface temperature and vegetation indices in a subtropical megacity. Urban Clim. 2019, 27, 105–123. [Google Scholar] [CrossRef]
- Fan, J.; Chen, X.; Xie, S.; Du, K. Mediating effect of air pollutants on urban morphology and air temperature. Atmos. Pollut. Res. 2025, 16, 102426. [Google Scholar] [CrossRef]
- Yan, H.; Fan, S.; Guo, C.; Hu, J.; Dong, L. Quantifying the Impact of Land Cover Composition on Intra-Urban Air Temperature Variations at a Mid-Latitude City. PLoS ONE 2014, 9, e102124. [Google Scholar] [CrossRef] [PubMed]
- Ulpiani, G. On the linkage between urban heat island and urban pollution island: Three-decade literature review towards a conceptual framework. Sci. Total Environ. 2020, 751, 141727. [Google Scholar] [CrossRef]
- Liu, X.; Chen, X.; Tian, M.; De Vos, J. Effects of buffer size on associations between the built environment and metro ridership: A machine learning-based sensitive analysis. J. Transp. Geogr. 2023, 113, 103730. [Google Scholar] [CrossRef]
- James, P.; Berrigan, D.; Hart, J.E.; Aaron Hipp, J.; Hoehner, C.M.; Kerr, J.; Major, J.M.; Oka, M.; Laden, F. Effects of buffer size and shape on associations between the built environment and energy balance. Health Place 2014, 27, 162–170. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, Y.; Zheng, Z.; Huang, Q.; Wu, Z. Application of building geometry indexes to assess the correlation between buildings and air temperature. Build. Environ. 2020, 167, 106477. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Z.; Hu, D. Effects of urban morphology on thermal comfort at the micro-scale. Sustain. Cities Soc. 2022, 86, 104150. [Google Scholar] [CrossRef]
- Yang, C.; Kui, T.; Zhou, W.; Fan, J.; Pan, L.; Wu, W.; Liu, M. Impact of refined 2D/3D urban morphology on hourly air temperature across different spatial scales in a snow climate city. Urban Clim. 2023, 47, 101404. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; Liu, W.; Tan, Z.; Hu, S.; Ao, Z.; Li, J.; Xing, H. Exploring the seasonal effects of urban morphology on land surface temperature in urban functional zones. Sustain. Cities Soc. 2024, 103, 105268. [Google Scholar] [CrossRef]
- Zhou, D.; Bonafoni, S.; Zhang, L.; Wang, R. Remote sensing of the urban heat island effect in a highly populated urban agglomeration area in East China. Sci. Total Environ. 2018, 628-629, 415–429. [Google Scholar] [CrossRef] [PubMed]
- Qian, W.; Li, X. A cold island connectivity and network perspective to mitigate the urban heat island effect. Sustain. Cities Soc. 2023, 94, 104525. [Google Scholar] [CrossRef]
- Teufel, B.; Sushama, L.; Poitras, V.; Dukhan, T.; Bélair, S.; Miranda-Moreno, L.; Sun, L.; Sasmito, A.P.; Bitsuamlak, G. Impact of COVID-19-Related Traffic Slowdown on Urban Heat Characteristics. Atmosphere 2021, 12, 243. [Google Scholar] [CrossRef]
- Gao, J.; Gong, J.; Yang, J.; Li, J.; Li, S. Measuring Spatial Connectivity between patches of the heat source and sink (SCSS): A new index to quantify the heterogeneity impacts of landscape patterns on land surface temperature. Landsc. Urban Plan. 2022, 217, 104260. [Google Scholar] [CrossRef]
- Chen, S.; Feng, Y.; Guan, C.; Xu, Y.; Tan, Q.; Li, Y.; Yang, X. Machine learning approaches to predicting urban park attractiveness: Insights from Shanghai and Tokyo. Urban For. Urban Green. 2025, 112, 128921. [Google Scholar] [CrossRef]
- Han, L.; Zhao, J.; Gao, Y.; Gu, Z. Prediction and evaluation of spatial distributions of ozone and urban heat island using a machine learning modified land use regression method. Sustain. Cities Soc. 2022, 78, 103643. [Google Scholar] [CrossRef]
- Kammuang-Lue, N.; Sakulchangsatjatai, P.; Sangnum, P.; Terdtoon, P. Influences of population, building, and traffic densities on urban heat island intensity in Chiang Mai City, Thailand. Therm. Sci. 2015, 19, 445–455. [Google Scholar] [CrossRef]
- Elmarakby, E.; Elkadi, H. Impact of urban morphology on Urban Heat Island in Manchester’s transit-oriented development. J. Clean. Prod. 2023, 434, 140009. [Google Scholar] [CrossRef]
- Wen, C.; Mamtimin, A.; Feng, J.; Wang, Y.; Yang, F.; Huo, W.; Zhou, C.; Li, R.; Song, M.; Gao, J.; et al. Diurnal Variation in Urban Heat Island Intensity in Birmingham: The Relationship between Nocturnal Surface and Canopy Heat Islands. Land 2023, 12, 2062. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Zhang, C.; He, W. Influence of spatiotemporal changes of impervious surface on the urban thermal environment: A case of Huai’an central urban area. Sustain. Cities Soc. 2022, 79, 103710. [Google Scholar] [CrossRef]
- Duveiller, G.; Hooker, J.; Cescatti, A. The mark of vegetation change on Earth’s surface energy balance. Nat. Commun. 2018, 9, 679. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Ren, Z.; Dong, Y.; Zhang, P.; Guo, Y.; Wang, W.; Bao, G. Efficient cooling of cities at global scale using urban green space to mitigate urban heat island effects in different climatic regions. Urban For. Urban Green. 2022, 74, 127635. [Google Scholar] [CrossRef]
- Steeneveld, G.J.; Koopmans, S.; Heusinkveld, B.G.; Theeuwes, N.E. Refreshing the role of open water surfaces on mitigating the maximum urban heat island effect. Landsc. Urban Plan. 2014, 121, 92–96. [Google Scholar] [CrossRef]
- Peng, J.; Liu, Q.; Xu, Z.; Lyu, D.; Du, Y.; Qiao, R.; Wu, J. How to effectively mitigate urban heat island effect? A perspective of waterbody patch size threshold. Landsc. Urban Plan. 2020, 202, 103873. [Google Scholar] [CrossRef]
- Bavnbæk, K.F.; Thuesen, A.A. Navigating spatial justice: Exploring municipal planners’ logics in differentiated village planning. J. Rural. Stud. 2024, 114, 103496. [Google Scholar] [CrossRef]
- Li, J.; Zheng, B.; Bedra, K.B.; Li, Z.; Chen, X. Effects of residential building height, density, and floor area ratios on indoor thermal environment in Singapore. J. Environ. Manag. 2022, 313, 114976. [Google Scholar] [CrossRef] [PubMed]

| Instrument Model | Monitoring Data | Unit | Frequency of Monitoring | Precision | Image |
|---|---|---|---|---|---|
| Garmin Etrex 201 | Track recording | Track points | 1 s | 3 m |  |
| Kestrel nk5400 | Temperature | °C | 5 s | ±0.5 °C |  |
| Relative Humidity | %RH | ±0.2% RH | |||
| Kestrel nk5500 | Temperature | °C | 5 s | ±0.5 °C |  |
| Relative Humidity | m/s | ±0.2% | |||
| Wind speed | Wind direction point | ±0.3% | |||
| Wind direction | Wind direction point | 5° |
| Region | Abbreviation | Definition | Formula | Parameter |
|---|---|---|---|---|
| Park | GCR | The ratio of green space to buffer zone area in a single buffer zone | (%) | Where is the area of greening space in the i-th buffer (m2). A is the area of a buffer (m2). |
| WCR | The ratio of the area of a water body to the area of a buffer zone within a single buffer zone | (%) | Where is the area of watershed coverage of the i-th buffer (m2). | |
| Residential areas | BCR | The ratio of the total building footprint in a single buffer zone to the buffer zone area | (%) | Where Mi is the sum of the building areas of the i-th buffer (m2). |
| FCR | The ratio of the area of all floors within a single buffer zone to the area of the buffer zone | Where is the floor area of the j-th building in the i-th. Buffer (m2); is the number of floors of the j-th building. | ||
| Park/Residential | ISP | The ratio of the impervious area within a single buffer zone to the buffer zone area | (%) | Where is the sum of the impervious surface are of the i-th buffer (m2). |
| RD | The ratio of the length of the road in a single buffer zone to the area of the buffer zone | (m/m2) | Where is the sum of the lengths of all roads in the i-th buffer (m). | |
| Dist_W | The closest distance a single buffer is from a body of water | Where is the Euclidean distance between the i-th buffer zone and the k-th water area (m). |
| Name | Abbreviation | Description |
|---|---|---|
| Random Forest | RF | Constructs multiple decision trees and combines their results to reduce variance. |
| Extreme Gradient Boosting | XGBoost | Uses regularization and parallel computing to enhance performance. |
| Light Gradient Boosting Machine | LightGBM | Improves speed and performance through histogram optimization and parallel computing. |
| Date | Temperature | Weather | Wind Speed | Morning Monitoring Period | Afternoon Monitoring Period |
|---|---|---|---|---|---|
| 2 July 2023 | 16–25 °C | sunny | 1–3 level | 8:30:00–10:53:20 | 15:00:00–17:18:05 |
| 3 July 2023 | 17–31 °C | sunny | 1–3 level | 8:30:00–10:49:05 | 15:00:00–17:19:25 |
| 4 July 2023 | 20–29 °C | sunny | 1–3 level | 8:30:00–10:48:25 | 15:00:00–17:22:10 |
| 5 July 2023 | 20–31 °C | sunny | 2–4 level | 8:30:00–10:48:00 | 15:00:00–17:15:30 |
| 6 July 2023 | 19–30 °C | sunny | 1–4 level | 8:30:00–10:50:50 | 15:00:00–17:21:20 |
| 1 October 2023 | 3–12 °C | sunny | 1–3 level | 8:30:00–10:52:20 | 15:00:00–17:20:30 |
| 2 October2023 | 4–14 °C | sunny | 1–3 level | 8:30:00–10:48:10 | 15:00:00–17:15:45 |
| 3 October2023 | 5–16 °C | sunny | 1–3 level | 8:30:00–10:50:25 | 15:00:00–17:23:15 |
| Morning | Afternoon | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| LM | LightGBM | RF | XGBoost | LM | LightGBM | RF | XGBoost | ||
| Park | 0.216 | 0.713 | 0.678 | 0.629 | 0.251 | 0.220 | 0.531 | 0.520 | |
| RMSE | 0.785 | 0.475 | 0.492 | 0.553 | 0.785 | 0.801 | 0.630 | 0.640 | |
| 5-fold CV | 0.201 | 0.612 | 0.625 | 0.585 | 0.301 | 0.209 | 0.529 | 0.511 | |
| RMSE | 0.782 | 0.474 | 0.498 | 0.568 | 0.779 | 0.798 | 0.621 | 0.662 | |
| Time Cost | 0.1 s | 2.86 s | 2.33 s | 13.21 s | 0.1 s | 2.37 s | 2.25 | 13.60 s | |
| Residential | 0.493 | 0.714 | 0.775 | 0.736 | 0.233 | 0.476 | 0.492 | 0.462 | |
| RMSE | 0.654 | 0.499 | 0.433 | 0.433 | 0.685 | 0.583 | 0.548 | 0.580 | |
| 5-fold CV | 0.312 | 0.682 | 0.763 | 0.697 | 0.221 | 0.402 | 0.483 | 0.460 | |
| RMSE | 0.597 | 0.527 | 0.429 | 0.434 | 0.703 | 0.592 | 0.551 | 0.577 | |
| Time Cost | 0.2 s | 2.33 s | 2.45 s | 13.05 s | 0.1 s | 2.49 s | 2.34 s | 13.51 s | |
| Morning | Afternoon | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| LM | LightGBM | RF | XGBoost | LM | LightGBM | RF | XGBoost | ||
| Park | 0.396 | 0.575 | 0.601 | 0.746 | 0.074 | 0.251 | 0.358 | 0.303 | |
| RMSE | 0.540 | 0.451 | 0.438 | 0.470 | 0.515 | 0.456 | 0.419 | 0.452 | |
| 5-fold CV | 0.235 | 0.485 | 0.582 | 0.632 | 0.162 | 0.214 | 0.349 | 0.294 | |
| RMSE | 0.526 | 0.453 | 0.427 | 0.532 | 0.507 | 0.477 | 0.417 | 0.477 | |
| Time Cost | 0.1 s | 2.31 s | 2.33 s | 13.21 s | 0.05 s | 2.55 s | 2.31 s | 13.60 s | |
| Residential | 0.517 | 0.783 | 0.756 | 0.580 | 0.580 | 0.764 | 0.782 | 0.773 | |
| RMSE | 0.645 | 0.435 | 0.450 | 0.424 | 0.424 | 0.327 | 0.321 | 0.326 | |
| 5-fold CV | 0.434 | 0.774 | 0.714 | 0.522 | 0.492 | 0.721 | 0.770 | 0.752 | |
| RMSE | 0.582 | 0.459 | 0.447 | 0.424 | 0.533 | 0.334 | 0.319 | 0.325 | |
| Time Cost | 0.1 s | 2.29 s | 2.85 s | 13.63 s | 0.1 s | 2.08 s | 2.24 s | 13.23 s | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Chen, X.; Xie, S. Comparing Multiple Machine Learning Models to Investigate Thermal Drivers in an Arid-Oasis Urban Park and Its Surroundings Using Mobile Monitoring. Appl. Sci. 2025, 15, 11417. https://doi.org/10.3390/app152111417
Feng Y, Chen X, Xie S. Comparing Multiple Machine Learning Models to Investigate Thermal Drivers in an Arid-Oasis Urban Park and Its Surroundings Using Mobile Monitoring. Applied Sciences. 2025; 15(21):11417. https://doi.org/10.3390/app152111417
Chicago/Turabian StyleFeng, Yunyao, Xuegang Chen, and Siqi Xie. 2025. "Comparing Multiple Machine Learning Models to Investigate Thermal Drivers in an Arid-Oasis Urban Park and Its Surroundings Using Mobile Monitoring" Applied Sciences 15, no. 21: 11417. https://doi.org/10.3390/app152111417
APA StyleFeng, Y., Chen, X., & Xie, S. (2025). Comparing Multiple Machine Learning Models to Investigate Thermal Drivers in an Arid-Oasis Urban Park and Its Surroundings Using Mobile Monitoring. Applied Sciences, 15(21), 11417. https://doi.org/10.3390/app152111417





