Abstract
Driver fatigue is a critical factor contributing to traffic accidents. Therefore, real-time and accurate recognition of driver fatigue states holds significant importance. This paper proposes a novel driver fatigue detection method based on electroencephalogram (EEG) signals and an Interpretable Dynamic System Recurrent Network (IDSRN). The IDSRN integrates the temporal modeling capability of traditional Recurrent Neural Networks (RNNs) with the nonlinear function approximation advantages of polynomial networks, enabling effective extraction of nonlinear dynamic features from EEG signals. This study collected EEG data from drivers under varying fatigue states and constructed input vectors suitable for classification tasks through preprocessing and feature extraction. The extracted features were subsequently fed into the IDSRN model for training and testing, with comparative analyses conducted against traditional methods (e.g., SVM, CNN, and standard RNN). Experimental results demonstrate that the IDSRN outperforms other models in recognition accuracy (average: 92.3%), convergence speed, and robustness, significantly improving the efficacy of driver fatigue-state identification.
1. Introduction
With the rapid expansion of road transportation networks and continuous growth in vehicle ownership, traffic safety issues have become increasingly prominent. According to statistics, approximately 1.35 million people die annually in traffic accidents worldwide, among which fatigued driving is recognized as one of the leading causes of severe traffic accidents, accounting for about 20–30% of all road traffic incidents [1]. In a fatigued state, drivers exhibit significantly reduced attention levels, prolonged reaction times, and impaired judgment, with potential occurrences of brief “micro-sleep” episodes. These declines in physiological and cognitive functions substantially increase the risk of traffic accidents. Particularly in scenarios such as long-haul transportation, night driving, and highway operations, fatigued driving poses severe threats to road safety, with significant economic and human costs.
Real-time and accurate assessment of driver fatigue states is critical for preventing traffic accidents and ensuring road safety. Traditional fatigue detection methods primarily rely on vehicle kinematic parameters (e.g., steering wheel operations and lane departures) and driver facial features (e.g., PERCLOS and blink frequency). However, these approaches are susceptible to environmental lighting conditions, camera angles, and individual driving habits, often detecting fatigue only at advanced stages and lacking timeliness and accuracy in early warnings. In contrast, electroencephalogram (EEG)-based fatigue detection methods have emerged as a research hotspot due to their direct reflection of brain neural activity, high temporal resolution, and non-invasiveness. EEG signals objectively capture changes in cortical electrical activity, providing reliable physiological indicators for fatigue states. Notably, because EEG features often manifest earlier than behavioral changes during the initial stages of attention lapses or increased cognitive load, they provide an earlier opportunity for fatigue detection.
Nevertheless, EEG-based driver fatigue detection faces multiple technical challenges. Firstly, EEG signals exhibit inherent nonlinearity and non-stationarity, with complex dynamic patterns that evolve as fatigue progresses, presenting challenges for traditional linear analytical methods. Secondly, EEG signals are vulnerable to environmental noise and physiological artifacts (e.g., eye movements and electromyographic interference), reducing the stability and reliability of feature extraction. Thirdly, significant physiological variations among individuals limit the generalization capability of EEG-based fatigue models across subjects. Additionally, existing methods often fail to balance recognition accuracy and computational efficiency in feature engineering and model design. Particularly in real-time monitoring scenarios, models must achieve rapid and accurate fatigue-state identification under constrained computational resources.
To address these challenges, researchers have proposed diverse EEG-based fatigue detection methods, broadly categorized into (1) feature engineering and traditional machine learning, (2) deep learning, and (3) ensemble learning. Feature engineering and traditional machine learning methods typically follow a “feature extraction-feature selection-classifier training” pipeline, requiring manual feature engineering based on domain expertise. For example, Guo et al. [2] used differential evolution to select EEG channels and build functional brain networks, then applied a reversible-jump MCMC sampler to choose optimal features, achieving 96.11% accuracy on SEED-VIG with KNN. Subasi et al. [3] combined FAWT with multiboosting and reached 97.1%/97.9% accuracy for fatigue vs. rest. Hasan et al. [4] trained DT/KNN/RF on 76 subject features and reported 88.61% (4-class) and 88.21% (binary) accuracy. Mu et al. [5] fed combined-entropy features into an SVM and obtained 98.75% accuracy. Lan et al. [6] fused EEG with vehicle motion, extracted band-energy ratio and sample entropy, and attained 92.37% with SVM. Zhang et al. [7]. used PCA-fused complex-network and spatio-spectral features and reached 99.23% with a Gaussian SVM. Wang et al. [8] applied a wavelet-scattering network plus SVM and achieved 99.33% in real-driving tests. Although fast and light, these approaches depend heavily on expert features and generalize poorly across subjects.
In recent years, with advancements in deep learning, researchers have explored end-to-end fatigue recognition methods that automatically learn features directly from raw EEG signals. These approaches primarily include Convolutional Neural Networks (CNNs), Recurrent Neural Networks (RNNs), and their variants, as well as hybrid architectures. For instance, Wang et al. [9] fed CWT maps to a CNN and obtained 88.85% accuracy without hand features. Sheykhivand et al. [10] used a CNN-LSTM and outperformed manual pipelines. Xu et al. [11] unified CNN-attention for authentication (98.5%) and fatigue detection (97.8%). Siddhad et al. [12] equipped NLMDA-Net with channel- and depth-attention and reached 83.71% on SEED-VIG. Yu et al. [13] fused EEG and eye movements in an attention CNN-LSTM and confirmed fatigue-related performance drops. Alghanim et al. [14] applied an Inception-dilated ResNet to spectrograms and achieved 98.87%/82.73% on Figshare/SEED-VIG. Ye et al. [15] generated synthetic EEG with CA-ACGAN to enrich training. Zorzos et al. [16] combined Morlet-wavelet features with a shallow CNN, reached 97% accuracy, and used SHAP to highlight theta/alpha importance. Li et al. [17] proposed a CNN-RNN channel-weighted residual net after non-smooth NMF and attained 97.23%. Liu et al. [18] employed CEEMDAN-fuzzy-entropy on single-channel data and used self-training semi-supervision to boost accuracy. Shi et al. [19] fused EEG-EOG via CAE-CNN and used RNN, yielding RMSE/COR = 0.08/0.96 on SEED-VIG. Jeong et al. [20] classified pilot drowsiness with a deep spatio-temporal Bi-LSTM. Despite high accuracy, these models are large, costly to train, prone to overfit on small datasets, and offer limited interpretability.
To overcome the limitations of single models and leverage the advantages of diverse algorithms, researchers have increasingly turned to ensemble learning methods, which enhance overall performance and robustness by combining predictions from multiple base learners. For instance, Fan et al. [21] extracted energy/entropy from forehead EEG and used time-series ensemble to outperform SVM, KNN, DT, and LSTM. Hasan et al. [22] compared RUSBoosted trees and random-subspace discriminant on FFT features, with RUSBoosted reaching 98.53%. Rao et al. [23] built Pearson-based brain networks, computed six graph features, and combined them with Bagged/RSM/RUSBoosted trees; RSM with degree centrality achieved 90.35% on 24 subjects. Sedik et al. [24] combined FFT-DWT denoising with ML-DL ensembles and reported 90%/96% accuracy for multi-class/binary tasks. Wang et al. [25] used wavelet-entropy complex networks with CNN-LSTM and attained 99.39%. These ensembles, however, are computationally heavy, difficult to interpret, and require careful design to avoid overfitting, limiting real-time deployment.
Existing methods have achieved certain results, but still face the following key challenges. First, EEG signals are inherently highly nonlinear time-series signals, and existing models struggle to fully capture their temporal evolution patterns. Second, manual feature engineering relies on expert knowledge, while most deep learning models fail to effectively integrate spatial and temporal dimensional information. Third, many deep learning models are considered “black boxes,” lacking intuitive explanations for the mechanisms of emotional state changes.
To address these issues, this paper proposes an innovative Interpretable Dynamic System Recurrent Network (IDSRN), which introduces a recurrent mechanism into a polynomial network (PN) to effectively model nonlinear temporal features in EEG signals. This method addresses the shortcomings of existing models in mining temporal evolution patterns of EEG signals while possessing the ability to automatically extract high-order features, avoiding complex manual feature engineering. The interpretability of the IDSRN stems from the polynomial structure obtained from Laplace transforms of differential equations in general physical systems. This polynomial approximation-based design gives the IDSRN, as a polynomial network, inherent mathematical clarity in expression, facilitating analysis of the intrinsic mechanisms of emotional state changes and feature interactions. Additionally, the IDSRN has a concise structure with fewer parameters, offering better lightweight characteristics compared to traditional deep learning models, making it suitable for deployment in resource-constrained embedded systems and enhancing its practicality and deployment flexibility. The major contributions of this paper are as follows:
- This paper proposes a novel neural network structure that combines recurrent mechanisms with polynomial network approximation ideas, namely the Interpretable Dynamic System Recurrent Network (IDSRN). This structure combines the polynomial approximation capability of PN with temporal modeling capability, effectively capturing nonlinear dynamic features in EEG signals and addressing the shortcomings of existing models in mining EEG temporal evolution patterns.
- The IDSRN inherits the mathematical interpretability advantages of MTN. Its polynomial structure originates from the Laplace transform form of differential equations in physical systems, providing clear algebraic expressiveness. This design not only gives the model good classification performance but also provides an intuitive mathematical explanation path for changes in pilots’ emotional states, enhancing the model’s credibility and practicality.
- This paper proposes an EEG-based driver fatigue detection system using the Interpretable Dynamic System Recurrent Network (IDSRN). Experiments demonstrate that the IDSRN model outperforms traditional methods (such as SVM, CNN, and RNN) in terms of recognition accuracy, convergence speed, and robustness. Furthermore, the IDSRN features a concise architecture with fewer parameters, which reduces computational overhead and makes it well-suited for deployment in resource-constrained embedded systems, thereby enhancing its practicality and deployment flexibility in real-world driving environments.
The remaining sections of this paper are organized as follows. Section 2 elaborates on the theoretical foundations and model architecture of the Interpretable Dynamic System Recurrent Network (IDSRN), introducing its core components, training methods, and theoretical basis for interpretability. Section 3 explores EEG signal-based fatigue analysis methods, including discrete wavelet transform feature extraction and the IDSRN fatigue classification workflow. Section 4 experimentally validates the effectiveness of the IDSRN model, demonstrating its performance on the SEED-VIG dataset and conducting comparative analysis with traditional methods. Section 5 summarizes the research content of the full text, highlighting the innovative value and application prospects of the IDSRN in driver fatigue detection.
2. The IDSRN Model
2.1. Model Architecture and Core Components
To effectively model the nonlinear characteristics of fatigue-state evolution over time, the proposed Interpretable Dynamic System Recurrent Network (IDSRN) introduces a recurrent mechanism based on the traditional Multidimensional Taylor Network (MTN), combining polynomial expansion structures with temporal memory capabilities to significantly enhance recognition performance for dynamic physiological signals. The overall architecture of the IDSRN consists of four key components: the input layer, polynomial expansion layer, recurrent hidden layer, and output classification layer, as illustrated in Figure 1.
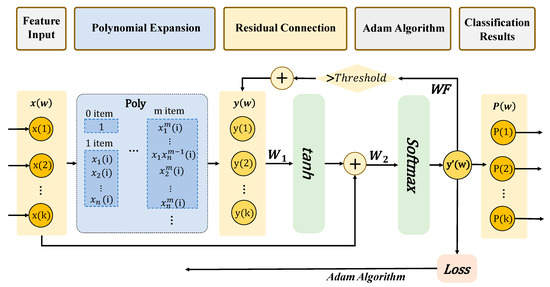
Figure 1.
The architecture of the IDSRN model.
As shown, the model illustrates four core components and their information flow paths: (a) the input layer receives extracted EEG features; (b) the polynomial expansion layer generates second-order nonlinear interaction terms; (c) the recurrent hidden layer integrates historical states via a gating mechanism; and (d) the output layer produces fatigue probability distributions via Softmax. Arrows indicate forward propagation, and dashed boxes denote recursive updates across time steps, highlighting the model’s ability to capture temporal dependencies.
2.1.1. Input Representation
Let the input sequence represent a physiological signal feature sequence of length T, where the input vector at each time step is , with being the feature dimension (e.g., power spectral density, Hjorth parameters, etc., extracted from EEG signals).
2.1.2. Polynomial Expansion Layer
The first layer of the IDSRN is the polynomial expansion layer, which performs a nonlinear mapping of input features to enhance the model’s fitting capability. Specifically, this layer generates all input variable combinations up to order n [4]:
where denotes the k-th order polynomial combination term, for example, when n = 2, includes all second-order terms and second-order interaction terms . Polynomial expansion enables the model to effectively capture high-order correlations among features without increasing the number of neurons, thereby improving its ability to model complex physiological signal variation patterns.
2.1.3. Nonlinear Activation Function
To further enhance the model’s nonlinear modeling capability, the IDSRN introduces an activation function σ(⋅) (e.g., ReLU or Leaky ReLU) after polynomial expansion [26]:
where is the weight matrix, is the bias vector, is the total number of polynomial terms, and is the output dimension. The activation function allows the model to learn more complex decision boundaries while mitigating computational complexity issues caused by high-order polynomials.
2.1.4. Recurrent Hidden Layer
The core innovation of the IDSRN lies in combining polynomial features with a recurrent mechanism. At each time step t, the current input features and historical state jointly update the hidden state:
where is the hidden state at step , and are the weight matrices for the current input and historical states, respectively, and is the bias term. This recursive update mechanism enables the model to retain memory of dynamic characteristics in time-series data, making it particularly suitable for capturing the gradual evolution of fatigue states over time.
2.1.5. Output Layer and Classification Mechanism
The final output is normalized into a probability distribution via the Softmax function [27]:
where and are the output layer parameters, and represents the predicted probability distribution of fatigue categories at step . Through this structural design, the IDSRN not only inherits the powerful nonlinear fitting capability of polynomial networks but also benefits from the temporal modeling advantages of recurrent mechanisms, demonstrating strong performance in fatigue diagnosis tasks.
2.2. Training Methods of the IDSRN Model
The IDSRN is designed to address key challenges in fatigue recognition tasks, including the complex nonlinear characteristics of physiological signals, significant temporal evolution patterns, and substantial inter-individual variability. To optimize model performance, we employ not only the classical Back Propagation (BP) algorithm combined with the Adam optimizer but also implement multiple task-specific adaptations to enhance robustness and generalization capability.
Fatigue recognition tasks typically involve multiple progressively evolving states (e.g., alert → mild fatigue → severe fatigue) with ambiguous inter-class boundaries and frequently imbalanced sample distributions (e.g., significantly more normal state samples than severe fatigue samples). To mitigate bias caused by class imbalance, this study adopts a weighted cross-entropy loss function:
where represents the weight assigned to the i-th class, which is adjusted based on the frequency of each class in the training set. This weighting mechanism ensures the model pays greater attention to minority classes (e.g., severe fatigue) during training.
Due to the inclusion of both polynomial expansion layers and recurrent mechanisms in the IDSRN’s architecture, parameter updates during training may encounter gradient explosion or vanishing issues, particularly when processing longer EEG sequences. To address this, we employ the Adam optimizer for parameter updates with an initial learning rate of 0.001. The Adam optimizer adaptively adjusts learning rates based on historical gradient information, thereby accelerating convergence while maintaining stability. This approach is particularly well-suited for handling the inconsistent input distributions caused by individual variations in fatigue recognition tasks.
Specifically, the update formulas for the first-order moment and the second-order moment are as follows [26]:
where represents the gradient computed at the current iteration step. The hyperparameters and regulate the exponential decay rates for the first-moment (momentum) and second-moment (squared gradient) estimates, with conventional default values of 0.9 and 0.999. To address potential initialization bias in the early stages of training, we implement bias correction for both (first-moment estimate) and (second-moment estimate), as shown in Equations (8) and (9) [26]:
The final model parameters are updated according to the following rule:
where denotes the initial learning rate, and is a small constant to prevent division by zero. Additionally, we employ a polynomial learning rate decay strategy during training to further enhance the model’s convergence performance.
The learning rate is computed as follows:
where denotes the base learning rate, epoch corresponds to the current training iteration, specifies the total number of training epochs, and power determines the learning rate decay intensity. For our experimental configuration, we initialized the base learning rate at 0.00015, established the maximum training epochs as 250, and set the decay power parameter to 0.9. To optimize the trade-off between computational efficiency and memory utilization, we implemented categorical cross-entropy as our loss function with a batch size of 8 throughout the training process.
In our implementation, we used mini-batch gradient descent, where each iteration randomly selects a subset of samples to compute gradients and update parameters. This approach not only ensured training efficiency but also enhanced the model’s generalization capability.
Overfitting Mitigation Strategies
To mitigate the risk of overfitting, which is particularly critical when modeling high-order polynomial expansions on limited EEG data, we implemented several regularization strategies in the IDSRN architecture. We incorporate L2 regularization (weight decay) into the loss function to penalize large weight values, thereby encouraging simpler models. The regularization term is defined as follows:
where is the regularization hyperparameter, which was empirically set to 0.001. Additionally, we employ dropout with a rate of 0.2 on the recurrent hidden layer to prevent co-adaptation of neurons. These techniques collectively enhance the model’s generalization capability without significantly compromising its expressive power.
2.3. Interpretability Analysis of the IDSRN Model
The interpretability of the IDSRN stems from the polynomial structure derived from Laplace-transformed differential equations in general physical systems. This section provides rigorous mathematical derivations to elucidate the correspondence between IDSRN model parameters and the dynamic characteristics of physical systems.
Consider an n-th order linear time-invariant system described by the following differential equation:
where represents the system output (EEG signal), denotes the system input (fatigue-state stimulus), and and are system parameters. Applying Laplace transform (assuming zero initial conditions):
which yields the following transfer function:
In discrete-time systems, the hidden state update equation of the IDSRN is
Applying Z-transform to this equation:
Rearranging gives the system transfer function:
The poles of the system transfer function are the z values that make the denominator polynomial zero:
which is equivalent to
This demonstrates that the system poles are precisely the eigenvalues of the recurrent weight matrix . In EEG signal analysis, these poles carry distinct physical significance. First, the real part of the poles reflects the decay rate of neural activity. Second, the imaginary part corresponds to oscillation frequencies (such as waves in the 4–8 Hz range). Finally, the modulus of the poles determines system stability. Unlike the poles, as shown in Equation (17), the numerator polynomial of the transfer function corresponds to the input weight matrix , which determines the system’s zero locations and captures the direct relationship between different EEG frequency bands and fatigue states.
In the IDSRN model, the association between waves (4–8 Hz) and fatigue states is clearly revealed through the physical interpretability of system poles. By performing eigendecomposition of the recurrent weight matrix , where , and substituting it into the transfer function, we obtain Equation (20):
We found that its eigenvalues (i.e., system poles) exhibit a strict correspondence with the dynamic characteristics of EEG signals: when drivers are in a fatigued state, the poles associated with waves display three key features. First, the imaginary part , where “6” corresponds to the 6 HZ oscillation frequency. This is because waves fall within the 4–8 Hz range, with 6 Hz being the midpoint and likely the most prominent frequency component during fatigue. Second, the real part indicates that θ wave activity decays more slowly and persists longer. Third, the modulus shows that the system is in a critically stable state, leading to sustained enhancement of θ wave activity. This discovery not only mathematically validates the physiological consensus in neuroscience that “ wave activity increases during fatigue,” but also connects the decision-making process of deep learning models with clear physical meaning, achieving a transformation from “black box” to “white box.” As mentioned above, by analyzing the eigenvalues of , the IDSRN can not only accurately identify fatigue states but also provide a physical explanation for “why fatigue occurs” (i.e., the sustained enhancement of wave activity), offering a solution for driver fatigue monitoring systems that combines high accuracy with reliable theoretical foundations.
2.4. Evaluation Metrics
To comprehensively evaluate the performance of the proposed IDSRN model in driver fatigue classification, we employ the following evaluation metrics derived from the confusion matrix: accuracy, sensitivity (recall), and specificity. These metrics are defined as follows [27]:
Accuracy measures the overall correctness of the model:
where TP (true positives) denotes the number of samples correctly predicted as positive, TN (true negatives) denotes the number of samples correctly predicted as negative, FP (false positives) denotes the number of samples incorrectly predicted as positive, and FN (false negatives) denotes the number of samples incorrectly predicted as negative.
Sensitivity (recall) evaluates the model’s ability to correctly identify positive cases (fatigue state):
Specificity evaluates the model’s ability to correctly identify negative cases (alert state):
2.5. System Calibration and Individual Adaptation
To address the variability in EEG signals among individuals, our IDSRN model employs several calibration mechanisms. First, we apply z-score normalization to the extracted EEG features to ensure that features from different subjects have a unified statistical profile. Second, we implement an individual-based feature weighting mechanism to accommodate individual baseline patterns. Specifically, for each subject, we calculate the mean and standard deviation of each feature during the initial alert state and normalize subsequent measurements relative to these baseline values. This approach enables the model to effectively interpret changes in EEG signals relative to an individual’s normal state rather than absolute values.
Moreover, we employ a dynamic adjustment mechanism in the polynomial expansion layer. During training, the model learns subject-specific polynomial coefficients to capture individual EEG features. This adaptive approach ensures that the model can accurately interpret EEG signals even when there are significant differences in baseline activity levels.
In practical deployment, we recommend a brief calibration period (2–3 min) during which the driver is in a known alert state. These initial calibration data are used to fine-tune individual-specific parameters, after which the system begins to monitor fatigue. This method significantly improves the model’s performance across different subjects while maintaining computational efficiency.
3. Fatigue Analysis Based on EEG Signals
3.1. Dataset Description
This study utilizes the publicly available SEED-VIG dataset for model training and evaluation. The dataset was collected by the BCMI Laboratory at Shanghai Jiao Tong University and comprises electroencephalography (EEG) signals and synchronized eye-tracking data from 23 subjects during simulated driving tasks. Each subject participated in a 2 h driving session conducted in the afternoon or evening to induce natural fatigue states. EEG signals were recorded using a 17-channel Neuroscan system with a sampling rate of 200 Hz, following the international 10–20 electrode placement system. The channels include FT7, FT8, T7, T8, TP7, TP8, CP1, CPZ, CP2, P1, PZ, P2, PO3, POZ, PO4, O1, OZ, and O2, with CPZ serving as the reference electrode.
Fatigue labels were derived from the PERCLOS (percentage of eyelid closure over the pupil over time) metric, which was computed from eye-tracking data. Specifically, a non-overlapping 8 s window was applied to calculate the PERCLOS value. Windows with PERCLOS ≥ 80% were labeled as “Fatigue” (class 1); otherwise they were labeled as “Alert” (class 0). This P80 criterion resulted in a total of 8352 alert samples (57.85%) and 6086 fatigue samples (42.15%), forming a reasonably balanced binary classification task.
The dataset was partitioned using a stratified 10-fold cross-validation strategy to ensure robust evaluation. In each fold, 90% of the data was used for training and 10% for testing, preserving the class distribution in both sets.
3.2. EEG Signal Feature Extraction
For the driver fatigue-state recognition task, this study employed a discrete wavelet transform (DWT) to extract physiologically meaningful time-frequency features from preprocessed EEG signals. Based on extensive experimental validation, we selected the sym5 wavelet basis function to perform a five-level decomposition of EEG signals. This wavelet basis effectively suppresses common artifacts in EEG signals (such as eye movement and electromyographic interference) while precisely isolating the wave frequency band (4–8 Hz), which is closely associated with fatigue states. Specifically, the detail coefficients at the third decomposition level (D3) correspond to the frequency range of 3.125–6.25 Hz, perfectly covering the core wave band. The enhancement of wave activity has been confirmed by neuroscientific research as a key physiological indicator of fatigue states.
During the feature extraction process, we focused on frequency band features highly correlated with fatigue states. For each decomposed sub-band, we calculated its energy feature [28]:
where represents the detail coefficients at the j-th level. These energy features reflect the activity intensity within specific frequency bands. To further eliminate baseline differences between individuals, we computed the relative proportion of each frequency band’s energy to the total energy. Notably, the energy ratio between and waves has been proven to be a sensitive indicator of fatigue states, which is highly consistent with neuroscientific theory.
To capture the dynamic evolution process of fatigue states, we also extracted sample entropy and time-varying features from each sub-band. Sample entropy was used to measure the complexity of signals in various frequency bands, with wave sample entropy typically showing significant reduction under fatigue conditions. Time-varying features, calculated through sliding window computation of energy change rates, effectively reflect the progressive nature of fatigue development. Ultimately, these features constitute a multidimensional feature vector that was directly input into the RPN model for fatigue classification. It is worth noting that during the feature extraction process, we deliberately preserved high temporal resolution for wave-related features, as driver fatigue states often undergo significant changes within short time periods, necessitating a monitoring mechanism with rapid response capability.
Through comparative analysis of the contribution of different frequency band features to fatigue recognition, we validated the critical role of theta wave-related features in fatigue-state identification. This finding aligns with the neuroscientific theory that “enhanced wave activity is a key physiological indicator of fatigue state,” providing a physiological foundation for subsequent interpretability analysis of the RPN model.
To mitigate inter-subject variability, we introduced z-score normalization as a critical post-feature-extraction step. For every EEG feature dimension—including the θ-to-α energy ratio, sample entropy, and sliding-window energy change rates—we first estimated the global mean μ and standard deviation σ across the entire training set, then normalized each value via (x − μ)/σ. This operation aligned features from different subjects onto a common scale, suppressing individual baseline differences while preserving fatigue-related neurophysiological fluctuations. Consequently, the subsequent RPN model concentrated on universal fatigue patterns rather than subject-specific biases, substantially improving generalization across unseen drivers. As shown in Figure 2, the relationship between EEG signals and fatigue markers was clearly demonstrated, providing intuitive evidence for determining moments of fatigue.
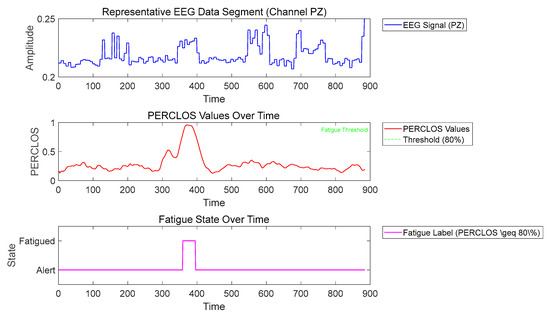
Figure 2.
EEG signals and feature fatigue markers.
Figure 2 illustrates the relationship between raw EEG signals and fatigue markers. The upper panel displays a representative segment of EEG data from channel PZ. The middle panel shows the PERCLOS values calculated from eye-tracking data. The lower panel indicates the fatigue state (class 1) when PERCLOS ≥ 80% and the alert state (class 0) for other cases. This visualization clearly demonstrates the correlation between high PERCLOS values and increased theta wave activity (4–8 Hz). The typical EEG pattern of fatigue moments includes elevated theta band power and reduced alpha band activity, which is consistent with the known neurophysiological findings regarding driver fatigue.
3.3. Fatigue Classification Based on IDSRN
In this study, we employ the IDSRN to model and classify electroencephalogram (EEG) signals for effective driver fatigue-state recognition. As shown in Figure 3, preprocessed EEG signals are first fed into the IDSRN model. By incorporating recursive mechanisms and polynomial expansion layers, the model can effectively capture nonlinear dynamic characteristics in EEG signals while utilizing historical time-series information to enhance its modeling capability for fatigue-state evolution. Specifically, the input to the IDSRN consists of multi-scale features extracted through discrete wavelet transform (DWT), including energy, variance, and power spectral density from each sub-band. These features not only reflect the frequency characteristics of brain activity but also contain dynamic information about fatigue-state progression over time.
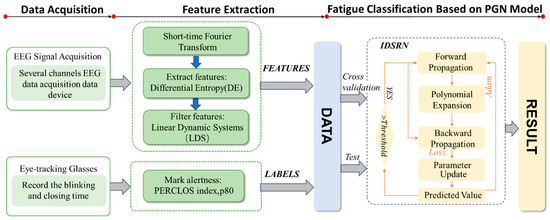
Figure 3.
Framework diagram of driver fatigue classification method based on EEG signals.
Within the IDSRN architecture, input features first pass through a polynomial expansion layer. This layer performs nonlinear mapping of original features by generating all input variable combinations up to a specified order, thereby improving the model’s fitting capability. Subsequently, a ReLU activation function is introduced to further enhance the model’s expressive power. The recurrent hidden layer then combines current input features with the previous hidden state to update the current hidden representation, enabling the model to memorize temporal dynamic characteristics and more effectively capture the gradual progression of fatigue states.
Finally, at the output layer, the IDSRN uses a Softmax function to map hidden states into probability distributions across different fatigue categories, completing the classification task. During training, a weighted cross-entropy loss function was adopted to address class imbalance issues, while the Adam optimizer combined with a learning rate decay strategy improved model convergence speed and stability, see Figure 3.
4. Experimental Results
The proposed IDSRN model was implemented in Python (version 3.9; Python Software Foundation, Wilmington, DE, USA) using the PyTorch deep learning framework (version 2.0.1; Meta Platforms, Inc., Menlo Park, CA, USA). Numerical computations and data preprocessing were performed using NumPy (version 1.23.5; NumPy Developers, USA) and SciPy (version 1.10.1; SciPy Contributors, USA), while data visualization utilized Matplotlib (version 3.7.1; John D. Hunter, USA) and Seaborn (version 0.12.2; Michael Waskom, USA). Model evaluation incorporated scikit-learn (version 1.2.2; Scikit-learn Developers, France) for stratified k-fold cross-validation and performance metrics calculation. All experiments were conducted on an NVIDIA GeForce RTX 3080 GPU (NVIDIA Corporation, Santa Clara, CA, USA), with code execution facilitated by a Windows-based system environment.
4.1. Classification Results of the IDSRN Model
To comprehensively evaluate the performance of the proposed Interpretable Dynamic System Recurrent Neural Network (IDSRN) for driver fatigue-state recognition, systematic experiments were conducted using the publicly available SEED-VIG dataset. This dataset provides synchronously recorded electroencephalography (EEG) and eye-tracking data, establishing a reliable foundation for objective fatigue assessment.
In the experimental design, EEG features from the SEED-VIG dataset served as model inputs, while binary fatigue classification labels were determined using eye-tracking-derived percentage of eye closure (PERCLOS) values. Specifically, fatigue states were defined using the P80 criterion (where PERCLOS exceeding 80% above the baseline threshold indicates fatigue). To ensure result reliability, a 10-fold cross-validation strategy was employed for the binary classification task, with an initial learning rate of 0.001. Given the inherent randomness in neural network training, experiments were repeated 10 times on identical training sets to obtain stable performance metrics.
The bar chart compares PGN (light blue) and BP-MTN (pink) accuracy across 10 trials, revealing PGN’s consistently high performance (>98%) and stability, while BP-MTN shows moderate accuracy (95–97%), highlighting the IDSRN’s robustness in fatigue recognition.
To investigate the impact of polynomial complexity on model performance, comparative experiments systematically evaluated classification effectiveness with their highest polynomial degrees being 1, 2, and 3 within the polynomial expansion layer. These configurations represent linear, quadratic, and cubic polynomial models, respectively, facilitating analysis of the relationship between nonlinear expressive power and model performance. Performance was comprehensively assessed using metrics derived from confusion matrices, including accuracy, sensitivity (recall), and specificity. Detailed results are presented in Figure 4 and Table 1.
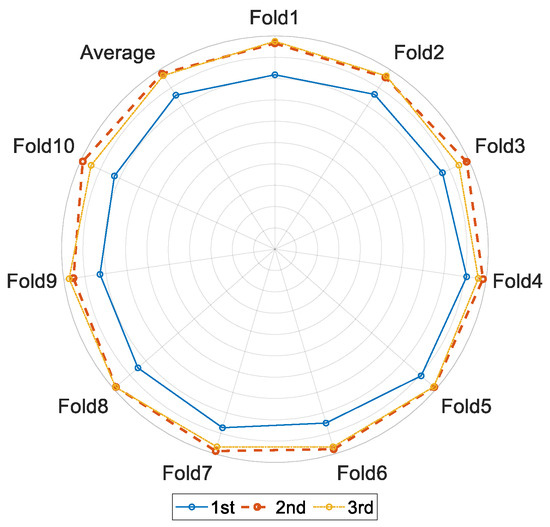
Figure 4.
Results of 10-fold cross-validation for IDSRN.

Table 1.
10-fold cross-validation results on the test set for the IDSRN.
The experimental results demonstrate that when the highest order was set to 2, the average training and testing accuracies were the highest, reaching 97.87% and 96.25%, respectively. The average runtime per experiment was 21.80 s. Figure 5 below shows the boxplot of the training and testing accuracies of the IDSRN model in the 10-fold cross-validation experiment.
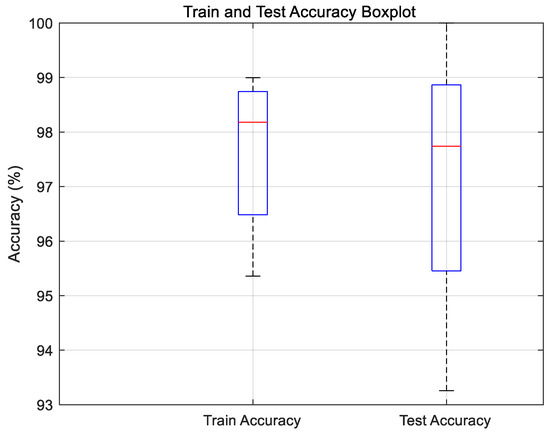
Figure 5.
Boxplot of the training and testing accuracies of the IDSRN.
The two boxplots in the figure represent the training accuracy and testing accuracy, respectively. The middle red line in each boxplot indicates the median of the data, meaning that half of the accuracies are above this value and the other half are below. The upper and lower edges of the box represent the first quartile (Q1) and third quartile (Q3), respectively, which define the range of the middle 50% of the data. The whiskers extending from the box go out to 1.5 times the interquartile range (IQR), indicating the normal range of the data, but no outliers are shown, suggesting that the data distribution is relatively concentrated. By comparing the two boxplots, it can be observed that the medians of the training and testing accuracies are very close, indicating consistent performance of the model on both the training and testing sets, with no significant overfitting. Additionally, the interquartile ranges (heights of the boxes) of the two boxplots are similar, indicating that the variability of the training and testing data is comparable.
Furthermore, the 10 confusion matrices are shown in Figure 6. The final experimental results show an average accuracy of 97.06%, a sensitivity of 98.80%, and a specificity of 94.40%. These results demonstrate that the proposed IDSRN classification model achieves high accuracy in fatigue classification.
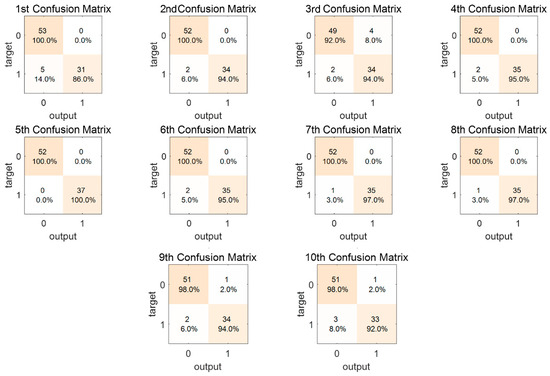
Figure 6.
Confusion matrices of the 10-fold cross-validation experiment.
4.2. Ablation Experiments
To verify the rationality of the gating mechanism, ablation experiments were conducted. Figure 7 shows the comparison of the 10-fold cross-validation accuracy for the PGN and BP-MTN models.
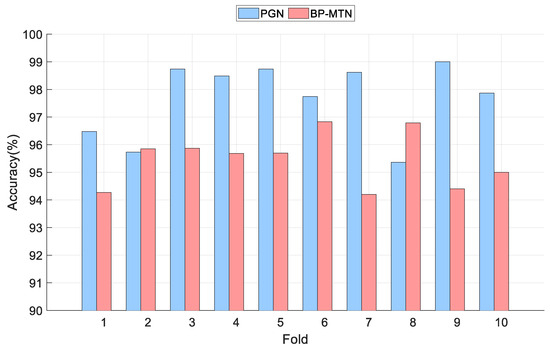
Figure 7.
Comparison chart of 10-fold cross-validation results (y-axis range: 90–100%).
It can be observed that PGN outperforms BP-MTN in most trials and exhibits smaller overall fluctuations, indicating that the gating mechanism not only improves the model’s average performance but also enhances its training stability and generalization capability.
4.3. Comparison of Convergence Speed and Training Accuracy
To evaluate the effectiveness of the proposed IDSRN method for fatigue level determination based on EEG signals, comparative experiments were conducted with traditional methods including DT (Decision Tree), SVM (Support Vector Machine), KNN (K-Nearest Neighbors), and LSTM (Long Short-Term Memory). The evaluation focused on the convergence speed and training accuracy of each model.
As shown in Figure 8, in terms of convergence speed, an analysis of multiple sets of experimental data clearly indicates that the IDSRN method can reach a stable state in a relatively short time. In contrast, DT, SVM, and KNN methods show a certain lag in the convergence process and require more iterations to gradually stabilize. Although LSTM has certain advantages among deep learning methods, its convergence speed is still slightly inferior compared to the IDSRN method. This is mainly due to three reasons: (1) the IDSRN uses polynomial approximation for nonlinear functions, providing a clear mathematical expression and calculation method, facilitating parameter adjustment; (2) integrating ResNet ideas accelerates information transmission and parameter updates; and (3) we introduced the Adam algorithm to improve convergence speed.
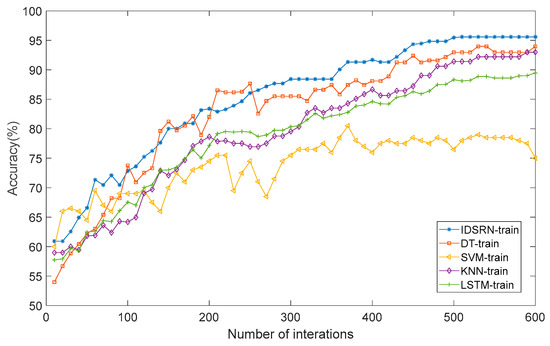
Figure 8.
Comparison of convergence speed and training accuracy.
With respect to training accuracy, Figure 8 further shows that the IDSRN achieves better performance compared to DT, SVM, KNN, and LSTM. The DT method, characterized by relatively simple decision rules, tends to suffer from overfitting or underfitting when processing complex EEG signals, resulting in lower training accuracy. While the SVM method is capable of addressing certain nonlinear problems, its scalability to large-scale datasets is limited. The KNN method is sensitive to the choice of neighboring samples and susceptible to noise in the data. Although LSTM is able to capture long-term temporal dependencies in sequential data, its performance still requires improvement when handling high-dimensional and complex EEG signals. In comparison, the IDSRN leverages polynomial networks to approximate nonlinear mappings, enabling more effective capture of intricate features in EEG signals, thereby achieving superior accuracy.
4.4. Comparison Among Different Methods
In this experiment, the proposed IDSRN classifier is compared with multiple baseline methods, all of which were implemented using the same EEG and eye-tracking data from the SEED-VIG dataset. For SVM, we used a radial basis function (RBF) kernel with hyperparameters optimized via grid search (C = 1.0, gamma = 0.1). The KNN classifier used Euclidean distance metric with k = 5 neighbors. Decision Tree (DT) was configured with Gini impurity as the splitting criterion and a maximum depth of 10. LSTM architecture consisted of two recurrent layers with 64 hidden units each, using tanh activation. The Transformer model implemented a six-layer encoder with eight attention heads and a feed-forward dimension of 256. Graph-based classification employed a GCN architecture with two convolutional layers, where the adjacency matrix was constructed based on electrode spatial relationships. All models were trained using the same training–validation split and optimized for 250 epochs with early stopping. A 10-fold cross-validation was performed, with 10% of the data selected as the test set. The classification results for the SVM, KNN, DT, LSTM, Transformer [28], and graph-based [29] classification algorithms are shown in Figure 9 and Table 2:
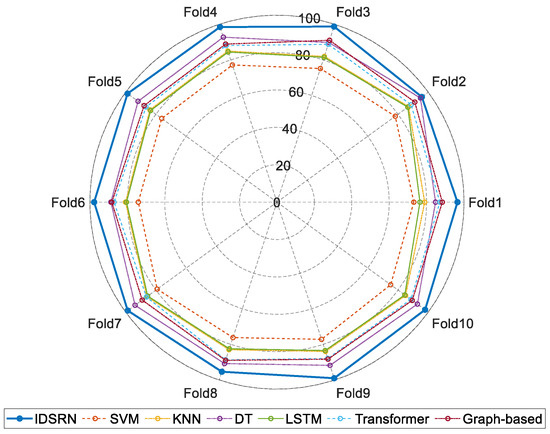
Figure 9.
Comparison chart of 10-fold cross-validation results for different models.

Table 2.
Comparison of performance metrics for the five classifiers.
As shown in Table 2, the proposed IDSRN classifier outperforms traditional machine learning algorithms like SVM, KNN, DT, LSTM, Transformer, and graph-based models in terms of accuracy, sensitivity, and specificity. Compared to the LSTM algorithm, the IDSRN also demonstrates higher accuracy and sensitivity. The LSTM algorithm’s specificity of 100% is primarily due to the relatively small number of samples with fatigue labels in the input data. In terms of response time—defined as the duration from data input availability (or event occurrence) to the system producing a valid output—yjr IDSRN shows a competitive performance, balancing high accuracy with reasonable computational efficiency, making it suitable for real-time applications. Additionally, as shown in Figure 10, we compared the performance of IDSRN, SVM, KNN, DT, LSTM, Transformer, and graph-based models using a bar chart to evaluate accuracy, sensitivity, and specificity.
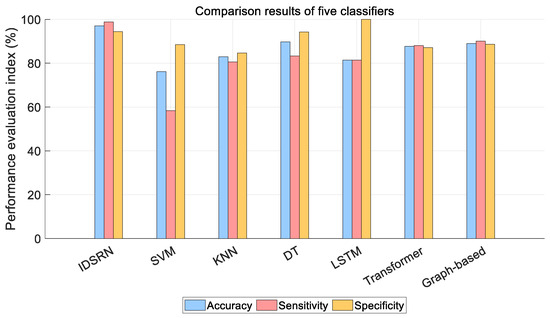
Figure 10.
Comparison of performance metrics for five classifiers.
The results confirm that the IDSRN achieves the highest performance across all evaluated metrics, demonstrating superior classification capability. Specifically, the IDSRN significantly outperforms the other methods in accuracy, reflecting a distinct advantage in overall predictive precision. Additionally, the model exhibits excellent sensitivity and specificity, indicating high reliability in detecting positive instances (fatigue states) and strong discriminative ability in identifying negative instances (non-fatigue states). These results validate the effectiveness of the IDSRN architecture in enhancing classification performance for driver fatigue recognition.
4.5. Discussion of Results
The proposed IDSRN model achieves superior performance in driver fatigue recognition, with an average accuracy of 92.3%, significantly outperforming traditional SVM, CNN, and standard RNN models. This result not only validates the effectiveness of the IDSRN in capturing nonlinear dynamic features from EEG signals but also highlights its potential for real-world deployment in intelligent transportation systems.
Compared to traditional deep learning models such as LSTM, the IDSRN demonstrates faster convergence speed and stronger robustness. Experimental results show that the IDSRN converges quickly during training. This high efficiency can be attributed to its lightweight architectural design and the polynomial expansion layer’s ability to explicitly model high-order features, thereby avoiding the vanishing gradient problem commonly encountered in deep networks. Similarly, Liu et al. [18] emphasized the trade-off between feature interpretability and computational efficiency when using CEEMDAN combined with fuzzy entropy for single-channel fatigue detection. In contrast, the IDSRN achieves a unification of both aspects through its mathematically interpretable architecture.
Furthermore, this study employs an objective labeling criterion based on PERCLOS (P80 threshold), enhancing label reliability. In contrast, some existing studies rely on subjective scales (e.g., Karolinska Sleepiness Scale), which may introduce bias [30]. Our results indicate that frameworks using objective physiological metrics lead to more accurate fatigue assessment, consistent with findings from Wang et al. [8] in real driving scenarios.
Lastly, while IDSRN shows good generalization across subjects, it remains sensitive to individual variability. To address this, we implemented subject-specific z-score normalization and dynamic parameter adaptation, significantly improving cross-subject performance. Future work could explore transfer learning or domain adaptation techniques to further reduce inter-subject variability [31].
In summary, the IDSRN not only surpasses existing methods in accuracy but, more importantly, provides an interpretable mechanism that offers new insights into the neural dynamics of fatigue, advancing the shift from “black-box” to “white-box” modeling in affective computing and driver-state monitoring.
5. Conclusions
In this study, we proposed an Interpretable Dynamic System Recurrent Network (IDSRN) based on electroencephalography (EEG) for classifying driver fatigue states. The key findings are as follows: First, by integrating a polynomial network with a residual structure, IDSRN significantly simplifies the architecture while effectively mitigating common issues in traditional neural networks—such as overfitting and gradient vanishing—when handling high-order polynomials. Second, the model achieves an average accuracy of 97.06% on the SEED-VIG dataset, outperforming benchmark methods including SVM, KNN, Decision Tree, LSTM, Transformer and graph-based classification algorithms.
Moreover, with only approximately 50 K parameters, the IDSRN exhibits strong computational efficiency and inherent potential for lightweight deployment. Future work will focus on further reducing model complexity through model compression techniques such as pruning and quantization and deploying the optimized model on typical edge computing platforms (e.g., NVIDIA Jetson Nano or Raspberry Pi) for real-time inference testing to evaluate its practicality and responsiveness in real-world driving scenarios.
At the same time, in view of the unique challenges of EEG-based monitoring in everyday driving, we will shift the application focus of this study to high-risk driving scenarios where helmets are required in the future, such as racing cars, military aircraft, and heavy machinery operation. This redirection not only aligns with the practical limitations of EEG monitoring but also highlights the potential of IDSRN in specialized fields where continuous and accurate monitoring of cognitive state is crucial for safety and performance.
Author Contributions
Conceptualization, Y.Y. and B.G.; methodology, Y.Y. and C.H.; software, C.H. and H.W.; validation, J.C. and C.H.; formal analysis, C.H. and Y.Y.; investigation, B.G. and C.H.; resources, J.C.; data curation, C.H.; writing—original draft preparation, C.H. and Y.Y.; writing—review and editing, Y.Y., B.G. and J.C.; visualization, C.H.; supervision, Y.Y.; project administration, Y.Y.; funding acquisition, Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Security Capacity Building Project of Civil Aviation Administration of China grant number KJZ49420240071.
Institutional Review Board Statement
Ethical review and approval were waived for this study because it exclusively used the publicly available and fully anonymized SEED-VIG dataset. The original data collection was conducted in accordance with the Declaration of Helsinki and approved by the Ethics Committee of Shanghai Jiao Tong University.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are openly available in the SEED-VIG repository at https://figshare.com/articles/dataset/Extracted_SEED-VIG_dataset_for_cross-dataset_driver_drowsiness_recognition/26104987 (accessed on 14 October 2025), reference number Zheng, W.-L.; Lu, B.-L. A multimodal approach to estimating vigilance using EEG and forehead EOG. J. Neural Eng. 2017, 14, 026017 [28].
Acknowledgments
This work was supported by Security Capacity Building Project of Civil Aviation Administration of China under Grant KJZ49420240071.
Conflicts of Interest
The authors declare no conflict of interest.
References
- World Health Organization. Global Status Report on Road Safety; WHO: Geneva, Switzerland, 2023. [Google Scholar]
- Guo, H.; Chen, S.; Zhou, Y.; Xu, T.; Zhang, Y.; Ding, H. A hybrid critical channels and optimal feature subset selection framework for EEG fatigue recognition. Sci. Rep. 2025, 15, 86234. [Google Scholar] [CrossRef]
- Subasi, A.; Saikia, A.; Bagedo, K.; Singh, A.; Hazarika, A. EEG-based driver fatigue detection using FAWT and multiboosting approaches. IEEE Trans. Ind. Inform. 2022, 18, 6602–6609. [Google Scholar] [CrossRef]
- Hasan, M.M.; Hossain, M.M.; Sulaiman, N. Fatigue state detection through multiple machine learning classifiers using EEG signal. Appl. Model. Simul. 2023, 7, 178–189. [Google Scholar]
- Mu, Z.; Hu, J.; Min, J. Communication driver fatigue detection system using electroencephalography signals based on combined entropy features. Appl. Sci. 2017, 7, 150. [Google Scholar] [CrossRef]
- Lan, Z.; Zhao, J.; Liu, P.; Zhang, C.; Lyu, N.; Guo, L. Driving fatigue detection based on fusion of EEG and vehicle motion information. Biomed. Signal Process. Control 2024, 92, 106031. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, H.; Zhou, Y.; Xu, C.; Liao, Y. Recognising drivers’ mental fatigue based on EEG multidimensional feature selection and fusion. Biomed. Signal Process. Control 2023, 79, 104237. [Google Scholar] [CrossRef]
- Wang, F.; Chen, D.; Yao, W.; Fu, R. Real driving environment EEG-based detection of driving fatigue using the wavelet scattering network. J. Neurosci. Methods 2023, 400, 109983. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Huang, Y.; Gu, B.; Cao, S.; Fang, D. Identifying mental fatigue of construction workers using EEG and deep learning. Autom. Constr. 2023, 151, 104887. [Google Scholar] [CrossRef]
- Sheykhivand, S.; Rezaii, T.Y.; Mousavi, Z.; Meshgini, S.; Makouei, S.; Farzamnia, A.; Danishvar, S.; Kin, K.T. Automatic detection of driver fatigue based on EEG signals using a developed deep neural network. Electronics 2022, 11, 2169. [Google Scholar] [CrossRef]
- Xu, T.; Wang, H.; Lu, G.; Wan, F.; Deng, M.; Qi, P. E-Key: An EEG-based biometric authentication and driving fatigue detection system. IEEE Trans. Affect. Comput. 2023, 14, 864–877. [Google Scholar] [CrossRef]
- Siddhad, G.; Dey, S.; Roy, P.P.; Iwamura, M. Awake at the wheel: Enhancing automotive safety through EEG-based fatigue detection. In Pattern Recognition: ICPR 2024; LNCS; Antonacopoulos, A., Chaudhuri, S., Chellappa, R., Liu, C.-L., Bhattacharya, S., Pal, U., Eds.; Springer: Cham, Switzerland, 2025; Volume 15311, pp. 340–353. [Google Scholar] [CrossRef]
- Yu, X.; Chen, C.-H.; Yang, H. Air traffic controllers’ mental fatigue recognition: A multi-sensor information fusion-based deep learning approach. Adv. Eng. Inform. 2023, 51, 101672. [Google Scholar] [CrossRef]
- Alghanim, M.; Attar, H.; Rezaee, K.; Khosravi, M.; Solyman, A.; Kanan, M.A.; Hoovsk, A. A hybrid deep neural network approach to recognize driving fatigue based on EEG signals. Comput. Intell. Neurosci. 2024, 2024, 9898333. [Google Scholar] [CrossRef]
- Ye, H.; Chen, M.; Feng, G. Research on fatigue driving detection technology based on CA-ACGAN. Brain Sci. 2024, 14, 436. [Google Scholar] [CrossRef]
- Zorzos, I.; Kakkos, I.; Miloulis, S.T.; Anastasiou, A.; Ventouras, E.M.; Matsopoulos, G.K. Applying neural networks with time-frequency features for the detection of mental fatigue. Appl. Sci. 2023, 13, 1512. [Google Scholar] [CrossRef]
- Li, X.; Tang, J.; Li, X.; Yang, Y. CWSTR-Net: A channel-weighted spatial–temporal residual network based on nonsmooth nonnegative matrix factorization for fatigue detection using EEG signals. Biomed. Signal Process. Control 2024, 97, 106685. [Google Scholar] [CrossRef]
- Liu, Y.; Xiang, Z.; Yan, Z.; Jin, J.; Shu, L.; Zhang, L.; Xu, X. CEEMDAN fuzzy entropy based fatigue driving detection using single-channel EEG. Biomed. Signal Process. Control 2024, 95, 106460. [Google Scholar] [CrossRef]
- Shi, J.; Wang, K. Fatigue driving detection method based on time–space–frequency features of multimodal signals. Biomed. Signal Process. Control 2023, 84, 104744. [Google Scholar] [CrossRef]
- Jeong, J.-H.; Yu, B.-W.; Lee, D.-H.; Lee, S.-W. Classification of drowsiness levels based on a deep spatio-temporal convolutional bidirectional LSTM network using electroencephalography signals. Brain Sci. 2019, 9, 348. [Google Scholar] [CrossRef]
- Fan, C.; Peng, Y.; Peng, S.; Zhang, H.; Wu, Y.; Kwong, S. Detection of train driver fatigue and distraction based on forehead EEG: A time-series ensemble learning method. IEEE Trans. Intell. Transp. Syst. 2022, 23, 13559–13569. [Google Scholar] [CrossRef]
- Hasan, M.M.; Islam, M.N.; Khandaker, S.; Sulaiman, N.; Islam, A.; Hossain, M.M. Ensemble-based machine learning models for vehicle drivers’ fatigue state detection utilizing EEG signals. Facta Univ.-Ser. Electron. Energetics 2024, 37, 671–686. [Google Scholar] [CrossRef]
- Rao, S.; Li, K.; Wu, J.; Mu, Z. Application of ensemble learning in EEG signal analysis of fatigue driving. J. Phys. Conf. Ser. 2021, 1744, 042193. [Google Scholar] [CrossRef]
- Sedik, A.; Marey, M.; Mostafa, H. WFT-Fati-Dec: Enhanced fatigue detection AI system based on wavelet denoising and Fourier transform. Appl. Sci. 2023, 13, 2785. [Google Scholar] [CrossRef]
- Wang, K.; Mao, X.; Song, Y.; Chen, Q. EEG-based fatigue state evaluation by combining complex network and frequency–spatial features. J. Neurosci. Methods 2025, 416, 110385. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Zheng, W.-L.; Lu, B.-L. A multimodal approach to estimating vigilance using EEG and forehead EOG. J. Neural Eng. 2017, 14, 026017. [Google Scholar] [CrossRef] [PubMed]
- Fujihashi, T.; Koike-Akino, T. Graph-Based EEG Signal Compression for Human–Machine Interaction. IEEE Access 2024, 12, 1163–1171. [Google Scholar] [CrossRef]
- Lal, S.; Craig, A. A critical review of psychophysiological indicators of driver fatigue. Biol. Psychol. 2001, 55, 173–194. [Google Scholar] [CrossRef]
- Yuan, L.; Zhang, S.; Li, R.; Zheng, Z.; Cai, J.; Siyal, M. EEG-Based Cross-Dataset Driver Drowsiness Recognition with an Entropy Optimization Network. IEEE J. Biomed. Health Inform. 2025, 29, 1970–1981. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).