Pre-Determining the Optimal Number of Clusters for k-Means Clustering Using the Parameters Package in R and Distance Metrics
Abstract
1. Introduction
2. Materials and Methods
2.1. The Distance Metrics
2.1.1. The Euclidean Distance
2.1.2. The Manhattan Distance
2.1.3. The Canberra Distance
3. The Datasets Used in the Study
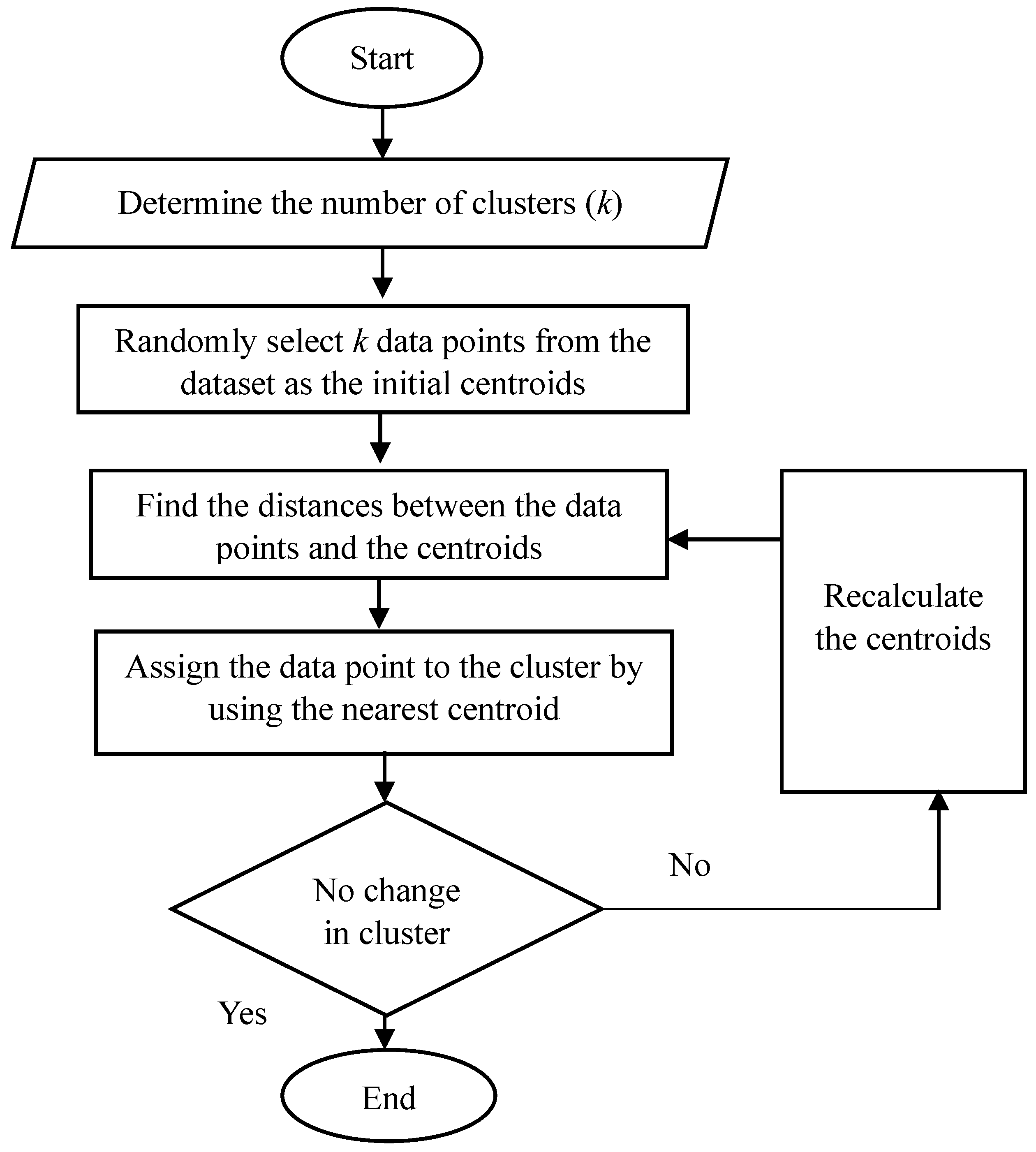
4. The Methodology for K-Means Clustering
The Parameters Package for Determining the Number of Clusters
- 1.
- Comprehensive Evaluation: Various validation techniques consider different aspects of clustering quality, including compactness, separation, density, and statistical significance. Using a wide range of metrics ensures a more thorough and robust evaluation of the optimal number of clusters.
- 2.
- Mitigation of Method-Specific Biases: Each approach has its own assumptions and sensitivities; using multiple methods helps reduce dependence on any one approach, making the results more reliable and less biased.
- 3.
- Consensus-Based Determination: Combining results from different methods helps find a more stable and agreed-upon estimate of the best number of clusters, especially in complex datasets.
- 4.
- Flexibility and Adaptability: Different datasets may require different methods, providing users with many options to select the most appropriate metrics for their data, making the tool more flexible.
- 5.
- Facilitating Comparative Analysis: Having multiple validation results enables users to compare and understand differences, leading to better and more confident choices for the optimal number of clusters.
5. Performance Metrics
5.1. Confusion Matrix
5.2. Accuracy
5.3. Precision and Recall
5.4. F1-Score
5.5. Numerical Study
6. Results and Discussion
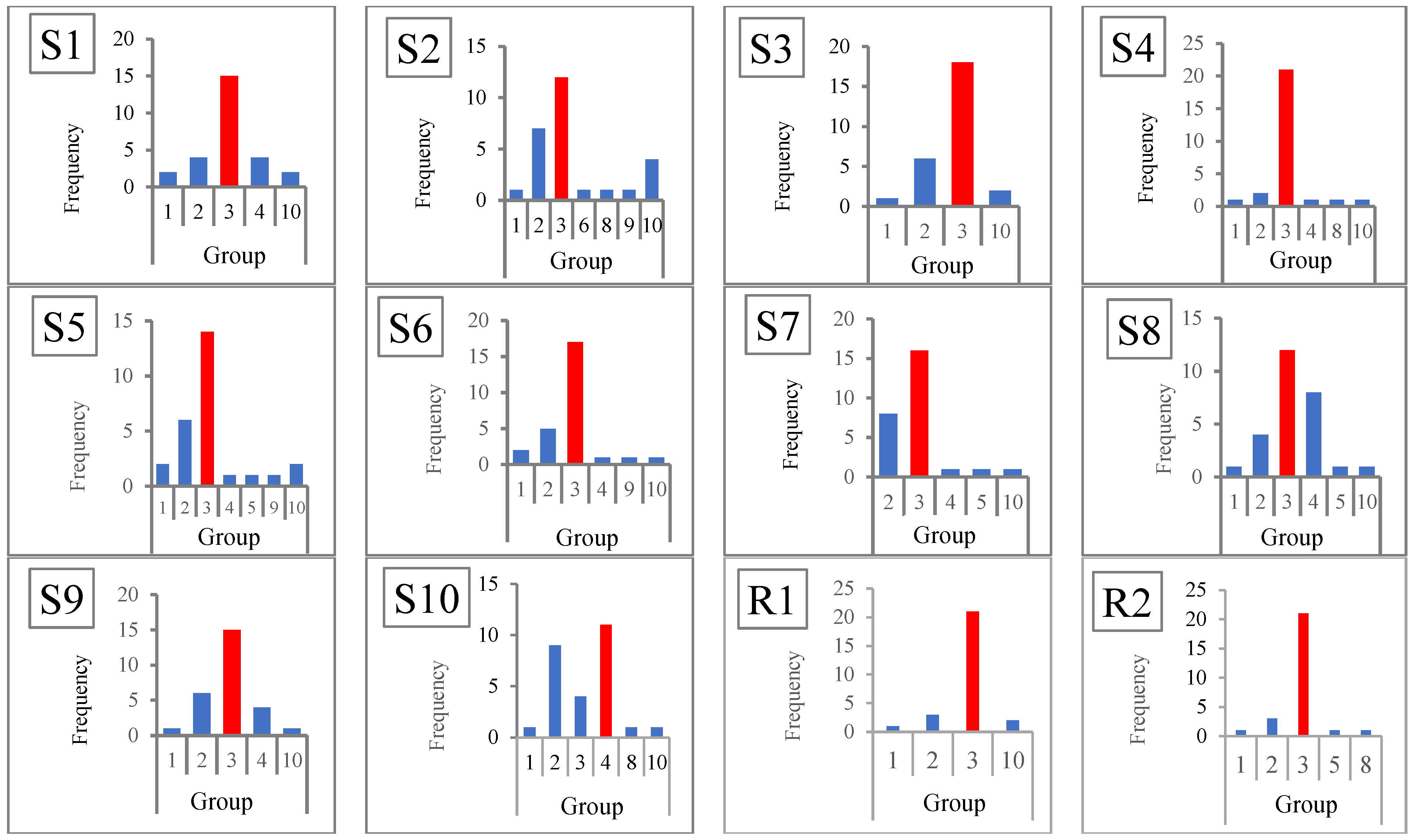
6.1. The Optimal Number of Clusters
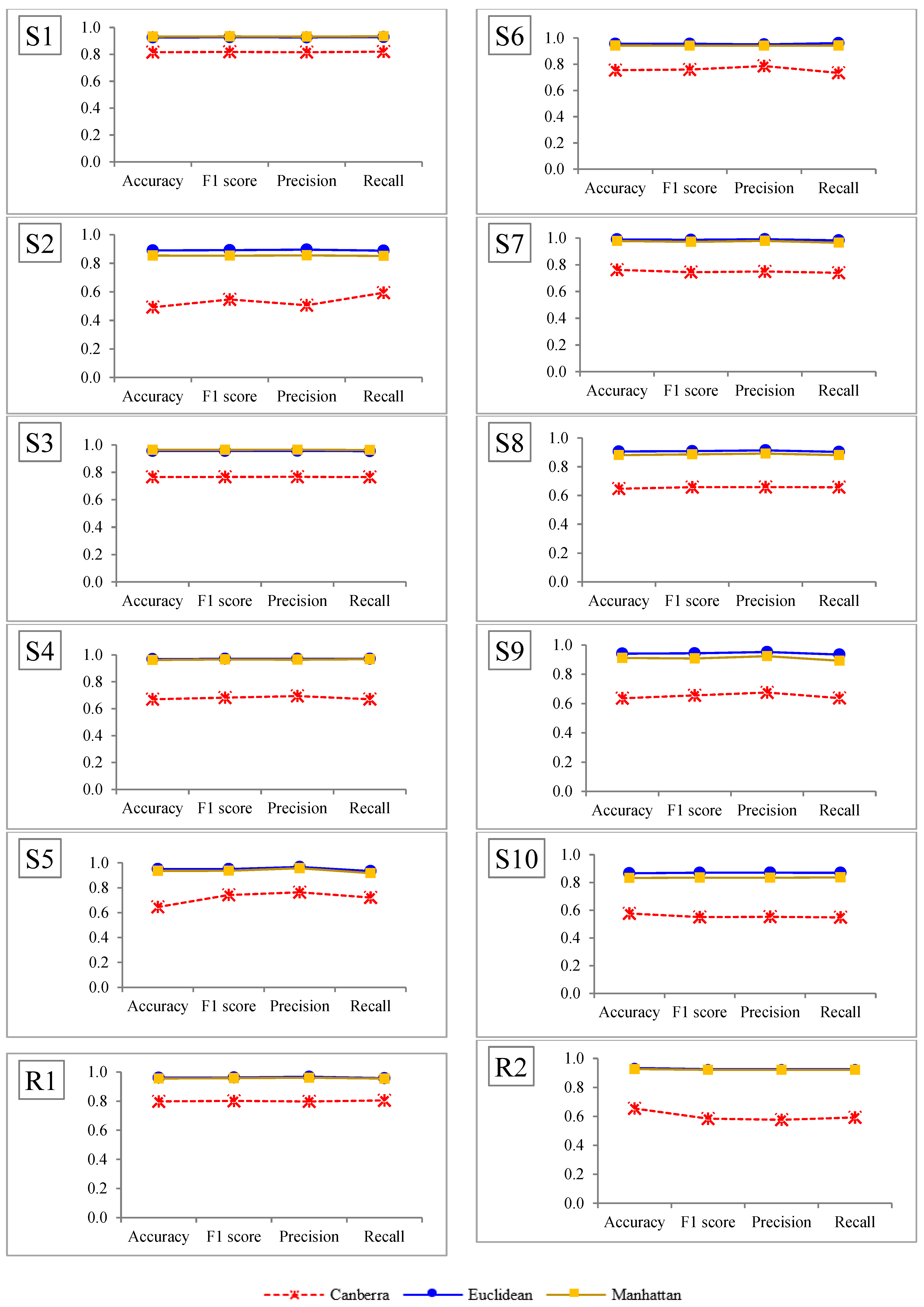
6.2. The Three Distance Metrics
6.3. Comparison of the Results Using the Three Distance Metrics with the True Group
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rodriguez, M.Z.; Comin, C.H.; Casanova, D.; Bruno, O.M.; Amancio, D.R.; Costa, L.D.; Rodrigues, F.A. Clustering algorithms: A comparative approach. PLoS ONE 2019, 14, e0210236. [Google Scholar] [CrossRef]
- Singh, S.; Srivastava, S. Review of clustering techniques in control system. Procedia Comput. Sci. 2020, 173, 272–280. [Google Scholar] [CrossRef]
- Sun, S.; Wang, K. Multi-view clustering: A survey. IEEE Trans. Knowl. Data Eng. 2013, 29, 5184–5197. [Google Scholar]
- Xu, C.; Tao, D.; Li, J. Multi-view learning overview: Recent progresses and future directions. Neurocomputing 2013, 130, 1–13. [Google Scholar]
- Zhang, T.; Lin, N. Multi-view clustering via graph fusion. Pattern Recognit. 2018, 78, 172–182. [Google Scholar]
- Radhakrishnan, S.; Zheng, D.; Wu, J.; Sangaiah, A.K. Multimodal deep learning: Techniques and applications. IEEE Trans. Multimed. 2021, 23, 2764–2777. [Google Scholar]
- Murtagh, F.; Contreras, P. Algorithms for hierarchical clustering: An overview. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2017, 7, e1219. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Sculley, D. Web-scale k-means clustering. In Proceedings of the 19th International Conference on World Wide Web, Raleigh, NC, USA, 26–30 April 2010; pp. 1177–1178. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the KDD’96: Proceedings of the Second International Conference on Knowledge Discovery and Data Mining; Portland, OR, USA, 2–4 August 1996, pp. 226–231.
- Ng, A.Y.; Jordan, M.I.; Weiss, Y. On spectral clustering: Analysis and an algorithm. Adv. Neural Inf. Process Syst. 2002, 14, 849–856. [Google Scholar]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Wongoutong, C. The impact of neglecting feature scaling in k-means clustering. PLoS ONE 2024, 19, e0310839. [Google Scholar] [CrossRef]
- Annas, M.; Wahab, S.N. Data mining methods: K-means clustering algorithms. Int. J. Cyber IT Serv. Manag. 2023, 3, 40–47. [Google Scholar] [CrossRef]
- Silitonga, P. Clustering of patient disease data by using K-means clustering. Int. J. Comput. Sci. Inf. Secur. 2017, 15, 219–221. [Google Scholar]
- Herman, E.; Zsido, K.E.; Fenyves, V. Cluster analysis with k-mean versus k-medoid in financial performance evaluation. Appl. Sci. 2022, 12, 7985. [Google Scholar] [CrossRef]
- Ali, H.H.; Kadhum, L.E. K-means clustering algorithm applications in data mining and pattern recognition. Int. J. Sci. Res. 2017, 6, 1577–1584. [Google Scholar]
- Shan, P. Image segmentation method based on k-mean algorithm. EURASIP J. Image Video Process. 2018, 2018, 81. [Google Scholar] [CrossRef]
- Ahmed, M.; Seraj, R.; Islam, S.M. The k-means algorithm: A comprehensive survey and performance evaluation. Electronics 2020, 9, 1295. [Google Scholar] [CrossRef]
- Kuncheva, L.I.; Vetrov, D.P. Evaluation of stability of k-means cluster ensembles with respect to random initialization. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1798–1808. [Google Scholar] [CrossRef]
- Arthur, D.; Vassilvitskii, S. K-means++: The Advantages of Careful Seeding. Stanford 2006. Available online: https://theory.stanford.edu/~sergei/papers/kMeansPP-soda.pdf (accessed on 11 May 2025).
- Mahmud, M.S.; Rahman, M.M.; Akhtar, M.N. Improvement of k-means clustering algorithm with better initial centroids based on weighted average. In Proceedings of the 7th International Conference on Electrical and Computer Engineering, Dhaka, Bangladesh, 20–22 December 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 647–650. [Google Scholar]
- Forgy, E.W. Cluster analysis of multivariate data: Efficiency versus interpretability of classifications. Biometrics 1965, 21, 768–769. [Google Scholar]
- Ahmad, A.; Khan, S.S. InitKmix—A novel initial partition generation algorithm for clustering mixed data using k-means-based clustering. Expert Syst. Appl. 2021, 167, 114149. [Google Scholar] [CrossRef]
- Milligan, G.W.; Cooper, M.C. An examination of procedures for determining the number of clusters in a data set. Psychometrika 1985, 50, 159–179. [Google Scholar] [CrossRef]
- Humaira, H.; Rasyidah, R. Determining the appropriate cluster number using Elbow method for k-means algorithm. In Proceedings of the 2nd Workshop on Multidisciplinary and Applications (WMA), Padang, Indonesia, 24–25 January 2018; EAI: Gent, Belgium, 2018; pp. 1–8. [Google Scholar]
- Gupta, U.D.; Menon, V.; Babbar, U. Detecting the number of clusters during expectation-maximization clustering using information criterion. In Proceedings of the Second International Conference on Machine Learning and Computing, Bangalore, India, 9–11 February 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 169–173. [Google Scholar]
- Gokcay, E.; Principe, J.C. Information theoretic clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 158–171. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Fu, W.; Perry, P.O. Estimating the number of clusters using cross-validation. J. Comput. Graphical Stat. 2020, 29, 162–173. [Google Scholar] [CrossRef]
- Saunders, C.; Castro, T.; Gama, J.; van der Bogaard, K.J.M.H. Challenges in clustering high-dimensional data. J. Data Sci. 2019, 17, 255–272. [Google Scholar]
- Shi, L.; Cao, L.; Ye, Y.; Zhao, Y.; Chen, B. Tensor-based Graph Learning with Consistency and Specificity for Multi-View Clustering. arXiv 2024, arXiv:2403.18393. [Google Scholar]
- Shi, L.; Cao, L.; Wang, J.; Chen, B. Enhanced latent multi-view subspace clustering. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 12480–12495. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Y. Model-based clustering algorithms: A review and new developments. Statist. Sci. 2018, 33, 543–558. [Google Scholar]
- Stergoulis, S.; Sgouros, N. Fuzzy clustering and the challenge of determining the number of clusters in high-dimensional data. Expert Syst. Appl. 2019, 132, 163–177. [Google Scholar]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Singh, A.; Yadav, A.; Rana, A. K-means with three different distance metrics. Int. J. Comput. Appl. 2013, 67, 13–17. [Google Scholar] [CrossRef]
- Gupta, M.K.; Chandra, P. Effects of similarity/distance metrics on k-means algorithm with respect to its applications in IoT and multimedia: A review. Multimed. Tools Appl. 2022, 81, 37007–37032. [Google Scholar] [CrossRef]
- Ghazal, T.M. Performances of k-means clustering algorithm with different distance metrics. Intell. Autom. Soft Comput. 2021, 30, 735–742. [Google Scholar] [CrossRef]
- Kumar, S. Efficient k-mean clustering algorithm for large datasets using data mining standard score normalization. Int. J. Recent Innov. Trends Comput. Commun. 2014, 2, 3161–3166. [Google Scholar]
- Dudek, A.; Walesiak, M. The choice of variable normalization method in cluster analysis. In Proceedings of the 35th International Business Information Management Association Conference (IBIMA), Seville, Spain, 1–2 April 2020; Curran Associates, Inc.: Red Hook, NY, USA, 2020; pp. 325–340. [Google Scholar]
- Lüdecke, D.; Ben-Shachar, M.S.; Patil, I.; Waggoner, P.; Makowski, D. Parameters: A package to easily extract, summarize, and display model parameters. J. Open Source Softw. 2020, 5, 2445. [Google Scholar] [CrossRef]
- Faisal, M.; Zamzami, E.M. Comparative analysis of inter-centroid k-means performance using Euclidean distance, Canberra distance and Manhattan distance. J. Phys. Conf. Ser. 2020, 1566, 012112. [Google Scholar] [CrossRef]
- Thakare, Y.S.; Bagal, S.B. Performance evaluation of k-means clustering algorithm with various distance metrics. Int. J. Comput. Appl. 2015, 110, 12–16. [Google Scholar] [CrossRef]
- Suhaeri, M.E.; Alimudin, J.A.; Ismail, M.T.; Ali, M.K. Evaluation of clustering approach with Euclidean and Manhattan distance for outlier detection. AIP Conf. Proc. 2021, 2423, 070025. [Google Scholar] [CrossRef]
- Yilmaz, S.; Chambers, J.; Cozza, S.; Patel, M.K. Exploratory study on clustering methods to identify electricity use patterns in building sector. J. Phys. Conf. Ser. 2019, 1343, 012044. [Google Scholar] [CrossRef]
- Melnykov, V.; Chen, W.C.; Maitra, R. MixSim: An R package for simulating data to study performance of clustering algorithms. J. Stat. Softw. 2012, 51, 1–25. [Google Scholar] [CrossRef]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.; Silverman, R.; Wu, A.Y. The analysis of a simple k-means clustering algorithm. In Proceedings of the Sixteenth Annual Symposium on Computational Geometry, Hong Kong, 12–14 June 2000; ACM: New York, NY, USA, 2000; pp. 100–109. [Google Scholar]
- Wu, J.; Chen, J.; Xiong, H.; Xie, M. External validation measures for K-means clustering: A data distribution perspective. Expert Syst. Appl. 2009, 36, 6050–6061. [Google Scholar] [CrossRef]
- Susmaga, R. Confusion matrix visualization. In Proceedings of the International Intelligent Information Processing and Web Mining (IIPWM)’04 Conference, Zakopane, Poland, 17–20 May 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 107–116. [Google Scholar]
- Diallo, R.; Edalo, C.; Awe, O.O. Machine learning evaluation of imbalanced health data: A comparative analysis of balanced accuracy, MCC, and F1 score. In Practical Statistical Learning and Data Science Methods; Springer: Cham, Switzerland, 2024; pp. 283–312. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing: Vienna, Austria, 2021. Available online: https://www.R-project.org/ (accessed on 11 March 2025).
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Kuhn, H.W. The Hungarian Method for the Assignment Problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Grötschel, M.; Lovász, L.; Schrijver, A. Geometric Algorithms and Combinatorial Optimization; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Hsu, J.; Hoi, S.C. Automatic determination of the number of clusters in large-scale data. IEEE Trans. Knowl. Data Eng. 2021, 33, 2674–2687. [Google Scholar]
- Ketchen, D.J.; Shook, C.L. The application of cluster analysis in strategic management research. Strat. Manag. J. 1996, 17, 441–458. [Google Scholar] [CrossRef]
- Rosenberg, A.; Hirschberg, J. The SDbw cluster validity index. In Proceedings of the Sixth International Conference on Fuzzy Systems and Knowledge Discovery, Tianjin, China, 14–16 August 2007; pp. 391–395. [Google Scholar]
- Steinley, D.; Brusco, M.J. Choosing the number of clusters in Κ-means clustering. Psychol. Methods 2011, 16, 285. [Google Scholar] [CrossRef]
- Sun, L.; Li, Z.; Zhang, H. A robust cluster validation method based on statistical criteria for high-dimensional data. Expert Syst. Appl. 2020, 162, 113716. [Google Scholar]
- Nguyen, T.; Lee, S. Improving cluster validity indices with statistical measures for complex datasets. Knowl.-Based Syst. 2022, 244, 108679. [Google Scholar]
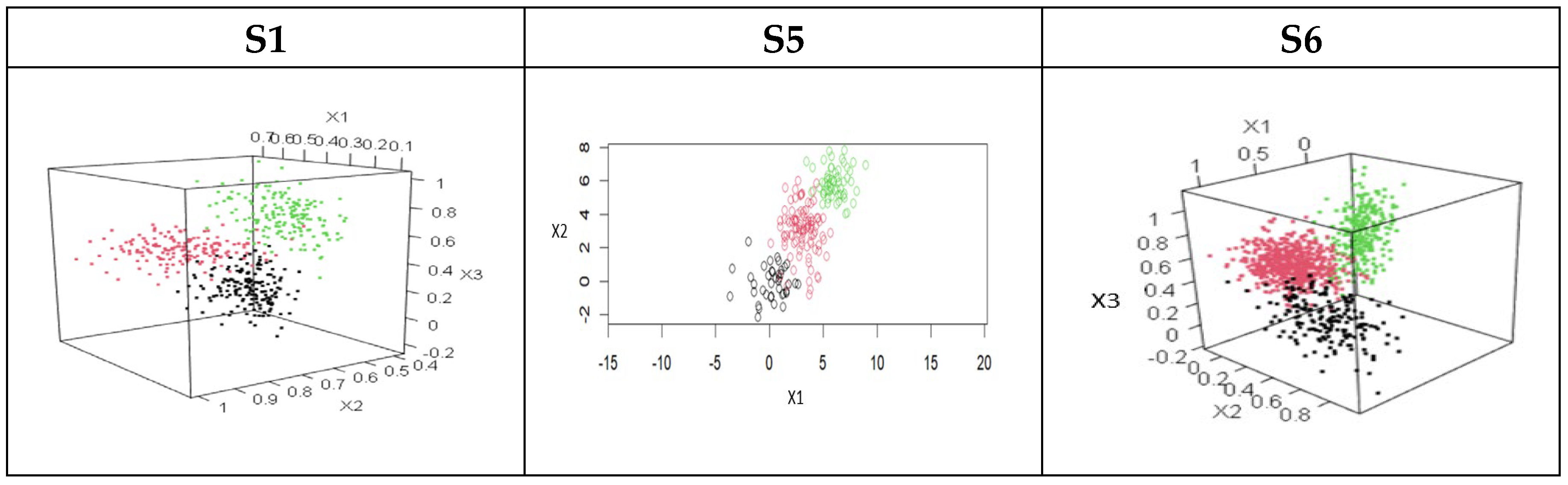



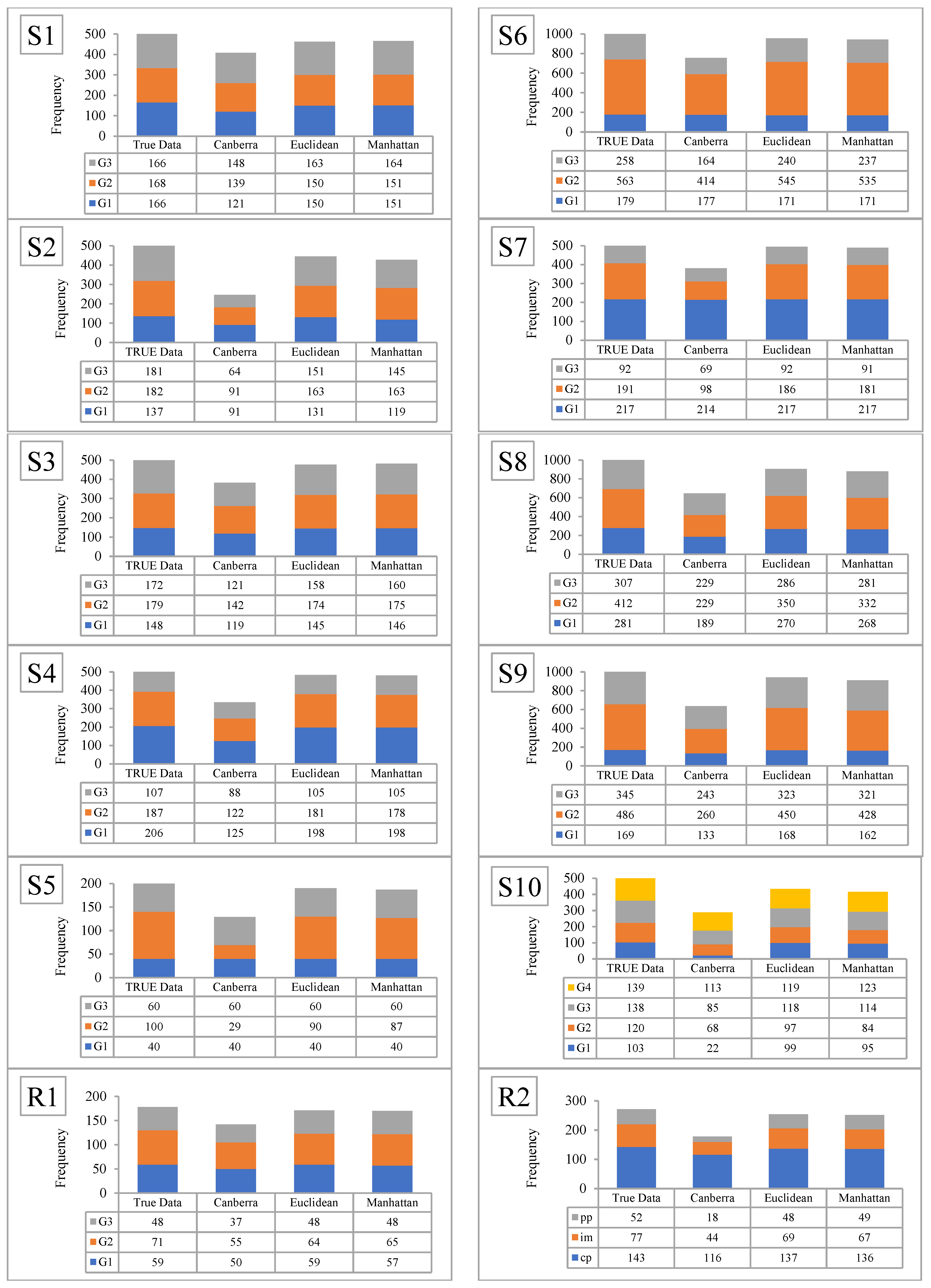

| Dataset | No. of Features | No. of Classes | No. of Data Items | No. of Objects in Each Class |
|---|---|---|---|---|
| S1 | 3 | 3 | 500 | 166, 168 166 |
| S2 | 10 | 3 | 500 | 137, 182, 181 |
| S3 | 10 | 3 | 500 | 148, 180, 172 |
| S4 | 10 | 3 | 500 | 206, 187, 107 |
| S5 | 2 | 3 | 200 | 40, 100, 60 |
| S6 | 3 | 3 | 1000 | 179, 563, 258 |
| S7 | 5 | 3 | 500 | 217, 191, 92 |
| S8 | 8 | 3 | 1000 | 320, 291, 389 |
| S9 | 8 | 3 | 1000 | 169, 486, 345 |
| S10 | 5 | 4 | 500 | 103, 120, 138, 139 |
| R1 | 13 | 3 | 178 | 59, 71, 48 |
| R2 | 4 | 3 | 272 | 143, 77, 52 |
| Method | Description |
|---|---|
| Elbow | The WCSS values are plotted on the y-axis against different values of k on the x-axis. The optimal k value is identified at the point where the graph shows an “elbow” shape, indicating a change in the rate of decrease in WCSS. |
| Silhouette | A silhouette score for each data point is calculated ranging from −1 to +1. The k value that yields the highest average silhouette score is identified by averaging these scores for different values of k and plotting them. |
| CH | The best k value is the one with the maximal CH index. |
| DB | The best k value is the one with the lowest Davies–Bouldin Index (DBI). |
| Ratkowsky | The best k value is the one with the highest Ratkowsky index. |
| PtBiserial | This involves using the Point-Biserial Correlation Coefficient to assess the quality of clustering. The k value that produces the highest Point-Biserial score is selected. |
| McClain | This index evaluates the clustering quality by comparing the distances within clusters (compactness) to the distances between clusters (separation). The k value with the lowest McClain index value is chosen. |
| Dunn | The k value that yields the highest Dunn index is selected. |
| Gap_Maechler2012 | This method utilizes a bootstrap-based comparison against a null (random) model and employs the firstSEmax rule to choose the smallest value of k. |
| Gap_Dudoit2002 | This method builds upon the original gap statistic by incorporating practical refinements and a focus on high-dimensional biological data. The goal is to select the smallest value of k for which the gap statistic falls within one standard error of the maximum observed gap. |
| kl | This method measures the improvement in clustering quality as the number of clusters increases and identifies the point at which the improvement begins to slow down, commonly referred to as the “elbow.” The optimal k value is selected when the value of kl is maximal. |
| Hartigan | This method evaluates the improvement in the total within-cluster sum of squares when adding another cluster. A Hartigan value of 10 or less indicates that adding another cluster does not significantly enhance the clustering quality. |
| Scott | An adaptation of Scott’s Rule, which was originally designed for estimating histogram bin widths, this method uses the spread and dimensionality of the data to estimate the optimal value of k. |
| Marriot | The aim of this method is to identify the point at which adding more clusters no longer significantly enhances their compactness. The optimal value of k is determined at the point where adding additional clusters does not noticeably improve the Marriot index. |
| trcovw | The value of k is selected where the trcovw plot either has a sharp drop (the Elbow point) or stabilizes, thereby indicating that adding more clusters does not significantly reduce the within-cluster covariance. |
| Tracew | This method analyzes the trace of the within-cluster dispersion matrix. The optimal value of k is identified when adding more clusters does not reduce the Trace(W) value by much, thus indicating diminishing returns. |
| Friedman | This evaluates the clustering results by analyzing dispersion matrixes, focusing on compactness and separation. The k value with the lowest Friedman index value is chosen. |
| Rubin | Closely related to the Friedman method, the value of k that maximizes the Rubin index is selected. |
| Duda | This approach evaluates whether splitting a cluster into two significantly improves the quality of the clusters. |
| Pseudot2 | The optimal value of k is identified at a local minimum on the Pseudot2 curve, which is followed by a sudden increase at the next value of k. |
| Beale | This method compares the residual sum of squares when using k clusters versus k + 1 clusters and uses an F-test to determine whether the improvement is statistically significant. |
| Ball | This is an internal cluster validation technique based on analyzing the ratio of within-cluster to between-cluster variation, with the aim of finding a balance between cluster compactness and separation. |
| Frey | The Frey method establishes a stopping rule by examining how much the WCSS decreases when increasing from k to k + 1. The goal is to stop increasing k when the percentage decrease in WCSS becomes consistently small, indicating that adding more clusters does not significantly improve data modeling. |
| SDindex | The best value for k is indicated by choosing the one that corresponds to the lowest SD index. |
| Cindex | This method compares the distances between points within the same cluster to the minimum and maximum possible distances among all data points. The best value of k has the lowest C-index. |
| CCC | The Cubic Clustering Criterion (CCC) method determines the optimal value for k by identifying the point where the CCC value reaches a local maximum or exhibits a significant peak for the first time. |
| SDbw | The Scattering-Density between-within (SDbw) index is a cluster validity index used to assess both the compactness (density) and separation (scatter) of clusters. The best value for k has the lowest SDbw value. |
| Predicted Values | Actual Values | ||
| Positive | Negative | ||
| Positive | TP | FP | |
| Negative | FN | TN | |
| Method | Number of Groups by Dataset | True Group Detection Frequency (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 (3) | S2 (3) | S3 (3) | S4 (3) | S5 (3) | S6 (3) | S7 (3) | S8 (3) | S9 (3) | S10 (4) | R1 (3) | R2 (3) | ||
| Elbow | 3 * | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 (8.33) |
| Silhouette | 3 * | 2 | 3 * | 3 * | 3 * | 3 * | 2 | 4 | 3 * | 2 | 2 | 3 * | 7 (58.33) |
| Ch | 3 * | 2 | 3 * | 3 * | 3 * | 3 * | 2 | 3 * | 2 | 2 | 2 | 3 * | 7 (58.33) |
| DB | 4 | 10 | 3 * | 3 * | 3 * | 3 * | 2 | 3 * | 3 * | 2 | 2 | 3 * | 7 (58.33) |
| Ratkowsky | 3 * | 3 * | 3 * | 3 * | 2 | 3 * | 2 | 3 * | 3 * | 2 | 2 | 3 * | 8 (66.67) |
| PtBiserial | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 2 | 4 | 3 * | 4 * | 2 | 3 * | 9 (75.00) |
| Mcclain | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 0 (0.00) |
| Dunn | 10 | 8 | 2 | 3 * | 3 * | 3 * | 2 | 2 | 4 | 4 * | 2 | 3 * | 5 (41.67) |
| Gap_Maechler2012 | 1 | 3 * | 3 * | 3 * | 1 | 1 | 3 * | 4 | 3 * | 4 * | 4 | 3 * | 7 (58.33) |
| Gap_Dudoit2002 | 3 * | 6 | 3 * | 3 * | 3 * | 3 * | 3 * | 4 | 3 * | 4 * | 6 | 3 * | 9 (75.00) |
| kl | 3 * | 3 * | 3 * | 3 * | 4 | 3 * | 3 * | 5 | 4 | 4 * | 5 | 3 * | 8 (66.67) |
| Hartigan | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 4 * | 3 * | 3 * | 12 (100) |
| Scott | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 3 | 3 * | 3 | 3 * | 3 * | 11 (91.67) |
| Marriot | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 4 | 3 * | 4 * | 3 * | 3 * | 11 (91.67) |
| trcovw | 4 | 3 * | 3 * | 3 * | 5 | 3 * | 3 * | 3 | 3 * | 3 | 3 * | 3 * | 9 (75.00) |
| Tracew | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 3 | 3 * | 4 * | 3 * | 3 * | 12 (100) |
| Friedman | 3 * | 3 * | 3 * | 3 * | 9 | 3 * | 3 * | 3 | 3 * | 3 | 3 * | 3 * | 10 (83.33) |
| Rubin | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 4 | 4 | 4 * | 5 | 3 * | 9 (75.00) |
| Duda | 2 | 2 | 2 | 3 * | 2 | 2 | 3 * | 3 * | 2 | 2 | 3 * | 3 * | 5 (41.67) |
| Pseudot2 | 2 | 2 | 2 | 3 * | 2 | 2 | 3 * | 3 * | 2 | 2 | 3 * | 3 * | 5 (41.67) |
| Beale | 2 | 2 | 2 | 3 * | 2 | 2 | 3 * | 2 | 2 | 2 | 2 | 2 | 2 (16.67) |
| Ball | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 3 * | 11 (91.67) |
| Frey | 1 | 1 | 1 | 1 | 1 | 1 | 3 * | 1 | 1 | 1 | 3 * | 1 | 2 (16.67) |
| SDindex | 4 | 10 | 3 * | 3 * | 3 * | 3 * | 3 * | 4 | 3 * | 4 * | 3 * | 3 * | 9 (75.00) |
| Cindex | 4 | 9 | 10 | 4 | 10 | 9 | 4 | 3 * | 3 * | 8 | 4 | 5 | 2 (16.67) |
| CCC | 3 * | 10 | 3 * | 8 | 3 * | 4 | 5 | 4 | 4 | 4 * | 5 | 3 * | 5 (41.67) |
| SDbw | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 8 | 0 (0.00) |
| Dataset | Distance Metric | Accuracy | F1-Score | Precision | Recall |
|---|---|---|---|---|---|
| S1 | Canberra | 0.8160 | 0.8181 | 0.8160 | 0.8202 |
| Euclidean | 0.9260 | 0.9275 | 0.9261 | 0.9288 | |
| Manhattan | 0.9320 | 0.9334 | 0.9321 | 0.9346 | |
| S2 | Canberra | 0.4920 | 0.5463 | 0.5059 | 0.5936 |
| Euclidean | 0.8900 | 0.8918 | 0.8954 | 0.8883 | |
| Manhattan | 0.8540 | 0.8531 | 0.8551 | 0.8512 | |
| S3 | Canberra | 0.7655 | 0.7658 | 0.7669 | 0.7647 |
| Euclidean | 0.9559 | 0.9558 | 0.9568 | 0.9547 | |
| Manhattan | 0.9639 | 0.9638 | 0.9648 | 0.9628 | |
| S4 | Canberra | 0.6700 | 0.6821 | 0.6939 | 0.6707 |
| Euclidean | 0.9680 | 0.9708 | 0.9701 | 0.9715 | |
| Manhattan | 0.9620 | 0.9663 | 0.9648 | 0.9678 | |
| S5 | Canberra | 0.6450 | 0.7417 | 0.7633 | 0.7212 |
| Euclidean | 0.9500 | 0.9499 | 0.9667 | 0.9337 | |
| Manhattan | 0.9350 | 0.9366 | 0.9567 | 0.9174 | |
| S6 | Canberra | 0.7550 | 0.7595 | 0.7866 | 0.7341 |
| Euclidean | 0.9560 | 0.9563 | 0.9512 | 0.9616 | |
| Manhattan | 0.9430 | 0.9421 | 0.9414 | 0.9428 | |
| S7 | Canberra | 0.7620 | 0.7449 | 0.7498 | 0.7400 |
| Euclidean | 0.9900 | 0.9870 | 0.9913 | 0.9828 | |
| Manhattan | 0.9780 | 0.9720 | 0.9789 | 0.9652 | |
| S8 | Canberra | 0.6470 | 0.6578 | 0.6581 | 0.6574 |
| Euclidean | 0.9060 | 0.9087 | 0.9140 | 0.9034 | |
| Manhattan | 0.8810 | 0.8864 | 0.8916 | 0.8813 | |
| S9 | Canberra | 0.6360 | 0.6559 | 0.6754 | 0.6374 |
| Euclidean | 0.9410 | 0.9432 | 0.9521 | 0.9345 | |
| Manhattan | 0.9110 | 0.9076 | 0.9232 | 0.8925 | |
| S10 | Canberra | 0.5760 | 0.5499 | 0.5523 | 0.5476 |
| Euclidean | 0.8660 | 0.8698 | 0.8702 | 0.8695 | |
| Manhattan | 0.8320 | 0.8348 | 0.8333 | 0.8363 | |
| R1 | Canberra | 0.7978 | 0.8013 | 0.7976 | 0.8050 |
| Euclidean | 0.9607 | 0.9624 | 0.9671 | 0.9577 | |
| Manhattan | 0.9551 | 0.9577 | 0.9605 | 0.9549 | |
| R2 | Canberra | 0.6544 | 0.5843 | 0.5763 | 0.5924 |
| Euclidean | 0.9265 | 0.9212 | 0.9212 | 0.9212 | |
| Manhattan | 0.9338 | 0.9255 | 0.9257 | 0.9253 |
| Null Hypothesis | Test Statistic (p-Value) | |||
|---|---|---|---|---|
| Accuracy | F1-Score | Precision | Recall | |
| The performances of the three methods follow the same distribution | 23.473 K (<0.0001) *** | 23.502 K (<0.0001) *** | 23.536 K (<0.0001) *** | 23.502 K (<0.0001) *** |
| The performances of Canberra and Manhattan follow the same distribution | −17.250 M (<0.0001) *** | −17.167 M (<0.0001) *** | −17.083 M (<0.0001) *** | −17.167 M (<0.0001) *** |
| The performances of Canberra and Euclidean follow the same distribution | −18.750 M (<0.0001) *** | −18.833 M (<0.0001) *** | −18.817 M (<0.0001) *** | −18.833 M (<0.0001) *** |
| The performances of Manhattan and Euclidean follow the same distribution | 1.500 M (0.727) ns | 1.667 M (0.698) ns | 1.833 M (0.670) ns | 1.667 M (0.727) ns |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Junthopas, W.; Wongoutong, C. Pre-Determining the Optimal Number of Clusters for k-Means Clustering Using the Parameters Package in R and Distance Metrics. Appl. Sci. 2025, 15, 11372. https://doi.org/10.3390/app152111372
Junthopas W, Wongoutong C. Pre-Determining the Optimal Number of Clusters for k-Means Clustering Using the Parameters Package in R and Distance Metrics. Applied Sciences. 2025; 15(21):11372. https://doi.org/10.3390/app152111372
Chicago/Turabian StyleJunthopas, Wannaporn, and Chantha Wongoutong. 2025. "Pre-Determining the Optimal Number of Clusters for k-Means Clustering Using the Parameters Package in R and Distance Metrics" Applied Sciences 15, no. 21: 11372. https://doi.org/10.3390/app152111372
APA StyleJunthopas, W., & Wongoutong, C. (2025). Pre-Determining the Optimal Number of Clusters for k-Means Clustering Using the Parameters Package in R and Distance Metrics. Applied Sciences, 15(21), 11372. https://doi.org/10.3390/app152111372






