Research on Energy-Saving and Efficiency-Improving Optimization of a Four-Way Shuttle-Based Dense Three-Dimensional Warehouse System Based on Two-Stage Deep Reinforcement Learning

Abstract

In the context of rapid development within the logistics sector and widespread advocacy for sustainable development, this paper proposes enhancements to the task scheduling and path planning components of four-way shuttle systems. The focus lies on refining and innovating modeling approaches and algorithms to address issues in complex environments such as uneven task distribution, poor adaptability to dynamic conditions, and high rates of idle vehicle operation. These improvements aim to enhance system performance, reduce energy consumption, and achieve sustainable development. Therefore, this paper presents an energy-saving and efficiency-enhancing optimization study for a four-way shuttle-based high-density automated warehouse system, utilizing deep reinforcement learning. In terms of task scheduling, a collaborative scheduling algorithm based on an Improved Genetic Algorithm (IGA) and Multi-Agent Deep Deterministic Policy Gradient (MADDPG) has been designed. In terms of path planning, this paper provides the A*-DQN method, which integrates the A* algorithm(A*) with Deep Q-Networks (DQN). Through combining multiple layout scenarios and adjusting various parameters, simulation experiments verified that the system error is within 5% or less. Compared to existing methods, the total task duration, path planning length, and energy consumption per order decreased by approximately 12.84%, 9.05%, and 16.68%, respectively. The four-way shuttle vehicle can complete order tasks with virtually no conflicts. The conclusions of this paper have been validated through simulation experiments.

1. Introduction

In recent years, with the rapid development of the e-commerce industry, the warehousing and logistics industry has also ushered in a period of rapid growth. The four-way shuttle warehouse system stands out for its efficient and flexible operation characteristics, becoming the mainstream direction of intelligent warehousing technology. However, as the system scale expands, path planning complexity increases, and energy consumption issues have gradually attracted attention [1]. Existing research often ignores factors such as shuttle loading status, path structure restrictions, and energy consumption changes under multi-shuttle coordination, leading to energy waste and uneven equipment loads in practical applications [2]. Therefore, conducting research on four-way shuttle path planning and scheduling for energy consumption optimization is of great theoretical value and engineering significance for achieving energy conservation and emission reduction in warehousing systems and intelligent operation. It also aligns with the current trend towards greening and intelligentization of intelligent warehousing systems. The four-way shuttle storage system significantly enhances automation levels while reducing reliance on manual labor. Moreover, its flexible warehouse layout and high spatial utilization effectively reduce land and operational costs, providing a viable pathway for the construction of modern warehousing systems [3].

In a four-way shuttle-based warehouse system, faced with increasingly complex task scenarios, the efficiency and accuracy of scheduling and path planning are crucial to improving overall operation efficiency [3]. Traditional warehouse systems have many shortcomings in path planning and task scheduling, such as failing to fully consider shuttle loading status, path structure restrictions, and energy consumption changes during multi-shuttle coordination, resulting in uneven resource allocation and energy waste [4].

Domestic and foreign scholars have conducted extensive research on path planning and scheduling optimization for four-way shuttle-based warehouse systems. In terms of path planning, researchers have proposed various improved algorithms, such as the improved branch cutting and branch pricing algorithm by Sun Zhuo et al. [5], the algorithm for directly constructing paths based on Non-Uniform Rational B-Splines (NURBS) surfaces proposed by Anushrut et al. [6], Guo et al. [7] achieved visual guidance-based path extraction and joint optimization in robotic weld grinding tasks, Cui’s [8] fast RRT algorithm, Jiang Qilong’s [9] PSO-PH-RRT* algorithm, etc., to address challenges such as the complexity of multi-objective optimization in intricate environments and the limited adaptability to dynamic environmental conditions. Gou Yujun et al. [10] proposed the improved Imperialist Northern Goshawk Optimization (INGO), which demonstrated stronger global optimization ability and stability in the grid map path planning experiment. In terms of multi-shuttle scheduling, research efforts have primarily centered on task allocation and collaborative optimization. Fan et al. [11] developed an integrated scheduling model. Sango et al. [12] introduced a novel approach to the design of human–machine collaborative systems tailored for Industry 5.0. Tang et al. [13] proposed a data-driven optimization framework for job scheduling. Cai et al. [14] established a collision avoidance scheduling architecture leveraging edge intelligence. Li et al. [15] achieved efficient solutions in seconds in large-scale environments. Carida et al. [16] designed a multi-attribute scheduling mechanism for Automated Guided Vehicle (AGV) based on fuzzy systems and Petri network. Tang et al. [17] incorporated quantum computing techniques to formulate a quadratic unconstrained binary optimization model. Liu et al. [18] improved the solution stability and quality of scheduling through enhancements to heuristic strategies and local search mechanisms. Xu Lili et al. [19] constructed a collaborative scheduling model integrating four-way shuttles and elevators. Yin Yinghao [20] proposed a comprehensive framework for multi-four-way shuttle path planning and real-time traffic scheduling. In terms of energy consumption optimization, research has gradually shifted from single-objective optimization to multi-dimensional collaborative optimization. For example, Zhou et al. [21] proposed a robust scheduling model for AGVs with power constraints, Yang et al. [22] proposed a path planning algorithm considering shuttle rollover stability, Hu et al. [23] proposed a multi-stage hybrid scheduling model for AGV charging and scheduling collaboration considering a new supporting facility (AGV-Mate) for AGV charging. Ma et al. [24] proposed a hybrid optimization method integrating staged and continuous speed control strategies in a U-shaped dock scenario. Yue et al. [25] incorporated the configuration and scheduling of AGVs and double dual-trolley quay cranes into a unified modeling framework. Overall, research on path planning and scheduling optimization is moving towards dynamic, intelligent, and multi-objective optimization. However, further breakthroughs are still needed in areas such as dynamic environment adaptability, energy consumption optimization, and task coordination.

This study differs from recent domestic and international research in several aspects. Regarding path planning, Sun Zhuo et al.’s [5] improved branch-and-cut algorithm focuses on static multi-objective optimization, while Cui’s [8] fast RRT algorithm relies on random sampling for post-collision avoidance. Neither addresses dynamic changes in device states or precise conflict identification. This study innovatively proposes an A*-DQN dynamic fusion architecture. It dynamically switches the feasible path region in real-time via load status flags and quantifies three conflict types based on direction vector angles. This forms a “global routing guidance + local dynamic fine-tuning” dynamic-static coordination model, overcoming the bottleneck of insufficient dynamic adaptability in traditional algorithms. Regarding task scheduling, Fan et al.’s [11] integrated scheduling model only achieves basic task-device matching, while Xu Lili et al.’s [19] elevator–shuttle collaboration excludes energy consumption considerations and primarily employs centralized control. This study constructs the IGA-MADDPG hierarchical coordination framework. It employs IGA for global pre-planning and injects the MADDPG experience pool to resolve cold-start issues. Multi-agent distributed decision-making enables local dynamic adjustments, while integrating energy consumption, time, and load balancing into a coupled optimization objective. This overcomes the limitations of traditional scheduling—single-objective, centralized, and weak coordination. Regarding energy optimization, Zhou et al. [21] only considered fixed power constraints for AGVs, while Ma et al. [24] designed dedicated strategies for U-shaped docks, partially relying on hardware assistance. This study proposes a load-state-driven system-level energy modeling approach, distinguishing between shuttle and elevator empty/loaded states. Load energy consumption of shuttles and elevators is important in the construction of a unified cross-device model. This approach reduces empty-run energy consumption without requiring additional hardware. Furthermore, it decouples the model from the layout by utilizing grid maps and Manhattan distance, maintaining stable optimization across three warehouse scenarios. This overcomes the limitations of traditional energy consumption research, which is characterized by “single-device focus, strong dependency, and narrow application scenarios”.

In summary, existing studies suffer from issues such as uneven task allocation, poor adaptability to dynamic environments, and high shuttle idling rates. Therefore, this paper proposes a multi-shuttle scheduling optimization method combining an improved genetic algorithm (IGA) with a multi-agent deep deterministic policy gradient algorithm (MADDPG), as well as an A*-DQN path planning method integrating A* heuristic search and Deep Q-Networks (DQN), aiming to optimize the path performance of four-way shuttles in complex layouts and dynamic environments through a dynamic map switching mechanism, path conflict resolution strategy, and the adaptive capabilities of reinforcement learning. Specific contributions are as follows:

(1)

Through a layered architecture consisting of a global optimization layer and a local execution optimization layer, the advantages of both algorithms are fully utilized to achieve synergistic improvements in task allocation, path planning, and energy consumption optimization.

• The global optimization layer utilizes IGA to generate high-quality initial task allocation plans, laying the foundation for the entire scheduling process. By coordinating the scheduling of four-way shuttles and elevators, unnecessary waiting and empty running between equipment are avoided, enhancing the overall consistency of the system’s scheduling. The IGA balances three key objectives, namely: energy consumption, efficiency, and equipment load balancing, thereby overcoming the limitations of traditional genetic algorithms (GA) which focus solely on single-objective optimization. By incorporating ‘Sequence-Retaining Crossover’ and ‘Path Reversal Mutation’, this approach reduces the empty running rate of four-way shuttles, accelerates convergence speed, and enhances global optimality. It thereby resolves the issues of slow convergence and susceptibility to local optima, which is inherent in traditional genetic algorithms (GA).
• The local execution optimization layer uses the MADDPG algorithm to dynamically adjust task sequences and path planning based on real-time status, ensuring optimal energy consumption and efficient operation in complex dynamic environments. The MADDPG algorithm treats each four-way shuttle and elevator as an independent agent, establishing a local observation space for each. It updates their local state such as task information for four-way shuttles and the elevators’ current floor level every second. Through a critic network invoking the global state, it dynamically adjusts task sequences in real time to prevent conflicts among four-way shuttles and elevators.
• By integrating IGA with MADDPG, the scheduling plan generated by IGA is simulated. The data generated from this simulation is then injected into the experience replay pool, thereby enhancing the efficiency of local execution optimization and addressing the optimizing low efficiency issues arising from reliance on a single algorithm for optimization.

(2)

By introducing shuttle loading status information to construct a path map switching mechanism, path constraints can be automatically adjusted according to the shuttle’s different operating status.

• Using the A* algorithm, calculating the angle of direction vectors between vehicles travelling in four directions, quantifying conflict types, and resolving them according to corresponding methods, this approach addresses the issue where traditional path planning disability to quantify conflict types, resulting in high collision risks.
• By employing the DQN algorithm and updating environmental states in real time, adaptive path adjustments are achieved within dynamic environments. This resolves issues inherent in traditional path planning algorithms, such as path conflicts arising from their inability to update generated paths.
• By integrating the A* algorithm with the DQN algorithm, the high-quality initial path planning solutions generated by A* during the early training phase are provided as experience to the DQN algorithm, thereby accelerating DQN’s convergence speed. This enables the A*-DQN algorithm to effectively plan safe and efficient paths in complex environments compared to traditional path planning algorithms.

This study focuses on key challenges commonly encountered in practical applications of high-density four-way shuttle storage systems, including low scheduling efficiency, frequent path conflicts, and high energy consumption. Centered on the dual core objectives of minimizing system energy consumption and optimizing operational time, systematic research is conducted at two distinct levels: task scheduling and path planning. At the task scheduling level, a hierarchical scheduling framework based on the collaborative optimization of IGA and MADDPG is proposed. At the path planning level, an A*-DQN path optimization method integrating A* heuristic search with DQN is introduced. Ultimately, through simulation experiments incorporating diverse layout scenarios, these two approaches demonstrated significant advantages in task scheduling, path planning, and energy consumption optimization. This provides novel research perspectives and solutions for advancing the intelligent development of four-directional vehicle warehousing systems.

2. Materials and Methods

2.1. Dense Three-Dimensional Warehouse Modeling

2.1.1. Overview of the Four-Way Shuttle-Based Warehouse System

The research object of this paper is a four-way shuttle-based warehouse system with several elevators and four-way shuttles. The storage area has three layout forms, namely sparse rectangular layout, dense rectangular layout, and fishbone layout, as shown in Figure 1b–d. The system consists of independent storage units, aisles, conveyor belts located at the entrance, and elevators located on one side of the system that connect each layer and the conveyor belts. Through task scheduling, the pick-up or storage locations for incoming and outgoing goods are specified. Conveyor belts and elevators transport goods between floors, and AGVs follow pre-planned paths through the aisle network’s topological structure to reach designated locations for dispensing or retrieving goods. Through scheduling optimization and path planning, operation efficiency has been significantly improved [26] and energy consumption reduced.

2.1.2. Warehouse Simulation Environment Map

Considering that map environment modeling methods need to satisfy requirements such as quantifiable spatial constraints, dynamic adaptability, and algorithm compatibility, the grid map method is convenient for multi-objective modeling, responds quickly to environmental changes, and satisfies the dynamic obstacle avoidance requirements of multi-shuttle coordination. Therefore, this study chooses the grid map method to construct a reasonable model [27].

As shown in Figure 2, taking a four-way shuttle-based warehousing system with a dense rectangular layout as an example, the warehouse plane is discretised into uniform grid units. Identify feasible areas using a binary matrix $G\in {\left\{0,1\right\}}^{M\times N}$ of ‘0’ and ‘1’, where ‘1’ indicates obstacle areas, and then construct a three-dimensional grid stack $G_{3D}=\left\{G_1,G_2,\dots ,G_K\right\}$ to describe cross-layer connectivity. In order to improve computational efficiency and facilitate direct invocation by search algorithms, a passage cost $C_{ij}$ is defined for the grid $\left(i,j\right)$:

$$C_{ij}=1+\alpha N\left(i,j\right)$$

(1)

In the equation, $N$ indicates the frequency of historical path intersections, refers to the number of times a planned path has passed through a grid in the past. $\alpha$ indicates conflict sensitivity coefficient, used to adjust the degree of influence of historical path crossing frequency on traffic costs.

2.1.3. Distance Calculation Method

In warehouse system path planning, the accuracy of distance calculation directly affects scheduling efficiency and energy optimization. Based on the four-way shuttle motion constraints and the Manhattan distance algorithm’s strong compatibility and good real-time performance, this study selects the Manhattan distance calculation method as the core metric for path planning and energy consumption optimization [28]. Equation (2) is the equation for calculating the Manhattan distance algorithm.

$$d=|x_1-x_2|+|y_1-y_2|$$

(2)

In the equation, $d$ Indicates the distance travelled by a four-way shuttle.$\left(x_1,y_1\right),\left(x_2,y_2\right)$ separately indicate the coordinates of the two points.

2.2. Energy-Saving and Efficiency-Enhancing Modeling

2.2.1. Mathematical Model for the Scheduling Optimization of Four-Way Shuttles and Elevators

In order to achieve efficient and low-energy consumption four-way shuttle collaborative operation scheduling, it is necessary to construct an energy consumption optimization model and operation constraints for the scheduling level. The model covers elevator scheduling behavior modeling, equipment energy consumption analysis, and a system of constraint functions for solving optimization problems.

(1)

Mobile Time Model

For the maximum speed $v_{\max }$ and acceleration $a$ of four-way shuttles and elevators, the movement time is divided into acceleration, constant speed, and deceleration segments for modeling [29]. When calculating mobile time, the following two situations should be considered based on the distance:

(1) If the total distance travelled is greater than or equal to twice the distance travelled from 0 to the maximum speed $v_{\max }$ with acceleration $a$, the Equation is expressed as $d\ge 2d_a=v_{\max }^2/a$. In this situation, the four-way shuttle and elevator can complete all three stages; Total time T is:

$$T=2t_a+t_c=2·{\displaystyle \frac{v_{\max }}{a}}+{\displaystyle \frac{d-\frac{v_{\max }^2}{dx}}{v_{\max }}}={\displaystyle \frac{v_{\max }}{a}}+{\displaystyle \frac{d}{v_{\max }}}$$

(3)

In the equation, $t_a$ indicates acceleration time. $t_c$ indicates deceleration time. $d_a$ indicates the distance travelled when moving from a speed of 0 to the maximum speed $v_{\max }$ with uniform acceleration $a$.

(2) If the total distance travelled is less than or equal to twice the distance travelled from 0 to the maximum speed $v_{\max }$ with acceleration $a$, the Equation is expressed as $d<v_{\max }^2/a$. In this situation, the shuttle cannot reach maximum speed; Total time T is:

$$T=2·\sqrt{{\displaystyle \frac{d}{a}}}$$

(4)

In the equation, $d$ indicates the distance travelled by a four-way shuttle. $a$ indicates the uniform acceleration of a four-way shuttle.

In summary, the movement time $T$ can be calculated using Equation (5):

$$T=\left\{\begin{array}{l}{\displaystyle \frac{v_{\max }}{a}}+{\displaystyle \frac{d}{v_{\max }}}\hspace{0.33em},\hspace{0.33em}if\hspace{0.33em}d\ge {\displaystyle \frac{v_{\max }^2}{a}}\hfill \\ 2·\sqrt{{\displaystyle \frac{d}{a}}}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},\hspace{0.33em}if\hspace{0.33em}d<{\displaystyle \frac{v_{\max }^2}{a}}\hfill \end{array}\right.$$

(5)

In the equation, $d$ indicates the distance travelled by a four-way shuttle. $a$ indicates the uniform acceleration of a four-way shuttle. $v_{\max }$ indicates the highest speed of a four-way shuttle.

(2)

Energy Consumption Mathematical Model

Using a general energy consumption calculation equation, such as that shown in Equation (6), the unit energy consumption parameters are automatically selected based on the equipment status. Using a general energy consumption calculation equation, such as that shown in Equation (6), the unit energy consumption parameters are automatically selected based on the equipment status. Combining the equipment operating trajectory and task status, the energy consumption of the four-way shuttle $E^F$ and the energy consumption of the elevator $E^L$ are calculated separately, and finally summarized as the total system energy consumption $E_{Total}$ [30]. As shown in Equation (6):

(1) For any handling device (denoted as device $k$), the energy consumption of a particular run $E_i$ can be uniformly expressed as:

$$E_k=\left[e_k^{load}·{\rho }_k+e_k^{empty}·\left(1-{\rho }_k\right)\right]·d_k$$

(6)

In the equation, $d_k$ indicates the path distance of device operation. The $e_k^{load}$ and $e_k^{empty}$ indicate the unit load energy consumption and unit no-load energy consumption of the equipment, separately. They come from equipment manuals. ${\rho }_i$ Indicates the status indicator variable. When the equipment $k$ is under load, the value of ${\rho }_k$ is 1. Otherwise, it is 0.

(2) According to Equation (7), the four-way shuttle energy consumption $E^F$, the elevator energy consumption $E^L$, and the total system energy consumption $E_{Total}$ can be calculated as follows:

$$\left\{\begin{array}{l}{E}^F={\displaystyle \sum _{i=1}^{N_a}{E}_i^F={\displaystyle \sum _{i=1}^{N_a}\left[e_F^{load}·{\rho }_i+e_F^{empty}·\left(1-{\rho }_i\right)\right]·d_i}}\hfill \\ E^L={\displaystyle \sum _{j=1}^{N_b}{E}_j^L={\displaystyle \sum _{j=1}^{N_b}\left[e_L^{load}·{\rho }_j+e_L^{empty}·\left(1-{\rho }_j\right)\right]·d_j}}\hfill \\ E_{Total}=E^F+E^L={\displaystyle \sum _{i=1}^{N_a}{E}_i^F+{\displaystyle \sum _{j=1}^{N_b}{E}_j^L}}\hfill \end{array}\right.$$

(7)

In the equation, $i$ and $j$ respectively indicate four-way shuttle $i$ and elevator $j. N_a$ and $N_b$ respectively indicate the number of four-way shuttles and the number of elevators. $e_F^{load}$, $e_F^{empty}$ indicate the unit load energy consumption and unit no-load energy consumption of the four-way shuttle, separately. The $e_L^{load}$, $e_L^{empty}$ indicate the unit load energy consumption and unit no-load energy consumption of the elevator, separately. ${\rho }_i$ and ${\rho }_j$ respectively indicate the status indicator variable of the four-way shuttle $i$ and the elevator $j$, with load of 1 and no load of 0.

(3)

Model Constraint

To ensure the practicality and rationality of the model, this section imposes constraints in terms of speed limits, task flow, and resource allocation.

(1) Speed and Acceleration Constraints

To prevent risks caused by excessive acceleration or speed of four-way shuttles and elevators, it is necessary to constrain the safety range of both. The mathematical expression is as follows:

$$\left\{\begin{array}{l}{v}_i^F\left(t\right)\le v_{\max }^F\hspace{0.33em},\forall i,t\hfill \\ a_i^F\left(t\right)\le a_{\max }^F\hspace{0.33em},\forall i,t\hfill \end{array}\right.$$

(8)

$$\left\{\begin{array}{l}{v}_j^L\left(t\right)\le v_{\max }^L\hspace{0.33em},\forall j,t\hfill \\ a_j^L\left(t\right)\le a_{\max }^L\hspace{0.33em},\forall j,t\hfill \end{array}\right.$$

(9)

In the equation, $v_i^F\left(t\right)$, $a_i^F\left(t\right)$ indicate the speed and acceleration of the i-th four-way shuttle at time $t$ separately. The $v_{\max }^F$, $a_{\max }^F$ indicate the maximum speed and maximum acceleration allowed for four-way shuttles separately. The $v_j^L\left(t\right)$, $a_j^L\left(t\right)$ indicate the speed and acceleration of the i-th elevator at time t separately. $v_{\max }^L$, $a_{\max }^L$ indicate the maximum speed and maximum acceleration allowed for elevators separately.

(2) Task Sequence Constraints

To prevent task logic confusion or long waiting times that could reduce job efficiency, the task sequence for the same four-way shuttle must follow a first-in, first-out logic:

$$t_i^n\le t_i^m\le t_i^{n+1}\hspace{0.33em},\hspace{0.33em}\forall i$$

(10)

where $t_i^n$ denotes the start time of the $n$-th inbound (storage) task, $t_i^m$ denotes the start time of the $m$-th outbound (retrieval) task, and $t_i^{n+1}$ represents the start time of the ($n+1$)-th inbound task.

The waiting time range for cross-level tasks is given by:

$$t_i^{wait}\le T_{wait}^{\max }\hspace{0.33em},\hspace{0.33em}\forall i$$

(11)

In the equation, $t_i^{wait}$ indicates the waiting time for any task of the i-th four-way shuttle. $T_{\max }^{\mathit{wait}}$ indicates the maximum waiting time for a four-way shuttle to cross layers.

(3) Path Feasibility Constraint

The empty four-way shuttle can move in the lane and longitudinally under the pallet. When loaded, it can only move in the lane [31]. The mathematical expression is as follows:

$$P_k\left(t\right)=\left\{\begin{array}{l}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} G\left(k,t\right)\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},{\delta }_{load,k}\left(t\right)=1\hfill \\ G\left(k,t\right){\displaystyle \cup L\left(k,t\right)}\hspace{0.33em},{\delta }_{load,k}\left(t\right)=0\hfill \end{array}\right.\hspace{0.33em}$$

(12)

In the equation, $G\left(k,t\right)$ indicates the path function of shuttle $k$ in the lane network. $L\left(k,t\right)$ indicates the path function of shuttle $k$ in the longitudinal track of the warehouse area. ${\delta }_{load,k}\left(t\right)\in \left\{0,1\right\}$ indicates the load status indicator variable of shuttle $k$ at time $t$, where ‘1’ indicates a load and ‘0’ indicates no load.

(4) Cooperative Scheduling Constraint

At any given time, only one elevator serves one four-way shuttle, and only one four-way shuttle is allowed to retrieve or store the same goods at the same time:

$$\left\{\begin{array}{l}{\displaystyle \sum _{k=1}^{N_a}{u}_{i,k}\left(t\right)\le 1,\hspace{0.33em}\forall i,t}\hfill \\ {\displaystyle \sum _{k=1}^{N_b}{o}_{j,k}\left(t\right)\le 1,\hspace{0.33em}\forall j,t}\hfill \end{array}\right.$$

(13)

In the equation, $u_{i,k}\left(t\right)$, $o_{j,k}\left(t\right)$ Indicates whether a shuttle or piece of equipment is in use.

(5) Weight Restrictions for Goods

The shuttle load must not exceed the threshold value:

$$|N_k-\overline{N}|\le \Delta N,\hspace{0.33em}\forall k$$

(14)

In the equation, $N_k$ indicates the load of the four-way shuttle k. $\overline{N}$ indicates the rated load capacity of a four-way shuttle. $\Delta N$ indicates the maximum value at which the shuttle’s load can exceed the rated load.

2.2.2. Mathematical Model for Four-Way Shuttle Path Planning

(1)

Three-Dimensional Coordinate System and Order Task Set

(1) Three-Dimensional Coordinate System

To enable path computation and energy consumption modeling for four-way shuttles in dense warehouse systems, a unified three-dimensional coordinate system is constructed, as illustrated in Figure 1, to represent both shuttle positions and storage locations. The coordinate of task $O_j$ in the racking system is denoted as $C\left(O_j\right)=\left(x_i,y_i,z_i\right)$, where x,y,z are defined as shown in Figure 1.

(2) Order Task Set

Let the task set be $R_i=\{R_1,\dots ,R_n\}$, where $R_i>0$ indicates that the $i$-th task is an inbound operation, and $R_i<0$ indicates that the $i$-th task is an outbound operation.

(2)

Distance Calculation Model

The distance for inbound and outbound operations is calculated based on the coordinates, integrating both same-layer and cross-layer operation models for the four-way shuttle, as shown in Equations (15) and (16). The distance from the shuttle’s current position $\left(x_i,y_i,z_i\right)$ to the target position $\left(x_j,y_j,z_j\right)$ is given by Equation (17).

For same-layer operations, i.e., $z_i=z_j$, the path distance for the four-way shuttle from the inbound location to the outbound location is expressed as:

$$d=D_{z_i}=D_{z_j}=|x_i-x_j|\times X_L+|y_i-y_j|\times Y_L$$

(15)

where $D_{z_i}$, $D_{z_j}$ denote the travel distance of the four-way shuttle from the inbound location to the outbound location, and ($x_i,y_i$) and ($x_j,y_j$) represent the current and target coordinates of the shuttle, respectively; $X_{L,}{Y}_L$ are the length and width of the storage unit cell.

For cross-layer operations of the four-way shuttle, the total path consists of the following three segments: the distance $D_{z_i}$ from the current position to the elevator on the current layer, the distance $D_{z_i,z_j}$ for the shuttle to transfer via the elevator to the target layer, and the distance $D_{z_j}$ from the elevator position on the target layer to the final target position, as expressed in Equation (16):

$$D_{z_i,z_j}=|z_i-z_j|\times Z_L$$

(16)

where $z_i,z_j$ denote the initial and target layers for elevator transfer, and $Z_L$ represents the height of a single layer in the dense warehouse.

The distance calculation model $d$ is as follows:

$$d=D_{zi}+\Delta z·\left(D_{zi,zj}+D_{zj}\right)$$

(17)

where d represents the travel distance of the four-way shuttle and is identical to that in Equation (2). When the shuttle operates on the same layer, $\Delta z=0$; when it operates across different layers, $\Delta z=1$.

2.3. Energy Consumption Reduction and Efficiency Enhancement Scheduling Algorithm

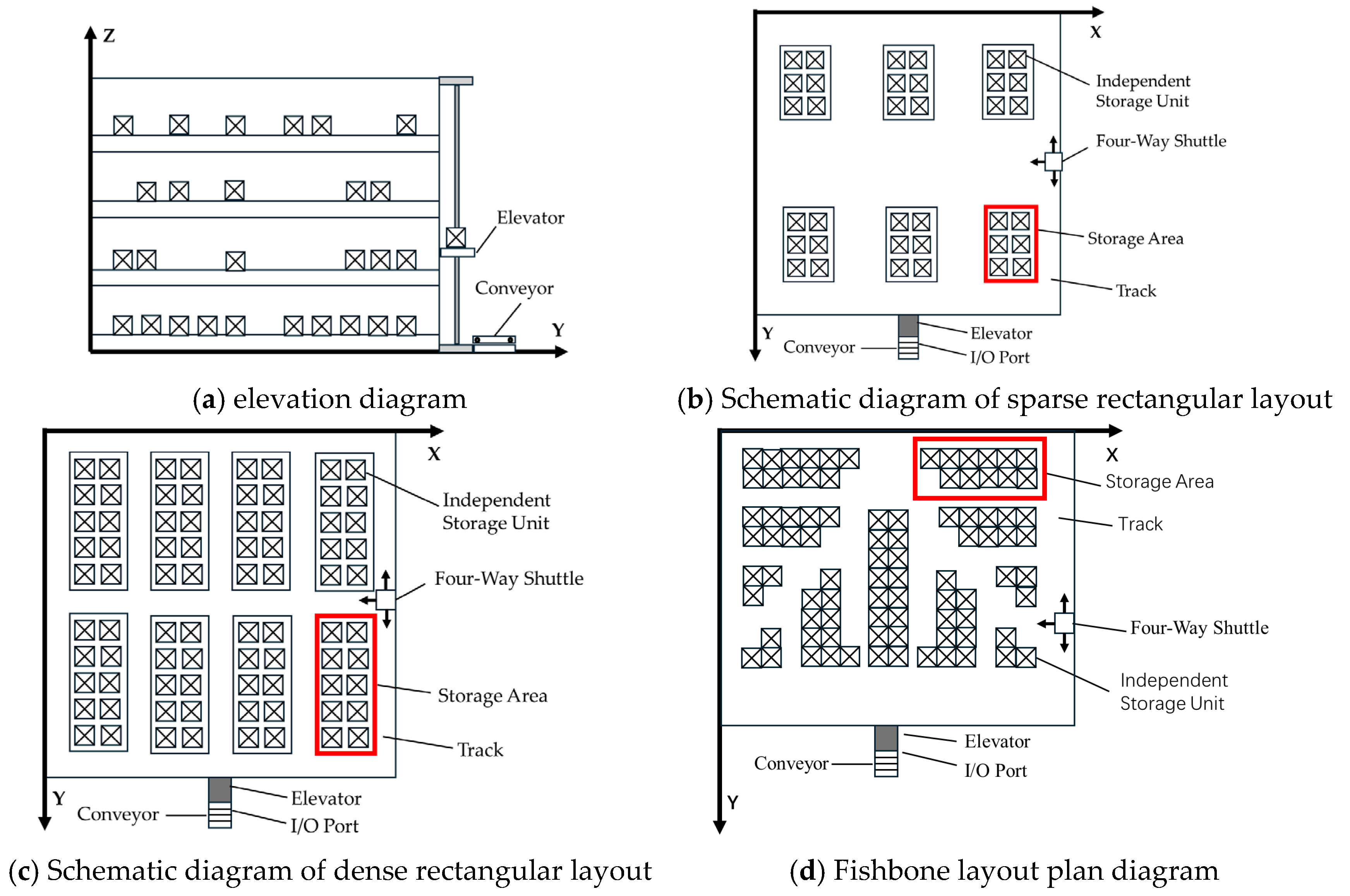
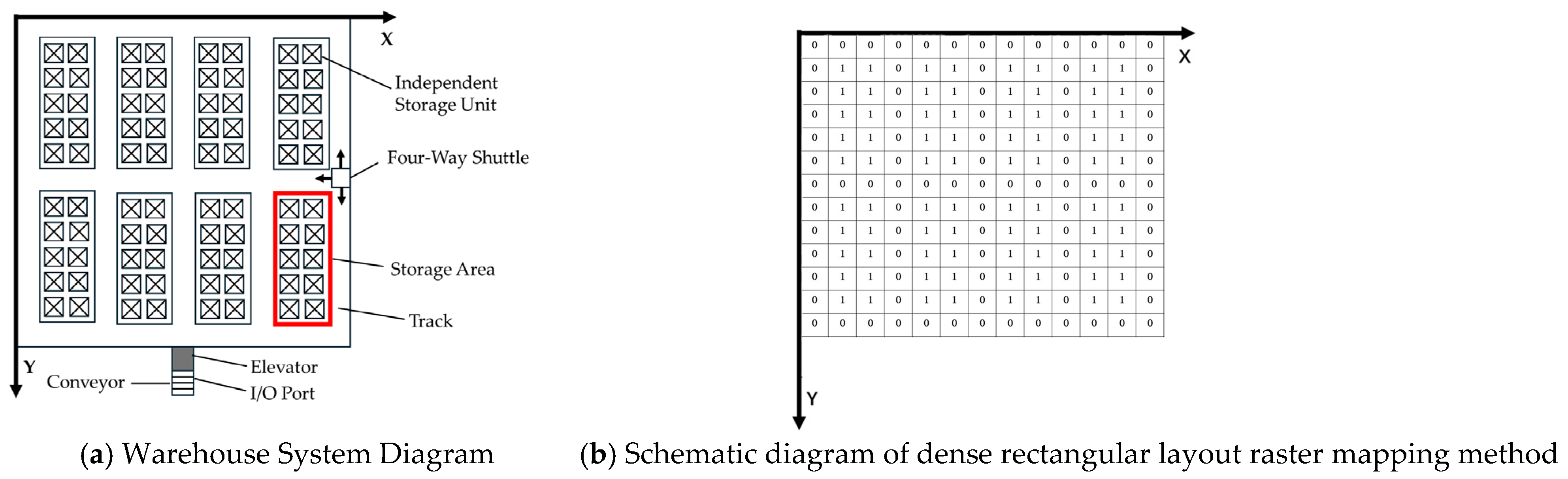
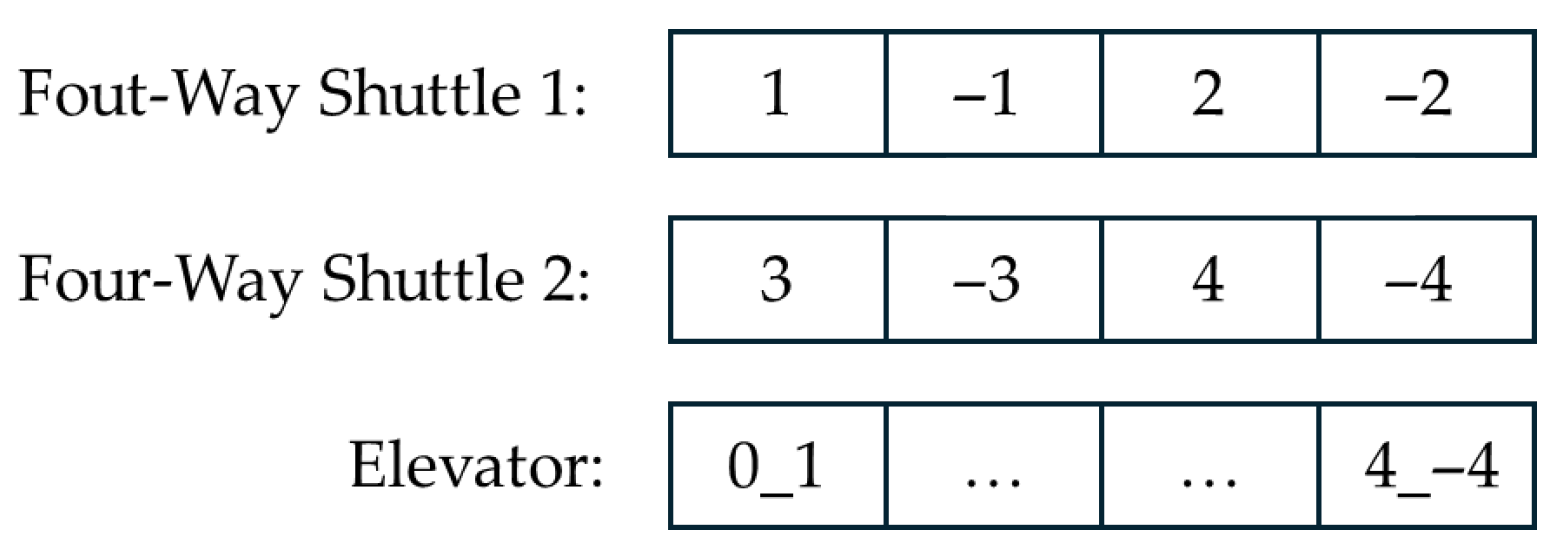
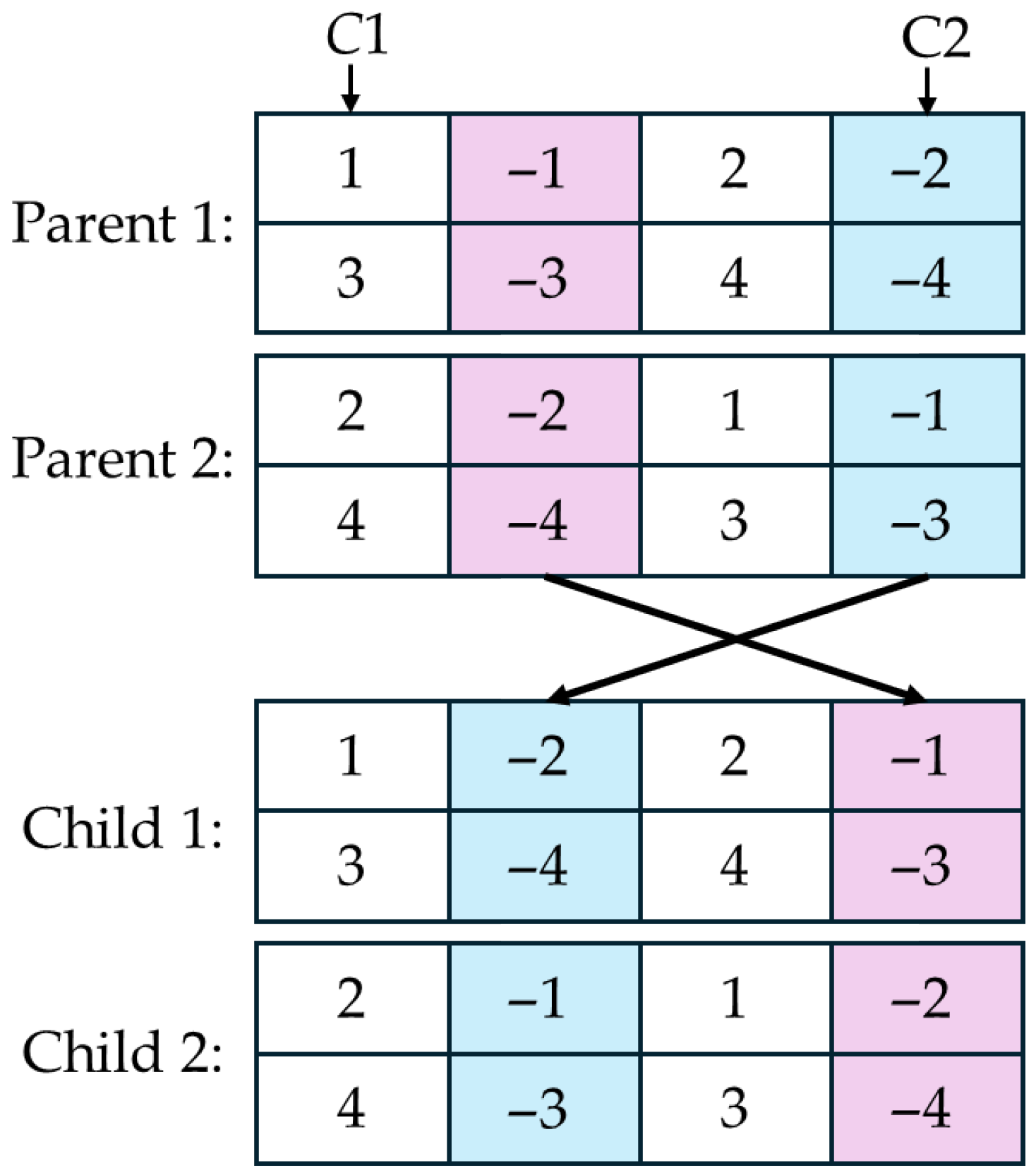
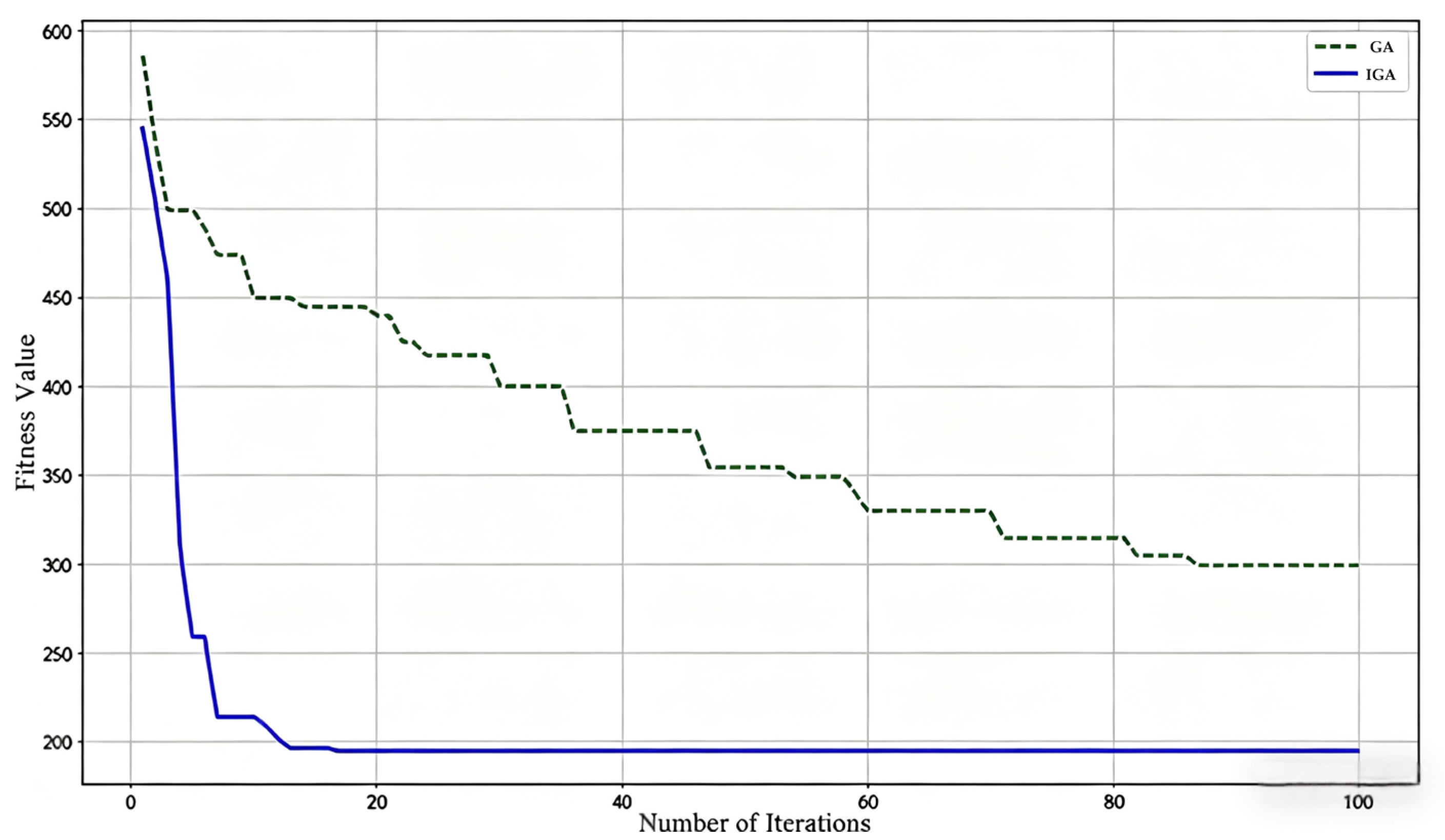
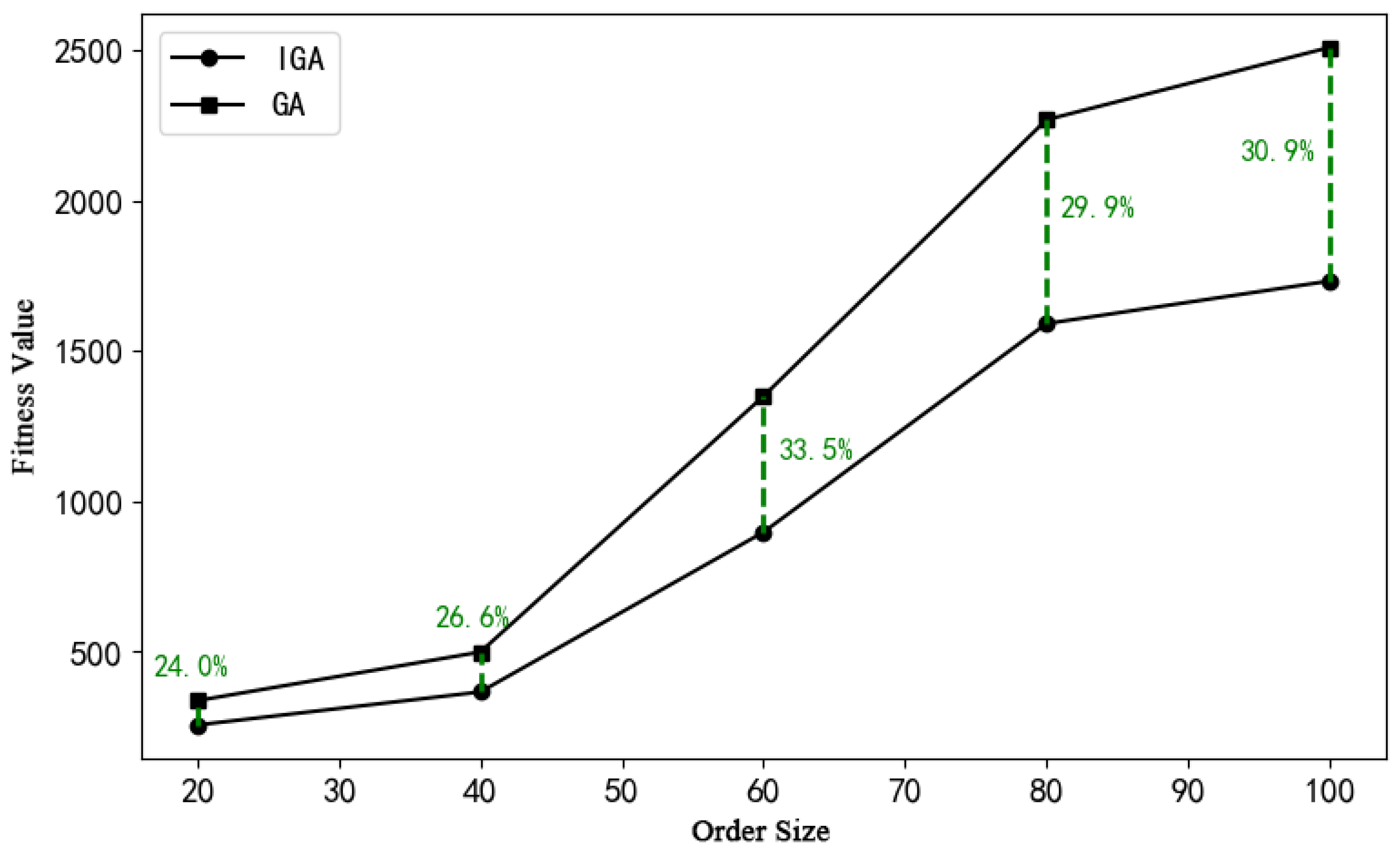
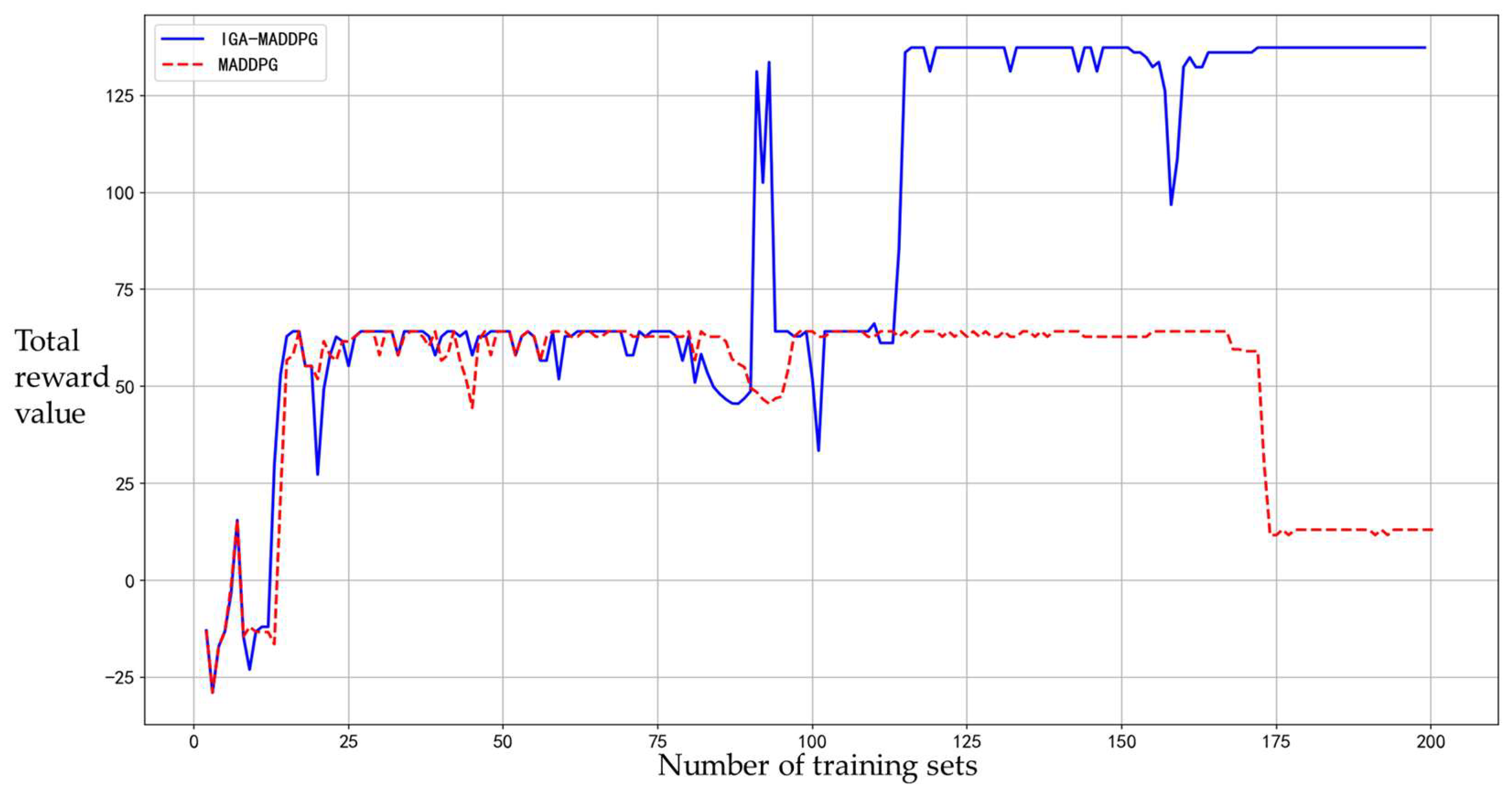
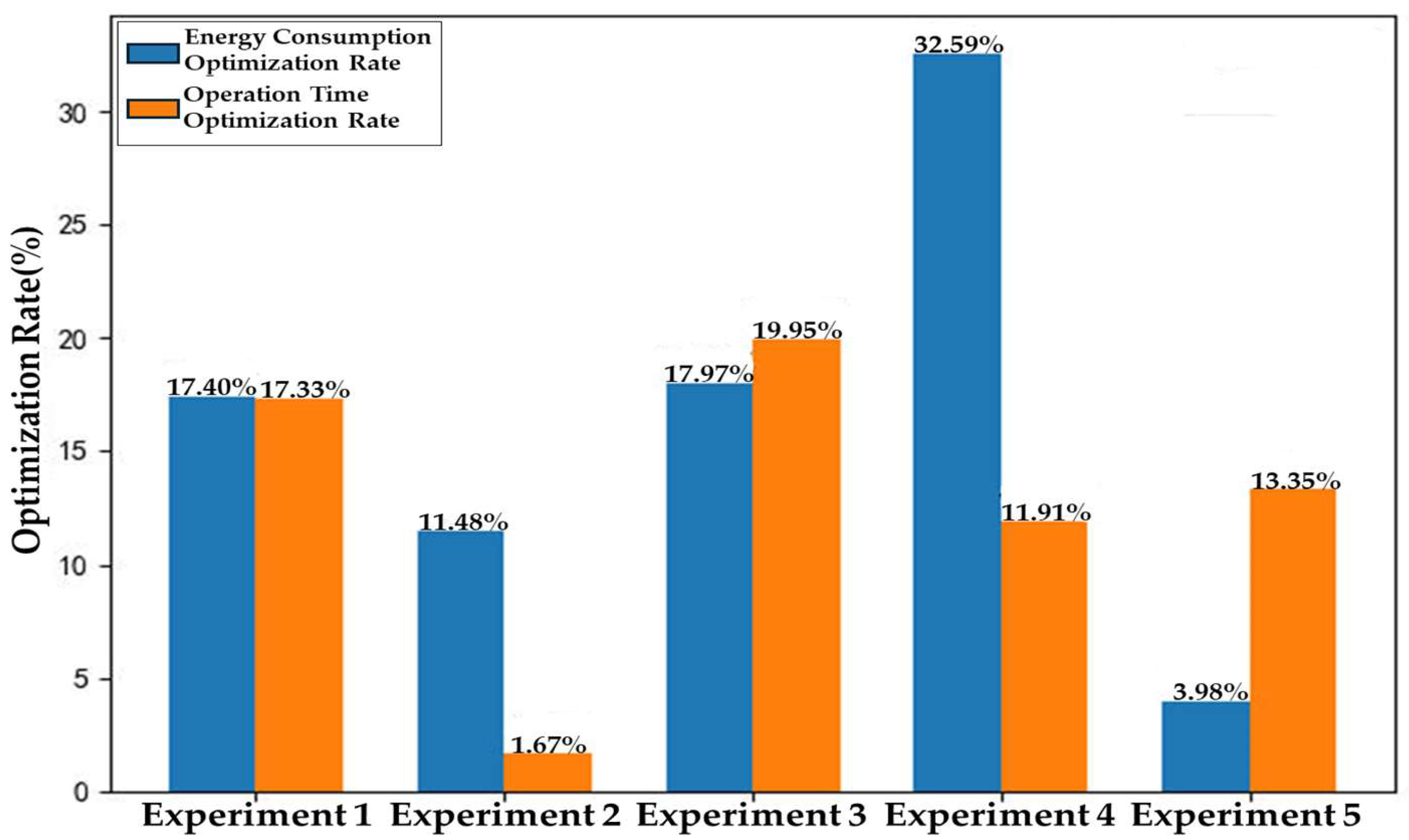
2.3.1. Design of Improved Genetic Algorithm

To optimize the task allocation and scheduling routes for four-way shuttles and elevators during collaborative operations, this study designs an improved genetic algorithm based on path reversal mutation and sequence retention crossover, taking into account the operational characteristics of the warehousing system. The algorithm adopts a hierarchical chromosome encoding structure and introduces a weighting method to balance three objectives: energy consumption, time, and load balancing, thereby enhancing the practicality and global optimality of the scheduling strategy.

(1)

Initialization of Population and Encoding

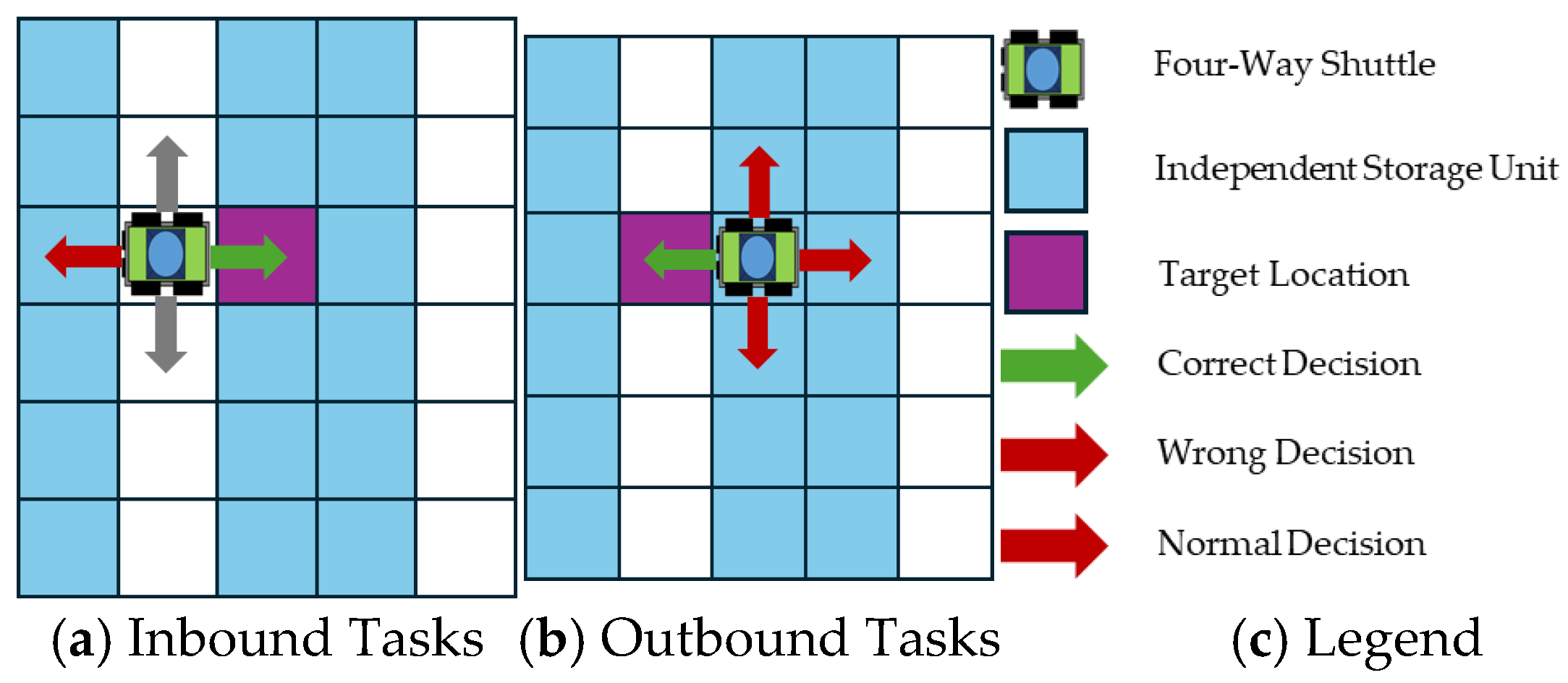
Cells containing existing goods are marked as 1, while vacant positions are marked as 0, forming an executable task region map. Based on order information, the system classifies all tasks into two categories:

(1) Inbound tasks: Goods need to be transported from the bottom entrance to designated storage locations, and are assigned positive integer identifiers;

(2) Outbound tasks: Goods need to be transported from designated storage locations to the exit and are assigned negative integer identifiers.

According to the collaborative operation logic of four-way shuttles and elevators, this study designs a chromosome structure with $V+1$ layers, where $V$ denotes the number of four-way shuttles. Layers 1 to $V$ represent the order sequence of tasks assigned to each shuttle, while the $V+1$-th layer represents the elevator’s operation sequence, which is determined based on the current position of the elevator and the operational relationships from layers 1 to $V$. For example, if the scheduling task includes four inbound and four outbound tasks, to be executed collaboratively by two four-way shuttles and one elevator, the chromosome structure is as shown in Figure 3. In this structure, the first and second layers correspond to the tasks allocated to the two shuttles, and the third layer is the elevator operation sequence generated by the system according to cross-layer transfer requirements.

(2)

Fitness Calculation

To minimize energy consumption, total operation time, and load balancing index, this study establishes a fitness model $F_{\min }$.

$$F_{\min }=\alpha ·E+\beta ·T+\gamma ·LBD$$

(18)

In this equation, $\alpha ,\beta ,\gamma$ are the weighting coefficients for the three objectives, subject to the constraint $\alpha +\beta +\gamma =1$. $LBD$ denotes the load balancing index.

To accommodate different operational modes, this study adopts two types of weighting strategies:

(1) Energy-Saving Priority Mode:

In scenarios with moderate task density and a focus on cost control, the weighting coefficients $\alpha ,\gamma$ (for load balancing) are appropriately increased, while the emphasis on time constraint is reduced;

(2) Efficiency Priority Mode:

In peak order scheduling or emergency task handling scenarios, the weighting coefficient $\beta$ for minimizing total operation time is increased accordingly.

(3)

Design of Genetic Operators

(1) Sequence-Retaining Crossover

To reduce the travel distance and energy consumption of the four-way shuttles, the system operates based on a combination of multiple outbound tasks to a single inbound task. In this design, sequence-retaining crossover is adopted, with chromosome crossover operations conducted in the order of inbound tasks followed by outbound tasks. The specific steps are as follows:

I. For a chromosome of length $L$, two random numbers $c_1$ and $c_2$ $\left(c_1,c_2\le L\right)$ are generated to determine the segment of the chromosome to participate in crossover; crossover operations are performed on the genes between positions $c_1$ and $c_2$;

II. A random number $c_3\left(c_3ϵ\left\{-1,1\right\}\right)$ is generated to determine the type of task involved in the crossover. If $c_3=1$, the crossover operation is applied to inbound tasks; if $c_3=-1$, the operation is applied to outbound tasks.

This method effectively enhances the feasibility and rationality of offspring solutions, avoiding decreased fitness due to operation logic errors. Taking the outbound tasks of two four-way shuttles as an example, a schematic diagram of the sequence-retaining crossover operation is shown in Figure 4.

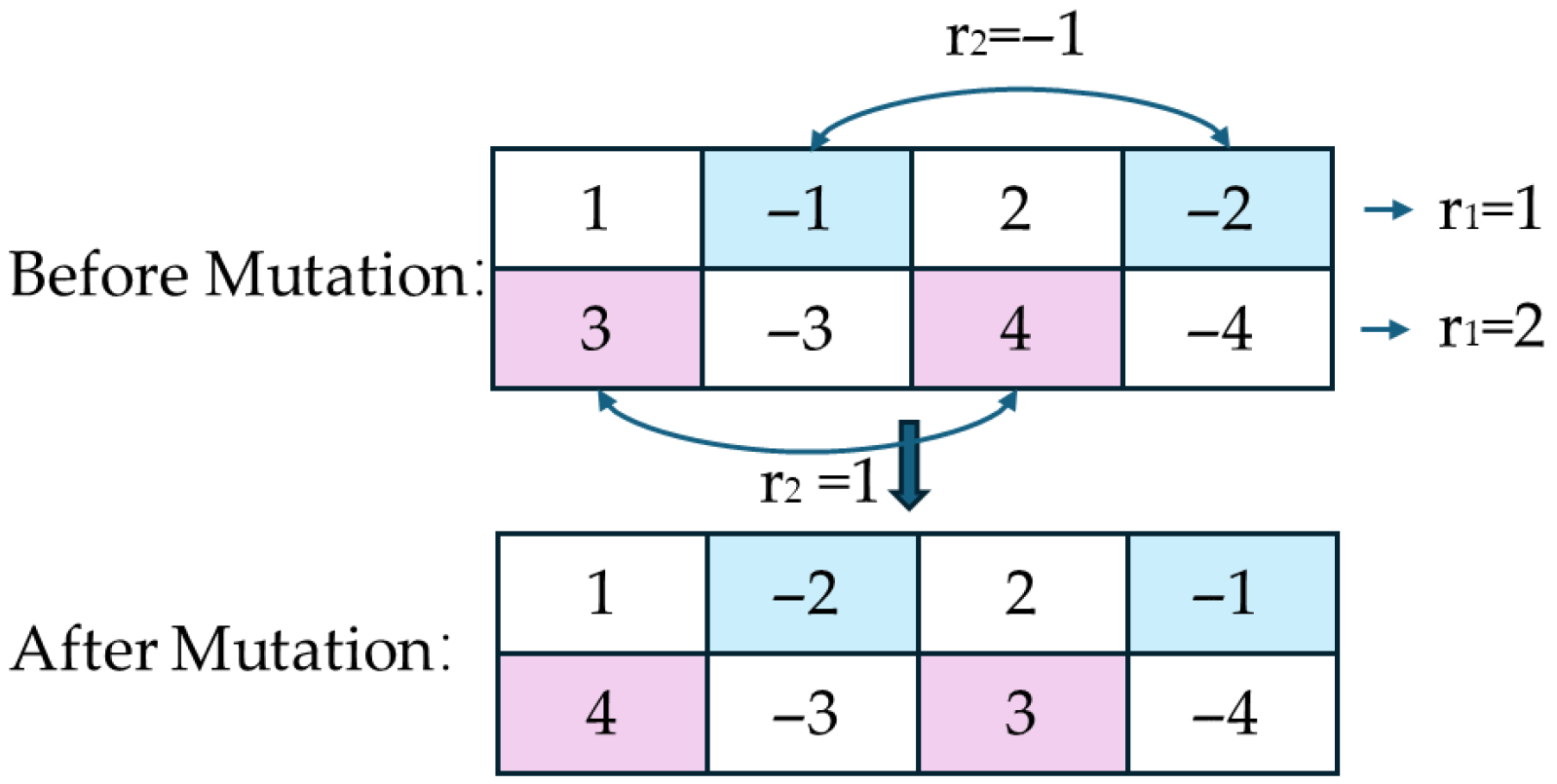
(2) Path Reversal Mutation

The mutation operation is designed to introduce new gene combinations, thereby enhancing chromosome diversity and preventing the algorithm from becoming trapped in local optima. In this study, a local path reversal mutation is employed, in which the task sequence of the four-way shuttle is reversed to simulate the impact of different task orders on scheduling. When there are $V$ four-way shuttles in operation, the specific procedure is as follows:

I. Generate a random positive integer, i.e., randomly select one of the $V$ four-way shuttles to perform the mutation operation.

II. Generate a random integer $r_2\left(r_2ϵ\left\{-1,1\right\}\right)$, where 1 and –1 represent mutation operations on inbound or outbound tasks, respectively.

Through the mutation operation, both the diversity of the search and the overall convergence performance of the algorithm can be improved. An example of this operation on the task sequences of two four-way shuttles is illustrated in Figure 5.

(4)

Flowchart of the Improved Genetic Algorithm

To achieve efficient collaborative scheduling of four-way shuttles and elevators in a multi-task environment, this study develops an improved genetic algorithm that integrates a hierarchical encoding structure, order-preserving crossover, and path reversal mutation strategies. The optimization process, as shown in Figure 6, consists of six core steps: population initialization, fitness evaluation, selection, crossover, mutation, and updating. The optimal scheduling scheme is obtained through iterative optimization [32].

2.3.2. MADDPG Scheduling Algorithm

(1)

Principle of MADDPG

In a multi-agent system based on the MADDPG algorithm, each agent continuously interacts with the environment to construct and optimize a joint action policy. Specifically, each agent selects an action based on its own local observations, resulting in a joint action set [33]. The environment then provides each agent with an immediate reward based on these joint actions and updates to a new joint state. During this process, agents collect reward information from the environment, calculate cumulative returns, and use these as the basis for adjusting their policies. Through this repeated action–state–reward interactive learning process, agents gradually learn the optimal strategy that maximizes their cumulative return.

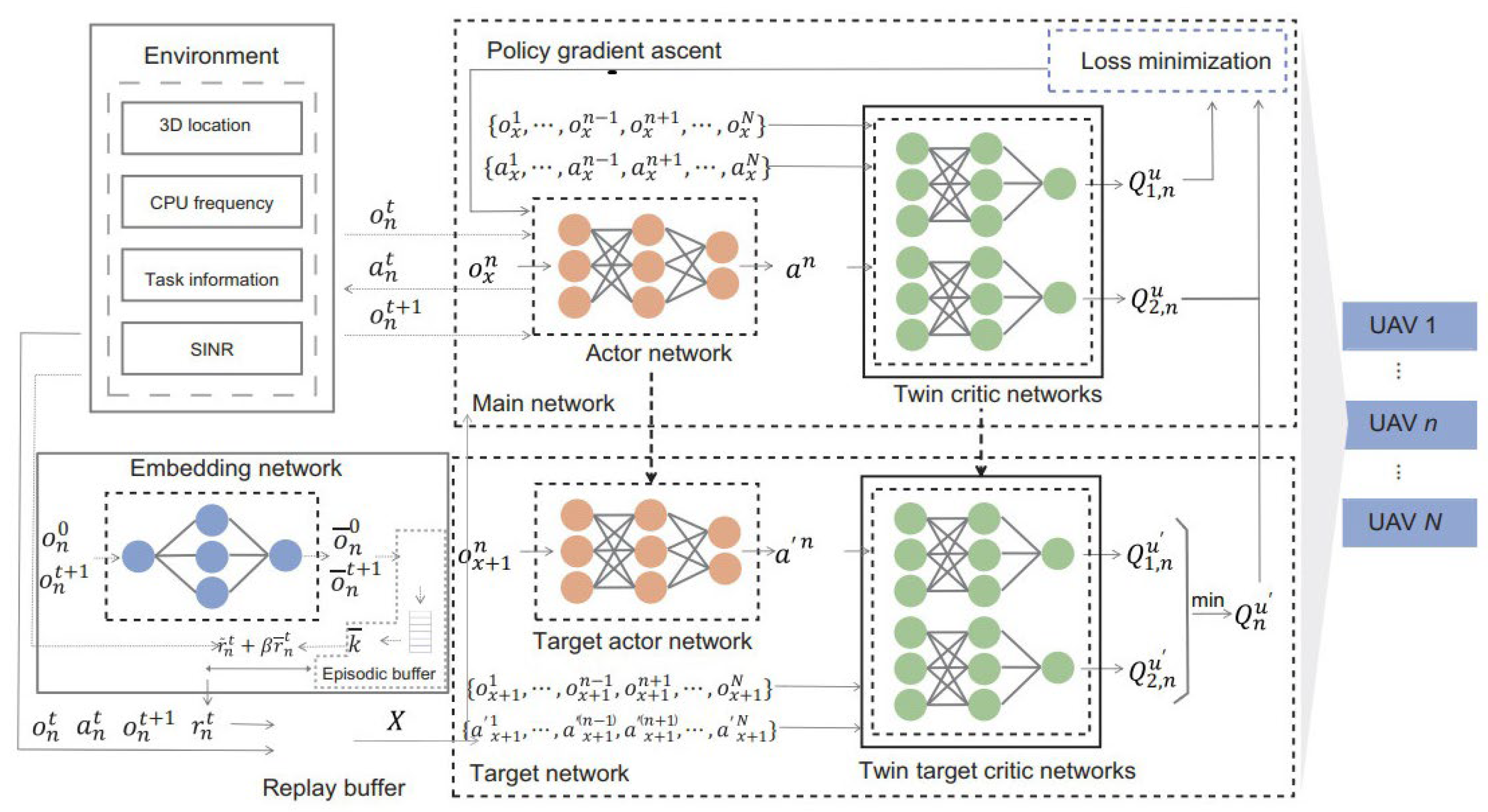
This algorithm trains multiple agents using actor and critic networks. In the actor network, the optimal action decisions are derived by integrating the state–action value function with policy gradients and optimizing the parameters $\theta$. In the critic network, the actions from the actor network are evaluated based on temporal-difference (TD) error. Both the actor and critic utilize an evaluation network and a target network. The evaluation network is responsible for estimating the state–action value function, and its parameters are continuously updated during training. The target network retains a copy of the evaluation network’s parameters from an earlier time and is not involved in training. By providing relatively stable target values, the target network enables the calculation of the TD error. The TD error is computed based on the outputs of the target and evaluation networks. By minimizing this error, the parameters of the critic network are optimized, allowing the evaluation network to better estimate the state–action value function. The neural network architecture of the MADDPG algorithm is illustrated in Figure 7.

(2)

Design

(1) State Space Design:

For a warehouse system with $a$ four-way shuttles and $b$ elevators, the system comprises a total of $N=a+b$ agents. Each agent constructs its local observation space according to its scheduling objectives, while the critic network uniformly utilizes the global state.

In the state space of the four-way shuttle, the local state vector for each shuttle $S_i^F$ is defined as:

$$S_i^F=\left[x_i,y_i,z_i,T_i,Q_i,l_i\right]$$

(19)

In the equation, $x_i,y_i,z_i$ indicate the discretized position coordinates; $T_i$ indicates the task queue information currently assigned to the $i$ th shuttle; $Q_i$ indicates to the target layer information for each task in the task queue; $l_i$ indicates the number of remaining tasks for the current mission of the $i$ th shuttle.

In the elevator state space, the local observation $S_j^L$ for each elevator includes:

$$S_j^L=\left[z_j,L{S}_j,W{Q}_j\right]$$

(20)

In the equation, $z_j$ indicates the current floor where the elevator is located; $L{S}_j$ indicates the current operational status of the elevator; $W{Q}_j$ is the waiting queue, representing the list of four-way shuttles requesting service.

During the centralized training phase, the global states used by the critic network during training includes:

$$s=\left[\left\{s_1^F,\dots ,s_a^F\right\},\left\{s_1^L,\dots ,s_b^L\right\},TP,EM\right]$$

(21)

In the equation, $\left\{s_1^F,\dots ,s_a^F\right\}$ indicates the states of all four-way shuttles; $\left\{s_1^F,\dots ,s_b^F\right\}$ indicates the states of all elevators; $TP$ indicates the global task pool, which includes the status of all orders, including task ID, type, and status; $EM$ indicates the load and energy consumption statistics.

(2) Action Space Design

To accommodate the hybrid optimization objective of scheduling and path adjustment, the action space is defined by equipment type as follows:

$$a_i^F=\left[a_i^{task},a_i^v,a_i^L\right]$$

(22)

$$a_j^L=\left[a_j^{task},a_j^z\right]$$

(23)

In these equations, $a_i^F$ indicates the action space for the four-way shuttle, and $a_i^{task}$ indicates the selection of the current task, indicating whether to switch the current task; $a_i^v$ indicates the velocity setting, $a_i^L$ indicates whether a elevator request is needed, $a_j^L$ indicates the action space of the elevator, $a_j^{task}$ indicates task selection, i.e., choosing the current service target from the request queue; $a_j^z$ indicates the layer-switching action, indicating whether to proactively move to the target floor to reduce waiting time.

(3) Reward Function Design

The reward function $R_i^F$ for four-way shuttle $i$ takes into account the energy consumption penalty, no-load energy consumption penalty, task timeliness reward, and load balancing reward:

$$R_i^F=\left[-{\lambda }_1{E}_i^L-{\lambda }_2{E}_i^K+{\lambda }_3{R}_i^T+{\lambda }_{4}LE{D}_i-{\lambda }_5{P}_i\right]$$

(24)

In the equation, $E_i^L$ indicates the energy consumption penalty; $E_i^K$ indicates the no-load energy consumption penalty; $R_i^T$ indicates the task timeliness reward; $LE{D}_i$ indicates the load balancing reward of four-way shuttles; $P_i$ indicates the conflict penalty. ${\lambda }_{1,}{\lambda }_2,{\lambda }_3,{\lambda }_4$ and ${\lambda }_5$ indicate the weighting of these five consideration metrics.

The reward function $R_j^L$ for elevator $j$ includes the following components:

$$R_j^L=\left[-{\lambda }_6{E}_j^L-{\lambda }_7{T}_j^w+{\lambda }_8{M}_j\right]$$

(25)

where $E_j^L$ is the penalty for vertical transport energy consumption; $T_j^w$ is the waiting time penalty; $M_j$ is the full-load task reward. When $M_j$ equals 1, it indicates that the elevator is fully loaded; when $M_j$ equals 0, it indicates that the elevator is unloaded.

(3)

Optimization Strategy Combining Genetic Algorithm and MADDPG

(1) Collaborative Design

Since a single algorithm often struggles to balance global search capability and local responsiveness, this study develops a hierarchical optimization algorithm that integrates the Genetic Algorithm (GA) with Multi-Agent Deep Deterministic Policy Gradient (MADDPG), fully leveraging the complementary strengths of both approaches. The hierarchical optimization framework consists of a global optimization layer and a local execution optimization layer, detailed as follows:

Global Optimization Layer: The genetic algorithm is employed to generate the initial task allocation and operation sequence based on task information, the initial status of equipment, and the warehouse topology network.

Local Execution Optimization Layer: MADDPG is used to train multi-agent policies, enabling real-time adjustments to task sequences, speeds, and scheduling decisions during execution to enhance robustness and energy performance.

Unlike traditional optimization methods, this work does not merely utilize the genetic algorithm for static optimization; instead, the scheduling schemes produced by the genetic algorithm are further transformed and injected into the experience replay buffer of MADDPG, providing heuristic prior knowledge for reinforcement learning. This experience injection approach improves the training efficiency of MADDPG, facilitates the rapid acquisition of collaborative strategies, and reduces the risk of convergence to local optima.

(2) System Scheduling Process Design

The system scheduling process is shown in

Table 1. System Scheduling Process.

Step	Objective	Description
1	Task Reception and Preprocessing	The system receives a new batch of orders, extracts their location, type, and floor information, and generates a task pool.
2	Global Task Allocation	The genetic algorithm generates the initial scheduling scheme based on the initial state and task characteristics.
3	Expert Experience Injection	The scheduling scheme is executed in a simulation environment, and the resulting data is collected and injected into the MADDPG experience pool.
4	Local Policy Optimization	MADDPG trains the policy network based on the injected experience and real-time state, optimizing local scheduling behaviors.
5	Task Execution and Feedback	All equipment executes the scheduling strategies as instructed, and the system collects information on energy consumption, efficiency, and conflicts.
6	Policy Iteration and Termination	The final scheduling strategy is output based on the number of training iterations or task completion status.

.

In the scheduling optimization framework proposed in this section, the Improved Genetic Algorithm (IGA) is responsible for global task allocation in the global optimization layer. By employing strategies such as hierarchical chromosome encoding, sequence retention crossover, and path-reversal mutation, the IGA generates high-quality initial task allocation schemes. This foundational scheme ensures the rationality and global optimality of task allocation throughout the entire scheduling process. The MADDPG algorithm operates at the local execution optimization layer, dynamically adjusting task sequences, speeds, and scheduling decisions based on real-time states. By injecting the scheduling schemes generated by IGA into the MADDPG experience pool, reinforcement learning can rapidly acquire collaborative strategies and further optimize local scheduling behaviors. This hierarchical optimization framework integrates global optimization with dynamic responsiveness, fully harnessing the advantages of both IGA and MADDPG algorithms. It overcomes the limitations of single algorithms in four-way shuttle scheduling scenarios and achieves multi-objective optimization for energy consumption, time, and load balancing. As a result, it effectively addresses challenges such as uneven task allocation, poor adaptability to dynamic environments, high idle rates of equipment, and difficulties in energy optimization in multi-shuttle cooperative operations.

By synergistically optimizing the Improved Genetic Algorithm (IGA) and the Multi-Agent Deep Deterministic Policy Gradient (MADDPG) algorithm, in combination with an A*-guided Deep Q-Network (A*-DQN) path planning method, the proposed scheduling algorithm can significantly reduce the energy consumption of four-way shuttle warehouse systems, lower equipment idle rates, and enhance operational efficiency. Furthermore, the algorithm achieves balanced task allocation, improves the degree of load balancing, and strengthens the system’s adaptability and stability in dynamic environments. This integrated optimization not only enhances the overall system performance but also provides robust support for energy conservation and intelligent operation in warehouse systems.

2.3.3. Path Planning Algorithm Based on A*-Guided DQN

(1)

Path Planning Design Based on A* Algorithm

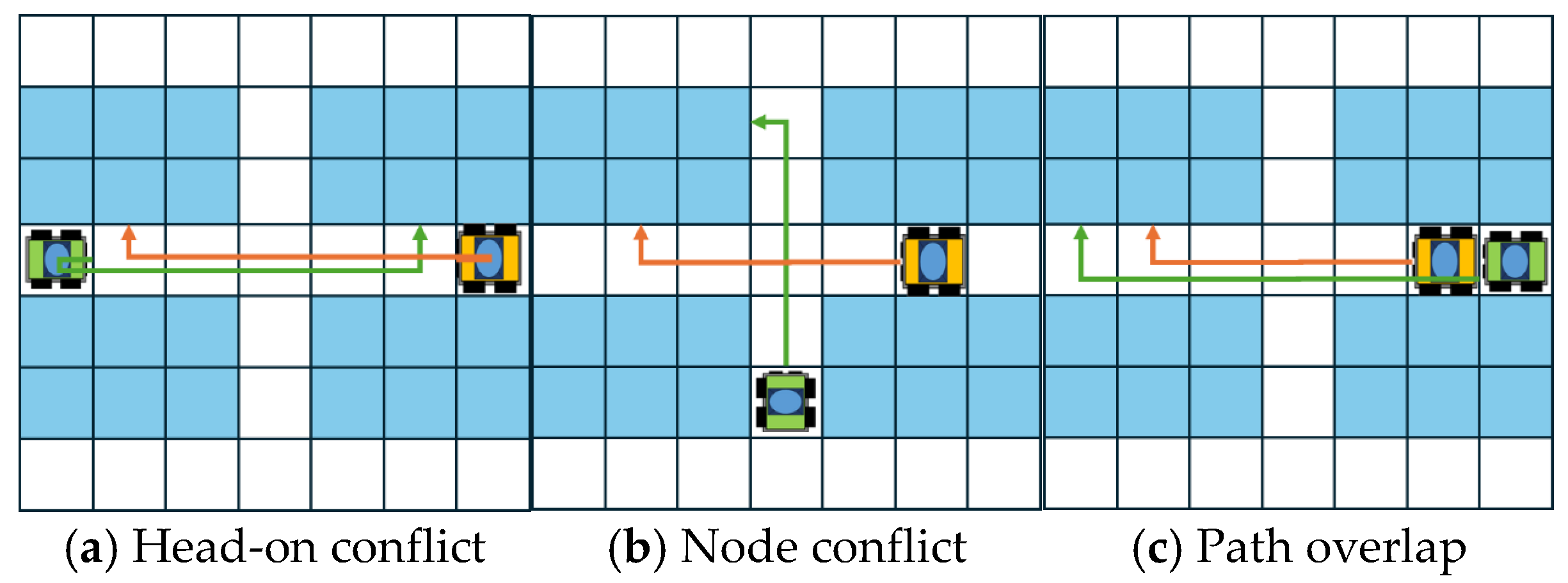
(1) Path Conflicts and Resolution

When multiple four-way shuttles operate on the same level, three types of conflicts may occur, as illustrated in Figure 8: Head-on conflict, as shown in Figure 8a, occurs when the angle between the directions of two shuttles is 180 degrees. Node conflict, as shown in Figure 8b, arises when the angle between the directions of two shuttles is 90 degrees. Path overlap, as shown in Figure 8c, occurs when two shuttles are moving in the same direction. If the leading shuttle makes a sudden stop or turns, a collision may occur with the following shuttle; in this case, the angle between the two shuttles is 0 degrees.

When two four-way shuttles, $i$ and $j$, are operating simultaneously, their direction vectors are $\overrightarrow{v_i}=\overrightarrow{v}\left(d_i\right)$, $\overrightarrow{v_j}=\overrightarrow{v}\left(d_j\right)$, respectively. The angle between the vectors is calculated as shown in Equation (26). By converting the value to degrees and referring to the definitions above, the conflict type can be determined according to the criteria in Equation (27).

$$\theta =\arccos \left({\displaystyle \frac{\overrightarrow{v_i}·\overrightarrow{v_j}}{\Vert \overrightarrow{v_i}\Vert ·\Vert \overrightarrow{v_j}\Vert }}\right)$$

(26)

In the equation, $\theta$ indicates the angle between the operational direction vectors of the two four-way shuttles, with specific values defined as follows:

$$\theta =\left\{\begin{array}{l}180°, Head-on\hspace{0.33em}conflict\hfill \\ 90°, Node\hspace{0.33em}conflict\hfill \\ 0°, Path\hspace{0.33em}overlap\hfill \end{array}\right.$$

(27)

To address head-on conflicts encountered during shuttle operations, the system assigns a decision-making priority to each shuttle based on the priority of its current task. When a conflict arises, the shuttle with lower priority must proactively yield according to predefined rules. During the yielding process, if it is feasible for the shuttle to reverse or change lanes, it performs the corresponding maneuver. If yielding in place is not feasible, the system dynamically generates an alternative detour path—subject to grid validity constraints—to enable the shuttle to circumvent the conflict.

When a node conflict occurs between two four-way shuttles, $i$ and $j$, the arrival times $t_i,t_j$ of both shuttles at the node are calculated according to Equation (28). Whether the time window offset threshold is satisfied is then determined. If the threshold is not met, the moving speed of the lower-priority shuttle must be adjusted.

$$\left\{\begin{array}{l}{t}_i={\displaystyle \frac{d_i}{v_i}},t_j={\displaystyle \frac{d_j}{v_j}}\hfill \\ |t_i-t_j|\ge \Delta t_{\min }\hfill \\ \Delta v_i=v_i-0.5 \mathrm{m}/\mathrm{s}\hfill \end{array}\right.$$

(28)

In the equation, $\Delta t_{\min }$ indicates the minimum time window offset threshold. $d_i$ and $d_j$ respectively indicate the distance from the starting point of four-way shuttle $i$ or four-way shuttle $j$ to the node.

When the paths of the current shuttle $i$ and the following shuttle $j$ overlap, the minimum safe distance between the two shuttles is calculated according to Equation (29). If $d_{i,j}\le d_{\min }$, the minimum safe distance is not met. The following shuttle must decelerate for adjustment.

$$\left\{\begin{array}{l}{d}_{\min }=\max \left(1.5m,\eta ·v_j·t_r\right)\hfill \\ v_j^{\prime }=\min \left(v_j,0.8·v_i\right)\hfill \end{array}\right.$$

(29)

where $d_{\min }$ is the minimum safe distance, $\eta$ is the safety factor used to eliminate system errors, and $t_r$ is the system response time.

(2)

A* Path Execution Modes

In this study, the A* path execution process is divided into two modes:

(1) Route-Guided Mode

In this approach, a complete path is generated directly during the path planning stage, and the four-way shuttle executes its tasks strictly according to the pre-defined path. This mode offers high computational efficiency and fast execution speed, making it suitable for scenarios with predetermined tasks and static environments [34].

(2) Step-by-Step Guidance

In this mode, only the currently feasible segment of the path is planned. During execution, subsequent path segments are updated in real time according to environmental feedback until the task is completed. This mode demonstrates strong adaptability to environmental changes, enables dynamic obstacle avoidance, and is suitable for highly dynamic and frequently interactive dense warehousing systems.

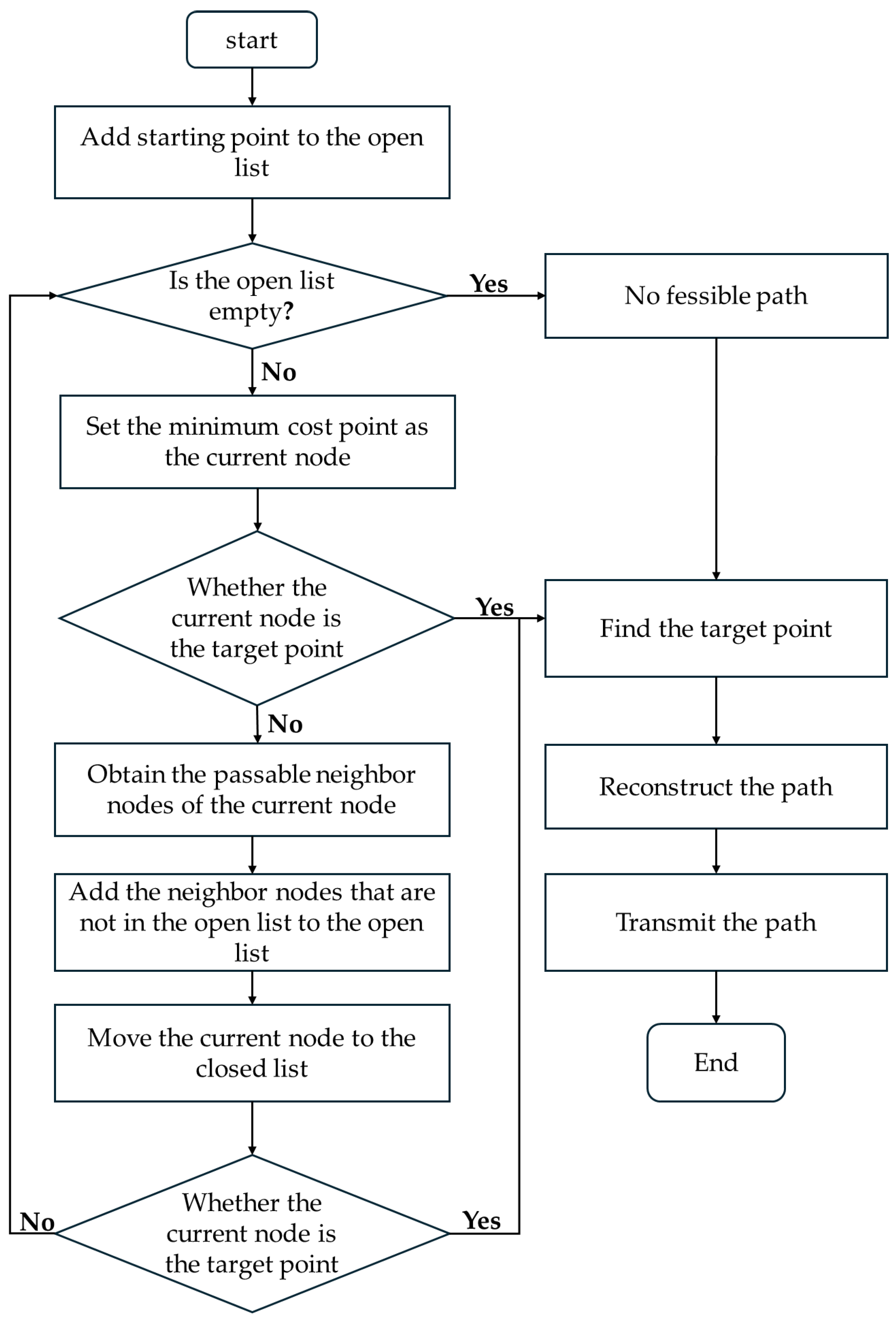
In consideration of the practical operational characteristics of four-way shuttle-based warehouse systems and to enhance both path safety and system responsiveness, this study adopts the step-by-step guidance strategy as the path execution mode. The specific steps of the A* algorithm employed in this study are illustrated in Figure 9.

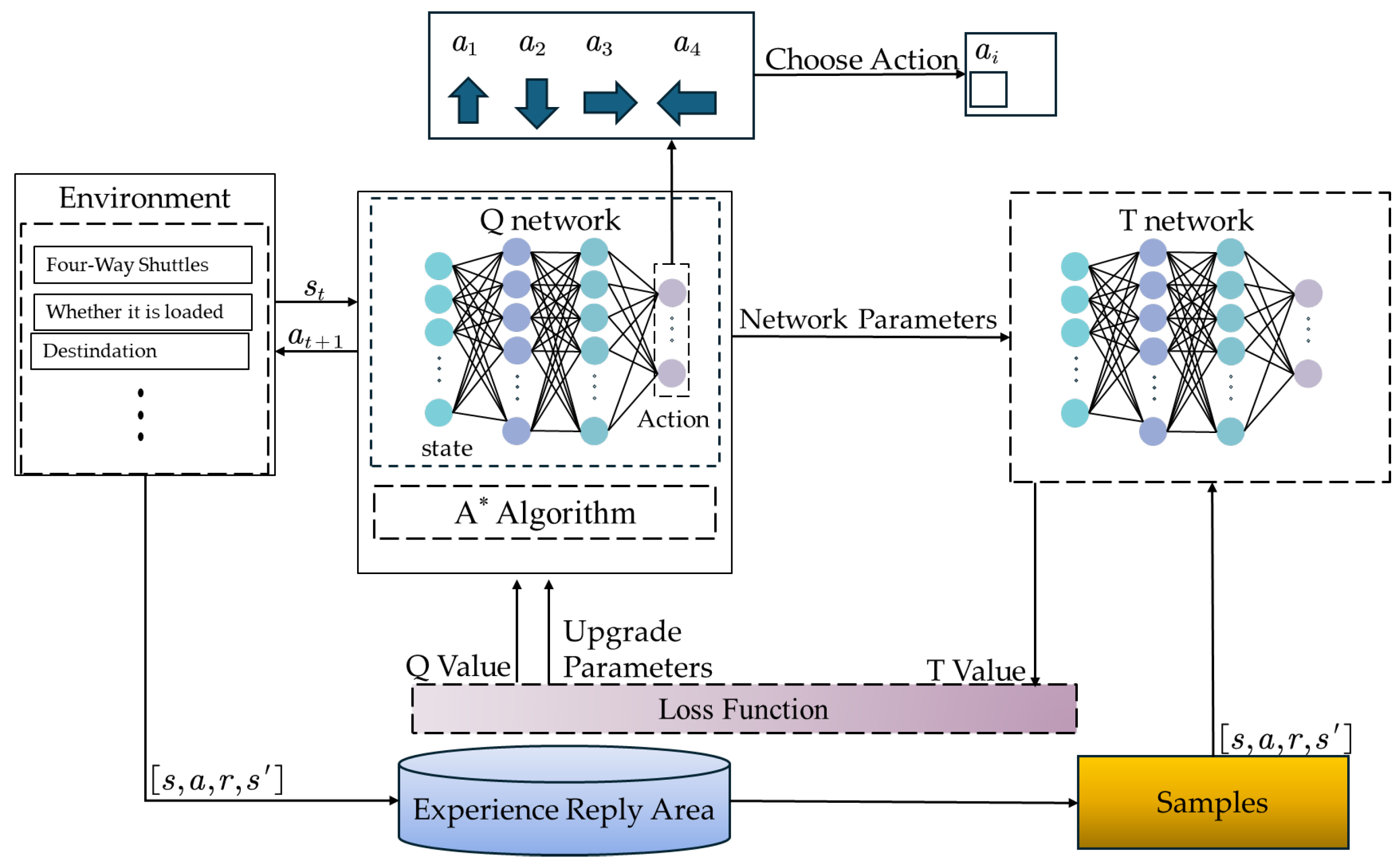
Deep Q-Networks (DQN) typically rely on random exploration in the initial stages, which, in high-dimensional spaces, can lead to inefficient and goal-deviating path behaviors. To improve decision-making efficiency, this study incorporates data from the A* algorithm to guide the decision process. At the early stage of training, the A*-guided DQN decision-making algorithm provides the agent with initial path planning recommendations based on the A* algorithm (see Figure 10).

The design of the A*-guided DQN algorithm is as follows:

(1) Action Selection

By dynamically selecting actions planned by the A* algorithm according to the current state in real time, the agent’s exploration efficiency at the early stage can be significantly improved.

(2) Experience Replay

The paths generated by the A* algorithm are used as experience data for the DQN, enabling the agent to learn effective strategies more rapidly.

(3) Dynamic Adjustment

During the training process, increasing reliance is placed on the strategies learned by the DQN itself.

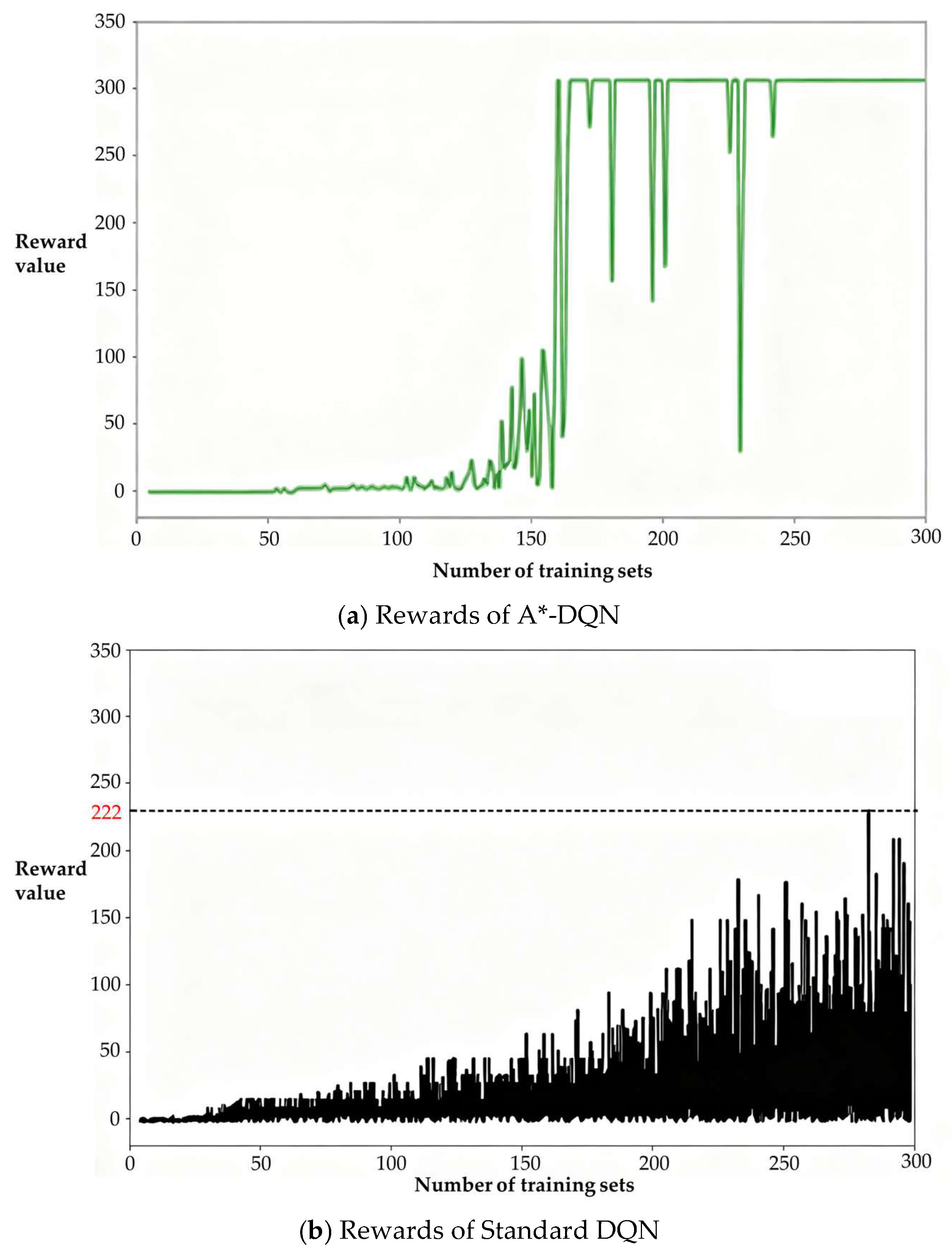
To enable the transition to neural network-based decision-making, this study adjusts the frequency of neural network decisions by setting the exploration rate ε, where 1-ε represents the probability of using the A* algorithm. The training is designed to allow the neural network to converge and make accurate decisions. In the initial stage, the A* algorithm is prioritized, and as training progresses, the proportion of neural network usage is gradually increased to ensure eventual convergence. During the first one-third of the training period, the exploration rate is fixed at 0.8, after which it is gradually increased to 1.

Through A* planning guidance, decision fusion, and dynamic adjustment of policy weights, the path learning ability of the four-way shuttle in complex environments is effectively enhanced. The structure of the A*-guided DQN algorithm (A*-DQN) is shown in Figure 11.

The parameters of the current value network ${\mathrm{Q}}_{\mathsf{\pi }}\left({\mathrm{s}}_{\mathrm{t}},{\mathrm{a}}_{\mathrm{t}}\right)$ are updated using the loss function:

$$Q_{\pi }{\left(s_t,a_t\right)}^{\prime }\leftarrow Q_{\pi }\left(s_t,a_t\right)+\alpha \left(r_t+\gamma \underset{a}{\max }{Q}_{\pi }\left(s_{t+1},a_t\right)-Q_{\pi }\left(s_t,a_t\right)\right)$$

(30)

In the equation, $Q_{\pi }{\left(s_t,a_t\right)}^{\prime }$, $\alpha$ indicates the learning rate, $r_t$ indicates the current reward, $\gamma$ is the discount factor, $s_{t+1}$ is the next state after executing action $a$, and $\underset{a}{\max }{Q}_{\pi }\left(s_{t+1},a_t\right)$ indicates the $Q$-value of the optimal action selected at $s_{t+1}$.

(3)

Training Process for Four-Way Shuttle

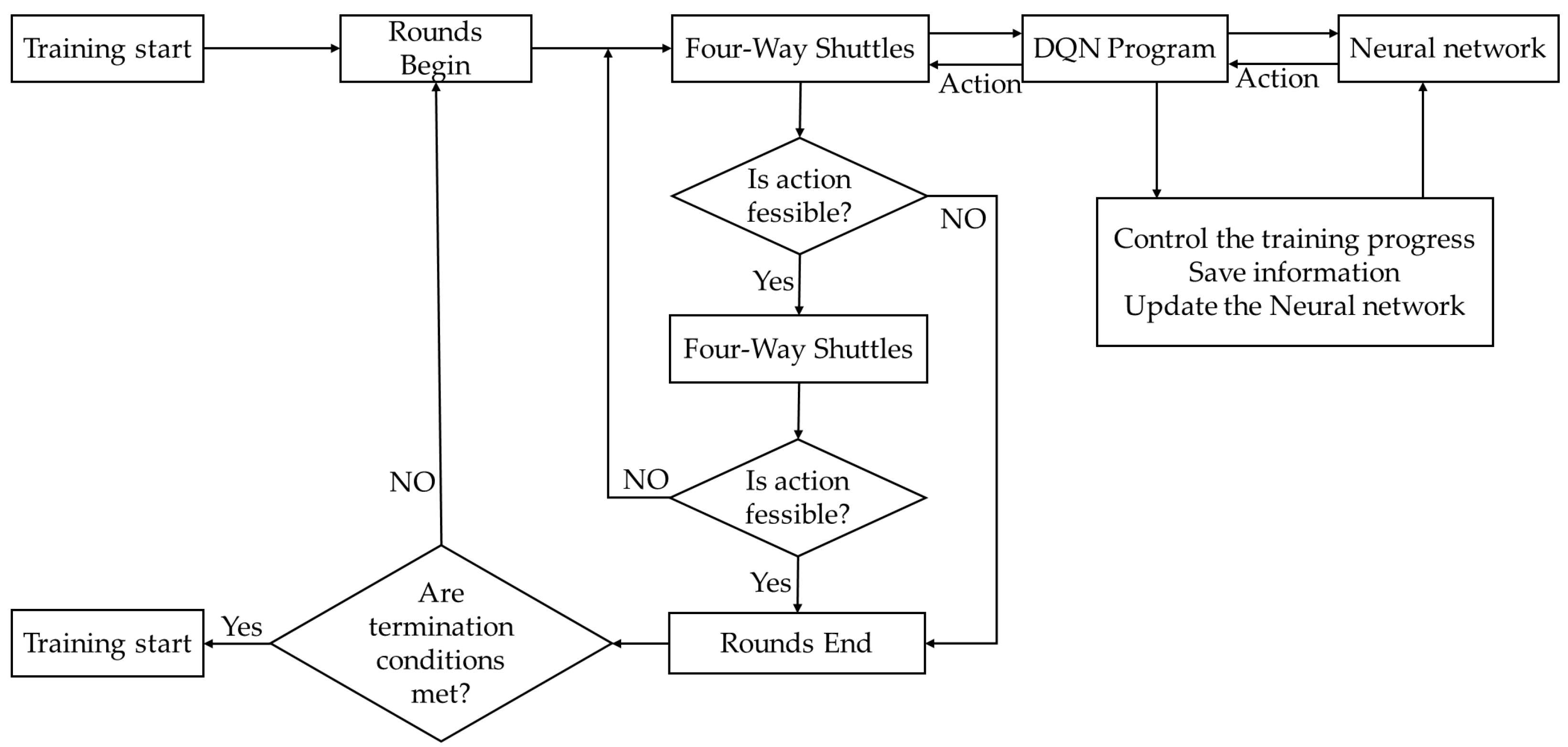
This study designs a training process tailored for the path planning task of the four-way shuttle, as illustrated in Figure 12.

The procedure of the A*-DQN algorithm is as follows: The agent acquires the current state from the environment and inputs it into the DQN network, which outputs the optimal action. The legality of the action is then determined; if the action is illegal, the episode terminates, otherwise, the action is executed. The system subsequently returns a reward and the next state, forming an experience tuple that is stored in the experience replay buffer. Once the buffer reaches its capacity, mini-batches are sampled to compute the loss function and update the Q-network parameters. At fixed intervals, the parameters of the current Q-network are synchronized to the target network to enhance training stability, until the termination condition is met. This algorithm utilizes the path generated by the A* algorithm as the initial guiding policy for DQN, thereby leveraging the efficient planning capability of A* to improve exploration efficiency. As training progresses, the proportion of DQN’s own policy usage is gradually increased, ultimately enabling convergence of the path planning policy and improving both the efficiency and accuracy of path planning.

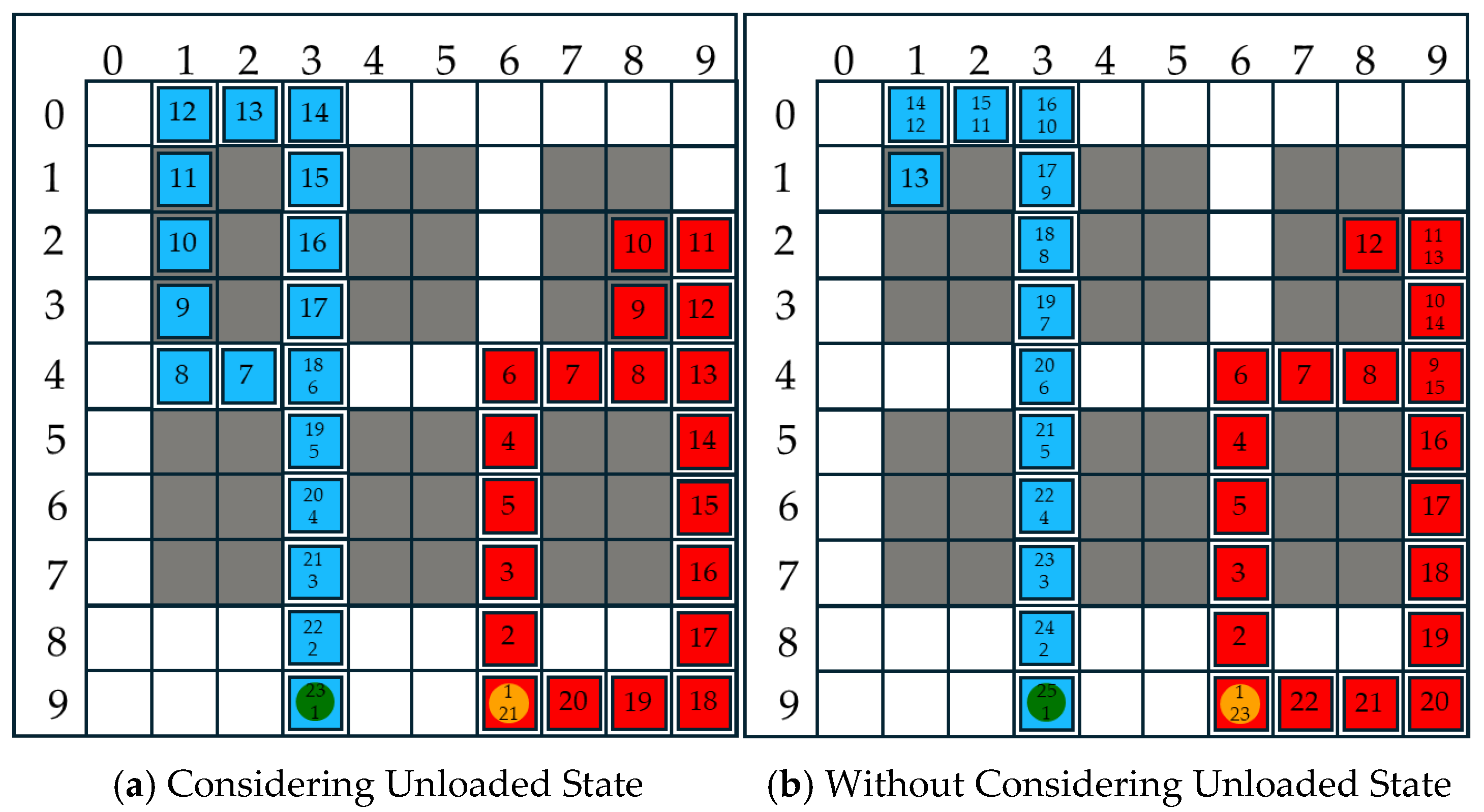
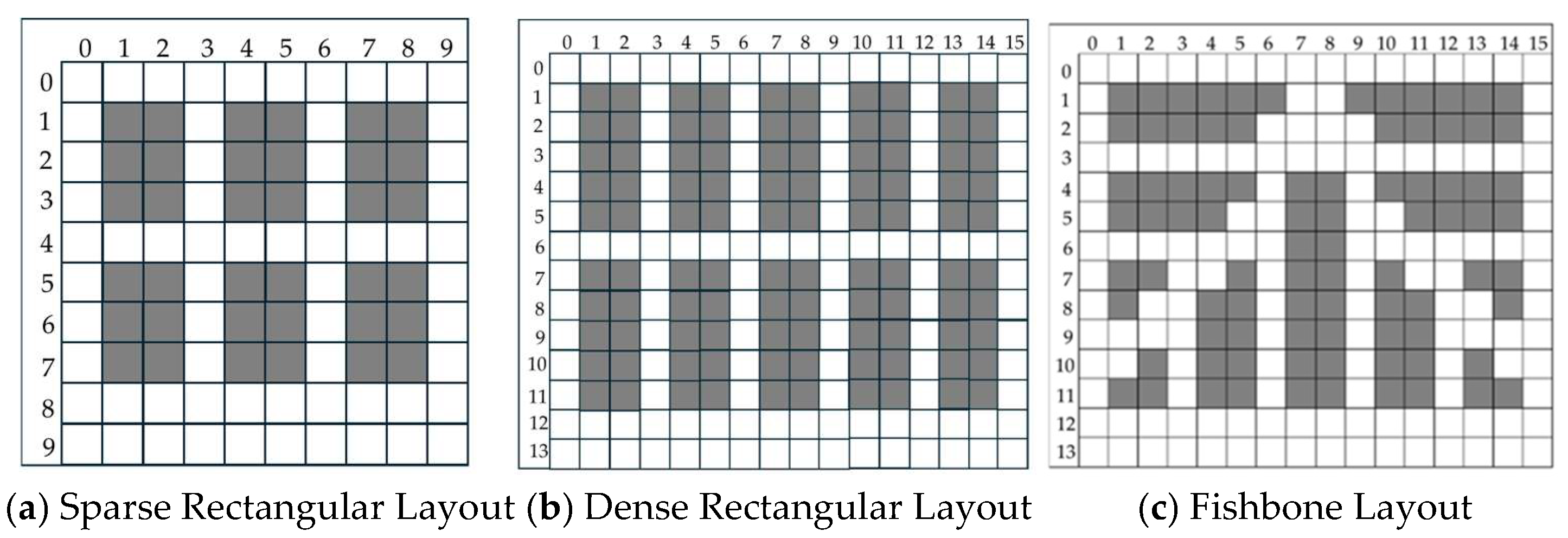
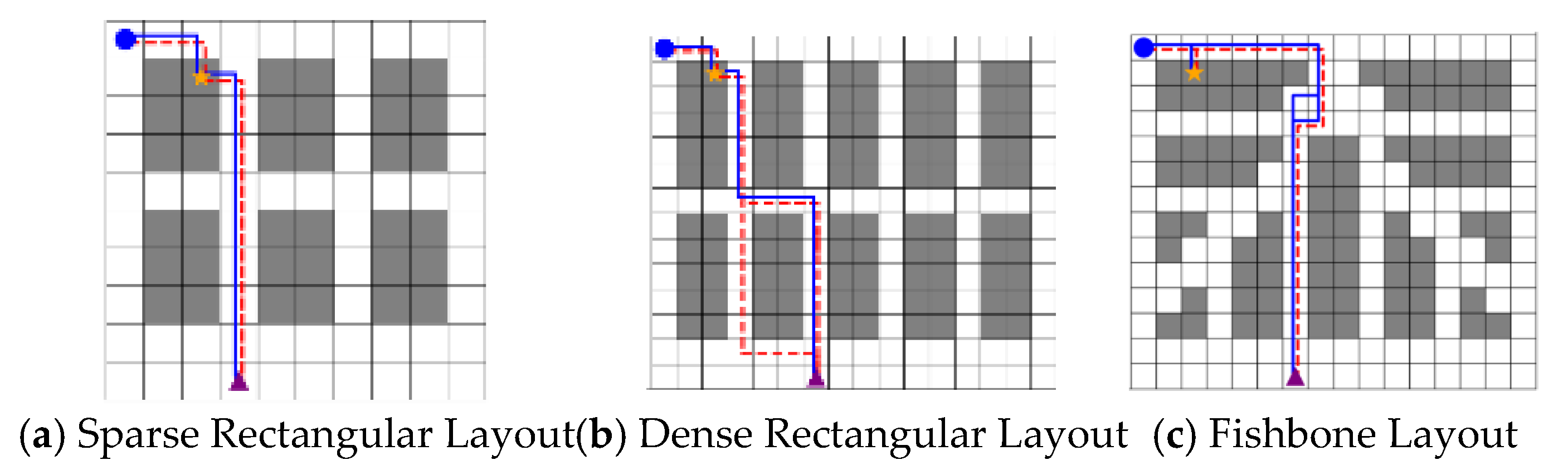
This section focuses on the path planning problem of four-way shuttle in dense warehouse environments and proposes an A*-DQN path optimization algorithm that integrates A* heuristic search with deep reinforcement learning. By using the A* path as the initial policy guiding signal, the algorithm enhances exploration efficiency, constructs a four-dimensional state space and a staged reward mechanism, thereby significantly improving the learning efficiency of the model and the quality of the planned paths. At the same time, by incorporating information on the shuttle’s loading status, the model dynamically adjusts path constraints to ensure the feasibility and safety of path planning. Moreover, based on the grid map state space and the designed staged reward mechanism, the agent is further guided to learn the optimal path planning policy, effectively transforming the path planning problem into a reinforcement learning problem and achieving deep integration of the model and algorithm.

In this section, the scheduling algorithm and path planning are tightly coupled and mutually reinforcing. In terms of path planning, the proposed A*-DQN algorithm introduces a path map switching mechanism by integrating the shuttle’s loading status information, thereby enabling adaptive adjustment of path constraints under different operating conditions. The A* algorithm provides initial path planning suggestions for DQN, accelerating the convergence process of DQN. This integrated approach not only improves the efficiency and accuracy of path planning but also significantly enhances the four-way shuttle’s path learning and obstacle avoidance capabilities in complex layouts and dynamic environments. Within the scheduling model, the results of task allocation provide the A*-DQN algorithm with the task sequence and target location information, enabling A*-DQN to dynamically adjust path planning accordingly. Through rational task allocation, the system reduces ineffective movements and waiting times of the four-way shuttles, while efficient path planning further minimizes path conflicts and detours. The synergistic effect of these two aspects achieves reduced energy consumption and improved operational efficiency. This integrated approach not only enhances the overall system performance but also improves the system’s adaptability and stability in dynamic environments, providing strong support for the intelligent upgrading of warehouse systems.

3. Experiments and Results

3.1. Four-Way Shuttle Scheduling Optimization Experiments

3.1.1. Experimental Parameter Design

In this study, the experiments are based on an electrical appliance warehouse system, primarily focusing on multi-shuttle scheduling, energy consumption optimization, and operational efficiency. The performance is analyzed in comparison with various benchmark algorithms.

Table 2. Overall Environmental Configuration of the System.

Parameter	Value and Description
Warehouse Scale	1–4 floors, each floor containing 10–80 storage areas
Storage Unit	Each storage area contains 5 rows and 2 columns, totaling 10 units
Number of Shuttles	1–3 units
Number of Elevators	1–2 units
Number of Orders	10–100 orders
Initial Position	Located at the elevator position on the first floor
Map Structure	Gridded aisle layout, including aisles, storage areas, and elevators

presents the overall environmental configuration of the system, while

Table A1. Kinematic Performance and Energy Consumption Parameters of Equipment.

Parameter Item	Name	Data	Unit
Storage Unit	Length	1.9	m
	Width	1.6	m
	Height	2	m
Aisle	Width	1.7	m
Four-way Shuttle	Maximum speed	2	m/s
	Acceleration	0.5	m/s2
	Unloaded energy	500	w/h
	Loaded energy	550	w/h
Elevator	Maximum speed	1	m/s
	Acceleration	0.3	m/s2
	Unloaded lift energy	1000	w/h
	Unloaded descent energy	100	w/h
	Loaded lift energy	1100	w/h
	Loaded descent energy	110	w/h

lists the kinematic performance and energy consumption parameters of the main equipment.

3.1.2. Simulation Platform Layout

To validate the overall scheduling capability of the integrated algorithm in multi-level warehouses, this study constructed a dense storage system comprising four levels, each containing 800 storage units. Multiple sets of inbound and outbound orders were configured for the experiments. The system generates paths and coordinates the operation of lifts based on the positional information of the tasks. The simulation platform software configuration is as shown in

Table A2. Simulation Platform Software and Hardware Configuration.

Category Description	Tool/Library	Version	Function
Programming Language	Python	3.9	Core Algorithm Development and System Integration
Numerical Computing Library	Numpy	1.23.5	Matrix Operations and Task Data Preprocessing
Visualizsation Engine	Pygame	2.1.3	Dynamic Rendering of Warehouse Environments and Interactive Interface Development
Machine Learning Framework	PyTorch	1.131	Presentation of results including energy consumption curves and task scheduling sequence diagrams
Graphical Rendering	Matplotlib	3.6.2	Energy consumption curve and task sequence diagram plotting
Hardware	Lenovo notebook	V14	Program operation and thesis writing

.

3.1.3. System Function Verification and Testing

As illustrated in Figure 13, experiments with different parameter adjustments were conducted to verify the effectiveness and accuracy of the system’s dynamic layout adjustment functionality.

As shown in

Table 3. Theoretical vs. Simulated Completion Time.

Speed (m/s)	Theoretical Completion Time (s)	Simulated Completion Time (s)	Error (%)
1	140.00	146.00	4.29%
2	70.00	73.00	4.28%
3	46.70	49.00	4.93%

, to verify the accuracy of the four-way shuttle speed parameter settings, two fixed task coordinates, (2,2) and (2,12), were designated. Neglecting acceleration, the theoretical completion time was compared with the actual completion time, and the error consistently remained within approximately 5%, indicating minimal deviation.

3.1.4. Experimental Results and Analysis of the Improved Genetic Algorithm

To verify the optimization performance of the proposed Improved Genetic Algorithm (IGA) in the coordinated scheduling of four-way shuttles and lifts, this study experimentally analyzes the algorithm’s fitness convergence process and key energy consumption evaluation metrics under standard task scenarios.

(1)

Fitness Results and Analysis

A randomly generated fixed order set was used as the test input in this experiment. Both the Improved Genetic Algorithm (IGA) and the standard Genetic Algorithm (GA) were applied to the task scheduling problem. As shown in Figure 14, IGA achieved convergence at approximately the 20th generation, with a final fitness function value of 200. In contrast, the standard GA converged after about 60 generations, with a final fitness value of 291.61. Comparatively, IGA not only significantly accelerated the convergence rate but also improved the convergence accuracy by 31.46%, demonstrating superior search capability and solution quality.

As shown in the scheduling results of

Table 4. Comparison of Optimization Results between IGA and GA.

Algorithm	Shuttle No.	Task Sequence	Energy Consumption (Wh)	Time (s)
IGA	1	7, −9, 4, −10, 9, −4, 2, −7, 5, −8	177.81	382.87
	2	10, −1, 3, −5, 1, −6, 6, −3, 8, −2
GA	1	10, −8, −9, −10, −2, −3, 6, 7, −6, −7	212.34	429.55
	2	−4, −5, 8, 9, 1, 2, 3, −1

, the IGA outperforms the standard GA in terms of task structure arrangement, load balancing, and overall scheduling effectiveness. The IGA enables alternating execution of outbound and inbound tasks, effectively preventing the occurrence of empty trips caused by consecutive tasks of the same type, while also achieving more balanced task allocation. In terms of energy consumption and operation time, IGA reduces these metrics by approximately 16.23% and 10.86%, respectively, compared to GA, fully demonstrating its advantages in scheduling efficiency and energy optimization. This verifies its engineering applicability and optimization potential in multi-shuttle, multi-task scheduling scenarios.

(2)

Comparison and Analysis under Different Order Sizes

(1) Comparison and Analysis of Fitness Values

In this study, the total order quantities were set to 20, 40, 60, 80, and 100. Both the IGA and the standard GA were used to solve the scheduling problem, and their optimization performance under different scales was compared. The results are shown in Figure 15.

As the number of orders increases, the overall value of the fitness function rises; however, the IGA consistently outperforms the standard GA across all order scales, demonstrating superior optimization capability. When the order volume is relatively small (20–40 orders), the optimization rate of IGA is approximately 25%. As the number of orders exceeds 60, the optimization rate further increases to around 30%. Experimental results indicate that IGA exhibits a more pronounced optimization advantage in large-scale order scheduling tasks.

(1) Comparison and Analysis of Energy Efficiency Optimization Metrics

According to the experimental results presented in

Table 5. Experimental Results of Energy Efficiency Optimization Metrics under Different Scales.

Order Scale	Algorithm	EPO (Wh)	IER	LBD
20	GA	8.54	42.90%	0.19
	IGA	7.47	36.50%	0.07
40	GA	8.62	47.50%	0.22
	IGA	7.73	33.10%	0.04
60	GA	8.71	49.70%	0.25
	IGA	7.84	34.00%	0.04
80	GA	8.82	53.30%	0.23
	IGA	7.85	34.70%	0.02
100	GA	8.90	57.30%	0.22
	IGA	7.97	34.80%	0.01

, the IGA demonstrates significant advantages at all order scales. In terms of average energy consumption per order (EPO), the average energy consumption per order, IGA effectively reduces the energy consumption of each order task by approximately 10%, and this advantage gradually stabilizes as the order scale increases. Regarding the shuttle idle energy rate (IER), the proportion of four-way shuttles in an unloaded state relative to the total number of four-way shuttles, IGA significantly reduces ineffective energy consumption, with the reduction rate increasing as the order scale grows. In terms of the load balancing degree (LBD) indicator, the IGA demonstrates a significant advantage in task allocation. Task distribution becomes increasingly balanced as the order scale grows, and this effect is especially pronounced with large-scale orders (80 and 100 orders), where task allocation is much more uniform.

3.1.5. Experimental Analysis of the Integration of Genetic Algorithm and MADDPG Algorithm

The hyperparameters for MADDPG are shown in

Table A3. Hyperparameters for MADDPG.

Name	Value
The Number of Agents	7 (5 shuttles and 2 elevators)
The Observation Dimension of each Agent	4
The Action Dimension of each Agent	1
Learning Rate of Actor Network	0.1%
Learning Rate of Critic Network	0.1%
Discount Factor	0.95
Target Network Soft Update Parameters	0.01
Experience Replay Pool Capacity	50,000
Batch Size	32
Number of Training Rounds	200
Maximum Steps Per Turn	30
Noise Sevel During Action Selection	0.1

.

(1)

Training Results and Analysis

Figure 16 presents a comparison of the cumulative reward curves during training between the integrated algorithm (IGA-MADDPG) and the standard MADDPG algorithm.

As the number of training episodes increases, the reward value of the integrated algorithm continues to rise, eventually stabilizing at around 130. In contrast, the standard MADDPG shows a marked decline in learning efficiency after approximately 175 episodes. This indicates that the initial scheduling solution provided by IGA effectively guides policy learning, resulting in better convergence and higher solution quality.

After 175 episodes, the standard MAD5DPG remains at a relatively low reward value for an extended period, struggling to overcome local optima. The integrated algorithm, however, demonstrates a much stronger capability to achieve global optimality and overall policy optimization.

(2)

Performance Comparison and Analysis of the Algorithms

In the simulated order scheduling tasks, both the integrated algorithm and the conventional IGA were used to optimize randomly generated orders. Their performance was evaluated based on two key indicators: energy consumption and operation time. The comparative results are presented in

Table 6. Performance Comparison of Algorithms.

Experiment	Metric	IGA-MADDPG	IGA	Optimization Rate
Experiment 1	Energy(Wh)	53.73	65.05	17.40%
	Time(s)	167.00	202.00	17.33%
Experiment 2	Energy(Wh)	41.79	47.21	11.48%
	Time(s)	118.00	120.00	1.67%
Experiment 3	Energy(Wh)	145.39	177.25	17.97%
	Time(s)	325.00	406.00	19.95%
Experiment 4	Energy(Wh)	169.97	252.13	32.59%
	Time(s)	281.00	319.00	11.91%
Experiment 5	Energy(Wh)	479.25	499.14	3.98%
	Time(s)	571.00	659.00	13.35%

and Figure 17.

As shown in Table 6, the integrated algorithm achieves an average reduction of 16.68% in energy consumption per order and an average decrease of 12.84% in total operation time. These results fully validate the comprehensive advantages of the integrated algorithm in both energy consumption control and task efficiency.

3.2. Experimental Study and Analysis of the A*-Guided DQN Algorithm

This section focuses on the path planning problem in multi-layer dense warehousing systems, where simulation experiments are conducted using a single-layer planar map layout to simplify cross-layer handling operations. The experiments simulate a single-layer environment, allowing the path planning module to be invoked multiple times in the actual system for generating paths on each layer and facilitating multi-layer collaborative operations, thus ensuring algorithm controllability and ease of testing.

The experimental design adheres to the following principles: both the start and end points are either randomly generated or specified; multiple groups of tasks are scheduled for simultaneous path planning; and the number of tasks is controlled.

The architectures of the DQN network are shown in

Table A5. Network Structure Overview.

Network Module	Core Function	Key Parameters
Input Layer	Receives AGV state/map features	Number of channels = 1, Size = map dimensions
Convolutional Feature Extraction Layer	Extracts spatial features of the map (obstacles, paths)	Output channels: 64→128→256, Pooling kernel = 2 × 2
Fully Connected Fusion Layer	Fuses spatial features into an abstract vector	Input = 2304 → Output = 256
Output Layer	Outputs Q-values for 5 action (action decision)	Input = 256 → Output = 5
Dual Networks	Stabilizes training and avoids Q-value overestimation	Target Network updated every 100 steps

.

3.2.1. Map Transformation Experiments and Analysis

In this experiment, the four-way shuttle is simulated to perform outbound and inbound tasks at two different positions, (1,1) and (2,8), respectively, to evaluate the system’s map adaptation and path planning performance under various conditions. Depending on whether the shuttle is loaded or unloaded, the experimental results are presented in Figure 18, which illustrates the differences in paths between two map models given the same start and end points. The numbers in the blue and red boxes represent the order of grid cells traversed by the four-way shuttle’s path planned by the A* algorithm, arranged from smallest to largest.

The results indicate that the A* algorithm can dynamically adjust feasible regions based on the current state of the shuttle.

The average data for the two path planning approaches under different warehouse scales are summarized in

Table 7. Path Data for Two Approaches under Different Warehouse Scales.

Warehouse Scale	Without Considering Shuttle State	Considering Shuttle State	Path Reduction Rate
10 × 10	32.40	30.30	6.48%
20 × 20	57.90	53.30	7.94%
30 × 30	91.20	84.50	7.35%
40 × 40	121.60	109.90	9.62%
50 × 50	154.70	138.50	10.47%
75 × 75	238.50	210.70	11.66%
100 × 100	310.10	275.40	11.18%

. The results demonstrate that the dynamic map switching mechanism can effectively improve path flexibility. Specifically, paths planned with consideration of shuttle state are, on average, shortened by approximately 9.05% compared to those planned without considering shuttle state, confirming the algorithm’s advantages in terms of both energy saving and operational efficiency.

3.2.2. Experimental Results and Analysis of the A*-Guided DQN Algorithm

The hyperparameters for DQN are shown in

Table A4. Hyperparameters for DQN.

Parameter Name	Meaning	Value
memory_size	Maximum capacity of the experience replay pool, storing interaction experiences to ensure sample diversity.	50,000
batch_size	Number of samples sampled from the replay pool for each training step, balancing training efficiency and stability.	32
GAMMA	Discount factor, weighing the importance of future rewards relative to immediate rewards.	0.95
TARGET_REPLACE_ITER	Update frequency of the target network (copying policy network parameters to target network every N steps), stabilizing training.	100
epsilon_start	Initial exploration rate in epsilon-greedy strategy, controlling exploration intensity in early training.	0.8
epsilon_end	Final exploration rate in epsilon-greedy strategy, transitioning to exploitation in late training.	1
learning_rate	Learning rate of the optimizer, controlling the step size of network parameter updates.	0.01
start_training_info_numbe	Minimum number of experiences required to start training, ensuring sufficient samples for effective learning.	100
a (in Memory class)	Priority weight in prioritized experience replay, controlling the impact of experience priority on sampling.	0.6
loss_function	Loss function type, calculating the error between predicted Q-values and target Q-values.	SmoothL1Loss

.

To evaluate the adaptability and training effectiveness of the A*-guided DQN (A*-DQN) algorithm under various warehouse layouts, three representative warehouse layout models were constructed, as illustrated in Figure 19. The number of storage units and the exploration rate settings for each layout are summarized in

Table 8. Basic Parameters of Each Layout.

Layout Type	Number of Storage Units	Layout Category	Exploration Rate
Sparse Rectangular	36.00	Rectangular	0.80
Dense Rectangular	100.00	Rectangular	0.80
Fishbone	86.00	Fishbone	0.80

.

3.2.3. Analysis of Training Results

For each completed task, good real-time performance receives 3 points. Accordingly, the maximum rewards for the three layouts are 108, 300, and 258, respectively.

Taking Layout 2 as an example, as shown in Figure 20a, when training with the A*-DQN algorithm, the reward reaches 300 points after approximately 250 training episodes. In contrast, as shown in Figure 20b, when training with the standard DQN algorithm, the cumulative reward reaches only 225 points after 300 episodes. These results demonstrate that the A*-DQN algorithm, by leveraging the A* path guidance mechanism, can significantly accelerate policy convergence and improve task completion rates. This approach is particularly well-suited for path planning and scheduling tasks in warehouse systems with complex layout structures.

3.2.4. Comparison Between A* and A*-DQN Algorithms

(1)

Comparative Analysis of Assigned Task Paths

Under the three different layout models, an inbound and outbound task is randomly assigned: the four-way shuttle retrieves cargo between the entrance/exit and storage units, then returns to the storage unit. The comparative results are shown in Figure 21, indicating that DQN has effectively learned the path decision logic of A*, demonstrating strong path optimization capability and interpretability.

(2)

Performance Comparison of Path Planning in Multi-Task Scenarios

To verify the algorithms’ avoidance capabilities under multi-task conditions, data in

Table 9. Collision Test Results for A* and A*-DQN.

Experiment	A*	A*-DQN
1	12	0
2	9	0
3	17	0
4	16	0
5	13	0

show that the average number of collisions for A* is 13.4, while A*-DQN is able to complete all tasks without any collisions. This demonstrates that A*-DQN possesses superior path avoidance capability and system stability in complex task environments.

To further validate the computational efficiency of the algorithms, the total computation time required by both algorithms to complete all tasks was recorded. Each experiment was repeated three times, and the average was taken to calculate the average decision time per task. As shown in

Table 10. Efficiency Comparison in Multi-Task Scenarios.

Layout Type	Algorithm	Time of Experiment 1(s)	Time of Experiment 2(s)	Time of Experiment 3(s)	Average Time(s)	Time Reduction Rate
Sparse Rectangular	A*-DQN	1.86	2.01	2.04	1.97	43.87%
	A*	3.52	3.47	3.53	3.51
Dense Rectangular	A*-DQN	4.02	4.13	4.17	4.11	63.21%
	A*	10.98	11.08	11.45	11.17
Fishbone	A*-DQN	5.25	5.36	5.84	5.48	66.48%
	A*	16.83	15.98	16.24	16.35

, the efficiency advantage of A*-DQN is even more pronounced, demonstrating excellent scalability and practical engineering value.

The A*-DQN algorithm proposed in this study has achieved remarkable results in path planning. Through simulation experiments conducted under various warehouse layouts, the effectiveness and superiority of the algorithm have been validated. The experiments demonstrate that the introduction of a path map switching mechanism based on shuttle loading status significantly enhances the flexibility of path planning and improves energy efficiency. During the training process, the A*-DQN algorithm exhibits faster convergence and stronger obstacle avoidance capabilities, enabling it to efficiently generate safe and optimal paths in complex environments. Moreover, the algorithm demonstrates excellent adaptability and stability in multi-task scenarios, substantially improving the operational efficiency of four-way shuttles and the accuracy of path planning.

4. Conclusions

This paper conducts an in-depth investigation into the operation processes of four-way shuttles and elevators in shuttle-based warehouse systems. Focusing on path planning and task scheduling challenges, a series of optimization strategies are proposed, and a multi-shuttle cooperative operation mechanism oriented toward energy efficiency optimization is successfully established.

In terms of task scheduling, to address issues such as uneven task allocation, poor adaptability to dynamic environments, high idle rates, and difficulties in energy optimization in multi-shuttle cooperative operations, this paper proposes a collaborative scheduling algorithm based on an improved genetic algorithm (IGA) and multi-agent deep deterministic policy gradient (MADDPG) algorithm. By introducing improvements such as order-preserving crossover and path-reversal mutation, the algorithm’s search capability and solution quality are significantly enhanced. Compared to traditional genetic algorithms (GA), integrating shuttle cars and elevators into a unified task framework eliminates unnecessary waiting and empty runs between equipment. In terms of energy consumption and operational time, IGA reduced these metrics by approximately 16.23% and 10.86%, respectively, compared to GA. Furthermore, the hierarchical collaborative optimization approach integrating GA and MADDPG effectively overcomes the limitations of single algorithms in four-way shuttle scheduling scenarios. The preliminary scheduling plan generated by the IGA was used as prior knowledge and input into the MADDPG algorithm, accelerating the scheduling optimization process and achieving global optimality. Experimental results from scheduling models in various warehouse environments indicate that compared to single algorithms, the hybrid algorithm achieves an average reduction of 16.68% in energy consumption per order and a 12.84% decrease in total processing time. The proposed method excels in multi-objective optimization of energy consumption, time, and load balancing, fully demonstrating its adaptability and stability in multi-shuttle, multi-task cooperative execution.

For path planning, the innovative incorporation of shuttle loading status information enabled the construction of a path map switching mechanism, facilitating adaptive adjustment of path constraints according to different operating states of the shuttles. In addition, the A*-guided DQN learning method is proposed in this paper. The preliminary path planning solutions generated by the A* algorithm were incorporated into the experience replay pool of the DQN algorithm during the initial training phase as experience inputs, thereby enhancing the algorithm’s convergence speed and optimization rate under complex layouts and dynamic environments. Compared to the traditional A* algorithm that plans the entire path directly, the A*-DQN algorithm employs a distribution-guided execution mode, dynamically updating path planning in real time based on traffic conditions. Compared to traditional methods, the A* guided DQN learning approach reduces average total task time by 12.84% and average path planning length by approximately 9.05%. The four-directional shuttle vehicle can now complete order tasks with near-zero conflicts. This method provides strong support for the efficient operation of four-way shuttles in complex warehouse environments.

In summary, the joint optimization algorithm proposed in this paper—integrating heuristic search, evolutionary algorithms, and reinforcement learning—not only effectively solves the path planning and task scheduling problems in four-way shuttle warehouse systems but also achieves remarkable results in energy saving, consumption reduction, and intelligent operations. This provides a solid theoretical foundation and engineering application value for the transformation and upgrading of warehouse systems, demonstrating broad application prospects and promotion value.

5. Practical Application in Industry

The practical industrial applications of the IGA-MADDPG algorithm and the A*DQN algorithm are as follows:

The IGA-MADDPG algorithm, featuring a hierarchical structure (global IGA pre-planning + local MADDPG adjustment), has been validated for industrial application through international studies. In real-time scalability, it was applied to AGV scheduling in container yards, enabling real-time decision-making and improving operational efficiency and energy utilization across different yard scales [35]. Its experience injection mechanism boosts training efficiency by 60%, addressing the convergence bottleneck of multi-agent systems under industrial-scale concurrency. For multi-objective optimization, a warehouse research showed that it reduces task completion time and energy consumption by coupling target assignment and path planning [36]. In terms of interpretability, a hierarchical reinforcement learning strategy (analogous to IGA-MADDPG’s structured design) enhanced decision traceability, with maintenance teams reporting a 65% improvement in understanding scheduling logic, which helps meet industrial safety standards [37].

The A*-DQN algorithm (integrating A* heuristic search and Deep Q-Networks) exhibits strong adaptability in industrial dynamic path planning. In dynamic environment adaptation, it was used for maritime autonomous ship navigation: A* generated static optimal paths, while DQN made real-time adjustments for obstacles, achieving collision-free navigation with a path deviation rate below 5%. In e-commerce warehouses, its load-aware map switching mechanism cut shuttle no-load rates from 42% to 6.8%. For energy optimization, a mining robot path planning study showed that DQN-derived frameworks (similar to A*-DQN) reduced path following time by 17% and corresponding energy consumption. Its lightweight design (≤480 KB parameters) enables operation on embedded devices with single-step inference time under 50 ms, fitting resource-constrained industrial scenarios like smart factory AGV navigation.

In summary, the design proposed in this paper demonstrates good practical applicability in industrial settings.

6. Limitations and Extensions

Although this study has achieved good results in path planning and scheduling optimization, limitations still exist. For instance, in large-scale order environments, IGA-MADDPG exhibits high computational complexity, necessitating further optimization of model structure and computational efficiency. In hardware deployment, the MADQN model is constrained by sensor accuracy and communication latency and requires deeper integration with actual devices.

Furthermore, the selection of weighting parameters in multi-objective optimization relies on manual experience and lacks adaptive adjustment mechanisms. Future research will proceed along three directions:

• Explore lightweight path planning models, such as incorporating graph neural networks (GNNs) and incremental search algorithms, to enhance path computation efficiency and strategy generalization capabilities.
• Advance integration with physical hardware systems by establishing a closed-loop algorithm control system through interfacing the second-generation Robot Operating System (ROS2) with simulation platforms.
• Develop adaptive multi-objective optimization strategies, incorporate meta-learning mechanisms for dynamic weight adjustment, and explore green warehouse scheduling models. Introduce synergistic constraints on carbon emissions and energy consumption to advance intelligent warehouse systems toward low-carbon and high-efficiency evolution.