Application of a Multi-Objective Optimization Algorithm Based on Differential Grouping to Financial Asset Allocation
Abstract
1. Introduction
2. Related Work
2.1. Traditional Financial Asset Allocation Methods
2.2. Multi-Objective Optimization Methods in Financial Asset Allocation
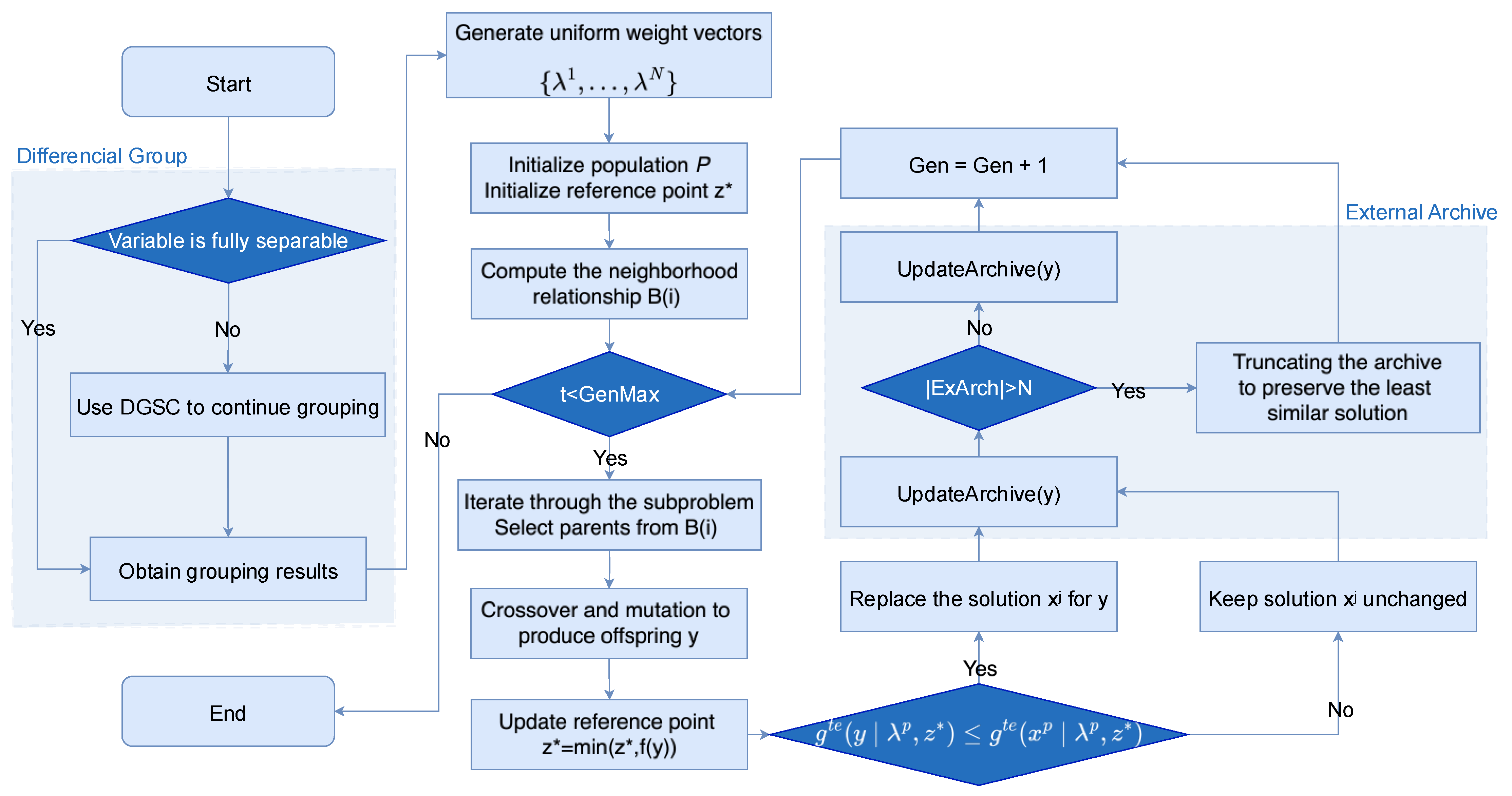
3. The Framework of MOEA/D Combined with Differential Grouping
3.1. General Framework
| Algorithm 1: DG-MOEA/D Algorithm |
| Input: (Population size) (Neighborhood size) (Group number) (Problem dimension) Output: (Final population) 2 Groups do ; ; ); InitializeReferencePoint( ); ; 9 end for |
3.2. Recursive Spectral Clustering Differential Grouping
| Algorithm 2: RDGSC Algorithm |
| Input: Output: Groups in vars do then Groups[fully_separable] 4 remaining_vars ← vars- Groups[fully_separable] 5 end for then ); , len (remaining_vars))); |
| Algorithm 3: DGSC Algorithm |
| Input: Output: Groups Θ; ; do 5 end for 6 L = D − W; , ’SA’); ); ; 12 end for |
3.3. MOEA/D Algorithm Combined with External Archives
| Algorithm 4: External Archive Mechanism |
| Input: (Selected set of non-dominated layer solutions); (The last nondominated layer of the Nth selected solution); (Maximum archive capacity) Output: ExArchCollection (Updated collection of external archives) then to ExArchCollection; then do ; then to ExArchCollection; then are deleted; are non-dominated then ; 12 end for then ExArchCollection do do Calculate the angle between each pair of solutions; 17 end for 18 Delete the solution with minimum angle; 19 end for 20 end while |
| Algorithm 5: MOEA/D-UTEA Algorithm |
| Input: (Neighborhood size); (Population size); max_gen (Maximum number of iterations) Output: (Final population) ); ; ); InitializeReferencePoint( ); ; 7 While gen < max_gen do do )); RecombinationAndMutation(parents); UpdateReferencePoint(z*, y); do then 15 end for 16 end for 17 end while |
3.4. Computational Complexity Analysis
3.5. Three-Objective Portfolio Model
4. Experiments and Analysis
4.1. Test Functions
4.2. Evaluation Metrics
4.3. Comparison Algorithms
- Multi-Objective Evolutionary Algorithm Based on Decomposition (MOEA/D): Utilizes weight vectors or decomposition strategies to convert complex multi-objective problems into multiple single-objective sub-problems, and shares information through a neighborhood collaboration mechanism, thereby improving search efficiency while ensuring uniformity in the solution set distribution.
- Nondominated Sorting Genetic Algorithm II (NSGA-II): Achieves efficient multi-objective optimization through rapid nondominated sorting and crowding distance calculation, while utilizing an elite retention strategy to ensure solution diversity and convergence.
- Nondominated Sorting Genetic Algorithm III (NSGA-III): Proposed for high-dimensional multi-objective optimization problems, it introduces a reference point mechanism to guide population evolution, combining nondominated sorting with adaptive normalization strategies to achieve uniform solution distribution while maintaining solution set diversity.
- Strength Pareto Evolutionary Algorithm 2 (SPEA2): By introducing a fine-grained fitness allocation strategy, density estimation techniques, and an enhanced archive truncation method, it enhances population diversity while preserving Pareto solutions, thereby avoiding premature convergence.
- MOEA/D with a Distance-Based Updating Strategy (MOEA/D-DU): Updates individuals in the population using distance metrics. This strategy randomly selects a solution in each iteration and updates it based on its distance from other solutions in the population.
- An Inverse Modelling Constrained MOEA/D (IM-C-MOEA/D): A multi-objective evolutionary algorithm combining decomposition strategies with constraint handling mechanisms, it uses inverse modelling techniques to map the objective space to the decision space, effectively addressing constrained real-world optimization problems.
- Large-scale Multi-objective Optimization via Reformulated Decision Variable Analysis (LERD): This algorithm reformulates the decision variable analysis process into an optimization problem with binary decision variables, enabling efficient large-scale multi-objective optimization, significantly reducing computational complexity, and improving optimization efficiency.
4.4. Comparative Analysis of Experimental Results
4.4.1. Analysis of Experimental Results for the DTLZ Test Function
4.4.2. Analysis of Experimental Results for the LSMOP Test Function
4.5. Ablation Experiment
5. Application of DG-MOEA/D in Financial Asset Allocation
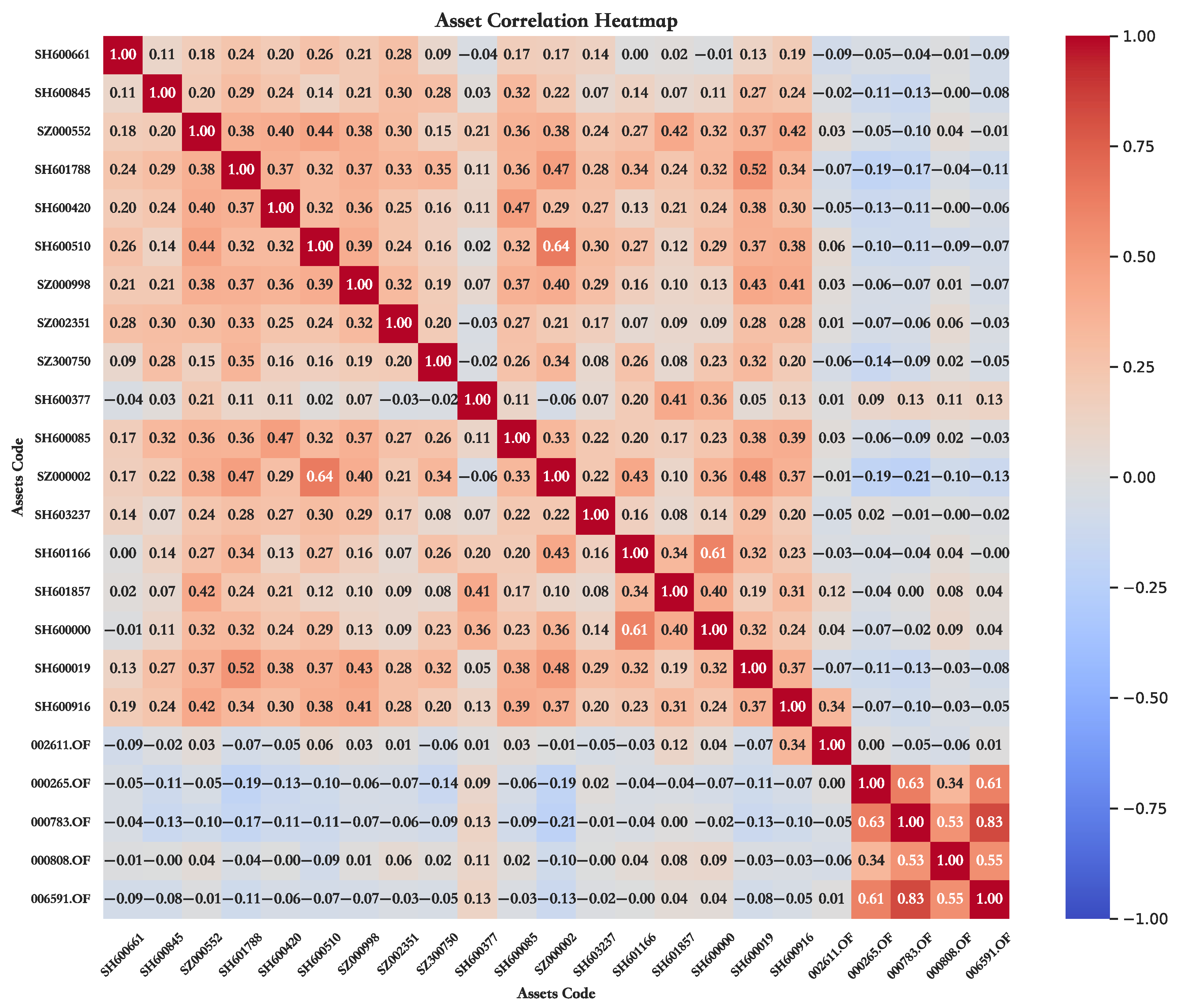
5.1. Data Sources and Preprocessing
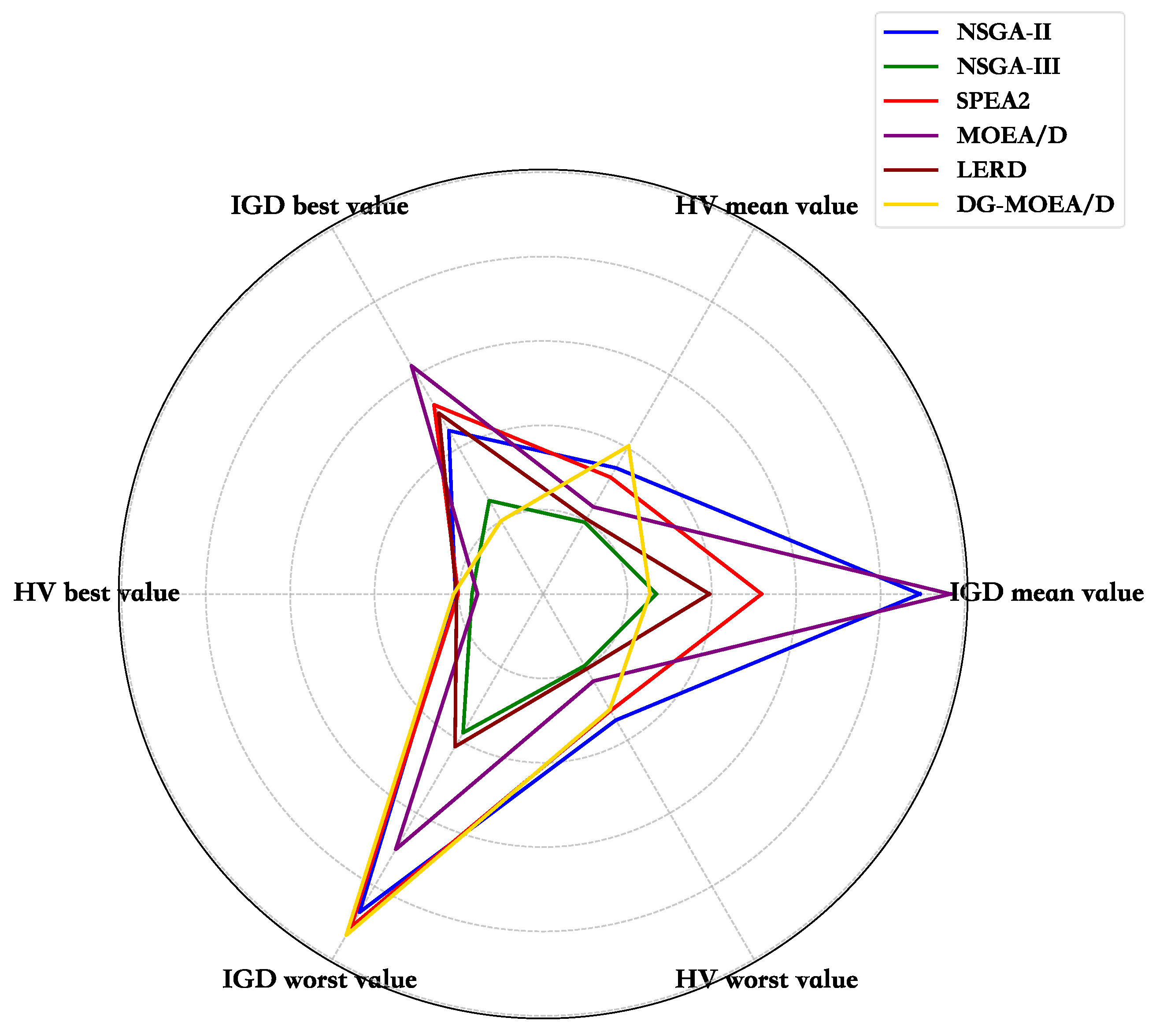
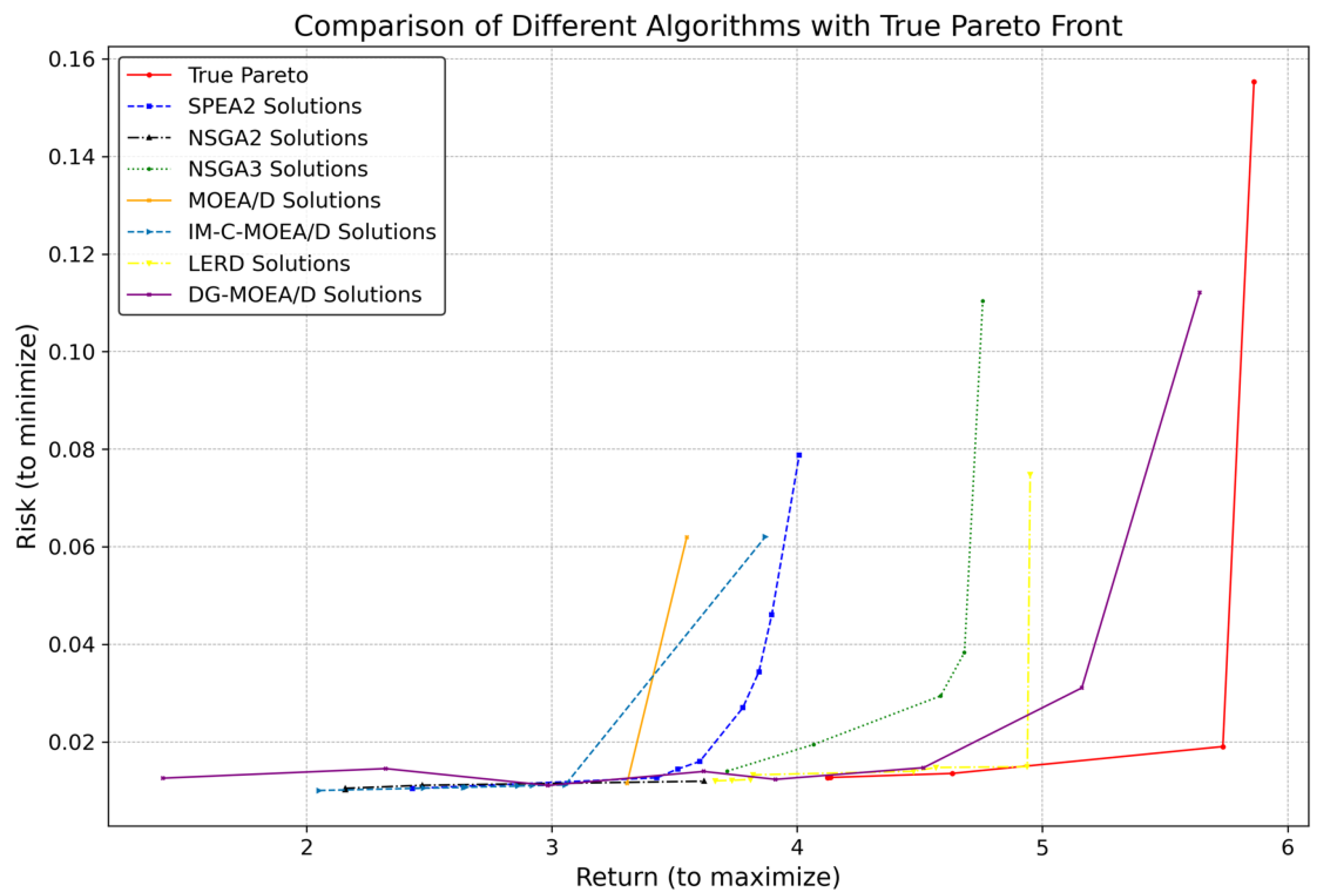
5.2. Performance Comparison of Algorithms
5.2.1. Comparison and Analysis of Model Evaluation Metrics
5.2.2. Selection and Analysis of the Optimal Investment Portfolio
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Acharya, A.; Sidnal, N.S. High Frequency Trading with Complex Event Processing. In Proceedings of the 2016 IEEE 23rd International Conference on High Performance Computing Workshops (HiPCW), Hyderabad, India, 19–22 December 2016; pp. 39–42. [Google Scholar]
- Wang, H. Leontief Model-based Research on the Input Structure of Three Industries: A Markowitz Optimization Perspective. Appl. Math. Nonlinear Sci. 2024, 9. [Google Scholar] [CrossRef]
- Song, M.; Lin, J.; Liu, X.; Jia, H.; Luo, S. Octopus Optimization Algorithm: A Novel Single- and Multi-objective Optimization Algorithm for Optimization Problems. Clust. Comput. 2025, 28, 484. [Google Scholar] [CrossRef]
- Romanyuk, Y. Liquidity, Risk, and Return: Specifying an Objective Function for the Management of Foreign Reserves. Appl. Stoch. Models Bus. Ind. 2012, 28, 175–193. [Google Scholar] [CrossRef]
- Jiao, Y.; Liu, H. Optimal Portfolio Choice with ESG Considerations and Asymmetric Information. Quant. Financ. 2025, 25, 1163–1176. [Google Scholar] [CrossRef]
- Huang, G.; Hu, M.; Yang, X.; Wang, X.; Wang, Y.; Huang, F. A Review of Constrained Multi-Objective Evolutionary Algorithm-Based Unmanned Aerial Vehicle Mission Planning: Key Techniques and Challenges. Drones 2024, 8, 316. [Google Scholar] [CrossRef]
- Wang, H.; Chen, L.; Hao, X.; Yu, T.; Qian, Y.; Yang, R.; Liu, W. Meta-knowledge-assisted Sampling with Variable Sorting for Large-scale Multi-objective Optimization. Appl. Soft Comput. 2025, 181, 113386. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Deb, K.; Agarwal, S.; Pratap, A.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Cheng, G.H.; Wang, G.G.; Hwang, Y.M. Multi-Objective Optimization for High-Dimensional Expensively Constrained Black-Box Problems. J. Mech. Des. 2021, 143, 111704. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio Selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Sawik, B. A Bi-objective Portfolio Optimization with Conditional Value-at-risk. Decis. Mak. Manuf. Serv. 2010, 4, 47–69. [Google Scholar] [CrossRef]
- Chung, M.; Lee, Y.; Kim, J.H.; Kim, W.C.; Fabozzi, F.J. The Effects of Errors in Means, Variances, and Correlations on the Mean-variance Framework. Quant. Financ. 2022, 22, 1893–1903. [Google Scholar] [CrossRef]
- Dai, M.; Jin, H.; Kou, S.; Xu, Y. A Dynamic Mean-Variance Analysis for Log Returns. Manag. Sci. 2020, 67, 1093–1108. [Google Scholar] [CrossRef]
- Andrei, D.; Cujean, J.; Wilson, M. The Lost Capital Asset Pricing Model. Rev. Econ. Stud. 2023, 90, 2703–2762. [Google Scholar] [CrossRef]
- Vasicek, O.A. A Note on Using Cross-sectional Information in Bayesian Estimation of Security Betas. J. Financ. 1973, 28, 1233–1239. [Google Scholar]
- Smith, W.S.; Harter, C. An Empirical Investigation of the Option-Adjusted Realized Return. Rev. Quant. Financ. Acc. 2002, 19, 379–398. [Google Scholar] [CrossRef]
- Behera, J.; Pasayat, A.K.; Behera, H.; Kumar, P. Prediction based Mean-value-at-risk Portfolio Optimization Using Machine Learning regression Algorithms for Multi-national Stock Markets. Eng. Appl. Artif. Intell. 2023, 120, 105843. [Google Scholar] [CrossRef]
- Chebbi, A.; Hedhli, A. Revisiting the Accuracy of Standard VaR Methods for Risk Assessment: Using the Copula–EVT Multi-dimensional Approach for Stock Markets in the MENA Region. Q. Rev. Econ. Financ. 2022, 84, 430–445. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Uryasev, S. Optimization of Conditional Value-at-risk. J. Risk 2000, 2, 21–42. [Google Scholar] [CrossRef]
- Wang, G.J.; Zhu, C.L. BP-CVaR: A Novel Model of Estimating CVaR with Back Propagation Algorithm. Econ. Lett. 2021, 209, 110125. [Google Scholar] [CrossRef]
- Anagnostopoulos, K.P.; Mamanis, G. A Portfolio Optimization Model with Three Objectives and Discrete Variables. Comput. Oper. Res. 2010, 37, 1285–1297. [Google Scholar] [CrossRef]
- Tobin, J. Liquidity Preference as Behavior towards Risk. Rev. Econ. Stud. 1958, 25, 65–86. [Google Scholar] [CrossRef]
- Amihud, Y.; Mendelson, H. Liquidity and Stock Returns. Financ. Anal. J. 1986, 42, 43–48. [Google Scholar] [CrossRef]
- Goldstein, I.; Jiang, H.; Ng, D.T. Investor Flows and Fragility in Corporate Bond Funds. J. Financ. Econ. 2017, 126, 592–613. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, H.; Huang, L.; Qu, R.; Nojima, Y. A Pareto Front Grid Guided Multi-objective Evolutionary Algorithm. Appl. Soft Comput. 2023, 136, 110095. [Google Scholar] [CrossRef]
- Cui, T.; Du, N.; Yang, X.; Ding, S. Multi-period Portfolio Optimization Using a Deep Reinforcement Learning Hyper-heuristic Ap-proach. Technol. Forecast. Soc. Change 2024, 198, 122944. [Google Scholar] [CrossRef]
- Chen, Y.T.; Yang, H.Q. Multi-period Mean-variance Portfolio Selection with Practical Constraints Using Heuristic Genetic Algorithms. Int. J. Comput. Econ. Econom. 2020, 10, 209–221. [Google Scholar] [CrossRef]
- Mishra, S.K.; Panda, G.; Meher, S.; Panda, A. Comparative Performance Evaluation of Multiobjective Optimization Algorithms for Portfolio Management. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 1337–1341. [Google Scholar]
- Anagnostopoulos, K.P.; Mamanis, G. Multiobjective Evolutionary Algorithms for Complex Portfolio Optimization Problems. Comput. Manag. Sci. 2011, 8, 259–279. [Google Scholar] [CrossRef]
- Mishra, S.K.; Panda, G.; Majhi, R. A Comparative Performance Assessment of a Set of Multiobjective Algorithms for Con-strained Portfolio Assets Selection. Swarm Evol. Comput. 2014, 16, 38–51. [Google Scholar] [CrossRef]
- Mane, S.U.; Rao, M.R.N. A non-dominated Sorting based Evolutionary Algorithm for Many-objective Optimization Problems. Sci. Iran. 2022, 28, 3293–3314. [Google Scholar] [CrossRef]
- Mishra, S.K.; Panda, G.; Majhi, R. Constrained Portfolio Asset Selection Using Multiobjective Bacteria Foraging Optimization. Oper. Res. 2014, 14, 113–145. [Google Scholar] [CrossRef]
- Kumar, D.; Mishra, K.K. Portfolio Optimization Using Novel Co-variance Guided Artificial Bee Colony Algorithm. Swarm Evol. Comput. 2017, 33, 119–130. [Google Scholar] [CrossRef]
- Leung, M.; Wang, J.; Che, H. Cardinality-constrained Portfolio Selection Via Two-timescale Duplex Neurodynamic Optimiza-tion. Neural Netw. 2022, 153, 399–410. [Google Scholar] [CrossRef] [PubMed]
- Chu, X.; Han, X.; Zhang, M.; Li, M. Improving Decomposition-based MOEAs for Combinatorial Optimization by Intensifying Corner Weights. Swarm Evol. Comput. 2024, 91, 101722. [Google Scholar] [CrossRef]
- Yang, M.; Qian, W.; Yang, L.; Hou, X.; Yuan, X.; Dong, Z. A Synergistic Multi-Objective Evolutionary Algorithm with Diffusion Population Generation for Portfolio Problems. Mathematics 2024, 12, 1368. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, A. Multiobjective Portfolio Optimization via Pareto Front Evolution. Complex Intell. Syst. 2022, 8, 4301–4317. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Tang, K.; Yao, X. Large Scale Evolutionary Optimization Using Cooperative Coevolution. Inf. Sci. 2008, 178, 2985–2999. [Google Scholar] [CrossRef]
- Van den Bergh, F.; Engelbrecht, A.P. A Cooperative Approach to Particle Swarm Optimization. IEEE Trans. Evol. Comput. 2004, 8, 225–239. [Google Scholar] [CrossRef]
- Omidvar, M.N.; Li, X.; Mei, Y.; Yao, X. Cooperative Co-Evolution with Differential Grouping for Large Scale Optimization. IEEE Trans. Evol. Comput. 2014, 18, 378–393. [Google Scholar] [CrossRef]
- Sun, Y.; Kirley, M.; Halgamuge, S.K. Extended Differential Grouping for Large Scale Global Optimization with Direct and Indirect Variable Interactions. In Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation, Madrid, Spain, 11–15 July 2015; pp. 313–320. [Google Scholar]
- Mei, Y.; Omidvar, M.N.; Li, X.; Yao, X. A Competitive Divide-and-Conquer Algorithm for Unconstrained Large-Scale Black-Box Opti-mization. ACM Trans. Math. Softw. 2016, 42, 13. [Google Scholar] [CrossRef]
- Sun, Y.; Kirley, M.; Halgamuge, S.K. A Recursive Decomposition Method for Large Scale Continuous Optimization. IEEE Trans. Evol. Comput. 2018, 22, 647–661. [Google Scholar] [CrossRef]
- Li, L.; Fang, W.; Wang, Q.; Sun, J. Differential Grouping with Spectral Clustering for Large Scale Global Optimization. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 334–341. [Google Scholar]
- Michalak, K. Improving the NSGA-II Performance with An External Population. In Proceedings of the International Conference on Intelligent Data Engineering and Automated Learning, Wroclaw, Poland, 14–16 October 2015; pp. 273–280. [Google Scholar]
- Knowles, J.D.; Corne, D.W. Approximating the Nondominated Front Using the Pareto Archived Evolution Strategy. Evol. Comput. 2000, 8, 149–172. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive Differential Evolution with Optional External Archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Nguyen, P.; Mitchell, D. Conditional Value-at-Risk Robust Optimization. SSRN Electron. J. 2022, 1–34, preprint. [Google Scholar] [CrossRef]
- Yu, C.; Liu, Y. A Personalized Mean-CVaR Portfolio Optimization Model for Individual Investment. Math. Probl. Eng. 2021, 2021, 8863597. [Google Scholar] [CrossRef]
| Grouping Method | XDG | RDG | RDGSC |
|---|---|---|---|
| Core Mechanism | Detects direct and indirect interactions | Recursively identifies nonlinear interactions between variables | Recursive spectral clustering with similarity matrix grouping |
| Accuracy Enhancement | High, though threshold-dependent | High, suitable for most CEC benchmarks | Superior, particularly in complex coupling and redundant variable scenarios |
| Feature Vector/Dimension Processing | No explicit dimensionality reduction | No explicit dimensionality reduction | Effectively reduces feature dimensions via spectral clustering |
| Suitable Problem Types | Moderate-scale problems with clear structure | Large-scale problems with separability | High-dimensional problems with complex coupling and nonlinearity |
| Problem | IGD/HV Mean | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| MOEA/D | MOEA/D-DU | NSGA-II | NSGA-III | SPEA2 | IM-C-MOEA/D | LERD | DG-MOEA/D | ||
| DTLZ 1 | IGD | 4.11 × 102= | 2.29 × 10−2= | 1.28 × 10−1- | 2.27 × 10−2= | 2.36 × 10−2= | 2.27 × 101- | 8.84 × 100- | 3.97 × 10−2 |
| HV | 7.87 × 101- | 8.30 × 10−1= | 6.48 × 10−1- | 8.31 × 10−1= | 8.29 × 10−1= | 0.00 × 100- | 1.36 × 10−1- | 8.41 × 10−1 | |
| DTLZ 2 | IGD | 5.45 × 102= | 5.45 × 10−2= | 7.32 × 10−2= | 5.45 × 10−2= | 5.70 × 10−2= | 1.20 × 10−1- | 6.64 × 10−2= | 5.05 × 10−2 |
| HV | 5.60 × 101= | 5.60 × 10−1= | 5.28 × 10−1= | 5.60 × 10−1= | 5.53 × 10−1= | 4.70 × 10−1- | 5.35 × 10−1= | 5.60 × 10−1 | |
| DTLZ 3 | IGD | 1.63 × 10−1- | 6.03 × 10−2= | 8.68 × 10−2= | 6.15 × 10−2= | 6.37 × 10−2= | 8.61 × 101- | 1.46 × 101- | 6.03 × 10−2 |
| HV | 4.67 × 10−1- | 5.43 × 10−1= | 4.83 × 10−1- | 5.29 × 10−1= | 5.36 × 10−1= | 0.00 × 100- | 1.52 × 10−1- | 5.54 × 10−1 | |
| DTLZ 4 | IGD | 2.87 × 10−1- | 5.45 × 10−2+ | 1.30 × 10−1+ | 1.52 × 10−1+ | 2.51 × 10−1= | 1.19 × 10−1+ | 2.93 × 10−1- | 2.42 × 10−1 |
| HV | 4.46 × 10−1= | 5.60 × 10−1+ | 4.99 × 10−1= | 5.16 × 10−1+ | 4.70 × 10−1= | 4.75 × 10−1= | 4.45 × 10−1= | 4.68 × 10−1 | |
| DTLZ 5 | IGD | 3.39 × 10−2= | 2.87 × 10−2= | 6.39 × 10−3= | 1.33 × 10−2= | 4.86 × 10−3= | 3.36 × 10−2= | 2.40 × 10−2= | 3.89 × 10−3 |
| HV | 1.82 × 10−1= | 1.87 × 10−1= | 1.99 × 10−1= | 1.93 × 10−1= | 1.99 × 10−1= | 1.74 × 10−1= | 1.89 × 10−1= | 2.02 × 10−1 | |
| DTLZ 6 | IGD | 3.39 × 10−2= | 3.31 × 10−2= | 6.68 × 10−3= | 1.95 × 10−2= | 4.49 × 10−3= | 7.05 × 100- | 2.39 × 10−2= | 3.39 × 10−3 |
| HV | 1.82 × 10−1= | 1.83 × 10−1= | 1.99 × 10−1= | 1.91 × 10−1= | 2.00 × 10−1= | 0.00 × 100- | 1.90 × 10−1= | 2.00 × 10−1 | |
| DTLZ 7 | IGD | 1.76 × 10−1- | 3.70 × 100- | 8.04 × 10−2= | 7.61 × 10−2= | 6.59 × 10−2= | 1.58 × 10−1- | 7.34 × 10−1- | 6.38 × 10−2 |
| HV | 2.55 × 10−1= | 7.75 × 10−2- | 2.66 × 10−1= | 2.69 × 10−1= | 2.75 × 10−1= | 2.47 × 10−1= | 2.07 × 10−1- | 2.75 × 10−1 | |
| +/-/= | 0/5/9 | 2/2/10 | 1/3/10 | 2/0/12 | 0/0/14 | 1/9/4 | 0/7/7 | ||
| Problem | IGD/HV Mean | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| MOEA/D | MOEA/D-DU | NSGA-II | NSGA-III | SPEA2 | IM-C-MOEA/D | LERD | DG-MOEA/D | ||
| LSMOP1 | IGD | 2.036 × 10−1- | 2.182 × 10−1- | 3.132 × 10−1- | 2.416 × 10−1- | 2.638 × 10−1- | 7.928 × 10−1- | 4.798 × 10−1- | 1.390 × 10−1 |
| HV | 6.021 × 10−1= | 5.670 × 10−1= | 4.456 × 10−1- | 5.146 × 10−1- | 5.267 × 10−1- | 7.637 × 10−2- | 2.078 × 10−1- | 6.050 × 10−1 | |
| LSMOP2 | IGD | 1.655 × 10−1- | 1.062 × 10−1= | 1.874 × 10−1- | 1.458 × 10−1= | 1.620 × 10−1- | 1.649 × 10−1- | 1.744 × 10−1- | 1.061 × 10−1 |
| HV | 6.884 × 10−1= | 6.767 × 10−1= | 6.406 × 10−1- | 6.908 × 10−1= | 6.893 × 10−1= | 6.340 × 10−1- | 6.647 × 10−1= | 7.080 × 10−1 | |
| LSMOP3 | IGD | 6.155 × 10−1- | 5.995 × 10−1- | 1.184 × 100- | 8.339 × 10−1- | 7.209 × 10−1- | 3.318 × 100- | 5.346 × 100- | 5.439 × 10−1 |
| HV | 2.068 × 10−1= | 1.589 × 10−1- | 6.014 × 10−2- | 8.510 × 10−2- | 1.517 × 10−1- | 0.000 × 100- | 2.121 × 10−2- | 2.198 × 10−1 | |
| LSMOP4 | IGD | 3.972 × 10−1- | 2.277 × 10−1+ | 4.673 × 10−1- | 4.018 × 10−1- | 3.870 × 10−1= | 3.821 × 10−1= | 3.609 × 10−1= | 3.429 × 10−1 |
| HV | 3.594 × 10−1= | 5.969 × 10−1+ | 2.832 × 10−1- | 4.393 × 10−1+ | 3.631 × 10−1= | 3.038 × 10−1= | 4.196 × 10−1+ | 3.464 × 10−1 | |
| LSMOP5 | IGD | 8.023 × 10−1= | 2.634 × 10−1+ | 3.205 × 10−1+ | 3.117 × 10−1+ | 3.831 × 10−1+ | 7.030 × 10−1+ | 3.689 × 10−1+ | 8.241 × 10−1 |
| HV | 9.806 × 10−2= | 2.158 × 10−1+ | 2.298 × 10−1+ | 1.992 × 10−1+ | 2.978 × 10−1+ | 5.065 × 10−2- | 3.549 × 10−1+ | 9.750 × 10−2 | |
| LSMOP6 | IGD | 9.645 × 10−1- | 1.120 × 100- | 1.319 × 100- | 1.714 × 100- | 1.521 × 100- | 4.231 × 100- | 1.869 × 100- | 9.116 × 10−1 |
| HV | 7.371 × 10−3= | 0.000 × 100= | 0.000 × 100= | 2.334 × 10−4= | 0.000 × 100= | 0.000 × 100= | 1.376 × 10−4= | 1.663 × 10−2 | |
| LSMOP7 | IGD | 8.130 × 10−1- | 6.937 × 10−1= | 2.073 × 100- | 2.436 × 100- | 2.239 × 100- | 2.021 × 100- | 1.208 × 100- | 6.526 × 10−1 |
| HV | 8.875 × 10−2= | 8.955 × 10−2= | 0.000 × 100- | 0.000 × 100- | 0.000 × 100- | 0.000 × 100- | 2.898 × 10−2- | 9.089 × 10−2 | |
| LSMOP8 | IGD | 7.966 × 10−1= | 2.366 × 10−1+ | 3.548 × 10−1+ | 3.406 × 10−1+ | 3.530 × 10−1+ | 4.030 × 10−1+ | 3.622 × 10−1+ | 8.158 × 10−1 |
| HV | 8.109 × 10−2= | 2.984 × 10−1+ | 3.228 × 10−1+ | 2.907 × 10−1+ | 3.121 × 10−1+ | 1.627 × 10−1+ | 3.303 × 10−1+ | 8.230 × 10−2 | |
| LSMOP9 | IGD | 4.765 × 10−1- | 8.840 × 101- | 1.334 × 100- | 1.196 × 100- | 1.395 × 100- | 1.581 × 100- | 1.828 × 100- | 4.244 × 10−1 |
| HV | 7.852 × 10−2- | 0.000 × 100- | 1.030 × 10−1= | 1.213 × 10−1= | 1.099 × 10−1= | 1.070 × 10−2- | 1.125 × 10−1= | 1.282 × 10−1 | |
| +/-/= | 0/8/10 | 6/6/6 | 4/12/2 | 5/9/4 | 4/9/5 | 3/12/3 | 5/9/4 | ||
| Problem | IGD Mean | ||
|---|---|---|---|
| DG-MOEA/D1 | DG-MOEA/D2 | DG-MOEA/D3 | |
| DTLZ1 | 4.57 × 10−2 | 3.30 × 101 | 2.16 × 101 |
| DTLZ2 | 7.45 × 10−2 | 3.27 × 10−1 | 5.66 × 10−2 |
| DTLZ3 | 6.96 × 10−2 | 1.91 × 102 | 7.92 × 101 |
| DTLZ4 | 4.11 × 10−1 | 3.53 × 10−1 | 7.09 × 10−1 |
| DTLZ5 | 5.39 × 10−2 | 1.87 × 10−1 | 3.04 × 10−2 |
| DTLZ6 | 5.39 × 10−2 | 1.37 × 101 | 1.77 × 100 |
| DTLZ7 | 1.54 × 10−1 | 5.34 × 10−1 | 1.73 × 10−1 |
| LSMOP1 | 6.02 × 10−1 | 5.67 × 10−1 | 4.46 × 10−1 |
| LSMOP2 | 7.08 × 10−1 | 7.27 × 10−1 | 6.41 × 10−1 |
| LSMOP3 | 2.07 × 10−1 | 1.59 × 10−1 | 6.01 × 10−2 |
| LSMOP4 | 3.59 × 10−1 | 5.97 × 10−1 | 3.93 × 10−1 |
| LSMOP5 | 8.98 × 10−1 | 1.22 × 100 | 1.23 × 100 |
| LSMOP6 | 1.01 × 100 | 2.50 × 100 | 2.26 × 100 |
| LSMOP7 | 6.89 × 10−1 | 1.09 × 100 | 1.97 × 100 |
| LSMOP8 | 8.21 × 10−1 | 2.30 × 100 | 1.82 × 100 |
| LSMOP9 | 4.99 × 10−1 | 9.53 × 10−1 | 1.10 × 100 |
| +/−/= | 1/9/6 | 1/15/0 | 1/13/2 |
| Asset Name | Asset Code | Asset Name | Asset Code | Asset Name | Asset Code |
|---|---|---|---|---|---|
| Only Education | 600661.SH | China Gold | 600916.SH | Contemporary Amperex Technology | 300750.SZ |
| Baoxin Software | 600845.SH | Ninghu Expressway | 600377.SH | Pudong Development Bank | 600000.SH |
| China Vanke | 000002.SZ | Shanghai Airport | 600019.SH | Bosera Gold ETF Link C | 002611.OF |
| Tong Ren Tang | 600085.SH | Longping High-Tech | 000998.SZ | E Fund Everlasting Bond A | 000265.OF |
| Sinopharm Group | 600420.SH | Wufangzhai Industry | 603237.SH | Bosera Enjoyment Holding Period A | 000783.OF |
| Black Peony | 600510.SH | Everbright Securities | 601788.SH | CMF Wealth Management Bond A | 000808.OF |
| Industrial Bank | 601166.SH | PetroChina Company | 601857.SH | GF Jingming Bond A | 006591.OF |
| Edifier Technology | 002351.SZ | Gansu Energy Chemical | 000552.SZ |
| Algorithm | Average Value | Best Value | Worst Value | |||
|---|---|---|---|---|---|---|
| IGD | HV | IGD | HV | IGD | HV | |
| NSGA-II | 8.9354 × 10−1 | 3.4524 × 10−1 | 4.4742 × 10−1 | 4.4524 × 10−1 | 8.7129 × 10−1 | 2.1210 × 10−1 |
| NSGA-III | 2.5827 × 10−1 | 1.9652 × 10−1 | 2.5577 × 10−1 | 2.2652 × 10−1 | 3.7981 × 10−1 | 1.6889 × 10−1 |
| SPEA2 | 5.1803 × 10−1 | 3.1955 × 10−1 | 5.1803 × 10−1 | 3.4955 × 10−1 | 9.1152 × 10−1 | 2.0136 × 10−1 |
| MOEA/D | 9.6598 × 10−1 | 2.3837 × 10−1 | 6.2494 × 10−1 | 2.8837 × 10−1 | 6.9913 × 10−1 | 1.5555 × 10−1 |
| IM-C-MOEA/D | 3.6480 × 100 | 3.5529 × 10−1 | 2.4600 × 100 | 5.4945 × 10−1 | 5.4636 × 100 | 3.4846 × 10−1 |
| LERD | 3.9411 × 10−1 | 2.0537 × 10−1 | 4.9534 × 10−1 | 2.0537 × 10−1 | 4.1792 × 10−1 | 2.0535 × 10−1 |
| DG-MOEA/D | 2.0025 × 10−1 | 4.0549 × 10−1 | 2.9327 × 10−1 | 5.1627 × 10−1 | 8.3399 × 10−1 | 2.0830 × 10−1 |
| Asset Code | Asset Weighting | Asset Code | Asset Weighting |
|---|---|---|---|
| 600661.SH | 29.375% | 000808.OF | 1.973% |
| 000002.SZ | 24.050% | 600019.SH | 1.489% |
| 600845.SH | 17.187% | 002351.SZ | 1.485% |
| 600000.SH | 6.409% | 601857.SH | 0.518% |
| 000265.OF | 5.332% | 600510.SH | 0.250% |
| 601788.SH | 4.290% | 000998.SZ | 0.234% |
| 000783.OF | 2.652% | 000552.SZ | 0.152% |
| 006591.OF | 2.556% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, P.; Jiang, Q.; Wang, H.; Guo, W.; Ding, W.; Wang, Z. Application of a Multi-Objective Optimization Algorithm Based on Differential Grouping to Financial Asset Allocation. Appl. Sci. 2025, 15, 11341. https://doi.org/10.3390/app152111341
Jia P, Jiang Q, Wang H, Guo W, Ding W, Wang Z. Application of a Multi-Objective Optimization Algorithm Based on Differential Grouping to Financial Asset Allocation. Applied Sciences. 2025; 15(21):11341. https://doi.org/10.3390/app152111341
Chicago/Turabian StyleJia, Peng, Qiting Jiang, Haodong Wang, Weibin Guo, Weichao Ding, and Zhe Wang. 2025. "Application of a Multi-Objective Optimization Algorithm Based on Differential Grouping to Financial Asset Allocation" Applied Sciences 15, no. 21: 11341. https://doi.org/10.3390/app152111341
APA StyleJia, P., Jiang, Q., Wang, H., Guo, W., Ding, W., & Wang, Z. (2025). Application of a Multi-Objective Optimization Algorithm Based on Differential Grouping to Financial Asset Allocation. Applied Sciences, 15(21), 11341. https://doi.org/10.3390/app152111341




