Abstract
When using optical remote sensing methods for Kelvin wake imaging, the imaging is affected by sea-surface stochastic fluctuation, imaging noise, and weak reflectivity contrast, resulting in weak wake image signals. In order to better obtain wake optical remote sensing images, this article proposes a multi-objective parameter stochastic optimization method for a time-delayed integration optical remote sensing imaging system. By constructing the wake imaging mechanism framework integrating a hydrodynamic model, rough sea surface probability and statistics model, and Time-Delay Integration Charge-Coupled Device (TDI-CCD) imaging link model, a stochastic multi-objective optimization model with constraints is established. The multi-objective function of this model is specifically defined as follows: maximizing the digital number difference between the crest and trough of Kelvin wakes in imaging results, maximizing the F number, minimizing the integration stages, and minimizing the quantization bits. Meanwhile, a two-stage solution method based on sample average approximation (SAA), branch and bound method (B&B), and the complex method is designed. The model can be used to obtain optimized design results for remote sensing imaging parameters, providing theoretical and methodological support for the design of remote sensing imaging systems. Numerical simulation results show that the optimized parameter combination can achieve clear imaging of the Kelvin wake, and the core indicators meet the design requirements.
1. Introduction
When a ship navigates in the sea, the interaction between the hull and the seawater will form a wake behind it. According to the formation mechanism of wakes, the common wake can be divided into three categories, namely, surface wave wake, turbulent wake, and internal wave wake. Among them, the Kelvin wake has become the focus of remote sensing research due to its high detectability in visible spectrum remote sensing. The spatial shape and radiation characteristics of Kelvin wake are influenced by many factors, including sea surface wind speed, ship geometric parameters (such as captain and draft) and ship motion parameters (such as speed and course). The detection of the Kelvin wake can enable wide area ship target detection and ship motion state inversion, and provide key information for marine monitoring, traffic supervision, and other applications [1,2]. Therefore, it is of great research value to carry out the remote sensing detection of the Kelvin wake.
The detection of a sea wake based on optical remote sensing mainly depends on the different characteristics of sea surface reflectance. However, the characteristics of wakes are usually weak due to the influence of sea surface background wave, low reflectivity of sea surface, and other factors. In addition, under the action of dynamic sea conditions such as wind waves and gravity waves, the sea surface reflectance shows the characteristics of stochastic fluctuations, which further weaken the characteristics of the wake [3]. At the same time, imaging system noise and other interference factors cause the detection ability of the wake target imaging system to decline. Based on the above background, how to obtain imaging results with clear Kelvin wake characteristics under the influence of complex noise, that is, the clear imaging of Kelvin wake, is an urgent problem to be solved.
Currently, the wake target clearness processing methods in the field of remote sensing can be divided into image-processing-based methods and imaging-based methods [4]. The wake target clearness processing methods based on image processing can be further divided into traditional algorithms and methods based on deep learning [5]. The traditional algorithm mainly relies on Radon transform, Hough transform and other transform methods to enhance the linear features in the image, and then uses constant false alarm rate (CFAR) and other threshold technology to process the transformed image to enhance the wake characteristics [5,6,7,8,9]. The method based on deep learning is widely used in wake enhancement tasks under complex environmental conditions [10,11,12,13]. However, it should be pointed out that if the wake signal obtained by the detector is too weak, the imaging system cannot detect the wake signal, resulting in the captured image not displaying the wake information, and the subsequent image processing will also fail.
The wake target clearness processing methods based on imaging can be divided into two types: the imaging mode optimization method and the imaging mechanism modeling method. The former mainly enhances the wake characteristics by optimizing the observation angle and imaging mode of the remote sensing imaging system (such as polarization imaging, spectral imaging, etc.) [14,15,16,17]. The latter focuses on building a complete physical model from the target radiation characteristics to the system imaging output, systematically analyzing the quantitative relationship between imaging parameters and imaging quality, and using parameter optimization to improve the imaging performance of the remote sensing system for wake targets, so as to achieve clear imaging of wake characteristics [4,18,19,20,21].
The current imaging-based wake clarification methods generally fail to fully consider the stochastic characteristics of wake targets, which will significantly constrain the detection capability of wake imaging systems. In the design process of remote sensing imaging systems, in addition to meeting the basic performance requirements for clear imaging, it is also necessary to consider diverse user needs. Therefore, it is urgent to conduct a systematic analysis of the characteristics of wake targets and imaging links under the influence of sea-surface stochastic fluctuation and establish a stochastic multi-objective parameter optimization design method based on this to achieve the best tradeoff design.
In order to address the above issues and meet the demand for clearness and high-quality imaging of Kelvin wake using optical remote sensing systems, this article systematically carries out the research on the optimization method of optical remote sensing system parameters for wake imaging coupling the effects of sea-surface stochastic fluctuation and imaging noise. Specifically, this article first constructs a wake imaging mechanism framework including a hydrodynamic model, a probabilistic statistical model of the rough sea surface, and a Time-Delay Integration Charge-Coupled Device (TDI-CCD) imaging link model. Then, aiming at the multiple random factors in the imaging process, a stochastic multi-objective parameter optimization model with constraints is established. The key issues and contributions discussed in this article can be summarized as follows:
- (1)
- Construction of mathematical optimization model. Firstly, the Kelvin wake full-link imaging model of the TDI-CCD optical remote sensing imaging system under the condition of sea-surface stochastic fluctuation is established. Then, based on the stochastic characteristics of the wake target and the noise characteristics of the imaging system, the system parameter optimization problem is modeled as a multi-objective mathematical optimization problem. This model takes the user’s requirements for system parameters and imaging output as the optimization goal, and the performance requirements of the imaging system as the constraint condition. Specifically, the user’s requirements for system parameters include maximizing the F number, minimizing the integration stages, and minimizing the quantization bits, while the requirement for imaging output refers to the digital number difference between the crests and troughs of Kelvin wakes.
- (2)
- Proposal of the solution method. For this multi-objective integer stochastic optimization problem, a two-stage solution method is designed. This method combines sample average approximation (SAA), branch and bound (B&B), and the complex method. Firstly, the stochastic optimization problem is transformed into a deterministic optimization problem by the sample average approximation, and then it is divided into two sub-problems by the problem decomposition strategy. Finally, the branch and bound and the complex method are used to solve the problem, so as to obtain the best tradeoff solution. This method effectively solves the dual challenges of meeting the performance index and user requirements in the design of an imaging system.
- (3)
- Numerical simulation verification. The effectiveness of the proposed parameter optimization scheme is verified by numerical simulation experiments. The simulation results show that the optimized system parameter combination not only realizes the clear imaging of the wake target but also shows better performance in the key parameters of the optical remote sensing imaging system, ensuring that the imaging performance of the system meets the requirements of clear imaging.
The rest of this article is organized as follows: Section 2 details the parameter optimization model for the optical remote sensing system used for Kelvin wake imaging. Section 3 presents the solution method for the optimization model. Section 4 conducts model simulation, analysis, and discussion. Finally, Section 5 concludes this article.
2. Problem Description
This section systematically describes the parameter optimization of the optical remote sensing system used for Kelvin wake imaging based on a hydrodynamic model, a probabilistic statistical model of rough sea surface, and a TDI-CCD imaging link model, and then proposes a stochastic multi-objective optimization model under opportunity constraints.
2.1. Imaging Mechanism Modeling
2.1.1. Kelvin Wake Modeling
Firstly, based on the theory of potential flow, the ship is simplified as a slender ellipsoid moving in a uniform straight line in an incompressible flow field at infinite depth [22]. Then, by deploying different point sources/sinks, combined with appropriate boundary conditions, the free surface velocity potential and its corresponding elevation distribution solution are derived [23]. The elevation distribution solutions calculated are also different due to the different deployment modes of point source/sink. In this article, the ship wake is modeled as the wake generated by the joint action of the point source at the bow and the point sink at the stern. Assuming that the ship is sailing at a constant speed in the negative direction of the X axis, the velocity potential of the Kelvin wake of the ship can be expressed as the following expression [14]:
where is the half-length of the ship, is the half-breadth of the ship, is the speed of the ship, and is the Green’s function.
After obtaining the velocity potential of the wake, the free surface velocity field and elevation distribution solution can be derived as [14,22]
where is the free surface velocity field, and is the elevation distribution solution.
2.1.2. Reflection Model
According to the Cox–Munk model [24], the sea surface is a collection of a large number of randomly inclined small facets influenced by wind, and the sea surface presents a dynamic and changing state. The geometry of the facet is shown in Figure 1. In time , the radiance reflected from the surface element with a projected area of to the receiver is a random variable, and its expression is [3]
where represents the radiance reflected by the sea surface (the apostrophe represents a random variable), is the Fresnel reflectivity, is the irradiance of the light source on the plane, is the solid angle of the light source with reflection as the vertex, and is the pulse function describing whether the slope meets the specular reflection condition; when the slope meets the specular reflection condition at time , there is , otherwise .
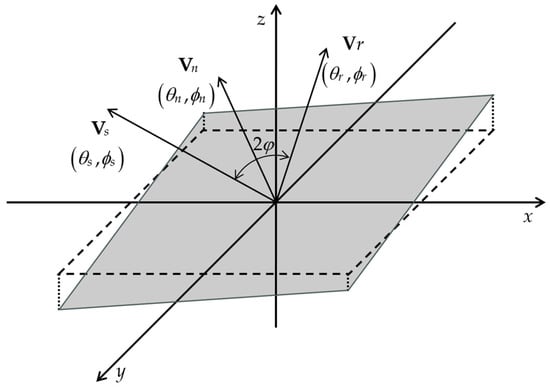
Figure 1.
The geometry of a sea surface facet.
The expectation and variance of the average radiance received by the imaging system are [3,24]
where is the time–space correlation scale of the flare, which is a function related to the wind wave spectrum and the wind speed on the sea surface. Under the condition of low wind speed, the approximate value of can be taken as . and are the slopes in the X and Y directions of the inclined plane, respectively; and represent the slopes that can produce a flare, respectively; and is the slope distribution function of the rough sea surface. Considering the modulation effect of Kelvin wake on sea surface roughness, the slope distribution function can be expressed as [14]
where is the standard deviation in the upwind direction, is the standard deviation in the crosswind direction, is the wind speed, and and represent the change value of roughness after being modulated by Kelvin wake.
2.1.3. Noise Model
Shot noise, dark current noise, and readout noise play a major role in the imaging link.
- Shot Noise
The process of photogenerated electrons in the photosensitive region of the sensor can be regarded as an independent, uniform, and continuous random process. Under stable illumination, the number of photogenerated electrons fluctuates slightly near an average value per unit time, which forms shot noise, and the number of photoelectrons generated follows the Poisson distribution [25]:
where is the number of signal electrons.
- 2.
- Dark Current Noise
The dark current noise is generated by the sensor itself. The generation process of dark current noise is independent of the generation process of photogenerated electrons, and also follows the Poisson distribution. The equivalent number of electrons of dark current noise is [26]
where is the number of dark current electrons.
- 3.
- Readout Noise
Readout noise mainly includes amplifier noise and reset noise (KTC noise) [27]. Its equivalent electron number can be expressed as
where is the root mean square noise, and is the charge conversion scale factor.
2.1.4. Imaging Link Model
The imaging process of the TDI-CCD remote sensing imaging system for the wake is that the light source (sun) shines on the sea surface, then the light reflected from the sea surface propagates to the TDI-CCD of the imaging system, next the photosensitive unit of each detector of the TDI-CCD generates photo-generated electrons in turn, and outputs the digital signal value after multi-level integration. The digital signal value () output by TDI-CCD on the sea surface with radiance can be expressed as
where is the atmospheric transmittance, is the total transmittance of the optical system, is the F number of the optical system, is integration stages, is the average spectral responsivity of TDI-CCD, is the maximum integration stages, is the total charge transfer efficiency, is the charge conversion factor, is the quantization bits, is the full well capacity of the TDI-CCD.
According to Functions (4)~(13), the probability mass function (PMF) of the unquantized and sampled digital signal value of the imaging system when imaging the sea surface with radiance under the influence of the sea-surface stochastic fluctuation and the noise of the imaging link can be obtained as follows:
where is the unquantized and sampled digital signal value, is the probability density function (PDF) of a random variable , and is the parameter with .
The expectation and variance of are
Considering the readout noise, the PMF of the digital signal value finally output by the imaging system is
The expectation and variance of are
2.2. Formulation of the Optimization Problem
The goal of the optimization problem constructed in this article is to determine the appropriate remote sensing imaging system parameters to meet the performance requirements of clear imaging and diversified user needs. Based on the analysis of the imaging process, a multi-objective stochastic optimization model is proposed to solve the optimal tradeoff design of the wake imaging system under different conditions. In this optimization model, the objective function is defined based on user requirements, and the constraints are determined by the clear imaging requirements of the imaging system and the range of parameters.
2.2.1. Optimization Constraints
The clarity of remote sensing imaging results is closely related to the noise level and radiation resolution of the imaging system. Among them, the requirement for noise level is to ensure that the imaging system can detect clear wake signals. The requirement of radiation resolution is to ensure that the crest and trough of reflectivity can be effectively distinguished after the wake signal is detected. It should be noted that sea-surface stochastic fluctuation will directly affect the imaging results, which will lead to differences in the clarity of the imaging results under different sea conditions. This characteristic determines that when selecting the optimization index of an imaging system, the index that can cover random factors must be selected first. Specifically, the detective signal-to-noise ratio (DSNR) includes the difference between the target and the background and random noise, so it can be directly used as the index to evaluate whether the imaging system can detect clear wake signals. Although the traditional radiometric resolution index can measure the resolution of the system to different radiances, it cannot meet the evaluation requirements under different sea conditions due to the lack of consideration of stochastic fluctuations. Based on this, it is necessary to use the probabilistic radiation resolution (PRR) index, which can be used to evaluate whether the imaging system can stably distinguish the radiation difference between the wake reflectivity crest and trough.
Based on the above analysis, we use the detective signal-to-noise ratio and probabilistic radiation resolution as the evaluation index of the imaging system’s ability to image wake targets, and as the constraints of the optimization model. These two constraints are described below.
- Detective Signal-to-Noise Ratio
The mathematical expression of DSNR of imaging system can be defined as
where represents the number of signal electrons generated by the target, represents the number of signal electrons generated by the background, and represents the noise equivalent electrons.
For the wake imaging system, the wake crest is regarded as the target, and the wake trough is regarded as the background. DSNR can be expressed as
where is the crest of wake radiance, and is the trough of wake radiance.
In the optimization design of the wake imaging system, the conditions that the DSNR of the imaging system needs to meet can be expressed as
- 2.
- Probabilistic Radiometric Resolution
In the study of wake remote sensing imaging, the core observation object is the periodic radiance distribution of the wake. In order to achieve clear imaging of the Kelvin wake, the imaging system should be able to distinguish the radiance difference between the crest and trough. Therefore, the radiometric resolution of the imaging system should be less than the radiance difference between the crest and trough.
For the wake with crest radiance and trough radiance , the difference between the digital signal values of the crest and trough output by the imaging system can be expressed as
where is the digital signal value corresponding to the radiance crest, is the corresponding digital signal value at the radiance trough, and is the difference between the digital signal values at the crest and trough.
Since both and are random variables influenced by the stochastic fluctuations of wake targets and random noise in the imaging system, we introduce the probabilistic radiometric resolution (PRR) model. The probability that is greater than 1 is used to measure the discrimination ability of the imaging system to radiation differences. PRR can be expressed as
From Functions (14)~(20), it can be seen that PRR can only be calculated by multiple integration. Therefore, in the actual numerical calculation, the value of PRR can be calculated by the Monte Carlo method.
In the optimization design of the wake imaging system, the conditions that the PRR of the imaging system needs to meet can be expressed as
2.2.2. Optimization Model
In this article, an optimization model based on user requirements, performance indicators, and imaging parameters is proposed to achieve the optimal tradeoff design of optical remote sensing systems for wake imaging. In the process of parameter optimization of the wake imaging system, the primary consideration is to ensure that the system can effectively detect clear wake signals, which requires that the design of the imaging system must meet DSNR and PRR indicators. In addition, the system design also needs to take into account the user’s requirements for system parameters, including the requirements of a larger F number, smaller integration stages, and smaller quantization bits, and at the same time, it needs to maximize the difference between the digital signal values at the crest and trough in the imaging results. Among them, DSNR and PRR are all functions related to F numbers , integration stages , quantization bits , crest radiance , trough radiance , and random noise. and are also influenced by the sea-surface stochastic fluctuation. Based on the above analysis, the parameter optimization problem of the wake imaging system is modeled as a multi-objective discrete optimization problem with chance constraints, and its mathematical model is described as follows:
where are decision variables, and are the value ranges of decision variables.
This optimization problem has four optimization objectives: maximize and while minimizing and under the constraints. The optimization problem has two optimization constraints: a deterministic constraint on the DSNR and a chance constraint on the PRR, which ensure the imaging system’s ability to clearly image wake targets.
The key input parameters of the optimization model are shown in Table 1.

Table 1.
Key input parameters.
The decision variables of the optimization model are shown in Table 2.

Table 2.
Decision variables.
3. Problem Solution
For the constrained multi-objective integer stochastic optimization problem described in Function (26), the SAA method is used to transform the original stochastic optimization model to obtain its corresponding deterministic optimization model. Then, a two-stage solution method is used to solve the transformed deterministic optimization model.
3.1. Deterministic Approximation of Stochastic Optimization Models
The SAA method is used to transform the stochastic optimization model into the deterministic optimization model. Specifically, based on the Kelvin wake model and reflection model, a large-scale random scene sample set is generated by the Monte Carlo method. Then, the imaging results of each scene sample are calculated based on the imaging link model. Finally, by replacing the random variables and chance constraints in the original model with the sample average, the transformation from a stochastic optimization model to a deterministic model is completed.
For random variable , the following approximate calculation equation can be used:
where is the sample observation value of the random variable , and is the sample size.
For the chance constraint (25), the following approximate calculation equation can be used:
where is the indicator function when , ; otherwise, .
The approximate deterministic optimization model can be expressed as
3.2. Two-Stage Solution Methodology
Function (29) is a multi-objective integer optimization problem, including four optimization objectives and three optimization variables. In this optimization model, , , and are both optimization variables and objectives. In addition, , PRR, and DSNR are functions of , , and . Therefore, for the multivariable optimization problem, the four optimization objectives are prioritized. Since the system parameters , , and directly affect the system performance and imaging quality, the requirements for system parameters will be the first priority. , which is influenced by system parameters, is the second priority.
Based on the priority of optimization variables, a two-stage solution method is designed. In the first stage, optimize the optimization objectives of the first priority. In the second stage, the optimization objectives of the second priority are optimized, and the optimization results of the first stage are taken as the constraints of the second stage. The specific solution stages are as follows:
Stage (1): The multi-objective optimization problem considering only the first priority can be expressed as
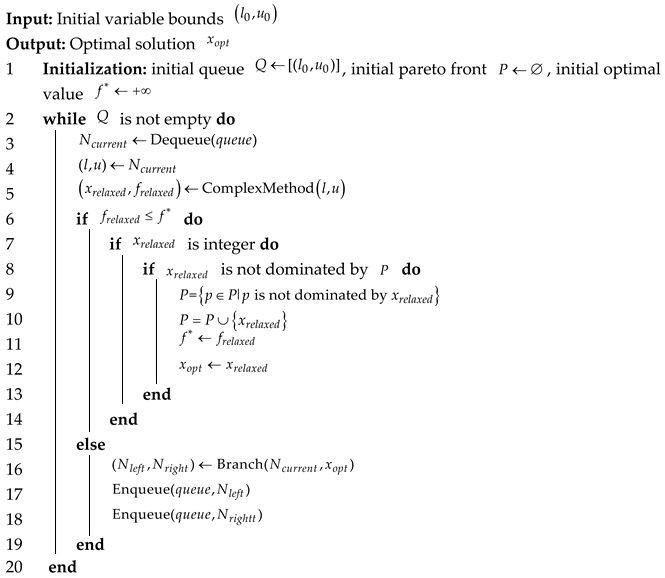
In the optimization problem described by Function (30), the three optimization objectives have the same priority, and the goal at this stage is to obtain the Pareto frontier of the problem. In this article, we use B&B to solve the Pareto frontier optimization problem of Function (30). The specific steps are as follows:
- Node initialization: First, define the definition domain of the optimization variable, and set its value range constraint and performance constraint. Then, set the upper and lower bounds of the root node of the branch and bound tree, and initialize the Pareto frontier set (initially empty).
- Linear relaxation Transformation: For the current node, relax the integer decision variables into continuous variables, and then transform the integer programming problem into a continuous programming problem.
- Embedding solution of complex method: Generate the initial complex vertices that meet the constraints in the relaxed continuous space, reduce the complex through iterative operations such as reflection, expansion, and contraction, and output the relaxation solution of the current node when the diameter of the complex is less than the threshold.
- Checking and processing of solutions: When the relaxation solution is a feasible integer solution, judge the dominant relationship between the feasible solution and the existing solution in the current Pareto frontier set. If the current feasible solution is dominated by at least one non-dominated solution in the Pareto frontier set, maintain the composition of the current Pareto frontier. If there is no dominating relationship between the current feasible solution and all non-dominating solutions in the Pareto frontier set, add the current feasible solution to the Pareto frontier set. If the current feasible solution can dominate part of the non-dominated solutions in the Pareto frontier set, delete all the solutions dominated by the feasible solution in the set, and add the current feasible solution to the Pareto frontier set to ensure the non-domination of the solutions in the set.
- Branching and pruning decision: If the relaxed solution is dominated by the non-dominated solution in the current Pareto front set, or the linear relaxation subproblem has no feasible solution, prune the node. Otherwise, select variables that do not meet the integer constraint to branch, generate child nodes, and update the upper and lower bounds.
- Algorithm termination: When all nodes are processed, the iteration is terminated and the optimal integer solution is output.
In the relaxation model in each node, the objective approximation method is used to solve the Pareto front of the optimization problem. The optimization objective can be expressed as
The optimization constraint conditions can be expressed as
where is the vector composed of three optimization variables, and is the target point, corresponding to the maximum number of F number, the minimum number of integration stages, and quantization bits that can be obtained.
Stage (2): The Pareto frontier obtained in the first stage is taken as the constraint condition of the optimization problem, and the optimization target of the second priority is taken as the only optimization target. The optimization problem model can be expressed as
where is the Pareto front, obtained in the first stage.
Since all the non-dominated solutions contained in the Pareto frontier have been traversed when solving the Pareto frontier in the first stage, there is no need to recalculate the Pareto frontier in this stage, and only the obtained non-dominated solution set needs to be filtered to obtain the solution that meets the requirements of this stage.
For the specific implementation process of the above two-stage solution algorithm, see the pseudo code shown in Algorithms 1 and 2.
| Algorithm 1: Branch and Bound Method |
 |
| Algorithm 2: Complex Method |
 |
3.3. Algorithm Complexity Analysis
The two-stage algorithm proposed in this article consists of two parts: the B&B, which is the main body of the algorithm, and the complex method, which is used to deal with the sub-optimization problems in the nodes of the B&B.
The total time complexity of the B&B is determined by the total number of search tree nodes and the processing complexity of a single node. The total number of search tree nodes is affected by the size of solution space and pruning efficiency, which can be expressed as
where is the solution space scale of variable ; is the solution space scale of variable ; is the scale of solution space of variable ; and is the pruning rate.
In a single node, the subproblem is solved by the complex method, and its complexity is related to the number of complex vertices , the cost of evaluating the objective function of a single vertex, and the number of iterations of the algorithm . The evaluation cost of the objective function for a single vertex is the sample size corresponding to the sample average approximation. The time complexity of the complex method can be expressed as
The overall time complexity of the algorithm is
4. Numerical Simulation
In this section, an example of a hypothetical ship and imaging conditions is used to simulate and analyze the Kelvin wake remote sensing imaging model and the optimization method.
4.1. Simulation Setup
We assume a scenario in which the half length and half width of the ship are 15 m and 3 m, respectively, the draft is 2 m, and the sailing speed is 6 m/s. The wind speed on the sea surface is 7 m/s, and the environmental illumination is 10 W/s2. When observed by the imaging system, the zenith angle of the source is 30°, the azimuth angle of the source is 182°, the zenith angle of the receiver is 3°, and the azimuth angle of the receiver is 132°. The size of the observation area is 800 m × 800 m. The settings of imaging simulation parameters in the TDI-CCD remote sensing imaging system are shown in Table 3.

Table 3.
Fixed simulation parameters.
4.2. Kelvin Wake Imaging Model
In this section, we use the imaging scene, ship parameters, and imaging parameters shown in the previous section to simulate and analyze the imaging model of Kelvin wake on the rough sea surface.
4.2.1. Reflectance Model of Kelvin Wake
Based on the Kelvin wake model and the sea surface reflection statistical model, the Kelvin wake field is simulated. In the simulation process, the elevation distribution of Kelvin wake is calculated by Functions (1)~(3), and the expectation and variance of the radiation of the wake are calculated by Functions (6) and (7). The numerical simulation results are shown in Figure 2, which shows the elevation distribution and radiation characteristics of the Kelvin wake.
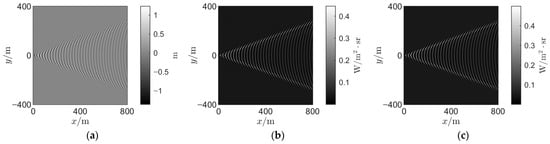
Figure 2.
Simulation results of Kelvin wake: (a) Elevation simulation of Kelvin wake; (b) Radiance expectation of Kelvin wake; (c) Radiance variance of Kelvin wake.
According to Figure 2, it can be concluded that the elevation distribution, radiance expectation and variance of the Kelvin wake show significant periodic characteristics. The Kelvin wake arm region shows the most significant periodicity, while the region farthest from the ship in the X axis direction shows the weakest periodicity.
Therefore, in the subsequent parameter optimization method, we selected the range of 700~800 m in the X axis and −50~50 m in the Y axis as the main observation area. The selection basis of this region is that it represents the weakest part of the whole wake field. If the imaging system can still clearly show the periodic characteristics of the region, it indicates that the system has the ability to clearly depict the wake target.
4.2.2. Imaging Link Model Analysis
In order to evaluate the clarity of wake imaging, we use as a quantitative index. The larger the , the stronger the imaging ability of the imaging system to the wake target, and the clearer the wake characteristics in the imaging results. The key parameters of the imaging system include F number, integration stages, and quantization bits. Six F numbers (5, 6, 7, 8, 9, and 10), twelve integration stages (8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, and 96) and four quantization bits (8, 10, 12, and 14) were selected for numerical simulation. Under the above imaging targets and imaging conditions, combined with the Kelvin wake reflection model, the digital signal value output by the imaging system is calculated according to the imaging link model (Functions (10)~(20)), and the simulation results are shown in Figure 3.
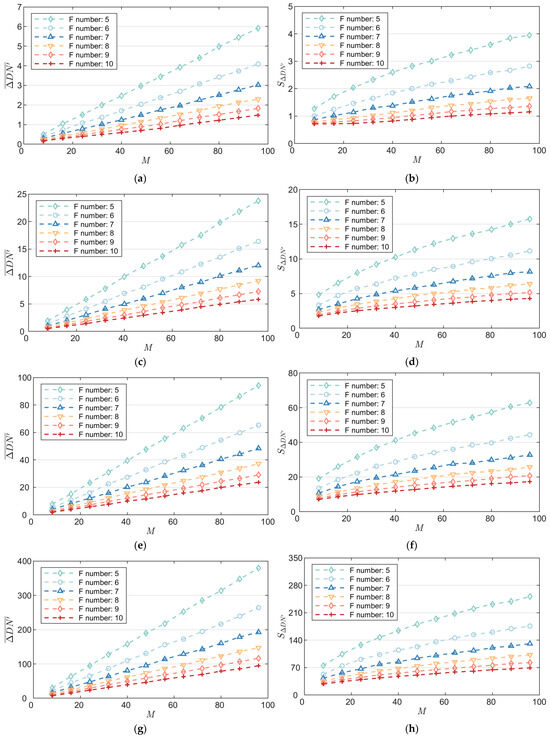
Figure 3.
Of different imaging system parameters: (a) vs. TDI stages under different F numbers (8-bit); (b) vs. TDI stages under different F numbers (8-bit); (c) vs. TDI stages under different F numbers (10-bit); (d) vs. TDI stages under different F numbers (10-bit); (e) vs. TDI stages under different F numbers (12-bit); (f) vs. TDI stages under different F numbers (12-bit); (g) vs. TDI stages under different F numbers (14-bit); (h) vs. TDI stages under different F numbers (14-bit).
Figure 3 shows the variation in the mean and standard deviation of with integration stages at different F numbers under different quantization bits. The experimental results show that the quantization bits have a significant effect on the mean and standard deviation of under the condition of any F numbers and integration stages. When the quantization bits are increased from 8 bits to 14 bits, the mean of () increases from a range of 0.17–5.92 to 7.45–379.27, and the standard deviation of () increases from a range of 0.72–3.95 to 27.99–251.15, showing the advantage of the dynamic range of a high-quantization-bits system. In addition, with the increase in integration stages, the mean and standard deviation of shows an upward trend, indicating that integration stages plays a key role in regulating signal strength and noise level.
Under different F numbers, the curve distribution in each sub-figure shows obvious differences: the smaller the F number, the greater the increase in the mean and standard deviation of with the increase in integration stages. And this difference is more significant with the increase in quantization bits, indicating that the F number has a certain impact on the signal strength and noise level of the imaging system. The synergy of quantization bits, integration stages, and F number provides theoretical guidance and experimental support for the optimization of imaging parameters.
4.3. Optimization Method
In this section, for the simulation scene, based on the imaging link model of the TDI-CCD remote sensing imaging system, the parameter optimization method proposed in this article is used to optimize the wake imaging system.
4.3.1. Optimization Constraints Analysis
In the optimization model, the constraint conditions are designed to ensure the imaging performance of the system to ensure that the output results clearly show wake characteristics. To achieve this goal, we first analyze the relationship between the DSNR values, the PRR values, and the system parameters. Then, the influence of parameters and on the optimization model is analyzed, and the parameter selection scheme is given.
- Detective Signal-to-Noise Ratio
Based on the Function (21), the DSNR values under different system parameter configurations are calculated. The numerical simulation results are shown in Figure 4.
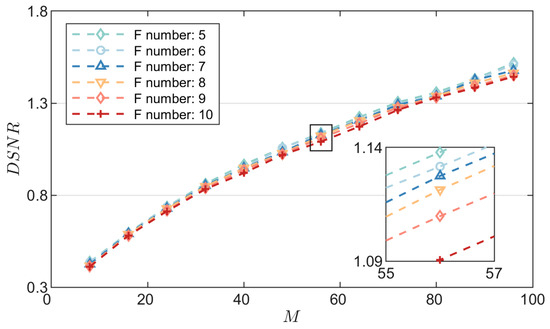
Figure 4.
DSNR values of different imaging system parameters.
Figure 4 shows the variation in DSNR values with integration stages under different F numbers. Figure 4 shows the variation in DSNR with integration stages under different F numbers. When integration stages increase from 8 to 96, DSNR shows an overall upward trend. For example, at an F number of 5, the DSNR increases from 0.43 to 1.52, which shows that under the selected parameters and scene conditions in this article, increasing the integration stages can effectively enhance the detection ability of the imaging system for wake signals. The partial enlarged image in Figure 4 shows that there are some differences in DSNR curves corresponding to different F numbers. With the decrease in the F number, DSNR values show a slight increasing trend. When the integration stages are 32, the F number decreases from 10 to 5, and the increase in DSNR value is less than 0.05. The results show that under the selected parameters and scene conditions in this article, the influence of the F number on the DSNR value is weaker than that of the integration stages within this parameter range. The above results show that under the selected parameters and scene conditions in this article, for the wake imaging system, integration stages are the dominant factor affecting the DSNR value, while the influence of the F number on the DSNR value is relatively weak.
To determine the value of parameter , the imaging results of the imaging system for wake targets at different DSNR values are calculated according to the Kelvin wake imaging mechanism model and Function (21). The simulation results are shown in Figure 5. Figure 5a,c,e show the digital signal values without final quantization and sampling under several typical DSNR values. Figure 5b,d,f show the frequency histogram of digital signal values without final quantization and sampling at the wake radiance crest and trough. Table 4 shows the relevant indicators of the simulation results under different DSNR values, including the mean () and standard deviation () of the digital signal values without final quantization and sampling, the min–max normalized contrast () between the crest and trough in the imaging results, and the overlap area () of the frequency histogram of the digital signal values at the crest and trough.
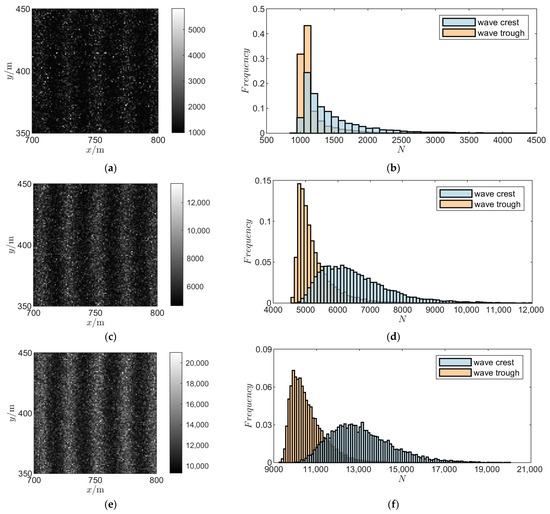
Figure 5.
Simulation results of wake imaging at different DSNR values: (a) , imaging results; (b) , frequency histogram of imaging results; (c) , imaging results; (d) , frequency histogram of imaging results; (e) , imaging results; (f) , frequency histogram of imaging results.

Table 4.
Relevant evaluation indicators of simulation results under different DSNR.
When , the imaging results in Figure 5a show that the of the image is 0.34, and the identifiability of periodic wake characteristics is very low. The frequency histogram (Figure 5b) shows that the of the probability distribution of the digital signal value at the crest and trough is 0.62, and the probability distribution of the two is almost completely coincident, indicating that the signal strength of the target in the imaging result is weak, resulting in low imaging quality.
When , the of the imaging results in Figure 5c is 0.43, and obvious wake characteristics can be observed. The frequency histogram (Figure 5d) shows that, compared with , the of the probability distribution of the digital signal value at the crest and trough is reduced to 0.41, and the peaks are completely separated, indicating that the intensity of the wake signal in the imaging results is strong, and clear wake characteristics can be observed.
When , the wake characteristics in the imaging results of Figure 5e are clearer, and the in the image is 0.50. The frequency histogram (Figure 5f) shows that the of the probability distribution of the digital signal value at the crest and trough is further reduced to 0.26, and the peak spacing is increased, indicating that the signal strength of the target in the imaging results is stronger, and the recognition degree of the wake feature is further enhanced.
Based on the above analysis, in the subsequent optimization design of this article, we set the value of as 1 and use as the constraint condition of the optimization model.
- 2.
- Probabilistic Radiometric Resolution
According to the calculation Function (25), the PRR values of different system parameters under the above imaging targets and imaging conditions are calculated. The numerical simulation results are shown in Figure 6.
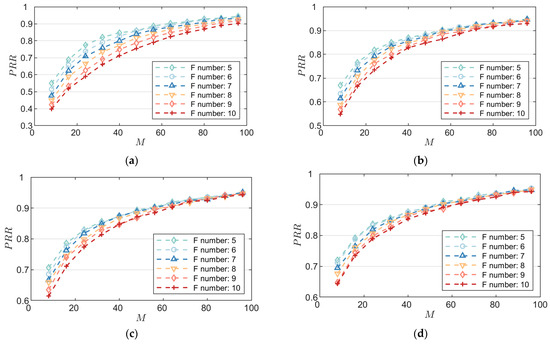
Figure 6.
PRR of different imaging system parameters: (a) ; (b) ; (c) ; (d) .
Figure 6 shows the variation in PRR values with integration stages at different F numbers under the conditions of different quantization bits of the system. The results show that under the selected parameters and scene conditions in this article, PRR values are positively correlated with integration stages and quantization bits, and negatively correlated with F numbers. In addition, comparing the simulation results of different parameter combinations, it can be seen that with the decrease in F number, the increase in integration stages, and the increase in quantization bits, the influence of integration stages, F number, and quantization bits on PRR values shows a weakening trend.
The above results show that under the selected parameters and scene conditions in this article, for the wake imaging system, PRR values are influenced by integration stages, F number, and quantization bits. This rule provides a reference for the optimization of imaging system parameters. In the process of system design, it is necessary to comprehensively consider the values of the three and their mutual influence.
To determine the value of parameter a, the imaging results of the wake target when the imaging system is at different PRR values are calculated according to the Kelvin wake imaging mechanism model and Function (25). The simulation results are shown in Figure 7. Figure 7a,c,e show the digital signal values under several typical PRR values. Figure 7b,d,f show the frequency histogram of digital signal values at the wake radiance crest and trough. Table 5 shows the relevant indicators of the simulation results under different PRR values.
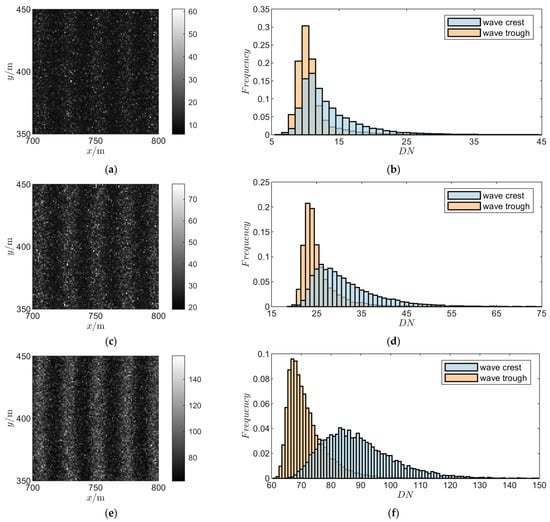
Figure 7.
Simulation results of wake imaging at different PRR values: (a) , imaging results; (b) , frequency histogram of imaging results; (c) , imaging results; (d) , frequency histogram of imaging results; (e) , imaging results; (f) , frequency histogram of imaging results.

Table 5.
Relevant evaluation indicators of simulation results under different PRR.
When , the of the imaging results in Figure 7a is 0.24, and the identifiability of periodic wake characteristics in the image is low. The frequency histogram (Figure 7b) shows that the of the probability distribution of the digital signal value at the crest and trough is 0.64, and the probability distribution of the two is almost completely overlapped, indicating that it is difficult to effectively distinguish the two through the digital signal value, resulting in low imaging quality.
When , the of the imaging results in Figure 7c is 0.31, and obvious wake characteristics can be observed from the image. The frequency histogram (Figure 7d) shows that compared with , the of the probability distribution of digital signal value at the crest and trough is reduced to 0.51, and the peak is completely separated, indicating that the two can be distinguished by digital signal value.
When , the of the imaging results in Figure 7e is 0.46, and a clearer periodic wake structure can be observed from the image. The frequency histogram (Figure 7f) shows that the of the probability distribution of the digital signal value at the crest and trough is reduced to 0.33, and the distance between the peaks increases, indicating that the digital signal values of the two are more distinguishable.
Based on the above analysis, in the subsequent optimization design of this article, we set the value of as 0.8 and use as the constraint condition of the optimization model.
4.3.2. Optimization Problem Solving
Based on engineering experience, six F numbers (5, 6, 7, 8, 9, 10), six integration stages (8, 16, 32, 48, 64, 96), and three quantization bits (8, 10, 12) were selected as the value range of optimization variables for numerical simulation. Based on the optimization model and algorithm proposed in this article, the optimization results of the optimization problem are shown in Table 6. Table 6 lists the values of the optimization parameters, objectives, and constraints of the optimization results in the first stage, where bold indicates the optimization results in the second stage.

Table 6.
Results of the two-stage optimization algorithm.
The optimization results of the first stage represent the parameter boundary that can clearly image the wake target under the current imaging conditions. The optimization results of the second stage represent the parameter combination with the largest in the optimization results of the first stage.
In order to verify the effectiveness of the parameter optimization scheme, the imaging performance of the optimal parameter combination and the non-optimized parameter combination was compared. The simulation results are shown in Figure 8 and Figure 9. The relevant indicators of simulation results are shown in Table 7.
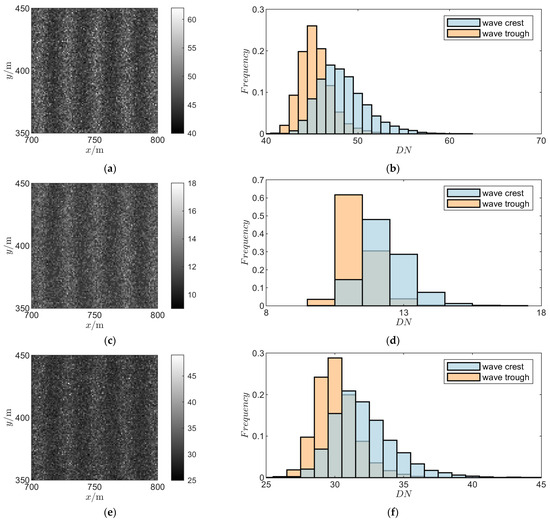
Figure 8.
Simulation results of wake imaging at different imaging system parameters: (a) , imaging results; (b) , frequency histogram of imaging results; (c) , imaging results; (d) , frequency histogram of imaging results; (e) , imaging results; (f) , frequency histogram of imaging results.
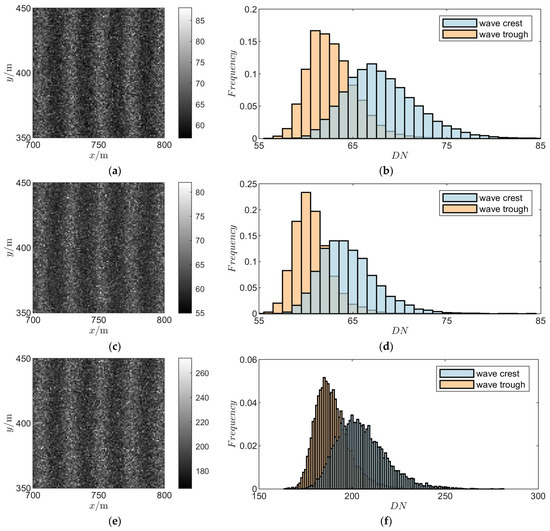
Figure 9.
Simulation results of wake imaging at different imaging system parameters: (a) , imaging results; (b) , frequency histogram of imaging results; (c) , imaging results; (d) , frequency histogram of imaging results; (e) , imaging results; (f) , frequency histogram of imaging results.

Table 7.
Relevant indicators of simulation results.
It can be seen from Table 7 that the optimal solution is better than all other non-optimized parameter combinations that meet the constraints. The of the imaging results of Figure 8a is 0.29, and obvious wake characteristics can be observed. The of the probability histogram in Figure 8b is 0.45, and the peak value of the digital signal at the crest and trough is completely separated.
In Table 7, there are two sets of parameter combinations (; ) whose performance is inferior to the optimal solution, and they fail to meet the constraints. In the imaging results in Figure 8c,e, the is lower than 0.29, and only relatively vague wake characteristics can be observed. The of the probability distribution in Figure 8d,f is greater than 0.45, and the peak value of the digital signal at the crest and trough is not completely separated.
In Table 7, there are three parameter combinations (; ; and ) with better performance than the optimal solution. In the imaging results in Figure 9a,c,e, the is greater than 0.29, and a clearer wake signal can be observed. In Figure 9b,d,f, the of probability distribution is less than 0.45, and the peak value of the digital signal at the crest and trough is completely separated. But in the first priority optimization objectives (maximize F, minimize M, and minimize n), they are still dominated by the optimal solution.
Based on the above analysis, under the selected parameters and scene conditions in this article, the optimal parameter combination can achieve clear imaging of wake targets. The combination of parameters with imaging performance lower than the optimal solution cannot obtain recognizable wake characteristics. The combination of parameters with imaging performance higher than the optimal solution can obtain identifiable wake characteristics. This conclusion verifies the effectiveness of the proposed optimization design method.
4.4. Wave Fluctuation Analysis
In order to study the influence of sea-surface stochastic fluctuation on the optimization method in this article, the corresponding comparative experiments are designed. In the numerical simulation stage, the influence of random fluctuations is ignored to complete the parameter optimization of the imaging system, and then the optimization results are compared with the optimization method in this article. The experimental results are shown in Figure 10. The relevant indicators of experimental results are shown in Table 8.
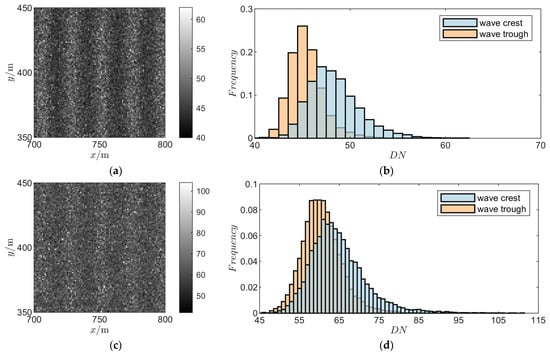
Figure 10.
Simulation results of wake imaging at different imaging system parameters: (a) , imaging results; (b) , frequency histogram of imaging results; (c) , imaging results; (d) , frequency histogram of imaging results.

Table 8.
Relevant indicators of experimental results.
Figure 10a,b shows the imaging results of the optimal solution when considering the sea-surface stochastic fluctuation. Figure 10c,d shows the imaging results of the optimal solution without considering the sea-surface stochastic fluctuation. The in the imaging results in Figure 10a is 0.29, and wake characteristics can be observed. The frequency histogram in Figure 10b shows that the of the probability distribution of the digital signal value at the crest and trough is 0.45. Figure 10c shows that without considering stochastic fluctuations, the of the wake image obtained based on the parameter optimization scheme is 0.12, and the recognizability of the periodic wake characteristics is low. Figure 10d shows that the of the probability distribution of the digital signal value at the crest and trough in the imaging results is 0.69, resulting in a significant reduction in the identifiability of the periodic wake characteristics. The experimental results verify that it is reasonable and necessary to introduce the sea-surface stochastic fluctuation factor into the parameter optimization of the wake imaging system under the selected parameters and scene conditions in this article. The effectiveness of the proposed method is also proved.
4.5. Algorithm Comparisons
To further verify the effectiveness of this algorithm (B&B-CM), we compare it with three well-known optimization algorithms, namely, multi-objective particle swarm optimization (MOPSO) [28], non-dominated sorting genetic algorithm II (NSGA-II) [29], and the -constraint method (-CM) [30]. In the optimization model in this article, the key is the accuracy and stability of the first-stage Pareto frontier solution. Therefore, we use inverse generation distance to measure the accuracy of each run result and use the Jaccard similarity coefficient to measure the similarity of each solution result to characterize the stability of the algorithm.
In the experiment, the imaging scene consistent with Section 4.3 is used to evaluate the performance of the algorithm under different lighting environments and sea conditions by adjusting the irradiance and wind speed of the sea surface. Table 9 summarizes the comparison results. The last three columns of data are as follows: the average inverse generation distance () of Pareto fronts across 10 runs for all algorithms, the average Jaccard similarity coefficient () of Pareto fronts across 10 runs, and the average time () consumption across 10 runs.

Table 9.
Algorithm comparison results.
In the scenario of , B&B-CM achieves optimal accuracy () and optimal stability (). The average calculation time () is higher than -CM (), but significantly lower than MOPSO () and NSGA-II (), reflecting a good balance between accuracy and efficiency.
In the scenarios of , B&B-CM still has the advantage in the accuracy () and stability (), and the calculation time () is significantly lower than that in the scenarios of , and the efficiency gap with -CM () is also significantly reduced.
In the scenario of , B&B-CM () is still better than MOPSO (), NSGA-II (), and -CM () in accuracy and stability. The calculation time () was significantly lower than that of MOPSO () and NSGA-II (). Although -CM maintains the shortest calculation time (), its accuracy and stability are still not as good as B&B-CM.
In summation, in all test scenarios, the Pareto front solution accuracy and solution stability of the B&B-CM algorithm are better than MOPSO, NSGA-II, and -CM. Although the calculation time is higher than -CM, it is far lower than MOPSO and NSGA-II. Especially in some scenarios, due to the pruning effect, the calculation efficiency can be greatly improved, which provides basic advantages for the parameter optimization of an actual TDI-CCD remote sensing system.
The optimization method described in this article is mainly used to guide and assist the parameter design of a remote sensing imaging system. In the imaging scenario set in this article, the average calculation time of B&B-CM is about 100 s, which can meet the requirements of the application scenario. In addition, based on the balance performance of the optimization method in solving accuracy, stability, and calculation time, its application scenario can also be extended to the integration with airborne platforms or satellite systems. On the one hand, this method can be embedded into the airborne platform or satellite system, and the adjustable parameters can be adjusted according to the current environmental parameters to meet the requirements of imaging performance. On the other hand, it can combine the collected image data to match the optimal imaging parameters for the scene on the fixed path.
5. Conclusions
This article proposes a multi-objective parameter stochastic optimization method for the time-delayed integration optical remote sensing system used for Kelvin wake imaging. By establishing a full-chain remote sensing imaging model of the Kelvin wake using TDI-CCD under sea surface wave conditions, a mathematical optimization framework based on stochastic programming is constructed to achieve the clear imaging of wake targets. For this stochastic integer nonlinear optimization problem, a two-stage solution algorithm, integrating SAA, B&B, and the complex method, is designed. Simulation experiments demonstrate that the system parameter combinations optimized by this method exhibit the appropriate F number, integration stages, and quantization bits. This study provides theoretical foundations and methodological support for parameter design and attitude control in remote sensing imaging systems.
Furthermore, the optimization model proposed in this article can be integrated with the satellite system to improve the environmental adaptability of the imaging system. On the one hand, the model can be embedded into the satellite system, collect the current environmental parameters, and dynamically adjust the adjustable parameters, so as to meet the imaging performance requirements in different environments. On the other hand, according to the historical image data collected by the satellite, the typical scenes on the orbit can be preset and the optimal imaging parameters of each scene can be calculated and matched through the model so as to preset the parameters for the subsequent orbit transit observation and ensure that the observation parameters are suitable for the scene.
However, it should be noted that the core of the optimization method provided in this article is the collaborative design of a general optimization framework and scene model input. The core optimization logic, such as multi-objective function construction, random constraint transformation, and two-stage solution method, is universal. In practical application, users do not need to redesign the framework but only need to adjust the model input parameters according to the specific detection scene. However, it should be noted that the specific parameter combination obtained by the method depends on the input parameters of the three core models, so there are some limitations, mainly reflected in the following:
- Kelvin wake model: This model adopts a simplified model based on potential flow theory (assuming that the ship is a slender ellipsoid, the seawater is incompressible, and the viscous force is ignored), which is only applicable to ships sailing at a constant speed in a straight line and infinite deep waters. The model needs to be replaced for non-slender ships, shallow water areas, or ship-maneuvering scenarios.
- Rough-sea-surface probability and statistics model: The model calculates the sea surface slope based on the Cox–Munk model, which is suitable for open sea areas with wind speeds of 3–14 m/s. Extreme wind speed ( or ), inshore breaking wave area, or uneven sea surface needs to introduce wave spectrum correction.
- TDI-CCD imaging link model: All imaging and environmental parameter settings in this model are assumed conditions, such as the total charge transfer efficiency and constant atmospheric transmittance. In practical applications, it is necessary to set parameters based on the selection of TDI-CCD and simulate atmospheric and lighting conditions using models such as MODTRAN. The higher the similarity between the set parameters and the real situation, the better the effectiveness of the results obtained.
Based on the above limitations analysis, in order to ensure the effectiveness of the method in different actual scenarios, this study further proposes the targeted adjustment steps of the model:
- Update input parameters: Select the appropriate Kelvin wake model, rough sea surface probability and statistics model, and TDI-CCD imaging link model according to the characteristics of the detection scene, and configure the input parameters in line with the actual scene.
- Adjust constraint parameter threshold: Set the constraint parameter threshold matching the current scene according to the model input parameters determined in step 1.
- Verification and iterative adjustment: Substitute the adjusted parameters and thresholds into the two-stage optimization algorithm to solve the candidate parameter combination and verify the evaluation indicators in several random scene samples. If the performance requirements are not met, return to the first step to readjust until the indicators meet the requirements.
In order to further verify and improve the optimization method, subsequent verification experiments could be carried out through water tank experiments and airborne experiments. Specifically, the water tank experiments would build an experimental platform, including a wave-making flume, a lighting system, a ship model and supporting towing system, and a TDI-CCD imaging system. Different sea conditions would be simulated by the wave-making flume, and different illuminance would be simulated by the lighting system. The imaging results of the wake target by the TDI-CCD camera under different parameter combinations would then be collected. By comparing the imaging results of the optimal parameter combination and the non-optimized parameter combination, the accuracy of the parameter optimization model in this article would be verified. The airborne experiment would be carried out using a TDI-CCD imaging system in conjunction with UAV, small aircraft, and other airborne remote sensing platforms. The wake target would be imaged in the environment of different sea conditions and different illuminances. By comparing the imaging results of the optimal parameter combination and the non-optimized parameter combination, the application effectiveness of the parameter optimization model in complex real scenes would then be verified.
Author Contributions
Conceptualization, M.S.; methodology, L.L. and M.S.; software, L.L.; validation, L.L. and M.S.; formal analysis, L.L. and M.S.; investigation, L.L., M.S. and X.Z.; resources, L.L. and M.S.; data curation, M.S. and L.L.; writing—original draft preparation, M.S., L.L., X.Z. and J.W.; writing—review and editing, M.S., L.L., X.Z. and J.W.; visualization, L.L.; supervision, J.W.; project administration, M.S.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (62205046) and the Dalian Youth Science and Technology Star Project Support Program (2023RQ021).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Guo, Y.; Li, Y.; Xue, A.; Tharmarasa, R.; Kirubarajan, T. Simultaneous Tracking of a Maneuvering Ship and Its Wake Using Gaussian Processes. Signal Process. 2020, 172, 107547. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, R. Ship Wakes in Optical Images. J. Atmos. Ocean. Technol. 2018, 35, 1633–1648. [Google Scholar] [CrossRef]
- Titov, V.I. On the accuracy of determining the distribution function of sea-surface slopes by sun glitters. Izv. Akad. Nauk SSSR Fiz. Atmos. Okeana. 1980, 16, 178–185. [Google Scholar]
- Ying, S.; Qu, H.; Tao, S.; Zheng, L.; Wu, X. Radiation Sensitivity Analysis of Ocean Wake Information Detection System Based on Visible Light Remote Sensing. Remote Sens. 2022, 14, 4054. [Google Scholar] [CrossRef]
- Mazzeo, A.; Renga, A.; Graziano, M.D. A Systematic Review of Ship Wake Detection Methods in Satellite Imagery. Remote Sens. 2024, 16, 3775. [Google Scholar] [CrossRef]
- Guan, Y.; Xu, H.; Li, W.; Li, C. Ship Wake Detection in a Single SAR Image via a Modified Low-Rank Constraint. Remote Sens. 2024, 16, 3487. [Google Scholar] [CrossRef]
- Ai, J.; Qi, X.; Yu, W.; Deng, Y.; Liu, F.; Shi, L.; Jia, Y. A Novel Ship Wake CFAR Detection Algorithm Based on SCR Enhancement and Normalized Hough Transform. IEEE Geosci. Remote Sens. Lett. 2011, 8, 681–685. [Google Scholar] [CrossRef]
- Srivastava, R.; Christmas, J. Analysis of Sea Waves and Ship Wake Detection. In Proceedings of the Oceans 2022, Chennai, India, 21–24 February 2022; IEEE: New York, NY, USA, 2022. [Google Scholar]
- Arivazhagan, S.; Sundari, M.S.; Selvi, M.R.T.; Anilkumar, K.; Vasanthanathan, A. Modeling and Theoretical Exploration of Free Surface Manifestation of Submarines in Presence and Absence of Ocean Waves. Ocean Eng. 2024, 301, 117552. [Google Scholar] [CrossRef]
- Xue, F.; Jin, W.; Qiu, S.; Yang, J. Rethinking Automatic Ship Wake Detection: State-of-the-Art CNN-Based Wake Detection via Optical Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5613622. [Google Scholar] [CrossRef]
- Xu, C.; Wang, Q.; Wang, X.; Chao, X.; Pan, B. Wake2Wake: Feature-Guided Self-Supervised Wave Suppression Method for SAR Ship Wake Detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5108114. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, H.; Wang, L.; Ohtsuki, T.; Adachi, F. SAR Image Wake Detection Based on Pseudo-Siamese Structure and Multidomain Feature Fusion. IEEE Geosci. Remote Sens. Lett. 2024, 21, 4015605. [Google Scholar] [CrossRef]
- Song, M.; Qu, H.; Zhang, G.; Tao, S.; Jin, G. A Variational Model for Sea Image Enhancement. Remote Sens. 2018, 10, 1313. [Google Scholar] [CrossRef]
- Xue, F.; Jin, W.; Qiu, S.; Yang, J. Airborne Optical Polarization Imaging for Observation of Submarine Kelvin Wakes on the Sea Surface: Imaging Chain and Simulation. ISPRS J. Photogramm. Remote Sens. 2021, 178, 136–154. [Google Scholar] [CrossRef]
- Jiang, Y.; Yang, Z.; Li, K.; Liu, T. Pre-Processing of Simulated Synthetic Aperture Radar Image Scenes Using Polarimetric Enhancement for Improved Ship Wake Detection. Remote Sens. 2024, 16, 658. [Google Scholar] [CrossRef]
- Li, D.; Jiang, Y.; Zhou, Z.; Deng, H.; Lin, M. Research on Ship Wake Measurement in Sea Based on Hyperspectral Imaging. In Proceedings of the 2024 4th International Conference on Industrial Automation, Robotics and Control Engineering (IARCE), Chengdu, China, 15–17 November 2024; IEEE Computer Soc: Los Alamitos, CA, USA, 2024; pp. 445–449. [Google Scholar]
- Sun, Y.-X.; Liu, P.; Jin, Y.-Q. Ship Wake Components: Isolation, Reconstruction, and Characteristics Analysis in Spectral, Spatial, and TerraSAR-X Image Domains. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4209–4224. [Google Scholar] [CrossRef]
- Song, M.; Wang, S.; Zhao, P.; Chen, Y.; Wang, J. Modeling Kelvin Wake Imaging Mechanism of Visible Spectral Remote Sensing. Appl. Ocean Res. 2021, 113, 102712. [Google Scholar] [CrossRef]
- Shi, Z.; Li, J. Detectability of the Infrared Surface Features of the Wake behind a Moving Underwater Body. In Proceedings of the AOPC 2015: Optical and Optoelectronic Sensing and Imaging Technology, Beijing, China, 5–7 May 2015; Gong, H., Wu, N., Ni, Y., Chen, W., Lu, J., Eds.; SPIE-Int Soc Optical Engineering: Bellingham, WA, USA, 2015; Volume 9674, p. 967436. [Google Scholar]
- Haghshenas, J. On-Board TDI Stage Estimation and Calibration Using SNR Analysis. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XXI; Neeck, S.P., Bezy, J.L., Kimura, T., Shimoda, H., Meynart, R., Eds.; SPIE-Int Soc Optical Engineering: Bellingham, WA, USA, 2017; Volume 10423, p. UNSP 104231U. [Google Scholar]
- Wei, Y.; Wu, Z.; Li, H.; Wu, J.; Qu, T. Application of Periodic Structure Scattering in Kelvin Ship Wakes Detection. Sustain. Cities Soc. 2019, 47, 101463. [Google Scholar] [CrossRef]
- Xue, F.; Jin, W.; Qiu, S.; Yang, J. Wake Features of Moving Submerged Bodies and Motion State Inversion of Submarines. IEEE Access 2020, 8, 12713–12724. [Google Scholar] [CrossRef]
- Sun, X.; Cai, M.; Wang, J.; Liu, C. Numerical Simulation of the Kelvin Wake Patterns. Appl. Sci. 2022, 12, 6265. [Google Scholar] [CrossRef]
- Cox, C.; Munk, W. Measurement of the Roughness of the Sea Surface from Photographs of the Sun’s Glitter. J. Opt. Soc. Am. 1954, 44, 838. [Google Scholar] [CrossRef]
- Wang, D.-J.; Zhang, T. Noise Analysis and Measurement of Time Delay and Integration Charge Coupled Device. Chin. Phys. B 2011, 20, 87202. [Google Scholar] [CrossRef]
- Li, Y.-F.; Li, M.-F.; Si, G.-L.; Guo, Y.-F. Noise analyzing and processing of TDI-CCD image sensor. Opt. Precis. Eng. 2007, 15, 1196–1202. [Google Scholar]
- Akiba, M. Theory and Measurement of Reset Noise Suppression in CTIA Readout Circuits. IEICE Trans. Electron. 2015, E98C, 899–902. [Google Scholar] [CrossRef]
- Coello Coello, C.A.; Lechuga, M.S. MOPSO: A Proposal for Multiple Objective Particle Swarm Optimization. In Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02 (cat. No.02th8600), Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1051–1056. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Mavrotas, G. Effective Implementation of the ε-Constraint Method in Multi-Objective Mathematical Programming Problems. Appl. Math. Comput. 2009, 213, 455–465. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).