A Comparative Analysis of Preprocessing Filters for Deep Learning-Based Equipment Power Efficiency Classification and Prediction Models
Abstract
1. Introduction
- Challenging Model-Centrism: Through extensive experiments on a real-world industrial power-efficiency dataset, the study empirically demonstrates that a data-centric preprocessing approach yields more significant and robust performance gains than relying on model complexity, validated across diverse architectures like the Transformer and R-Linear.
- The Surprising Effectiveness of Simplicity: Grounded in our empirical analysis, the study reveals the counter-intuitive result that the Simple Moving Average (SMA)—a traditional and efficient filter—consistently outperforms more complex filtering techniques on real-world industrial data.
- A Practical Framework for Preprocessing: Based on the comprehensive results of our scenario-based experiments, the study provides an empirically validated framework that offers actionable guidelines for practitioners to select optimal filtering strategies by analyzing the trade-offs between performance, stability, and window sizes.
2. Related Works
2.1. Data-Driven Approaches for Industrial Predictive Maintenance
2.2. Deep Learning Models for Industrial Time-Series Analysis
2.3. Filtering Methodologies for Time-Series Preprocessing
2.3.1. SMA
2.3.2. Median Filter
2.3.3. Hampel Filter
2.3.4. Kalman Filter
3. Experiments
3.1. Dataset
- Normal: This class represents states where the system is operating within optimal efficiency parameters, indicated by an average power factor of 80% or higher.
- Caution: This class indicates minor but significant deviations from optimal efficiency, suggesting that future maintenance may be required. This corresponds to an average power factor between 60% and 80%.
- Warning: This class signifies a state of severe inefficiency that requires immediate attention, defined by an average power factor below 60%.
3.2. Pre-Processing Pipeline and Model Architecture
3.3. Experimental Setup
3.4. Evaluation
- : Measures the overall proportion of correctly classified instances across all three classes, as defined in Equation (5),
- : A key metric for imbalanced datasets, the is the harmonic mean of and . measures the proportion of positive identifications that were actually correct, while measures the proportion of actual positives that were correctly identified. The is then calculated with Equation (6). For this multi-class problem, the macro-averaged is used.where , , and represent True Positives, False Positives, and False Negatives, respectively.
- Training Time: Measures the average training time for each iteration of the experiment.
4. Results
4.1. Experimental Results by Window Size
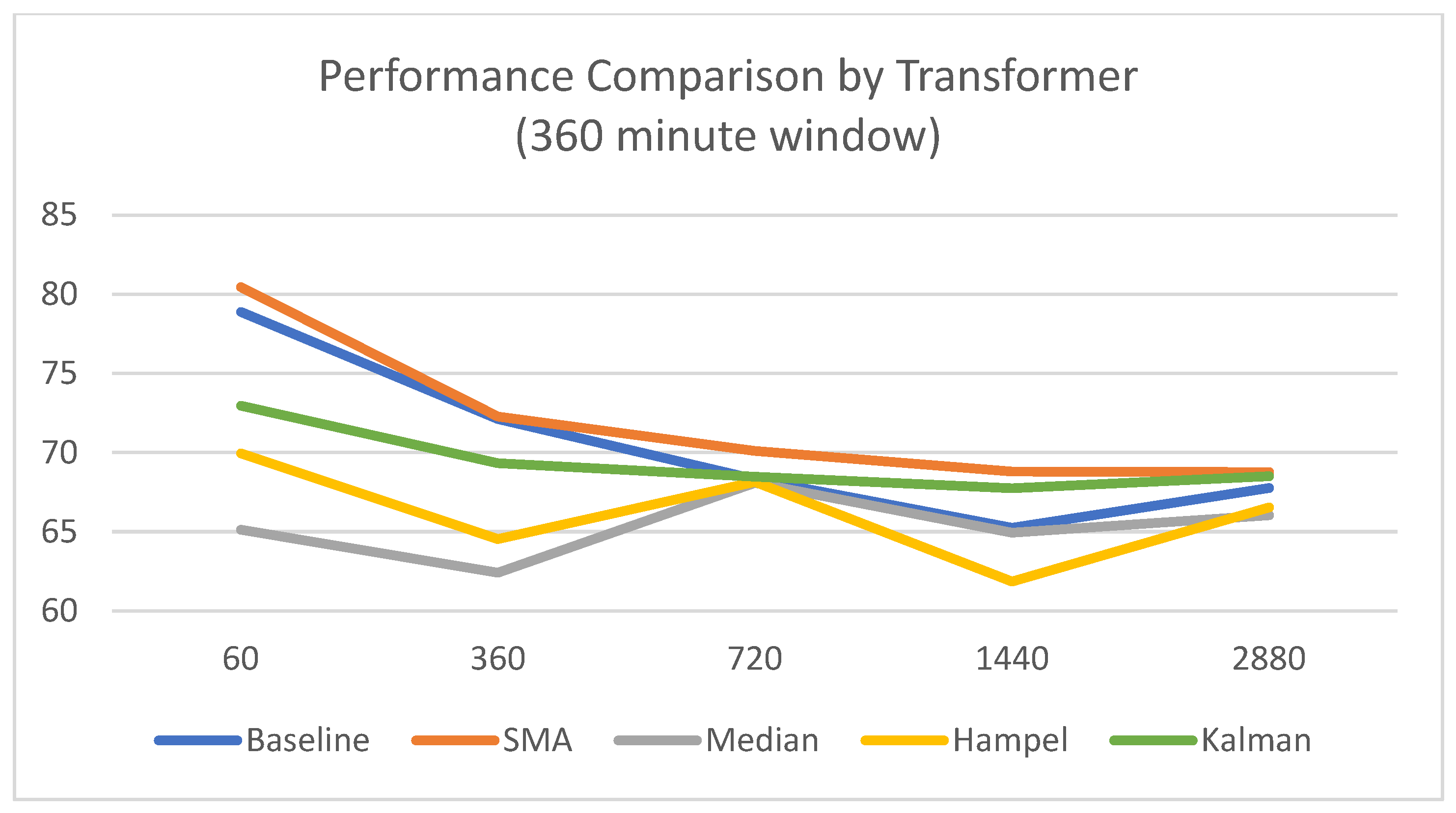
4.1.1. Results Based on a 360 min Window
- The Simple Moving Average (SMA) filter achieved the highest mean accuracy of 80.45% and the lowest standard deviation of 1.94%, establishing it as the most effective and reliable preprocessing technique for short-term predictions.
- In contrast, other filters demonstrated clear limitations, particularly in terms of stability. The Median filter was highly unstable with an extreme accuracy standard deviation of 11.60%, and the Kalman filter also showed high instability in short-term predictions with a standard deviation of 10.62%.
- A consistent trend emerged across most techniques where mean performance gradually decreased as the prediction offset became longer, highlighting the increased difficulty of long-term forecasting.
- The R-Linear model showed an overall decrease in performance compared to the Transformer model. Its peak accuracy was 75.15% with the Median filter, which was significantly lower than the Transformer’s peak of 80.45%.
- Due to its simpler linear architecture, the R-Linear model was less sensitive to the different preprocessing techniques, resulting in smaller performance variations among them.
- Despite lower sensitivity, data preprocessing still provided meaningful performance improvements. The Median filter was effective for short-term predictions, while the SMA technique showed improved accuracy for long-term predictions.
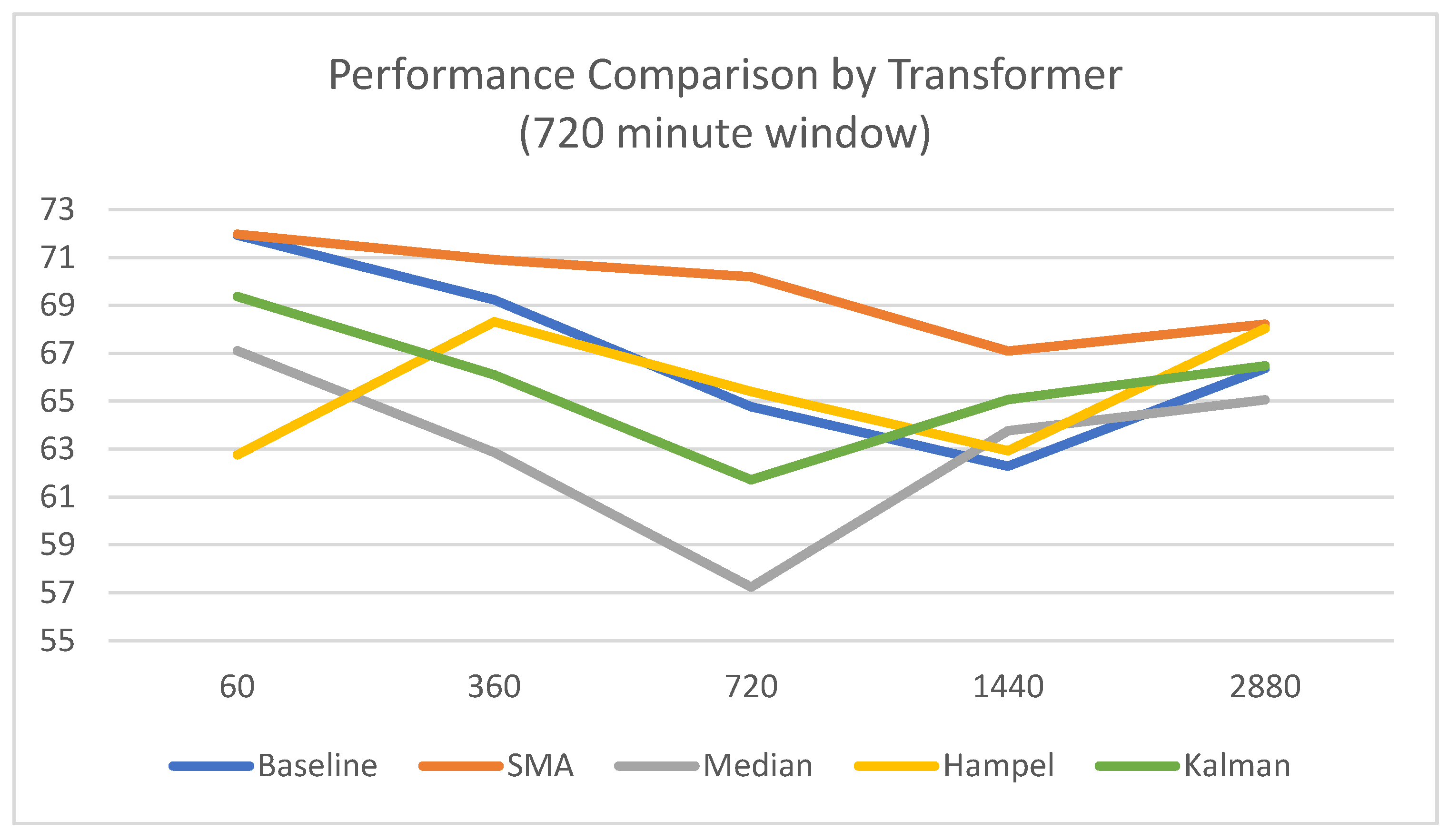
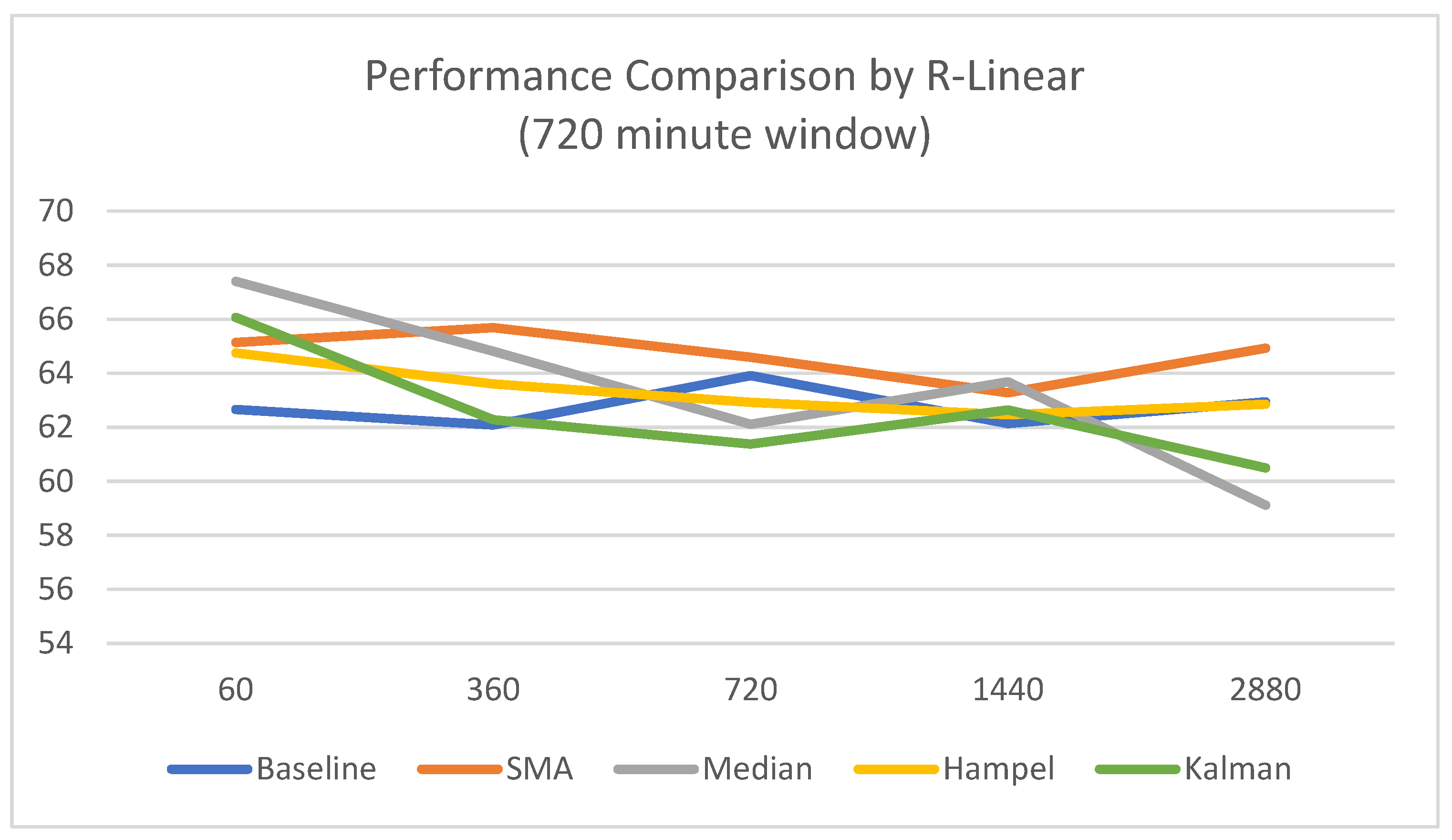
4.1.2. Results Based on a 720 min Window
- The longer window degraded performance, with the baseline model’s peak accuracy dropping to 71.94% and its stability decreasing significantly with a standard deviation as high as 12.03%. This supports the hypothesis that excessively long windows can introduce performance-hindering noise.
- The SMA filter achieved the highest mean accuracy (71.98%) but exhibited significant instability in short-term predictions, with a high standard deviation of 13.73%.
- Other preprocessing methods, including Median, Hampel, and Kalman, failed to surpass the baseline in terms of mean accuracy and consistently showed elevated standard deviations, confirming they were ineffective in this scenario.
- For the shortest prediction horizon (60 min offset), the Median filter recorded the highest mean accuracy (67.41%) but was also highly unstable, with a standard deviation of 11.08%.
- The SMA filter once again proved to be the most robust technique, consistently achieving the best accuracy across most mid-to-long-term prediction horizons (360, 720, and 2880 min).
- This confirms that even under inefficient input conditions, SMA is the superior technique for providing reliable and consistently high performance for long-term predictions with the R-Linear model.
4.2. Results for Optimal Scenarios by Preprocessing Technique
5. Discussion
- First, the SMA can be a more effective alternative to complex techniques. SMA provided an ideal balance between performance and stability by reducing unnecessary volatility while preserving key data trends.
- Second, optimizing model performance requires not only selecting the right filter but also the appropriate length of the input data.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar, A.; Selvakumar, V.; Lavanya, P.; Lakshmi, S.; Uma, S.; Naidu, K.B.; Srivastava, R. Optimizing Power Management in IoT Devices Using Machine Learning Techniques. J. Electr. Syst. 2024, 20, 2929–2940. [Google Scholar] [CrossRef]
- Ethan, A.; Karan, D. Energy-Efficient IoT Systems Using Machine Learning for Real-Time Analysis. Int. J. Mach. Learn. Res. Cybersecur. Artif. Intell. 2023, 14, 1307–1322. [Google Scholar]
- Solanki, A. Sensor Data Analysis for Enhanced Decision-Making in Industry. Int. J. Manag. IT Eng. 2024, 14, 1–14. [Google Scholar]
- Bilgili, M.; Arslan, N.; Şekertekin, A.; Yaşar, A. Application of long short-term memory (LSTM) neural network based on deeplearning for electricity energy consumption forecasting. Turk. J. Electr. Eng. Comput. Sci. 2022, 30, 140–157. [Google Scholar] [CrossRef]
- Kim, K.; Kim, D.K.; Noh, J.; Kim, M. Stable forecasting of environmental time series via long short term memory recurrent neural network. IEEE Access 2018, 6, 75216–75228. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, W.; Rahayu, W.; Dillon, T. An evaluative study on IoT ecosystem for smart predictive maintenance (IoT-SPM) in manufacturing: Multiview requirements and data quality. IEEE Internet Things J. 2023, 10, 11160–11184. [Google Scholar] [CrossRef]
- Liu, Y.; Dillon, T.; Yu, W.; Rahayu, W.; Mostafa, F. Noise removal in the presence of significant anomalies for industrial IoT sensor data in manufacturing. IEEE Internet Things J. 2020, 7, 7084–7096. [Google Scholar] [CrossRef]
- Goknil, A.; Nguyen, P.; Sen, S.; Politaki, D.; Niavis, H.; Pedersen, K.J.; Suyuthi, A.; Anand, A.; Ziegenbein, A. A systematic review of data quality in CPS and IoT for industry 4.0. ACM Comput. Surv. 2023, 55, 1–38. [Google Scholar] [CrossRef]
- Patel, J.M.; Ramezankhani, M.; Deodhar, A.; Birru, D. State of Health Estimation of Batteries Using a Time-Informed Dynamic Sequence-Inverted Transformer. arXiv 2025, arXiv:2507.18320. [Google Scholar]
- Noura, N.; Boulon, L.; Jemeï, S. A review of battery state of health estimation methods: Hybrid electric vehicle challenges. World Electr. Veh. J. 2020, 11, 66. [Google Scholar] [CrossRef]
- Safavi, V.; Bazmohammadi, N.; Vasquez, J.C.; Guerrero, J.M. Battery state-of-health estimation: A step towards battery digital twins. Electronics 2024, 13, 587. [Google Scholar] [CrossRef]
- Oji, T.; Zhou, Y.; Ci, S.; Kang, F.; Chen, X.; Liu, X. Data-driven methods for battery soh estimation: Survey and a critical analysis. IEEE Access 2021, 9, 126903–126916. [Google Scholar] [CrossRef]
- Iurilli, P.; Brivio, C.; Carrillo, R.E.; Wood, V. Physics-based soh estimation for li-ion cells. Batteries 2022, 8, 204. [Google Scholar] [CrossRef]
- Jo, S.; Jung, S.; Roh, T. Battery state-of-health estimation using machine learning and preprocessing with relative state-of-charge. Energies 2021, 14, 7206. [Google Scholar] [CrossRef]
- Acurio, B.A.A.; Barragán, D.E.C.; Rodríguez, J.C.; Grijalva, F.; Pereira da Silva, L.C. Robust Data-Driven State of Health Estimation of Lithium-Ion Batteries Based on Reconstructed Signals. Energies 2025, 18, 2459. [Google Scholar] [CrossRef]
- Tang, X.; Liu, K.; Li, K.; Widanage, W.D.; Kendrick, E.; Gao, F. Recovering large-scale battery aging dataset with machine learning. Patterns 2021, 2, 100302. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Ji, T.; Yu, S.; Liu, G. Accurate prediction approach of SOH for lithium-ion batteries based on LSTM method. Batteries 2023, 9, 177. [Google Scholar] [CrossRef]
- Cui, S.; Joe, I. A dynamic spatial-temporal attention-based GRU model with healthy features for state-of-health estimation of lithium-ion batteries. IEEE Access 2021, 9, 27374–27388. [Google Scholar] [CrossRef]
- Cao, K.; Zhang, T.; Huang, J. Advanced hybrid LSTM-transformer architecture for real-time multi-task prediction in engineering systems. Sci. Rep. 2024, 14, 4890. [Google Scholar] [CrossRef]
- Wen, Q.; Zhou, T.; Zhang, C.; Chen, W.; Ma, Z.; Yan, J.; Sun, L. Transformers in time series: A survey. arXiv 2022, arXiv:2202.07125. [Google Scholar]
- Fatima, S.S.W.; Rahimi, A. A review of time-series forecasting algorithms for industrial manufacturing systems. Machines 2024, 12, 380. [Google Scholar] [CrossRef]
- Meng, F.; Wang, P.; Wang, J. Lithium-ion battery state of health estimation based on LSTM-transformer. In Proceedings of the 2024 IEEE 13th International Conference on Communication Systems and Network Technologies (CSNT), Jabalpur, India, 6–7 April 2024; pp. 1305–1310. [Google Scholar]
- Wang, M.; Sui, Z.; Zhang, L. State-of-Health Estimation of Lithium-Ion Batteries Based on EIS and CNN-Transformer Network. In Proceedings of the 2024 Global Reliability and Prognostics and Health Management Conference (PHM-Beijing), Beijing, China, 11–13 October 2024; pp. 1–7. [Google Scholar]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. itransformer: Inverted transformers are effective for time series forecasting. arXiv 2023, arXiv:2310.06625. [Google Scholar]
- Eivazi, H.; Hebenbrock, A.; Ginster, R.; Blömeke, S.; Wittek, S.; Herrmann, C.; Spengler, S.T.; Turek, T.; Rausch, A. DiffBatt: A diffusion model for battery degradation prediction and synthesis. arXiv 2024, arXiv:2410.23893. [Google Scholar] [CrossRef]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are transformers effective for time series forecasting? In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 11121–11128. [Google Scholar] [CrossRef]
- Li, Z.; Qi, S.; Li, Y.; Xu, Z. Revisiting long-term time series forecasting: An investigation on linear mapping. arXiv 2023, arXiv:2305.10721. [Google Scholar] [CrossRef]
- Johnston, F.R.; Boyland, J.E.; Meadows, M.; Shale, E. Some properties of a simple moving average when applied to forecasting a time series. J. Oper. Res. Soc. 1999, 50, 1267–1271. [Google Scholar] [CrossRef]
- Astola, J.; Neuvo, Y. Matched median filtering. IEEE Trans. Commun. 2002, 40, 722–729. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, H.; Wang, J.; Long, M. Non-stationary transformers: Exploring the stationarity in time series forecasting. Adv. Neural Inf. Process. Syst. 2022, 35, 9881–9893. [Google Scholar]
- Yin, L.; Yang, R.; Gabbouj, M.; Neuvo, Y. Weighted median filters: A tutorial. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 1996, 43, 157–192. [Google Scholar] [CrossRef]
- Roos-Hoefgeest Toribio, M.; Garnung Menéndez, A.; Roos-Hoefgeest Toribio, S.; Álvarez García, I. A Novel Approach to Speed Up Hampel Filter for Outlier Detection. Sensors 2025, 25, 3319. [Google Scholar] [CrossRef] [PubMed]
- Hampel, F.R. The influence curve and its role in robust estimation. J. Am. Stat. Assoc. 1974, 69, 383–393. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Fluids Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Blázquez-García, A.; Conde, A.; Mori, U.; Lozano, J.A. A review on outlier/anomaly detection in time series data. ACM Comput. Surv. (CSUR) 2021, 54, 1–33. [Google Scholar] [CrossRef]
- Yasaei, R.; Hernandez, F.; Faruque, M.A.A. IoT-CAD: Context-aware adaptive anomaly detection in IoT systems through sensor association. In Proceedings of the 39th International Conference on Computer-Aided Design, San Diego, CA, USA, 2–5 November 2020; pp. 1–9. [Google Scholar]
- Owen, A.; Doe, J. Forecasting Supply Chain Trends Using Time Series Analysis. 2024. Available online: https://www.researchgate.net/profile/Antony-Owen/publication/390300976_Forecasting_Supply_Chain_Trends_Using_Time_Series_Analysis/links/67e817c9e8041142a14f08d0/Forecasting-Supply-Chain-Trends-Using-Time-Series-Analysis.pdf (accessed on 16 October 2025).
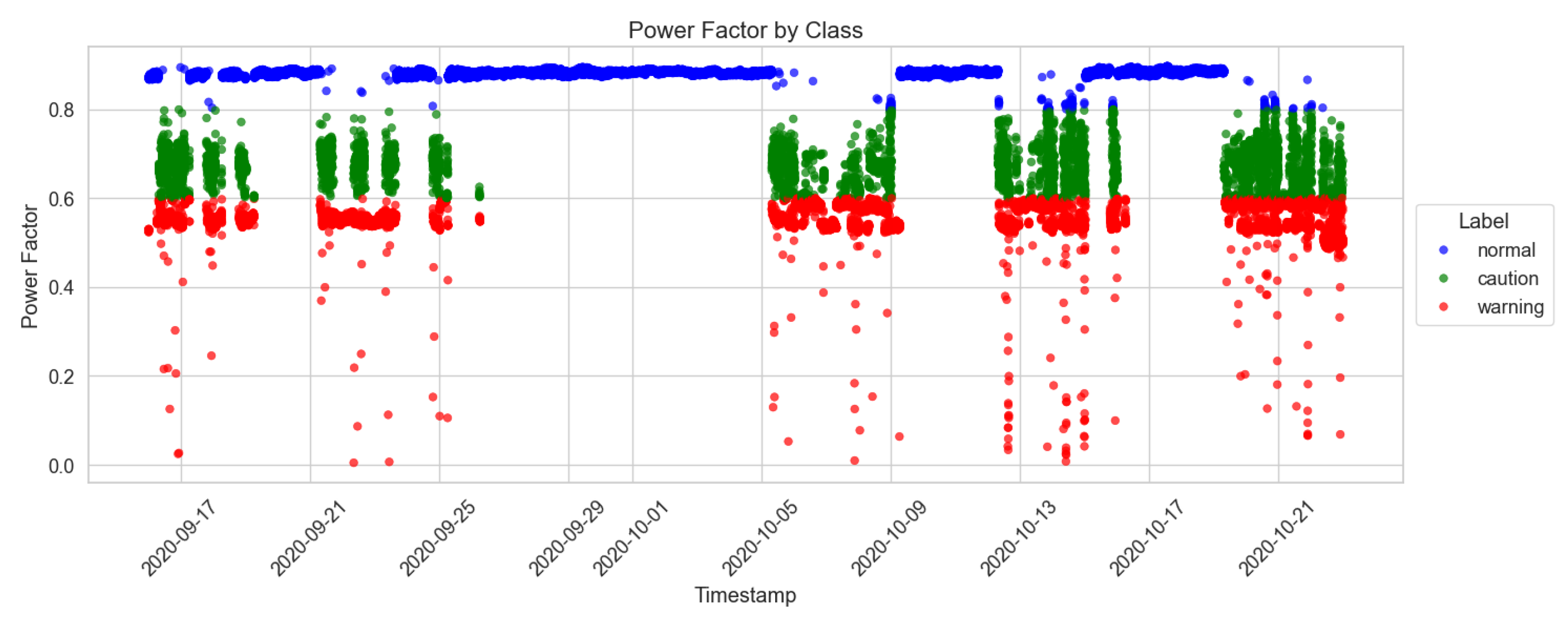

| Normal | Caution | Warning | Total | |
|---|---|---|---|---|
| Count | 31,256 | 14,347 | 7677 | 53,280 |
| Percentage | 58.7% | 26.9% | 14.4% | 100.0% |
| Preprocessing | Window/ Offset | Accuracy (%) | Accuracy Std. (%) | F1 Score (%) | F1 Score Std. (%) | Training Time (s) |
|---|---|---|---|---|---|---|
| Baseline | 360/60 | 78.88 | 4.26 | 59.58 | 6.30 | 367.9 |
| 360/360 | 72.12 | 3.91 | 52.64 | 6.48 | 367.8 | |
| 360/720 | 68.31 | 7.71 | 49.88 | 7.18 | 354.4 | |
| 360/1440 | 65.25 | 3.44 | 41.15 | 7.12 | 341.4 | |
| 360/2880 | 67.76 | 1.11 | 45.93 | 2.71 | 333.1 | |
| SMA | 360/60 | 80.45 | 1.94 | 60.39 | 2.18 | 382.9 |
| 360/360 | 72.27 | 8.17 | 54.66 | 6.08 | 373.9 | |
| 360/720 | 70.10 | 2.59 | 53.27 | 2.45 | 369.1 | |
| 360/1440 | 68.80 | 3.07 | 48.30 | 5.47 | 381.2 | |
| 360/2880 | 68.78 | 2.16 | 49.92 | 3.04 | 384.7 | |
| Median | 360/60 | 65.12 | 11.60 | 39.11 | 15.89 | 347.4 |
| 360/360 | 62.42 | 5.39 | 32.77 | 11.20 | 348.3 | |
| 360/720 | 68.09 | 8.46 | 49.35 | 10.30 | 343.0 | |
| 360/1440 | 64.94 | 5.95 | 38.34 | 13.64 | 334.5 | |
| 360/2880 | 66.03 | 5.77 | 44.27 | 7.32 | 326.0 | |
| Hampel | 360/60 | 69.96 | 7.74 | 48.13 | 11.47 | 343.0 |
| 360/360 | 64.53 | 8.26 | 40.15 | 11.38 | 341.9 | |
| 360/720 | 68.14 | 2.85 | 48.63 | 5.89 | 336.2 | |
| 360/1440 | 61.86 | 9.64 | 40.44 | 7.66 | 337.9 | |
| 360/2880 | 66.54 | 2.25 | 44.64 | 2.69 | 336.9 | |
| Kalman | 360/60 | 72.96 | 10.62 | 52.45 | 11.67 | 354.3 |
| 360/360 | 69.32 | 5.08 | 47.37 | 9.37 | 353.3 | |
| 360/720 | 68.47 | 7.94 | 49.71 | 8.53 | 345.0 | |
| 360/1440 | 67.75 | 3.32 | 46.23 | 5.71 | 346.5 | |
| 360/2880 | 68.50 | 2.24 | 47.65 | 2.96 | 336.6 |
| Preprocessing | Window/ Offset | Accuracy (%) | Accuracy Std. (%) | F1 Score (%) | F1 Score Std. (%) | Training Time (s) |
|---|---|---|---|---|---|---|
| Baseline | 360/60 | 72.25 | 5.89 | 51.06 | 9.26 | 145.3 |
| 360/360 | 65.58 | 4.00 | 41.75 | 8.07 | 141.4 | |
| 360/720 | 63.83 | 1.97 | 36.94 | 4.06 | 141.1 | |
| 360/1440 | 63.29 | 1.95 | 35.15 | 4.30 | 139.8 | |
| 360/2880 | 61.56 | 3.07 | 34.85 | 5.29 | 136.3 | |
| SMA | 360/60 | 72.61 | 9.14 | 49.50 | 13.04 | 143.6 |
| 360/360 | 64.41 | 8.37 | 39.38 | 10.76 | 141.7 | |
| 360/720 | 62.50 | 10.71 | 37.88 | 7.89 | 140.9 | |
| 360/1440 | 63.66 | 2.26 | 36.00 | 4.51 | 138.7 | |
| 360/2880 | 63.68 | 3.10 | 38.67 | 5.45 | 138.5 | |
| Median | 360/60 | 75.15 | 10.85 | 55.05 | 11.57 | 145.9 |
| 360/360 | 67.41 | 4.72 | 46.38 | 6.49 | 144.2 | |
| 360/720 | 64.60 | 3.30 | 38.71 | 7.28 | 142.3 | |
| 360/1440 | 63.61 | 2.02 | 35.18 | 4.04 | 142.1 | |
| 360/2880 | 62.71 | 3.12 | 37.46 | 4.62 | 138.2 | |
| Hampel | 360/60 | 72.26 | 4.71 | 51.41 | 7.50 | 144.9 |
| 360/360 | 61.95 | 8.90 | 38.59 | 9.01 | 141.8 | |
| 360/720 | 62.57 | 2.71 | 33.98 | 5.94 | 141.2 | |
| 360/1440 | 62.73 | 2.04 | 32.72 | 4.97 | 139.1 | |
| 360/2880 | 62.23 | 3.32 | 33.07 | 7.20 | 135.7 | |
| Kalman | 360/60 | 74.79 | 6.33 | 53.47 | 8.54 | 191.2 |
| 360/360 | 63.89 | 8.07 | 39.52 | 9.84 | 204.6 | |
| 360/720 | 59.99 | 8.40 | 33.39 | 7.21 | 198.7 | |
| 360/1440 | 62.76 | 2.17 | 34.41 | 5.34 | 178.2 | |
| 360/2880 | 61.07 | 7.12 | 36.14 | 5.53 | 161.8 |
| Preprocessing | Window/ Offset | Accuracy (%) | Accuracy Std. (%) | F1 Score (%) | F1 Score Std. (%) | Training Time (s) |
|---|---|---|---|---|---|---|
| Baseline | 720/60 | 71.94 | 4.11 | 52.56 | 6.60 | 891.8 |
| 720/360 | 69.23 | 3.61 | 48.32 | 6.66 | 866.0 | |
| 720/720 | 64.77 | 12.03 | 46.28 | 10.25 | 878.3 | |
| 720/1440 | 62.29 | 9.72 | 40.73 | 8.49 | 867.4 | |
| 720/2880 | 66.37 | 4.37 | 46.31 | 5.36 | 843.1 | |
| SMA | 720/60 | 71.98 | 13.73 | 54.75 | 10.22 | 893.3 |
| 720/360 | 70.91 | 7.86 | 54.23 | 6.44 | 886.6 | |
| 720/720 | 70.19 | 2.77 | 52.13 | 4.50 | 877.2 | |
| 720/1440 | 67.10 | 3.10 | 45.88 | 5.31 | 854.9 | |
| 720/2880 | 68.21 | 6.05 | 48.64 | 5.40 | 832.3 | |
| Median | 720/60 | 67.11 | 10.12 | 44.80 | 13.06 | 894.8 |
| 720/360 | 62.86 | 10.77 | 41.13 | 10.98 | 886.1 | |
| 720/720 | 57.24 | 15.71 | 39.60 | 13.86 | 875.6 | |
| 720/1440 | 63.76 | 5.45 | 40.17 | 10.42 | 856.8 | |
| 720/2880 | 65.05 | 5.11 | 40.93 | 11.44 | 830.9 | |
| Hampel | 720/60 | 62.76 | 8.57 | 38.46 | 11.33 | 881.6 |
| 720/360 | 68.32 | 3.90 | 45.60 | 7.85 | 884.0 | |
| 720/720 | 65.40 | 7.86 | 46.75 | 7.90 | 877.6 | |
| 720/1440 | 62.93 | 7.22 | 40.00 | 7.40 | 864.2 | |
| 720/2880 | 68.04 | 3.79 | 46.55 | 6.59 | 834.5 | |
| Kalman | 720/60 | 69.37 | 7.35 | 45.37 | 11.46 | 1007.6 |
| 720/360 | 66.10 | 10.74 | 44.35 | 11.08 | 999.2 | |
| 720/720 | 61.72 | 12.55 | 41.84 | 10.91 | 969.2 | |
| 720/1440 | 65.06 | 6.96 | 43.69 | 6.35 | 929.3 | |
| 720/2880 | 66.48 | 5.81 | 46.57 | 3.81 | 869.5 |
| Preprocessing | Window/ Offset | Accuracy (%) | Accuracy Std. (%) | F1 Score (%) | F1 Score Std. (%) | Training Time (s) |
|---|---|---|---|---|---|---|
| Baseline | 720/60 | 62.66 | 13.06 | 40.09 | 12.54 | 232.9 |
| 720/360 | 62.09 | 7.34 | 34.90 | 9.59 | 230.5 | |
| 720/720 | 63.92 | 2.96 | 36.12 | 7.33 | 225.4 | |
| 720/1440 | 62.14 | 7.10 | 35.59 | 6.05 | 214.5 | |
| 720/2880 | 62.94 | 2.69 | 37.05 | 5.96 | 206.9 | |
| SMA | 720/60 | 65.14 | 6.91 | 37.68 | 13.31 | 220.9 |
| 720/360 | 65.69 | 4.94 | 39.11 | 10.51 | 217.8 | |
| 720/720 | 64.59 | 2.48 | 37.66 | 6.32 | 216.3 | |
| 720/1440 | 63.28 | 2.53 | 33.59 | 5.86 | 212.5 | |
| 720/2880 | 64.93 | 8.75 | 46.55 | 7.77 | 206.7 | |
| Median | 720/60 | 67.41 | 11.08 | 46.55 | 11.00 | 220.4 |
| 720/360 | 64.81 | 8.61 | 39.19 | 11.28 | 216.5 | |
| 720/720 | 62.11 | 6.94 | 33.40 | 8.50 | 216.6 | |
| 720/1440 | 63.68 | 2.32 | 36.00 | 5.66 | 227.0 | |
| 720/2880 | 59.12 | 10.77 | 33.59 | 7.79 | 219.6 | |
| Hampel | 720/60 | 64.76 | 7.57 | 40.75 | 10.12 | 235.4 |
| 720/360 | 63.60 | 3.54 | 36.39 | 7.68 | 235.2 | |
| 720/720 | 62.92 | 3.86 | 35.22 | 8.15 | 234.9 | |
| 720/1440 | 62.47 | 2.44 | 34.40 | 5.87 | 227.5 | |
| 720/2880 | 62.85 | 3.06 | 35.84 | 7.26 | 211.4 | |
| Kalman | 720/60 | 66.07 | 9.23 | 40.24 | 12.48 | 273.4 |
| 720/360 | 62.28 | 7.03 | 36.17 | 8.37 | 276.7 | |
| 720/720 | 61.38 | 2.55 | 30.27 | 7.44 | 262.7 | |
| 720/1440 | 62.64 | 2.42 | 34.95 | 5.88 | 255.9 | |
| 720/2880 | 60.50 | 10.65 | 37.49 | 8.13 | 248.5 |
| Model | Preprocessing | Configuration (Window/Offset) | Accuracy |
|---|---|---|---|
| Transformer | Baseline | 360/60 | 78.88% |
| SMA | 360/60 | 80.45% | |
| Median | 360/720 | 68.09% | |
| Hampel | 360/60 | 69.96% | |
| Kalman | 360/60 | 72.96% | |
| R-Linear | Baseline | 360/60 | 72.25% |
| SMA | 360/60 | 72.61% | |
| Median | 360/60 | 75.15% | |
| Hampel | 360/60 | 72.26% | |
| Kalman | 360/60 | 74.79% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sung, S.-H.; Seo, C.-S.; Pokojovy, M.; Kim, S. A Comparative Analysis of Preprocessing Filters for Deep Learning-Based Equipment Power Efficiency Classification and Prediction Models. Appl. Sci. 2025, 15, 11277. https://doi.org/10.3390/app152011277
Sung S-H, Seo C-S, Pokojovy M, Kim S. A Comparative Analysis of Preprocessing Filters for Deep Learning-Based Equipment Power Efficiency Classification and Prediction Models. Applied Sciences. 2025; 15(20):11277. https://doi.org/10.3390/app152011277
Chicago/Turabian StyleSung, Sang-Ha, Chang-Sung Seo, Michael Pokojovy, and Sangjin Kim. 2025. "A Comparative Analysis of Preprocessing Filters for Deep Learning-Based Equipment Power Efficiency Classification and Prediction Models" Applied Sciences 15, no. 20: 11277. https://doi.org/10.3390/app152011277
APA StyleSung, S.-H., Seo, C.-S., Pokojovy, M., & Kim, S. (2025). A Comparative Analysis of Preprocessing Filters for Deep Learning-Based Equipment Power Efficiency Classification and Prediction Models. Applied Sciences, 15(20), 11277. https://doi.org/10.3390/app152011277






