Multi-Parameter Synchronous Identification Method for Dual Metal Rubber Clamps Considering Directional Differences in Mechanical Properties
Abstract
Featured Application
Abstract
1. Introduction
2. Dynamic Parameter Identification Model
2.1. Dynamic Constitutive Model for the Connection Between DMRC and Pipe
2.2. FEM of the Pipe
2.3. FEM of DMRC-Pipeline System
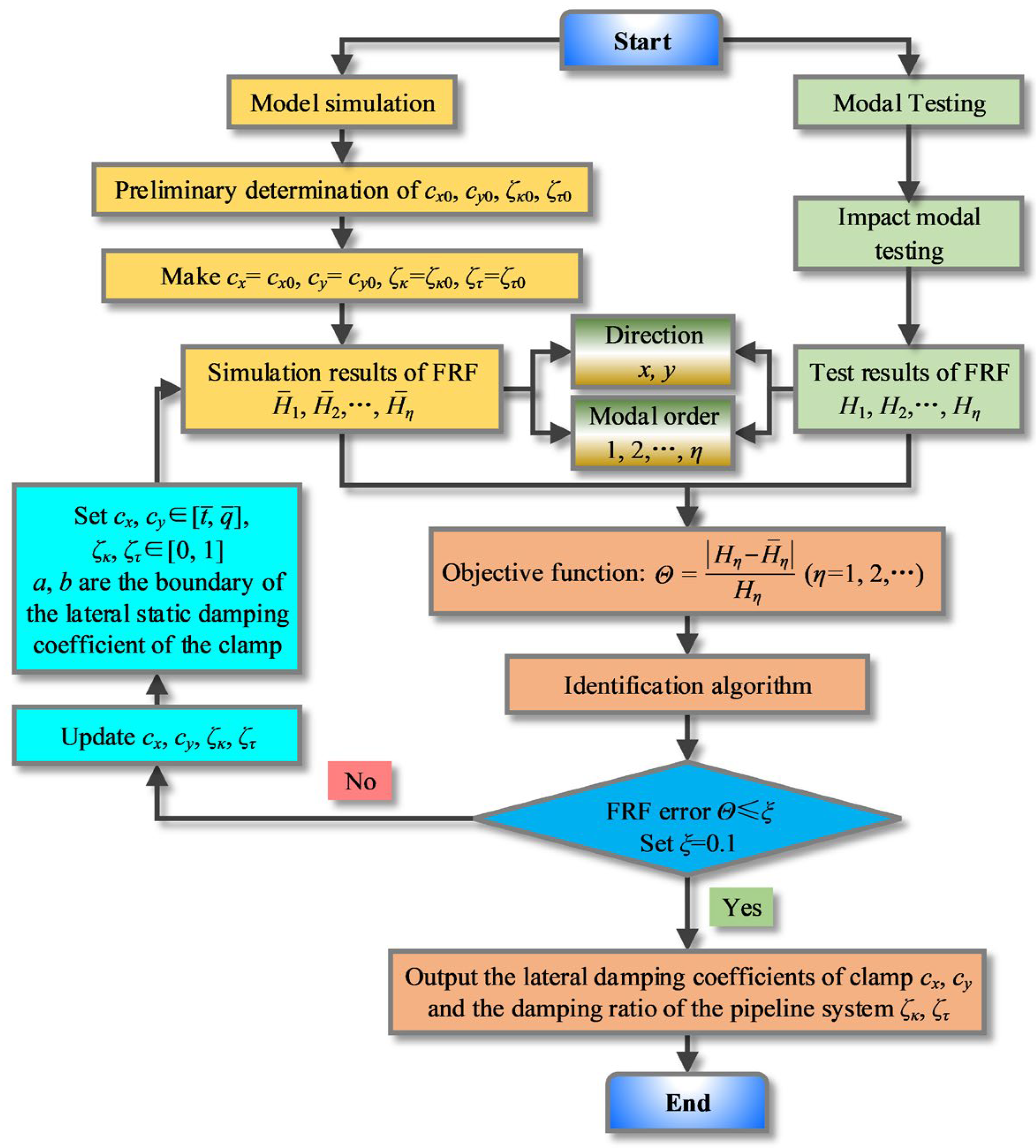
3. Algorithm and Procedure for Identifying Mechanical Parameters of Clamps
3.1. Identification Algorithm
3.2. The Stiffness Identification Procedure of the Clamp
3.3. The Damping Identification Procedure of the Clamp
4. Experimental Verification
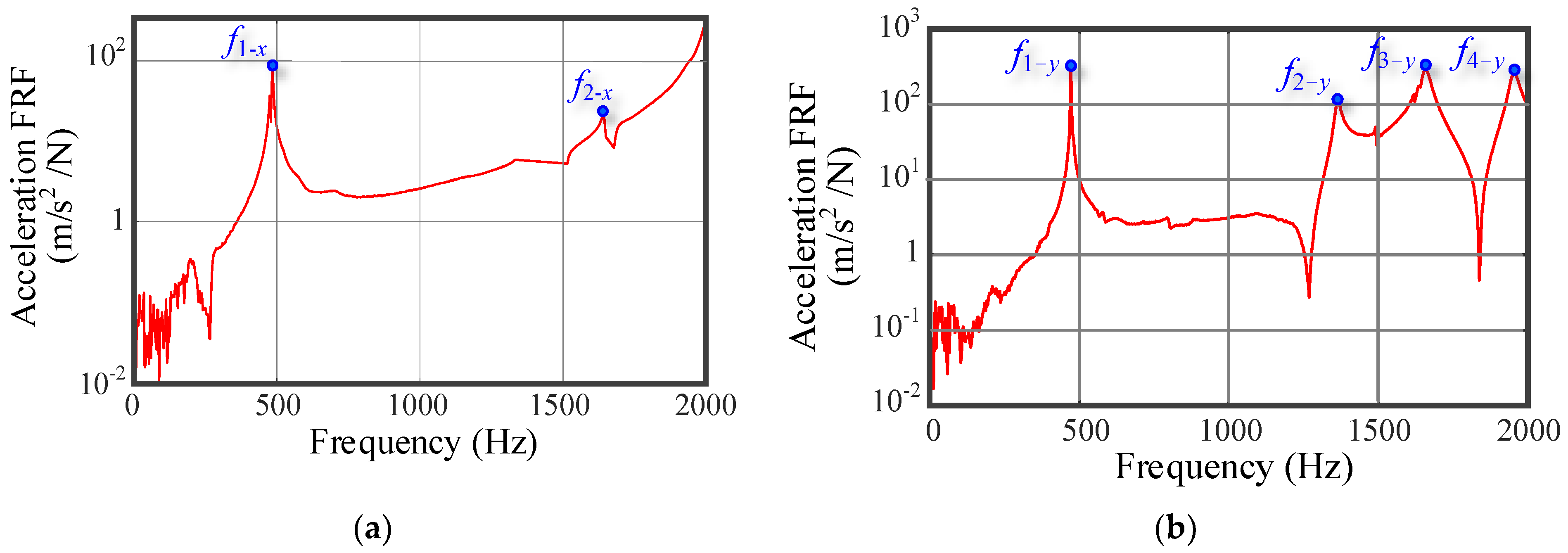
4.1. Experimental System and Testing Results
4.2. The Process and Results of Identifying Mechanical Parameters of Clamp
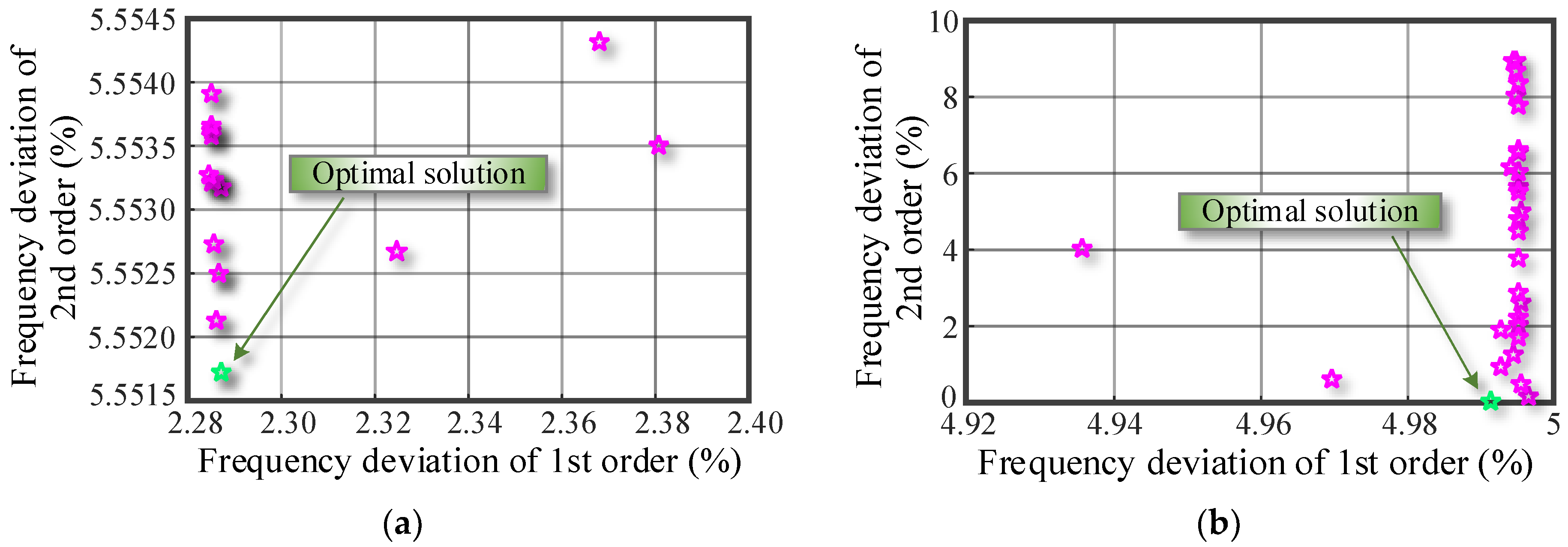
4.2.1. Stiffness Identification
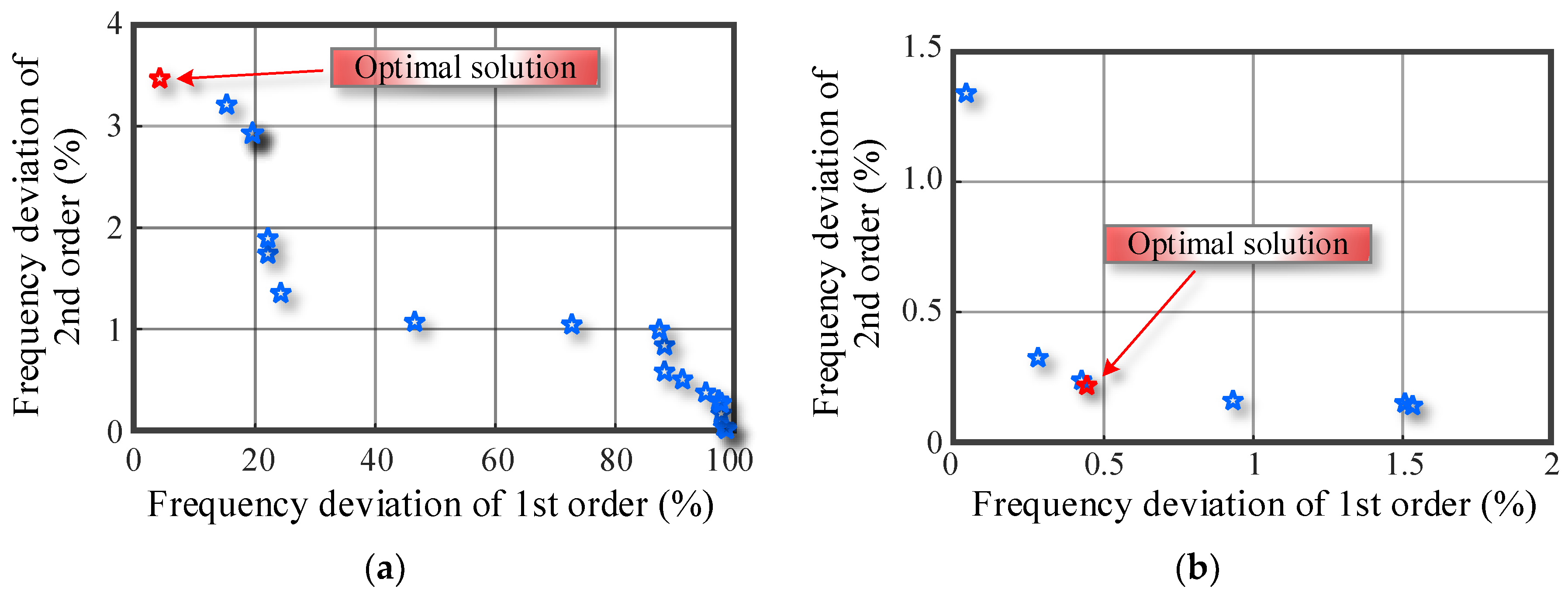
4.2.2. Damping Identification
5. Discussion on Method Limitations
6. Conclusions
- A DMRC-pipeline system is established for the identification of dynamic parameters of DMRCs, which can effectively reflect the differences in dynamic parameters of DMRC in different directions;
- A dynamic model of the DMRC-pipeline system is established based on the finite element method, and the stiffness and damping effects of the clamps in different directions are effectively simulated through two spring-damping modules. Based on a Pareto multi-objective genetic algorithm, an algorithm and process for identifying dynamic parameters of the DMRC using modal data (natural frequency and FRF) of the DMRC-pipeline system are proposed;
- The dynamic parameter identification process of the DMRC is carried out through experimental research, and the identification results are incorporated into the FEM of the pipeline system for simulation analysis. Furthermore, a comparative analysis is conducted on the system’s natural characteristic parameters (natural frequency and peak frequency response function) of the testing and simulation. The maximum and average deviations of the natural frequency are 5.55% and 3.21%, respectively, while the maximum and average deviations of the peak of FRF are 3.86% and 1.995%, respectively. The comparative analysis results show that the identification results of the clamp parameters have good accuracy and also verify the effectiveness of the identification method proposed in this paper.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ji, W.H.; Sun, W.; Wang, D.H. A hybrid finite element and extended transfer matrix method for breathing cracks. Mech. Syst. Sig. Process. 2024, 212, 111276. [Google Scholar] [CrossRef]
- Yang, T.G.; Li, G.C.; Yuan, S.Y. The LST-SATM-net: A new deep feature learning framework for aero-engine hydraulic pipeline systems intelligent faults diagnosis. Appl. Acoust. 2023, 210, 109436. [Google Scholar] [CrossRef]
- Zhang, X.T.; Liu, W.; Zhang, Y.M. Experimental Investigation and Optimization Design of Multi-Support Pipeline System. Chin. J. Mech. Eng. 2021, 34, 10. [Google Scholar] [CrossRef]
- Liu, Q.; Tang, Z.; Liu, H.J. Integrated Optimization of Pipe Routing and Clamp Layout for Aeroengine Using Improved MOALO. Int. J. Aerosp. Eng. 2021, 2021, 6681322. [Google Scholar] [CrossRef]
- Li, X.; Li, W.H.; Shi, J. Pipelines vibration analysis and control based on clamps’ locations optimization of multi-pump system. Chin. J. Aeronaut. 2022, 35, 352–366. [Google Scholar] [CrossRef]
- Sun, A.H.; Yu, R.Y.; Wang, X. Dynamic analysis of liquid-filled clamp-pipe systems based on the spectral element method. Arch. Appl. Mech. 2025, 95, 24. [Google Scholar] [CrossRef]
- Yang, Y.B.; Sui, G.H.; Zhang, Y.H. Response spectrum method for fatigue damage assessment of aero-hydraulic pipeline systems. Comput. Struct. 2023, 287, 107119. [Google Scholar] [CrossRef]
- Liu, J.Z.; Zhao, Y.L.; Zhu, Q.G. Nonlinear characteristic of clamp loosing in aero-engine pipeline system. IEEE Access 2021, 9, 64076–64084. [Google Scholar]
- Chen, W.J.; Cao, Y.M.; Guo, X.M. Nonlinear vibration analysis of pipeline considering the effects of soft nonlinear clamp. Appl. Math. Mech. 2022, 43, 1555–1568. [Google Scholar] [CrossRef]
- Jin, J.; Zhu, Z.B.; Cao, Y.L. Dynamic property evaluation of pipeline clamp based on analyzing the propagation characteristics of flexural wave in pipeline. NDT E Int. 2024, 145, 103097. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, W.; Ma, H.W. Semi-analytical modeling and vibration analysis for U-shaped, Z-shaped and regular spatial pipelines supported by multiple clamps. Eur. J. Mech. A-Solids 2023, 97, 104797. [Google Scholar] [CrossRef]
- Cao, Y.M.; Guo, X.M. Semi-analytical dynamic modeling and fluid-structure interaction analysis of L-shaped pipeline. Thin-Walled Struct. 2024, 196, 111485. [Google Scholar]
- Chen, W.J.; Guo, Z.W.; Chen, S. Semi-analytic modeling and experimental verification of arbitrary aero-engine complex spatial pipeline. Appl. Math. Model. 2024, 131, 505–534. [Google Scholar] [CrossRef]
- Ma, H.W.; Sun, W.; Ji, W.H. Nonlinear vibration analysis of Z-shaped pipes with CLD considering amplitude-dependent characteristics of clamps. Int. J. Mech. Sci. 2024, 262, 108739. [Google Scholar] [CrossRef]
- Guo, X.M.; Gu, J.F.; Li, H. Dynamic modeling and experimental verification of an L-shaped pipeline in aero-engine subjected to base harmonic and random excitations. Appl. Math. Model. 2024, 126, 249–256. [Google Scholar] [CrossRef]
- Guo, X.M.; Cao, Y.M.; Ma, H. Vibration analysis for a parallel fluid-filled pipelines-casing model considering casing flexibility. Int. J. Mech. Sci. 2022, 231, 107606. [Google Scholar] [CrossRef]
- Cao, Y.M.; Chai, Q.D.; Guo, X.M. Comparative study on two finite element models for multi-clamp pipeline system. J. Mech. Sci. Technol. 2022, 36, 1157–1169. [Google Scholar] [CrossRef]
- Cao, Y.M.; Guo, X.M.; Ma, H. Dynamic modelling and natural characteristics analysis of fluid conveying pipeline with connecting hose. Mech. Syst. Sig. Process. 2023, 193, 110244. [Google Scholar] [CrossRef]
- Guo, X.M.; Ma, H.; Zhang, X.F. Uncertain frequency responses of clamp-pipeline systems using an interval-based method. IEEE Access 2020, 8, 29370–29384. [Google Scholar] [CrossRef]
- Liu, Z.H.; Shan, Z.C.; Zhang, X.F. Uncertain frequency response analysis of clamp-pipe systems via the coordinate transformed polynomial chaos expansion. Int. J. Press. Vessel. Pip. 2022, 19, 104720. [Google Scholar] [CrossRef]
- Ma, H.W.; Sun, W.; Ji, W.H. Dynamic modeling and vibration analysis of planar pipeline with partial constrained layer damping treatment: Theoretical and experimental studies. Compos. Struct. 2023, 323, 117476. [Google Scholar] [CrossRef]
- Ma, H.W.; Sun, W.; Wang, D. Finite element modeling of straight pipeline with partially attached viscoelastic damping patch based on variable thickness laminated element. Compos. Struct. 2022, 314, 116944. [Google Scholar] [CrossRef]
- Liu, Y.; Wei, J.T.; Du, H. An analysis of the vibration characteristics of an aviation hydraulic pipeline with a clamp. Aerospace 2023, 10, 900. [Google Scholar] [CrossRef]
- Ji, W.H.; Sun, W.; Zhang, Y. Parametric model order reduction and vibration analysis of pipeline system based on adaptive dynamic substructure method. Structures 2023, 50, 689–706. [Google Scholar] [CrossRef]
- Zhang, X.T.; Liu, W. The effect of pipeline layout parameters on mode and dynamic stress of “airframe-clamps-pipeline” structure. Multidiscip. Model. Mater. Struct. 2020, 16, 373–389. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, T.; Ouyang, H.J. Natural frequency assignment of a pipeline through structural modification in layout optimization of elastic supports. J. Sound Vib. 2023, 561, 117702. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, W.; Ji, W.H. Hoop layouts optimization for vibration reduction of L-shaped pipeline based on substructure-analytical model and genetic algorithm. J. Braz. Soc. Mech. Sci. 2023, 45, 243. [Google Scholar] [CrossRef]
- Chen, H.T.; Zhang, L.; Zhang, T. FRF-based model updating of liquid-filled pipeline system considering tolerance intervals of test errors in the antiresonant frequencies. Eng. Struct. 2024, 307, 117818. [Google Scholar] [CrossRef]
- Gao, P.X.; Li, J.W.; Zhai, J.Y. A Novel Optimization Layout Method for Clamps in a Pipeline System. Appl. Sci. 2020, 10, 390. [Google Scholar] [CrossRef]
- Liu, F.M.; Sun, W.; Zhang, H. Dynamic modeling and stress reduction optimization of parallel pipelines based on pipe-solid element coupling. Int. J. Press. Vessel. Pip. 2024, 207, 105107. [Google Scholar] [CrossRef]
- Chen, W.J.; Cao, Y.M.; Chen, S. Semi-analytical dynamic modeling of parallel pipeline considering soft nonlinearity of clamp: A simulation and experimental study. Mech. Syst. Sig. Process. 2023, 201, 110648. [Google Scholar] [CrossRef]
- Guo, X.M.; Xiao, C.L.; Ge, H. Dynamic modeling and experimental study of a complex fluid-conveying pipeline system with series and parallel structures. Appl. Math. Model. 2022, 109, 186–208. [Google Scholar] [CrossRef]
- Gao, P.X.; Zhang, Y.L.; Liu, X.F. Vibration analysis of aero parallel-pipeline systems based on a novel reduced order modeling method. J. Mech. Sci. Technol. 2020, 34, 3137–3146. [Google Scholar] [CrossRef]
- Chai, Q.D.; Zeng, J.; Ma, H. A dynamic modeling approach for nonlinear vibration analysis of the L-type pipeline system with clamps. Chin. J. Aeronaut. 2020, 33, 3253–3265. [Google Scholar] [CrossRef]
- Lin, J.Z.; Niu, Z.H.; Zhang, X.F. Clamp nonlinear modeling and hysteresis model parameter identification. IEEE Access 2021, 9, 47757–147767. [Google Scholar] [CrossRef]
- Cao, Y.M.; Chen, W.J.; Ma, H. Dynamic modeling and experimental verification of clamp-pipeline system with soft nonlinearity. Nonlinear Dyn. 2023, 111, 17725–17748. [Google Scholar] [CrossRef]
- Wang, Z.C.; Gao, P.X.; Zhou, Z.D. A numerically stable flexural dynamics model of complex multi-span fluid-conveying pipes with flexible components and its application to clamp stiffness identification. Thin-Walled Struct. 2024, 195, 111488. [Google Scholar] [CrossRef]
- Zhu, H.Y.; Liu, W.; Li, W.Z. Dynamic identification method for stiffness of duplex suspension clamp based on system modes. Structures 2023, 57, 105284. [Google Scholar] [CrossRef]

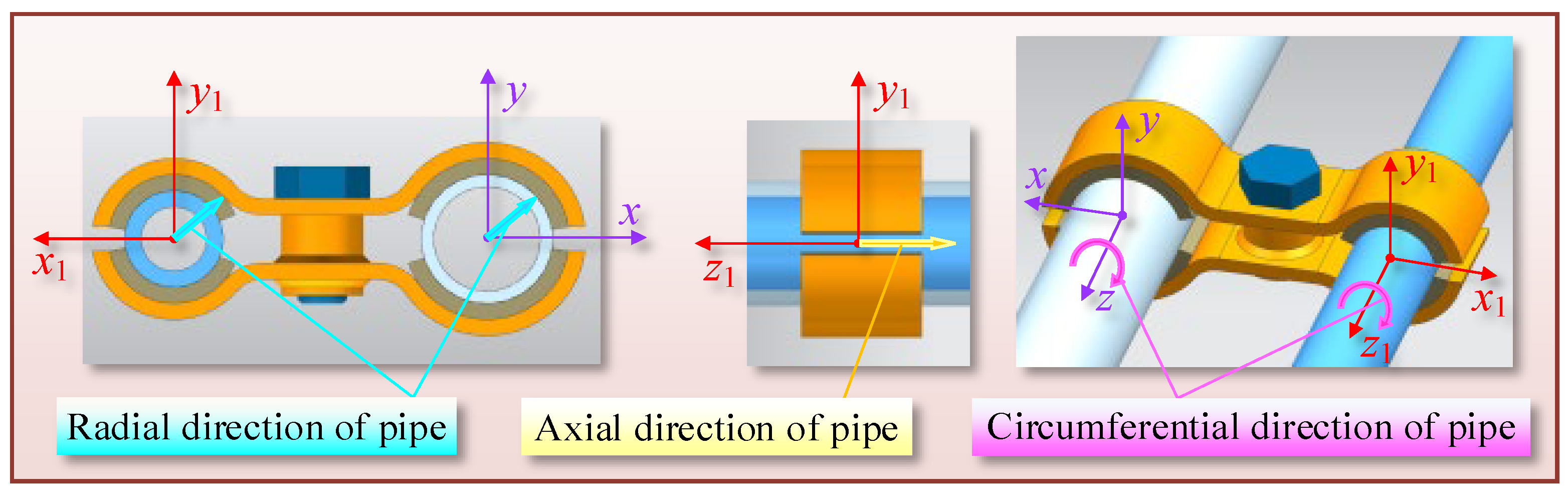



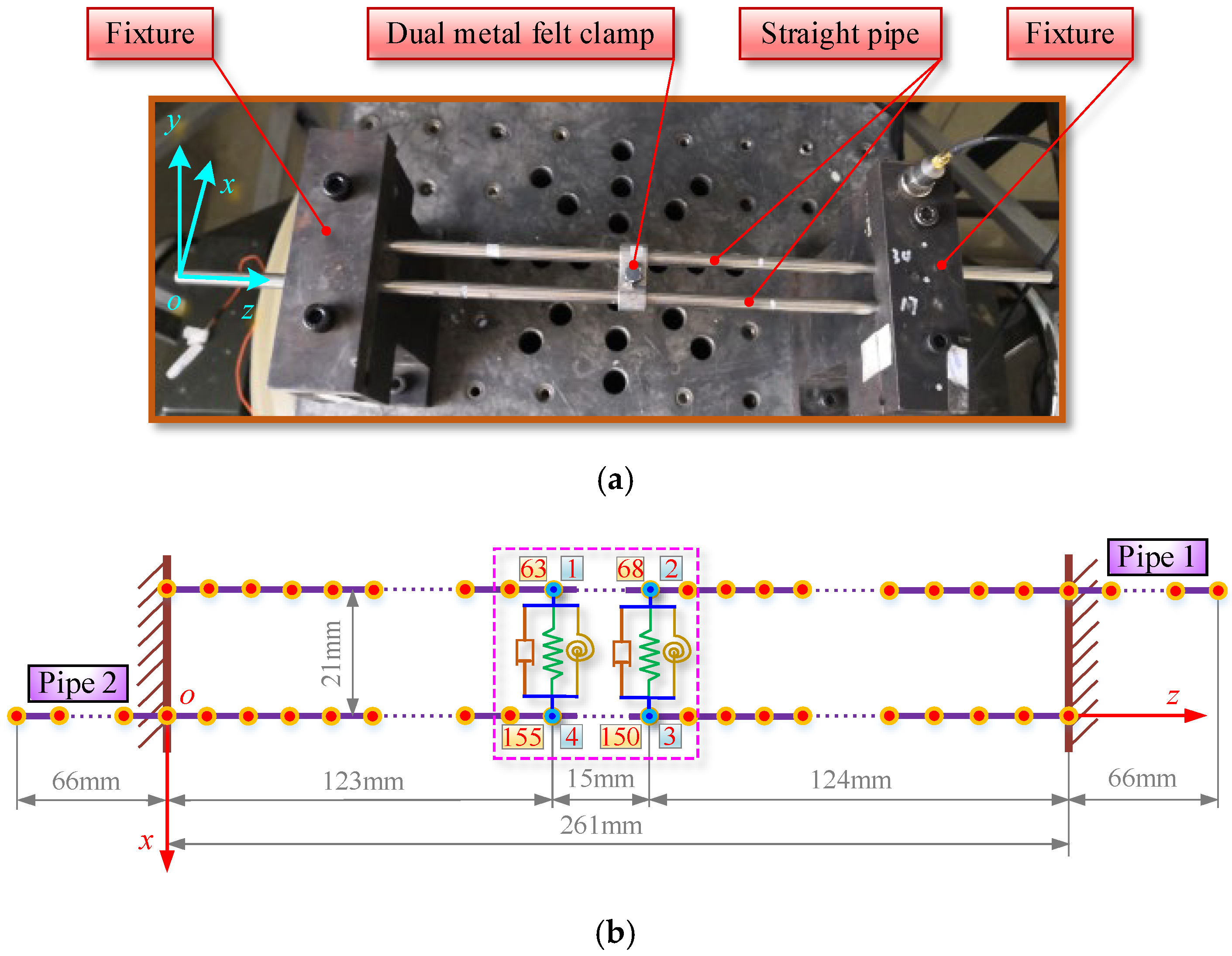
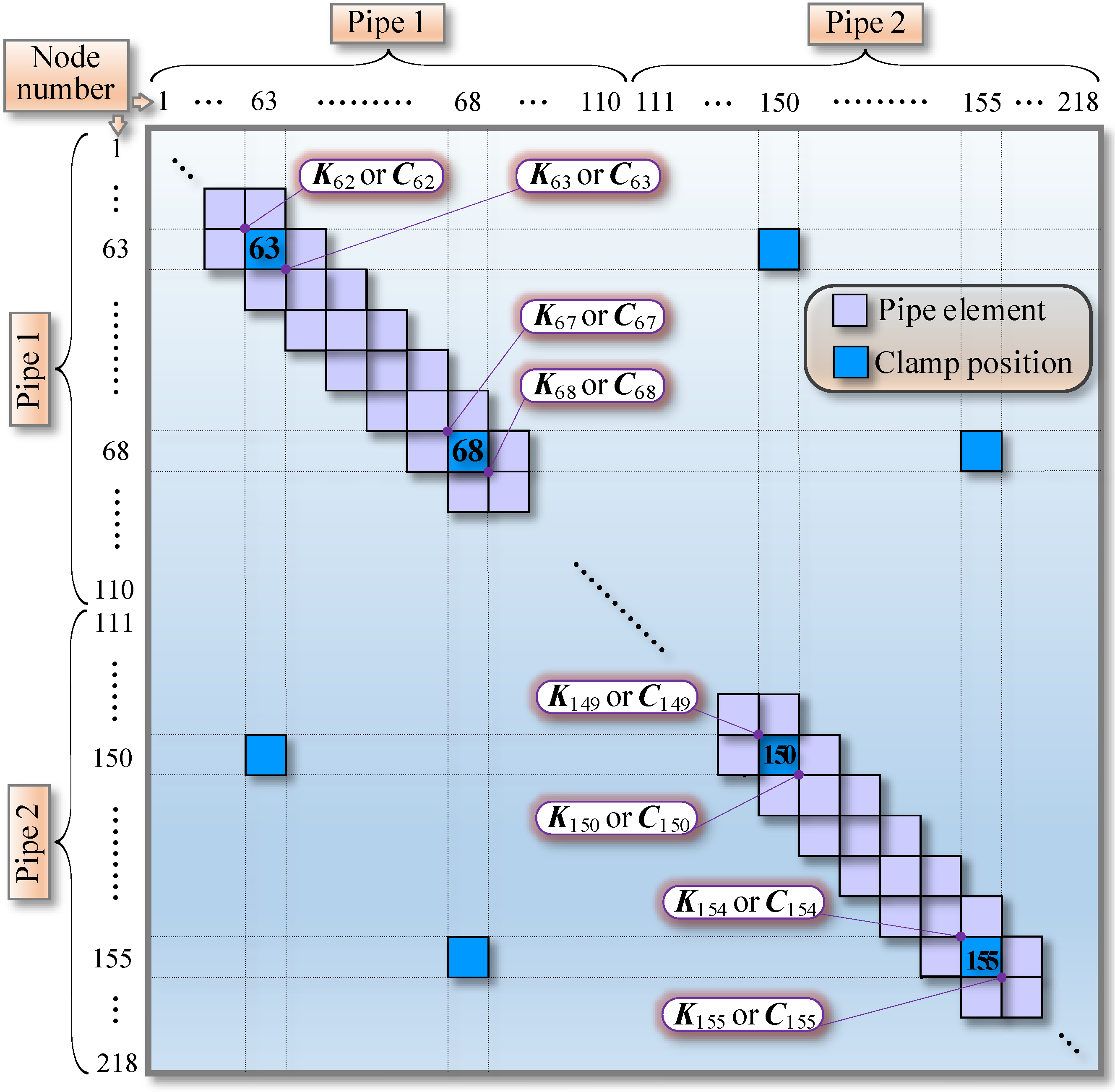
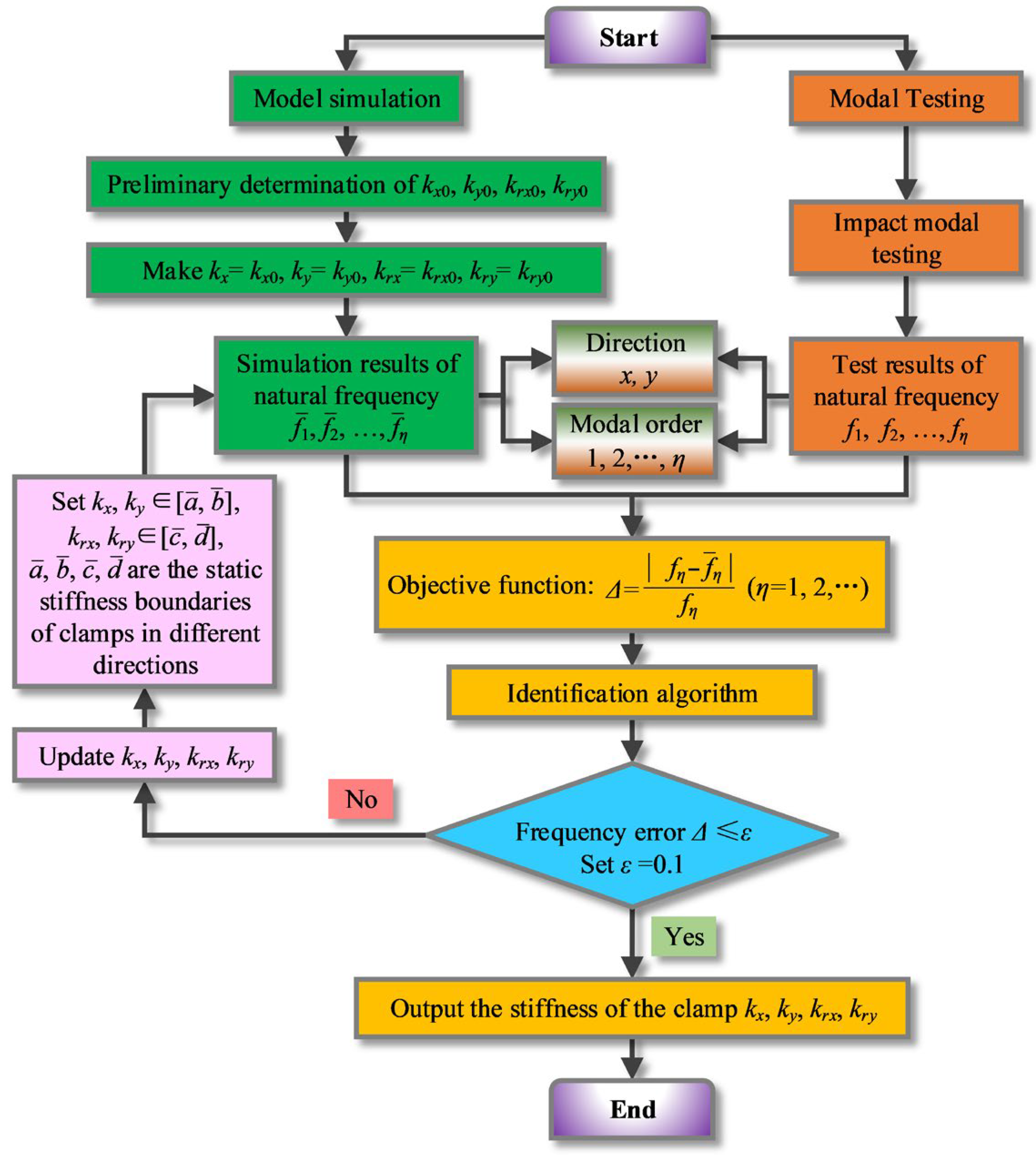



| Elastic Modulus (GPa) | Density (kg/m3) | Poisson’s Ratio | Length (mm) | Outer Diameter (mm) | Inner Diameter (mm) |
|---|---|---|---|---|---|
| 190 | 7850 | 0.3 | 403 | 8 | 6.4 |
| Serial Number | Instrument | Manufacturer |
|---|---|---|
| 1 | LMS SCADAS mobile front end | Siemens/Germany |
| 2 | Acceleration lightweight sensor | BK/Denmark |
| 3 | LMS Test. lab mobile workstation | Siemens/Germany |
| 4 | PCB 8206-001 54627 exciting hammer | PCB/USA |
| Order–Direction | f1−x | f2−x | f1−y | f2−y | f3−y | f4−y |
|---|---|---|---|---|---|---|
| Natural frequency (Hz) | 484.375 | 1640.625 | 471.875 | 1365.625 | 1659.375 | 1953.125 |
| Peak value of FRF (m/s2/N) | 76.8435 | 21.0613 | 304.4037 | 108.1294 | 290.1738 | 259.7483 |
| Order and Direction of Testing Data | 1st and 2nd Orders in x Direction | 1st and 2nd Orders in y Direction |
|---|---|---|
| Stiffness in (N/m) | 3.2 × 106 | 3.683 × 106 |
| Stiffness in (N/m) | 7.0 × 105 | 8.929 × 105 |
| (N·m/rad) | 103.84 | 104.741 |
| (N·m/rad) | 44.00 | 56.814 |
| Order and Direction of Testing Data | 1st and 2nd Orders in x Direction | 1st and 2nd Orders in y Direction |
|---|---|---|
| 2.97 × 10−3 | 6.33 × 10−4 | |
| 7.63 × 10−2 | 4.72 × 10−3 | |
| Damping coefficient of clamp (N·s/m) | 38.53 | 37.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, K.; Wang, R.; Wang, B. Multi-Parameter Synchronous Identification Method for Dual Metal Rubber Clamps Considering Directional Differences in Mechanical Properties. Appl. Sci. 2025, 15, 11239. https://doi.org/10.3390/app152011239
Xu K, Wang R, Wang B. Multi-Parameter Synchronous Identification Method for Dual Metal Rubber Clamps Considering Directional Differences in Mechanical Properties. Applied Sciences. 2025; 15(20):11239. https://doi.org/10.3390/app152011239
Chicago/Turabian StyleXu, Kunpeng, Ruize Wang, and Bo Wang. 2025. "Multi-Parameter Synchronous Identification Method for Dual Metal Rubber Clamps Considering Directional Differences in Mechanical Properties" Applied Sciences 15, no. 20: 11239. https://doi.org/10.3390/app152011239
APA StyleXu, K., Wang, R., & Wang, B. (2025). Multi-Parameter Synchronous Identification Method for Dual Metal Rubber Clamps Considering Directional Differences in Mechanical Properties. Applied Sciences, 15(20), 11239. https://doi.org/10.3390/app152011239





