Sliding Mode Observer-Based Sensorless Control Strategy for PMSM Drives in Air Compressor Applications
Abstract
1. Introduction
2. Mathematical Model and Vector Control of PMSM
2.1. Mathematical Model of PMSM
2.2. Vector Control of PMSM
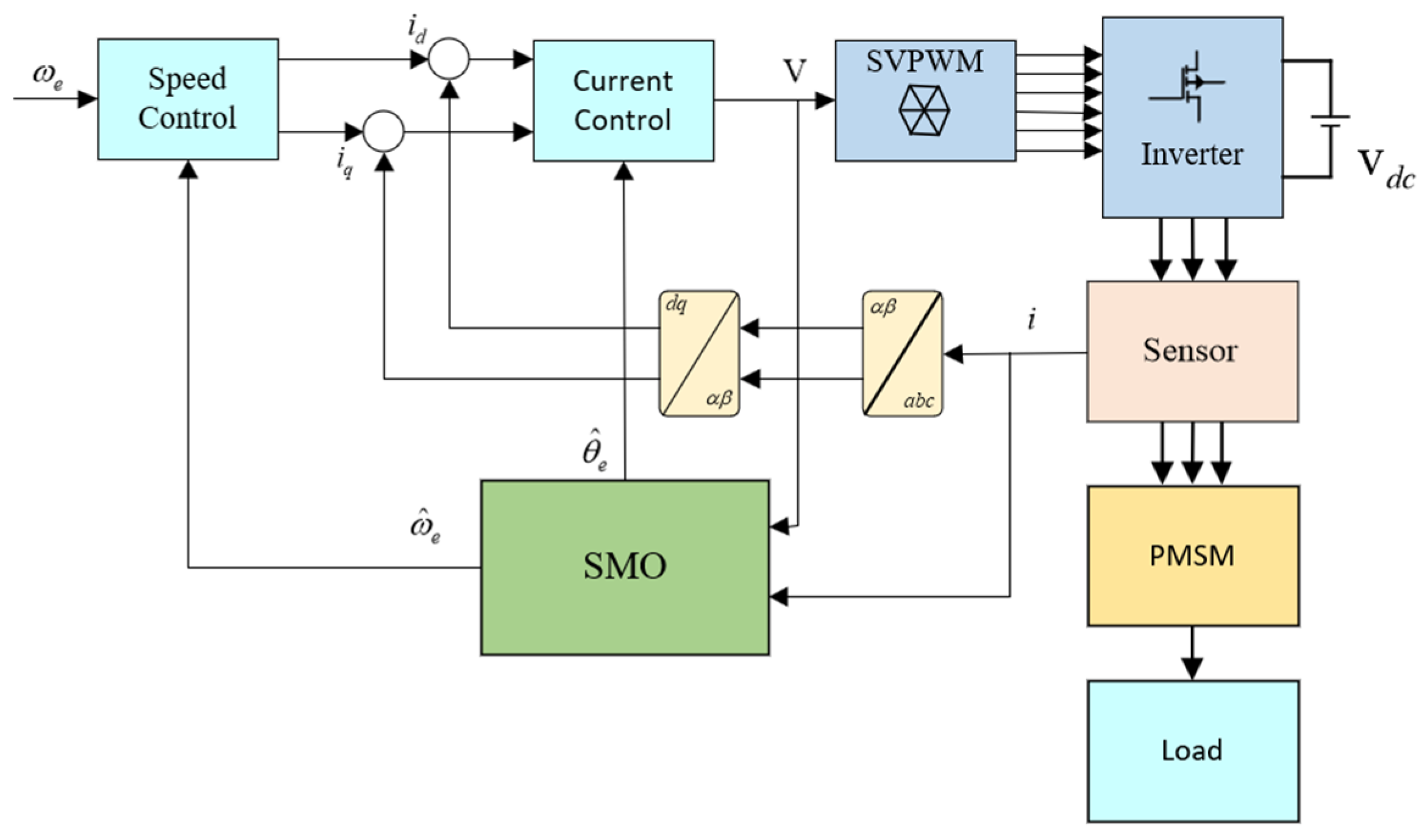
3. Sensorless Control Based on SMO
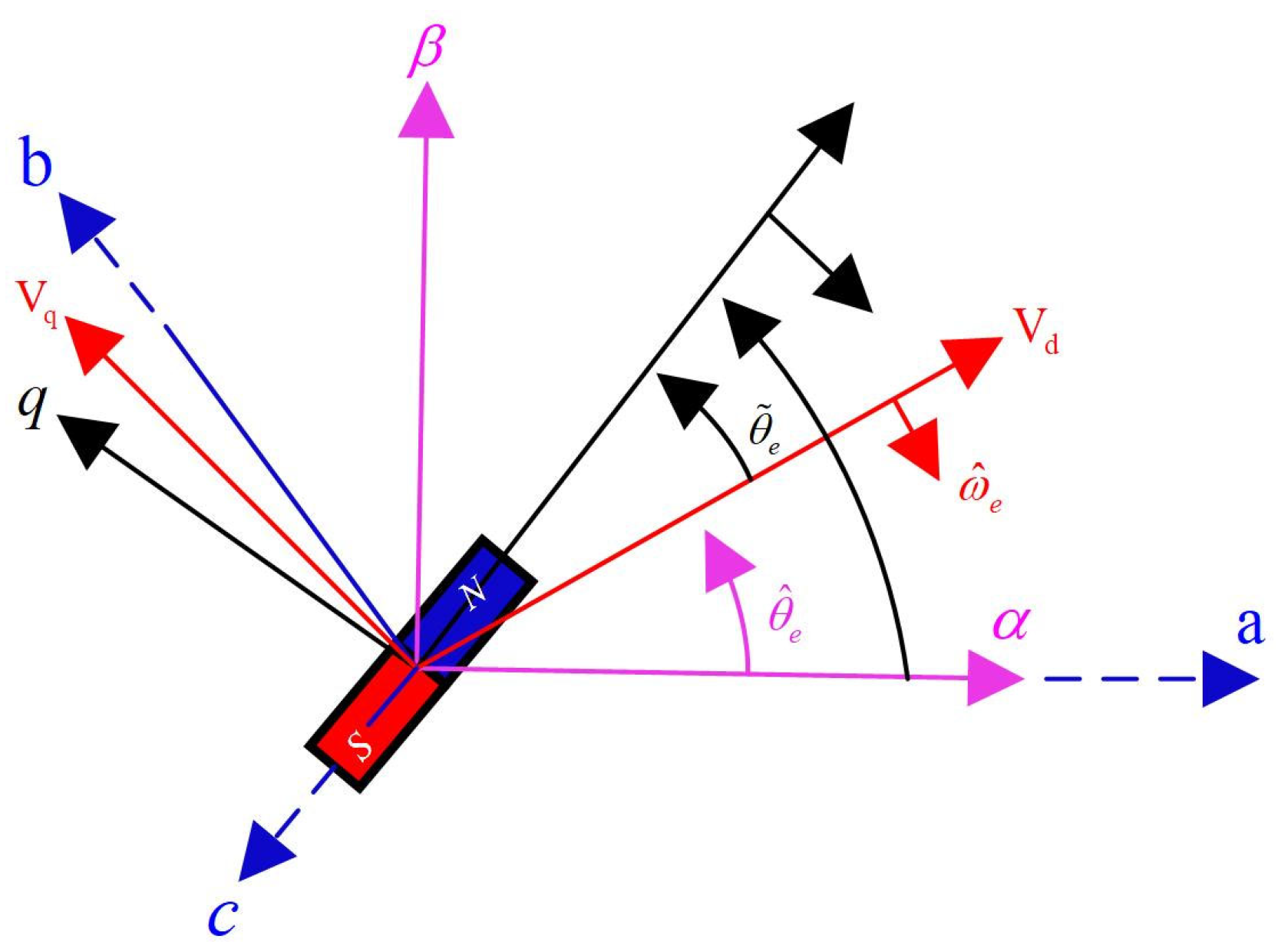
3.1. Sliding Mode Observer Design in Stationary αβ-Frame
3.2. Conventional Sliding Mode Observer
3.3. Design of Higher-Order Sliding Mode Observers for Sensorless PMSM Control
3.4. Adaptive Gain Methodologies for Chattering Suppression
3.5. Adaptive Gain Mechanism for Enhanced SMO in PMSM Drives
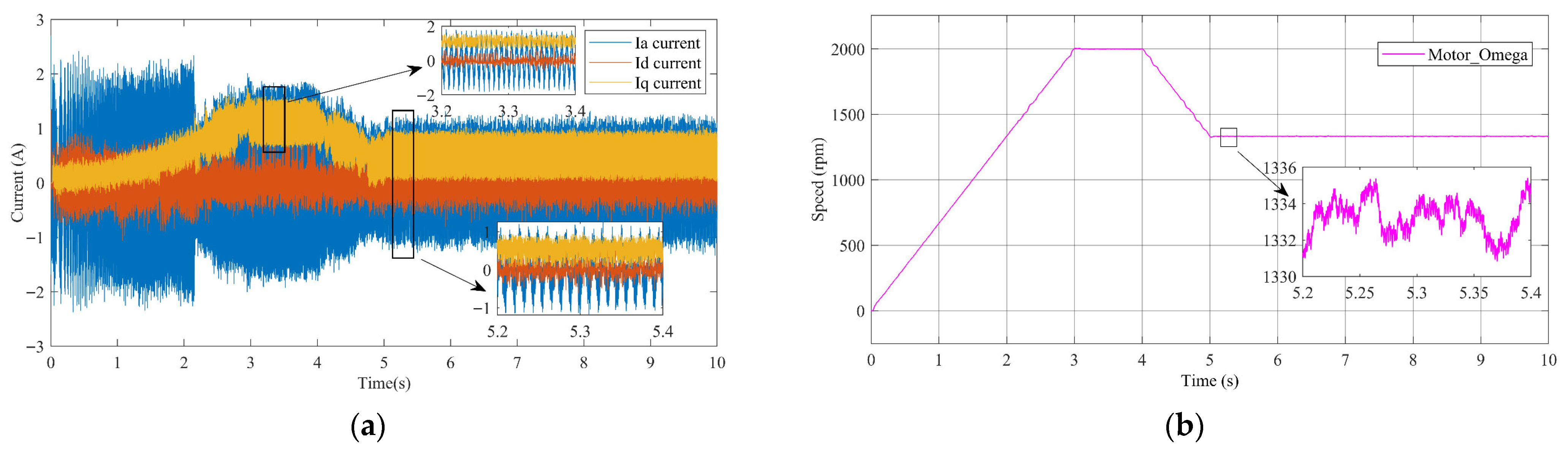
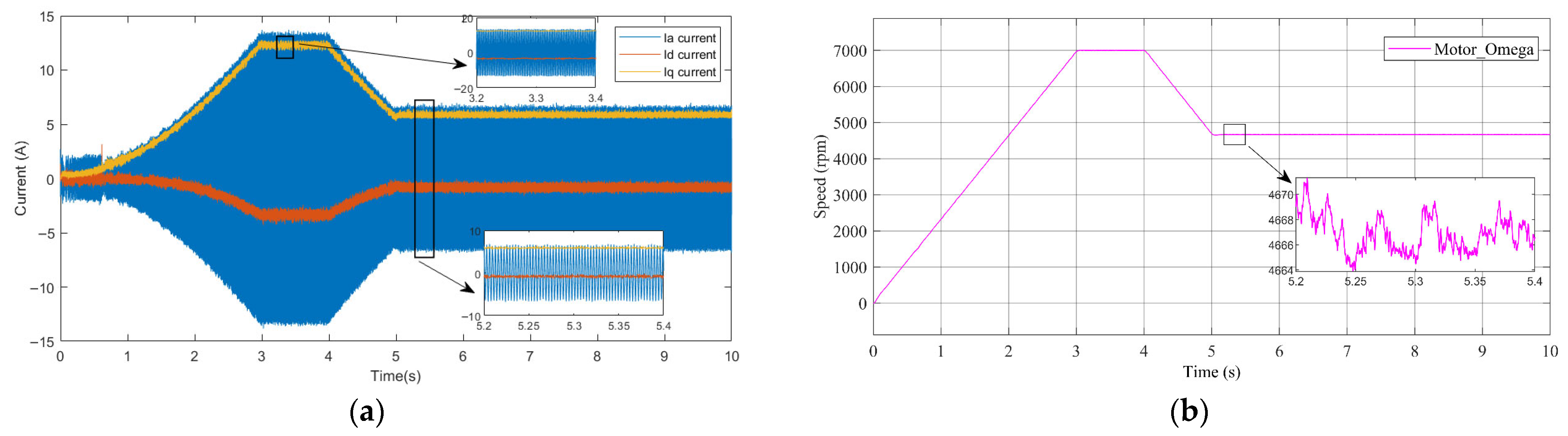
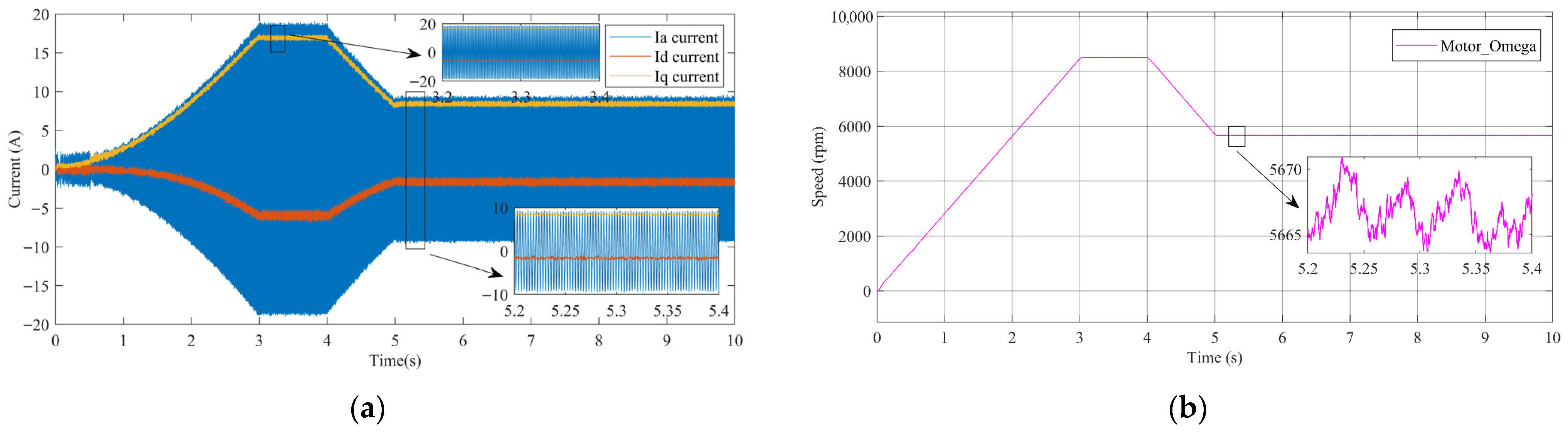
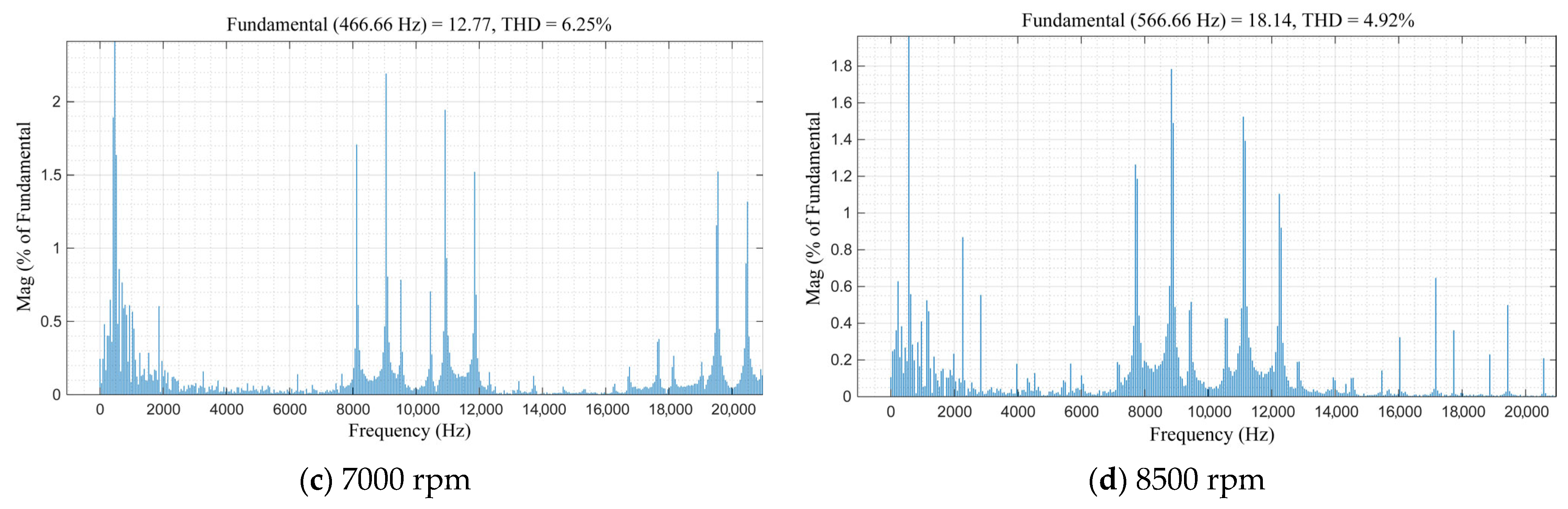
4. Simulation
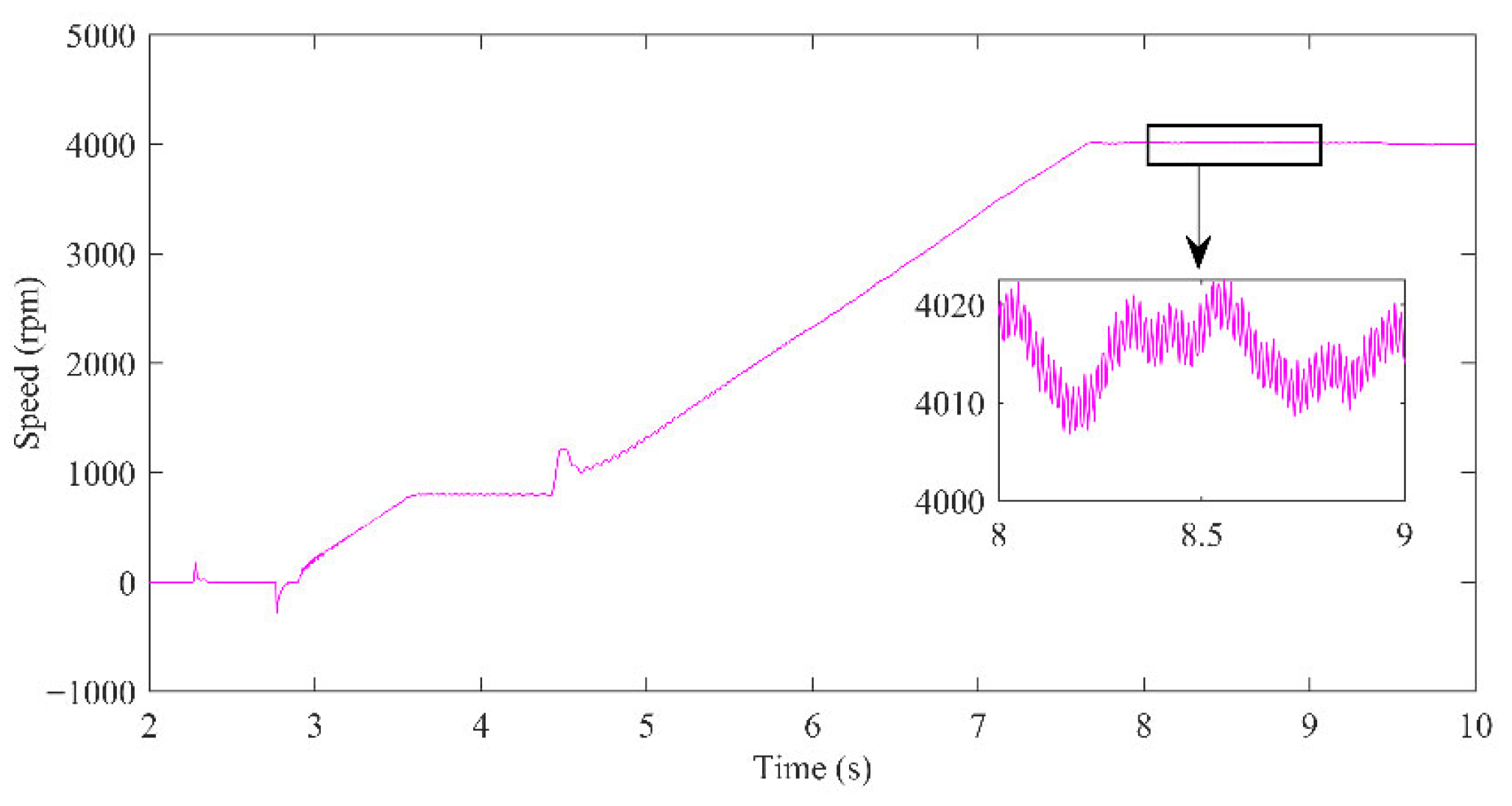
5. Experiment Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jena, S.; Kumar, S.; Deshmukh, A.V.; Hava, A.M.; Akin, B.; Gabrys, C.; Rodgers, T. Design and Control of High-Frequency Buck Converter Fed Six-Step Drive for Air-Core PMSM. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 1144–1157. [Google Scholar] [CrossRef]
- Ha, V.T. Drive Control of a Permanent Magnet Synchronous Motor Fed by a Multi-level Inverter for Electric Vehicle Application. Eng. Technol. Appl. Sci. Res. 2022, 12, 8658–8666. [Google Scholar] [CrossRef]
- Yoon, K.-Y.; Lee, S.-T. Performance Improvement of Permanent-Magnet-Synchronous Motors through Rotor Shape Optimization of Marine Blowing System with High-Speed Rotation. Energies 2023, 16, 5486. [Google Scholar] [CrossRef]
- Wen, D.; Wang, W.; Zhang, Y. Sensorless Control of Permanent Magnet Synchronous Motor in Full Speed Range. Chin. J. Electr. Eng. 2022, 8, 97–107. [Google Scholar] [CrossRef]
- Chen, F.; Li, C.; Li, Z.; Du, Q.; Yin, W. Robust predictive torque control of switched reluctance motor based on linear extended state observer. Electr. Eng. 2024, 106, 7973–7984. [Google Scholar] [CrossRef]
- Dang, C.; Dou, M.; Yan, S.; Dang, M.; Wang, Y.; Zhao, D.; Hua, Z. An Improved Adaptive Sliding Mode Speed Control of PMSM Drives with an Extended State Observer. IEEE Trans. Energy Convers. 2024, 39, 2349–2361. [Google Scholar] [CrossRef]
- Dei, G.; Gupta, D.K.; Sahu, B.K.; Bajaj, M.; Blazek, V.; Prokop, L. A novel TID + IDN controller tuned with coatis optimization algorithm under deregulated hybrid power system. Sci. Rep. 2025, 15, 4838. [Google Scholar] [CrossRef]
- Akundi, S.S.; Braniff, A.; Dantas, B.; Liu, Y.; Tian, Y.; Niknezhad, S.S.; Khan, F.I.; Pistikopoulos, E.N. Chapter Eight—Advanced system control strategies for enhanced safety and efficiency of energy systems. In Methods in Chemical Process Safety; Khan, F.I., Pistikopoulos, E.N., Sajid, Z., Eds.; Elsevier: Amsterdam, The Netherlands, 2024; Volume 8, pp. 243–260. ISBN 9780443297748. [Google Scholar] [CrossRef]
- Jin, S.; Jin, W.; Wang, H.; Yu, S.; Zhang, Z. Maximum torque per ampere control of permanent magnet/reluctance hybrid rotor dual stator synchronous motor. IET Electr. Power Appl. 2024, 18, 1021–1032. [Google Scholar] [CrossRef]
- Khan, M.Y.A. A Review of Analysis and Existing Simulation Model of Three Phase Permanent Magnet Synchronous Motor Drive (PMSM). Control Syst. Optim. Lett. 2024, 2, 349–356. [Google Scholar] [CrossRef]
- Tarczewski, T.; Lisinski, H.; Grzesiak, L.M. Performance analysis of PMSM servo-drive with state feedback and hybrid position controllers. IEEE Trans. Ind. Electron. Res. 2025, 12, 100116. [Google Scholar] [CrossRef]
- Shuang, B.; Zhu, Z.-Q. Simultaneous Sensorless Rotor Position and Torque Estimation for IPMSM at Standstill and Low Speed Based on High-Frequency Square Wave Voltage Injection. IEEE Trans. Ind. Electron. 2022, 69, 8791–8802. [Google Scholar] [CrossRef]
- Rahman, S.U.; Xia, C. Rotor Speed and Position Estimation Analysis of Interior PMSM Machines in Low and Medium-High Speed Regions Adopting an Improved Flux Observer for Electric Vehicle Applications. Machines 2023, 11, 574. [Google Scholar] [CrossRef]
- Aminzadeh, A.; Sattarpanah Karganroudi, S.; Majidi, S.; Dabompre, C.; Azaiez, K.; Mitride, C.; Sénéchal, E. A Machine Learning Implementation to Predictive Maintenance and Monitoring of Industrial Compressors. Sensors 2025, 25, 1006. [Google Scholar] [CrossRef] [PubMed]
- Shokrani, A.; Dogan, H.; Burian, D.; Nwabueze, T.D.; Kolar, P.; Liao, Z.; Sadek, A.; Teti, R.; Wang, P.; Pavel, R.; et al. Sensors for in-process and on-machine monitoring of machining operations. CIRP J. Manuf. Sci. Technol. 2024, 51, 263–292. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Q.; Li, K. Fault-Tolerant Control of PMSM Drives Under Sensor Failures for Aerospace Applications. IEEE Trans. Transp. Electrif. 2022, 8, 2055–2067. [Google Scholar]
- Beheshti Asl, M.; Fofana, I.; Meghnefi, F. Review of Various Sensor Technologies in Monitoring the Condition of Power Transformers. Energies 2024, 17, 3533. [Google Scholar] [CrossRef]
- Yue, W.; Guo, Y.; Lee, J.; Ganbold, E.; Wu, J.-K.; Li, Y.; Wang, C.; Kim, H.S.; Shin, Y.-K.; Liang, J.-G.; et al. Advancements in Passive Wireless Sensing Systems in Monitoring Harsh Environment and Healthcare Applications. Nano-Micro Lett. 2025, 17, 106. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Chen, F. Sensorless Control of PMSM Based on an Improved Super-Twisting Sliding Mode Observer. J. Electrotechnol. Electr. Eng. Manag. 2025, 8, 45–54. [Google Scholar] [CrossRef]
- Sumika, C.; Govind, V.; Radoslaw, Z. Analysing Recent Breakthroughs in Fault Diagnosis through Sensor: A Comprehensive Overview. Comput. Model. Eng. Sci. 2024, 141, 1983–2020. [Google Scholar] [CrossRef]
- Huang, Y.; Su, Z.; Chang, D.; Sun, Y.; Tan, J. Error Analysis of an Economical On-Site Calibration System for Linear Optical Encoders. Metrology 2024, 4, 131–140. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, X.; Liu, X.; Su, H. Adaptive Robust Sensorless Control for PMSM Based on Improved Back EMF Observer and Extended State Observer. IEEE Trans. Ind. Electron. 2024, 71, 16635–16643. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Z.; Wang, W.; Lv, Y.; Yuan, B.; Wang, S.; Li, W.; Li, Q.; Zhang, Q.; Chen, Q. SMO-Based Sensorless Control of a Permanent Magnet Synchronous Motor. Front. Energy Res. 2022, 10, 839329. [Google Scholar] [CrossRef]
- Ran, Y.; Qiao, M.; Sun, L.; Xia, Y. Review of Position Sensorless Control Technology for Permanent Magnet Synchronous Motors. Energies 2025, 18, 2302. [Google Scholar] [CrossRef]
- Ferdiansyah, I.; Hanamoto, T. An Improved Extraction Scheme for High-Frequency Injection in the Realization of Effective Sensorless PMSM Control. World Electr. Veh. J. 2025, 16, 326. [Google Scholar] [CrossRef]
- Cao, X.; Ye, Y.; Duan, Y.; Wu, Y.; Yang, X. Sensorless control of permanent magnet synchronous motor based on adaptive back-EMF observer. Adv. Mech. Eng. 2023, 15, 168781322311516. [Google Scholar] [CrossRef]
- Yao, G.; Yang, Z.; Han, S.; Wang, Z. Full-speed domain position sensorless control strategy for PMSM based on a novel phase-locked loop. Control Eng. Pract. 2024, 152, 106058. [Google Scholar] [CrossRef]
- Xu, Y.; Lin, C.; Xing, J.; Zhang, H.; Zhuang, X. Robustness Enhancement of Position Sensorless Super-High-Speed Pmsm for Hydrogen Fuel Cell Air Compressors Based on Linear Extended State Observer. Appl. Energy 2025, 400, 126560. [Google Scholar] [CrossRef]
- Rahman, S.U.; Xia, C.; Shah, S.H.; Abubakar, U.; Hassan, M.U. Improving the Low-Speed Operation Performance of IPMSM Sensorless Vector Control with ADRC DC-Offset Compensation Loop. Eng. Proc. 2023, 46, 17. [Google Scholar] [CrossRef]
- Xu, S.; Shen, A.; Zhang, M.; Tang, Q.; Luo, X.; Xu, J. Dual-Sliding-Mode-Observer-Based IPMSM Sensorless Control Technique. Complexity 2024, 2024, 5512231. [Google Scholar] [CrossRef]
- Wei, X.; Mei, K.; Ding, S.; Jiang, L. Sensorless control of permanent magnet synchronous motor based on fixed-time terminal sliding mode observer. Asian J. Control 2024, 26, 1771–1786. [Google Scholar] [CrossRef]





| Name of the Parameter | Parameter Value |
|---|---|
| Stator Resistance (Rs) | 0.00031 Ω |
| Stator Inductance (Ls) | 0.445 mH |
| Permanent Magnet Flux Linkage (ψf) | 0.00954 Wb |
| Sampling Time (Ts) | 0.0001 ns |
| Viscous Damping Coefficient (B) | 0.000213 N·m·s/rad |
| Simulation Step Size | 5 × 10−7 ns |
| Rotor Moment of Inertia (J) | 2.8 × 10−7 kg·m2 |
| Number of poles (Pn) | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sohel, R.M.; Wu, W.; Ji, R.; Fang, Z.; Liu, K. Sliding Mode Observer-Based Sensorless Control Strategy for PMSM Drives in Air Compressor Applications. Appl. Sci. 2025, 15, 11206. https://doi.org/10.3390/app152011206
Sohel RM, Wu W, Ji R, Fang Z, Liu K. Sliding Mode Observer-Based Sensorless Control Strategy for PMSM Drives in Air Compressor Applications. Applied Sciences. 2025; 15(20):11206. https://doi.org/10.3390/app152011206
Chicago/Turabian StyleSohel, Rana Md, Wenhao Wu, Renzi Ji, Zihao Fang, and Kai Liu. 2025. "Sliding Mode Observer-Based Sensorless Control Strategy for PMSM Drives in Air Compressor Applications" Applied Sciences 15, no. 20: 11206. https://doi.org/10.3390/app152011206
APA StyleSohel, R. M., Wu, W., Ji, R., Fang, Z., & Liu, K. (2025). Sliding Mode Observer-Based Sensorless Control Strategy for PMSM Drives in Air Compressor Applications. Applied Sciences, 15(20), 11206. https://doi.org/10.3390/app152011206








