Application of FEM Analyses and Neural Networks Approach in Multi-Stage Optimisation of Notched Steel Structures Subjected to Fatigue Loadings
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Procedures
2.2. Finite Element Analyses
2.2.1. Ansys APDL Approaches
- Simple search method (SSM) with a gradual narrowing of the search area, Ansys APDL;
- Ansys parametric optimisation (APO), Ansys APDL;
- Goal-driven optimisation (GDO), Ansys Workbench.
- Plate width W = 45 mm;
- Semi-axis of the elliptical hole perpendicular to tensile loading direction—a = 0.167/W = 7.5 mm;
- Second semi-axis of elliptical hole—b = 1.5a = 0.25/W = 11.25 mm.
- Maximum number of iterations—30;
- Maximum number of consecutive infeasible solutions—7.
- Maximum number of iterations—10;
- Limit of design variable changes for the design space at each iteration—100%;
- Forward difference applied to the design variable range that was used to compute the gradient—0.2%.
2.2.2. Ansys Workbench Model
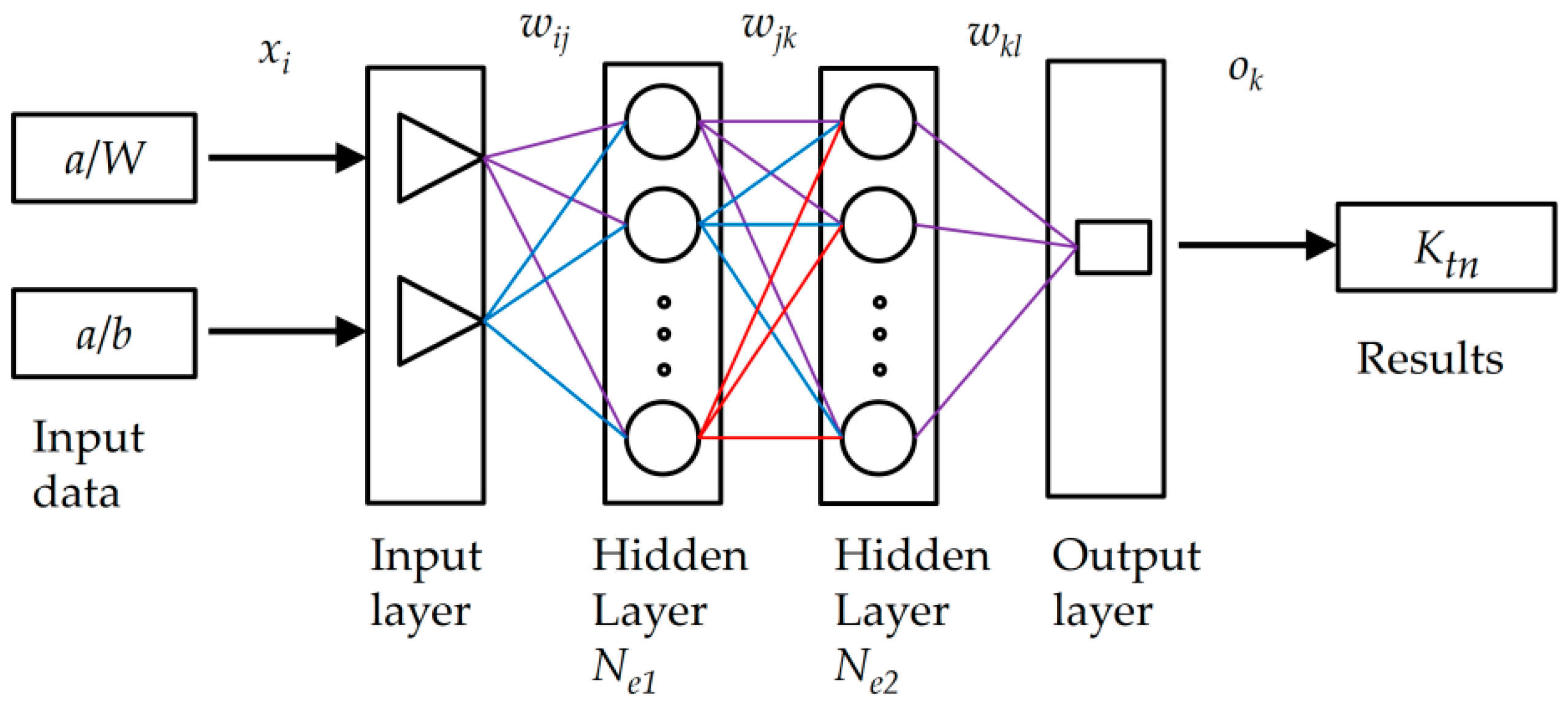
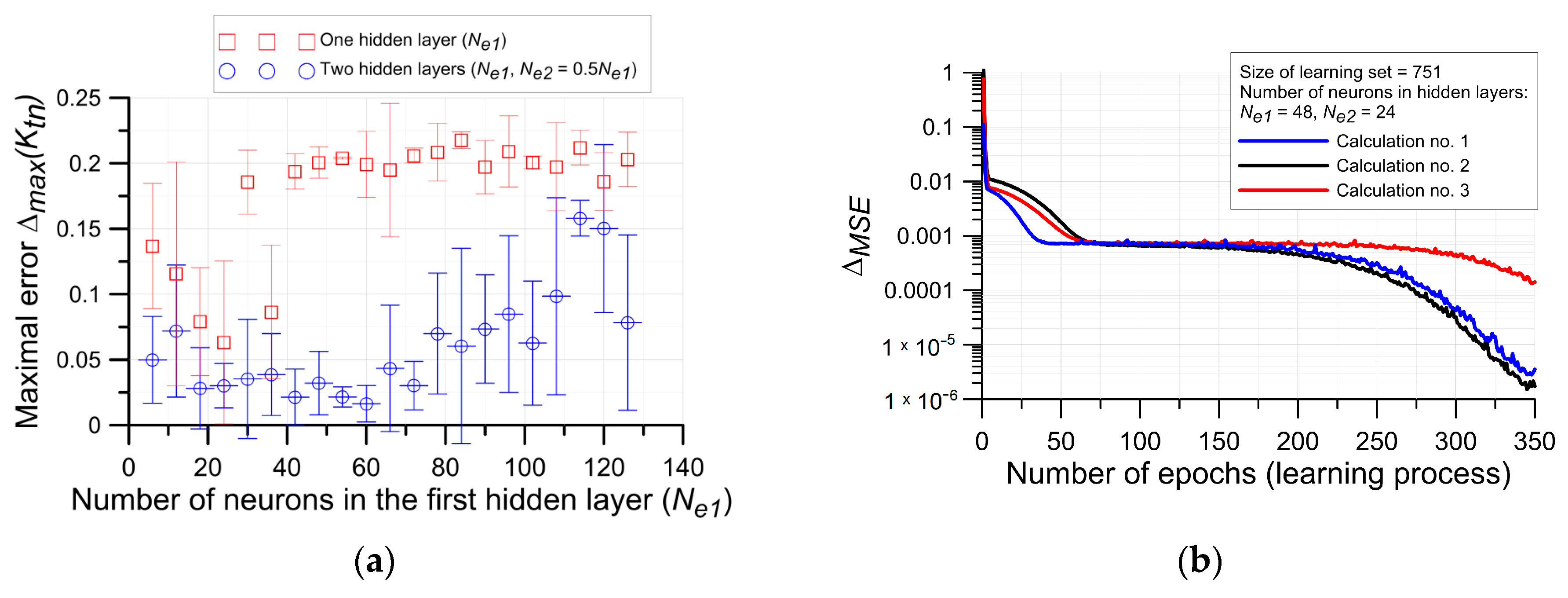
2.3. Neural Network
Error Estimation
3. Results of FEM Optimisation
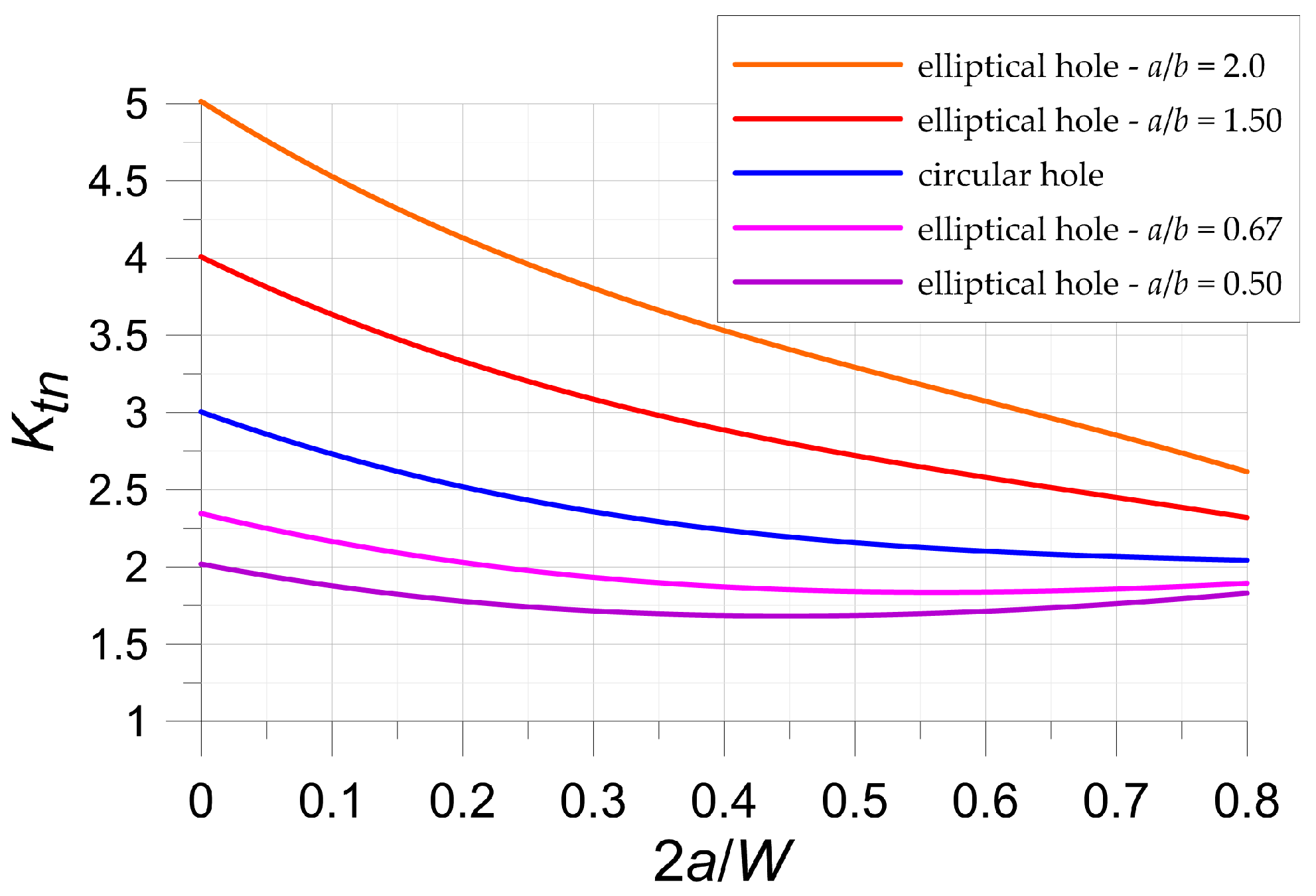
3.1. Stress Concentration Around Circular and Elliptical Holes—Theoretical Study
3.2. Simple Search Optimisation Method
3.3. Parametric Optimisation Results
3.4. Results of GDO Optimisation Process (Ansys Workbench)
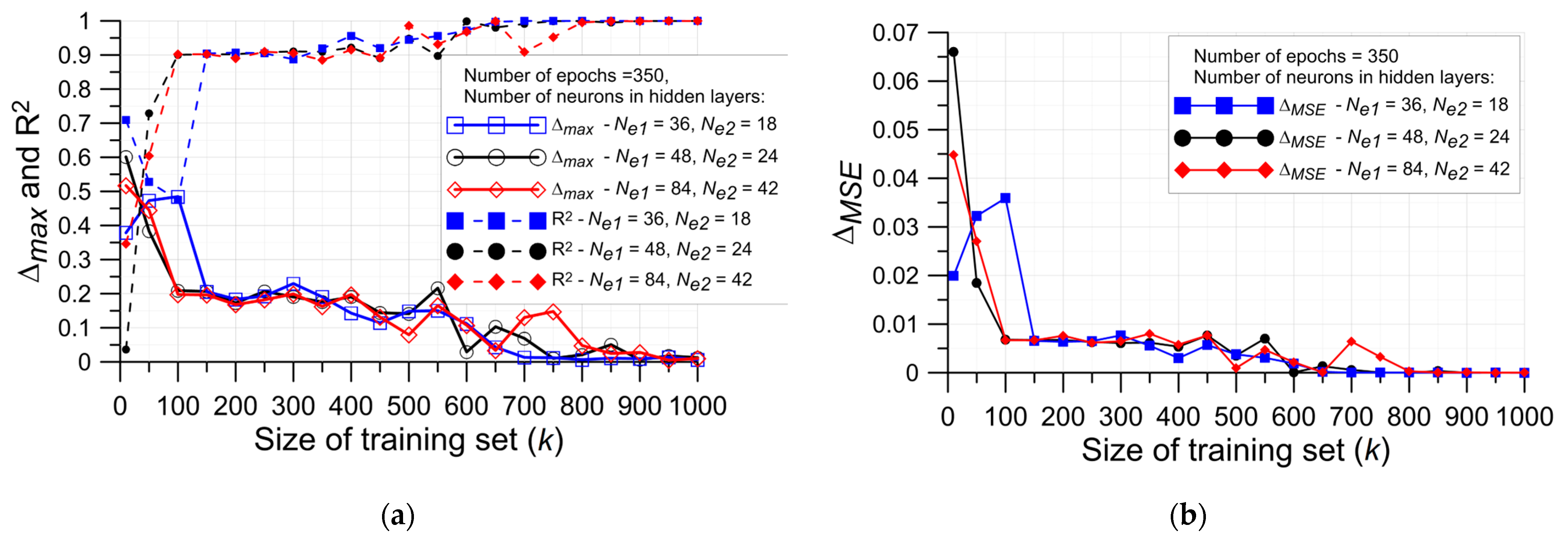
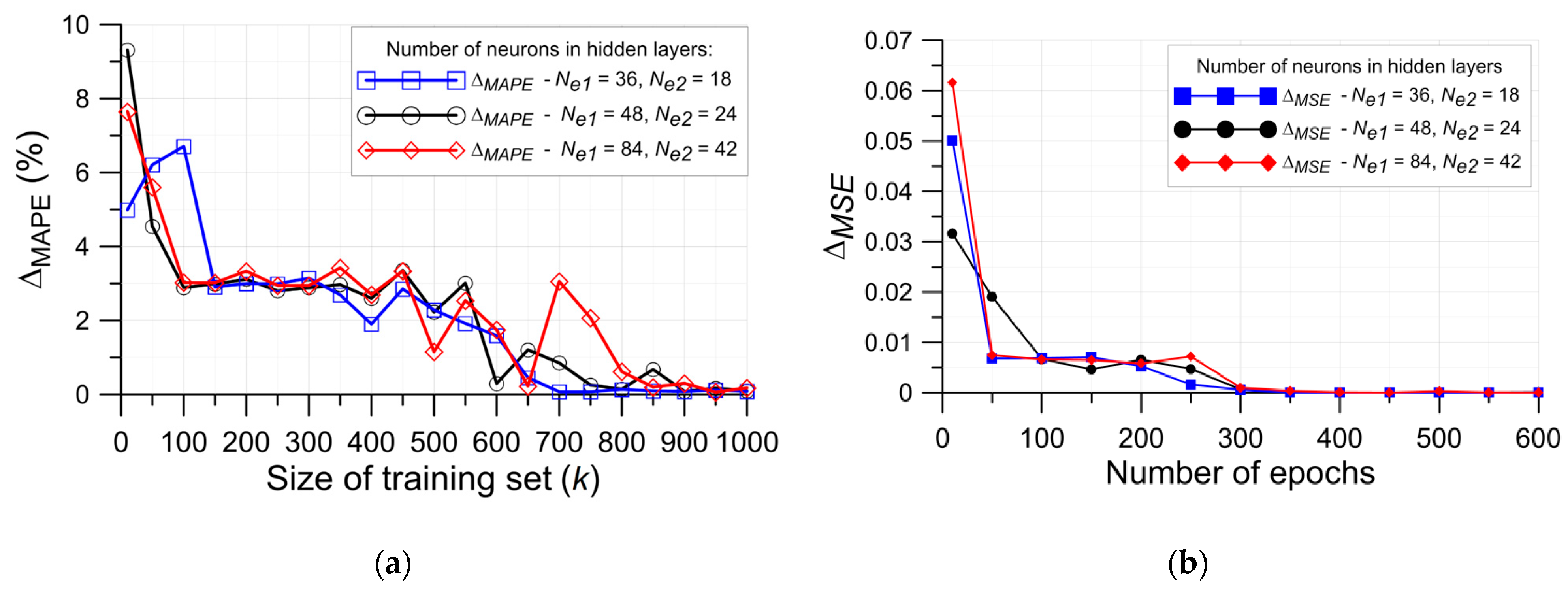
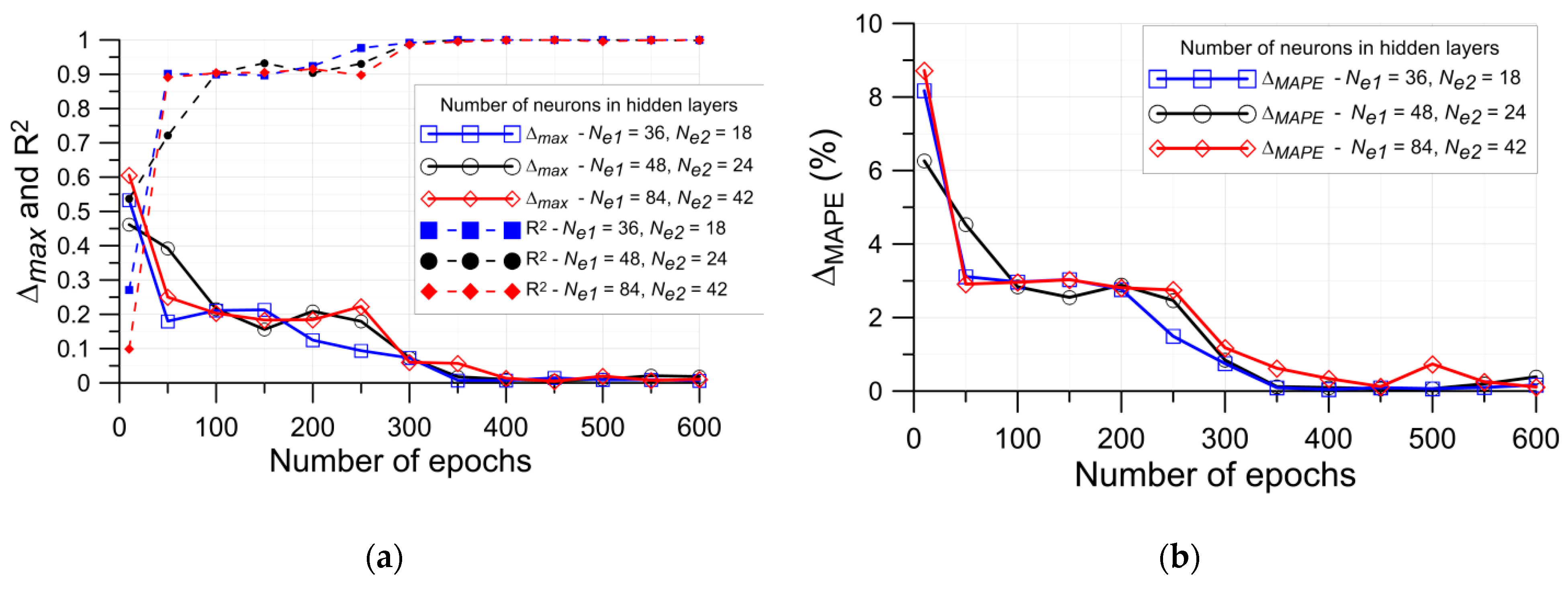
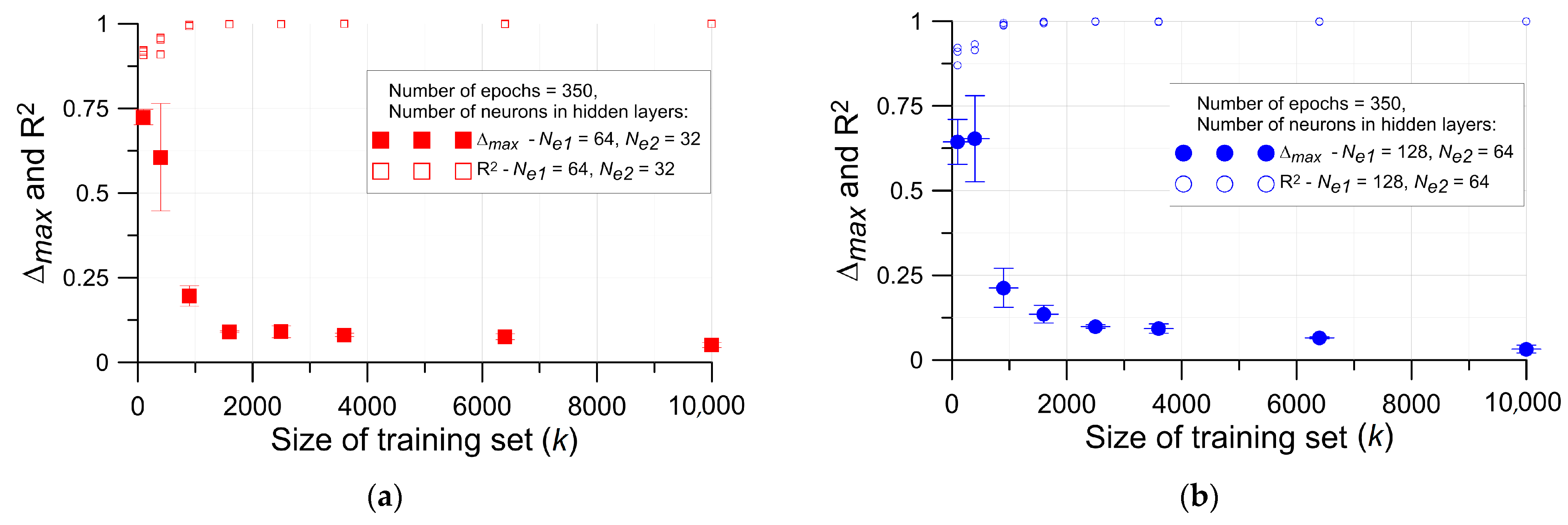
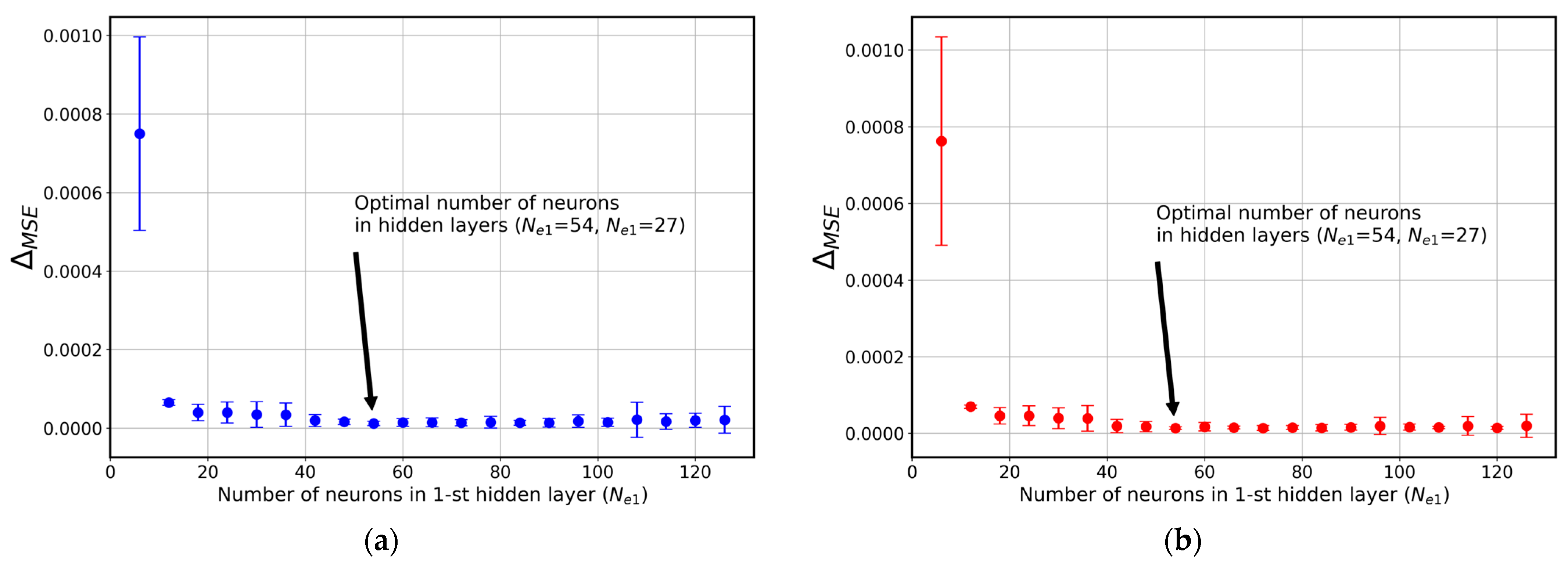
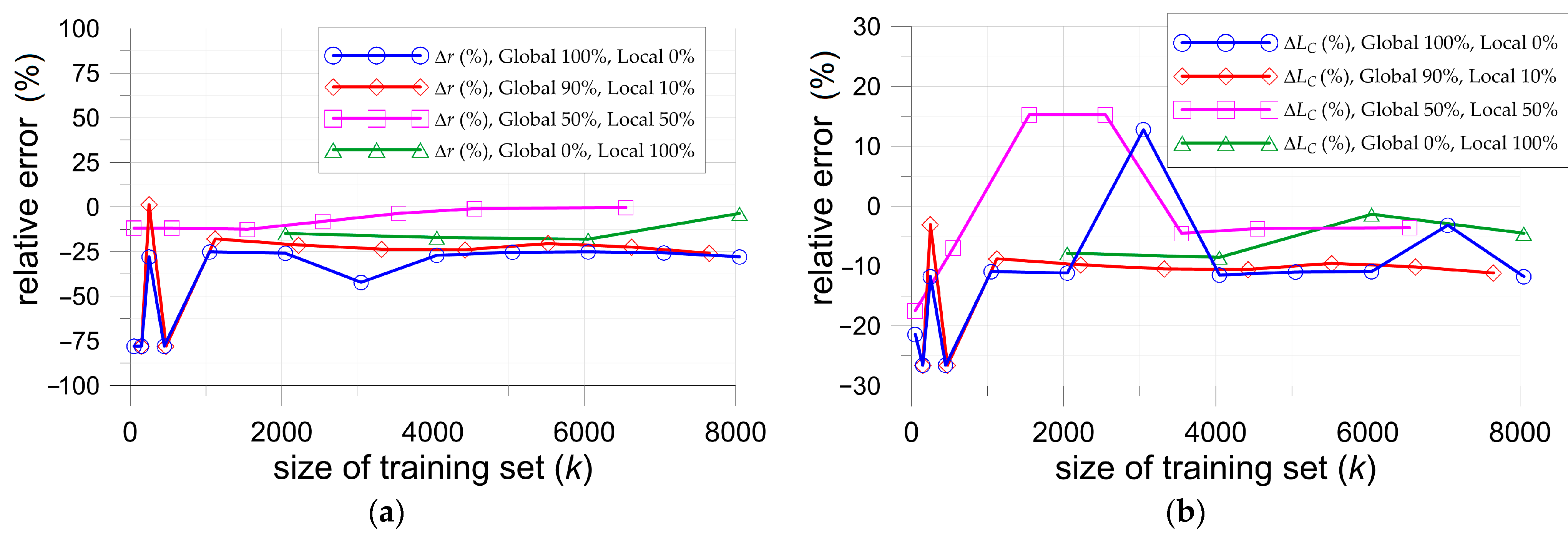
4. Results of Neural Network Approach
4.1. Specimen with Single Circular Opening
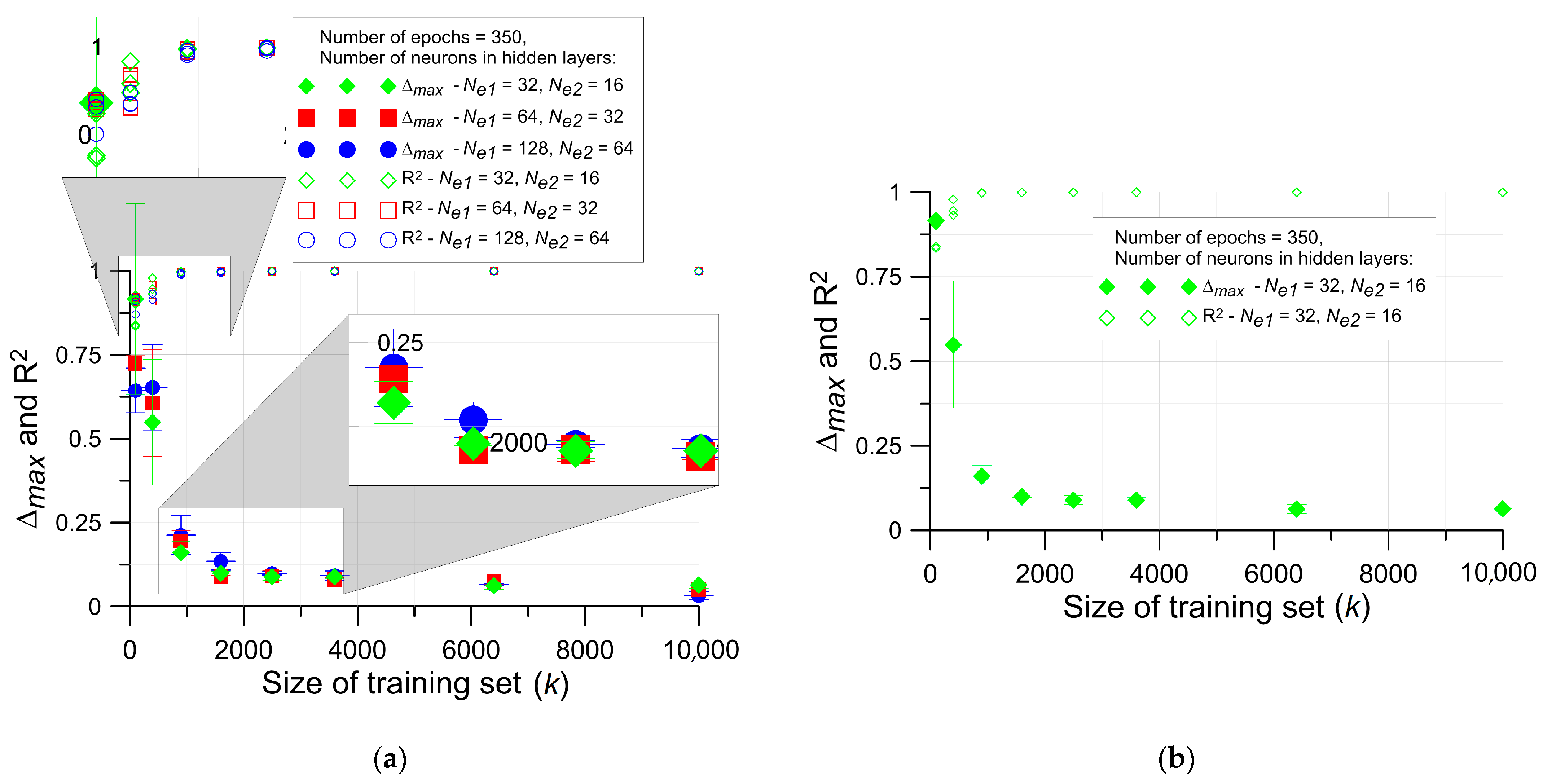
4.2. Specimen with Single Elliptical Opening
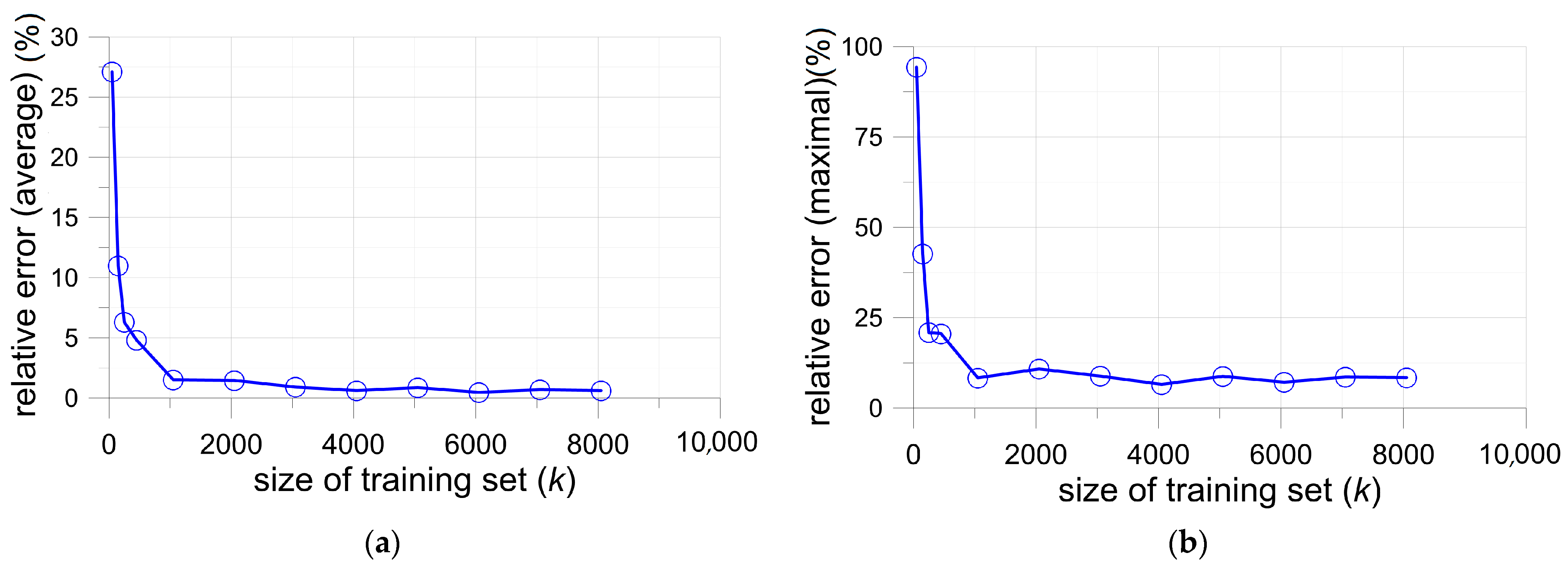
- for (Ne1 = 128, Ne2 = 64)—k ≥ 2500,
- for (Ne1 = 64, Ne2 = 32)—k ≥ 1600,
- for (Ne1 = 32, Ne2 = 16)—k ≥ 1600.
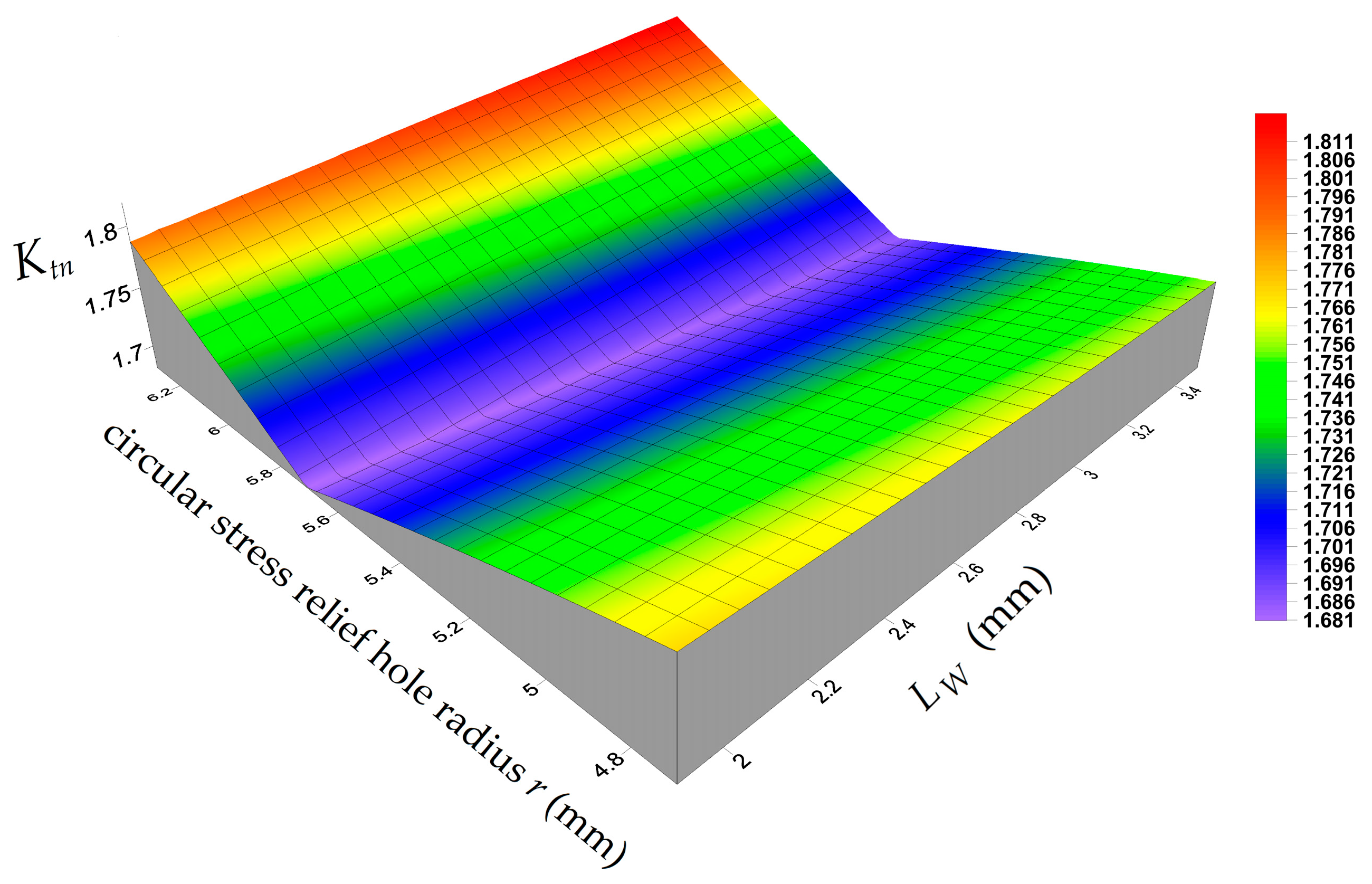
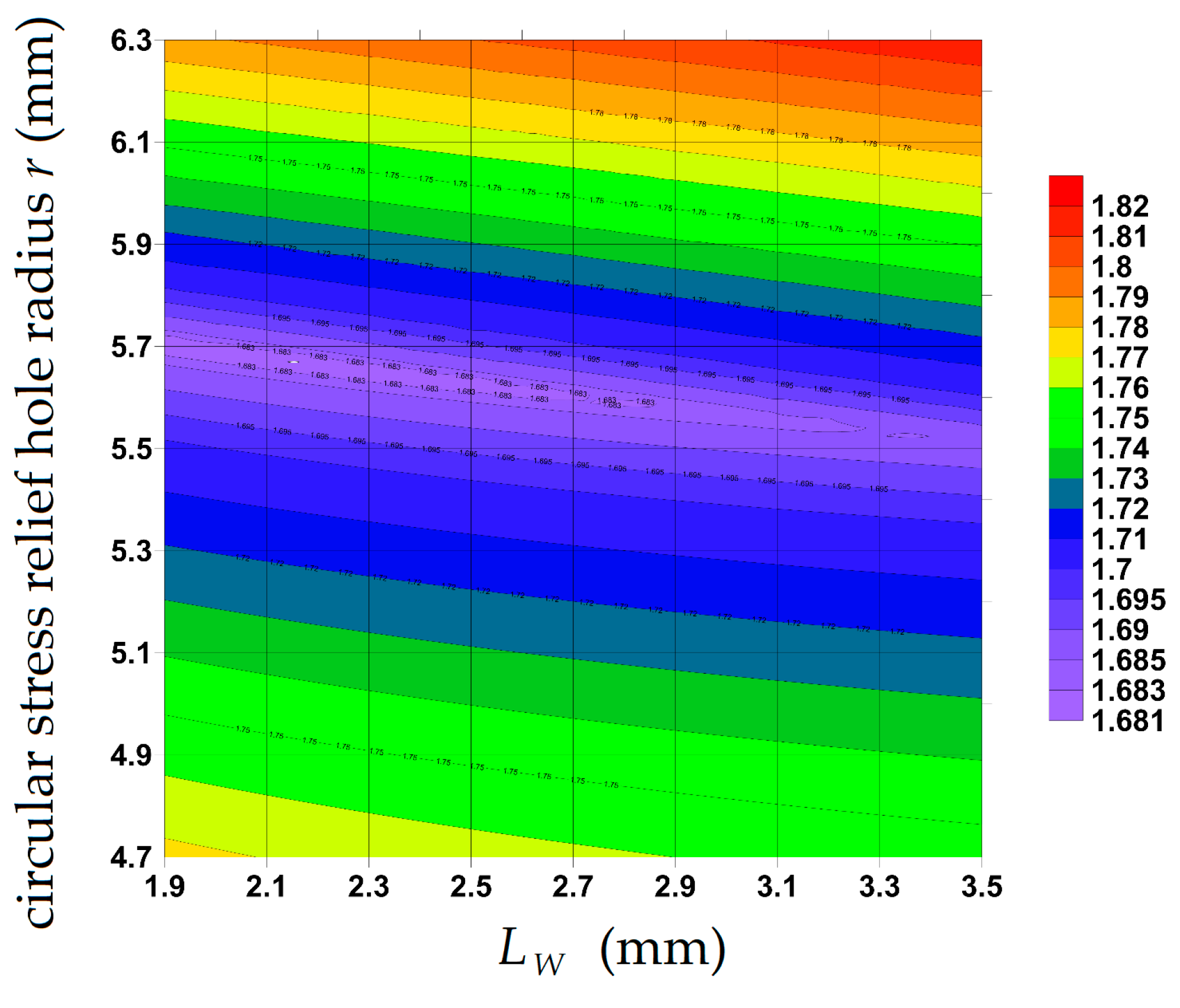
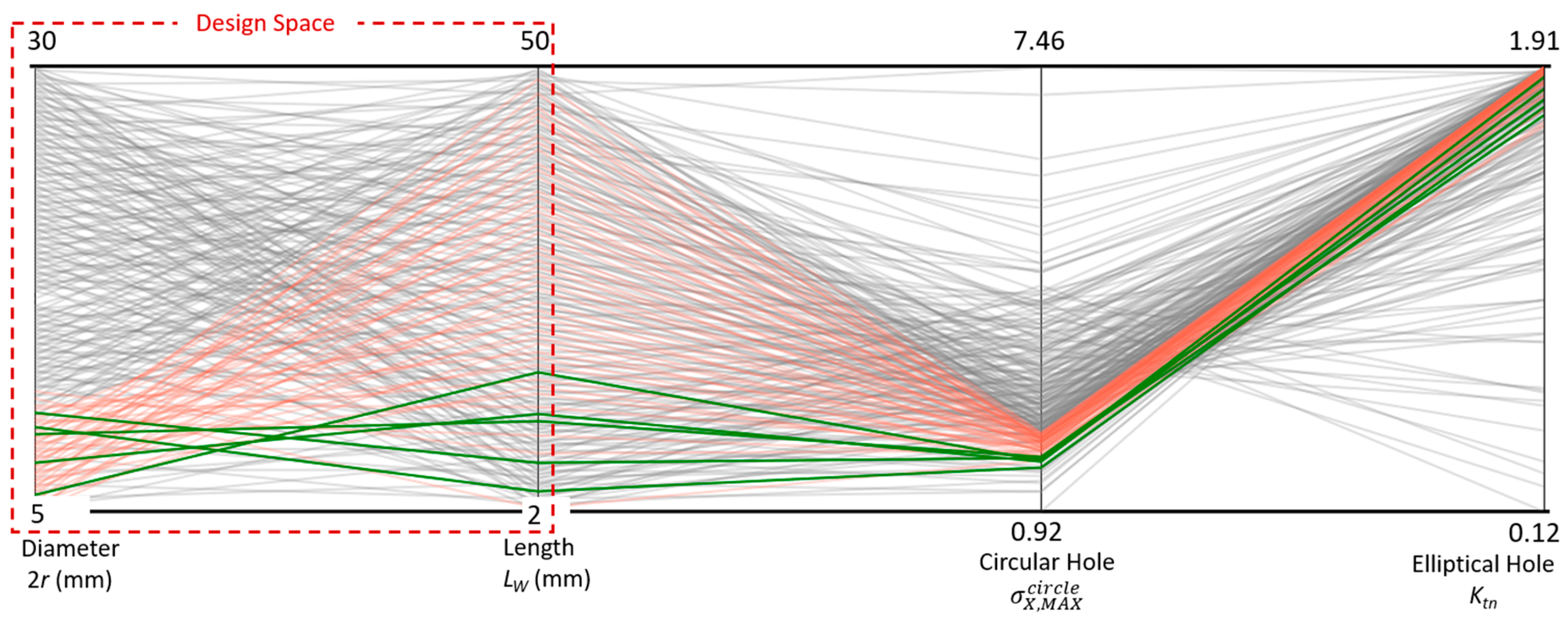
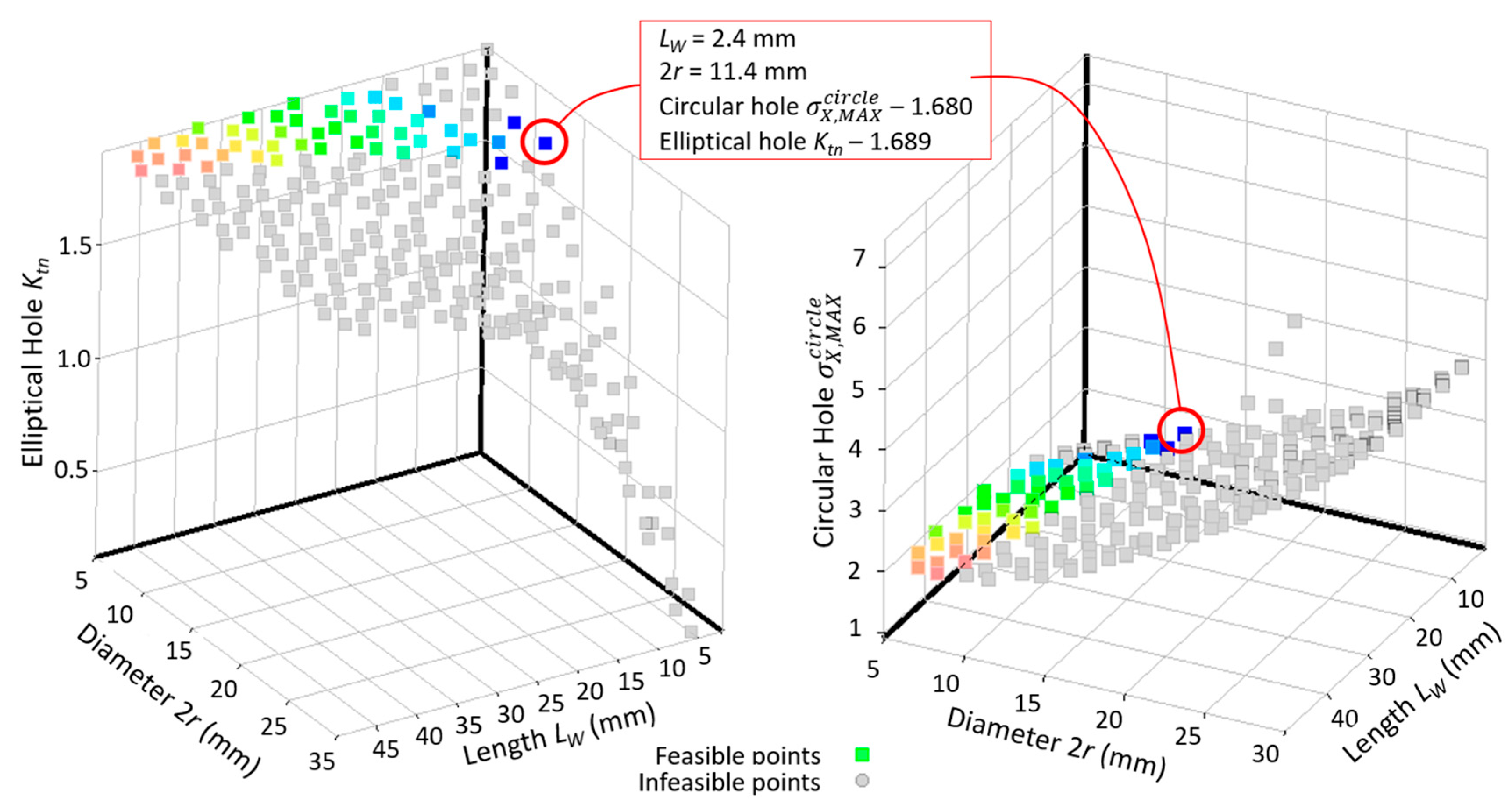
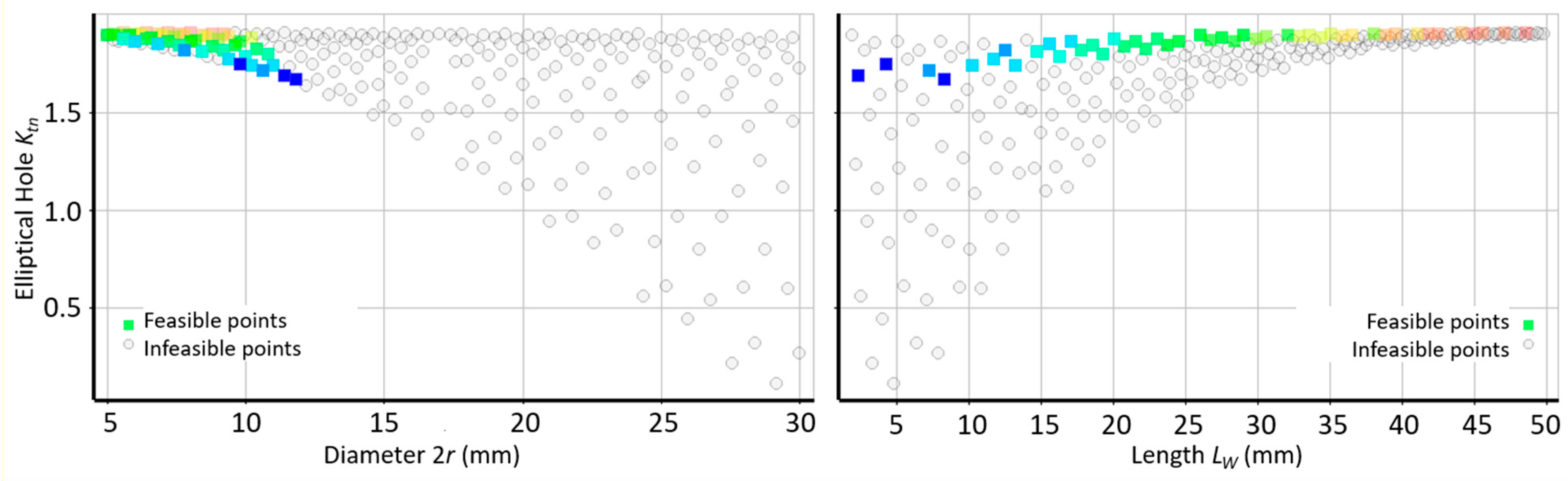
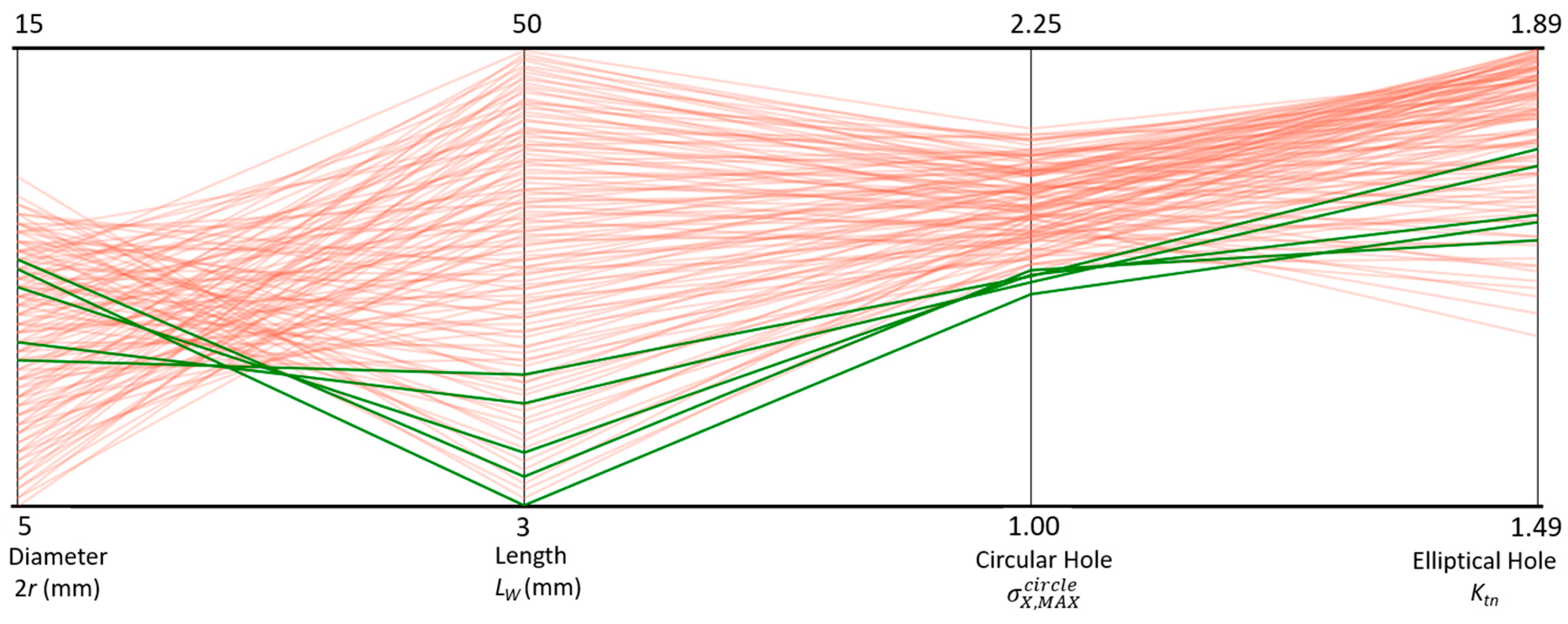
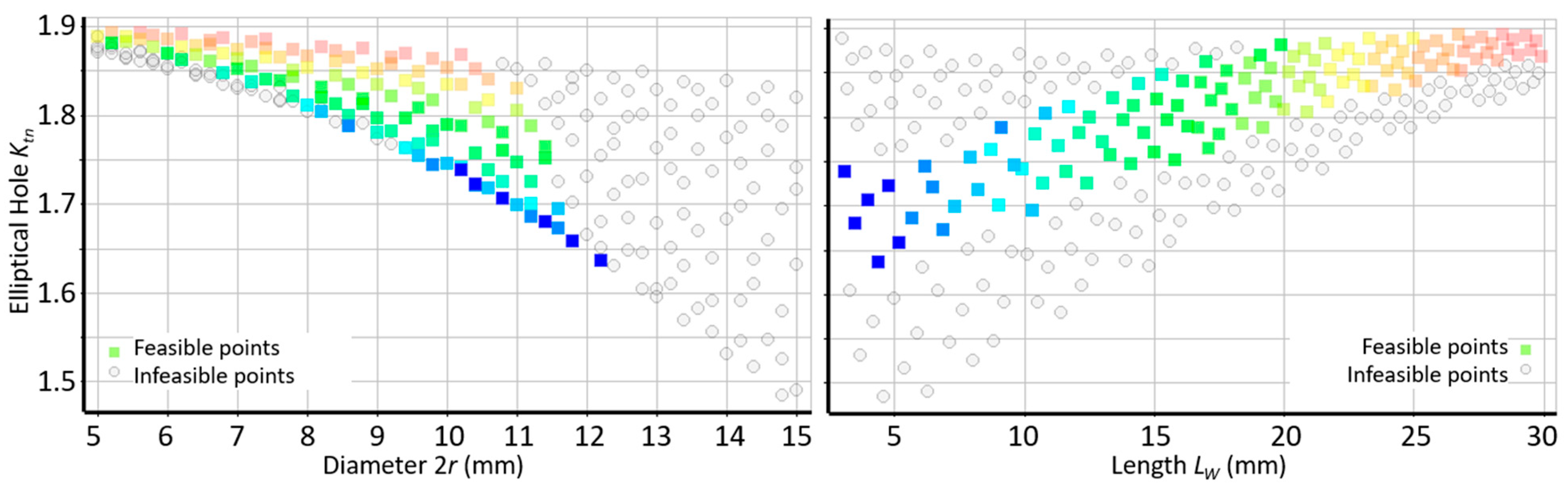
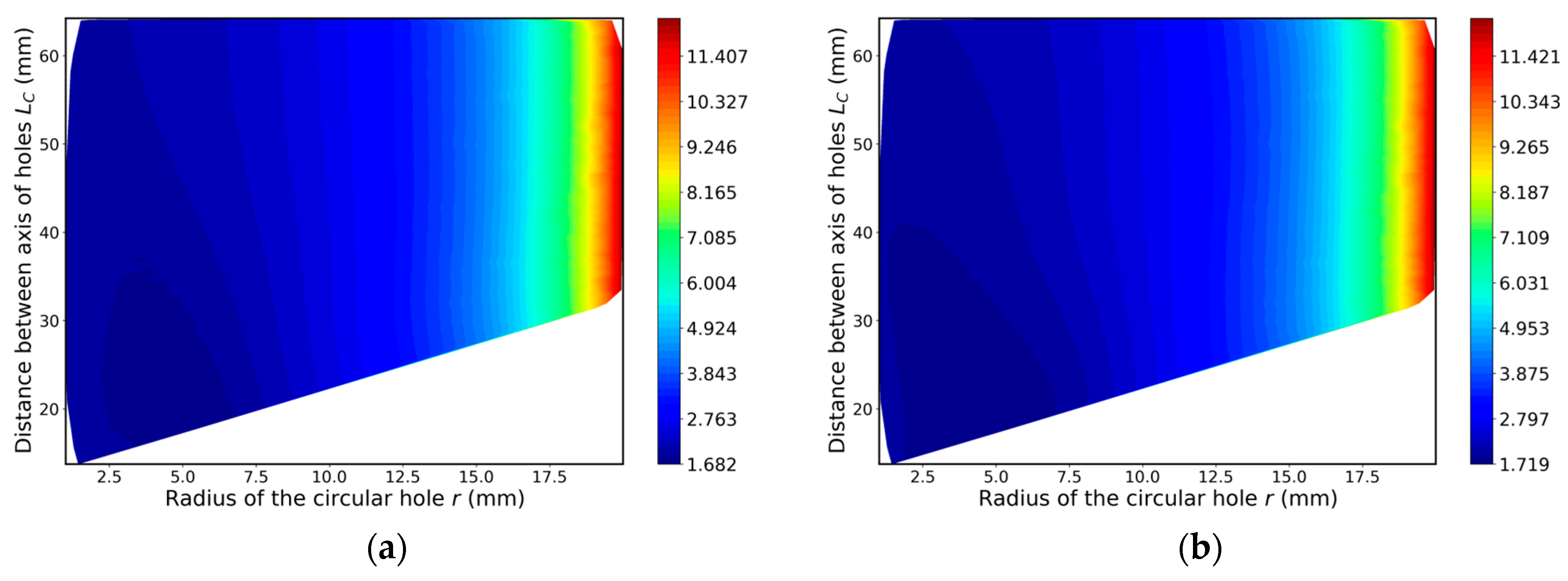
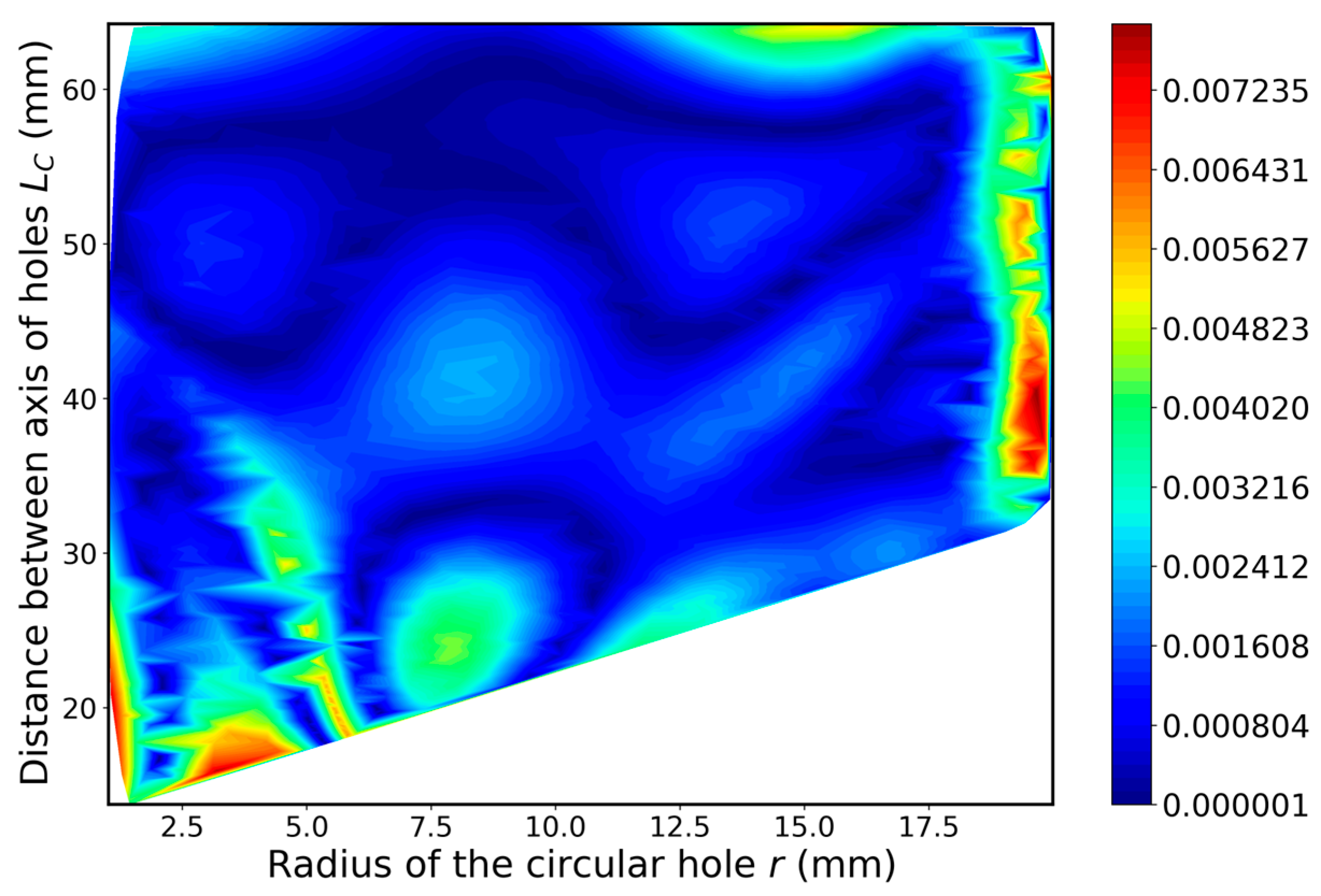
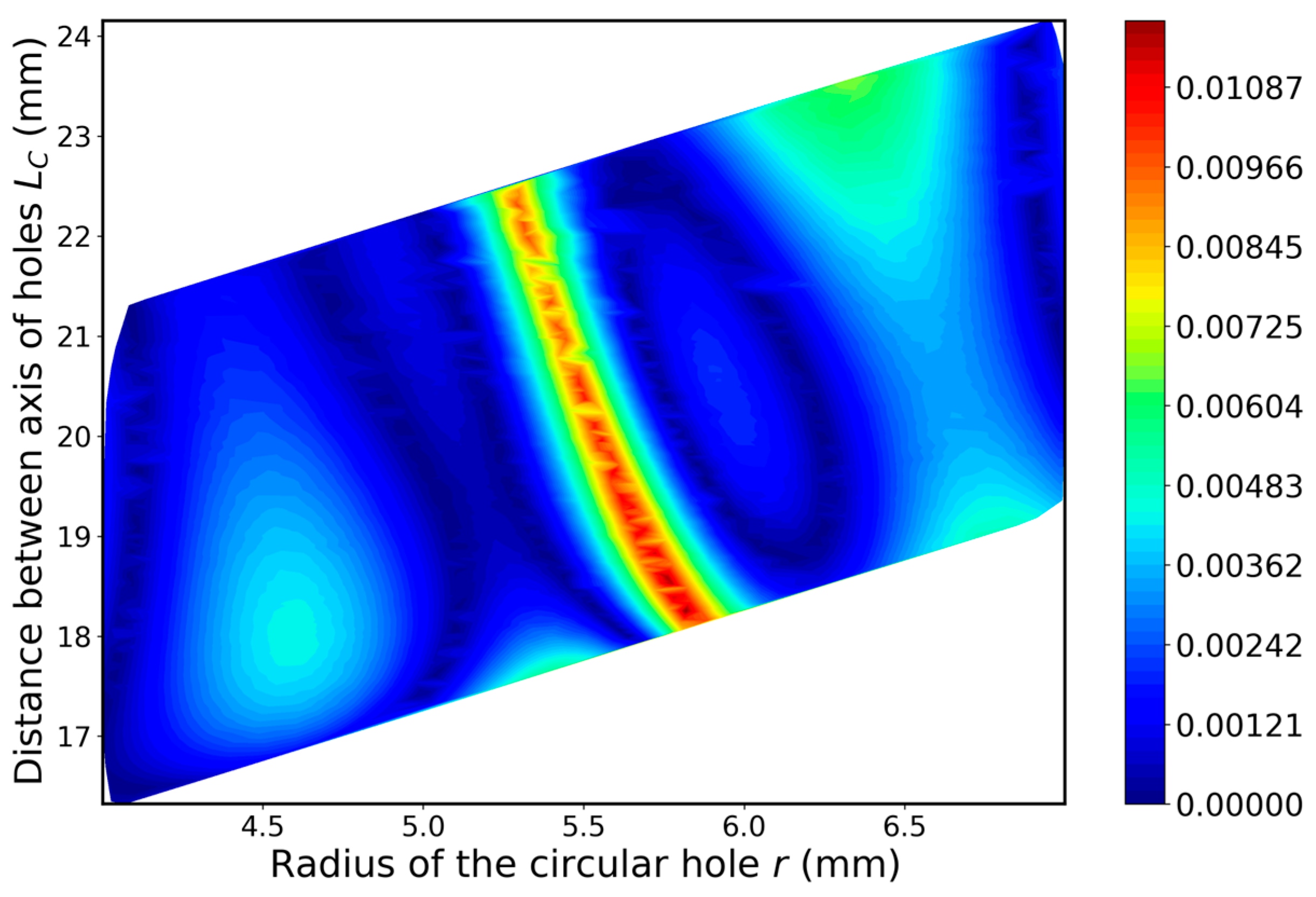
4.3. Determination of Optimal Configuration of Stress Relief Holes and Maximal Ktn Value
4.3.1. Sub–Variant 1: Extended Feasible Range of the Input Parameters
4.3.2. Sub-Variant 2: Narrowed Feasible Range of the Input Parameters
5. Experimental Results of Fatigue Tests and FEM Analyses of Notched Specimens Reinforced by Composite Overlays
6. Discussion
- Error of radius r determination: –15.6%;
- Error of stress relief hole position LC: –9.5%.
7. Conclusions
- (1)
- The cutting of additional circular stress relief holes reduces the stress concentration around the elliptical opening by about 12% and leads to an increase in fatigue life by about 79% for the applied material.
- (2)
- The use of composite overlays additionally decreases Ktn in relation to specimens with stress relief holes by about 6%. This should also increase the fatigue life.
- (3)
- In the investigated case, in which the radius and position of stress relief holes are assumed as decision variables, the shape of the objective function (Ktn) does not have a clear absolute optimum and has the shape of a narrow strip in which only slight differences in the value of Ktn appear.
- (4)
- All methods ensured the achievement of an optimal solution. Differences between the applied methods occurred in terms of the time spent on model preparation and calculations.
- (5)
- The application of ANN serving as a surrogate model requires the preparation of a large set of training data; however, once learned, it allows for performing calculations in a short time with high accuracy.
- (6)
- As shown in the FEM analyses, it is possible to find the optimal or quasi-optimal configuration, but the solution is time-consuming. The alternative in this case seems to be the use of the ANN approach. Such an approach is particularly suitable when the optimisation analyses must be repeated for different sets of geometrical parameters or boundary conditions. It is enough to apply only one ANN learning procedure (which is the most time-consuming), and after that, the solution can be obtained in a relatively short time.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| mean absolute error | |
| mean absolute percentage error | |
| maximal difference between true and predicted data | |
| mean squared error | |
| error of radius r determination | |
| error of stress relief hole position (LC) | |
| maximal stress in the notch | |
| σnom | nominal stress in the weakened cross-section |
| maximal σx stress around circular hole | |
| σx | stress in x-direction |
| ν | Poisson’s ratio |
| a – | semi-axis of the elliptical hole perpendicular to tensile loading |
| b | semi-axis of elliptical hole parallel to tensile loading |
| coefficients | |
| d | diameter of circular hole |
| E | Young’s modulus |
| Eadh | adhesive stiffness |
| F | tension force |
| k | number of input data (size of training set) |
| Ktn | stress concentration factor |
| LC | distance between the axes of circular and elliptical openings |
| LW | smallest thickness between an elliptical and circular hole |
| Nei | number of neurons in the i-th hidden layer |
| Nf,avg | average fatigue life |
| R | stress ratio |
| R | radius of circular hole |
| amount of variability in the data accounted by the regression model | |
| t | thickness |
| W | plate width |
| i-th output (predicted) data | |
| mean value of predicted values | |
| i-th input data |
Abbreviations
| SCF | Stress Concentration Factor |
| FEM | Finite Element Method |
| ANN | Artificial Neural Network |
| DIC | Digital Image Correlation |
| APDL | Ansys Parametric Design Language |
| SSM | Simple Search Method |
| APO | Ansys Parametric Optimisation |
| ZOOM | Zero-Order Optimisation Method |
| FOOM | First-Order Optimisation Method |
| GDO | Goal-Driven Optimisation |
| LF | Loss Function |
| MSE | Mean Square Error |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
References
- Kirsch, E.G. Die Theorie der Elastizitat und die Bedurfnisse der Festigkeitslehre. Z. Des Vereines Dtsch. Ingenieure 1898, 42, 797–807. [Google Scholar]
- Inglis, C.E. Stress in a plane due to the presence of cracks and sharp corners. Trans. Inst. Nav. Arch. 1913, 55, 219–230. [Google Scholar]
- Pilkey, W.D.; Pilkey, D.F. Peterson’s Stress Concentration Factors; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Young, W.C.; Budynas, R.G. Roark’s Formulas for Stress and Strain; McGraw-Hill Book Company Inc.: New York, NY, USA, 2002. [Google Scholar]
- Ozkan, M.T.; Toktas, I. Determination of the stress concentration factor in rectangular plate with a hole under tensile stress using different methods. Fract. Mech. Model. 2016, 58, 839–847. [Google Scholar] [CrossRef]
- Zheng, Y.; Chang-Boo, K.; Chonhdu, C.; Hyeon, G.B. The concentration of stress and strain in a finite-thickness elastic plate containing a circular hole. Int. J. Solids Struct. 2008, 45, 713–731. [Google Scholar] [CrossRef]
- Toubal, L.; Karama, M.; Lorrain, B. Stress concentration in a circular hole in a composite plate. Comp. Struct. 2005, 68, 31–36. [Google Scholar] [CrossRef]
- Khechai, A.; Tati, A.; Guettala, A. Finite element analysis of stress concentrations and failure criteria in composite plates with circular holes. Front. Mech. Eng. 2014, 9, 281–294. [Google Scholar] [CrossRef]
- Zhong, H.; Brett, A.; Fereidoon, D. Stress concentration in laminated composites with an elliptical hole under uniaxial load. In Proceedings of the IMECE: 2004 ASME International Mechanical Engineering Congress, Anaheim, CA, USA, 13–19 November 2004; pp. 1–6. [Google Scholar] [CrossRef]
- Khechai, A.; Tati, A.; Ouejdi-Belarbi, M.; Guettala, A. Numerical analysis of stress concentration in isotropic and laminated plates with inclined elliptical holes. J. Inst. Eng. India Ser. C 2019, 100, 511–522. [Google Scholar] [CrossRef]
- Jafari, M.; Ardalani, E. Stress concentration in finite metallic plates with regular holes. Int. J. Mech. Sci. 2016, 106, 220–230. [Google Scholar] [CrossRef]
- Rezaeepazhand, J.; Jafari, M. Stress concentration in metallic plates with special-shaped cut-out. Int. J. Mech. Sci. 2010, 52, 96–102. [Google Scholar] [CrossRef]
- Romanowicz, P.J.; Szybiński, B.; Wygoda, M. Fatigue performance of open-hole structural elements reinforced by CFRP overlays. Int. J. Adhes. Adhes. 2024, 130, 103606. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Zhang, T.; Li, X.; Wang, Q.Y.; Huang, W.; Shen, M. Characterization of the effect of CFRP reinforcement on the fatigue strength of aluminum alloy plates with fastener holes. Eng. Struct. 2018, 177, 739–752. [Google Scholar] [CrossRef]
- Romanowicz, P.J.; Szybiński, B.; Wygoda, M. Static and Fatigue Behaviour of Double-Lap Adhesive Joints and Notched Metal Samples Reinforced by Composite Overlays. Materials 2022, 15, 3233. [Google Scholar] [CrossRef] [PubMed]
- Romanowicz, P.J.; Szybiński, B.; Wygoda, M. Preliminary Experimental and Numerical Study of Metal Element with Notches Reinforced by Composite Materials. J. Compos. Sci. 2021, 5, 134. [Google Scholar] [CrossRef]
- Ribeiro, J.P.A.; Gomes, L.F.F.; Tavares, S.M.O. Artificial neural networks applied in mechanical structural design. Comput. Methods Biomech. Biomed. Eng. 2021, 1, 14–21. [Google Scholar] [CrossRef]
- Eren, M.; Toktas, I.; Ozkan, M.T. Modelling of stress concentration factor using artificial neural networks for a flat tension bar with opposite V-shaped notches. J. Polytech. 2023, 26, 1199–1205. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Okuda, H. Prediction of stress concentration at fillets using a neural network for efficient finite element analysis. Mech. Eng. Lett. 2020, 6, 20-00318. [Google Scholar] [CrossRef]
- Zhao, J.; Xiao, L.; Wei, X.; Li, X. Parametric study and neural network-based prediction for stress concentration factor of concreto-filled steel tubular T-joint. Ocean Eng. 2024, 305, 117972. [Google Scholar] [CrossRef]
- Hou, J.; Zhao, M.; Chen, Y.; Li, Q.; Wang, C. Prediction of mechanical property of open-hole composite laminates using generalized regression neural network method. Acta Mech. 2024, 235, 7553–7568. [Google Scholar] [CrossRef]
- Fan, H.T.; Wang, H. Predicting the open-hole tensile strength of composite plates based on Probabilistic Neural Network. Appl. Compos. Mater. 2014, 21, 827–840. [Google Scholar] [CrossRef]
- Rezasefat, M.; Hogan, J.D. A finite element-convolutional neural network model (FE-CNN) for stress field analysis around an arbitrary inclusion. Mech. Learn. Sci. Technol. 2023, 4, 045052. [Google Scholar] [CrossRef]
- Zhang, K.; Ma, L.; Song, Z.; Gao, H.; Zhou, W.; Liu, J.; Tao, R. Strength prediction and progressive damage analysis of carbon fiber reinforced polymer-laminate with circular holes by an efficient Artificial Neural Network. Compos. Struct. 2022, 296, 115835. [Google Scholar] [CrossRef]
- Marković, E.; Marohnić, T.; Basan, R. A surrogate artificial neural network model for estimating the fatigue life of steel components based on finite element simulations. Materials 2025, 18, 2756. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhu, Z.; Sha, A.; Hao, W. Low-cycle fatigue life prediction of titanium alloy using genetic algorithm-optimized BP artificial neural network. Int. J. Fatigue 2023, 172, 107609. [Google Scholar] [CrossRef]
- Soyer, M.S.; Tuzun, N.; Karakas, O.; Berto, F. An investigation of artificial neural network structure and its effects on the estimation of low-cycle fatigue parameters of various steels. Fatigue Fract. Eng. Mater Struct. 2023, 46, 2929–2948. [Google Scholar] [CrossRef]
- Pujol, J.C.F.; Pinto, J.M.A. A neural network approach to fatigue life prediction. Int. J. Fatigue 2011, 33, 313–322. [Google Scholar] [CrossRef]
- Gbagba, S.; Maccioni, L.; Concli, F. Advances in machine learning techniques used in fatigue life prediction of welded structures. Appl. Sci. 2024, 14, 398. [Google Scholar] [CrossRef]
- Giannella, V.; Bardozzo, F.; Postiglione, A.; Tagliaferri, R.; Sepe, R.; Armentani, E. Neural networks for fatigue crack propagation predictions in real-time under uncertainty. Comput. Struct. 2023, 288, 107157. [Google Scholar] [CrossRef]
- Zhang, W.; Bao, Z.; Jiang, S.; He, J. An artificial neural network-based algorithm for evaluation of fatigue crack propagation considering nonlinear damage accumulation. Materials 2016, 9, 483. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, J.; Guo, W.; Guo, W. A machine learning-based approach to predict the fatigue life of three-dimensional cracked specimens. Int. J. Fatigue 2022, 159, 106808. [Google Scholar] [CrossRef]
- Zhang, H.; Deng, Y.; Chen, F.; Luo, Y.; Xiao, X.; Lu, N.; Liu, Y.; Deng, Y. Fatigue life prediction for orthotropic steel bridge decks welds using a Gaussian variational bayes network and small sample experimental data. Reliab. Eng. Syst. Saf. 2025, 264, 111406. [Google Scholar] [CrossRef]
- Mohammadi, M.; Dryden, J.R.; Jiang, L. Stress concentration around a hole in a radially inhomogeneous plate. Int. J. Solids Struct. 2011, 48, 483–491. [Google Scholar] [CrossRef]
- Nagpal, S.; Jain, N.; Sanyal, S. Stress Concentration and its Mitigation Techniques in Flat Plate with Singularities—A Critical Review. Eng. J. 2012, 16, 2–15. [Google Scholar] [CrossRef]
- Monti, S. Reduction of the Local Stress Field Around Holes Through Porous Shaped Structures. Communications 2018, 3, 36–41. [Google Scholar] [CrossRef]
- Picelli, R.; Townsend, S.; Kim, H.A. Stress and strain control via level set topology optimization. Struct. Multidisc. Optim. 2018, 58, 2037–2051. [Google Scholar] [CrossRef]
- Szybiński, B.; Romanowicz, P.J. Optimization of Flat Ends in Pressure Vessels. Materials 2019, 12, 4194. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Yuan, H.; Li, X.; Shi, P. Stress Concentration and Damage Factor Due to Central Elliptical Hole in Functionally Graded Panels Subjected to Uniform Tensile Traction. Materials 2019, 12, 422. [Google Scholar] [CrossRef] [PubMed]
- Almeida, J.H.S., Jr.; Bittrich, L.; Spickenheuer, A. Improving the open-hole tension characteristics with variable-axial composite laminates: Optimization, progressive damage modeling and experimental observations. Compos. Sci. Technol. 2020, 185, 107889. [Google Scholar] [CrossRef]
- Yan, C.; Hao, W.; Yin, Y.; Zeng, N.; Du, H.; Song, D. Stress Optimization of Vent Holes with Different Shapes Using Efficient Switching Delayed PSO Algorithm. Appl. Sci. 2022, 12, 5395. [Google Scholar] [CrossRef]
- Romanowicz, P.J.; Szybiński, B. Determination of Optimal Flat-End Head Geometries for Pressure Vessels Based on Numerical and Experimental Approaches. Materials 2021, 14, 2520. [Google Scholar] [CrossRef]
- AFV. Accialerie Beltrame SpA Vicenza, Material Certificate No. 450947, 4 November 2024. Available online: https://gruppobeltrame.com/en/afv-acciaierie-beltrame-spa/ (accessed on 20 May 2025).
- EN 10025-2:2019; Hot Rolled Products of Structural Steels—Part 2: Technical Delivery Conditions for Non-Alloy Structural Steels. European Committee for Standardization: Brussels, Belgium, 2019.
- ANSYS. Campus Release 2024 R2 July 2024; ANSYS, Inc.: Canonsburg, PA, USA, 2024. [Google Scholar]
- ANSYS. Campus Release 2025 R1 July 2025; ANSYS, Inc.: Canonsburg, PA, USA, 2025. [Google Scholar]
- ANSYS. 2025 R1 Design Xplorer User’s Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2025. [Google Scholar]
- Tensorflow. Available online: https://www.tensorflow.org (accessed on 10 September 2025).
- PyTorch. Available online: https://pytorch.org (accessed on 10 September 2025).
- PyCharm. Available online: https://www.jetbrains.com/pycharm (accessed on 10 September 2025).
- Spyder-ide. Available online: https://www.spyder-ide.org (accessed on 10 September 2025).
- Terven, J.; Cordova-Esparza, D.-M.; Romero-Gonzalez, J.-A.; Ramirez-Pedraza, A.; Chavez-Uriola, E.A. A comprehensive survey of loss functions and metrics in deep learning. Artif. Intell. Rev. 2025, 58, 195. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1999. [Google Scholar]
- GOM Software 2018 Hotfix 1. Available online: www.gom.com (accessed on 26 September 2018).
- Romanowicz, P.J.; Szybiński, B.; Wygoda, M. Assessment of Digital Image Correlation Effectiveness and Quality in Determination of Surface Strains of Hybrid Steel/Composite Structures. Materials 2024, 17, 3561. [Google Scholar] [CrossRef]
- Romanowicz, P.J.; Szybiński, B.; Wygoda, M. Fracture Mechanism of Adhesive Layers in Fatigue-Loaded Steel Structures Reinforced by the CFRP Overlays. Appl. Sci. 2025, 15, 3435. [Google Scholar] [CrossRef]
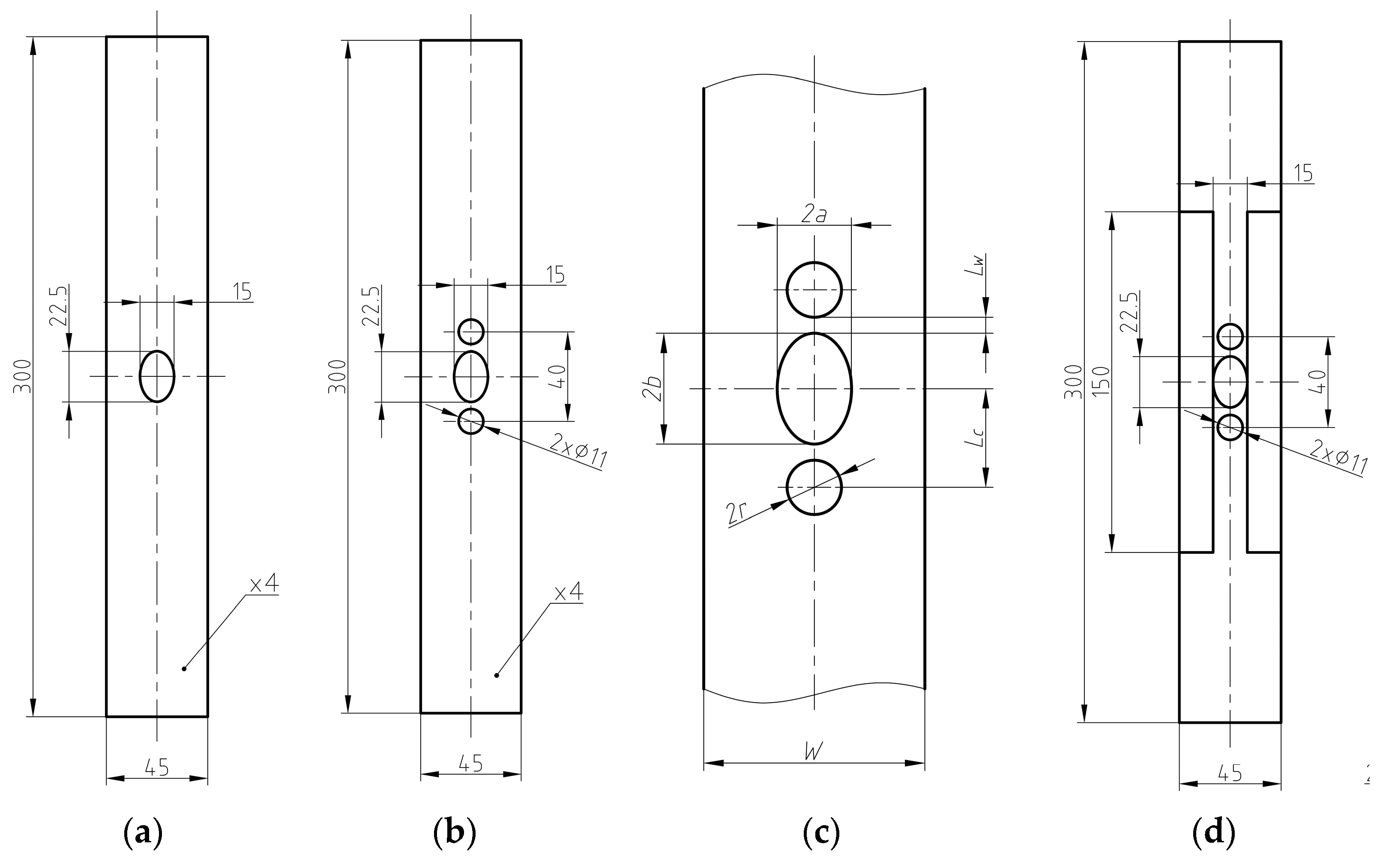

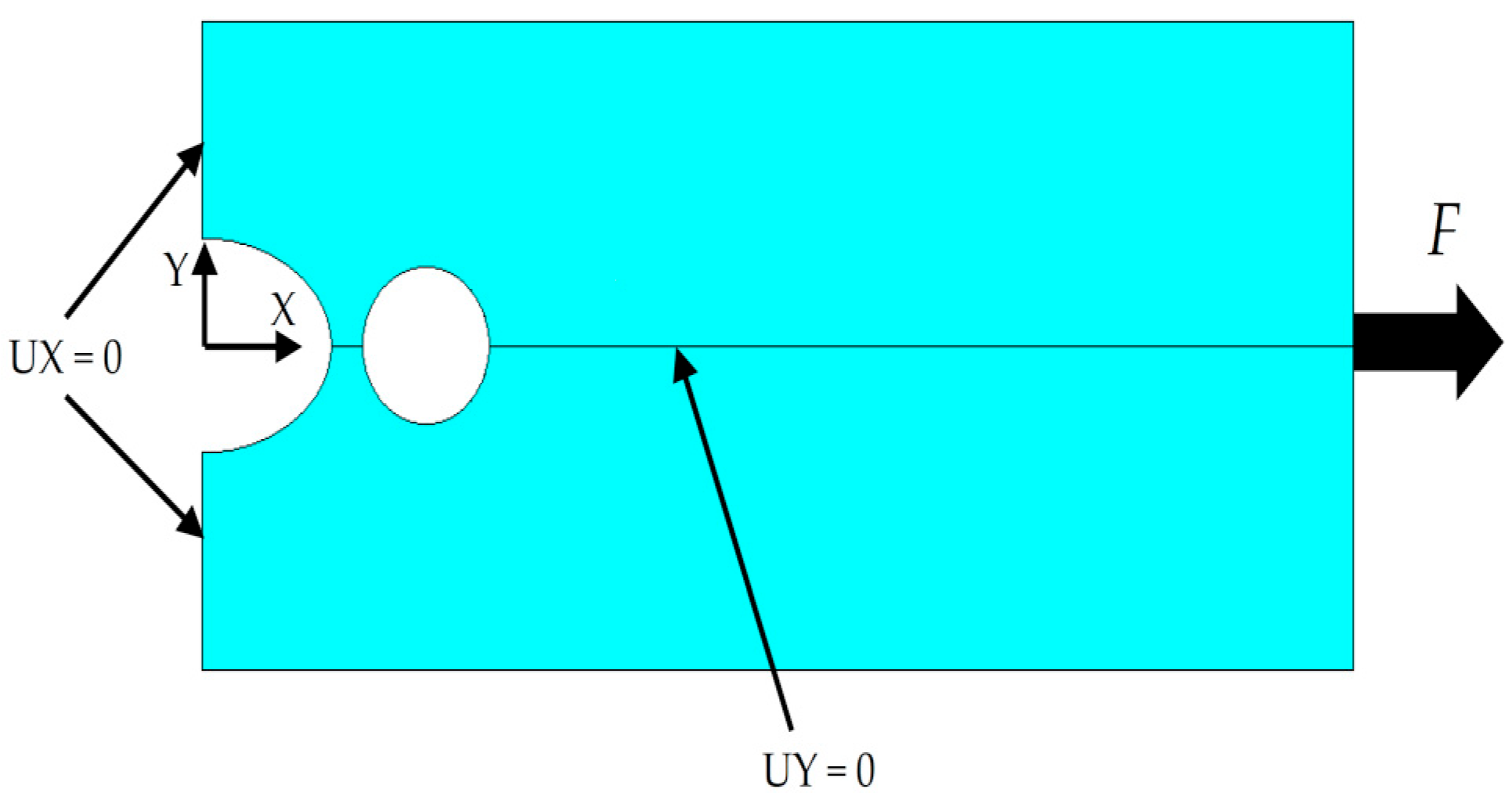





| Material | C | Si | Mn | P | S | Cu | Cr | Ni | V | Mo | N |
|---|---|---|---|---|---|---|---|---|---|---|---|
| S235JR [43] | 0.11 | 0.19 | 0.92 | 0.022 | 0.024 | 0.30 | 0.12 | 0.12 | 0.004 | 0.03 | 0.0116 |
| S235JR (Standards [44]) | 0.19 | - | 1.50 | 0.045 | 0.045 | 0.60 | 0.34 | 0.47 | - | 0.14 | 0.014 |
| Material | E (GPa) | ν | Yield Limit (MPa) | Ultimate Tensile Strength (MPa) | Elongation at Failure (%) |
|---|---|---|---|---|---|
| S235JR [43] | 210 | 0.3 | 344 | 492 | 33 |
| S235JR (Standards [44]) | 210 | 0.3 | ≥235 | 360–510 | ≥26 |
| Specimen No. | Sample Geometry | Test Type | Comments |
|---|---|---|---|
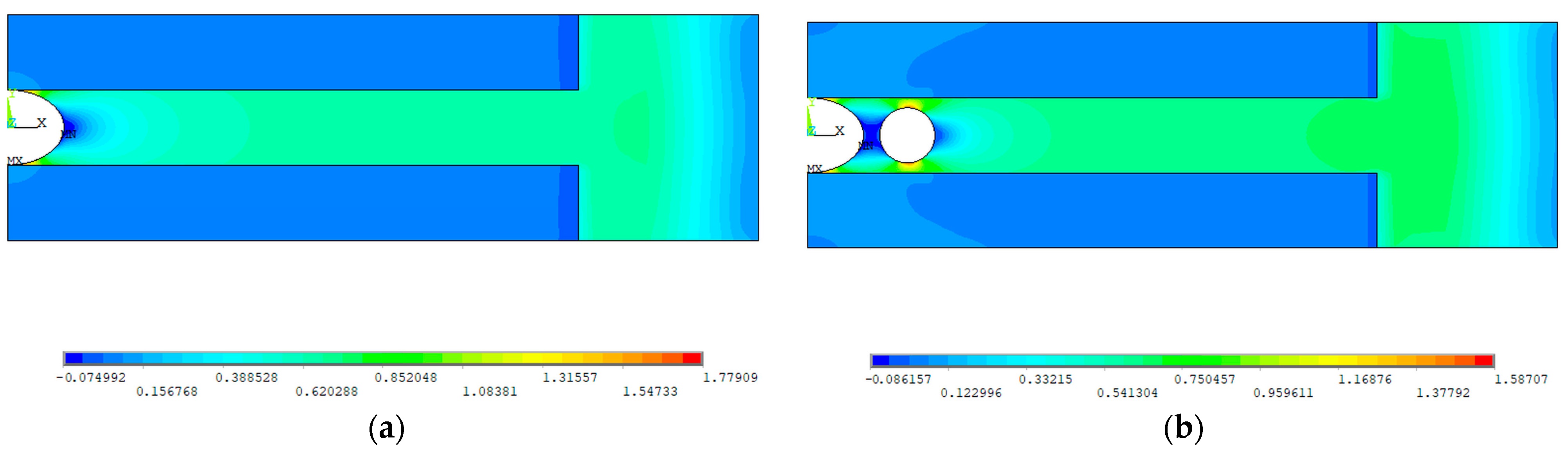
| 1–3 | Notched—elliptical hole | Fatigue, tensile | Figure 1a and Figure 2a |
| 4–6 | Notched—elliptical hole with two stress relief holes | Fatigue, tensile | Figure 1b and Figure 2b |
| Studied Case | Input Parameter (s) | Output Parameter (s) |
|---|---|---|
| 1. Circular hole | d/W | Ktn |
| 2. Elliptical hole | a/b, a/W | Ktn |
| 3. Elliptical hole with circular relief holes | a/W, r/W | Ktn and 5 other quantities |
| No. | r (mm) | LC (mm) | LW (mm) | Ktn (Elliptical) | (MPa) | ||
|---|---|---|---|---|---|---|---|
| Value | SMXB | Value | SMXB | ||||
| 1 | 5.749 | 18.532 | 1.533 | 1.6825 | 1.6825 | 1.6787 | 1.6788 |
| 2 | 5.687 | 18.982 | 2.044 | 1.6806 | 1.6806 | 1.6803 | 1.6803 |
| 3 | 5.672 | 19.085 | 2.163 | 1.6806 | 1.6806 | 1.6806 | 1.6805 |
| 4 | 5.597 | 19.882 | 3.035 | 1.6879 | 1.6879 | 1.6879 | 1.6879 |
| 5 | 5.551 | 19.977 | 3.176 | 1.6835 | 1.6835 | 1.6831 | 1.6831 |
| 6 | 5.510 | 20.260 | 3.500 | 1.6855 | 1.6855 | 1.6837 | 1.6837 |
| 7 | 5.458 | 20.750 | 4.042 | 1.6880 | 1.6880 | 1.6874 | 1.6874 |
| 8 (tested) | 5.500 | 20.000 | 3.250 | 1.6879 | 1.6879 | 1.6760 | 1.6760 |
| Samples Set | Hole Diameter | Length | Circular Hole | Elliptical Hole | Difference |
|---|---|---|---|---|---|
| 2R (mm) | LW (mm) | (MPa) | Ktn | (%) | |
| 1 | 9.8 | 4.3 | 1.582 | 1.750 | 9.6 |
| 2 | 7.8 | 12.6 | 1.667 | 1.820 | 8.4 |
| 3 | 6.0 | 17.1 | 1.684 | 1.867 | 9.8 |
| 4 | 10.6 | 7.3 | 1.721 | 1.717 | 0.3 |
| 5 | 11.4 | 2.4 | 1.680 | 1.689 | 0.5 |
| Samples Set | Hole Diameter | Length | Circular Hole | Elliptical Hole | Difference |
|---|---|---|---|---|---|
| 2r [mm] | LW (mm) | (MPa) | Ktn | (%) | |
| 1 | 10.2 | 3.1 | 1.582 | 1.740 | 9.1 |
| 2 | 8.6 | 9.1 | 1.615 | 1.789 | 7.2 |
| 3 | 9.8 | 6.2 | 1.634 | 1.746 | 6.4 |
| 4 | 10.4 | 4.8 | 1.647 | 1.723 | 4.4 |
| 5 | 8.2 | 10.8 | 1.631 | 1.805 | 9.6 |
| Samples Set | Hole Diameter | Length | Circular Hole | Ellitptical Hole | Difference |
|---|---|---|---|---|---|
| 2r [mm] | LW (mm) | (MPa) | Ktn | (%) | |
| 1 | 9.6 | 11.3 | 1.743 | 1.768 | 1.4 |
| 2 | 9.8 | 13 | 1.790 | 1.773 | 1.0 |
| 3 | 10 | 9.6 | 1.725 | 1.747 | 1.3 |
| 4 | 10.2 | 9.9 | 1.751 | 1.742 | 0.5 |
| 5 | 10.6 | 8.2 | 1.740 | 1.720 | 1.1 |
| Minimal Value of Ktn | Optimal Radius r of Hole (mm) | Optimal Distance LC (mm) | |
|---|---|---|---|
| Numerical study | 1.682 | 5.643 | 19.185 |
| Sub-variant 1 | 1.719 | 4.800 | 17.184 |
| Sub-variant 2 | 1.702 | 5.590 | 18.910 |
| No | Specimen Type | Eadh (GPa) | Ktn | Nf (Cycles) | Nf,avg (Cycles) | (Cycles) | |
|---|---|---|---|---|---|---|---|
| 1–3 | With singular elliptical hole | Exp. | - | 1.908 (theoretical) 1.922 (FEM) | 41,234, 52,516, 62,306 | 52018 | 10.55 |
| 4–6 | With elliptical hole with two circular relief holes | Exp. | - | 1.688 | 84,652, 91,987, 102,910 | 93183 | 9.15 |
| - | With elliptical hole strengthened by composite overlays | FEM | 0.355 | 1.790 | - | - | - |
| FEM | 0.590 | 1.787 | - | - | - | ||
| FEM | 3.600 | 1.779 | - | - | - | ||
| - | With elliptical hole with two circular relief holes strengthened by composite overlays | FEM | 0.355 | 1.596 | - | - | - |
| FEM | 0.590 | 1.594 | - | - | - | ||
| FEM | 3.600 | 1.587 | - | - | - |
| Method | Scale | Optimal Decision Variables (mm) | Ktn | ||
|---|---|---|---|---|---|
| r (mm) | LW (mm) | LC (mm) | |||
| Simple-search method (SSM) | Global | 5.672 | 2.163 | 19.085 | 1.6806 |
| 5.687 | 2.044 | 18.982 | 1.6806 | ||
| Parametric optimisation (Ansys APDL- PO) | Global | 5.692 | 2.001 | 18.944 | 1.6807 |
| Local | 5.551 | 3.176 | 19.977 | 1.6835 | |
| Goal-driven optimisation (GDO) (Ansys Workbench) | Global | 5.7 | 2.4 | 19.35 | 1.689 |
| Local | 5.2 | 4.8 | 21.25 | 1.723 | |
| ANN—macro | Global | 4.800 | 1.134 | 17.184 | 1.7185 |
| Local | 4.576 | 3.002 | 18.828 | 1.7270 | |
| ANN—local | Global | 5.590 | 2.070 | 18.910 | 1.7020 |
| Local | 5.486 | 3.000 | 19.736 | 1.7029 | |
| Tested | - | 5.50 | 3.25 | 20.00 | 1.6879 |
| Specimen with singular elliptical opening | - | - | - | 1.908 | |
| SSM | APDL-PO | GDO | ANN | |
|---|---|---|---|---|
| Precision in global optimum search | very high | moderate | moderate | moderate |
| Computational time | very high | high | high |
|
| Sensitivity for stacking in local minimum | not applicable | high | low | not applicable |
| Number of analyses required | very high | high | moderate | moderate |
| Sensitivity for input data | low | high | low | moderate |
| Practical applicability | low | moderate | high | high |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romanowicz, P.J.; Szybiński, B.; Barski, M.; Stawiarski, A.; Pałac, M. Application of FEM Analyses and Neural Networks Approach in Multi-Stage Optimisation of Notched Steel Structures Subjected to Fatigue Loadings. Appl. Sci. 2025, 15, 11194. https://doi.org/10.3390/app152011194
Romanowicz PJ, Szybiński B, Barski M, Stawiarski A, Pałac M. Application of FEM Analyses and Neural Networks Approach in Multi-Stage Optimisation of Notched Steel Structures Subjected to Fatigue Loadings. Applied Sciences. 2025; 15(20):11194. https://doi.org/10.3390/app152011194
Chicago/Turabian StyleRomanowicz, Paweł J., Bogdan Szybiński, Marek Barski, Adam Stawiarski, and Mateusz Pałac. 2025. "Application of FEM Analyses and Neural Networks Approach in Multi-Stage Optimisation of Notched Steel Structures Subjected to Fatigue Loadings" Applied Sciences 15, no. 20: 11194. https://doi.org/10.3390/app152011194
APA StyleRomanowicz, P. J., Szybiński, B., Barski, M., Stawiarski, A., & Pałac, M. (2025). Application of FEM Analyses and Neural Networks Approach in Multi-Stage Optimisation of Notched Steel Structures Subjected to Fatigue Loadings. Applied Sciences, 15(20), 11194. https://doi.org/10.3390/app152011194






