1. Introduction
Modern architecture faces the dual challenge of pursuing efficiency and standardization in design and construction, while simultaneously satisfying diverse user demands and complex functional relationships [
1,
2,
3]. Against this backdrop, modular construction and grid-based design approaches have emerged as robust alternatives. However, the Spatial Allocation Problem (SAP), optimally positioning various required functions under given constraints, still necessitates complex decision-making [
4,
5]. The complexity of this problem increases exponentially in multistory buildings, where factors such as vertical continuity (e.g., cores and staircases), circulation efficiency, and functional zoning across different floors must be considered concurrently.
This study addresses these challenges by presenting a procedure for implementing a Generative Design (GD) methodology to optimize spatial allocation in multi-story buildings within a Building Information Modeling (BIM) environment [
6,
7,
8]. This approach goes beyond the mere application of new technology; it is an attempt to integrate the architectural intellectual tradition of systematically generating space through rules—exemplified by Alexander’s ‘A Pattern Language’ and Stiny’s ‘Shape Grammar’—with contemporary BIM workflows [
9,
10]. Specifically, we aimed to derive optimal spatial configurations amid complex geometric and functional constraints by rapidly exploring and quantitatively evaluating numerous design alternatives using GD.
To establish an automated design pipeline, this study seeks to answer the following key research questions:
Q1. In the context of multistory SAPs, how can essential geometric constraints (boundary compliance) and structural constraints (vertical alignment of fixed elements) be formalized as hard constraints within a GD algorithm?
Q2. How can adjacency, departmental grouping, and positional preference be defined and calculated as quantitative soft objectives for evaluating the functional efficiency of spatial layouts?
Q3. How can a reproducible BIM-integrated pipeline be constructed and verified to generate and optimize alternatives based on defined constraints and objectives?
The primary contribution of this research lies in the clear separation and application of the complex SAP to hard constraints and soft objectives [
11]. Specifically, we secured geometric validity by (1) implementing a boundary constraint (‘boxedin’) to ensure that none of the spaces exceeded the defined boundaries. We maintained structural consistency by (2) implementing a vertical alignment constraint to align the positions of fixed elements, such as cores, across multiple floors.
Furthermore, to evaluate the functional efficiency of the space, we established a multi-objective optimization framework by (3) defining adjacency (ADJACENT, minimizing circulation length), departmental grouping (DEPARTMENT, minimizing group area), and core position (CORE, optimizing location) as quantitative metrics, and simultaneously optimizing them. In conclusion, this study presents an integrated workflow that successfully implements and validates a procedure for automatically generating alternatives that optimize these three soft objectives while satisfying all hard constraints in a multistory scenario (four-story scale).
2. Literature Review
To systematically position this research and verify its originality, a comprehensive literature review was conducted. The review process targeted two primary academic databases, Google Scholar and Web of Science, to ensure broad coverage of relevant scientific publications. The search strategy involved a combination of keywords centered on the core topics of this study, including “Generative Design”, “Spatial Allocation Problem (SAP)”, “Building Information Modeling (BIM)”, “Design Automation”, and “Multi-objective Optimization”. The selection process was performed in stages. An initial search yielded a large volume of records, which were then filtered by title and abstract to identify those directly relevant to automated spatial planning in architecture. The inclusion criteria for full-text analysis were: (1) peer-reviewed articles focusing on the application of generative or algorithmic techniques to architectural layout problems; (2) studies that explicitly discussed integration with or application within a BIM framework; and (3) research employing multi-objective optimization to evaluate design alternatives. Studies were excluded if they were purely theoretical, not applied to the architectural domain, or did not involve a computational implementation.
The selected literature was then thematically analyzed to map the evolution of computational design methodologies, from foundational theories to contemporary hybrid approaches. A summary of this analysis is presented in
Table 1, which organizes the most influential projects by main category, year, author(s), and journal. Each entry includes a brief summary that outlines the key contribution of the work and clarifies how it informed the development of the methodology proposed in this study.
2.1. Formalization of Architectural Design Rules: Theoretical Foundations of Knowledge-Based Generation
The rule-based generative approach adopted in this study is rooted in the intellectual tradition of describing the design process as a set of explicit rules that aim to generate architectural space through consistent grammar. The seminal work in this field is ‘Shape Grammars’, which established the design process as a formal grammar by applying generation and substitution rules to geometric shapes [
10]. While shape grammars constructed a formal syntax for the design process, ’A Pattern Language’ imbued that syntax with functional and experiential semantics [
9]. This work systematized the recurring relationships of context–problem–solution in space as ’patterns’ and linked designs ranging from urban scales to furniture through their networks. It provides the philosophical foundation for this study’s approach of treating practical knowledge, such as certain spaces must be adjacent, as rules (soft objectives).
The structural framework for applying these rules to actual architectural systems can be found as ’Supports’ theory [
12]. This theory introduced the ‘Open Building’ concept, separating a building into a fixed support and variable infill, allowing spaces to be customized according to user needs atop a standardized structural system. The 3.3 × 3.3 m modular grid (support), and the layout strategy of combining various programs within it (infill) in this study directly corresponds to this systemic framework. Therefore, this is a practical successor to the theoretical tradition using the modern BIM technology platform [
13,
14]. The formality of ‘Shape Grammars’, the functional knowledge of ‘Pattern Language’, and the systemic separation of ‘Supports’ are materialized in this study as machine-verifiable ’Hard Constraints,’ such as the boundary constraint and the vertical alignment constraint.
2.2. Advancements in Computational Methodologies for Design Automation
Computational methodologies for solving the SAP have evolved primarily around approaches that combine explicit knowledge with optimization algorithms GD. Recently, data-driven approaches that learn implicit patterns from large-scale data have been utilized [
15]. Both trends have increasingly leveraged graphs as core data structures to systematically handle architectural constraints.
In the realm of knowledge-based optimization, Cao et al. recently proposed a method combining graph-based representations with a multi-objective genetic algorithm (MOGA), targeting the hybrid modularization of architectural floor plans [
17]. This study extracts wall attributes, junctions, and adjacency relationships from BIM, encodes them into graphs, and explores various modularization strategies using time and cost evaluation functions. It demonstrates a framework that simultaneously improves constructability and economy while maintaining topological constraints, suggesting that requirements like this study’s ‘Vertical Alignment Constraint’ or ‘ADJACENT Objective’ can also be naturally translated into graph constraints [
16,
20].
Data-driven generative models complement knowledge-based optimization. Wang et al. proposed a pipeline that combines deep learning and graph algorithms to model spatial units as graphs and used learned features to generate and modify room layouts and adjacency relationships [
21]. Su et al. introduced a hybrid configuration that learns the topological patterns of floor plans through a discrete denoising diffusion model and applies explicit rules (e.g., windows and circulation) as post-processing constraints [
22]. This approach combines the creative exploration capabilities of probabilistic models with the precision of explicit rules to enhance the quality of the final output, offering insights into the design of soft objective scorers (e.g., circulation efficiency and cohesion). In summary, recent research has converged on a framework that (a) structures architectural rules and constraints through graph modeling, (b) broadens the scope of exploration using generative models such as optimization algorithms or deep learning, and (c) considers practical judgment indicators (time, cost, and quality) through multi-objective optimization.
2.3. Integration of Constraints and Design Objectives: Hybrid Approaches
The central trend in recent spatial allocation research is converging on hybrid approaches that combine the reliability of satisfying mandatory constraints with the exploratory power to optimize design objectives. This is an attempt to respect the architect’s rules while exploring new possibilities, sharing the same critical perspective as this study’s approach of utilizing hard constraints and soft objectives within a GD environment [
18,
19]. Recent studies on injecting architectural knowledge (constraints and objectives) into computational models present two main methods.
The first involves embedding rules directly into the generation process. For example, Aalaei et al. utilized graph neural networks (GNN) to transform architectural rules such as boundaries and adjacencies into graph constraints and integrated them into a conditional generative adversarial network (CGAN) model to generate rule-compliant floor plans [
23]. Rules such as this study’s vertical alignment constraint or boundary constraint can be modeled as graph constraints.
The second is a more flexible approach that utilizes rules as input conditions or evaluation criteria for generation. Zeng et al. proposed a diffusion model that accepts various conditions such as boundaries, areas, and functions and integrated heterogeneous conditions such as boundaries, graphs, and text into a single pipeline [
24]. This approach culminated in the recent work by Qin et al., who introduced LLMs to automatically convert natural language prompts into javascript object notation conditions, illustrating a future in which humans and AI interactively develop designs [
25]. Soft objectives in this study, such as CORE positional preference and DEPARTMENT cohesion, can be naturally converted into these condition vectors or evaluation criteria.
Beyond these knowledge integration methods, a common workflow pattern of Initialization → Exploration → Constraint-based refinement and evaluation has been emerging in recent studies. First, Luo et al. researched a method to provide a good seed, or initial solution, to start the exploration by automatically generating bubble diagrams using GNNs [
26]. This aligns directly with the Initialization phase of this study. Next, after various algorithms generate creative alternatives (Exploration), the process undergoes a Refinement stage in which the generated results are adjusted to meet the constraints again. This process enhances the completeness of the results by reinforcing consistency in topology and geometry, which precisely matches the meta-pattern of the workflow in hard constraint check (Feasibility Filtering) to soft objective calculation (Performance Evaluation and Ranking). In summary, the tradition of formalizing architectural design (
Section 2.1) has been succeeded by diverse modern computational methodologies (
Section 2.2) and has recently evolved into methods that effectively integrate constraints and design objectives (
Section 2.3). Within this context, this study focuses on the reliability and controllability of explicit rule-based optimization rather than the implicit learning of data-driven AI models. Specifically, it focuses on clearly defining the complex requirements of multistory buildings as Hard Constraints and soft objectives within a BIM environment and establishing a practical and reproducible pipeline to solve SAP.
3. Methods
This study proposes a methodology that utilizes GD to address the architectural SAP. The SAP is well-recognized in operations research and architectural design as a complex, often NP-hard, combinatorial optimization challenge, necessitating efficient computational strategies [
27]. The primary objective was to optimize spatial layout efficiency while satisfying the complex geometric constraints and functional requirements of multistory buildings. This methodology involves computationally defining the design problem (
Section 3.1), modeling constraints and objectives for optimization (
Section 3.2), and employing an efficient exploration strategy (
Section 3.3), as illustrated in
Figure 1.
3.1. Design Problem Formalization and Spatial Model Definition
This study defines the design challenge as a spatial allocation optimization problem. This is a combinatorial optimization problem focused on assigning the required program elements to optimal locations within a given boundary. To solve this problem, the architectural requirements were translated into algorithmically interpretable models.
3.1.1. Spatial Model
The design domain was conceptualized as a discretized 3D grid system (G). This approach, utilizing grid-based discretization or voxelization, is a common strategy in automated layout generation as it simplifies geometric representation and facilitates the application of combinatorial optimization algorithms [
28]. Within this system, the target area is represented by a collection of grid cells, where each cell C(x,y,z) defines a minimum allocatable spatial unit. The coordinates (x,y) denote the horizontal position and z represents the vertical floor (layer). Consequently, a multistory building was configured as a vertical stack of floor grids, as illustrated in
Figure 2.
Concurrently, the set of spaces required for allocation (P), known as program elements, was predefined. Each program element pi ∈ P was characterized by specific attributes, including the required area (expressed as a number of cells), the assigned functional group (Department), and adjacency requirements with other spaces. Thus, the SAP was formalized as the process of identifying an optimal mapping function that assigned all the elements of set P to the cells of grid G without overlap.
3.1.2. Classification of Spaces in Multi-Story Structures
To define the SAP in multistory buildings, spaces must be classified according to their vertical mobility, and the characteristics of each type must be reflected as constraints. Accordingly, the spaces can be divided into two main types. The first type comprises fixed elements, such as stairwells or elevator cores, which require mandatory vertical continuity across all floors. These elements are strongly constrained in that they must maintain the same horizontal position (x,y) on each floor. The second type consists of flexible elements that refer to general functional spaces. These spaces are allocated relatively freely within the remaining available area according to the design objectives after the positions of the fixed elements have been determined.
3.2. Optimization Model: Constraints and Objectives
The GD process is composed of hard constraints, which define the design space, and soft objectives, which evaluate the design quality. Hard constraints act as filters to determine the feasibility of an alternative, whereas soft objectives serve as criteria for ranking the feasible alternatives, as shown in
Figure 3.
3.2.1. Hard Constraints: Feasibility Conditions
Hard constraints are mandatory conditions that a generated design must satisfy to be physically and structurally viable. Alternatives that violate these constraints are considered infeasible and excluded from the search space. This study applies three primary hard constraints.
The most fundamental constraint is ensuring geometric integrity. This includes the non-overlap principle, stating that two different spaces cannot occupy the same grid cell simultaneously, and the complete allocation principle, requiring all program elements to be fully placed on the grid without omission.
Next, all spaces must comply with the boundary constraint, that is, they must be located within a predefined building envelope or floor grid boundary. The system enforces this through an intersection check (e.g., the ’boxedin’ parameter), disallowing layouts that exceed the boundaries.
Finally, a vertical alignment constraint is applied to ensure the realism of the multistory structure. This constraint forces fixed elements, such as cores, to be placed in identical horizontal positions across all floors. To achieve this, the algorithm uses the positions of the fixed elements determined on a reference floor as a mandatory condition for the layout process on other floors, thereby maintaining structural consistency.
3.2.2. Soft Objectives: Performance Metrics
Soft objectives are quantitative indicators for evaluating the design quality. This study defined three key metrics related to the functional efficiency of spatial layouts. These metrics—adjacency, cohesion (compactness), and positional preference—are standard evaluation criteria widely adopted in architectural layout optimization research [
29]. Optimization was performed to minimize these metrics, as illustrated in
Figure 4.
The first metric is adjacency and circulation Efficiency. Based on a predefined list of adjacency requirements, this metric evaluates the circulation efficiency by measuring the distance between functionally connected spaces. Typically, the distance between the centroids of two spaces (e.g., Manhattan or Euclidean distance) is calculated to minimize the average travel distance (fADJ) between related spaces.
The second metric is functional cohesion and departmental grouping, which assesses how closely spaces belonging to the same functional group (Department) are located. Because higher functional cohesion enables more efficient space utilization, the area of the bounding box or convex hull (fDEPT) encompassing all spaces in the group is calculated to minimize this area.
The final metric is positional preference, which is used to guide specific spaces toward particular areas of a building according to the design intent. For example, if the core is to be placed in the northwestern section, a preference map with location-specific scores will be predefined across the entire grid. The scores of the locations where the space is placed are then summed to optimize (minimize or maximize) the positional score (fCORE).
3.2.3. Multi-Objective Optimization Formulation
The goal of this study is to optimize (minimize) the defined performance indicator vector F(x) = (fADJ(x), fDEPT(x), fCORE(x)) for a design alternative x that satisfies the hard constraints H(x).
Minimize F(x)
The multi-objective optimization algorithm derives a pareto optimal set that illustrates the trade-offs between objectives rather than a single optimal solution, allowing the designer to review various superior alternatives.
3.3. Exploration Strategy and Process
The SAP is a combinatorial optimization problem with a vast search space that necessitates an efficient exploration strategy. This study utilized a metaheuristic-based GD approach to address this challenge.
3.3.1. Search Algorithm
This study employs a metaheuristic approach, specifically utilizing the Non-dominated Sorting Genetic Algorithm II (NSGA-II). NSGA-II is a widely recognized evolutionary algorithm known for its effectiveness in solving complex multi-objective optimization problems. It mimics the process of biological evolution by generating an initial population of solutions and progressively exploring better solutions over several generations. It is specifically designed to efficiently find a diverse set of trade-off solutions along the Pareto front, which is crucial for architectural design decision-making.
3.3.2. Generative Design Process
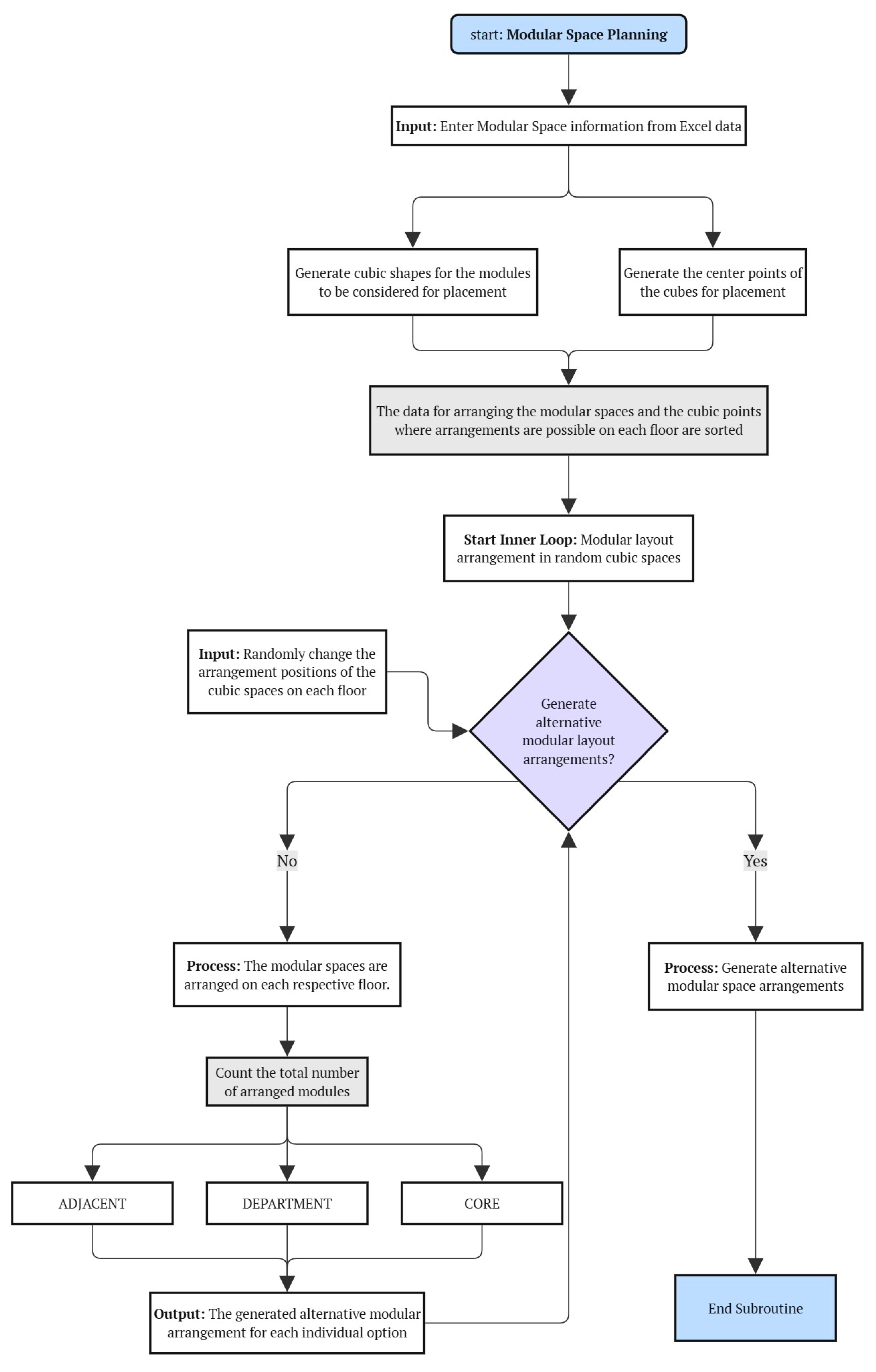
The overall exploration process follows an iterative structure consisting of four stages: initialization, generation, evaluation, and optimization, as shown in
Figure 5. The process begins at the initialization stage. At this stage, the designer inputs the parameters and sets up the exploration environment, such as a grid system, based on which the algorithm generates an initial set of solutions. Particularly for multistory structures, the logic to satisfy the vertical alignment constraint can be applied in this stage. This involves prioritizing the determination of fixed element positions on a reference floor and propagating them to other floors.
Following the initialization, the system enters the core loop of generation and evaluation. In the generation stage, diverse spatial layout alternatives are created either randomly or by modifying the superior solutions from the previous generation. Each generated alternative proceeds to the evaluation stage, where its feasibility is checked by verifying its compliance with the hard constraints. Only the feasible alternatives that pass this check proceed to calculation of soft objective metrics and quantitative evaluation of their performances.
In the final optimization stage, superior alternatives are selected based on the evaluation results. Transformation operators, such as swapping or shifting spatial positions, are applied to create new alternatives for the next generation. The system iteratively performs the ’Generation-Evaluation-Optimization’ process until a predefined termination condition (e.g., maximum number of generations) is met, progressively exploring better solutions and ultimately deriving the optimal alternatives.
4. Implementation and Case Study
This section describes the system environment and architecture for implementing the GD methodology, as shown in
Figure 6. It also details the phased setup of the case study designed to validate the implemented system. Specifically, it addresses the handling of basic geometric constraints using a spatial allocation algorithm, the process of expansion to multistory structures, and specific metrics defined for optimization.
4.1. System Implementation Environment and Architecture
4.1.1. Implementation Environment
The spatial allocation and optimization algorithms used in this study were implemented using Dynamo 3.5 a visual programming tool integrated into the Autodesk Revit 2026 environment. The optimization process utilized the Generative Design (GD) for Revit engine, which interfaces with Dynamo and employs the NSGA-II algorithm as its underlying optimization engine.
This integrated approach was specifically chosen over other intelligent methods, such as Particle Swarm Optimization (PSO) or Artificial Neural Networks (ANNs), for several key reasons. First, a primary objective of this study was to establish a practical pipeline directly within a BIM environment. Utilizing GD for Revit ensures seamless data continuity and immediate visualization, which is crucial for practical application. Second, the nature of the SAP addressed here is a multi-objective combinatorial optimization problem. While PSO is generally more effective for continuous optimization problems and ANNs (or other machine learning approaches) excel at learning implicit patterns from data [
23,
24], NSGA-II is a robust standard for exploring trade-offs and identifying Pareto-optimal solutions in scenarios like this study (balancing CORE, ADJACENT, and DEPARTMENT). Furthermore, as this study focused on the explicit formalization of rules (hard constraints and soft objectives), the chosen methodology provides the necessary control and reliability for enforcing mandatory geometric and structural constraints.
Complex data processing and geometric calculation logic were developed using a combination of Dynamo nodes and Python 3.12 scripts where necessary.
4.1.2. System Architecture and Data Flow
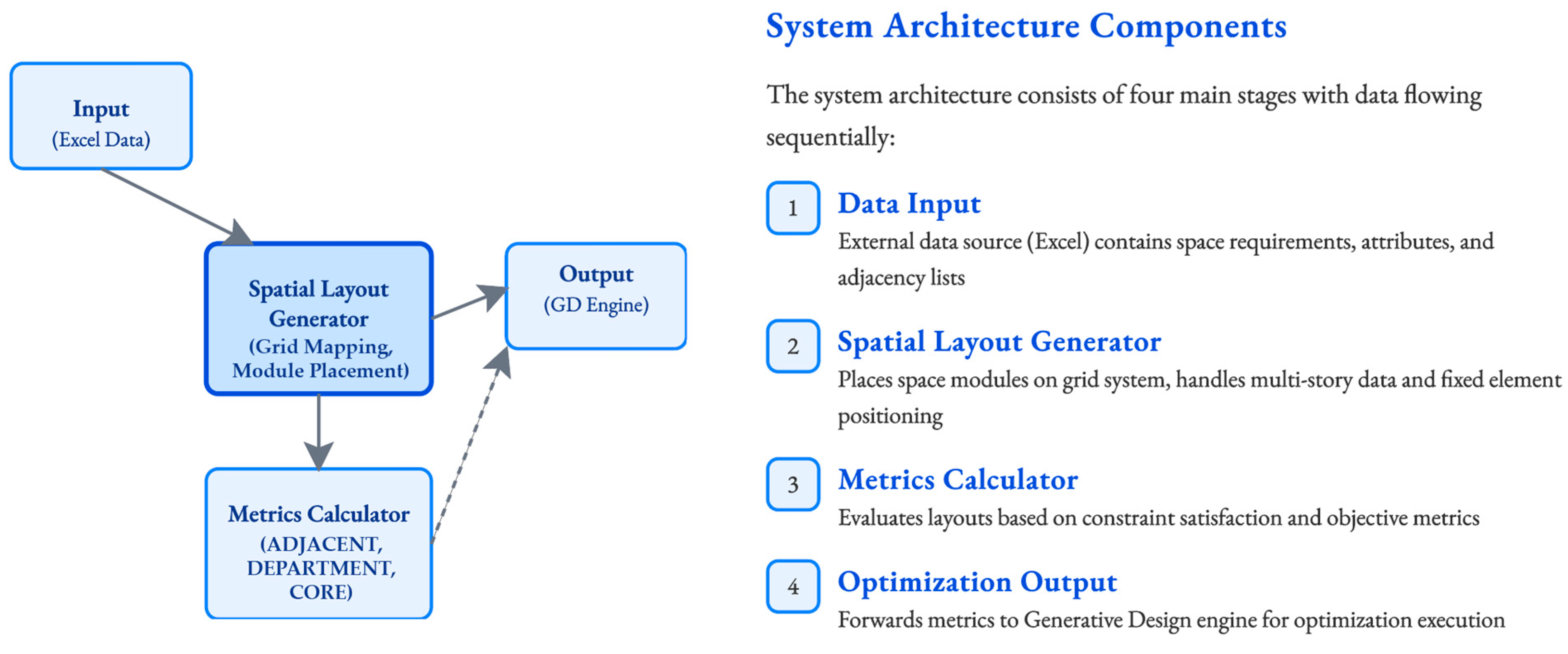
The system architecture implemented in this study features a sequential data flow across the four main stages, as illustrated in
Figure 7. The overall process consists of Data Input → Spatial Layout Generation → Metrics Calculation → Optimization Execution.
The first stage is Data Input. All design requirements, including attributes such as the name, quantity, and department of required spaces per floor, as well as interspace adjacency requirements, were input via an external data source. Dynamo read the data and converted them into a data structure that could be processed using subsequent algorithms.
Next, the converted data were passed to the spatial layout generation stage. This stage generates various design alternatives by placing the spatial modules onto a defined grid system based on the input information. Crucially, the core logic for handling multistory structures and controlling the position of fixed elements such as cores was included in this process.
Each generated layout underwent metrics calculation. Here, the satisfaction of predefined hard constraints (e.g., boundary violations) and the achievement level of soft objectives (e.g., adjacency and cohesion) were calculated as quantitative values to evaluate the performance of each alternative.
In the final optimization execution stage, the calculated metric values were transferred to the GD engine. Goals (minimize or maximize) were set and constraints based on these metrics were applied, then the optimization process was executed to explore design alternatives and determine which were superior.
4.2. Case Study Design
A two-phase case study was conducted to verify the validity and performance of the implemented system. Phase 1 aimed to validate the system’s ability to handle basic geometric constraints, whereas Phase 2 aimed to validate the multi-objective optimization performance by expanding the system to a multi-story structure.
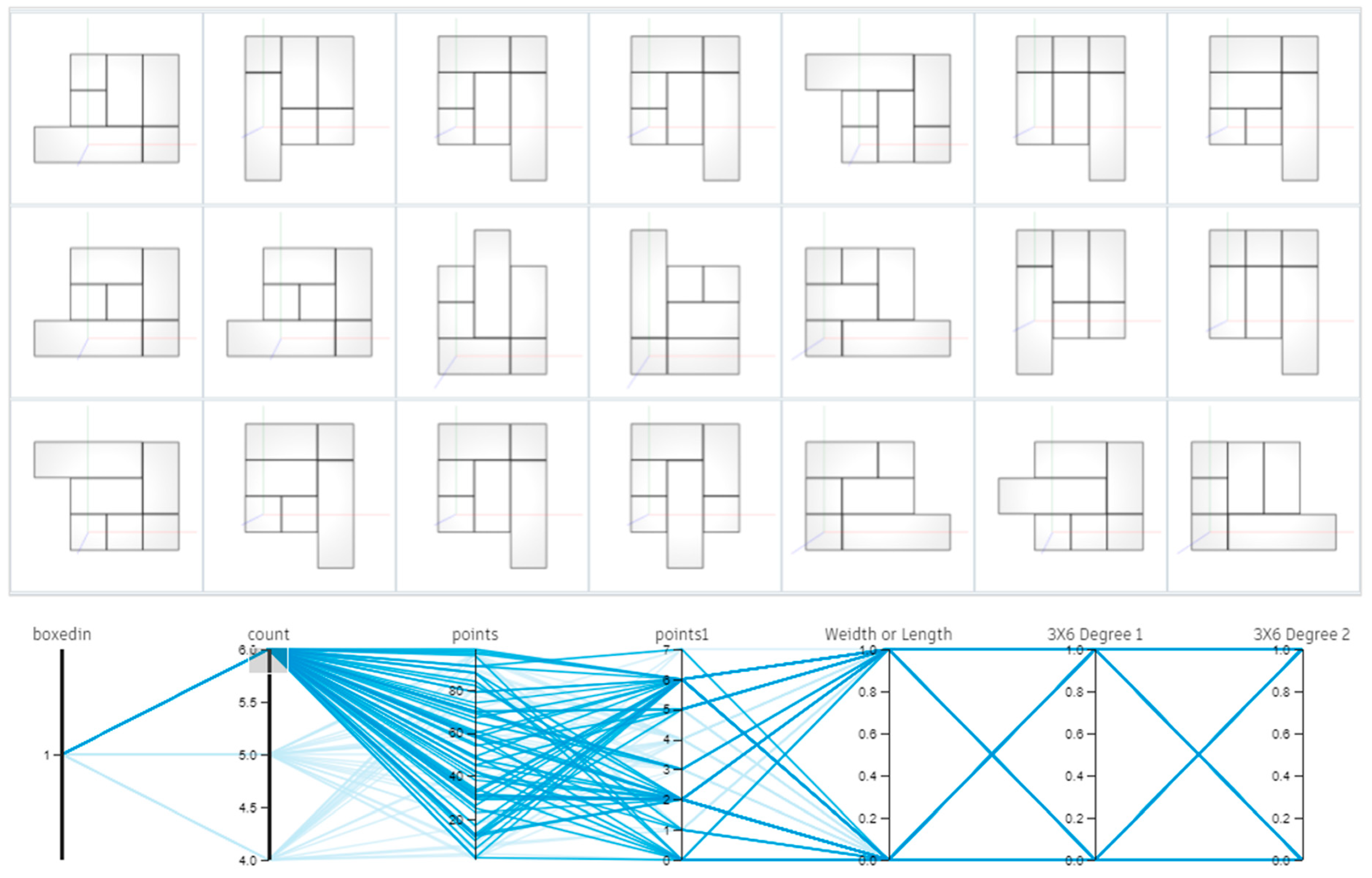
4.2.1. Basic Module Composition
Prior to the main case study, a module library based on a 3.3 m grid was established to ensure diversity in spatial combinations and generate practical design alternatives. This process began with the classification of primary spatial functions into five types: bedroom; entrance and laundry room; kitchen and dining room; terrace; and living room. For each functional type, 1–4 modules were combined in various ways, resulting in approximately 5–10 unique designs per type. A foundation for rich spatial configurations in the subsequent optimization phase was established by predefining the diversified basic module library according to its function and size.
4.2.2. Phase 1: Geometric Constraint Validation
The objective of Phase 1 of the case study was to validate the system’s capability to handle hard constraints, ensuring that all required spaces were correctly placed within the given boundaries. Two scenarios were designed and tested for this purpose.
The first scenario, the grid size limitation test (Scenario P-1), intentionally set conditions that exceed the system’s physical capacity. As shown in
Figure 8, by attempting to allocate a physically impossible quantity of space to a 3 × 3 grid, we verified whether the system accurately recognized this limitation and treated it as a constraint violation.
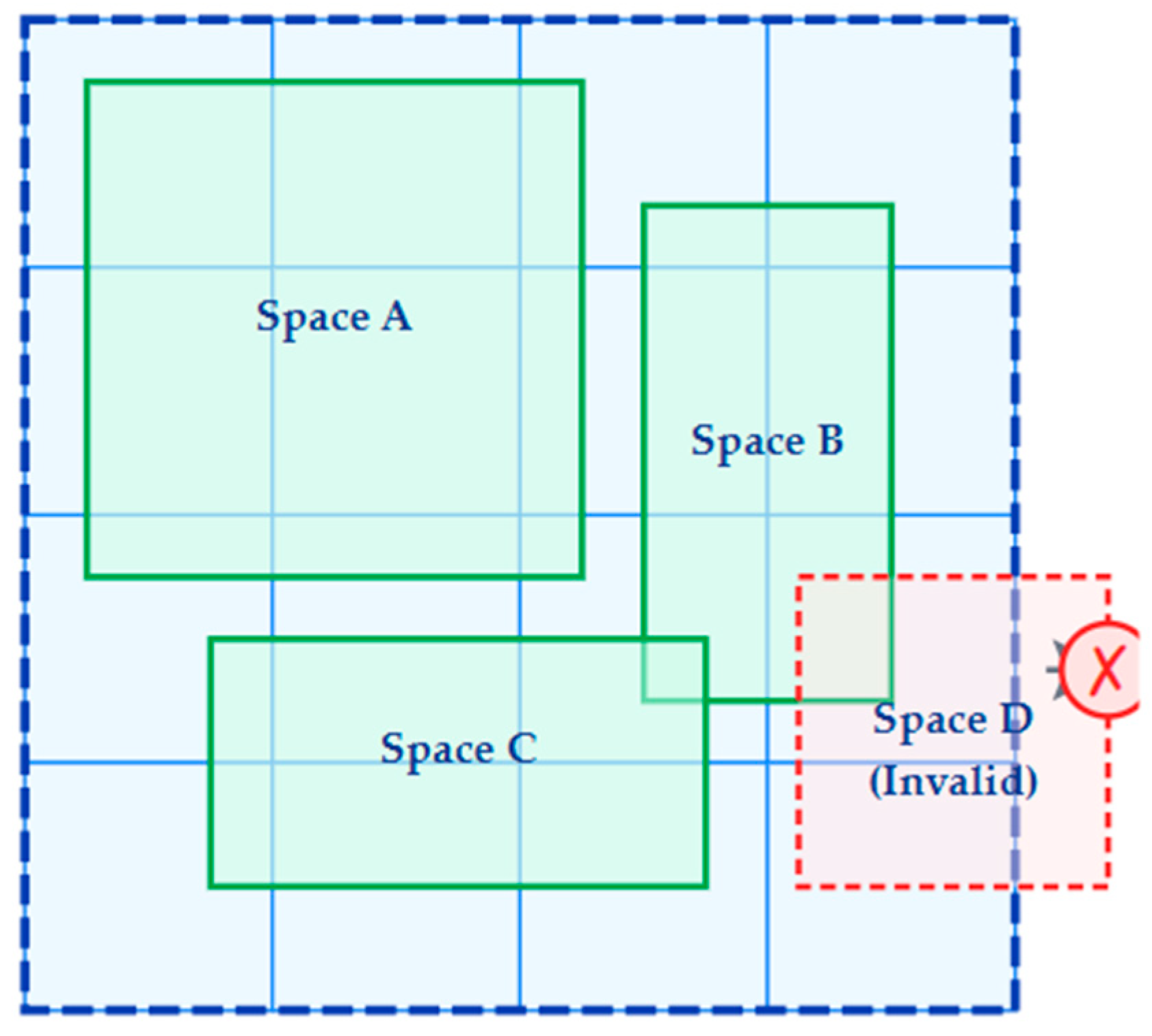
Next, in the boundary constraint test (Scenario P-2), the ‘boxedin’ constraint was activated in a 4 × 4 grid environment to ensure that all spaces do not exceed the defined boundaries. The purpose of this scenario was to verify whether the GD engine successfully filtered out invalid alternatives that violated the boundaries, as shown in
Figure 9, and only derived results that satisfied the constraints.
4.2.3. Phase 2: Multi-Story Multi-Objective Optimization
Following the validation of the geometric constraints, Phase 2 aimed to verify the performance of the algorithm in simultaneously optimizing the practical design objectives by expanding it to a multistory structure.
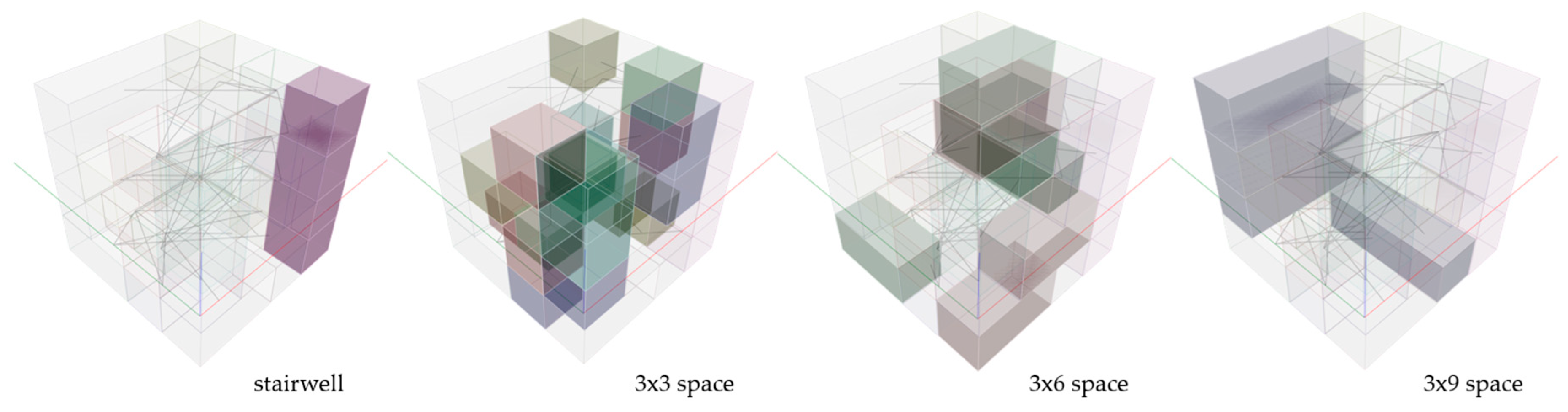
The first step, multi-story expansion and fixed element handling (Scenario M-1), involved extending the algorithm previously applied to a single floor to a multi-story building. The core objective of this process was to validate the logic for placing elements that required fixed vertical positions, such as stairwells, at the same location on every floor.
After verifying the multi-story handling capability, the four-story multi-objective optimization (Scenario M-2) was conducted to perform complex optimization similar to real-world design problems. Targeting a four-story building, as shown in
Figure 10, three potentially conflicting practical design objectives were applied simultaneously. These included core location optimization (CORE), adjacency optimization for circulation efficiency (ADJACENT), and spatial group cohesion optimization for functional efficiency (DEPARTMENT). The ultimate goal of this scenario was to derive a balanced optimal layout by considering all three metrics.
4.3. Case Study: Optimization Model Implementation
The core components of the optimization model implemented in this case study, hard constraints and soft objectives (metrics)are as follows.
4.3.1. Hard Constraints
Hard constraints are mandatory conditions that must be satisfied by each generated design alternative to be physically valid. In this study, two key hard constraints were defined and implemented in the system.
The first is the boundary constraint, which forces all the spatial modules to remain within the given grid boundaries. To implement this, Dynamo’s geometric operation node (DoesIntersect) was used to check whether each spatial module intersected the outer boundary line. If a module intersects the boundary (true), it is considered to have violated the constraint; if it does not intersect (false), it is considered valid. This boolean value is output as a parameter named ‘boxedin’. By setting a constraint during the optimization process such that this value must always be zero (false), the generation of alternatives exceeding the boundaries is fundamentally prevented.
The second is the vertical-alignment constraint aimed at securing the structural consistency of a multistory building. This constraint ensures that fixed elements that require vertical continuity across multiple floors, such as stairwells or cores, maintain the same horizontal position on all floors. The implementation method involves first determining the position (Point) of the fixed element on a reference floor (e.g., 1st floor) and passing this positional information to all other floors as a mandatory constraint. Consequently, when allocating spaces on the upper floors, the predetermined coordinates of the fixed element from the reference floor are excluded from the allocatable area before the remaining spaces are allocated, thereby guaranteeing vertical alignment.
4.3.2. Soft Objectives and Metrics
Hard constraints are absolute criteria for determining the validity of a design alternative, whereas soft objectives are quantitative metrics for evaluating the relative performance of valid alternatives in design selection. In this case study, three key metrics reflecting practical design intentions were set as soft objectives, and the optimization f minimized the values of all three metrics.
The first objective was the ‘CORE’ score, established to guide the location of the core, such as a stairwell, to a specific area of the building (e.g., the northwest side). To achieve this, a virtual score distribution (Preference Map) was defined across the entire grid, assigning the most favorable score (−1 point) to the preferred location (northwest corner) and progressively less favorable scores toward the opposite location (southeast corner). The system summed the scores of the locations where the core was placed and, by minimizing this score, guided the core placement to the area intended by the designer.
The second objective was the ’ADJACENT’ average length, a metric evaluating the circulation efficiency between spaces. According to the predefined list of adjacency requirements, the centroids of the spaces that needed to be connected were linked by lines, and the average length of all connection lines was calculated. A shorter average length indicates that the related functional spaces are closer together, implying higher circulation efficiency. Therefore, the optimization aimed to minimize this value.
The third objective was the ‘DEPARTMENT’ group area, which measured functional cohesion by evaluating how closely spaces belonging to the same functional group were located. The calculation method involved creating the smallest polygon encompassing all spaces belonging to the same group and determining its area. A smaller area suggests that the spaces of the group are cohesively arranged, indicating high functional efficiency. Thus, minimizing this area was also set as an objective.
4.3.3. Optimization Settings
To derive efficient optimization results, it is essential to set reasonable target ranges and constraints for each metric. Setting unrealistic goals may result in a failure to find valid solutions, whereas allowing overly broad ranges may diminish the significance of optimization. To address this, a preliminary analysis phase was conducted prior to the main optimization execution. First, the randomize function of the system was used to generate hundreds of diverse spatial layout alternatives. This process aimed to understand the natural distribution of the ADJACENT, CORE, and DEPARTMENT metric values in alternatives generated without specific objectives.
Figure 11 illustrates the visualization and calculation of these metrics for the floor plan.
ADJACENT is quantified as the length of the connection lines linking the centroids of spaces requiring adjacency, DEPARTMENT as the area of the polygon encompassing spaces belonging to the same group, and CORE as the preference score of the location where the fixed element is placed. Based on the data distribution obtained through preliminary analysis, a realistic range of values for each metric was identified, and the optimization goals and constraints were specifically set, as shown in
Figure 11 and
Table 2. For example, a range of 55–75 was set as the promising solution range for the ADJACENT average length, and the range corresponding to the northwest outermost area (−1.0 point) and its adjacent line (−0.5 point) was targeted for the CORE score. These specific settings guide the GD engine to focus on meaningful regions within a vast search space to efficiently find optimal alternatives.
5. Results and Discussion
This section presents and analyzes the implementation and test results of the GD system.
Section 5.1 validates the basic spatial allocation constraints through preliminary experiments.
Section 5.2 extends this to a multistory structure to optimize the core placement, spatial adjacency, and cohesion. Finally, the optimization results are analyzed in
Section 5.3, and the implications and limitations of this study are discussed in
Section 5.4.
5.1. Preliminary Testing and Geometric Constraint Validation
5.1.1. Verification of Grid Size Constraints and Limitations
The most fundamental constraint in the SAP is that all required spaces must be placed within the given boundaries. In the preliminary testing phase, when attempting to allocate the specified quantity of program elements to a 3 × 3 grid, a problem arose in which some modules extended beyond the grid boundaries or could not be placed because of insufficient space, as shown in
Figure 12.
Figure 13 illustrates a scenario in which the constraints are violated because of insufficient space. When attempting to place the required number of modules into a 3 × 3 grid, some were positioned outside the boundary or omitted entirely, thus failing to produce a valid allocation.
Figure 14 shows that the placement sequence can lead to an undeployable state within the 3 × 3 grid. When a module cannot be placed, the process halts and only the previously allocated modules are displayed. This demonstrates that a valid solution cannot be obtained if the grid size is too small for the required total area. This result suggests that it is essential to either set an appropriate grid size (e.g., expanding to 4 × 4 or larger) or adjust the program requirements before starting exploration.
5.1.2. Implementation of Boundary Constraints
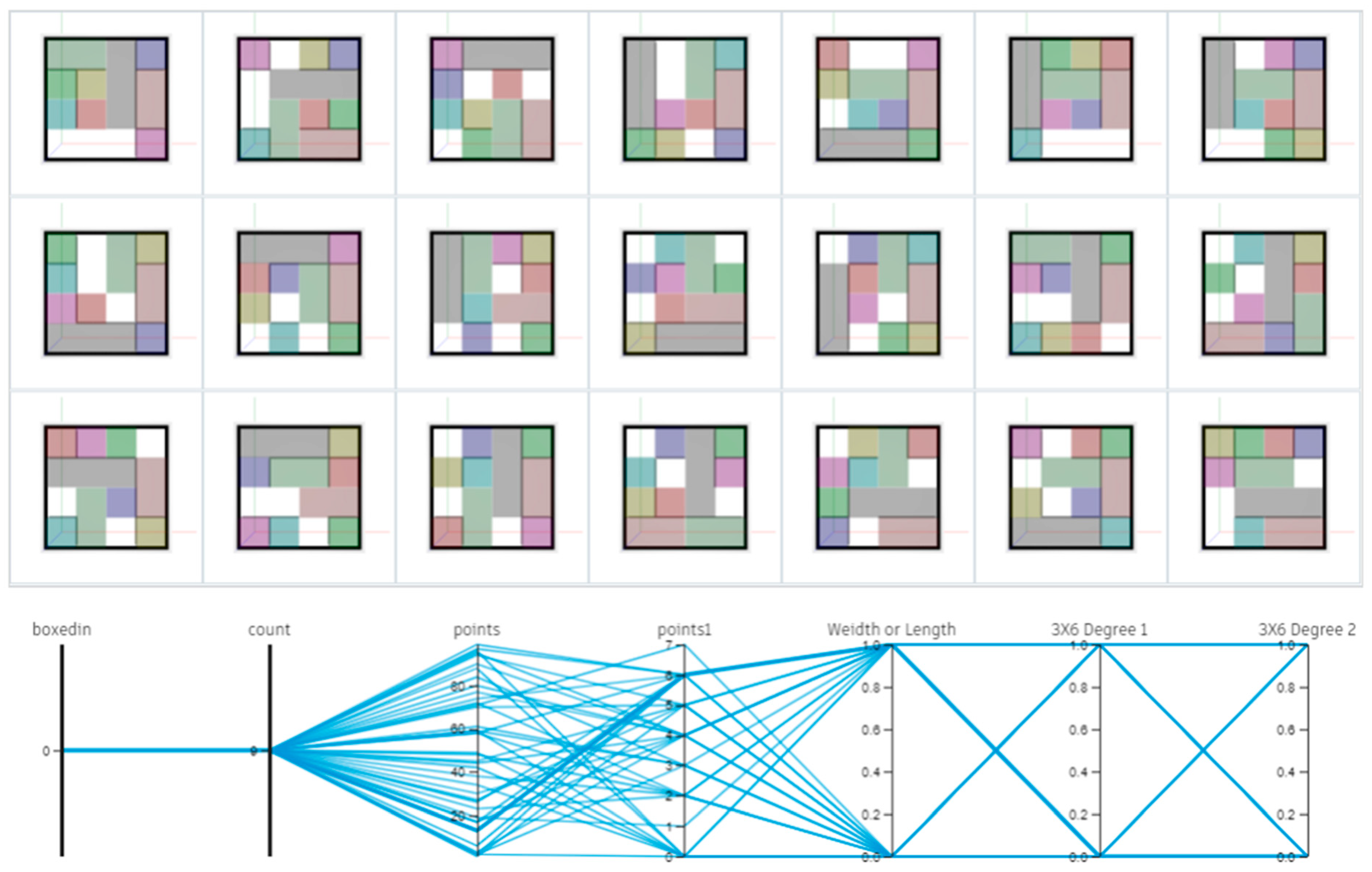
To resolve the boundary violation issue and search for valid alternatives, a hard constraint was implemented in a 4 × 4 grid environment to ensure that all the spaces were placed within the boundaries. Using the Dynamo’s ‘DoesIntersect’ node, the system checks whether each spatial module overlaps with the outer boundary (true if it overlaps, false if not). Based on this Boolean value, an output parameter named ’boxedin’ was defined.
Subsequently, a constraint was set using the Optimize function in GD to fix the ’boxedin’ value to 0 (no boundary violation) as shown in
Figure 15. This shows the successful placement of all the spaces within the 4 × 4 boundary. This was achieved by using the ‘DoesIntersect’ node for the boundary check logic and applying a GD optimization constraint that set the ’boxedin’ parameter to 0. Through this process, it was confirmed that the system could successfully filter and derive only valid alternatives that satisfied the boundary constraints from the various alternatives generated during the Randomize process.
5.1.3. Visualization of Results
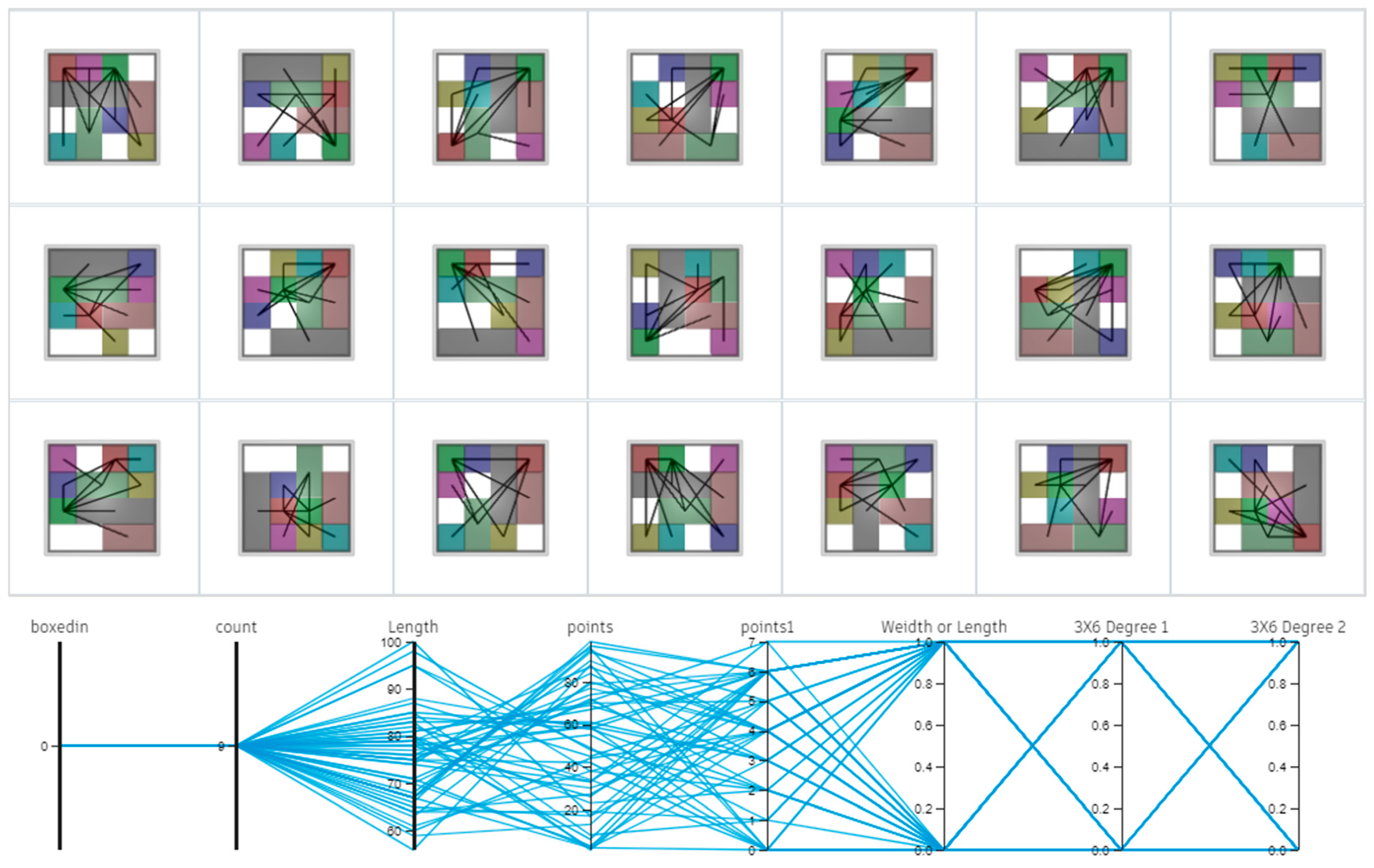
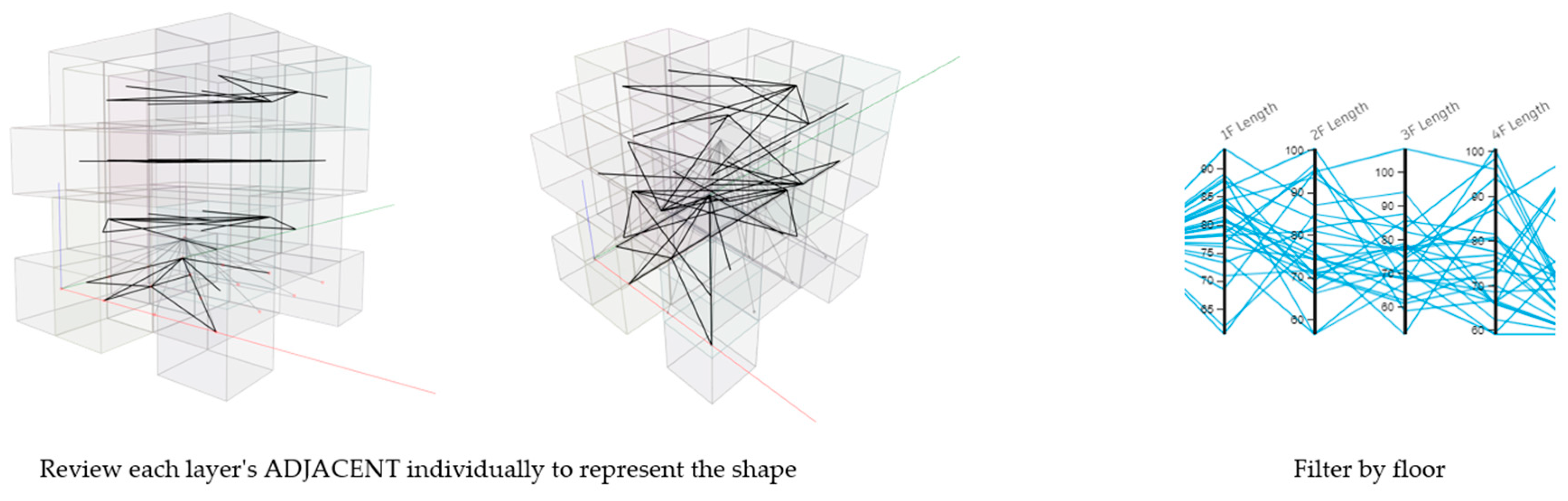
A visualization method was applied to effectively analyze the generated alternatives. Each space was assigned a unique color based on its ’Space Name,’ allowing for an intuitive understanding of the spatial distribution. Furthermore, lines were used to connect spaces with adjacency requirements and visually represent their relationships, as shown in
Figure 16. This is a visualization of the generated floor plan alternatives. The spaces were colored according to their type, and those with adjacent requirements were connected by lines. Additionally, to represent accessibility, lines were generated, and the total sum of their lengths is the output, which is useful for visually examining the circulation efficiency and functional connectivity of the generated alternatives.
In
Figure 17, a length value between 85 and 100 signifies a layout where spaces are distributed too far apart, indicating poor accessibility. The range of 70–85 contains a mix of inadequate and adequate alternatives, requiring further review. Finally, the range of 65–75 indicates that the generated alternatives feature appropriately clustered spatial distributions.
5.2. Expansion to Multi-Story Structure and Optimization Setup
5.2.1. Implementation of Multi-Story Algorithm
Experiments were conducted to extend the basic spatial allocation algorithm to multistory structures. In multistory buildings, certain elements, such as stairwells or utility cores, must remain fixed in the same vertical position across all floors. The logic for implementing this is illustrated in
Figure 18.
- -
Placement and extraction of fixed elements: The stairwell space is placed on the first floor, and its location point is extracted.
- -
Setting multi-story placement constraints: For the other floors, the point of the fixed element, as determined on the first floor, was excluded from the available placement area.
- -
Placement of remaining spaces: The remaining spaces are allocated to the remaining area after excluding the fixed element’s point, while also considering the adjacent requirements for each floor.
Through this process, it was confirmed that the system could effectively handle fixed elements while maintaining the vertical consistency of spatial layouts across floors in a multistory structure.
Figure 19 shows that the placement of the stairwell affected the layouts of the other spaces on all floors. The layout was system-generated by excluding the stairwell area, then creating alternatives by placing the remaining spatial modules of various sizes according to this rule.
5.2.2. Multi-Objective Optimization Setup
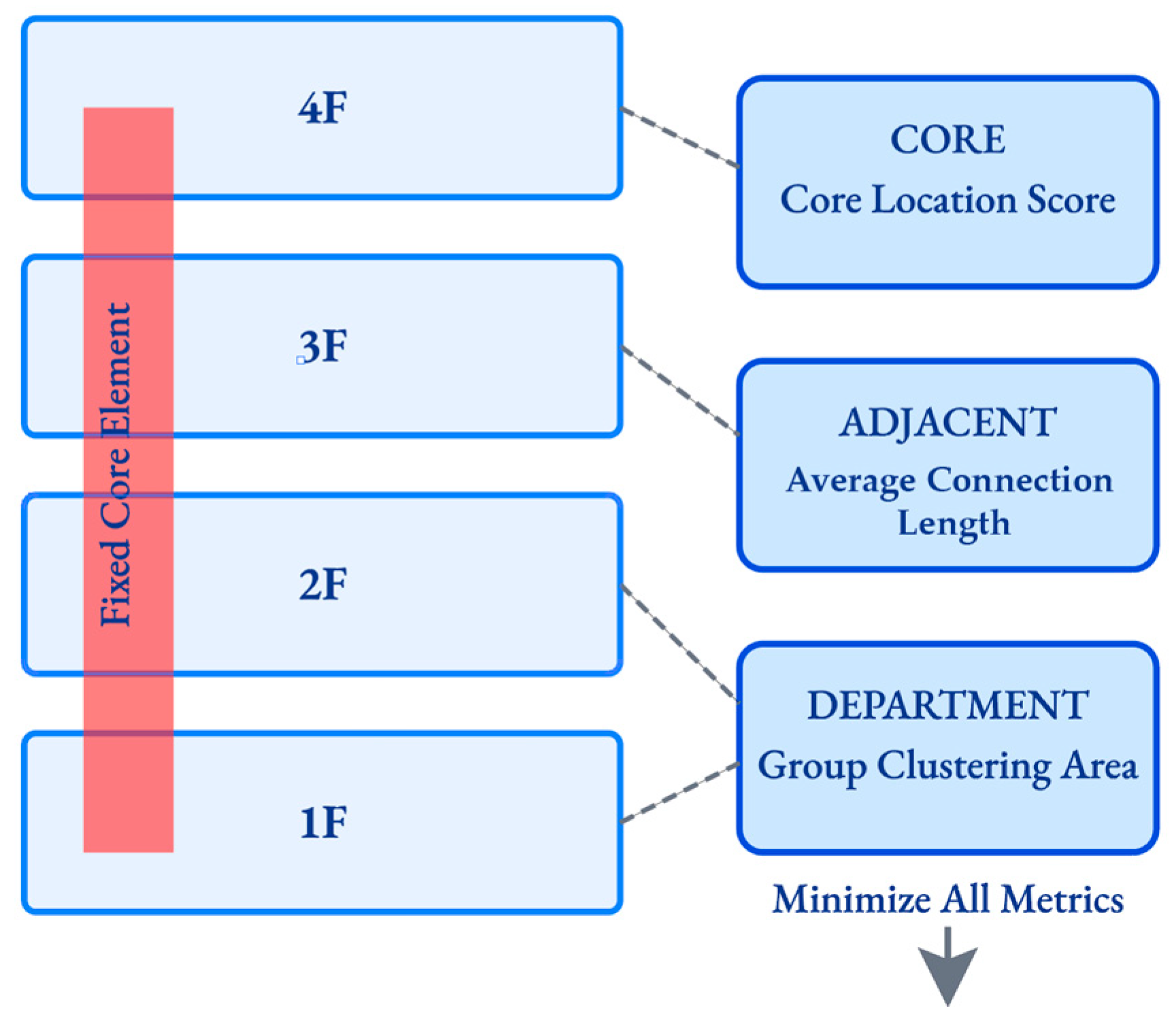
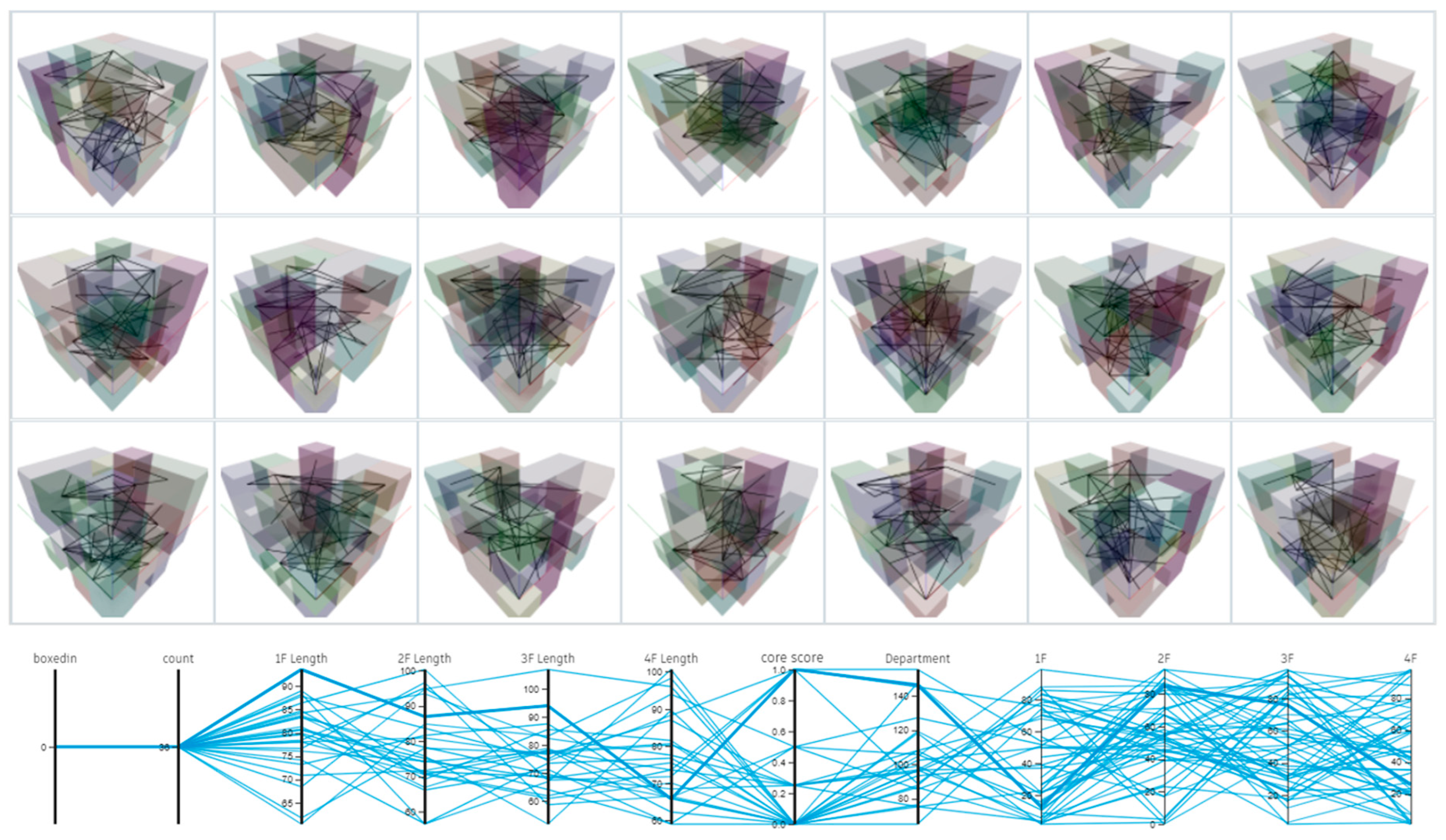
The multistory experiment was adjusted to a four-story scale, and three key optimization objectives were established to guide the generation of practical spatial layouts beyond simple allocation.
Figure 20 shows Aa example layout of a four-story building where optimizations for ADJACENT (connection line length) and DEPARTMENT (polygon area) have been applied while CORE was guided toward the northwest.
CORE (Core Position Optimization): It is generally preferable to place the core on the north or west side, where conditions for natural light and views are relatively unfavorable. To guide this, the northwest corner was assigned the highest score (e.g., 1 point), with scores decreasing toward the southeast. (Goal: Maximize).
ADJACENT (Adjacency/Circulation Optimization): This measures the average length of the connecting lines that represent accessibility between spaces. A shorter length indicates that the related spaces are placed closer together, signifying a higher circulation efficiency. (Goal: Minimize)
DEPARTMENT (Spatial Group Cohesion Optimization): This evaluates the degree of clustering of spaces belonging to the same department or functional group. It is calculated using the area of a polygon enclosing the group; a smaller area indicates that the group is more tightly clustered, indicating higher functional efficiency. (Goal: Minimize)
As shown in
Figure 21, because the rules are executed individually for each floor, specific module layout alternatives can be reviewed by filtering the ADJACENT values on a floor-by-floor basis.
As shown in
Figure 22, the DEPARTMENT values by floor are represented by the polygons as the rules are executed individually on each floor. Alternatives can be filtered by the DEPARTMENT value for each floor or by the sum of the values for all floors.
As shown in
Figure 23, verifying CORE count results by adjusting visibility has been conducted and the placement of the stairwell in the intended location can be confirmed by filtering the CORE score values (1, 0.5, 0.25, and 0.1).
5.3. Implementation and Optimization Results
5.3.1. System Implementation and Data Flow
An integrated Dynamo workflow was constructed to perform multi-objective optimization.
Figure 24 shows an image of the final Dynamo script structure, including logic for processing Excel data input, per-floor spatial allocation (outlining, organizing spaces, list restructuring), and the calculation of ADJACENT and DEPARTMENT metrics. An end-to-end pipeline was built to receive per-floor spatial requirements (Point Input) via Excel data, allocate the multistory spaces based on this input, and then calculate the CORE, ADJACENT, and DEPARTMENT metrics to be passed to the GD optimization engine. The process also included list restructuring and organization for efficient data handling.
5.3.2. Analysis of Optimization Results
The optimization process in the GD was executed for three established objectives. To determine the optimal range of the layouts, the results of a ’Randomize’ run were first analyzed to identify the realistic range of each metric. Based on this analysis, goals (e.g., Minimize) and constraints were set, as shown in
Figure 25. An image from the GD interface shows the optimization goals (Maximize Core, Minimize Adjacent and Department), constraint ranges, and performance distribution of the alternatives derived from the exploration.
The optimization goals were entered as numerical values at the GD interface, as shown in
Figure 26. After setting the three goals (Maximize Core, Minimize Adjacent, and Maximize Department) and their constraints, the results were confirmed, verifying that the process works effectively for the expanded scope of the multistory structure.
The optimization results were derived from the following set ranges:
CORE Score: Range [1–0.5]. This indicated that the core was successfully placed in the outermost northwest corner (1) or in the line adjacent to it (0.5). This indicates that the system effectively controlled the core position according to the design intent.
Adjacent average length: range [55, 75]. The explored alternatives had average lengths within this range, indicating that the spaces requiring connections were placed relatively close to each other, thereby securing circulation efficiency.
Average department area: Range [80, 100]. This suggests that spaces belonging to the same group were effectively clustered, thereby achieving a layout with high functional cohesion.
In summary, the system successfully generated balanced and optimal spatial layout alternatives by simultaneously considering three potentially conflicting objectives: the core position, circulation, and cohesion.
In comparison with existing literature on Spatial Allocation Problems (SAP), the optimization results demonstrate the efficacy of the proposed BIM-integrated approach utilizing NSGA-II. While the reviewer inquired about comparisons regarding the reduction in emissions, it is important to clarify that the metrics in this study focused on functional efficiency rather than environmental performance. However, the performance of the optimization in managing complex constraints is notable. Many studies utilize Genetic Algorithms (GA) or MOGAs for floor plan optimization; however, they often focus on single-floor scenarios or face challenges with the direct implementation of complex multi-story constraints within a practical design environment. Our approach successfully integrated the vertical alignment constraint, ensuring structural consistency across four stories—a challenge often simplified in other models.
Furthermore, compared to recent data-driven approaches using GANs or diffusion models, which excel at generating diverse layouts but may struggle to guarantee strict adherence to hard constraints, our explicit rule-based optimization ensures that 100% of the optimized solutions are geometrically and structurally feasible. The simultaneous optimization of location, circulation, and cohesion within the targeted ranges confirms the robustness of this methodology.
5.4. Discussion
The implementation and experimental results of this study substantiate the efficacy of the Generative Design (GD) methodology in solving complex architectural Spatial Allocation Problems (SAP). The core strategy of this research—the clear distinction and application of ‘Hard Constraints’ and ‘Soft Objectives’—proved crucial in balancing essential geometric validity with the optimization of functional performance. This aligns with the recent consensus in computational design favoring hybrid approaches that combine the reliability of explicit rules with the exploratory power of optimization algorithms [
18,
19].
A key insight derived from this study is the paramount importance of formalized constraint definition. The failure of the initial 3 × 3 grid experiment (
Section 5.1.1) underscored the necessity of reconciling physical limitations with program requirements prior to optimization. The subsequent successful implementation of the boundary constraint (‘boxedin’) ensured fundamental geometric validity. This emphasizes that machine-verifiable, explicit constraints are essential for the reliability of the GD process. This approach is deeply rooted in the tradition of formal design grammars, such as Stiny’s ‘Shape Grammars’ [
10], which hold that the formalization of clear rules is foundational to successful design automation. This provides greater controllability compared to purely data-driven generative models, which can struggle to satisfy strict hard constraints [
23].
Furthermore, the methodology demonstrated significant scalability. By extending the pipeline to a four-story case study and successfully implementing the vertical alignment constraint for fixed elements (e.g., cores, stairwells), the study addressed the inherent complexities of multi-story SAP, such as maintaining structural and functional continuity. The systematic handling of fixed and variable elements reflects Habraken’s ‘Supports’ theory [
12]. While recent studies often employ graph-based representations to manage such topological constraints [
17,
20], this study achieved vertical consistency through direct integration within the BIM workflow, demonstrating a practical approach applicable to actual multi-story building design.
Moreover, this study validated a concrete methodology for improving design quality beyond simple automation by quantifying design intent. By formalizing practical goals—positional preference (CORE), circulation efficiency (ADJACENT), and functional cohesion (DEPARTMENT)—the system successfully navigated the trade-offs between conflicting objectives. This quantification translates the functional and experiential knowledge embedded in architectural traditions, such as Alexander’s ‘A Pattern Language’ [
9], into computable metrics, enabling the systematic evaluation and improvement of design performance during the early design stages.
Despite these contributions, this study has limitations that suggest directions for future research. First, a scope mismatch exists between the initial ambition to optimize modular residential quality (e.g., daylighting and void utilization) and the actual implementation, which focused on general functional efficiency (adjacency and cohesion). Future research should integrate environmental performance indicators or constraints tailored to specific building typologies. Second, the current evaluation metrics rely on basic geometric calculations (centroid distance and polygon area). Future work necessitates the integration of more sophisticated simulation-based metrics that account for actual walking paths, inter-floor travel times, and evacuation regulations. Finally, the scope of automation should be expanded from generating spatial configurations to automatically converting these layouts into detailed BIM objects (e.g., walls, windows, rooms) and integrating Multidisciplinary Optimization (MDO), including structural and energy analysis.
6. Conclusions
This study proposed and validated an automated design pipeline implementing Generative Design (GD) methodologies within a Building Information Modeling (BIM) environment to address the complex Spatial Allocation Problem (SAP) in 3.3 m module-based, multi-story buildings. By systematically formalizing intricate design requirements into machine-interpretable hard constraints and soft objectives, this study established a structured approach to balancing geometric validity and functional efficiency during the early design stages.
The principal achievements include the successful implementation of critical hard constraints to ensure fundamental validity. Specifically, the boundary constraint (‘boxedin’) secured geometric feasibility by ensuring all spaces were placed within defined boundaries, while the vertical alignment constraint maintained structural consistency by aligning fixed elements across floors. Furthermore, to evaluate layout quality, practical design goals were quantified as performance metrics: positional preference (CORE), circulation efficiency (ADJACENT), and functional cohesion (DEPARTMENT). Multi-objective optimization was performed to successfully derive optimal alternatives that balanced design intent and functional efficiency. The end-to-end workflow, from data input through generation and evaluation to optimization execution, was fully integrated within the BIM environment, providing a reproducible and practical pipeline that maintains data continuity and allows for immediate visualization of results.
In conclusion, by clearly defining the complex multi-story SAP through the structured application of hard constraints and soft objectives within a BIM environment, this study successfully demonstrated the substantial potential and scalability of rule-based design automation.
Author Contributions
Conceptualization, Y.H., J.L. and W.C. (WonSeok Cho); methodology, W.C. (Wonho Cho) and M.J.; formal analysis, W.C. (Wonho Cho) and M.J.; investigation, W.C. (Wonho Cho) and W.C. (WonSeok Cho); resources, Y.H.; writing—original draft preparation, W.C. (Wonho Cho) and W.C. (WonSeok Cho); writing—review and editing, J.L. and Y.H.; visualization, W.C. (Wonho Cho); supervision, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by Samsung Electronics Co., Ltd. (IO250102-11622-01).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
Author Yeongyu Hwang, WonSeok Choi and Minhyuk Jung was employed by the company Construction Team, Samsung Electronics Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The authors declare that this study received funding from Samsung Electronics. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.
References
- Smith, R.E. Prefab Architecture: A Guide to Modular Design and Construction; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Parracho, D.F.; Nour El-Din, M.; Esmaeili, I.; Freitas, S.S.; Rodrigues, L.; Poças Martins, J.; Corvacho, H.; Delgado, J.M.; Guimarães, A.S. Modular Construction in the Digital Age: A Systematic Review on Smart and Sustainable Innovations. Buildings 2025, 15, 765. [Google Scholar] [CrossRef]
- Djukanovic, M.; Alegre, A.; Teixeira Bastos, F. Prefabricated Solutions for Housing: Modular Architecture and Flexible Living Spaces. Buildings 2025, 15, 862. [Google Scholar] [CrossRef]
- Picard, J.-C.; Queyranne, M. On the one-dimensional space allocation problem. Oper. Res. 1981, 29, 371–391. [Google Scholar] [CrossRef]
- Cai, Y.; Chen, J.; Zhang, C.; Wang, B. A parking space allocation method to make a shared parking strategy for appertaining parking lots of public buildings. Sustainability 2018, 11, 120. [Google Scholar] [CrossRef]
- Lee, J.; Cho, W.; Kang, D.; Lee, J. Simplified methods for generative design that combine evaluation techniques for automated conceptual building design. Appl. Sci. 2023, 13, 12856. [Google Scholar] [CrossRef]
- Weber, R.E.; Mueller, C.; Reinhart, C. Automated floorplan generation in architectural design: A review of methods and applications. Autom. Constr. 2022, 140, 104385. [Google Scholar] [CrossRef]
- Ma, W.; Wang, X.; Wang, J.; Xiang, X.; Sun, J. Generative design in building information modelling (BIM): Approaches and requirements. Sensors 2021, 21, 5439. [Google Scholar] [CrossRef]
- Alexander, C. A Pattern Language: Towns, Buildings, Construction; Oxford University Press: Oxford, UK, 1977. [Google Scholar]
- Stiny, G. Introduction to shape and shape grammars. Environ. Plan. B Plan. Des. 1980, 7, 343–351. [Google Scholar] [CrossRef]
- Berrada, I.; Ferland, J.A.; Michelon, P. A multi-objective approach to nurse scheduling with both hard and soft constraints. Socio-Econ. Plan. Sci. 1996, 30, 183–193. [Google Scholar] [CrossRef]
- Habraken, N.J. Supports: An Alternative to Mass Housing; Routledge: London, UK, 2021. [Google Scholar]
- Li, S.; Jiang, Z.; Xu, Z. BIM-Based Model Checking: A Scientometric Analysis and Critical Review. Appl. Sci. 2024, 15, 49. [Google Scholar] [CrossRef]
- Alnajjar, O.; Atencio, E.; Turmo, J. Framework for Optimizing the Construction Process: The Integration of Lean Construction, Building Information Modeling (BIM), and Emerging Technologies. Appl. Sci. 2025, 15, 7253. [Google Scholar] [CrossRef]
- Atencio, E.; Lozano, F.; Alfaro, I.; Lozano-Galant, J.A.; Muñoz-La Rivera, F. Integrating web-based weather data into building information modeling models through robot process automation. Appl. Sci. 2024, 14, 9109. [Google Scholar] [CrossRef]
- Cho, J.; Kim, S.; Kang, S. Development of a Spatial Alignment System for Interacting with BIM Objects in Mixed Reality. Appl. Sci. 2025, 15, 9713. [Google Scholar] [CrossRef]
- Cao, K.; Batty, M.; Huang, B.; Liu, Y.; Yu, L.; Chen, J. Spatial multi-objective land use optimization: Extensions to the non-dominated sorting genetic algorithm-II. Int. J. Geogr. Inf. Sci. 2011, 25, 1949–1969. [Google Scholar] [CrossRef]
- Krish, S. A practical generative design method. Comput.-Aided Des. 2011, 43, 88–100. [Google Scholar] [CrossRef]
- Mountstephens, J.; Teo, J. Progress and challenges in generative product design: A review of systems. Computers 2020, 9, 80. [Google Scholar] [CrossRef]
- Wang, B.; Lu, W.; Zhang, Y. A graph-enabled parametric modeling approach for façade layout generative design. J. Build. Eng. 2025, 105, 112481. [Google Scholar] [CrossRef]
- Wang, B.; Liang, Y.; Zheng, T.; Yuan, M.; Zhang, H. Optimisation of a downstream oil supply chain with new pipeline route planning. Chem. Eng. Res. Des. 2019, 145, 300–313. [Google Scholar] [CrossRef]
- Su, X.; Cai, H. Enabling construction 4D topological analysis for effective construction planning. J. Comput. Civ. Eng. 2016, 30, 04014123. [Google Scholar] [CrossRef]
- Aalaei, M.; Saadi, M.; Rahbar, M.; Ekhlassi, A. Architectural layout generation using a graph-constrained conditional Generative Adversarial Network (GAN). Autom. Constr. 2023, 155, 105053. [Google Scholar] [CrossRef]
- Zeng, P.; Gao, W.; Yin, J.; Xu, P.; Lu, S. Residential floor plans: Multi-conditional automatic generation using diffusion models. Autom. Constr. 2024, 162, 105374. [Google Scholar] [CrossRef]
- Qin, S.; Guan, H.; Liao, W.; Gu, Y.; Zheng, Z.; Xue, H.; Lu, X. Intelligent design and optimization system for shear wall structures based on large language models and generative artificial intelligence. J. Build. Eng. 2024, 95, 109996. [Google Scholar] [CrossRef]
- Luo, G.; Zhou, X.; Liao, Y.; Ding, Y.; Liu, J.; Xia, Y.; Qi, H. Automated Residential Bubble Diagram Generation Based on Dual-Branch Graph Neural Network and Variational Encoding. Appl. Sci. 2025, 15, 4490. [Google Scholar] [CrossRef]
- Drira, A.; Pierreval, H.; Hajri-Gabouj, S. Facility layout problems: A survey. Annu. Rev. Control 2007, 31, 255–267. [Google Scholar] [CrossRef]
- Nagy, D.; Lau, D.; Locke, J.; Stoddart, J.; Villaggi, L.; Wang, R.; Zhao, D.; Benjamin, D. Project discover: An application of generative design for architectural space planning. In Proceedings of the Symposium on Simulation for Architecture and Urban Design, Toronto, ON, Canada, 22–24 May 2017; pp. 1–8. [Google Scholar]
- Michalek, J.; Choudhary, R.; Papalambros, P. Architectural layout design optimization. Eng. Optim. 2002, 34, 461–484. [Google Scholar] [CrossRef]
Figure 1.
Key components of overall methodology.
Figure 1.
Key components of overall methodology.
Figure 2.
Grid system definition and program elements.
Figure 2.
Grid system definition and program elements.
Figure 3.
Components of the optimization model.
Figure 3.
Components of the optimization model.
Figure 4.
Conceptual diagram of evaluation metrics: Illustrations showing (a) Adjacency (measuring distance between spaces), (b) Departmental Grouping (measuring group area), and (c) Positional Preference (location evaluation based on a score map) on a sample grid plane.
Figure 4.
Conceptual diagram of evaluation metrics: Illustrations showing (a) Adjacency (measuring distance between spaces), (b) Departmental Grouping (measuring group area), and (c) Positional Preference (location evaluation based on a score map) on a sample grid plane.
Figure 5.
Generative Design Process Flowchart: A flow diagram illustrating the sequence.
Figure 5.
Generative Design Process Flowchart: A flow diagram illustrating the sequence.
Figure 6.
Key components of implementation and validation.
Figure 6.
Key components of implementation and validation.
Figure 7.
System architecture and data flow diagram.
Figure 7.
System architecture and data flow diagram.
Figure 8.
Testing grid size limitations.
Figure 8.
Testing grid size limitations.
Figure 9.
Boundary constraint test.
Figure 9.
Boundary constraint test.
Figure 10.
Conceptual diagram of the four-story multi-objective optimization.
Figure 10.
Conceptual diagram of the four-story multi-objective optimization.
Figure 11.
Metric Visualization on floor layout (adjacent connection, core fixed element, department grouping, functional space).
Figure 11.
Metric Visualization on floor layout (adjacent connection, core fixed element, department grouping, functional space).
Figure 12.
Cubic reference configuration and length and number of modules.
Figure 12.
Cubic reference configuration and length and number of modules.
Figure 13.
3 × 3 images of situations in which space is out of bound or impossible to deploy on a grid.
Figure 13.
3 × 3 images of situations in which space is out of bound or impossible to deploy on a grid.
Figure 14.
Situational images placed within a 3 × 3 grid, but not deployable and causing an error.
Figure 14.
Situational images placed within a 3 × 3 grid, but not deployable and causing an error.
Figure 15.
Implementation and results of the ‘boxedin’ constraint in a 4 × 4 grid.
Figure 15.
Implementation and results of the ‘boxedin’ constraint in a 4 × 4 grid.
Figure 16.
Visualization of space colors and adjacency.
Figure 16.
Visualization of space colors and adjacency.
Figure 17.
Reviewing alternatives by filtering the output length value.
Figure 17.
Reviewing alternatives by filtering the output length value.
Figure 18.
Multi-story extension and handling of fixed elements such as the stairwell.
Figure 18.
Multi-story extension and handling of fixed elements such as the stairwell.
Figure 19.
Placement of other modules avoiding the fixed stairwell space.
Figure 19.
Placement of other modules avoiding the fixed stairwell space.
Figure 20.
Conceptual explanation of ADJACENT, DEPARTMENT, and CORE.
Figure 20.
Conceptual explanation of ADJACENT, DEPARTMENT, and CORE.
Figure 21.
Individual filtering of ADJACENT by floor.
Figure 21.
Individual filtering of ADJACENT by floor.
Figure 22.
Individual filtering of DEPARTMENT by floor.
Figure 22.
Individual filtering of DEPARTMENT by floor.
Figure 23.
Verifying CORE count results by adjusting visibility.
Figure 23.
Verifying CORE count results by adjusting visibility.
Figure 24.
Final Dynamo script process overview.
Figure 24.
Final Dynamo script process overview.
Figure 25.
Verifying result distribution for setting GD optimization conditions.
Figure 25.
Verifying result distribution for setting GD optimization conditions.
Figure 26.
Input values and results in the Generative Design interface.
Figure 26.
Input values and results in the Generative Design interface.
Table 1.
Thematic Analysis of Key Literature.
Table 1.
Thematic Analysis of Key Literature.
| Category | Author/Year | Journal/Publisher | Summary |
|---|
| Theoretical Foundations | Alexander, 1977 [9] | Oxford University Press | Systematized the recurring ‘context-problem-solution’ relationships in space as ‘patterns’, providing functional/experiential semantics (A Pattern Language). |
| Theoretical Foundations | Stiny [10] | Environment and planning B: planning and design | Established the design process as a formal grammar by applying generation and substitution rules to geometric shapes (Shape Grammars). |
| Theoretical Foundations | Habraken [12] | Routledge | Introduced the ‘Open Building’ concept, separating a building into a fixed ‘support’ and variable ‘infill’. |
| BIM Integration & Tools | Li [13] | Applied Sciences | Practical successor to theoretical traditions using the modern BIM technology platform (BIM-Based Model Checking). |
| BIM Integration & Tools | Alnajjar [14] | Applied Sciences | Practical successor to theoretical traditions using the modern BIM technology platform (Optimizing the Construction Process). |
| BIM Integration & Tools | Atencio [15] | Applied Sciences | Data-driven approaches that learn implicit patterns from large-scale data. |
| BIM Integration & Tools | Cho [16] | Applied Sciences | Suggests that requirements like the ‘Vertical Alignment Constraint’ can be translated into graph constraints. |
| Optimization & Generative Design | Cao [17] | Int. Journal of Geographical Information Science | Proposed a method combining graph-based representations with a multi-objective genetic algorithm (MOGA) for hybrid modularization of architectural floor plans. |
| Optimization & Generative Design | Krish [18] | Computer-aided design | Hybrid approaches (Generative Design) that combine satisfying mandatory constraints with optimizing design objectives. |
| Optimization & Generative Design | Mountstephens [19] | Computers | Hybrid approaches that combine satisfying mandatory constraints with optimizing design objectives. |
| Advanced AI/ML Automation | Wang [20] | Journal of Building Engineering | Suggests that requirements like the ‘ADJACENT Objective’ can be naturally translated into graph constraints. |
| Advanced AI/ML Automation | Wang [21] | Chemical Engineering Research and Design | Proposed a pipeline combining deep learning and graph algorithms to generate and modify room layouts. |
| Advanced AI/ML Automation | Su [22] | Journal of Computing in Civil Engineering | Introduced a hybrid configuration learning topological patterns via a diffusion model and applying explicit rules as post-processing constraints. |
| Advanced AI/ML Automation | Aalaei [23] | Automation in Construction | Utilized GNNs and CGAN to transform architectural rules (boundaries, adjacencies) into graph constraints to generate rule-compliant floor plans. |
| Advanced AI/ML Automation | Zeng [24] | Automation in Construction | Proposed a diffusion model that integrates heterogeneous conditions (boundaries, graphs, text) into a single pipeline. |
| Advanced AI/ML Automation | Qin [25] | Journal of Building Engineering | Introduced LLMs to automatically convert natural language prompts into JSON conditions. |
| Advanced AI/ML Automation | Luo [26] | Applied Sciences | Researched a method to provide a good initial solution (seed) by automatically generating bubble diagrams using GNNs. |
Table 2.
Optimization goals and setting ranges for the case study (Phase 2).
Table 2.
Optimization goals and setting ranges for the case study (Phase 2).
| Metric | Goal | Description | Constraint Range
(Based on Preliminary Analysis) |
|---|
| CORE | Minimize | Core Location (Guided to Northwest) | Min: −1.0/Max: −0.5 |
| ADJACENT | Minimize | Average Length between Adjacent Spaces | Min: 55/Max: 75 |
| DEPARTMENT | Minimize | Clustering Area of Space Groups | Min: 10/Max: 25 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).