Enhanced Velocity Extraction of Moving Subject Using Through-Wall-Imaging Radar

Abstract

Detecting human movement through walls is vital for disaster response and security, where obstacles obscure visibility and endanger rescue operations, necessitating advanced through-wall radar (TWR) solutions. This study introduces a novel method to enhance velocity estimation accuracy in TWR systems despite signal attenuation caused by walls. Our proposed method dynamically adjusts the beamforming range based on radar-target distance, improving point cloud reconstruction and enabling precise velocity measurements. We conducted experiments in 1D and 2D indoor environments, with and without a brick wall, to validate the proposed method’s effectiveness. In both 1D and 2D experiments, the proposed method successfully restored the velocity information of five subjects located behind a brick wall, achieving root mean square error (RMSE) values of approximately 0.1–0.2 m/s in most cases. Furthermore, statistical comparisons before and after applying the proposed method in the brick wall environment revealed significant reductions in RMSE (p < 0.05) and significant increases in the number of detected point clouds (p < 0.05), confirming the method’s effectiveness in enhancing both velocity extraction accuracy and detection capability.

1. Introduction

Through-wall motion detection and tracking technology has recently gained significant attention due to its potential applications in various fields, such as counter-terrorism, disaster rescue, and building safety diagnostics. In disaster scenarios like terrorism or natural calamities, survivors may be trapped in spaces obscured by walls or structures, making rapid and accurate detection critical for effective rescue operations. However, direct human intervention in such environments poses risks to rescue personnel, including secondary collapses or falling debris. Additionally, conventional imaging equipment or sensor-based systems cannot penetrate opaque structures, limiting the ability to acquire information beyond the line of sight. These constraints have spotlighted radar sensors capable of penetrating walls as a promising alternative.

In recent years, advancements in ultra-wideband radar technologies, such as Impulse Radio Ultra-WideBand (IR-UWB) and Stepped Frequency Continuous Wave (SFCW), which offer high temporal resolution and wide frequency bandwidth, have enabled precise detection and tracking of human presence and movement behind obstacles [1]. However, despite their promising wall-penetration capabilities, these radar types often involve complex hardware configurations, trade-offs in temporal resolution, and limitations in real-time processing performance. In contrast, Frequency-Modulated Continuous Wave (FMCW) radar offers high range resolution and precise Doppler measurements while maintaining relatively simple hardware architecture and suitability for real-time applications. Therefore, a 4D imaging radar based on FMCW was selected for this study. Existing studies on radar-based through-wall sensing can be categorized into preprocessing for noise reduction [2,3], vital sign detection [4,5], target tracking [6,7,8], motion recognition [9,10], and spatial mapping [11,12]. Among these, target tracking research has focused on tracking moving objects using Through-Wall Imaging Radar (TWIR/TWR) systems. These studies have proposed customized methods to effectively handle changes in target image size and orientation within compact TWIR systems. For instance, some research has utilized statistical information within a mean-shift framework for target tracking or dynamically estimated target size and orientation to propose stable tracking methods in small antenna array environments [13,14,15,16]. Other studies have addressed multipath interference issues during tracking by leveraging human movement patterns to calculate and infer delays in radar signals or by applying motion correlation filters to compensate for real-time variations in radar signal amplitude and direction for more accurate target tracking [17,18,19].

However, a common challenge in through-wall radar research is the significant reduction in point cloud data due to signal power attenuation caused by wall penetration and increasing distance, which is a primary factor in reducing target detection accuracy. As radar signals weaken during wall penetration, the number of point clouds decreases, and noise increases. Additionally, as the target moves farther from the radar, signal power further diminishes, exacerbating the reduction in point cloud data. This study focuses on extracting target velocity information rather than positional data in environments where point cloud reduction is inevitable. Since velocity information is calculated based on the average velocity of the entire point cloud, it is likely to maintain consistency even when the number of point clouds decreases. However, velocity information is not immune to data loss caused by wall penetration. While some previous studies have investigated velocity information in through-wall radar systems [20], few have specifically focused on improving the accuracy of velocity data. Recently, research has begun to focus on improving the accuracy of velocity information in through-wall radar systems. For instance, one approach has utilized the joint spatiotemporal characteristics of MIMO radar to enhance range–velocity measurement accuracy [21]. In line with this growing trend, this study also focuses on improving the accuracy of velocity estimation in through-wall scenarios.

This study proposes a technique to enhance the accuracy of velocity information in through-wall environments. The proposed method improves upon existing beamforming techniques by dynamically adjusting the beamforming range based on the distance between the radar and the target. This approach effectively compensates for the loss of point clouds caused by wall penetration or increased distance, thereby enabling more accurate velocity measurements of moving targets. To demonstrate that the proposed method effectively increases target point clouds and improves velocity accuracy, experiments were designed and conducted across various environments and scenarios. These experiments were performed in environments with and without a brick wall to analyze the ability to detect target movement behind a wall. The experiments observed velocity changes corresponding to various target movements, including Normal Walk and Walk-Stop motions. Additionally, experiments in both 1D and 2D environments were conducted to analyze the accuracy of target velocity information extraction.

The main contributions of this study are as follows: (1) A beamforming-based algorithm is proposed to enable robust velocity estimation despite signal attenuation and distortion in through-wall scenarios. (2) The proposed method is validated in both 1D and 2D experimental setups, and its accuracy is verified against motion sensor-based ground truth data. (3) The effectiveness of the proposed method in improving velocity estimation accuracy compared to existing methods is quantitatively demonstrated.

2. Signal Processing for FMCW Radar

Radar is a device that can detect not only the presence of an object but also its direction, distance, and other information by transmitting electromagnetic waves and receiving the signals reflected from the object. Radars can be classified into several types depending on the modulation scheme of the transmitted and received signals. In this study, a Frequency Modulated Continuous Wave (FMCW) radar, whose transmitted signal frequency varies linearly with time, was employed. Since the frequency of the transmitted signal increases at a constant rate, the information of the detected object can be effectively obtained by analyzing the frequency difference between the transmitted and received signals. The transmitted signal $m_s\left(t\right)$ and the received signal $m_r\left(t\right)$ can be expressed as Equations (1) and (2), respectively.

$$m_s\left(t\right)=M_s\left(t\right)·cos\left(2\pi (f_c+{\displaystyle \frac{BW·t}{2T_c}})t\right)$$

(1)

$$m_r\left(t\right)=M_r\left(t\right)·cos\left(2\pi (f_c+f_d+{\displaystyle \frac{BW·(t-t_d)}{2T_c}})(t-t_d)\right)$$

(2)

Here, t denotes time, $t_d$ represents the time delay between the transmitted and received signals, $T_c$ is the chirp duration, $f_c$ is the carrier frequency, $BW$ is the bandwidth, and $f_d$ is the Doppler frequency. $M_s\left(t\right)$ is the time-varying envelope (amplitude) of the transmitted signal, and $M_r\left(t\right)$ is the time-varying envelope (amplitude) of the received signal; their magnitudes may vary over time due to system characteristics or environmental influences. In this case, the FMCW radar continuously transmits the transmitted signal $m_s\left(t\right)$, and the received signal $m_r\left(t\right)$ is processed through a mixer and a low-pass filter (LPF) to generate the intermediate frequency (IF) signal $x\left(t\right)$.

$$x\left(t\right)=M_x\left(t\right)·cos\left(2\pi ({\displaystyle \frac{BW·t_d}{T_c}}-f_d)t+2\pi (f_c+f_d)t_d\right)$$

(3)

By applying a fast Fourier transform (FFT) to the intermediate frequency (IF) signal $x\left(t\right)$, the range information can be obtained. Specifically, the range FFT extracts the beat frequency $f_b$, from which the time delay $t_d$ is derived to estimate the range $R\left(t\right)$. Furthermore, a second FFT is performed along the slow-time dimension to obtain the Doppler spectrum. This spectrum provides the velocity information of the target. The beat frequency is given by the following:

$$f_b={\displaystyle \frac{BW·t_d}{T_c}}-f_d={\displaystyle \frac{BW·t_d}{T_c}}\left(\because {\displaystyle \frac{BW·t_d}{T_c}}\gg f_d\right)$$

(4)

In general FMCW radar systems, the carrier frequency $f_c$ typically operates in the 76–81 GHz band, and the radar module used in this study operates at a center frequency of 79 GHz. Assuming that a target is moving toward the radar at 1 m/s, the Doppler frequency shift can be estimated using the standard Doppler equation:

$$f_d=\left({\displaystyle \frac{2v}{c}}\right)·f_c$$

(5)

Substituting the values gives the following:

$$f_d=\left({\displaystyle \frac{2\times 1}{3\times {10}^8}}\right)·79\times {10}^9\approx 527\mathrm{Hz}$$

Meanwhile, the radar system used in this study has a bandwidth of $BW=3$ GHz and a chirp duration of $T_c=256\mathrm{\mu }\mathrm{s}$. For a target located approximately 4 m away, the time delay is estimated as $t_d\approx 26.7$ ns. Substituting these values yields the following:

$${\displaystyle \frac{BW·t_d}{T_c}}={\displaystyle \frac{3\times {10}^9·26.7\times {10}^{-9}}{256\times {10}^{-6}}}\approx 312.89\mathrm{kHz}$$

This value is over 590 times greater than the estimated Doppler frequency ($f_d\approx 527$ Hz), confirming that the assumption $\left({\displaystyle \frac{BW·t_d}{T_c}}\gg f_d\right)$ is valid under the system conditions considered in this study. Based on this assumption, the range $R\left(t\right)$ can be simplified as follows:

$$R\left(t\right)={\displaystyle \frac{c·t_d}{2}}={\displaystyle \frac{c}{2}}·{\displaystyle \frac{f_b·T_c}{BW}}={\displaystyle \frac{f_b·T_c·c}{2BW}}$$

(6)

The velocity $v\left(t\right)$ is obtained by analyzing the phase change between two chirps within the signal $x\left(t\right)$.

$$\Delta \varphi =2\pi (f_c+f_d)\Delta t_d=2\pi f_c\Delta t_d(\because f_c\gg f_d)$$

(7)

Here, the additional time delay $\Delta t_d$ arises from the extra path length $2v{T}_c$ traveled by the target during the chirp interval, which is expressed as a time delay by dividing by the propagation speed c. $\Delta t_d$ can be converted to the time interval $T_c$ between two chirps. Assuming that the target moves with a velocity v (m/s) during this time, Equation (7) can be computed as Equation (8).

$$\Delta \varphi =2\pi f_c\Delta t_d=2\pi f_c·\left({\displaystyle \frac{2v{T}_c}{c}}\right)={\displaystyle \frac{4\pi v{f}_c{T}_c}{c}}$$

(8)

In Equation (9), by additionally applying the Fast Fourier Transform (FFT), the frequency components can be analyzed to estimate the phase change frequency.

$$v={\displaystyle \frac{c\Delta \varphi }{4\pi f_c{T}_c}}$$

(9)

As described above, FMCW radar can precisely acquire information on the target’s range and velocity through signal processing utilizing FFT. Based on this, it is possible to detect and estimate the position and movement status of objects.

3. Proposed Through-the-Wall Velocity Detection Method

3.1. Point Cloud and Velocity Information Due to Wall Penetration

Radar observations indicate that, as the distance between the radar and the target increases, or when penetrating a wall, the density of the target’s point cloud decreases and noise increases. These issues serve as major obstacles to effectively detecting the movement of the target. Therefore, methods to reduce noise and to detect the target’s point cloud more effectively are necessary.

Figure 1 shows a graph illustrating the change in the number of point clouds according to the target’s moving distance, both when there is no wall present and when a wall is present. In the graph, the black line represents the distance between the radar and the target, and the red line represents the number of point clouds respectively. Figure 1 confirms that regardless of the presence of a wall, the number of point clouds tends to decrease as the distance between the radar and the target increases. In particular, in the environment with a wall, the number of point clouds converges nearly to zero as the distance between the radar and the target increases.

Additionally, when examining the maximum number of point clouds, it can be observed that the maximum number decreases from approximately 250 to 150 when comparing the case without a wall (Figure 1a) to the case with a brick wall (Figure 1b).

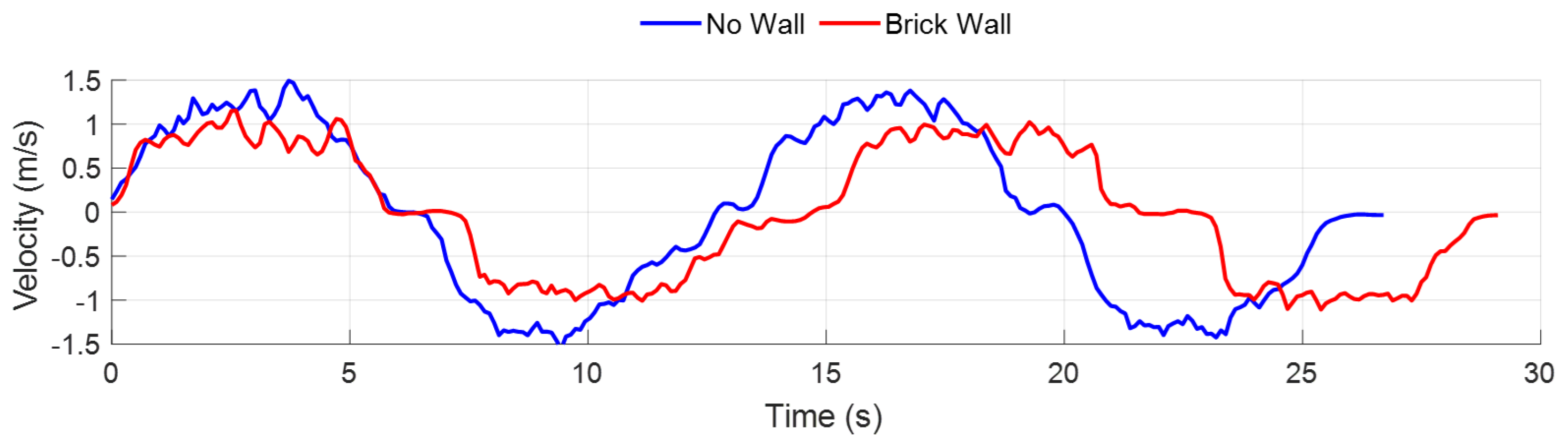
Figure 2 illustrates the average velocity of the point cloud under each condition. It can be observed that the velocity changes in the two conditions exhibit a similar trend.

As shown in Figure 2, the velocity graphs exhibit similar patterns in both wall-free and brick wall conditions, indicating that the loss of velocity information is relatively minor despite a decrease in the number of point clouds. This is because the velocity information is computed based on the average velocity of the entire point cloud, allowing it to maintain consistency even when some point clouds are lost. Based on this observation, this study proposes a method that leverages velocity information to effectively detect the motion of targets located behind a wall.

3.2. Proposed Velocity Enhancement Method

Signal attenuation through walls is modeled as a function of material, frequency, and thickness d, using the expression $e^{-2\alpha d}$, where $\alpha$ denotes the attenuation constant of the material. It is assumed that the signal passes through the wall twice (forward and backward) during transmission and reflection. The received power in this study follows the radar equation and is expressed as follows:

$$P_r\approx P_t·G_t\left({\theta }_0\right)·G_r\left({\theta }_0\right)·{\displaystyle \frac{{\lambda }^2\sigma }{{\left(4\pi \right)}^3{R}^4}}·e^{-2\alpha d}$$

(10)

Here, $G_t\left({\theta }_0\right)$ and $G_r\left({\theta }_0\right)$ denote the transmit and receive antenna gains, R is the radar–target distance, $\lambda$ is the wavelength, and $\sigma$ is the radar cross section (RCS) of the target. When array beamforming is applied, an additional beamforming gain $G^{\mathrm{bf}}\left({\theta }_0\right)$ is introduced, which is given by the following:

$$G^{\mathrm{bf}}\left({\theta }_0\right)={\displaystyle \frac{|w^{H}a\left({\theta }_0\right){|}^2}{{\parallel w\parallel }^2}}$$

(11)

Under uniform weighting, the beamforming gain increases proportionally with the number of array elements N, and the corresponding 3-dB mainlobe width can be approximated as follows:

$$\Delta {\theta }_{3\mathrm{dB}}\approx 0.886·{\displaystyle \frac{\lambda }{N{d}_e}}$$

(12)

where $d_e$ is the element spacing. Therefore, the effective SNR degradation due to wall attenuation $e^{-2\alpha d}$ can be compensated by beamforming gain $G^{\mathrm{bf}}$, and the expansion of the virtual array $N_{\mathrm{virt}}$ in this study contributes to improved spatial resolution and estimation stability.

In practice, conventional fixed beamforming techniques are limited in their ability to cope with target distance variations and the resulting signal degradation. To address this, the proposed Ramp-up Beamforming adaptively adjusts its beamforming parameters based on the radar-target distance.

The block diagram of the proposed velocity enhancement method for targets behind a wall is shown in Figure 3. The proposed method improves velocity estimation accuracy in through-wall scenarios by employing ramp-up beamforming to increase the number of point clouds.

3.2.1. Experimental Environment

Figure 4 illustrates a detailed schematic of the experimental environment, showing the arrangement of key equipment and structures. The experimental methods, detailed radar specifications, and the actual environment are presented in Section 4. The experimental environment is divided into one-dimensional and two-dimensional settings, with distinct procedures systematically applied for each.

In the one-dimensional setting, the subject starts from a point 3.8 m away from the radar and walks back and forth twice along a straight line covering a distance of 4.5 m. The experiment is conducted under two conditions: without a brick wall and with a brick wall present. Subsequently, in the two-dimensional experiment, the subject moves laterally within a 2 m wide space. The movement follows a systematic path in the order indicated by the numbers in Figure 4b, where numbers 1–8 illustrate the sequential walking paths of the subject.

3.2.2. Proposed Ramp-Up Beamforming

The core principle of conventional beamforming techniques is to form beams at specific angles and consider the angle with the highest received beam intensity as the direction of the target. However, conventional beamforming maintains a fixed beamforming range, which leads to increased noise within the detection range as the target moves farther away. Therefore, by dynamically adjusting the detection range according to the target’s movement distance, target detection can be made more effective.

Figure 5 illustrates the horizontal and vertical detection ranges in one-dimensional and two-dimensional environments. Ensure that the azimuth width A and the elevation height E remain constant regardless of the distance $R_i$ the beamforming angles, ${\theta }_{azi}$ and ${\theta }_{ele}$, are adjusted as follows.

$$\begin{array}{cc}\hfill {\theta }_{azi}& ={tan}^{-1}\left({\displaystyle \frac{A}{R_i}}\right)\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\theta }_{ele}& ={tan}^{-1}\left({\displaystyle \frac{E}{R_i}}\right)\hfill \end{array}$$

(14)

Here, $R_i$ denotes the distance between the radar and the target, and i represents the scan index. In Equations (13) and (14), the process of calculating the displacement of the target and the value of $R_i$ is described in Equation (15).

$$R_i=\left\{\begin{array}{cc}{\displaystyle \frac{b_e+b_s}{2}},\hfill & \mathrm{if}\mathrm{data}\mathrm{exist}\hfill \\ R_{i-1},\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(15)

In Equation (15), $b_e$ denotes the starting value of the section with the maximum number of point clouds, and $b_s$ represents the ending value of the same section. The median value of the section with the largest number of collected point clouds is used as the distance between the radar and the target. If scan data is not available, the previously calculated value of $R_i$ is used instead. To prevent abrupt changes in $R_i$, additional processing as described in Equation (16) is performed before applying the results to Equations (13) and (14).

$$R_i=\left\{\begin{array}{cc}{R}_i,\hfill & \mathrm{if}\left|R_i-R_{i-1}\right|\le T\hfill \\ R_{i-1},\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(16)

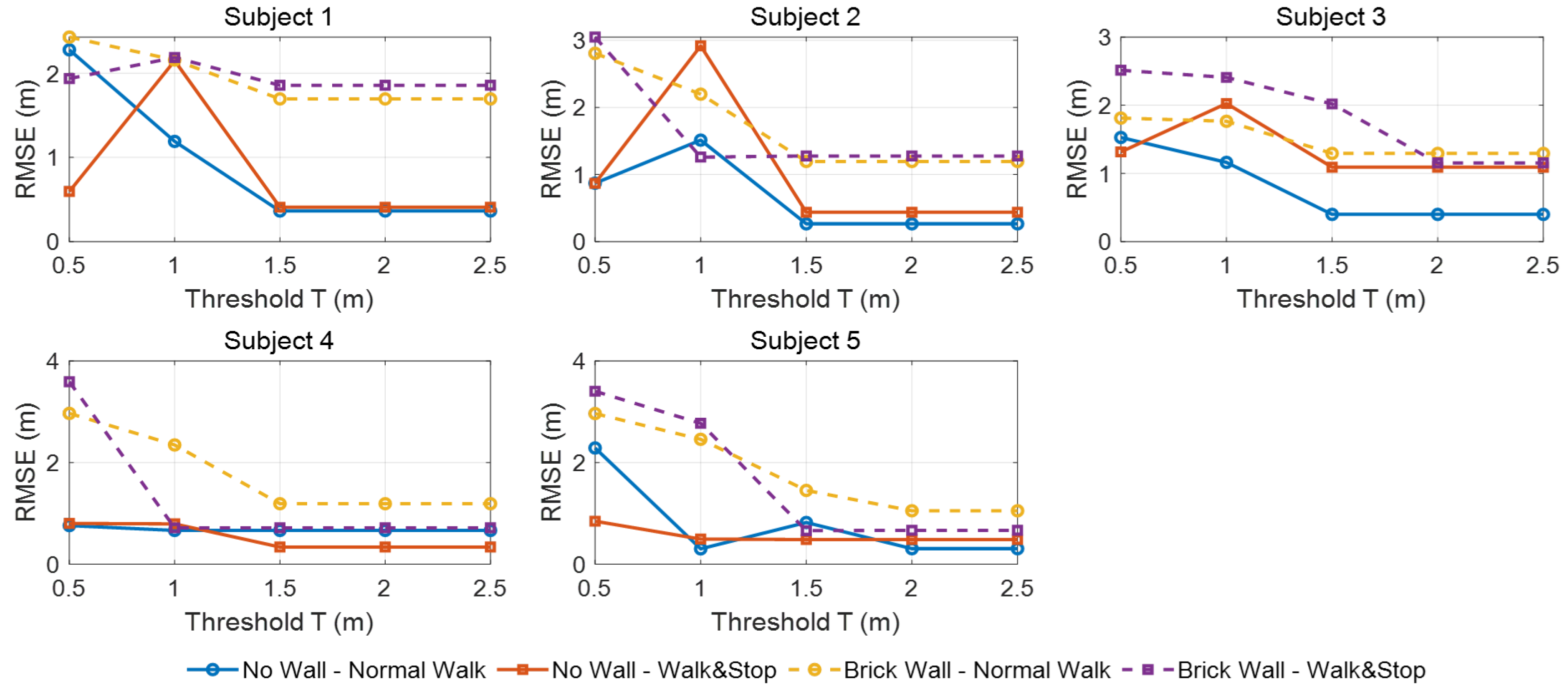
In this study, the threshold T for distance filtering was set to 1.8 m. Figure 6 visualizes the changes in RMSE according to different threshold values for each participant and experimental condition, providing an intuitive justification for the chosen setting. To quantitatively assess the validity of the threshold T and evaluate the generality of the proposed method, RMSE of distance estimation was compared by varying T from 0.5 m to 2.5 m in increments of 0.5 m. The experiments were conducted under four conditions, which combined the presence or absence of a wall and two types of motion (Normal-Walk and Walk-Stop), across five participants.The results showed that in most cases, RMSE remained stable when $T\ge 1.5$ m. In contrast, excessively small T values tended to suppress normal distance variations excessively, leading to increased errors. On the other hand, an appropriately chosen threshold T effectively mitigated instability in distance estimation, contributing to reduced errors and more consistent distance information. These findings support the validity of the threshold setting adopted in this study from a sensitivity perspective.

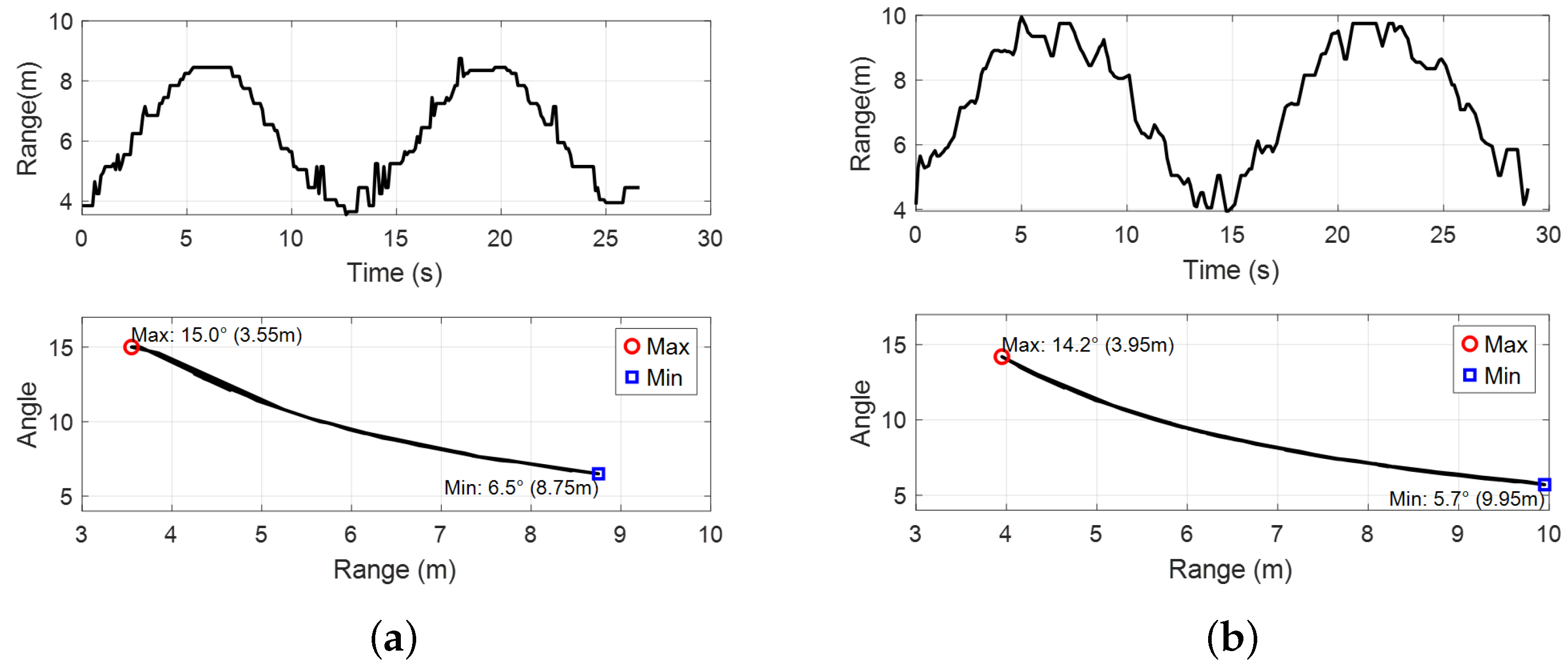
$R_i$ by extracting the point clouds within the azimuth beamforming angle $(-{\theta }_{azi},{\theta }_{azi})$ and the elevation beamforming angle $(-{\theta }_{ele},{\theta }_{ele})$, background noise is reduced and the number of target-related point clouds is increased. Figure 7 shows the variation of ${\theta }_{azi}$ and ${\theta }_{ele}$ with respect to distance, when $A=E=1$ in a one-dimensional environment. It can be observed from the figure that as the distance increases, the values of ${\theta }_{azi}$ and ${\theta }_{ele}$ decrease. To reflect the characteristic of the target moving left or right in a two-dimensional environment, unlike in the one-dimensional environment where the center angle is set to zero, the Azimuth detection angle is configured as $({\theta }_c-{\theta }_{azi},{\theta }_c+{\theta }_{azi})$ based on the center angle ${\theta }_c$. The center angle is calculated as the mean azimuth angle of each clustered point cloud within a scan as in Equation (17).

$${\theta }_c={\displaystyle \frac{1}{N}}\sum _{k=1}^N{\theta }_k$$

(17)

Here, N denotes the number of point clouds within the scan, and ${\theta }_k$ represents the azimuth angle of each point cloud.

Figure 8 and Figure 9, respectively, show the changes in the number of point clouds before and after the Ramp-up beamforming in one-dimensional and two-dimensional environments. Regardless of the presence of a wall, it was commonly observed in both environments that the number of point clouds increased by approximately twofold after the Ramp-up beamforming.

4. Experimental Results

The experiments were conducted using a commercial 4D imaging FMCW radar (AFI910, Bitsensing Inc., Seongnam, Republic of Korea) to observe the movement velocity of subjects under various walking conditions. The radar module is designed to operate in the 79 GHz band, which corresponds to the internationally standardized mmWave frequency range (77–81 GHz) widely adopted in ETSI regulations and automotive radar applications [22,23]. To obtain accurate ground truth data, Perception Neuron Studio motion sensors (Noitom Ltd., Beijing, China, sampling frequency: 100 Hz) were attached to the subjects’ bodies, and the experiments were performed while the subjects wore the sensors, as illustrated in Figure 10b.

As summarized in

Table 1. Radar parameters.

Center frequency ($f_c$)	79 GHz
Chirp duration ($T_c$)	256 μs
Sampling frequency ($f_s$)	4 MHz
Azimuth angle	$-{45}^{\circ }$ to ${45}^{\circ }$
Elevation angle	$-{15}^{\circ }$ to ${15}^{\circ }$
Number of samples	1024
Number of chirps	32
Number of channels	$192(12\mathrm{Tx}\times 16\mathrm{Rx})$
Bandwidth	3 GHz
Chirp interval	0.05 s (20 fps)

, the radar is equipped with 12 transmitting (Tx) and 16 receiving (Rx) antennas. Figure 11 illustrates the antenna array configuration of the radar used in this study. MIMO beamforming was applied, resulting in a total of 192 (=12 × 16) virtual array elements. The Tx antennas were arranged in two vertical columns, while the Rx antennas were configured as a uniform linear array (ULA) with equal spacing.

The experiments were conducted in both one-dimensional and two-dimensional motion environments, with and without a brick wall positioned approximately 0.5 m in front of the radar. The relative permittivity of the concrete bricks is typically in the range from 5 to 10, and the conductivity is approximately from ${10}^{-3}$ to ${10}^{-2}$ S/m [24,25]. These values are considered representative of the wall material used in this study. In the one-dimensional setup, participants started at a distance of approximately 3.8 m from the radar and walked back and forth twice along a linear path covering approximately 4.5 m. The two-dimensional experiments were performed under the same radar distance condition, with participants following a predefined zigzag path within a 2 m lateral width, completing a single round trip over a distance of approximately 4.8 m. The experiment was conducted in a corridor approximately 2 m wide, and the total zigzag walking path was about 4.8 m in length, with turning points placed at intervals of 1.2 m from the starting position. The participant started from the center and moved alternately to the left and right ends. The starting distance of 3.8 m (measured from the radar) was chosen considering the elevation angle range of the radar (from $-{15}^{\circ }$ to $+{15}^{\circ }$). Assuming an average adult height of 1.8 m, this distance ensures that the vertical height span of the body (approximately 0.9–1.0 m from the radar’s perspective) remains within the radar’s field of view. Participants executed two motion patterns in both environments: Normal-Walk and Walk-Stop. These combined motion patterns were selected to observe a variety of movements. For all experiments, the radar was mounted vertically at a height of approximately 1 m above the ground. In addition, motion sensors were attached to both the participants’ backs and legs, with the data from the back-mounted sensors used as ground truth.

4.1. One-Dimensional Experimental Results

Figure 12 shows one-dimensional experimental data of a single subject among five participants under the Normal Walk and Walk-Stop scenarios. In the Normal Walk scenario, the overall tendency of the subject’s motion shows a gradual increase in velocity at the beginning of walking, followed by a steady velocity during continuous movement. When no wall was present, there was no significant difference between the velocity change before and after applying the proposed method. However, in the presence of a brick wall, the post-method velocity change exhibited a much closer resemblance to the Ground truth data. In the Walk-Stop scenario, the velocity change demonstrates an alternating increase and decrease, reflecting the walking and stopping intervals. Similar to the Normal Walk case, no meaningful differences were observed between pre- and post-method results without a wall. In contrast, when a brick wall was present, the velocity in the 5–10 s interval, which had previously appeared as 0 m/s, was successfully restored after applying the proposed method. These findings indicate that velocity change information lost due to the presence of a brick wall was effectively recovered through the Ramp-up Beamforming, and the restored data were accurately reflected in the velocity extraction.

Table 2. Velocity estimation accuracy (root mean square error, RMSE) in one-dimensional environment. The bold font was intentionally used to emphasize the significantly reduced p-values, highlighting the improvement in estimation performance after applying the proposed method.

	RMSE (No Wall)				RMSE (Brick Wall)
	Normal Walk		Walk-Stop		Normal Walk		Walk-Stop
	Before	After	Before	After	Before	After	Before	After
Subject 1	0.236 ± 0.24	0.230 ± 0.23	0.164 ± 0.16	0.182 ± 0.18	0.308 ± 0.30	0.151 ± 0.15	0.242 ± 0.24	0.154 ± 0.15
Subject 2	0.187 ± 0.19	0.187 ± 0.19	0.112 ± 0.11	0.148 ± 0.14	0.290 ± 0.29	0.131 ± 0.13	0.361 ± 0.36	0.208 ± 0.21
Subject 3	0.298 ± 0.29	0.382 ± 0.37	0.229 ± 0.22	0.285 ± 0.28	0.374 ± 0.37	0.192 ± 0.19	0.322 ± 0.32	0.170 ± 0.17
Subject 4	0.192 ± 0.19	0.188 ± 0.19	0.199 ± 0.20	0.215 ± 0.22	0.493 ± 0.49	0.291 ± 0.27	0.370 ± 0.37	0.290 ± 0.29
Subject 5	0.273 ± 0.27	0.306 ± 0.31	0.133 ± 0.13	0.134 ± 0.13	0.444 ± 0.43	0.186 ± 0.18	0.270 ± 0.27	0.169 ± 0.17
Mean	0.237	0.259	0.167	0.193	0.382	0.190	0.313	0.198
p-value	0.2810		0.0548		0.0005		0.0019

shows the comparison of the Root Mean Square Error (RMSE) of velocity estimates between radar data and motion sensor-based ground truth data for five subjects, before and after applying the Ramp-up Beamforming. In the environment without a wall, the average change in RMSE was negligible at approximately 0.02 m/s. However, in the environment with a brick wall, the RMSE values showed an average reduction of about 50% across all subjects. Furthermore, statistical analysis revealed that the brick wall environment exhibited p-values below 0.05 compared to environments without a wall, demonstrating the reliability of the Ramp-up Beamforming. Here, the p-values indicate the significance levels calculated from paired t-tests performed on the before–after values collected from all subjects.

Table 3. Changes in the number of point clouds in one-dimensional environment.

	No Wall				Brick Wall
	Normal Walk		Walk-Stop		Normal Walk		Walk-Stop
	Before	After	Before	After	Before	After	Before	After
Subject 1	127 ± 68	217 ± 83	99 ± 57	157 ± 56	35 ± 42	103 ± 65	45 ± 38	114 ± 52
Subject 2	127 ± 68	230 ± 81	99 ± 57	170 ± 61	31 ± 41	85 ± 72	31 ± 30	80 ± 66
Subject 3	143 ± 78	235 ± 86	109 ± 63	174 ± 63	56 ± 65	122 ± 106	50 ± 54	107 ± 91
Subject 4	112 ± 69	191 ± 74	77 ± 48	117 ± 44	43 ± 55	88 ± 82	67 ± 49	123 ± 67
Subject 5	137 ± 81	219 ± 86	87 ± 55	133 ± 52	54 ± 65	107 ± 78	68 ± 43	119 ± 62
Mean	129	218	94	150	44	101	52	109
p-value	$p<0.0001$		0.0006		0.0002		0.0001

presents the results of analyzing the number of point clouds per second for five subjects after applying the Ramp-up Beamforming. In the environment with a brick wall, the number of point clouds before applying Ramp-up Beamforming was generally lower compared to the environment without a wall, indirectly indicating information loss of the target due to the brick wall. However, after the application of Ramp-up Beamforming, an increasing trend in the number of point clouds was observed for all subjects, with the count rising up to approximately threefold in the brick wall environment. These results suggest that the Ramp-up Beamforming effectively increases the point clouds containing velocity information of the target, producing more point clouds than the original data and thereby enabling more accurate detection of movements of targets behind wall. Moreover, it is noteworthy that the increase in the number of point clouds was greater in the obstacle (brick wall) environment than in the environment without obstacles, indirectly demonstrating that the proposed method can effectively compensate for signal loss caused by obstacles.

4.2. Two-Dimensional Experiment

The Ramp-up Beamforming was modified and applied using the central angle and travel distance. In the one-dimensional experiment, the central angle was fixed at 0 degrees to implement the proposed method. However, in the two-dimensional experiment, the proposed method was adjusted to observe a range of 1 (m) left and right and 1 (m) up and down based on the central angle for more precise target detection.

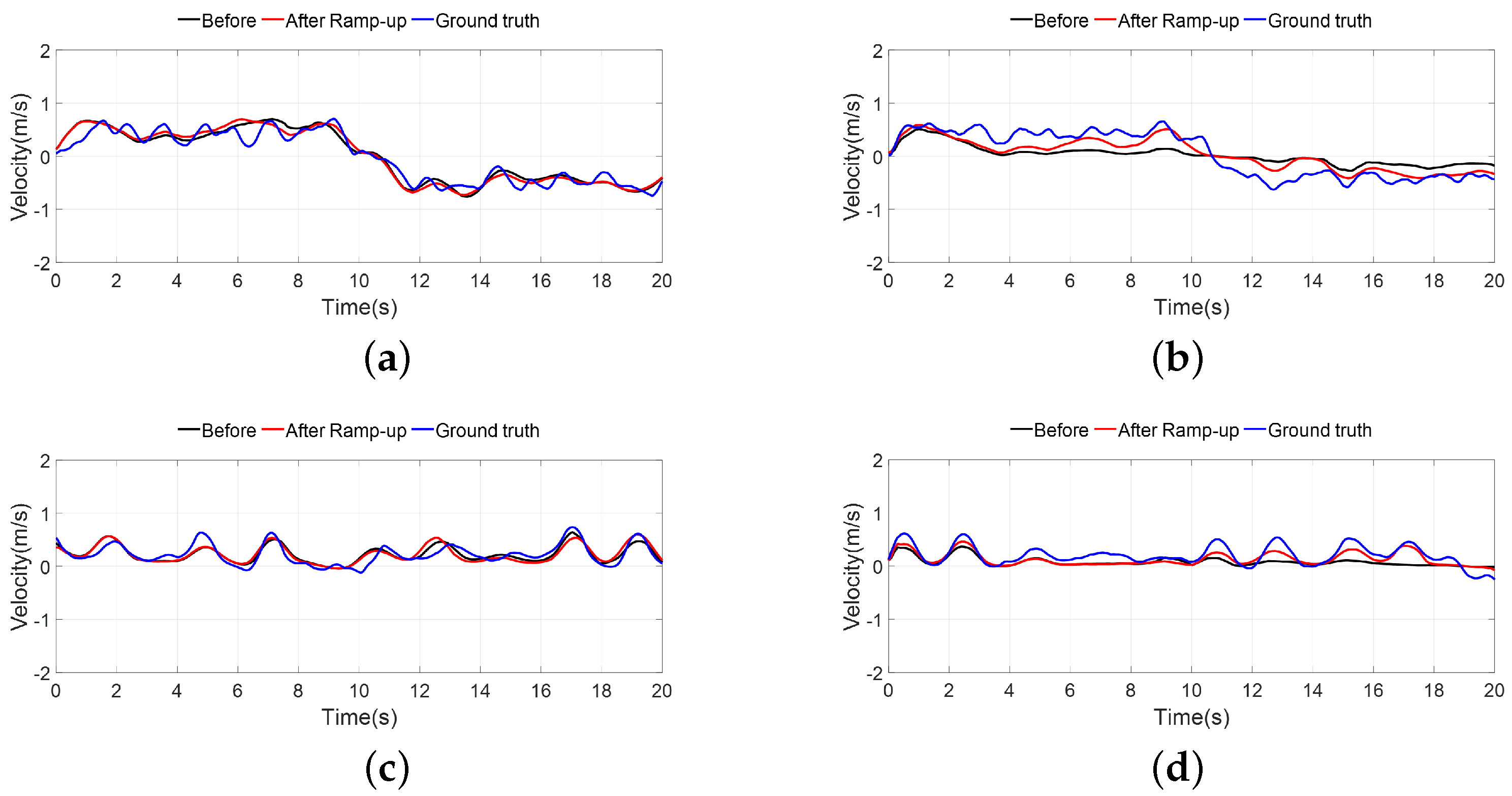
Figure 13 shows the 2D experimental data of one subject among five under Normal Walk and Walk-Stop scenarios. In the environment without a wall, discrepancies among Ground Truth data, radar data, and Ramp-up Beamforming processed data were minimal or negligible. In contrast, in the brick wall environment, some discrepancies were observed among the datasets, indicating that ignoring the central angle affected velocity estimation and accuracy. However, overall, data processed with Ramp-up Beamforming in the brick wall environment showed smaller discrepancies from the Ground Truth compared to the original data, with more pronounced velocity variations, implying sufficient velocity restoration performance of the proposed method.

Table 4. Velocity estimation accuracy (root mean square error, RMSE) in two-dimensional environment. The bold font was intentionally used to emphasize the significantly reduced p-values, highlighting the improvement in estimation performance after applying the proposed method.

	No Wall				Brick Wall
	Normal Walk		Walk-Stop		Normal Walk		Walk-Stop
	Before	After	Before	After	Before	After	Before	After
Subject 1	0.163 ± 0.16	0.154 ± 0.15	0.149 ± 0.15	0.168 ± 0.17	0.292 ± 0.29	0.197 ± 0.20	0.204 ± 0.20	0.144 ± 0.14
Subject 2	0.162 ± 0.16	0.131 ± 0.13	0.126 ± 0.13	0.121 ± 0.12	0.293 ± 0.29	0.214 ± 0.21	0.255 ± 0.25	0.185 ± 0.18
Subject 3	0.169 ± 0.17	0.188 ± 0.18	0.204 ± 0.20	0.258 ± 0.26	0.255 ± 0.26	0.184 ± 0.18	0.281 ± 0.28	0.198 ± 0.20
Subject 4	0.175 ± 0.17	0.213 ± 0.21	0.184 ± 0.18	0.180 ± 0.18	0.377 ± 0.38	0.292 ± 0.29	0.277 ± 0.28	0.238 ± 0.24
Subject 5	0.179 ± 0.18	0.191 ± 0.19	0.154 ± 0.15	0.155 ± 0.15	0.350 ± 0.35	0.229 ± 0.23	0.225 ± 0.22	0.187 ± 0.18
Mean	0.170	0.175	0.163	0.176	0.313	0.223	0.248	0.190
p-value	0.6510		0.3074		0.0005		0.0027

and

Table 5. Changes in the number of point clouds in two-dimensional environment.

	No Wall				Brick Wall
	Normal Walk		Walk-Stop		Normal Walk		Walk-Stop
	Before	After	Before	After	Before	After	Before	After
Subject 1	105 ± 61	160 ± 58	72 ± 44	119 ± 52	41 ± 34	110 ± 53	39 ± 26	102 ± 49
Subject 2	101 ± 68	148 ± 68	89 ± 60	130 ± 57	34 ± 33	89 ± 63	37 ± 37	90 ± 58
Subject 3	95 ± 65	151 ± 64	73 ± 51	118 ± 62	45 ± 43	96 ± 80	29 ± 26	76 ± 57
Subject 4	94 ± 56	139 ± 52	66 ± 53	99 ± 49	59 ± 44	110 ± 70	62 ± 43	109 ± 56
Subject 5	105 ± 71	162 ± 67	82 ± 59	124 ± 57	57 ± 38	115 ± 71	52 ± 36	95 ± 60
Mean	100	152	76	118	47	104	44	94
p-value	$p<0.0001$		0.0001		0.0001		0.0001

, respectively, show the changes in RMSE and the number of point clouds before and after applying the Ramp-up Beamforming in the two-dimensional environment. Notably, despite not reflecting the central angle, the Ramp-up Beamforming consistently reduced velocity errors relative to the ground truth for all experimental subjects in the brick wall environment. However, compared to the one-dimensional brick wall environment, the RMSE differences before and after the Ramp-up Beamforming in the two-dimensional brick wall environment were somewhat reduced, likely due to insufficient utilization of central angle information. Nonetheless, as in the one-dimensional experiment, statistical significance was confirmed in the two-dimensional brick wall environment with p-values below 0.05.

Regarding changes in the number of point clouds, similar to the one-dimensional experiment, fewer point clouds were recorded initially in the environment with walls, and this number increased by more than twice after applying the proposed method. These results statistically demonstrate that the Ramp-up Beamforming effectively restores velocity information lost due to walls and improves accuracy.

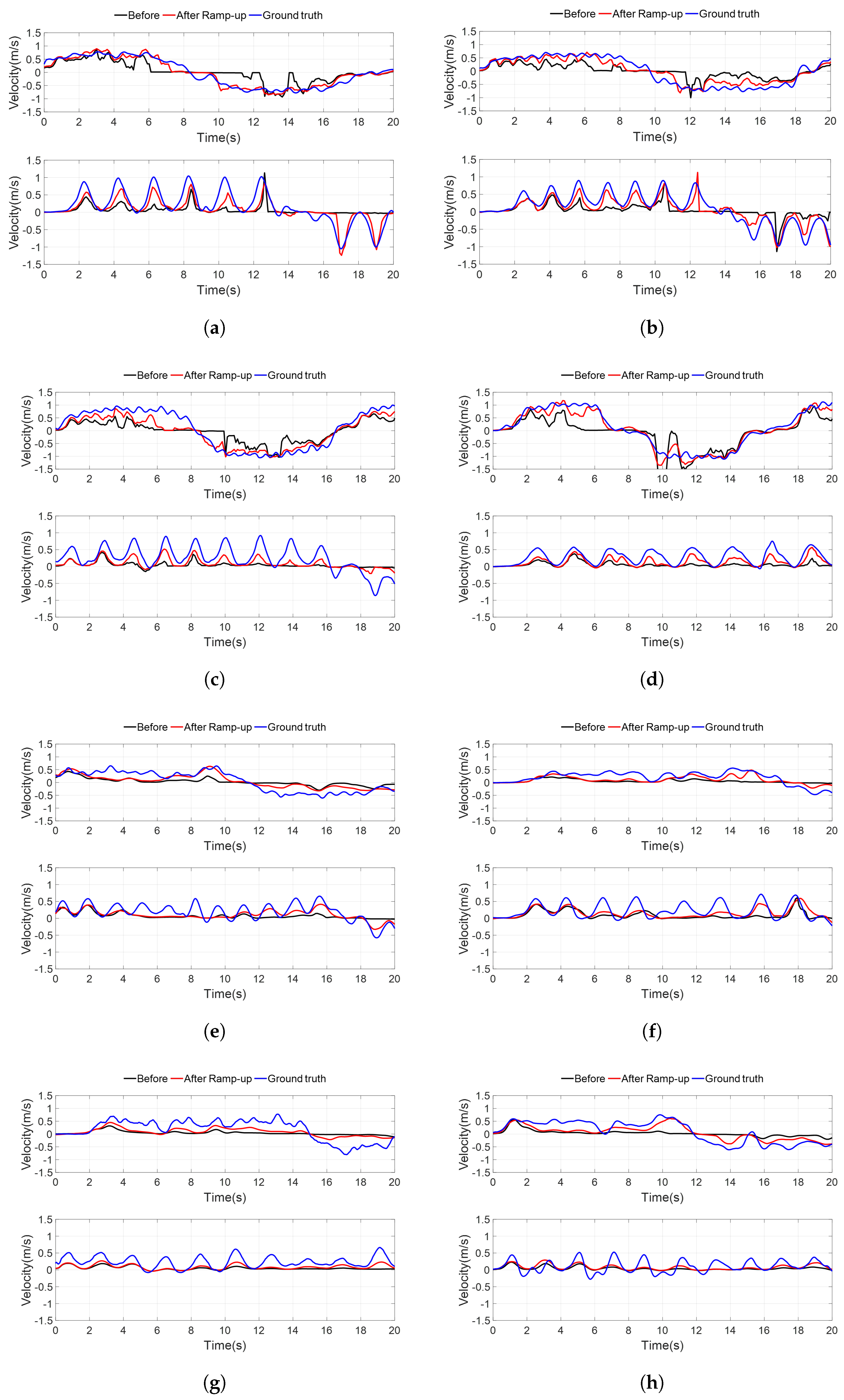
Figure 14 shows graphs of one-dimensional (a–d) and two-dimensional (e–h) experimental data for four subjects under the brick wall environment, excluding the single subject presented. The upper row corresponds to the Normal Walk scenario, while the lower row represents the Walk–Stop scenario.

5. Conclusions

This study aimed to overcome the limitations of conventional reflection power-based approaches in target tracking using through-wall radar, where the reduction of point clouds and increased noise due to walls make detecting movements behind the wall challenging. To address this, we proposed a method focusing on velocity information rather than power, enhancing velocity estimation accuracy. The proposed method, Ramp-up Beamforming, effectively restores velocity information even in environments with a wall between the radar and the target.

Experiments were conducted in one-dimensional and two-dimensional indoor environments to validate the proposed method, and performance was evaluated based on collected data. In the one-dimensional experiment, the velocities of five subjects located behind a brick wall were successfully restored using Ramp-up Beamforming, and the proposed method’s validity was confirmed by comparison with ground truth data from motion sensors. In the two-dimensional environment, smooth estimation of the subjects’ movement distance and central angle was possible without wall; however, in the brick wall environment, central angle estimation was limited and some velocity information was not fully restored. This indicates the need for a complementary algorithm optimized for two-dimensional spatial characteristics. Nonetheless, the Ramp-up Beamforming method maintained velocity restoration performance, showing reduced error compared to ground truth, similar to the one-dimensional case. These results suggest that the proposed method provides reliable velocity estimation even in environments with obstacles like a brick wall and extends the applicability of through-wall target tracking technologies.

Furthermore, the proposed method was implemented in MATLAB R2024a and executed on a system equipped with an AMD Ryzen 5 5600G CPU (6 cores, 12 threads, 3.9 GHz base/4.26 GHz boost), 16 GB RAM, and Windows 11 OS. GPU acceleration was not used. The average processing time per frame was measured to be approximately 237.3 ms per frame, which includes both dynamic beamforming operations and post-processing. This result supports the feasibility of applying the proposed method to real-time tracking of slowly moving targets such as pedestrians. In addition, since the radar module used in this study outputs Range–Doppler data by internally performing both range and Doppler FFTs, the additional computational overhead incurred by the proposed method is limited to the beamforming process. The computational complexity of the beamforming was confirmed to be on the order of $\mathcal{O}(N_{\mathrm{array}}·N_c)$, depending on the number of array elements and the slow-time length.

Nevertheless, this study has certain limitations. The experiments were conducted with a single-material brick wall environment and a limited number of subjects, which were intended to verify the fundamental validity of the proposed method under controlled conditions. For practical applications, however, it is important to extend the evaluation to more diverse wall configurations, including multi-layered or metal-reinforced structures of varying thicknesses, as well as to a broader range of subjects across different ages and body figures. These aspects will be addressed in future work to comprehensively assess the robustness and generalizability of the proposed method.

In addition, integrating the proposed method with AI-based tracking models or learning-based parameter tuning strategies may further enhance its adaptability and autonomous operation in complex environments. For example, deep learning approaches could enable more robust range–velocity estimation even under noisy or cluttered conditions. Moreover, recent studies have reviewed target detection techniques using Synthetic Aperture Radar (SAR) [26], including Polarimetric SAR (PolSAR), and discussed their applications in high-resolution remote sensing. In this context, the proposed radar–AI fusion approach may also hold promise for real-time and automated target detection in SAR-based systems.