Deep Learning Model Ensemble Applied to Modulus Back-Calculation of Old Cement Concrete Rubblized Overlay Asphalt Pavement
Abstract
1. Introduction
Objective
2. Methodology
2.1. Training Dataset Generation
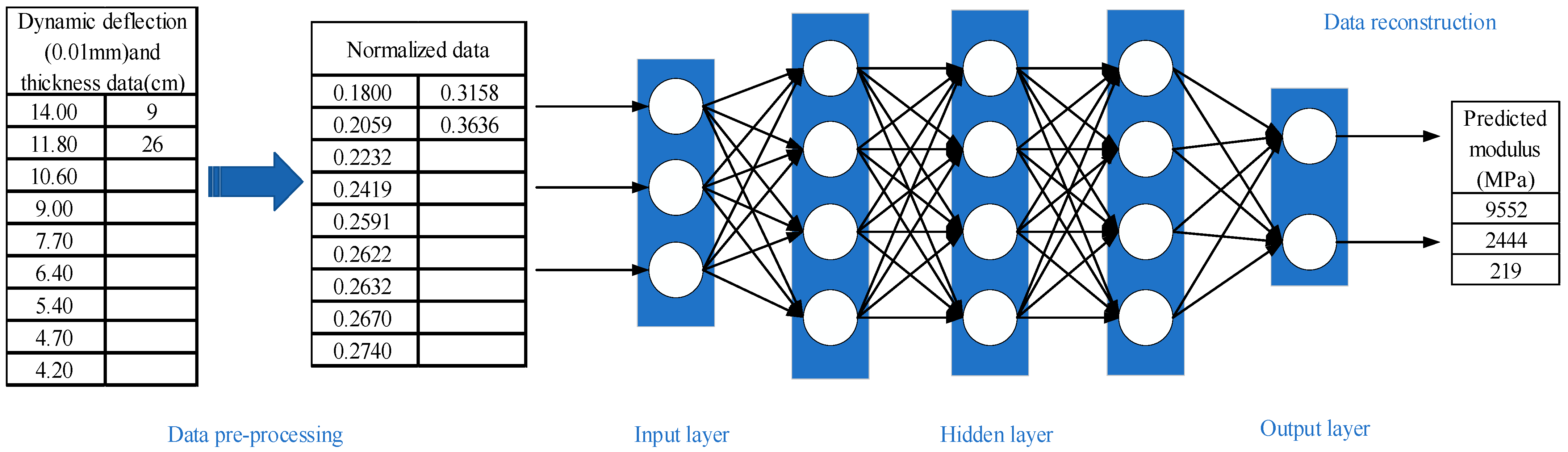
2.2. BP Neural Network Model
2.3. Development of a Genetic Algorithm for Optimizing the BP
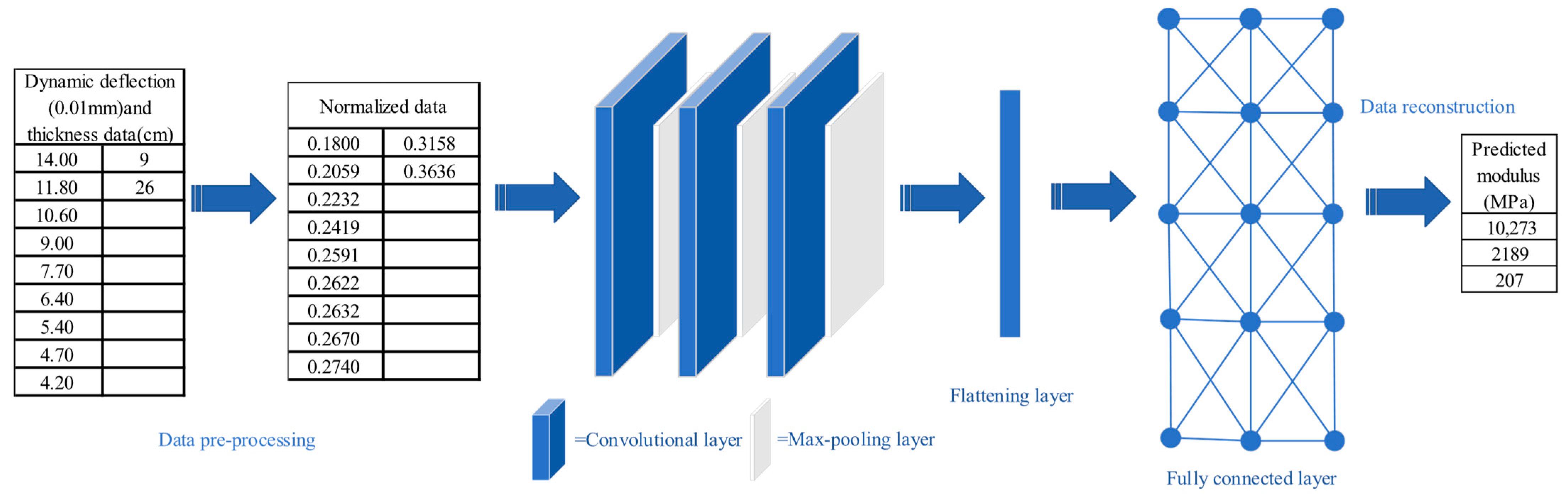
2.4. CNN Model
3. Results and Discussion
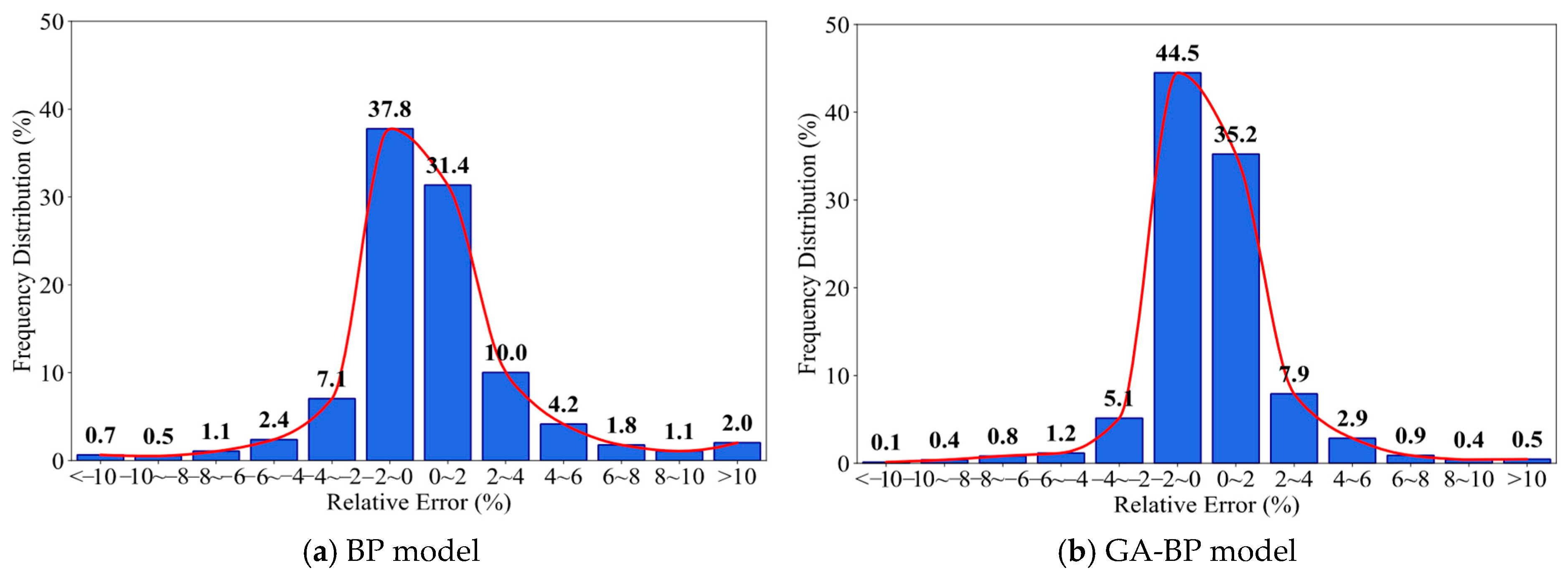
3.1. Performance Analysis of the Single Model
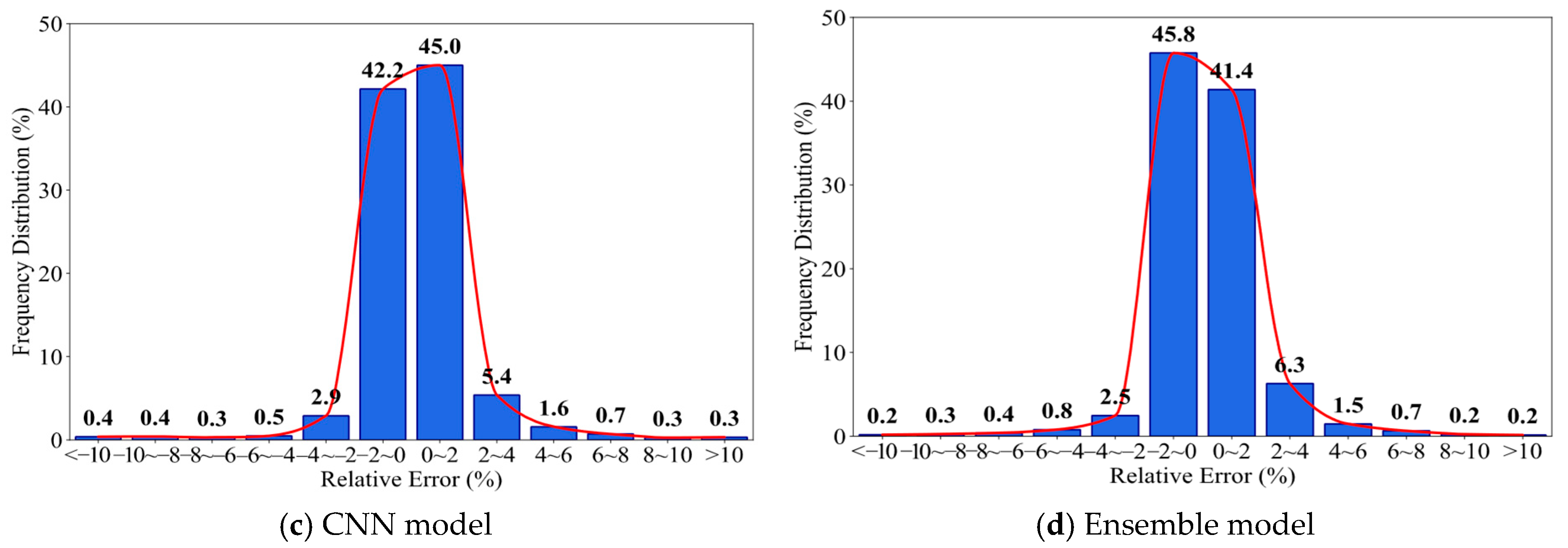
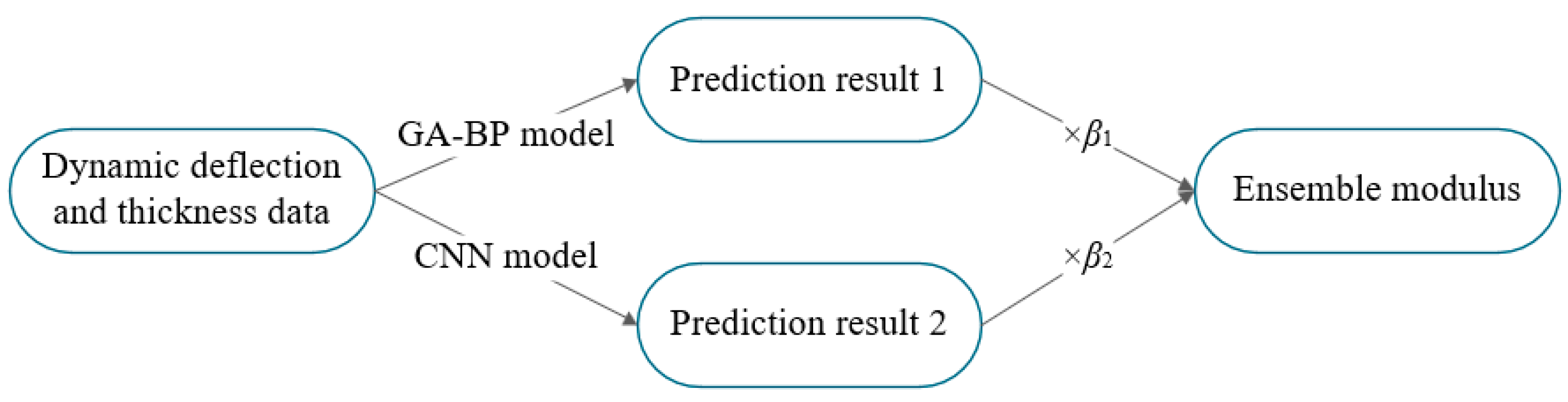
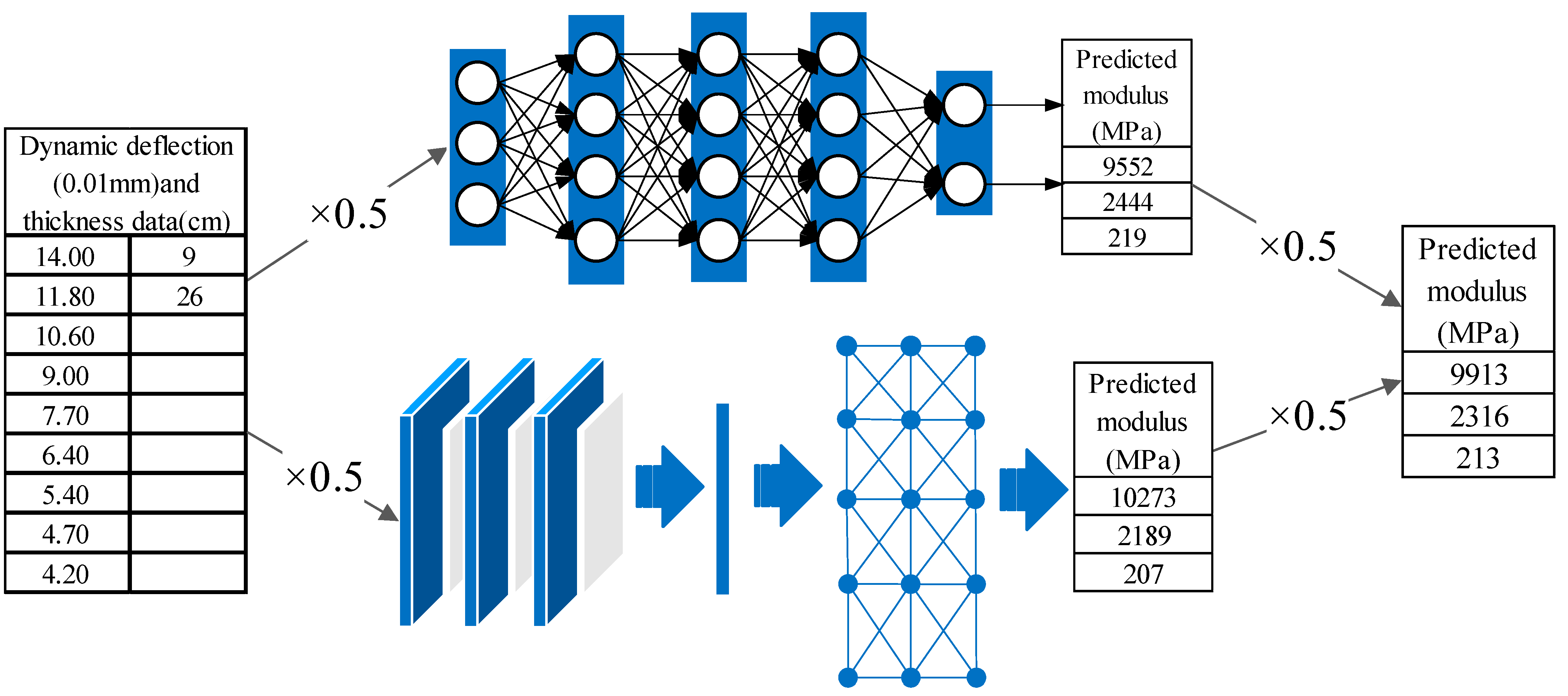
3.2. Analysis of the CNN and GA-BP Ensemble Model
3.3. Ensemble Model Engineering Validation
4. Summary and Conclusions
- Based on model-evaluation metrics and error-distribution analyses, all three models (BP, GA-BP, and CNN) trained on the large-scale FWD dynamic-deflection dataset exhibit high predictive performance (R2 > 0.981). The CNN back-calculation model attains lower mean errors than GA-BP, and both models outperform the plain BP model (R2 > 0.993 for CNN/GA-BP), indicating greater application potential for CNN in modulus back-calculation of asphalt overlays on rubblized concrete pavements.
- On the validation set, CNN and GA-BP display complementary maxima across layers and extreme parameter combinations. An equal-weight linear ensemble, motivated by this complementarity, substantially reduces tail risk: the maximum relative error drops from 25.9% (CNN) to 17.3%, and the share of cases with <5% error increases from 96.7% to 97.3%. Mean-based metrics (MAE, RMSE) and R2 also improve. These results indicate that the ensemble lowers worst-case errors while enhancing overall stability and accuracy.
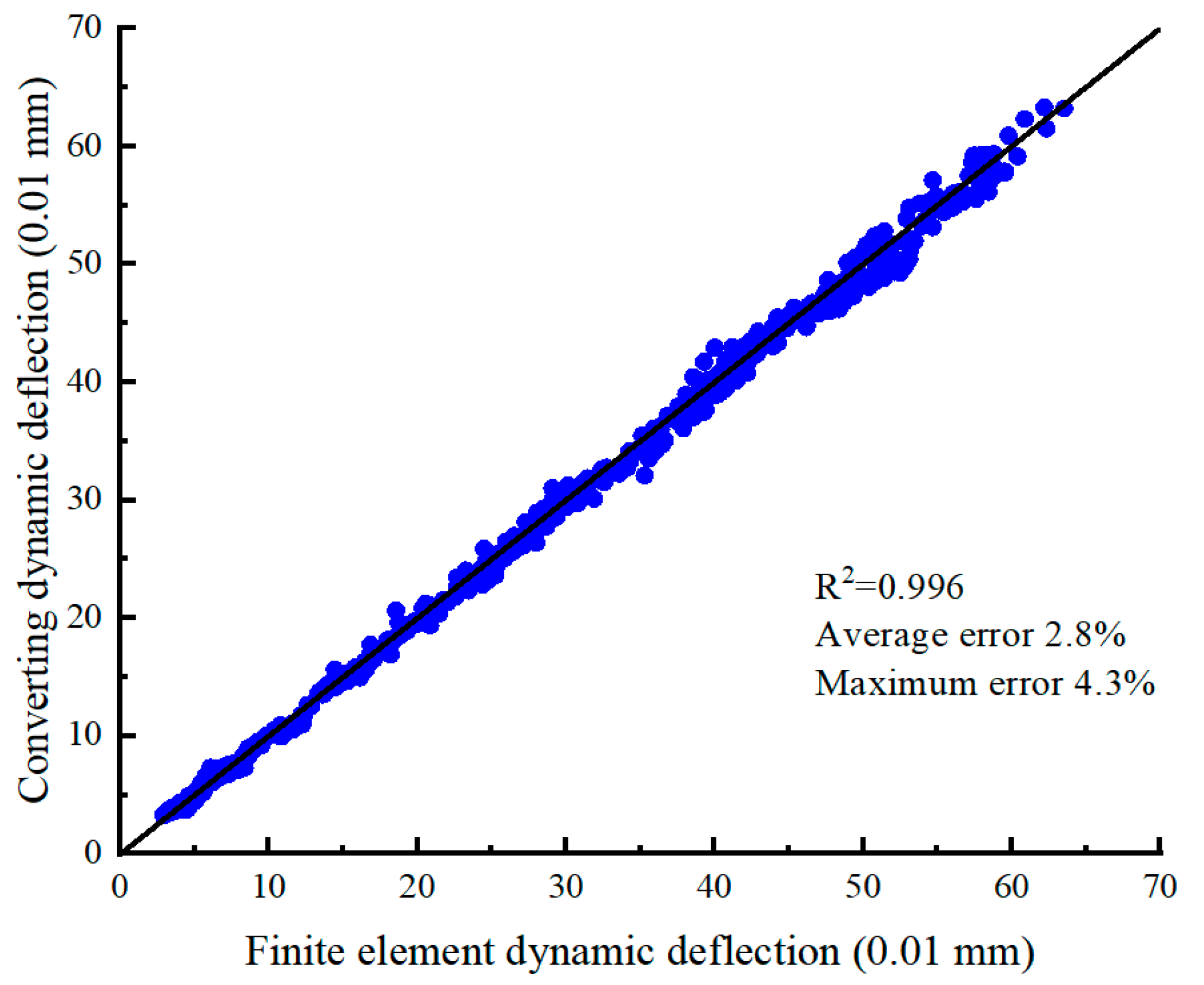
- External consistency checks and closed-loop field-segment validation using 3D dynamic finite-element analysis show strong agreement among simulation, back-calculation, and field measurements: the average dataset error is ≈2.8% (maximum ≈ 4.3%), and the RMSE for representative field deflection basins is ≈0.88%. Collectively, these findings demonstrate that the CNN + GA-BP ensemble model delivers high accuracy, reliability, and generalization for predicting dynamic moduli of pavement structural layers on rubblized concrete bases.
Limitations and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Papavasiliou, V.; Loizos, A. Field performance and fatigue characteristics of recycled pavement materials treated with foamed asphalt. Constr. Build. Mater. 2013, 48, 677–684. [Google Scholar] [CrossRef]
- El-Raof, H.S.A.; El-Hakim, R.T.A.; El-Badawy, S.M.; Afify, H.A. Simplified closed-form procedure for network-level determination of pavement layer moduli from falling weight deflectometer data. J. Transp. Eng. Part B Pavements 2018, 144, 04018052. [Google Scholar] [CrossRef]
- Zeiada, W.; Dabous, S.A.; Hamad, K.; Al-Ruzouq, R.; Khalil, M.A. Machine learning for pavement performance modelling in warm climate regions. Arab. J. Sci. Eng. 2020, 45, 4091–4109. [Google Scholar] [CrossRef]
- Zaman, M.; Solanki, P.; Ebrahimi, A.; White, L. Neural network modeling of resilient modulus using routine subgrade soil properties. Int. J. Geomech. 2010, 10, 1–12. [Google Scholar] [CrossRef]
- You, L.; Yan, K.; Liu, N. Assessing artificial neural network performance for predicting interlayer conditions and layer modulus of multi-layered flexible pavement. Front. Struct. Civ. Eng. 2020, 14, 487–500. [Google Scholar] [CrossRef]
- Tarefder, R.A.; Ahsan, S.; Ahmed, M.U. Neural network–based thickness determination model to improve back-calculation of layer moduli without coring. Int. J. Geomech. 2015, 15, 04014058. [Google Scholar] [CrossRef]
- Elbagalati, O.; Elseifi, M.A.; Gaspard, K.; Zhang, Z. Development of an artificial neural network model to predict subgrade resilient modulus from continuous deflection testing. Can. J. Civ. Eng. 2017, 44, 700–706. [Google Scholar] [CrossRef]
- Ceylan, H.; Schwartz, C.W.; Kim, S.; Gopalakrishnan, K. Accuracy of predictive models for dynamic modulus of hot-mix asphalt. J. Mater. Civ. Eng. 2009, 21, 286–293. [Google Scholar] [CrossRef]
- Sharma, S.; Das, A. Back-calculation of pavement layer moduli from falling weight deflectometer data using an artificial neural network. Can. J. Civ. Eng. 2008, 35, 57–66. [Google Scholar] [CrossRef]
- Wang, H.; Li, M.; Szary, P.; Hu, X. Structural assessment of asphalt pavement condition using backcalculated modulus and field data. Constr. Build. Mater. 2019, 211, 943–951. [Google Scholar] [CrossRef]
- Ghasemi, P.; Aslani, M.; Rollins, D.K.; Williams, R.C. Principal component neural networks for modeling, prediction, and optimization of hot-mix asphalt dynamic modulus. Infrastructures 2019, 4, 53. [Google Scholar] [CrossRef]
- Zhang, C.; Shen, S.; Huang, H.; Yu, S. In situ dynamic modulus prediction for asphalt pavement combining machine learning algorithm and sensing technology. IEEE Trans. Intell. Transp. Syst. 2024, 25, 8695–8704. [Google Scholar] [CrossRef]
- Fan, J.; Ma, T.; Zhu, J.; Zhu, Y.; Zhang, Y. Characteristics of high-speed deflection basin and structural-parameter back-calculation of asphalt pavement with different structural states. Constr. Build. Mater. 2022, 341, 127869. [Google Scholar] [CrossRef]
- Moussa, G.S.; Owais, M. Modeling hot-mix asphalt dynamic modulus using deep residual neural networks: Parametric and sensitivity analysis study. Constr. Build. Mater. 2021, 294, 123589. [Google Scholar] [CrossRef]
- Han, C.; Ma, T.; Chen, S.; Fan, J. Application of a hybrid neural network structure for FWD back-calculation based on LTPP database. Int. J. Pavement Eng. 2022, 23, 3099–3112. [Google Scholar] [CrossRef]
- Al-Qaili, A.H.; Al-Mansour, A.I.; Al-Solieman, H.; Alsharabi, K. RNN-based pavement moduli prediction for flexible pavement design enhancement. Case Stud. Constr. Mater. 2024, 20, e02811. [Google Scholar] [CrossRef]
- Al-Qaili, A.H.; Al-Mansour, A.I.; Al-Solieman, H.; Abduh, Z.; Lee, S.M. Adaptation of an alternative neural network instead of an ANN for back-calculating pavement layer moduli. Constr. Build. Mater. 2024, 438, 137281. [Google Scholar] [CrossRef]
- Ghorbani, B.; Arulrajah, A.; Narsilio, G.; Horpibulsuk, S.; Bo, M.W. Development of genetically based models for predicting the resilient modulus of cohesive pavement subgrade soils. Soils Found. 2020, 60, 398–412. [Google Scholar] [CrossRef]
- Li, M.; Wang, H. Development of ANN–GA program for back-calculation of pavement moduli under FWD testing with viscoelastic and nonlinear parameters. Int. J. Pavement Eng. 2019, 20, 490–498. [Google Scholar] [CrossRef]
- Li, M.; Wang, H. Prediction of asphalt pavement responses from FWD surface deflections using soft computing methods. J. Transp. Eng. Part B Pavements 2018, 144, 04018014. [Google Scholar] [CrossRef]
- Fan, H.; Zhang, J.; Zheng, J. Back-calculation of nonlinear properties of subgrade using a new in situ nondestructive testing approach based on loading sequence. Int. J. Geomech. 2024, 24, 04024235. [Google Scholar] [CrossRef]
- Li, M.; Dai, Q.; Su, P.; You, Z.; Ma, Y. Surface layer modulus prediction of asphalt pavement based on LTPP database and machine learning for mechanistic–empirical rehabilitation design applications. Constr. Build. Mater. 2022, 344, 128303. [Google Scholar] [CrossRef]
- Svilar, M.; Peško, I.; Šešlija, M. Model for estimating the modulus of elasticity of asphalt layers using machine learning. Appl. Sci. 2022, 12, 10536. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Y.; Sun, Q.; Wang, R. Intelligent back-calculation of elastic modulus for asphalt pavement structures with bedrock using a stacking ensemble learning model. Constr. Build. Mater. 2025, 491, 142704. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, D. Dynamic modulus analysis of the resonantly rubblized layer of old cement concrete slab based on BP neural network and deep learning model. Highway 2024, 69, 44–51. (In Chinese) [Google Scholar]
- Li, Q.; Chen, Z. Numerical analysis and conversion of dynamic and static deflection of asphalt pavement under FWD loading. Constr. Build. Mater. 2023, 367, 129513. [Google Scholar] [CrossRef]
- Tarefder, R.A.; Ahmed, M.U. Modeling of the FWD deflection basin to evaluate airport pavements. Int. J. Geomech. 2014, 14, 205–213. [Google Scholar] [CrossRef]
- JTG D50-2017; Specifications for Design of Highway Asphalt Pavement. China Standard Press: Beijing, China, 2017.
- Ling, C.; David, E.; Siddharthan, R. Comparison of dynamic and static back-calculation moduli for three-layer pavements. Transp. Res. Rec. 1991, 1293, 86–92. [Google Scholar]
- Wu, C.; Wang, H.; Zhao, J.; Jiang, X.; Qiu, Y. Asphalt pavement modulus back-calculation using surface deflections under moving loads. Comput.-Aided Civ. Infrastruct. Eng. 2020, 35, 1246–1260. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.S.; Talatahari, S.; Alavi, A.H. Metaheuristic algorithms. In Metaheuristic Applications in Structures and Infrastructures; Elsevier: Amsterdam, The Netherlands, 2013; pp. 1–24. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Ige, A.O.; Sibiya, M. State-of-the-art in 1D convolutional neural networks: A survey. IEEE Access 2024, 12, 144082–144105. [Google Scholar] [CrossRef]
- Almufti, S.M.; Shaban, A.A.; Ali, Z.A.; Ali, R.I.; Fuente, J.D. Overview of metaheuristic algorithms. Polaris Glob. J. Sch. Res. Trends 2023, 2, 10–32. [Google Scholar] [CrossRef]
- Ghanizadeh, A.R.; Heidarabadizadeh, N.; Jalali, F. Artificial neural network back-calculation of flexible pavements with sensitivity analysis using Garson’s and connection weights algorithms. Innov. Infrastruct. Solut. 2020, 5, 63. [Google Scholar] [CrossRef]
- Wang, X.; Hyndman, R.J.; Li, F.; Kang, Y. Forecast combinations: An over 50-year review. Int. J. Forecast. 2023, 39, 1518–1547. [Google Scholar] [CrossRef]

| No. | Pavement Structural Layers | Thickness (cm) | Poisson’s Ratio | Density (kg·m−3) |
|---|---|---|---|---|
| 1 | AC-16 medium-graded asphalt concrete surface layer | 4 | 0.25 | 2450 |
| 2 | AC-20 medium-graded asphalt concrete binder layer | 5 | 0.25 | 2450 |
| 3 | Resonance-crushed cement concrete layer | 26 | 0.30 | 2500 |
| 4 | Old cement-stabilized crushed stone base layer | 18 | 0.30 | 2400 |
| 5 | Graded crushed stone subbase layer | 18 | 0.35 | 2250 |
| 6 | Subgrade soil layer | - | 0.40 | 2100 |
| Pavement Structural Layer Division | Thickness (cm) | Poisson’s Ratio | Density (kg·m3) |
|---|---|---|---|
| Asphalt overlay layer | 9 | 0.25 | 2450 |
| Resonant-crushed stone layer | 26 | 0.30 | 2500 |
| Old cement-stabilized crushed stone layer + Old graded crushed stone layer + Soil base. | - | 0.35 | 2250 |
| Pavement Structural Layer | Thickness | Poisson’s Ratio | Modulus | ||
|---|---|---|---|---|---|
| Range (cm) | Number of Values | Range (MPa) | Number of Values | ||
| Asphalt overlay layer | 3–22 | 20 * | 0.25 | 5000–14,500 | 20 |
| Resonance-crushed stone layer | 18–40 | 12 | 0.30 | 800–4200 | 18 * |
| Subgrade | - | - | 0.35 | 80–420 | 18 |
| Sensor Position | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 |
|---|---|---|---|---|---|---|---|---|---|
| Distance to load center (cm) | 0 | 20 | 30 | 45 | 60 | 75 | 90 | 105 | 120 |
| Hardware and Software | Model and Version |
|---|---|
| GPU | Nvidia GeForce RTX 4060ti |
| CPU | 13th Gen Intel(R) Core(TM) i5-13400F |
| Operating system | Windows 11 professional |
| Pycharm | 2024.2.4 professional |
| Pytorch | 1.12.1 |
| Python | 3.8.20 |
| Scikit-lrean | 1.3.0 |
| Matplotlib | 3.7.2 |
| Numpy | 1.24.3 |
| Pandas | 2.0.3 |
| Tqdm | 4.66.5 |
| Optuna | 4.0.0 |
| Hyperparameters | Ranges | Results |
|---|---|---|
| Number of hidden layers | 1, 2, 3, 4, 5 | 3 |
| Number of hidden neurons | 64, 128, 256, 512, 1024 | 512 |
| Learning rate range | 0.001–0.00001 | 0.0001 |
| Dropout rate | 0.1, 0.2, 0.3 | 0.1 |
| Training batch size | 64, 128, 256, 512, 1024 | 1024 |
| Module | Construction Methods | Relevant Formulas |
|---|---|---|
| Genetic encoding | Real-number encoding | - |
| Fitness evaluation | - | |
| Selection operator | Tournament selection | - |
| Crossover operator | Arithmetic crossover | |
| Mutation operator | Uniform mutation | |
| Parameter configuration | Adaptive crossover rate | |
| Adaptive mutation rate | ||
| Population size | ||
| The encoding range, the number of iterations, and the neural network iteration count are determined empirically. | ||
| Hyperparameters | Ranges | Results |
|---|---|---|
| Number of convolutional layers | 1, 2, 3 | 3 |
| Number of hidden layers | 2, 3, 4, 5 | 3 |
| Number of neurons | 64, 128, 256, 512, 1024 | 1024 |
| Learning rate range | 0.001–0.00001 | 0.0002 |
| Dropout rate | 0.1, 0.2, 0.3 | 0.2 |
| Training batch size | 64, 128, 256, 512, 1024 | 1024 |
| Model | Pavement Structural Layers | Pavement Structure Scheme Quantity | Evaluation Parameter | Relative Error (%) | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | MAE | RMSE | MAPE | Average Value | Maximum Value | |||
| BP | Asphalt overlay layer | 3600 | 0.981 | 3.332 | 4.747 | 3.710 | 3.7 | 38.0 |
| Resonance-crushed stone layer | 0.996 | 4.480 | 7.520 | 1.940 | 1.9 | 21.7 | ||
| Subgrade | 0.987 | 3.161 | 5.730 | 1.196 | 1.2 | 21.9 | ||
| GA-BP | Asphalt overlay layer | 0.993 | 1.865 | 2.837 | 2.055 | 2.1 | 20.9 | |
| Resonance-crushed stone layer | 0.998 | 3.037 | 4.902 | 1.366 | 1.4 | 17.6 | ||
| Subgrade | 0.995 | 2.215 | 3.584 | 0.840 | 0.8 | 13.4 | ||
| CNN | Asphalt overlay layer | 0.994 | 1.717 | 2.763 | 1.816 | 1.8 | 20.3 | |
| Resonance-crushed stone layer | 0.998 | 2.231 | 4.731 | 0.871 | 0.9 | 18.1 | ||
| Subgrade | 0.994 | 1.590 | 3.762 | 0.614 | 0.6 | 25.9 | ||
| Ensemble model | Asphalt overlay layer | 0.995 | 1.522 | 2.366 | 1.642 | 1.6 | 17.3 | |
| Resonance-crushed stone layer | 0.999 | 2.148 | 4.026 | 0.908 | 0.9 | 13.1 | ||
| Subgrade | 0.996 | 1.556 | 3.190 | 0.599 | 0.6 | 14.9 | ||
| Pavement Structural Layers | BP Model | GA-BP Model | CNN Model | Ensemble Model | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| <2% | <5% | <10% | <2% | <5% | <10% | <2% | <5% | <10% | <2% | <5% | <10% | |
| Asphalt overlay layer | 41.6 | 77.0 | 93.0 | 65.7 | 90.5 | 98.8 | 71.9 | 92.5 | 98.6 | 73.8 | 94.1 | 99.4 |
| Resonance-crushed stone layer | 66.7 | 93.2 | 98.5 | 79.6 | 97.2 | 99.6 | 93.6 | 98.8 | 99.7 | 90.9 | 98.8 | 99.9 |
| Subgrade | 85.9 | 96.3 | 99.3 | 93.8 | 98.6 | 99.8 | 96.0 | 98.8 | 99.5 | 96.6 | 98.9 | 99.7 |
| Average value | 64.7 | 88.8 | 96.9 | 79.7 | 95.4 | 99.4 | 87.2 | 96.7 | 99.3 | 87.1 | 97.3 | 99.7 |
| Pavement Structural Layers | BP Maximum Relative Error Pavement Structure | GA-BP Maximum Relative Error Pavement Structure | CNN Maximum Relative Error Pavement Structure | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Structural Information | Back-Calculation Modulus (MPa) | Structural Information | Back-Calculation Modulus (MPa) | Structural Information | Back-Calculation Modulus (MPa) | ||||||||||
| Thickness (cm) | Modulus (MPa) | BP | GA-BP | CNN | Thickness (cm) | Modulus (MPa) | BP | GA-BP | CNN | Thickness (cm) | Modulus (MPa) | BP | GA-BP | CNN | |
| Asphalt overlay layer | 3 | 5000 | 6901 | 5715 | 5980 | 3 | 5000 | 5796 | 6043 | 5698 | 22 | 6920 | 7734 | 7415 | 8189 |
| Resonance-crushed stone layer | 40 | 4200 | 3939 | 4150 | 4131 | 18 | 800 | 801 | 818 | 794 | 32 | 4200 | 4300 | 4230 | 4939 |
| Subgrade | - | 350 | 349 | 347 | 348 | - | 292 | 289 | 293 | 291 | - | 274 | 298 | 294 | 345 |
| Sensor Position | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 |
|---|---|---|---|---|---|---|---|---|---|
| Mean deflection | 12.10 | 10.20 | 9.00 | 7.60 | 6.50 | 5.40 | 4.60 | 4.00 | 3.60 |
| The standard deviation of deflection | 1.78 | 1.56 | 1.50 | 1.32 | 1.14 | 0.93 | 0.80 | 0.63 | 0.55 |
| Coefficient of variation | 0.15 | 0.15 | 0.17 | 0.17 | 0.18 | 0.17 | 0.17 | 0.16 | 0.15 |
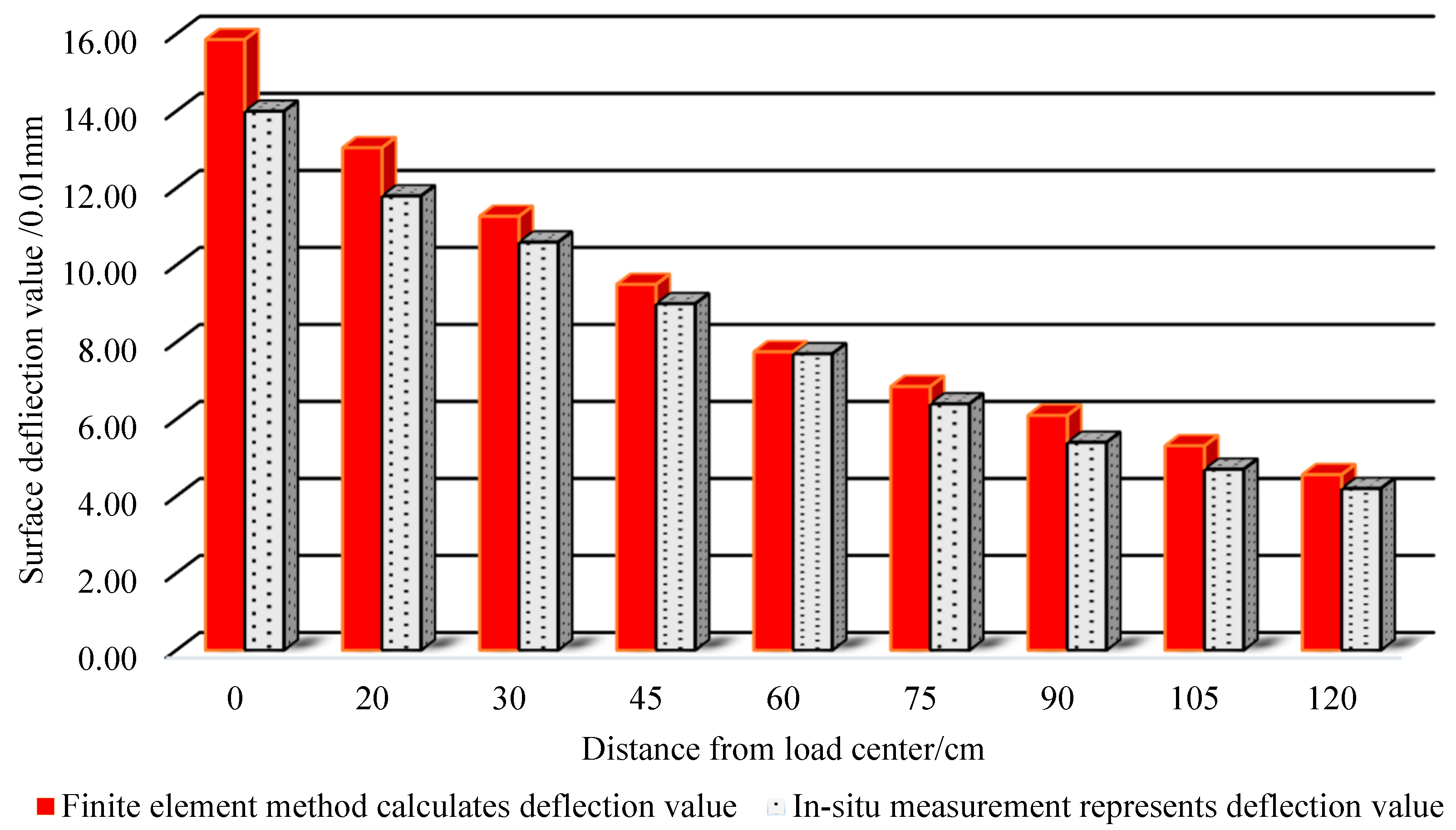
| Representative deflection | 14.00 | 11.80 | 10.60 | 9.00 | 7.70 | 6.40 | 5.40 | 4.70 | 4.20 |
| Sensor Position | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | RMSE of Measured Deflection (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| Dynamic deflection | 15.86 | 13.05 | 11.27 | 9.50 | 7.75 | 6.85 | 6.1 | 5.31 | 4.56 | 0.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Peng, P. Deep Learning Model Ensemble Applied to Modulus Back-Calculation of Old Cement Concrete Rubblized Overlay Asphalt Pavement. Appl. Sci. 2025, 15, 11115. https://doi.org/10.3390/app152011115
Li Q, Peng P. Deep Learning Model Ensemble Applied to Modulus Back-Calculation of Old Cement Concrete Rubblized Overlay Asphalt Pavement. Applied Sciences. 2025; 15(20):11115. https://doi.org/10.3390/app152011115
Chicago/Turabian StyleLi, Qiang, and Pai Peng. 2025. "Deep Learning Model Ensemble Applied to Modulus Back-Calculation of Old Cement Concrete Rubblized Overlay Asphalt Pavement" Applied Sciences 15, no. 20: 11115. https://doi.org/10.3390/app152011115
APA StyleLi, Q., & Peng, P. (2025). Deep Learning Model Ensemble Applied to Modulus Back-Calculation of Old Cement Concrete Rubblized Overlay Asphalt Pavement. Applied Sciences, 15(20), 11115. https://doi.org/10.3390/app152011115






