Sensor-Level Anomaly Detection in DC–DC Buck Converters with a Physics-Informed LSTM: DSP-Based Validation of Detection and a Simulation Study of CI-Guided Deception
Abstract
1. Introduction
1.1. Research Background
1.2. Limitations of Existing Research
1.3. Related Work and Context
Classical Detectors (EKF/Fuzzy/CUSUM)
1.4. Research Objectives and Contributions
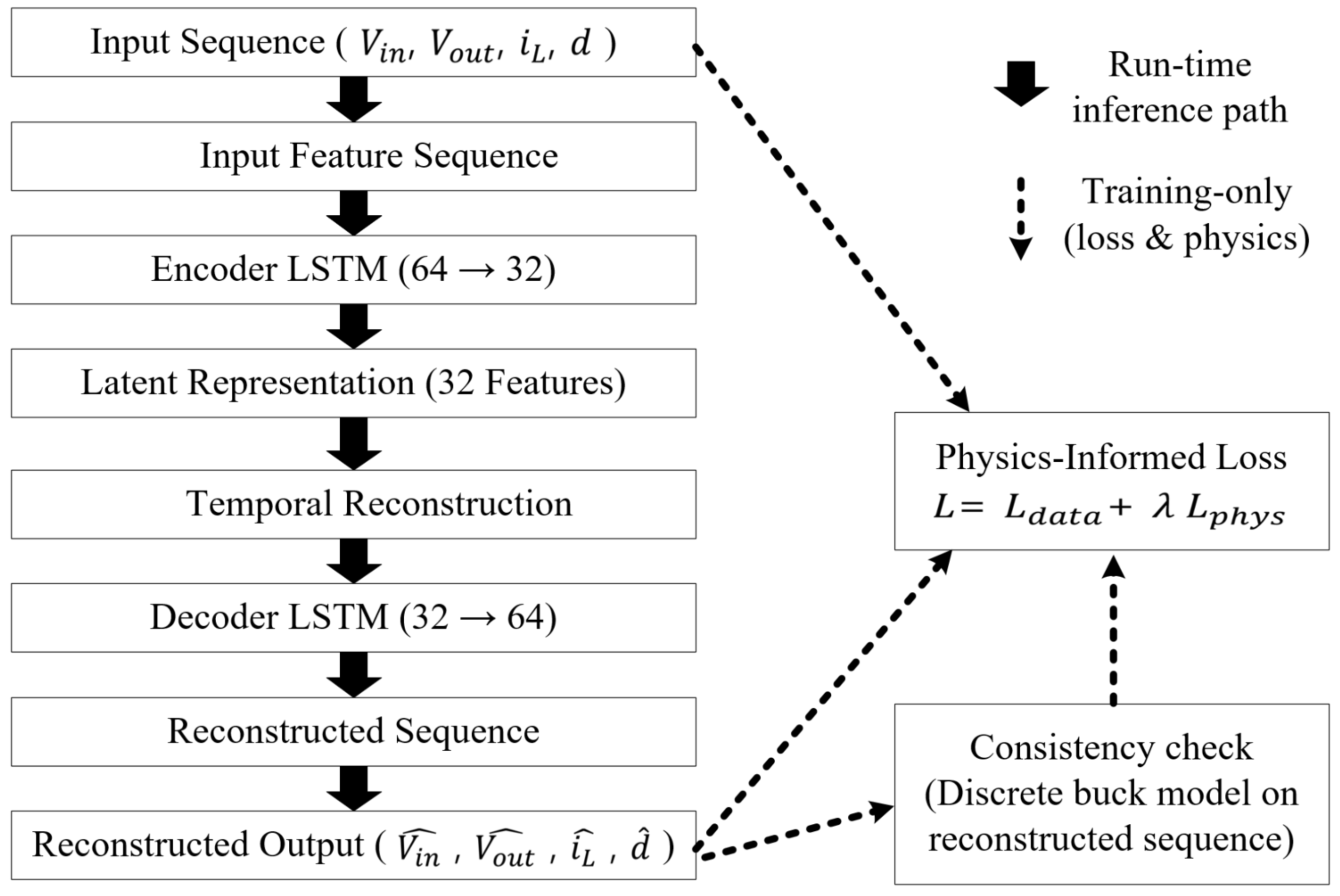
- Discrete-time physics-informed LSTM (PI–LSTM) for converters. We embed the averaged buck dynamics as residual penalties on decoder trajectories, avoiding label leakage and aligning with fixed-step embedded control; the residual template is topology-agnostic via the replacement of the discrete-time update map [23].
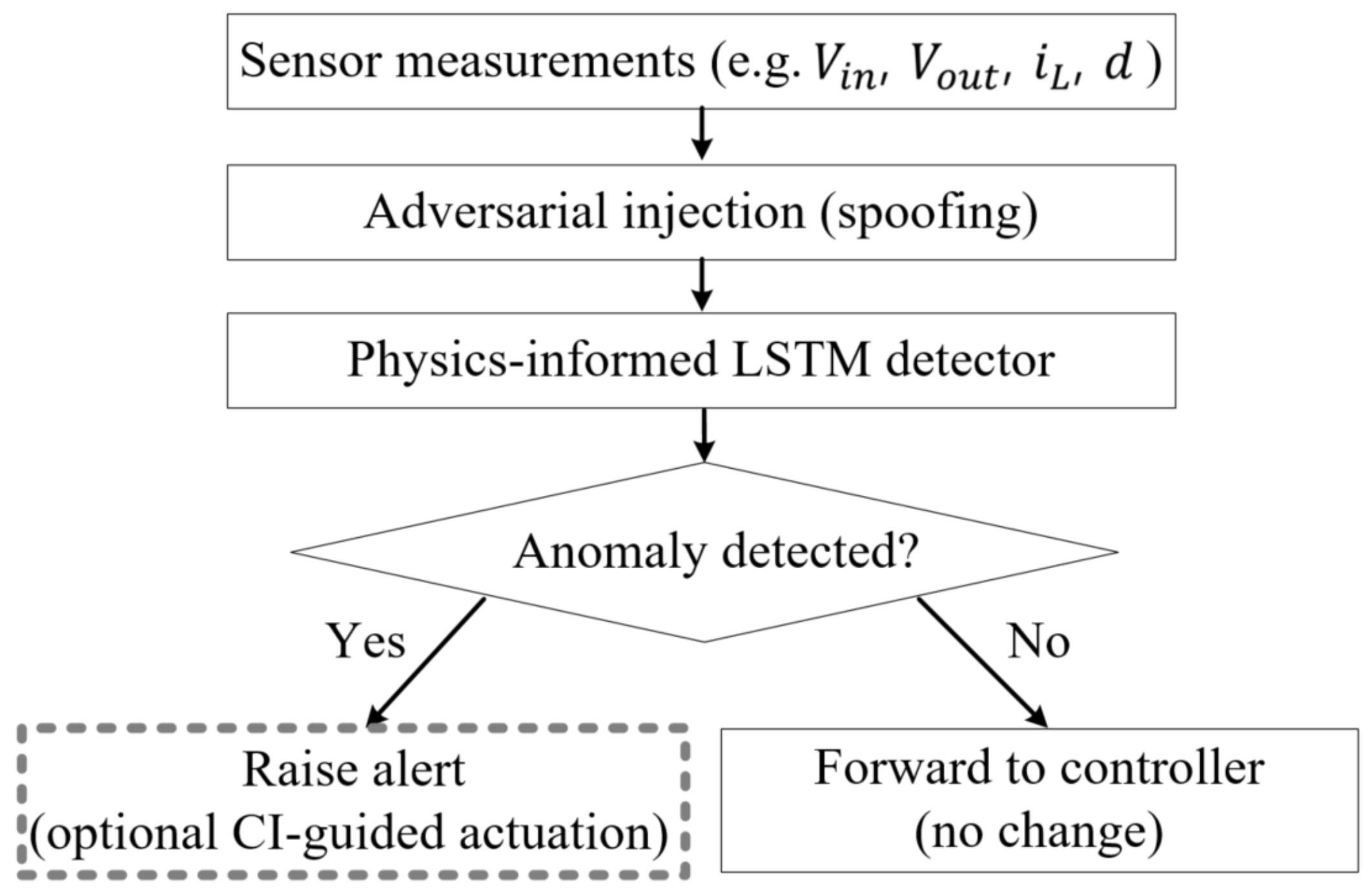
- Unified detection policy with DSP-grade deployment. A single detector covers DC bias, fixed-sample delay, and narrowband noise under a fixed decision rule (, ). On a TMS320F28379, a distilled model (, ) achieves 2.9–4.2 ms latency with an alarm-wise FPR of ≤1.2%.
- Unified safety box coherently tied to response. We formalize a safety box for DC rail quality and regulation—time-domain ripple , in-band ripple ratio , and a regulation window—and reuse the same normalizers inside the confusion index (CI), preventing metric–policy mismatch. See Section 2.5, Equations (5) and (6).
- CI-guided actuation policy (simulation) with rollback criteria. We specify a bounded actuation law tied to the safety box and demonstrate an operating point (CI ) in simulations, together with firmware-style rollback/hysteresis rules for hardware realization [24,25]. See Section 2.5, Equations (5) and (6).
- Measurement and reporting conventions for power quality-aware detection. We standardize (AC-coupled, 20 MHz bandwidth limit) and (Welch PSD around ) and report detection with fixed persistence, hardware compute budgets, and confidence intervals.
2. System Modeling and Design
2.1. Buck Converter Simulation Model
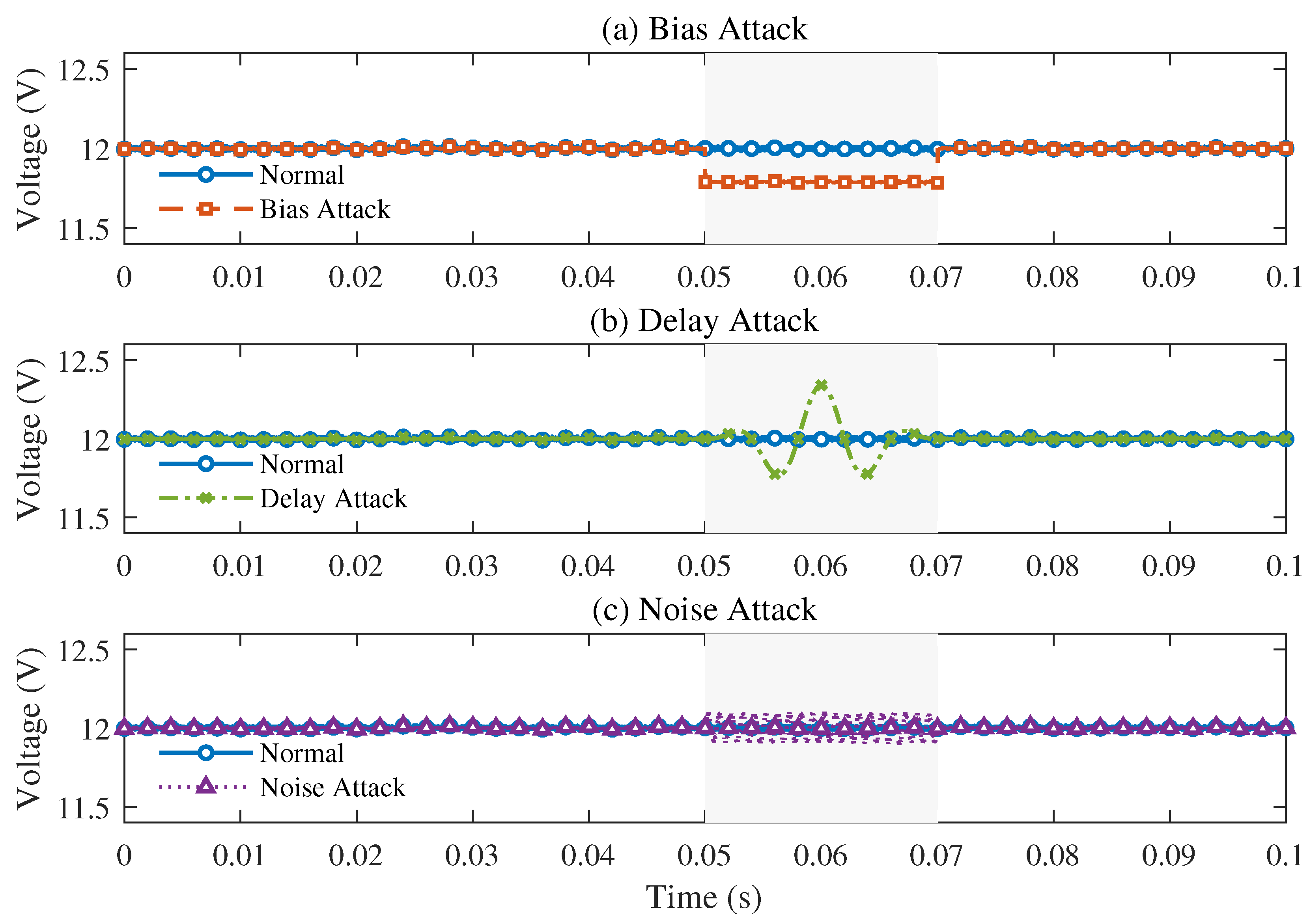
2.2. Sensor Attack Scenario Modeling
| Algorithm 1 Bias attack (voltage only, physically consistent) |
|
| Algorithm 2 Delay attack (ring buffer at sampling period ) |
|
| Algorithm 3 Noise attack (narrowband sinusoidal injection) |
|
2.2.1. Bias Attack Modeling
2.2.2. Delay Attack Modeling
2.2.3. Noise Injection Attack Modeling
2.2.4. Rationale for Attack Parameter Choices
2.2.5. Real-World Scenarios (EV/PV/ESS)
2.3. Physics-Informed LSTM Model Structure
2.3.1. Time-Base Convention (Simulation vs. Hardware)
2.3.2. Hyperparameter Selection and Validation Protocol
2.3.3. Cross-Validation and Leakage Control
2.4. Physics-Informed Learning Framework
Context in the Broader PINN Literature
2.5. CI-Guided Intentional Performance Degradation (Unified with DC Rail Ripple Metrics)
| Algorithm 4 CI-guided deception under a unified safety box |
|
3. Simulation Results and Analysis
3.1. Simulation Environment Setup
Classical Baselines (EKF Residual and Shewhart)
3.2. Benchmark Dataset Domain Alignment (Auxiliary Evaluation)
- 1.
- Signal mapping. Select PMSM signals that are physically analogous to our inputs (e.g., DC bus voltage/current and duty or normalized gate command). Exclude non-analogous mechanical variables from the core feature set.
- 2.
- Sampling (no upsampling). Use all PMSM signals at their native 10 Hz sampling rate (no upsampling or resampling). Apply per-window mean removal (AC coupling) and z-score normalization computed on benign segments. The decision rule is identical to the buck study: threshold and an consecutive-samples policy.
- 3.
- Attack semantics. When labels exist (bias/delay/noise), retain them. Otherwise, inject attacks consistent with our threat model (bias at the sensor tap; fixed-sample delay; a narrowband sinusoid at a frequency resolvable under 10 Hz Nyquist) to preserve semantic alignment.
- 4.
- Metrics separation. DC rail power quality metrics (, IRR) are not computed for PMSM. We report only detection metrics (accuracy, F1, AUC, alarm-wise FPR) for PMSM, and we do not compare the absolute latencies between the PMSM and buck domains.
3.2.1. Auxiliary PMSM Dataset: Sampling Rate Disclosure and Verification
3.2.2. Detector Configuration at Low Rate
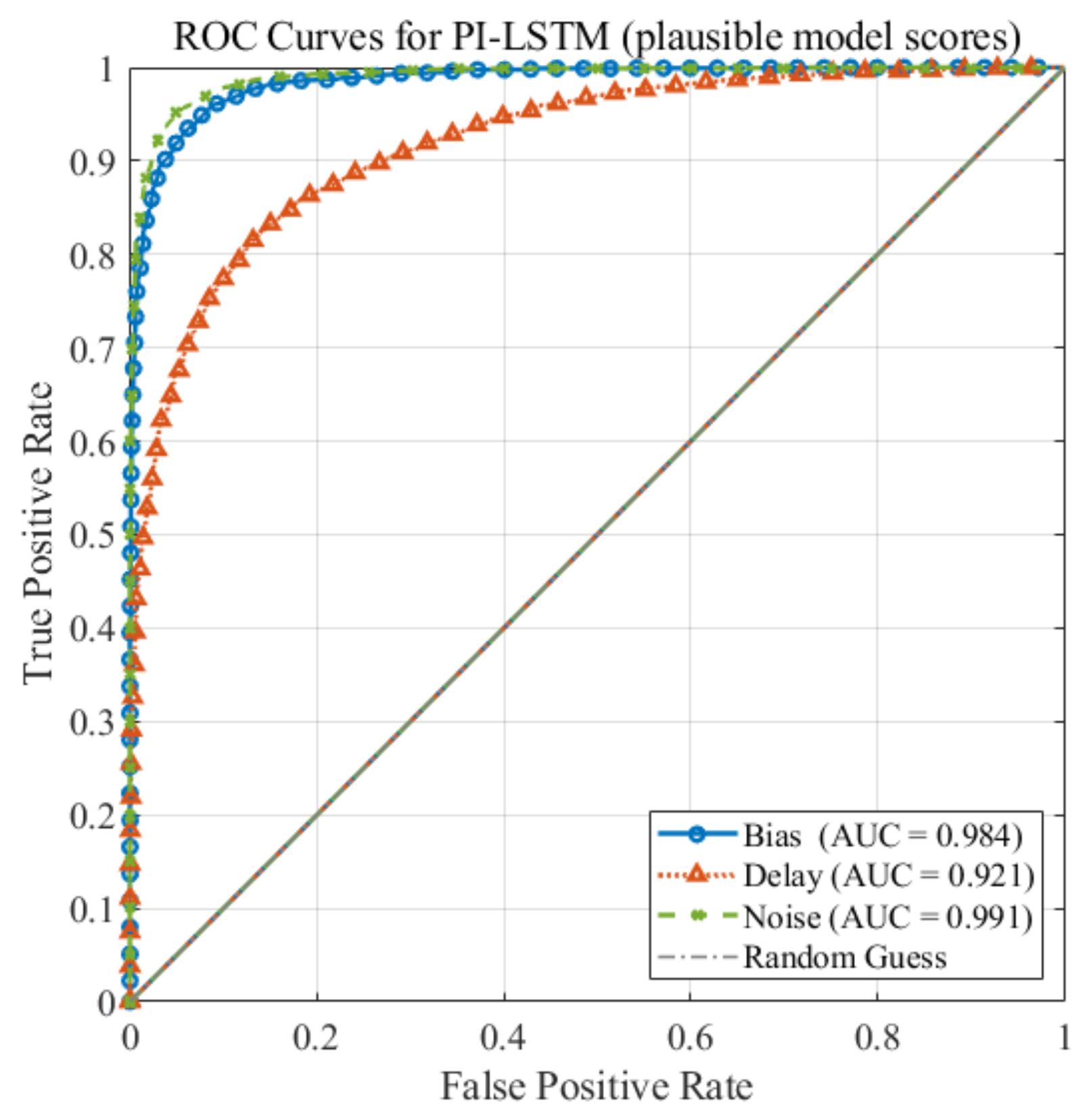
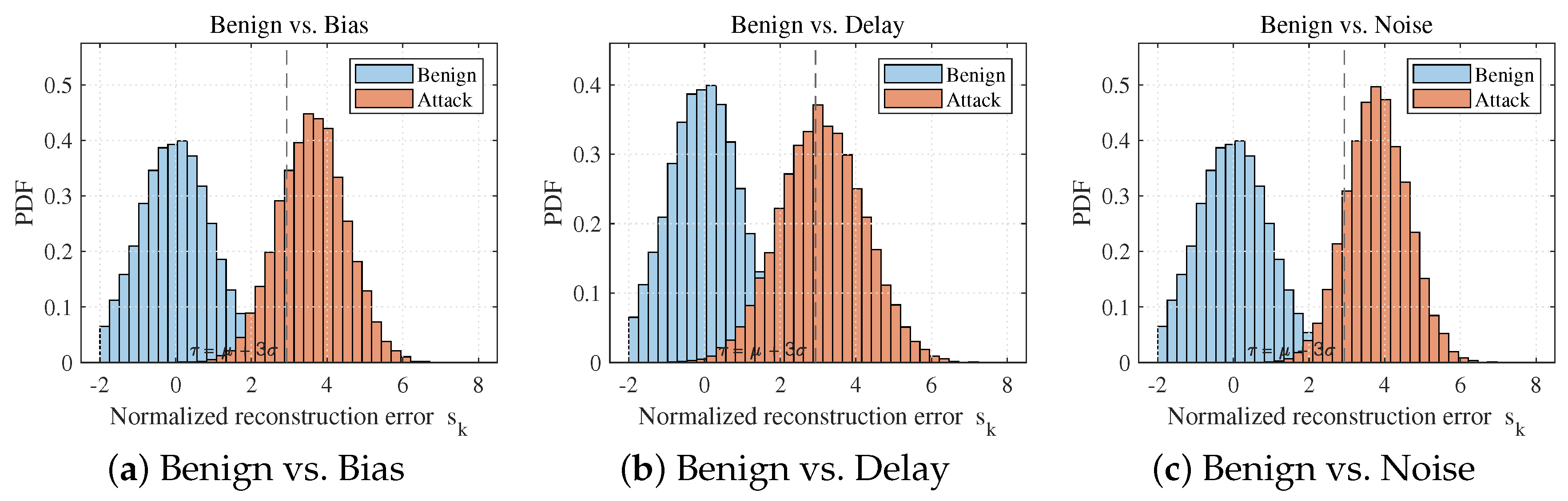
3.3. Attack Detection Performance Analysis
Additional Baselines: SVM and Random Forest
3.4. Public Benchmark Comparison
- ARIMA (residual threshold);
- Isolation Forest (100 trees, 4 features);
- CNN–LSTM Autoencoder (1D-CNN→LSTM; reimplementation of [44]);
- Proposed PI–LSTM ().
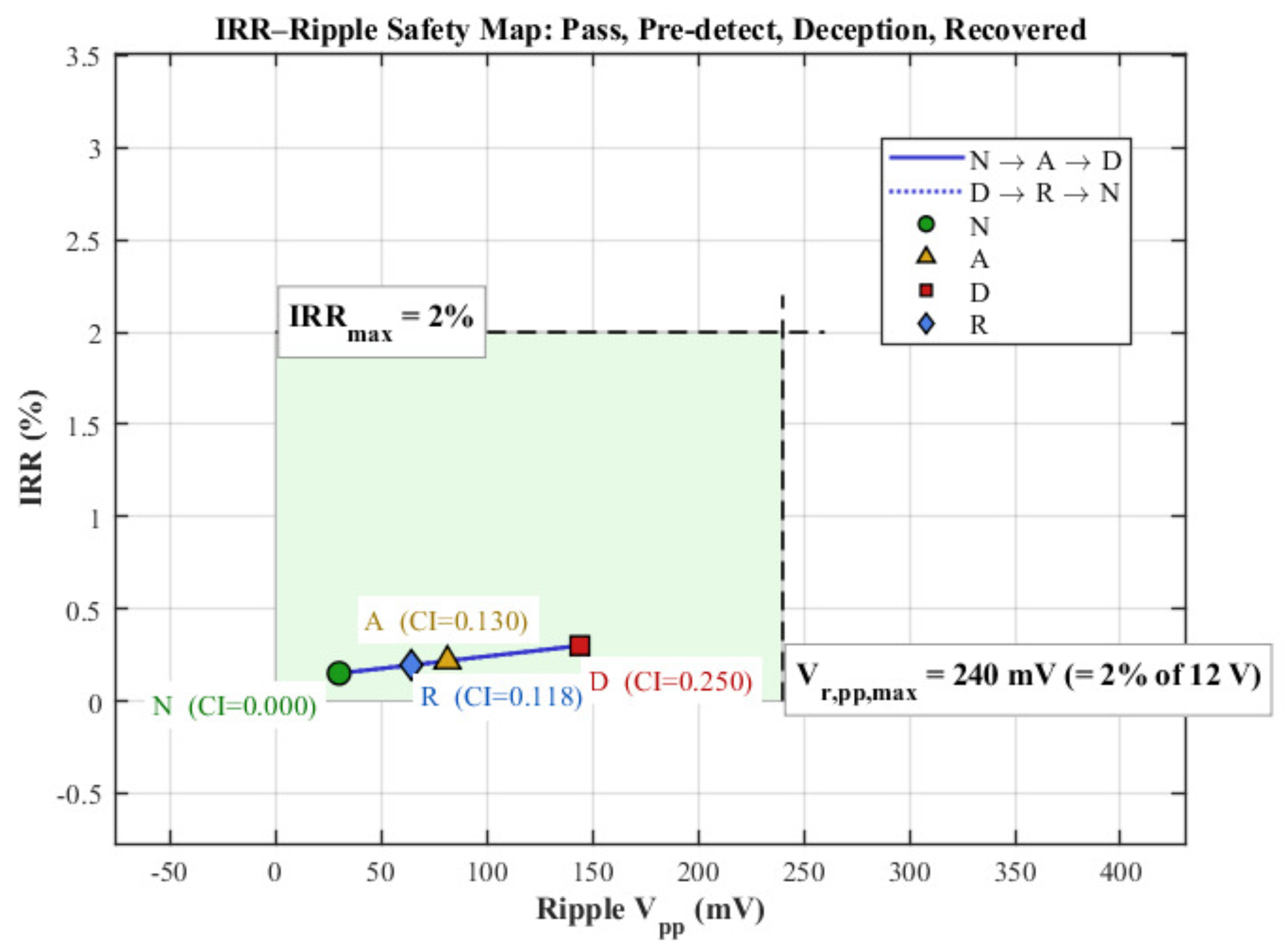
3.5. CI-Guided Deception Under a Unified Safety Box (Simulation Only)
Scope and Hardware Linkage
3.6. Effect of Physical Constraints
4. Experimental Setup and Results
4.1. Experimental Setup
- 1.
- DC bias with calibrated mapping to the feedback path;
- 2.
- Fixed sample delay ms (FIFO at kHz);
- 3.
- Narrowband sinusoidal injection at 1 kHz ( ).
4.1.1. Measurement Protocol and Definitions
4.1.2. Compliance and Interpretation
4.2. Real-Time Inference Budget on TMS320F28379
4.2.1. Analytic Complexity (per LSTM Layer)
4.2.2. Cycle Model
4.2.3. Deployment Configuration (Example)
4.2.4. On-Board Measurement Protocol
4.2.5. Bias Injection and Scaling
4.2.6. Delay Injection: Implementation and Validation
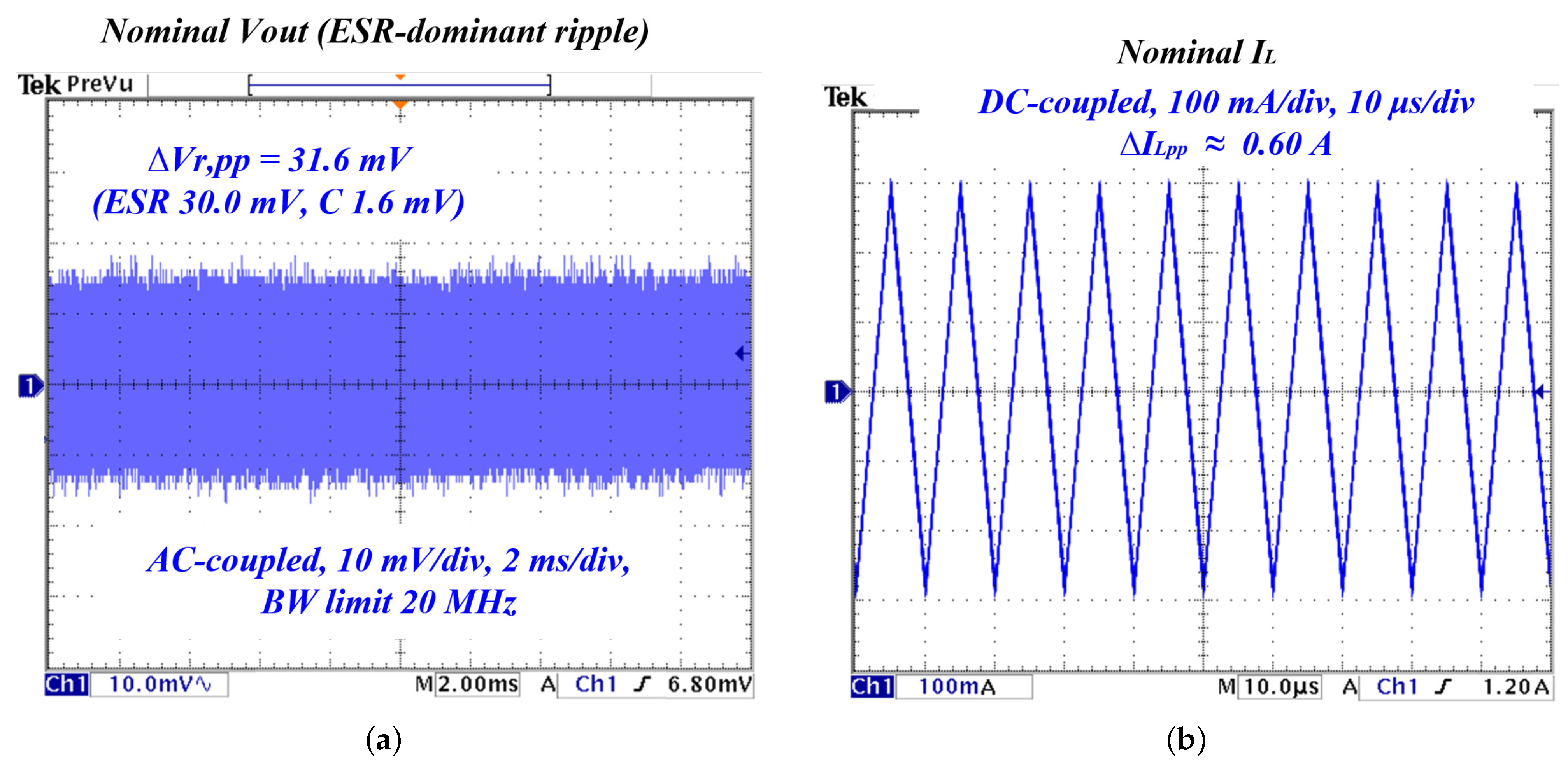
4.2.7. Oscilloscope and Probing Settings
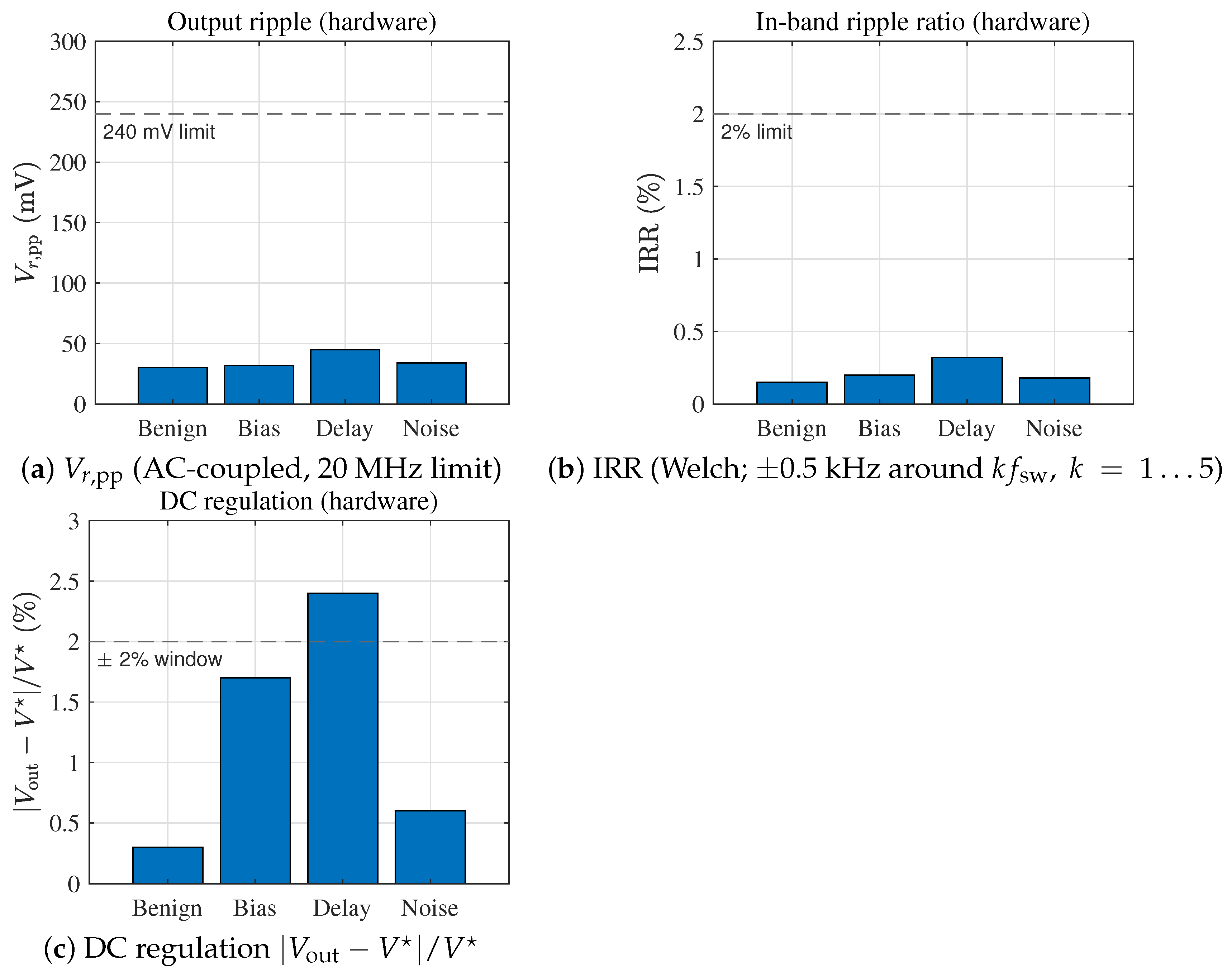
- : 10:1 passive probe with spring ground; bandwidth limit 20 MHz. AC coupling for ripple (); DC coupling for step/bias/delay tests.
- : 20 MHz current probe, deskewed to the probe using a common step.
- Time windows: ripple at 5–10 switching periods (50–100 s); low-frequency oscillation at 50–100 ms.
- Triggering: rising edge of the attack window marker or reference step; memory depth ≥1 Mpts; sample rate ≥10 MS/s (ripple captures often at 200 MS/s).
4.3. Detection Metrics: Latency and False Positives
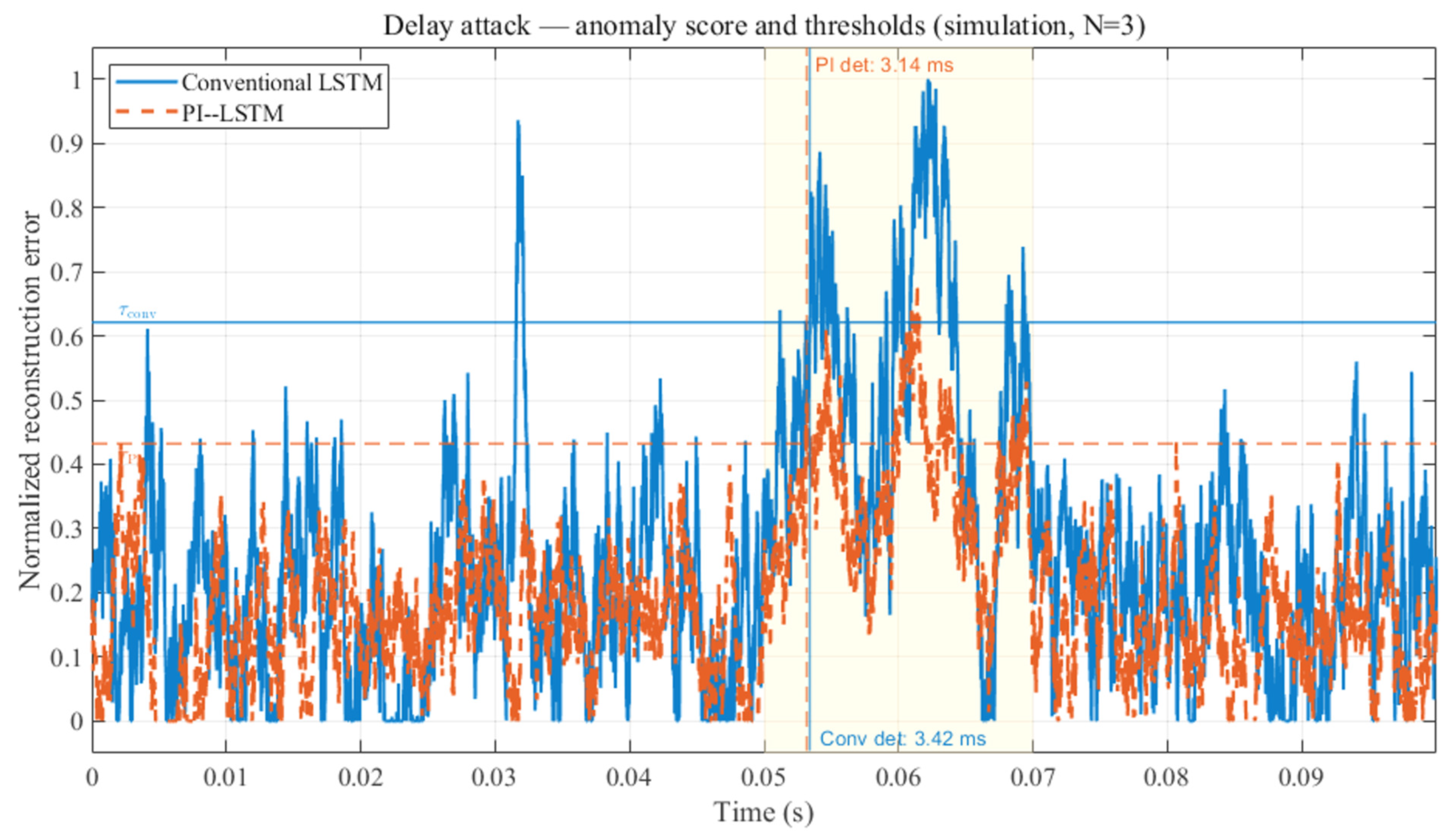
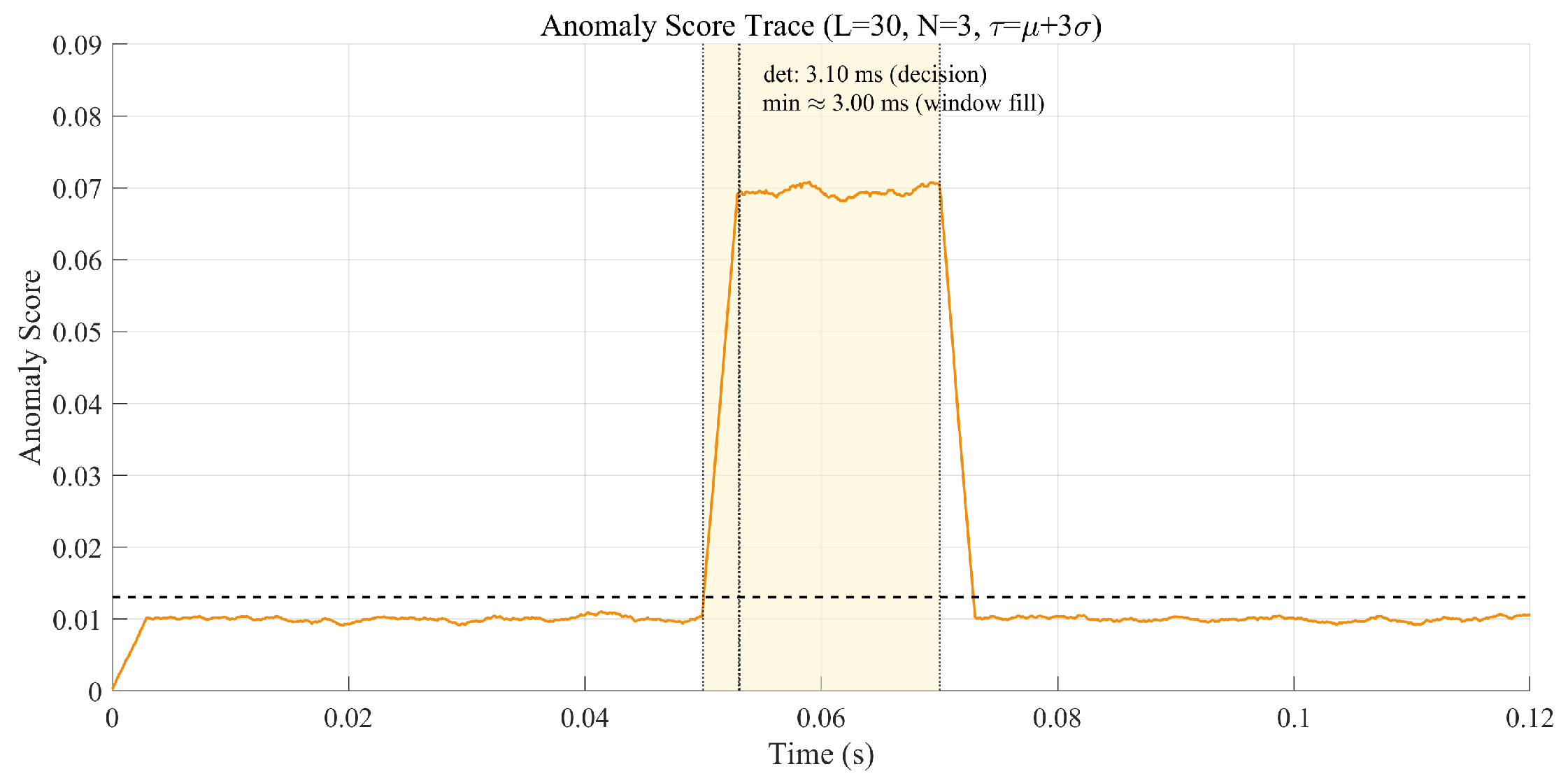
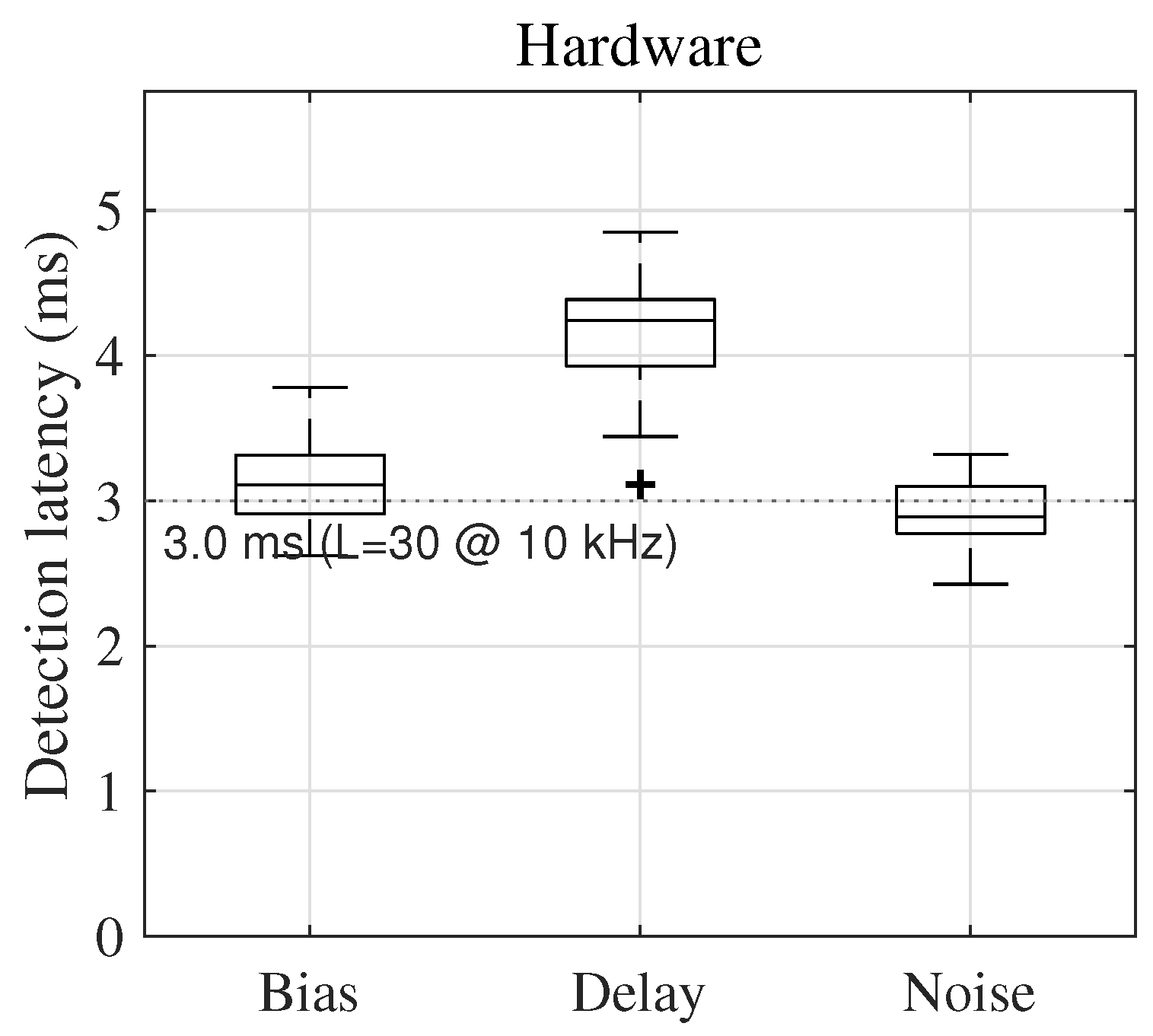
4.3.1. Detection Latency
4.3.2. False Positive Rate (Alarm-Wise)
4.3.3. Sample-Wise Exceedance (Secondary Descriptor)
4.3.4. Statistical Reporting Conventions
4.3.5. System-Level Impact and Resilience Metrics
4.4. Experimental Results
4.4.1. Baseline Operation
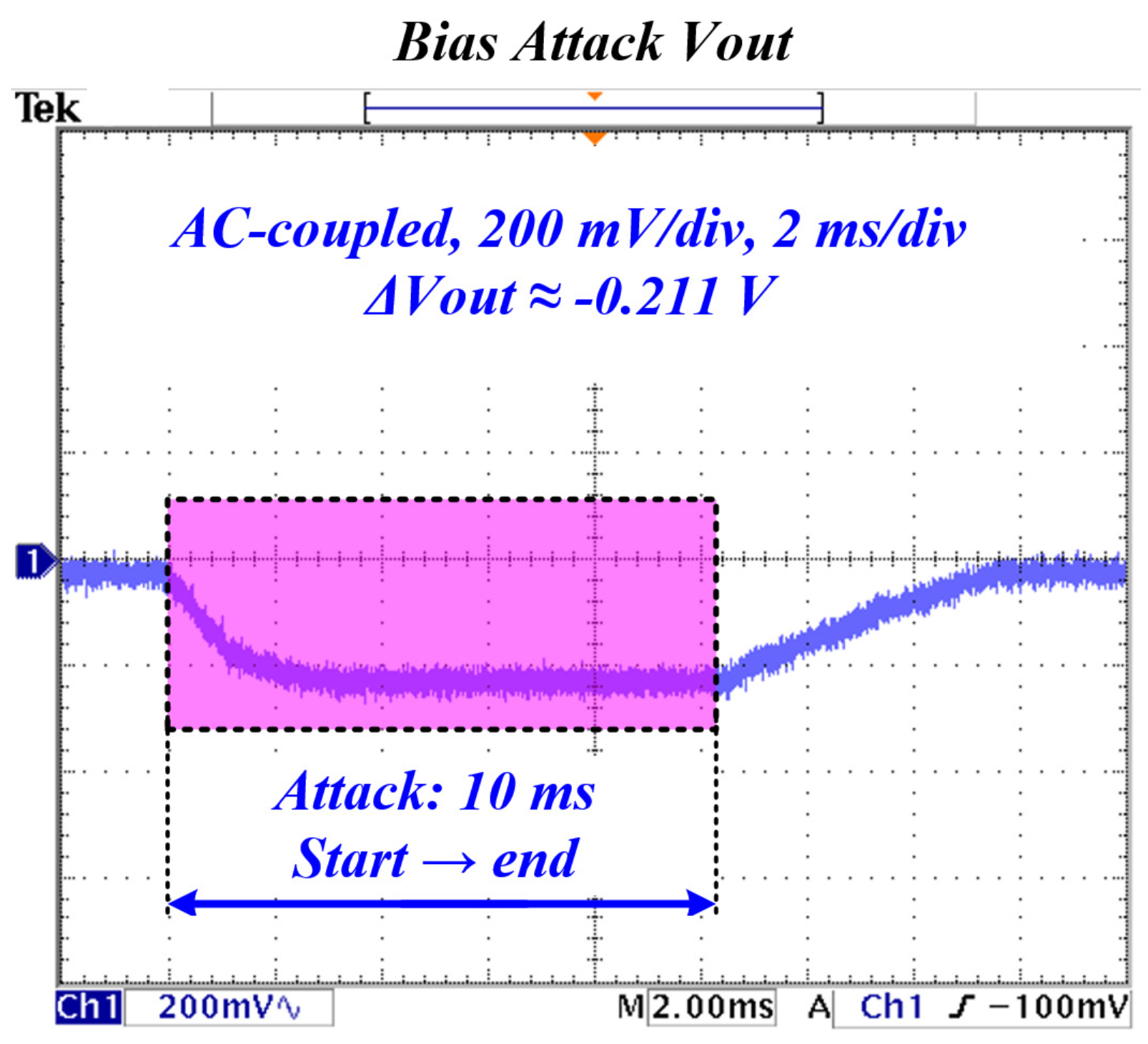
4.4.2. Bias Injection
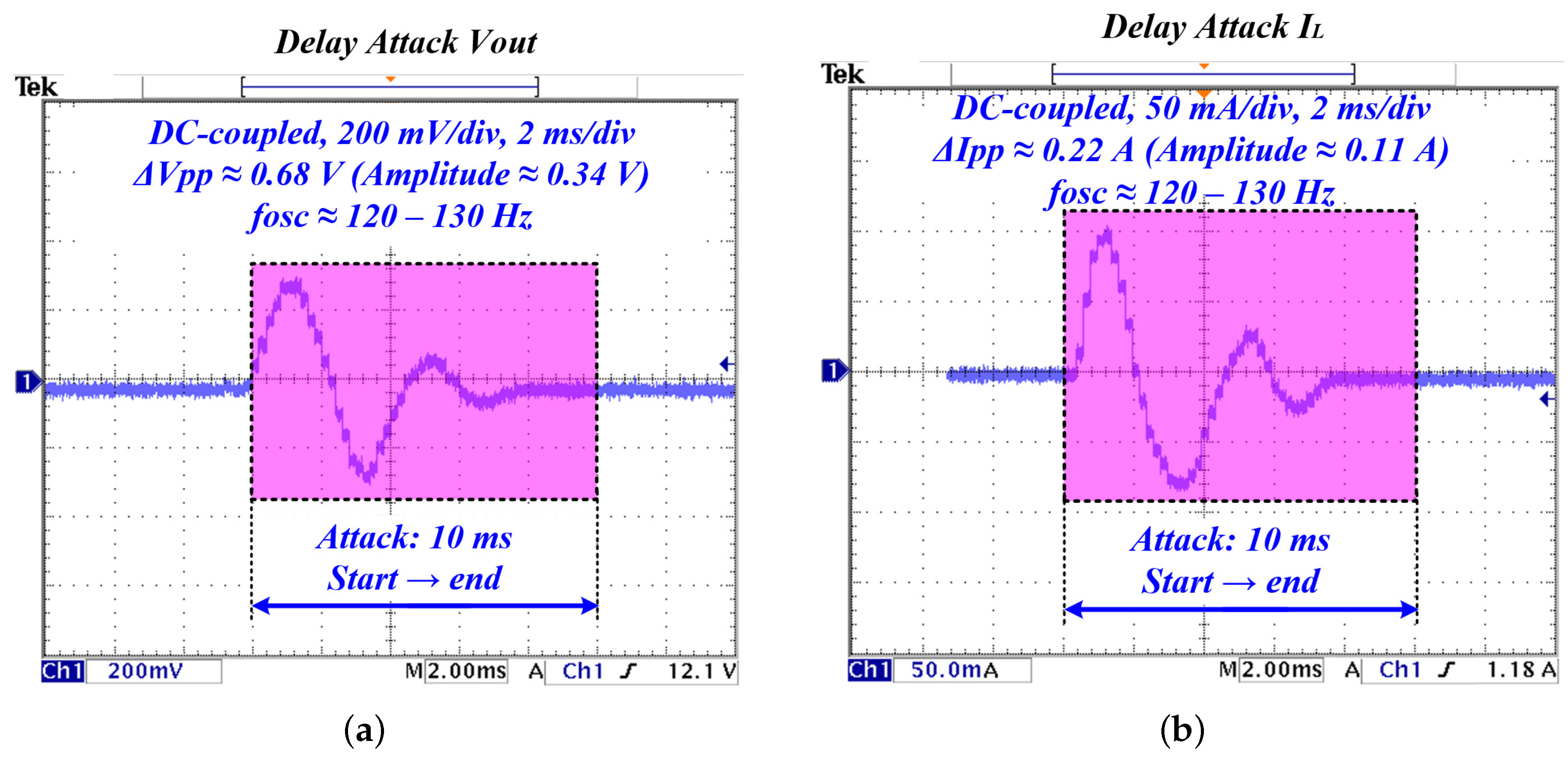
4.4.3. Delay Injection
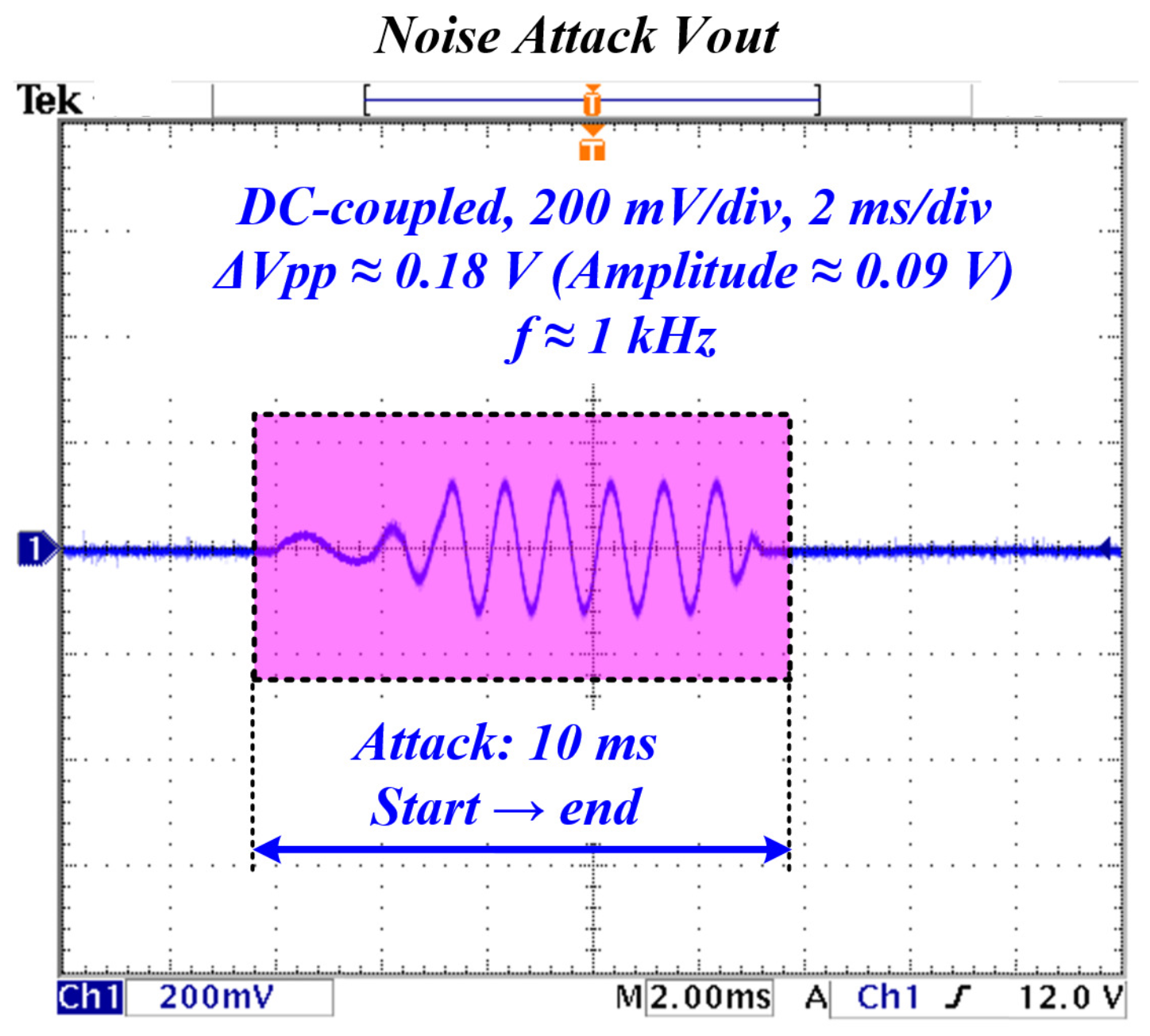
4.4.4. Noise Injection
4.4.5. Anomaly Score and Detection Performance
4.4.6. Hardware Results with Confidence Intervals
- Bias: latency ms; FPR ;
- Delay: latency ms; FPR ;
- Noise: latency ms; FPR .
4.4.7. CI-Based Actuation: Hardware Implementation Plan
4.4.8. Limitations and Robustness Considerations
5. Conclusions
- HIL/on-rig CI actuation under the unified safety box. Close the loop on HIL and hardware for CI-guided actuation while enforcing the same limits used in this paper: , , . Acceptance targets: median detection latency within the prior 2.9–4.2 ms band; alarm-wise FPR ; zero safety box violations during CI engagement with rollback/hysteresis enabled.
- Threat model and topology expansion. Evaluate more complex disturbances (multi-tone/near- EMI, sampled data jitter/delay spread, ADC range/quantization effects, sensor drift + load steps) and extend the residual template to boost, buck–boost, and multiphase VRM with optional multi-sensor fusion.
- System-level performance and resilience across environments. Quantify efficiency drop and energy overhead, delay-sensitive oscillation proxies, and fleet indicators (alarm density, MTTR, score drift index) across temperature/aging (e.g., –C), ESR/inductance drift, and EMI injection; retain the fixed decision policy (, ) with periodic benign rethresholding.
- Distributed integration (edge–gateway–cloud). Keep safety local on the controller (fail closed to ). Gateway aggregates 1–5 Hz summaries (OPC UA/MQTT/TLS), supports OTA with versioning/rollback; cloud performs drift monitoring and replay-based validation. Budgets: <0.1 ms/step at 10 kHz inference; ∼0.2–2.5 kB/s telemetry per node.
- Commercialization pilots. Run pilots in two–three domains (EV on-board DC–DC/charger, PV DC-link, ESS) to assess readiness. Targets: latency band preserved (median report), FPR , no safety box violations, and reduced nuisance trips vs. baseline. Deliverables: firmware library (porting guide), add-on module reference design, gateway/OTA workflows (audit logs, rollback).
- Industrial practice readiness. Prepare lightweight hardening and pre-compliance—QA test pack (temperature, aging, ESR and inductance (L) drift, EMI)—documentation for integration and O&M (commissioning: logging → shadow mode → gated actuation)—and pre-assess applicable standards (e.g., IEC 61204-3 [55], IEC 62443-2-1 [61], ISO 26262 [62], ISO/SAE 21434 [63]).
- Adaptive operations (optional). Operating mode-aware thresholds and change point detection while retaining the persistence policy; quantization/pruning for sub-40 µs/step at 200 MHz without loss of detection performance.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADC | Analog-to-Digital Converter |
| AE | Autoencoder |
| CCM | Continuous Conduction Mode |
| CI | Confusion Index (not a statistical confidence interval) |
| DSP | Digital Signal Processor |
| DSO | Digital Storage Oscilloscope |
| ESR | Equivalent Series Resistance |
| HIL | Hardware-in-the-Loop |
| IRR | In-Band Ripple Ratio |
| LSTM | Long Short-Term Memory |
| PI–LSTM | Physics-Informed LSTM |
| PSD | Power Spectral Density |
| PWM | Pulse Width Modulation |
References
- Mazumder, S.K.; Kulkarni, A.; Sahoo, S.; Blaabjerg, F.; Mantooth, H.A.; Balda, J.C.; Zhao, Y.; Ramos-Ruiz, J.A.; Enjeti, P.N.; Kumar, P.; et al. A review of current research trends in power-electronic innovations in cyber–physical systems. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5146–5163. [Google Scholar] [CrossRef]
- Parizad, A.; Baghaee, H.R.; Alizadeh, V.; Rahman, S. Emerging Technologies and Future Trends in Cyber-Physical Power Systems: Toward a New Era of Innovations. Smart-Cyber-Phys. Power Syst. Solut. Emerg. Technol. 2025, 2, 525–565. [Google Scholar]
- Chukwunweike, J.N.; Agosa, A.A.; Mba, U.J.; Okusi, O.; Safo, N.O.; Onosetale, O. Enhancing Cybersecurity in Onboard Charging Systems of Electric Vehicles: A MATLAB-based Approach. World J. Adv. Res. Rev. 2024, 23, 2661–2681. [Google Scholar] [CrossRef]
- Arena, G.; Chub, A.; Lukianov, M.; Strzelecki, R.; Vinnikov, D.; De Carne, G. A comprehensive review on DC fast charging stations for electric vehicles: Standards, power conversion technologies, architectures, energy management, and cybersecurity. IEEE Open J. Power Electron. 2024, 5, 1573–1611. [Google Scholar] [CrossRef]
- Yu, X.; Wang, H.; Dong, K.; Chen, C. A novel LDVP-based anomaly detection method for data streams. Int. J. Comput. Appl. 2024, 46, 381–389. [Google Scholar] [CrossRef]
- Tabassum, T.; Toker, O.; Khalghani, M.R. Cyber–physical anomaly detection for inverter-based microgrid using autoencoder neural network. Appl. Energy 2024, 355, 122283. [Google Scholar] [CrossRef]
- Hwang, S.Y.; Lee, J.c.; Lee, S.s.; Min, C. Anomaly-Detection Framework for Thrust Bearings in OWC WECs Using a Feature-Based Autoencoder. J. Mar. Sci. Eng. 2025, 13, 1638. [Google Scholar] [CrossRef]
- Alserhani, F. Intrusion Detection and Real-Time Adaptive Security in Medical IoT Using a Cyber-Physical System Design. Sensors 2025, 25, 4720. [Google Scholar] [CrossRef]
- Mahmoudi, I.; Boubiche, D.E.; Athmani, S.; Toral-Cruz, H.; Chan-Puc, F.I. Toward Generative AI-Based Intrusion Detection Systems for the Internet of Vehicles (IoV). Future Int. 2025, 17, 310. [Google Scholar] [CrossRef]
- Santoso, A.; Surya, Y. Maximizing decision efficiency with edge-based AI systems: Advanced strategies for real-time processing, scalability, and autonomous intelligence in distributed environments. Q. J. Emerg. Technol. Innov. 2024, 9, 104–132. [Google Scholar]
- Ottaviano, D. Real-Time Virtualization of Mixed-Criticality Heterogeneous Embedded Systems for Fusion Diagnostics and Control. 2025. Available online: https://www.research.unipd.it/handle/11577/3552539 (accessed on 23 September 2025).
- Isermann, R. Fault-Diagnosis Systems: An Introduction from Fault Detection to Fault Tolerance; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Givi, H.; Farjah, E.; Ghanbari, T. A Comprehensive Monitoring System for Online Fault Diagnosis and Aging Detection of Non-Isolated DC–DC Converters’ Components. IEEE Trans. Power Electron. 2019, 34, 6858–6875. [Google Scholar] [CrossRef]
- Geddam, K.K.; Elangovan, D. Review on fault-diagnosis and fault-tolerance for DC–DC converters. IET Power Electron. 2020, 13, 3071–3086. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A deep learning library for solving differential equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific Machine Learning Through Physics-Informed Neural Networks: Where we are and What’s next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: Learning velocity and pressure fields from scalar concentration only. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef] [PubMed]
- Karpatne, A.; Atluri, G.; Faghmous, J.H.; Steinbach, M.; Banerjee, A.; Ganguly, A.R.; Shekhar, S.; Samatova, N.; Kumar, V. Theory-Guided Data Science: A New Paradigm for Scientific Discovery from Data. IEEE Trans. Knowl. Data Eng. 2017, 29, 2318–2331. [Google Scholar] [CrossRef]
- Yang, S.; Bryant, A.; Mawby, P.; Xiang, D.; Ran, L.; Tavner, P. Condition Monitoring for Device Reliability in Power Electronic Converters: A Review. IEEE Trans. Power Electron. 2010, 25, 2734–2752. [Google Scholar] [CrossRef]
- Buiatti, G.M.; Martín-Ramos, J.A.; Rojas García, C.H.; Amaral, A.M.R.; Cardoso, A.J.M. An Online and Noninvasive Technique for the Condition Monitoring of Capacitors in Boost Converters. IEEE Trans. Instrum. Meas. 2010, 59, 2134–2143. [Google Scholar] [CrossRef]
- Elabid, Z. Informed Deep Learning for Modeling Physical Dynamics. Ph.D. Thesis, Sorbonne Université, Paris, France, 2025. [Google Scholar]
- Mansuri, A.; Maurya, R.; Suhel, S.M.; Iqbal, A. Random Switching Pulse Positioning based SVM Techniques for Six-Phase AC Drive to Spread Harmonic Spectrum. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 6531–6540. [Google Scholar] [CrossRef]
- Ekin, Ö.; Perez, F.; Wiegel, F.; Hagenmeyer, V.; Damm, G. Grid supporting nonlinear control for AC-coupled DC Microgrids. In Proceedings of the 2024 IEEE Sixth International Conference on DC Microgrids (ICDCM), Columbia, SC, USA, 5–8 August 2024; IEEE: New York, NY, USA, 2024; pp. 1–6. [Google Scholar]
- Ulrich, B. A low-cost setup and procedure for measuring losses in inductors. In Proceedings of the 2025 IEEE Applied Power Electronics Conference and Exposition (APEC), Atlanta, GA, USA, 16–20 March 2025; IEEE: New York, NY, USA, 2025; pp. 2502–2509. [Google Scholar]
- Bolatbek, Z. Single Shot Spectroscopy Using Supercontinuum and White Light Sources; University of Dayton: Dayton, OH, USA, 2024. [Google Scholar]
- Kim, H.; Bandyopadhyay, R.; Ozmen, M.O.; Celik, Z.B.; Bianchi, A.; Kim, Y.; Xu, D. A systematic study of physical sensor attack hardness. In Proceedings of the 2024 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 20–22 May 2024; IEEE: New York, NY, USA, 2024; pp. 2328–2347. [Google Scholar]
- Lian, Z.; Shi, P.; Chen, M. A Survey on Cyber-Attacks for Cyber-Physical Systems: Modeling, Defense and Design. IEEE Int. Things J. 2024, 12, 1471–1483. [Google Scholar] [CrossRef]
- Cao, H.; Huang, W.; Xu, G.; Chen, X.; He, Z.; Hu, J.; Jiang, H.; Fang, Y. Security analysis of WiFi-based sensing systems: Threats from perturbation attacks. arXiv 2024, arXiv:2404.15587. [Google Scholar]
- Jiang, D.; Zhang, M.; Xu, Y.; Qian, H.; Yang, Y.; Zhang, D.; Liu, Q. Rotor dynamic response prediction using physics-informed multi-LSTM networks. Aerosp. Sci. Technol. 2024, 155, 109648. [Google Scholar] [CrossRef]
- Atila, H.; Spence, S.M. Metamodeling of the response trajectories of nonlinear stochastic dynamic systems using physics-informed LSTM networks. J. Build. Eng. 2025, 111, 113447. [Google Scholar] [CrossRef]
- Ma, Z.; Jiang, G.; Chen, J. Physics-informed ensemble learning with residual modeling for enhanced building energy prediction. Energy Build. 2024, 323, 114853. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, J.; Bai, J.; Anitescu, C.; Eshaghi, M.S.; Zhuang, X.; Rabczuk, T.; Liu, Y. Kolmogorov–Arnold-Informed neural network: A physics-informed deep learning framework for solving forward and inverse problems based on Kolmogorov–Arnold Networks. Comput. Methods Appl. Mech. Eng. 2025, 433, 117518. [Google Scholar] [CrossRef]
- Fu, B.; Gao, Y.; Wang, W. A physics-informed deep reinforcement learning framework for autonomous steel frame structure design. Comput.-Aided Civ. Infrastruct. Eng. 2024, 39, 3125–3144. [Google Scholar] [CrossRef]
- Bagheri, A.; Patrignani, A.; Ghanbarian, B.; Pourkargar, D.B. A hybrid time series and physics-informed machine learning framework to predict soil water content. Eng. Appl. Artif. Intell. 2025, 144, 110105. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Kwak, S.; Choi, S. Model Predictive Virtual Flux Control Method for Low Switching Loss Performance in Three-Phase AC/DC Pulse-width-Modulated Converters. Machines 2024, 12, 66. [Google Scholar] [CrossRef]
- Fedele, E.; Spina, I.; Di Noia, L.P.; Tricoli, P. Multi-Port Traction Converter for Hydrogen Rail Vehicles: A Comparative Study. IEEE Access 2024, 12, 174888–174900. [Google Scholar] [CrossRef]
- Bacha, A. Comprehensive Dataset for Fault Detection and Diagnosis in Inverter-Driven PMSM Systems (Version 3.0) [Data set]. Zenodo. 2024. Available online: https://www.sciencedirect.com/science/article/pii/S2352340925000186 (accessed on 8 October 2025).
- Shaheed, K.; Szczuko, P.; Kumar, M.; Qureshi, I.; Abbas, Q.; Ullah, I. Deep learning techniques for biometric security: A systematic review of presentation attack detection systems. Eng. Appl. Artif. Intell. 2024, 129, 107569. [Google Scholar] [CrossRef]
- Rajendran, R.M.; Vyas, B. Detecting apt using machine learning: Comparative performance analysis with proposed model. In Proceedings of the SoutheastCon 2024, Atlanta, GA, USA, 15–24 March 2024; IEEE: New York, NY, USA, 2024; pp. 1064–1069. [Google Scholar]
- Kim, H.G.; Park, Y. Calibrating F1 Scores for Fair Performance Comparison of Binary Classification Models with Application to Student Dropout Prediction. IEEE Access 2025, 13, 136554–136567. [Google Scholar] [CrossRef]
- Xu, T. Credit risk assessment using a combined approach of supervised and unsupervised learning. J. Comput. Methods Eng. Appl. 2024, 4, 1–12. [Google Scholar] [CrossRef]
- Khanmohammadi, F.; Azmi, R. Time-series anomaly detection in automated vehicles using d-cnn-lstm autoencoder. IEEE Trans. Intell. Transp. Syst. 2024, 25, 9296–9307. [Google Scholar] [CrossRef]
- Long, S.; Zhou, Q.; Ying, C.; Ma, L.; Luo, Y. Rethinking domain generalization: Discriminability and generalizability. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 11783–11797. [Google Scholar] [CrossRef]
- Jiang, F.; Li, Q.; Wang, W.; Ren, M.; Shen, W.; Liu, B.; Sun, Z. Open-set single-domain generalization for robust face anti-spoofing. Int. J. Comput. Vis. 2024, 132, 5151–5172. [Google Scholar] [CrossRef]
- Arpinati, L.; Carradori, G.; Scherz-Shouval, R. CAF-induced physical constraints controlling T cell state and localization in solid tumours. Nat. Rev. Cancer 2024, 24, 676–693. [Google Scholar] [CrossRef]
- Jiang, L.; Hu, Y.; Liu, Y.; Zhang, X.; Kang, G.; Kan, Q. Physics-informed machine learning for low-cycle fatigue life prediction of 316 stainless steels. Int. J. Fatigue 2024, 182, 108187. [Google Scholar] [CrossRef]
- Kwon, Y.; Kim, W.; Kim, H. HARD: Hardware-Aware lightweight Real-time semantic segmentation model Deployable from Edge to GPU. In Proceedings of the Asian Conference on Computer Vision, Hanoi, Vietnam, 8–12 December 2024; pp. 3552–3569. [Google Scholar]
- Gao, B.; Kong, X.; Li, S.; Chen, Y.; Zhang, X.; Liu, Z.; Lv, W. Enhancing anomaly detection accuracy and interpretability in low-quality and class imbalanced data: A comprehensive approach. Appl. Energy 2024, 353, 122157. [Google Scholar] [CrossRef]
- Instruments, T. The TMS320F2837xD Architecture: Achieving a New Level of High Performance. Technical Article SPRT720, Texas Instruments. 2016. Available online: https://www.radiolocman.com/datasheet/data.html?di=333939&/TMS320F28379D (accessed on 23 September 2025).
- Instruments, T. TMS320C28x Extended Instruction Sets Technical Reference Manual; Texas Instruments: Dallas, TX, USA, 2019. [Google Scholar]
- ISO 16750-2:2023; Road Vehicles—Environmental Conditions and Testing for Electrical and Electronic Equipment—Part 2: Electrical Loads. International Organization for Standardization: Geneva, Switzerland, 2023.
- ISO 21780:2020; Road Vehicles—Supply Voltage of 48 V—Electrical Requirements and Tests. International Organization for Standardization: Geneva, Switzerland, 2020.
- IEC 61204-3:2016; Low-Voltage Power Supplies, DC Output—Part 3: Electromagnetic Compatibility (EMC). International Electrotechnical Commission: Geneva, Switzerland, 2016.
- Single Rail Power Supply ATX12VO Design Guide. In Design Guide; Intel Corporation: Santa Clara, CA, USA, 2020.
- Power Supply Measurement and Analysis with Bench Oscilloscopes. In Technical Report Application Note 3GW-23612-6; Tektronix, Inc.: Beaverton, OR, USA, 2014.
- Instruments, T. Cycle Scavenging on C2000™ MCUs, Part 5: TMU and CLA. Technical Article. 2017. Available online: https://www.ti.com/lit/ta/sszt866/sszt866.pdf?ts=1760149313235&ref_url=https%253A%252F%252Fwww.google.com.hk%252F (accessed on 7 September 2025).
- Instruments, T. TMS320F2837xD Dual-Core Real-Time Microcontrollers Technical Reference Manual; Texas Instruments: Dallas, TX, USA, 2024. [Google Scholar]
- MathWorks. C28x-Build Options—Enable FastRTS. Online Documentation. 2025. Available online: https://www.mathworks.com/help/ti-c2000/ref/sect-hw-imp-pane-c28x-build-options.html (accessed on 7 September 2025).
- IEC 62443-2-1:2024; Security for Industrial Automation and Control Systems—Part 2-1: Security Program Requirements for IACS Asset Owners. International Electrotechnical Commission: Geneva, Switzerland, 2024.
- ISO 26262:2018; Road Vehicles—Functional Safety (All Parts). International Organization for Standardization: Geneva, Switzerland, 2018.
- ISO/SAE 21434:2021; Road Vehicles—Cybersecurity Engineering. International Organization for Standardization and SAE International: Geneva, Switzerland; Warrendale, PA, USA, 2021.


| Category | Representative References |
|---|---|
| Model-/observer-based FDI | Fault diagnosis monographs and observer-based schemes [12]. |
| Rule/statistical detection | Residual thresholds; classical change detection surveys (e.g., CUSUM/GLR) [12]. |
| Classical ML for converters | SVM/RF/isolation forest baselines; PE monitoring surveys [13,14]. |
| Deep time-series AEs | CNN–LSTM and LSTM autoencoders in converter diagnostics [13,14]. |
| Physics-informed learning | PINNs and theory-guided data science [15,16,17,18,19,20]. |
| CPS security in PE | Device reliability/CM and DC–DC diagnosis overviews [14,21]. |
| Abbrev. | Definition |
|---|---|
| ADC | Analog-to-Digital Converter |
| AE | Autoencoder |
| AUC | Area Under the ROC Curve |
| CCM | Continuous Conduction Mode |
| CI | Confusion Index (policy metric; not a statistical confidence interval) |
| DSP | Digital Signal Processor |
| DSO | Digital Storage Oscilloscope |
| EMI/EMC | Electromagnetic Interference/Compatibility |
| ESR | Equivalent Series Resistance |
| FPR | False-Positive Rate (alarm-wise unless stated) |
| HIL | Hardware-in-the-Loop |
| IRR | In-band Ripple Ratio |
| LSTM | Long Short-Term Memory |
| PI–LSTM | Physics-Informed LSTM |
| PSD | Power Spectral Density |
| PWM | Pulse-Width Modulation |
| ROC | Receiver Operating Characteristic |
| SPF | Sample-wise Positive Fraction |
| VRM | Voltage Regulator Module |
| Parameter | Value | Unit |
|---|---|---|
| Input Voltage | 24 | V |
| Output Voltage | 12 | V |
| Inductance | 100 | µH |
| Capacitance | 470 | µF |
| Load Resistance | 10 | |
| Switching Frequency | 100 | kHz |
| Output Power | 14.4 | W |
| Domain | Typical Disturbance (Site) | Primary Effect |
|---|---|---|
| EV (12/48 V) | Supply ripple on ; harness/ground; 0.5–5 kHz | , IRR ; small regulation error unless severe; score rises at tone(s). |
| PV DC-link | MPPT/load transitions; sensor bias/drift (divider/ADC) | Transient regulation excursions; DC shift per bias; score increases after onset. |
| ESS/Industrial | Fixed delay (buffer/firmware); sense -line EMI (≈1 kHz) | Phase margin loss ⇒ ∼ Hz modulation (delay); narrowband component; few ms detection latency. |
| Item | Value |
|---|---|
| GPU/CPU/RAM | RTX 5070Ti (12 GB)/Core7 255HX/64 GB |
| Framework | PyTorch 2.2 (CUDA 12); data via MATLAB R2024a |
| Dataset windows () | ∼180,000 (80/10/10 split) |
| Batch/LR schedule | 128/ (cosine) |
| Early stopping | Patience 10 epochs |
| Epochs (median) | 35–55 (42) |
| Wall clock (median) | 65–85 min (74 min) |
| Peak GPU memory | 2.1–2.4 GB (FP32) |
| Checkpoint size | ∼7.5 MB (offline model) |
| Distillation time | 10–15 min → |
| Item | Value | Note |
|---|---|---|
| for | ||
| , | also used as CI normalizers | |
| deception cap | ||
| ref/duty/freq gains | ||
| 3 samples, 10 ms | persistence/hysteresis |
| Parameter | Value | Unit |
|---|---|---|
| Simulation time | 0.1 | s |
| Sampling interval | 10 | µs |
| Total samples | 10,000 | — |
| Attack start time | 50 | ms |
| Attack duration | 20 | ms |
| Sampling frequency | 100 | kHz |
| Measurement noise | 1 | % |
| Metric | Bias | Delay | Noise |
|---|---|---|---|
| Accuracy (%) | 96.24 | 91.98 | 97.51 |
| Precision (%) | 94.83 | 90.12 | 96.89 |
| Recall (%) | 97.45 | 93.78 | 98.12 |
| F1 score (%) | 96.12 | 91.91 | 97.50 |
| Detection latency after onset (ms) | 2.88 | 3.95 | 2.59 |
| Method | Accuracy (%) | FPR (%) | Latency (ms) | Hardware (Target/Footprint) |
|---|---|---|---|---|
| EKF (residual) | 90.5 | 3.8 | 3.6–5.0 | MCU/DSP; state+cov <10 kB |
| Shewhart (residual norm) | 88.0 | 6.7 | 3.8–5.2 | MCU/DSP; negligible |
| Fuzzy logic (rule-based) | 89.0 | 5.4 | 3.5–5.0 | MCU/DSP; ∼10–20 rules |
| PI–LSTM (ours) | ∼95.24 | ≤1.2 | 2.9–4.2 | TMS320F28379; ∼18.5 kB params |
| Method | Accuracy (%) | FPR (%) | Latency (ms) | Hardware (Target/Footprint) |
|---|---|---|---|---|
| SVM (linear) | 92.0 | 3.2 | 3.4–4.5 | MCU/DSP; weights <50 kB |
| Random Forest (200×, ) | 93.2 | 2.5 | 3.3–4.3 | MCU-class feasible; ∼300 kB |
| PI–LSTM (ours) | ∼95.24 | ≤1.2 | 2.9–4.2 | TMS320F28379; ∼18.5 kB |
| Method | Accuracy (%) | F1 (%) | AUC | FPR (%) |
|---|---|---|---|---|
| ARIMA | ||||
| Isolation Forest |
| Method | Accuracy (%) | F1 (%) | AUC | FPR (%) |
|---|---|---|---|---|
| CNN–LSTM AE | ||||
| PI–LSTM (proposed) |
| Metric | Normal | After Detection | Normalized Value |
|---|---|---|---|
| Efficiency (%) | 92.3 | 85.0 | |
| IRR (%) | 0.15 | 0.30 | |
| Output ripple (mV) | 30 | 144 | |
| Confusion index | 0 | – |
| Weights | CI (Computed) | |||
|---|---|---|---|---|
| Baseline (Table 6) | 0.50 | 0.30 | 0.20 | 0.25 |
| Ripple-heavy | 0.30 | 0.40 | 0.30 | 0.27 |
| Efficiency-heavy | 0.60 | 0.20 | 0.20 | 0.24 |
| Equal weights | 0.33 | 0.33 | 0.34 | 0.26 |
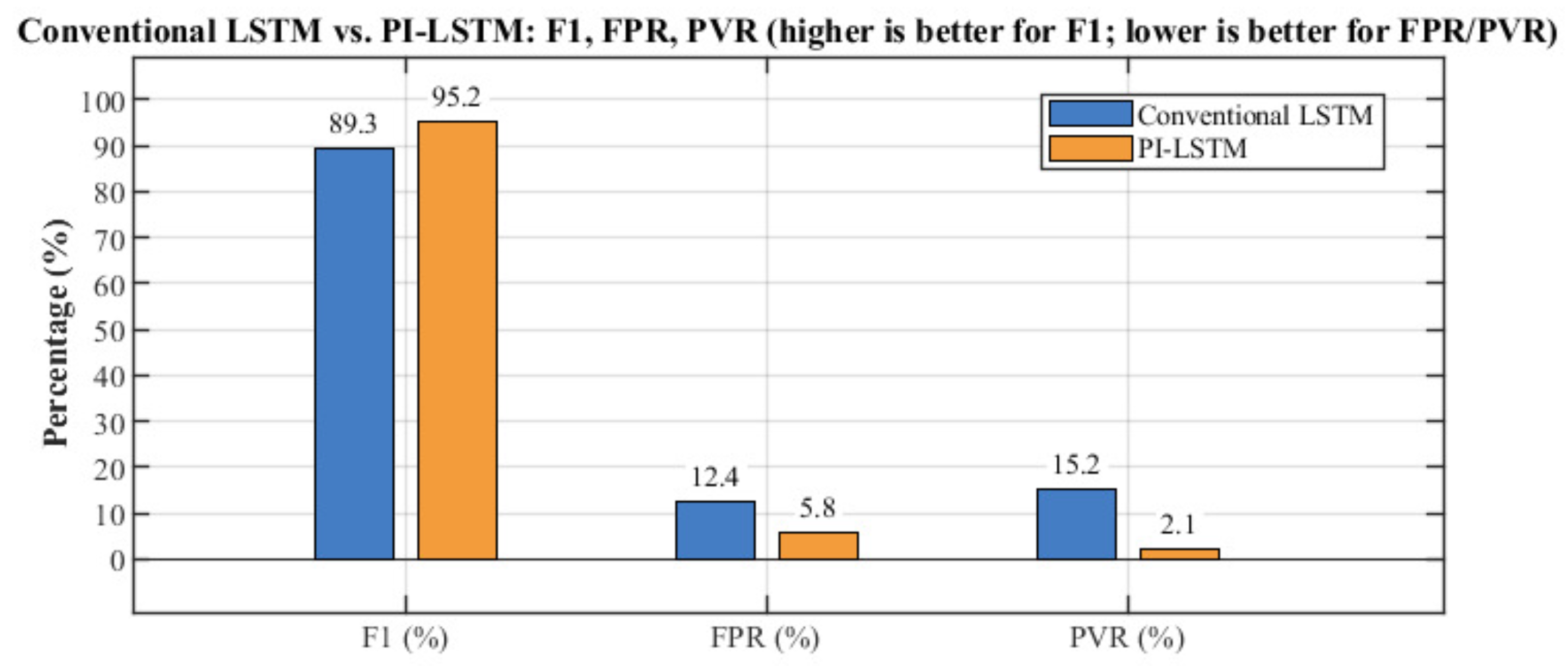
| Metric | Conventional LSTM | PI–LSTM |
|---|---|---|
| F1 score (%) | 89.3 | 95.2 |
| FPR (alarm-wise, %, ) | 12.4 | 5.8 |
| PVR (%) | 15.2 | 2.1 |
| Item | Setting |
|---|---|
| Scope sampling rate | ≥10 MS/s |
| Record length | ≥1 Mpts |
| Welch estimator | Hann, 50% overlap |
| Integration band | kHz around () |
| Normalization | (mean of DC-coupled record) |
| Time-domain ripple | from AC-coupled trace (20 MHz limit) |
| Item | Value |
|---|---|
| Model config | |
| Arithmetic/activations | FP32/PWL (DSPLib GEMM) |
| Per-step MACs | 4608 |
| Per-step cycles (estimate) | ≈11 kcycles |
| Per-step time @ 200 MHz (estimate) | ≈55 µ |
| Parameter memory (FP32) | ≈18.5 kB |
| Item | Value |
|---|---|
| Measured step time (median) | 54–58 µs ( calls, optimized build) |
| Jitter (peak-to-peak) | <4 µs |
| CPU load (LSTM only) | ≈55% |
| Streaming predictor | kHz; decim. ( kHz); |
| Decision rule | ; ; ms |
| KPI | Symbol | Unit | Definition/Purpose |
|---|---|---|---|
| Efficiency drop | %, % | Baseline ; ; maps to CI via . | |
| Ripple and spectrum | mV, % | Time-domain peak-to-peak; in-band ratio around . | |
| Regulation error | % | Compliance to the DC window. | |
| Oscillation index | % | RMS in 100–150 Hz band/; delay stress proxy. | |
| Phase margin bound | deg | ≈ (surrogate). | |
| Alarm density | during benign operation. | ||
| MTB alarms | h | . | |
| MTT recovery | s | Alarm → within-limit restoration (incl. hysteresis). | |
| Score drift | – | on benign segments. |
| Quantity | Reported | Computed (Model) | Verdict |
|---|---|---|---|
| Inductor ripple () | Consistent | ||
| Output ripple () | Consistent (ESR-dominant) | ||
| Bias (V) | Consistent (scaled) | ||
| Delay (ms) | µs = 1.020 | Consistent | |
| Noise (1 kHz) level () | ∼0.18 | N/A | Consistent (qual.) |
| Attack | Latency (ms), Median [IQR] | Latency, 95% CI (Bootstrap) | FPR (%), 95% CI (Wilson) |
|---|---|---|---|
| Bias | 3.1 [2.7–3.5] | 2.9–3.4 | 0.8 (0.2–2.9) |
| Delay | 4.2 [3.7–4.9] | 3.9–4.6 | 1.2 (0.3–3.3) |
| Noise | 2.9 [2.5–3.2] | 2.7–3.1 | 0.6 (0.1–2.4) |
| Scenario | DC Regulation () | ||
|---|---|---|---|
| Hardware (no CI actuation) | Fail (delay, up to ) | Pass | Pass |
| Simulation (with CI actuation) | Pass | Pass | Pass |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moon, J.-H.; Kim, J.-H.; Lee, J.-H. Sensor-Level Anomaly Detection in DC–DC Buck Converters with a Physics-Informed LSTM: DSP-Based Validation of Detection and a Simulation Study of CI-Guided Deception. Appl. Sci. 2025, 15, 11112. https://doi.org/10.3390/app152011112
Moon J-H, Kim J-H, Lee J-H. Sensor-Level Anomaly Detection in DC–DC Buck Converters with a Physics-Informed LSTM: DSP-Based Validation of Detection and a Simulation Study of CI-Guided Deception. Applied Sciences. 2025; 15(20):11112. https://doi.org/10.3390/app152011112
Chicago/Turabian StyleMoon, Jeong-Hoon, Jin-Hong Kim, and Jung-Hwan Lee. 2025. "Sensor-Level Anomaly Detection in DC–DC Buck Converters with a Physics-Informed LSTM: DSP-Based Validation of Detection and a Simulation Study of CI-Guided Deception" Applied Sciences 15, no. 20: 11112. https://doi.org/10.3390/app152011112
APA StyleMoon, J.-H., Kim, J.-H., & Lee, J.-H. (2025). Sensor-Level Anomaly Detection in DC–DC Buck Converters with a Physics-Informed LSTM: DSP-Based Validation of Detection and a Simulation Study of CI-Guided Deception. Applied Sciences, 15(20), 11112. https://doi.org/10.3390/app152011112






