Enhanced UAV Trajectory Tracking Using AIMM-IAKF with Adaptive Model Transition Probability
Abstract
1. Introduction
2. The Improved Adaptive Kalman Filter: From Foundations to Implementation
2.1. UAV Motion Models
2.2. Basic Filtering Algorithms and Improvements
2.2.1. Standard Kalman Filter
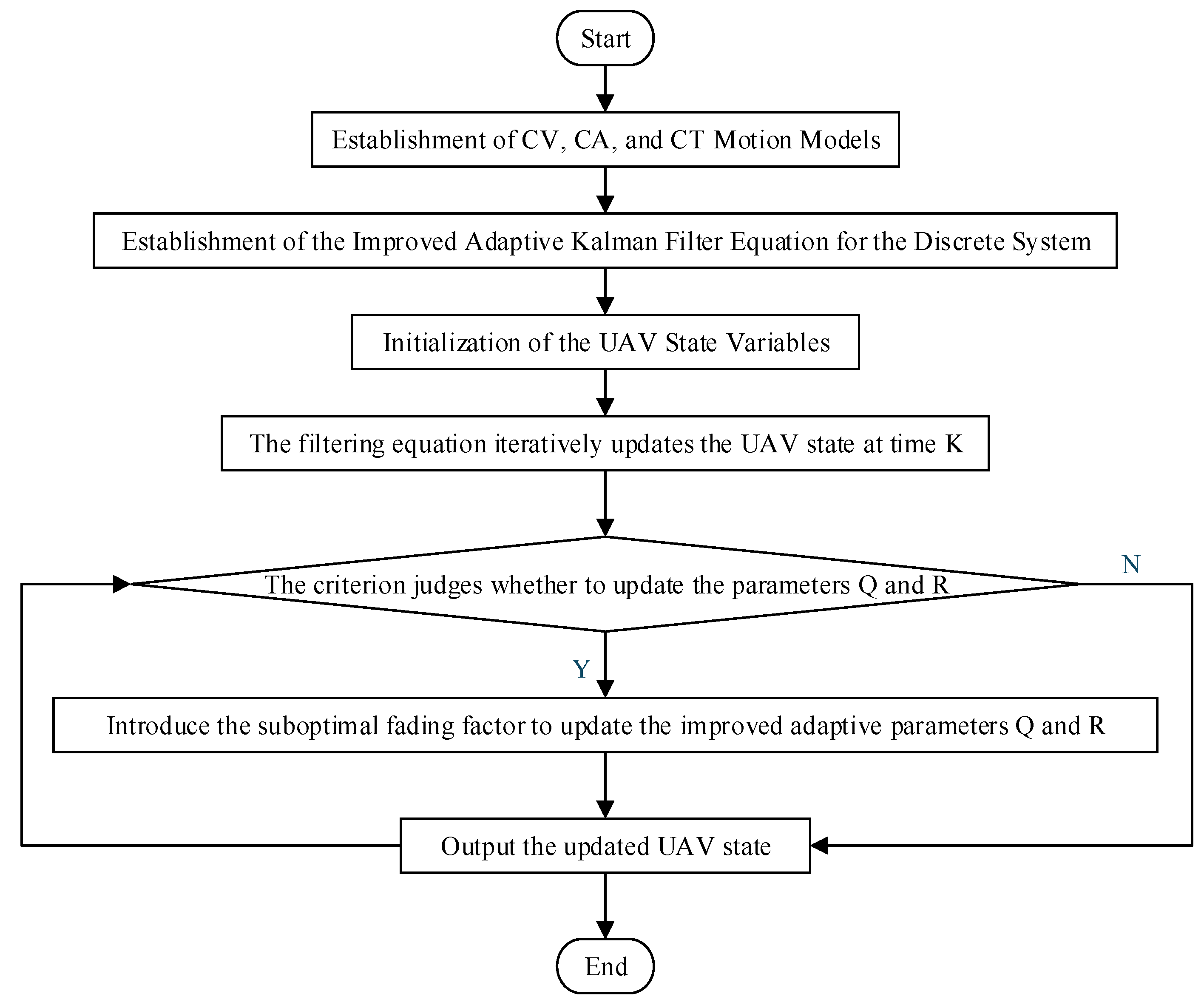
2.2.2. Improved Adaptive Kalman Filter
3. The Adaptive IMM (AIMM) Strategy: Formulation and Integration
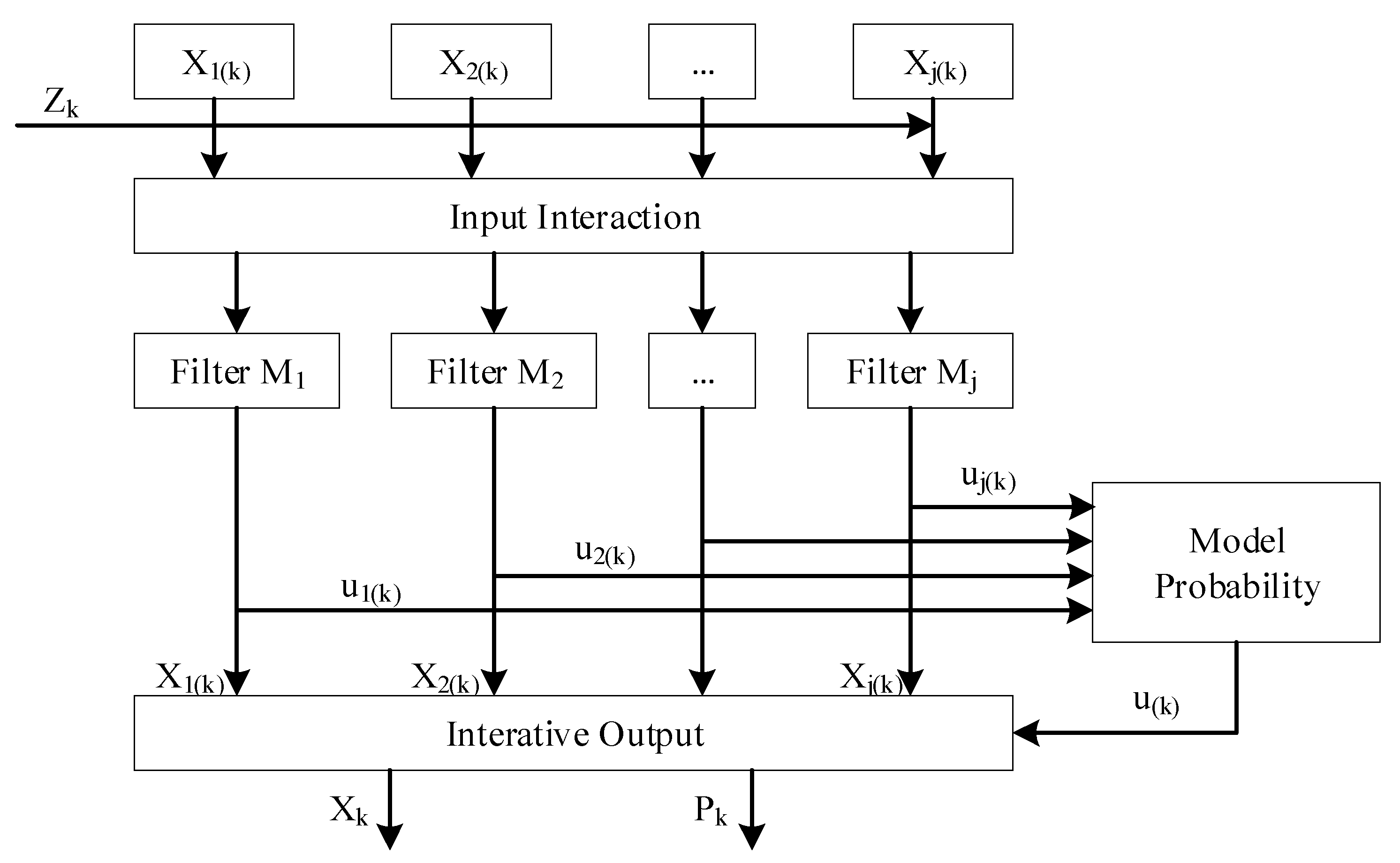
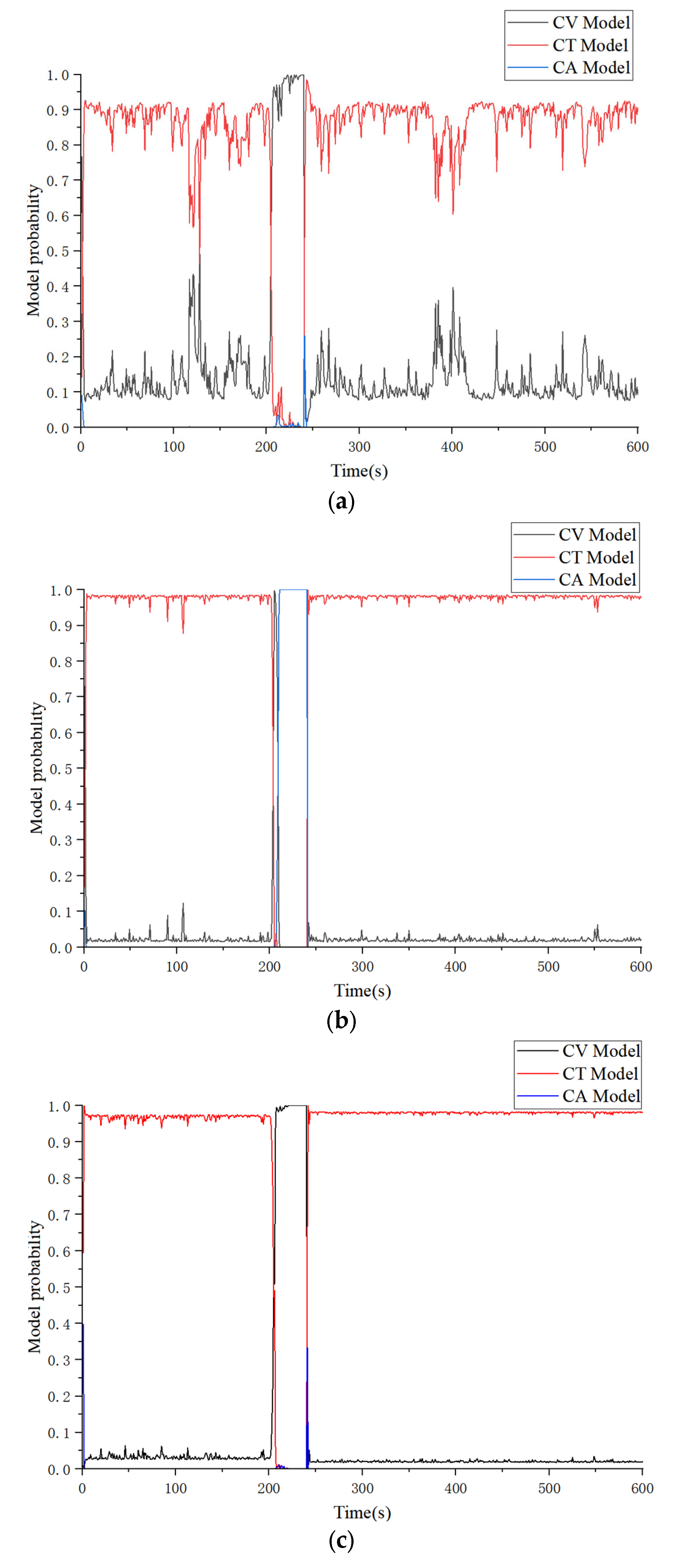
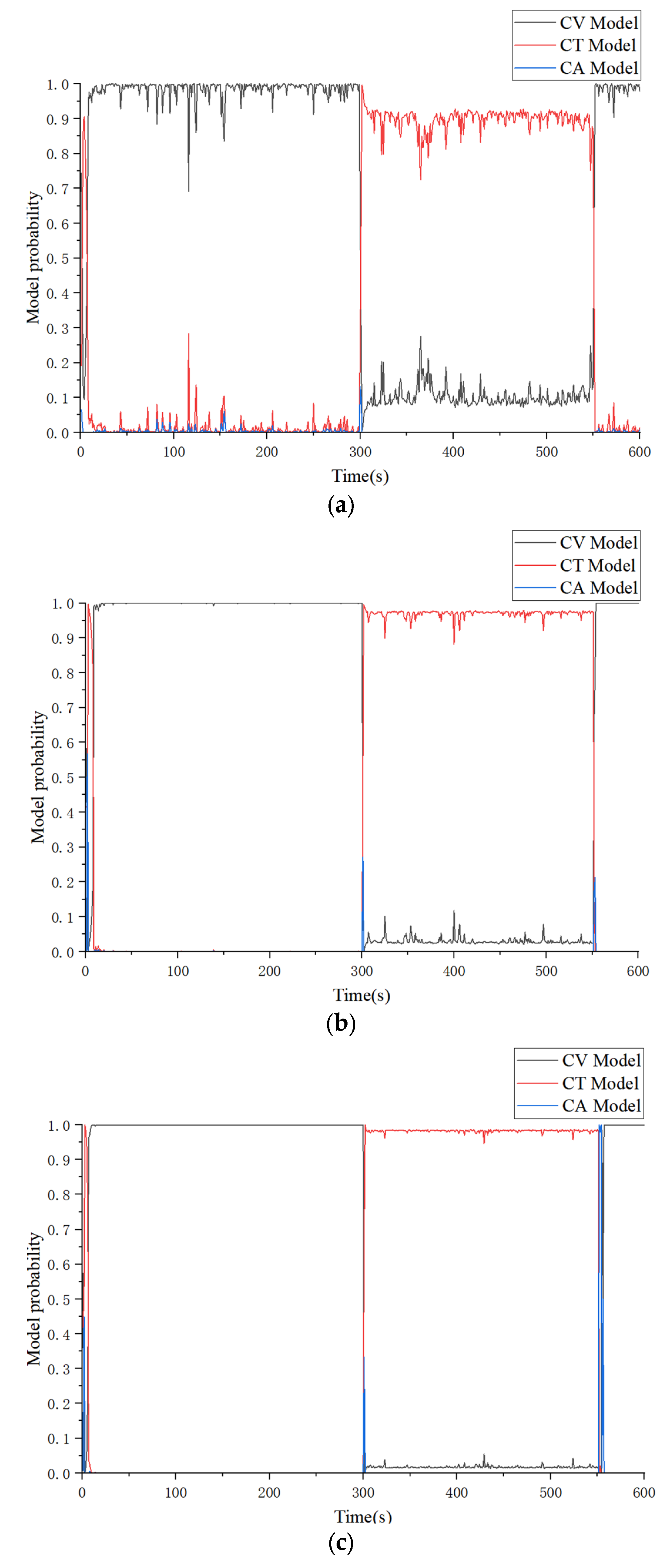
3.1. Basic IMM Algorithm
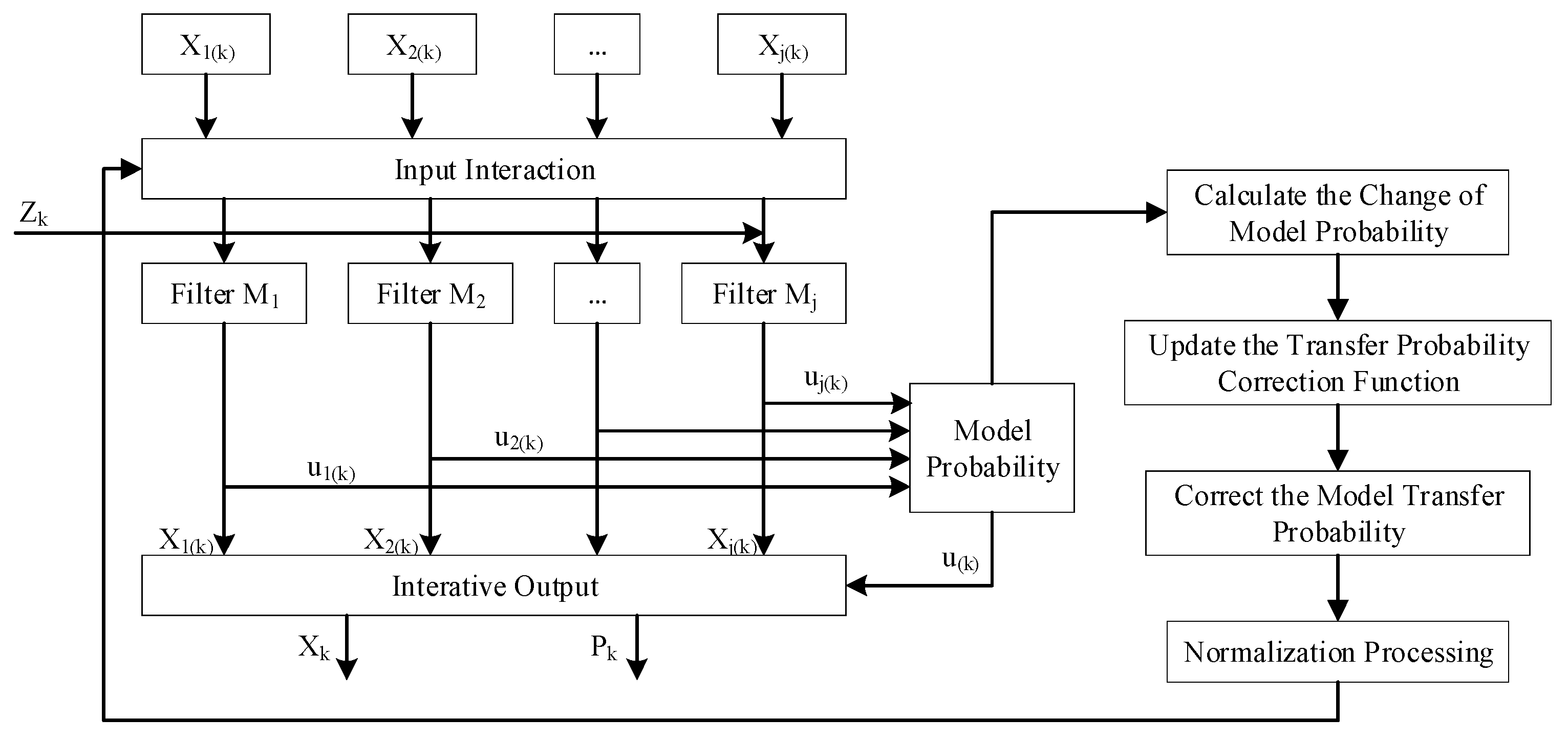
3.2. AIMM Algorithm
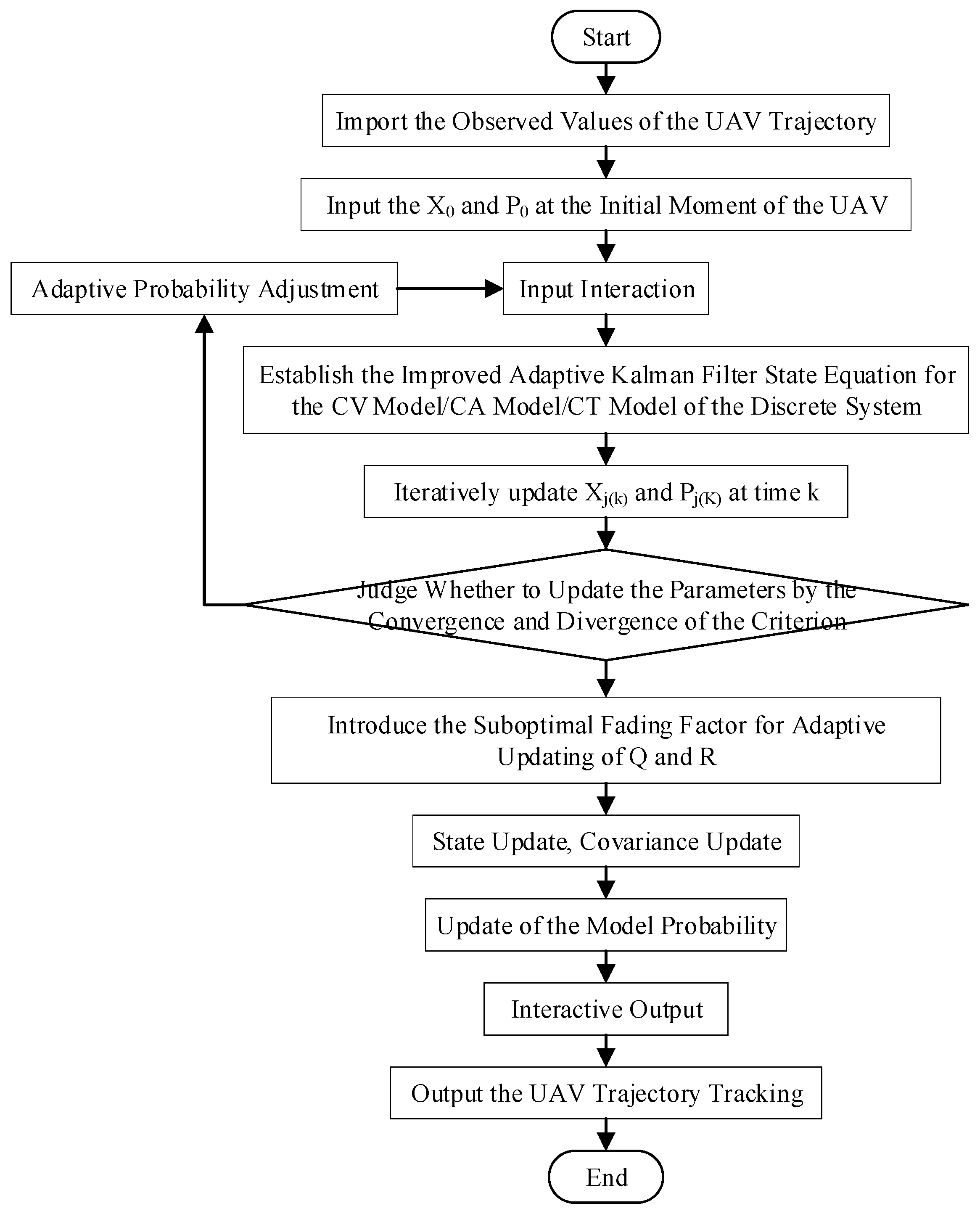
3.3. UAV Trajectory Tracking Using AIMM-IAKF Algorithm
| Algorithm 1: The AIMM-IAKF Algorithm |
| Input: Initial state X0, covariance P0, model set M = {CV, CA, CT}, initial model probabilities μ0, initial transition matrix Π0. Output: Fused state estimate Xk, covariance Pk. 1: for each time step k do 2: // AIMM: Input Interaction (Mixing) 3: Calculate mixed estimates Xj(0) and covariances Pj(0) for each model using Equations (19)–(22). 4: // Parallel IAKF Filtering 5: for each model j in M do 6 Perform prediction step using Xj(0) and Pj(0). 7: // IAKF Adaptation 8: Compute innovation εk and innovation covariance Sk. 9: if convergence criterion (Equation (11)) is violated then 10: Calculate weight bk based on the fading factor λk. 11: Adapt Qk and Rk using Equations (14)–(15). 12: end if 13: Perform update step to get Xj(k) and Pj(k). 14: Compute model likelihood Lj(k) (Equation (23). 15: end for 16: // AIMM: Probability Update & Adaptive Transition Matrix 17: Update model probabilities μj(k) (Equation (24). 18: Adapt the transition matrix Π using the new probabilities and Equations (27)–(33). 19: // Output Fusion 20: Fuse state and covariance estimates across all models (Equations (25)–(26) to get Xk and Pk. 21: end for |
4. Results and Discussion
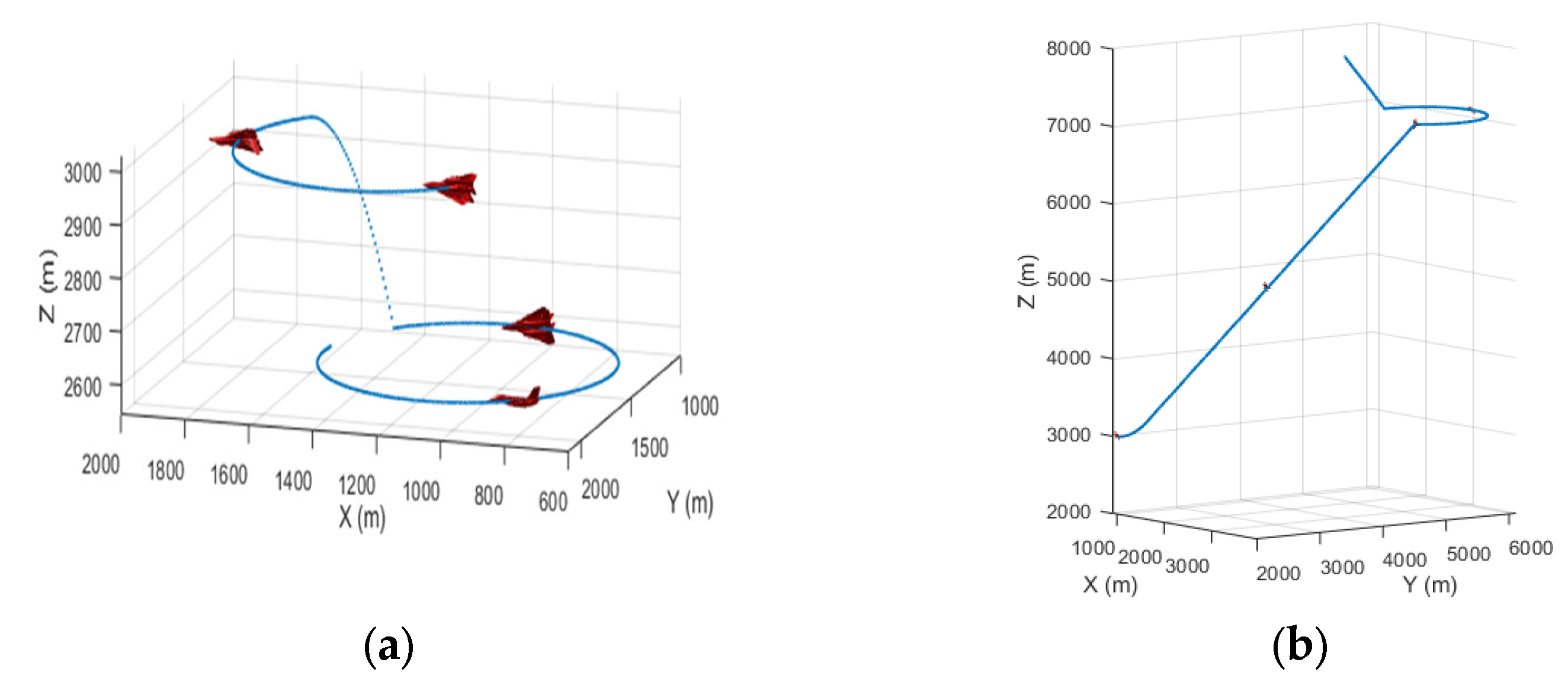
4.1. Simulation Setup
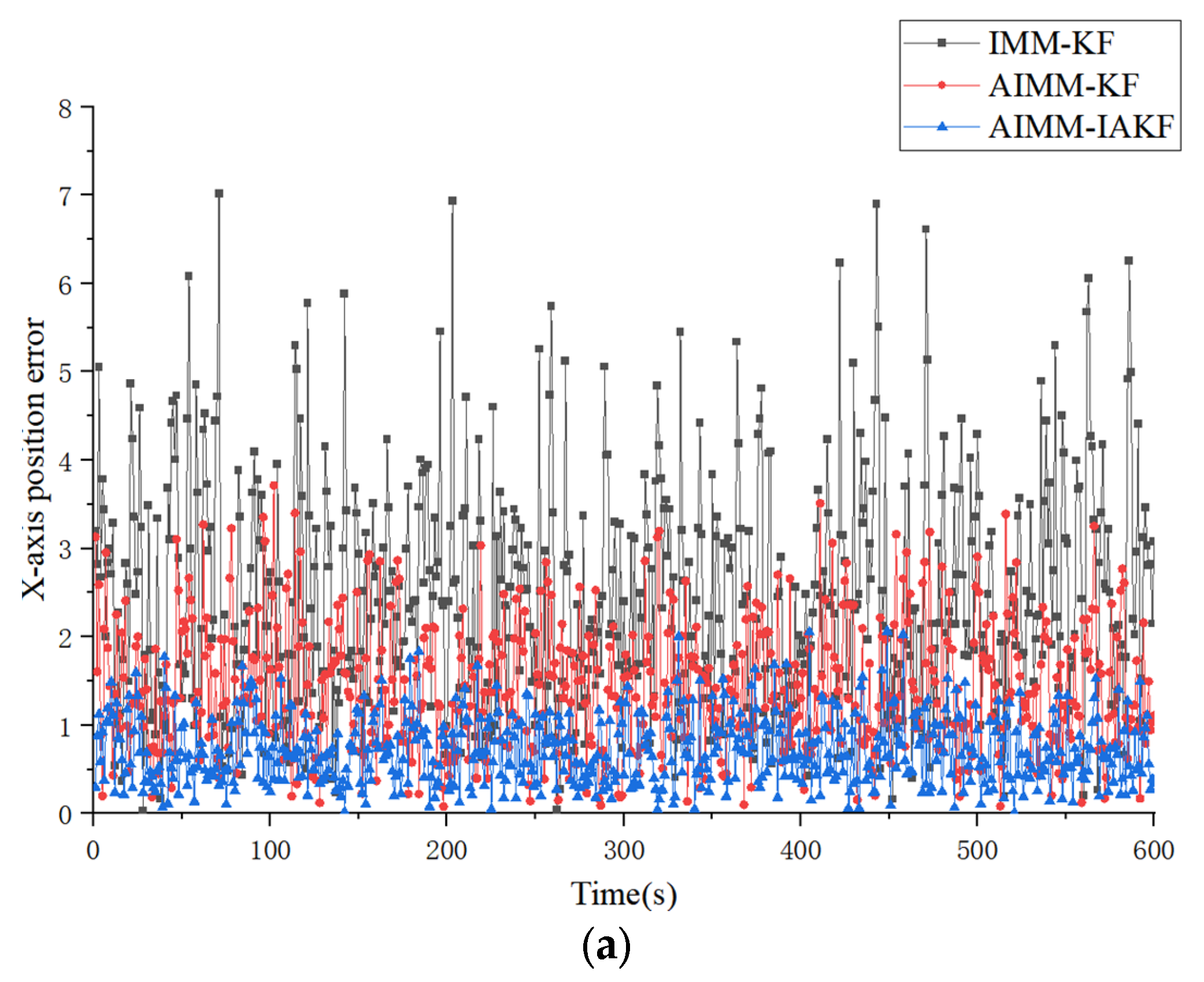
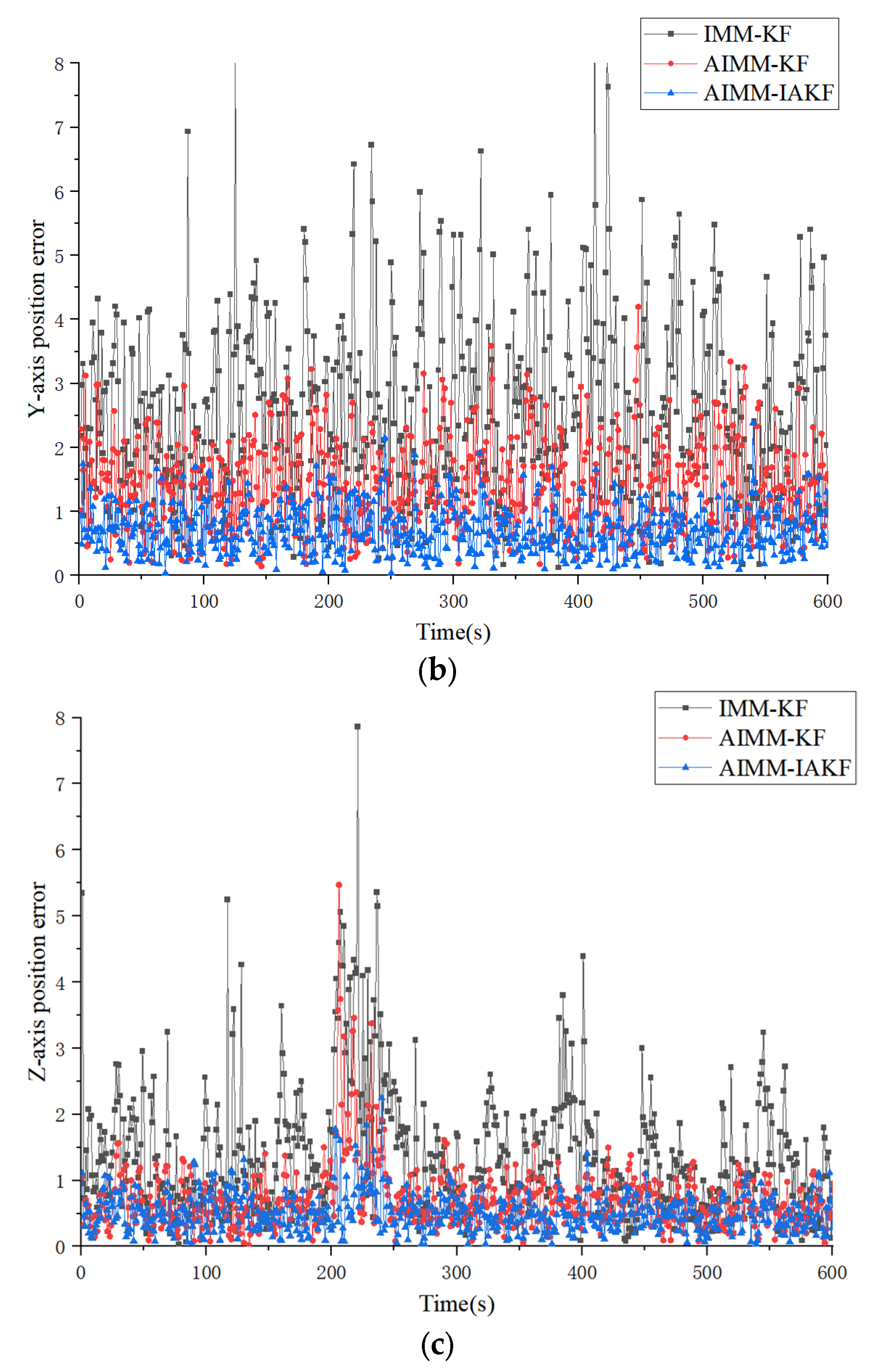
4.2. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description |
| Xk | System state vector at time k |
| Φk | State transition matrix |
| Zk | Measurement vector |
| H | Observation matrix |
| Q, R | System and measurement noise covariance matrices |
| Kk | Kalman gain matrix |
| Pk | State estimation error covariance matrix |
| λk | Suboptimal fading factor |
| εk | Innovation (residual) sequence |
| μj(k) | Probability of model j at time k |
| Π, pij | Model transition matrix and its elements |
| α | Transition probability adjustment speed parameter |
| T | Sampling interval |
| ω | Yaw rate |
| CV | Constant Velocity model |
| CA | Constant Acceleration model |
| CT | Constant Turn model |
| IMM | Interacting Multiple Model |
| KF | Kalman Filter |
| IAKF | Improved Adaptive Kalman Filter |
| AIMM | Adaptive Interacting Multiple Model |
| RMSE | Root Mean Square Error |
| ARMSE | Average Root Mean Square Error |
References
- Semenov, S.; Krupska-Klimczak, M.; Frontczak, M.; Yu, J.; He, J.; Chernykh, O. Adaptive Stochastic GERT Modeling of UAV Video Transmission for Urban Monitoring Systems. Appl. Sci. 2025, 15, 9277. [Google Scholar] [CrossRef]
- Yao, A.; Pal, S.; Li, G.; Li, X.; Zhang, Z.; Jiang, F.; Dong, C.; Xu, J.; Liu, X. FedShufde: A Privacy Preserving Framework of Federated Learning for Edge-Based Smart UAV Delivery System. Future Gener. Comput. Syst. 2025, 166, 107706. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, Z.; Huang, Q.; Liu, X.; Wang, B.; Hu, B. Real-Time Visual Monitoring and High Spatiotemporal-Resolution Mapping of Air Pollutants Using a Drone-Mass Spectrometer System. Environ. Sci. Technol. 2025, 59, 8099–8107. [Google Scholar] [CrossRef]
- Labib, N.S.; Brust, M.R.; Danoy, G.; Bouvry, P. The Rise of Drones in Internet of Things: A Survey on the Evolution, Prospects and Challenges of Unmanned Aerial Vehicles. IEEE Access 2021, 9, 115466–115487. [Google Scholar] [CrossRef]
- Ren, W.; Wei, Y.; Wang, C. Design of a Morphing Aircraft Based on Model Predictive Control. Appl. Sci. 2025, 15, 4380. [Google Scholar] [CrossRef]
- Shukla, P.; Shukla, S.; Singh, A.K. Trajectory-Prediction Techniques for Unmanned Aerial Vehicles (UAVs): A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2024, 27, 1867–1910. [Google Scholar] [CrossRef]
- Savino, A. Multi-Fidelity Aerodynamic Optimization of the Wing Extension of a Tiltrotor Aircraft. Appl. Sci. 2025, 15, 9491. [Google Scholar] [CrossRef]
- Yuan, X.; Xu, J.; Li, S. Design and Simulation Verification of Model Predictive Attitude Control Based on Feedback Linearization for Quadrotor UAV. Appl. Sci. 2025, 15, 5218. [Google Scholar] [CrossRef]
- Kiciński, Ł.; Topczewski, S. Fuzzy Model Predictive Control for Unmanned Helicopter. Appl. Sci. 2025, 15, 8120. [Google Scholar] [CrossRef]
- Tkach, M. Trends in the Global Arms Market, Development of the Combat Drone Market: Impact and Consequences for Ukraine. Political Sci. Secur. Stud. J. 2023, 4. [Google Scholar] [CrossRef]
- Oprean, L.-G. Artillery and Drone Action Issues in the War in Ukraine. Sci. Bull. 2023, 28, 73–78. [Google Scholar] [CrossRef]
- Petrovski, A.; Delchev, G. Application of Drones with Artificial Intelligence for Military Purposes. In Proceedings of the 10th International Scientific Conference on Defensive Technologies (OTEH 2022), Belgrade, Serbia, 13–14 October 2022; pp. 92–100. [Google Scholar]
- Czarnecki, T.; Stawowy, M.; Kadłubowski, A. Cost-Effective Autonomous Drone Navigation Using Reinforcement Learning: Simulation and Real-World Validation. Appl. Sci. 2024, 15, 179. [Google Scholar] [CrossRef]
- Raj, A.; Ahuja, K.; Busnel, Y. AI Algorithm for Predicting and Optimizing Trajectory of Massive UAV Swarm. Robot. Auton. Syst. 2025, 186, 104910. [Google Scholar] [CrossRef]
- Carbone, M.R. When Not to Use Machine Learning: A Perspective on Potential and Limitations. MRS Bull. 2022, 47, 968–974. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Wang, X.; Wang, A.; Wang, D.; Xiong, Y.; Liang, B.; Qi, Y. A Modified Sage-Husa Adaptive Kalman Filter for State Estimation of Electric Vehicle Servo Control System. Energy Rep. 2022, 8, 20–27. [Google Scholar] [CrossRef]
- Sun, D.; Yu, X.; Wang, C.; Zhang, C.; Huang, R.; Zhou, Q.; Amietszajew, T.; Bhagat, R. State of Charge Estimation for Lithium-Ion Battery Based on an Intelligent Adaptive Extended Kalman Filter with Improved Noise Estimator. Energy 2021, 214, 119025. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, W.; Wang, X. UAV Swarm Navigation Using Dynamic Adaptive Kalman Filter and Network Navigation. Sensors 2021, 21, 5374. [Google Scholar] [CrossRef]
- Fraser, C.T.; Ulrich, S. Adaptive Extended Kalman Filtering Strategies for Spacecraft Formation Relative Navigation. Acta Astronaut. 2021, 178, 700–721. [Google Scholar] [CrossRef]
- Jiang, L.; Wu, L. Enhanced Yolov8 Network with Extended Kalman Filter for Wildlife Detection and Tracking in Complex Environments. Ecol. Inform. 2024, 84, 102856. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, S.; Wang, X.; Wang, H. Self-Tuning Process Noise in Variational Bayesian Adaptive Kalman Filter for Target Tracking. Electronics 2023, 12, 3887. [Google Scholar] [CrossRef]
- Sterpu, D.-A.; Măriuța, D.; Cican, G.; Larco, C.-M.; Grigorie, L.-T. Machine Learning Prediction of Airfoil Aerodynamic Performance Using Neural Network Ensembles. Appl. Sci. 2025, 15, 7720. [Google Scholar] [CrossRef]
- Singh, R.; Bhushan, B. Evolving Intelligent System for Trajectory Tracking of Unmanned Aerial Vehicles. IEEE Trans. Automat. Sci. Eng. 2022, 19, 1971–1984. [Google Scholar] [CrossRef]
- Urrea, C.; Agramonte, R. Kalman Filter: Historical Overview and Review of Its Use in Robotics 60 Years after Its Creation. J. Sens. 2021, 2021, 9674015. [Google Scholar] [CrossRef]
- Limaverde Filho, J.O.A.; Fortaleza, E.L.F.; Silva, J.G.; De Campos, M.C.M.M. Adaptive Kalman Filtering for Closed-Loop Systems Based on the Observation Vector Covariance. Int. J. Control 2022, 95, 1731–1746. [Google Scholar] [CrossRef]
- Akbaş, E.M.; Çifdalöz, O.; Üçüncü, M. Improving the Performance of a MEMS-IMU System Based on a False State-Space Model by Using a Fading Factor Adaptive Kalman Filter. Meas. Control 2024, 57, 1243–1251. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, S.; Wang, X.; Wang, H.; Yang, H. Kalman Filter with Adaptive Covariance Estimation for Carrier Tracking under Weak Signals and Dynamic Conditions. Electronics 2024, 13, 1288. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, Z.; Qiao, D.; Mu, X.; Hu, X. An Improved Innovation Adaptive Kalman Filter for Integrated INS/GPS Navigation. Sustainability 2022, 14, 11230. [Google Scholar] [CrossRef]
- Blom, H.A.P.; Bar-Shalom, Y. The Interacting Multiple Model Algorithm for Systems with Markovian Switching Coefficients. IEEE Trans. Automat. Contr. 1988, 33, 780–783. [Google Scholar] [CrossRef]
- Granstrom, K.; Willett, P.; Bar-Shalom, Y. Systematic Approach to IMM Mixing for Unequal Dimension States. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2975–2986. [Google Scholar] [CrossRef]
- Zhao, B. Multisensor Maneuvering Target Fusion Tracking Using Interacting Multiple Model. Aut. Control Comp. Sci. 2024, 58, 303–312. [Google Scholar] [CrossRef]
- Wang, J.; He, J.; Peng, B.; Wang, G. Generalized Interacting Multiple Model Kalman Filtering Algorithm for Maneuvering Target Tracking under Non-Gaussian Noises. ISA Trans. 2024, 155, 148–163. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Wang, H.; Shi, Z. Interacting Multiple Model Adaptive Robust Kalman Filter for Process and Measurement Modeling Errors Simultaneously. Signal Process. 2025, 227, 109743. [Google Scholar] [CrossRef]
- Xie, G.; Sun, L.; Wen, T.; Hei, X.; Qian, F. Adaptive Transition Probability Matrix-Based Parallel IMM Algorithm. IEEE Trans. Syst. Man Cybern, Syst. 2021, 51, 2980–2989. [Google Scholar] [CrossRef]
- Sun, M.; Duan, Q.; Xia, W.; Bao, Q.; Mao, Y. Multiple Adaptive Factors Based Interacting Multiple Model Estimator. IET Control Theory Amp; Appl 2024, 18, 1059–1069. [Google Scholar] [CrossRef]
- Lee, I.H.; Park, C.G. An Improved Interacting Multiple Model Algorithm with Adaptive Transition Probability Matrix Based on the Situation. Int. J. Control Autom. Syst. 2023, 21, 3299–3312. [Google Scholar] [CrossRef]
- Emambakhsh, M.; Bay, A.; Vazquez, E. Convolutional Recurrent Predictor: Implicit Representation for Multi-Target Filtering and Tracking. IEEE Trans. Signal Process. 2019, 67, 4545–4555. [Google Scholar] [CrossRef]
- Delande, E.; Houssineau, J.; Franco, J.; Frueh, C.; Clark, D.; Jah, M. A New Multi-Target Tracking Algorithm for a Large Number of Orbiting Objects. Adv. Space Res. 2019, 64, 645–667. [Google Scholar] [CrossRef]
- Mazor, E.; Averbuch, A.; Bar-Shalom, Y.; Dayan, J. Interacting Multiple Model Methods in Target Tracking: A Survey. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 103–123. [Google Scholar] [CrossRef]
- Yaacoub, J.-P.; Noura, H.; Salman, O.; Chehab, A. Security Analysis of Drones Systems: Attacks, Limitations, and Recommendations. Internet Things 2020, 11, 100218. [Google Scholar] [CrossRef]
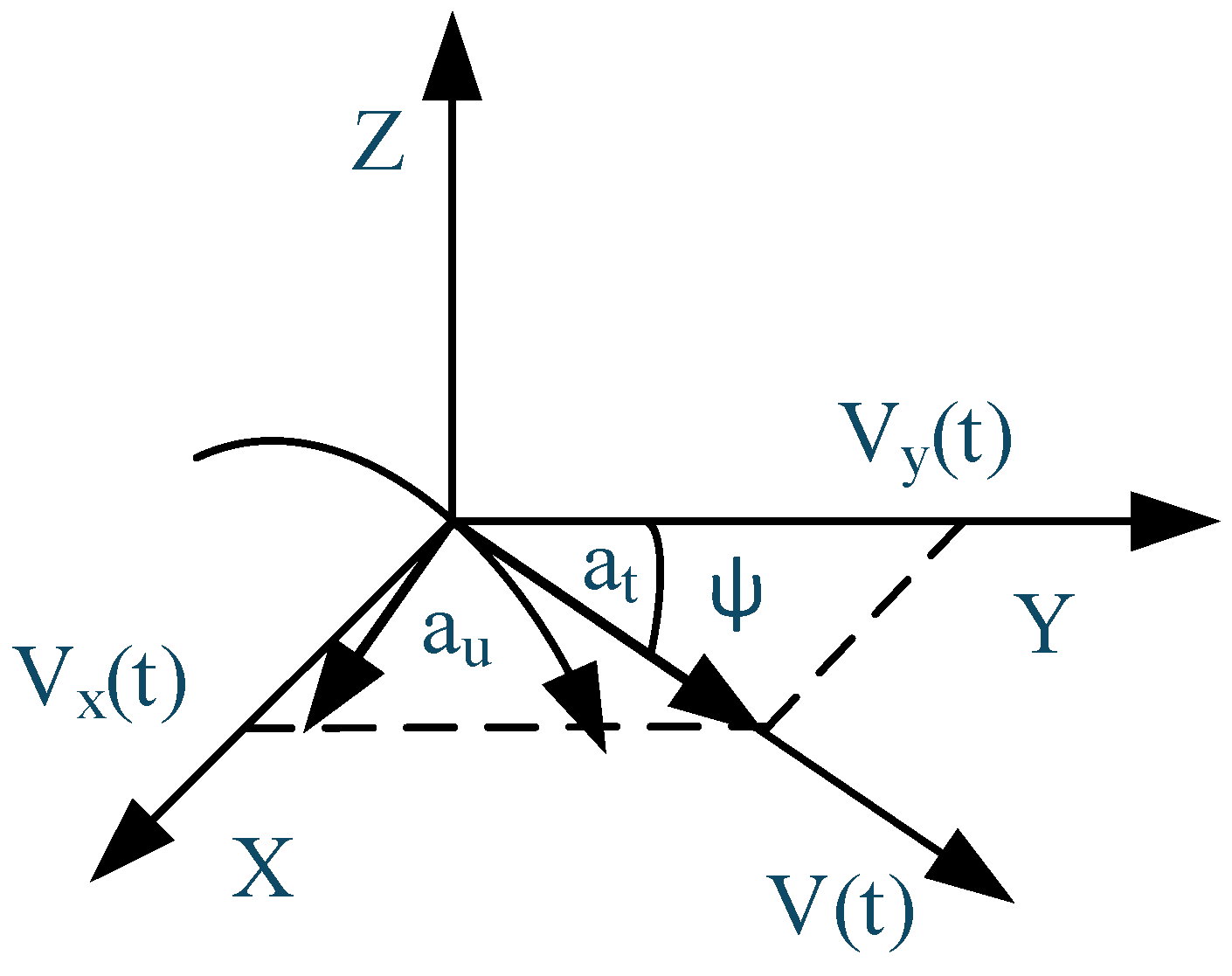

| Method | Adaptive Transition Matrix? | Adaptive Noise Tuning? | Key Limitation Addressed |
|---|---|---|---|
| Xie et al. [35] | Yes (Correction Function) | No | Improves switching but not filter robustness |
| Sun et al. [36] | No | Yes (Adaptive Factors) | Wastes resources with stable noise |
| Lee et al. [37] | Yes (Polarization Function) | No | Does not optimize noise characteristics |
| Proposed AIMM-IAKF | Yes (Exponential Adjustment) | Yes (Fading Factor and Criterion) | Simultaneously optimizes model switching and noise adaptation |
| Parameter | Symbol | Value | Units |
|---|---|---|---|
| Sampling Interval | T | 1 | s |
| Total Sampling Points | N | 600 | - |
| Montecarlo Runs | M | 100 | - |
| Initial State Covariance | P0 | 100 · eye(9) | - |
| System Noise Covariance (Initial) | Q | eye(3) | m2 |
| Measurement Noise Covariance (Initial) | R | diag([20, 20, 20]) | m2 |
| Fading Factor Bounds | λk | [0.95, 0.995] | - |
| Adjustment Speed Parameter | α | 10 | - |
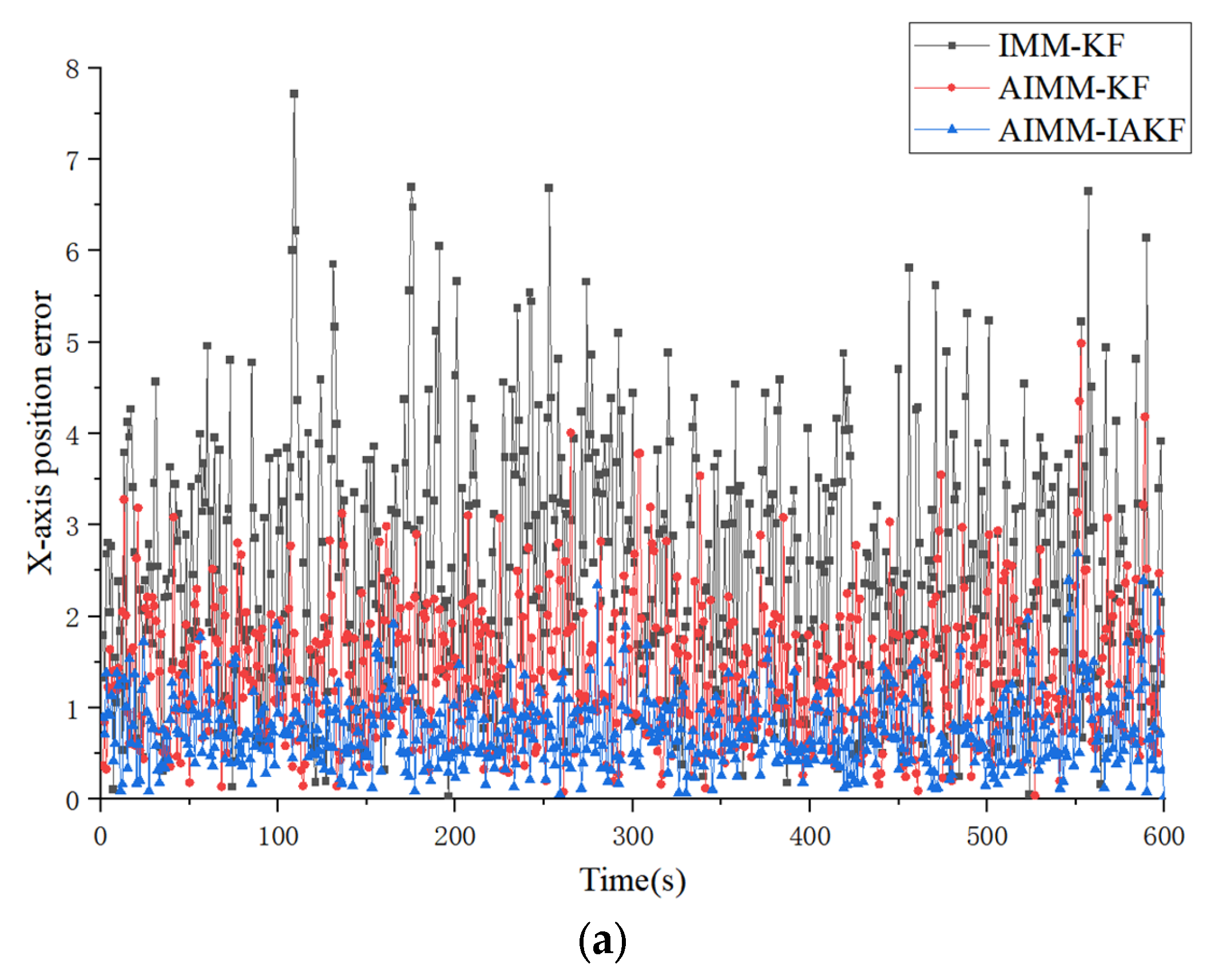
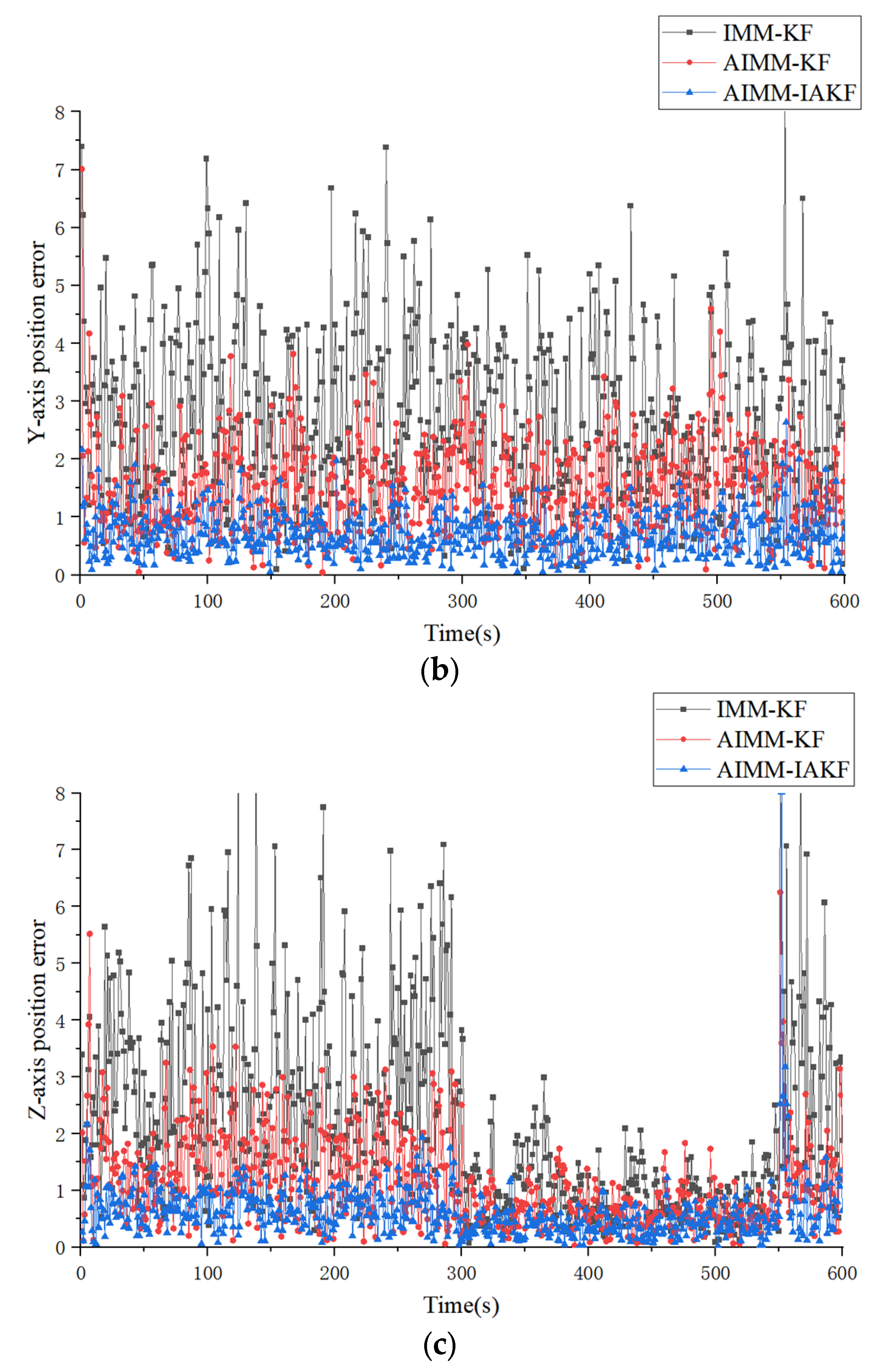
| Algorithms & Models | Type of Trajectory | X-Axis (ARMSE/m) | Y-Axis (ARMSE/m) | Z-Axis (ARMSE/m) |
|---|---|---|---|---|
| IMM-KF | Type I | 2.937584 | 2.948784 | 1.648211 |
| Type II | 2.666003 | 2.725856 | 2.333053 | |
| AIMM-KF | Type I | 1.436144 | 1.422095 | 0.711672 |
| Type II | 1.398113 | 1.504259 | 1.126852 | |
| AIMM-IAKF | Type I | 0.717412 | 0.713891 | 0.507468 |
| Type II | 0.757225 | 0.705126 | 0.612758 |
| Comparison | X-Axis | Y-Axis | Z-Axis | |||
|---|---|---|---|---|---|---|
| Type I | Type II | Type I | Type II | Type I | Type II | |
| AIMM-KF over IMM-KF | 51% | 48% | 52% | 45% | 56% | 52% |
| AIMM-IAKF over AIMM-KF | 50% | 46% | 50% | 52% | 30% | 46% |
| AIMM-IAKF over IMM-KF | 76% | 72% | 76% | 74% | 69% | 74% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Liu, C.; Ji, Y.; Wang, Z.; Li, Y. Enhanced UAV Trajectory Tracking Using AIMM-IAKF with Adaptive Model Transition Probability. Appl. Sci. 2025, 15, 11111. https://doi.org/10.3390/app152011111
Zhang P, Liu C, Ji Y, Wang Z, Li Y. Enhanced UAV Trajectory Tracking Using AIMM-IAKF with Adaptive Model Transition Probability. Applied Sciences. 2025; 15(20):11111. https://doi.org/10.3390/app152011111
Chicago/Turabian StyleZhang, Pengfei, Cong Liu, Yunbiao Ji, Zhongliu Wang, and Yawen Li. 2025. "Enhanced UAV Trajectory Tracking Using AIMM-IAKF with Adaptive Model Transition Probability" Applied Sciences 15, no. 20: 11111. https://doi.org/10.3390/app152011111
APA StyleZhang, P., Liu, C., Ji, Y., Wang, Z., & Li, Y. (2025). Enhanced UAV Trajectory Tracking Using AIMM-IAKF with Adaptive Model Transition Probability. Applied Sciences, 15(20), 11111. https://doi.org/10.3390/app152011111





