Thermodynamics of Liquid Uranium from Atomistic and Ab Initio Modeling
Abstract
1. Introduction
2. Classical Molecular Dynamics Methodology
3. Ab Initio Computational Methodology
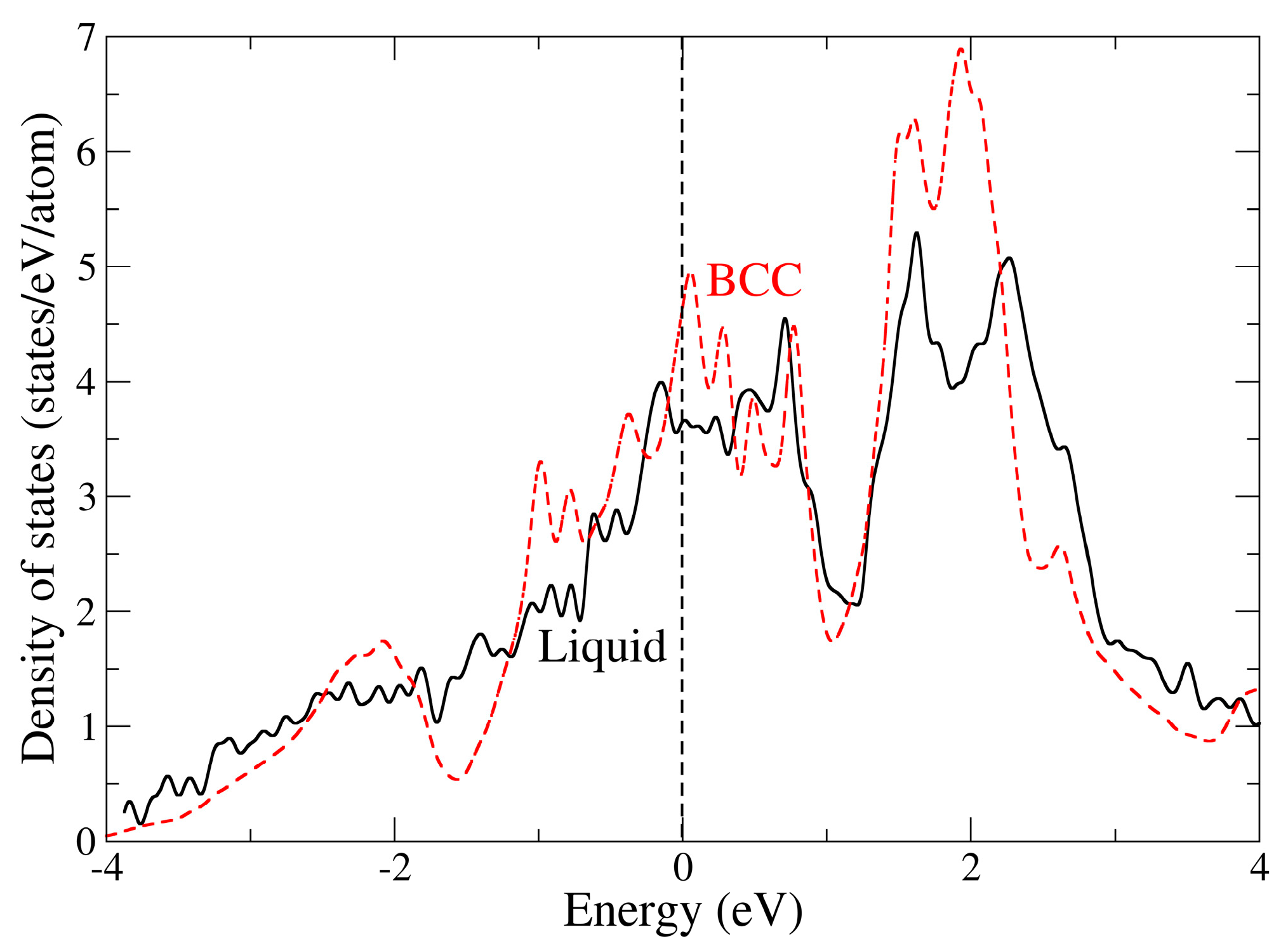
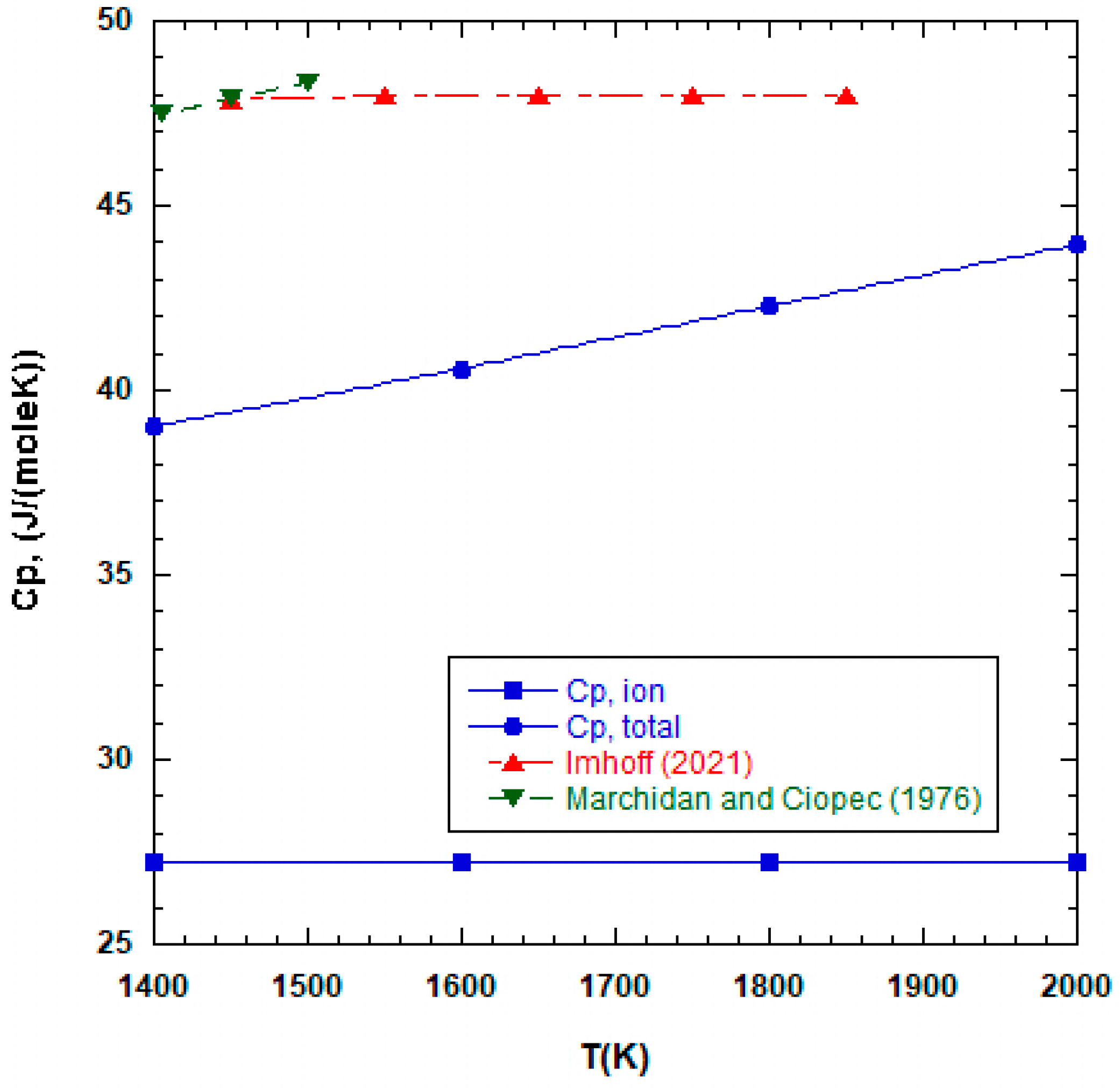
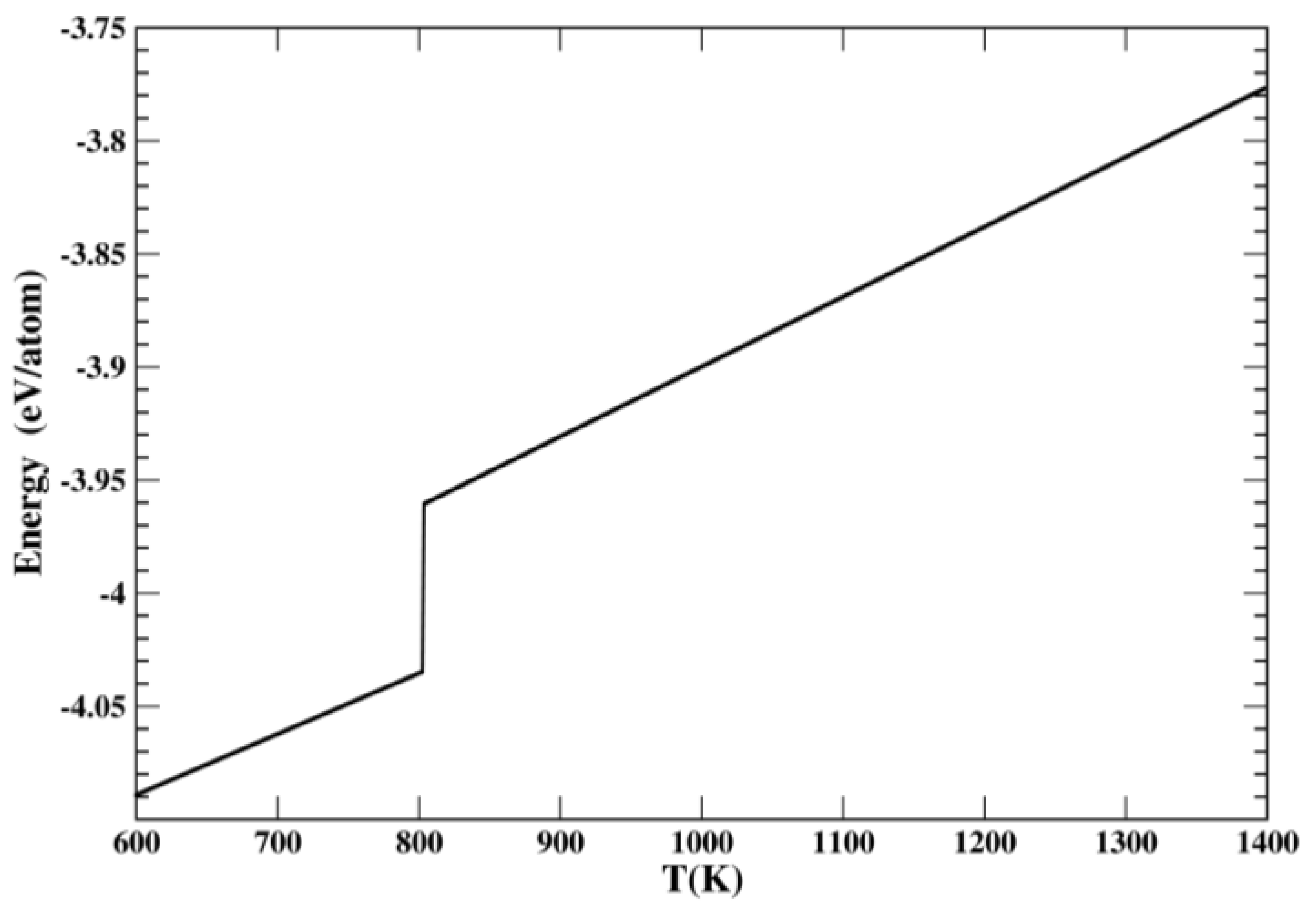
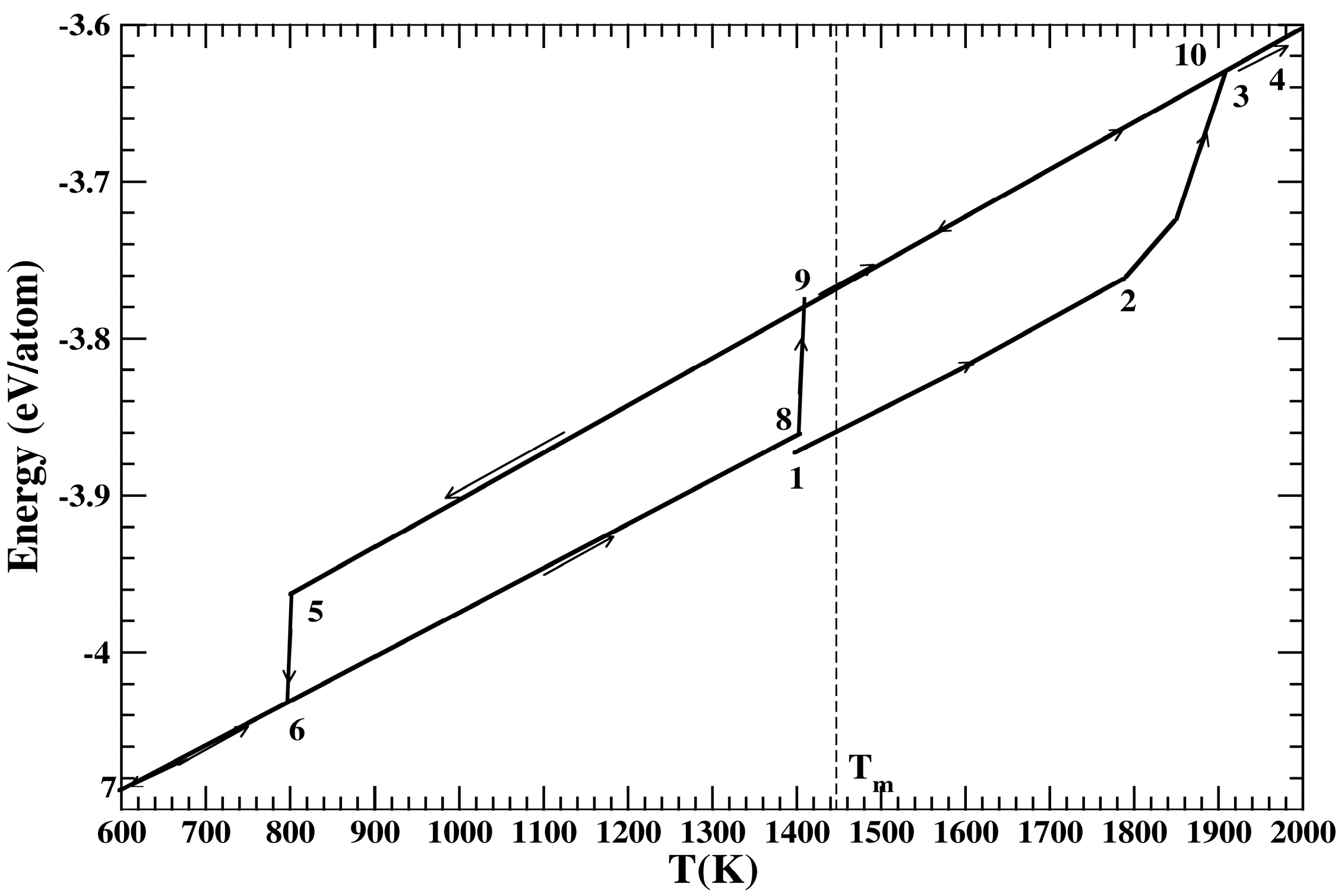
4. Results
5. Discussion
6. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Söderlind, P.; Landa, A.; Moore, E.E.; Perron, A.; Roehling, J.; McKeown, J.T. High-temperature thermodynamics of uranium from ab initio modeling. Appl. Sci. 2023, 13, 2123. [Google Scholar] [CrossRef]
- Pascuet, M.I.; Bonny, G.; Fernández, J.R. Many-body interatomic U and Al–U potentials. J. Nucl. Mater. 2012, 424, 158–163. [Google Scholar] [CrossRef]
- Belaschenko, D.K.; Smirnova, D.E.; Ostrovsky, O.I. Molecular-dynamic simulation of the thermophysical properties of liquid uranium. High Temp. 2010, 48, 363–375. [Google Scholar] [CrossRef]
- Smirnova, D.E.; Starikov, S.V.; Stegailov, V.V. Interatomic potential for uranium in a wide range of pressures and temperatures. J. Phys. Condens. Matter. 2012, 24, 015702. [Google Scholar] [CrossRef][Green Version]
- Beeler, B.; Deo, C.; Baskes, M.; Okuniewski, M. Atomistic properties of γ uranium. J. Phys. Condens. Matter 2012, 24, 075401. [Google Scholar] [CrossRef] [PubMed]
- Moore, A.P.; Beeler, B.; Deo, C.; Baskes, M.I.; Okuniewski, M.A. Atomistic modeling of high temperature uranium-zirconium alloy structure and thermodynamics. J. Nucl. Mater. 2015, 467, 802–819. [Google Scholar] [CrossRef]
- Pascuet, M.I.; Fernández. Atomic interaction of the MEAM type for the study of intermetallics in the Al-U alloy. J. Nucl. Mater. 2015, 467, 229–239. [Google Scholar] [CrossRef]
- Hood, R.; Yang, L.H.; Moriarty, J. Quantum molecular dynamics simulations of uranium at high pressure and temperature. Phys. Rev. B 2008, 78, 024116. [Google Scholar] [CrossRef]
- Yanilkin, A.V. Investigation of a-phase and liquid uranium by the method of quantum molecular dynamics. High Temp. 2017, 55, 40–46. [Google Scholar] [CrossRef]
- Del Rio, B.G.; González, L.E.; Gonzales, D.J. First principles study of liquid uranium at temperatures up to 2050 K. J. Phys. Cond. Matter. 2020, 32, 304001. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Sun, H.; Li, Q.; Wang, L. Origin of local structures of u-co melts: A first-principles study. Front. Mater. 2022, 8, 821306. [Google Scholar] [CrossRef]
- Minakov, D.; Paramonov, M.; Levashov, P. Effect of the spin-orbit interaction on thermodynamic properties of liquid uranium. arXiv 2020, arXiv:2005.05468. [Google Scholar]
- Levinson, L.S. Heat content of molten uranium. J. Chem Phys. 1964, 40, 3584–3585. [Google Scholar] [CrossRef]
- Gathers, G.R. Dynamic methods for investigating thermophysical properties of matter at very high temperatures and pressures. Rep. Prog. Phys. 1986, 49, 341–396. [Google Scholar] [CrossRef]
- Marchidan, D.; Ciopec, M. Enthalpy of uranium to 1500 K by drop calorimetry. J. Chem. Thermodyn. 1976, 8, 691–701. [Google Scholar] [CrossRef]
- Mulford, R.N.R.; Sheldon, R.I. Densi1y and heat capacity of liquid uranium at high temperatures. J. Nucl. Mater. 1988, 154, 268–275. [Google Scholar] [CrossRef]
- Dinsdale, A.T. SGTE data for pure elements. Calphad 1991, 15, 317–425. [Google Scholar] [CrossRef]
- Gurvich, L.V.; Veits, I.V.; Medvedev, V.A. Thermodynamic Properties of Individual Substances, 4th ed.; Gurvich, L.V., Veits, I.V., Alcock, C.B., Eds.; Begell House: Danbury, CT, USA, 1994; Volume 4, Part 1–2; 448p. [Google Scholar]
- Grimvall, G. Thermophysical Properties of Materials; Elsevier BV: Amsterdam, The Netherlands, 1999; pp. 157–172. [Google Scholar]
- Crangle, J.; Temporal, J. Heat capacity and transformations in alpha uranium at low temperature. J. Phys. F Met. Phys. 1973, 3, 1097–1105. [Google Scholar] [CrossRef]
- Stewart, G.R. Measurement of low-temperature specific heat. Rev. Sci. Instrum. 1983, 54, 1–20. [Google Scholar] [CrossRef]
- Xiong, W.; Xie, W.; Shen, C.; Morgan, D. Thermodynamic modeling of the U–Zr system—A revisit. J. Nucl. Mater. 2013, 443, 331–341. [Google Scholar] [CrossRef]
- Wills, J.M.; Eriksson, O.; Andersson, P.; Delin, A.; Grechnyev, O.; Alouani, M. Full-Potential Electronic Structure Method; Springer Series in Solid-State Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 167. [Google Scholar]
- Plimpton, S. Fast parallel algorithms for short range molecular dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; In’T Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Morris, J.R.; Wang, C.Z.; Ho, K.M.; Chan, C.T. Melting line of aluminum from simulations of coexisting phases. Phys. Rev. B 1994, 49, 3109–3115. [Google Scholar] [CrossRef]
- Morris, J.R.; Song, X. The melting lines of model systems calculated from coexistence simulations. J. Chem. Phys. 2002, 116, 9352–9358. [Google Scholar] [CrossRef]
- Mendelev, M.I.; Han, S.; Srolovitz, J.; Ackland, G.J.; Sun, D.Y.; Asta, M. Development of new interatomic potentials appropriate for crystalline and liquid iron. Phil Mag. 2003, 83, 3977–3994. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Verlet, P. Computer "Experiments" on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev B 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Verlet, P. Computer "Experiments" on Classical Fluids. II. Equilibrium Correlation Functions. Phys. Rev. 1968, 165, 201–214. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed]
- Söderlind, P. Theory of the crystal structures of cerium and the light actinides. Adv. Phys. 1998, 47, 959–998. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Xie, W.; Xiong, W.; Marianetti, C.A.; Morgan, D. Correlation and relativistic effects in U metal and U-Zr alloy: Validation of ab initio approaches. Phys. Rev. B 2013, 88, 235128. [Google Scholar] [CrossRef]
- Söderlind, P.; Landa, A.; Turchi, P.E.A. Comment on “Correlation and relativistic effects in U metal and U-Zr alloy. Phys. Rev. B 2014, 90, 157101. [Google Scholar] [CrossRef]
- Sadigh, B.; Kutepov, A.; Landa, A.; Söderlind, P. Assessing relativistic effects and electron correlation in the actinide metals Th-Pu. Appl. Sci. 2019, 9, 5020. [Google Scholar] [CrossRef]
- Hu, G.; Luo, C.; Wu, L.; Tang, Q.; Ren, Z.; Xu, B. Molecular dynamics simulation of solid/liquid interfacial energy of metallic uranium. J. Nucl. Mater. 2020, 538, 152183. [Google Scholar] [CrossRef]
- Stephens, H. Determination of the Enthalpy of Liquid Copper and Uranium with a Liquid Argon Calorimeter. High Temp. Sci. 1974, 6, 156–166. [Google Scholar]
- Fokin, L.R. Liquid Uranium, Density Isobar, 1406-3500 K. Analysis and Generalization of the Experimental data. In Problems of Atomic Science and Technology. Serie: Nuclear-Reactor Constants; 2016; Issue 3, pp. 24–36. Available online: https://vant.ippe.ru/en/year2016/3/thermal-physics-hydrodynamics/1188-2.html (accessed on 18 December 2024).
- Shapiro, A.B.; Summers, L.T.; Eckels, D.J.; Sahai, V. Modeling of Casting Microstructures and Defects; UCRL-ID-128519; LLNL Internal Report: Livermore, CA, USA, 1997. [Google Scholar]
- Shaner, J.W. Thermal expansion of metals over the entire liquid range. In Thermal Expansion; Peggs, I.D., Ed.; Plenum Publishing Company: New York, NY, USA, 1978; Volume 6, pp. 69–81. [Google Scholar]
- Grosse, A.V.; Cahill, J.A.; Kirshenbaum, A.D. Density of liquid uranium. J. Am. Chem. Soc. 1961, 83, 4665–4666. [Google Scholar] [CrossRef]
- Söderlind, P.; Eriksson, O.; Wills, J.; Boring, A. A unified picture of the crystal structures of metals. Nature 1995, 374, 524–525. [Google Scholar] [CrossRef]
- Imhoff, S.D. Uranium Density, Thermal Conductivity, Specific Heat, and Thermal Diffusivity. 2021, Report, LA-UR-21-21810, 02.24.2021, 20p. Available online: https://www.osti.gov/biblio/1768421 (accessed on 18 December 2024).
- Gurvich, L.V.; Veits, I.V.; Medvedev, V.A.; Yungman, V.S.; Bergman, G.A.; Iorish, V.S.; Gusarov, A.V.; Leonidov, V.Y.; Dorofeeva, O.V.; Nazarenko, I.I.; et al. Thermodynamic Properties of Individual Substances: Handbook; Glushko, V.P., Ed.; USSR: Nauka, Moscow, 1982; Volume 4. (In Russian) [Google Scholar]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef]
- Ofte, D. The viscosity of liquid uranium, gold and lead. J. Nucl Mater. 1967, 22, 28–32. [Google Scholar] [CrossRef]
- Luo, S.-N.; Strachan, A.; Swift, D.C. Nonequilibrium melting and crystallization of a model Lennard-Jones system. J. Chem. Phys. 2004, 120, 11640–11649. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.-N.; Swift, D.C. On asymmetry between superheating and supercooling in solid-liquid transitions: Landau models. J. Chem. Phys. 2004, 121, 7387–7389. [Google Scholar] [CrossRef]
- Kelton, K.F. Crystal Nucleation in Liquids and Glasses. Solid St. Phys. 1991, 45, 75–177. [Google Scholar]
- Luo, S.-N.; Ahrens, T.J.; Çaĝin, T.; Strachan, W.; Goddard III, W.A.; Swift, D.C. Maximum superheating and undercooling: Systematics, molecular dynamics simulations, and dynamic experiments. Phys. Rev. B 2003, 68, 134206. [Google Scholar] [CrossRef]
- Luo, S.-N.; Ahrens, T.J. Shock-induced superheating and melting curves of geophysically important minerals. Phys. Earth Planet. Inter. 2004, 143–144, 369–386. [Google Scholar] [CrossRef]
- Zhang, W.-J.; Liu, Z.-Y.; Liu, Z.-L.; Cai, L.-C. Melting curves and entropy of melting of iron under Earth’s core. Phys. Earth Planet. Inter. 2015, 244, 69–77. [Google Scholar] [CrossRef]
- Zhang, H.; Kalvapalle, P.; Douglas, J.F. String-like collective atomic motion in the melting and freezing of nanoparticles. J. Phys. Chem. 2011, 115, 14068–14076. [Google Scholar] [CrossRef]
- Thermophysical Properties of Materials for Nuclear Engineering: A Tutorial and Collection of Data; International Atomic Energy Agency (IAEA): Vienna, Austria, 2008.
- Beeler, B.; Casagranda, A.; Aagesen, L.; Zhang, Y.; Novascone, S. Atomistic calculations of the surface energy as a function of composition and temperature in g U-Zr to inform fuel performance modeling. J. Nucl. Mater. 2020, 540, 152271. [Google Scholar] [CrossRef]
- Aly, A.; Beeler, B.; Avramova, M. Ab initio molecular dynamics investigation of γ-(U,Zr) structural and thermal properties as a function of temperature and composition. J. Nucl. Mater. 2022, 561, 153523. [Google Scholar] [CrossRef]
- Starikov, S.V.; Kolotova, L.N.; Kuksin, A.Y.; Smirnova, D.E.; Tseplyaev, V.I. Atomistic simulation of cubic and tetragonal phases of U-Mo alloy: Structure and thermodynamic properties. J. Nucl. Mater. 2018, 499, 451–463. [Google Scholar] [CrossRef]
- Kolotova, L.; Gordeev, I. Structure and phase transition features of monoclinic and tetragonal phases in U–Mo alloys. Crystals 2020, 10, 69–77. [Google Scholar] [CrossRef]
- Starikov, S.; Smirnova, D. Details of structure transformations in pure uranium and U-Mo alloys: Insights from classical atomistic simulation. J. Nucl. Mater. 2023, 576, 154265. [Google Scholar] [CrossRef]
- Duong, T.C.; Hackenberg, R.E.; Attari, V.; Landa, A.; Turchi, P.E.; Arroyave, R. Investigation of the discontinuous precipitation of U-Nb alloys via thermodynamic analysis and phase-field modeling. Comput. Mater. Sci. 2020, 175, 109573. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Landa, A.; Söderlind, P.; Roehling, J.; McKeown, J.T. Thermodynamics of Liquid Uranium from Atomistic and Ab Initio Modeling. Appl. Sci. 2025, 15, 896. https://doi.org/10.3390/app15020896
Landa A, Söderlind P, Roehling J, McKeown JT. Thermodynamics of Liquid Uranium from Atomistic and Ab Initio Modeling. Applied Sciences. 2025; 15(2):896. https://doi.org/10.3390/app15020896
Chicago/Turabian StyleLanda, Alexander, Per Söderlind, John Roehling, and Joseph T. McKeown. 2025. "Thermodynamics of Liquid Uranium from Atomistic and Ab Initio Modeling" Applied Sciences 15, no. 2: 896. https://doi.org/10.3390/app15020896
APA StyleLanda, A., Söderlind, P., Roehling, J., & McKeown, J. T. (2025). Thermodynamics of Liquid Uranium from Atomistic and Ab Initio Modeling. Applied Sciences, 15(2), 896. https://doi.org/10.3390/app15020896






