Next Article in Journal
Optimizing Growth Conditions and Biochemical Properties of Chondracanthus acicularis (Rhodophyta) in Laboratory Settings
Previous Article in Journal
Catalytic Screening for 1,2-Diol Protection: A Saccharose-Derived Hydrothermal Carbon Showcases Enhanced Performance
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 15
Issue 2
10.3390/app15020808
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Influences of Different Factors and Sensitivity Analysis of Permeability of Gassy Coal

by
Bo Li
1,2,3,*,
Yong Yuan
1,2,3,*,
Yunpei Liang
4 and
Zhenghan Qin
1,2,3
1
State Key Laboratory for Fine Exploration and Intelligent Development of Coal Resources, China University of Mining and Technology, Xuzhou 221116, China
2
School of Mines, China University of Mining and Technology, Xuzhou 221116, China
3
Key Laboratory of Deep Coal Resource, Ministry of Education of China, China University of Mining and Technology, Xuzhou 221116, China
4
State Key Laboratory of Coal Mine Disaster Dynamics and Control, School of Resources and Safety Engineering, Chongqing University, Chongqing 400044, China
*
Authors to whom correspondence should be addressed.
Appl. Sci. 2025, 15(2), 808; https://doi.org/10.3390/app15020808
Submission received: 14 December 2024 / Revised: 8 January 2025 / Accepted: 14 January 2025 / Published: 15 January 2025
Browse Figures
Versions Notes

Abstract

:
Influencing factors and sensitivity analysis of coal permeability are significant for reasonably setting coalbed methane (CBM) extraction parameters and increasing CBM output. Seepage tests were conducted on gassy coal using a seepage test system for damaged coal and rock mass under various conditions of axial pressure, confining pressure, and gas pressure. Moreover, the influences of different factors on the permeability of gassy coal and the sensitivity of permeability to these factors were analyzed. Research results show that under the same confining pressure, the relationship between permeability and axial pressure of gassy coal meets the quadratic polynomial function; under the same axial pressure, the permeability changes with the confining pressure as a power function. The permeability of gassy coal is far more sensitive to confining pressure than to axial pressure during axial seepage. Under the same axial pressure and confining pressure (same stress), the permeability of gassy coal reduces at first and then increases in a V-shaped trend with growing gas pressure. There is a turning point in the seepage tests, that is, the critical gas pressure. When the gas pressure is lower than the critical value, the slippage effect plays the leading role in the variation of permeability of the coal; on the contrary, effective stress plays the dominant role. In the non-isobaric deviatoric stress state, the permeability of gassy coal is most sensitive to the confining pressure, followed successively by gas pressure and axial pressure. The research results provide a theoretical basis for precise gas extraction and control in coal seams.

1. Introduction

Coalbed methane (CBM) is a new, clean, and efficient energy source, with China’s CBM reserves exceeding 40 trillion m3, making it an abundant resource with significant potential for utilization. At present, the main utilization method of CBM is CBM extraction, and permeability is a key parameter describing the mobility performance of methane in coal, which has an important impact on CBM extraction [1,2,3,4,5,6,7]. There are many factors influencing the permeability of gas-containing coal, such as axial pressure, confine pressure, temperature, gas pressure, etc., and the sensitivity of each influencing factor to the permeability of gas-containing coal varies [8,9,10,11,12,13,14]. Therefore, it is of great significance to analyze the factors that influence and sensitivity of the permeability of gas-containing coal for the efficient extraction of coalbed methane.
The permeability of gas-containing coal is influenced by various factors, such as gas pressure, effective stress, temperature, water content, etc. Many scholars have carried out extensive research on the influence of these factors on the permeability of gas-containing coal [15,16,17,18], yielding valuable results. Stress, as an important factor affecting permeability, influences coal body permeability in five main ways: the stress state of the coal body, stress-induced damage, physical properties of the coal body, matrix deformation, and methane adsorption capacity [19,20]. Meng et al. [21] research concluded that the porosity and permeability of anthracite coal decrease exponentially with increasing effective stress, with significant changes observed below 5–6 MPa and enhanced stress sensitivity at higher moisture content and temperature. Zou et al. [22] concluded that both the effective stress coefficient and gas slippage have a significant influence on coal permeability, with the slippage effect being more pronounced at low gas pressures and the cleat exhibiting more vulnerability to deformation compared to the bedding. The effects of temperature on the permeability of the coal body mainly include thermal expansion and deformation of the coal body, changes in methane adsorption, and thermal cracking damage [23,24]. Wang et al. [25] research concluded that the cyclic temperature impact significantly enhances coal permeability, with new fractures and increased permeability observed as the temperature difference rises. Cai et al. [26] measured the porosity of the coal body after heat treatment by the NMR method and found that the porosity of the coal body showed a general increase with the increase in temperature. The effect of water content on the permeability of the coal body mainly includes filling pores, swelling effect, reducing friction, and changing the coals’ physical properties [27,28]. Braga and Kudasik [29] found that temperature significantly influences coal permeability, with higher temperatures leading to a marked decrease in the absolute permeability of raw coal to gases, while the effect on briquette coal permeability is negligible and can be compensated by changes in the dynamic viscosity factor. Zhang et al. [30] research concluded that the peak strength, axial strain, and permeability of water-bearing raw coal decrease with water content and confining pressure, while permeability increases with unloading and exhibits volatility with axial strain, following an exponential decay function with effective stress. Yin et al. [31] research concluded that the effective gas permeability of coal cores decreases with increasing water content and effective stress, with a linear relationship to water content and an exponential relationship to effective stress, influenced by changes in permeation pore structure.
In addition, many permeability models have been developed to quantitatively characterize seepage in coal seams. Zhao et al. [32] conducted unsteady state displacement tests on coal samples based on the NMR technique to establish and validate a relative permeability model considering interfacial effects. Zhou et al. [33] proposed and validated a new permeability model for deep coal, which incorporates matrix–fracture interaction and creep deformation, showing improved performance over classical models, with the internal swelling coefficient playing a key role in permeability evolution. Jia and Zou [34] studied permeability evolution in mining-disturbed coal under triaxial stress, with permeability models accounting for stress state and path, showing good agreement with experimental data and providing insights for coal mine disaster prevention and coal–CBM exploitation. Liu et al. [35] proposed the use of modulus loss rate to represent the variation in elastic modulus in different directions and developed an anisotropic permeability model by relating permeability to strain based on the modulus loss rate. Wang et al. [36] constructed an anisotropic permeability model for the permeability evolution induced by directional compression by deriving the fracture aperture diameter during compression and introducing the strain ratio between the matrix and fracture unit. Wu et al. [37] constructed an anisotropic permeability model for a doubly porous coal body by integrating the flow and migration of compressible gases in the coal matrix and fracture system, assuming unequal thermal expansion and adsorption in each direction. Xue et al. [38] defined damage by modulus loss and coupled the damage parameters into the C-B model to construct a permeability evolution model for damaged coal seams that considered the effect of damage on permeability.
In summary, while numerous studies have been conducted on the permeability of gas-containing coal, yielding a wealth of valuable insights, there remains a relative lack of comprehensive analyses that specifically address the combined effects of various influencing factors on coal permeability. Moreover, few studies have delved into the sensitivity of these factors, leaving a gap in understanding how each factor individually and interactively impacts the permeability of gas-containing coal under different conditions. Therefore, in this study, seepage tests were performed using a damaged coal rock seepage test system to investigate the impact of various factors on the permeability of gas-containing coal and the sensitivity of permeability to these factors. The findings offer valuable insights to analyze the influencing factors and sensitivity of the permeability of gas-containing coal for the efficient extraction of coalbed methane.

2. Test Equipment and Sample Preparation

2.1. Test Equipment

A seepage test system designed for damaged coal and rock mass was employed, as shown in Figure 1; its main components are described in detail in the previously published reference [18] and will not be repeated here. This system allows for the examination of seepage in both intact and fractured coal and rock under varying conditions of gas pressure, axial pressure, confining pressure, and temperature.

2.2. Preparation of Test Coal Samples

The preparation process of test coal samples is described as follows. At first, large raw coal blocks were collected from 4# coal seam in 24,312 working faces of a 1930 coal mine in Urumqi City, Xinjiang Uygur Autonomous Region, China. Then, a ZS-100 core drilling rig was adopted to drill coal samples measuring 50 mm × 100 mm, which were then ground to obtain standard coal samples. Finally, an ultrasonic detector was utilized to detect and classify coal samples. Coal samples with similar fracture distribution were selected to carry out seepage tests to avoid the influence of the difference in fracture distribution in coal samples on the test results. The preparation process of coal samples is displayed in Figure 2.

3. Influences of Axial Pressure and Confining Pressure on the Permeability of Gassy Coal

3.1. Test Schemes

To explore the influences of axial pressure and confining pressure on the permeability of gassy coal, two groups of seepage tests were conducted on gassy coal under different axial pressures and confining pressures. The stress loading paths are shown in Figure 3. In the tests, the gas pressure was 1 MPa; confining pressure was 2, 4, 6, 8, and 10 MPa; under each confining pressure, the axial pressure was separately increased from 1 to 10 MPa, with an interval of 1 MPa.

3.2. Test Results and Discussion

Two groups of seepage tests were conducted on gassy coal under different axial pressures and confining pressures following test schemes in Figure 3, thus obtaining the axial pressure–permeability curves under different confining pressures, as illustrated in Figure 4. The fitting formulas for axial pressure and permeability are shown in Table 1. The confining pressure–permeability curves under different axial pressures are shown in Figure 5. The fitting formulas for confining pressure and permeability are listed in Table 2.
It can be seen from Figure 4 that under the same confining pressure, the permeability of gassy coal decreases with the growing axial pressure, and so does the decrease rate. Meanwhile, the overall decreased amplitude of permeability with increasing axial pressure is not large, particularly under high confining pressure, when the permeability basically remains unchanged with growing axial pressure. This indicates that the permeability is less sensitive to axial pressure during axial seepage. As shown in Table 1, the fitting formula for permeability and axial pressure of gassy coal under the same confining pressure is a quadratic polynomial function, and the correlation coefficients are always higher than 0.98. This suggests that under the same confining pressure, the relationship between permeability and axial pressure of gassy coal meets the quadratic polynomial function.
As shown in Figure 5, the permeability of gassy coal decreases with the increment of confining pressure, and so does the decrease rate under the same axial pressure. The permeability reduces substantially with the increasing confining pressure on the whole, almost in an exponential manner. This indicates that the axial permeability is far more sensitive to confining pressure than to axial pressure; that is, the axial seepage is greatly affected by confining pressure, whose reason is as follows: In the seepage test, the gas seepage occurs parallel to the axial pressure and perpendicular to the confining pressure. Consequently, changes in the confining pressure have a more pronounced effect on the fissure opening in the direction of gas seepage, leading to a greater sensitivity of permeability to the confining pressure. It can be seen from Table 2 that under the same axial pressure, the fitting formula for permeability and confining pressure of gassy coal is a power function, and the correlation coefficients are always higher than 0.97. This shows that, at constant axial pressure, the permeability of gassy coal is governed by a power function with respect to confining pressure.
In summary, the permeability of gassy coal during axial seepage is far more sensitive to confining pressure than to axial pressure. To further study the quantitative relationship between sensitivities of axial permeability of gassy coal to confining pressure and axial pressure, the quantitative relationship between the above sensitivities was explored by tests. In the tests, the gas pressure was 0.5 MPa. Prior to each test, the initial axial pressure and confining pressure were set at 10 MPa and 2 MPa, respectively. Seepage tests were conducted with varying unloading rates of axial pressure and loading rates of confining pressure, as detailed in Table 3.
Tests on the quantitative relationship between sensitivities of permeability to the axial pressure and confining pressure were performed according to test schemes in Table 3, thus attaining permeability curves at different unloading rates of axial pressure and loading rates of confining pressure (Figure 6).
It can be seen from Figure 6 that as the axial pressure is unloaded from 10 to 1.5 MPa and confining pressure is increased from 2 to 3 MPa, that is, when the ratio of the unloading rate of axial pressure to the loading rate of confining pressure is 8.5:1, the permeability of gassy coal remains unchanged and is basically identical (7.68 md). This suggests that, during axial seepage, the permeability of gassy coal is significantly more responsive to confining pressure than to axial pressure, with the sensitivity to confining pressure being approximately 8.5 times greater than that to axial pressure.
In general cases, during pressure-relief gas extraction in protective layer mining, the seepage path of gas extracted from boreholes in the protected layer is generally parallel to the protected layer, as shown in Figure 7. Therefore, in protective layer mining, reducing vertical stress in the protected layer is more effective than decreasing horizontal stress in terms of pressure relief and permeability enhancement.

4. Influences of Gas Pressure on the Permeability of Gassy Coal

4.1. Test Schemes

To study the influences of gas pressure on the permeability of gassy coal, two groups of seepage tests were carried out on gassy coal under identical axial pressure and confining pressure with different gas pressures. The stress loading paths are shown in Figure 8.

4.2. Test Results and Discussion

Two groups of seepage tests were performed on gassy coal under different gas pressures following the test schemes in Figure 8. In this way, the gas pressure–permeability curves under different axial pressures and confining pressures were plotted, as shown in Figure 9. The fitting formulas for gas pressure and permeability are shown in Table 4.
As shown in Figure 9, with the same axial and confining pressures (identical stress conditions), the permeability of gassy coal reduces at first and then increases in a V-shaped trend with growing gas pressure. In addition, the value and change trend of permeability decline with the growing stress. The quadratic polynomial function was adopted to model the relationship between permeability and gas pressure in Figure 9, with the fitting results presented in Table 4.
It can be seen from Table 4 that the quadratic polynomial function can fit changes of permeability with gas pressure under the same stress well, and the correlation coefficients are all higher than 0.8. Because the permeability declines at first and then increases with increasing gas pressure, there is a turning point in the seepage test process, that is, the critical gas pressure. The values of critical gas pressure of gassy coal in each stress state calculated using the fitting formulas for permeability and gas pressure are listed in Table 4. The table shows that the critical gas pressure of coal samples grows with the increment of the stress of coal samples.
Factors that influence the permeability of gassy coal during variations of gas pressure include changes in the effective stress, adsorption of coal, and the Klinkenberg effect (slippage effect) under low atmospheric pressure [39]. Under the same stress, the effective stress of gassy coal samples declines with the increasing gas pressure, and the permeability should enlarge. Whereas, the gas adsorption of coal samples also increases as the gas pressure augments, so the coal matrix expands and internal pore space shrinks, thus leading to the decreased permeability of coal samples, which is the slippage effect. The slippage effect is generally more obvious under low gas pressure and low stress, as evident in Figure 9, which is consistent with the findings of reference [40]. Therefore, the critical gas pressure of gassy coal functions as a boundary between the slippage effect and effective stress. When the gas pressure is lower than the critical value, the slippage effect and the adsorption and expansion of the substrate dominate, with lower gas and annular pressures amplifying the influence of these factors on permeability. However, when the gas pressure exceeds the critical value, the reduction in effective stress leads to the expansion of pore spaces, which becomes the primary mechanism driving changes in permeability.
To further study the influence of the slippage effect on the permeability of gassy coal, seepage tests with different gas pressures under constant effective stress were conducted. The test results are displayed in Figure 10.
It can be seen from Figure 10 that the permeability of gassy coal decreases with growing gas pressure under the same effective stress and does not increase. This indicates that the reduction of permeability of gassy coal with increasing gas pressure before reaching the critical gas pressure is not determined by the effective stress but by the slippage effect instead. Moreover, this also suggests that after reaching the critical gas pressure, the permeability is determined by effective stress.

5. Sensitivity Analysis of Permeability of Gassy Coal to Axial Pressure, Confining Pressure, and Gas Pressure

5.1. Experimental Schemes

The above tests and analysis reveal that when the gassy coal is under the isobaric condition (axial pressure is equal to confining pressure), the permeability of gassy coal before reaching the critical gas pressure is determined by the slippage effect caused by the gas pressure, that is, determined by the gas pressure. Meanwhile, the permeability of gassy coal after reaching critical gas pressure is determined by effective stress. If the gassy coal is in the non-isobaric deviatoric stress state (axial pressure is unequal to confining pressure), the sensitivities of permeability of gassy coal to axial pressure, confining pressure, and gas pressure remain unclear. Hence, to carry out sensitivity analysis on the permeability of gassy coal to axial pressure, confining pressure, and gas pressure in seepage tests in the non-isobaric deviatoric stress state, gassy coal should be selected to carry out seepage tests under different axial pressures, confining pressures, and gas pressures. Considering that this calls for multi-factor (axial pressure, confining pressure, and gas pressure) tests many times, which is tedious, orthogonal experiments were selected.
The influences of three factors, namely, the axial pressure, confining pressure, and gas pressure, on the permeability of gassy coal need to be studied in the experiments, while their interactions are not considered. Therefore, three-factor and four-level L16(43) orthogonal experimental tables were used, which could meet the experimental requirements. In the meanwhile, the above analysis reveals that there is a critical point of gas pressure in terms of its influence on the permeability, so two orthogonal experimental tables were designed: one with low gas pressure (lower than the critical value) and the other with high gas pressure (higher than the critical value). The factors and levels in the two orthogonal experimental tables are shown in Table 5.

5.2. Experimental Results and Discussion

Two methods, namely, range analysis and variance analysis, are generally used to process the orthogonal experimental tables. Range analysis was only performed here for the orthogonal experimental tables to determine the order of various factors according to their influences on the permeability of gassy coal. The permeability test results, according to the two orthogonal experimental tables, are displayed in Table 6 and Table 7. The range R is calculated according to the difference between the optimal and worst levels, which reflects how significantly a level of a factor influences the experimental index. That is, the larger the range of a factor is, the greater the influence of the factor on the experimental index, and vice versa. According to the permeability test results based on the two orthogonal experimental tables, the ranges R of the two orthogonal experimental tables were calculated, as listed in Table 6 and Table 7.
It can be seen from Table 6 and Table 7 that either under low or high gas pressure, the confining pressure always exerts the largest influence on the permeability of gassy coal in the non-isobaric deviatoric stress state, followed by gas pressure and, finally, axial pressure. More specifically, ranges of various factors are listed in descending orders as RB (0.33255), RC (0.12545), and RA (0.1037) according to orthogonal experimental Table 1 and as RB (0.3651), RC (0.014375), and RA (0.0119) according to orthogonal experimental Table 2. The influence trends of various factors on the permeability were drawn in accordance with Table 6 and Table 7, as shown in Figure 11.
It can be seen from Figure 11 that various factors are listed in descending order, such as the confining pressure, gas pressure, and axial pressure, according to their influences on permeability. That is to say, the permeability of gassy coal is most sensitive to the confining pressure, followed successively by gas pressure and axial pressure.

6. Conclusions

The seepage test system for damaged coal and rock mass was used to carry out seepage tests on gassy coal under different factors (axial pressure, confining pressure, and gas pressure). The influence of these factors on the permeability of gassy coal and the sensitivity of permeability to each factor were analyzed. The following main conclusions are drawn:
(1)
The relationship between permeability and axial pressure in gassy coal follows a quadratic polynomial function under constant confining pressure, while the relationship between permeability and confining pressure is described by a power function under constant axial pressure. During axial seepage, gassy coal’s permeability is significantly more sensitive to confining pressure than axial pressure, with the sensitivity to confining pressure being approximately 8.5 times greater. Therefore, reducing vertical stress in the protected layer has a more pronounced pressure-relief and permeability-enhancing effect compared to decreasing horizontal stress in protective layer mining;
(2)
At constant axial and confining pressures (same stress), the permeability of gassy coal initially decreases and then increases, following a V-shaped pattern as gas pressure increases. There is a turning point in the seepage tests, that is, the critical gas pressure, which is the boundary between the slippage effect and effective stress. When the gas pressure is lower than the critical value, the slippage effect plays the leading role, and the lower the stress and gas pressure are, the more significant the influence of the slippage effect on the permeability; on the contrary, the effective stress plays a dominant role in the variation of permeability of coal when the gas pressure exceeds the critical value;
(3)
Under a non-isobaric deviatoric stress state, the permeability of gassy coal is primarily influenced by confining pressure, followed by gas pressure and axial pressure in decreasing order of sensitivity.

Author Contributions

Data curation, B.L.; Funding acquisition, B.L. and Y.L.; Methodology, Y.Y.; Validation, Z.Q.; Writing—original draft, B.L.; Writing—review and editing, Y.L. and Y.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (52204132 and 52174166), the Independent research project of State Key Laboratory for Fine Exploration and Intelligent Development of Coal Resources, CUMT (SKLCRSM24X002), Hunan Provincial Natural Science Foundation of China (2023JJ40285), Scientific Research Foundation of Hunan Provincial Education Department (22B0469).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Jiang, C.; Yang, Y.; Wei, W.; Duan, M.; Yu, T. A new stress-damage-flow coupling model and the damage characterization of raw coal under loading and unloading conditions. Int. J. Rock Mech. Min. Sci. 2021, 138, 104601. [Google Scholar] [CrossRef]
  2. Wei, J.; Su, E.; Xu, G.; Yang, Y.; Han, S.; Chen, X.; An, F. Comparative analysis of permeability rebound and recovery of tectonic and intact coal: Implications for coalbed methane recovery in tectonic coal reservoirs. Energy 2024, 301, 131702. [Google Scholar] [CrossRef]
  3. Salmachi, A.; Karacan, C.Ö. Cross-formational flow of water into coalbed methane reservoirs: Controls on relative permeability curve shape and production profile. Environ. Earth Sci. 2017, 76, 200. [Google Scholar] [CrossRef]
  4. Shevtsov, A.; Khyamyalyaynen, V. Geomechanical Estimation of the Influence of Horizontal Coalbed Methane Well Design on Coal Seam Permeability. E3S Web Conf. 2019, 105, 01014. [Google Scholar] [CrossRef]
  5. Li, B.; Zou, Q.; Liang, Y. Experimental Research into the Evolution of Permeability in a Broken Coal Mass under Cyclic Loading and Unloading Conditions. Appl. Sci. 2019, 9, 762. [Google Scholar] [CrossRef]
  6. Li, G.; Wang, Y.; Wang, J.; Zhang, H.; Shen, W.; Jiang, H. Coupled Effects of Stress, Moisture Content and Gas Pressure on the Permeability Evolution of Coal Samples: A Case Study of the Coking Coal Resourced from Tunlan Coalmine. Water 2021, 13, 1653. [Google Scholar] [CrossRef]
  7. Su, E.; Wei, J.; Chen, H.; Chen, X.; Liang, Y.; Zou, Q.; Zhu, X. Effect of CO2 injection on Coalbed Permeability Based on a Thermal–Hydraulic–Mechanical Coupling Model. Energy Fuels 2024, 38, 11078–11092. [Google Scholar] [CrossRef]
  8. Bai, X.; Wang, Y.; He, G.; Zhou, Z.; Wang, D.; Zhang, D. Research on a permeability model of coal damaged under triaxial loading and unloading. Fuel 2023, 354, 129375. [Google Scholar] [CrossRef]
  9. Wang, F.; Liang, Y.; Li, X.; Li, L.; Li, J.; Chen, Y. Study on the change of permeability of gas-containing coal under many factors. Energy Sci. Eng. 2019, 7, 194–206. [Google Scholar] [CrossRef]
  10. Thararoop, P.; Karpyn, Z.T.; Ertekin, T. Development of a multi-mechanistic, dual-porosity, dual-permeability, numerical flow model for coalbed methane reservoirs. J. Nat. Gas Sci. Eng. 2012, 8, 121–131. [Google Scholar] [CrossRef]
  11. Zakharov, V.N.; Malinnikova, O.N.; Trofimov, V.A.; Filippov, Y.A. Effect of gas content and actual stresses on coalbed permeability. J. Min. Sci. 2016, 52, 218–225. [Google Scholar] [CrossRef]
  12. Zeng, S.; Zhang, L.; Luo, L.; Ye, Z.; Wang, C. Permeability Evolution of Anthracite Subjected to Liquid Nitrogen Treatment under Repeated Loading–Unloading Conditions. Nat. Resour. Res. 2023, 32, 2753–2767. [Google Scholar] [CrossRef]
  13. Zhang, C.; Tu, S.; Zhao, Y. Compaction characteristics of the caving zone in a longwall goaf: A review. Environ. Earth Sci. 2019, 78, 27. [Google Scholar] [CrossRef]
  14. Peng, K.; Shi, S.; Zou, Q.; Wang, G.; Jiang, Z. Disaster-Triggering Mechanisms Based on Interaction of Various Factors in Structured Gas Migration in Coal Seams Under Loading and Unloading Conditions. Nat. Resour. Res. 2021, 30, 1445–1465. [Google Scholar] [CrossRef]
  15. Pan, Z.; Connell, L.D. Modelling permeability for coal reservoirs: A review of analytical models and testing data. Int. J. Coal Geol. 2012, 92, 1–44. [Google Scholar] [CrossRef]
  16. Lu, S.; Li, M.; Ma, Y.; Wang, S.; Zhao, W. Permeability changes in mining-damaged coal: A review of mathematical models. J. Nat. Gas Sci. Eng. 2022, 106, 104739. [Google Scholar] [CrossRef]
  17. Luo, L.; Zhang, L.; Pan, J.; Li, M.; Tian, Y.; Wang, C.; Li, S. Evolution of Broken Coal’s Permeability Characteristics under Cyclic Loading–Unloading Conditions. Nat. Resour. Res. 2024, 33, 2279–2297. [Google Scholar] [CrossRef]
  18. Li, B.; Liang, Y.; Zhang, L.; Zou, Q. Experimental investigation on compaction characteristics and permeability evolution of broken coal. Int. J. Rock Mech. Min. Sci. 2019, 118, 63–76. [Google Scholar] [CrossRef]
  19. Ye, Z.W.; Zhang, L.; Hao, D.Y.; Zhang, C.; Wang, C. Experimental study on the response characteristics of coal permeability to pore pressure under loading and unloading conditions. J. Geophys. Eng. 2017, 14, 1020–1031. [Google Scholar] [CrossRef]
  20. Zhang, L.; Hao, D.; Ye, Z.; Zhang, C.; Chen, S. Experimental study of gas pressure and effective stress influencing on gas seepage characteristics of bituminous coal in both axial and radial directions. Int. J. Oil Gas Coal Technol. 2019, 22, 527–553. [Google Scholar] [CrossRef]
  21. Meng, Y.; Li, Z.; Lai, F. Experimental study on porosity and permeability of anthracite coal under different stresses. J. Pet. Sci. Eng. 2015, 133, 810–817. [Google Scholar] [CrossRef]
  22. Zou, J.; Chen, W.; Yang, D.; Yu, H.; Yuan, J. The impact of effective stress and gas slippage on coal permeability under cyclic loading. J. Nat. Gas Sci. Eng. 2016, 31, 236–248. [Google Scholar] [CrossRef]
  23. Li, B.; Ren, C.; Wang, Z.; Li, J.; Yang, K.; Xu, J. Experimental study on damage and the permeability evolution process of methane-containing coal under different temperature conditions. J. Pet. Sci. Eng. 2020, 184, 106509. [Google Scholar] [CrossRef]
  24. Ren, C.; Li, B.; Xu, J.; Zhang, Y.; Li, J.; Gao, Z.; Yu, J. A novel damage-based permeability model for coal in the compaction and fracturing process under different temperature conditions. Rock Mech. Rock Eng. 2020, 53, 5697–5713. [Google Scholar] [CrossRef]
  25. Wang, D.; Yao, B.; Gao, Y.; Li, W.; Lv, R. Effect of cyclic temperature impact on coal seam permeability. Therm. Sci. 2017, 21 (Suppl. S1), 351–357. [Google Scholar] [CrossRef]
  26. Cai, Y.; Liu, D.; Pan, Z.; Yao, Y.; Li, J.; Qiu, Y. Petrophysical characterization of Chinese coal cores with heat treatment by nuclear magnetic resonance. Fuel 2013, 108, 292–302. [Google Scholar] [CrossRef]
  27. Li, J.; Li, B.; Pan, Z.; Wang, Z.; Yang, K.; Ren, C.; Xu, J. Coal permeability evolution under different water-bearing conditions. Nat. Resour. Res. 2020, 29, 2451–2465. [Google Scholar] [CrossRef]
  28. Chao, J.; Yu, M.; Chu, T.; Han, X.; Teng, F.; Li, P. Evolution of broken coal permeability under the condition of stress, temperature, moisture content, and pore pressure. Rock Mech. Rock Eng. 2019, 52, 2803–2814. [Google Scholar] [CrossRef]
  29. Braga, L.T.P.; Kudasik, M. Permeability measurements of raw and briquette coal of various porosities at different temperatures. Mater. Res. Express 2019, 6, 105609. [Google Scholar] [CrossRef]
  30. Zhang, Z.; Wang, H.; Wang, L.; Zhang, D. Experimental Study on Mechanics and Permeability Properties of Water-Bearing Raw Coal Samples Under In-Situ Stress. Appl. Sci. 2019, 9, 2549. [Google Scholar] [CrossRef]
  31. Yin, G.; Jiang, C.; Xu, J.; Guo, L.; Peng, S.; Li, W. An experimental study on the effects of water content on coalbed gas permeability in ground stress fields. Transp. Porous Media 2012, 94, 87–99. [Google Scholar] [CrossRef]
  32. Zhao, T.; Xu, H.; Tang, D.; Zong, P. A new relative permeability model of coal reservoir considering interface effect. J. Pet. Sci. Eng. 2021, 207, 109082. [Google Scholar] [CrossRef]
  33. Zhou, H.W.; Zhang, L.; Wang, X.Y.; Rong, T.L.; Wang, L.J. Effects of matrix-fracture interaction and creep deformation on permeability evolution of deep coal. Int. J. Rock Mech. Min. Sci. 2020, 127, 104236. [Google Scholar] [CrossRef]
  34. Jia, H.; Zou, D. Study on the Permeability Evolution Model of Mining-Disturbed Coal. Geofluids 2021, 2021, 1810915. [Google Scholar] [CrossRef]
  35. Liu, J.; Chen, Z.; Elsworth, D.; Miao, X.; Mao, X. Linking gas-sorption induced changes in coal permeability to directional strains through a modulus reduction ratio. Int. J. Coal Geol. 2010, 83, 21–30. [Google Scholar] [CrossRef]
  36. Wang, J.G.; Liu, J.; Kabir, A. Combined effects of directional compaction, non-Darcy flow and anisotropic swelling on coal seam gas extraction. Int. J. Coal Geol. 2013, 109, 1–14. [Google Scholar] [CrossRef]
  37. Wu, Y.; Liu, J.; Elsworth, D.; Miao, X.; Mao, X. Development of anisotropic permeability during coalbed methane production. J. Nat. Gas Sci. Eng. 2010, 2, 197–210. [Google Scholar] [CrossRef]
  38. Xue, Y.; Gao, F.; Gao, Y.; Cheng, H.; Liu, Y.; Hou, P.; Teng, T. Quantitative evaluation of stress-relief and permeability-increasing effects of overlying coal seams for coal mine methane drainage in Wulan coal mine. J. Nat. Gas Sci. Eng. 2016, 32, 122–137. [Google Scholar] [CrossRef]
  39. Xiao, W.; Bernabé, Y.; Evans, B.; Mok, U.; Zhao, J.; Ren, X.; Chen, M. Klinkenberg effect and effective pressure for gas permeability of tight sandstones. J. Geophys. Res. Solid Earth 2019, 124, 1412–1429. [Google Scholar] [CrossRef]
  40. Lv, Q.; Chen, Z.; Wang, M. An improved elastic-tubes model for the correlation of permeability and stress with correction for the Klinkenberg effect. J. Nat. Gas Sci. Eng. 2017, 48, 24–35. [Google Scholar] [CrossRef]
Applsci 15 00808 g001
Figure 1. Schematic representation of the seepage test system for damaged coal and rock mass. For a description of the system, please refer to reference [18].
Figure 1. Schematic representation of the seepage test system for damaged coal and rock mass. For a description of the system, please refer to reference [18].
Applsci 15 00808 g001
Applsci 15 00808 g002
Figure 2. Preparation process of test coal samples, including raw coal collection, drilling of coal samples, and coal sample screening.
Figure 2. Preparation process of test coal samples, including raw coal collection, drilling of coal samples, and coal sample screening.
Applsci 15 00808 g002
Applsci 15 00808 g003
Figure 3. Stress loading paths in seepage tests on gassy coal under different axial pressures and confining pressures.
Figure 3. Stress loading paths in seepage tests on gassy coal under different axial pressures and confining pressures.
Applsci 15 00808 g003
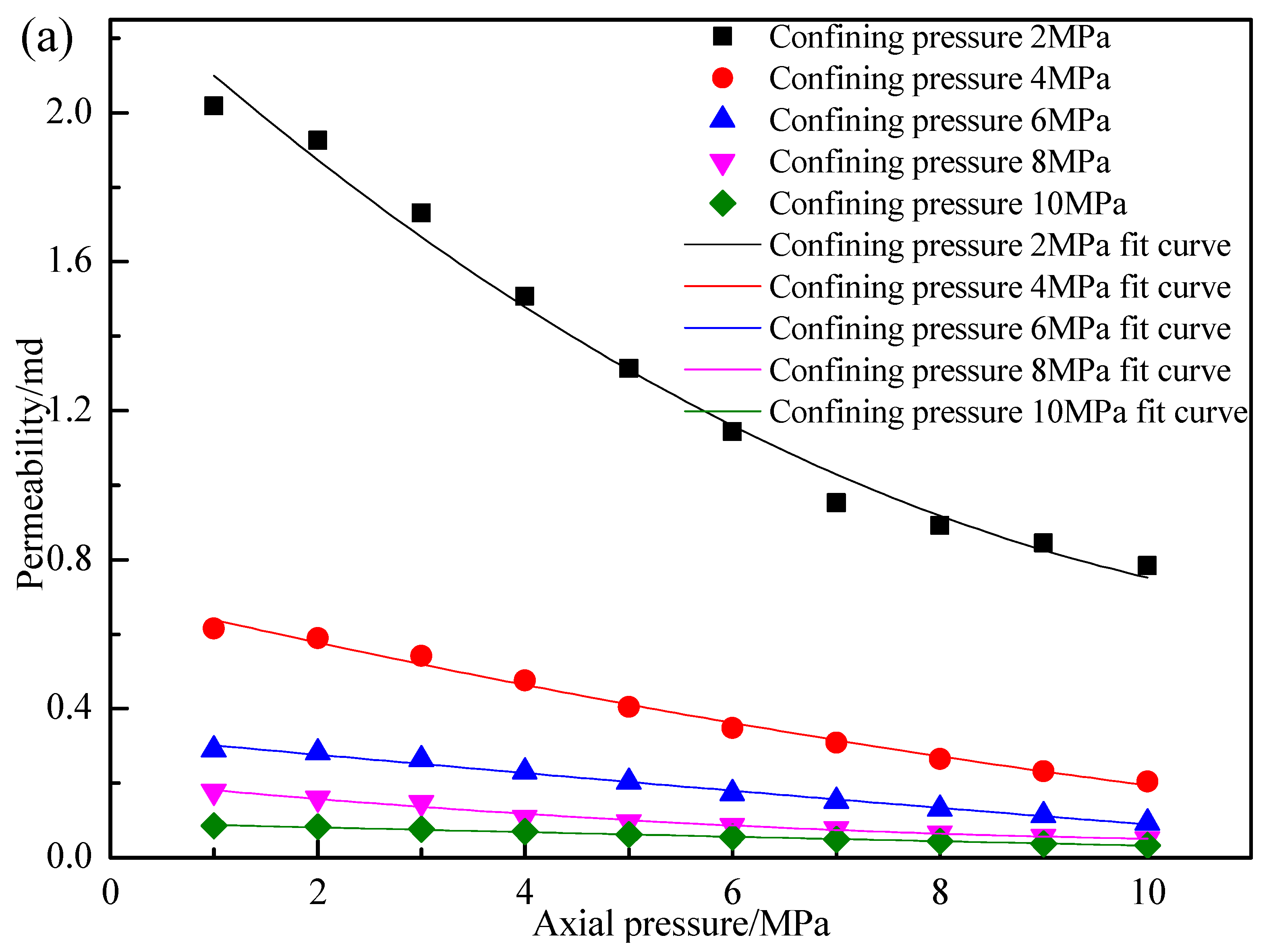
Applsci 15 00808 g004aApplsci 15 00808 g004b
Figure 4. Axial pressure–permeability curves of gassy coal under different confining pressures. (a) Z1 coal samples; (b) Z2 coal samples.
Figure 4. Axial pressure–permeability curves of gassy coal under different confining pressures. (a) Z1 coal samples; (b) Z2 coal samples.
Applsci 15 00808 g004aApplsci 15 00808 g004b
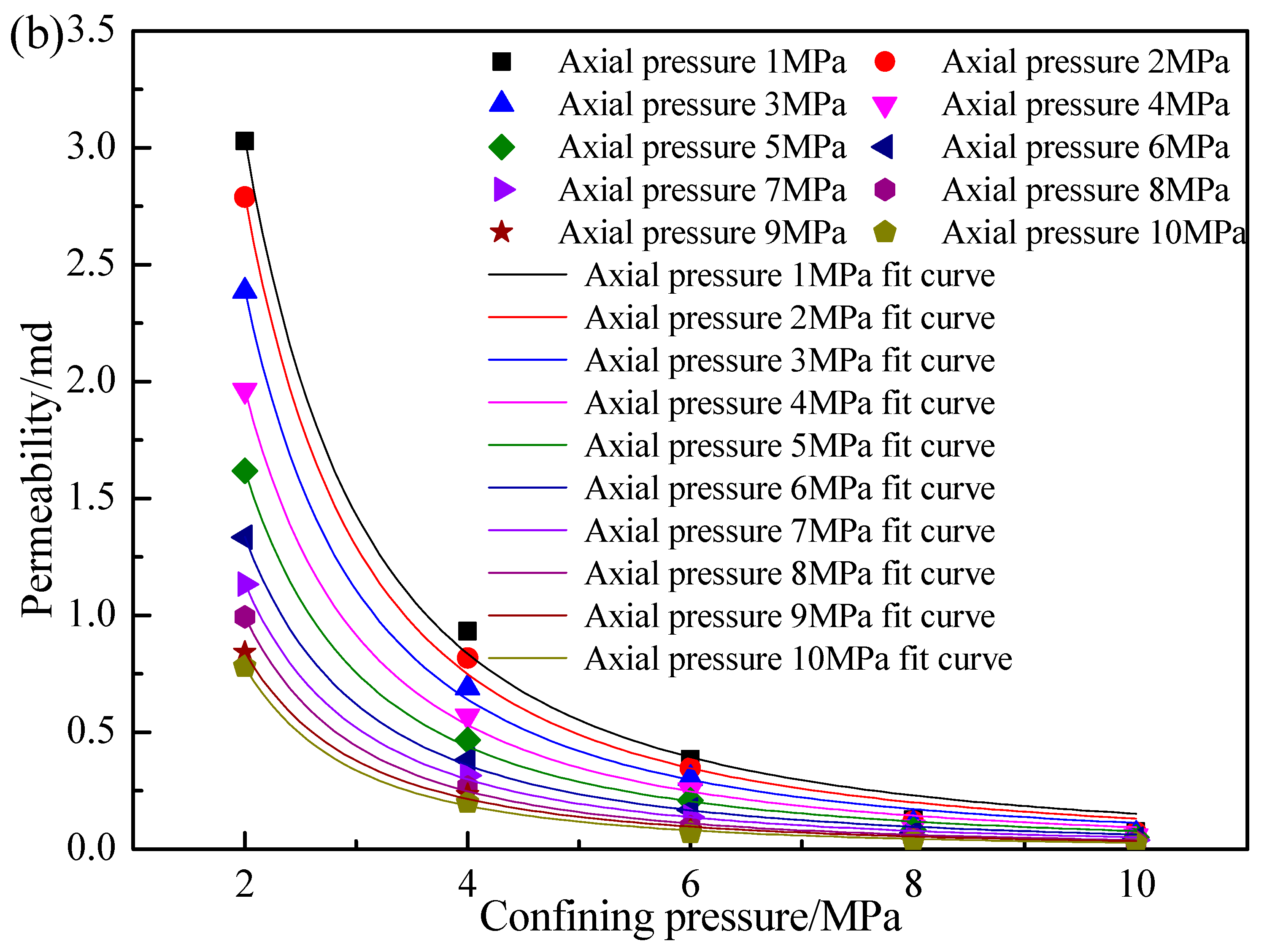
Applsci 15 00808 g005aApplsci 15 00808 g005b
Figure 5. Confining pressure–permeability curves of gassy coal under different axial pressures. (a) Z1 coal samples; (b) Z2 coal samples.
Figure 5. Confining pressure–permeability curves of gassy coal under different axial pressures. (a) Z1 coal samples; (b) Z2 coal samples.
Applsci 15 00808 g005aApplsci 15 00808 g005b
Applsci 15 00808 g006
Figure 6. Permeability curves of gassy coal at different unloading rates of axial pressure and loading rates of confining pressure.
Figure 6. Permeability curves of gassy coal at different unloading rates of axial pressure and loading rates of confining pressure.
Applsci 15 00808 g006
Applsci 15 00808 g007
Figure 7. Seepage paths of gas extracted from the protected layer during pressure-relief protective layer mining.
Figure 7. Seepage paths of gas extracted from the protected layer during pressure-relief protective layer mining.
Applsci 15 00808 g007
Applsci 15 00808 g008
Figure 8. Seepage test schemes for the influence of gas pressure on the permeability of gassy coal.
Figure 8. Seepage test schemes for the influence of gas pressure on the permeability of gassy coal.
Applsci 15 00808 g008
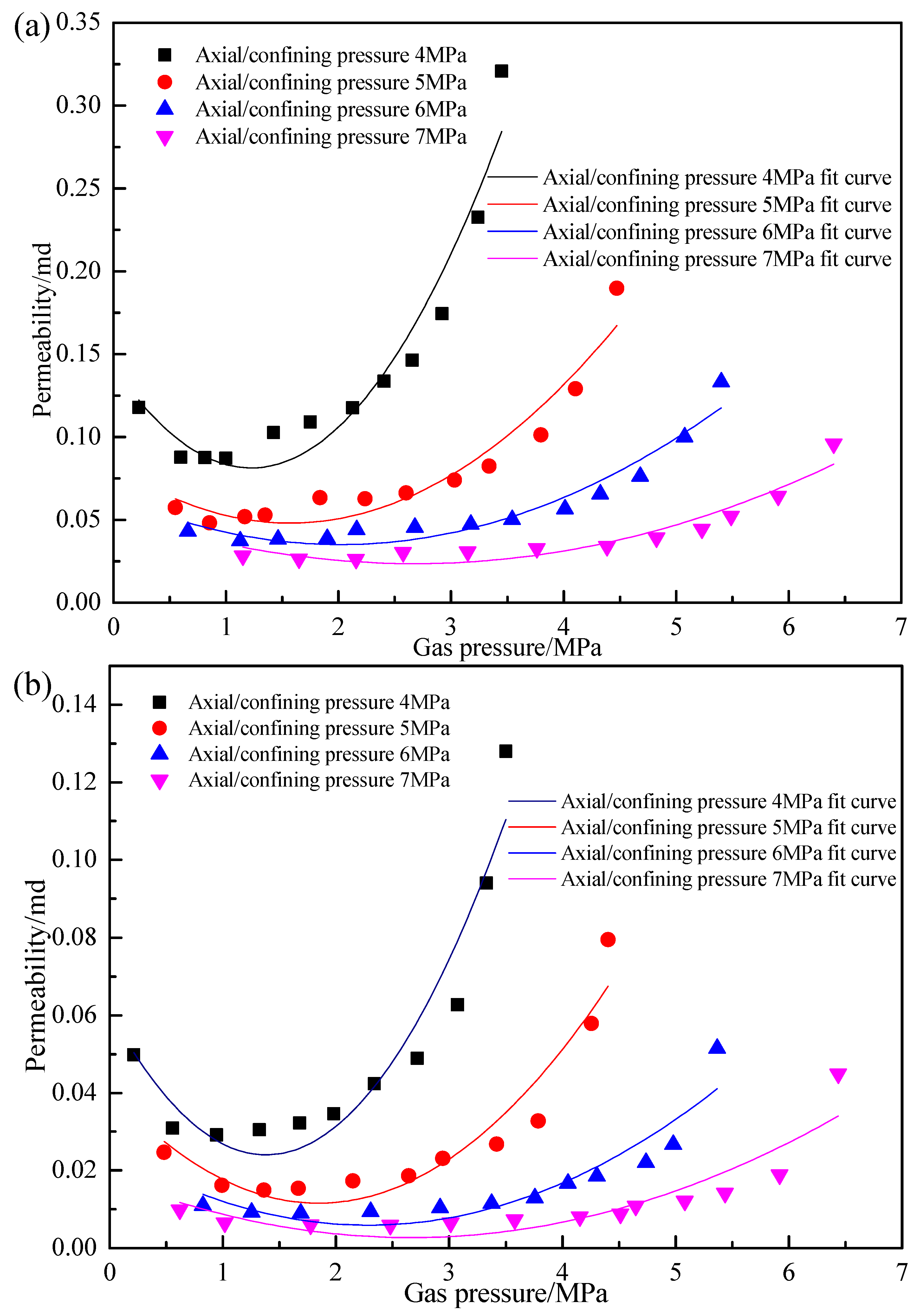
Applsci 15 00808 g009
Figure 9. Permeability–gas pressure curves of gassy coal in different stress states. (a) W1 coal samples; (b) W2 coal samples.
Figure 9. Permeability–gas pressure curves of gassy coal in different stress states. (a) W1 coal samples; (b) W2 coal samples.
Applsci 15 00808 g009
Applsci 15 00808 g010
Figure 10. Permeability–gas pressure curves of gassy coal under the same effective stress. (a) Y1 coal samples; (b) Y2 coal samples.
Figure 10. Permeability–gas pressure curves of gassy coal under the same effective stress. (a) Y1 coal samples; (b) Y2 coal samples.
Applsci 15 00808 g010
Applsci 15 00808 g011
Figure 11. Influence trends of various factors on the permeability. (a) Orthogonal experiment Table 1, (b) orthogonal experiment Table 2.
Figure 11. Influence trends of various factors on the permeability. (a) Orthogonal experiment Table 1, (b) orthogonal experiment Table 2.
Applsci 15 00808 g011
Table 1. Fitting formulas for permeability and axial pressure of gassy coal under different confining pressures.
Table 1. Fitting formulas for permeability and axial pressure of gassy coal under different confining pressures.
Coal Sample NumberConfining Pressure/MPaPermeability–Axial Pressure Fitting
Formula		Correlation Coefficient
Z12K = 0.0096σ12 − 0.2549σ1 + 2.3451R2 = 0.9882
4K = 0.0015σ12 − 0.0657σ1 + 0.7028R2 = 0.9911
6K = 0.0002σ12 − 0.0257σ1 + 0.3268R2 = 0.991
8K = 0.0011σ12 − 0.0267σ1 + 0.2064R2 = 0.9868
10K = 3 × 10−5σ12 − 0.0065σ1 + 0.094R2 = 0.9959
Z22K = 0.0214σ12 − 0.4995σ1 + 3.6111R2 = 0.9949
4K = 0.0071σ12 − 0.1608σ1 + 1.0985R2 = 0.999
6K = 0.002σ12 − 0.0586σ1 + 0.4521R2 = 0.9963
8K = 0.0003σ12 − 0.0142σ1 + 0.1452R2 = 0.9952
10K = 0.0002σ12 − 0.0083σ1 + 0.086R2 = 0.9975
Table 2. Fitting formulas for permeability and confining pressure of gassy coal under different axial pressures.
Table 2. Fitting formulas for permeability and confining pressure of gassy coal under different axial pressures.
Coal Sample
Number		Axial Pressure/MPaPermeability–Confining Pressure Fitting
Formula		Correlation Coefficient
Z11K = 8.0727σ2−1.896R2 = 0.9894
2K = 7.7766σ2−1.905R2 = 0.9918
3K = 6.975σ2−1.891R2 = 0.9903
4K = 6.1974σ2−1.915R2 = 0.9925
5K = 5.2467σ2−1.893R2 = 0.9935
6K = 4.4602σ2−1.878R2 = 0.9957
7K = 3.6655σ2−1.84R2 = 0.9945
8K = 3.4334σ2−1.879R2 = 0.9972
9K = 3.3461σ2−1.939R2 = 0.9981
10K = 3.0957σ2−1.968R2 = 0.9997
Z21K = 18.31σ2−2.312R2 = 0.9754
2K = 16.224σ2−2.292R2 = 0.98
3K = 13.436σ2−2.26R2 = 0.9815
4K = 10.582σ2−2.217R2 = 0.9833
5K = 8.2168σ2−2.163R2 = 0.9875
6K = 6.5522σ2−2.138R2 = 0.9905
7K = 5.4545σ2−2.134R2 = 0.9928
8K = 4.673σ2−2.152R2 = 0.9976
9K = 4.0289σ2−2.159R2 = 0.9954
10K = 3.6822σ2−2.185R2 = 0.9971
Table 3. Test schemes for the quantitative relationship between sensitivities of permeability of gassy coal to axial pressure and confining pressure.
Table 3. Test schemes for the quantitative relationship between sensitivities of permeability of gassy coal to axial pressure and confining pressure.
NumberGas
Pressure/MPa		Initial Axial
Pressure/MPa		Initial Confining
Pressure/MPa		Ratio of Axial Unloading Rate to Confining Pressure Loading Rate
10.51021:1
20.51021.5:1
30.51022:1
40.51022.5:1
50.51023:1
60.51023.5:1
70.51024:1
80.51024.5:1
90.51025:1
100.51025.5:1
110.51026:1
120.51026.5:1
130.51027:1
140.51027.5:1
150.51028:1
160.51028.5:1
170.51029:1
Table 4. Fitting formulas for permeability and gas pressure of gassy coal under different stresses.
Table 4. Fitting formulas for permeability and gas pressure of gassy coal under different stresses.
Coal Sample NumberAxial
Pressure/MPa		Confining
Pressure/MPa		Permeability–Gas
Pressure Fitting Formula		Correlation CoefficientCritical Gas
Pressure/MPa
W144K = 0.0409P2 − 0.1003P + 0.1427R2 = 0.92471.226
55K = 0.0141P2 − 0.0440P + 0.0828R2 = 0.90941.560
66K = 0.0072P2 − 0.0290P + 0.0644R2 = 0.91882.014
77K = 0.0043P2 − 0.0231P + 0.0544R2 = 0.88982.686
W244K = 0.0193P2 − 0.0532P + 0.0609R2 = 0.89601.378
55K = 0.0086P2 − 0.0316P + 0.0407R2 = 0.89331.837
66K = 0.0037P2 − 0.0169P + 0.0253R2 = 0.82982.284
77K = 0.0021P2 − 0.0116P + 0.0181R2 = 0.83822.762
Table 5. Factors and levels of the two orthogonal experimental tables.
Table 5. Factors and levels of the two orthogonal experimental tables.
Orthogonal Test Table
Number		LevelInfluencing Factor (A)
Axial Pressure/MPa		Influencing Factor (B)
Confining Pressure/MPa		Influencing Factor (C)
Gas Pressure/MPa
11330.5
2441
3551.5
4662
21663
2773.5
3884
4994.5
Table 6. Permeability test results and order of various influencing factors based on orthogonal experimental Table 1.
Table 6. Permeability test results and order of various influencing factors based on orthogonal experimental Table 1.
Influencing Factor (A)
Axial Pressure/MPa		Influencing Factor (B)
Confining Pressure/MPa		Influencing Factor (C)
Gas Pressure/MPa		Permeability/md
1330.50.7388
2440.50.5873
3550.50.2674
4660.50.1917
53410.343
64310.4843
75610.2264
86510.255
9351.50.2701
10461.50.2204
11531.50.3126
12641.50.4803
133620.2272
144520.2696
155420.366
166320.6602
k10.3947750.5489750.4463
k20.39040.444150.327175
k30.29310.2655250.32085
k40.39680.2164250.38075
Extreme value (R)0.10370.332550.12545
Ranking of influencing factorsConfining pressure > Gas pressure > Axial pressure
Table 7. Permeability test results and order of various influencing factors based on orthogonal experimental Table 2.
Table 7. Permeability test results and order of various influencing factors based on orthogonal experimental Table 2.
Influencing Factor (A)
Axial Pressure/MPa		Influencing Factor (B)
Confining Pressure/MPa		Influencing Factor (C)
Gas Pressure/MPa		Permeability/md
16630.2081
27730.1766
38830.1443
49930.1093
5673.50.1533
6763.50.195
7893.50.1135
8983.50.1252
96840.1346
107940.1171
118640.2013
129740.1587
13694.50.1206
14784.50.1376
15874.50.1651
16964.50.2212
k10.61660.82560.159575
k20.62630.65370.14675
k30.62420.54170.152925
k40.61440.46050.161125
Extreme value (R)0.01190.36510.014375
Ranking of influencing factorsConfining pressure > Gas pressure > Axial pressure
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Li, B.; Yuan, Y.; Liang, Y.; Qin, Z. Influences of Different Factors and Sensitivity Analysis of Permeability of Gassy Coal. Appl. Sci. 2025, 15, 808. https://doi.org/10.3390/app15020808

AMA Style

Li B, Yuan Y, Liang Y, Qin Z. Influences of Different Factors and Sensitivity Analysis of Permeability of Gassy Coal. Applied Sciences. 2025; 15(2):808. https://doi.org/10.3390/app15020808

Chicago/Turabian Style

Li, Bo, Yong Yuan, Yunpei Liang, and Zhenghan Qin. 2025. "Influences of Different Factors and Sensitivity Analysis of Permeability of Gassy Coal" Applied Sciences 15, no. 2: 808. https://doi.org/10.3390/app15020808

APA Style

Li, B., Yuan, Y., Liang, Y., & Qin, Z. (2025). Influences of Different Factors and Sensitivity Analysis of Permeability of Gassy Coal. Applied Sciences, 15(2), 808. https://doi.org/10.3390/app15020808

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop