Abstract
This paper introduces shadow filters that employ multiple-input operational transconductance amplifiers (MI-OTAs) as the active component. Two configurations of shadow filters are proposed. The first configuration, in contrast to previous designs, enables the adjustment of the quality factor without affecting the passband gains of the BPF, LPF, and HPF, thus achieving optimal frequency responses for these filters. The second configuration allows for the variation of the natural frequency without impacting the passband gains of the HPF, LPF, and BPF, maintaining constant passband gains. Moreover, the natural frequency can be electronically controlled by modifying parameters of the original biquad filters, providing advantages in compensating for process, voltage, and temperature variations. The MI-OTA is designed to provide multiple-input differential terminals using the multiple-input bulk-driven MOS transistor (MIBD-MOST) technique, allowing differential input signals to be converted into current output through its transconductance gain. The OTA operates at a supply voltage of 450 mV and consumes 81 nW of power, with the MOS transistors operating in weak inversion. The OTA and shadow filters were designed and simulated using a 0.18 µm CMOS process to validate the functionality and performance of the proposed circuits.
1. Introduction
Universal filters typically provide second-order transfer functions for low-pass filters (LPFs), high-pass filters (HPFs), band-pass filters (BPFs), band-stop filters (BSFs), and all-pass filters (APFs), all within the same topology under suitable conditions. Filters that allow for the electronic and orthogonal control of both the natural frequency and the quality factor are particularly desirable, as they enable the desired natural frequency and quality factor to be achieved without the need to redesign the passive components. The natural frequency and quality factor of universal filters are typically adjustable through internal parameters such as resistors, capacitors, and transconductances [1,2,3,4,5]. However, adjusting these internal parameters can also alter the performance of the filters, affecting factors like dynamic range, operating frequency, and power consumption.
Shadow filters, also known as frequency-agile filters, are techniques that use external amplifiers to adjust the natural frequency and quality factor of conventional universal filters. Two primary techniques for shadow filters have been described in the literature [6,7]. The first shadow filter concept, presented in [6], involves a second-order filter with low-pass filter (LPF) and band-pass filter (BPF) outputs, along with an external amplifier. The output signals from the LPF and BPF are summed, and this summed output is amplified by an external amplifier before being fed back to the input of the original second-order filter. By adjusting the gain of the amplifier, the quality factor of the LPF and BPF can be modified. However, this method only allows for the adjustment of the quality factor, without providing control over the natural frequency. To address this limitation, the shadow filter concept was further developed in [7] to allow for the modification of both the natural frequency and the quality factor using external amplifiers. In this second approach, the second-order filter includes LPF, high-pass filter (HPF), and BPF outputs, and it utilizes two external amplifiers. The BPF output is amplified by the first external amplifier, while the LPF output is amplified by the second external amplifier. These two amplified output signals are then fed back to the input of the original second-order filter, enabling control over both the natural frequency and the quality factor.
Numerous shadow filters have been proposed in the literature, utilizing the concepts from [6,7] to implement these filters using various active elements [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. For example, the shadow filter in [8] employs second-generation current conveyors, while the shadow filters in [9,10,11] make use of current-feedback operational amplifiers. Additionally, the shadow filter in [12] uses operational transresistance amplifiers, and the one in [13] uses operational floating current conveyors. However, in the case of shadow filters using these active devices [8,9,10,11,12,13], the natural frequency of the original second-order filters cannot be electronically controlled. The ability to electronically tune the natural frequency of the original second-order filters in shadow filters offers significant advantages, such as compensating for variations in the natural frequency due to temperature and process changes. This electronic tuning capability enhances the robustness and stability of the filter’s performance across varying temperature and process conditions.
Numerous shadow filters with electronic tuning capabilities have been proposed in the literature [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. For example, the shadow filters presented in [14,15,16,17] are designed to deliver high-quality-factor (high-Q) band-pass filters (BPFs). Those in [18,19,20,21,22,23,24] provide low-pass filters (LPFs) and band-pass filters (BPFs) based on the foundational principles outlined in [6], while the designs in [25,26] extend the concept to include LPFs, BPFs, and high-pass filters (HPFs) using the approach described in [7]. Additionally, the current-mode shadow filters in [27,28,29,30,31,32] support LPFs, BPFs, HPFs, band-stop filters (BSFs), and all-pass filters (APFs) within the same topology.
Shadow filters can be categorized into three main types. The first category consists of filters that adjust the natural frequency using an amplifier [14,15,16,17,18,19,20,21,22,23,24]. However, altering the natural frequency in this approach also impacts the quality factor. The second category includes filters that modify the quality factor via an amplifier [25,26]. In this case, adjusting the quality factor results in an increase or decrease in the passband gains of the LPF and HPF, depending on whether positive or negative feedback is applied. Consequently, only the BPF maintains a standard form. The third category comprises filters capable of varying both the natural frequency and the quality factor through amplifiers [25,26,27,28,29,30,31,32]. However, changing the natural frequency in these filters affects both the quality factor and the passband gain. Fortunately, the quality factor can be adjusted to remain constant while varying the natural frequency. However, the passband gain cannot be maintained at unity; it will either increase or decrease depending on the feedback connections.
To address these limitations, shadow filters with a constant passband gain are proposed in this work. Two types of shadow filters are introduced. The first shadow filter allows the quality factor to be adjusted without affecting the passband gains of the BPF, LPF, and HPF when the input signals are appropriately applied. Consequently, the frequency responses of this shadow filter maintain the standard forms of BPF, LPF, and HPF. The second shadow filter enables the natural frequency to be adjusted without influencing the passband gains of the HPF, BPF, and LPF under proper input signal conditions. Both the natural frequency and the quality factor of the second-order shadow filter can be independently and electronically controlled. These proposed shadow filters are proposed using multiple-input operational transconductance amplifiers (MI-OTAs). The use of MI-OTAs allows for the realization of multiple filtering responses and the incorporation of external amplifiers, as demonstrated in this study.
2. Proposed Circuit
2.1. MI-OTA
The electrical symbol of the MI-OTA is presented in Figure 1. The general expression for the output current of the OTA can be written as a sum of three differential input voltages multiplied by a circuit transconductance :
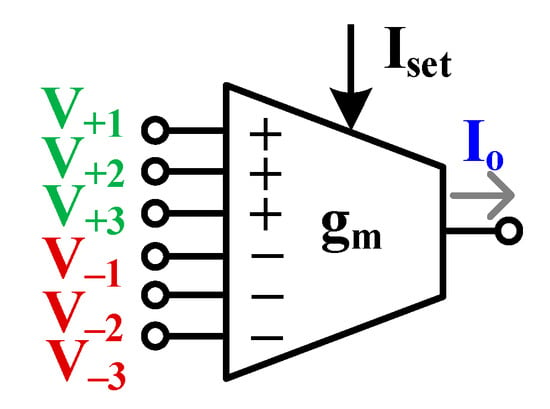
Figure 1.
Electrical symbol of MI-OTA.
The CMOS circuit schematic of the MI-OTA is presented in Figure 2a. This CMOS structure is a modified version of the two-input, one-output MI-OTA, which was first experimentally verified in [33]. In the proposed MI-OTA, an additional input voltage was incorporated to facilitate filter applications. This modification, which increases the number of inputs, resulted in a simplified filter topology and a reduction in the number of OTAs required.
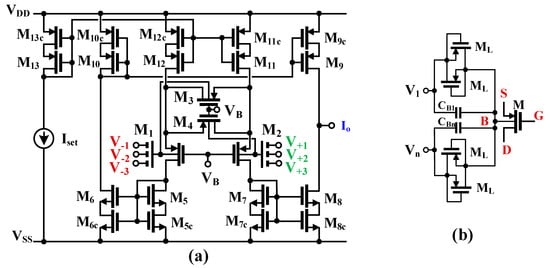
Figure 2.
Proposed MI-OTA, (a) CMOS implementation, (b) MIBD MOST technique.
The design features a linearized bulk-driven (BD) input stage (M1–M4) coupled with a set of current mirrors (M5–M12) configured in a current mirror topology with a single output. The linearization technique employed relies on the principle of source degeneration, wherein transistors M3 and M4 operate in the triode region and are regulated by input signals. This approach enhances linearity and improves immunity to common-mode signals. The underlying concept was initially introduced for conventional gate-driven (GD) circuits operating in the strong inversion region [34]. In this design, a similar topology is adapted for bulk-driven (BD) devices operating in the weak inversion region, which aligns with the extremely low bias currents required for ultra-low-power applications. Additionally, the input transistors M1 and M2 were replaced with multiple-input devices. These devices were formed by conventional BD transistors enhanced with capacitive voltage divider/summing circuits connected to their bulk terminals, as depicted in Figure 2b. This approach, referred to as the MI-BD-MOS technique [35], streamlines the multiple-input structure and reduces overall power dissipation.
The summing circuits comprise capacitors CBi in parallel with large resistances RL, implemented using anti-parallel connections of transistors ML operating in the cutoff region with VGS = 0. For the frequency range of interest (ω >> 1/CBRL), the summing coefficients are determined solely by the capacitor values. The large resistances RL ensure the proper DC biasing of the bulk terminals of M1 and M2. Notably, the application of the BD technique not only extends the OTA’s common-mode range but also enhances its linear range. To enhance the DC voltage gain without restricting the output swing of the OTA, the current mirror transistors are implemented as composite devices using a self-cascode (SC) configuration. In this design, the transistors Mic (i = 5–13) operate in the triode region, functioning as source-degenerative resistors for their counterparts Mi. This configuration effectively increases the output resistance of the device, contributing to improved overall voltage gain while maintaining adequate output swing capabilities.
The quasi-static I–V transfer characteristics of the OTA, corresponding to the i-th input, can be expressed for unity-gain current mirrors and under the condition ω >> 1/CBRL as follows [33]:
where
- at the operating point;
- is the subthreshold slope factor for p-channel transistors;
- is the thermal potential;
- = (W3,4/L3,4)/(W1,2/L1,2) is the relative aspect ratio of the two matched transistor pairs M3,4 − M1,2;
- is the AC voltage gain of the input capacitive divider.
The ideal value of , assuming no parasitic capacitance effects, is given by the following:
For = 3, as in the given example, and assuming identical capacitances , .
To achieve optimal linearity, the coefficient m should equal 0.5 regardless of the biasing current Iset [33].
The small-signal transconductance is expressed as follows:
Its value is times smaller compared to that of its single-input GD counterpart. This reduction arises due to the following:
- The input capacitive divider (), which attenuates the input signal.
- The control of transistors M1 and M2 through their bulk terminals, in which the bulk transconductance is inherently of the gate transconductance.
The transconductance is proportional to the biasing current Iset, allowing straightforward electronic tuning by adjusting Iset. It is important to note that signal attenuation at the input stage increases the input-referred noise of the circuit by a factor of . This is due to the lower transconductance, which results from the combination of an input capacitive divider and the bulk-driven (BD) technique. However, since the linear range also increases by the same proportion, the dynamic range (DR) remains unchanged compared to the single-input gain-differential (GD) counterpart [33]. A detailed analysis of the noise performance of the MI-OTA is provided in [33].
It is worth pointing out, that, as long as the circuit operates in weak inversion, i.e., its transfer characteristic is described by (2), the linear range does not depend on Iset and transistors aspect ratios, provided that m = 0.5 = const., which ensures optimal linearity. On the other hand, provided that the transistor channel areas are sufficiently large, the dominant source of noise in the considered frequency range is thermal noise. For constant m, which is required for optimum linearity, assuming, for simplicity, identical slope factors for n- and p-channel transistors, np = nn = n, the input referred noise of the circuit can be expressed as follows:
where C is a constant and q is the electron charge and Δf is the noise bandwidth. Consequently, the DR can be expressed in the following form:
where Vinm is the rms value of the input differential signal for the assumed nonlinear distortion, which, with m = 0.5, depends on the number of inputs but does not depend on the biasing currents and transistor aspect ratios. As can be concluded from (6), with the above assumptions, the DR is proportional to the square root of the biasing current Iset. However, since the specific value of Iset results from the required transconductance value, one can conclude that, for the given number of inputs and assumed transconductance, the DR of the circuit is constant and does not depend on other design parameters.
The differential low-frequency voltage gain of the OTA can be approximated as follows:
where rout is the output resistance of the OTA, given by the following:
Note that this gain is also reduced by the input divider, which lowers the circuit’s transconductance. However, the self-cascode composite transistors boost the output resistance and consequently the voltage gain to an acceptable level, sufficient for the intended application, without compromising the OTA’s output voltage swing.
2.2. Proposed First Shadow Filters
Referring to the block diagram of the shadow filter in Figure 3a [7], the outputs of the HPF and LPF are summed and amplified by amplifier A. The resulting amplified output is then summed with the input . In this shadow filter, the gain of amplifier A controls the quality factor () of the filter. However, adjusting the quality factor can influence the passband gain of both the HPF and LPF, either increasing or decreasing it [8,25,31]. To address this, the shadow filter in Figure 3a [7] has been modified to maintain a constant passband gain for the HPF and LPF even as the quality factor is varied through the amplifier gain. The updated block diagram of the shadow filter is shown in Figure 3b. To keep the passband gain constant, a negative amplifier () and an additional input, , are introduced. If a band-pass filter (BPF) is needed, can be connected to ground. For the HPF and LPF configurations, both and can be driven by the same input signal ( = = ).
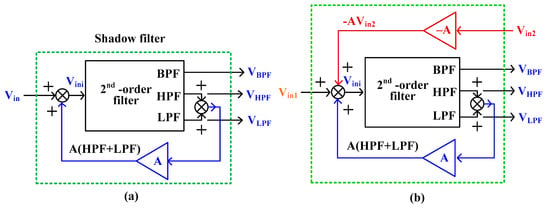
Figure 3.
Block diagram of (a) first shadow filter and (b) shadow filter with improved passband gain.
Figure 4 illustrates the proposed first shadow filter using MI-OTAs. The circuit consists of four MI-OTAs, two grounded capacitors, and one grounded resistor. Compared to Figure 3b, the components and function as amplifiers and , with their roles slightly interchanged to facilitate easier control of the quality factor, i.e., .
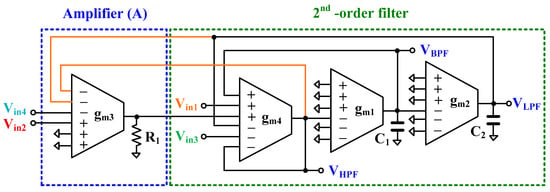
Figure 4.
Proposed first shadow filter using MI-OTAs.
Thanks to the multiple inputs of the OTA, various filter functions can be easily realized. By connecting and to ground and using Equation (1) along with nodal analysis, the output voltage of the band-pass filter (BPF) can be expressed as follows:
If is driven by the input signal, an inverting BPF is obtained, whereas applying the input signal to produces a non-inverting BPF.
Using Equation (1) and applying nodal analysis, the output voltage of the LPF can be expressed as follows:
If and are simultaneously driven by input signals while and are grounded, a non-inverting LPF is obtained. Conversely, if and are applied with input signals while and are grounded, an inverting LPF is achieved.
Using Equation (1) and nodal analysis, the output voltage of the HPF can be expressed as follows:
For a non-inverting HPF, and are applied with input signals together, while and are grounded. For an inverting HPF, and are applied with input signals while and are grounded.
It should be noted that the shadow filter in Figure 4 allows the quality factors of the BPF, LPF, and HPF to be adjusted without affecting the passband gain of their transfer functions. Additionally, both non-inverting and inverting configurations of the BPF, LPF, and HPF can be achieved under appropriate conditions, facilitated by the MI-OTA-based circuit. Any unused input terminals can be connected to ground.
If a band-stop filter (BSF) is required, it can be realized by summing and . Similarly, an all-pass filter (APF) can be achieved by summing , and . In both cases, an additional summing amplifier is necessary, which can be implemented using an MI-OTA in a negative feedback configuration similar to .
The natural frequency () and the quality factor () of filters are expressed as follows:
It can be observed that the quality factor can be controlled via . According to Equation (4), , , and can be individually controlled via the bias currents , , and corresponding to their respective ( = 1, 2, 3). For independent control of the parameters and , capacitors and can be fixed. The parameter can be controlled by (where ), while the parameter can be independently adjusted via or . However, varying using may impact the stability, power consumption, and dynamic range of the original second-order filter. Therefore, the primary purpose of the first shadow filter is to control only the parameter via an external amplifier. If independent control of both and is required, this can be achieved using the second proposed shadow filter. In this case, varying both are will only affect the power consumption of the filter.
Equations (9)–(11) demonstrate that varying the filter response’s quality factor by a factor of also scales their transfer functions by the same factor. This adjustment enables the achievement of a unity passband gain. Unlike previous shadow filters (e.g., [8,15,16,17,20,21,23,25,26,29,31,32]), in which variations in the quality factor resulted in changes to the passband gain of the transfer function, the proposed design maintains a consistent passband gain despite such variations.
2.3. Proposed Second Shadow Filters
The shadow filter depicted in Figure 4 employs an external amplifier solely to adjust the quality factor. As illustrated in the block diagram of the shadow filter in Figure 5a [7], the output signals BPF and LPF are amplified by amplifiers A1 and A2, respectively, and then combined with the input signal. This design enables independent control of the quality factor and natural frequency using A1 and A2. However, modifying the natural frequency can influence the passband gain of both the BPF and LPF, potentially causing it to either increase or decrease [8,25,26,31,32]. To address this issue, the updated block diagram of the shadow filter, shown in Figure 5b, introduces A1 and A2, and additional inputs and to stabilize the passband gain. For an HPF configuration, the input signal is applied to , with and grounded. In contrast, for the BPF and LPF configurations, and can be driven by the same input signal under appropriate conditions.
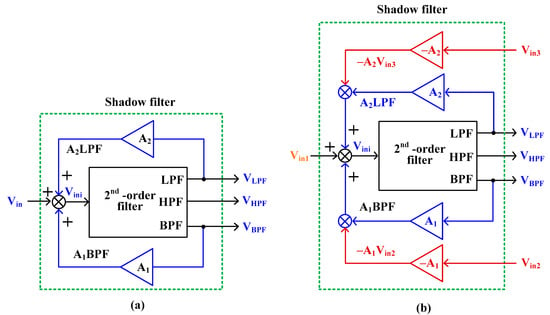
Figure 5.
Block diagram of (a) second shadow filter in [2] and (b) shadow filter with improved passband gain.
Figure 6 presents the proposed second shadow filter using MI-OTAs. The circuit comprises five MI-OTAs, two grounded capacitors, and one grounded resistor. Leveraging the multiple-input capability of the OTAs, this design facilitates the straightforward implementation of various filter functions. By grounding and and applying Equation (1) with nodal analysis, the output voltage of the HPF can be expressed as follows:
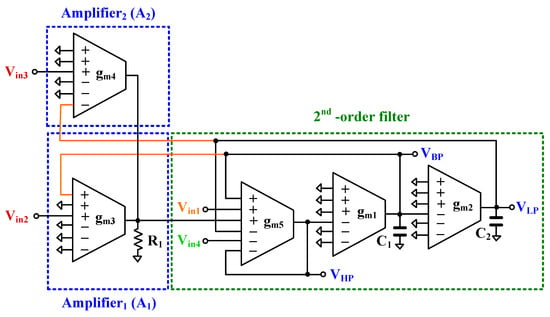
Figure 6.
Proposed second shadow filter using MI-OTAs.
If is the input signal, a non-inverting HPF is obtained. Alternatively, applying the input signal to results in a non-inverting BPF.
Case 1.
When is grounded and
is connected to either
or , nodal analysis gives the BPF output voltage as follows:
If is the input signal (with also connected to ), an inverting BPF is obtained with grounded. Conversely, if is the input signal (with also connected to and grounded), a non-inverting BPF is achieved. In this configuration, the BPF gain remains constant when the natural frequency is adjusted by amplifier .
Case 2.
When
is grounded and
is connected to either
or
, the BPF output voltage is as follows:
The conditions for obtaining a BPF in this case are similar to those for Case 1, except that
is connected to either
or
. Here, the BPF gain remains constant when the quality factor is adjusted using amplifier
, while
is fixed.
By grounding
and connecting
to either
or
, the LPF output voltage is expressed as follows:
If is the input signal (with also connected to ), a non-inverting LPF is obtained, with grounded. Conversely, if is the input signal (with also connected to and grounded), an inverting LPF is realized.
The parameters and of filters are given, respectively, by the following:
These equations highlight how can be adjusted using , while depends on .
Equations (14)–(17) reveal that, when the natural frequency of the filter responses is adjusted by a factor of , this modification directly impacts their transfer functions. Consequently, unity passband gains can be realized. This behavior contrasts with that of the earlier shadow filters (e.g., [8,25,26,31,32]), in which changes in the natural frequency result in variations in the passband gain.
2.4. Non-Ideal Analysis
The non-ideal transconductance of the MI-OTA at a frequency near its cutoff can be expressed as follows [36]:
where and represents the first pole frequency of .
Considering the non-idealities in (20) for and (while neglecting and ), the non-idealities can be approximated as and , and the denominator of transfer functions (6)–(8) can be then written as follows:
The denominator of transfer functions (14)–(17) can be written as follows:
From Equations (21) and (22), the non-ideal effects of the transconductances and can be mitigated by satisfying the following conditions:
These conditions can be achieved by appropriately selecting the values of , and capacitances , to create large time constants, which are significantly greater than the small time constants associated with non-ideal effects.
3. Simulation Results
The proposed CMOS circuit and filter applications were designed and simulated using the Cadence Virtuoso Design Environment, utilizing TSMC’s 0.18 µm CMOS technology. The circuit is capable of operating with either a single supply voltage of 450 mV or dual supply voltages of ±225 mV, as utilized in the presented simulations. The transistor aspect ratios are detailed in Table 1. Notably, relatively long channel lengths (L = 1 µm) were selected for the devices to achieve both higher voltage gain and larger device areas, which help mitigate flicker noise and mismatch effects. The channel widths of M1, M2, and Mic (i = 5–13) were determined during the simulation phase to provide quiescent VGS voltages of the above transistors equal to around VDD/3, which provides the maximum headroom for possible PVT variations and signal swing. The aspect ratios of M3 and M4 were half of the ones for M1 and M2, which provides m = 0.5, required for optimal linearity. The channel widths of Mi were twice as large as those for Mic, which provided VDS of Mic equal to around 25 mV—a good compromise between voltage gain and signal swing of the OTA. The input metal–insulator–metal (MIM) capacitor CBi was set to 0.5 pF, and the bias voltage VB = −50 mV. It is important to note that the simulation and experimental results for the MI-OTA with two inputs are provided in [33]. Consequently, this section focuses on the simulation results for filter applications.

Table 1.
Transistor aspect ratios of the proposed MI-OTA.
For the first shadow filter, with C1,2 = 18 pF, R1 = 5 MΩ, Iset3 = 12 nA, and Iset1,2,4 = 6 nA, the frequency responses of the LPF, BPF, and BPF are illustrated in Figure 7. The cutoff frequency was determined to be 106 Hz, with a total power consumption of 81 nW. Figure 8 depicts the frequency responses of the first shadow filter with a constant Iset3 = 12 nA and varying Iset = Iset1,2,4 = [1.5, 3, 6, 12, 24, 48] nA. The corresponding cutoff frequencies were [26.6, 53, 106, 199.5, 398.1, 708] Hz, respectively. This figure validates the filter’s tunable natural frequency, as described in Equation (9). With a frequency range spanning from subhertz to 10 kHz, the proposed filter is suitable for bio-signal processing applications. This work introduces a universal filter that integrates low-pass (LPF), high-pass (HPF), and band-pass (BPF) functionalities within a single topology. The specific application depends on the user’s requirements. For instance, a low-pass filter can be utilized to remove interference noise, while a band-pass filter can be employed to isolate the desired frequency range.
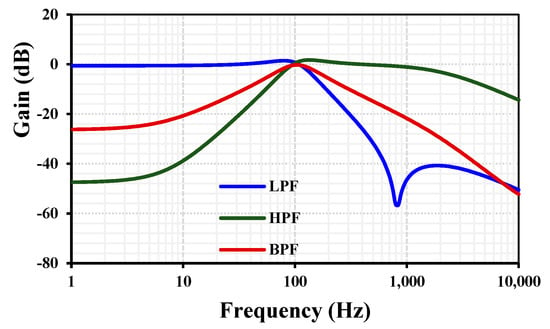
Figure 7.
Frequency responses of the first shadow filter with Iset3 = 12 nA and Iset1,2,4 = 6 nA.
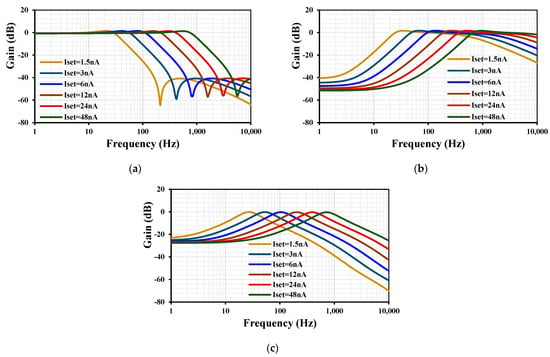
Figure 8.
Frequency responses of the first shadow filter with varying Iset = Iset1,2,4 for (a) LPF, (b) HPF, and (c) BPF.
Figure 9 presents the frequency responses of the first shadow filter with R1 = 5 MΩ, a constant Iset1,2,4 = 6 nA, and varying Iset = Iset3 = [1.5, 3, 6, 12, 24, 48] nA. This figure demonstrates the tunability of the filter’s quality factor Q, as described in Equation (10).
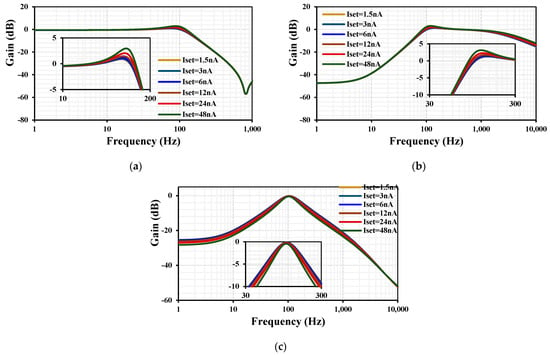
Figure 9.
Frequency responses of the first shadow filter with varying Iset = Iset3 for (a) LPF, (b) HPF, and (c) BPF.
The filter can achieve broader tunability of the quality factor Q, if required, by adjusting R1, as demonstrated in Figure 10. For this analysis, Iset1,2,4 = 6 nA, Iset3 = 48 nA, and various R1 = [2.5, 5, 10, 20] MΩ were used.
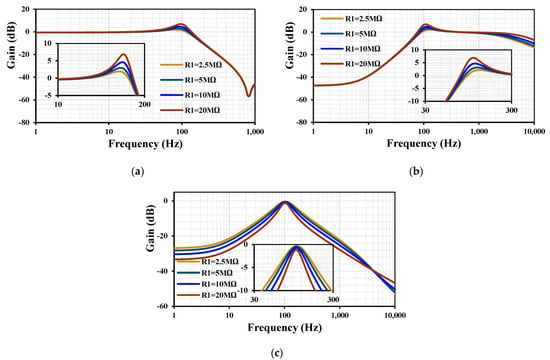
Figure 10.
Frequency responses of the first shadow filter with various R1 for (a) LPF, (b) HPF, and (c) BPF.
Figure 11, showing the frequency responses of the first shadow filter with C1,2 = 18 pF, R1 = 5 MΩ, Iset3 = 12 nA, and Iset1,2,4 = 6 nA, was repeated using Monte Carlo (MC) analysis, which included mismatch and process variations over 200 runs. As shown in Figure 11, the filter circuit exhibited an acceptable variation across these runs.
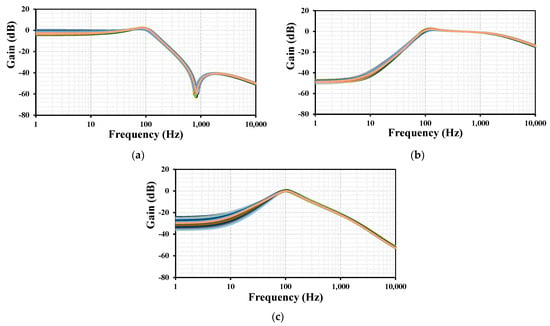
Figure 11.
Frequency responses of the first shadow filter with MC for (a) LPF, (b) HPF, and (c) BPF.
Figure 12 was also repeated using process, voltage, and temperature (PVT) analysis, which included the following conditions: fast–fast, slow–fast, fast–slow, and slow–slow transistor process corners, ±10% variations in supply voltage, and temperature corners of –10 °C and 60 °C. As shown in Figure 12, the filter circuit again demonstrated an acceptable variation across these PVT corners.
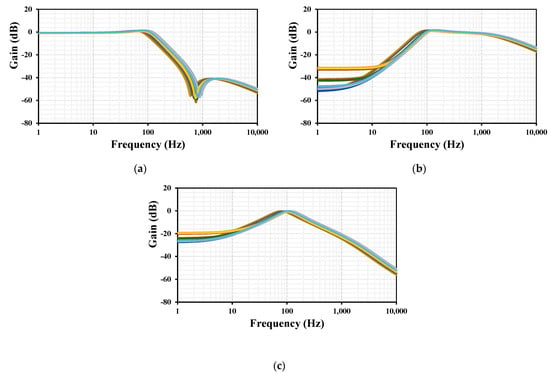
Figure 12.
Frequency responses of the first shadow filter with PVT for (a) LPF, (b) HPF, and (c) BPF.
The transient performance of the LPF in the first shadow filter, configured as depicted in Figure 13, was evaluated. As shown in Figure 13a, the input signal featured a 300 mV peak-to-peak amplitude at a frequency of 10 Hz. The results show that the input and output waveforms closely overlapped, with a total harmonic distortion (THD) of 1.8%. Figure 12b illustrates the relationship between the THD and the peak-to-peak amplitude of the input signal at 10 Hz. Notably, the circuit maintained a THD of 1% for a 200 mV peak-to-peak input, despite operating at a low supply voltage of 450 mV.
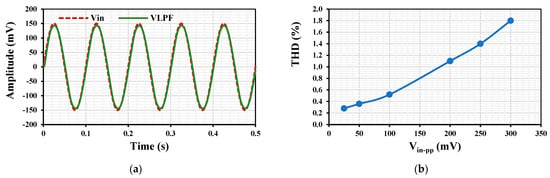
Figure 13.
(a) Transient response of the LPF in the first shadow filter and (b) the THD.
Figure 14 presents the frequency response of the output noise for the LPF in the first shadow filter. The integrated noise within the frequency range of 1 Hz to 106 Hz was determined to be 264 µV, yielding a dynamic range (DR) of 54.5 dB for 1% THD.
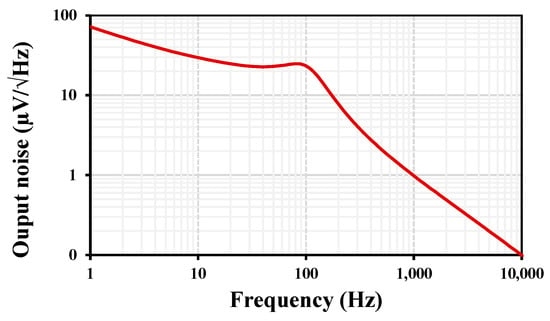
Figure 14.
Frequency response of the output noise for the LPF in the first shadow filter.
Figure 15 presents the frequency responses of the second first shadow filter with C1,2 = 18 pF, R1 = 20 MΩ, a constant Iset1,2,5 = 6 nA, Iset4 = 12 nA, and varying Iset = Iset3 = [1.5, 3, 6, 12, 24, 48] nA. This figure demonstrates the tunability of the filter’s quality factor Q, as described in Equation (16).
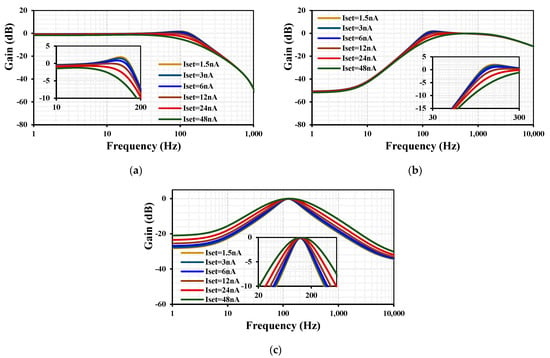
Figure 15.
Frequency responses of the second shadow filter with varying Iset = Iset3 for (a) LPF, (b) HPF, and (c) BPF.
The proposed shadow filter was compared with previously reported shadow filters, as summarized in Table 2. Recent shadow filters from [8,18,25,27,29], which provide voltage-mode transfer functions, were selected for the comparison. It is evident that the proposed shadow filter allows the parameters or to be adjusted without affecting the passband magnitude of the transfer functions. Although the circuit in [27] can compensate for the passband magnitude using amplifiers, the adjustment must be performed manually. This underscores the novel solution provided by the proposed circuit. The shadow filter demonstrated the lowest supply voltage and power consumption among its counterparts, as shown in comparison with [8,18,25,27,29]. Additionally, compared to [8], the proposed circuit offers the added benefit of electronic control.

Table 2.
Comparison of the properties of the proposed shadow filter with those of filters from selected previous works.
4. Conclusions
This paper introduces novel shadow filters based on multiple-input operational transconductance amplifiers (MI-OTAs) and presents two configurations of these shadow filters. In contrast to previous shadow filters, the proposed structure enables independent control of the natural frequency and the quality factor via external amplifiers, without affecting the passband magnitude responses of the filters. The first shadow filter allows the quality factor to be varied without affecting the passband gains, while the second shadow filter enables the natural frequency to be varied without altering the passband gains. In both cases, the passband gains are nearly unity. The proposed shadow filters are implemented using MI-OTAs. The use of multiple inputs in the OTA facilitates the realization of various filter responses both non-inverting and inverting transfer functions and external amplifiers with ease. These multiple inputs are achieved through the multiple-input bulk-driven MOS transistor technique. The simulation results confirm the functionality of the filter, demonstrating its operation under low voltage supply and low power consumption.
Author Contributions
Conceptualization, M.K., F.K. and T.K.; methodology, M.K., F.K. and T.K.; software, M.K. and F.K.; validation, M.K., F.K. and N.W.; formal analysis, M.K. and T.K.; investigation, M.K., F.K. and T.K.; resources, M.K.; data curation, M.K. and F.K.; writing—original draft preparation, M.K., F.K., T.K. and N.W.; writing—review and editing, M.K., F.K., T.K. and N.W.; visualization, M.K. and F.K.; supervision, M.K. and F.K.; project administration, M.K. and F.K.; funding acquisition, M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the University of Defence within the Organization Development Project VAROPS.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, C.; Liu, H.; Zhao, Y. A New Current-Mode Current-Controlled Universal Filter Based on CCCII(±). Circuits Syst. Signal Process. 2008, 27, 673–682. [Google Scholar] [CrossRef]
- Hassan, T.M.; Mahmoud, S.A. Fully Programmable Universal Filter with Independent Gain-ωo-Q Control Based on New Digitally Programmable CMOS CCII. J. Circuits Syst. Comput. 2009, 18, 875–897. [Google Scholar] [CrossRef]
- Prommee, P.; Pattanatadapong, T. Realization of Tunable Pole-Q Current-Mode OTA-C Universal Filter. Circuits Syst. Signal Process. 2010, 29, 913–924. [Google Scholar] [CrossRef]
- Jaikla, W.; Khateb, F.; Kulej, T.; Pitaksuttayaprot, K. Universal Filter Based on Compact CMOS Structure of VDDDA. Sensors 2021, 21, 1683. [Google Scholar] [CrossRef]
- Kumngern, M.; Khateb, F.; Kulej, T.; Knobnob, B. 1 V Tunable High-Quality Universal Filter Using Multiple-Input Operational Transconductance Amplifiers. Sensors 2024, 24, 3013. [Google Scholar] [CrossRef]
- Lakys, Y.; Fabre, A. Shadow Filters: New Family of Second-Order Filters. Electron. Lett. 2010, 46, 276–277. [Google Scholar] [CrossRef]
- Biolkova, V.; Biolek, D. Shadow Filters for Orthogonal Modification of Characteristic Frequency and Bandwidth. Electron. Lett. 2010, 46, 830–831. [Google Scholar] [CrossRef]
- Khateb, F.; Jaikla, W.; Kulej, T.; Kumngern, M.; Kubánek, D. Kubanek. Shadow Filters Based on DDCC. IET Circuits Devices Syst. 2017, 11, 631–637. [Google Scholar] [CrossRef]
- Abuelma’Atti, M.T.; Almutairi, N. New CFOA-Based Shadow Banpass Filter. In Proceedings of the 2016 International Conference on Electronics, Information, and Communications (ICEIC), Danang, Vietnam, 27–30 January 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Abuelma’atti, M.T.; Almutairi, N.R. Almutairi. New Current-Feedback Operational-Amplifier Based Shadow Filters. Analog. Integr. Circuits Signal Process. 2016, 86, 471–480. [Google Scholar] [CrossRef]
- Nako, J.; Psychalinos, C.; Minaei, S. First-Order Universal Shadow Filter Designs with Scaled Time Constants. Int. J. Circuit Theory Appl. 2024, 52, 4040–4053. [Google Scholar] [CrossRef]
- Anurag, R.; Pandey, R.; Pandey, N.; Singh, M.; Jain, M. OTRA Based Shadow Filters. In Proceedings of the 2015 Annual IEEE India Conference (INDICON), New Delhi, India, 17–20 December 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Nand, D.; Pandey, N. New Configuration for OFCC-Based CM SIMO Filter and Its Application as Shadow Filter. Arab. J. Sci. Eng. 2018, 43, 3011–3022. [Google Scholar] [CrossRef]
- Buakaew, S.; Narksarp, W.; Wongtaychatham, C. Fully Active and Minimal Shadow Bandpass Filter. In Proceedings of the 2018 International Conference on Engineering, Applied Sciences, and Technology (ICEAST), Phuket, Thailand, 4–7 July 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Buakaew, S.; Narksarp, W.; Wongtaychatham, C. Shadow Bandpass Filter with Q-Improvement. In Proceedings of the 2019 5th International Conference on Engineering, Applied Sciences and Technology (ICEAST), Luang Prabang, Laos, 2–5 July 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Buakaew, S.; Narksarp, W.; Wongtaychatham, C. High Quality-Factor Shadow Bandpass Filters with Orthogonality to the Characteristic Frequency. In Proceedings of the 2020 17th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Phuket, Thailand, 24–27 June 2020; pp. 372–375. [Google Scholar] [CrossRef]
- Buakaew, S.; Wongtaychatham, C. Boosting the Quality Factor of the Shadow Bandpass Filter. J. Circuits Syst. Comput. 2022, 31, 2250248. [Google Scholar] [CrossRef]
- Moonmuang, P.; Pukkalanun, T.; Tangsrirat, W. Voltage Differencing Gain Amplifier-Based Shadow Filter: A Comparison Study. In Proceedings of the 2020 6th International Conference on Engineering, Applied Sciences and Technology (ICEAST), Chiang Mai, Thailand, 1–4 July 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Varshney, G.; Pandey, N.; Pandey, R. Generalization of Shadow Filters in Fractional Domain. Int. J. Circuit Theory Appl. 2021, 49, 3248–3265. [Google Scholar] [CrossRef]
- Pandey, N.; Pandey, R.; Choudhary, R.; Sayal, A.; Tripathi, M. Realization of CDTA Based Frequency Agile Filter. In Proceedings of the 2013 IEEE International Conference on Signal Processing, Computing and Control (ISPCC), Solan, India, 26–28 September 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Pandey, N.; Sayal, A.; Choudhary, R.; Pandey, R. Design of CDTA and VDTA Based Frequency Agile Filters. Adv. Electron. 2014, 2014, 176243. [Google Scholar] [CrossRef]
- Atasoyu, M.; Kuntman, H.; Metin, B.; Herencsar, N.; Cicekoglu, O. Design of Current-Mode Class 1 Frequency-Agile Filter Employing CDTAs. In Proceedings of the 2015 European Conference on Circuit Theory and Design (ECCTD), Trondheim, Norway, 24–26 August 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Alaybeyoğlu, E.; Kuntman, H. A New Frequency Agile Filter Structure Employing CDTA for Positioning Systems and Secure Communications. Analog. Integr. Circuits Signal Process. 2016, 89, 693–703. [Google Scholar] [CrossRef]
- Chhabra, K.; Singhal, S.; Pandey, N. Realisation of CBTA Based Current Mode Frequency Agile Filter. In Proceedings of the 2019 6th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 7–8 March 2019; pp. 1076–1081. [Google Scholar] [CrossRef]
- Kumngern, M.; Khateb, F.; Kulej, T. Shadow Filters Using Multiple-Input Differential Difference Transconductance Amplifiers. Sensors 2023, 23, 1526. [Google Scholar] [CrossRef]
- Khateb, F.; Kumngern, M.; Kulej, T.; Ranjan, R.K. Ranjan. 0.5 V Multiple-Input Multiple-Output Differential Difference Transconductance Amplifier and Its Applications to Shadow Filter and Oscillator. IEEE Access 2023, 11, 31212–31227. [Google Scholar] [CrossRef]
- Huaihongthong, P.; Chaichana, A.; Suwanjan, P.; Siripongdee, S.; Sunthonkanokpong, W.; Supavarasuwat, P.; Jaikla, W.; Khateb, F. Single-Input Multiple-Output Voltage-Mode Shadow Filter Based on VDDDAs. AEU-Int. J. Electron. Commun. 2019, 103, 13–23. [Google Scholar] [CrossRef]
- Singh, D.; Paul, S.K. Realization of Current Mode Universal Shadow Filter. AEU-Int. J. Electron. Commun. 2020, 117, 153088. [Google Scholar] [CrossRef]
- Singh, D.; Paul, S.K. Mixed-Mode Universal Filter Using FD-CCCTA and Its Extension as Shadow Filter. Inf. MIDEM 2022, 52, 239–262. [Google Scholar] [CrossRef]
- Singh, D.; Paul, S.K. Improved Current Mode Biquadratic Shadow Universal Filter. Inf. MIDEM 2022, 52, 51–66. [Google Scholar] [CrossRef]
- Kumngern, M.; Khateb, F.; Kulej, T.; Kyselak, M.; Lerkvaranyu, S.; Knobnob, B. Current-Mode Shadow Filter with Single-Input Multiple-Output Using Current-Controlled Current Conveyors with Controlled Current Gain. Sensors 2024, 24, 460. [Google Scholar] [CrossRef] [PubMed]
- Kumngern, M.; Khateb, F.; Kulej, T. A Novel Multiple-Input Single-Output Current-Mode Shadow Filter and Shadow Oscillator Using Current-Controlled Current Conveyors. Circuits Syst. Signal Process. 2024, 43, 5438–5462. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Akbari, M.; Tang, K.-T. A 0.5-V multiple-input bulk-driven OTA in 0.18-μm CMOS. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2022, 30, 1739–1747. [Google Scholar] [CrossRef]
- Krummenacher, F.; Joehl, N. A 4-MHz CMOS continuous-time filter with on-chip automatic tuning. IEEE J. Solid-State Circuits 1988, 23, 750–758. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Kumngern, M.; Psychalinos, C. Multiple-input bulk-driven MOS transistor for low-voltage low-frequency applications. Circuits Syst. Signal Process. 2019, 38, 2829–2845. [Google Scholar] [CrossRef]
- Nevárez-Lozano, H.; Sánchez-Sinencio, E. Minimum parasitic effects biquadratic OTA-C filter architectures. Analog. Integr. Circuits Signal Process. 1991, 1, 297–319. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).