Model-Free Speed Control for Pumping Kite Generator Systems Based on Nonlinear Hyperbolic Tangent Tracking Differentiator
Abstract
1. Introduction
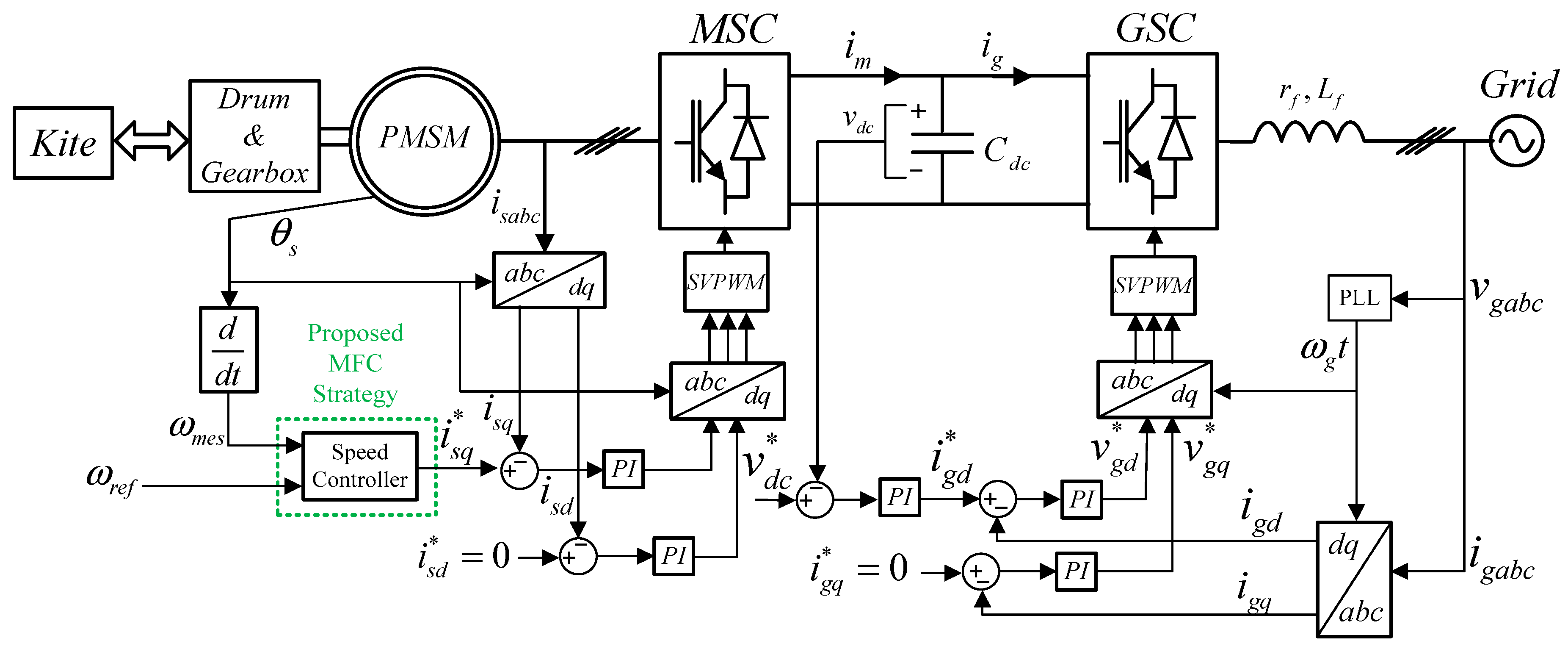
2. Power Kite Generator System Modeling
- Precise tracking of a periodically varying reference speed during power generation phases.
- Ensuring stable transitions between generation and recovery phases.
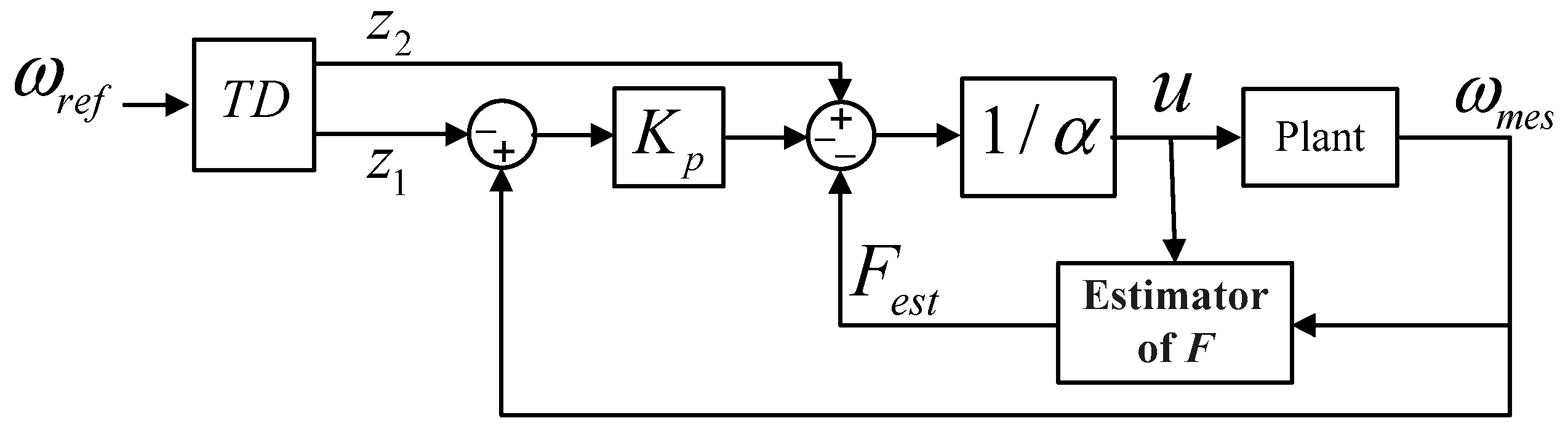
3. Model-Free Control
3.1. Ultra Local Model
3.2. Intelligent Controllers
3.3. Online Estimation of F
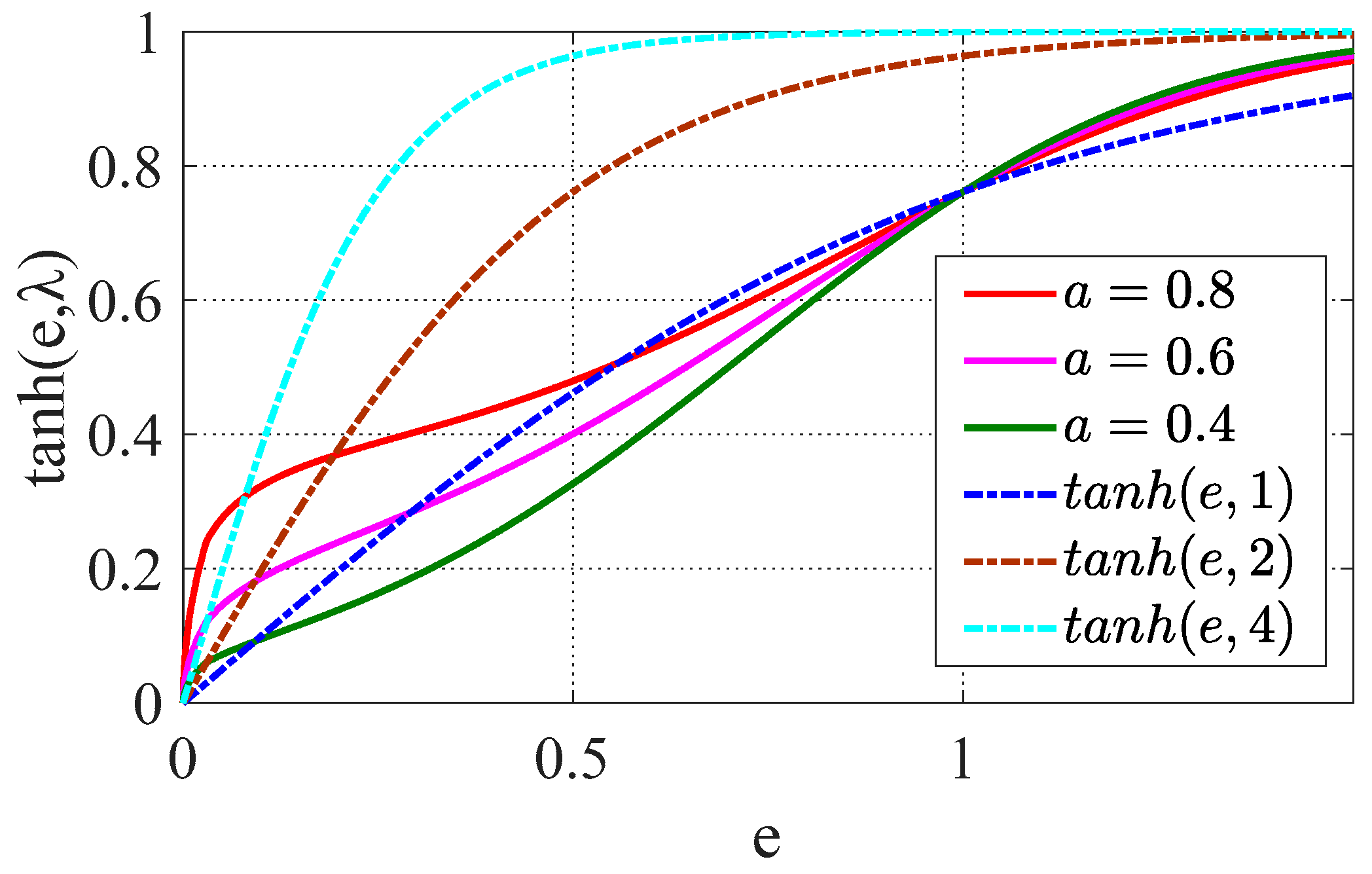
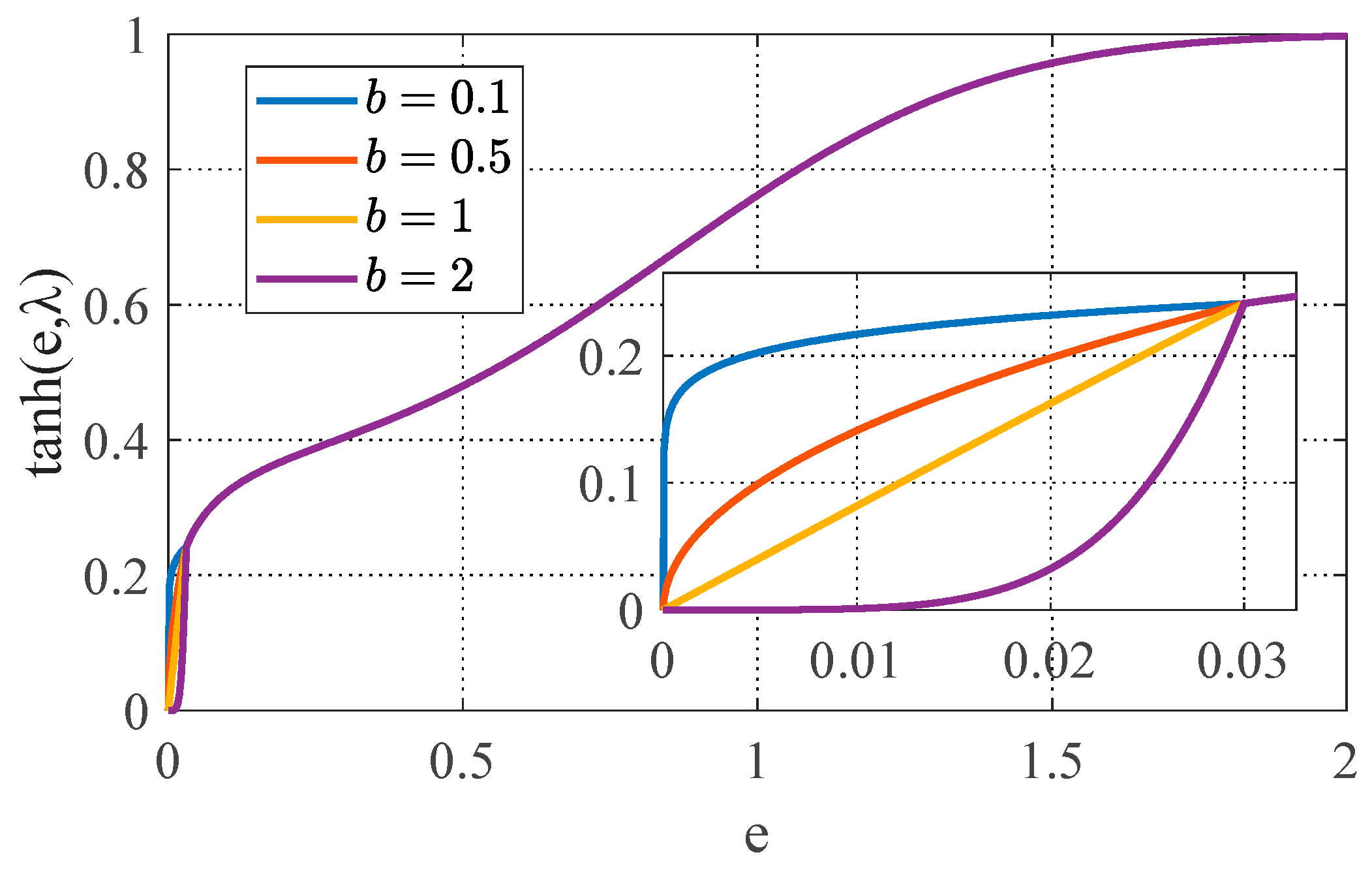
3.4. Tracking Differentiator Design Based on Hyperbolic Tangent Function
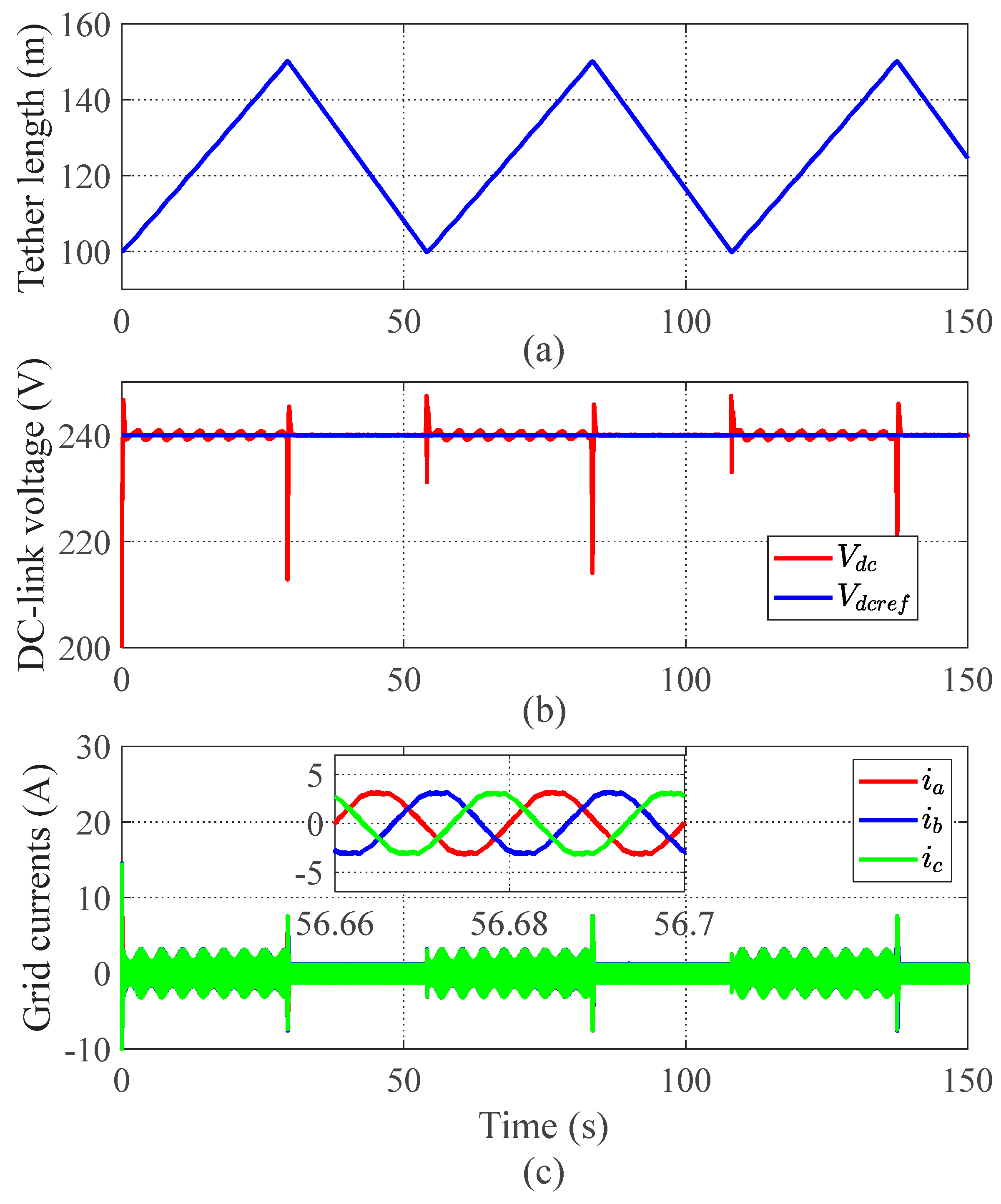
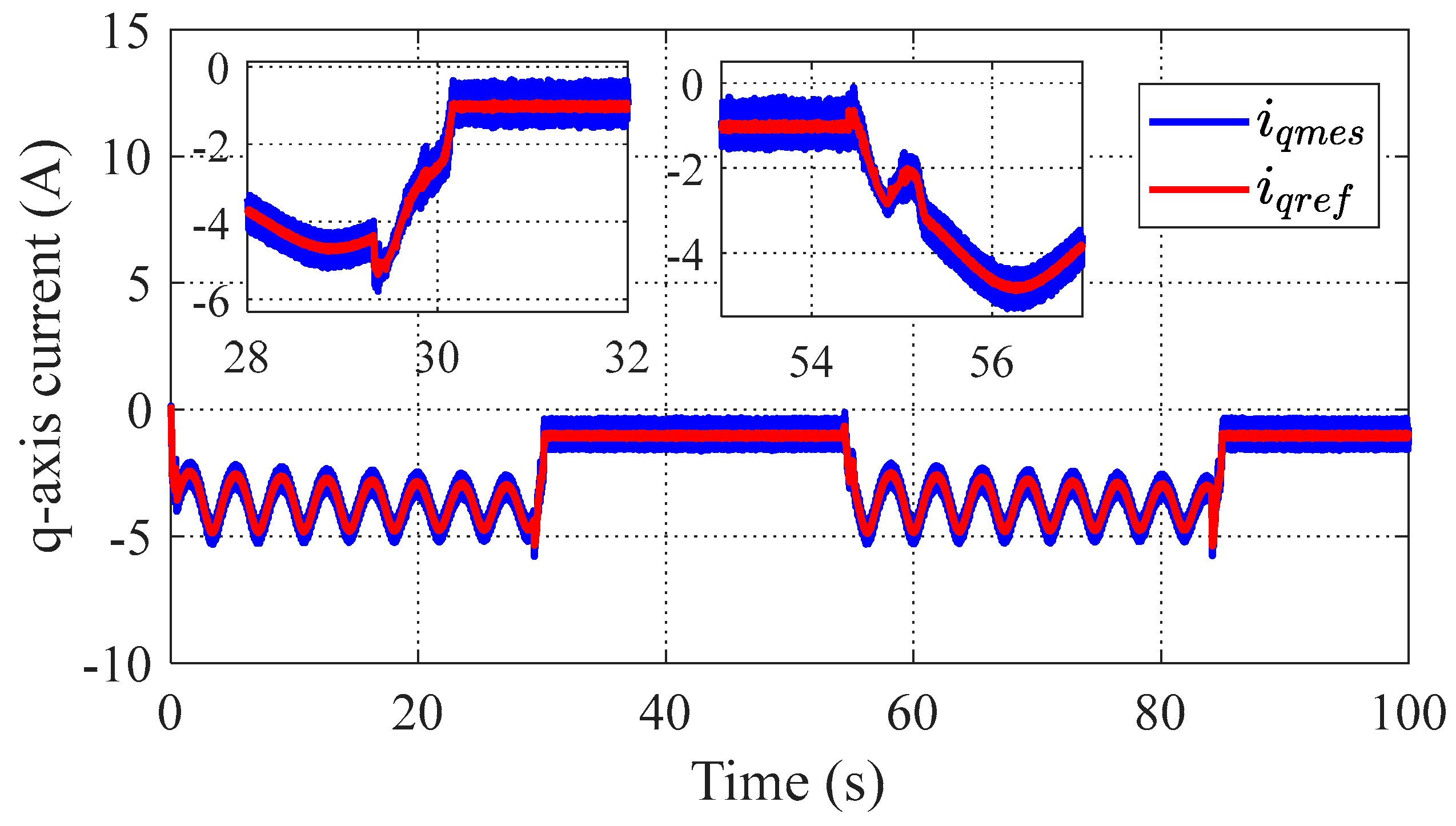
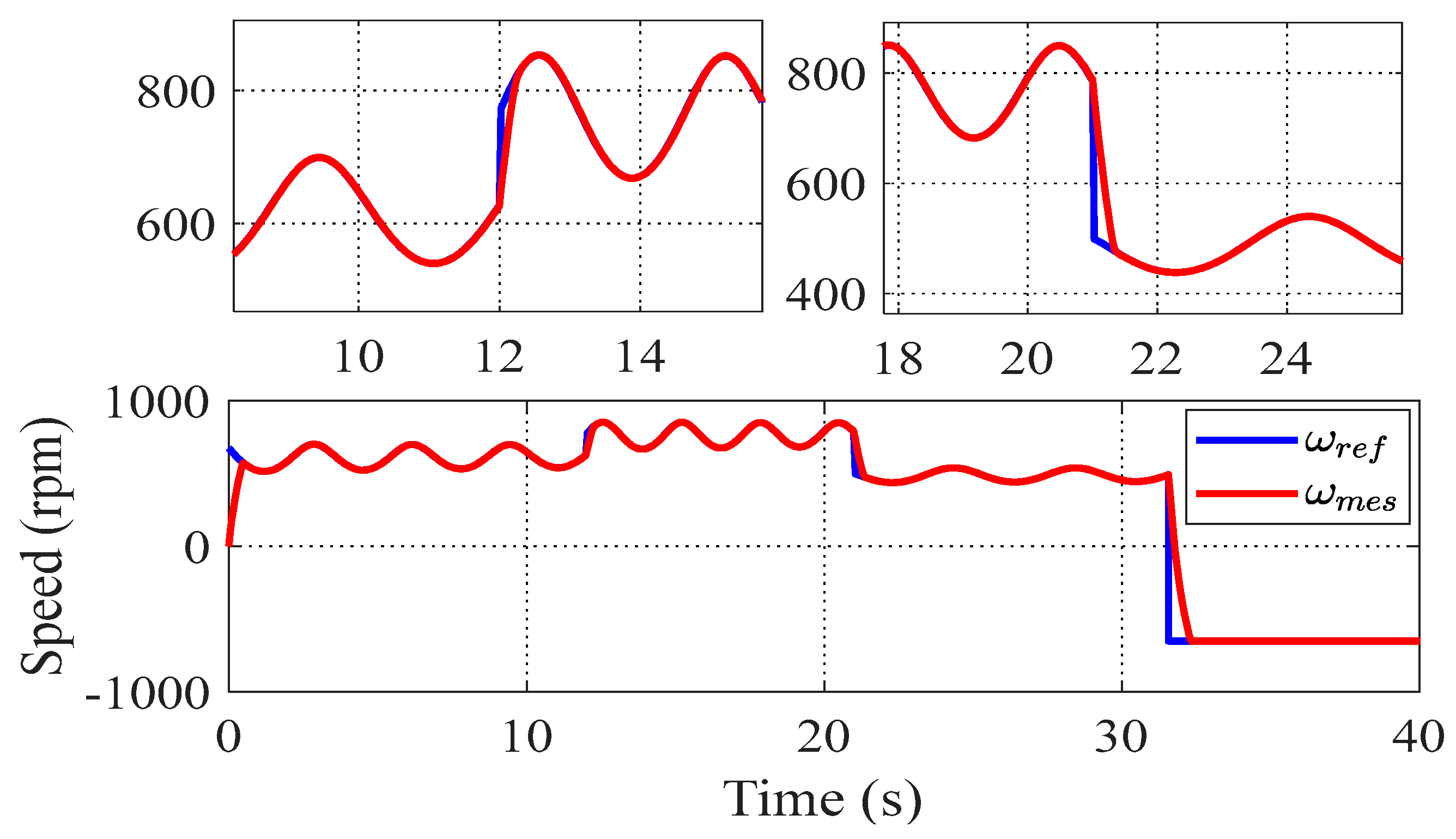
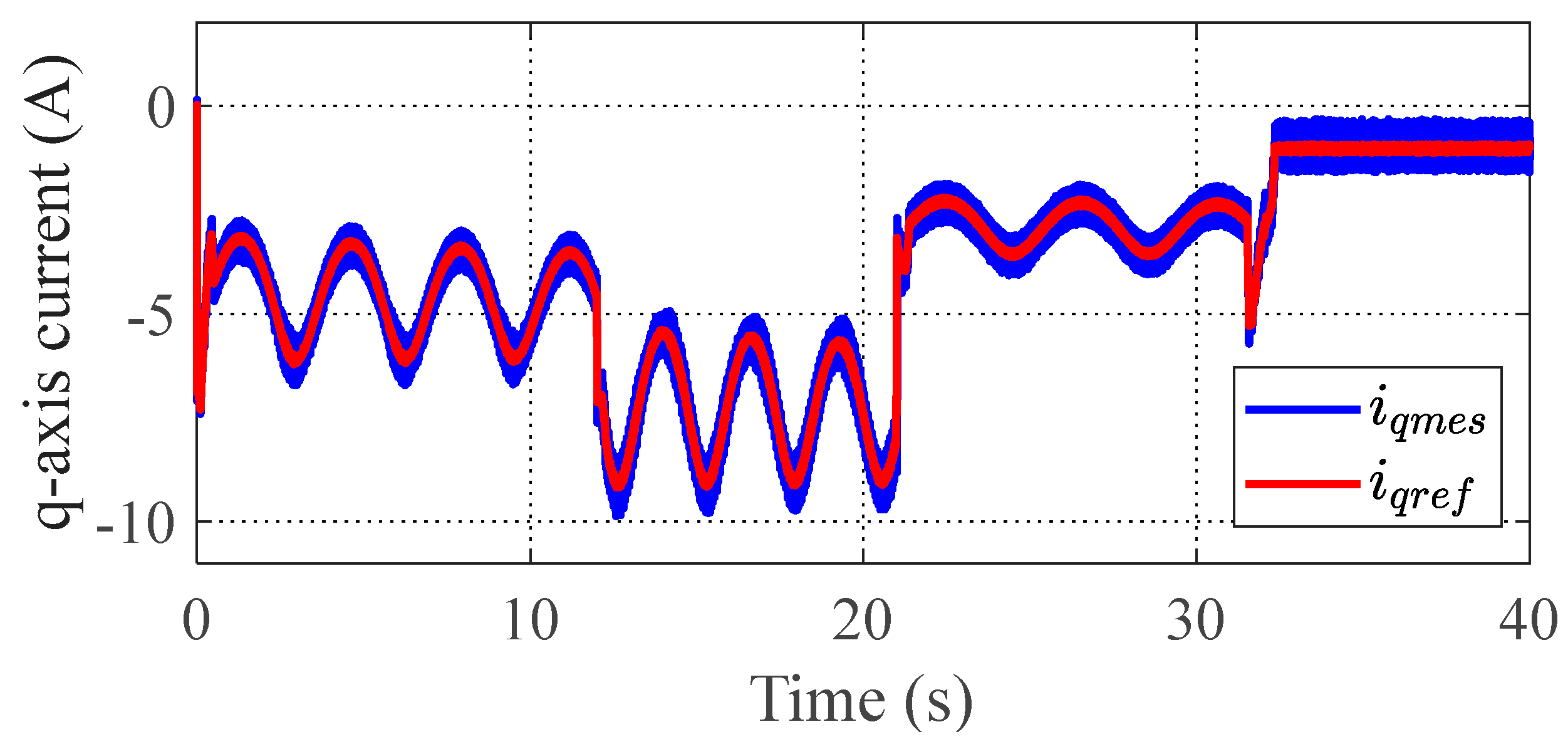
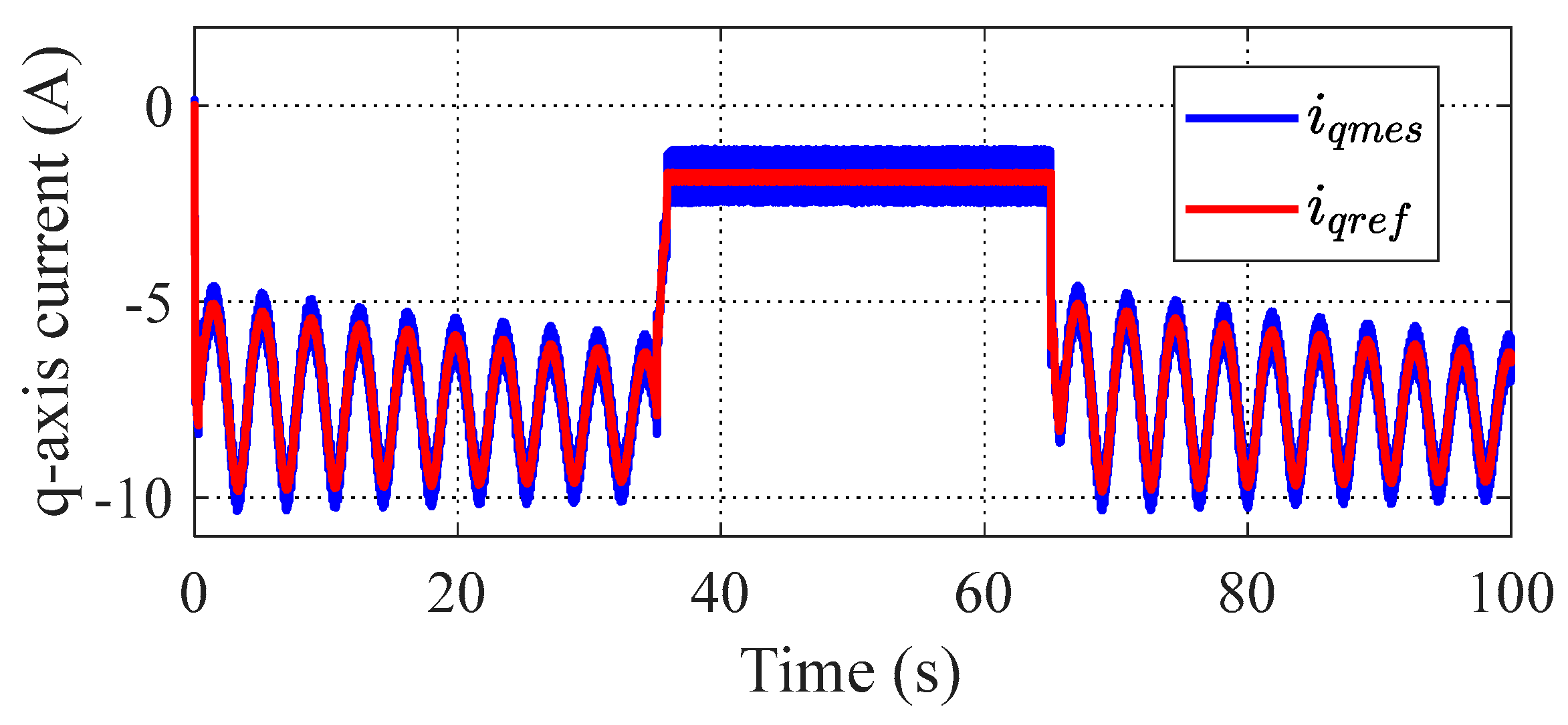
4. Simulation Results
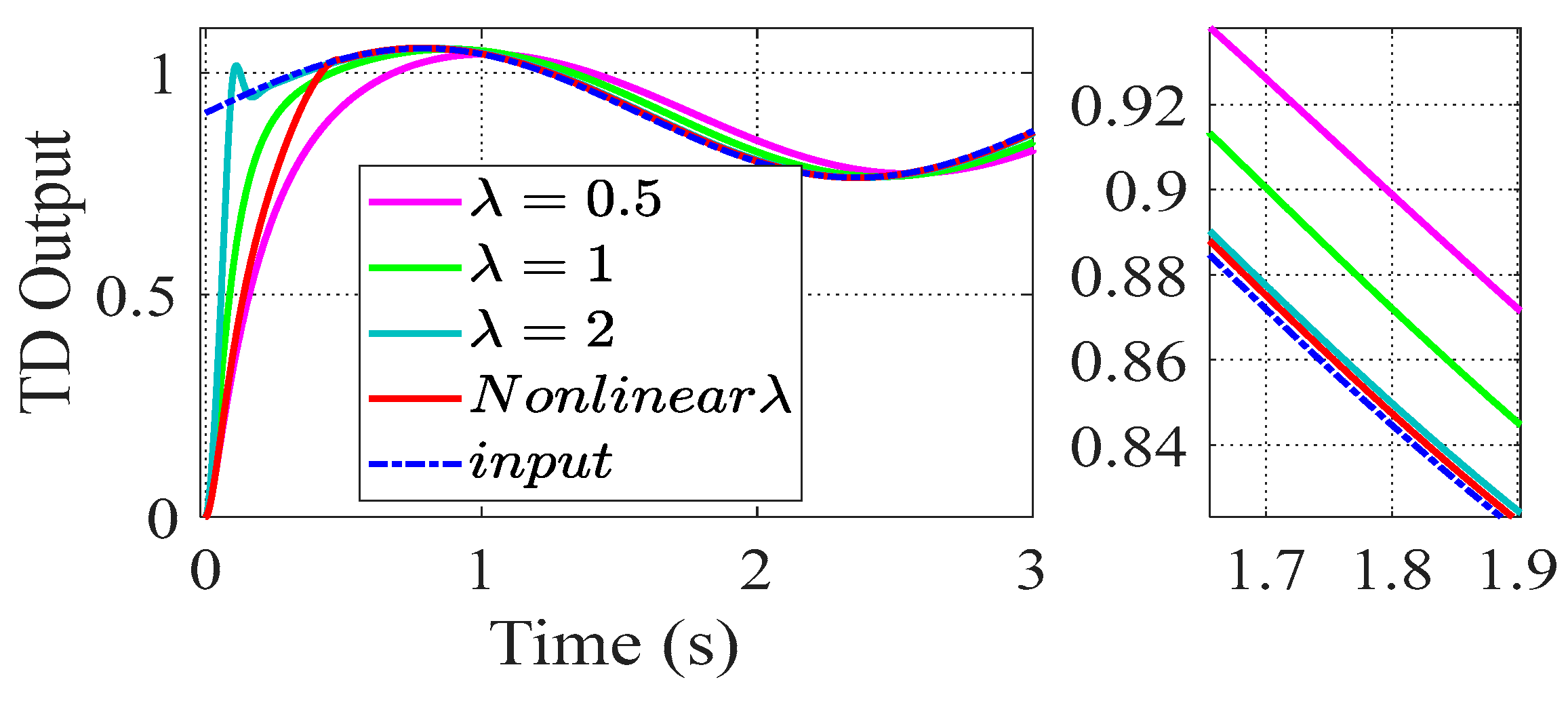
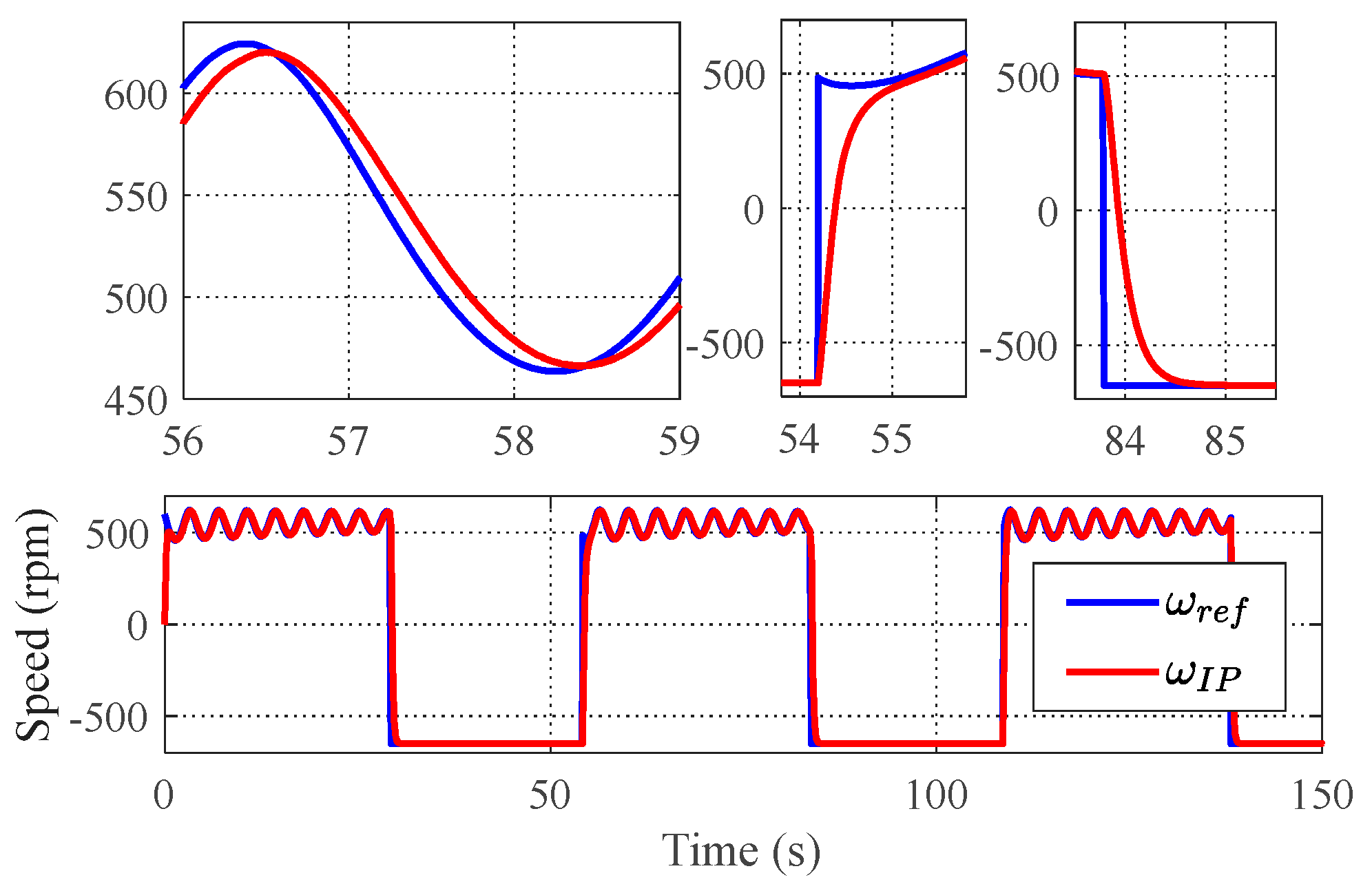
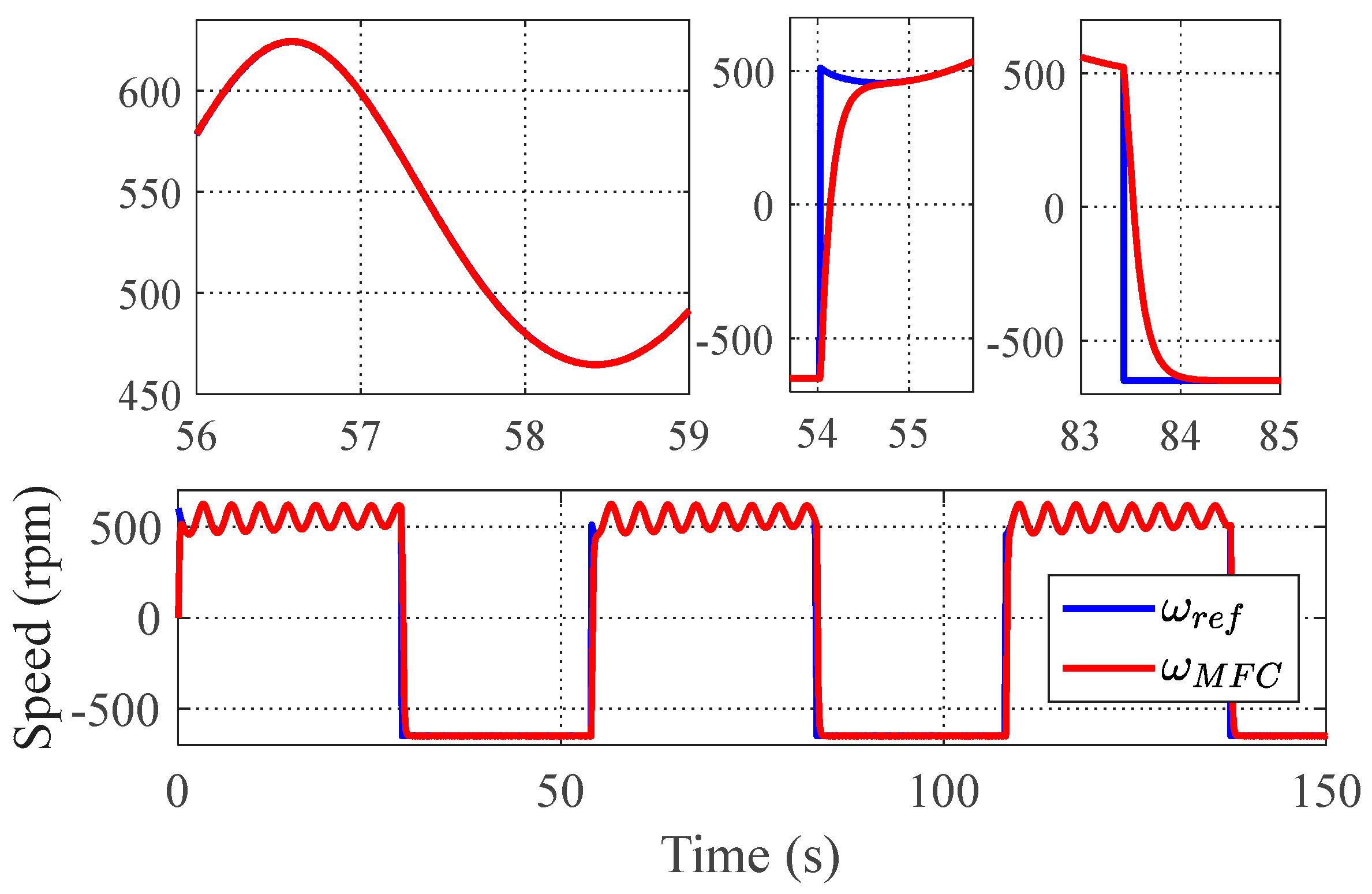
4.1. Tracking Performance
4.2. Scalability in Varying Environmental Conditions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tang, Z.; Yang, Y.; Blaabjerg, F. Power electronics: The enabling technology for renewable energy integration. CSEE J. Power Energy Syst. 2021, 8, 39–52. [Google Scholar]
- Badihi, H.; Zhang, Y.; Jiang, B.; Pillay, P.; Rakheja, S. A comprehensive review on signal-based and model-based condition monitoring of wind turbines: Fault diagnosis and lifetime prognosis. Proc. IEEE 2022, 110, 754–806. [Google Scholar] [CrossRef]
- Saberi, S.; Rezaie, B. Robust adaptive direct speed control of PMSG-based airborne wind energy system using FCS-MPC method. ISA Trans. 2022, 131, 43–60. [Google Scholar] [CrossRef]
- Vermillion, C.; Cobb, M.; Fagiano, L.; Leuthold, R.; Diehl, M.; Smith, R.S.; Wood, T.A.; Rapp, S.; Schmehl, R.; Olinger, D. Electricity in the air: Insights from two decades of advanced control research and experimental flight testing of airborne wind energy systems. Annu. Rev. Control 2021, 52, 330–357. [Google Scholar] [CrossRef]
- Malz, E.C.; Verendel, V.; Gros, S. Computing the power profiles for an Airborne Wind Energy system based on large-scale wind data. Renew. Energy 2020, 162, 766–778. [Google Scholar] [CrossRef]
- Malz, E.C.; Walter, V.; Göransson, L.; Gros, S. The value of airborne wind energy to the electricity system. Wind Energy 2022, 25, 281–299. [Google Scholar] [CrossRef]
- Schmidt, E.; de Oliveira, M.D.L.C.; da Silva, R.S.; Fagiano, L.; Neto, A.T. In-flight estimation of the aerodynamics of tethered wings for airborne wind energy. IEEE Trans. Control Syst. Technol. 2019, 28, 1309–1322. [Google Scholar] [CrossRef]
- Akberali, A.F.K.; Kheiri, M.; Bourgault, F. Generalized aerodynamic models for crosswind kite power systems. J. Wind Eng. Ind. Aerodyn. 2021, 215, 104664. [Google Scholar] [CrossRef]
- Yan, C.; Zhang, H. Analysis of the work performance of the lift mode crosswind kite power system based on aerodynamic parameters. Energy Rep. 2022, 8, 40–52. [Google Scholar] [CrossRef]
- Zempoalteca-Jimenez, M.-A.; Castro-Linares, R.; Alvarez-Gallegos, J. Trajectory Tracking Flight Control of a Tethered Kite Using a Passive Sliding Mode Approach. IEEE Lat. Am. Trans. 2021, 20, 133–140. [Google Scholar] [CrossRef]
- Costello, S.; François, G.; Bonvin, D. Real-time optimizing control of an experimental crosswind power kite. IEEE Trans. Control Syst. Technol. 2017, 26, 507–522. [Google Scholar] [CrossRef]
- Bari, S.; Khan, M.U. Sliding mode control for autonomous flight of tethered kite under varying wind speed conditions. In Proceedings of the 2020 17th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 14–18 January 2020; pp. 315–320. [Google Scholar]
- Todeschini, D.; Fagiano, L.; Micheli, C.; Cattano, A. Control of a rigid wing pumping Airborne Wind Energy system in all operational phases. Control Eng. Pract. 2021, 111, 104794. [Google Scholar] [CrossRef]
- Siddiqui, A.; Borek, J.; Vermillion, C. A Fused Gaussian Process Modeling and Model Predictive Control Framework for Real-Time Path Adaptation of an Airborne Wind Energy System. IEEE Trans. Control Syst. Technol. 2022, 31, 475–482. [Google Scholar] [CrossRef]
- Belguedri, M.; Benrabah, A.; Khoucha, F.; Benbouzid, M.; Benmansour, K. An improved uncertainty and disturbance estimator-based speed control for grid-connected pumping kite wind generator. Control Eng. Pract. 2024, 143, 105795. [Google Scholar] [CrossRef]
- Schechner, K.; Bauer, F.; Hackl, C.M. Nonlinear DC-link PI control for airborne wind energy systems during pumping mode. In Airborne Wind Energy: Advances in Technology Development and Research; Springer: Singapore, 2018; pp. 241–276. [Google Scholar]
- Belguedri, M.; Amirat, Y.; Benrabah, A.; Khoucha, F.; Benbouzid, M.; Benmansour, K. Active Disturbance Rejection Control with a Cascaded Extended State Observer for Pumping Kite Generator Systems Robust DC-Link Voltage Control. IEEE Trans. Energy Convers. 2024, 1–12. [Google Scholar] [CrossRef]
- Zhao, Y.; Wei, C.; Zhang, Z.; Qiao, W. A review on position/speed sensorless control for permanent-magnet synchronous machine-based wind energy conversion systems. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 203–216. [Google Scholar] [CrossRef]
- Berra, A.; Fagiano, L. An optimal reeling control strategy for pumping airborne wind energy systems without wind speed feedback. In Proceedings of the 2021 European Control Conference (ECC), Rotterdam, The Netherlands, 29 June–2 July 2021; pp. 1199–1204. [Google Scholar]
- Argatov, I.; Silvennoinen, R. Energy conversion efficiency of the pumping kite wind generator. Renew. Energy 2010, 35, 1052–1060. [Google Scholar] [CrossRef]
- Fagiano, L.; Milanese, M. Airborne wind energy: An overview. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 3132–3143. [Google Scholar]
- Ahmed, M.S.; Hably, A.; Bacha, S. Kite generator system modeling and grid integration. IEEE Trans. Sustain. Energy 2013, 4, 968–976. [Google Scholar] [CrossRef]
- Mademlis, G.; Liu, Y.; Chen, P.; Singhroy, E. Generator speed control and experimental verification of tidal undersea kite systems. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 1531–1537. [Google Scholar]
- Fliess, M.; Join, C. Model-free Control and Intelligent PID Controllers: Towards a Possible Trivialization of Nonlinear Control? IFAC Proc. Vol. 2009, 42, 1531–1550. [Google Scholar] [CrossRef]
- Fliess, M.; Join, C. Model-free control. Int. J. Control 2013, 86, 2228–2252. [Google Scholar] [CrossRef]
- Gédouin, P.-A.; Delaleau, E.; Bourgeot, J.-M.; Join, C.; Arbab Chirani, S.; Calloch, S. Experimental comparison of classical PID and model-free control: Position control of a shape memory alloy active spring. Control Eng. Pract. 2011, 19, 433–441. [Google Scholar] [CrossRef]
- Yahagi, S.; Suzuki, M. Intelligent PI control based on the ultra-local model and Kalman filter for vehicle yaw-rate control. SICE J. Control Meas. Syst. Integr. 2023, 16, 38–47. [Google Scholar] [CrossRef]
- Hamon, P.; Michel, L.; Plestan, F.; Chablat, D. Model-free based control of a gripper actuated by pneumatic muscles. Mechatronics 2023, 95, 103053. [Google Scholar] [CrossRef]
- Scherer, P.M.; Othmane, A.; Rudolph, J. Combining model-based and model-free approaches for the control of an electro-hydraulic system. Control Eng. Pract. 2023, 133, 105453. [Google Scholar] [CrossRef]
- Carvalho, A.D.; Pereira, B.S.; Angélico, B.A.; Laganá, A.A.M.; Justo, J.F. Model-free control applied to a direct injection system: Experimental validation. Fuel 2024, 358, 130071. [Google Scholar] [CrossRef]
- Carvalho, A.D.; Angélico, B.A.; Laganá, A.A.M. Model-Free Control for High Pressure in a Direct Injection System. J. Control Autom. Electr. Syst. 2023, 34, 689–699. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, X.; Wang, J. Extremum-Seeking-Based Adaptive Model-Free Control and Its Application to Automated Vehicle Path Tracking. IEEE/ASME Trans. Mechatron. 2022, 27, 3874–3884. [Google Scholar] [CrossRef]
- Ahmed, M.; Hably, A.; Bacha, S. Power maximization of a closed-orbit kite generator system. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 7717–7722. [Google Scholar]
- Fagiano, L.; Milanese, M.; Piga, D. High-altitude wind power generation. IEEE Trans. Energy Convers. 2009, 25, 168–180. [Google Scholar] [CrossRef]
- Ahmed, M.; Hably, A.; Bacha, S. High altitude wind power systems: A survey on flexible power kites. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 2085–2091. [Google Scholar]
- Park, B.; Olama, M.M. A Model-Free Voltage Control Approach to Mitigate Motor Stalling and FIDVR for Smart Grids. IEEE Trans. Smart Grid 2021, 12, 67–78. [Google Scholar] [CrossRef]
- Haddar, M.; Chaari, R.; Baslamisli, S.C.; Chaari, F.; Haddar, M. Intelligent PD controller design for active suspension system based on robust model-free control strategy. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4863–4880. [Google Scholar] [CrossRef]
- Barth, J.M.O. Algorithmes de Contrôle sans Modèle pour les Micro Drones de Type Tail-Sitter; Institut Supérieur de l’Aéronautique et de l’Espace Toulouse: Toulouse, France, 2020. [Google Scholar]
- Yang, Z.; Ji, J.; Sun, X.; Zhu, H.; Zhao, Q. Active Disturbance Rejection Control for Bearingless Induction Motor Based on Hyperbolic Tangent Tracking Differentiator. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2623–2633. [Google Scholar] [CrossRef]
- Ane, T.; Loron, L. Easy and efficient tuning of PI controllers for electrical drives. In Proceedings of the IECON 2006—32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006; pp. 5131–5136. [Google Scholar]
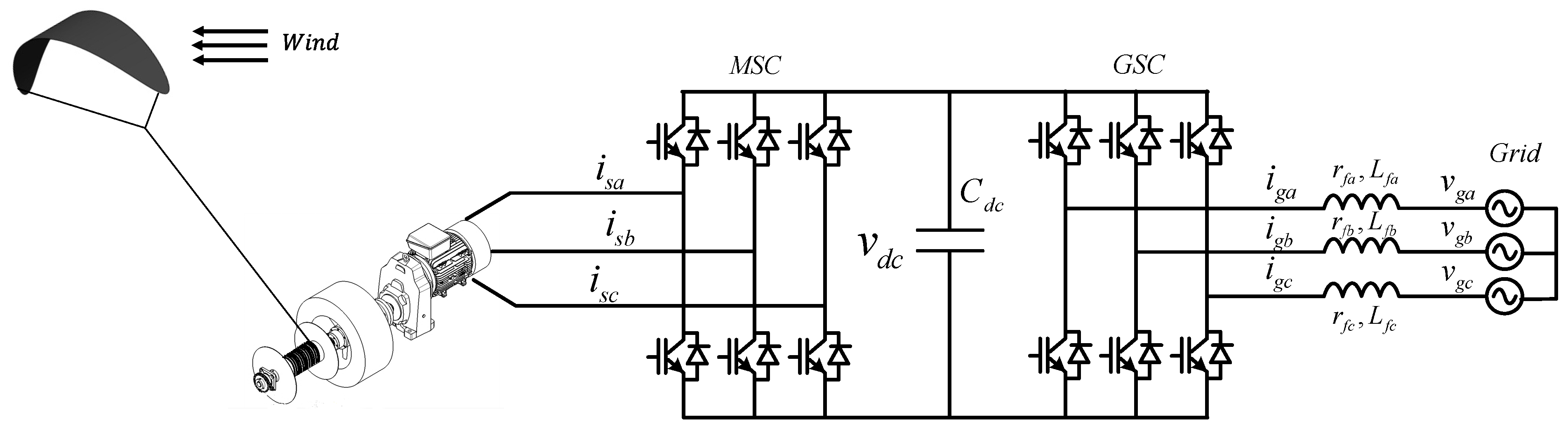

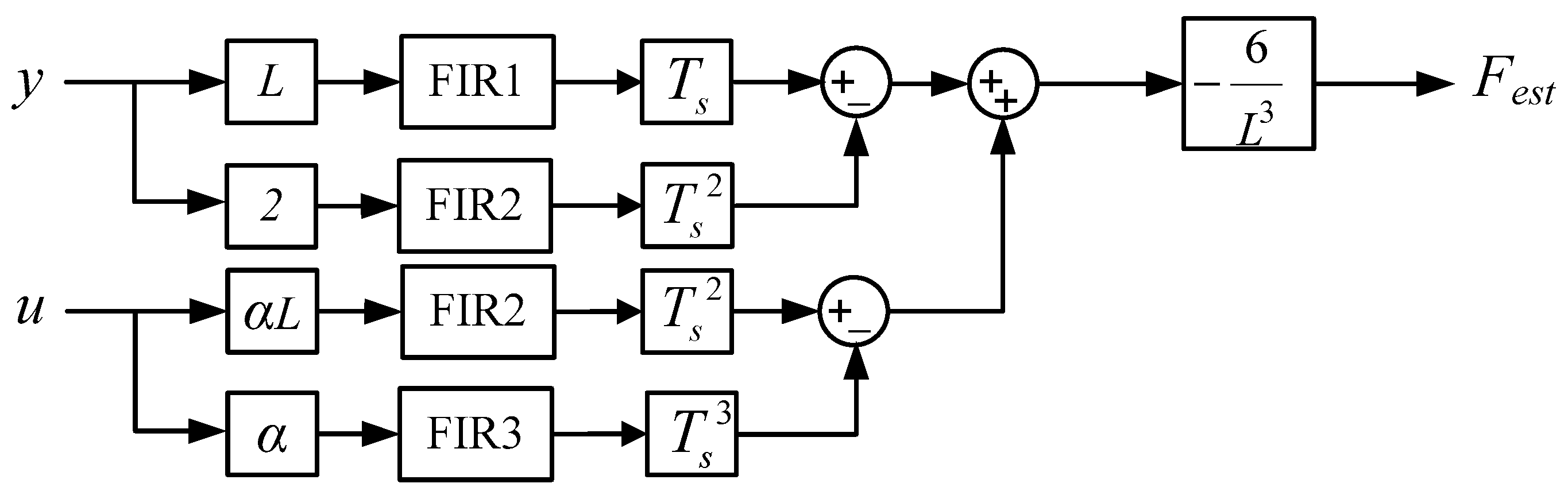

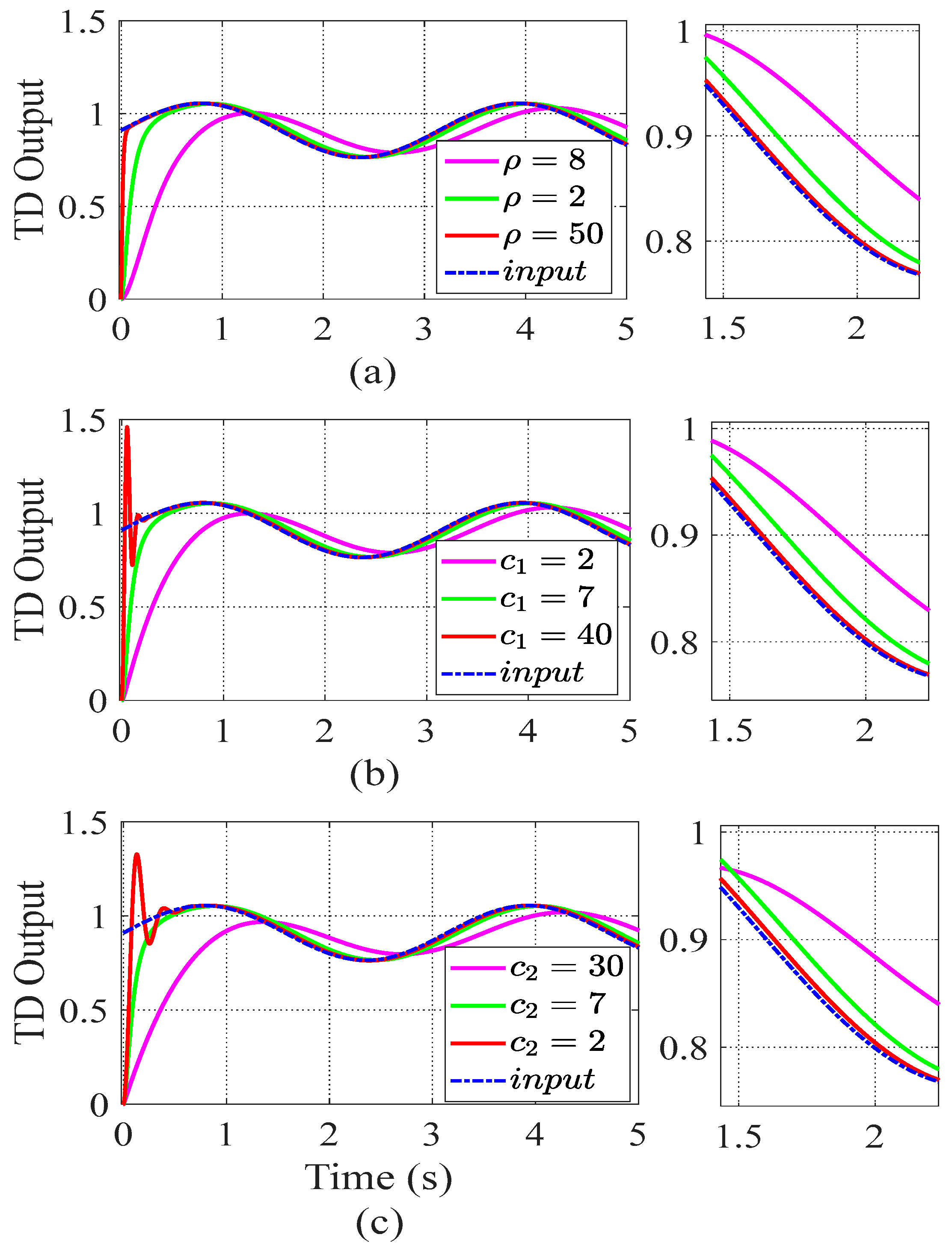
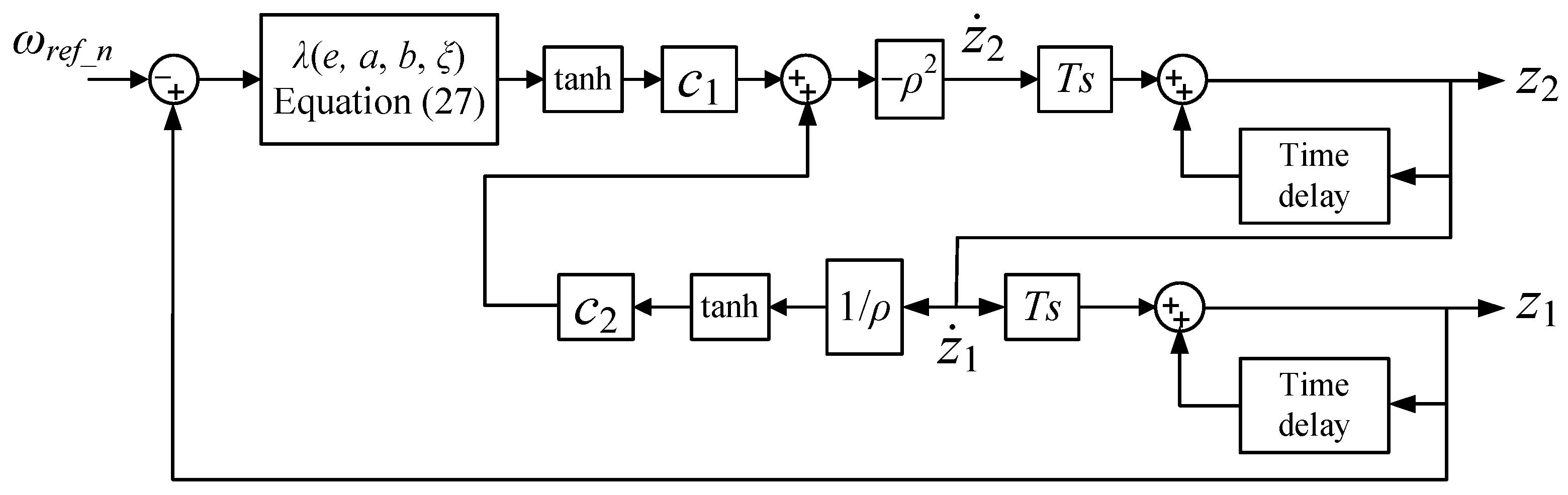






| Parameters | Symbol | Value |
|---|---|---|
| Kite’s area | A | 3 m2 |
| Air density | ρair | 1.225 kg/ |
| Lift coefficient | CL | 1 |
| Drag coefficient | CD | 0.33 |
| Pole pair number | p | 2 |
| System total inertia | J | 0.03 kg m2 |
| Viscous damping | D | 0.005 N.m.s |
| Machine inductance | Ls | 6 mH |
| Machine resistance | Rs | 0.2 Ω |
| Machine flux linkage | φm | 0.6 Wb |
| DC-link capacitance | C | 4700 μF |
| Grid-side filter inductance | Lf | 20 mH |
| Grid-side filter resistance | Rf | 0.5 Ω |
| Carrier frequency | Fc | 5 kHz |
| Sampling time | TS | 5 × 10−6 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belguedri, M.; Benrabah, A.; Khoucha, F.; Delaleau, E.; Benbouzid, M.; Benmansour, K. Model-Free Speed Control for Pumping Kite Generator Systems Based on Nonlinear Hyperbolic Tangent Tracking Differentiator. Appl. Sci. 2025, 15, 685. https://doi.org/10.3390/app15020685
Belguedri M, Benrabah A, Khoucha F, Delaleau E, Benbouzid M, Benmansour K. Model-Free Speed Control for Pumping Kite Generator Systems Based on Nonlinear Hyperbolic Tangent Tracking Differentiator. Applied Sciences. 2025; 15(2):685. https://doi.org/10.3390/app15020685
Chicago/Turabian StyleBelguedri, Mouaad, Abdeldjabar Benrabah, Farid Khoucha, Emmanuel Delaleau, Mohamed Benbouzid, and Khelifa Benmansour. 2025. "Model-Free Speed Control for Pumping Kite Generator Systems Based on Nonlinear Hyperbolic Tangent Tracking Differentiator" Applied Sciences 15, no. 2: 685. https://doi.org/10.3390/app15020685
APA StyleBelguedri, M., Benrabah, A., Khoucha, F., Delaleau, E., Benbouzid, M., & Benmansour, K. (2025). Model-Free Speed Control for Pumping Kite Generator Systems Based on Nonlinear Hyperbolic Tangent Tracking Differentiator. Applied Sciences, 15(2), 685. https://doi.org/10.3390/app15020685








