Parametric Analysis of Control Techniques for 15 MW Semi-Submersible Floating Wind Turbine
Abstract
1. Introduction
2. Target Floating Wind Turbine
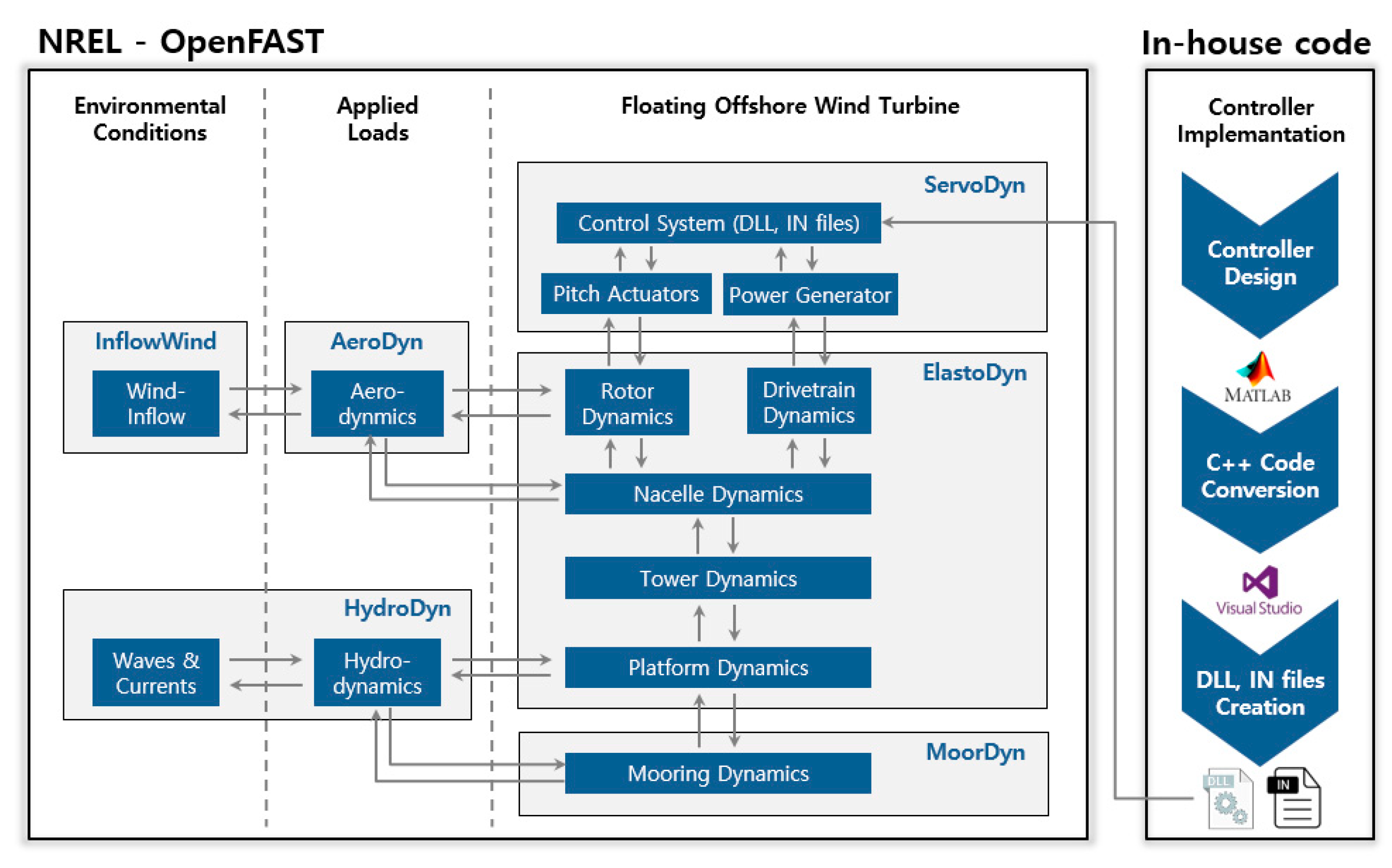
2.1. Numerical Modeling
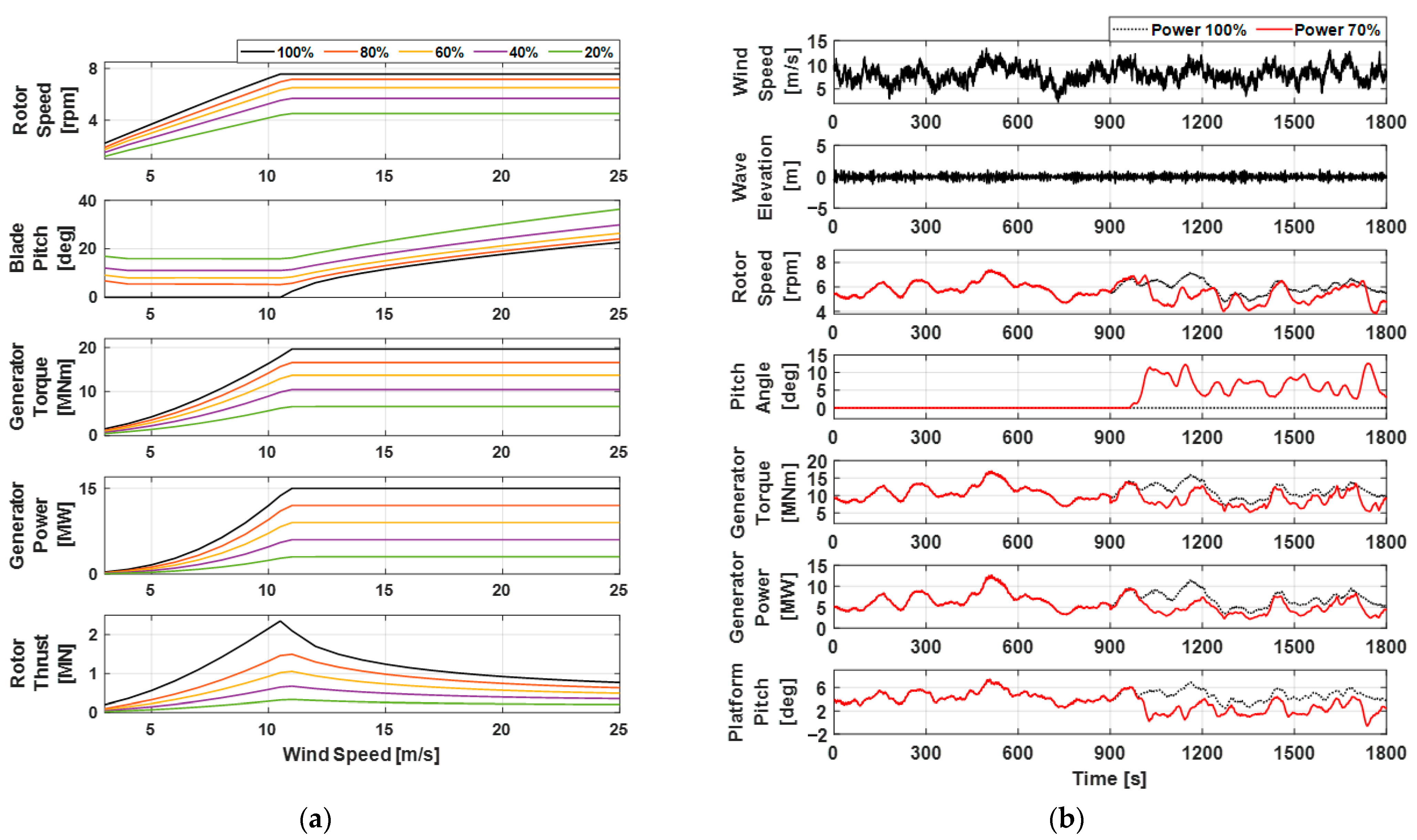
2.2. Verification of OWT Numerical Modeling
2.3. Verification of FOWT Numerical Modeling
3. Control Algorithms
3.1. Baseline Control
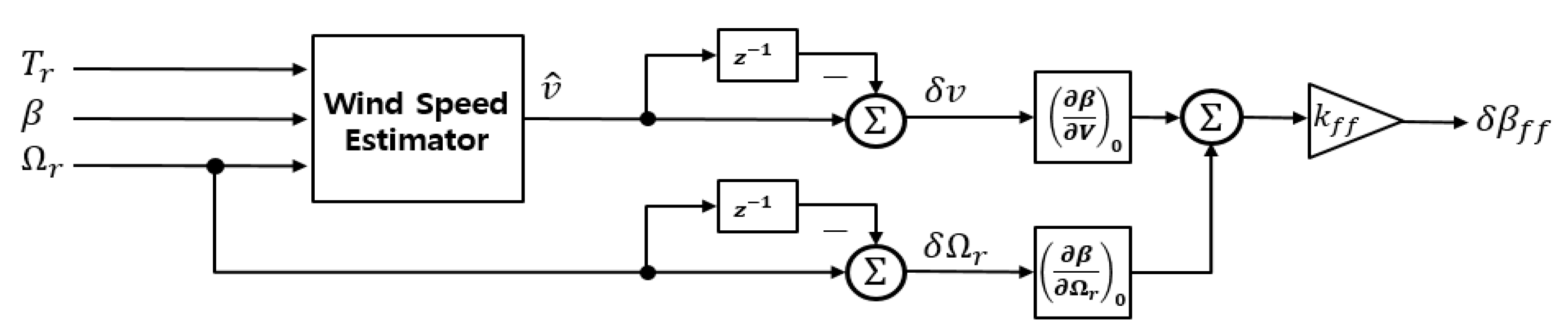
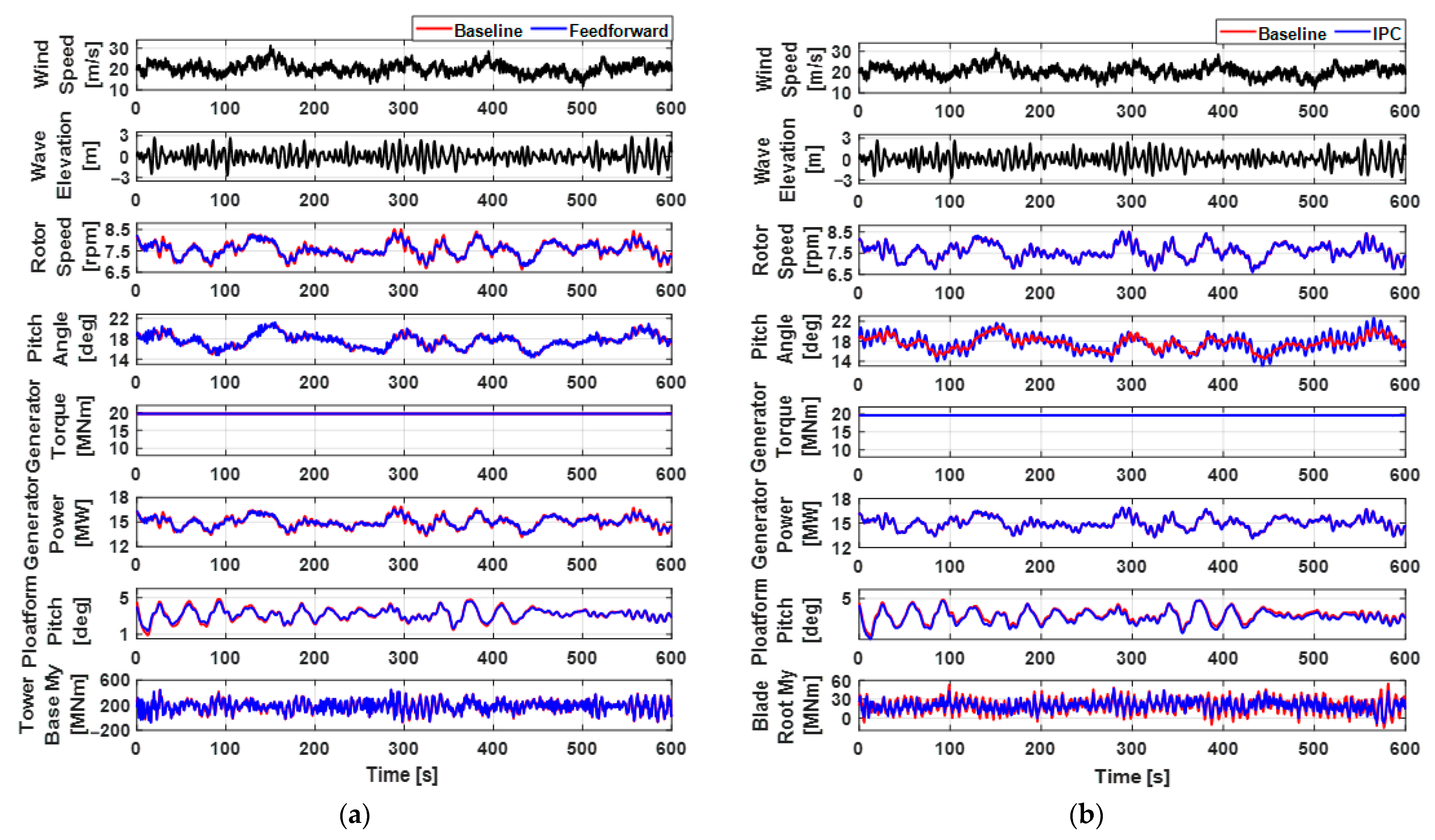
3.2. Feedforward Control
3.3. Individual Pitch Control
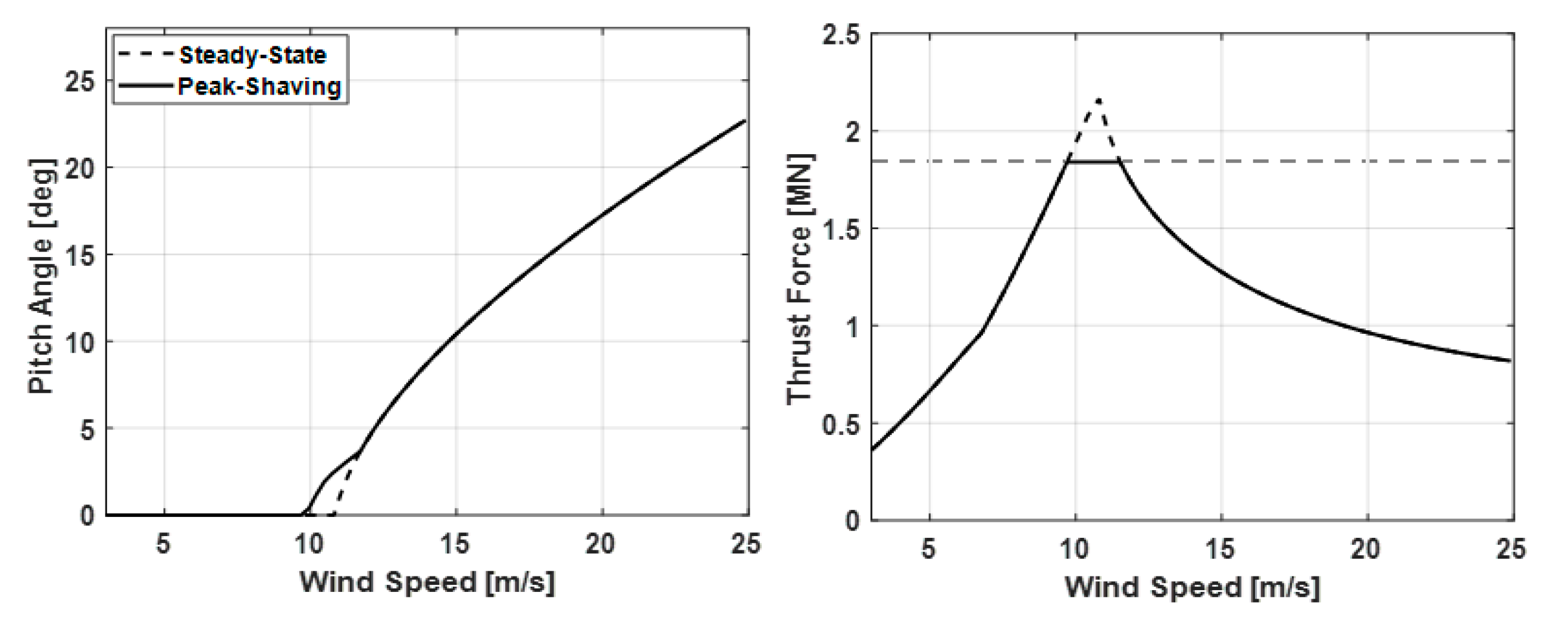
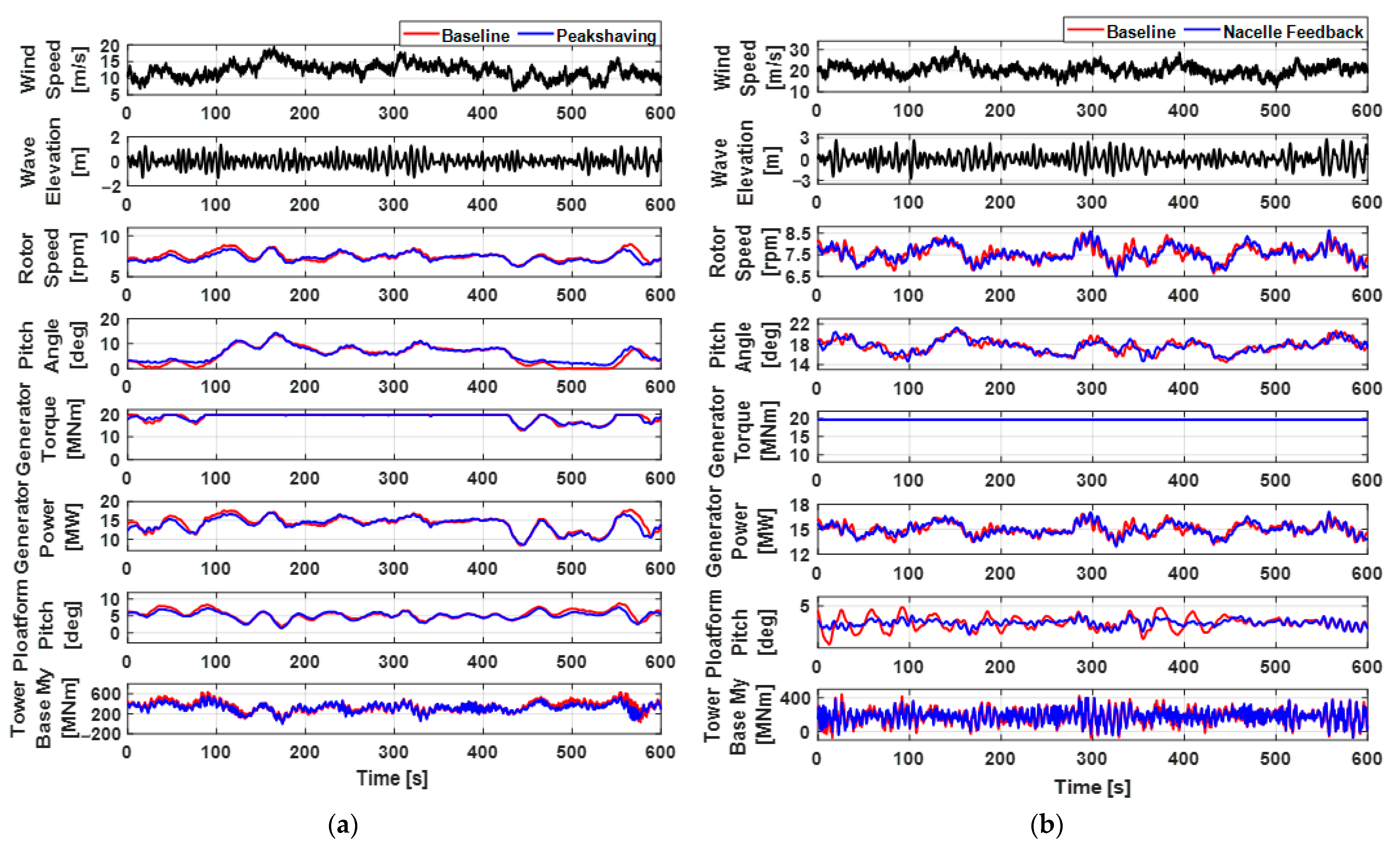
3.4. Peak Shaving
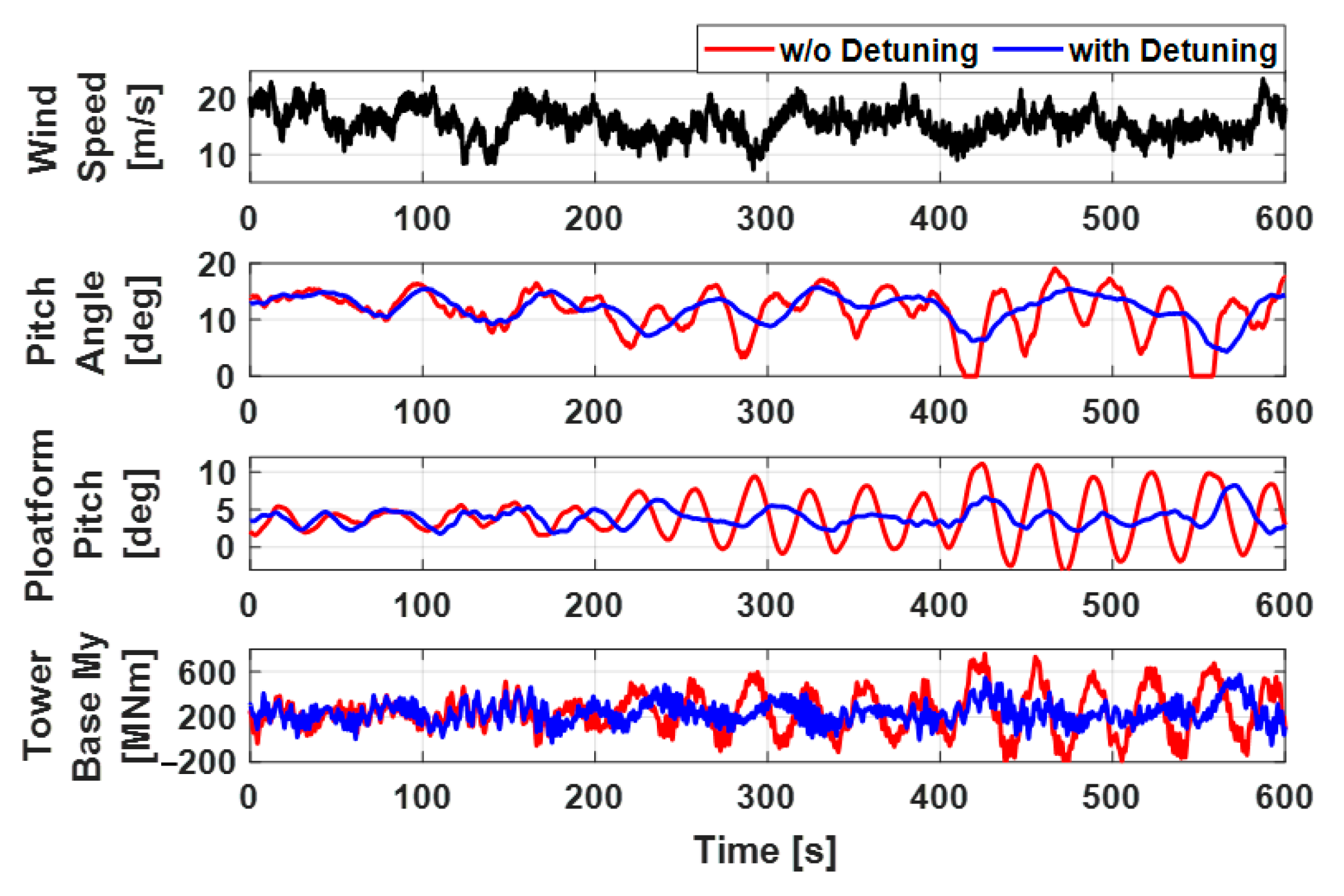
3.5. Nacelle Feedback Control
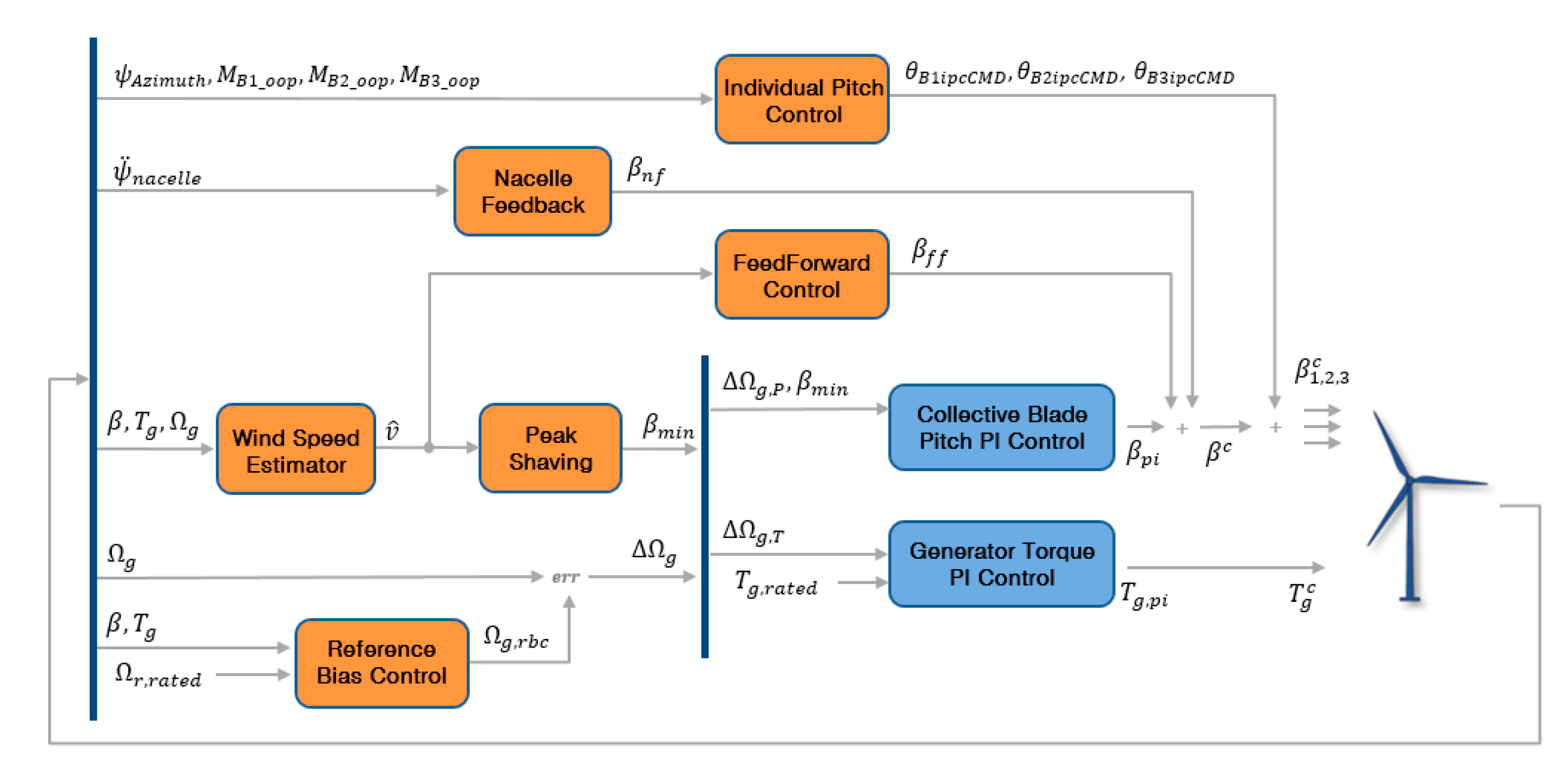
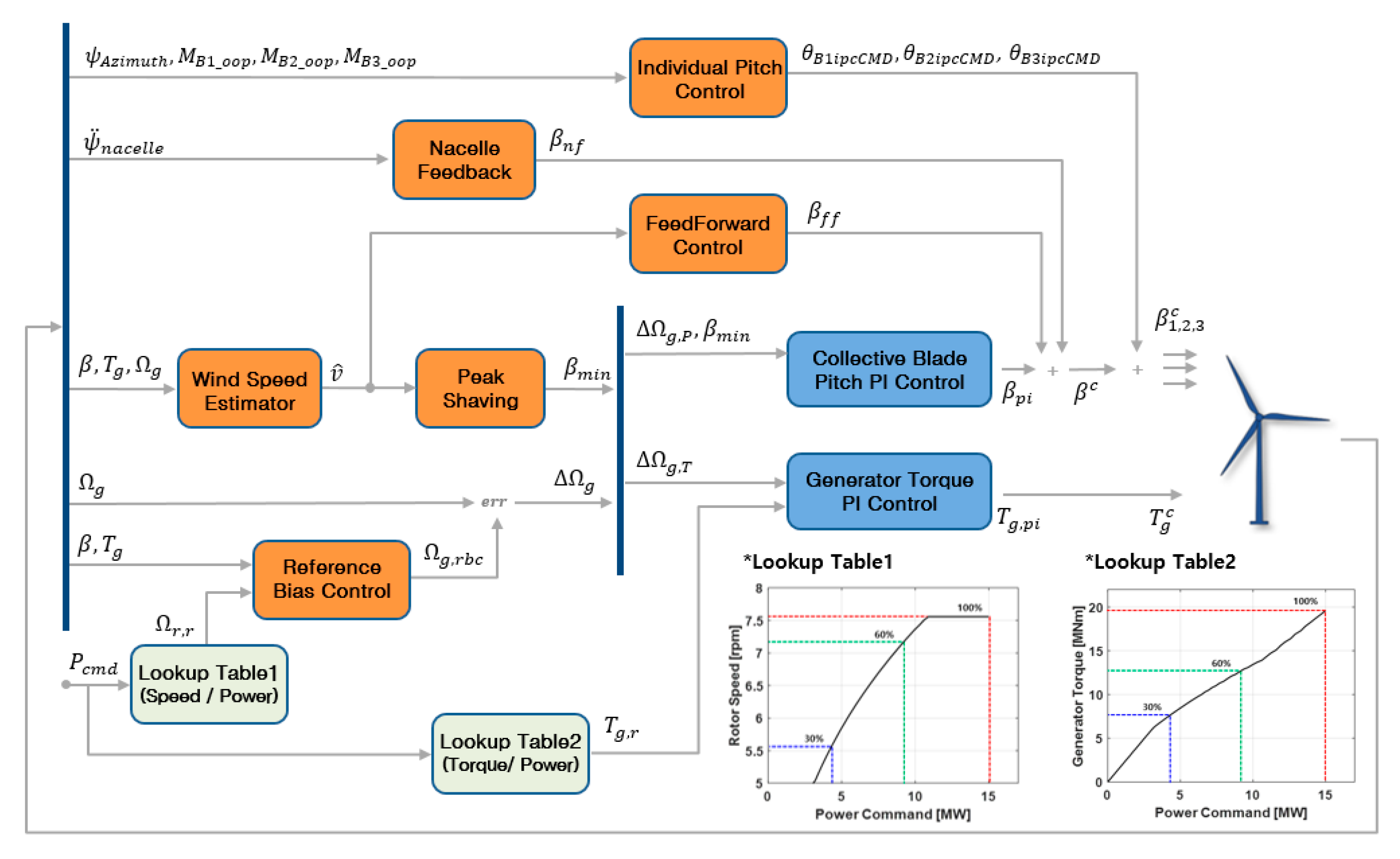
3.6. Whole Control Algorithm and Its Implementation
4. Controller Evaluation
4.1. Parametric Study
4.2. DLC Simulation
5. Discussion
6. Conclusions
- To meet these control objectives, the feedforward, IPC, peak shaving, and nacelle feedback control algorithms were incorporated into the detuned baseline controller.
- The parametric simulations using the wind turbine simulation tool OpenFAST were conducted to analyze the performance changes with control parameters and determine the optimal parameters. The parametric simulations were performed under the NTM and NSS conditions, using four levels of control parameter cases for each control technique. Control performance indicators, including the mean power, the standard deviation of the rotor speed, platform motion, and the tower and the blade loads, were compared. The results showed that, while increasing the control parameters improved control performance, excessively high values led to degradation in aspects unrelated to the primary control objectives. Consequently, the control parameters for each control technique were selected to avoid adversely affecting other performance indicators.
- To verify the performance of the overall control algorithm with the selected control parameters from the parametric study, simulations under DLC 1.2 and DLC 1.6 were carried out. The results demonstrated that the proposed control algorithm achieved significant load and motion reductions compared with the ROSCO controller. Specifically, while the mean power was decreased by 5%, the rotor speed deviation was reduced by 49%, platform pitch motion by 20%, tower loads by 15%, blade loads by 17%, RNA acceleration by 22%, and the mooring line tension by 38%.
- In addition to the power production and the load and motion reductions, the DPPT control algorithm was implemented to consider the additional control objective. The simulation results under power curtailment showed that the difference between the demanded power command and the produced power was within 1%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Aerodynamic torque | |
| Blade pitch angle | |
| Rotor speed | |
| Estimated wind speed | |
| Feedforward control gain | |
| Blade pitch angle increment by feedforward control | |
| Azimuth angle | |
| Blade1-root flap-wase bending moment | |
| Rotor tilt moment | |
| Rotor yaw moment | |
| Rotor tilt angle for rotor tilt control | |
| Rotor yaw angle for rotor yaw control | |
| IPC command for Blade1 | |
| Nacelle angular acceleration | |
| Nacelle angular velocity | |
| Nacelle feedback control gain | |
| Blade pitch angle increment by nacelle feedback control | |
| Generator torque | |
| Generator speed | |
| Rated rotor speed | |
| Rotor speed reference by RBC | |
| Minimum blade pitch angle limit | |
| Rated generator torque | |
| Blade pitch command by PI control | |
| Generator toqrue command by PI control | |
| Individual blade pitch command | |
| Generator torque command | |
| Demanded power command | |
| Rotor speed reference by DPPT contorl | |
| Generator torque reference by DPPT contorl |
References
- Manwell, J.F.; Mcgowan, J.G.; Rogers, A.L. Wind Energy Explained, 2nd ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Bossanyi, E.A. The design of closed loop controllers for wind turbines. Wind Energy 2000, 3, 149–163. [Google Scholar] [CrossRef]
- Fateh, F.; White, W.N.; Gruenbacher, D. Torsional vibrations mitigation in the drivetrain of DFIG-based grid-connected wind turbine. IEEE Trans. Ind. Appl. 2017, 53, 5760–5767. [Google Scholar] [CrossRef]
- Pascu, V.; Kanev, S.; Van Wingerden, J.-W. Adaptive tower damping control for offshore wind turbines. Wind Energy 2016, 20, 765–781. [Google Scholar] [CrossRef]
- Mohammadi, E.; Fadaeinedjad, R.; Moschopoulos, G. Implementation of internal model based control and individual pitch control to reduce fatigue loads and tower vibrations in wind turbines. J. Sound Vib. 2018, 421, 132–152. [Google Scholar] [CrossRef]
- Kim, K.; Kim, H.-G.; Paek, I. Application and Validation of Peak Shaving to Improve Performance of a 100 KW Wind Turbine. Int. J. Precis. Eng. Manuf. Green Technol. 2020, 7, 411–421. [Google Scholar] [CrossRef]
- Meng, F.; Wenske, J.; Gambier, A. Wind turbine loads reduction using feedforward feedback collective pitch control based on the estimated effective wind speed. In Proceedings of the American Control Conference, Boston, MA, USA, 6–8 July 2016. [Google Scholar]
- Zhang, H.; Wen, B.; Tian, X.; Li, X.; Dong, Y.; Wang, M.; Peng, Z. Experimental study on mitigating vibration of floating offshore wind turbine using tuned mass damper. Ocean Eng. 2023, 288, 115974. [Google Scholar] [CrossRef]
- Chapain, S.; Aly, A.M. Vibration Attenuation in Wind Turbines: A Proposed Robust Pendulum Pounding TMD. Eng. Struct. 2021, 233, 111891. [Google Scholar] [CrossRef]
- Han, D.; Wang, W.; Li, X.; Su, X. Optimization Design of Multiple Tuned Mass Dampers for Semi-Submersible Floating Wind Turbine. Ocean Eng. 2022, 264, 112536. [Google Scholar] [CrossRef]
- Stockhouse, D.; Phadnis, M.; Grant, E.; Johnson, K.; Damiani, R.; Pao, L. Control of a floating wind turbine on a novel actuated platform. In Proceedings of the 2022 American Control Conference (ACC), Atlanta, GA, USA, 8–10 June 2022. [Google Scholar]
- Lenfest, E.; Goupee, A.J.; Wright, A.; Abbas, N. Tuning of nacelle feedback gains for floating wind turbine controllers using a two-DOF model. In Proceedings of the ASME 2020 39th International Conference on Offshore Mechanics and Arctic Engineering, Virtual, 3–7 August 2020. [Google Scholar]
- Oh, Y.; Kim, K.; Kim, H.; Paek, I. Control Algorithm of a Floating Wind Turbine for Reduction of Tower Loads and Power Fluctuation. Int. J. Precis. Eng. Manuf. 2015, 16, 2041–2048. [Google Scholar] [CrossRef]
- Schipf, D.; Simley, E.; Lemmer, F.; Pao, L.; Cheng, P.W. Collective Pitch Feedforward Control of Floating Wind Turbines Using Lidar. In Proceedings of the Twenty-Fifth International Ocean and Polar Engineering Conference, Kona, HI, USA, 21 June 2015. [Google Scholar]
- Hawari, Q.; Kim, T.; Ward, C.; Fleming, J. LQG control for hydrodynamic compensation on large floating wind turbines. Renew. Energy 2023, 205, 1–9. [Google Scholar] [CrossRef]
- Shah, K.; Li, Y.; Nagamune, R.; Zhou, Y.; Rehman, W. Platform motion minimization using model predictive control of a floating offshore wind turbine. Theor. Appl. Mech. Lett. 2021, 11, 100295. [Google Scholar] [CrossRef]
- Fleming, P.A.; Peiffer, A.; Schlipf, D. Wind turbine controller to mitigate structural loads on a floating wind turbine platform. J. Offshore Mech. Arct. Eng. 2019, 141, 061901. [Google Scholar] [CrossRef]
- Abbas, N.J.; Zalkind, D.S.; Pao, L.; Wright, A. A reference open-source controller for fixed and floating offshore wind turbines. Wind Energy Sci. 2022, 7, 53–73. [Google Scholar] [CrossRef]
- Rodríguez-Pérez, Á.M.; Pulido-Calvo, I. Analysis and Viability of Microturbines in Hydraulic Networks: A Case Study. J. Water Supply Res. Technol. Aqua. 2019, 68, 474–482. [Google Scholar] [CrossRef]
- Allen, C.; Viscelli, A.; Dagher, H.; Goupee, A.; Gaertner, E.; Abbas, N.; Hall, M.; Barter, G. Definition of the UMaine VolturnUSS Reference Platform Developed for the IEA Wind 15Megawatt Offshore Reference Wind Turbine; 2020 Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2020. [Google Scholar]
- Ramachandran, G.K.V.; Robertson, A.; Jonkman, J.M.; Masciola, M.D. Investigation of Response Amplitude Operators for Floating Offshore Wind Turbines (No. NREL/CP-5000-58098); National Renewable Energy Lab. (NREL): Golden, CO, USA, 2013. [Google Scholar]
- Larsen, T.J.; Hanson, T.D. A method to avoid negative damped low frequent tower vibrations for a floating, pitch controlled wind turbine. J. Phys. Conf. Ser. 2007, 75, 012073. [Google Scholar] [CrossRef]
- van Hooft, E.L.; van Engelen, T.G. Feed Forward Control of Estimated Wind Speed; Technical Report ECN-C–03-137; ECN Wind Energy: Kreilerood, The Netherlands, 2003. [Google Scholar]
- Jeon, T.; Paek, I. Design and verification of the LQR controller based on fuzzy logic for large wind turbine. Energies 2021, 14, 230. [Google Scholar] [CrossRef]
- Jeon, T.; Song, Y.; Paek, I. A Study on H-infinity Controller for a Non-Linear Wind Turbine with Uncertainty. Appl. Sci. 2023, 13, 11930. [Google Scholar] [CrossRef]
- Bossanyi, E.A. Individual Blade Pitch Control for Load Reduction. Wind Energy 2003, 6, 119–128. [Google Scholar] [CrossRef]
- Coleman, R.P.; Feingold, A.M. Theory of Self-Excited Mechanical Oscillations of Helicopter Rotors with Hinged Blades; National Advisory Committee for Aeronautics (NACA): Washington, DC, USA, 1957. [Google Scholar]
- Jeon, T.; Kim, D.; Paek, I. Improvements to and Experimental Validation of PI Controllers Using a Reference Bias Control Algorithm for Wind Turbines. Energies 2022, 15, 8298. [Google Scholar] [CrossRef]
- Kim, K.; Kim, H.; Paek, I.; Kim, H.-G.; Son, J. Field Validation of Demanded Power Point Tracking Control Algorithm for Medium-Capacity Wind Turbine. Int. J. Precis. Eng. Manuf. Green Technol. 2019, 6, 875–881. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Wind Energy Generation Systems—Part 3-1: Design Requirements for Fixed Offshore Wind Turbines, IEC 61400-3-1, 1st ed.; International Electrotechnical Commission: Geneva, Switzerland, 2019. [Google Scholar]
- International Electrotechnical Commission. Wind Energy Generation Systems—Part 3-2: Design Requirements for Floating Offshore Wind Turbines, IEC 61400-3-2, 1st ed.; International Electrotechnical Commission: Geneva, Switzerland, 2019. [Google Scholar]
- van Wingerden, J.W.; Pao, L.; Aho, J.; Fleming, P. Active power control of waked wind farms. IFAC-PapersOnLine 2017, 50, 4484–4491. [Google Scholar] [CrossRef]
- Jeon, T.; Kim, D.; Song, Y.; Paek, I. Design and Validation of Demanded Power Point Tracking Control Algorithm for MIMO Cpontrollers in Wind Turbines. Energies 2021, 14, 5818. [Google Scholar] [CrossRef]
- Bottasso, C.L.; Campagnolo, F.; Petrovi’c, V. Wind tunnel testing of scaled wind turbine models: Beyond aerodynamics. Wind. Eng. Ind. Aerodyn. 2014, 127, 11–28. [Google Scholar] [CrossRef]
- Fontanella, A.; Facchinetti, A.; Di Carlo, S.; Belloli, M. Wind Tunnel Investigation of the Aerodynamic Response of Two 15 MW Floating Wind Turbines. Wind Energy Sci. 2022, 7, 1711–1729. [Google Scholar] [CrossRef]
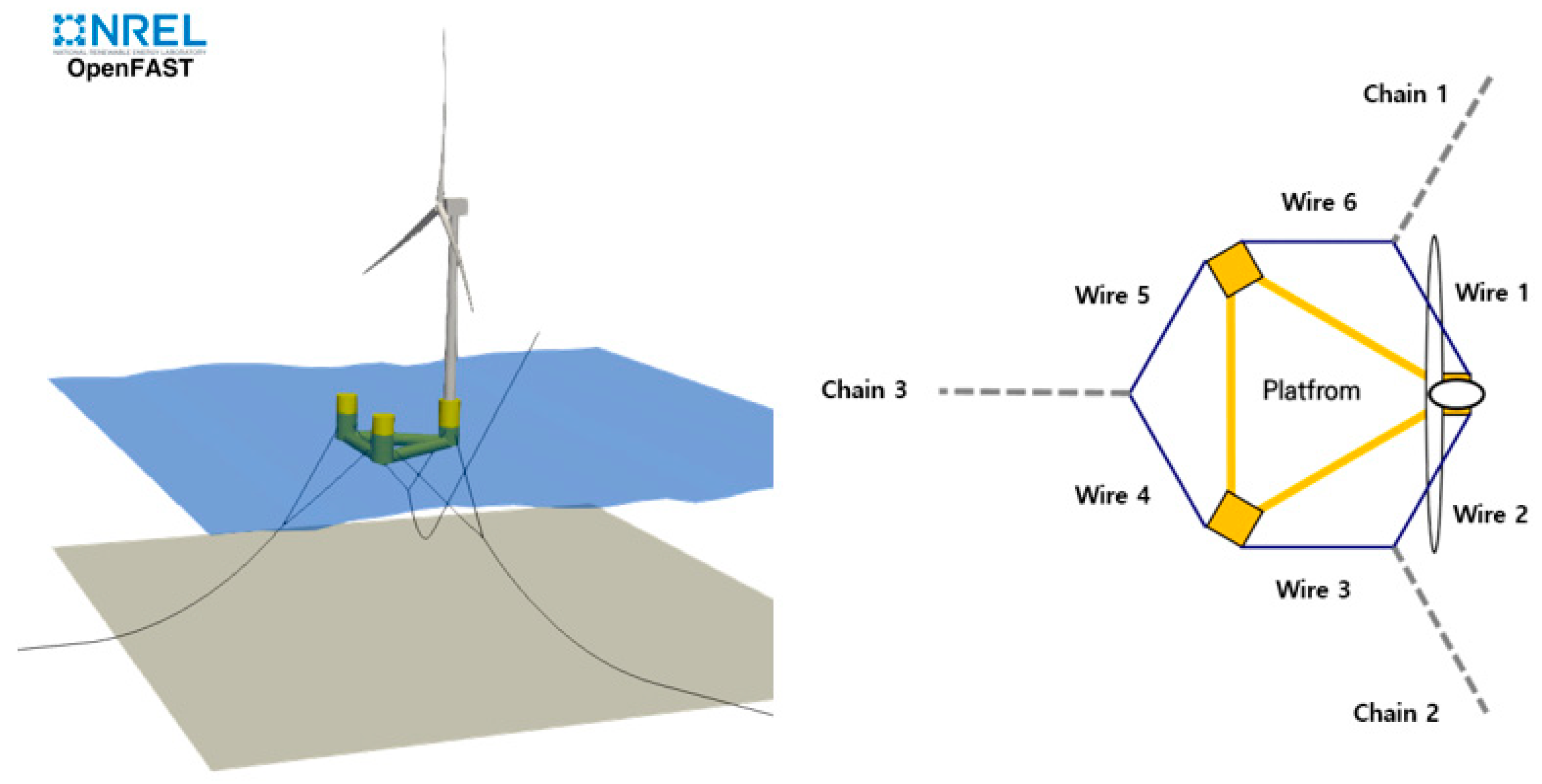
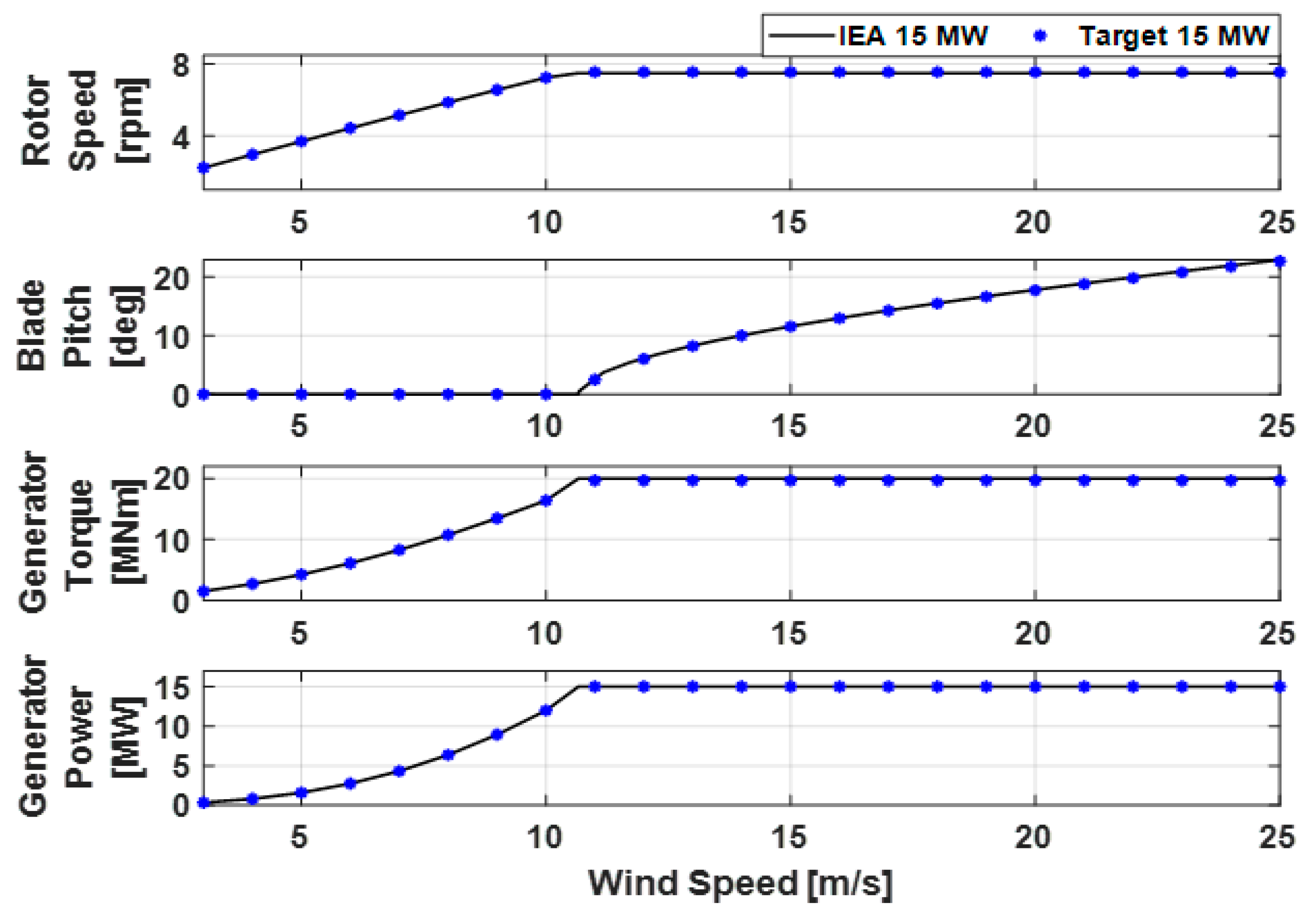
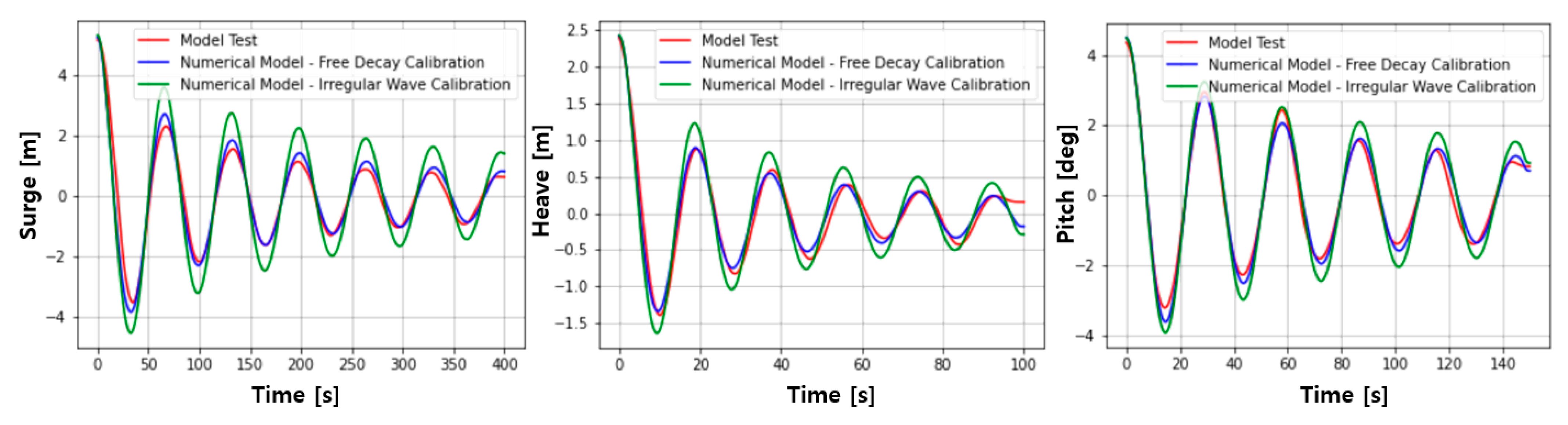

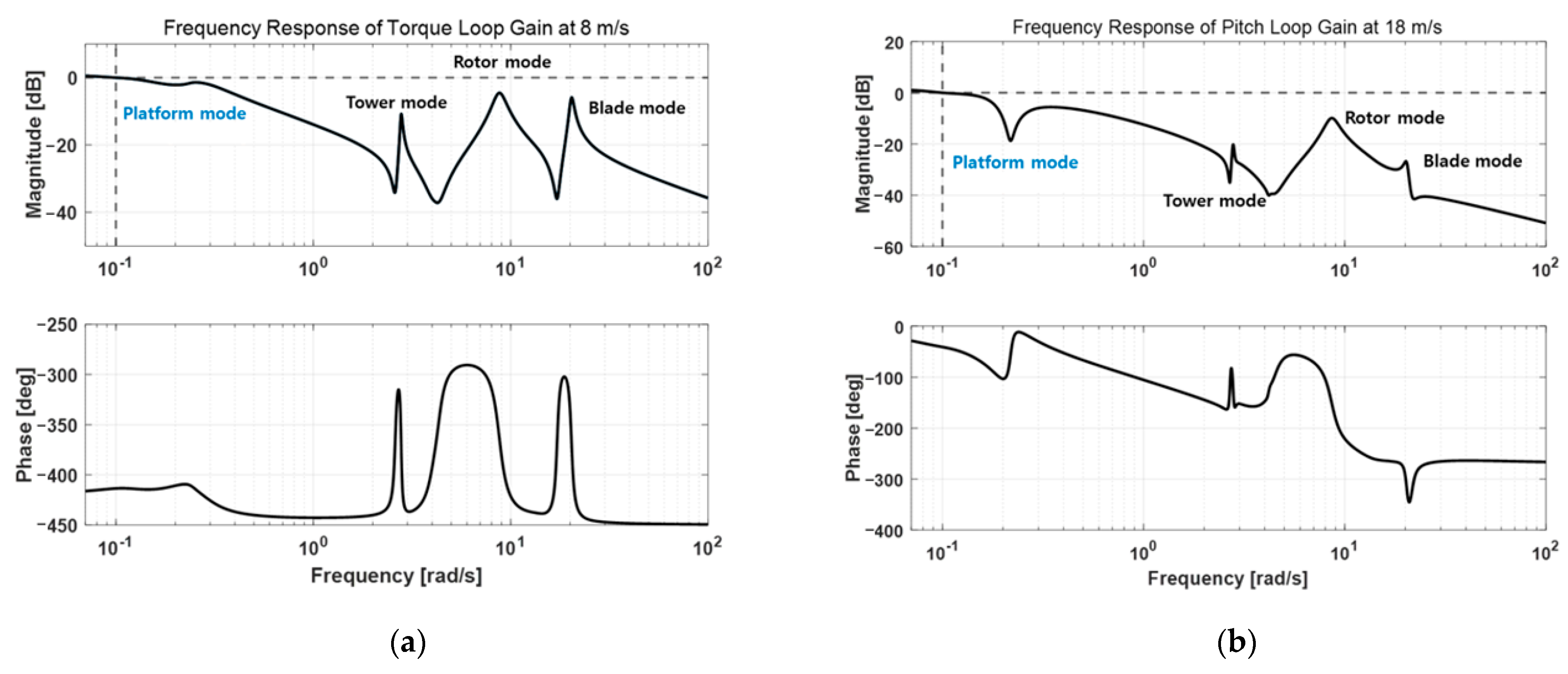


| Specifications | Units | Values |
|---|---|---|
| Rated Power | MW | 15 |
| Rated Rotor Speed | rpm | 7.55 |
| Rated Generator Torque | MNm | 19.63 |
| Gear Ratio | - | 1 |
| Rotor Diameter | m | 240 |
| Hub Height | m | 150 |
| Cut-in/Rated/Cut-out Wind Speed | m/s | 3, 10.59, 25 |
| Controllers | Control Parameters | Control Performance in Dynamic Simulation [%] (Controllers − Baseline)/Baseline * 100 | ||||
|---|---|---|---|---|---|---|
| Mean | Standard Deviation | Damage Equivalent Load | ||||
| Generator Power | Rotor Speed | Platform Pitch | Tower-Base FA Bending | Blade-Root FW Bending | ||
| Feed Forward | 1 | 0.0 | −4.4 | −5.8 | −0.8 | −1.5 |
| 2 | 0.0 | −7.3 | −11.1 | −0.4 | −1.8 | |
| 3 | 0.0 | −11.2 | −20.1 | 3.6 | 1.8 | |
| 4 | −1.0 | 3.8 | −31.4 | 84.2 | 200.1 | |
| IPC | 1 | 0.0 | 0.1 | 0.6 | −0.1 | −5.5 |
| 2 | 0.0 | 1.1 | 6.7 | 0.8 | −27.2 | |
| 3 | 0.0 | 4.6 | 28.5 | 4.9 | −38.9 | |
| 4 | −69.9 | −15.4 | 17.7 | 92.2 | −20.8 | |
| Peak Shaving | 1 | −1.2 | −18.4 | −9.8 | −6.9 | −3.4 |
| 2 | −1.8 | −9.8 | −15.2 | −9.1 | −1.3 | |
| 3 | −2.8 | −4.2 | −20.9 | −14.4 | −4.2 | |
| 4 | −4.4 | 2.9 | −25.5 | −18.3 | −3.6 | |
| Nacelle Feedback | 1 | 0.0 | −2.5 | −30.9 | −4.2 | −0.8 |
| 2 | 0.0 | −2.9 | −41.5 | −5.3 | −1.3 | |
| 3 | 0.0 | 1.9 | −50.2 | −8.8 | −1.2 | |
| 4 | 0.1 | 69.2 | −38.7 | −8.5 | 23.3 | |
| DLC | No. | Wind [m/s] | Wave | Current [m/s] | |||
|---|---|---|---|---|---|---|---|
| Hs [m] | Tp [s] | Duration [min] | Gamma [-] | ||||
| 1.2 | 1 | 9.0 | 1.50 | 8.00 | 60.0 | 1.00 | 0.00 |
| 2 | 11.0 | 1.75 | 8.25 | 60.0 | 1.00 | 0.00 | |
| 3 | 13.0 | 2.00 | 8.25 | 60.0 | 1.00 | 0.00 | |
| 1.6 | 4 | 11.0 | 10.72 | 14.08 | 180.0 | 2.50 | 0.00 |
| 5 | 11.0 | 4.50 | 9.00 | 180.0 | 2.50 | 0.00 | |
| 6 | 25.0 | 10.72 | 14.08 | 180.0 | 2.50 | 0.00 | |
| Control Performance [%] (Proposed Control − ROSCO)/ROSCO * 100 | DLC 1.2 | DLC 1.6 | ||||||
|---|---|---|---|---|---|---|---|---|
| No. 1 | No. 2 | No. 3 | No. 4 | No. 5 | No. 6 | |||
| Power Production | Mean | Gen. Power | −1.38 | −4.40 | −2.69 | −4.95 | −4.06 | 0.17 |
| Std.Dev. | Rot. Speed | −9.93 | −23.64 | −9.97 | −11.32 | −24.68 | −49.37 | |
| RNA Acc. | Max. | X-Direction | 4.41 | −17.15 | −22.10 | −4.14 | −15.87 | −8.15 |
| Platform Motion | Std.Dev. | Pitch | −12.94 | −19.76 | −9.69 | −9.31 | −20.28 | −8.23 |
| Yaw | −4.56 | −5.95 | −10.18 | −10.83 | −9.10 | −13.50 | ||
| Mooring Tension | Std.Dev. | Chain 3 | 0.27 | −3.45 | −1.28 | −1.29 | −1.22 | 0.47 |
| Wire 4 | −12.35 | −29.25 | −36.34 | −11.18 | −28.82 | −2.73 | ||
| Wire 5 | −7.21 | −27.34 | −38.75 | −8.63 | −27.80 | 1.73 | ||
| Fatigue Load | DEL | Blade My | −12.34 | −17.61 | −17.48 | −17.73 | −23.38 | −14.43 |
| Tower My | −2.45 | −15.7 | −8.61 | −0.25 | −6.30 | −2.47 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, T.; Kim, B.-S.; Kim, J.; Paek, I.; Lim, C.-H. Parametric Analysis of Control Techniques for 15 MW Semi-Submersible Floating Wind Turbine. Appl. Sci. 2025, 15, 519. https://doi.org/10.3390/app15020519
Jeon T, Kim B-S, Kim J, Paek I, Lim C-H. Parametric Analysis of Control Techniques for 15 MW Semi-Submersible Floating Wind Turbine. Applied Sciences. 2025; 15(2):519. https://doi.org/10.3390/app15020519
Chicago/Turabian StyleJeon, Taesu, Byung-Soo Kim, Jaecheon Kim, Insu Paek, and Chang-Hyuck Lim. 2025. "Parametric Analysis of Control Techniques for 15 MW Semi-Submersible Floating Wind Turbine" Applied Sciences 15, no. 2: 519. https://doi.org/10.3390/app15020519
APA StyleJeon, T., Kim, B.-S., Kim, J., Paek, I., & Lim, C.-H. (2025). Parametric Analysis of Control Techniques for 15 MW Semi-Submersible Floating Wind Turbine. Applied Sciences, 15(2), 519. https://doi.org/10.3390/app15020519






