A Deviation Correction Technique Based on Particle Filtering Combined with a Dung Beetle Optimizer with the Improved Model Predictive Control for Vertical Drilling
Abstract
1. Introduction
1.1. General Background
1.2. Literature Review
1.3. The Hypothesis of This Study
2. Assumptions and Limitations in Research
2.1. Assumptions
2.2. Limitations
3. Process Analysis with Problem Description
3.1. Problem Description
Model Robustness to Small-Angle Approximation
4. Deviation Correcting Technique
4.1. Design of Control System
4.2. Design of Dung Beetle Optimizer Particle Filter
4.2.1. Prediction Step
4.2.2. Update Step
4.2.3. Comparison with Bayesian Filtering Methods
| Algorithm 1 DBOPF for vertical drilling | |
| 1: | Require: values of measurement |
| 2: | Ensure: estimated variables |
| 3: | (a) Initializing: |
| 4: | Transform angles from measurements by (2) |
| 5: | |
| 6: | Establish prior probability distributions for process and measurement noise. |
| 7: | |
| 8: | (10) |
| 9: | Initialize a dung beetle set from the prior probability distribution of process |
| 10: | (6) |
| 11: | (7) |
| 12: | for do |
| 13: | (b) Importance sampling |
| 14: | One step prediction from prediction function (1) |
| 15: | |
| 16: | |
| 17: | (c) Updating the weights |
| 18: | convert the angles from measurement by (2) |
| 19: | |
| 20: | |
| 21: | |
| 22: | |
| 23: | |
| 24: | (d) Resampling and estimating |
| 25: | |
| 26: | |
| 27: | convert the angles to inclination and azimuth by (2) |
| 28: | (11) |
| 29: | end for |
4.3. Design of Model Predictive Controller
4.3.1. The Objective of the Model Predictive Controller
4.3.2. Incorporating Real-World Errors
Measurement Tool Alignment Errors
Local Gravity Variations
Magnetic Field Bias
4.3.3. The Modified MPC
Filter Enhancement
MPC Constraints
Sigmoid Weight Adjustment:
5. Discussion of Results
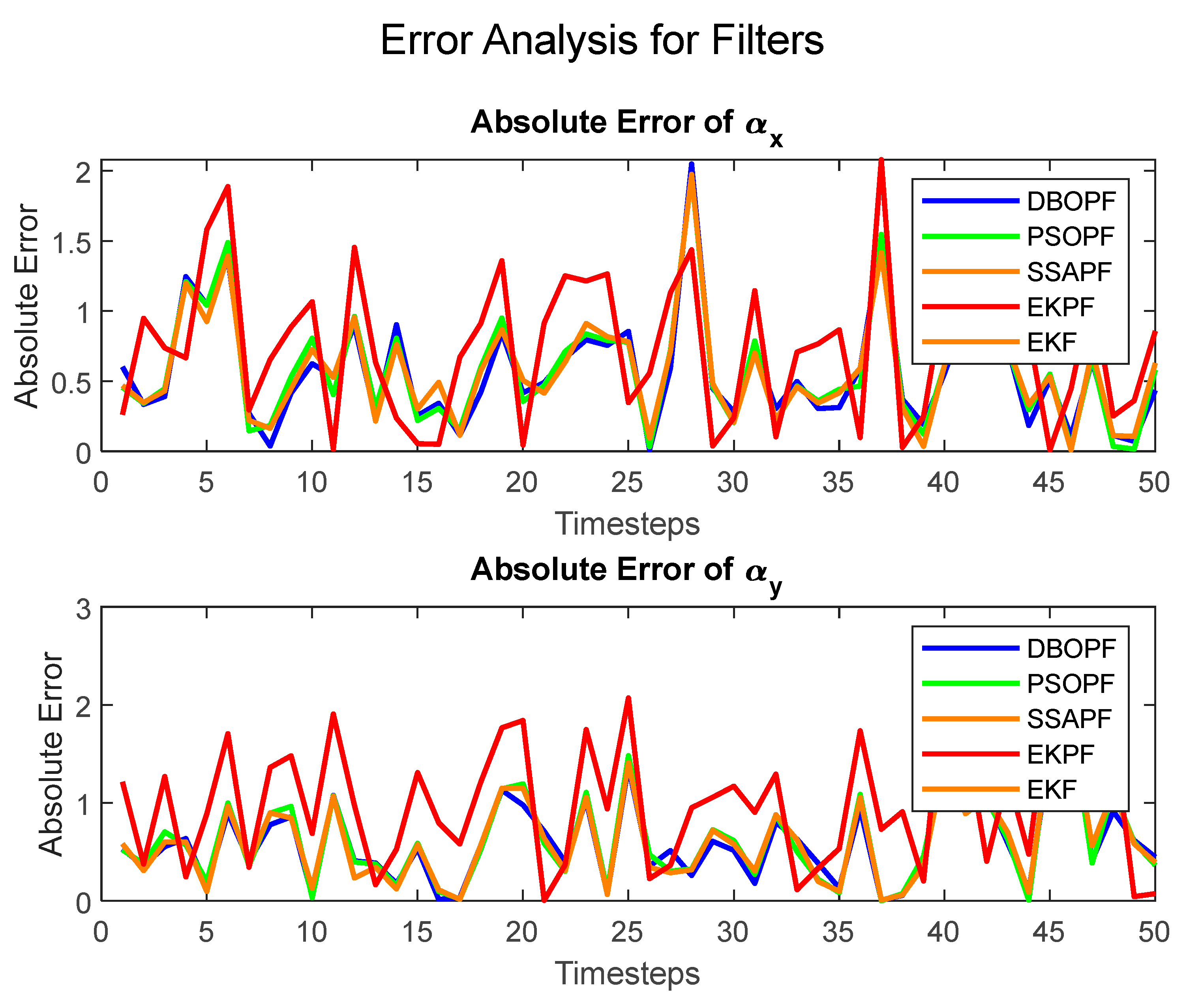
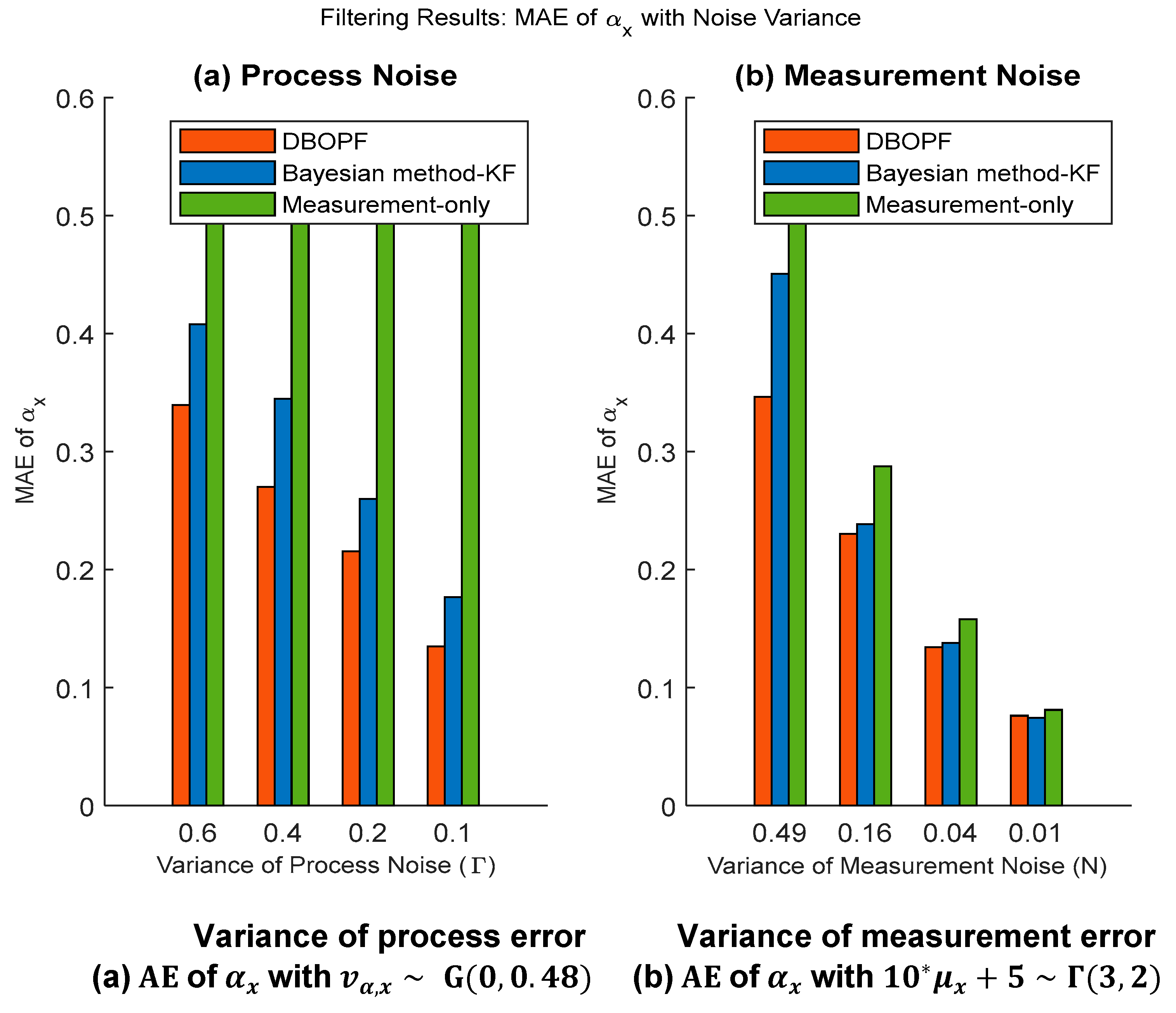
5.1. Analysis of Filtering
5.2. Dynamic Response of Correction Technique
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclatures
| BHA | bottom hole assembly |
| DBO | dung beetle optimizer |
| EKF | extended Kalman filter |
| EKPF | extended Kalman particle filter |
| IPC | industrial personal computer |
| KF | Kalman filter |
| MPC | model predictive control |
| MAE | mean absolute error |
| PF | particle filter |
| PSO | particle swarm optimizer |
| RMSE | root mean square error |
| SSA | sparrow search algorithm |
| SIR | sampling importance resampling |
References
- Tian, J.; Dheyaa, A. State-of-the-art review on Automatic Vertical Drilling Tools: Addressing vibrational load challenges in oil and gas operations. Results Eng. 2025, 25, 104416. [Google Scholar] [CrossRef]
- Mahmoud, A.; Gajbhiye, R.; Elkatatny, S. Novel Approach to Enhancing Oil-Based Drilling Fluids Properties Using Combined Organoclays. Arab. J. Sci. Eng. 2025, published. [Google Scholar] [CrossRef]
- Lu, C.; Wu, M.; Chen, X.; Cao, W.; Gan, C.; She, J. Torsional vibration control of drill-string systems with time-varying measurement delays. Inf. Sci. 2018, 467, 528–548. [Google Scholar] [CrossRef]
- Bagheri, M.A.H.; Ashoori, S.; Abdideh, M. Stress field analysis and its effect on wellbore stability and selection of optimal wellbore trajectory in the Asmari Formation of Ahvaz oil field. J. Adv. Appl. Geol. 2024, 14, 202–221. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, C.; Zhang, K.; Liu, B. Measurement Method of Whole Mechanical Automatic Vertical Drilling Tools. Appl. Sci. 2024, 14, 7129. [Google Scholar] [CrossRef]
- Liang, H.; Yin, C.-C.; Su, Y.; Liu, Y.-H.; Li, J.; Gao, R.-Y.; Wang, L.B. Fast simulation of EM telemetry in vertical drilling: A semi-analytical finite-element method with virtual layering technique. Pet. Sci. 2025, 22, 3304–3314. [Google Scholar] [CrossRef]
- Qin, L.; Wang, W.; Shi, M.; Liang, Y.; Tan, P. Attitude Calculation Method of Drilling Tools Based on Cross-Correlation Extraction and ASRUKF. Electronics 2024, 13, 1707. [Google Scholar] [CrossRef]
- Huang, S.; Xu, Z.; Li, Y.; Gou, T.; Yuan, Z.; Shi, J.; Gao, H. Real-Time Model—Data Fusion for Accurate Wellbore Pressure Prediction in HTHP Wells. Appl. Sci. 2025, 15, 9911. [Google Scholar] [CrossRef]
- Wang, G.; Fan, X.; Zhao, J.; Yang, C.; Ma, L.; Dai, W. Iterated Maximum Mixture Correntropy Kalman Filter and Its Applications in Tracking and Navigation. IEEE Sens. J. 2024, 24, 27790–27802. [Google Scholar] [CrossRef]
- Meddah, S.; Doghmane, M.Z.; Ahmed, S.; Abdelhakim, T.; Kidouche, M.; Fah, K. Fractional-order PID controller design for strongly coupled high-frequency axial—Torsional vibrations in drill string system. Int. J. Dyn. Control 2025, 13, 94. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Zhang, J.; Cao, J. Geoenergy Science and Engineering Real-time estimation of geomechanical characteristics using drilling parameter data and LWD. Geoenergy Sci. Eng. 2025, 244, 213450. [Google Scholar] [CrossRef]
- Barjini, A.H.; Khoshnazar, M.; Moradi, H. Design of a sliding mode controller for suppressing coupled axial & torsional vibrations in horizontal drill strings using Extended Kalman Filter. J. Sound Vib. 2024, 586, 118477. [Google Scholar] [CrossRef]
- Kamel, J.M.; Muthalif, A.G.A.; Falah, A.H. A review of vertical drill-string mathematical modelling. Appl. Eng. Sci. 2025, 22, 100227. [Google Scholar] [CrossRef]
- Guo, Q.; Liu, G.; Zhu, J.; Cai, X.; Men, M.; Liang, L.; Wang, A.; Xu, B. Stick–Slip Prevention of Drill Strings Using Model Predictive Control Based on a Nonlinear Finite Element Reduced-Order Model. Processes 2025, 13, 1418. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, W.; Chen, Y.; Shi, S.; Wang, J.; Zhao, R. DNN–GA–RF prediction model for rock strength indicators based on sound level and drilling parameters. Bull. Eng. Geol. Environ. 2024, 83, 360. [Google Scholar] [CrossRef]
- Zhang, K.; Huo, A. Deep reinforcement learning attitude control of stabilized platform for rotary steerable system based on extended state observer. J. Eng. Res. 2025, 13, 2777–2789. [Google Scholar] [CrossRef]
- Nour, M.; Elsayed, S.K.; Mahmoud, O. A supervised machine learning model to select a cost-effective directional drilling tool. Sci. Rep. 2024, 14, 26624. [Google Scholar] [CrossRef]
- Saadeldin, R.; Gamal, H.; Elkatatny, S. Detecting downhole vibrations through drilling horizontal sections: Machine learning study. Sci. Rep. 2023, 13, 6204. [Google Scholar] [CrossRef]
- Alrushud, A.; Mohammad, M.; Oliveira, V.; Zahrani, B. Effect of the rotary steerable system steering mechanism on wellbore tortuosity in Horizontal Wells. In Proceedings of the Offshore Technology Conference Asia, OTCA 2018, Kuala Lumpur, Malaysia, 20–23 March 2018. [Google Scholar] [CrossRef]
- Litvinenko, V.S.; Dvoinikov, M.V. Justification of the technological parameters choice for well drilling by rotary steerable systems. J. Min. Inst. 2019, 235, 24–29. [Google Scholar] [CrossRef]
- Huo, A.; Zhang, K.; Jiang, X. Enhanced toolface angle control of stabilized platform using I_DDPG in rotary steerable system. Int. J. Mach. Learn. Cybern. 2025, 16, 5493–5507. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, N.; Li, F. Steering drilling wellbore trajectory prediction based on the NOA-LSTM-FCNN method. Sci. Rep. 2025, 15, 5215. [Google Scholar] [CrossRef]
- Zhang, D.; Wu, M.; Lu, C.; Chen, L.; Cao, W. A deviation correction strategy based on particle filtering and improved model predictive control for vertical drilling. ISA Trans. 2021, 111, 265–274. [Google Scholar] [CrossRef] [PubMed]
- Meng, S.; Wang, C.; Zhou, Y.; Hou, L. Research on Data-Driven Drilling Safety Grade Evaluation System. Processes 2025, 13, 2469. [Google Scholar] [CrossRef]
- Cao, W.; Mei, D.; Guo, Y.; Ghorbani, H. Deep learning approach to prediction of drill-bit torque in directional drilling sliding mode: Energy saving Total Strokes per Minute. Measurement 2025, 250, 117144. [Google Scholar] [CrossRef]
- Ye, M.; Zhou, H.; Yang, H.; Hu, B. Multi-Strategy Improved Dung Beetle Optimization Algorithm and Its Applications. Biomimetics 2024, 9, 291. [Google Scholar] [CrossRef]
- Xu, H.; Xu, L.; Shen, S. Online identification methods for a class of Hammerstein nonlinear systems using the adaptive particle filtering. Chaos Solitons Fractals 2024, 186, 115181. [Google Scholar] [CrossRef]
- Kuptametee, C.; Michalopoulou, Z.H.; Aunsri, N. A review of efficient applications of genetic algorithms to improve particle filtering optimization problems. Meas. J. Int. Meas. Confed. 2024, 224, 113952. [Google Scholar] [CrossRef]
- Ejike, C.; Obuobi, I.F.; Avinu, S.; Abid, K.; Teodoriu, C. Investigation and Analysis of Influential Parameters in Bottomhole Stick–Slip Calculation during Vertical Drilling Operations. Energies 2024, 17, 622. [Google Scholar] [CrossRef]
- Ao, Y.; Köhler, J.; Prajapat, M.; As, Y.; Zeilinger, M.; Fürnstahl, P.; Krause, A. Stochastic Model Predictive Control for Sub-Gaussian Noise. arXiv 2025, arXiv:2503.08795. [Google Scholar] [CrossRef]

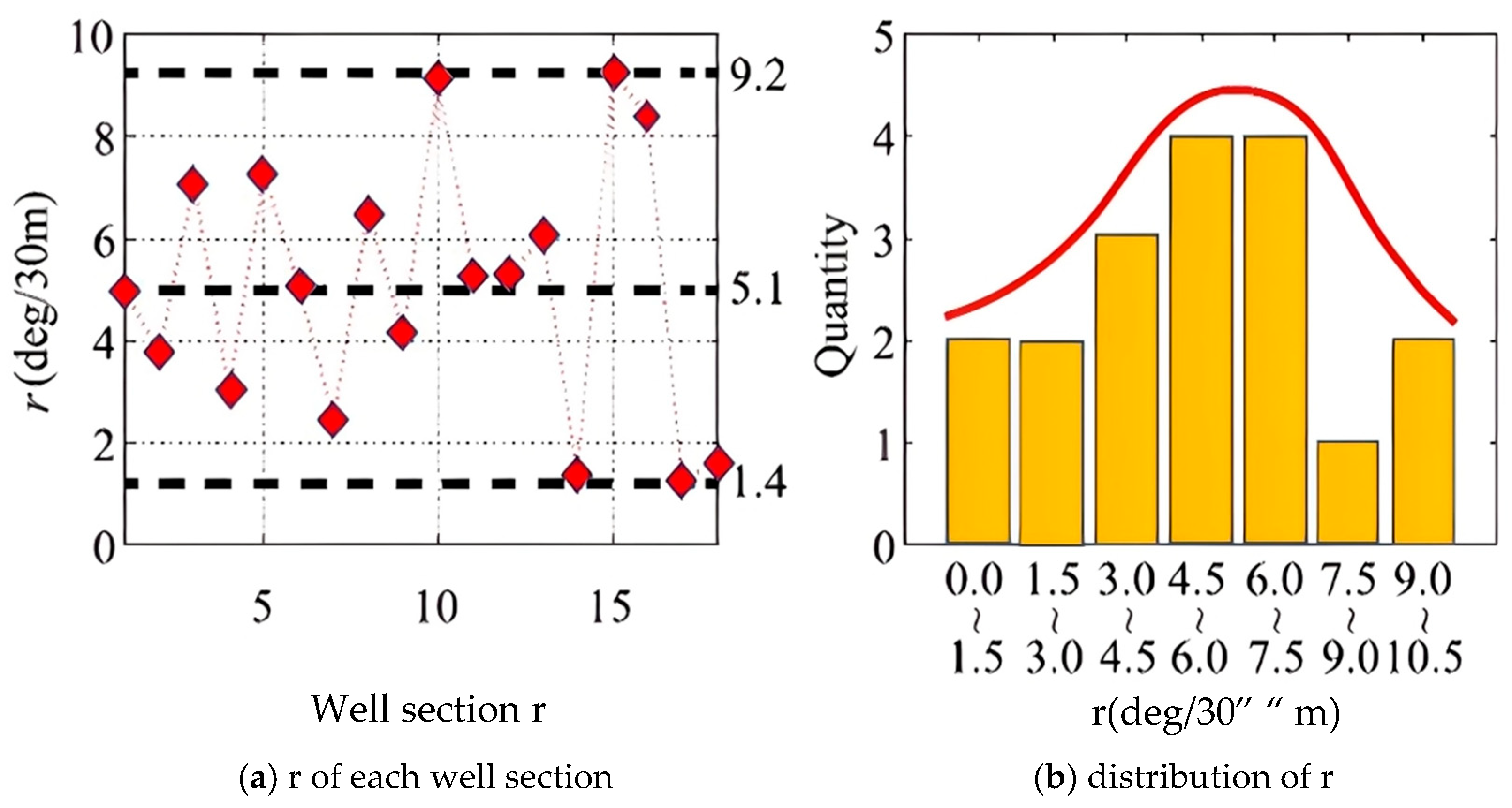

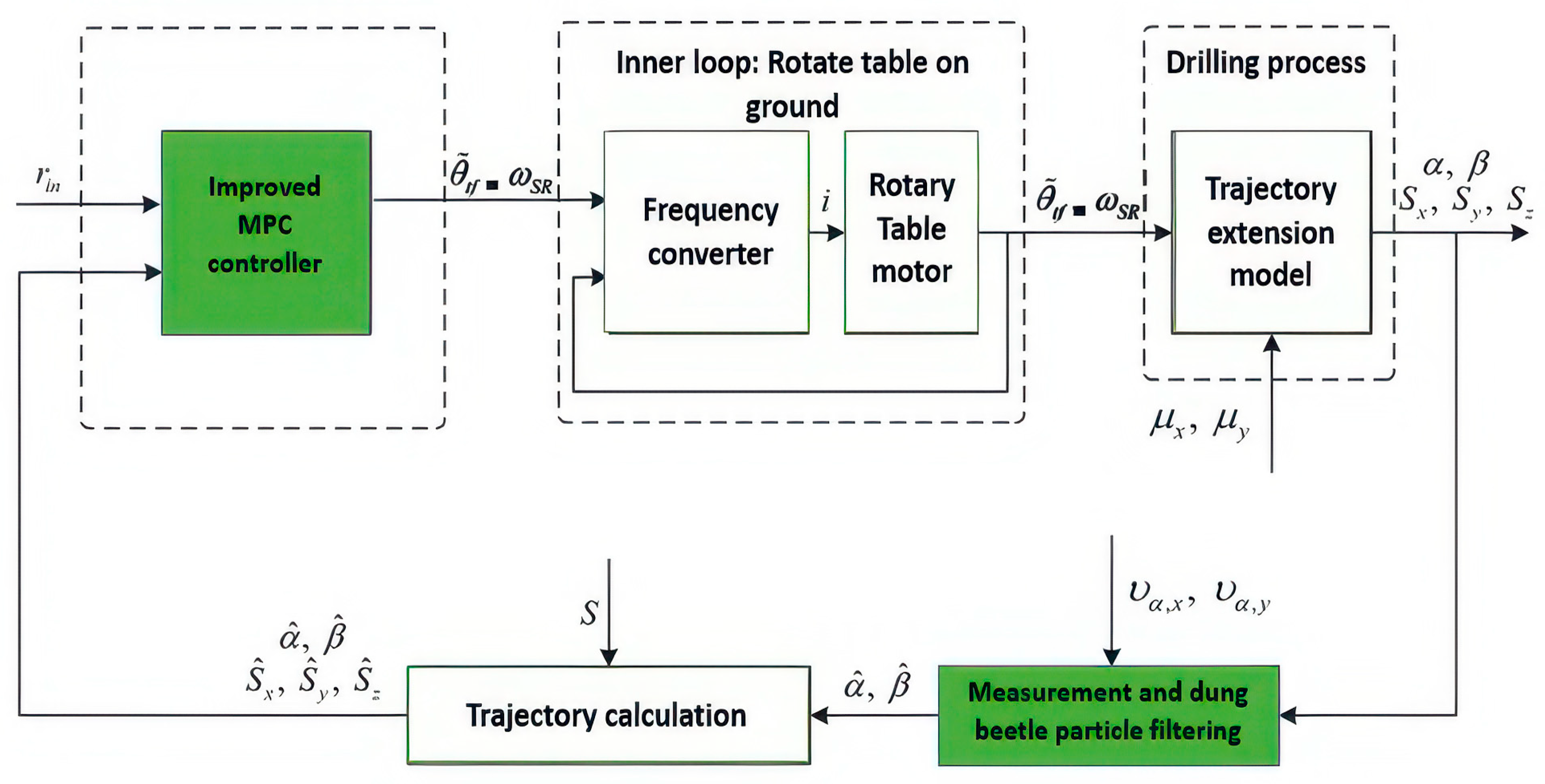
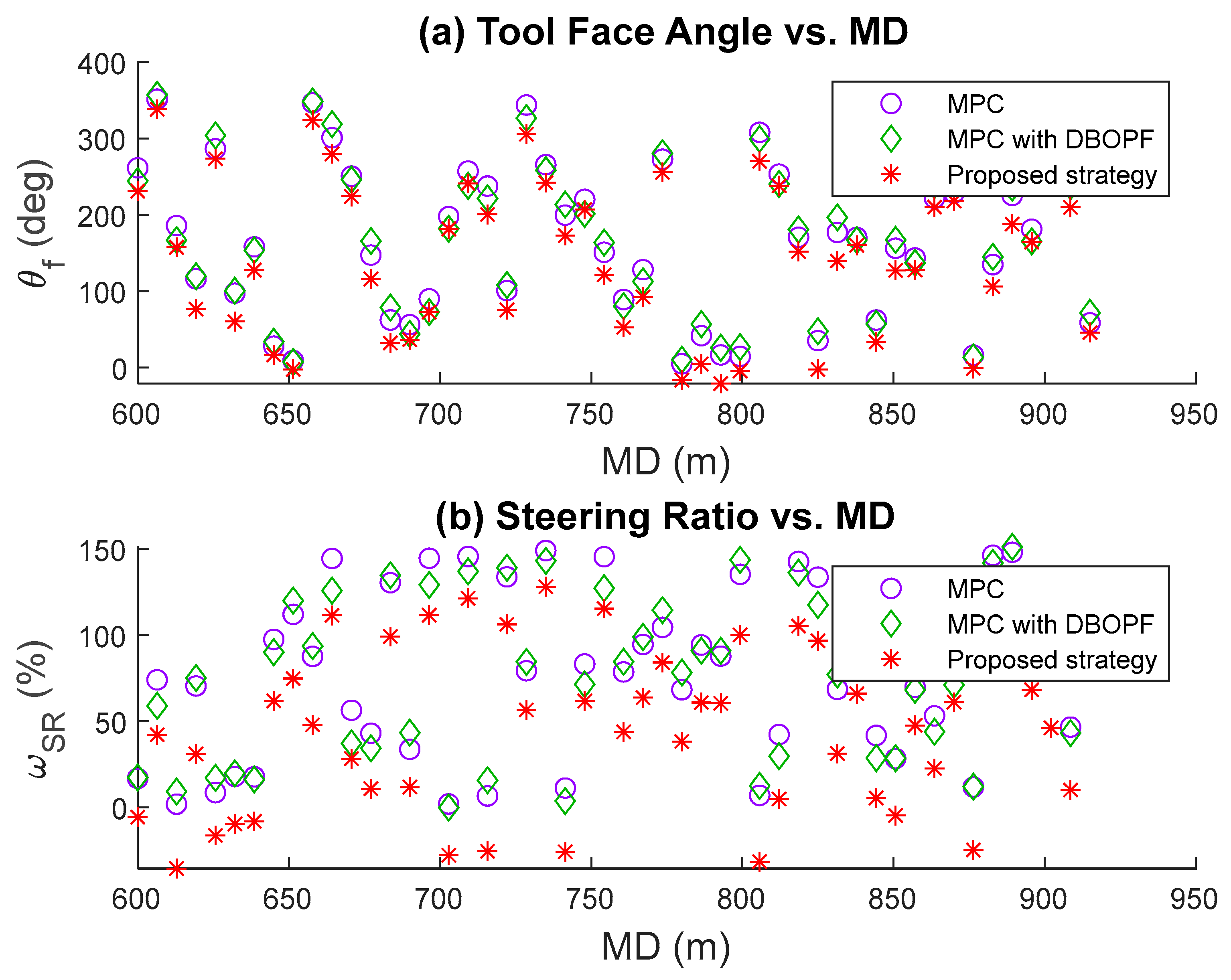
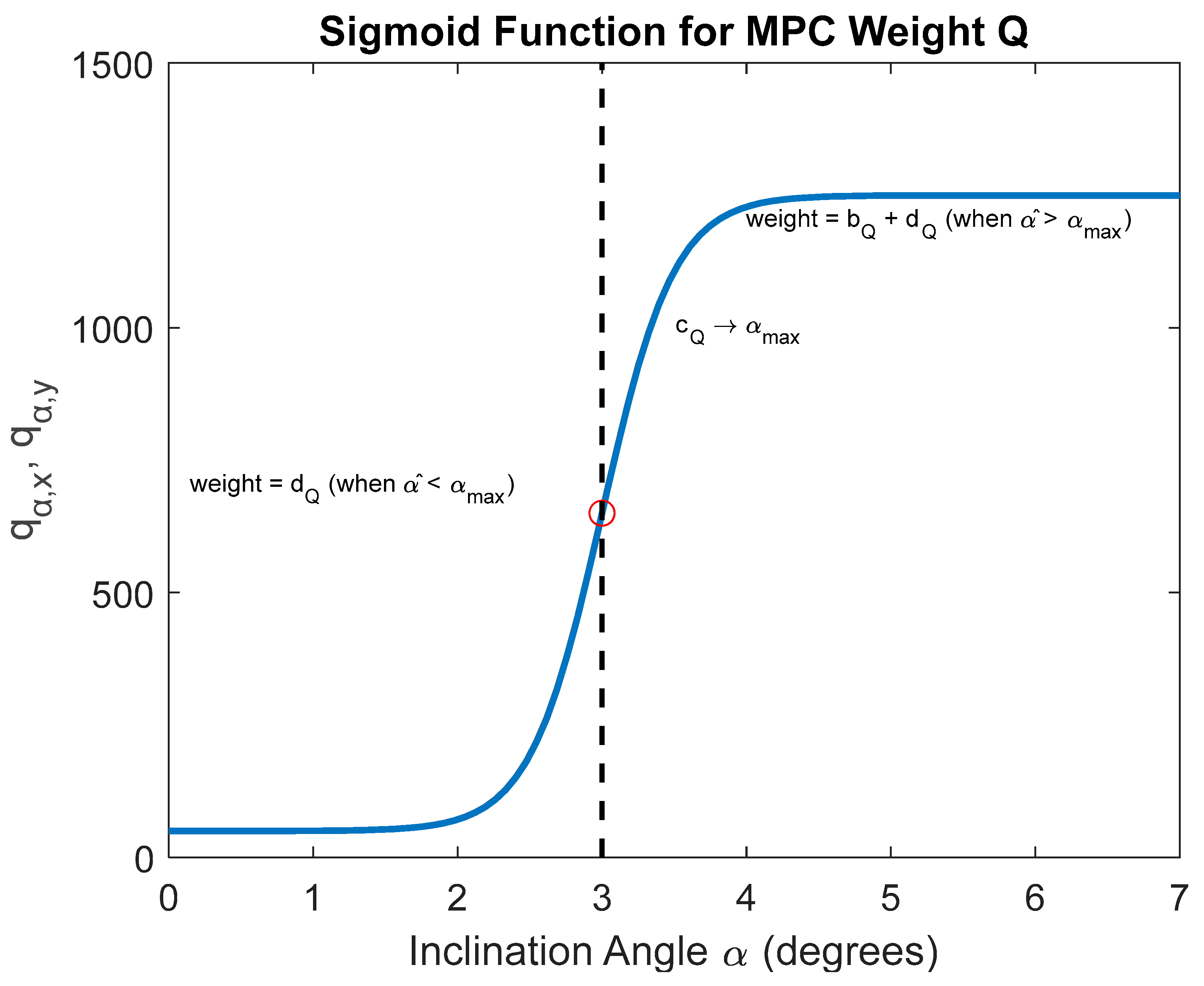

| Parameter | Description |
|---|---|
| 0.3 h | |
| 6 | |
| [40,000,40,000] | |
| Monte Carlo | 1000 iteration, the convergence criterion was set to a maximum difference of 0.01 |
| Dung beetle optimizer | 100 particles, 500 iterations, coefficients of = 0.5 and b = 0.3, process noise was adjusted to 0.05 |
| Filter | ||||
|---|---|---|---|---|
| Mean Absolute Error | Root Mean Square Error | Mean Absolute Error | Root Mean Square Error | |
| DBO | 0.26353 | 0.33564 | 0.27816 | 0.35095 |
| PSO | 0.35853 | 0.43881 | 0.36174 | 0.42351 |
| SSA | 0.36541 | 0.44032 | 0.35976 | 0.43674 |
| EKPF | 0.45944 | 0.47738 | 0.44664 | 0.48287 |
| EKF | 0.73652 | 0.92605 | 1.00715 | 1.2682 |
| DBOPF | Bayesian Method (Kalman Filter) | ||
|---|---|---|---|
| * | 0.32822 | 0.38354 | 0.54774 |
| * | 0.26789 | 0.33776 | 0.56223 |
| * | 0.21055 | 0.23565 | 0.53594 |
| * | 0.13326 | 0.15849 | 0.54381 |
| DBOPF | Bayesian Method (Kalman Filter) | ||
|---|---|---|---|
| 0.33657 | 0.42846 | 0.54987 | |
| 0.22094 | 0.25547 | 0.29076 | |
| 0.13006 | 0.14309 | 0.16034 | |
| 0.06983 | 0.08123 | 0.09134 |
| α/∘ | α/∘ | |||||
|---|---|---|---|---|---|---|
| 600 | 9.82 | 1.55 | 1.6 | 9.82 | 1.52 | 1.5 |
| 700 | 12.61 | 1.42 | 1.7 | 4.39 | 0.94 | 3.1 |
| 800 | 16.26 | 1.15 | 2.2 | 0.13 | 0.03 | 0.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albabo, A.; Wen, G.; Cheng, S.; Mustafa, A.; Qiu, W. A Deviation Correction Technique Based on Particle Filtering Combined with a Dung Beetle Optimizer with the Improved Model Predictive Control for Vertical Drilling. Appl. Sci. 2025, 15, 10773. https://doi.org/10.3390/app151910773
Albabo A, Wen G, Cheng S, Mustafa A, Qiu W. A Deviation Correction Technique Based on Particle Filtering Combined with a Dung Beetle Optimizer with the Improved Model Predictive Control for Vertical Drilling. Applied Sciences. 2025; 15(19):10773. https://doi.org/10.3390/app151910773
Chicago/Turabian StyleAlbabo, Abobaker, Guojun Wen, Siyi Cheng, Asaad Mustafa, and Wangde Qiu. 2025. "A Deviation Correction Technique Based on Particle Filtering Combined with a Dung Beetle Optimizer with the Improved Model Predictive Control for Vertical Drilling" Applied Sciences 15, no. 19: 10773. https://doi.org/10.3390/app151910773
APA StyleAlbabo, A., Wen, G., Cheng, S., Mustafa, A., & Qiu, W. (2025). A Deviation Correction Technique Based on Particle Filtering Combined with a Dung Beetle Optimizer with the Improved Model Predictive Control for Vertical Drilling. Applied Sciences, 15(19), 10773. https://doi.org/10.3390/app151910773





