Investigation on Ground Collapse Due to Exfiltration of Shallowly Buried Water-Supply Pipeline
Abstract
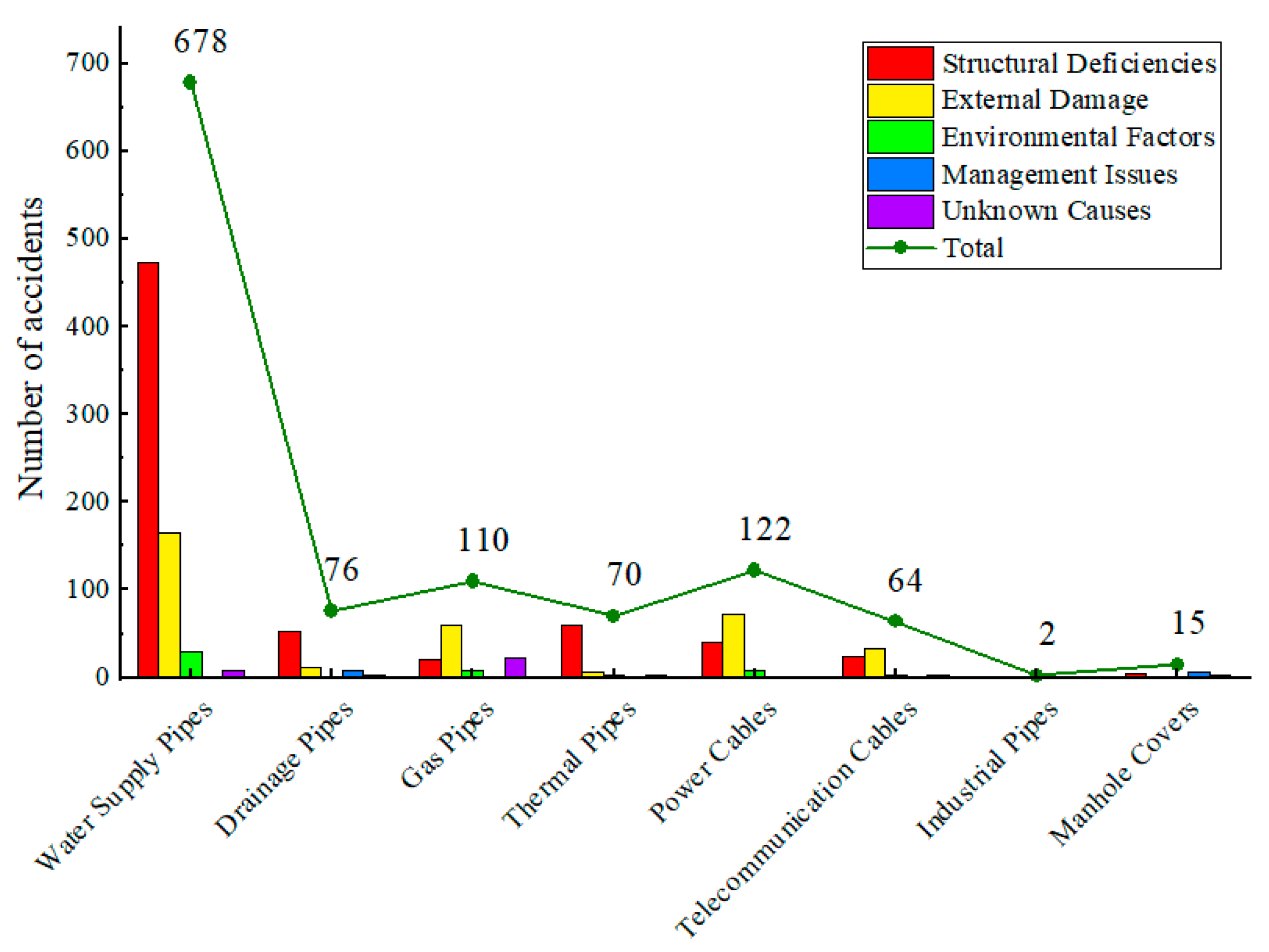
1. Introduction
2. Laboratory Model Test
2.1. Similarity Law
2.2. Model Setup
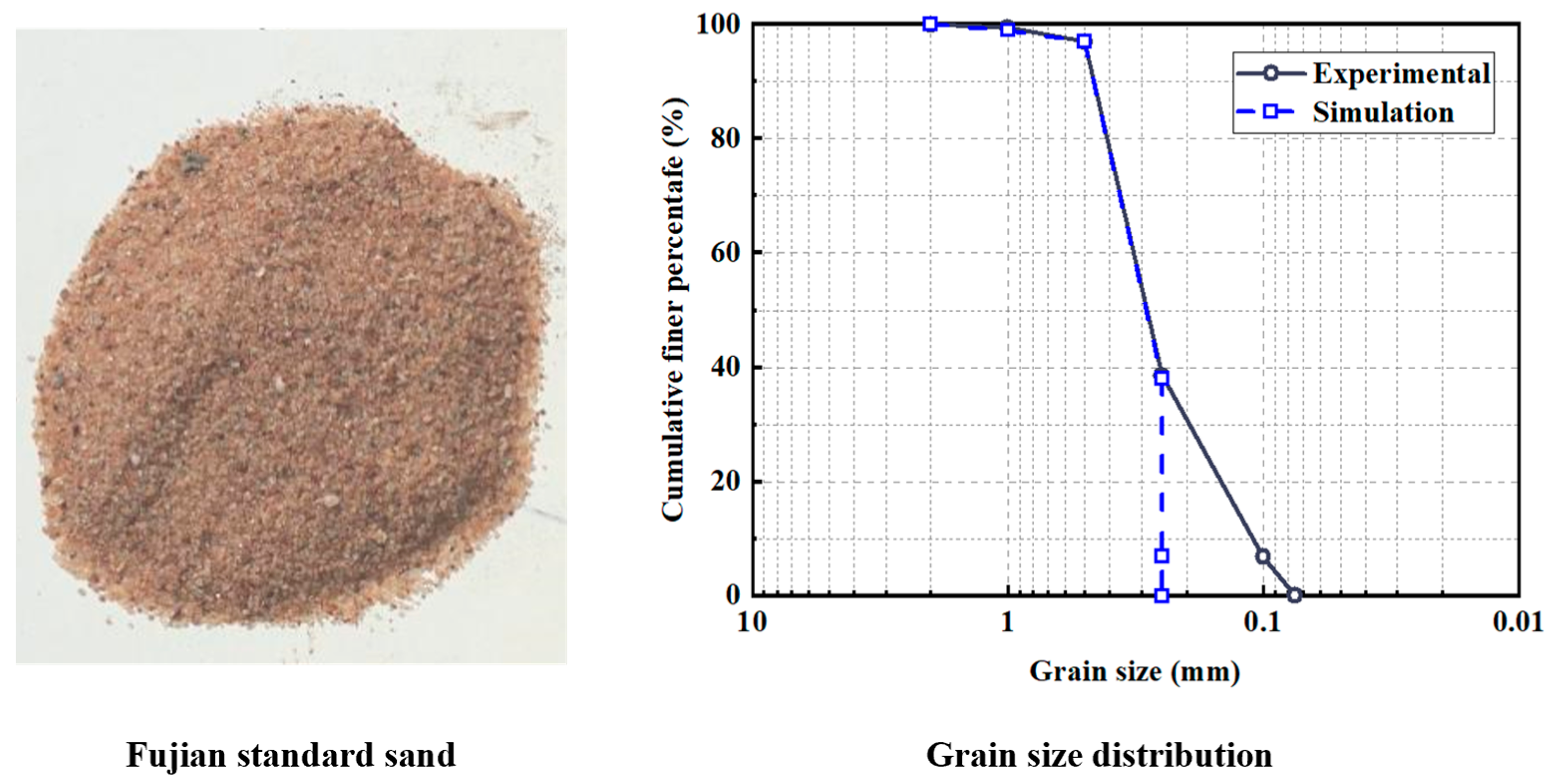
2.3. Test Materials and Parameters
3. Analyses on Test Results
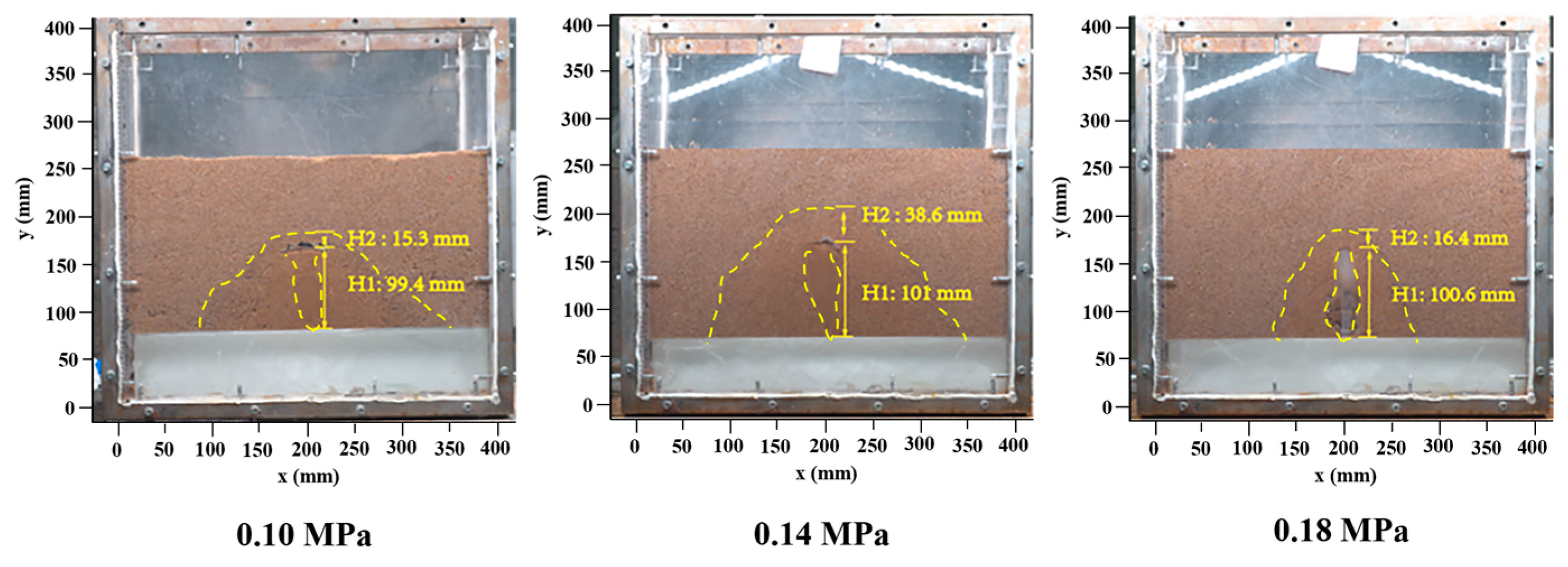
3.1. Influence of Water Pressure
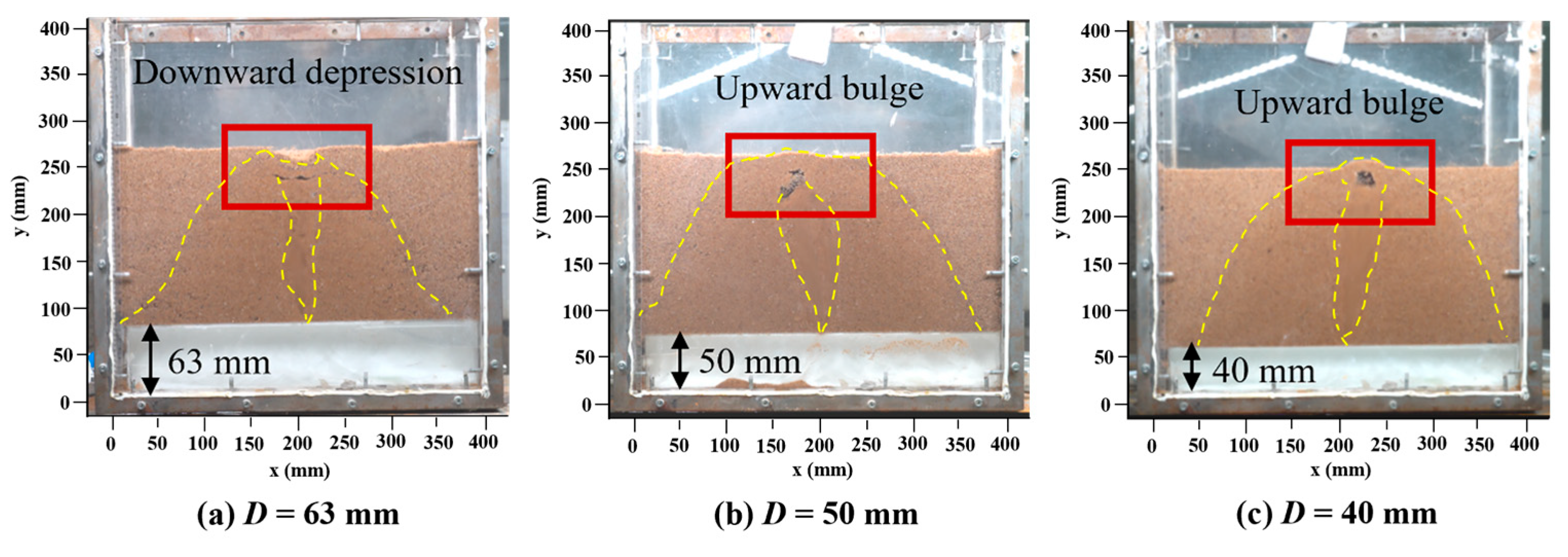
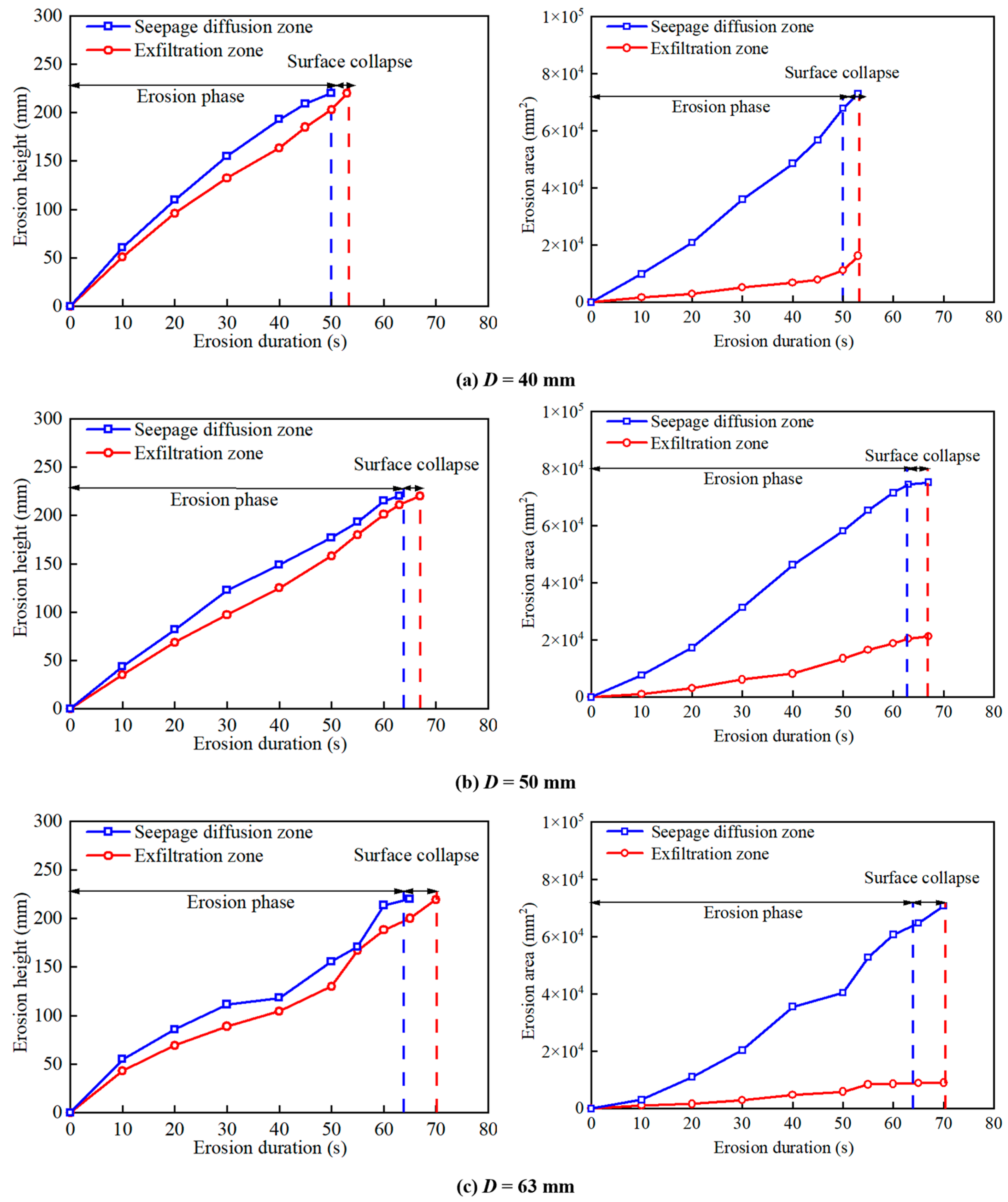
3.2. Influence of Pipe Diameter
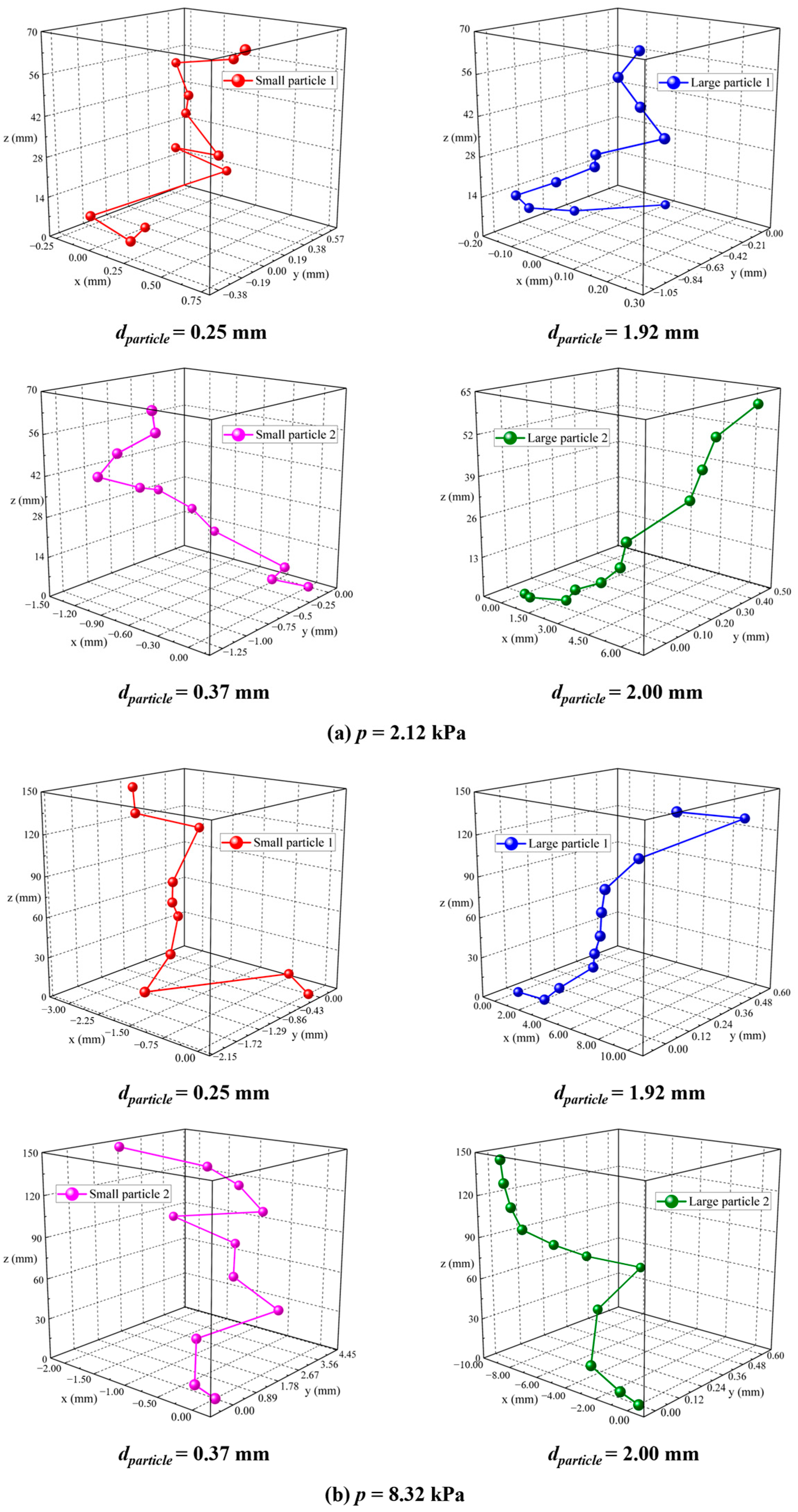
4. Numerical Simulation
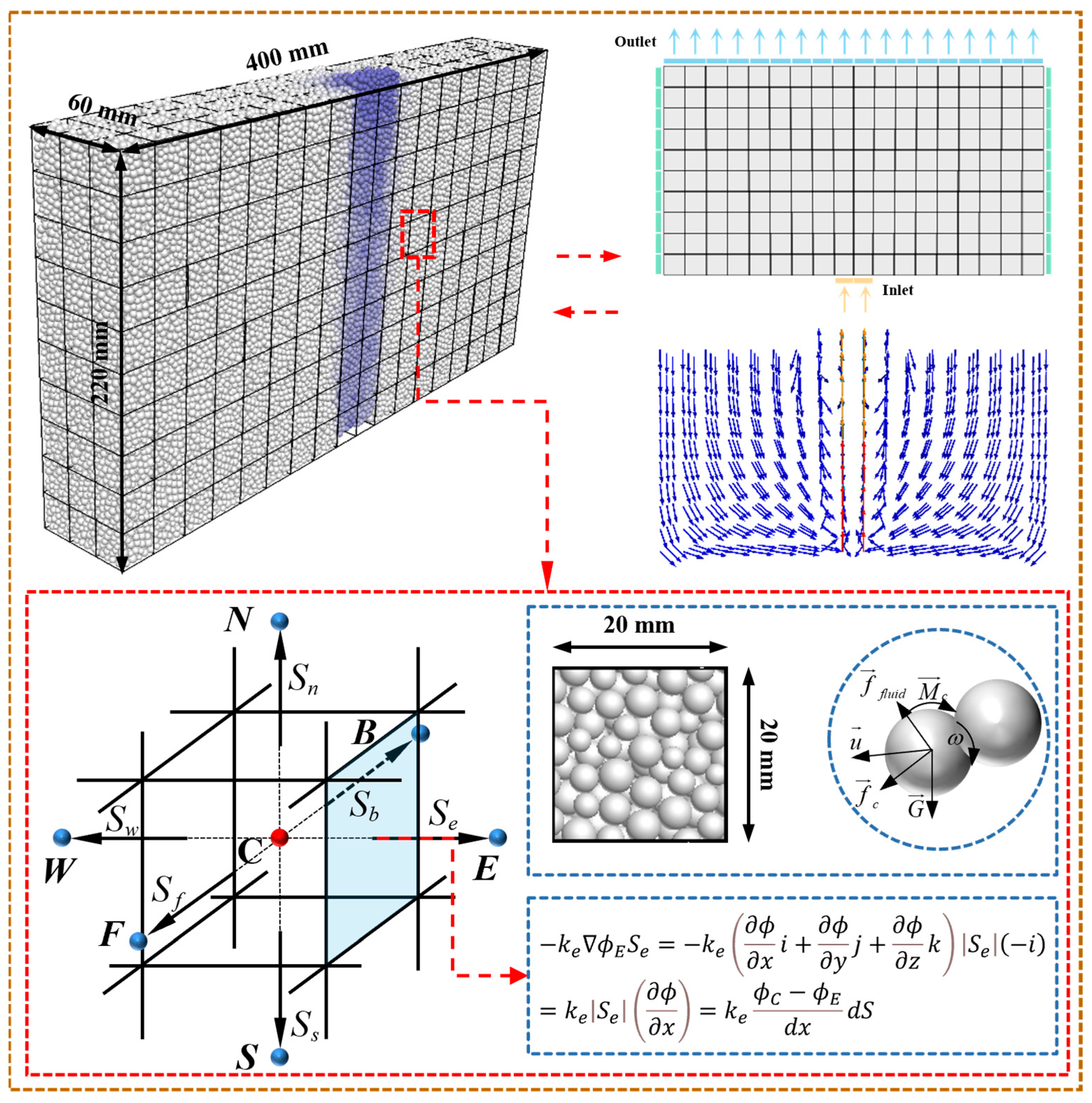
4.1. Model Setup
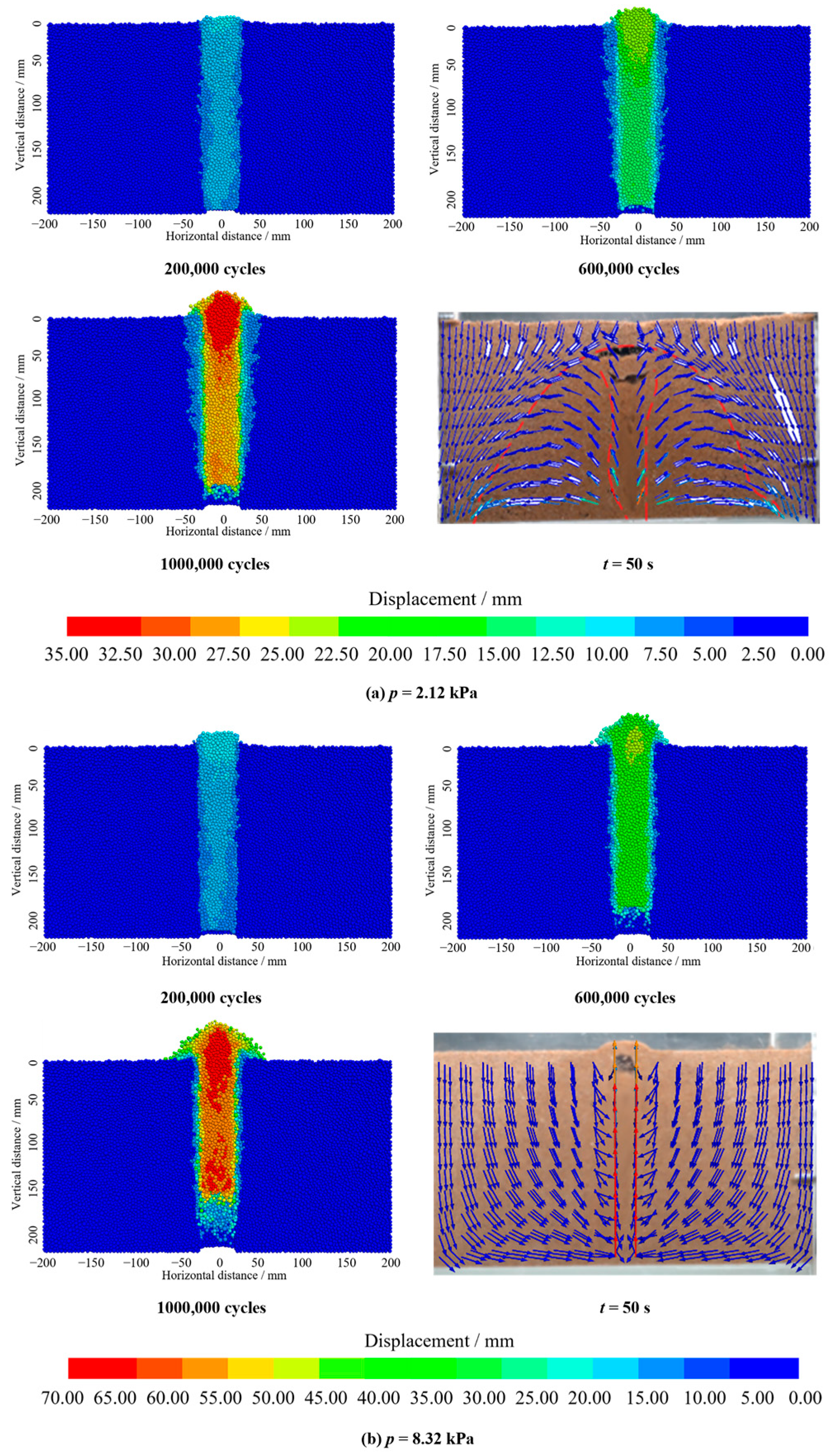
4.2. Influence of Water Pressure
5. Conclusions
- (1)
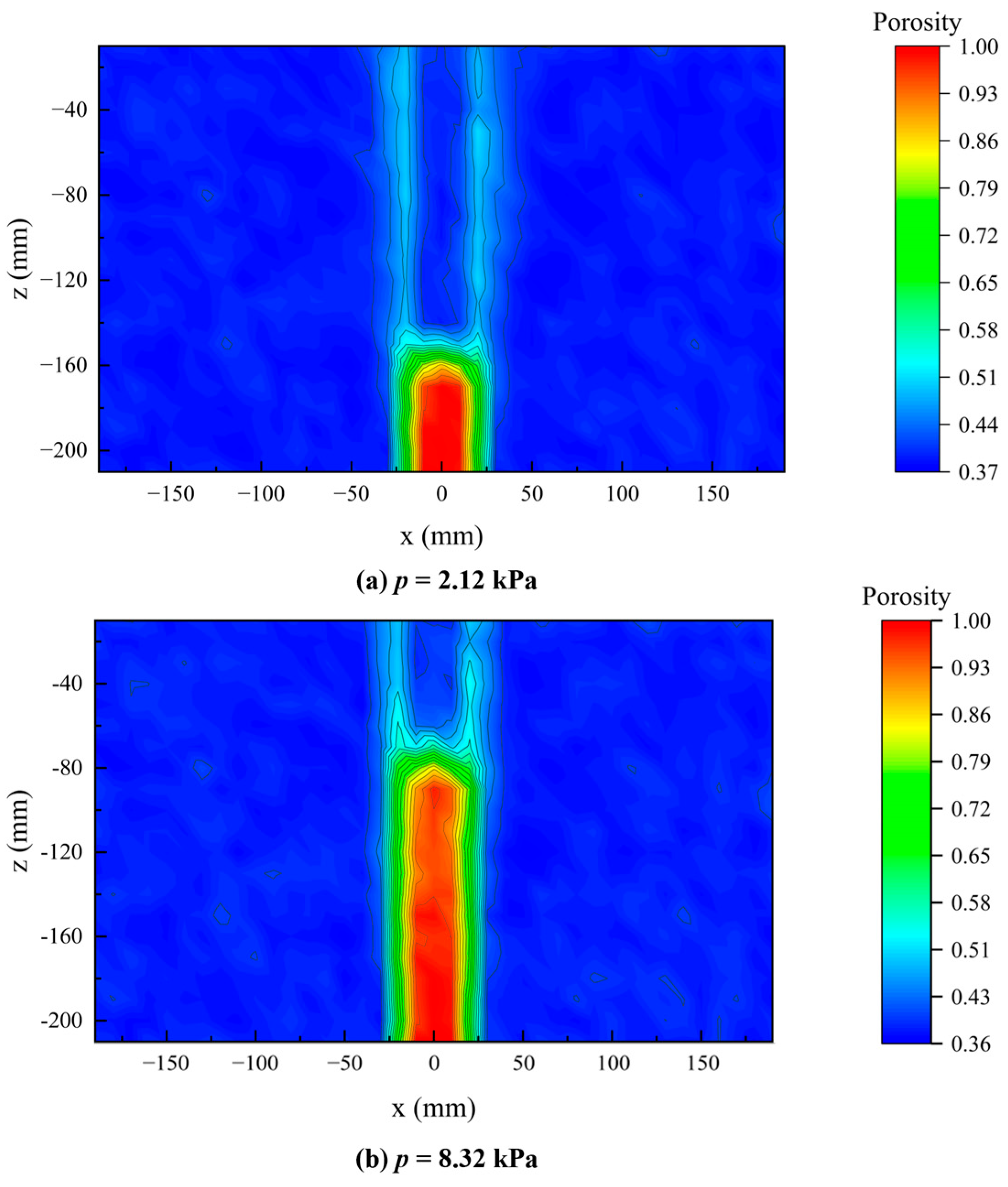
- Both the laboratory model tests and numerical simulation show that the erosion zone can be divided into two zones, the exfiltration zone and the seepage diffusion zone. Within the exfiltration zone, an entrainment phenomenon occurred in the lateral section, while a vortex-induced soil–water mixture formed in the middle section due to resistance from the soil weight. Soil erosion was rapid in the exfiltration zone, resulting in a significant increase in local porosity. In some cases, local porosity in exfiltration zone could reach 1.0, meaning there were no soil particles remaining in those regions.
- (2)
- Under high inlet pressure (pc = 0.18 MPa), pressurized water flow from the fracture strongly inhibited lateral seepage diffusion of water, resulting in a height difference of 16.4 mm between the exfiltration zone and seepage diffusion zone. Under low inlet pressure (pc = 0.10 MPa), there was an extended seepage diffusion zone, and the height difference between the exfiltration zone and seepage diffusion zone increased to 38.6 mm. This phenomenon was related to the balance between hydraulic gradient and critical shear stress of soil.
- (3)
- The inlet pressure had an effect on the ground collapse process; when the inlet pressure of the laboratory test model increased from 0.10 MPa to 0.18 MPa, the ground collapse duration time of the fractured prototype pipe was reduced by 22–28% (from 125 s to 98 s, and the initial exfiltration velocity increased from 5.2 mm/s to 9.4 mm/s. According to the laboratory test results, the erosion velocity was exponentially related to time. Reducing the pipe diameter was equivalent to increasing the water pressure. Under a small pipe diameter, there was a cavity between the exfiltration zone and the ground surface, which caused ground bulging. Under a large pipe diameter, the cavity diminished and ground subsidence occurred. The formation of the cavity was related to the erosion height and flow pressure of the erosion process.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peng, S.; Huang, W.; Luo, G.; Cao, H.; Pan, H.; Mo, N. Failure mechanisms of ground collapse caused by shield tunnelling in water-rich composite sandy stratum: A case study. Eng. Fail. Anal. 2023, 146, 107100. [Google Scholar] [CrossRef]
- Zhang, C.P.; Zhang, D.L.; Wang, M.S.; Li, Q.Q. Catastrophe mechanism and control technology of ground collapse induced by urban tunneling. Rock Soil Mech. 2010, 31, 303–309. [Google Scholar]
- Alarifi, H.; Mohamad, H.; Nordin, N.F.; Yusoff, M.; Rafindadi, A.D.; Widjaja, B. A large-scale model of lateral pressure on a buried pipeline in medium dense sand. Appl. Sci. 2021, 11, 5554. [Google Scholar] [CrossRef]
- China Association of City Planning. Urban Planning Association Statistical Analysis Report of Underground Pipeline Accidents in China in 2023; Underground Pipeline Comprehensive Management Research Center: Beijing, China, 2024. [Google Scholar]
- Barfuss, S.L.; Fugal, M. Water main break rates in the United States and Canada. J. Am. Water Work. Assoc. 2025, 117, 22–33. [Google Scholar] [CrossRef]
- Dastpak, P.; Sousa, R.L.; Dias, D. Soil erosion due to defective pipes: A hidden hazard beneath our feet. Sustainability 2023, 15, 8931. [Google Scholar] [CrossRef]
- Tan, Y.; Long, Y.Y. Review of cave-in failures of urban roadways in China: A database. J. Perform. Constr. Facil. 2021, 35, 4021080. [Google Scholar] [CrossRef]
- Liu, C.; Chen, B.; Luo, H.; Ruan, J. Experimental study on seepage erosion induced by pipeline damage under full pipe flow condition. Rock Soil Mech. 2020, 41, 1. [Google Scholar]
- Shao, Y.; Yao, T.; Gong, J.; Liu, J.; Zhang, T.; Yu, T. Impact of main pipe flow velocity on leakage and intrusion flow: An experimental study. Water 2019, 11, 118. [Google Scholar] [CrossRef]
- Yu, T.; Zhang, X.; Neto, I.E.L.; Zhang, T.; Shao, Y.; Ye, M. Impact of orifice-to-pipe diameter ratio on leakage flow: An experimental study. Water 2019, 11, 2189. [Google Scholar] [CrossRef]
- Zhang, T.; Jiang, S.; Wu, F.; Shao, Y.; Chu, S. Experimental Study of External Pipe Wall Erosion due to Water Pipe Leakage. J. Pipeline Syst. Eng. Pract. 2023, 14, 4022071. [Google Scholar] [CrossRef]
- Ben-Mansour, R.; Habib, M.; Khalifa, A.; Youcef-Toumi, K.; Chatzigeorgiou, D. Computational fluid dynamic simulation of small leaks in water pipelines for direct leak pressure transduction. Comput. Fluids 2012, 57, 110–123. [Google Scholar] [CrossRef]
- Aghda, S.M.F.; GanjaliPour, K.; Nabiollahi, K. Assessing the accuracy of TDR-based water leak detection system. Results Phys. 2018, 8, 939–948. [Google Scholar] [CrossRef]
- Ozevin, D.; Harding, J. Novel leak localization in pressurized pipeline networks using acoustic emission and geometric connectivity. Int. J. Press. Vessel. Pip. 2012, 92, 63–69. [Google Scholar] [CrossRef]
- Lu, W.; Liang, W.; Zhang, L.; Liu, W. A novel noise reduction method applied in negative pressure wave for pipeline leakage localization. Process Saf. Environ. Prot. 2016, 104, 142–149. [Google Scholar] [CrossRef]
- Long, Y.Y.; Tan, Y. Soil arching due to leaking of tunnel buried in water-rich sand. Tunn. Undergr. Space Technol. 2020, 95, 103158. [Google Scholar] [CrossRef]
- Tang, Y.; Zhu, D.Z.; Chan, D.H.; Zhang, S. Physical and analytical modeling of soil loss caused by a defective sewer pipe with different defect locations. Acta Geotech. 2023, 18, 2639–2659. [Google Scholar] [CrossRef]
- Guo, S.; Zhu, D.Z. Soil and groundwater erosion rates into a sewer pipe crack. J. Hydraul. Eng. 2017, 143, 6017008. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Liu, J.C.; Tan, Y.; Long, Y.-Y. Experimental and numerical investigation on internal erosion induced by infiltration of defective buried pipe. Bull. Eng. Geol. Environ. 2025, 84, 38. [Google Scholar] [CrossRef]
- Chao, H.; Tan, Y.; Su, Z.K. Ground failure and soil erosion caused by bursting of buried water pipeline: Experimental and numerical investigations. Eng. Fail. Anal. 2025, 167, 108965. [Google Scholar] [CrossRef]
- Duan, Y.; Zhang, W.; Liu, H.; Chem, J. Dynamics of soil erosion due to underground pipeline fractures: A transparent soil study under varied hydraulic conditions. J. Comput. Methods Sci. Eng. 2024, 24, 2429–2445. [Google Scholar] [CrossRef]
- Chen, B.; Liu, C.; Li, Q.; Onyekwena, C.C. Experimental and theoretical investigations of ground settlement around submerged defective pipelines. Transp. Geotech. 2024, 49, 101395. [Google Scholar] [CrossRef]
- Karoui, T.; Jeong, S.-Y.; Jeong, Y.-H.; Kim, D.S. Experimental study of ground subsidence mechanism caused by sewer pipe cracks. Appl. Sci. 2018, 8, 679. [Google Scholar] [CrossRef]
- Lee, S.; Kang, J.; Kim, J. A Study on Factors Influencing Ground Subsidence and a Risk Analysis Method Using the Attributes of Sewer Pipes. Appl. Sci. 2023, 13, 9714. [Google Scholar] [CrossRef]
- Hall, S.; Bornert, M.; Desrues, J.; Pannier, Y.; Lenoir, N.; Viggiani, G.; Bésuelle, P. Discrete and continuum analysis of localised deformation in sand using X-ray μCT and volumetric digital image correlation. Géotechnique 2010, 60, 315–322. [Google Scholar] [CrossRef]
- Lu, Y.; Huang, Y.; Hu, Y. Characterization of initialization and formation of shear zones in sandy slopes. Arab. J. Sci. Eng. 2023, 48, 5019–5035. [Google Scholar] [CrossRef]
- Hu, Y.; Lu, Y. Study on soil-rock slope instability at mesoscopic scale using discrete element method. Comput. Geotech. 2023, 157, 105268. [Google Scholar] [CrossRef]
- Liu, F. Multi-scale analyses of granular flows for disaster resilience enhancement. Ga. Inst. Technol. 2019. [Google Scholar]
- Avci, B.; Gurbuz, A. Modulus of subgrade reaction that varies with magnitude of displacement of cohesionless soil. Arab. J. Geosci. 2018, 11, 351. [Google Scholar] [CrossRef]
- Xu, T. Similarity Theory and Model Test; China Agricultural Machinery Press: Beijing, China, 1982. [Google Scholar]
- Heller, V. Self-similarity and Reynolds number invariance in Froude modelling. J. Hydraul. Res. 2017, 55, 293–309. [Google Scholar] [CrossRef]
- Heller, V. Scale effects in physical hydraulic engineering models. J. Hydraul. Res. 2011, 49, 293–306. [Google Scholar] [CrossRef]
- Hughes, S.A. Physical Models and Laboratory Techniques in Coastal Engineering; World Scientific: Singapore, 1993. [Google Scholar]
- Guo, S.; Shao, Y.; Zhang, T.; Zhu, D.Z.; Zhang, Y. Physical modeling on sand erosion around defective sewer pipes under the influence of groundwater. J. Hydraul. Eng. 2013, 139, 1247–1257. [Google Scholar] [CrossRef]
- Yuan, P. Study on Collapse Mechanism of Soil Subgrade of City Roads by Water Erosion; China University of Mining & Technology: Beijing, China, 2015. [Google Scholar]
- Cui, X. Numerical Simulation of Internal Fluidisation and Cavity Evolution Due to a Leaking Pipe Using the Coupled DEM-LBM Technique; University of Birmingham: Birmingham, UK, 2013. [Google Scholar]
- GB 50289-2016; Code for Comprehensive Planning of Urban Engineering Pipeline. China Architecture & Building Press: Beijing, China, 2016.
- Zhao, Z.Y. The Study About Liquid-Pipeline Specification Small Hole Leakage Law and Pressure Calculation Method After Leakage; China University of Petroleum: Qingdao, China, 2018. [Google Scholar]
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- GB/T 50145-2007; Standard for Engineering Classification of Soil. Ministry of Housing and Urban-Rural Development of the People’s Republic of China, China Standard Press: Beijing, China, 2007.
- Tan, X.; Hu, Z.; Cao, M.; Chen, C. 3D discrete element simulation of a geotextile-encased stone column under uniaxial compression testing. Comput. Geotech. 2020, 126, 103769. [Google Scholar] [CrossRef]
- Itasca Consulting Group, INC. PFC3D: Particle Flow Code in 3 Dimensions, Version 9.0; Itasca Consulting Group, Inc.: Minneapolis, MN, USA, 2022; Available online: https://www.itascacg.com/software/pfc (accessed on 15 January 2025).
- Hu, Y.; Lu, Y. A novel framework for calibrating DEM parameters: A case study of sand and soil-rock mixture. Comput. Geotech. 2024, 174, 106619. [Google Scholar] [CrossRef]
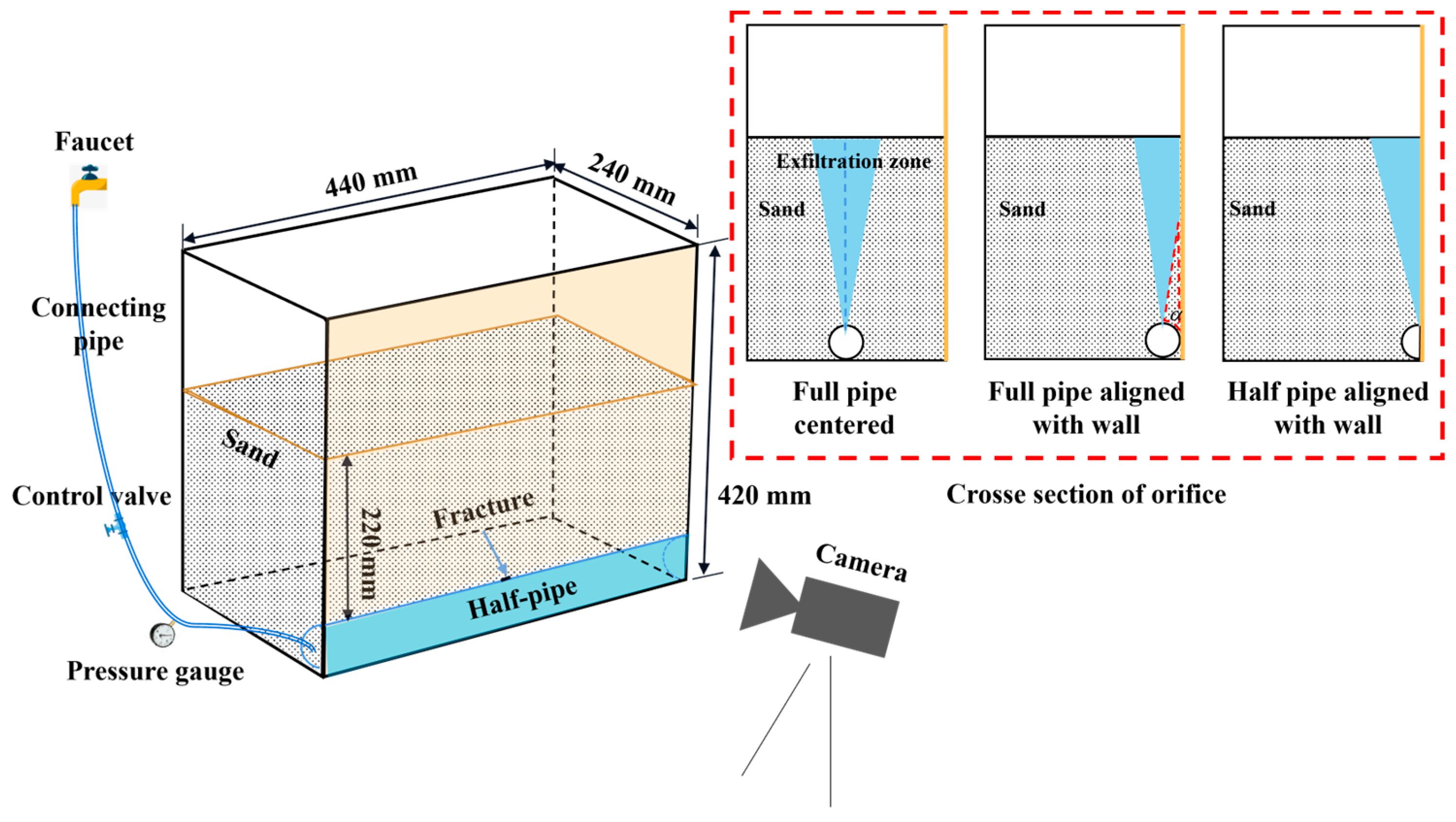







| Connecting Pipe | Half-Pipe Water-Supply System | ||||||
|---|---|---|---|---|---|---|---|
| Diameter Dc (12 mm) | Diameter D (63 mm) | Diameter D (50 mm) | Diameter D (40 mm) | ||||
| Inlet Pressure pc (MPa) | Flow Velocity vc (m/s) | Flow Pressure p (MPa) | Flow Velocity v (m/s) | Flow Pressure p (MPa) | Flow Velocity v (m/s) | Flow Pressure p (MPa) | Flow Velocity v (m/s) |
| 0.10 | 1 | 2.122 × 10−3 | 0.09 | 7.166 × 10−3 | 0.14 | 1.872 × 10−2 | 0.22 |
| 0.14 | 2 | 8.320 × 10−3 | 0.18 | / | / | / | / |
| 0.18 | 3 | 2.412 × 10−2 | 0.27 | / | / | / | / |
| Soil Type | d10 (mm) | d30 (mm) | d50 (mm) | d60 (mm) | Cu | Cc | γ (kN/m3) | c (kPa) | φ (°) |
|---|---|---|---|---|---|---|---|---|---|
| Sand | 0.11 | 0.21 | 0.28 | 0.34 | 3.09 | 1.07 | 19.1 | 0 | 33.5 |
| Test No. | Half-Pipe Diameter D (mm) | Overlaying Soil Thickness H (mm) | Flow Pressure in Connecting Pipe pc (MPa) |
|---|---|---|---|
| 1 | 63 | 220 | 0.10 |
| 2 | 220 | 0.14 | |
| 3 | 220 | 0.18 | |
| 4 | 50 | 220 | 0.10 |
| 5 | 40 | 220 | 0.10 |
| Micro-Parameters | Soil Sample |
|---|---|
| PFC model objects | Ball |
| Density (kg⋅m−3) | 2650 |
| Effective modulus (Pa) | 1 × 106 |
| Stiffness ratio | 1.214 |
| Ball–ball friction coefficient | 0.65 |
| Rotational friction coefficient | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, F.; Lu, Y.; Lu, X. Investigation on Ground Collapse Due to Exfiltration of Shallowly Buried Water-Supply Pipeline. Appl. Sci. 2025, 15, 10736. https://doi.org/10.3390/app151910736
Bai F, Lu Y, Lu X. Investigation on Ground Collapse Due to Exfiltration of Shallowly Buried Water-Supply Pipeline. Applied Sciences. 2025; 15(19):10736. https://doi.org/10.3390/app151910736
Chicago/Turabian StyleBai, Fenghao, Ye Lu, and Xiuying Lu. 2025. "Investigation on Ground Collapse Due to Exfiltration of Shallowly Buried Water-Supply Pipeline" Applied Sciences 15, no. 19: 10736. https://doi.org/10.3390/app151910736
APA StyleBai, F., Lu, Y., & Lu, X. (2025). Investigation on Ground Collapse Due to Exfiltration of Shallowly Buried Water-Supply Pipeline. Applied Sciences, 15(19), 10736. https://doi.org/10.3390/app151910736





