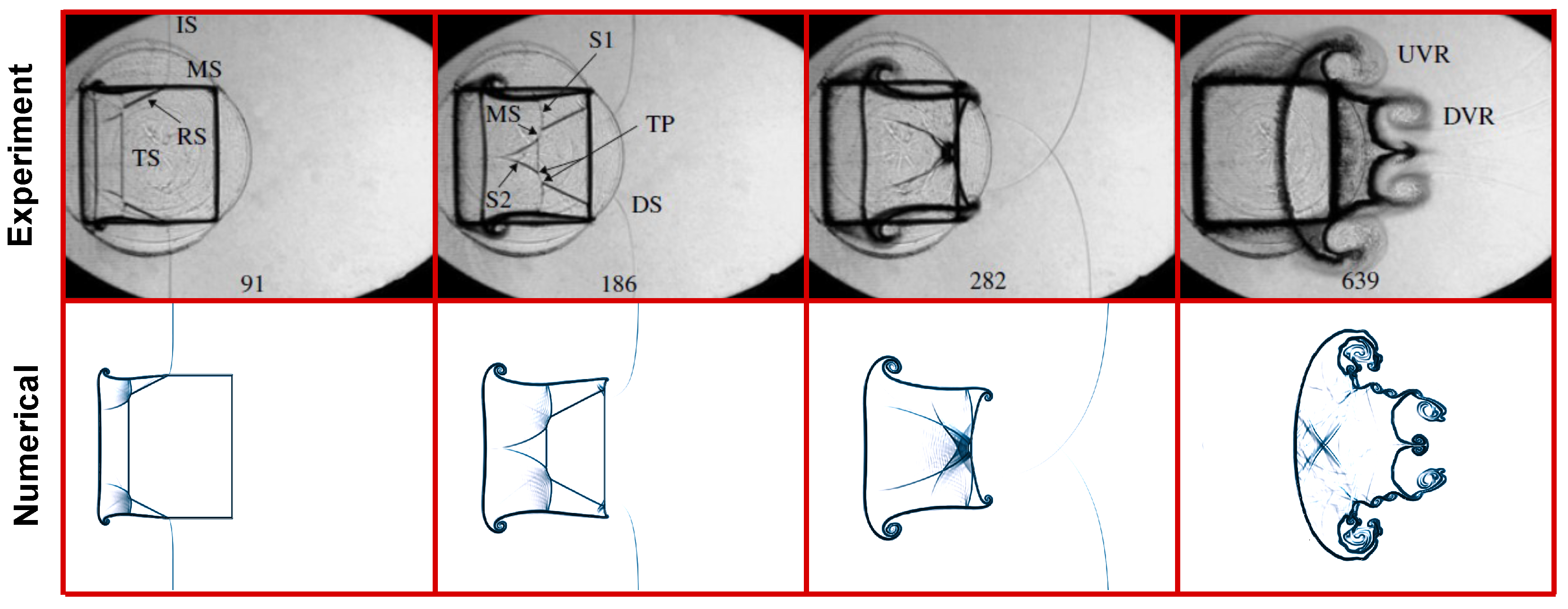
In this section, we analyze the shock-accelerated interfacial instabilities in single-mode stratifications, detailing the shock–interface interaction dynamics and the resulting patterns of vorticity deposition that govern early impulse and subsequent wave-driven modulation. We then quantify the evolution using integral diagnostics and assess interface characteristics to isolate the role of layer thickness.
4.1. Shock–Interface Interaction Dynamics
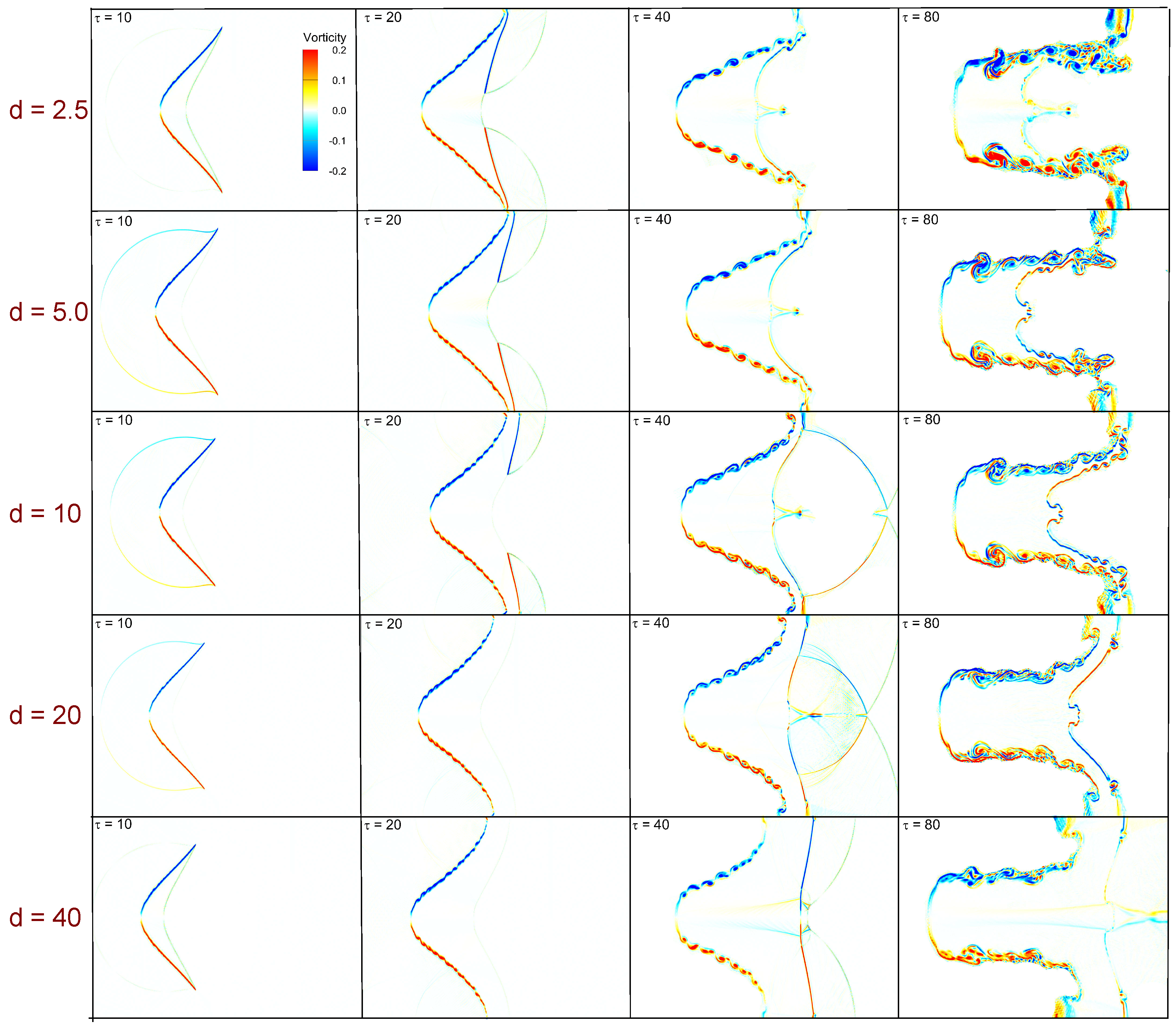
This subsection examines how the heavy-layer thickness
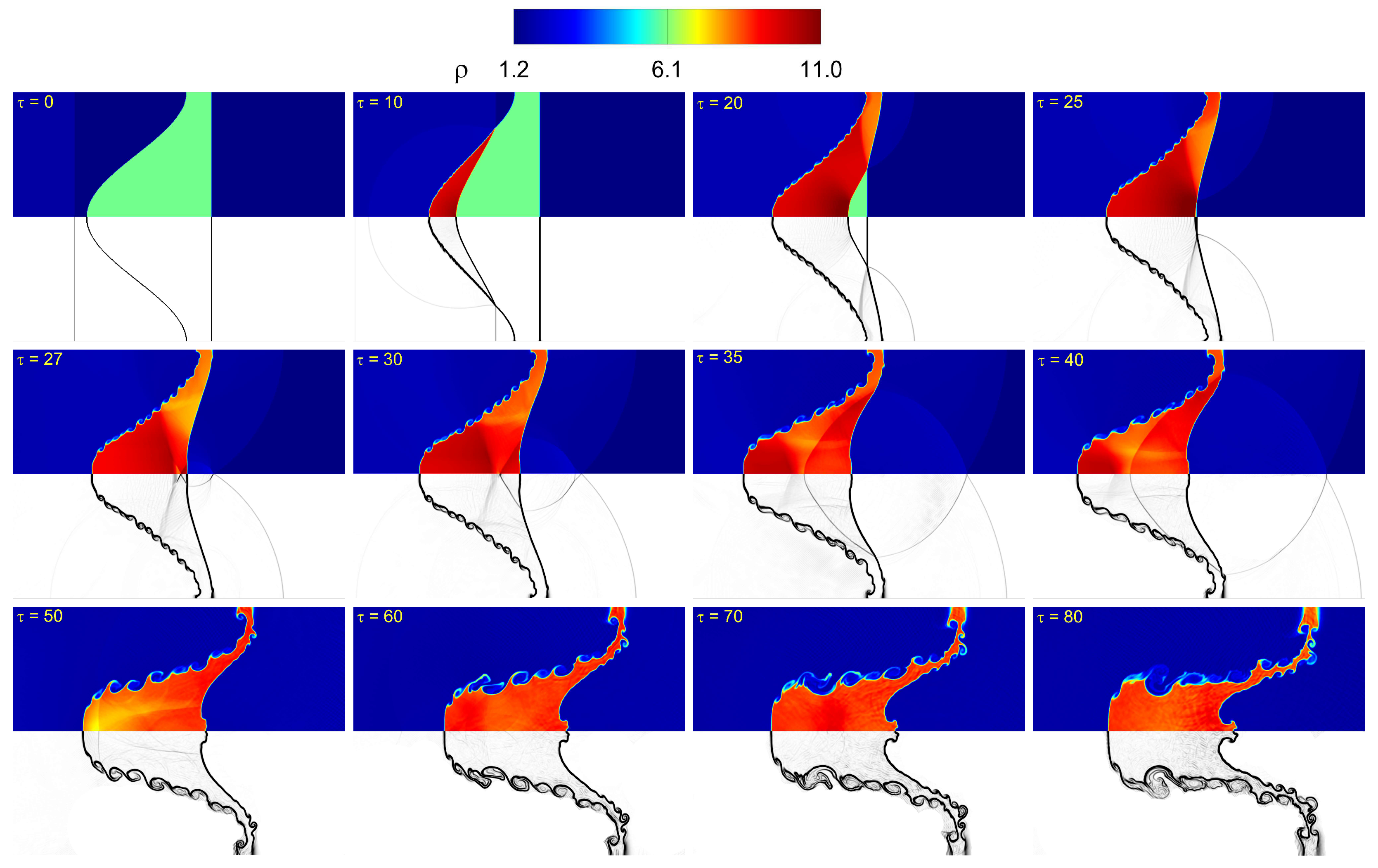
d modulates the sequence of wave–interface events and the ensuing small-scale structures in single-mode stratifications, using time-resolved density/Schlieren fields (
Figure 7,
Figure 8 and
Figure 9). Throughout, we use the following notation: IS (incident shock),
(upstream wavy interface) and
(downstream interface), RS (reflected shock in the shocked ambient), TS1 (shock transmitted into the heavy layer after the first impact), DS (diffracted shock emitted into the ambient at
), RTS/TS2 (reflected/transmitted pair launched at
upon arrival of TS1 or its returns), IRR (interface re-impact generated by reverberations), KH (Kelvin–Helmholtz) shear layers/billows, and SF (local shock focusing near the bulge tip).
For thin layers (
and
as illustrated in
Figure 7), the IS first impinges on
, splitting into RS and TS1. The baroclinic torque due to
misalignment deposits a vorticity sheet along
, impulsively accelerating the interface and forming a bulge–spike pair. The post-shock slip initiates KH shear layers that promptly roll up into billows. Because the acoustic path across the layer is short, TS1 reaches
early, launching DS into the ambient and an RTS/TS2 pair that begins to reverberate within the layer. These returns phase-lock with the interface motion, producing frequent IRR events that reinforce the circulation sheet, sharpen SF at the bulge tip, and hasten billow amplification and shedding. The thinner case (
) exhibits the earliest and strongest reverberation cycle, with accelerated amplitude growth, more intense KH roll-up, and jet pairing already by
. For
, the same mechanisms occur but with slightly delayed timing and somewhat reduced intensity over the same interval.
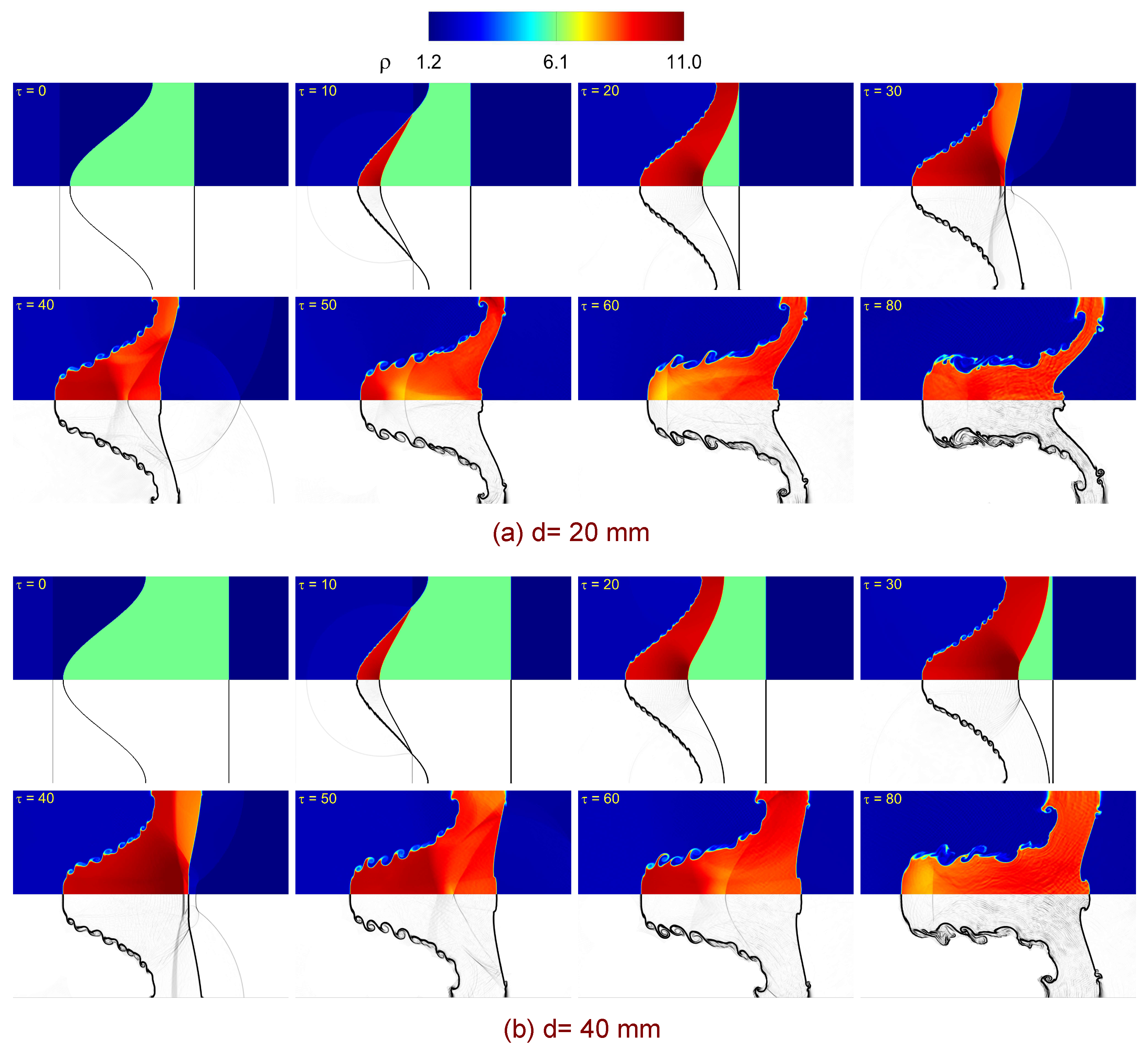
For the intermediate layer (
) as illustrated in
Figure 8, the leading front remains comparatively smooth up to
because TS1 requires a longer acoustic transit to reach
in contrast to
Figure 7. When TS1 finally strikes
(
), DS is emitted into the ambient, and an RTS/TS2 pair is launched, but the returns arrive less frequently and with reduced strength. Consequently, the added impulses are phase-lagged relative to the interfacial motion, and the cumulative baroclinic deposition proceeds in smaller, temporally separated bursts. The slip layer along
thickens more gradually; KH billows remain short and weak through
, with larger spacing and later saturation. Attenuation of the transmitted wave across the thicker heavy gas further reduces the circulation injected per re-impact, postponing jet formation and pairing until
. The SF region at the bulge tip is broader, and its curvature is gentler than in the thinner cases.
For thick layers (
and
as illustrated in
Figure 9), the initial IS impact at
again seeds a vorticity sheet and forms a bulge–spike pair, but the much longer transit distance across the heavy gas substantially delays the first
interaction. For
, TS1 reaches
only at
; for
, this encounter is pushed toward the end of the plotted window. As a result, the RTS/TS2 reverberations are infrequent and weak, their impulses poorly synchronized with the interface motion. The leading front remains smooth for a longer duration, the shock foot broadens, and the slip layer thickens slowly. KH corrugations emerge late and remain short; for
, small billows appear only after
, whereas for
, they are barely initiated, and no jet pairing is observed within
.
Relative to the thin layers in
Figure 7 (
), where early reverberations drive strong, phase-coherent IRR and rapid KH roll-up with jet pairing by
, increasing
d (
Figure 8 and
Figure 9) systematically: (i) lengthens the acoustic transit time across the heavy layer (scaling approximately with
d), (ii) increases attenuation of the transmitted wave, (iii) dephases the returns relative to the evolving interface, and (iv) reduces the circulation input per IRR event. Collectively, these effects weaken baroclinic vorticity reinforcement, broaden the SF region, delay KH onset and saturation, and suppress early jet formation. At matched
, larger
d yields smaller bulge amplitudes, smoother leading morphology, larger billow spacing, and fewer/smaller shed structures over the time window considered.
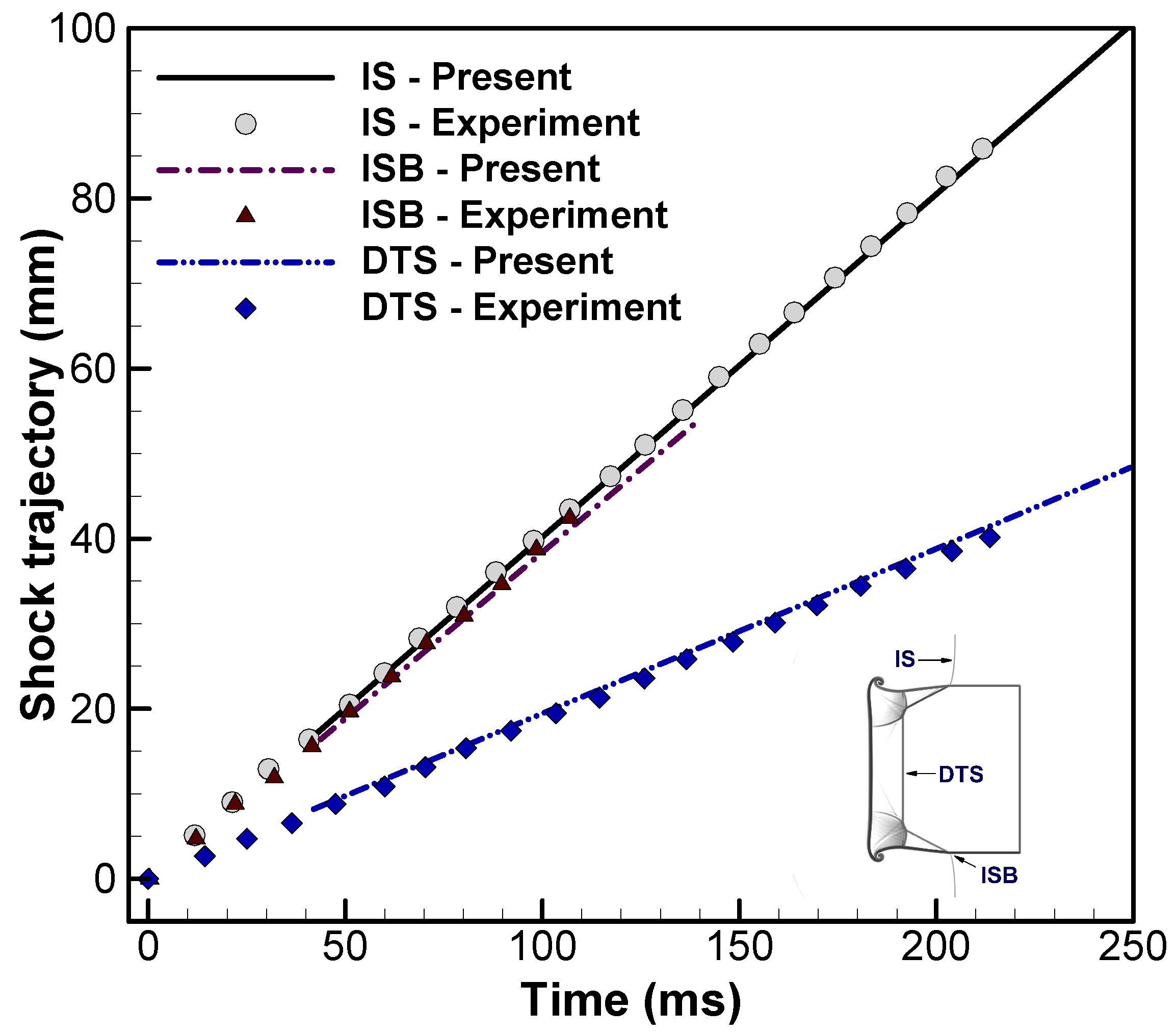
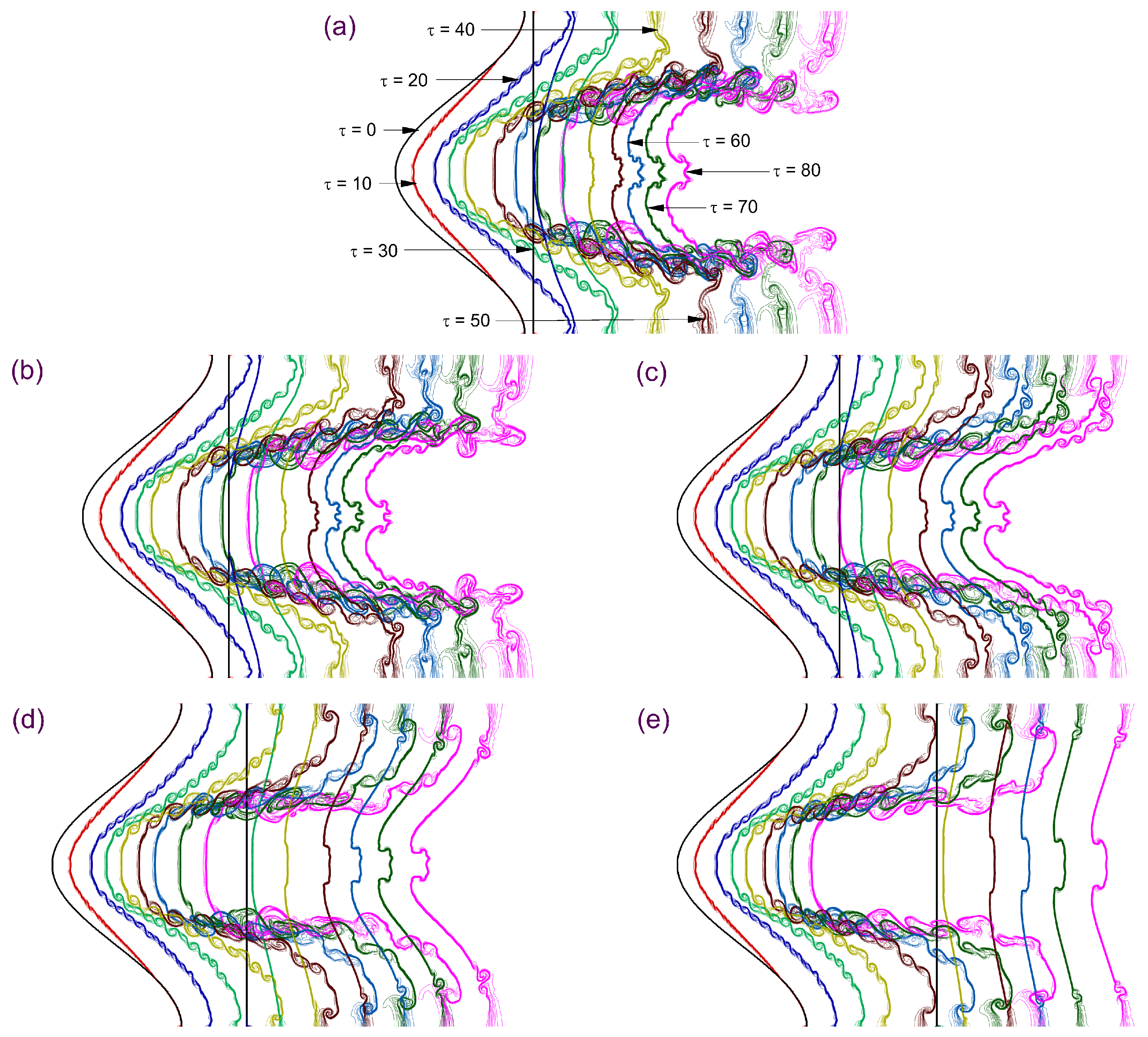
Figure 10 overlays instantaneous interface locations to show how heavy-layer thickness
d governs wave–interface coupling and the emergence of small-scale structure: The incident shock (IS) first impacts the upstream interface
, depositing a baroclinic vorticity sheet that forms a bulge–spike pair; the transmitted shock (TS1) then crosses the heavy layer and, upon reaching the downstream interface
, emits a diffracted shock (DS) into the ambient and an RTS/TS2 pair that reverberates between
and
. For thin layers (
and
), the short acoustic path yields early, strong, and phase-coherent returns, producing frequent interface re-impacts (IRR), sharp shock focusing (SF) near the bulge tip, rapid contour spreading with
, vigorous KH roll-up, and jet pairing by
. At
, longer transit time and attenuation render the returns less frequent and phase-lagged, so the slip layer thickens gradually, KH billows remain short and widely spaced up to
, and jet pairing is postponed beyond
with gentler tip curvature. For thicker layers (
and
), the first
encounter is delayed to
or later, reverberations are sparse and weak, and the interface retains a smooth, slowly advancing envelope with muted KH corrugations and no jet pairing within
. Overall, increasing
d lengthens the acoustic transit, dephases and attenuates the returns, reduces circulation input per IRR, broadens SF, delays KH onset and saturation, and thus suppresses early growth and small-scale shedding at matched
.
4.2. Dynamics of Vorticity Deposition
The generation and evolution of vorticity in shock-accelerated multi-fluid flows are governed by the complex interplay between baroclinic torque, compressibility, vortex stretching, and viscous diffusion. When a shock wave encounters a perturbed density interface, the misalignment between the shock-induced pressure gradient and the pre-existing density gradient produces a baroclinic torque that deposits a sheet of vorticity along the interface. This initial impulse drives the deformation of the interface into bulge–spike structures and seeds the subsequent development of shear layers.
The evolution of deposited vorticity can be described by the vorticity transport equation (VTE) for compressible viscous fluids:
where the first term represents vortex stretching and tilting, which redistribute vorticity and play a central role in turbulence development. The second term accounts for dilatational effects due to compressibility, which can amplify or attenuate vorticity depending on local flow divergence. The third term embodies baroclinic generation, the dominant source of circulation at shocked density interfaces. Finally, the last term captures viscous diffusion, which acts to smooth sharp gradients and broaden vorticity layers. Together, these mechanisms dictate how circulation is injected, redistributed, and dissipated in shocked stratifications. Baroclinic deposition provides the primary impulse for instability growth, while vortex stretching, compressibility, and viscosity modulate its subsequent evolution, shaping the emergence of secondary shear-layer roll-ups and eventual transition toward mixing.
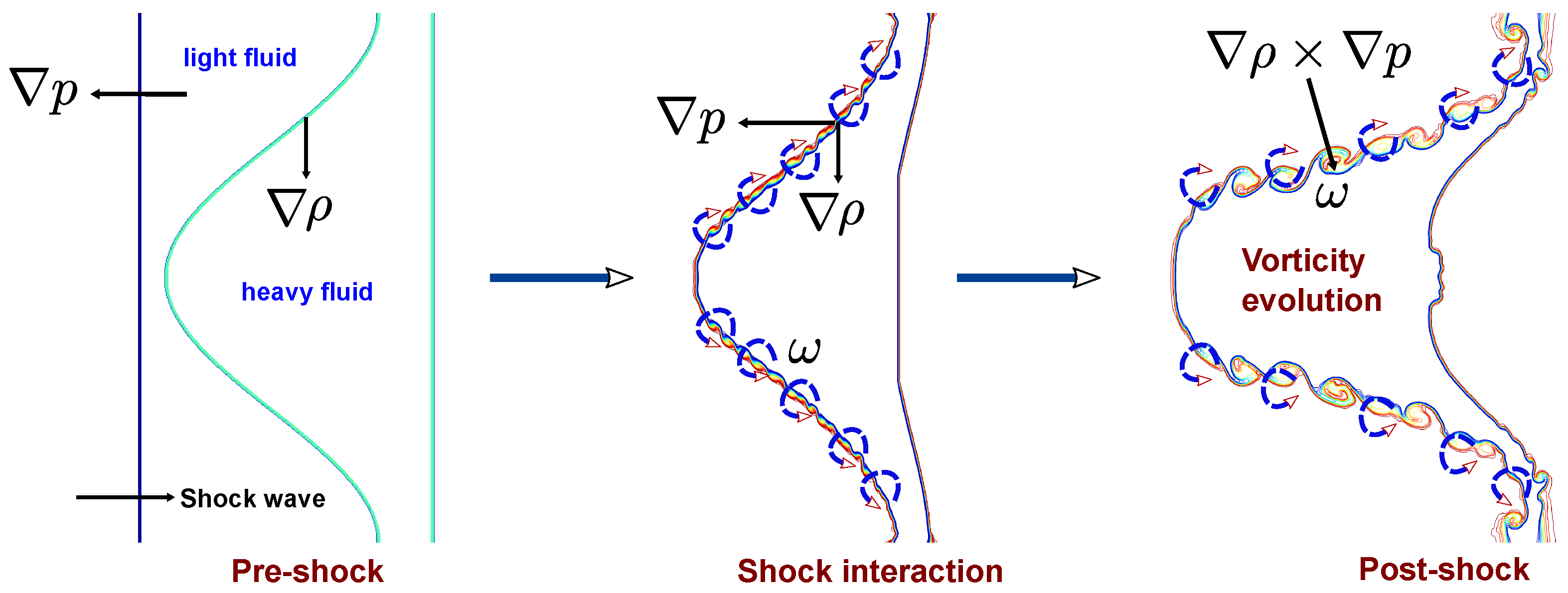
Figure 11 provides a schematic representation of the mechanisms responsible for vorticity deposition in a shock-accelerated heavy–light stratified interface. In the pre-shock state, a density gradient
exists across the perturbed interface between the heavy and light gases, while the pressure gradient
is aligned with the incident planar shock. During shock interaction, the shock front refracts across the perturbed interface, creating a local misalignment between
and
. This misalignment gives rise to a baroclinic torque
, which deposits a sheet of vorticity
along the interface. The deposited vorticity drives the initial bulge–spike morphology and seeds the growth of shear layers. In the post-shock stage, this circulation evolves dynamically: the vorticity sheet rolls up into small-scale vortices, shear layers thicken, and secondary vortical structures emerge along the distorted interface. These processes are central to the subsequent development of RM instability, feeding into KH roll-ups, jet formation, and enhanced interfacial mixing.
For a finite-thickness heavy layer, the strength and coherence of baroclinic deposition are governed by the acoustic transit time
where
d denotes the heavy-layer thickness and
is the sound speed in SF
6. The efficiency of baroclinic vorticity reinforcement can be interpreted as a competition between the acoustic transit time
and the characteristic KH growth time
. When
, reverberations occur frequently and remain phase-coherent, leading to enhanced baroclinic amplification. In contrast, when
, the reverberations become phase-lagged and attenuated, resulting in reduced baroclinic deposition. Accordingly, thin layers (
–5 mm) generate synchronized baroclinic peaks and rapid KH roll-up, whereas thick layers (
–40 mm) delay and suppress these mechanisms due to increased
and shock attenuation.
Figure 12 depicts the temporal evolution of vorticity distribution in shock-accelerated single-mode heavy–light stratifications for different heavy-layer thicknesses (
d = 2.5, 5, 10, 20, 40 mm). At early times (
), baroclinic torque, represented by the
term in Equation (
20), dominates the dynamics by depositing circulation along the perturbed upstream interface, forming a vorticity sheet of alternating sign aligned with interface crests and troughs. As the flow evolves (
), this sheet amplifies and begins to roll up due to shear instabilities, while the vortex stretching and tilting contribution
redistributes vorticity around the bulge and spike tips. At later stages (
), interactions with secondary shock reverberations further intensify the circulation, promoting vortex pairing and the emergence of Kelvin–Helmholtz billows. In parallel, the compressibility term
modulates vorticity in regions of local expansion and compression, while viscous diffusion
acts to broaden shear layers and smooth sharp gradients. Collectively, these mechanisms explain the contrasting structures observed across layer thicknesses: thin layers favor rapid and coherent roll-up driven by strong baroclinic reinforcement, whereas thick layers exhibit attenuated circulation, delayed roll-up, and weaker small-scale vortical structures due to enhanced diffusion and longer acoustic transit times.
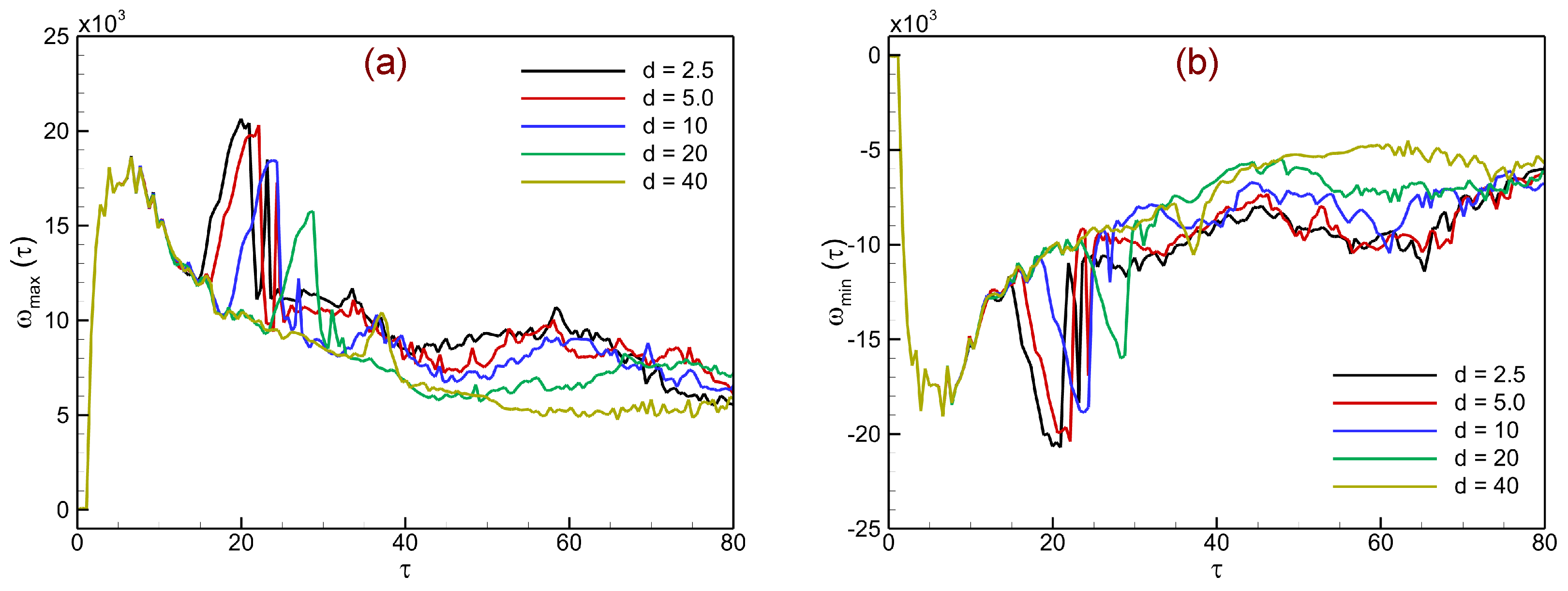
To further quantify the intensity of vortical structures generated during shock-accelerated instability, we examine the temporal evolution of the maximum and minimum vorticity within the computational domain. These extrema provide direct measures of the strength of circulation deposited along the perturbed interface and serve as indicators of the subsequent roll-up and amplification of small-scale vortices. Mathematically, the extrema are defined as
where
denotes the scalar vorticity field in two dimensions, and
D represents the computational domain. In the discrete form used for numerical simulations, the extrema are evaluated at each time step as
with
denoting the computed vorticity at grid location
and time
. Tracking
and
highlights the asymmetry between positive and negative vortical regions and provides a quantitative measure of how shock-driven baroclinic deposition evolves into nonlinear roll-up and mixing.
Figure 13 presents the temporal evolution of vorticity extrema in shock-accelerated single-mode light–heavy stratifications for different heavy-layer thicknesses.
Figure 13a shows the maximum vorticity
, while
Figure 13b shows the minimum vorticity
. Immediately after shock impact, sharp peaks appear in both
and
, reflecting the strong baroclinic deposition of circulation at the perturbed upstream interface. Thin layers (
mm) exhibit higher initial peaks, indicating stronger and more localized vorticity sheets, consistent with the rapid roll-up and intense shear-layer evolution observed in the corresponding flow fields. For intermediate thickness (
mm), the peak values are slightly reduced and spread over a longer time, while for thicker layers (
mm) the extrema are considerably weaker, reflecting attenuated baroclinic input and slower growth of small-scale vortical structures.
As time progresses toward , both and gradually decrease in magnitude, indicating a redistribution of circulation into larger-scale structures and dissipation by viscous effects. The asymmetry between the maximum and minimum curves highlights the imbalance between positive and negative vortical regions, which develops as shear instabilities amplify along the spike and bulge tips. To sum up, the vorticity extrema offer a quantifiable indicator of how layer thickness affects baroclinic deposition: bigger layers slow down the commencement of nonlinear roll-up and inhibit vorticity increase, whereas thinner layers maintain higher, early-time circulation amplification.
4.3. Integral Diagnostics
Integral diagnostics provide a global perspective on shock-accelerated instabilities by condensing spatially distributed fields into domain-integrated measures. These quantities capture the cumulative effects of key physical mechanisms and enable direct comparison across cases. In particular, they highlight the roles of dilatational, baroclinic, and viscous sources in vorticity production, as well as the evolution of circulation, enstrophy, and kinetic energy that govern instability growth and mixing efficiency.
To quantify the mechanisms of vorticity generation, we analyze the integral contributions of the principal production terms in the vorticity transport equation (VTE). Specifically, we consider the dilatational (), baroclinic (), and viscous () components, each spatially integrated over the computational domain D. This diagnostic framework provides a consistent basis for evaluating how the relative importance of these mechanisms evolves across different layer configurations.
The integrated quantities are defined as
where
denotes the scalar vorticity,
is the density,
p the pressure, and
the dynamic viscosity. The use of absolute values ensures that the contributions reflect the net production magnitude, independent of sign. Collectively, these measures allow for a systematic comparison of compressibility, baroclinic torque, and viscous diffusion in driving the evolution of instability across different layer thicknesses.
Figure 14 illustrates the temporal evolution of the spatially integrated vorticity source terms in shock-accelerated single-mode light–heavy stratifications for varying heavy-layer thicknesses (
mm). The dilatational contribution (
Figure 14a) remains negligible before shock impact but rises sharply once the shock interacts with the perturbed interface. Thin layers (
mm) exhibit the strongest and earliest amplification due to rapid reverberations between interfaces that intensify compressibility-driven vorticity modulation, while thicker layers (
mm) respond more slowly and with smaller magnitudes because of longer acoustic transit times and stronger wave attenuation. The baroclinic contribution (
Figure 14b) dominates the early stages, reflecting the misalignment of density and pressure gradients at the shocked interface. Thin layers again produce higher peaks from stronger and more coherent baroclinic torque deposition, whereas intermediate and thick layers (
–40 mm) display a gradual rise, indicative of weaker synchronization between reverberated shocks and interface motion. This delayed and attenuated baroclinic input accounts for the slower roll-up and suppressed fine-scale vortex formation observed in the corresponding flow fields. The viscous contribution (
Figure 14c) grows steadily throughout the evolution as a diffusive mechanism that broadens shear layers and smooths gradients. Its magnitude follows the same thickness-dependent trend, with larger values in thinner layers where intense small-scale activity enhances vorticity gradients, and weaker contributions in thicker layers where vortical structures remain subdued. Hence, the comparative trends show that thinner layers generate stronger dilatational, baroclinic, and viscous contributions, driving rapid vorticity amplification, vigorous shear roll-up, and early jet pairing, while thicker layers delay the onset and reduce the intensity of instability growth, leading to smoother interfaces and weaker mixing.
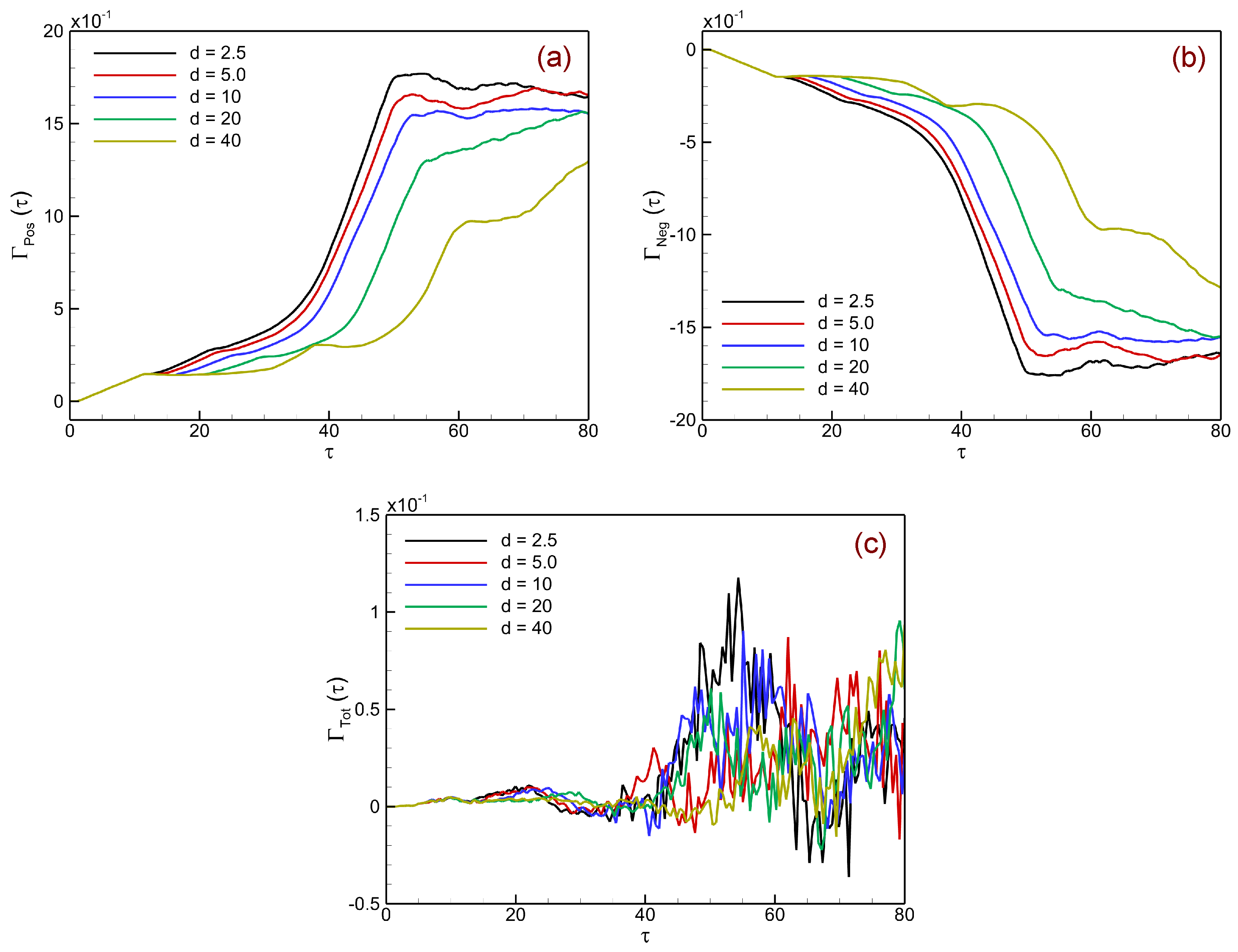
Circulation is a key diagnostic for quantifying the strength and evolution of vortical structures in shock-driven flows. In the context of instability evolution, it directly measures the baroclinically generated vortices deposited at the perturbed interface and reveals the balance between counter-rotating motions. The total circulation in the flow field is expressed as the spatial integral of vorticity over the computational domain
D:
For a more detailed characterization, circulation can be decomposed into its positive and negative components, corresponding to contributions from oppositely rotating vortical regions:
These diagnostics quantify the circulation deposited along the interface by baroclinic torque. While
and
track the evolution of positive and negative vortical structures, their sum yields the net circulation
, providing an integrated measure of the overall rotational strength in the shocked stratification.
Figure 15 presents the temporal evolution of spatially integrated circulation in shock-accelerated single-mode heavy–light stratifications for different heavy-layer thicknesses (
mm).
Figure 15a shows the positive circulation
, which grows rapidly after shock impact due to baroclinic vorticity deposition along interface crests. Thin layers (
mm) reach higher values at earlier times, reflecting strong baroclinic reinforcement from frequent reverberations, while thicker layers (
mm) exhibit delayed and weaker growth because of longer acoustic transit times and wave attenuation.
Figure 15b displays the negative circulation
, generated along interface troughs, which follows similar trends with thin layers producing stronger counter-rotating vortices and thick layers showing weaker, delayed growth.
Figure 15c reports the net circulation
, defined as the sum of
and
. Owing to the near-symmetric production of positive and negative vortices,
remains close to zero, with only small fluctuations at later times arising from nonlinear roll-up, vortex pairing, and secondary shock interactions. Hence, thin layers generate stronger circulation and earlier roll-up, while thick layers suppress vorticity deposition and delay instability growth, consistent with the integrated source-term behavior shown in
Figure 14.
The integral decomposition of the vorticity source terms further reinforces the mechanistic picture outlined in
Section 4.2. As shown in
Figure 14, thin layers exhibit sharp and synchronized peaks in the baroclinic contribution, consistent with short acoustic transit times (
) that allow frequent, phase-coherent reverberations. This repeated reinforcement enhances circulation growth and accelerates the onset of secondary Kelvin–Helmholtz instabilities. By contrast, thick layers display weaker and broadened baroclinic peaks, as the longer transit times (
) produce phase-lagged reverberations and attenuated deposition. The dilatational term is also amplified in thin layers, reflecting stronger compressibility effects due to tighter vortex roll-up, whereas the viscous contribution grows steadily with increased small-scale activity. Together, these trends provide a quantitative link between layer thickness, baroclinic forcing, and the subsequent evolution of circulation (
Figure 15). In this way, the integral diagnostics confirm that acoustic transit time and phase synchronization are key parameters governing the thickness-dependent dynamics of RM instability.
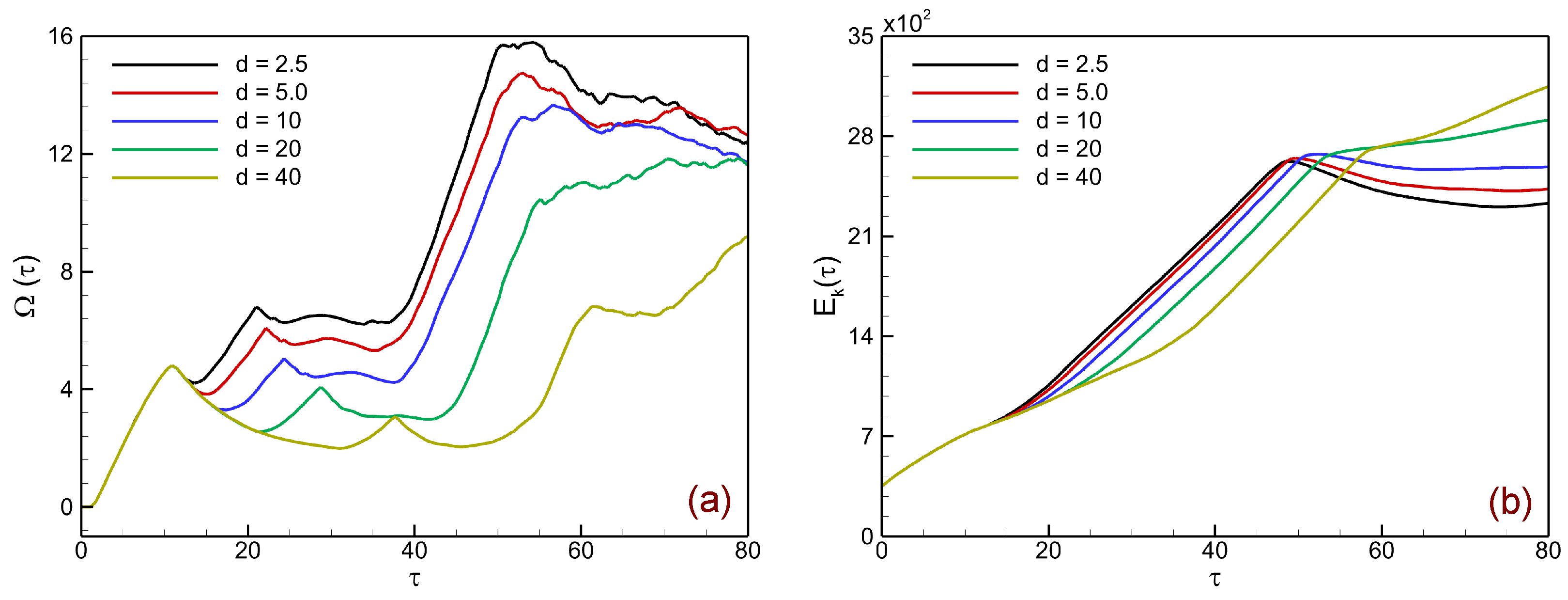
Enstrophy and kinetic energy are essential diagnostics for shock-accelerated instabilities. Enstrophy quantifies the growth of baroclinically generated vortical structures, while kinetic energy measures the redistribution of bulk flow energy into interface deformation and small-scale motions. For a two-dimensional flow, the enstrophy is defined as the spatial integral of the squared vorticity over the computational domain
D:
which serves as a measure of the cumulative strength of vortical activity throughout the flow field. The total kinetic energy in the domain is expressed as
providing a global measure of the bulk momentum and its progressive transfer into interface deformation, shear layers, and small-scale vortices that emerge during the nonlinear stage of RMI growth.
Figure 16 presents the temporal evolution of enstrophy
and kinetic energy
in shock-accelerated single-mode light–heavy stratifications for varying heavy-layer thicknesses (
mm). In
Figure 16a, the enstrophy evolution reflects the amplification of vortical structures generated at the perturbed interface. Immediately after shock impact, enstrophy rises rapidly due to strong baroclinic deposition and shear-layer formation. Thin layers (
mm) exhibit the largest and earliest growth, as frequent shock reverberations reinforce vorticity deposition and trigger rapid Kelvin–Helmholtz roll-up, leading to intense small-scale vortical activity. Intermediate and thick layers (
d = 10–40 mm) show progressively delayed and weaker growth, since longer acoustic transit times and stronger attenuation of transmitted shocks reduce the synchronization and strength of baroclinic forcing. At later times (
), enstrophy in thinner layers reaches higher peaks but eventually decays slightly as vortex pairing and viscous diffusion redistribute circulation into larger scales.
Figure 16b shows the evolution of total kinetic energy. Unlike enstrophy, the growth of
is smoother and more gradual across all cases, reflecting the continuous redistribution of bulk shock energy into interface deformation and small-scale motions. Initially, all cases follow similar trends, dominated by the incident shock input. As time progresses, differences emerge: Thinner layers exhibit slightly higher saturation levels due to stronger interface deformation and shear amplification, whereas thicker layers reach lower levels of
, consistent with their weaker vortex activity and suppressed mixing.
4.4. Interface Characteristics
This subsection analyzes the evolution of interface trajectories, normalized length, and perturbation amplitude in shock-accelerated single-mode stratifications. These measures capture how baroclinic vorticity deposition and shock interactions drive interface displacement, deformation, and the emergence of small-scale structures that govern instability growth and mixing.
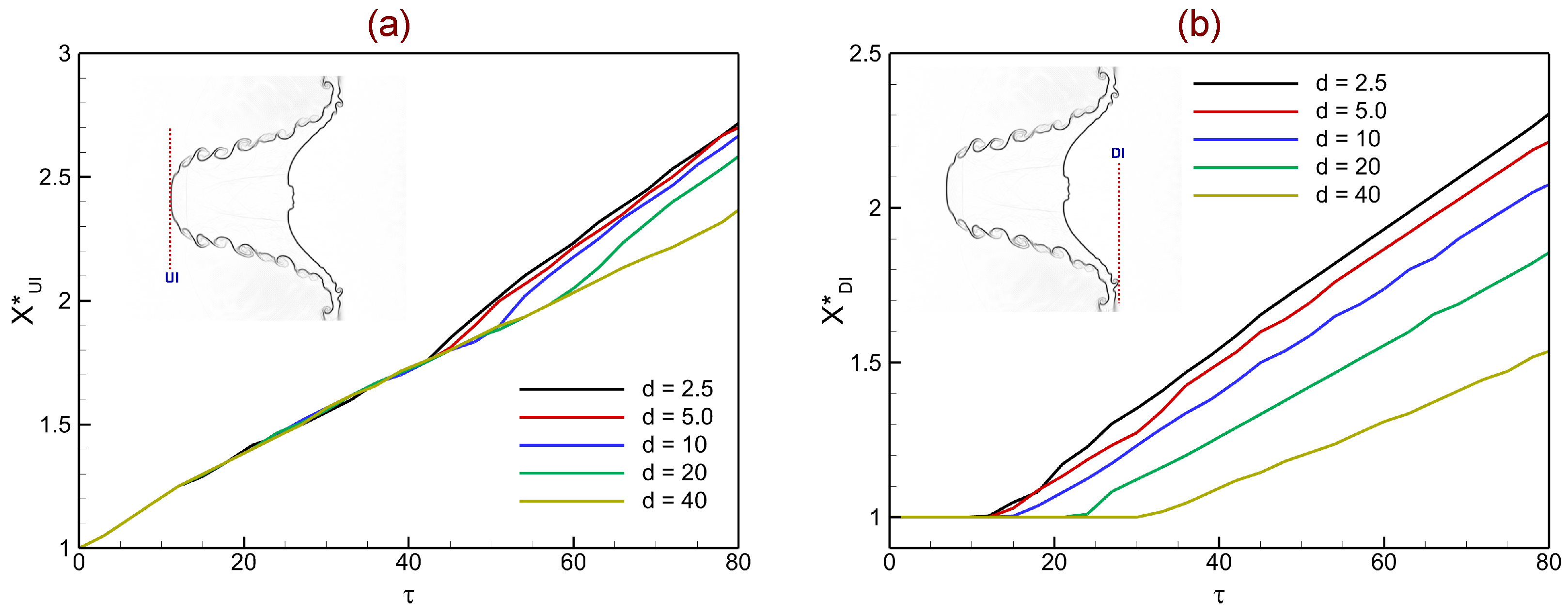
Figure 17 shows the temporal evolution of the normalized upstream (
) and downstream (
) interfaces in shock-accelerated single-mode light–heavy stratifications for varying heavy-layer thicknesses (
mm). In
Figure 17a, the upstream interface displacement
initially grows nearly linearly with time for all cases, reflecting the impulsive acceleration imparted by the incident shock. Thin layers (
mm) exhibit faster growth after
due to strong reverberations and repeated shock–interface interactions that reinforce baroclinic vorticity deposition. For thicker layers (
mm), the displacement rate decreases, as transmitted shocks are attenuated and arrive later at the interface, resulting in weaker circulation input and smoother evolution.
Figure 17b shows the normalized downstream interface displacement
. Similarly to the upstream case, thin layers undergo rapid displacement driven by strong transmitted and reflected shocks that enhance interfacial acceleration. Thick layers, however, display slower and more gradual displacement because of reduced shock strength and phase-lagged reverberations. The gap between thin and thick cases widens with time, underscoring the role of layer thickness in modulating interface motion. According to the numerical results, thick layers reduce displacement because of delayed and weaker shock–interface coupling, but thin heavy layers promote rapid and sustained interface acceleration, driven by coherent shock reverberations and strong baroclinic forcing.
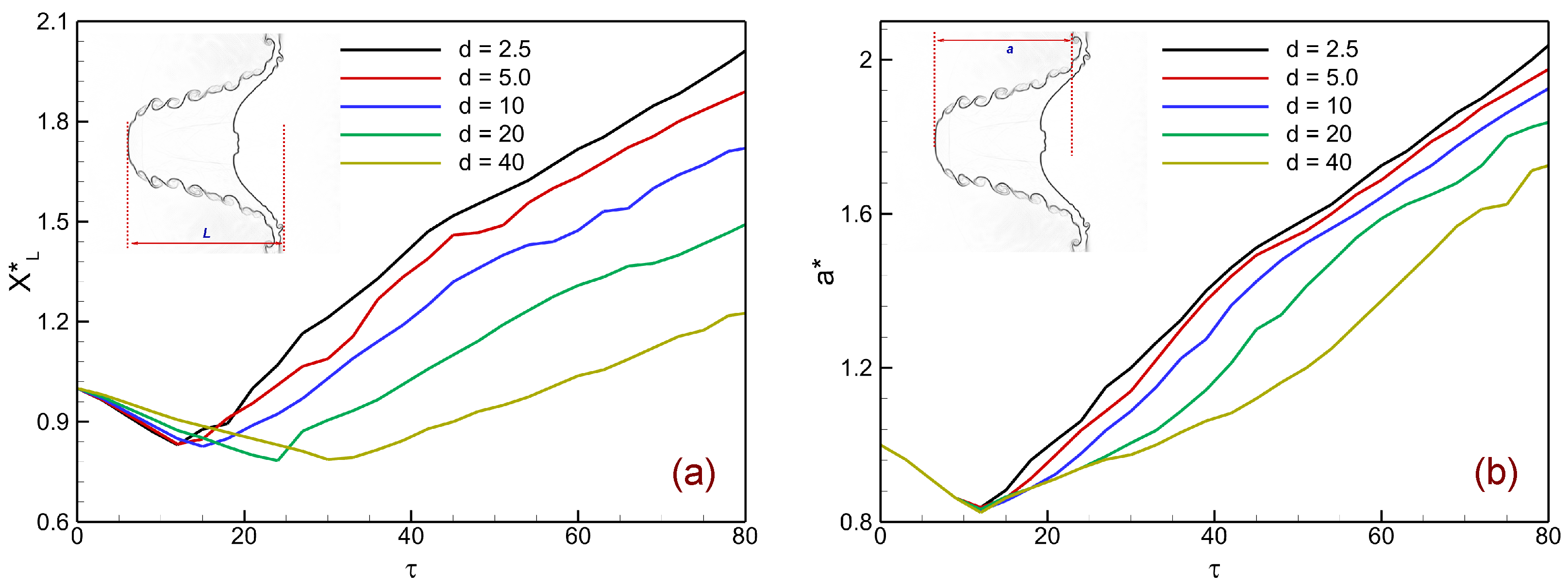
Figure 18 depicts the temporal evolution of the normalized interface length (
) and normalized perturbation amplitude (
) in shock-accelerated single-mode light–heavy stratifications for varying heavy-layer thicknesses (
mm). In
Figure 18a, the normalized interface length
characterizes the development of small-scale interfacial structures. After an initial slight decrease immediately following shock impact,
increases steadily due to interface stretching and the growth of Kelvin–Helmholtz roll-ups. Thin layers (
mm) exhibit the most rapid growth, reflecting strong baroclinic vorticity reinforcement from repeated reverberations that promote enhanced billow formation and fine-scale deformation. For thicker layers (
mm), the growth of
is delayed and weaker, consistent with suppressed shock–interface coupling and reduced small-scale activity.
Figure 18b shows the evolution of the normalized perturbation amplitude
, which measures the large-scale displacement of the perturbed interface. Following an initial dip during shock compression, the amplitude grows rapidly, especially for thinner layers where reverberations drive strong baroclinic torque and accelerated spike-bubble growth. In contrast, thicker layers display slower amplitude growth due to weaker and phase-lagged circulation input from transmitted shocks.