Channel Optimization of Sandwich Double-Sided Cold Plates for Electric Vehicle Battery Cooling
Abstract
1. Introduction
1.1. Background
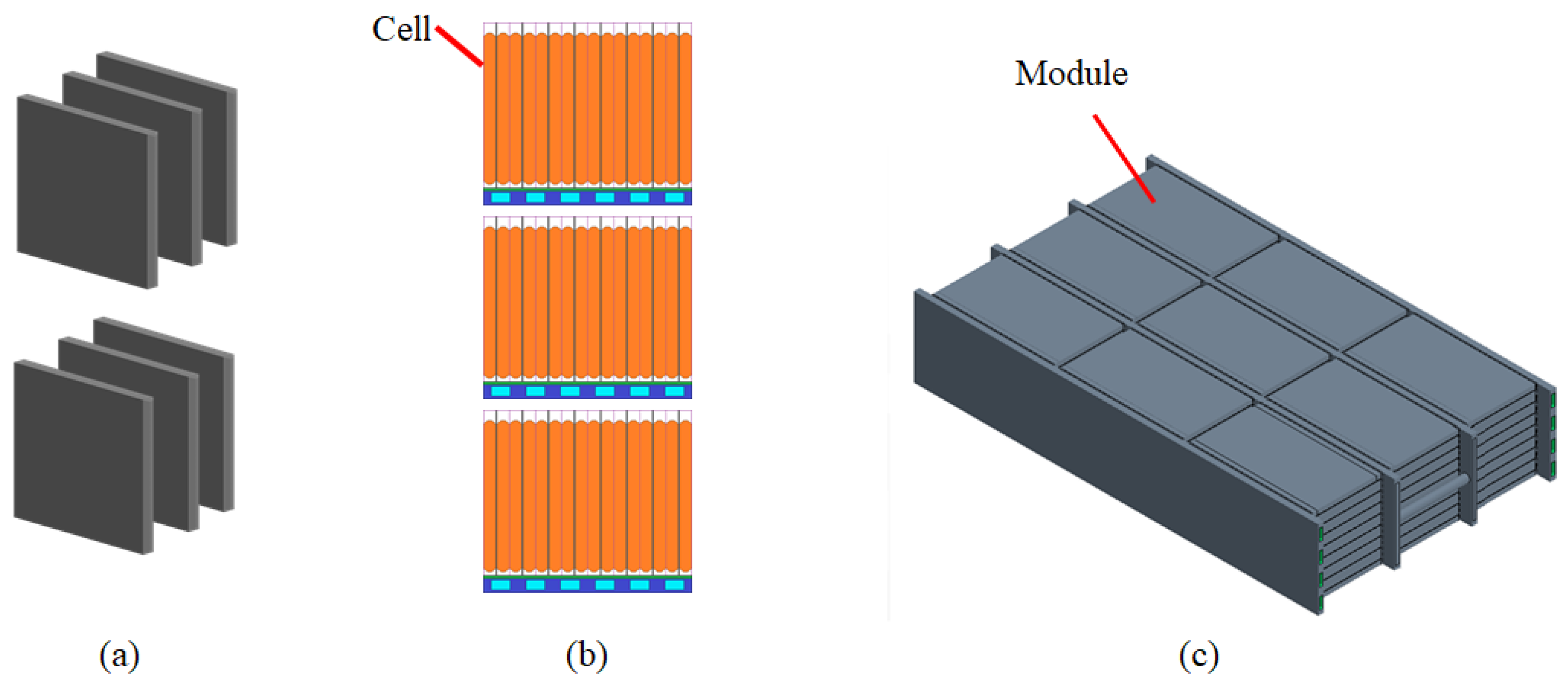
1.2. Research Cases
2. Methodology
3. Numerical Method
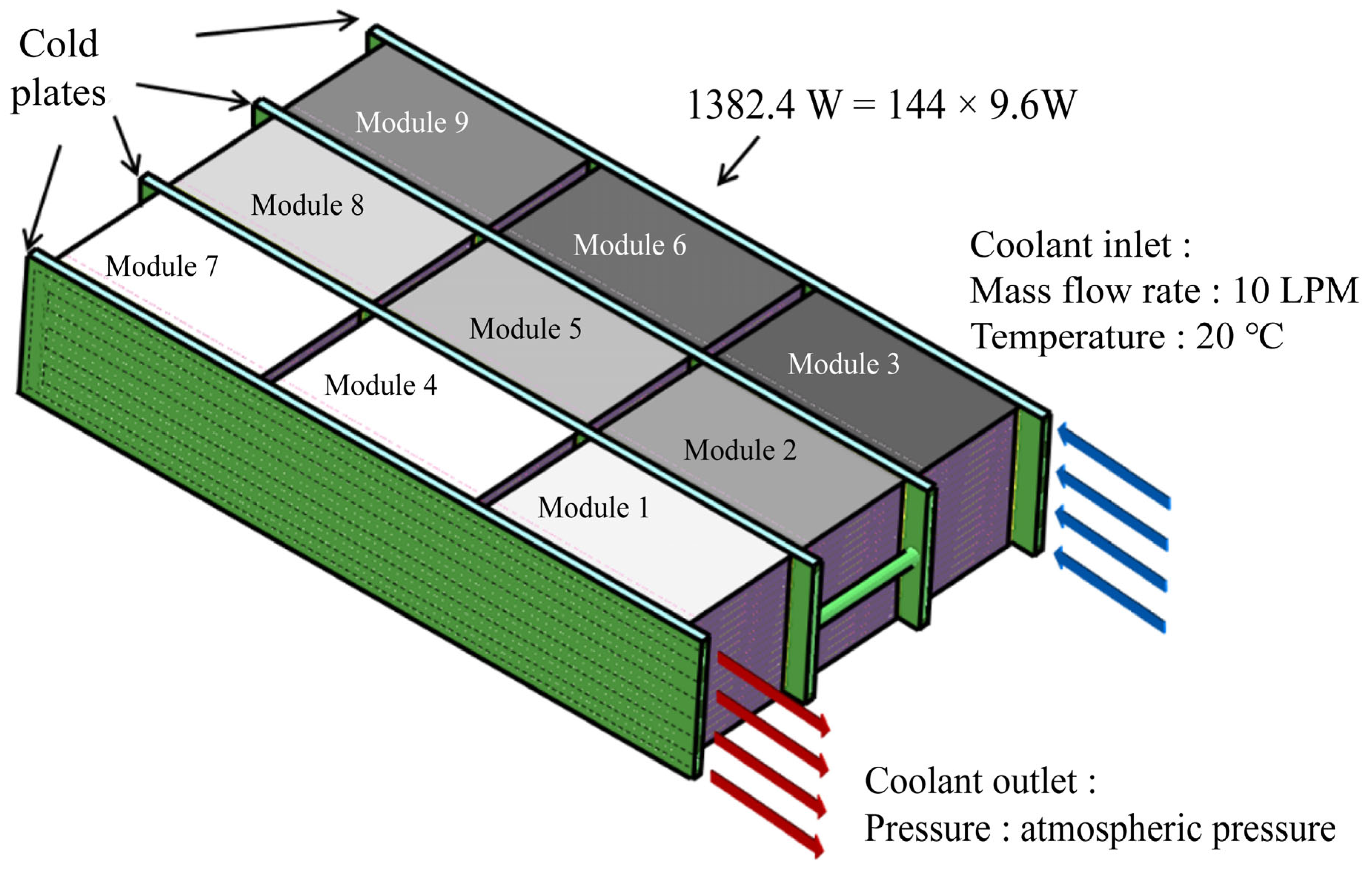
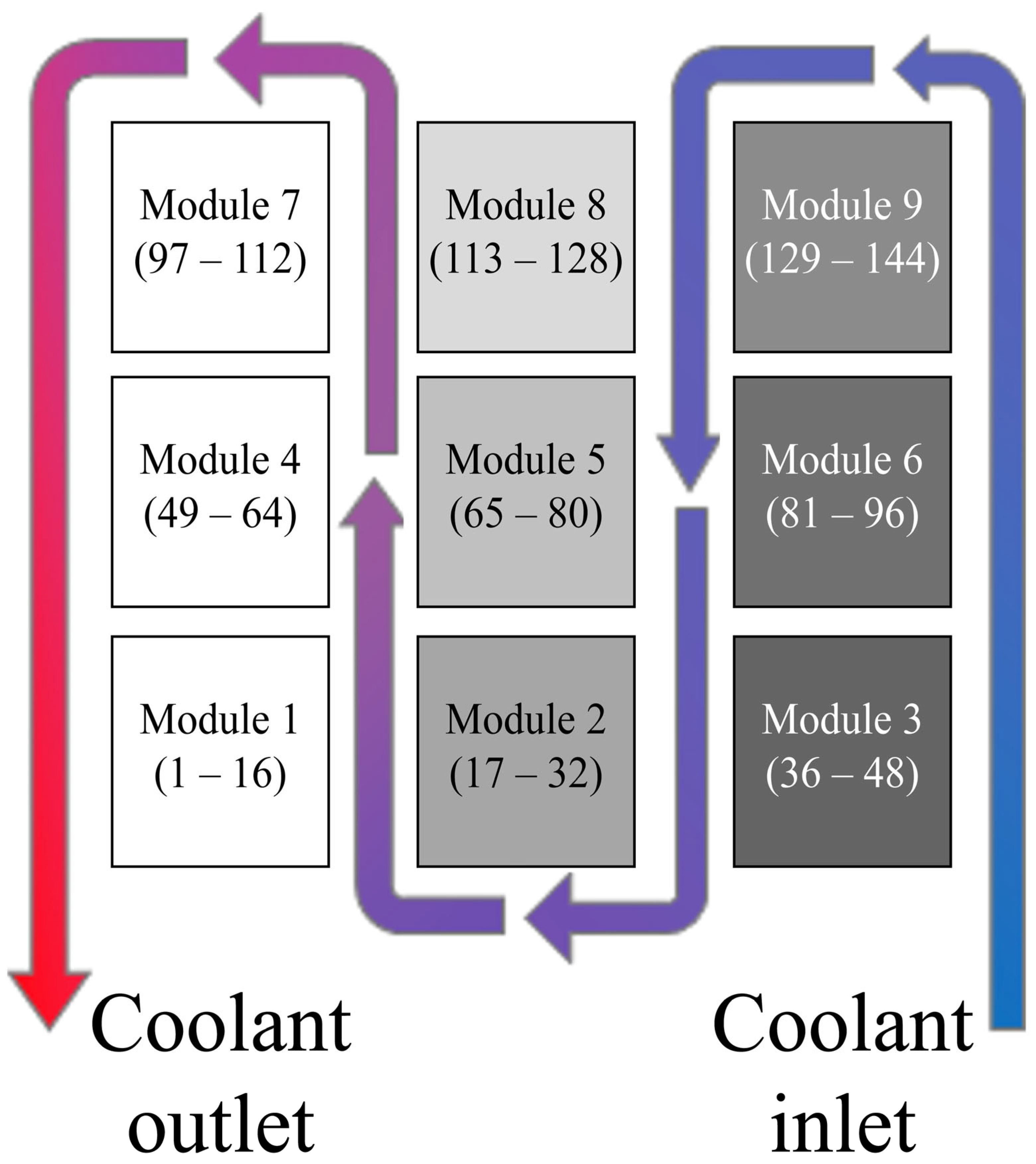
3.1. Pack-Level Boundary Conditions
3.2. Module-Level Boundary Conditions
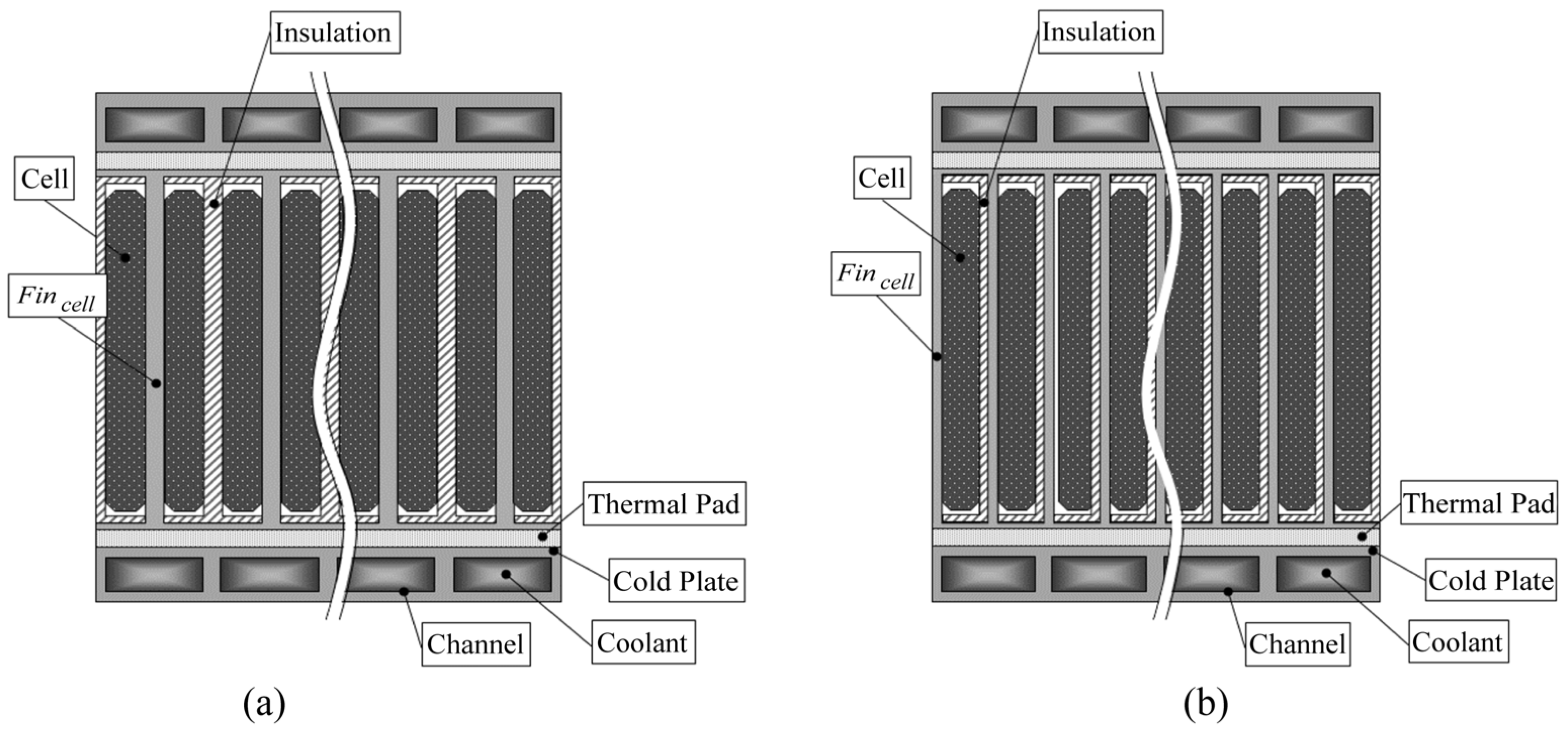
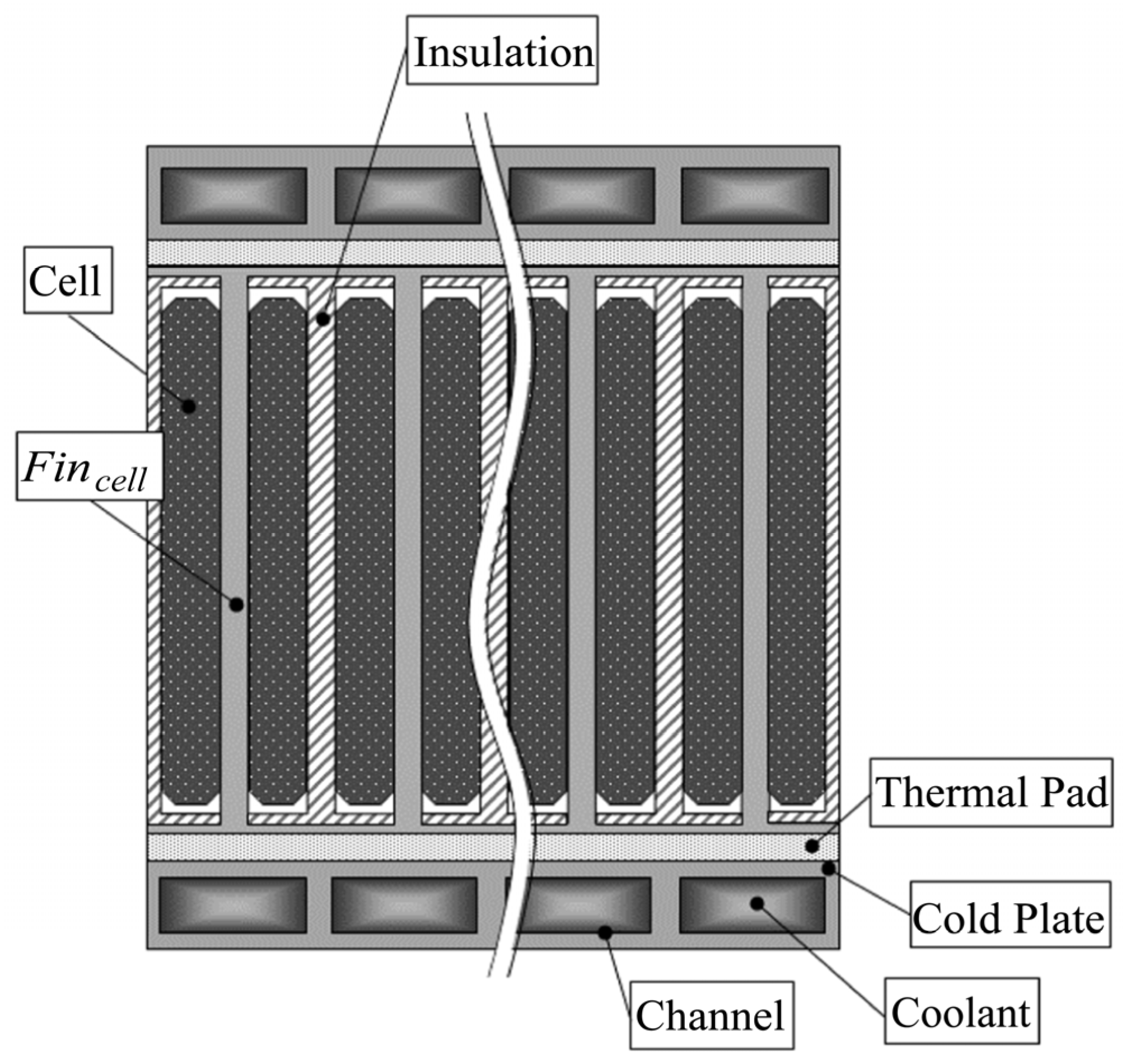
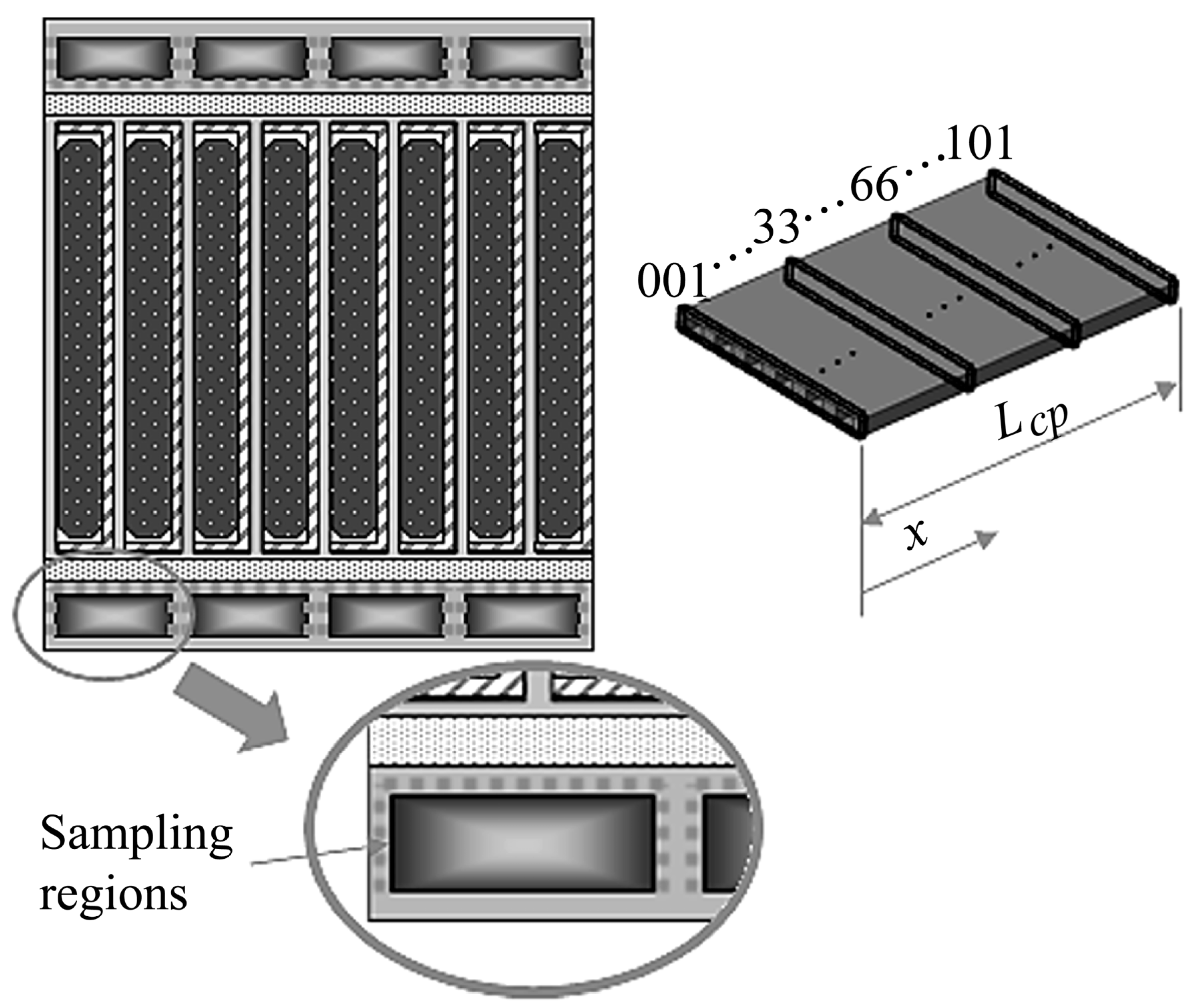
3.3. Fincell Arrangements
3.4. Orthogonal Array for Channel
3.5. Material Properties and Governing Equations
4. Results and Discussion
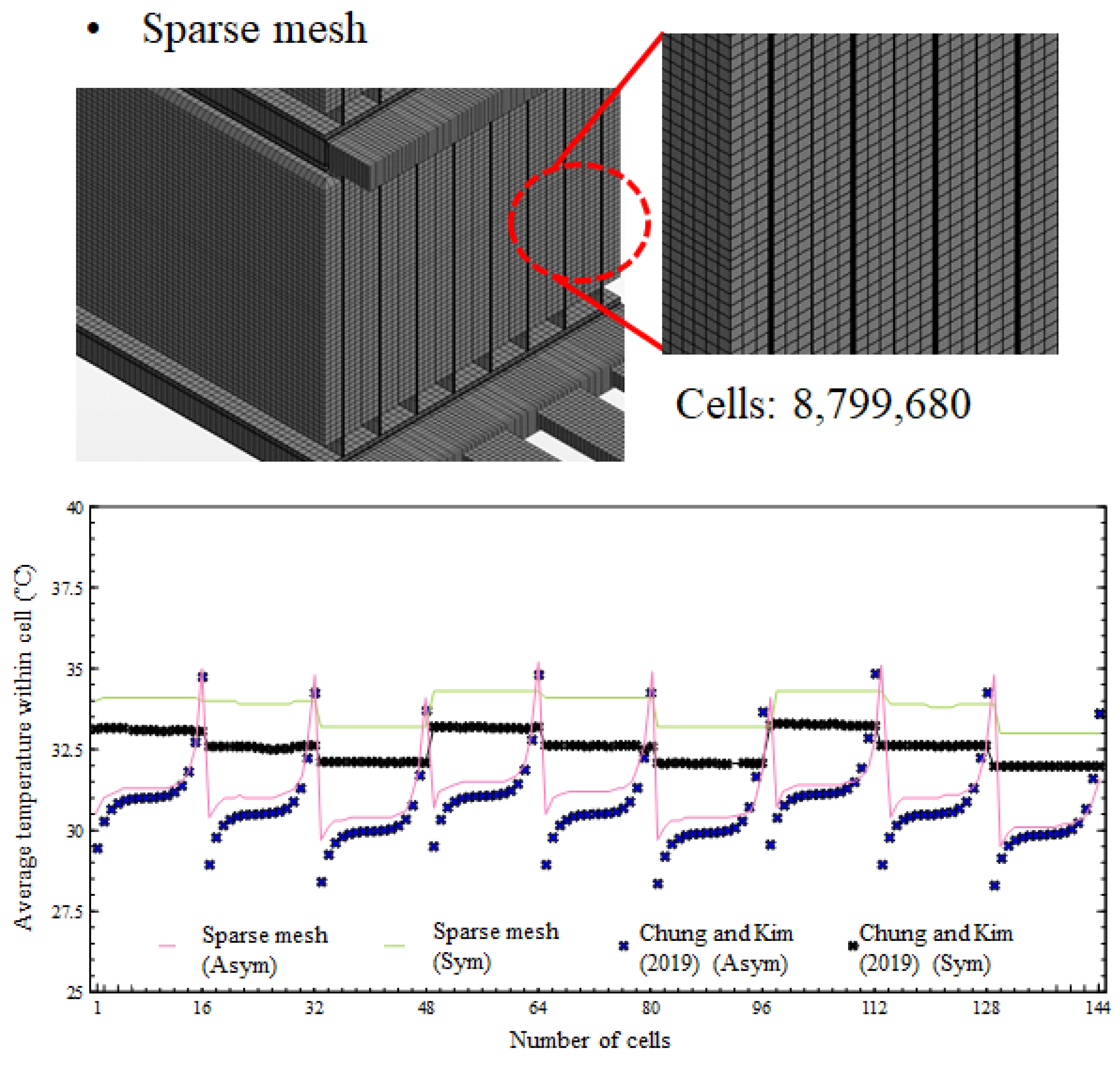
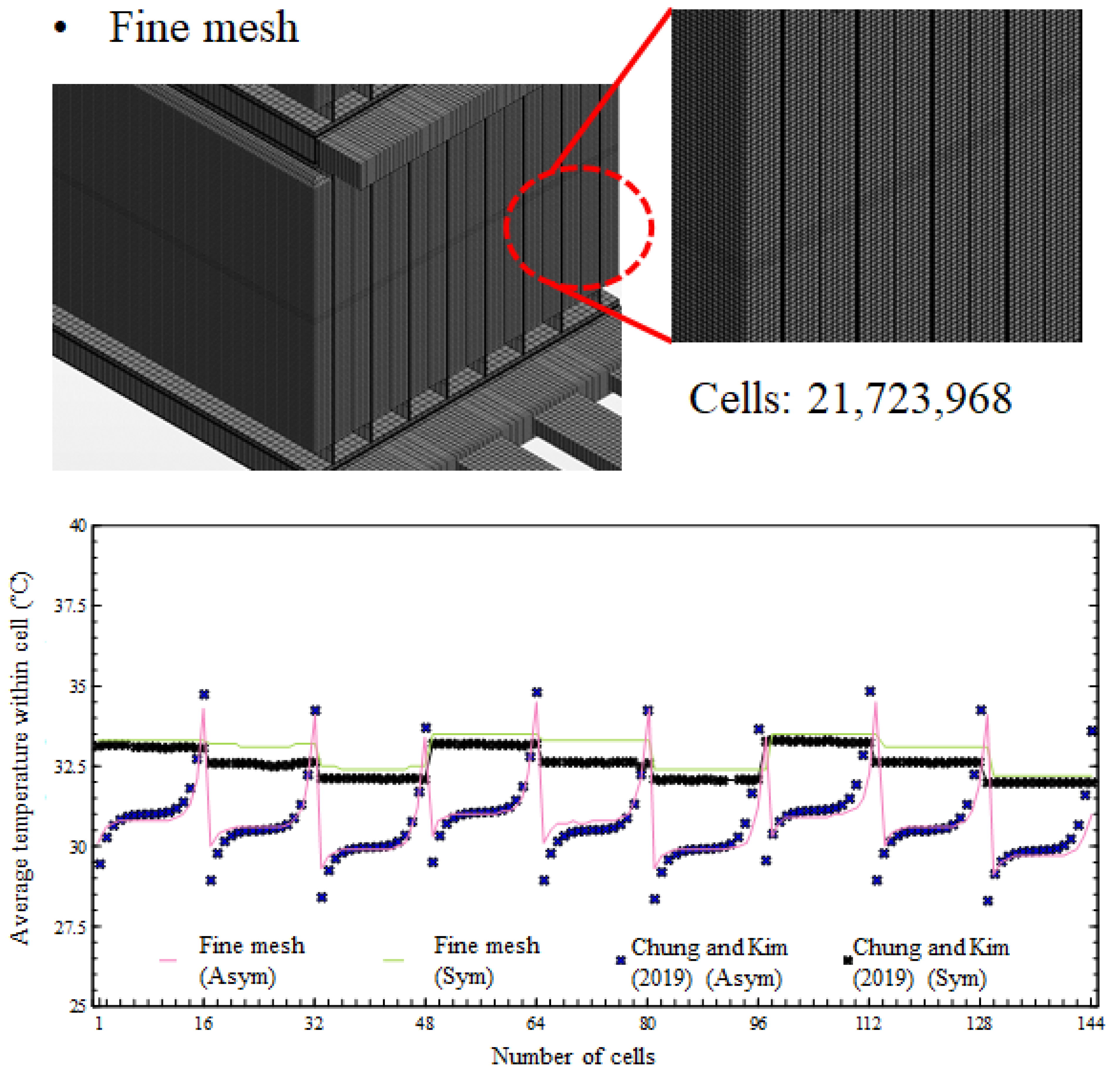
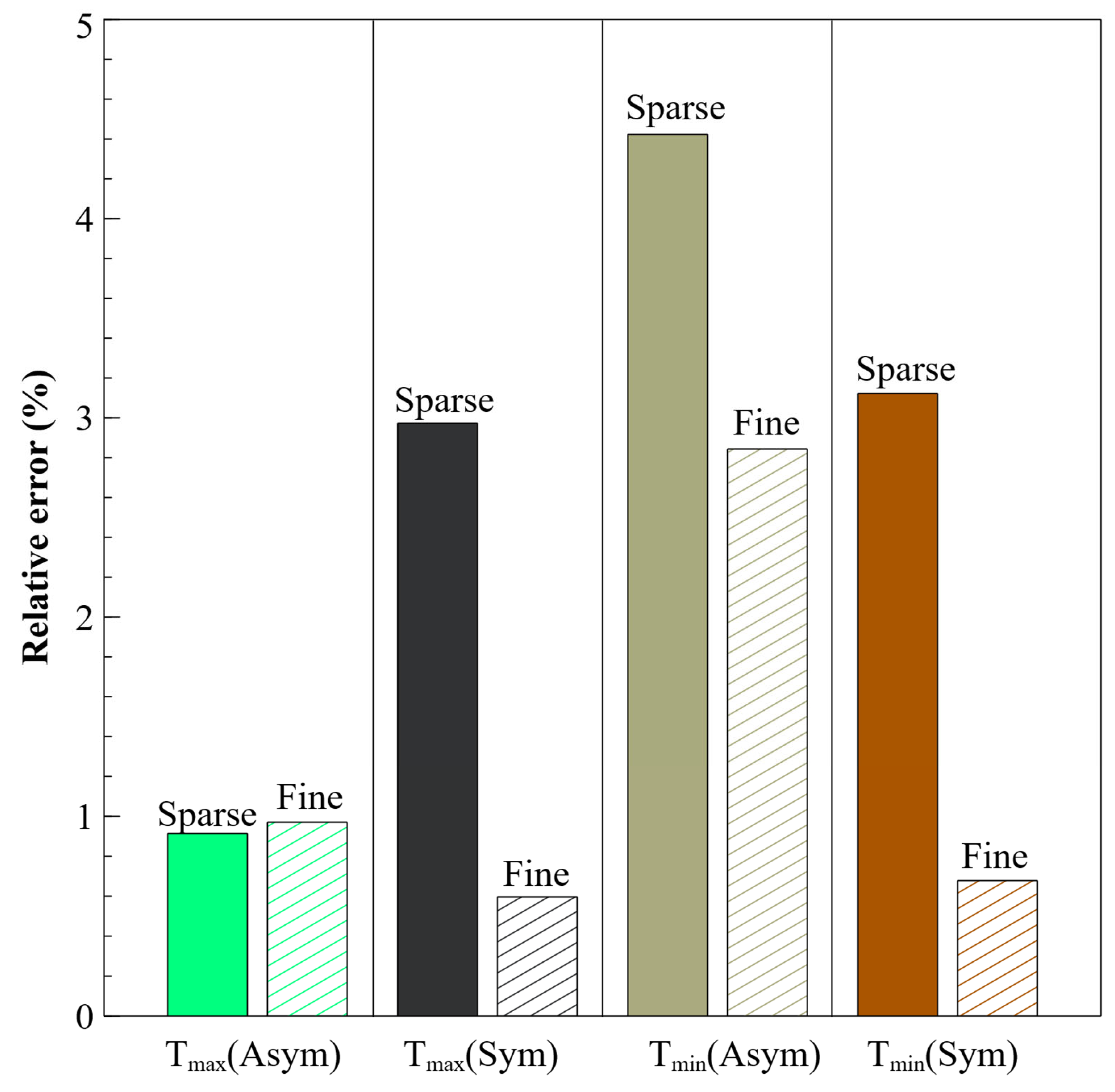
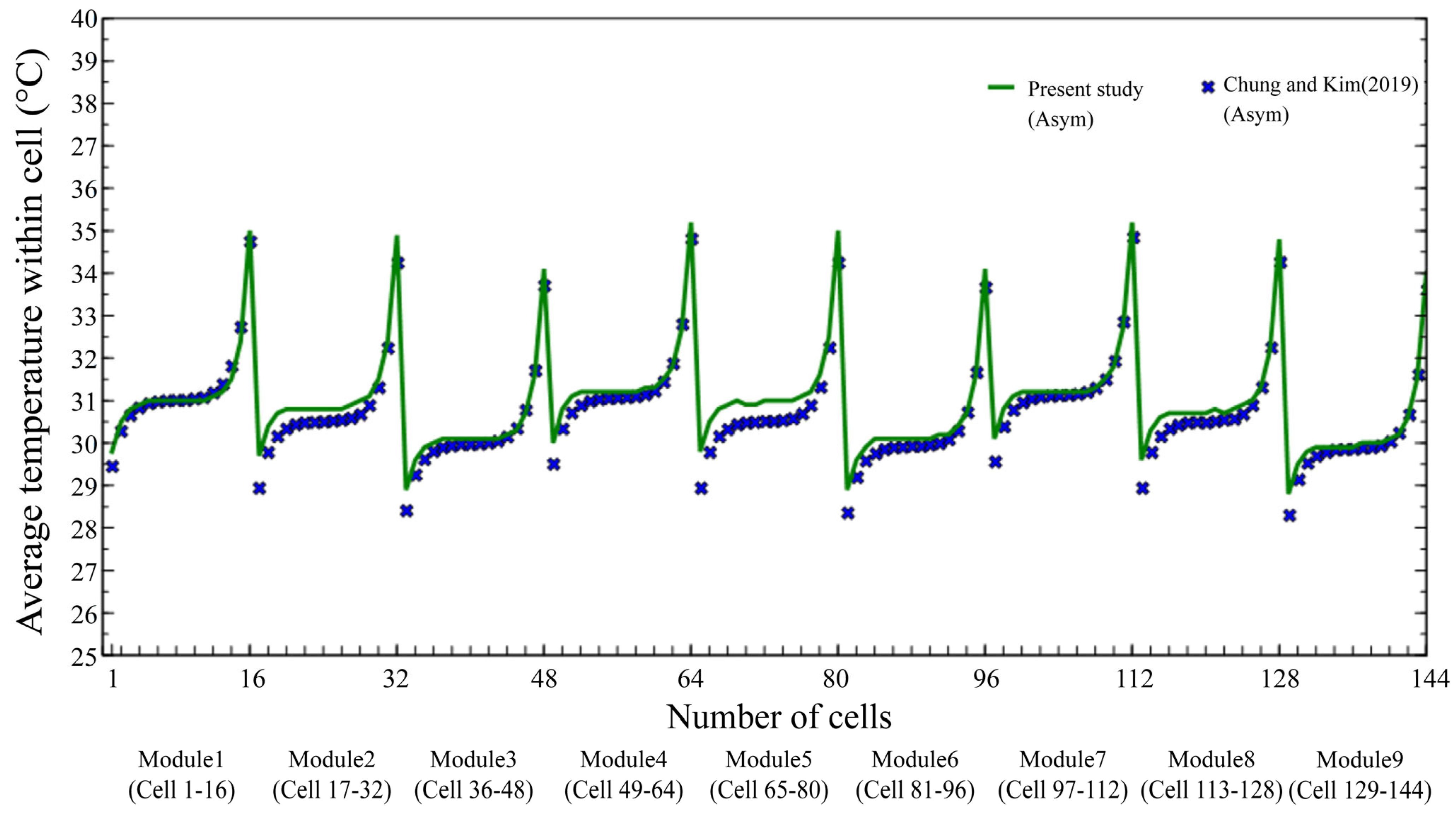
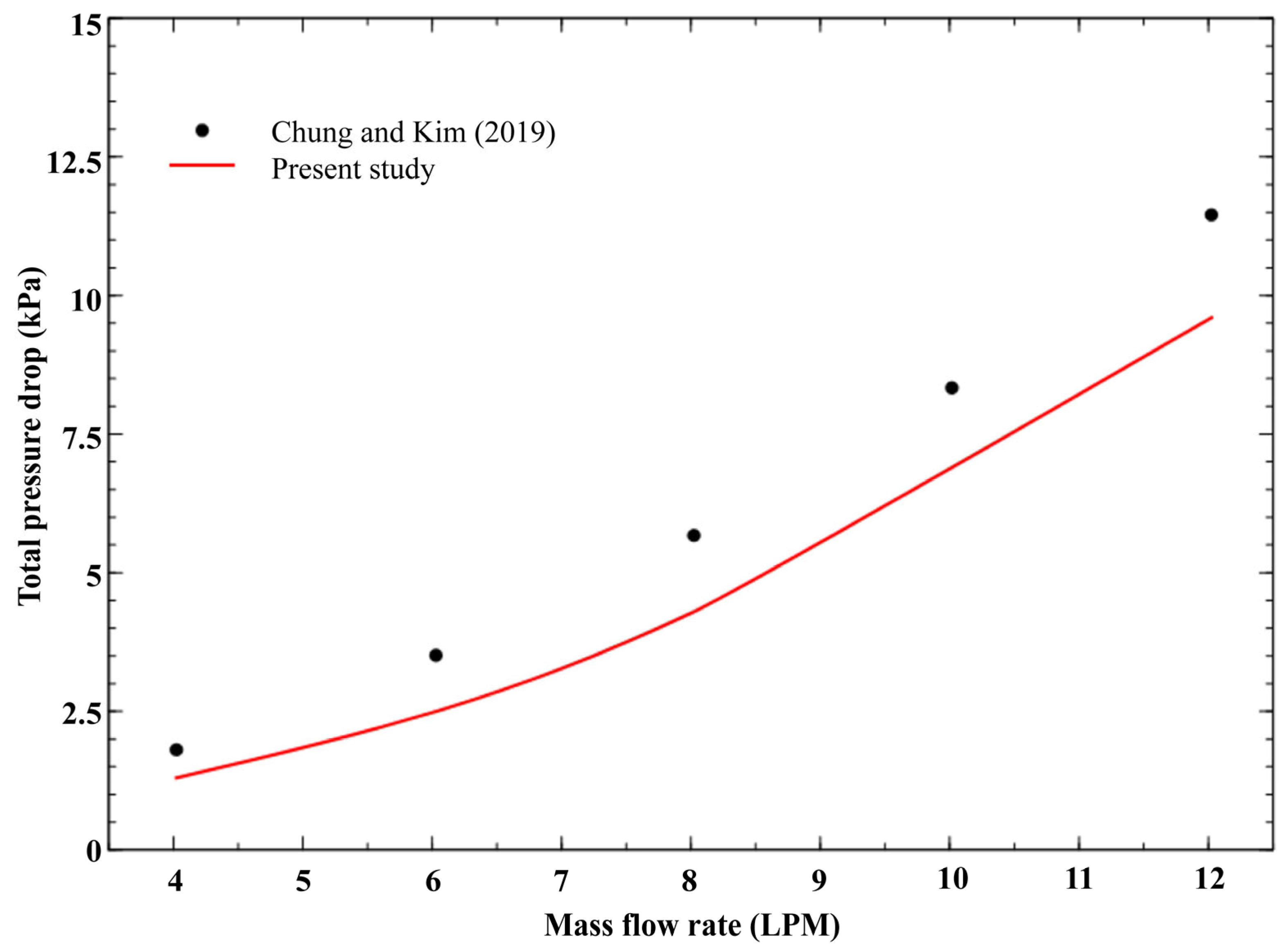
4.1. Grid Dependency
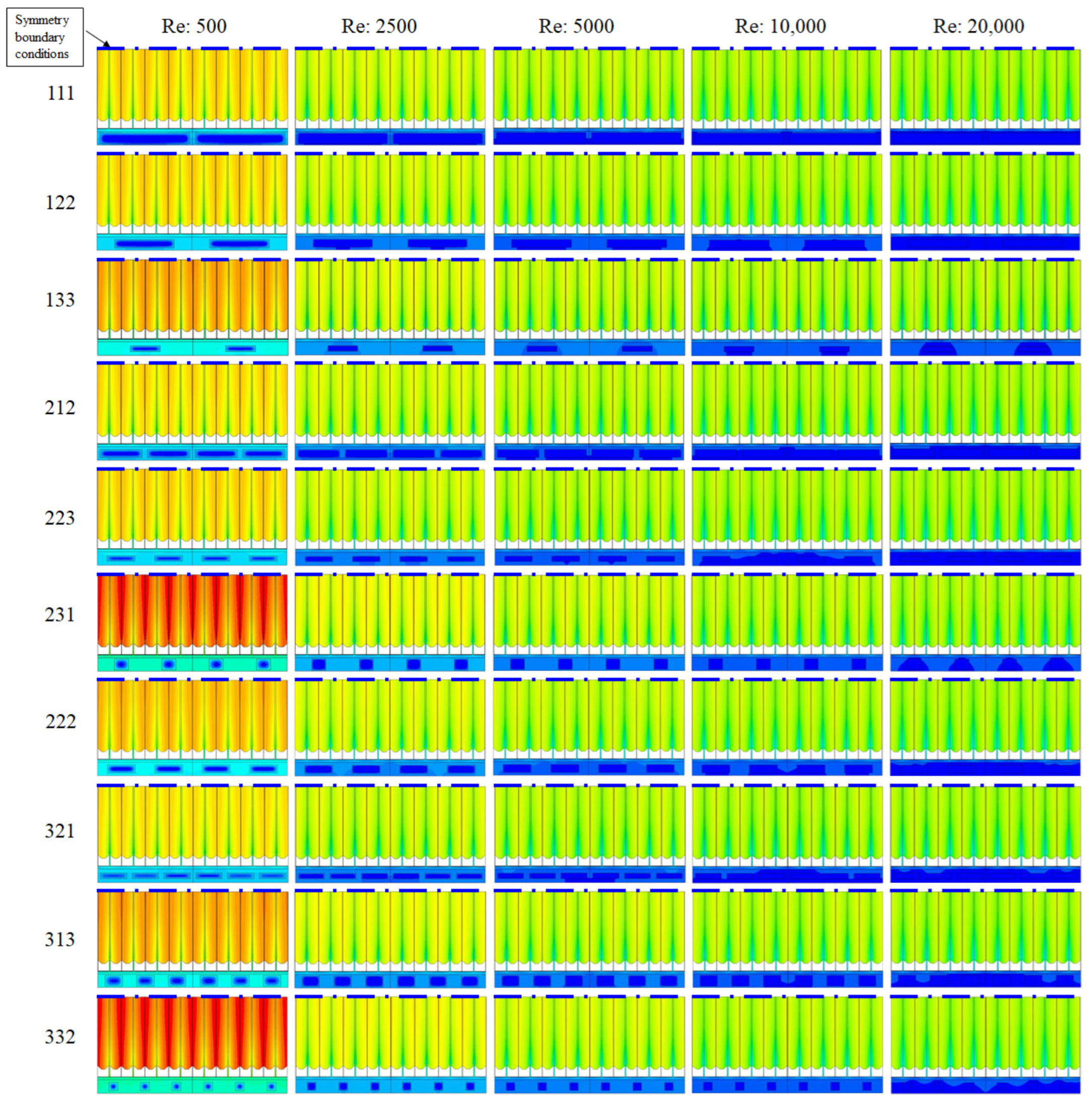
4.2. Section of Temperature Distributions
4.3. Calculation of h and Nusselt Number
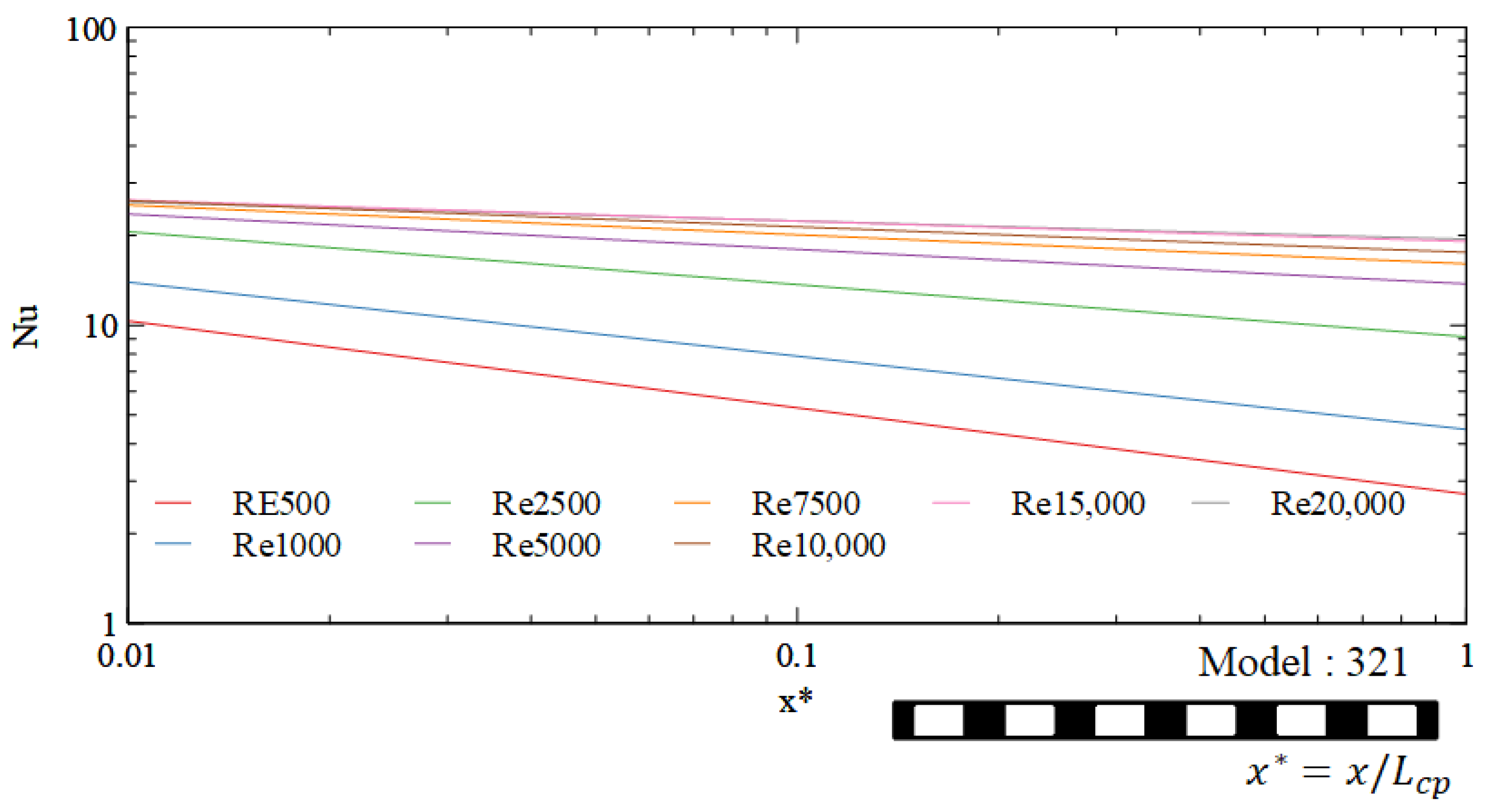
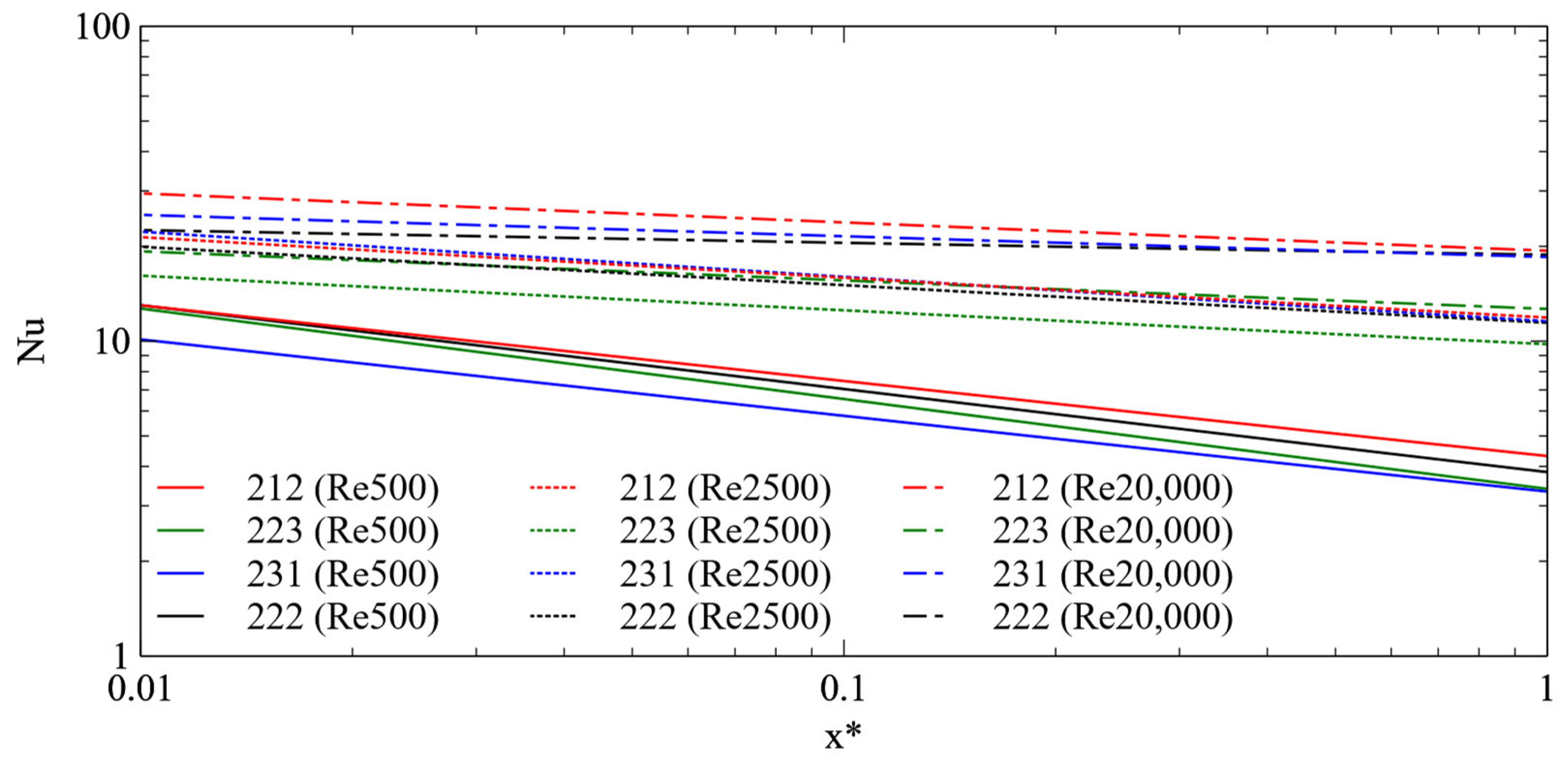
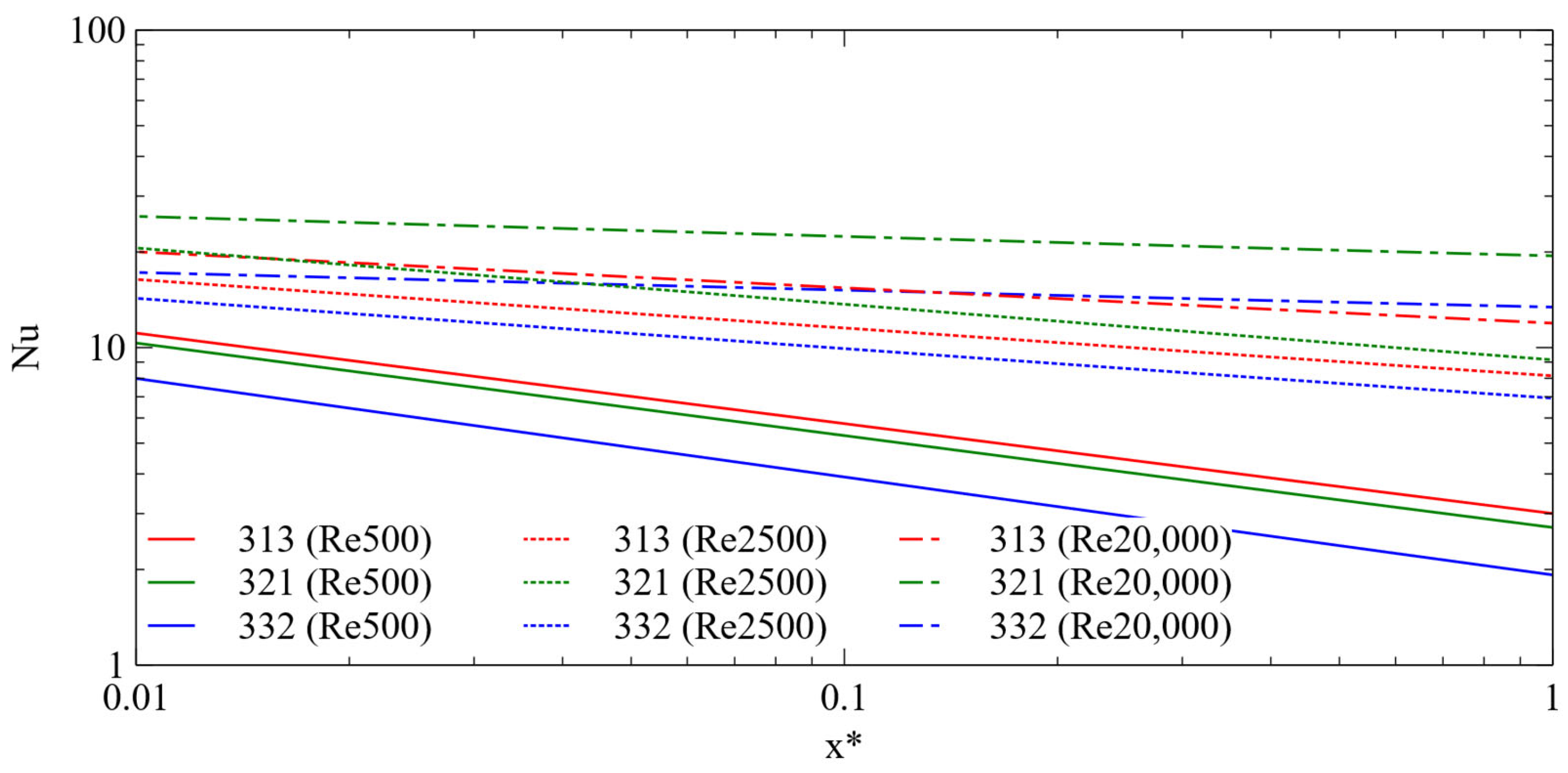
4.4. Development of Nusselt Number Correlations
4.5. Development of Fanning f-factor Correlations
4.6. Correlation Between Fanning f-factor and Colburn j-factor
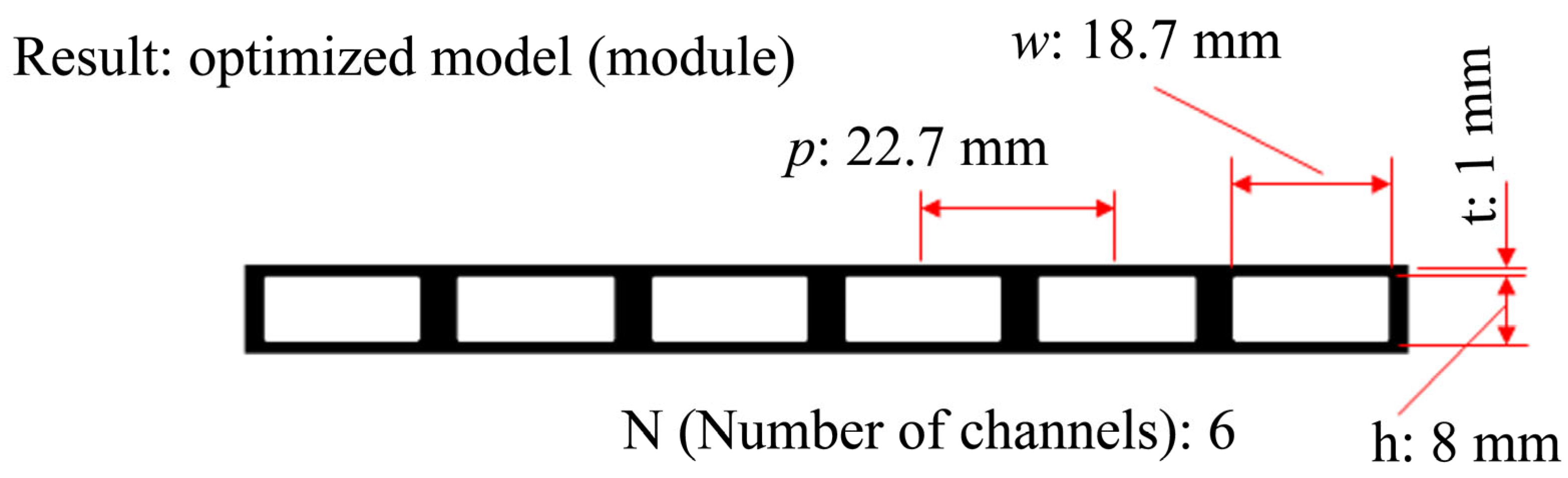
4.7. Channel Optimization
5. Conclusions
- -
- For a fixed number of channels, the Nusselt number increases with wetted area.
- -
- As the Re increases, the decrease in Nusselt number along the non-dimensionalized distance x* decreases.
- -
- Maintaining a high Re helps minimize inlet effects and ensures uniform heat dissipation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Specific heat capacity [J/kg·K] | |
| C-rate | Rate of charge |
| f | Fanning f-factor |
| Fin on the cell | |
| GF | Goodnesss factor |
| Production of turbulent kinetic energy | |
| H | Height of cold plate [mm] |
| h | Height of channel [mm] |
| j | Colburn j-factor |
| k | Thermal conductivity [W/m·K] |
| Lch | Length of channel [mm] |
| N | Number of channels |
| Number of cases with above 10% error | |
| Nu | Nusselt number |
| Number of total cases | |
| P | Pressure [Pa] |
| Pressure drop [Pa] | |
| Pitch of channel | |
| Reynolds number | |
| t | Thickness between top surface of the cold plate and channel [mm] |
| Temperature [K] | |
| Average temperature of cell | |
| Temperature difference of cell | |
| Maximum temperature of cell | |
| Minimum temperature of cell | |
| Time-averaged velocity [m/s] | |
| Reynolds stress tensor [m2/s2] | |
| Turbulent heat flux component [K·m/s] | |
| Volume of coolant region | |
| Width of cold plate [mm] | |
| Width of channel [mm] | |
| Maximum width of channel [mm] | |
| directions [m] | |
| Dissipation rate of turbulent kinetic energy | |
| Viscosity | |
| Turbulent eddy viscosity | |
| density |
References
- König, A.; Mayer, S.; Nicoletti, L.; Tumphart, S.; Lienkamp, M. The impact of HVAC on the development of autonomous and electric vehicle concepts. Energies 2022, 15, 441. [Google Scholar] [CrossRef]
- Evtimov, I.; Ivanov, R.; Sapundjiev, M. Energy consumption of auxiliary systems of electric cars. MATEC Web Conf. EDP Sci. 2017, 133, 06002. [Google Scholar] [CrossRef]
- Cavalcante, I.; Rodrigues da Silva, A.; Zajc, M.; Mendek, I.; Calearo, L.; Malkova, A.; Ziras, C.; Pediaditis, P.; Michos, K.; Mateus, J.; et al. Dataset on electric road mobility: Historical and evolution scenarios until 2050. Sci. Data 2024, 11, 1019. [Google Scholar] [CrossRef] [PubMed]
- Oech, A.K.; Mwandila, G.; Mulolani, F. A review of improvements on electric vehicle battery. Heliyon 2024, 10, e34806. [Google Scholar] [CrossRef] [PubMed]
- Chung, Y.; Kim, M.S. Thermal analysis and pack level design of battery thermal management system with liquid cooling for electric vehicles. Energy Convers. Manag. 2019, 196, 105–116. [Google Scholar] [CrossRef]
- Guo, Q.; Liu, S.; Zhang, J.; Huang, Z.; Han, D. Effects of charging rates on heat and gas generation in lithium-ion battery thermal runaway triggered by high temperature coupled with overcharge. J. Power Sources 2024, 600, 234237. [Google Scholar] [CrossRef]
- Kampker, A.; Heimes, H.H.; Offermanns, C.; Vienenkötter, J.; Robben, T. Framework and classification of battery system architectures. World Electr. Veh. J. 2023, 14, 88. [Google Scholar] [CrossRef]
- Ma, Y.; Teng, H.; Thelliez, M. Electro-thermal modeling of a lithium-ion battery system. SAE Int. J. Engines 2010, 3, 306–317. [Google Scholar] [CrossRef]
- Hettesheimer, T.; Neef, C.; Rosellón Inclán, I.; Link, S.; Schmaltz, T.; Schuckert, F.; Stephan, A.; Stephan, M.; Thielmann, A.; Weymann, L.; et al. Lithium-Ion Battery Roadmap-Industrialization Perspectives Toward 2030; Fraunhofer: Munich, Germany, 2023. [Google Scholar] [CrossRef]
- Yi, Z.; Wei, P.; Zhang, H.; Sun, H.; Zeng, S.; Yu, H. Wide range temperature thermal performance of power battery module with double-sided thermoelectric device system with high energy efficiency. Appl. Therm. Eng. 2023, 227, 120375. [Google Scholar] [CrossRef]
- Cai, Y.; Sun, Q.; Gu, X.; Li, Y.; Luo, W.; Zhang, Y.; Zhang, B.; Huang, G.; Dong, K. Multi-objective optimization of battery thermal management system based on a novel embedded hybrid cooling plate considering time-based early shutdown strategy. Energy 2024, 312, 133419. [Google Scholar] [CrossRef]
- Madaoui, S.; Guzowski, B.; Gozdur, R.; Dimitrova, Z.; Audiot, N.; Sabatier, J.; Vinassa, J.M.; Guillemard, F. Evaluation of dual side cooling system for prismatic batteries for vehicle applications. In Proceedings of the 36th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact on Energy Systems (ECOS 2023), Las Palmas de Gran Canaria, Spain, 25–30 June 2023; pp. 2218–2228. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H. Thermal characteristics of power battery module with composite phase change material and external liquid cooling. Int. J. Heat Mass Transf. 2020, 156, 119820. [Google Scholar] [CrossRef]
- Zhao, J.; Rao, Z.; Li, Y. Thermal performance of mini-channel liquid cooled cylinder based battery thermal management for cylindrical lithium-ion power battery. Energy Convers. Manag. 2015, 103, 157–165. [Google Scholar] [CrossRef]
- Zhang, C.; Li, K.; Mcloone, S.; Yang, Z. Battery modelling methods for electric vehicles–A review. In Proceedings of the European Control Conference (ECC 2014), Strasbourg, France, 24–27 June 2014; pp. 2673–2678. [Google Scholar] [CrossRef]
- Liu, G.; Ouyang, M.; Lu, L.; Li, J.; Han, X. Analysis of the heat generation of lithium-ion battery during charging and discharging considering different influencing factors. J. Therm. Anal. Calorim. 2014, 116, 1001–1010. [Google Scholar] [CrossRef]
- Aruna, P.; Vasan Prabhu, V.; Krishnakumar, V.; Velmurugan, P. Review on lithium-ion battery modeling techniques for electric vehicle applications. In Lecture Notes in Electrical Engineering; Dhar, S., Do, D.T., Sur, S.N., Liu, C.M., Eds.; Springer: Singapore, 2022; Volume 1037, pp. 551–565. ISBN 978-981-99-1983-3. [Google Scholar] [CrossRef]
- Saw, L.H.; Ye, Y.; Tay, A.A.O. Electro-thermal characterization of lithium iron phosphate cell with equivalent circuit modeling. Energy Convers. Manag. 2014, 87, 367–377. [Google Scholar] [CrossRef]
- Bamrah, P.; Kumar Chauhan, M.; Singh Sikarwar, B. CFD analysis of battery thermal management system. J. Phys. Conf. S. 2022, 2178, 012035. [Google Scholar] [CrossRef]
- Shang, Z.; Qi, H.; Liu, X.; Ouyang, C.; Wang, Y. Structural optimization of lithium-ion battery for improving thermal performance based on a liquid cooling system. Int. J. Heat Mass Transf. 2019, 130, 33–41. [Google Scholar] [CrossRef]
- Nigel. 2020 Rimac Nevera. 2023. Available online: https://www.batterydesign.net/2020-rimac-nevera/#:-:text=Liquid%20Cooling%20%C2%B7%20Flow%20rate,4 (accessed on 3 August 2025).
- Gotion. Multi-National Academicians Discussed the Development of New Energy in Hefei, Gotion Astroinno Batteries Will Be in Mass Production Next Year. 2023. Available online: https://en.gotion.com.cn/news/company-news-260.html (accessed on 3 August 2025).
- Contemporary Amperex Technology Co., Limited; Song, F.T. Water Cooling Plate Assembly, Cooling System, Battery and Enclosure, and Electrical Device. Patent CN114497826A, 18 April 2022. [Google Scholar]
- Gao, H.; Hou, X.; Ma, W.; Ma, Y. Design and Thermal Performance Analysis of a Liquid Cooling Plate Based on Gradually Varied Circular Notched Fins for Lithium-Ion Batteries. Processes 2025, 13, 924. [Google Scholar] [CrossRef]
- Mokhtari, A.; Jalalvand, M. Effect of flow pattern and channel cross section on thermal management of cylindrical batteries with solid blocks containing liquid channels: A Mokhtari and M Jalalvand. Indian J. Phys. 2025, 99, 4223–4238. [Google Scholar] [CrossRef]
- Zhang, H.; Ganesan, P.; Sharma, R.; Zubir, M.N.B.M.; Badruddin, I.A.; Chong, W.T. A novel overflow channel design of manifold cold plate for lithium-ion battery: A CFD study. Process Saf. Environ. Prot. 2024, 189, 648–663. [Google Scholar] [CrossRef]
- Alvarez, S. Tesla 4680 Cells Compared with BYD Blade and CATL Qilin Structural Batteries. 2022. Available online: https://www.teslarati.com/tesla-4680-vs-byd-blade-vs-catl-qilin-structural-batteries-video/ (accessed on 3 August 2025).
- Ye, Y.; Saw, L.H.; Shi, Y.; Tay, A.A. Numerical analyses on optimizing a heat pipe thermal management system for lithium-ion batteries during fast charging. Appl. Therm. Eng. 2015, 86, 281–291. [Google Scholar] [CrossRef]
- Zuo, W.; Zhang, Y.; E, J.; Huang, Y.; Li, Q.; Zhou, K.; Zhang, G. Effects of multi-factors on performance of an improved multi-channel cold plate for thermal management of a prismatic LiFePO4 battery. Energy 2022, 261, 125384. [Google Scholar] [CrossRef]
- Hosseinzadeh, E.; Barai, A.; Marco, J.; Jennings, P.A. A comparative study on different cooling strategies for lithium-ion battery cells. In Proceedings of the European Battery, Hybrid and Fuel Cell Electric Vehicle Congress (EEVC 2017) Proceedings, Geneva, Switzerland, 14–16 March 2017; pp. 1–9. [Google Scholar]
- Alzwayi, A.; Paul, M.C. Heat transfer enhancement of a lithium-ion battery cell using vertical and spiral cooling fins. Therm. Sci. Eng. Prog. 2024, 47, 102304. [Google Scholar] [CrossRef]
- Choi, H.; Lee, H.; Han, U.; Jung, J.; Lee, H. Comparative Evaluation of Liquid Cooling-Based Battery Thermal Management Systems: Fin Cooling, PCM Cooling, and Intercell Cooling. Int. J. Energy Res. 2024, 2024, 5395508. [Google Scholar] [CrossRef]
- Kuznetcov, A.; Telichev, I.; Wu, C.Q. Effect of thin-walled tube geometry on its crashworthiness performance. In Proceedings of the International LS-DYNA Users Conference, Dearborn, MI, USA, 12–14 June 2016; pp. 1–12. [Google Scholar]
- GW. Understanding the Minimum Wall Thickness for Aluminum Extrusion. 2025. Available online: https://hplmachining.com/blog/the-minimum-thickness-for-aluminum-extrusion/#:~:text=match%20at%20L316%20minimum%20wall,Meeting%20international%20requirements%20like%20ISO (accessed on 3 August 2025).
- Schadegg, J. Common Design Mistakes to Avoid in Extruded Parts. 2022. Available online: https://www.xometry.com/resources/extrusion/extrusion-design-tips/#:~:text=Wall%20thickness%20and%20balance%20play,help%20avoid%20costly%20secondary%20operations (accessed on 3 August 2025).
- Ortega, A.; Caceres, C.; Uras, U.; Kisitu, D.; Chowdhury, U.; Radmard, V.; Heydari, A. Determination of the thermal performance limits for single phase liquid cooling using an improved effectiveness-NTU cold plate model. In Proceedings of the International Electronic Packaging Technical Conference and Exhibition, Garden Grove, CA, USA, 25–27 October 2022; p. V001T01A008. [Google Scholar] [CrossRef]
- Dudchenko, A.V.; Hardikar, M.; Anand, A.; Xin, R.; Wang, R.; Gopu, C.; Mauter, M.S. Guidance on Nusselt number correlation selection in membrane distillation. ACS EST Eng. 2022, 2, 1425–1434. [Google Scholar] [CrossRef]
- Stephan, K. Wärmeübergang und Druckabfall bei nicht ausgebildeter Laminarströmung in Rohren und in ebenen Spalten: Wärmeübergang und Druckabfall bei nicht ausgebildeter Laminarströmung in Rohren und in ebenen Spalten. Chem. Ing. Tech. 1959, 31, 773–778. [Google Scholar] [CrossRef]
- Mortean, M.V.V.; Mantelli, M.B.H. Nusselt number correlation for compact heat exchangers in transition regimes. Appl. Therm. Eng. 2019, 151, 514–522. [Google Scholar] [CrossRef]
- Churchill, S.W.; Usagi, R. A general expression for the correlation of rates of transfer and other phenomena. AIChE J. 1972, 18, 1121–1128. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Principles of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: Singapore, 2013; pp. 484–485. ISBN 978-04-7064-615-1. [Google Scholar]
- Vijayan, P.K.; Nayak, A.K.; Kumar, N. Single-Phase, Two-Phase and Supercritical Natural Circulation Systems; Elsevier: Duxford, UK, 2019; pp. 69–118. ISBN 978-00-8102-487-4. [Google Scholar]
- Jones, O.C. An improvement in the calculation of turbulent friction in rectangular ducts. J. Fluids Eng. 1976, 98, 173–180. [Google Scholar] [CrossRef]










| Number of Channels | Dh (m) | Reference |
|---|---|---|
| 3–5 | 0.008 | [28] |
| 3–6 | 0.001 | [29] |
| 4 | 0.011 | [5] |
| 3 | 0.001 | [30] |
| 1 | 0.03 | [31] |
| 1 | 0.005 | [32] |
| No. | Name | h/t | Reynolds number (Re) | |||
|---|---|---|---|---|---|---|
| 1 | 111 | 1/1 | 8/1 | 500, 1000, 2500, 5000, 7500, 10,000, 15,000, 20,000 | 214.2 | |
| 2 | 122 | 2/3 | 6/2 | 500, 1000, 2500, 5000, 7500, 10,000, 15,000, 20,000 | 107.1 | |
| 3 | 133 | 1/3 | 4/3 | 500, 1000, 2500, 5000, 7500, 10,000, 15,000, 20,000 | 35.7 | |
| 4 | 212 | 1/1 | 6/2 | 500, 1000, 2500, 5000, 7500, 10,000, 15,000, 20,000 | 150.6 | |
| 5 | 223 | 2/3 | 4/3 | 500, 1000, 2500, 5000, 7500, 10,000, 15,000, 20,000 | 66.9 | |
| 6 | 231 | 1/3 | 8/1 | 500, 1000, 2500, 5000, 7500, 10,000, 15,000, 20,000 | 66.9 | |
| 7 | 313 | 1/1 | 4/3 | 500, 1000, 2500, 5000, 7500, 10,000, 15,000, 20,000 | 93.7 | |
| 8 | 321 | 2/3 | 8/1 | 500, 1000, 2500, 5000, 7500, 10,000, 15,000, 20,000 | 124.9 | |
| 9 | 332 | 1/3 | 6/2 | 500, 1000, 2500, 5000, 7500, 10,000, 15,000, 20,000 | 46.8 | |
| 10 [5] | 222 | 34 | 2/3 | 6/2 | 500, 1000, 2500, 5000, 7500, 10,000, 15,000, 20,000 | 100.4 |
| Part | [] | Cp [] | [] |
|---|---|---|---|
| Cold plate and Fincell | 2700 | 893 | 170 |
| Thermal pad | 3100 | 930 | 5 |
| Insulation | 2300 | 1430 | 1.5 |
| Battery cell | 1780 | 1000 | 30/0.5 (in/cross-plane) |
| Coolant | 997.6 | 4181.7 | 0.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, H.-I.; Choi, T.S.; Kook, J.-K.; Kim, T.K. Channel Optimization of Sandwich Double-Sided Cold Plates for Electric Vehicle Battery Cooling. Appl. Sci. 2025, 15, 10653. https://doi.org/10.3390/app151910653
Choi H-I, Choi TS, Kook J-K, Kim TK. Channel Optimization of Sandwich Double-Sided Cold Plates for Electric Vehicle Battery Cooling. Applied Sciences. 2025; 15(19):10653. https://doi.org/10.3390/app151910653
Chicago/Turabian StyleChoi, Hyoung-In, Tae Seung Choi, Jeong-Keun Kook, and Taek Keun Kim. 2025. "Channel Optimization of Sandwich Double-Sided Cold Plates for Electric Vehicle Battery Cooling" Applied Sciences 15, no. 19: 10653. https://doi.org/10.3390/app151910653
APA StyleChoi, H.-I., Choi, T. S., Kook, J.-K., & Kim, T. K. (2025). Channel Optimization of Sandwich Double-Sided Cold Plates for Electric Vehicle Battery Cooling. Applied Sciences, 15(19), 10653. https://doi.org/10.3390/app151910653







