Critical Data Discovery for Self-Driving: A Data Distillation Approach

Abstract

Deep learning models have achieved significant progress in developing self-driving algorithms. Despite their advantages, these algorithms typically require substantial amounts of data for effective training. Critical driving data, in particular, is essential for enhancing training efficiency and ensuring driving safety. However, existing methods for identifying critical data often rely on human prior knowledge or are disconnected from the training of self-driving algorithms. In this paper, we introduce a novel data distillation technique designed to autonomously identify critical data for training self-driving algorithms. We conducted experiments with both numerical simulations and the NGSIM dataset, which consists of real-world car trajectories on highway US-101, to validate our approach. In the numerical experiments, the distillation method achieved a test root mean squared error of 1.933 using only 200 distilled training data samples, demonstrating a significant improvement in data efficiency compared to the 1.872 test error obtained with 20,000 randomly sampled training samples. The distilled critical data represents only 1% of the original dataset, optimizing data usage and significantly enhancing computational efficiency. For real-world NGSIM data, we demonstrate the performance of the proposed method in scenarios with extremely sparse data availability and show that our proposed data distillation method outperforms other sampling baselines, including Herding and K-centering. These experimental results highlight the capability of the proposed method to autonomously identify critical data without relying on human prior knowledge.

1. Introduction

Recent years have witnessed breakthroughs in applying deep learning models to develop self-driving algorithms. However, training these algorithms requires a large amount of naturalistic driving data, which is expensive and inefficient to collect as the critical driving data only accounts for a small portion of it. Thus, discovering critical data becomes important for improving training efficiency and ensuring driving safety.

Critical driving data usually includes corner cases, without which the trained algorithms may not perform well in worst-case scenarios or may have safety issues. Existing methods for discovering critical data can be divided into two categories: sampling-based and generation-based methods. The sampling-based method aims to directly identify critical data by directly sampling it from naturalistic datasets by utilizing manually defined metrics like time to collision (TTC) [1,2,3] or adaptive algorithms such as importance sampling [4,5,6,7] and clustering [8,9,10,11,12]. However, this method has two major drawbacks. First, it heavily relies on human prior knowledge to identify critical data. The manually defined metrics require extensive human knowledge and are not flexible enough to handle the complex patterns of human driving behavior. Adaptive sampling methods also depend on human knowledge to select key characteristic variables (e.g., TTC and space headway) for adjusting sampling weights or clustering. Second, this method samples original data rather than learning data patterns. It may encounter issues when naturalistic data lacks certain scenarios and does not consider the ratio of critical to non-critical data.

Different from the sampling-based methods, generation-based methods aim to synthesize critical driving data using simulators [13,14,15] or deep generative models [16,17,18,19,20]. Compared to the sampling-based approach, generation-based methods can learn data patterns and generate critical scenarios that are not originally collected in naturalistic data. However, like sampling-based methods, they still require human prior knowledge to identify critical data. Additionally, most methods of this kind decouple the upstream critical data generation from the downstream self-driving algorithm training processes and use independent metrics for these two processes. Due to this decoupling, the generated critical data may not be optimal for training self-driving algorithms.

To fill these research gaps, in this paper we propose a unified framework to discover critical data while training self-driving algorithms using the data distillation approach. The data distillation approach was originally used to find parsimonious training data that can achieve a similar training efficacy to the original training data, and it is primarily used to condense image datasets in image classification tasks. We have reformulated the data distillation framework to discover critical data. In this process, we do not provide any prior knowledge, and our proposed framework can identify critical data, the size of which is an order of magnitude smaller than the original, thus enhancing training efficiency.

Our contributions are as follows:

• We are the first to formulate the data distillation framework for a regression problem;
• We apply the data distillation framework to self-driving critical data discovery;
• Our proposed method is evaluated using numerical and real-world datasets. We show that the data distillation framework can identify the most critical data with a minimal size.

The rest of this paper is organized as follows: Section 2 reviews the related work on self-driving critical data discovery. Section 3 introduces the preliminaries and problem statement of data distillation. Section 4 introduces the methodology of our proposed data distillation framework. Section 5 introduces both numerical and real-world experiments and results. Section 7 concludes and projects future research directions.

2. Related Work

2.1. Critical Data Generation

Sampling-based methods include rule-based and adaptive ones. Rule-based sampling methods use human experience and prior knowledge to define criteria for critical data. Time to collision (TTC) is the most widely used metric to find collision or near-collision driving scenarios [1,2,3]. Additionally, some studies use overlapped vehicle bounding boxes to identify collision data [21]. Unlike rule-based methods, adaptive methods do not specifically propose metrics to filter critical data. For example, importance sampling aims to progressively replace the original data distribution with a new one that has a higher ratio of critical data occurrence [4,5,6,7]. While the sampling ratio of critical data is adaptively increased, this method still requires human experience to define what constitutes critical data. Clustering methods [8,9,10,11,12] use differences within the data and divide them into clusters, requiring human guidance to select the variables to decide the cluster boundary. After the clusters are separated, human prior knowledge is still necessary to determine which clusters contain critical data.

Table 1. Comparison among related work.

Method	Automatic	Generates New Data	Covers Long-Tail
Rule-based (e.g., TTC, overlap) [1,2,3,21]	✗	✗	✗
Adaptive sampling (importance) [4,5,6,7]	✓	✗	✗
Clustering-based [8,9,10,11,12]	✓	✗	✗
Simulator-based (e.g., CARLA, perturbation) [13,14]	✓	✓	✗
Deep generative models (GAN, VAE) [5,15]	✓	✓	✗
GradMatch [22]	✓	✗	✓
Dataset distillation (DD) [17,19]	✓	✓	✓  (classification only)
Our work	✓	✓	✓ (first in regression/self-driving)

Table 1. Comparison among related work.

Method	Automatic	Generates New Data	Covers Long-Tail
Rule-based (e.g., TTC, overlap) [1,2,3,21]	✗	✗	✗
Adaptive sampling (importance) [4,5,6,7]	✓	✗	✗
Clustering-based [8,9,10,11,12]	✓	✗	✗
Simulator-based (e.g., CARLA, perturbation) [13,14]	✓	✓	✗
Deep generative models (GAN, VAE) [5,15]	✓	✓	✗
GradMatch [22]	✓	✗	✓
Dataset distillation (DD) [17,19]	✓	✓	✓  (classification only)
Our work	✓	✓	✓ (first in regression/self-driving)

Generation-based methods use simulators or deep generative models to synthesize critical driving data. Simulators like CARLA [14] incorporate built-in physics models to simulate driving dynamics. In [13], critical driving scenarios are generated by perturbing non-critical driving data. A learnable perturbation framework is proposed to accelerate this generation process [14]. Additionally, some researchers have further improved generation efficiency using causal inference [15]. Yang et al. (2025) [23] employed deep learning techniques to enhance recommender systems using large language models. While large language models have been primarily investigated in natural language processing tasks [24]. Deep generative models, such as generative adversarial networks (GANs) and variational autoencoders (VAEs), learn to synthesize data from naturalistic samples. In existing studies, conditional variables are usually used to specify critical scenarios [5].

2.2. Data Distillation

Dataset distillation (DD) was first proposed by [17]. The goal is to generate a parsimonious synthetic dataset such that models trained on it perform comparably to those trained on the original dataset. Unlike the above-mentioned sampling-based and generation-based methods, DD unifies the data generation and model training processes. For example, DD is applied to condensing images for image classification tasks [19], where cross-entropy is used as a single metric for both filtering critical data and also for training classification models. In this study, the generated data contain more information compared to the original data with a significantly smaller size. Recently, a variety of works have extended the application of dataset distillation (DD) in different research fields, including continuous learning and federated learning [25,26,27,28,29,30]. More recent studies have also focused on improving generalization through coarse-to-fine regularization [31]. Table 1 summarizes the above-mentioned related work. Despite these advances, the majority of existing works remain within a classification framework, focusing primarily on image recognition benchmarks. To the best of our knowledge, there are no studies that investigate regression-oriented tasks, such as self-driving trajectory prediction, where capturing continuous dynamics and long-tailed behaviors is crucial. In parallel, theoretical studies of mean-field approximations and Langevin sampling [32,33,34] have highlighted the importance of scalable probabilistic frameworks.

3. Preliminaries and Problem Statement

3.1. Driving Scenario

A driving scenario can be described by different modalities of data, such as images and lidar points, depending on how the data is collected. Despite the existence of different data modalities, all these data can be universally represented by a driving state. A driving state describes the scenario using its relative positions and velocities and its neighbours. In this paper, we focus on the distilling of driving states to demonstrate that our method is generalized to all data modalities. We define $x=[h,v,\Delta v]$ as the driving state, where h, $\Delta v$, and v stand for spacing headway, velocity difference from the leading vehicle, and the velocity of the current vehicle, respectively.

3.2. Car-Following

Car-following accounts for a major part of a self-driving algorithm, and in this paper we aim to apply data distillation to generate critical data to train a CF model. Define y as the acceleration of the next time step. A CF model aims to $f_{\lambda }$ learn the mapping from the state x to the action y, $f:x\to y$. An example of a CF model is the intelligent driving model (IDM) [35], which is depicted as follows:

$$\begin{array}{c}\hfill y=a_{max}\left[1-{\left({\displaystyle \frac{v\left(t\right)}{v_0}}\right)}^4-{\left({\displaystyle \frac{s_0+v{T}_0+\frac{v\left(t\right)\Delta v\left(t\right)}{2\sqrt{a_{max}b}}}{\Delta x\left(t\right)}}\right)}^2\right]\end{array}$$

(1)

which has five parameters: $v_0$ is the desired velocity, $T_0$ is the desired time headway, $s_0$ is the minimum spacing in congested traffic, $a_{max}$ is the maximum acceleration allowed, and b is the comfortable deceleration.

3.3. Problem Statement

Define the original dataset as $\mathcal{T}=\{X,Y\}={\{x^{\left(i\right)},y^{\left(i\right)}\}}_{i=1}^{N_T}$, where $N_T=\left|\mathcal{T}\right|$ is the data size. Similarly define the critical dataset as $\mathcal{S}=\{\tilde{X},\tilde{Y}\}={\{{\tilde{x}}^{\left(i\right)},{\tilde{y}}^{\left(i\right)}\}}_{i=1}^{N_S}$, with $N_S$ being the dataset size. The problem of critical data discovery is to identify $\mathcal{S}$ that is the most representative of the original data $\mathcal{T}$:

$$\mathcal{S}=\underset{\mathcal{S}}{argmin}D(\mathcal{S},\mathcal{T}),$$

(2)

where D stands for a measurement of the representativeness of the generated $\mathcal{S}$ compared to the original data $\mathcal{T}$, e.g., reconstruction error together with cluster diversity. To avoid learning trivial results that $\mathcal{S}$ is equivalent to $\mathcal{T}$, the size of the generated data is usually constrained, i.e., $\left|\mathcal{S}\right|<<\left|\mathcal{T}\right|$.

4. Methodology

In this section, we will introduce the framework of our proposed data distillation for critical driving data discovery. On a high-level view, we formulate the original problem as a bi-level optimization problem. The inner loop is illustrated in blue in Figure 1, which includes training a CF model $f_{\theta }$, where $\theta$ is the parameter for the CF model. The real-world data and the randomly initialized data are denoted as X and $\widehat{X}$, respectively. $f_{\theta }\left(X\right)$ represents the predicted acceleration, which is compared with the real acceleration Y to calculate the loss $\mathcal{L}$. Similarly, $f_{\theta }\left(\widehat{X}\right)$ denotes the predicted acceleration using the distilled features $\widehat{X}$ and is compared to the distilled acceleration $\tilde{Y}$, which is derived from domain knowledge such as the real-world acceleration distribution, to calculate the loss ${\mathcal{L}}_{syn}$. In the outer loop, we measure the representativeness of generated data $(\tilde{X},\tilde{Y})$ with a differentiable approximation D, which measures the CF modeling performance difference between using the original data and the synthetic data. In this framework, the upstream of data generation and downstream CF model training are united, and the whole framework can be updated by gradient descent. In the following part of this section, we will detail each component.

4.1. Data Parameterization

This subsection will discuss how to set the trainable data $(\tilde{X},\tilde{Y})$. On one hand, we randomly initialize $\tilde{X}$ and update its value in each iteration. The size of $\tilde{X}$ is pre-defined as a hyperparameter $N_T$ that can be tuned. On the other, we set the value of $\tilde{Y}$ by prior knowledge and fix its value during training. We make such a design to balance the flexibility and reliability of the generated data. If both $\tilde{X}$ and $\tilde{Y}$ are trainable parameters, this framework may encounter convergence issues with a lack of supervision signal. We make the feature $\tilde{X}$ variant instead of $\tilde{Y}$ because the feature contains more information than the label, thus increasing the flexibility of data generation. The domain knowledge of $\widehat{Y}$ includes the prior assumption of what a suitable $\widehat{Y}$ may contain; e.g., $\widehat{Y}$ should cover both the acceleration and deceleration driving scenarios. To mitigate overfitting, we assign the value of Y to $\left|S\right|$ values that adhere to a Gaussian distribution ranging within $(-1,1)$. This parameterization is inspired by and modified from the original data distillation work for image classification. In the original DD paper, the target $\tilde{Y}$ is defined as a discretized variable with equal frequencies for each image class.

4.2. Car-Following Surrogate Model

To evaluate the performance of the data parameterization, a downstream CF model is used. The CF model $f_{\theta }$ is a neural network parameterized by $\theta$. The output of the neural network is compared to its ground truth, and the loss function is calculated.

$${\mathcal{L}}_{\mathrm{syn}}\left(\mathcal{S},{\theta }_t\right)={\displaystyle \frac{1}{\left|\mathcal{S}\right|}}\sum _{(\tilde{x},\tilde{y})\in \mathcal{S}}\mathcal{l}\left(f_{{\theta }_t}\left(\tilde{x}\right),\tilde{y}\right)$$

(3)

This neural network is also applied to the original data, and the loss function is calculated.

$$\mathcal{L}\left(\mathcal{T},{\theta }_t\right)={\displaystyle \frac{1}{\left|\mathcal{T}\right|}}\sum _{(x,y)\in \mathcal{T}}\mathcal{l}\left(f_{{\theta }_t}\left(x\right),y\right)$$

(4)

The objective of data distillation is to generate a synthetic dataset $\mathcal{S}$ such that neural networks trained on $\mathcal{S}$ achieve performance similar to those trained on the entire dataset. This objective can be described as follows:

$${\mathbb{E}}_{x\sim P_{\mathcal{D}}}\left[\mathcal{l}\left(f_{{\theta }^{\mathcal{T}}}\left(x\right),y\right)\right]\simeq {\mathbb{E}}_{x\sim P_{\mathcal{D}}}\left[\mathcal{l}\left(f_{{\theta }^{\mathcal{S}}}\left(x\right),y\right)\right]$$

(5)

where ${\theta }^{\mathcal{T}}$ and ${\theta }^{\mathcal{S}}$ represent the parameters in deep neural networks $f_{{\theta }^{\mathcal{T}}}$ and $f_{{\theta }^{\mathcal{S}}}$ that are trained on $\mathcal{T}$ and $\mathcal{S}$. $P_{\mathcal{D}}$ represents the real data distribution and ℓ represents the Mean Squared Loss (MSE), since we face a regression question.

The core idea of DD is that the CF model itself can be used to measure the quality of the generated data. In other methods, this process is usually replaced by human guidance. Directly measuring the difference between these two loss functions is computationally expensive. Below we will introduce how to approximate this difference using a differentiable framework.

4.3. Differentiable Representiveness Approximation

To realize the specified objective, the research presented in [26] elucidates an intriguing method. It suggests that a comparable solution can be drawn when the parameter updates for both ${\theta }_t^T$ and ${\theta }_t^S$ are nearly identical at every training iteration t, given a shared initial condition where ${\theta }_0^T={\theta }_0^S$. This premise operates on the foundational belief that ${\theta }_t^T$ and ${\theta }_t^S$ can consistently maintain equivalence across all iterations. Building upon this foundation, the authors further streamlined the learning process. Instead of juggling multiple neural network parameters, they integrated the framework into a singular neural network, parameterized by $\theta$. They then articulated this unification by proposing the following minimization problem:

$$\underset{\mathcal{S}}{min}D\left({\nabla }_{\theta }{\mathcal{L}}_{\mathrm{syn}}\left(\mathcal{S},{\theta }_t\right),{\nabla }_{\theta }\mathcal{L}\left(\mathcal{T},{\theta }_t\right)\right).$$

(6)

$D(·,·)$ quantifies the discrepancy between the gradient vectors of ${\mathcal{L}}^{\mathcal{S}}$ and ${\mathcal{L}}^{\mathcal{T}}$ with respect to $\theta$. In cases where $f_{\theta }$ represents a multilayer neural network, these gradients represent a series of trainable weights applicable to each fully connected (FC) and convolutional layer, respectively. The matching loss is expressed as a summation of individual losses per layer: $D\left({\nabla }_{\theta }{\mathcal{L}}^{\mathcal{S}},{\nabla }_{\theta }{\mathcal{L}}^{\mathcal{T}}\right)={\sum }_{l=1}^{L}d\left({\nabla }_{{\theta }^{\left(l\right)}}{\mathcal{L}}^{\mathcal{S}},{\nabla }_{{\theta }^{\left(l\right)}}{\mathcal{L}}^{\mathcal{T}}\right)$, where l denotes the layer index and L the total number of layers containing weights. The function $d(\mathbf{A},\mathbf{B})={\sum }_{i=1}^{\mathrm{out}}\left(1-{\displaystyle \frac{{\mathbf{A}}_{\mathbf{i}}·{\mathbf{B}}_{\mathbf{i}}}{∥{\mathbf{A}}_{\mathbf{i}}∥∥{\mathbf{B}}_{\mathbf{i}}∥}}\right)$ calculates the sum across output channels, where ${\mathbf{A}}_i$ and ${\mathbf{B}}_i$ are flattened gradient vectors corresponding to each output channel i.

4.4. Training Algorithms

The training algorithm is shown in Algorithm 1.

Algorithm 1. Data distillation with DSA.

Require: Training Set T, with parameter Input X and Output Y Ensure: Initialize synthesis Data Parameter: $\widehat{X}$, deep neural network $f_{\theta }$, number of training  iterations K, number of inner-loop steps T, number of steps for updating weights ${\zeta }_{\theta }$ and  synthetic samples ${\zeta }_{\widehat{X}}$, in each inner-loop step respectively, learning rates for updating  weights ${\eta }_{\theta }$ and synthetic samples ${\zeta }_{\widehat{X}}$  for k from 0 to $K-1$ do    Initialize $\theta$ and $f_{\theta }$    for t from 0 to $T-1$ do      Compute $\mathcal{L}\leftarrow {\displaystyle \frac{1}{\left|T\right|}}\sum \mathcal{l}(f_{{\theta }_t}\left(X\right),Y)$      Compute ${\mathcal{L}}_{syn}\leftarrow {\displaystyle \frac{1}{\left|S\right|}}\sum \mathcal{l}(f_{{\theta }_t}\left(\widehat{X}\right),Y)$      Use a optimizer sgd to update $\widehat{X}$$\leftarrow {\mathrm{sgd}}_{X_{\mathrm{syn}}}(D({\nabla }_{\theta }{\mathcal{L}}_{syn}\left(\theta \right),{\nabla }_{\theta }\mathcal{L}\left(\theta \right)),{\zeta }_{\widehat{X}},{\eta }_{\widehat{X}})$      Update ${\theta }_{t+1}\leftarrow {\mathrm{sgd}}_{\theta }({\mathcal{L}}_{\mathrm{syn}}\left({\theta }_t\right),{\zeta }_{\theta },{\eta }_{\theta })$      Update $f_{\theta }$    end for  end for  Output: $\widehat{X}$

5. Numerical Experiment

In this section, we evaluate our method using numerical data generated from an IDM model. The reason for using numerical data is that we can explicitly generate safety-critical data as a benchmark to evaluate if our algorithm can identify them. In the next section, we will use a real-world dataset to demonstrate the effectiveness of our proposed method for real-world generation.

5.1. Dataset

We assessed our approach using the car-following datasets mentioned earlier. The training set comprises 20,000 rows of data, and the validation set and test set have 5000 rows of data points.

5.2. Experiment Setting

We evaluated our approach using a multilayer perceptron (MLP) network architecture, implemented via Keras’ Sequential API. This network comprises two hidden layers, the first with 64 neurons and the second with 32 neurons, both employing the Rectified Linear Unit (ReLU) activation function. To handle regression tasks, the output layer is equipped with a single neuron. Throughout the training, we utilize MSE as the loss function and employ the Adam optimizer to adjust weights.

By initializing the deep neural network $f_{\theta }$, using TensorFlow’s Keras API, the model begins with an input shaped by three. This input passes through three dense layers with 64, 128, and 64 neurons, respectively, all employing the ReLU activation function. Each dense layer is succeeded by batch normalization for efficient training. The architecture culminates in a single-neuron output layer, indicating its regression-focused design. $\widehat{X}$ was constructed as a matrix where all elements are set to 1 for initialization, while $Y_{\mathrm{syn}}$ followed a Gaussian distribution ranging within (−1, 1).

Finally, we use the evaluation method: root mean squared error (RMSE). Our evaluation comprises two phases. In the first phase, we generate a compact synthetic dataset (roughly 200 rows) derived from the large real training dataset. Subsequently, we employ this synthesized dataset to train the initial neural networks with specific parameters and gauge their RMSE on both the real training and real testing sets. Instead of evaluating the accuracy of predicted acceleration, we conducted a one-second rolling simulation and evaluated performance by comparing the predicted position with the ground truth. This comparison is more aligned with real-world performance, i.e., next-position prediction. To mitigate overfitting, we contrast these RMSE results with those obtained from the synthetic dataset. In the following phase, we engage with the large real dataset, training it on the same pre-set neural network parameters. We then assess its performance on the real testing dataset, observing the RMSE disparities stemming from the two diverse training datasets.

5.3. Numerical Experiment Results

In this subsection, we present experimental results to demonstrate two key benefits of our proposed methods: improved data efficiency and an increased proportion of up-sampled critical driving data.

For improved data efficiency, the performance of training the downstream car-following model using the distilled data is illustrated in

Table 2. Comparison of model performance on original and distilled datasets.

Dataset	Training Size	RMSE (m)
Original Dataset	20,000	1.872
Random Sampling	200	4.696
Distillation	200	1.933

. This table clearly demonstrates that with merely $1\%$ of the original dataset, we can achieve a performance level comparable to that of the model trained on the original full-size dataset, albeit with a minor decrease in performance metrics. This indicates the efficacy of our data distillation technique in retaining significant informational content despite the drastic reduction in data volume. In contrast, when we randomly sampled 200 rows of data to train the same model, the performance was significantly poorer. This underlines the importance of our distillation method over arbitrary sampling, which fails to capture the essential dynamics and relationships within the data that are critical for maintaining performance in predictive modeling. Thus, our approach not only conserves resources but also ensures the robustness of the model by focusing on the most informative parts of the dataset.

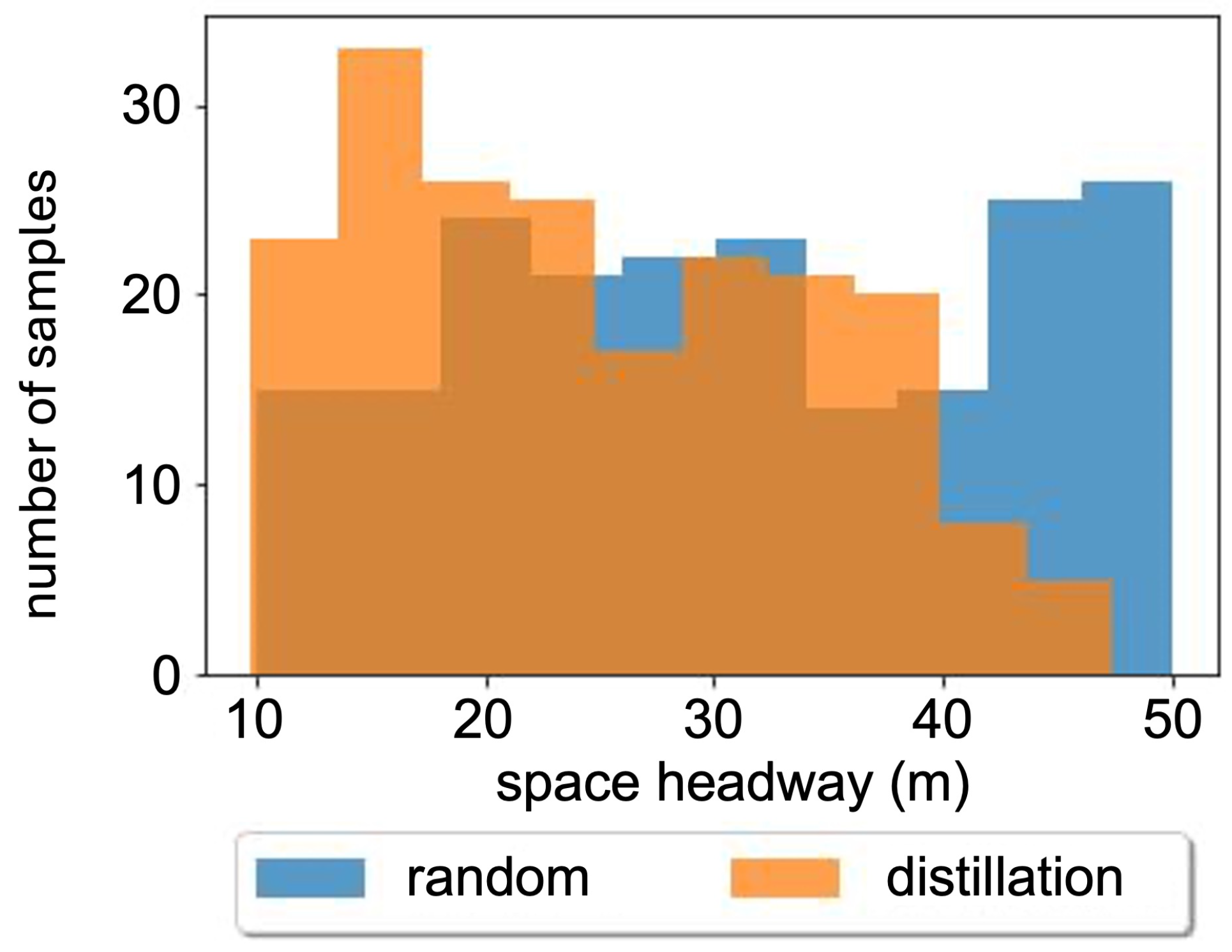
To demonstrate the increased proportion of up-sampled critical driving data, we analyzed the distribution of the space headway generated from the data distillation process in comparison to that of the randomly sampled data. This comparative analysis is visually represented in Figure 2. From this figure, it is evident that the data distillation process tends to prioritize data points with closer space headways. This prioritization occurs because the algorithm identifies these data points as more critical for training, especially in scenarios where there is a scarcity of available data. The tendency to focus on closer space headways suggests that such conditions are deemed by the algorithm to have a higher impact on the model’s learning and accuracy. This automatic weighting toward more significant, informative instances demonstrates the intelligence of the distillation process in effectively harnessing limited data to optimize training outcomes. By doing so, it ensures that the distilled dataset, though smaller, is still highly representative and effective for training robust models.

6. Case Study with NGSIM Dataset

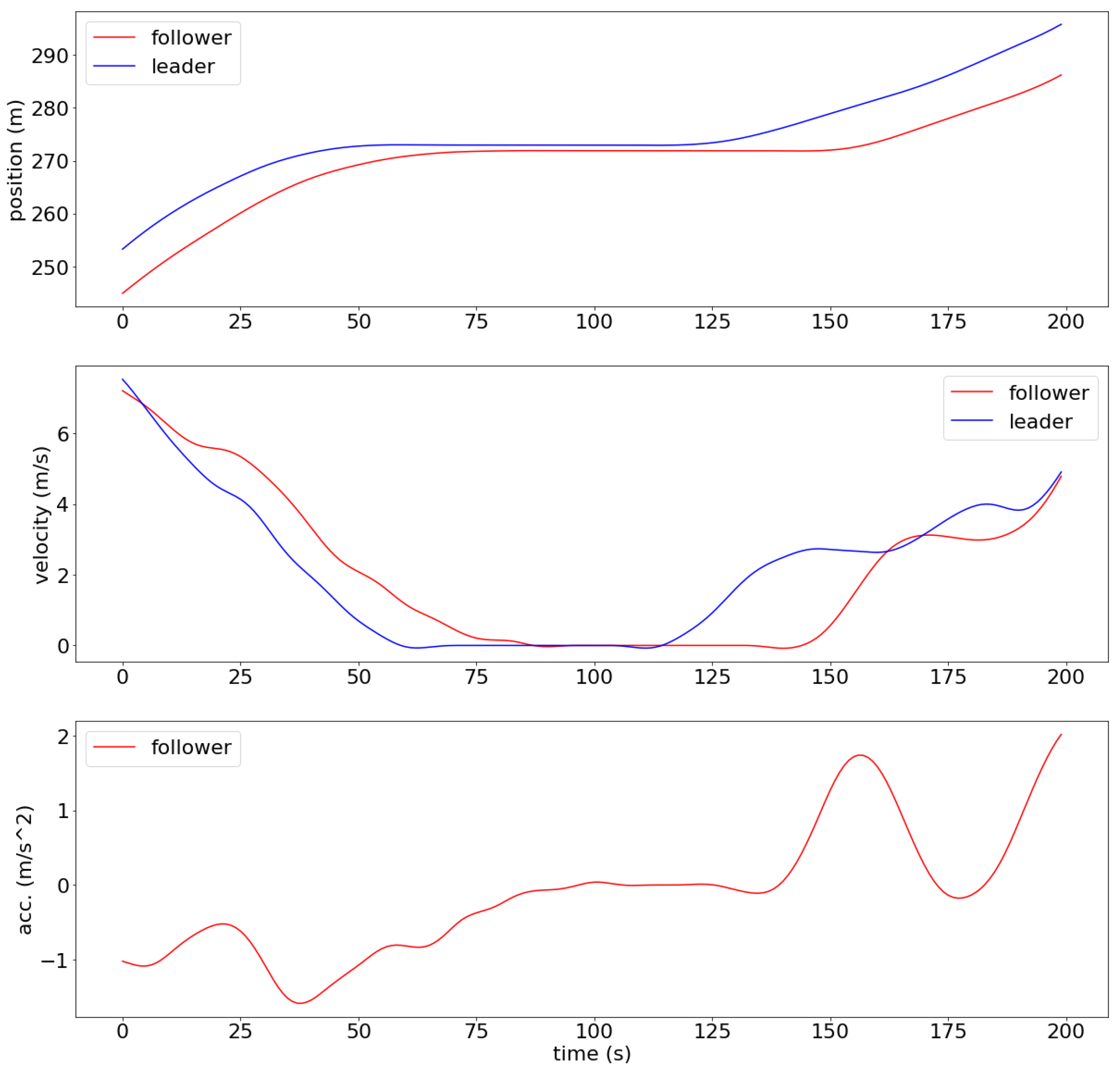
In this section, we evaluate our proposed method using the NGSIM dataset. The Next Generation SIMulation (NGSIM) dataset we utilized was collected from a segment of US Highway 101 using a camera mounted atop a high building on 15 June 2005. This particular section of the highway includes five main lanes along with an auxiliary lane situated between an on-ramp and an off-ramp. The dataset offers detailed vehicular data every 0.1 s, such as position, velocity, acceleration, lane occupancy, spacing, and vehicle type (including automobiles, trucks, and motorcycles). An example of the NGSIM car-following data is illustrated in Figure 3. Our analysis primarily focuses on the leftmost lane, as its distance from the ramp facilitates easier platoon formation. We applied the same data filtering technique as described in [19].

The experimental setting is the same as in the numerical experiments. In addition to random sampling, we use three baseline models. The Herding baseline [36], which selects samples closest to the cluster center, has been applied in various studies. K-Center [37] selects multiple center points to minimize the maximum distance between any data point and its nearest center. GradMatch [22] selects optimal data subsets by approximately matching the gradients of the subset to those of the full dataset, focusing on data selection rather than generating new data. For all baselines, we use models trained on the entire dataset to extract features and compute the L2 distance to centers. All experiments are repeated 10 times to calculate the standard deviation.

6.1. Case Study Results

The performance comparison of our data distillation method is presented in

Table 3. Comparison of model performance on original and distilled datasets.

Dataset	Training Size	RMSE (m)
Original Dataset	20,000	2.635 ± 0.041
Random Sampling	200	7.632 ± 0.152
Herding	200	4.386 ± 0.097
K-Center	200	4.634 ± 0.083
GradMatch	200	4.435 ± 0.072
Distillation	200	4.137 ± 0.065

. The results show that our method consistently outperforms all baseline approaches, including GradMatch, when trained on the same reduced dataset size. Importantly, although there remains a performance gap compared to training on the full dataset, our method narrows this gap more effectively than the baselines. This improvement can be attributed to the ability of our distillation process to capture meaningful patterns in driving behavior that are often missed by sampling-based methods.

In particular, while GradMatch selects optimal subsets of the data by approximately matching gradients, it does not synthesize new data. Our method, in contrast, generates distilled datasets, which is especially important for self-driving applications where the data are long-tailed. Even if long-tailed samples are up-sampled, they may still be insufficient to cover the entire subspace and to train a strong model. By generating new datasets, our method effectively serves as data augmentation for the long-tailed data, thereby achieving better results. These findings suggest that data distillation not only enhances model accuracy under limited data conditions but also provides a more reliable way to handle the complexity of real-world driving data, which is essential for advancing autonomous driving technology.

6.2. Ablation Studies

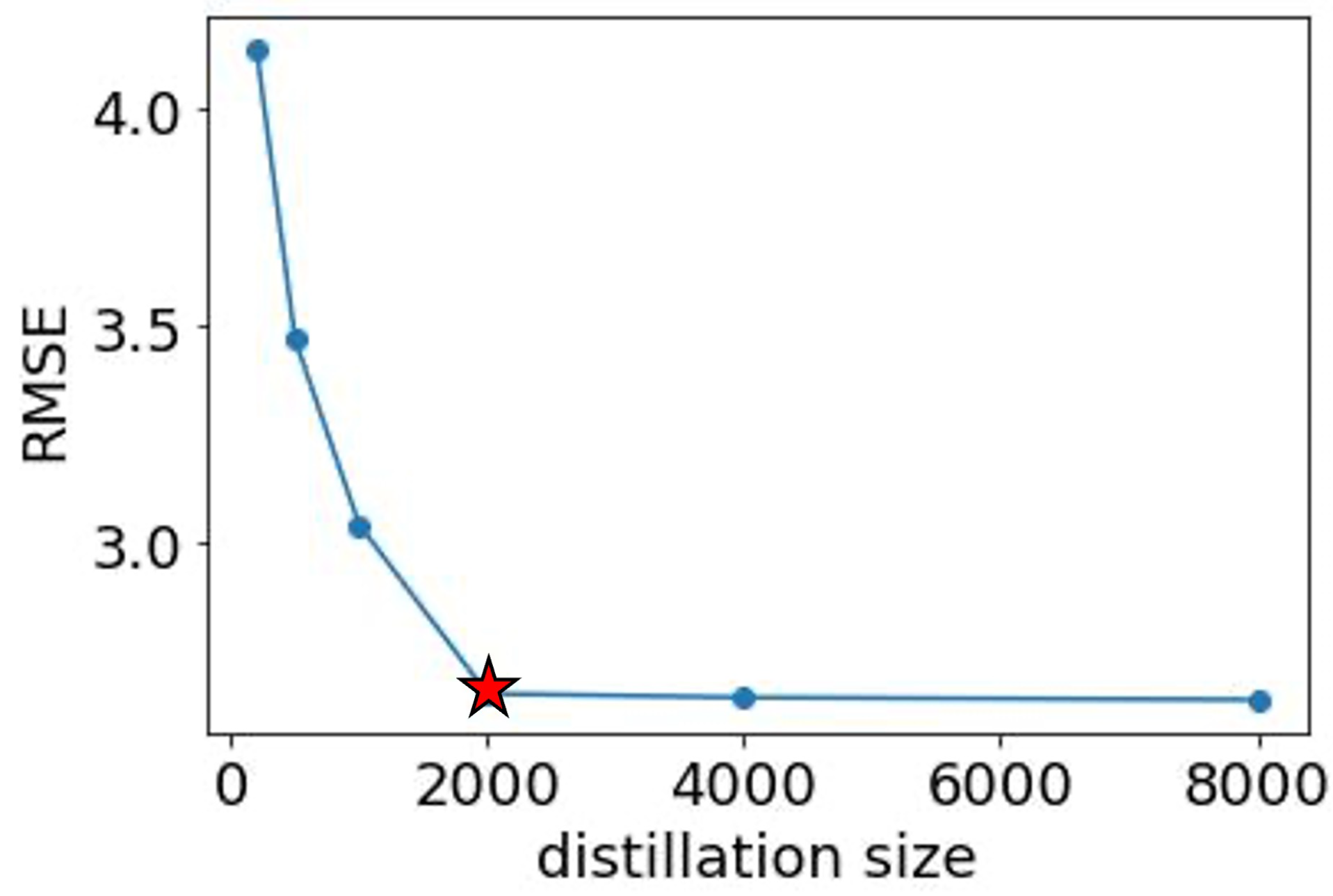
We conducted an ablation study on the compression ratio to evaluate its impact on the model’s performance. The results, depicted in Figure 4, show an optimal compression ratio of about $10\%$, marked with a red star. Beyond this point, increasing the amount of data does not contribute additional benefits to the training process. This finding suggests that a careful balance must be struck between data quantity and model efficiency. Excess data beyond the optimal threshold does not enhance training efficacy, indicating that the model has reached a saturation point where additional information no longer improves learning. This insight is crucial for optimizing data usage and computational resources in machine learning models, particularly in scenarios where data acquisition and storage may be costly or constrained.

7. Conclusions

In conclusion, the development of self-driving algorithms requires significant data for effective training, particularly critical driving data to boost training efficiency and ensure safety. Traditional methods for identifying this crucial data often rely on human prior knowledge or are disconnected from the actual training processes of these algorithms. In response, this study introduced a novel data distillation technique designed specifically to identify and utilize critical data for training self-driving systems. Through experiments that included both numerical simulations and real-world data from the NGSIM dataset, we validated our approach. The findings confirmed that our proposed methods could effectively identify critical data autonomously, without the need for human input. Moreover, the critical data discovered was just $1\%$ the size of the original dataset, significantly optimizing data usage and enhancing computational efficiency. This breakthrough not only supports the advancement of autonomous driving technologies but also contributes to the broader field of machine learning by offering a scalable and efficient approach to data handling.

This work can be extended in two directions. First, controlled generation of distilled data can be performed, allowing for content generation in specific contexts, such as the follower’s speed. Second, a theoretical analysis of distillation in regression problems can be conducted.