Secure and Efficient Data Encryption for Internet of Robotic Things via Chaos-Based Ascon

Abstract

The increasing adoption of digital technologies, robotic systems, and IoT applications in sectors such as medicine, agriculture, and industry drives a surge in data generation and necessitates secure and efficient encryption. For resource-constrained systems, lightweight yet robust cryptographic algorithms are critical. This study addresses the security demands of IoRT systems by proposing an enhanced chaos-based encryption method. The approach integrates the lightweight structure of NIST-standardized Ascon-AEAD128 with the randomness of the Zaslavsky map. Ascon-AEAD128 is widely used on many hardware platforms; therefore, it must robustly resist both passive and active attacks. To overcome these challenges and enhance Ascon’s security, we integrate into Ascon the keys and nonces generated by the Zaslavsky chaotic map, which is deterministic, nonperiodic, and highly sensitive to initial conditions and parameter variations.This integration yields a chaos-based Ascon variant with a higher encryption security relative to the standard Ascon. In addition, we introduce exploratory variants that inject non-repeating chaotic values into the initialization vectors (IVs), the round constants (RCs), and the linear diffusion constants (LCs), while preserving the core permutation. Real-time tests are conducted using Raspberry Pi 3B devices and ROS 2–based IoRT robots. The algorithm’s performance is evaluated over 100 encryption runs on 12 grayscale/color images and variable-length text transmitted via MQTT. Statistical and differential analyses—including histogram, entropy, correlation, chi-square, NPCR, UACI, MSE, MAE, PSNR, and NIST SP 800-22 randomness tests—assess the encryption strength. The results indicate that the proposed method delivers consistent improvements in randomness and uniformity over standard Ascon-AEAD128, while remaining comparable to state-of-the-art chaotic encryption schemes across standard security metrics. These findings suggest that the algorithm is a promising option for resource-constrained IoRT applications.

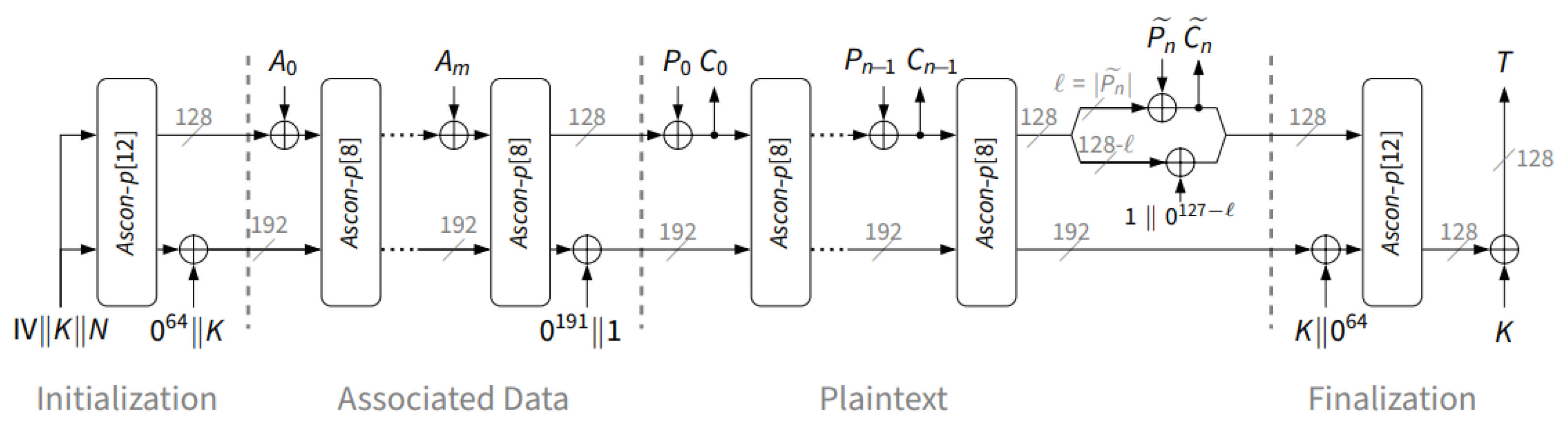
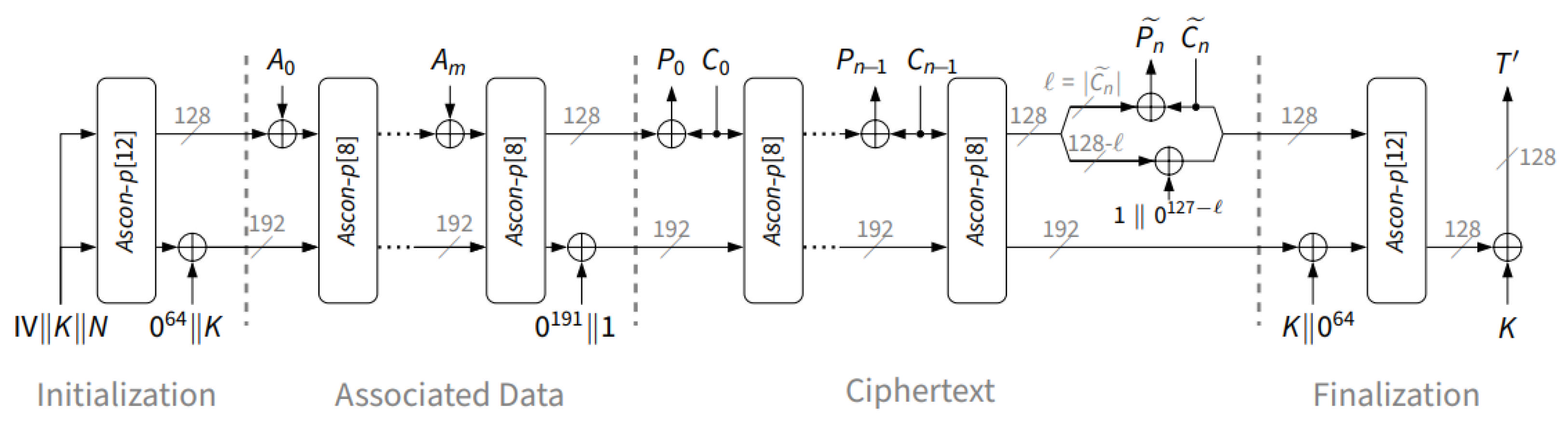
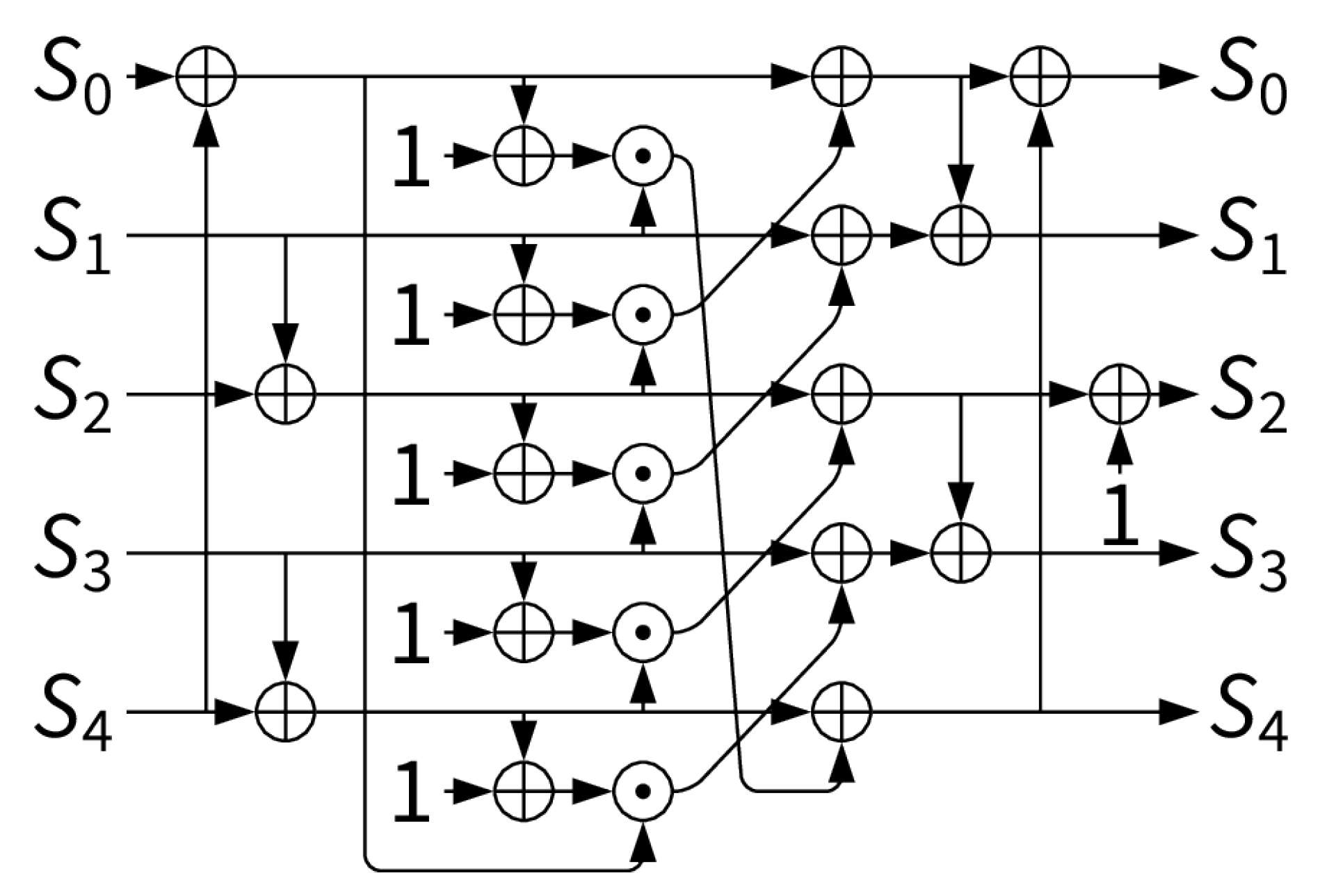
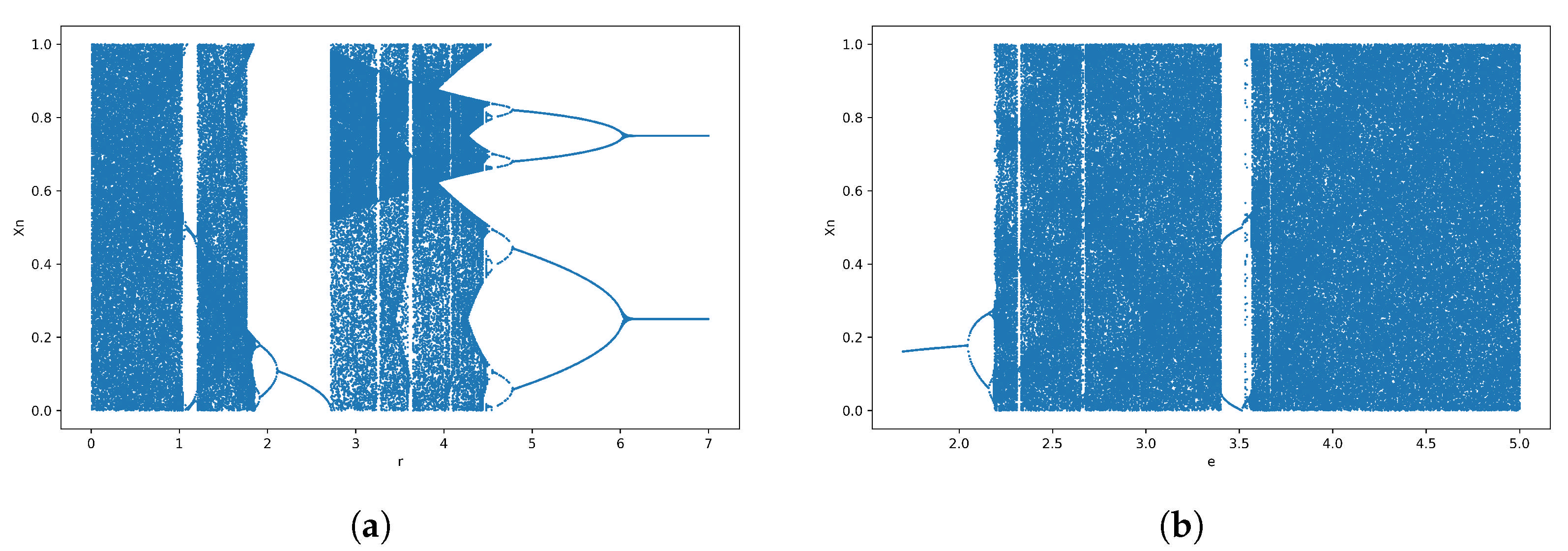
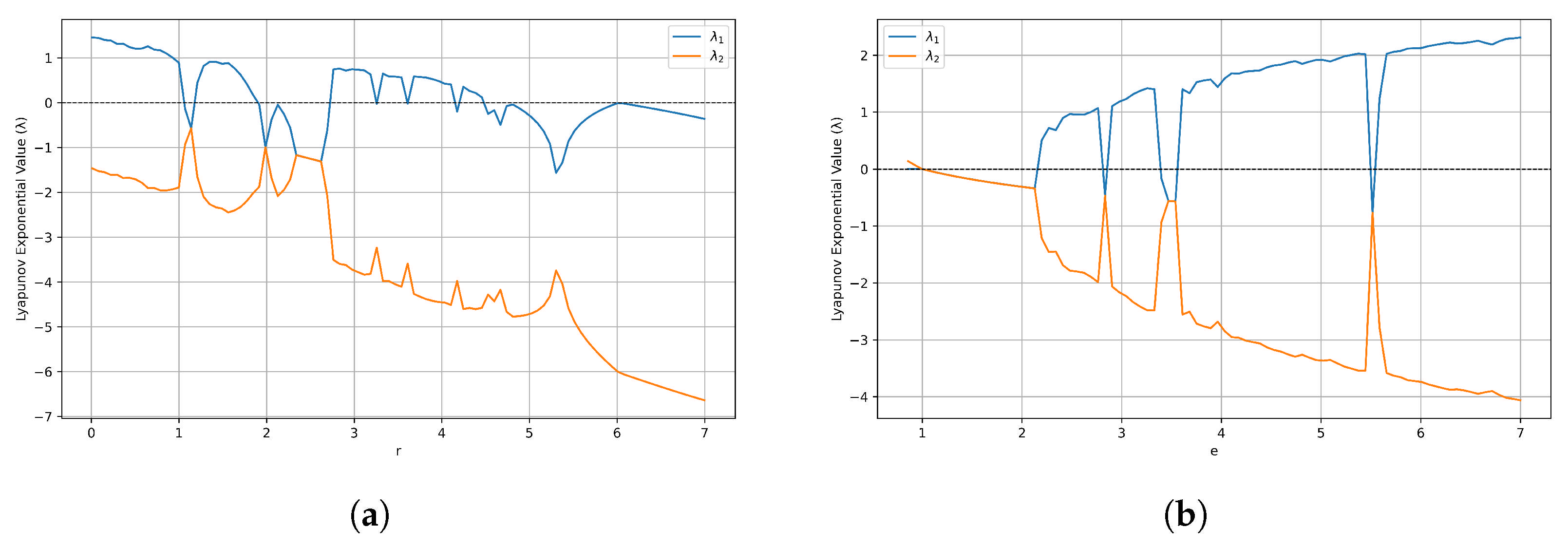
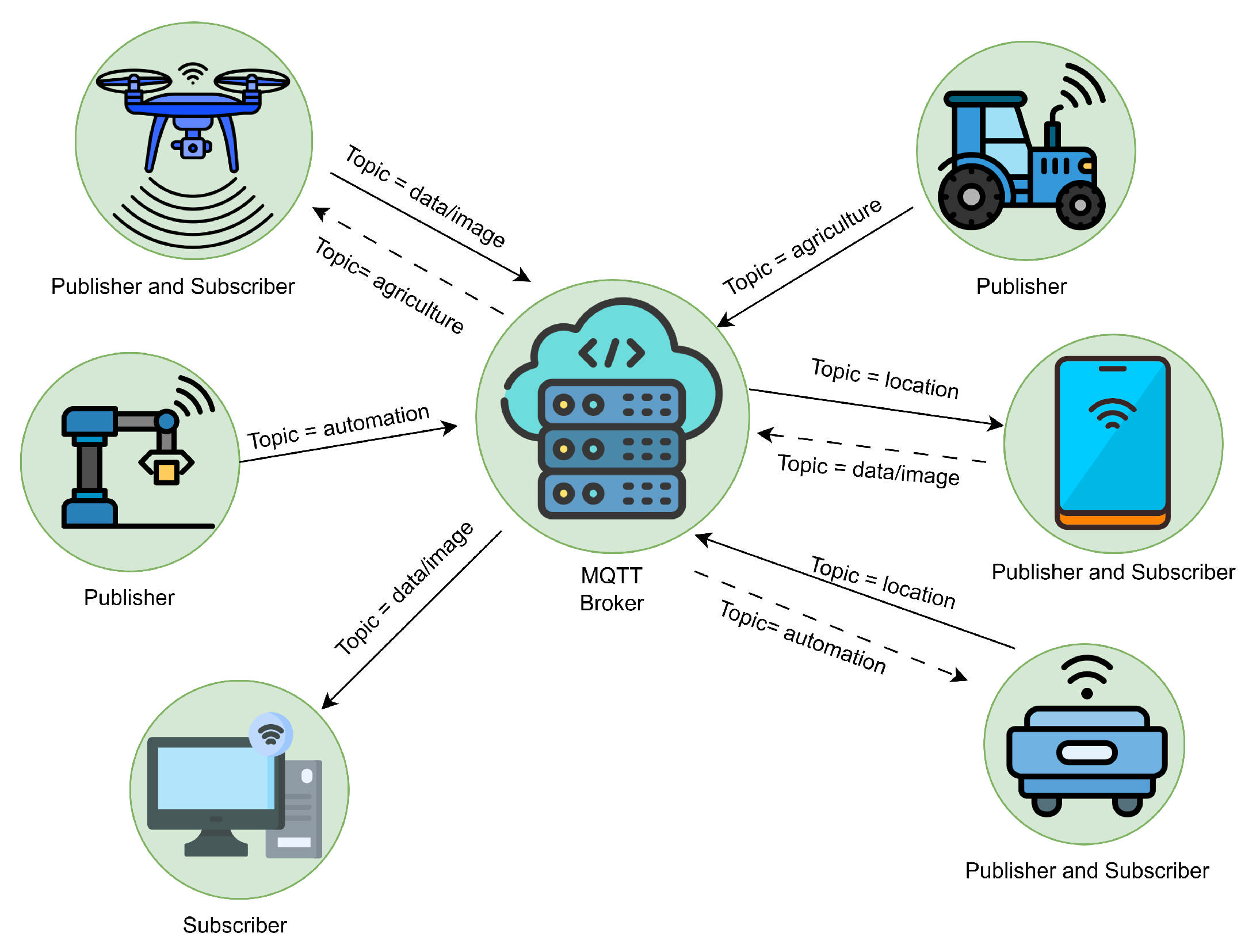
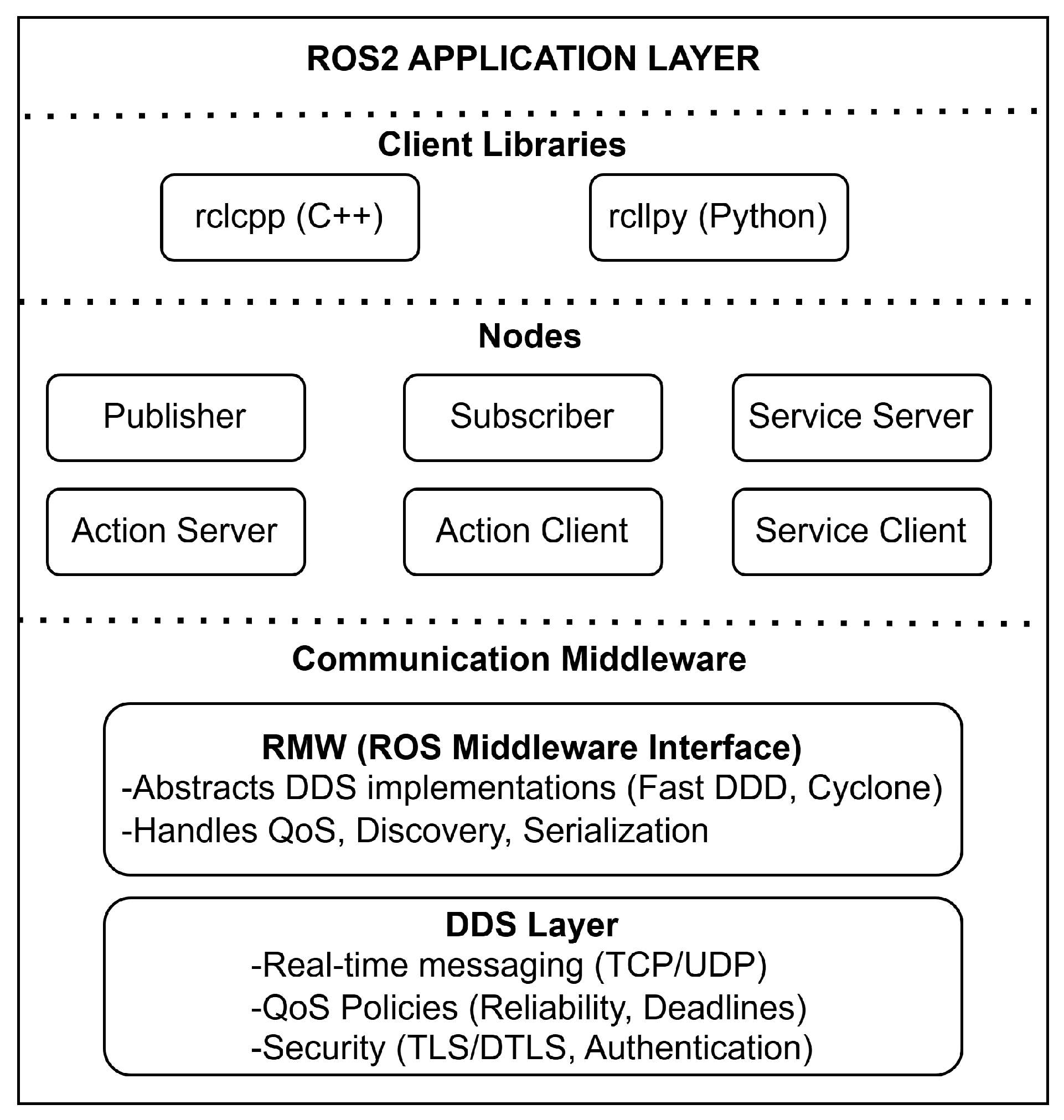
1. Introduction

The rapid proliferation of Internet of Things (IoT) devices, driven by artificial intelligence and machine learning, is taking place in a wide range of applications from industrial solutions to personal assistants, revolutionizing many industries [1]. One of these sectors is the robotics industry. Today, robots are widely used in various industries such as manufacturing, healthcare, agriculture, and space exploration. Their purpose is to provide information services for detection, sensing, and tracking and to create motion and interaction behavior [2]. In this way, robotic technologies provide ways to improve the performance and capabilities of the user, product, or process. However, the integration of IoT into everyday environments through robots raises significant concerns about data security. As robots from industrial devices collect, transmit, and process sensitive information collected through IoT, protecting these data has become crucial to prevent unauthorized access and ensure user privacy. Therefore, encryption methods are used to enhance data security, data integrity, and confidentiality.

Data security has long been a fundamental aspect of digital communication, prompting the advancement of various encryption and decryption methods over the years. Encryption transforms data into an encrypted structure and makes them unintelligible without the corresponding decryption key. In the literature, methods such as Data Encryption Standard (DES) [3], the RSA method [4], Advanced Encryption Standard (AES) [5,6], SNOW-V [7,8], and S-box [9] can be found. In order to increase the data security of the algorithms used in encryption, chaotic systems are often utilized, which have the characteristics of randomness, ergodicity, unpredictability, deterministicness, and extreme sensitivity to initial conditions [10,11,12,13,14,15]. Arab et al. performed an encryption study by applying random numbers from the Arnold chaotic system to the modified AES method. They showed that small changes in the initial values lead to significant differences in the encrypted image [16]. Inam et al. used the random values obtained from chaotic maps to encrypt images in the AES algorithm. This integration strengthens the security by increasing the randomness and complexity of the encryption process, thereby significantly reducing the likelihood of successful cryptographic attacks [17]. Tang et al. proposed a chaotic cryptographic algorithm based on the Lorenz system by combining the Lorenz system with Arnold mapping and DNA coding. The performance analysis included histogram analysis, correlation coefficient analysis, information entropy analysis, noise attack testing, clipping attack testing, key space analysis, and key sensitivity analysis. The experimental results show that the proposed algorithm has good security performance and is suitable for cloud platform robots with high information security requirements [18]. Wang et al. proposed an image encryption method utilizing S-boxes constructed from chaotic time series generated by their novel system, enhancing both unpredictability and security in the encryption process [19]. The proposed Permuted Cellular Automata (pCA) S-box was evaluated against graph-based, chaos-based, and linear transformation-based alternatives. It demonstrated strong resistance to linear and correlation attacks, all while maintaining resource efficiency [20]. Gafsi et al. developed an FPGA-based chaos-based encryption system specifically designed for image encryption and decryption. In this system, the authors generated pseudo-random numbers using the Lorenz chaotic system and performed encryption and decryption using the XOR operation with the keys obtained from these values with images [21]. As efforts have increasingly focused on reducing the computational overhead, lightweight encryption techniques have gained attention. In this context, Gilmolk et al. proposed a novel lightweight chaotic encryption approach specifically designed for securing light images in IoT environments. The effectiveness of the proposed scheme was validated through comprehensive analyses such as histogram distribution, pixel correlation, and mean square error evaluation, revealing notable improvements in image quality metrics—including homogeneity, energy, and contrast—while also demonstrating high robustness against various cryptographic attacks [22]. Similarly, Mohammed et al. proposed a chaos-based lightweight image encryption and decryption scheme for IoT applications, utilizing data generated from a five-dimensional chaotic system to construct an S-box. The newly designed S-box exhibits strong cryptographic properties, including high nonlinearity and resilience against statistical and differential attacks. These strengths are validated through performance metrics such as peak signal-to-noise ratio (PSNR), low correlation coefficients, and high NPCR and UACI values, confirming its suitability for secure image transmission over public communication channels [23]. Abbood et al. proposed a novel and efficient cryptographic system that combines stream-cipher principles with chaotic encryption and is specifically designed to address the challenges of securing data on resource-limited IoT devices. The system’s performance was validated using various evaluation metrics, including histogram and correlation analyses, NPCR, UACI, PSNR, and entropy. The results confirm that the proposed method ensures robust security, operational efficiency, and adaptability, making it a viable solution for protecting sensitive information in IoT-based environments [24]. Similarly, Aqeel et al. developed an image-encryption scheme tailored for IoT systems by utilizing a five-dimensional hyperchaotic map. The robustness and effectiveness of this method were thoroughly assessed using a range of security metrics, including information entropy, correlation analysis, histogram uniformity, and resistance to differential attacks, confirming a high level of security and suitability for IoT-based applications [25]. Nazish and Banday explored the application of lightweight one-dimensional chaotic maps, including Logistic, Sine, Tent, and Chebyshev maps, for image encryption. Their evaluation involved multiple performance and security metrics, such as PSNR, MSE, NPCR, UACI, entropy, and execution time, demonstrating the methods’ effectiveness and efficiency [26].

Traditional encryption techniques often lead to increased computational load and higher power consumption, creating challenges in protecting against evolving cyber threats. This issue is especially critical in IoT and embedded systems, where limited processing power and energy efficiency are paramount. To meet these needs, the Ascon algorithm is adopted as a lightweight and secure encryption method. Recognized for its effectiveness, Ascon was officially chosen by the National Institute of Standards and Technology (NIST) in 2023 as the Lightweight Cryptography Standard, underscoring its importance for safeguarding resource-constrained devices [27]. Ascon not only employs authenticated encryption with associated data (AEAD) and hashing operations but also provides robust resistance to attacks such as differential and linear cryptanalysis. Moreover, Ascon delivers enhanced security while maintaining minimal computational and communication overhead [28]. NIST identified Ascon as a leading candidate in its competition to establish a new lightweight encryption standard tailored for IoT devices; it was selected over other finalists primarily due to its strong resistance to side-channel attacks [29]. Wurity and Sumalatha analyzed the Ascon-128, Ascon-128a, and Ascon-80pq variants. Key performance indicators—including encryption and decryption times, memory consumption, and throughput—were evaluated across different data sizes [30]. Athanasiou et al. presented a coprocessor designed to implement the Ascon lightweight-cryptography algorithm, addressing security issues in IoT environments. The design incorporates features such as AEAD, hashing, and MAC, enhancing Ascon’s performance for devices with limited resources [31]. Koppuravuri et al. proposed an FPGA architecture for Ascon that delivers up to a 31.77% increase in throughput, enhancing its suitability for secure edge computing in IoT applications [32]. Rahul et al. adapted IoT communication for smart agriculture applications. Ascon encryption enabled data authentication and secure data transmission [33]. Nooruddin and Valles used a LoRa-based IoT framework and Ascon encryption for secure data transmission, integrating an ESP32 and environmental sensors with a Raspberry Pi Pico [34]. El-Hajj and Gebremariam applied the Ascon method to improve the security of resource-constrained IoT devices. In particular, they emphasized that the digital twin framework increases resilience against cyber threats in Industry 4.0. They also verified the effectiveness of Ascon compared with AES-GCM in terms of security [35]. Khan, Lee, and Hwang evaluated the performance of Ascon on various FPGA platforms for resource-constrained IoT platforms and implemented a recursive strategy to reduce area consumption [36]. Raj and Bodapati transmitted medical images over IoT networks using FPGA and employed the Ascon-128 version for data hiding [37]. Nguyen and Chen applied Ascon encryption for an automotive industry application on FPGA hardware. In this way, they demonstrated that the speed increased by a factor of 100 [38].

In recent years, the Internet of Robotic Things (IoRT) has advanced through the integration of IoT systems and robots. The IoRT combines various technologies, including cloud computing, robotics, the IoT, artificial intelligence (AI), and machine learning (ML). The IoRT plays an important role in manufacturing, healthcare, agriculture, space exploration, security, and transportation. Kanthimathi et al. stated in their study that the system integration of robots with IoT and AI has transformed industrial production. Efficiency gains and predictive maintenance have saved money and increased sustainability, making it an economically viable and environmentally friendly alternative [39]. Today, robots can be grouped into categories such as autonomous robots, humanoid robots, service robots, and pre-programmed robots. In particular, robots such as inspection robots have become essential tools in harsh environments such as remote-control decontamination, welding operations, leak inspections, radiation discovery and assessment, radiation-aware navigation, and characterization and inspection operations on land, in air, and in water [40]. The IoRT can be deployed in many different places, allowing robots to transmit and receive data to and from other devices and users. However, studies have highlighted weaknesses in ROS-based systems for self-driving cars, surgical robots, and eldercare robots, including unauthorized publishing, unauthorized data access, and denial-of-service (DoS) cyberattacks on these robots [41]. Here, IoRT security relies heavily on encryption. As IoRT systems connect to multiple devices and share sensitive data, encryption needs to provide a critical layer of defense against unauthorized access and data breaches [42]. Furthermore, beyond confidentiality, encryption and decryption algorithms also verify the authenticity and integrity of data to ensure that data remain unchanged during transmission [43]. Kamilarlis and Botteghi presented a secure communication protocol for the IoRT that uses encryption to protect data transmitted between devices. They tested the system in a simulated environment and demonstrated its effectiveness in securing the IoRT [44]. Chang et al. designed a data security robot for the IoRT using Raspberry Pi hardware for the healthcare sector. While performing this process, they used the AES algorithm and the EEC algorithms in encryption and compared their performance [45]. Additionally, MQTT (Message Queuing Telemetry Transport) is a lightweight publish-subscribe messaging protocol specifically designed for machine-to-machine (M2M) communication in IoT. Initially developed for telemetry in oil pipelines, MQTT enables efficient data exchange between devices, especially in scenarios with constrained bandwidth or high latency. Cameron utilized MQTT for communication between ESP32 microcontrollers operating on separate Wi-Fi networks [46]. Although MQTT serves as a lightweight messaging protocol for IoT devices, Buccafurri and Lazzaro have identified and proposed solutions to address its vulnerabilities related to weak authentication, security, and privacy [47]. Lightweight cryptography is a rapidly growing area dedicated to creating cryptographic methods optimized for resource-limited devices, such as those used in IoT and embedded systems. These methods aim to minimize the power consumption, processing time, and memory requirements, while ensuring strong security. In this context, Abubakar et al. enhanced the previously proposed PRESENT algorithm by modifying it to improve both its security and efficiency [48]. Similarly, Al-Azzawi et al. developed a novel lightweight encryption method by proposing a lightweight block cipher based on Type-2 Generalized Feistel Networks, aiming to improve the security while reducing the resource consumption [49].

The originality of this work is that it aims to study the application of the Ascon algorithm in encrypting images and data in IoT robots, specifically its integration with chaotic systems to strengthen security measures. By reviewing the existing literature on Ascon and chaotic systems and analyzing their combined effectiveness in IoT environments, this research aims to contribute to the ongoing discourse on improving data security in the rapidly evolving IoT robotics landscape. From a general perspective, the contributions of this study to the literature are as follows:

• A new lightweight encryption mechanism is proposed for IoRT-based robots by taking advantage of the lightweight structure of the Ascon-AEAD128 algorithm and the unique properties of a chaotic map.
• A pseudorandom number generator was implemented, and statistical tests were conducted to evaluate its properties.
• The developed algorithm was applied to color and grayscale images as well as text data; comprehensive security analyses were performed.
• An application enabling encrypted and secure data exchange over the MQTT protocol was implemented between ROS 2 Humble robots and Raspberry Pi 3 Model B IoT devices (İstanbul, Turkey).

The remainder of this study is organized as follows. In Section 2, we present the basic structure of the Ascon-AEAD128 lightweight authenticated-encryption algorithm, the properties of the Zaslavsky map used to provide pseudorandom number generation for integration into Ascon, the MQTT protocol enabling lightweight communication between robots and IoT devices, and the overall architecture of the ROS 2 middleware (İstanbul, Turkey). Section 3 specifies the threat model and security objectives for the proposed chaos-based encryption variants. Section 4 details the design and integration of the proposed chaos-based Ascon variants C1–C4. Section 5 presents the experimental setup and the main evaluation results, reporting comprehensive analyses across image and text experiments as well as performance measurements. Finally, Section 6 concludes with an interpretation of the results.

2. Preliminaries

2.1. Ascon-AEAD128

Ascon, the first choice in the CAESAR (Authenticated Encryption: Security, Applicability, and Robustness) competition, was optimized for security, efficiency, and flexibility and was standardized by NIST in 2023 as a lightweight encryption algorithm for use in low-power embedded systems, IoT devices, and other resource-constrained environments. The Ascon family consists of Ascon-AEAD128, Ascon-Hash256, Ascon-XOF128, and Ascon-CXOF128, which are lightweight symmetric algorithms designed to provide authenticated encryption with associated data (AEAD), hashing, and extendable-output function (XOF) functionality. The Ascon-AEAD128 algorithm, for encryption and authentication with associated data, employs a sponge construction. This construction operates on a 320-bit state vector, absorbing input data in blocks and generating output through compression. In the absorption phase of the sponge structure, input data (key, nonce, IV, message) are iteratively processed into the internal state. Each new input block contributes to updating the internal state. In the compression phase, a specific output is taken from the internal state to produce the ciphertext and authentication tag [27,32,50].

In the Ascon-AEAD128 algorithm, the key (K), nonce (N), and tag (T) are 128 bits, and the initialization vector ($IV$) is 64 bits; each data block is 128 bits. The algorithm comprises four stages: initialization, processing associated data, processing plaintext/ciphertext, and finalization. The number of internal permutation rounds is 12 in the initialization and finalization stages (Ascon-p[12]) and 8 in the associated-data and plaintext/ciphertext processing stages (Ascon-p[8]). Figure 1 shows the encryption scheme of the Ascon-AEAD128 algorithm.

2.1.1. Initialization

A 320-bit internal state (S) is initialized using K, N, and $IV$. The $IV$ constant 0x00001000808c0001 encodes the algorithm’s key size, rate, and internal permutation rounds. The symbol ∥ denotes the concatenation of the data. The state S is updated by applying the Ascon-p[12] permutation, and the key K is added to the last 128 bits of the internal state with XOR operation.

$$\begin{array}{cc}S\hfill & \leftarrow IV\Vert K\Vert N(S_0\leftarrow IV;S_1,S_2\leftarrow K;S_3,S_4\leftarrow N)\hfill \end{array}$$

(1)

2.1.2. Processing Associated Data

The processing of associated data absorbs into the internal state any associated data A that are not encrypted but need to be authenticated, thereby ensuring that the authentication tag is bound to these data and that any modification of A results in verification failure. In this phase, A is divided into 128-bit blocks; each block is XORed into the first 128 bits of the state, followed by application of the Ascon-p[8] permutation. At the end of the process, a one-bit marker is XORed into the state for domain separation. If A is empty, only this final step is performed.

2.1.3. Processing Plaintext/Ciphertext

During plaintext processing, the plaintext P is divided into 128-bit blocks for encryption, with the final block $P_n$ padded if necessary. Each block $P_i$ is XORed with the first 128 bits of the internal state to produce the corresponding ciphertext block $C_i$. The updated state is then processed by the Ascon-p[8] permutation, and all ciphertext blocks are concatenated to form the final ciphertext. During ciphertext processing, the ciphertext C is similarly divided into 128-bit blocks for decryption. Each block $C_i$ is XORed with the first 128 bits of the internal state to recover the corresponding plaintext block $P_i$. The state is subsequently updated with the ciphertext and permuted by Ascon-p[8], except after the final block $C_n$. All recovered plaintext blocks are concatenated to obtain the original message. The decryption scheme of the algorithm is given in Figure 2.

2.1.4. Finalization

In the final step of the encryption process, the authentication tag T is generated. The key K is injected into the internal state S through an XOR operation, after which the state is processed using the Ascon-p[12] permutation. The authentication tag T is generated by XORing the last 128 bits of S with K. The encryption process is completed by returning the ciphertext C and the authentication tag T.

In the finalization step of decryption, the authentication tag T is checked, and the procedure continues depending on whether integrity is ensured. First, the key K is XORed into the state S. Then, the state S is processed using the Ascon-p[12] permutation. The authentication tag $T^{\prime }$ is computed by XORing the last 128 bits of S with K. The computed $T^{\prime }$ is compared with the tag T provided with the ciphertext. Decryption is successful if they are equal and the plaintext is returned; otherwise, an error is returned.

2.1.5. Ascon Permutations

The permutation with 12 or 8 rounds, applied within the four stages of the Ascon-AEAD128 algorithm, performs the core cryptographic operations [32]. This permutation comprises three layers: constant addition, substitution, and linear diffusion; it is executed on the five 64-bit registers $S_0$, $S_1$, $S_2$, $S_3$, and $S_4$ of the 320-bit internal state S.

$$S\leftarrow S_0\Vert S_1\Vert S_2\Vert S_3\Vert S_4$$

(2)

Constant Addition Layer: In each round of the permutation, register $S_2$ is XORed with a round constant $c_i$. This operation ensures that every round is distinguished, preventing repeatable patterns and thereby enhancing the permutation’s resistance to differential and linear cryptanalysis. The round constants corresponding to different permutations are presented in

Table 1. Round constants for Ascon-p[8] and Ascon-p[12] [27].

p[12]	p[8]	Constant
0		0x00000000000000f0
1		0x00000000000000e1
2		0x00000000000000d2
3		0x00000000000000c3
4	0	0x00000000000000b4
5	1	0x00000000000000a5
6	2	0x0000000000000096
7	3	0x0000000000000087
8	4	0x0000000000000078
9	5	0x0000000000000069
10	6	0x000000000000005a
11	7	0x000000000000004b

.

$$S_2\leftarrow S_2\oplus c_i$$

(3)

The least significant 8 bits of the constants take values, and the remaining 56 bits are always zero. Therefore, in the constant addition layer, the XOR is applied to the least significant 8 bits of $S_2$.

Substitution Layer: In this stage, an update is performed by applying 64 parallel 5-bit substitution operations to state S. Each bit of the 5-bit input is taken from the same index of registers $S_0$, $S_1$, $S_2$, $S_3$, and $S_4$, respectively.

$$(s_{(0,j)},\dots ,s_{(4,j)})=\mathrm{SBOX}(s_{(0,j)},s_{(1,j)},\dots ,s_{(4,j)}),0\le j<64$$

(4)

The 5-bit input of the 5-bit SBOX is S = ($S_0$, $S_1$, $S_2$, $S_3$, $S_4$), and it calculates the 5-bit output using the circuit given in Figure 3.

Linear Diffusion Layer: In the final step of the permutation, rotation and XOR operations are applied to each of the five 64-bit registers in the internal state S. These operations diffuse the bits throughout the state, ensuring that any change in a single bit propagates broadly and contributes to effective mixing. This diffusion achieves uniform bit distribution and significantly strengthens the permutation against linear cryptanalysis.

$$\begin{array}{cc}{S}_0\hfill & \leftarrow S_0\oplus (S_0\gg 19)\oplus (S_0\gg 28)\hfill \\ S_1\hfill & \leftarrow S_1\oplus (S_1\gg 61)\oplus (S_1\gg 39)\hfill \\ S_2\hfill & \leftarrow S_2\oplus (S_2\gg 1)\oplus (S_2\gg 6)\hfill \\ S_3\hfill & \leftarrow S_3\oplus (S_3\gg 10)\oplus (S_3\gg 17)\hfill \\ S_4\hfill & \leftarrow S_4\oplus (S_4\gg 7)\oplus (S_4\gg 41)\hfill \end{array}$$

(5)

The Ascon permutation structure, optimized for lightweight cryptography, offers a well-balanced design in terms of both performance and security. It is particularly effective for low-cost hardware applications and IoT devices.

2.2. Zaslavsky Map

In 1978, George M. Zaslavsky introduced the two-dimensional, discrete-time, and nonlinear Zaslavsky map [51], whose mathematical formulation is presented in Equation (6).

$$\begin{array}{cc}{x}_{n+1}\hfill & =(x_n+v(1+\mu y_n)+ev\mu \cos \left(2\pi x_n\right))mod1\hfill \\ y_{n+1}\hfill & =e^{-r}\left(y_n+e\cos \left(2\pi x_n\right)\right)\hfill \\ \mu \hfill & ={\displaystyle \frac{1-e^{-r}}{r}}\hfill \end{array}$$

(6)

Here, $\mu$ depends on r. The parameters r, v, and e control the map’s chaotic behavior, and x and y denote the state variables. Throughout this study, the Zaslavsky map parameters are set to $e=2.718281828459045$, $r=0.9$, and $v=0.5$, with initial conditions $x_0=0.1234$ and $y_0=0.5678$. To demonstrate the sensitivity to the initial conditions, Figure 4 shows the effect of perturbing the initial conditions by $1\times {10}^{-15}$ in x and y.

Bifurcation diagrams graphically depict how a dynamical system’s behavior changes as parameters vary, providing essential insight into stability and qualitative dynamics under differing conditions. Figure 5 presents the diagrams for r and e; chaotic behavior is observed for $r\approx 0$–1, $1.3$–$1.9$, and $2.8$–$4.6$, and for $e\approx 2.3$–$3.4$ and $3.6$–5.

The chaotic nature of the Zaslavsky map is confirmed by its positive maximum Lyapunov exponent $({\lambda }_1>0)$. As shown in Figure 6, the Lyapunov spectra for parameters r and e$(0.01-7)$ align with the corresponding bifurcation diagrams, providing consistent evidence of chaos.

2.3. Message Queuing Telemetry Transport (MQTT)

Originally designed in 1999 by Andy Stanford-Clark and Arlen Nipper, MQTT enables communication over TCP/IP between low-bandwidth devices with limited processing power. With its lightweight architecture, MQTT facilitates fast message delivery for resource-constrained devices in real-time IoT applications by offering low-energy consumption and minimal data traffic. A large number of devices can securely communicate in real time using MQTT’s publish–subscribe protocol through a broker in fields such as agriculture, healthcare, and smart cities.

As shown in Figure 7, messages are published to a specific topic, and clients can receive data by subscribing to those topics. Topics enhance MQTT’s flexibility and scalability, making it widely used in IoT. A publisher need not know whether any subscriber exists. In the publish–subscribe model, because the parties are unaware of each other’s existence, either side can send or receive messages independently. The MQTT packet format consists of a fixed header, a variable header, and a payload; the payload carries the application message.

MQTT defines three Quality of Service (QoS) levels: QoS 0, QoS 1, and QoS 2. QoS 0 delivers a message at most once (best effort); the broker does not acknowledge receipt. QoS 1 guarantees delivery at least once; if no acknowledgment is received within the timeout, the sender retransmits. QoS 2 guarantees delivery exactly once using a four-message, two-phase handshake, which requires additional control packets. In this study, because a symmetric encryption scheme is used, QoS 1 was chosen to ensure that each message is delivered at least once.

2.4. Robot Operating System 2 (ROS 2)

ROS 2 is a versatile middleware framework specifically designed to facilitate the development of robotic applications in real-time environments. It features a data-centric architecture that leverages the Data Distribution Service (DDS) standard for efficient real-time communication. Widely used in autonomous vehicles, industrial robots, drones, and research prototypes, where modularity, scalability, and real-time performance are critical, ROS 2 adopts a publish–subscribe communication mechanism. An ROS 2 package is the fundamental organizational unit and contains nodes, libraries, configuration files, and dependencies. A node is the smallest executable unit in ROS 2 and is typically developed using C++ or Python programming languages. In ROS 2, all data flow operates by default over the publish–subscribe protocol. Publisher nodes send messages to a specific topic, while subscriber nodes receive messages from the topics they subscribe to. A node can function as both a publisher and a subscriber. ROS 2 also employs Quality of Service (QoS) policies for topics, enabling precise control over message delivery. Figure 8 illustrates the general architecture of ROS 2.

3. Threat Model and Security Goals

This section defines the security environment, adversary capabilities, and the specific goals for each of the four proposed variants of the chaos-enhanced Ascon scheme.

3.1. System Setting and Assets

The targeted scenario involves the secure exchange of image data among resource-constrained IoRT robots and IoT devices, using the MQTT protocol over ROS 2 middleware. The critical assets requiring protection are as follows: (i) the image payloads, (ii) the AEAD encryption keys, (iii) nonces, counters, and session identifiers, and (iv) associated metadata such as device IDs. We assume that the MQTT brokers and network routers are honest-but-curious: they will correctly relay messages but may attempt to passively learn information from the traffic they handle. End devices are trusted but may be physically accessible to operators.

3.2. Adversary Capabilities

We consider a powerful network-level adversary capable of both passive and active attacks. The adversary can eavesdrop on all communications and can intercept, replay, drop, or reorder messages. Furthermore, the adversary can adaptively issue chosen-plaintext and chosen-ciphertext queries (CPA/CCA setting) to devices under its control. Techniques such as traffic and timing analysis are also within the adversary’s capabilities. Within the scope of this work, we exclude physical side-channel attacks, hardware compromise, and Denial-of-Service (DoS) attacks aimed solely at disrupting availability.

3.3. Security Goals

Our design is driven by the following security goals:

Confidentiality and Integrity (C1): For the C1 (standard-compliant) variant, confidentiality and integrity are inherited directly from the standard unmodified Ascon-AEAD128 algorithm. This guarantee holds provided that the chaotic map supplies high-entropy, unpredictable keys and nonces, and the protocol ensures nonce uniqueness. The system must output $(\perp )$ and reject any ciphertext that fails authentication. All four variants (C1–C4) employ robust verification: any single-bit fault in the key, nonce, associated data, ciphertext, or tag induces authentication failure, prompting the receiver to output $(\perp )$ and release no plaintext.

Nonce Uniqueness (C1, C2): In both C1 and C2, N is unique per key. We use the same construction, $N=chaos\left[4B\right]$ ∥counter[4B]∥ $sessio{n}_{id}\left[8B\right]$. Uniqueness is guaranteed by the $(sessio{n}_{id},counter)$ pair; the 4-byte chaotic component serves only as an unpredictability salt. The counter is persistent across reboots; on wrap-around at $2^{32}$, the $sessio{n}_{id}$ is refreshed and the counter reset. The receiver maintains state at least as a map $(devic{e}_{id},sessio{n}_{id})\to counte{r}_{last}$ and rejects any packet with $counter⩽counte{r}_{last}$ as a replay; this policy prevents false positives from MQTT QoS duplicates by requiring equality (not window-based) for replay detection.

Clear Security Framing for Variants: This goal precisely defines the security claims for each variant, addressing the reviewer’s primary concern:

• C1 (Standard-Compliant): inherits the full IND-CPA and INT-CTXT security guarantees of Ascon-AEAD128.
• C2, C3, C4 (Exploratory Variants): Security arguments for these variants are strictly limited to demonstrating statistical strength through a battery of tests (NIST SP 800-22, ENT, NPCR, UACI, avalanche effect, entropy, chi-square). The goal is to explore whether chaos can enhance output randomness, diffusion, and differential properties in a measurable way, not to claim provable security against chosen-ciphertext attacks.

Structural Integrity of Dynamic Constants (C3, C4): The design of the chaotic generators for the round constant $\left(RC\right)$ and the linear constant $\left(LC\right)$ is guided by the need to preserve the structural integrity of the Ascon permutation. The $RC$ generator ensures the generation of unique nonzero values to maintain round differentiation. The $LC$ generator enforces constraints on rotation values (a, b) to preserve the bijectivity of the linear diffusion layer. The detailed algorithms for these generators are specified in Section 4.2.3.

4. Design and Integration of Chaos-Based Ascon Variants (C1–C4)

4.1. Zaslavsky Map-Based PRNG Structure and Randomness Evaluation

The Zaslavsky map is utilized as a chaotic pseudorandom number generator (PRNG) to produce two byte sequences, PRN1 and PRN2, from the state variables x and y, respectively. The randomness of the sequences PRN1 and PRN2 was evaluated using the NIST SP 800-22 statistical test suite and the ENT test. For NIST testing, the sequences were converted to binary streams of length 1,000,000 bits. The results, presented in

Table 2. NIST SP 800-22 test results for PRN1 and PRN2.

NIST-800-22 Tests	p-Value for PRN1	p-Value for PRN2	Result
Frequency Monobit	0.9856	0.9394	Pass
Block Frequency	0.9998	0.6591	Pass
Runs	0.1835	0.6643	Pass
Longest Run of Ones in a Block	0.7733	0.9080	Pass
Binary Matrix Rank	0.8251	0.5713	Pass
Discrete Fourier Transform	0.3493	0.1254	Pass
Non-Overlapping Template	0.2675	0.5525	Pass
Overlapping Template	0.4900	0.3253	Pass
Universal Statistical	0.3954	0.856	Pass
Linear Complexity	0.0813	0.7408	Pass
Serial 1	0.8143	0.0536	Pass
Serial 2	0.9514	0.0339	Pass
Approximate Entropy	0.5817	0.1361	Pass
Cumulative Sums Forward	0.5356	0.2997	Pass
Cumulative Sums Backward	0.5205	0.2590	Pass
Random Excursions (+4)	0.8585	0.4645	Pass
Random Excursions Variant (+4)	0.4800	0.093	Pass

, show that both sequences pass all 15 tests in the NIST suite with p-values exceeding 0.001, confirming their statistical randomness. Additionally, the ENT test was applied to 2,000,000-byte sequences from PRN1 and PRN2. The ENT test includes five components: entropy with the ideal value 8, chi-square testing uniformity where the p-value should be between 0.1 and 0.9, the arithmetic mean that should be near 127.5, the Monte Carlo estimation of $\pi$ that should be close to 3.14159265358979323846, and the serial correlation coefficient that should be near 0. The results, presented in

Table 3. ENT test results of PRN1 and PRN2.

Test Name	PRN1 (Average)	PRN2 (Average)	Result
Entropy	7.999914	7.999892	Successful
Chi-square	238.5144	299.1660	Successful
Arithmetic Mean	127.4067	127.4737	Successful
Monte Carlo Pi	3.134440	3.133576	Successful
Correlation	0.000127	−0.001172	Successful

, show that both sequences achieve near-ideal values across all tests, further validating their high randomness quality and suitability for cryptographic applications.

The successful outcomes of both test suites demonstrate that the Zaslavsky map-based PRNG produces outputs that are statistically random and suitable for cryptographic applications.

4.2. Dynamic Parameter Integration for Ascon-AEAD128

Details of the four variants integrated into the structure of the Ascon-AEAD128 algorithm using pseudorandom numbers generated by the Zaslavsky map are presented below.

4.2.1. C1: Standard-Compliant Integration with Chaotic Key and Nonce

The Zaslavsky chaotic map is employed to dynamically generate both the key and part of the nonce. This approach is outlined in Algorithm 1 and aims to enhance cryptographic strength through the unpredictability of chaotic systems while preserving the security properties of standard Ascon. Crucially, the IV, round constants $\left(RC\right)$, and linear constants $\left(LC\right)$ remain unchanged from the original Ascon specification, ensuring that the core permutation structure and its security guarantees are maintained.

The nonce value is constructed by combining 4 bytes of chaotic output with 12 bytes of system-managed values: a persistent 4-byte counter and an 8-byte session ID. This design guarantees nonce uniqueness for every encryption operation under the same key, which is a fundamental requirement for AEAD security. By leaving the IV, RC, and LC unchanged, this combination inherits the security proofs and authenticity assurances of the standard Ascon-AEAD128 algorithm.

Algorithm 1 ZaslavskyMap–Based Generation of key and nonce

1: Result: key (16 B), nonce (16 B), updated $(x,y)$   2: Start   3: Enter parameters →$(r,v,\mathrm{e})$   4: Enter initial condition →$(x_0,y_0)$   5: Number of steps → size=10   6: $\mu \leftarrow {\displaystyle \frac{1-{\mathrm{e}}^{-r}}{r}}$   7: $Scale\leftarrow (2^{35}-1)$   8: PRN1[16], PRN2[16], key[16], nonce_c[4]   9: for $t=0$ to size-1 do 10:       $x_{\mathrm{new}}\leftarrow \left(x+v(1+\mu y)+\mathrm{e}v\mu \cos \left(2\pi x\right)\right)\mathrm{mod}1$ 11:       $y_{\mathrm{new}}\leftarrow {\mathrm{e}}^{-r}\left(y+\mathrm{e}\cos \left(2\pi x\right)\right)$ 12:       $\mathtt{PRN}\mathtt{1}\left[t\right]\leftarrow \lfloor x_{\mathrm{new}}\times Scale\rfloor \mathrm{mod}256$ 13:       $\mathtt{PRN}\mathtt{2}\left[t\right]\leftarrow \lfloor y_{\mathrm{new}}\times Scale\rfloor \mathrm{mod}256$ 14:       $x\leftarrow x_{\mathrm{new}},y\leftarrow y_{\mathrm{new}}$ 15: end for 16: key←bytes(PRN1$[0:8]\parallel$PRN2$[0:8])$ 17: nonce_c←bytes(PRN1$[8:10]\parallel$PRN2$[8:10])$ 18: nonce←nonce_c∥$\mathtt{counter}$∥session_id 19: return key, nonce, x, y 20: End

4.2.2. C2: Experimental Variant with Dynamic IV, Key, and Nonce

The Ascon internal state S is initialized from the fixed IV, the secret key, and a public nonce; subsequent operations, including domain separation, round constants, and the permutation, act on S. In this variant, presented in Algorithm 2, the $IV$—which is constant in the specification—is generated per message from the Zaslavsky chaotic map, and the key and the nonce are likewise derived from chaos. The round constants and the linear diffusion parameters remain unchanged from the standard Ascon permutation. The objective is exploratory: to assess whether injecting variability into all inputs to the internal state S, in particular the otherwise static IV, yields measurable changes in ciphertext-domain statistics, such as entropy and diffusion, and in differential behavior, such as NPCR and UACI, relative to the unmodified algorithm.

4.2.3. C3: Experimental Variant with Dynamic RC and LC

This variant preserves the standard $IV$, $key$, and $nonce$, but it replaces Ascon’s fixed round constants $\left(RCs\right)$ and linear diffusion constants (LCs) with values derived from the Zaslavsky map. In the Ascon permutation, $RCs$ are injected each round to provide round separation and to break structural symmetries, whereas $LCs$ specify the bitwise rotations used by the linear diffusion layer. Algorithm 3 provides the pseudocode of the RC and LC generation procedure. The design rationale is exploratory: to examine whether dynamically varying these internal permutation parameters affects encrypted data statistics and diffusion metrics, such as entropy, NPCR, and UACI, relative to the unmodified permutation.

The round constants are derived from a 15-byte chaotic sequence generated by the Zaslavsky map. The process begins by extracting all unique values from the chaotic bytes that fall within the range $[1,255]$, maintaining their original order of occurrence. This ordered selection ensures that the chaotic dynamics are preserved in the resulting constant sequence. If the number of unique nonzero bytes from the chaotic source is fewer than 12, the algorithm proceeds to sequentially incorporate values from the ordered integer set $[1,2,3,\dots 255]$ until exactly 12 distinct bytes are obtained. This two-step approach guarantees that the final RC sequence consists of 12 nonzero unique bytes, thereby ensuring that each round constant contributes to round separation and symmetry breaking within the permutation.

Algorithm 2 Zaslavsky Map–Based Generation of IV, key, and nonce

1: Result: IV (8 B), key (16 B), nonce (16 B), updated $(x,y)$   2: Start   3: Enter parameters →$(r,v,\mathrm{e})$   4: Enter initial condition →$(x_0,y_0)$   5: Number of steps → size=16   6: $\mu \leftarrow {\displaystyle \frac{1-{\mathrm{e}}^{-r}}{r}}$   7: $Scale\leftarrow (2^{35}-1)$   8: PRN1[16], PRN2[16], IV[8], key[16], nonce_c[4]   9: for $t=0$ to size-1 do 10:      $x_{\mathrm{new}}\leftarrow \left(x+v(1+\mu y)+\mathrm{e}v\mu \cos \left(2\pi x\right)\right)\mathrm{mod}1$ 11:       $y_{\mathrm{new}}\leftarrow {\mathrm{e}}^{-r}\left(y+\mathrm{e}\cos \left(2\pi x\right)\right)$ 12:       $\mathtt{PRN}\mathtt{1}\left[t\right]\leftarrow \lfloor x_{\mathrm{new}}\times Scale\rfloor \mathrm{mod}256$ 13:       $\mathtt{PRN}\mathtt{2}\left[t\right]\leftarrow \lfloor y_{\mathrm{new}}\times Scale\rfloor \mathrm{mod}256$ 14:       $x\leftarrow x_{\mathrm{new}},y\leftarrow y_{\mathrm{new}}$ 15: end for 16: key←bytes(PRN1$[0:16])$ 17: nonce_c←bytes(PRN1$[4:8])$ 18: IV←bytes(PRN1$[8:16])$ 19: nonce←nonce_c∥$\mathtt{counter}$∥session_id 20: return IV, key, nonce, x, y 21: End

Algorithm 3 Zaslavsky Map–Based Generation of $RC$ and $LC$

1: Result: RC (12 B), LC (10 B as five rotation pairs), updated $(x,y)$   2: Start   3: Enter parameters →$(r,v,\mathrm{e})$;    initial condition →$(x_0,y_0)$   4: Number of steps → size $=15$;    $\mu \leftarrow {\displaystyle \frac{1-{\mathrm{e}}^{-r}}{r}}$;    $Scale\leftarrow 2^{35}-1$   5: PRN1[15], PRN2[15]   6: for $t=0$ to size $-1$ do   7:       $x_{\mathrm{new}}\leftarrow \left(x+v(1+\mu y)+\mathrm{e}v\mu \cos \left(2\pi x\right)\right)\mathrm{mod}1$   8:       $y_{\mathrm{new}}\leftarrow {\mathrm{e}}^{-r}\left(y+\mathrm{e}\cos \left(2\pi x\right)\right)$   9:       $\mathtt{PRN}\mathtt{1}\left[t\right]\leftarrow \lfloor x_{\mathrm{new}}·Scale\rfloor \mathrm{mod}256$;    $\mathtt{PRN}\mathtt{2}\left[t\right]\leftarrow \lfloor y_{\mathrm{new}}·Scale\rfloor \mathrm{mod}256$ 10:      $x\leftarrow x_{\mathrm{new}}$; $y\leftarrow y_{\mathrm{new}}$ 11: end for 12: // RC: stable de-dup of PRN1 (exclude 0), then append [1–255]; take first 12 13: $U\leftarrow \mathrm{OrderedUnique}\left({\mathrm{Filter}}_{[1,255]}\left(\mathtt{PRN}{\mathtt{1}}_{[0..\mathit{size}-1]}\right)\parallel [1,2,\dots ,255]\right)$ 14: $\mathrm{RC}\leftarrow \mathrm{Take}(U,12)$ 15: // LC: five rotation pairs $(a_i,b_i)$, values in $[1,63]$, with $a_i\ne b_i$ 16: $LC\_seed=PRN2[5:15]$ 17: for $j=0$ to 4 do 18:       $a\leftarrow (\mathtt{LC}\_\mathtt{seed}[2j\left]\mathrm{mod}63\right)+1$;    $b\leftarrow (\mathtt{LC}\_\mathtt{seed}[2j+1\left]\mathrm{mod}63\right)+1$ 19:       if $a=b$ then 20:            $b\leftarrow \left(b\mathrm{mod}63\right)+1$ 21:       end if 22:       set pair j of LC to $(a,b)$ 23: end for 24: return RC, LC, x, y 25: End

The $LCs$ consist of five rotation pairs $(a_i,b_i)$ for $i=0$ to 4, generated from the 10 chaotic bytes. Each pair is computed as follows:

$$a=\left(byt{e}_{2j}\mathrm{mod}63\right)+1,b=\left(byt{e}_{2j+1}\mathrm{mod}63\right)+1,$$

with a correction if $a=b$: b is set to $\left(b\mathrm{mod}63\right)+1$ to ensure distinctness. This guarantees that each pair lies in $[1,63]$ with $a\ne b$, preserving the bijectivity of the linear layer $L_{a,b}\left(x\right)=x\oplus \mathrm{ROR}(x,a)\oplus \mathrm{ROR}(x,b)$—a circulant linear operator proven invertible for any $a,b\in [1,63]$ with $a\ne b$.

4.2.4. C4: Experimental Variant with Dynamized Constants ($IV$, $RC$, $LC$)

This variant constitutes the most comprehensive architectural modification evaluated, wherein the standard $IV$, $RCs$, and $LCs$ are replaced with values dynamically generated by the Zaslavsky chaotic map. The key and nonce remain unaltered from the conventional Ascon specification and are processed using the algorithm’s standard mechanisms. The principal objective of this configuration is to facilitate an empirical investigation into the collective impact of constant dynamization on the core output properties. Specifically, the variant presented in Algorithm 4 enables a quantitative assessment of how pervasive parameter variability influences the statistical distribution and differential characteristics of the encrypted output.

Algorithm 4 Zaslavsky Map–Based Generation of RC, LC, and IV

1: Result: IV (8B), RC (12B), LC (10B), updated $(x,y)$   2: Start   3: Enter parameters →$(r,v,\mathrm{e})$;    initial condition →$(x_0,y_0)$   4: Number of steps → size $=20$;    $\mu \leftarrow {\displaystyle \frac{1-{\mathrm{e}}^{-r}}{r}}$;    $Scale\leftarrow 2^{35}-1$   5: PRN1[20], PRN2[20]   6: for $t=0$ to size $-1$ do   7:       $x_{\mathrm{new}}\leftarrow \left(x+v(1+\mu y)+\mathrm{e}v\mu \cos \left(2\pi x\right)\right)\mathrm{mod}1$   8:       $y_{\mathrm{new}}\leftarrow {\mathrm{e}}^{-r}\left(y+\mathrm{e}\cos \left(2\pi x\right)\right)$   9:       $\mathtt{PRN}\mathtt{1}\left[t\right]\leftarrow \lfloor x_{\mathrm{new}}·Scale\rfloor \mathrm{mod}256$;    $\mathtt{PRN}\mathtt{2}\left[t\right]\leftarrow \lfloor y_{\mathrm{new}}·Scale\rfloor \mathrm{mod}256$ 10:      $x\leftarrow x_{\mathrm{new}}$; $y\leftarrow y_{\mathrm{new}}$ 11: end for 12: // RC: stable de-dup of PRN1 (exclude 0), then append [1–255]; take first 12 13: $U\leftarrow \mathrm{OrderedUnique}\left({\mathrm{Filter}}_{[1,255]}\left(\mathtt{PRN}{\mathtt{1}}_{[0..\mathit{size}-1]}\right)\parallel [1,2,\dots ,255]\right)$ 14: $\mathtt{RC}\leftarrow \mathrm{Take}(U,12)$ 15: // LC: five rotation pairs $(a_i,b_i)$ from PRN2[2:12], map to $[1,63]$, ensure $a_i\ne b_i$ 16: for $j=0$ to 4 do 17:       $a\leftarrow \left(\mathtt{PRN}\mathtt{2}\right[2+2j\left]\mathrm{mod}63\right)+1$;    $b\leftarrow \left(\mathtt{PRN}\mathtt{2}\right[3+2j\left]\mathrm{mod}63\right)+1$ 18:       if $a=b$ then 19:            $b\leftarrow \left(b\mathrm{mod}63\right)+1$ 20:       end if 21:       set pair j of LC to $(a,b)$ 22: end for 23: IV←bytes(PRN2$[12:20])$ 24: return RC, LC, IV, x, y 25: End

5. Experimental Setup and Analysis

All experiments were conducted on an ROS 2 robot running Ubuntu 22.04.5 LTS with 7.1 of GiB RAM and an AMD Ryzen 5 4600G CPU (6 physical cores, 12 threads). The CPU uses dynamic frequency scaling, operating in the range 400 MHz–4.3 GHz, with an 8 MB L3 cache. The robot runs the ROS 2 Humble distribution. The software stack consisted of ROS 2 Humble, Python 3.10.12, and the following libraries: NumPy 1.21.5, OpenCV 4.5.4, and Paho-MQTT 2.0.0. The proposed standard-compliant baseline (C1) and the exploratory variants (C2–C4) were used to secure communication between ROS 2–based robots and other IoT devices. As the IoT endpoint, we used a Raspberry Pi 3 Model B running 64-bit Debian 12 as a lightweight device. We employed the MQTT protocol to bridge the Raspberry Pi and ROS 2–based robots, using the Paho-MQTT client library and Mosquitto as the broker. Text and image encryption, decryption, and analyses were performed in Python. ROS 2–based robot clients and IoT clients exchanged image and text data via the image and data topics, respectively.

The standard-compliant baseline (C1) and the exploratory variants (C2–C4) were instantiated using two Zaslavsky-derived pseudorandom byte streams, PRN1 and PRN2. Each configuration was evaluated over 100 consecutive runs. For every experimental condition, we performed distributional and statistical analyses (histograms, ${\chi }^2$, correlation, Shannon entropy, NIST SP 800-22), assessed the encryption quality via MSE, MAE, and PSNR, examined the differential behavior using the avalanche effect, NPCR, and UACI, and measured the performance in terms of the key space size, key sensitivity, and processing time. In each iteration, the reference Ascon-AEAD128 ran side by side with the standard-compliant baseline (C1). In all experiments, the associated data A were constructed per message as device_id∥session_id∥counter∥“ImageEncryption”, where the string literal “ImageEncryption” is constant, while device_id, session_id, and counter vary across devices, sessions, and messages. The same analyses were applied to the exploratory variants C2–C4, and the corresponding tables are presented in Appendix A. The experiments employed grayscale and color images at resolutions $256\times 256$, $512\times 512$, and $1024\times 1024$, sourced from the USC–SIPI Image Database and spanning a variety of styles [52].

5.1. Statistical Analysis

Shannon entropy, histogram, correlation coefficients, and the NIST SP 800-22 test suite were used as complementary diagnostics to characterize the output-distribution uniformity and randomness.

5.1.1. Histogram Analysis

The distribution of pixel values in the encrypted image or the character/bit distribution in the ciphertext is determined by histogram analysis. The histogram (pixel-density distribution) of the image obtained from a quality encryption algorithm should be uniform. Thus, attackers are hindered from extracting useful information from the encrypted image and recovering the original image. Figure 9 presents the histogram analysis results for the grayscale and color images. The results indicate that the ciphertexts effectively conceal visible structure in the plaintext images, exhibiting high uniformity and low residual correlation.

5.1.2. Chi-Square (${\chi }^2$) Test

The ${\chi }^2$ test assesses whether the pixel distributions in the encrypted images and the character/bit distributions in the ciphertext deviate from uniformity. A large ${\chi }^2$ value indicates that the distribution is concentrated at certain levels and the encryption is poor, whereas a small ${\chi }^2$ value indicates that the distribution is close to uniform and the encryption quality is good. The ${\chi }^2$ statistic is computed as in Equation (7).

$$\begin{array}{cc}{\chi }^2\hfill & ={\displaystyle \sum _{i=0}^{255}}{\displaystyle \frac{{(f_i-E)}^2}{E}},\hfill \\ E\hfill & ={\displaystyle \frac{H\times W\times C}{256}},\hfill \end{array}$$

(7)

where $f_i$ denotes the observed frequency, i.e., the number of times the pixel value i occurs in the image, and E represents the expected frequency of each value under the assumption of a uniform distribution.

We conducted 100 independent encryption runs for each image with C1 and with the standard Ascon-AEAD128.

Table 4. ${\chi }^2$ over 100 runs for C1 and standard Ascon: mean ± standard deviation; the minimum ${\chi }^2$ for C1 together with the corresponding Ascon value from the same run index; and counts of runs with ${\chi }^2>293.25$.

Size	Filename	Min ${\mathit{\chi }}^2$ (C1)	${\mathit{\chi }}^2$ (Ascon)	C1 (Mean ± Std)	Ascon (Mean ± Std)	χ2 > 293.25 (C1/Ascon)
256 × 256	4.1.05	183.375000	279.109375	$255.346354\pm 20.587984$	$255.992891\pm 22.169414$	2/6
	4.1.06	189.817708	262.390625	$255.691589\pm 21.032231$	$258.854844\pm 24.904865$	4/9
	5.1.10	198.453125	256.109375	$253.439766\pm 21.711427$	$254.315078\pm 23.558643$	4/7
	5.1.11	175.867188	228.132812	$253.485547\pm 22.631090$	$258.872891\pm 23.024797$	5/8
	5.1.12	196.906250	253.453125	$255.705703\pm 20.809372$	$252.539063\pm 20.915370$	3/5
512 × 512	4.2.03	190.095703	243.328125	$251.062741\pm 22.145573$	$256.615404\pm 22.230042$	1/4
	4.2.05	192.541016	298.611979	$251.123958\pm 23.646410$	$258.173398\pm 25.798108$	5/9
	4.2.07	201.750000	268.656250	$252.500781\pm 19.880233$	$254.381159\pm 22.577531$	1/6
	5.2.09	188.154297	272.183594	$252.726758\pm 23.885141$	$255.211563\pm 23.622717$	4/6
	Boat.512	186.468750	276.273438	$251.338203\pm 21.883113$	$258.089414\pm 22.648993$	2/6
1024 × 1024	5.3.01	199.912598	240.914062	$255.558154\pm 22.373090$	$257.324517\pm 21.351941$	5/7
	7.2.01	184.753418	264.894043	$254.597026\pm 19.827567$	$254.796816\pm 22.146297$	3/4

reports the chi-square results as run-averaged values expressed as the mean ± standard deviation, the minimum ${\chi }^2$ achieved by C1 together with the Ascon ${\chi }^2$ from the same run index, and the number of runs whose ${\chi }^2$ exceeds $293.25$ for each method.

A lower ${\chi }^2$ indicates a histogram closer to uniformity and, therefore, stronger diffusion. We adopted $293.25$ as the 5% critical value; results above this threshold lead to rejection of the null hypothesis of uniformity and indicate that the ciphertext histogram is not consistent with randomness. Table 4 shows that, when averaged over 100 runs, C1 attains a lower ${\chi }^2$ in 11 of the 12 images, and in every row, the number of runs exceeding $293.25$ is smaller under C1. Taken together, these findings indicate a consistent advantage of C1 in histogram uniformity and diffusion.

Equation (8) is used to calculate the ${\chi }^2$ statistic of the ciphertext. Here, $O_i$ calculates the observed frequency, i.e., the number of times each byte value occurs in the ciphertext. The expected frequency, E, is the total data length (N) divided by 256. As with image data, a small ${\chi }^2$ value for text data indicates that the bytes are close in frequency, and therefore, the distribution is uniform. Randomly generated plaintexts with different data lengths were encrypted, and the calculated ${\chi }^2$ metric values are given in Table 19.

$$\begin{array}{cc}{\chi }^2\hfill & ={\displaystyle \sum _{i=0}^{255}}{\displaystyle \frac{{(O_i-E)}^2}{E}}\hfill \\ E\hfill & ={\displaystyle \frac{N}{256}}\hfill \end{array}$$

(8)

Table 5. ${\chi }^2$ values of images encrypted with C1 and related works.

Size	Filename	Reference	${\mathit{\chi }}^2$
256 × 256	4.1.05	Proposed	183.375000
		[53]	225.9453
	4.1.06	Proposed	189.817708
		[53]	243.8515
	5.1.10	Proposed	198.453125
		[53]	258.4843
	5.1.12	Proposed	196.906250
		[54]	213.797
		[50]	249.199
512 × 512	4.2.03	Proposed	190.095703
		[50]	264.887
		[55]	248.74544
		[54]	241.091
	4.2.05	Proposed	192.541016
		[56]	249.7578
		[57]	216.5977
	4.2.07	Proposed	201.750000
		[55]	266.7067
		[25]	231.08
	5.2.09	Proposed	188.154297
		[11]	241.1348
	Boat.512	Proposed	186.468750
		[11]	243.1680
		[57]	280.6582
1024 × 1024	5.3.01	Proposed	199.912598
		[50]	262.222
		[54]	215.956
		[11]	226.1406
	7.2.01	Proposed	184.753418
		[53]	253.9165
		[11]	244.5845

demonstrates that, with respect to the ${\chi }^2$ metric, C1 consistently outperforms the related methods across all evaluated images, yielding ciphertext histograms that are closest to uniform.

5.1.3. Correlation Analysis

Images are composed of pixels, and the relationship between two adjacent pixels is quantified by the Pearson correlation coefficient ($\rho$). In the original images, adjacent pixels are usually close in color; so, their correlation is high. In the encrypted images, this relationship should be disrupted to achieve randomness, driving the correlation toward zero. $\rho$ is in the range [−1,1], with values of about 1 or −1 indicating a strong correlation, with values of about 0 indicating a very weak correlation.

The correlation coefficient between adjacent pixel values within a given image is given by Equation (9).

$${\rho }_{XY}={\displaystyle \frac{\mathrm{Cov}(X,Y)}{{\sigma }_X{\sigma }_Y}}={\displaystyle \frac{{\sum }_{i=1}^N(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{{\sum }_{i=1}^N{(X_i-\overline{X})}^2}\sqrt{{\sum }_{i=1}^N{(Y_i-\overline{Y})}^2}}}$$

(9)

Here, X and Y denote the datasets formed by pairs of adjacent pixel values (e.g., a pixel and its horizontal neighbor) in the image, and N is the number of adjacent pairs. $\overline{X}$ and $\overline{Y}$ represent the means of X and Y, respectively, and ${\sigma }_X$ and ${\sigma }_Y$ represent the standard deviations.

In the context of text encryption, Equation (9) is used to measure whether there exists any linear relationship between the bytes of the plaintext and ciphertext located at the same position/index. In text encryption, the correlation within bit sequences or between characters is ideally close to zero, indicating that the texts do not exhibit any linear relationship, effectively hiding any pattern in the plaintext. Randomly generated plaintexts of varying lengths were encrypted, and the calculated correlation coefficients are presented in Table 19.

Figure 10 illustrates the horizontal, vertical, and diagonal correlations for the R, G, and B channels of the color image 4.2.07 and its encrypted counterpart; it also shows the corresponding correlations for grayscale image 5.1.12 and its encrypted counterpart.

Using C1 (with keys and nonces derived from the chaotic map) and standard Ascon-AEAD128, we performed 100 encryption runs per image. In each run, we computed the horizontal, vertical, and diagonal adjacent-pixel correlation coefficients for both ciphers. Because these coefficients can take on negative as well as positive values, simple averaging across runs is uninformative. Accordingly,

Table 6. Horizontal, vertical, and diagonal correlation coefficients for C1 and standard Ascon; C1 is the closest-to-zero across 100 runs, and Ascon is taken from the same run index.

Size	Filename	Horizontal		Vertical		Diagonal
		Min $\mathit{\rho }$ (C1)	$\mathit{\rho }$ (Ascon)	Min $\mathit{\rho }$ (C1)	$\mathit{\rho }$ (Ascon)	Min $\mathit{\rho }$ (C1)	$\mathit{\rho }$ (Ascon)
256 × 256	4.1.05	$-0.000005$	$-0.000695$	$-0.000007$	$-0.001299$	$0.000003$	$-0.002696$
	4.1.06	$0.000006$	$-0.001075$	$0.000006$	$-0.002868$	$0.000012$	$-0.003306$
	5.1.10	$-0.000032$	$0.000184$	$-0.000005$	$-0.004635$	$0.000002$	$0.001521$
	5.1.11	$-0.000007$	$0.004630$	$-0.000006$	$0.003896$	$-0.000002$	$-0.005668$
	5.1.12	$-0.000001$	$-0.003839$	$0.000004$	$-0.000488$	$0.000011$	$-0.001680$
512 × 512	4.2.03	$-0.000009$	$0.001024$	$-0.000001$	$0.000993$	$-0.000001$	$0.000204$
	4.2.05	$0.000003$	$-0.000674$	$-0.000001$	$-0.002998$	$0.000002$	$0.000566$
	4.2.07	$-0.000002$	$0.001432$	$-0.000003$	$-0.000537$	$-0.000005$	$0.001575$
	5.2.09	$0.000011$	$-0.000045$	$0.000005$	$0.003435$	$0.000002$	$-0.000976$
	Boat.512	$-0.000003$	$0.000474$	$-0.000001$	$-0.000192$	$0.000001$	$-0.000781$
1024 × 1024	5.3.01	$-0.000001$	$0.000736$	$-0.000001$	$-0.000729$	$-0.000002$	$-0.001772$
	7.2.01	$0.000002$	$0.000489$	$0.000003$	$0.000694$	$-0.000007$	$-0.000364$

reports, for each direction, the correlation coefficient of C1 that is closest to zero among the 100 runs, together with the corresponding Ascon coefficient evaluated at the same run index.

The reported magnitudes in Table 6 are on the order of ${10}^{-6}$–${10}^{-5}$, effectively indistinguishable from zero at image scale. Such near-zero coefficients indicate that local linear dependencies between neighboring pixels are strongly suppressed. This behavior is consistent with strong diffusion, whereby small changes in local structure do not survive encryption as measurable linear correlations. In practical terms, the correlation plots and coefficients suggest that C1 ciphertexts leave no exploitable linear spatial signature, reducing the risk of correlation-based statistical analysis on the encrypted images. Comparing the correlation values in Table 6 with the corresponding results from prior studies in

Table 7. Correlation coefficients (horizontal, vertical, and diagonal) of encrypted images reported by related work.

Size	Filename	Reference	Horizontal	Vertical	Diagonal
256 × 256	4.1.05	[16]	0.0048	0.0039	0.0002507
		[53]	−0.00019	−0.00031	−0.00028
	5.1.10	[58]	−0.0014	−0.0008	−0.0038
		[12]	0.0008	0.0020	−0.0008
	5.1.11	[58]	0.0034	0.0026	−0.0046
	5.1.12	[54]	0.0003	0.0003	−0.0020
		[50]	0.0013	−0.0008	−0.0007
		[12]	−0.0024	0.0007	0.0018
512 × 512	4.2.03	[50]	−0.0001	0.0017	−0.00121
		[55]	0.004979382	−0.004313788	−0.002290213
		[54]	0.0004	−0.0005	0.0010
	4.2.05	[56]	−0.0046	−0.0078	−0.0004
		[57]	−0.0239	−0.0239	−0.036
	4.2.07	[55]	−0.002653	0.002852	0.0005539
	5.2.09	[58]	−0.0005	0.0018	0.0022
	Boat.512	[16]	0.0042	0.0037	0.0046
		[57]	−0.0215	−0.0215	−0.0636
		[11]	−0.0003	−0.0014	0.0006
1024 × 1024	5.3.01	[50]	0.0003	−0.0001	−0.0013
		[54]	0.0004	0.0003	0.0004
		[58]	0.0012	−0.0020	−0.0004
	7.2.01	[58]	0.0006	0.0012	0.0009
		[11]	−0.0019	0.0005	−0.0008

shows that the proposed approach more effectively disrupts inter-pixel relationships.

5.1.4. Entropy Analysis

Information entropy measures the uncertainty within a dataset. It is commonly used to assess whether the pixels in encrypted images or the bytes (characters) in text data are randomly distributed. Shannon entropy H, calculated as in Equation (10), is derived from the probability distribution of the pixel values in an image.

$$\begin{array}{cc}H\hfill & =-{\displaystyle \sum _{i=1}^{255}}{p}_i{\log }_2\left(p_i\right),\hfill \\ p_i\hfill & ={\displaystyle \frac{f_i}{H\times W\times C}},\hfill \end{array}$$

(10)

where the pixel probability $p_i$ is computed as the ratio of the number of pixels with value i to the total number of pixels in the image. Here, $f_i$ denotes the count of value i (i.e., the histogram frequency), and H, W, and C denote the image height, width, and number of channels, respectively.

The calculation of $p_i$, which denotes the probability of the ith byte value in the text data, is given by Equation (11). $O_i$ represents the observed frequency of the ith byte, and N represents the total number of bytes. Randomly generated plaintexts of varying lengths were encrypted, and the resulting entropy values are reported in Table 19.

$$p_i={\displaystyle \frac{O_i}{N}}$$

(11)

If an image has a completely random and uniform distribution of pixels, the entropy value is 8, which is the maximum value for an 8-bit image. In text data, the maximum entropy value for 256 different symbols (bytes) is likewise 8. The entropy in the range of 7.9-8 for image and text data generally indicates good randomness. A low entropy value indicates that encryption may fail, and information leakage may occur.

Table 8. Entropy values for images encrypted with C1 and with the standard Ascon.

Size	Filename	Max Entropy (C1)	Entropy (Ascon)	C1 (Mean ± Std)	Ascon (Mean ± Std)
256 × 256	4.1.05	7.999328	7.998979	$7.999071\pm 0.000086$	$7.999054\pm 0.000086$
	4.1.06	7.999304	7.999037	$7.999062\pm 0.000077$	$7.999050\pm 0.000091$
	5.1.10	7.997820	7.997306	$7.997211\pm 0.000265$	$7.997156\pm 0.000257$
	5.1.11	7.998070	7.997486	$7.997207\pm 0.000250$	$7.997148\pm 0.000254$
	5.1.12	7.997828	7.997221	$7.997211\pm 0.000273$	$7.997173\pm 0.000236$
512 × 512	4.2.03	7.999825	7.999777	$7.999770\pm 0.000020$	$7.999765\pm 0.000020$
	4.2.05	7.999823	7.999726	$7.999770\pm 0.000022$	$7.999763\pm 0.000024$
	4.2.07	7.999815	7.999754	$7.999767\pm 0.000018$	$7.999764\pm 0.000019$
	5.2.09	7.999482	7.999251	$7.999306\pm 0.000067$	$7.999290\pm 0.000058$
	Boat.512	7.999487	7.999239	$7.999308\pm 0.000060$	$7.999290\pm 0.000062$
1024 × 1024	5.3.01	7.999862	7.999834	$7.999824\pm 0.000015$	$7.999823\pm 0.000015$
	7.2.01	7.999873	7.999818	$7.999827\pm 0.000014$	$7.999823\pm 0.000014$

reports the entropy values for images encrypted with C1 and with the standard Ascon. The third column gives the maximum entropy observed over 100 runs for C1 (keys and nonces derived from the chaotic map). The fourth column provides the corresponding entropy value of the standard Ascon, taken from the same run index at which C1 attains its maximum. The next two columns summarize all 100 runs by reporting the mean and standard deviation of the entropy values for C1 and for the standard Ascon, respectively.

Table 8 shows that, for an 8-bit source, both schemes approach the theoretical maximum entropy of H = 8 bits. A more detailed comparison indicates that, in all 12 image-resolution pairs, the run-averaged entropy of C1 is higher than that of the standard Ascon. These findings suggest that integrating the chaotic map provides a consistent advantage in entropy across all cases, improving closeness to statistical uniformity without degrading security.

Table 9. Entropy values of images encrypted with C1 and the related work.

Size	Filename	Reference	Entropy
256 × 256	4.1.05	Proposed	7.999328
		[59]	7.9993
		[60]	7.99914
		[53]	7.997512
	4.1.06	Proposed	7.999304
		[60]	7.998936
		[59]	7.9994
	5.1.10	Proposed	7.997820
		[61]	7.9974
		[60]	7.997667
	5.1.11	Proposed	7.998070
		[61]	7.9969
		[60]	7.996775
	5.1.12	Proposed	7.997828
		[61]	7.9972
		[62]	7.9955
		[50]	7.9973
512 × 512	4.2.03	Proposed	7.999825
		[50]	7.9997
		[55]	7.297795295
		[54]	7.9998
		[60]	7.999765
	4.2.05	Proposed	7.999823
		[59]	7.99861
	4.2.07	Proposed	7.999815
		[25]	7.9994
		[55]	7.99926645
	5.2.09	Proposed	7.999482
		[58]	7.9992
		[61]	7.9993
		[11]	7.9994
	Boat.512	Proposed	7.999487
		[58]	7.9993
		[61]	7.9994
		[11]	7.9994
1024 × 1024	5.3.01	Proposed	7.999862
		[50]	7.9998
		[54]	7.9999
		[58]	7.9998
	7.2.01	Proposed	7.999873
		[58]	7.9998
		[61]	7.9998

further shows that C1’s entropy values for encrypted images are very close to the theoretical upper bound and competitive with the prior work.

5.1.5. NIST Statistical Test Suite

The NIST SP 800-22 test suite consists of 15 tests that focus on the different possible types of randomness of a sequence. Some of these tests may also consist of subtests [50]. Each test generates a p-value, and p takes values in the range [0,1]. If the p-value generated from a test is 1, it means that the sequence given to the test is completely random, while 0 means that the sequence is not random. In general, a test p-value greater than 0.01 indicates that the sequence is random and passes that test. Moreover, to claim randomness with respect to the suite, a sequence should pass all 15 tests.

Table 10. Results of the NIST SP 800-22 tests for images encrypted with C1.

NIST-800-22 Tests	4.2.03	4.2.05	4.2.07	5.2.09	5.3.01	7.2.01	Boat.512
Frequency Monobit	0.6789	0.3411	0.9601	0.3713	0.4877	0.2113	0.3351
Block Frequency	0.7768	0.2071	0.2360	0.0640	0.1891	0.1891	0.9311
Runs	0.8043	0.5558	0.5326	0.1805	0.7103	0.1286	0.6135
Longest Run of Ones in a Block	0.1938	0.0316	0.6852	0.0884	0.1210	0.8203	0.2473
Binary Matrix Rank	0.7187	0.3415	0.7148	0.2947	0.2173	0.8624	0.5399
Discrete Fourier Transform	0.9050	0.9050	0.1803	0.3833	0.0931	0.9050	0.2998
Non-Overlapping Template	0.9720	0.9085	0.3405	0.4217	0.5217	0.6706	0.3297
Overlapping Template	0.4050	0.3326	0.8010	0.5221	0.0833	0.0214	0.9193
Universal Statistical	0.9545	0.3257	0.8971	0.8131	0.2009	0.7851	0.7049
Linear Complexity	0.3369	0.9265	0.3737	0.7409	0.2754	0.9364	0.5520
Serial 1	0.3441	0.9333	0.7285	0.3049	0.7073	0.1353	0.4460
Serial 2	0.7676	0.7043	0.8464	0.6159	0.8691	0.2844	0.8462
Approximate Entropy	0.2772	0.3190	0.4496	0.5286	0.4644	0.0405	0.3566
Cumulative Sums Forward	0.9667	0.5323	0.7738	0.40154	0.3284	0.2058	0.3357
Cumulative Sums Backward	0.6329	0.4589	0.8192	0.6256	0.2958	0.1183	0.5264
Random Excursions (+4)	0.4030	0.4572	0.5355	0.2912	0.7972	0.5251	0.8033
Random Excursions Variant (+4)	0.3620	0.4587	0.3195	0.7953	0.6895	0.1304	0.9331

reports the NIST SP 800-22 test results for ciphertext bitstreams obtained by encrypting images with keys and nonces derived from the Zaslavsky map. Because the suite requires at least 1,000,000 bits per sequence, the tests were conducted on images of size $512\times 512$ and $1024\times 1024$.

Across all tested sequences, the resulting p-values exceeded 0.01, including for the more stringent families (Frequency/Block Frequency, Runs/Longest-Run, DFT, Serial-1/2, Linear Complexity, and Random Excursions). The NIST SP 800-22 outcomes indicate no statistically significant irregularities in the ciphertext bitstreams and support the conclusion that C1 produces outputs with consistently strong indicators of statistical randomness.

5.2. Encryption Quality Analysis

Tests on the mean square error (MSE), mean absolute error (MAE), and peak signal-to-noise ratio (PSNR) were performed on the original images and their encrypted versions to calculate the efficiency and quality of an image encryption method. A secure image cipher is expected to produce large differences between the input and output (i.e., high MSE/MAE and low PSNR relative to the plaintext), indicating effective concealment of the visual structure.

5.2.1. Mean Square Error (MSE)

The MSE, which measures the mean squared difference between the pixel values of the plaintext and ciphertext images, is computed as in Equation (12):

$$MSE={\displaystyle \frac{1}{H\times W}}{\displaystyle \sum _{i=1}^H}{\displaystyle \sum _{j=1}^W}{[P(i,j)-C(i,j)]}^2$$

(12)

Here, H and W denote the height and width of the image, respectively. $P(i,j)$ is the pixel value of the plaintext image, and $C(i,j)$ is the pixel value of the ciphertext image at location $(i,j)$. The MSE increases as the ciphertext image deviates further from the plaintext image; a high MSE therefore indicates good encryption quality.

Table 11. MSE values for images encrypted with C1 and the standard Ascon.

Size	Filename	Max MSE (C1)	MSE Ascon	C1 (Mean ± Std)	Ascon (Mean ± Std)
256 × 256	4.1.05	8416.539134	8365.144180	$8356.642789\pm 21.584277$	$8352.353064\pm 19.661101$
	4.1.06	9999.897202	9912.867350	$9930.880100\pm 26.134248$	$9925.352633\pm 25.116813$
	5.1.10	7798.144241	7753.826660	$7691.706813\pm 34.460185$	$7686.435038\pm 32.817423$
	5.1.11	11,063.073456	10,872.269806	$\mathrm{10,924.948178}\pm 49.833690$	$\mathrm{10,900.646140}\pm 48.911795$
	5.1.12	12,309.361771	12,097.973587	$\mathrm{12,164.498850}\pm 49.937794$	$\mathrm{12,151.840936}\pm 51.708691$
512 × 512	4.2.03	8655.809656	8599.133701	$8620.690864\pm 11.925301$	$8618.853004\pm 9.948338$
	4.2.05	10,399.355824	10,355.106950	$\mathrm{10,355.326264}\pm 10.881590$	$\mathrm{10,352.863329}\pm 12.239604$
	4.2.07	10,165.795052	10,138.277390	$\mathrm{10,126.022130}\pm 11.503382$	$\mathrm{10,124.520597}\pm 13.083722$
	5.2.09	9908.172035	9847.301613	$9835.579373\pm 21.324108$	$9830.850514\pm 22.443783$
	Boat.512	7701.595245	7639.867119	$7649.817102\pm 17.268532$	$7644.612824\pm 15.723253$
1024 × 1024	5.3.01	10,324.336185	10,295.933423	$\mathrm{10,300.708227}\pm 10.963870$	$\mathrm{10,296.975873}\pm 11.789043$
	7.2.01	15,178.014318	15,138.050726	$\mathrm{15,138.170951}\pm 15.137773$	$\mathrm{15,137.760237}\pm 15.188432$

reports the MSE values for images encrypted with C1 and the standard Ascon. The third column gives the maximum MSE value observed over 100 runs for C1 (with keys and nonces derived from the chaotic map). The fourth column provides the corresponding MSE value of the standard Ascon, taken from the same run index at which C1 attains its maximum. The next two columns summarize all 100 runs by reporting the mean and standard deviation of the MSE values for C1 and for the standard Ascon, respectively.

Across all test images in Table 11, C1 attains higher MSE values than the standard Ascon, both at the single-run maximum (matched at the same run index) and in the run-averaged metric (mean ± std over 100 runs). This consistent increase in MSE indicates enhanced image-domain obfuscation, i.e., stronger suppression of residual plaintext structure in the ciphertext.

5.2.2. Mean Absolute Error (MAE)

The MAE quantifies the average absolute difference between the pixel values of the plaintext and ciphertext images, as given by Equation (13). Larger MAE values indicate greater pixel-wise deviation between the plaintext and ciphertext images, which is desirable for image-domain obfuscation.

$$MAE={\displaystyle \frac{1}{H\times W}}{\displaystyle \sum _{i=1}^H}{\displaystyle \sum _{j=1}^W}|P(i,j)-C(i,j)|$$

(13)

Here, $P(i,j)$ and $C(i,j)$ denote the pixel values of the plaintext and ciphertext images at location $(i,j)$; H and W denote the image height and width, respectively.

Table 12. MAE values for images encrypted with C1 and the standard Ascon.

Size	Filename	Max MAE (C1)	MAE (Ascon)	C1 (Mean ± Std)	Ascon (Mean ± Std)
256 × 256	4.1.05	75.646840	75.396357	$75.310881\pm 0.110748$	$75.288045\pm 0.100983$
	4.1.06	81.844533	81.486074	$81.447423\pm 0.132837$	$81.419511\pm 0.116195$
	5.1.10	73.259811	73.015991	$72.723788\pm 0.189516$	$72.687783\pm 0.180907$
	5.1.11	86.029739	85.418350	$85.341995\pm 0.251771$	$85.237006\pm 0.246522$
	5.1.12	90.826691	90.493332	$90.191191\pm 0.238886$	$90.115985\pm 0.250891$
512 × 512	4.2.03	76.531690	76.321219	$76.342793\pm 0.060618$	$76.331566\pm 0.059051$
	4.2.05	83.350577	83.112209	$83.111848\pm 0.063390$	$83.098865\pm 0.061587$
	4.2.07	82.445412	82.265511	$82.221148\pm 0.059271$	$82.217268\pm 0.066503$
	5.2.09	81.446831	81.143066	$81.082095\pm 0.111680$	$81.061271\pm 0.118879$
	Boat.512	72.828041	72.482101	$72.555307\pm 0.098537$	$72.528990\pm 0.090561$
1024 × 1024	5.3.01	83.030689	82.796355	$82.905830\pm 0.051708$	$82.888254\pm 0.056970$
	7.2.01	102.003654	101.819471	$101.798477\pm 0.067874$	$101.797414\pm 0.064034$

reports the MAE values for images encrypted with C1 and the standard Ascon. The third column gives the maximum MAE value observed over 100 runs for C1 (with keys and nonces derived from the chaotic map). The fourth column provides the corresponding MAE of the standard Ascon, taken from the same run index at which C1 attains its maximum. The next two columns summarize all 100 runs by reporting the mean and standard deviation of the MAE values for C1 and for the unmodified Ascon, respectively.

Table 12 summarizes the image-domain distortion via the MAE. The run-averaged MAE (mean ± std over 100 runs) is consistently higher for C1. The absolute mean differences are small (on the order of ${10}^{-3}$ to ${10}^{-1}$ MAE units), with standard deviations of similar magnitude for both methods, indicating that the increase is achieved without sacrificing run-to-run consistency. Overall, the table shows a consistent but modest advantage for C1 in MAE—i.e., stronger image-domain obfuscation—across the evaluated images.

Table 13. MSE and MAE values of images encrypted with C1 and the related work.

Size	Filename	Reference	MSE	MAE
512 × 512	4.2.03	Proposed	8655.809656	76.531690
		[55]	8623.94	—
		[57]	7261.71	71.0481
	4.2.05	Proposed	10,399.355824	83.350577
		[57]	10,296.2	82.9506
	4.2.07	Proposed	10,165.795052	82.445412
		[55]	10,129.94712	—
		[25]	—	82.241
		[57]	8434.09	75.6136

reports the MAE values for images encrypted with C1, alongside comparable results from the literature.

Table 13 assesses the separation between the ciphertext and the original images using MSE and MAE; for these metrics, larger values indicate stronger concealment. C1 achieves values on par with those reported in prior work and slightly higher in many cases, indicating robust distortion and concealment.

5.2.3. Peak Signal-to-Noise Ratio (PSNR)

The PSNR quantifies the peak signal-to-noise ratio between the plaintext image and the ciphertext image and is computed as in Equation (14).

$$\mathrm{PSNR}\left(\mathrm{dB}\right)=10{\log }_{10}\left({\displaystyle \frac{{\mathrm{MAX}}_P^2}{\mathrm{MSE}}}\right)$$

(14)

Here, $MA{X}_p$ denotes the maximum possible pixel value. For 8-bit images $MA{X}_p$ equals 255. MSE is defined in Equation (12). In this context, a higher PSNR indicates lower pixel-wise distortion, whereas a lower PSNR indicates stronger image-domain obfuscation.

Table 14. PSNR (dB) for images encrypted with C1 and the standard Ascon.

Size	Filename	Min PSNR (C1)	PSNR (Ascon)	C1 (Mean ± Std)	Ascon (Mean ± Std)
256 × 256	4.1.05	8.879468	8.906069	$8.910500\pm 0.011216$	$8.912727\pm 0.010219$
	4.1.06	8.129434	8.160577	$8.161758\pm 0.011408$	$8.164775\pm 0.010213$
	5.1.10	9.210891	9.235643	$9.270620\pm 0.019464$	$9.273593\pm 0.018561$
	5.1.11	7.692046	7.767601	$7.746654\pm 0.019805$	$7.756324\pm 0.019484$
	5.1.12	7.228448	7.303677	$7.279898\pm 0.017833$	$7.284422\pm 0.018478$
512 × 512	4.2.03	8.757727	8.786257	$8.775184\pm 0.005461$	$8.776122\pm 0.006034$
	4.2.05	7.960739	7.979258	$7.979168\pm 0.004564$	$7.980202\pm 0.005134$
	4.2.07	8.059390	8.071162	$8.075896\pm 0.005278$	$8.076019\pm 0.005156$
	5.2.09	8.170868	8.197631	$8.202814\pm 0.009416$	$8.204904\pm 0.009911$
	Boat.512	9.264997	9.299946	$9.294304\pm 0.009806$	$9.297258\pm 0.008928$
1024 × 1024	5.3.01	7.992116	7.998385	$8.002135\pm 0.004623$	$8.003709\pm 0.004971$
	7.2.01	6.318654	6.330104	$6.329653\pm 0.004485$	$6.329427\pm 0.004340$

reports the PSNR (dB) for images encrypted with C1 and the standard Ascon. The third column gives the minimum PSNR observed across 100 runs for C1. The fourth column lists the matched PSNR of the standard Ascon, evaluated at the same run index at which C1 attains its minimum. The last two columns report the run-averaged PSNR values (mean ± std over 100 runs) for C1 and the standard Ascon, respectively.

Using PSNR, which in the context of image encryption means that lower values reflect the stronger concealment of the visible structure, we find that the C1 and standard Ascon perform comparably. Across all test images, both schemes achieve a consistently low PSNR, approximately 6 to 9 dB. The differences between the methods are marginal. These results suggest that the C1 modification preserves Ascon’s image-level concealment performance without degrading PSNR-based distortion characteristics.

Table 15. PSNR (dB) values for images encrypted with C1 and related work.

Size	Filename	Reference	PSNR (dB)
256 × 256	5.1.12	Proposed	7.228448
		[50]	7.2918
		[54]	8.2915
512 × 512	4.2.03	Proposed	8.757727
		[50]	8.7899
		[55]	8.78864
		[54]	8.7966
	4.2.07	Proposed	8.059390
		[25]	9.1185
		[55]	8.12625
1024 × 1024	5.3.01	Proposed	7.992116
		[50]	8.1126
		[54]	8.2112

reports the PSNR values for images encrypted with C1, alongside comparable results reported in the literature.

5.3. Differential Analysis

Cryptanalysts conduct differential attacks by introducing slight modifications to the original plaintext or image and encrypting it with the same key, in an attempt to identify relationships between the original and the resulting encrypted output (e.g., ciphertext for text, encrypted image for images). Therefore, an encryption algorithm must exhibit strong diffusion, such that a small change—for example, altering a single byte or pixel in the input—produces a significantly different output. To evaluate an algorithm’s resistance to such attacks, the avalanche effect test is employed for text data, while the NPCR and UACI metrics, image-domain analogs of the avalanche effect, are used for encrypted images. In this study, we introduced a slight modification by increasing the first pixel value of the red channel by 1 for color images, and the first pixel value by 1 for grayscale images.

5.3.1. Avalanche Effect

The avalanche effect is the phenomenon whereby a very small change in the encryption key or plaintext results in a significant change in the corresponding ciphertext. In encryption algorithms, a small change, such as inverting a single bit or increasing or decreasing a single pixel by 1, is intended to produce a large and widespread difference in the output. In plaintext data, the avalanche effect is calculated as in Equation (15).

$$\begin{array}{c}\mathrm{Number\_of\_changed\_bits}={\displaystyle \sum _{i=1}^L}\mathrm{bitcount}(C_1\left(i\right)\oplus C_2\left(i\right)),\hfill \\ \mathrm{Avalanche\_Effect}=\left({\displaystyle \frac{\mathrm{number\_of\_changed\_bits}}{\mathrm{total\_number\_of\_bits}}}\right)\times 100\%,\hfill \end{array}$$

(15)

where $C_1\left(i\right)$ denotes the $i^{\mathrm{th}}$ byte of the ciphertext obtained by encrypting the original plaintext, and $C_2\left(i\right)$ denotes the $i^{\mathrm{th}}$ byte of the ciphertext obtained by encrypting the plaintext in which one bit of the original was flipped. The function bitcount calculates the number of different bits in the $i^{\mathrm{th}}$ byte. L is the total number of bytes in the ciphertext.

For an encryption algorithm to be considered highly sensitive to input changes and to provide strong security, approximately 50% of the bits should change when a single input bit is flipped. The avalanche-effect results for randomly generated plaintexts of varying lengths are reported in Table 19. The avalanche effect for encrypted images is assessed using the NPCR and UACI metrics.

5.3.2. Number of Pixels Change Rate (NPCR)

The NPCR metric measures the percentage of pixels that differ between two encrypted images: one obtained by encrypting the original image and the other obtained by encrypting the image after randomly modifying a single pixel value. The NPCR is computed as in Equation (16).

$$\begin{array}{cc}NPCR\hfill & ={\displaystyle \frac{1}{H\times W}}{\displaystyle \sum _{i=1}^H}{\displaystyle \sum _{j=1}^W}D(i,j)\times 100\%\hfill \\ D(i,j)\hfill & =\left\{\begin{array}{cc}1\hfill & \mathrm{if}{C}_1(i,j)\ne C_2(i,j)\hfill \\ 0\hfill & \mathrm{if}{C}_1(i,j)=C_2(i,j)\hfill \end{array}\right.\hfill \end{array}$$

(16)

Here, $C_1$ denotes the ciphertext obtained by encrypting the original image, and $C_2$ denotes the ciphertext obtained after modifying a single pixel in the original image. For each pixel location $(i,j)$, $D(i,j)=0$ if the corresponding pixels in $C_1$ and $C_2$ are equal, and $D(i,j)=1$ otherwise. H and W denote the image height and width, respectively. NPCR measures the proportion of pixels that change between $C_1$ and $C_2$; values approaching its theoretical ideal indicate stronger sensitivity to plaintext changes and better diffusion. For 8-bit images under ideal diffusion, the theoretical NPCR is $99.609375\%$ [63].

For each run, we computed the absolute difference between the measured NPCR and the theoretical ideal. The mean absolute deviation ($\Delta$) was then calculated by averaging these differences over 100 runs, as given in Equation (17). Smaller values of $\Delta \mathrm{C}1$ and $\Delta \mathrm{Ascon}$ indicate closer proximity to the theoretical ideal.

$$\Delta A={\displaystyle \frac{1}{100}}{\displaystyle \sum _{i=1}^{100}}\left|x_i^{\left(A\right)}-ideal\right|,A\in \{\mathrm{C}1,\mathrm{Ascon}\},$$

(17)

where $x_i^{\left(A\right)}$ is the measured NPCR (in %) at run i for method A, and $\mathrm{ideal}=99.609375\%$.

Table 16. NPCR statistics for C1 and standard Ascon: mean and standard deviation over 100 runs and mean absolute deviation ($\Delta$) from the theoretical ideal.

Size	Filename	C1 (Mean ± Std)	Ascon (Mean ± Std)	ΔC1	ΔAscon
256 × 256	4.1.05	$99.602758\pm 0.012643$	$99.601669\pm 0.013455$	0.011195	0.012629
	4.1.06	$99.601593\pm 0.013320$	$99.600210\pm 0.014590$	0.012644	0.013906
	5.1.10	$99.585648\pm 0.024178$	$99.583374\pm 0.028278$	0.027390	0.031158
	5.1.11	$99.590301\pm 0.024476$	$99.582794\pm 0.025048$	0.024689	0.031311
	5.1.12	$99.588196\pm 0.022228$	$99.582886\pm 0.021738$	0.025055	0.028656
512 × 512	4.2.03	$99.608259\pm 0.006909$	$99.608162\pm 0.007332$	0.005229	0.006147
	4.2.05	$99.607320\pm 0.006568$	$99.606578\pm 0.006711$	0.005526	0.006081
	4.2.07	$99.607103\pm 0.006604$	$99.607288\pm 0.008792$	0.005352	0.006919
	5.2.09	$99.604866\pm 0.010829$	$99.603649\pm 0.012577$	0.009857	0.011234
	Boat.512	$99.602039\pm 0.010394$	$99.602234\pm 0.010944$	0.009960	0.010361
1024 × 1024	5.3.01	$99.608043\pm 0.006096$	$99.607971\pm 0.006359$	0.005033	0.005426
	7.2.01	$99.608650\pm 0.006688$	$99.608784\pm 0.007004$	0.005178	0.005615

presents, for both C1 and the standard Ascon, the mean ± standard deviation of the NPCR over 100 runs, together with the mean absolute deviation ($\Delta$) from the ideal value.

Across all twelve image–resolution pairs, the C1 exhibits consistently better diffusion than the standard Ascon. The run-averaged NPCR values of both schemes lie close to the theoretical ideal of $99.609375\%$, yet C1 is systematically closer to the ideal. In every row of Table 16, the mean absolute deviation from the ideal ($\Delta \mathrm{C}1$) is smaller than that of the standard Ascon ($\Delta \mathrm{Ascon}$). Taken together, this evidence indicates that C1 achieves marginal yet consistent gains in plaintext-change sensitivity as measured by the NPCR. Table 18 compares the NPCR (%) of images encrypted with C1 to values reported in the literature and shows that integrating chaotic parameters from the Zaslavsky map into Ascon-AEAD128 effectively propagates a single-bit change in the original image across the encrypted image.

5.3.3. Unified Average Changing Intensity (UACI)

UACI, another metric used in differential analysis, measures the average change in pixel intensity between two encrypted images. The first image is obtained by encrypting the original image. The second is obtained by modifying exactly one pixel in the original image and then encrypting it. The modification may consist of increasing or decreasing the intensity of a randomly selected pixel by 1 or setting it to 0 or 255. The UACI is computed as in Equation (18).

$$UACI={\displaystyle \frac{1}{H\times W}}{\displaystyle \sum _{i=1}^H}{\displaystyle \sum _{j=1}^W}{\displaystyle \frac{|C_1(i,j)-C_2(i,j)|}{255}}\times 100\%$$

(18)

Here, $C_1$ denotes the encrypted image obtained by encrypting the original image, and $C_2$ denotes the encrypted image obtained by first modifying one pixel of the original image and then encrypting it. In a secure image-encryption scheme, small changes in the plaintext should induce large changes in the ciphertext; accordingly, the term $|C_1(i,j)-C_2(i,j)|$ captures this per-pixel sensitivity and underlies the UACI metric. For 8-bit images under ideal diffusion, the theoretical UACI is $33.4635\%$[63]. For each run, we computed the absolute difference between the measured UACI and the theoretical ideal. The mean absolute deviation ($\Delta$) was then calculated by averaging these differences over 100 runs as given in Equation (17).

Table 17. UACI statistics for C1 and standard Ascon: mean and standard deviation over 100 runs and mean absolute deviation ($\Delta$) from the theoretical ideal.

Size	Filename	C1 (Mean ± Std)	Ascon (Mean ± Std)	$\Delta$C1	$\Delta$Ascon
256 × 256	4.1.05	$33.466973\pm 0.050994$	$33.463235\pm 0.062781$	0.037583	0.051471
	4.1.06	$33.459010\pm 0.046739$	$33.455147\pm 0.051320$	0.035629	0.042005
	5.1.10	$33.443481\pm 0.085011$	$33.438125\pm 0.095549$	0.069430	0.077853
	5.1.11	$33.471623\pm 0.087792$	$33.451122\pm 0.107773$	0.067486	0.086980
	5.1.12	$33.454695\pm 0.091704$	$33.464351\pm 0.095635$	0.075593	0.078244
512 × 512	4.2.03	$33.461308\pm 0.023904$	$33.457644\pm 0.028362$	0.019744	0.022880
	4.2.05	$33.460731\pm 0.025106$	$33.461981\pm 0.029608$	0.020286	0.022017
	4.2.07	$33.464314\pm 0.027801$	$33.460466\pm 0.029189$	0.021681	0.023990
	5.2.09	$33.457853\pm 0.043812$	$33.474550\pm 0.045279$	0.034608	0.038494
	Boat.512	$33.464995\pm 0.041639$	$33.455805\pm 0.044206$	0.032827	0.036596
1024 × 1024	5.3.01	$33.464791\pm 0.019406$	$33.458943\pm 0.022918$	0.015457	0.018286
	7.2.01	$33.460894\pm 0.021745$	$33.466677\pm 0.025126$	0.017613	0.019753

presents, for both C1 and standard Ascon, the mean ± standard deviation of the UACI together with $\Delta$ (deviation from the ideal) after 100 runs.

Table 17 provides a UACI-based assessment of the differential resistance for C1 and the standard Ascon. For all the tested images, the empirical mean UACI values of both schemes are close to the theoretical ideal of $33.4635\%$, indicating strong diffusion. A finer comparison based on the mean absolute deviation from the ideal ($\Delta$) shows a consistent advantage for C1: in all twelve image–resolution pairs, $\Delta \mathrm{C}1$ is lower than $\Delta \mathrm{Ascon}$, meaning C1’s UACI values are systematically closer to the ideal over 100 runs. Moreover, C1 exhibits lower run-to-run variability, with smaller standard deviations in every case. Overall, these findings indicate a small but uniform improvement in diffusion for C1. Table 18 compares the UACI (%) of images encrypted with C1 to the values reported in the literature.

Table 18. NPCR and UACI (%) values for images encrypted with C1 and the related work.

Size	Filename	Reference	NPCR (%)	UACI (%)
256 × 256	4.1.05	Proposed	99.609375	33.463831
		[60]	99.6028	33.4018
		[59]	99.6217	33.4176
		[53]	99.5941	33.4498
	4.1.06	Proposed	99.609375	33.463480
		[60]	99.5956	33.5235
		[59]	99.6101	33.5062
		[53]	99.6246	33.4227
	5.1.10	Proposed	99.609375	33.463763
		[58]	99.6094	33.4801
		[12]	99.6124	33.4835
		[64]	99.6017	33.5032
		[65]	99.6155	33.5115
	5.1.11	Proposed	99.609375	33.463368
		[58]	99.6189	33.5077
		[12]	99.5956	33.3793
		[64]	99.6139	33.4719
		[65]	99.6094	33.5174
	5.1.12	Proposed	99.609375	33.464008
		[58]	99.6178	33.4835
		[12]	99.6108	33.4883
		[64]	99.6185	33.4541
		[65]	99.5758	33.4202
512 × 512	4.2.03	Proposed	99.609375	33.463457
		[55]	99.61548	33.44075
		[50]	99.6249	33.5860
		[54]	99.6222	33.4901
	4.2.05	Proposed	99.609375	33.463546
		[60]	99.6231	33.4475
	4.2.07	Proposed	99.609375	33.463537
		[55]	99.60327	33.47308
		[25]	99.6128	33.4915
	5.2.09	Proposed	99.609375	33.463648
		[58]	99.585	33.4687
		[12]	99.617	33.4727
		[64]	99.5971	33.4757
		[65]	99.6094	33.4528
	Boat.512	Proposed	99.609375	33.463631
		[58]	99.6178	33.4590
		[12]	99.6140	33.4814
		[64]	99.6284	33.4568
		[65]	99.5998	33.4519
1024 × 1024	5.3.01	Proposed	99.609375	33.463550
		[58]	99.6082	33.4611
		[64]	99.6134	33.4943
		[65]	99.6035	33.4741
	7.2.01	Proposed	99.609375	33.463597
		[58]	99.6128	33.4289
		[64]	99.6072	33.4746
		[65]	99.6013	33.4548

Table 18. NPCR and UACI (%) values for images encrypted with C1 and the related work.

Size	Filename	Reference	NPCR (%)	UACI (%)
256 × 256	4.1.05	Proposed	99.609375	33.463831
		[60]	99.6028	33.4018
		[59]	99.6217	33.4176
		[53]	99.5941	33.4498
	4.1.06	Proposed	99.609375	33.463480
		[60]	99.5956	33.5235
		[59]	99.6101	33.5062
		[53]	99.6246	33.4227
	5.1.10	Proposed	99.609375	33.463763
		[58]	99.6094	33.4801
		[12]	99.6124	33.4835
		[64]	99.6017	33.5032
		[65]	99.6155	33.5115
	5.1.11	Proposed	99.609375	33.463368
		[58]	99.6189	33.5077
		[12]	99.5956	33.3793
		[64]	99.6139	33.4719
		[65]	99.6094	33.5174
	5.1.12	Proposed	99.609375	33.464008
		[58]	99.6178	33.4835
		[12]	99.6108	33.4883
		[64]	99.6185	33.4541
		[65]	99.5758	33.4202
512 × 512	4.2.03	Proposed	99.609375	33.463457
		[55]	99.61548	33.44075
		[50]	99.6249	33.5860
		[54]	99.6222	33.4901
	4.2.05	Proposed	99.609375	33.463546
		[60]	99.6231	33.4475
	4.2.07	Proposed	99.609375	33.463537
		[55]	99.60327	33.47308
		[25]	99.6128	33.4915
	5.2.09	Proposed	99.609375	33.463648
		[58]	99.585	33.4687
		[12]	99.617	33.4727
		[64]	99.5971	33.4757
		[65]	99.6094	33.4528
	Boat.512	Proposed	99.609375	33.463631
		[58]	99.6178	33.4590
		[12]	99.6140	33.4814
		[64]	99.6284	33.4568
		[65]	99.5998	33.4519
1024 × 1024	5.3.01	Proposed	99.609375	33.463550
		[58]	99.6082	33.4611
		[64]	99.6134	33.4943
		[65]	99.6035	33.4741
	7.2.01	Proposed	99.609375	33.463597
		[58]	99.6128	33.4289
		[64]	99.6072	33.4746
		[65]	99.6013	33.4548

The NPCR and UACI values closest to the ideal from the 100 encryption runs are listed in Table 18, alongside the results reported in the literature. Table 18 demonstrates the clear superiority of C1 on the differential metrics. For every image–size pair, C1 attains the theoretical ideal NPCR of 99.609375%, whereas the related works report lower values. For the UACI, C1 reaches or is closest to the ideal 33.4635% in most cases, yielding the best value in the corresponding entries. These findings indicate that C1 achieves stronger diffusion and differential resistance than the previously reported methods.

5.4. Key Space Analysis

In an encryption algorithm, the key space denotes the total number of all theoretically possible key combinations. The key space must be sufficiently large to make brute-force attacks computationally infeasible. Keys with a minimum of 128 bits should be used, making brute-force key scanning practically impossible [55,66].

In the case of Ascon-AEAD128, the secret key has a fixed size of 128 bits. The 128-bit nonce must be unique under the same key and can be public; therefore, it is not considered part of the secret key space. Hence, the brute-force security of the Ascon is strictly determined by the 128-bit secret key, yielding an effective key space of $2^{128}$.

In the proposed structure, the secret key is generated using parameters obtained from the Zaslavsky map. Each parameter is represented in IEEE-754 double-precision format, which provides 53 bits of significant precision. Since the chaotic map involves two state variables and three control parameters, the theoretical upper bound of the parameter space is ${\left(2^{53}\right)}^5=2^{265}$ states. Nevertheless, regardless of the size of this parameter space, the derived key is compressed into a 128-bit Ascon-AEAD128 key, and thus the overall brute-force security level of the system remains bounded by $2^{128}$.

5.5. Key Sensitivity Test

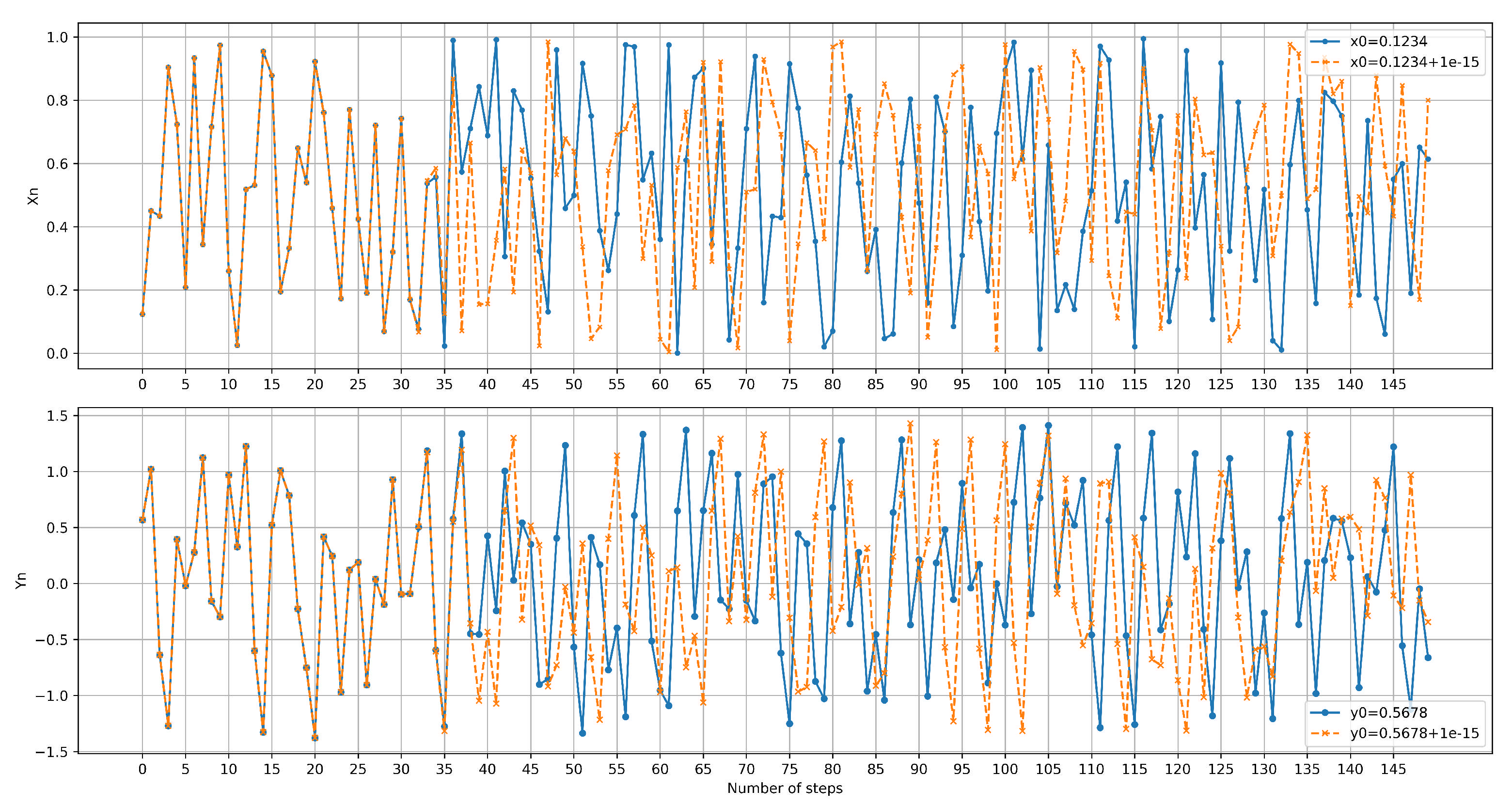
According to Shannon’s confusion principle, a secure image encryption algorithm must exhibit very high sensitivity to its secret key. In practice, even the slightest modification of the key or of the parameters used to generate the key should produce a completely different ciphertext image.

In our experiments, a secret key K was first derived from the Zaslavsky map parameters ($x_o$ = 0.1234, $y_o$ = 0.5678, r = 0.9, v = 0.5, e = 2.718281828459045). Each parameter was then minimally perturbed, and the modified values were used to generate new keys for encrypting the same test image. The differences between each encrypted images and the original encrypted image were computed and are shown in Figure 11. Throughout the key-sensitivity experiments, the nonce, associated data A, counter, and session-ID values were kept constant to isolate the impact of the key variations. Furthermore, to examine the sensitivity of the final 128-bit Ascon key, a one-bit flip was applied, and the modified key was used to re-encrypt the same image. The results clearly show that both a minimal change in any chaotic parameter and a single-bit change in the final key produce entirely different ciphertext images. These findings confirm that the proposed scheme satisfies Shannon’s confusion requirement.

Equation (19) is used to measure the sensitivity of the ciphertext to changes in the key. Each bit of the N-bit key is inverted one at a time, and the avalanche effect is measured after each inversion. Using Equation (15), the avalanche effect for each modified key bit is computed from the difference between the ciphertext produced with the original key and the ciphertext produced after flipping that bit. The final key-sensitivity score is then obtained by averaging these per-bit avalanche values over all N key bits, as given in Equation (19). Thus, on average, the number of output bits changed as a result of a single-bit modification is determined. When any bit of the key is changed, the average number of altered output bits should be approximately equal to half the number of plaintext bits. In this study, N = 128.

$$\mathrm{Key}\mathrm{Sensitivity}={\displaystyle \frac{{\sum }_{i=1}^N\mathrm{avalanche\_effect\_for\_bit\_i}}{N}}$$

(19)

5.6. Text Data Analysis

Randomly generated plaintexts of varying lengths were encrypted with C1 and with Ascon-AEAD128. The resulting ciphertexts were evaluated using entropy, correlation, chi-square, avalanche (bit level), key sensitivity, MSE, and MAE. The Zaslavsky map was initialized with $x_0=0.1234$, $y_0=0.5678$, $e=2.718281828459045$, $r=0.9$, and $v=0.5$. At each iteration, the updated $(x,y)$ served as the initial conditions for the next step, and the resulting chaotic sequences were used to derive the key and nonce. For both C1 and Ascon, after 100 runs, Table 19 reports the run-averaged results for the entropy, chi-square, avalanche, key sensitivity, MSE, and MAE, together with the minimum observed correlation.

Table 19. Evaluation across message lengths using matched random plaintexts with C1 and with the standard Ascon.

Metric	Length [B] = 256		Length [B] = 512		Length [B] = 1024		Length [B] = 10,240
	C1	Ascon	C1	Ascon	C1	Ascon	C1	Ascon
Entropy	7.1782	7.1647	7.5955	7.5891	7.8102	7.8064	7.9821	7.9817
Correlation	−0.0001	−0.0001	−0.0001	0.0001	−0.0001	0.0001	0.0001	0.0001
Chi-square	254.58	257.38	256.87	259.90	254.96	257.75	255.17	258.23
Avalanche (%)	50.07	49.81	50.17	49.86	50.04	49.99	50.00	49.96
Key Sensitivity	1024.13	1023.77	2048.34	2047.51	4096.88	4095.63	40,959.41	40,956.30
MSE	11,060.08	10,916.95	11,017.74	10,891.42	10,892.27	10,865.43	10,938.00	10,904.01
MAE	85.98	85.19	85.71	85.18	85.20	85.04	85.41	85.24

Table 19. Evaluation across message lengths using matched random plaintexts with C1 and with the standard Ascon.

Metric	Length [B] = 256		Length [B] = 512		Length [B] = 1024		Length [B] = 10,240
	C1	Ascon	C1	Ascon	C1	Ascon	C1	Ascon
Entropy	7.1782	7.1647	7.5955	7.5891	7.8102	7.8064	7.9821	7.9817
Correlation	−0.0001	−0.0001	−0.0001	0.0001	−0.0001	0.0001	0.0001	0.0001
Chi-square	254.58	257.38	256.87	259.90	254.96	257.75	255.17	258.23
Avalanche (%)	50.07	49.81	50.17	49.86	50.04	49.99	50.00	49.96
Key Sensitivity	1024.13	1023.77	2048.34	2047.51	4096.88	4095.63	40,959.41	40,956.30
MSE	11,060.08	10,916.95	11,017.74	10,891.42	10,892.27	10,865.43	10,938.00	10,904.01
MAE	85.98	85.19	85.71	85.18	85.20	85.04	85.41	85.24

Table 19 reports the run-averaged text-encryption metrics for C1 and standard Ascon-AEAD128 at plaintext lengths of 256, 512, 1024, and 10,240 bytes. For each message length, 100 independently generated random plaintexts were encrypted with C1 and with standard Ascon, using keys and nonces freshly derived from the chaotic map for each run. Across lengths, the ciphertext statistics exhibit the expected convergence: entropy approaches the 8-bit ideal, chi-square values remain comfortably below the critical threshold, correlation scores stay close to zero, and diffusion-oriented metrics concentrate around their nominal targets. Taken together, these results show no systematic irregularity and indicate that, under the tested conditions, C1 matches, and in several lengths marginally improves upon, the standard Ascon in terms of histogram uniformity and diffusion.

5.7. Performance Analysis

We analyze how Ascon-AEAD128, the standard-compliant C1 scheme, and the C4 variant (which dynamically generates IV, RC, and LC) affect the encryption and decryption times.

Table 20. Parameter generation times (ms) for use in encryption and decryption.

Scheme	Key/Nonce (CPU)	PRNG	Nonce Build	RC Build	LC Build
Ascon	0.003	—	—	—	—
C1	—	0.018	0.002	—	—
C4	0.003	0.024	—	0.015	1.407

reports the parameter-generation times (in milliseconds) used by the ciphers.

In the baseline Ascon, obtaining the key and nonce from the CPU RNG takes 0.003 ms. In C1, both parameters are derived from chaotic-map random numbers: the key is generated directly from chaotic outputs, while the nonce is constructed by concatenating chaotic outputs with a counter and a session identifier; this process takes 0.020 ms. C4 generates the key and nonce via the CPU and produces chaotic random numbers to construct RC and LC, requiring 1.449 ms. The dominant cost arises from enforcing bijectivity in the LC.

Table 21. Core encryption and decryption times for standard Ascon, C1, and C4.

Size	Filename	Type	Encryption (s)			Decryption (s)
			Ascon	C1	C4	Ascon	C1	C4
256 × 256	4.1.05	Color	0.343225	0.340722	0.340003	0.341618	0.345214	0.342501
	4.1.06	Color	0.340095	0.340567	0.340003	0.341406	0.341122	0.343501
	5.1.10	Gray	0.110192	0.108776	0.108494	0.109726	0.107887	0.108405
	5.1.11	Gray	0.111237	0.112445	0.109905	0.107642	0.109206	0.109846
	5.1.12	Gray	0.112024	0.111511	0.110007	0.110554	0.109421	0.109784
512 × 512	4.2.03	Color	1.849984	1.854430	1.833255	1.863040	1.860873	1.841330
	4.2.05	Color	1.846267	1.835167	1.828066	1.840492	1.852241	1.845257
	4.2.07	Color	1.842680	1.844640	1.843853	1.837909	1.850161	1.844626
	5.2.09	Gray	0.477924	0.475911	0.474500	0.474085	0.467480	0.471335
	Boat.512	Gray	0.476573	0.474380	0.472634	0.468591	0.471271	0.472336
1024 × 1024	5.3.01	Gray	2.828522	2.800080	2.807296	2.779824	2.796872	2.798440
	7.2.01	Gray	2.800914	2.819610	2.803640	2.790914	2.797895	2.802135

reports the encryption and decryption times for 12 images, in seconds. The parameter-generation overhead is excluded from these measurements. The results indicate that encryption and decryption exhibit comparable runtimes.

6. Conclusions and Future Work

In this study, we develop a chaos-based lightweight encryption approach by integrating pseudorandom numbers generated by the Zaslavsky map into Ascon-AEAD128 for key and nonce derivation (C1). In baseline Ascon-AEAD128, keys and nonces are generated per run, while the permutation, IV, round constants, and linear constants remain standard; the same core remains unchanged in C1. We implement MQTT-based communication between ROS 2 Humble robots and Raspberry Pi 3B devices and encrypt grayscale and color images of sizes 256 × 256, 512 × 512, and 1024 × 1024, as well as text of varying lengths. We conduct 100 runs per setting and evaluate the entropy, ${\chi }^2$, adjacent-pixel correlation, NPCR, UACI, PSNR, MSE, and MAE. For completeness, we also report exploratory variants (C2–C4) that modify internal constants as ablations. For C2–C4, analyses are limited to statistical and differential tests to examine chaos-induced improvements in randomness and diffusion.

Across the 100-run experiments, C1 produces ciphertexts whose statistical and differential indicators are consistently close to their theoretical ideals. Shannon entropy remains near 8 bits; ${\chi }^2$ averages are lower in most image–size pairs, with fewer exceedances of the 293.25 threshold; adjacent-pixel correlations are very close to zero across all images and directions; the NPCR and UACI reach near-ideal levels; the PSNR values are low, indicating strong concealment; and the MSE/MAE are comparable, often slightly higher than the baseline. Taken together, these results demonstrate a consistent and repeatable advantage of C1 in histogram uniformity and decorrelation over standard Ascon-AEAD128.

The appendices present exploratory results for C2–C4. Across the tested image–size pairs, these variants show clear instances of improvement in distributional and differential indicators relative to the corresponding standard Ascon runs, most notably lower ${\chi }^2$ averages or fewer exceedances of 293.25 in multiple cases, and correlation coefficients closer to zero for selected images and directions. The NPCR and UACI remain close to their theoretical ideals, with several cases exhibiting tighter proximity, while the PSNR and MSE/MAE are consistently comparable to the baselines. Although the gains are moderate and not uniform across all settings, the evidence indicates that chaos-driven parameterization delivers measurable benefits and is a promising direction for enhancing diffusion-oriented behavior. Consistent with the threat model, these findings are diagnostic and exploratory and do not extend AEAD security claims beyond those of the standard Ascon.

Future work will broaden the chaotic design space beyond the Zaslavsky map by exploring piecewise-linear maps and four- and five-dimensional hyperchaotic systems to enlarge the effective key space. We will also pursue dynamic parameter optimization and AI-based control mechanisms, with a C++ implementation targeting efficiency. In addition, we will investigate FPGA/ASIC implementations of the chaos-based Ascon design to evaluate resource utilization and power consumption at the hardware level.