Total Fuel Cost, Power Loss, and Voltage Deviation Reduction for Power Systems with Optimal Placement and Operation of FACTS and Renewable Power Sources
Abstract
1. Introduction
- Implement seven simulation cases with different assumptions regarding the existence of FACTS devices and RPPs: the separate and simultaneous use of SVC, TCSC, and RPPs is tried in seven cases.
- Propose different combinations of FACTS and wind power plants: three cases, including one, two, and three wind power plants, are integrated with different types of FACTS.
- Provide solutions with the same or better total fuel costs, power loss, and voltage deviation than previous studies.
- Find the best study case with the smallest total power loss. The best study case indicates the best plan for transmission power networks, which is the simultaneous installation of TCSC, FACTS, and renewable power plants.
- Indicate the best solution for selecting the most suitable buses and the rated parameters of TCSC, SVC, and wind power plants.
- The highest active power loss reduction and the most stable voltage profile are obtained when installing the simultaneous TCSC, SVC, and wind power plants. In addition, the rated power of the SVC and wind power plants is minimal.
2. Problem Description
2.1. Objective Function
- Reduction in power losses: Transmission lines connecting each pair of buses have active power losses due to their own parameters. So, the total losses are minimized as follows [8]:
- 2.
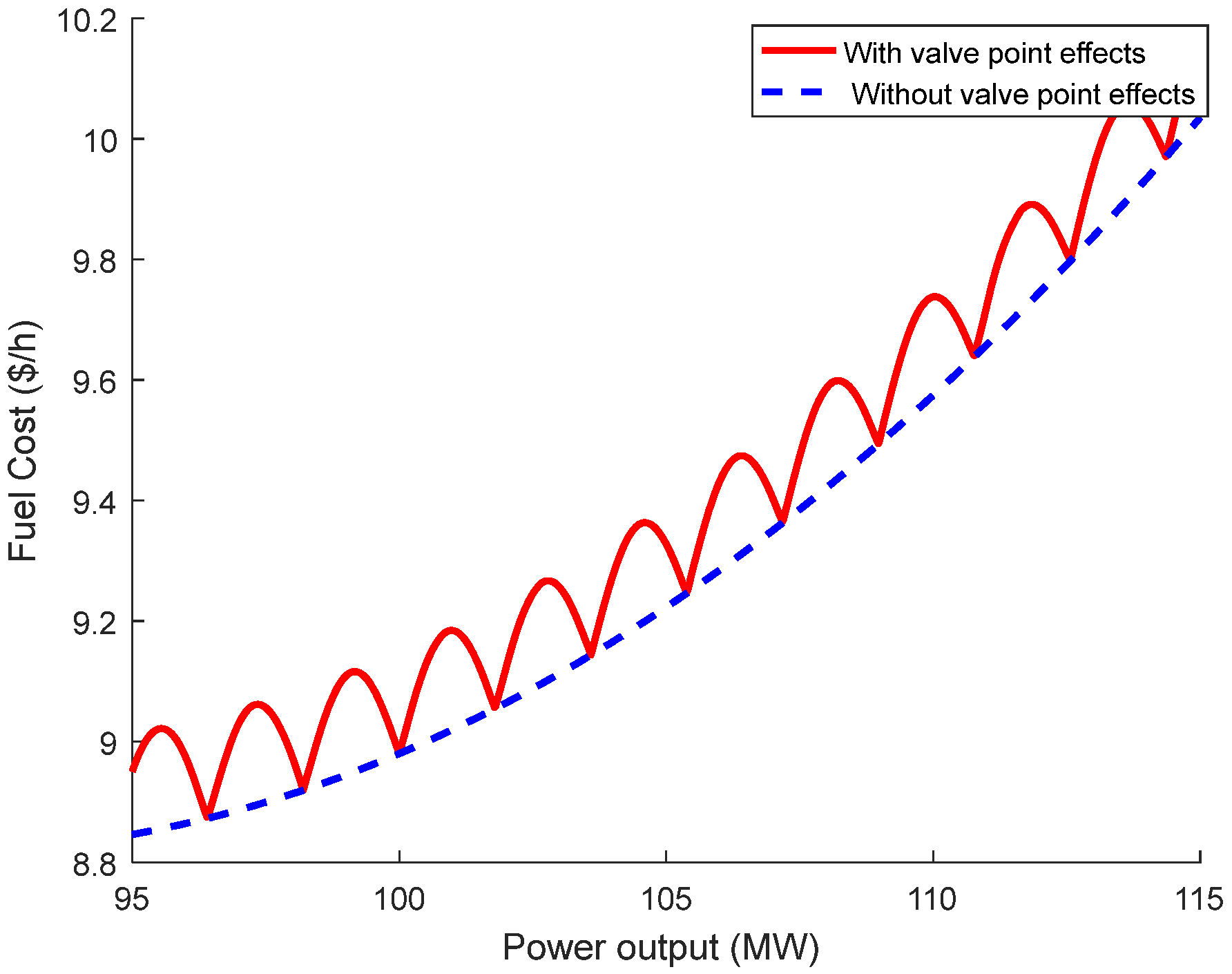
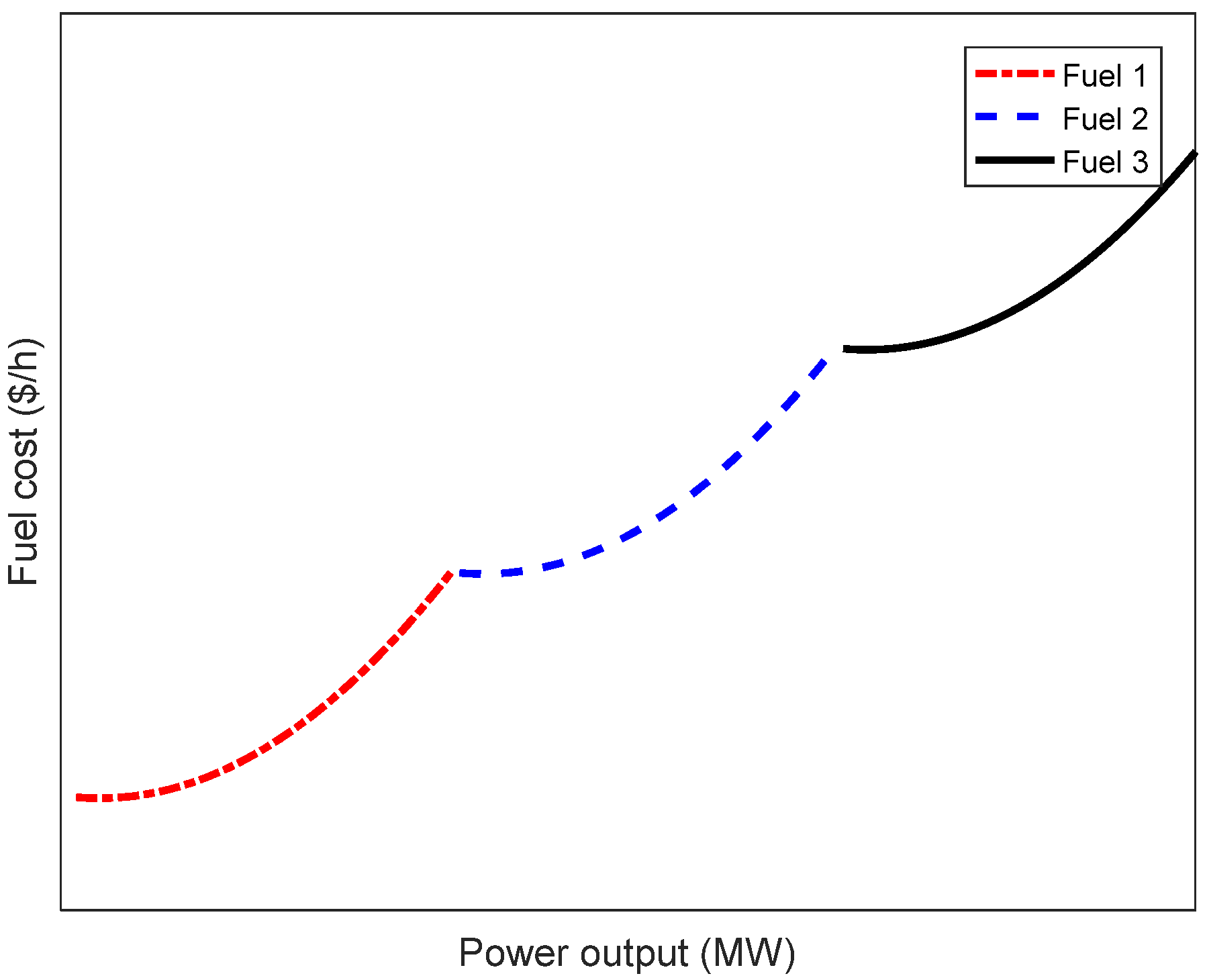
- Reduction in total fuel costs: TPPs working on buses in power systems are using fossil fuels, which cost a lot of money. So, reducing the total cost is very important. The study considers three fuel cost types, including the following: Case (1) using single fuel and neglecting valve point effects (VPES) of TPPs [9]; Case (2) using single fuel and considering VPES of TPPs [28]; and Case (3) using three fuels and neglecting VPES of TPPs [31]. In early 2025, multiple fuel-based thermal generation units were reapplied [56]. In practice, the Siemens SGT6-5000F gas turbine can use many types of fuels, such as natural gas, ethane, syngas, propane, distillates, crude oils, biodiesel, kerosene, alcohols, and so on [57].
- 3.
- Reduction in total voltage deviation: The voltage standard value, or the expected voltage, is assumed to be 1 Pu in power systems. The deviation of working voltage values and the expected value is called the voltage fluctuation. When the deviation is reduced at most, the voltage of the power systems can be stable. The target is mathematically expressed as follows:
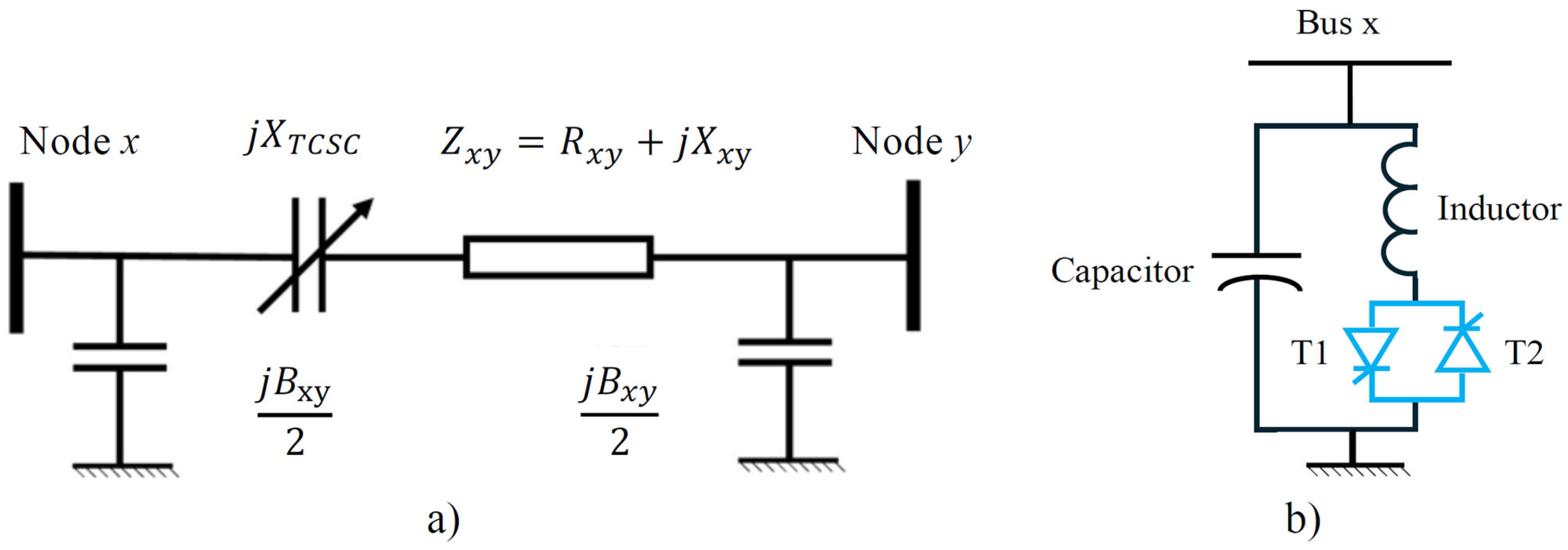
2.2. The Model of TCSC and SVC
2.3. Power Balance Constraint
2.4. Inequality Constraints
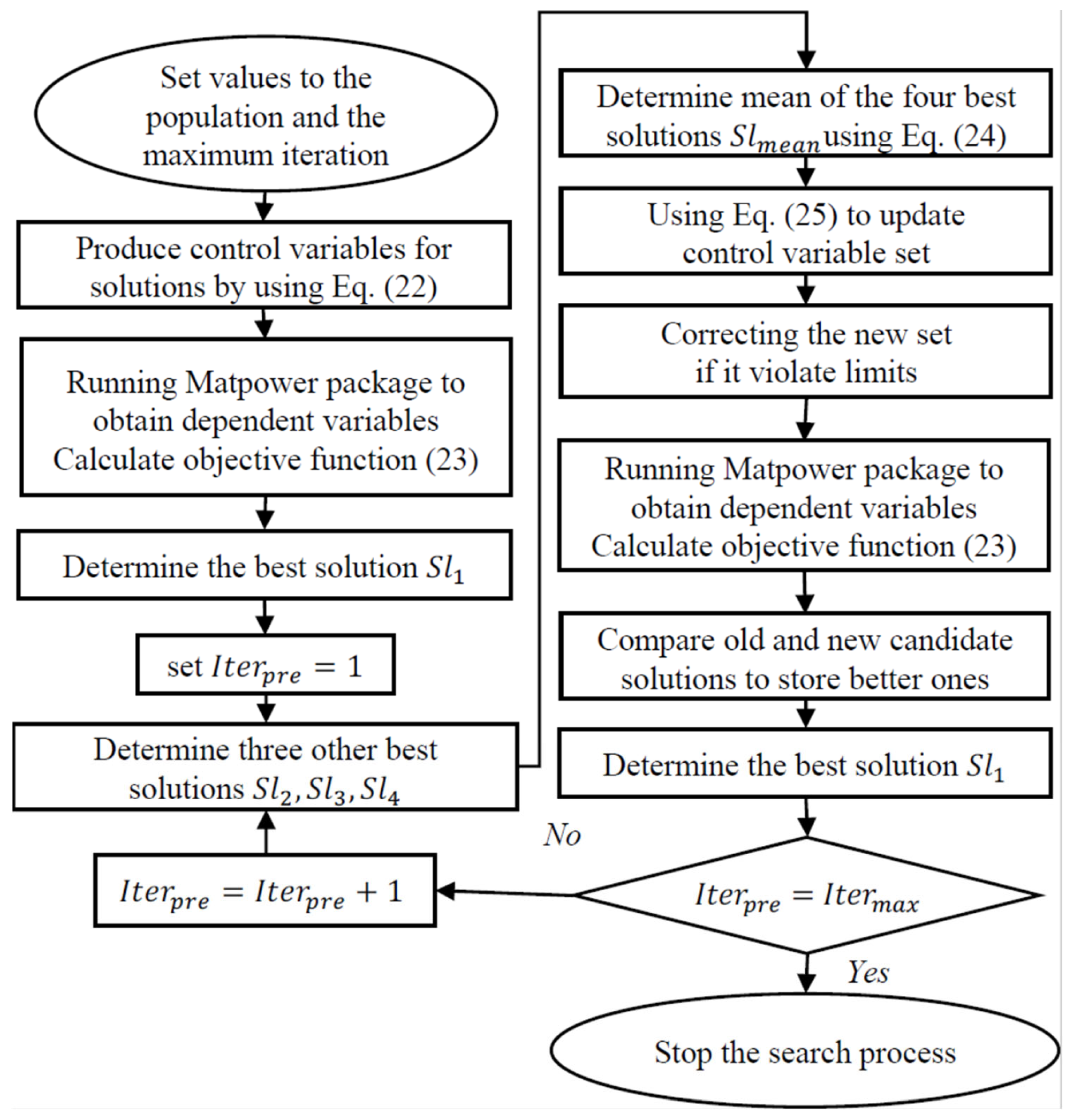
3. The Application of EO for the Placement of SVC, TCSC, and RPPs
3.1. Population Initialization
3.2. EO’s Solution-Updating Process
3.3. Computation Process Summary
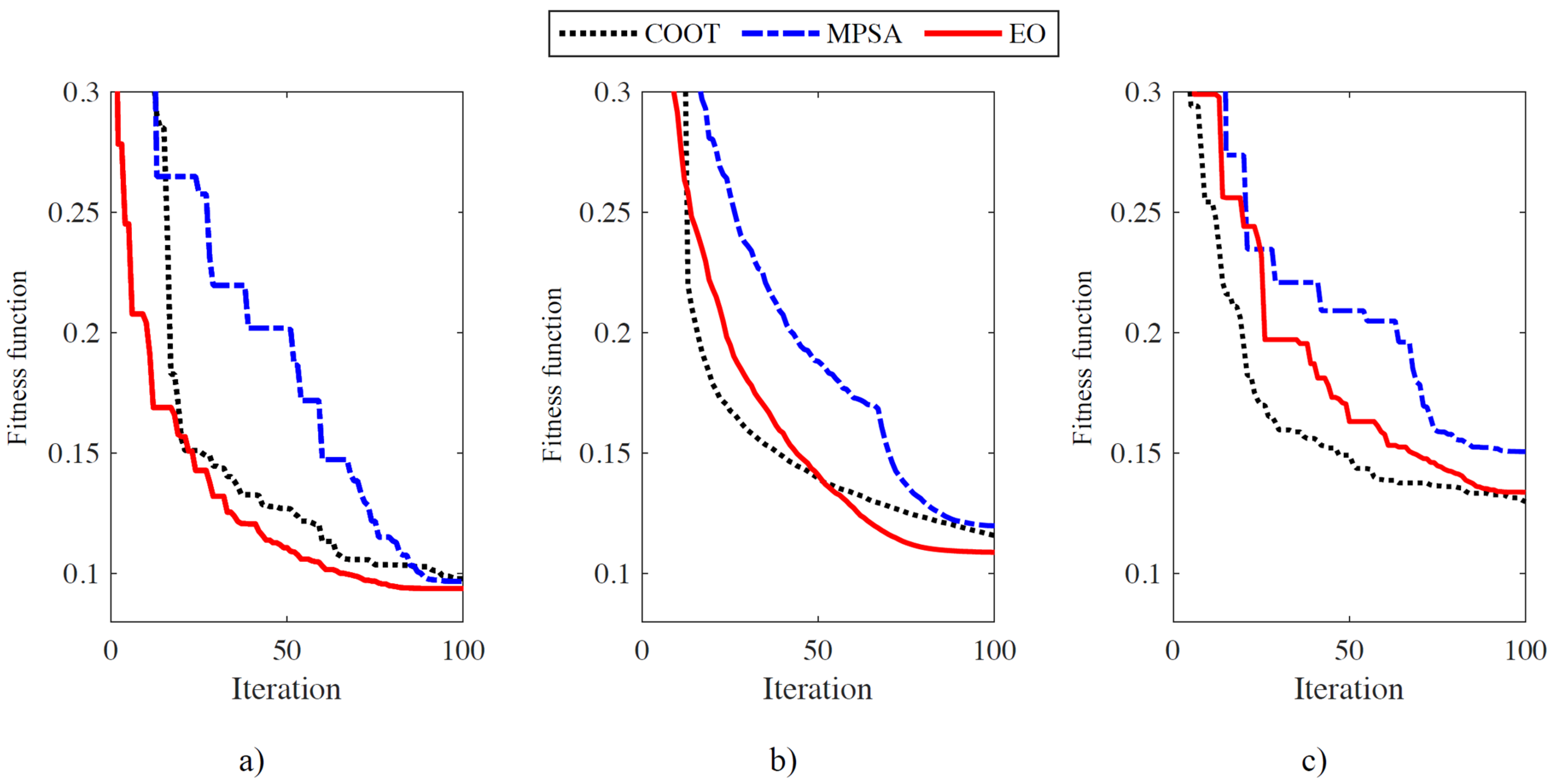
4. Results and Discussions
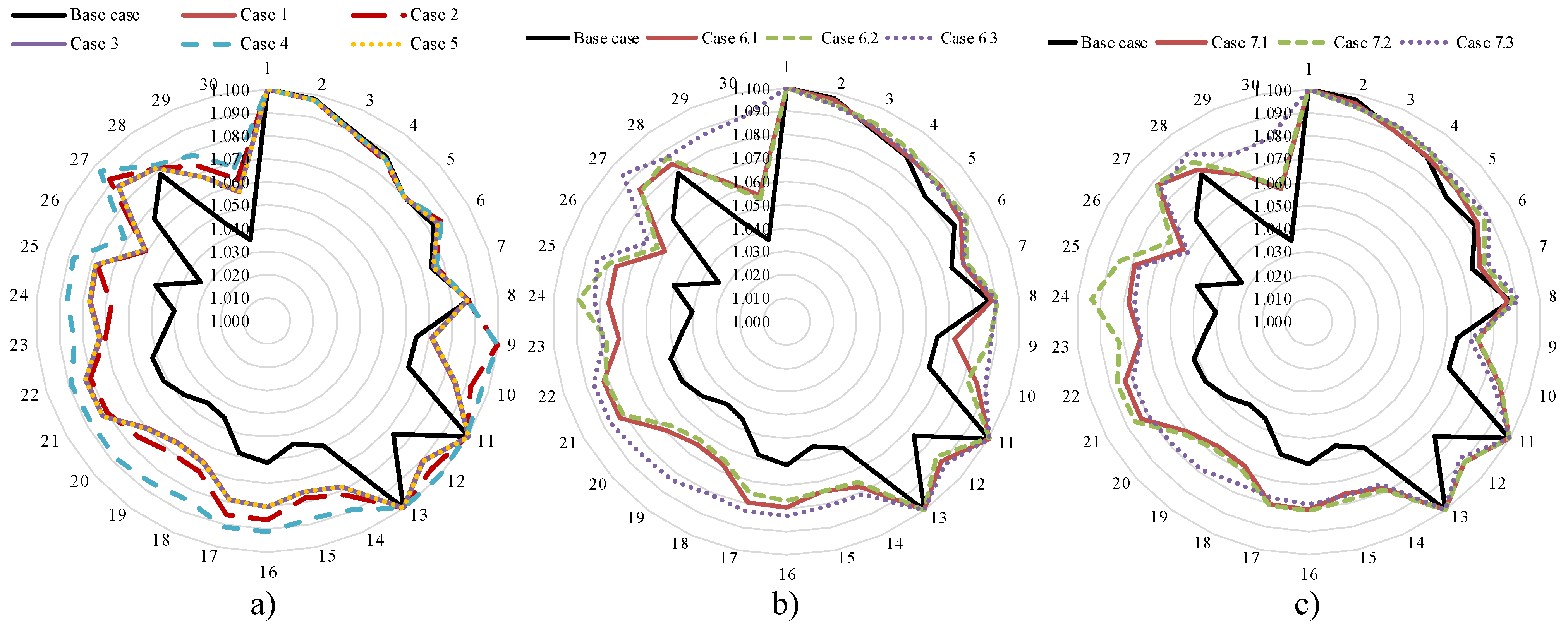
4.1. Result Comparisons for Study Cases Without FACTS and Renewable Power Sources
4.2. Study Cases with FACTS and Renewable Power Sources
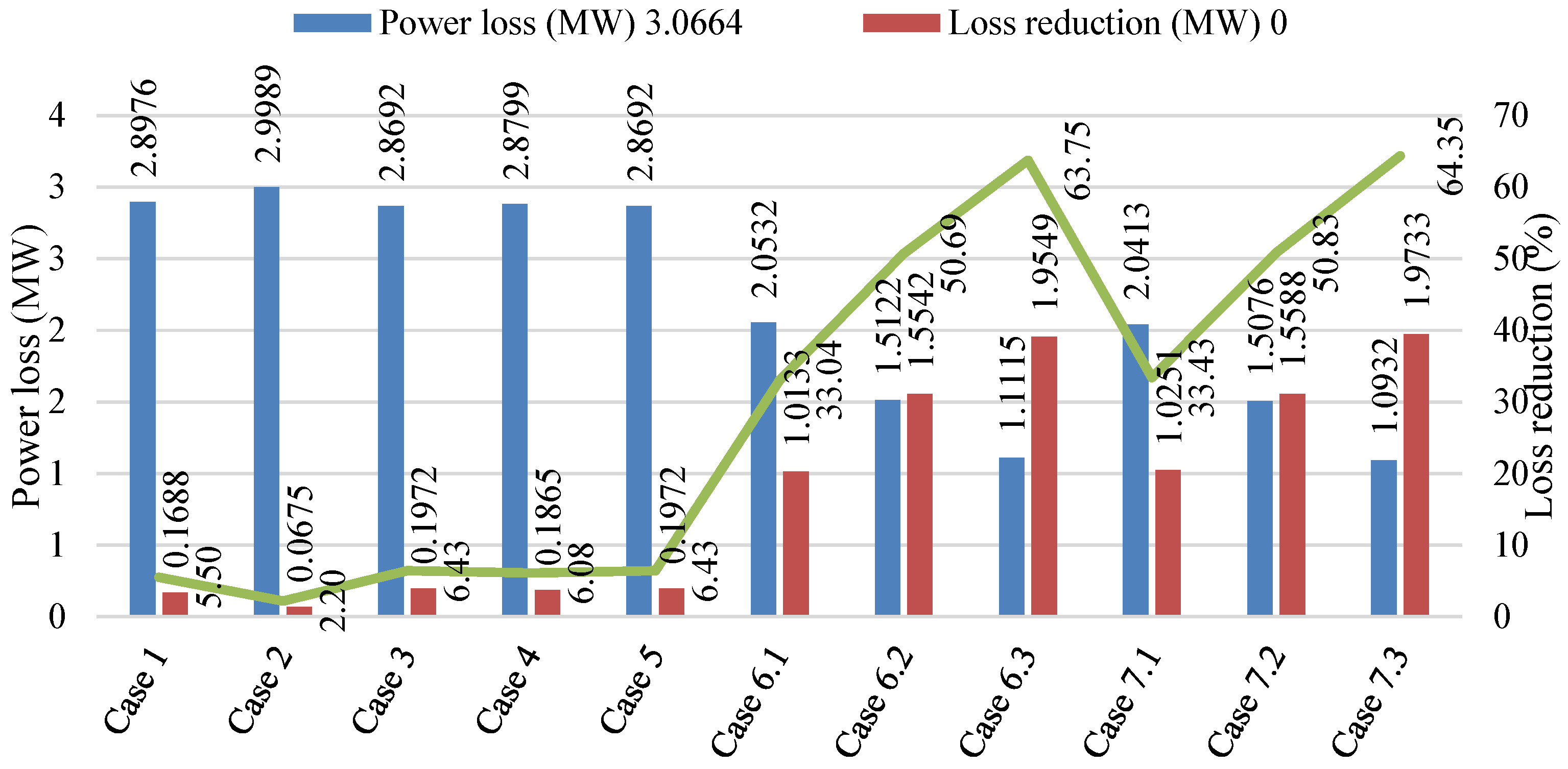
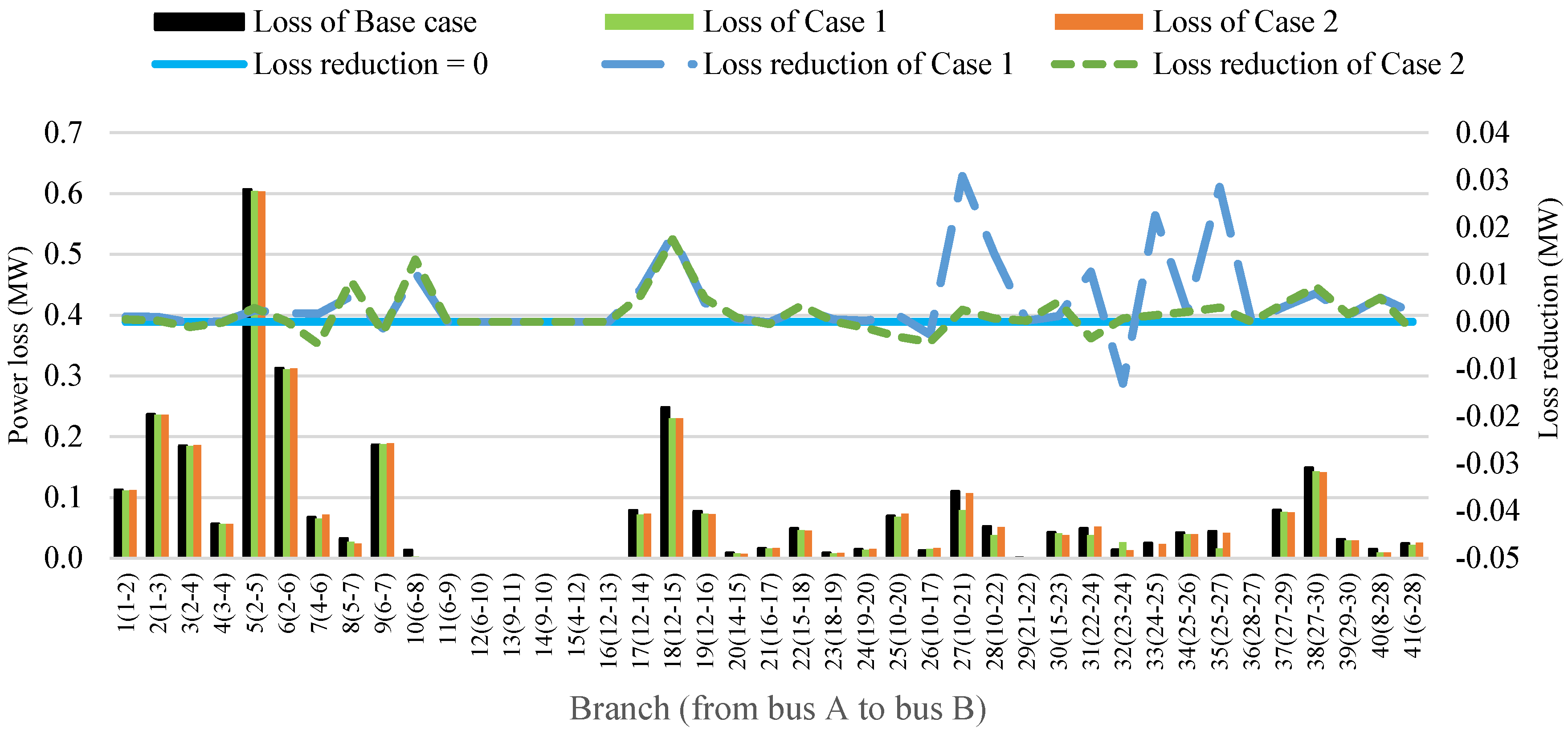
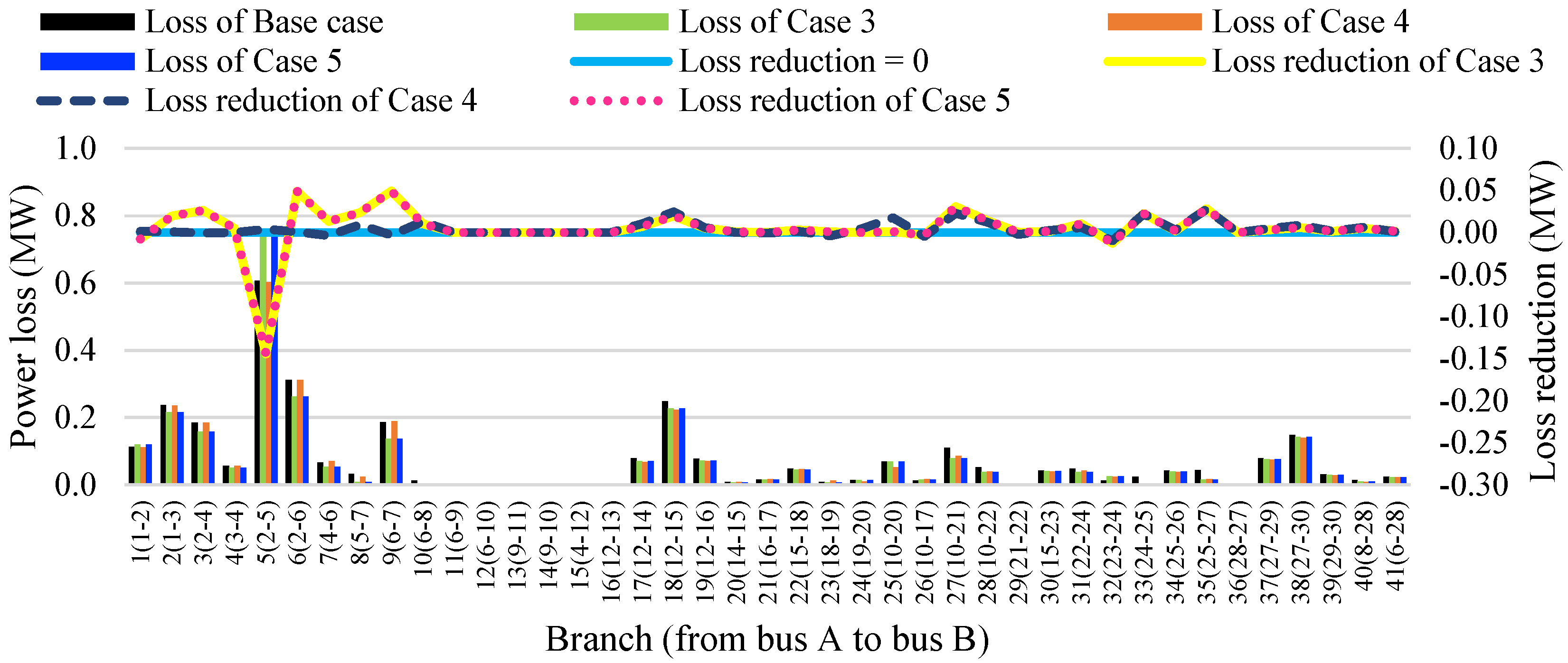
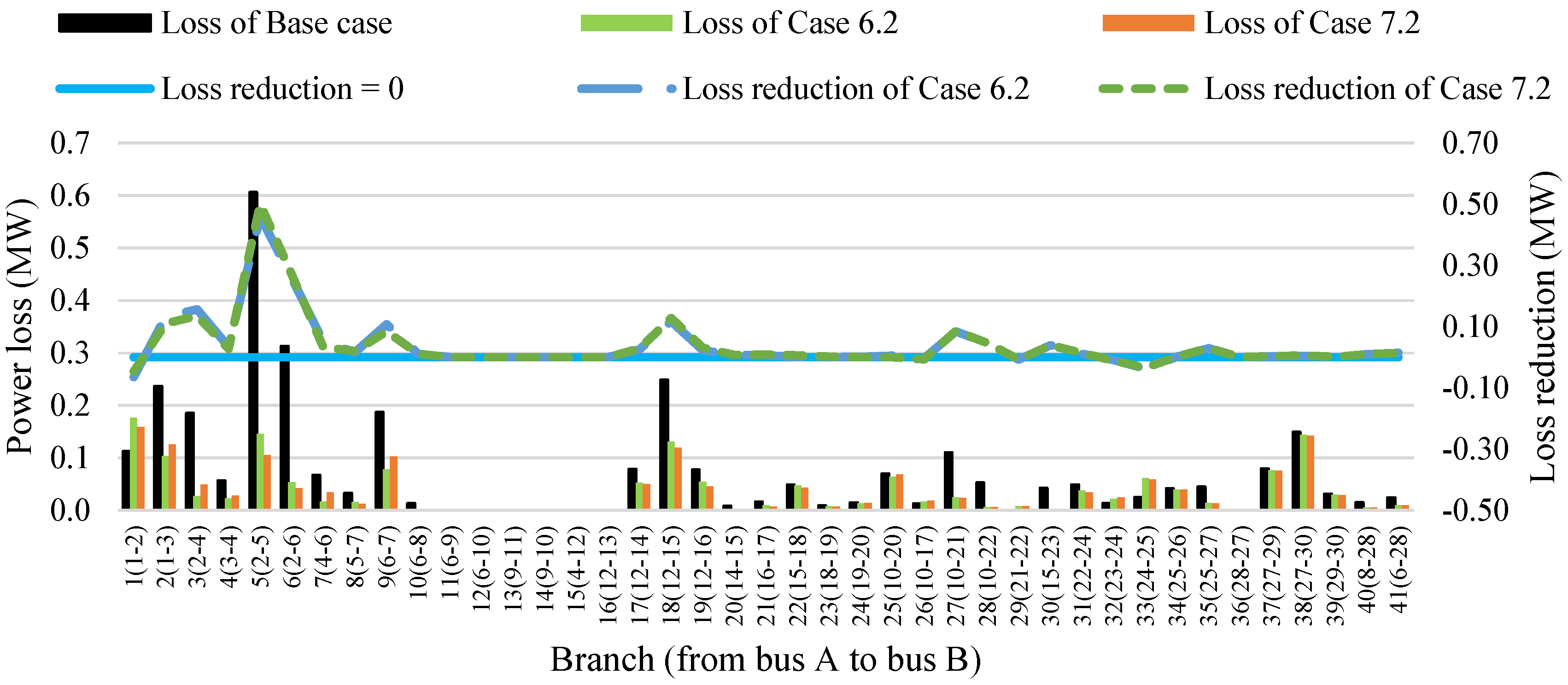
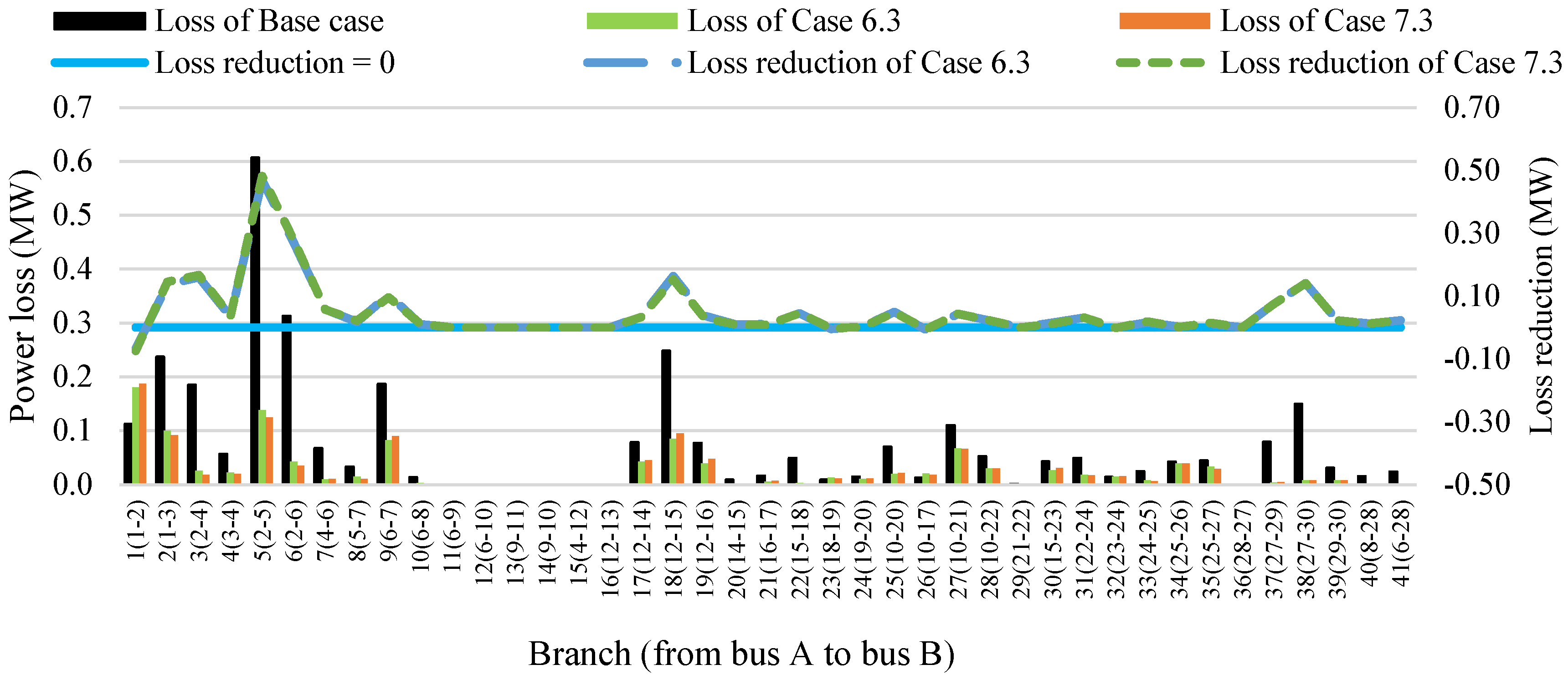
4.3. The Impact of FACTS and RPPs on the Power Loss
- (1)
- Case 7.1 used smaller SVCs and TCSCs but the same WPP as Case 6.1.
- (2)
- Case 7.2 used a smaller power of SVCs and wind power plants but a little greater TCSC than Case 6.2.
- (3)
- Case 7.3 used the same wind power, a smaller TCSC, and smaller SVCs than Case 6.3.
5. Conclusions
- The power loss of the base case is 3.066 MW, and the best loss is 2.869 MW for Cases 3 and 5 with two SVCs and one TCSC, in which Case 3 optimizes two SVCs in the first stage and one TCSC in the second stage, and Case 5 optimizes two SVCs and one TCSC simultaneously. When applying the obtained solution of Case 5 and optimizing the placement of one, two, and three WPPs, the power loss is, respectively, 2.053, 1.512, and 1.112 MW. When optimizing two SVCs, one TCSC, and WPPs simultaneously, the power loss is, respectively, 2.041, 1.508, and 1.093 MW for one, two, and three WPPs. When combining two SVCs, one TCSC, and wind power plants, the power loss is 2.041, 1.508, and 1.093 MW for one, two, and three WPPs. So, the installation of FACTS can reduce loss from 3.066 to 2.869 MW, and this loss can be reduced from 2.869 MW to 2.041 MW for one WPP, 1.508 MW for two WPPs, and 1.093 MW for three WPPs. The installation of more WPPs can reduce losses more significantly.
- Cases 7.1, 7.2, and 7.3 reach smaller losses than Cases 6.1, 6.2, and 6.3 by 0.0118 MW, about 0.59%, 0.0046 MW, about 0.3%, and 0.0004 MW, about 0.04%, respectively. Thus, the simultaneous placement of two SVCs, one TCSC, and wind power plants is more robust than the separated placement for every period.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameters | Single Fuel-Without VPES | Single Fuel-With VPES | Multiple Fuels | Power Loss | VD |
|---|---|---|---|---|---|
| Ps2 (Bus 2) MW | 48.890 | 44.153 | 55.000 | 80.000 | 43.339 |
| Ps3 (Bus 5) MW | 21.348 | 18.566 | 23.512 | 50.000 | 31.385 |
| Ps4 (Bus 8) MW | 21.010 | 10.001 | 34.158 | 35.000 | 30.055 |
| Ps5 (Bus 11) MW | 11.900 | 10.000 | 17.767 | 29.981 | 29.978 |
| Ps6 (Bus 13) MW | 12.000 | 12.006 | 19.599 | 39.868 | 13.109 |
| Vs1 (Bus 1) pu | 1.100 | 1.100 | 1.100 | 1.100 | 1.025 |
| Vs2 (Bus 2) pu | 1.087 | 1.079 | 1.086 | 1.097 | 1.017 |
| Vs3 (Bus 5) pu | 1.062 | 1.051 | 1.058 | 1.082 | 1.017 |
| Vs4 (Bus 8) pu | 1.070 | 1.060 | 1.069 | 1.090 | 1.000 |
| Vs5 (Bus 11) pu | 1.098 | 1.088 | 1.053 | 1.097 | 1.059 |
| Vs6 (Bus 13) pu | 1.100 | 1.100 | 1.098 | 1.100 | 0.999 |
| Tap1 (Bus 6–9)% | 4.759 | 4.023 | 4.302 | 4.744 | 4.746 |
| Tap2 (Bus 6–10)% | 4.852 | 4.639 | 4.607 | 2.367 | 0.078 |
| Tap3 (Bus 4–12)% | 4.086 | 4.635 | 4.042 | 4.429 | 4.951 |
| Tap4 (Bus 27–28)% | 4.941 | 4.970 | 0.705 | 4.878 | 0.038 |
| Qc1 (Bus 10) MVar | 4.951 | 4.719 | 0.560 | 4.338 | 4.969 |
| Qc2 (Bus 12) MVar | 4.976 | 3.815 | 0.103 | 5.000 | 4.697 |
| Qc3 (Bus 15) MVar | 3.336 | 4.682 | 4.637 | 3.279 | 4.974 |
| Qc4 (Bus 17) MVar | 4.920 | 4.782 | 0.002 | 4.997 | 4.985 |
| Qc5 (Bus 20) MVar | 2.244 | 4.224 | 0.322 | 2.755 | 2.303 |
| Qc6 (Bus 21) MVar | 1.048 | 1.077 | 1.098 | 1.012 | 1.079 |
| Qc7 (Bus 23) MVar | 0.901 | 0.900 | 0.936 | 0.951 | 0.904 |
| Qc8 (Bus 24) MVar | 0.983 | 1.020 | 1.069 | 0.984 | 0.955 |
| Qc9 (Bus 29) MVar | 0.964 | 0.992 | 0.988 | 0.979 | 0.964 |
| Parameters | Case Base | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 |
|---|---|---|---|---|---|---|
| Ps2 (Bus 2) MW | 80.0000 | 80.0000 | 79.9999 | 80.0000 | 79.9996 | 80.0000 |
| Ps3 (Bus 5) MW | 50.0000 | 50.0000 | 50.0000 | 50.0000 | 50.0000 | 50.0000 |
| Ps4 (Bus 8) MW | 35.0000 | 35.0000 | 35.0000 | 35.0000 | 35.0000 | 35.0000 |
| Ps5 (Bus 11) MW | 30.0000 | 30.0000 | 30.0000 | 30.0000 | 30.0000 | 30.0000 |
| Ps6 (Bus 13) MW | 40.0000 | 40.0000 | 40.0000 | 40.0000 | 40.0000 | 40.0000 |
| Vs1 (Bus 1) pu | 1.1000 | 1.1000 | 1.1000 | 1.1000 | 1.1000 | 1.1000 |
| Vs2 (Bus 2) pu | 1.0976 | 1.0976 | 1.0976 | 1.0975 | 1.0976 | 1.0975 |
| Vs3 (Bus 5) pu | 1.0796 | 1.0797 | 1.0799 | 1.0798 | 1.0799 | 1.0798 |
| Vs4 (Bus 8) pu | 1.0872 | 1.0869 | 1.0868 | 1.0868 | 1.0868 | 1.0868 |
| Vs5 (Bus 11) pu | 1.1000 | 1.1000 | 1.0995 | 1.1000 | 1.0993 | 1.1000 |
| Vs6 (Bus 13) pu | 1.1000 | 1.1000 | 1.1000 | 1.1000 | 1.1000 | 1.1000 |
| Tap1 (Bus 6–9)% | 1.0472 | 1.0649 | 1.0636 | 1.0637 | 1.0482 | 1.0637 |
| Tap2 (Bus 6–10)% | 0.9000 | 0.9000 | 0.9000 | 0.9000 | 0.9165 | 0.9000 |
| Tap3 (Bus 4–12)% | 1.0190 | 0.9844 | 0.9683 | 0.9837 | 0.9664 | 0.9837 |
| Tap4 (Bus 27–28)% | 0.9785 | 0.9733 | 0.9592 | 0.9729 | 0.9651 | 0.9729 |
| SVC1 (Location; size) | - | 21; 12.7030 | - | 21; 12.7030 | 19; 5.207 | 21; 12.6822 |
| SVC2 (Location; size) | - | 24; 8.8750 | - | 24; 8.8750 | 24; 9.548 | 24; 8.8682 |
| TCSC (Branch; reactance) | - | - | 13; 0.208 | 5; 0.0541 | 13; 0.208 | 5; 0.0541 |
| Parameters | Case 6.1 | Case 6.2 | Case 6.3 | Case 7.1 | Case 7.2 | Case 7.3 |
|---|---|---|---|---|---|---|
| Ps2 (Bus 2) MW | 50.4659 | 25.9217 | 23.438 | 50.4413 | 25.9076 | 20.0030 |
| Ps3 (Bus 5) MW | 50 | 50 | 50 | 50.0000 | 50.0000 | 50.0000 |
| Ps4 (Bus 8) MW | 35 | 35 | 35 | 35.0000 | 35.0000 | 35.0000 |
| Ps5 (Bus 11) MW | 30 | 30 | 29.9897 | 30.0000 | 30.0000 | 30.0000 |
| Ps6 (Bus 13) MW | 39.9857 | 40 | 33.0904 | 40.0000 | 40.0000 | 36.5081 |
| Vs1 (Bus 1) pu | 1.1 | 1.1 | 1.1 | 1.1000 | 1.1000 | 1.1000 |
| Vs2 (Bus 2) pu | 1.0968 | 1.0952 | 1.0947 | 1.0961 | 1.0948 | 1.0947 |
| Vs3 (Bus 5) pu | 1.0877 | 1.0872 | 1.0864 | 1.0856 | 1.0859 | 1.0871 |
| Vs4 (Bus 8) pu | 1.0882 | 1.0907 | 1.09 | 1.0863 | 1.0892 | 1.0911 |
| Vs5 (Bus 11) pu | 1.1 | 1.0998 | 1.1 | 1.1000 | 1.1000 | 1.1000 |
| Vs6 (Bus 13) pu | 1.1 | 1.1 | 1.1 | 1.1000 | 1.1000 | 1.1000 |
| Tap1 (Bus 6–9)% | 1.0634 | 1.0012 | 1.0125 | 1.0584 | 1.0641 | 1.0728 |
| Tap2 (Bus 6–10)% | 0.9 | 0.9949 | 0.9495 | 0.9000 | 0.9000 | 0.9000 |
| Tap3 (Bus 4–12)% | 0.9895 | 0.9969 | 0.983 | 0.9853 | 0.9876 | 0.9930 |
| Tap4 (Bus 27–28)% | 0.977 | 0.9819 | 0.9781 | 0.9719 | 0.9760 | 0.9876 |
| SVC1 (Location; size) | 21; 12.6822 | 21; 12.6822 | 21; 12.6822 | 21; 12.447 | 21; 11.832 | 24; 8.581 |
| SVC2 (Location; size) | 24; 8.8682 | 24; 8.8682 | 24; 8.8682 | 24; 8.832 | 24; 8.575 | 21; 11.141 |
| TCSC (Branch; reactance) | 5; 0.0541 | 5; 0.0541 | 5; 0.0541 | 7; 0.0508 | 7; 0.0559 | 5; 0.0445 |
| WPP1 (bus; power MW) | 5; 30 | 5; 30 | 5; 30 | 5; 30 | 5; 30 | 5; 30 |
| WPP2 (bus; power MW) | - | 24; 24 | 19; 20 | - | 24; 24 | 19; 20 |
| WPP3 (bus; power MW) | - | - | 30; 14 | - | - | 30; 14 |
References
- Venkatesan, R.; Kumar, C.; Balamurugan, C.R. FOPIR Controller for TCSC Based Gate Turn-off Switches to Control Power Quality in Transmission Line. Electr. Eng. 2024, 106, 4603–4616. [Google Scholar] [CrossRef]
- Rana, A.S.; Bajaj, M.; Gairola, S. Optimal Power Flow Solution in Smart Grid Environment Using SVC and TCSC; IntechOpen: London, UK, 2019; ISBN 1789841062. [Google Scholar]
- Farhat, M.; Kamel, S.; Atallah, A.M.; Hassan, M.H.; Agwa, A.M. ESMA-OPF: Enhanced Slime Mould Algorithm for Solving Optimal Power Flow Problem. Sustainability 2022, 14, 2305. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Vo, D.N.; Van Tran, H.; Van Dai, L. Optimal Dispatch of Reactive Power Using Modified Stochastic Fractal Search Algorithm. Complexity 2019, 2019, 4670820. [Google Scholar] [CrossRef]
- Devarapalli, R.; Venkateswara Rao, B.; Dey, B.; Vinod Kumar, K.; Malik, H.; García Márquez, F.P. An Approach to Solve OPF Problems Using a Novel Hybrid Whale and Sine Cosine Optimization Algorithm. J. Intell. Fuzzy Syst. 2022, 42, 957–967. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Hasanien, H.M.; Ginidi, A.R. An Improved Heap Optimization Algorithm for Efficient Energy Management Based Optimal Power Flow Model. Energy 2022, 250, 123795. [Google Scholar] [CrossRef]
- Su, H.; Wei, H.; Wei, X.; Wang, G.; Zhang, Y.; Wang, R. Long-Term Optimal Operation of the Cascade Hydro-Wind-Photovoltaic Hybrid System Considering Transmission Section Constraints. Math. Probl. Eng. 2023, 2023, 8484804. [Google Scholar] [CrossRef]
- Kumari, M.S.; Maheswarapu, S. Enhanced Genetic Algorithm Based Computation Technique for Multi-Objective Optimal Power Flow Solution. Int. J. Electr. Power Energy Syst. 2010, 32, 736–742. [Google Scholar] [CrossRef]
- Surender Reddy, S.; Bijwe, P.R.; Abhyankar, A.R. Faster Evolutionary Algorithm Based Optimal Power Flow Using Incremental Variables. Int. J. Electr. Power Energy Syst. 2014, 54, 198–210. [Google Scholar] [CrossRef]
- Reddy, S.S.; Bijwe, P.R. Efficiency Improvements in Meta-Heuristic Algorithms to Solve the Optimal Power Flow Problem. Int. J. Emerg. Electr. Power Syst. 2016, 17, 631–647. [Google Scholar] [CrossRef]
- Abido, M.A. Optimal Power Flow Using Particle Swarm Optimization. Int. J. Electr. Power Energy Syst. 2002, 24, 563–571. [Google Scholar] [CrossRef]
- Niknam, T.; Narimani, M.R.; Aghaei, J.; Azizipanah-Abarghooee, R. Improved Particle Swarm Optimisation for Multi-Objective Optimal Power Flow Considering the Cost, Loss, Emission and Voltage Stability Index. IET Gener. Transm. Distrib. 2012, 6, 515–527. [Google Scholar] [CrossRef]
- Vaisakh, K.; Srinivas, L.R.; Meah, K. Genetic Evolving Ant Direction Particle Swarm Optimization Algorithm for Optimal Power Flow with Non-Smooth Cost Functions and Statistical Analysis. Appl. Soft Comput. 2013, 13, 4579–4593. [Google Scholar] [CrossRef]
- Vo, D.N.; Schegner, P. An Improved Particle Swarm Optimization for Optimal Power Flow. In Meta-Heuristics Optimization Algorithms in Engineering, Business, Economics, and Finance; IGI Global: New York, NY, USA, 2013; pp. 1–40. [Google Scholar]
- Roberge, V.; Tarbouchi, M.; Okou, F. Optimal Power Flow Based on Parallel Metaheuristics for Graphics Processing Units. Electr. Power Syst. Res. 2016, 140, 344–353. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; Hasanien, H.M. Single and Multi-Objective Optimal Power Flow Using Grey Wolf Optimizer and Differential Evolution Algorithms. Electr. Power Compon. Syst. 2015, 43, 1548–1559. [Google Scholar] [CrossRef]
- Abou El Ela, A.A.; Abido, M.A.; Spea, S.R. Optimal Power Flow Using Differential Evolution Algorithm. Electr. Power Syst. Res. 2010, 80, 878–885. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Chattopadhyay, P.K. Application of Biogeography-Based Optimisation to Solve Different Optimal Power Flow Problems. IET Gener. Transm. Distrib. 2011, 5, 70–80. [Google Scholar] [CrossRef]
- Ramesh Kumar, A.; Premalatha, L. Optimal Power Flow for a Deregulated Power System Using Adaptive Real Coded Biogeography-Based Optimization. Int. J. Electr. Power Energy Syst. 2015, 73, 393–399. [Google Scholar] [CrossRef]
- Nayak, M.R.; Nayak, C.K.; Rout, P.K. Application of Multi-Objective Teaching Learning Based Optimization Algorithm to Optimal Power Flow Problem. Procedia Technol. 2012, 6, 255–264. [Google Scholar] [CrossRef]
- Daryani, N.; Hagh, M.T.; Teimourzadeh, S. Adaptive Group Search Optimization Algorithm for Multi-Objective Optimal Power Flow Problem. Appl. Soft Comput. 2016, 38, 1012–1024. [Google Scholar] [CrossRef]
- Younis, A.; Belabbes, F.; Cotfas, P.A.; Cotfas, D.T. Utilizing the Honeybees Mating-Inspired Firefly Algorithm to Extract Parameters of the Wind Speed Weibull Model. Forecasting 2024, 6, 357–377. [Google Scholar] [CrossRef]
- Lashkar Ara, A.; Kazemi, A.; Gahramani, S.; Behshad, M. Optimal Reactive Power Flow Using Multi-Objective Mathematical Programming. Sci. Iran. 2012, 19, 1829–1836. [Google Scholar] [CrossRef]
- Duman, S.; Güvenç, U.; Sönmez, Y.; Yörükeren, N. Optimal Power Flow Using Gravitational Search Algorithm. Energy Convers. Manag. 2012, 59, 86–95. [Google Scholar] [CrossRef]
- Rezaei Adaryani, M.; Karami, A. Artificial Bee Colony Algorithm for Solving Multi-Objective Optimal Power Flow Problem. Int. J. Electr. Power Energy Syst. 2013, 53, 219–230. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Ghanbarian, M.M.; Gharibzadeh, M.; Azizi Vahed, A. Multi-Objective Optimal Power Flow Considering the Cost, Emission, Voltage Deviation and Power Losses Using Multi-Objective Modified Imperialist Competitive Algorithm. Energy 2014, 78, 276–289. [Google Scholar] [CrossRef]
- El-Hana Bouchekara, H.R.; Abido, M.A.; Chaib, A.E. Optimal Power Flow Using an Improved Electromagnetism-like Mechanism Method. Electr. Power Compon. Syst. 2016, 44, 434–449. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.H.; Chaib, A.E.; Abido, M.A.; El-Sehiemy, R.A. Optimal Power Flow Using an Improved Colliding Bodies Optimization Algorithm. Appl. Soft Comput. 2016, 42, 119–131. [Google Scholar] [CrossRef]
- Ladumor, D.P.; Trivedi, I.N.; Bhesdadiya, R.H.; Jangir, P. A Grey Wolf Optimizer Algorithm for Voltage Stability Enhancement. In Proceedings of the 2017 Third International Conference on Advances in Electrical, Electronics, Information, Communication and Bio-Informatics (AEEICB), Chennai, India, 27–28 February 2017; pp. 278–282. [Google Scholar]
- Mohamed, A.-A.A.; Mohamed, Y.S.; El-Gaafary, A.A.M.; Hemeida, A.M. Optimal Power Flow Using Moth Swarm Algorithm. Electr. Power Syst. Res. 2017, 142, 190–206. [Google Scholar] [CrossRef]
- Nguyen, T.T. A High Performance Social Spider Optimization Algorithm for Optimal Power Flow Solution with Single Objective Optimization. Energy 2019, 171, 218–240. [Google Scholar] [CrossRef]
- Hassan, M.H.; Kamel, S.; Selim, A.; Khurshaid, T.; Domínguez-García, J.L. A Modified Rao-2 Algorithm for Optimal Power Flow Incorporating Renewable Energy Sources. Mathematics 2021, 9, 1532. [Google Scholar] [CrossRef]
- Ebeed, M.; Abdelmotaleb, M.A.; Khan, N.H.; Jamal, R.; Kamel, S.; Hussien, A.G.; Zawbaa, H.M.; Jurado, F.; Sayed, K. A Modified Artificial Hummingbird Algorithm for Solving Optimal Power Flow Problem in Power Systems. Energy Rep. 2024, 11, 982–1005. [Google Scholar] [CrossRef]
- Nkan, I.; Obi, P.; Natala, H.; Okoro, O. Investigation of the Transfer Capability of the Nigerian 330 KV, 58-Bus Power System Network Using FACTS Devices. Elektr. J. Electr. Eng. 2023, 22, 53–62. [Google Scholar] [CrossRef]
- Ibrahim, N.M.A.; El-said, E.A.; Attia, H.E.M.; Hemade, B.A. Enhancing Power System Stability: An Innovative Approach Using Coordination of FOPID Controller for PSS and SVC FACTS Device with MFO Algorithm. Electr. Eng. 2024, 106, 2265–2283. [Google Scholar] [CrossRef]
- Gupta, S.K.; Mallik, S.K. Enhancement in Voltage Stability Using FACTS Devices Under Contingency Conditions. J. Oper. Autom. Power Eng. 2024, 12, 365–378. [Google Scholar] [CrossRef]
- Daealhaq, H.M.; kfajey, Y.F.; Tukkee, A.S. Power Loss Reduction and Voltage Profile Improvement Using Optimal Placement of FACTS Devices. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1067, 012128. [Google Scholar] [CrossRef]
- Marouani, I.; Guesmi, T.; Alshammari, B.M.; Alqunun, K.; Alshammari, A.S.; Albadran, S.; Hadj Abdallah, H.; Rahmani, S. Optimized FACTS Devices for Power System Enhancement: Applications and Solving Methods. Sustainability 2023, 15, 9348. [Google Scholar] [CrossRef]
- Ćalasan, M.; Konjić, T.; Kecojević, K.; Nikitović, L. Optimal Allocation of Static Var Compensators in Electric Power Systems. Energies 2020, 13, 3219. [Google Scholar] [CrossRef]
- Dandotia, A.; Gupta, M.K.; Banerjee, M.K.; Singh, S.K.; Đurin, B.; Dogančić, D.; Kranjčić, N. Optimal Placement and Size of SVC with Cost-Effective Function Using Genetic Algorithm for Voltage Profile Improvement in Renewable Integrated Power Systems. Energies 2023, 16, 2637. [Google Scholar] [CrossRef]
- Okelola, M.O.; Ayanlade, S.O.; Ogunwole, E.I. Particle Swarm Optimization for Optimal Allocation of STATCOM on Transmission Network. J. Phys. Conf. Ser. 2021, 1880, 012035. [Google Scholar] [CrossRef]
- Khan, N.H.; Wang, Y.; Tian, D.; Jamal, R.; Kamel, S.; Ebeed, M. Optimal Siting and Sizing of SSSC Using Modified Salp Swarm Algorithm Considering Optimal Reactive Power Dispatch Problem. IEEE Access 2021, 9, 49249–49266. [Google Scholar] [CrossRef]
- Mostafa, A.; Ebeed, M.; Kamel, S.; Abdel-Moamen, M.A. Optimal Power Flow Solution Using Levy Spiral Flight Equilibrium Optimizer with Incorporating CUPFC. IEEE Access 2021, 9, 69985–69998. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Mohammadi, F. Optimal Placement of TCSC for Congestion Management and Power Loss Reduction Using Multi-Objective Genetic Algorithm. Sustainability 2020, 12, 2813. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Le, C.K.; Phan, M.T.; Nguyen, T.T. COOT Bird Behavior-Based Optimization Algorithm for Optimal Placement of Thyristor Controlled Series Compensator Devices in Transmission Power Networks. Adv. Electr. Electron. Eng. 2023, 21, 171–183. [Google Scholar] [CrossRef]
- Rambabu, M.; Kumar, G.V.N.; Sobhan, P.V.S. Optimal Power Flow with Renewable Energy Resources Using Static VAR Compensator and Grey Wolf Optimisation. Int. J. Intell. Enterp. 2022, 9, 357. [Google Scholar] [CrossRef]
- Rezaeian-Marjani, S.; Galvani, S.; Talavat, V.; Farhadi-Kangarlu, M. Optimal Allocation of D-STATCOM in Distribution Networks Including Correlated Renewable Energy Sources. Int. J. Electr. Power Energy Syst. 2020, 122, 106178. [Google Scholar] [CrossRef]
- Yang, N.-C.; Chang, Z.-H. Optimal Capacity and Location for STATCOM with Seasonal Wind Power Prediction Using C-Vine Copula. Mathematics 2023, 11, 2815. [Google Scholar] [CrossRef]
- Basu, J.B.; Dawn, S.; Saha, P.K.; Chakraborty, M.R.; Alsaif, F.; Alsulamy, S.; Ustun, T.S. Risk Mitigation & Profit Improvement of a Wind-Fuel Cell Hybrid System with TCSC Placement. IEEE Access 2023, 11, 39431–39447. [Google Scholar] [CrossRef]
- Faramarzi, Z.; Abazari, S.; Hoghoughi, S.; Abjadi, N.R. Improved Power System Dynamic Stability by DFIG in the Presence of SSSC Using Adaptive Nonlinear Multi-Input Backstepping. J. Oper. Autom. Power Eng. 2024, 12, 107–120. [Google Scholar]
- Rezaeian-Marjani, S.; Jalalat, S.M.; Tousi, B.; Galvani, S.; Talavat, V. A Probabilistic Approach for Optimal Operation of Wind-integrated Power Systems Including UPFC. IET Renew. Power Gener. 2023, 17, 706–724. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. A New Optimization Method Based on COOT Bird Natural Life Model. Expert Syst. Appl. 2021, 183, 115352. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium Optimizer: A Novel Optimization Algorithm. Knowl. Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A Nature-Inspired Metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- MATPOWER PGROGRAM. Available online: https://matpower.org/matpower-7-0-launch/ (accessed on 1 January 2025).
- Sharifzadeh, H. Handling Multiple-Fuel Options in Economic Dispatch of Thermal Power Plants Through a Tight Model Applying Indicator Variables. Int. Trans. Electr. Energy Syst. 2025, 2025, 1572487. [Google Scholar] [CrossRef]
- The Siemens SGT6-5000F Gas Turbine. Available online: https://www.siemens-energy.com/global/en/home/products-services/product/sgt6-5000f.html#/ (accessed on 20 September 2025).
- Shafik, M.B.; Chen, H.; Rashed, G.I.; El-Sehiemy, R.A. Adaptive Multi Objective Parallel Seeker Optimization Algorithm for Incorporating TCSC Devices into Optimal Power Flow Framework. IEEE Access 2019, 7, 36934–36947. [Google Scholar] [CrossRef]
- Le, L.D.; Vo, D.N.; Huynh, S.T.; Nguyen-Hoang, T.M.; Vasant, P. A Hybrid Differential Evolution and Harmony Search for Optimal Power Flow with FACTS Devices. Int. J. Oper. Res. Inf. Syst. 2020, 11, 39–65. [Google Scholar] [CrossRef]
- Mohamed, S.A.; Anwer, N.; Mahmoud, M.M. Solving Optimal Power Flow Problem for IEEE-30 Bus System Using a Developed Particle Swarm Optimization Method: Towards Fuel Cost Minimization. Int. J. Model. Simul. 2025, 45, 307–320. [Google Scholar] [CrossRef]
- Tran, V.H.; Truong, A.V.; Phan, T.M.; Nguyen, T.T. Minimize the One-Year Energy for Distribution Power Grids with Renewable Energies-Based Distributed Generators, Capacitors, and Soft Open Points. Int. J. Energy Res. 2025, 2025, 3457520. [Google Scholar] [CrossRef]
- Nagarajan, K.; Rajagopalan, A.; Bajaj, M.; Raju, V.; Blazek, V. Enhanced Wombat Optimization Algorithm for Multi-Objective Optimal Power Flow in Renewable Energy and Electric Vehicle Integrated Systems. Results Eng. 2025, 25, 103671. [Google Scholar] [CrossRef]
- Ali, I.I.; Al-kubragyi, S.S.A. Optimal Power Flow Solution Integrated with TCSC to Improved Voltage Profile and Losses Reduction in Power System Using Effective Intelligent Technique. Int. J. Intell. Eng. Syst. 2024, 17, 659–673. [Google Scholar] [CrossRef]

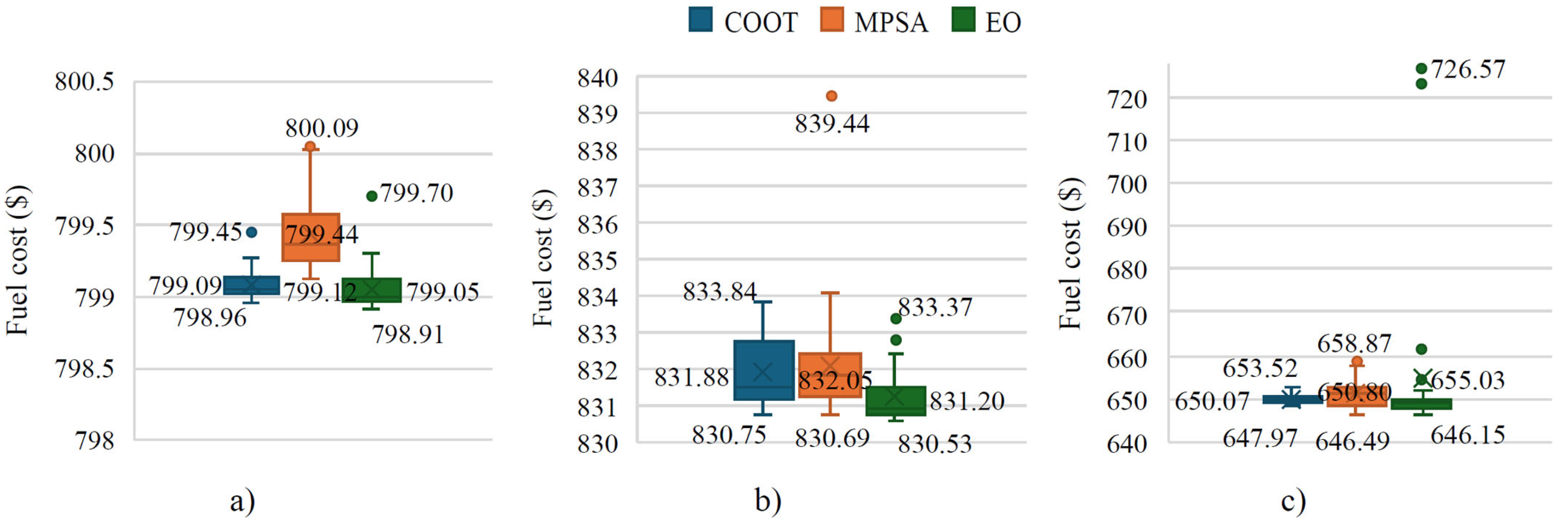

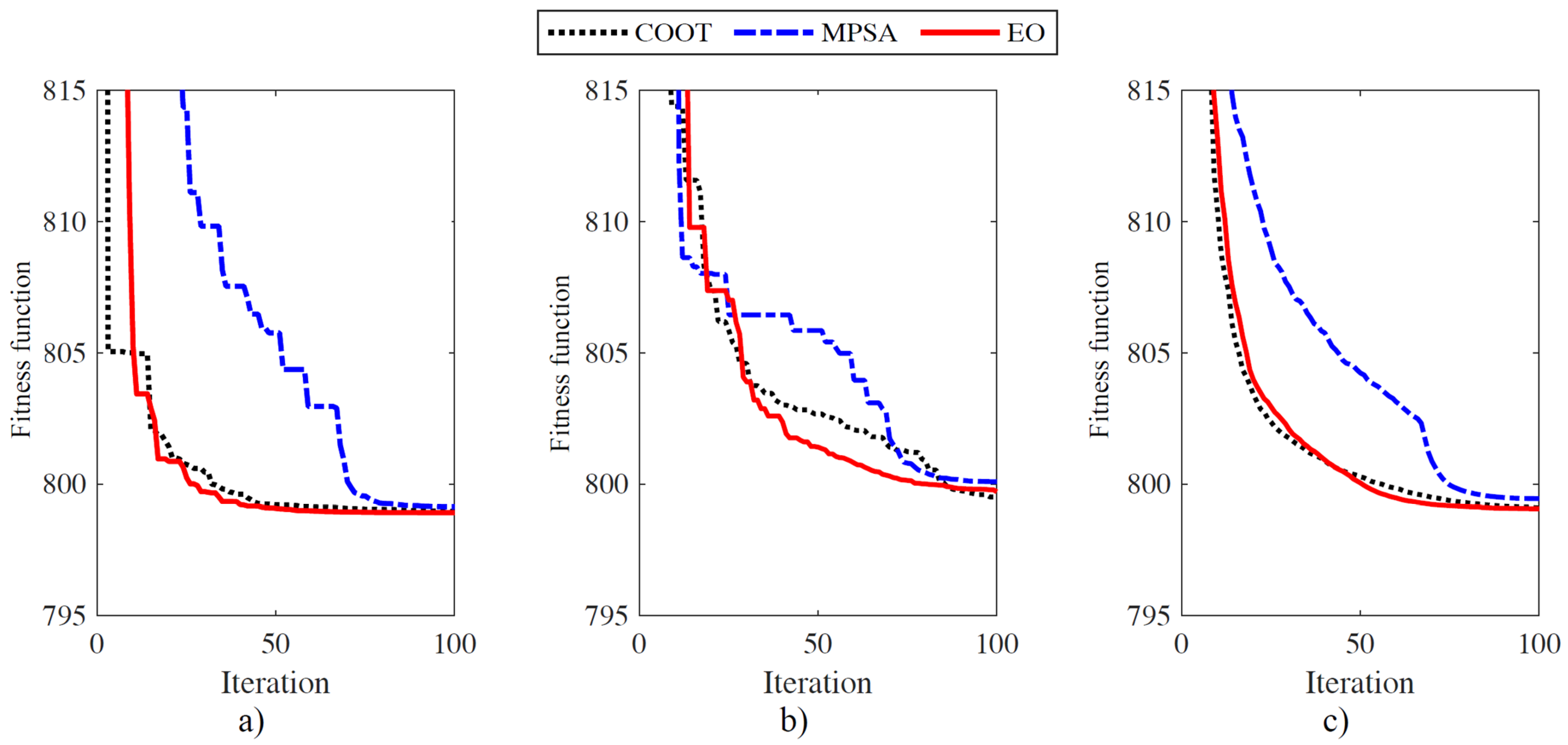
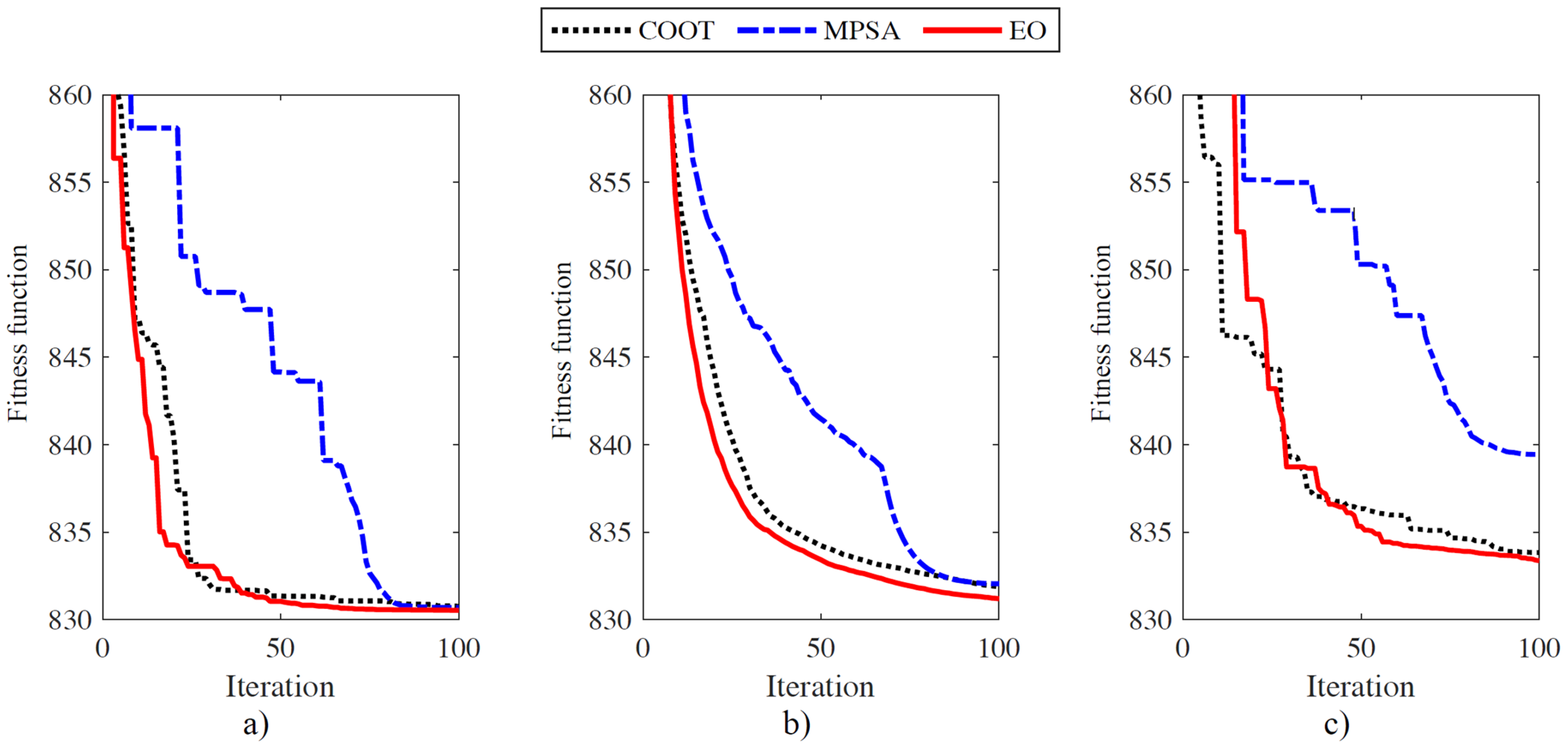

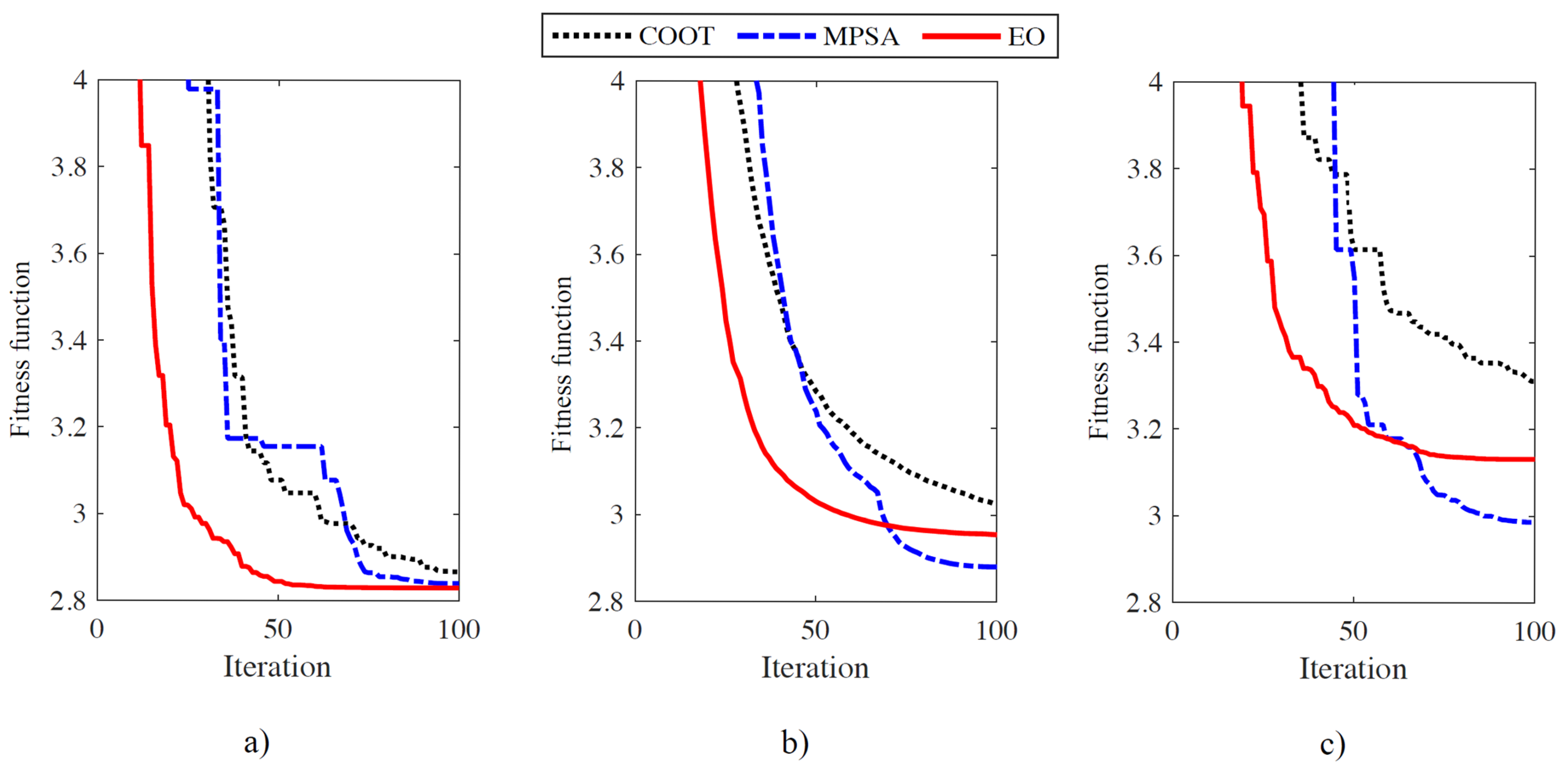

| Method | Single Fuel-Without VPES | Single Fuel-with VPES | Multiple Fuels |
|---|---|---|---|
| EGA [8] | 799.56 | - | - |
| IGA [9] | 799.56 | - | - |
| BIGA [10] | 800.0435 | - | - |
| CDE1 [16] | 801.23 | - | - |
| CDE2 [17] | 799.2891 | - | 650.8224 |
| WF-PSO [11] | 800.41 | - | 647.69 |
| AD-PSO [13] | 800.2276 | - | 629.4692 |
| GPUS-PSO [15] | 800.53 | - | - |
| BBO [18] | 799.1116 | - | 647.7437 |
| ABBO [19] | 800.5159 | - | - |
| TLBO [20] | 800.7257 | - | - |
| GSO [21] | 802.188 | - | - |
| AGSO [21] | 801.75 | - | - |
| MP [23] | 801.757 | - | - |
| GSA [24] | 798.675143 | - | 646.848066 |
| ABCA [25] | 800.6600 | - | 649.0855 |
| GWO [29] | 799.5585 | - | - |
| MEMLMA [27] | 800.0781 | - | 649.6309 |
| ICBOA [28] | 799.0353 | 830.4531 | 645.1668 |
| MSA [30] | 800.5099 | - | 646.8364 |
| OSSOA [31] | 802.2580 | 840.5816 | 657.1848 |
| MSSOA [31] | 798.9936 | 830.45 | 646.1758 |
| LD-FB-AHA [33] | 799.7633 | 833.7215 | - |
| OAHA [33] | 800.3203 | 835.7149 | - |
| FS-SFSOA [33] | 799.8328 | 833.9494 | - |
| ALO [33] | 802.2177 | 836.8568 | - |
| WOA [33] | 801.7535 | 837.0127 | - |
| SCFA [33] | 815.0065 | 869.8157 | - |
| FBL-ABCOA [33] | 799.7641 | 833.8195 | - |
| COOT | 798.957 | 830.746 | 647.967 |
| MPSA | 799.123 | 830.695 | 646.491 |
| EO | 798.912 | 830.532 | 646.152 |
| Method | Power Loss (MW) | VD |
|---|---|---|
| EGA [8] | 3.2008 | - |
| HEGA [9] | 3.244 | - |
| DE [16] | 3.38 | - |
| DE [17] | - | 0.1357 |
| CQS-PSO [12] | 5.0732 | - |
| AD-PSO [13] | - | 0.4952 |
| BBO [18] | - | 0.0951 |
| ABBO [19] | 3.1009 | 0.092 |
| TLBO [20] | 2.9501 | - |
| GSA [24] | - | 0.093269 |
| ABCA [25] | 3.1078 | |
| IICA [26] | - | 0.0952 |
| GWO [29] | - | 0.118736 |
| MEMLMA [27] | - | 0.1063 |
| MSA [30] | 3.1005 | - |
| OSSOA [31] | 3.8239 | 0.123551 |
| MSSOA [31] | 2.8678 | 0.09071 |
| COOT | 2.867 | 0.098 |
| MPSA | 2.840 | 0.097 |
| EO | 2.830 | 0.094 |
| Study Case | Description | |
|---|---|---|
| Base | Optimal power flow for the IEEE 30-bus system without capacitors, FACTS, and renewable energies | - |
| Case 1 | Optimal location and rated power of two SVCs | 60; 500 |
| Case 2 | Optimal location and parameter of 1 TCSC in the base system | 60; 500 |
| Case 3 | Using results from Case 1 and optimizing the location and parameter of 1 TCSC | 60; 500 |
| Case 4 | Using results from Case 2 and optimizing the location and rated power of two SVCs | 60; 500 |
| Case 5 | Simultaneously optimize two SVCs and one TCSC in the base system | 100; 1000 |
| Case 6 | Use the best solution from Case 3, Case 4, and Case 5, and then optimize different numbers of wind power plants | |
| Case 6.1 | Optimize the location and rated power of one wind power plant | 60; 500 |
| Case 6.2 | Optimize the location and rated power of two wind power plants | 60; 500 |
| Case 6.3 | Optimize the location and rated power of three wind power plants | 60; 500 |
| Case 7 | Simultaneously optimize two SVCs, one TCSC, and wind power plants | |
| Case 7.1 | One wind power plant | 100; 1000 |
| Case 7.2 | Two wind power plants | 100; 1200 |
| Case 7.3 | Three wind power plants | 100; 1500 |
| Case | Minimum Power Loss | Mean Power Loss | ||||
|---|---|---|---|---|---|---|
| COOT | MPSA | EO | COOT | MPSA | EO | |
| Base | 3.066 | 3.066 | 3.066 | 3.066 | 3.066 | 3.094 |
| Case 1 | 2.898 | 2.898 | 2.898 | 2.924 | 2.901 | 3.018 |
| Case 2 | 2.999 | 2.999 | 2.999 | 3.055 | 3.013 | 3.059 |
| Case 3 | 2.869 | 2.869 | 2.869 | 2.890 | 2.879 | 2.998 |
| Case 4 | 2.880 | 2.8797 | 2.881 | 2.918 | 2.886 | 3.097 |
| Case 5 | 2.869 | 2.869 | 2.869 | 2.905 | 2.890 | 2.906 |
| Case 6.1 | 2.055 | 2.053 | 2.053 | 2.245 | 2.089 | 2.225 |
| Case 6.2 | 1.523 | 1.513 | 1.512 | 1.704 | 1.544 | 1.717 |
| Case 6.3 | 1.124 | 1.117 | 1.112 | 1.332 | 1.197 | 1.300 |
| Case 7.1 | 2.041 | 2.042 | 2.041 | 2.053 | 2.044 | 2.042 |
| Case 7.2 | 1.523 | 1.510 | 1.508 | 1.523 | 1.516 | 1.510 |
| Case 7.3 | 1.114 | 1.108 | 1.093 | 1.122 | 1.117 | 1.109 |
| Case | The Best Solution | The Best Stabilization | ||||
|---|---|---|---|---|---|---|
| COOT | MPSA | EO | COOT | MPSA | EO | |
| Base | x | x | x | x | x | - |
| Case 1 | x | x | x | - | x | - |
| Case 2 | x | x | x | - | x | - |
| Case 3 | x | x | x | - | x | - |
| Case 4 | - | x | - | - | x | - |
| Case 5 | x | x | x | - | x | - |
| Case 6.1 | - | x | x | - | x | - |
| Case 6.2 | - | - | x | - | x | - |
| Case 6.3 | - | - | x | - | x | - |
| Case 7.1 | x | - | x | - | - | x |
| Case 7.2 | - | - | x | - | - | x |
| Case 7.3 | - | - | x | - | - | x |
| Case | Wind Power Plant | SVC | TCSC | |||
|---|---|---|---|---|---|---|
| Bus | Size (MW) | Bus | Size (MVAr) | Line | Size (Pu) | |
| 1 | - | - | 21; 24 | 12.7030; 8.8750 | - | - |
| 2 | - | - | - | - | 13 | 0.208 |
| 3 | - | - | 21; 24 | 12.7030; 8.8750 | 5 | 0.0541 |
| 4 | - | - | 19; 24 | 5.207; 9.548 | 13 | 0.208 |
| 5 | - | - | 21; 24 | 12.6822; 8.8682 | 5 | 0.0541 |
| 6.1 | 5 | 30 | 21; 24 | 12.6822; 8.8682 | 5 | 0.0541 |
| 6.2 | 5; 24 | 30; 24 | 21; 24 | 12.6822; 8.8682 | 5 | 0.0541 |
| 6.3 | 5; 19; 30 | 30; 20; 14 | 21; 24 | 12.6822; 8.8682 | 5 | 0.0541 |
| 7.1 | 5 | 30 | 21; 25 | 12.447; 8.832 | 7 | 0.051 |
| 7.2 | 5; 24 | 24; 24 | 21; 26 | 11.141; 8.581 | 7 | 0.0559 |
| 7.3 | 5; 19; 30 | 30; 20; 14 | 21; 27 | 10.785; 8.569 | 7 | 0.0445 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.A.; Kien, L.C.; Duong, M.Q.; Phan, T.M.; Nguyen, T.T. Total Fuel Cost, Power Loss, and Voltage Deviation Reduction for Power Systems with Optimal Placement and Operation of FACTS and Renewable Power Sources. Appl. Sci. 2025, 15, 10596. https://doi.org/10.3390/app151910596
Nguyen TA, Kien LC, Duong MQ, Phan TM, Nguyen TT. Total Fuel Cost, Power Loss, and Voltage Deviation Reduction for Power Systems with Optimal Placement and Operation of FACTS and Renewable Power Sources. Applied Sciences. 2025; 15(19):10596. https://doi.org/10.3390/app151910596
Chicago/Turabian StyleNguyen, Tuan Anh, Le Chi Kien, Minh Quan Duong, Tan Minh Phan, and Thang Trung Nguyen. 2025. "Total Fuel Cost, Power Loss, and Voltage Deviation Reduction for Power Systems with Optimal Placement and Operation of FACTS and Renewable Power Sources" Applied Sciences 15, no. 19: 10596. https://doi.org/10.3390/app151910596
APA StyleNguyen, T. A., Kien, L. C., Duong, M. Q., Phan, T. M., & Nguyen, T. T. (2025). Total Fuel Cost, Power Loss, and Voltage Deviation Reduction for Power Systems with Optimal Placement and Operation of FACTS and Renewable Power Sources. Applied Sciences, 15(19), 10596. https://doi.org/10.3390/app151910596







