Urban Eco-Network Traffic Control via MARL-Based Traffic Signals and Vehicle Speed Coordination

Abstract

This study proposes a Cooperative Traffic Controller System (CTS), an urban eco-network control system that leverages Multi-Agent Reinforcement Learning (MARL), to address urban road congestion and environmental pollution. The proposed system synergizes traffic signal timing optimization and speed guidance control, simultaneously enhancing network efficiency, reducing carbon emissions, and minimizing energy consumption. A Beta-enhanced Soft Actor-Critic (SAC) algorithm is applied to achieve the joint optimization of the traffic signal phasing and vehicle speed coordination. Experimental results show that in large-scale networks, the improved SAC reduces the average delay time per vehicle by approximately one minute, reduces CO₂ emissions by more than double, and reduces fuel consumption by 56%. Comparative analyses of the algorithm versus the PPO and standard SAC demonstrate its superior performance in complex traffic scenarios—specifically in congestion mitigation and emissions reduction.

1. Introduction

The rapid pace of urbanization and the escalating number of automobiles have rendered urban traffic congestion a ubiquitous challenge. The contradiction between limited road resources and a dense traffic flow has intensified regional congestion. Such congestion results in frequent vehicle idling, which not only extends commuting times but also causes a surge in regional CO₂ emissions and fuel consumption. This dual pressure not only degrades the air quality but also increases travel time costs and energy expenditure.

Over an extended period, scholars have consistently advanced their research on urban congestion. Laval [1] analogized traffic flow to a gas and put forward the phase transition theory of traffic flow, which elucidates the complex dynamic characteristics of urban traffic, and defined the boundaries of congestion. Relevant research has revealed the relationships between congestion and traffic flow—such as those between the maximum network throughput, congestion levels, and traffic flow normalization methods—and has also highlighted the implications of congestion for sustainable urban development [2].

Research indicates that traffic congestion directly increases vehicular emissions on urban roads, thereby exacerbating air pollution. Vehicles that frequently stop and start in congested areas significantly increase CO₂ emissions and particulate matter (PM2.5), further deteriorating the local air quality. Traffic congestion not only raises pollutant emissions but also indirectly affects public health. In 2020, excessive vehicle emissions caused by traffic congestion in China led to over 25,000 deaths [3]. Moreover, the noise generated by congestion, including driver honking, adversely impacts the daily lives of students and local residents.

Beyond environmental impacts, congestion also imposes economic costs by increasing fuel expenses and lost productivity due to longer travel times [4]. According to Ahn et al. [5], fuel consumption increases with the jerk of vehicles. That is, for a given distance, smoother driving results in lower fuel consumption. However, traffic congestion frequently induces unhealthy driving behaviors, such as repeated acceleration and braking. Under identical traffic conditions, variations in driving style can lead to fuel consumption differences of up to 29% [6]. Mohammadnazar et al. [7] demonstrated that, within urban networks, normal driving improves fuel economy by approximately 23% compared with unhealthy driving behavior. Marzet et al. [8] revealed that traffic conditions exert a substantial influence on both driving behavior and vehicle fuel consumption. Experimental results indicate that, relative to congested roads, vehicles operating under favorable traffic conditions achieve up to a 36% improvement in fuel efficiency. Therefore, developing a traffic control system aimed at mitigating congestion is of great significance for both environmental sustainability and economic efficiency.

Traffic light signal control represents an effective means of mitigating traffic congestion. By optimizing signal phase timing plans, researchers have enhanced the operational efficiency of individual intersections. Agand et al. [9] advanced environmental impact mitigation by pioneering a DRL-based traffic signal control framework that integrates a novel reward distribution mechanism, effectively reducing CO₂ emissions across diverse vehicle types while simultaneously shortening travel times in urban networks.

In recent years, the coordinated control of multi-intersection signals in large-scale urban networks has emerged as a prominent research direction. The optimization framework for coordinated multi-intersection signal control centers on two primary objectives: maximizing the green wave bandwidth and optimizing traffic performance metrics [10,11]. Recent developments in traffic signal coordination have seen substantial research dedicated to the development of Multi-Agent Reinforcement Learning (MARL) methodologies. Elise et al. [12] modeled the road network state space using a Deep Q-Network (DQN) and achieved significant reductions in travel time and queue length through dynamic policy optimization. Wei et al. [13] enhanced the DQN architecture by integrating Graph Convolutional Networks (GCNs) for topological feature extraction, introducing a dual-reward mechanism that jointly optimizes the vehicle waiting time and intersection throughput. Their approach reduced the average waiting time by 40–47% under high-density traffic conditions. Liang et al. [14] proposed a Double Dueling Deep Q-Network (3DQN) framework that employs Convolutional Neural Networks (CNNs) for grid-based traffic scenario representation, consistently reporting performance improvements, including more than a 20% reduction in the average vehicle delay across diverse traffic patterns.

While MARL has shown considerable potential in coordinated multi-intersection traffic signal control, it faces a fundamental challenge known as the curse of dimensionality. Existing mitigation strategies have converged into three primary technical approaches:

(1)

Decentralized Architecture: Chu et al. [15] proposed the Multi-Advantage Actor-Critic (MA2C) algorithm that enables independent agent learning through environmental dynamics modeling. Min et al. [16] yielded 10–25% improvements in traffic throughput metrics via a strategic state-reward system reconfiguration within the Advantage Actor-Critic (A2C) framework.

(2)

Hybrid Hierarchical Approach: Tan et al. [17] developed the Collaborative Deep Reinforcement Learning (Coder) framework, which decomposes complex tasks into single-agent subproblems and achieves large-scale traffic network optimization through the hierarchical aggregation of regional and global agents.

(3)

Collaborative Learning Innovation: Wang et al. [18] developed the Cooperative Double Q-Learning (Co-DQL) algorithm incorporating mean-field approximation, surpassing existing decentralized MARL algorithms across multiple traffic flow metrics [19].

The rapid advancement of Connected Autonomous Vehicle (CAV) technology has propelled intelligent transportation research into a new phase. Ghiasi et al. [20] proposed a hybrid traffic trajectory coordination algorithm leveraging CAV technology, which mitigates stop-and-go oscillations and reduces both fuel consumption and emissions. Arvin et al. [21] combined Adaptive Cruise Control (ACC) with Cooperative Adaptive Cruise Control (CACC) to enhance car-following models, thereby improving traffic efficiency and safety. Lin et al. [22] constructed an MARL-ES (Evolution Strategy) cooperative framework to optimize variable speed limits, significantly improving the throughput under high-density traffic flow conditions. Yu et al.’s [23] team developed a Mixed Integer Linear Programming (MILP) optimization model that improves the traffic capacity while reducing delays, fuel consumption, and CO₂ emissions. Guo et al. [24] proposed a Cooperative Traffic and Vehicle control (CoTV) framework, achieving the dual optimization of the travel time and energy consumption across diverse urban networks. Busch et al. [25] designed a DRL-based joint controller, significantly enhancing system efficiency by smoothing vehicle speed profiles.

Previous research has often employed grid networks composed of identical intersections. However, such grid networks fail to capture the complexity of real-world urban networks. Furthermore, an effective intelligent transportation system should not only improve the operational efficiency of the road networks but also encourage safe and sustainable driving behaviors. Accordingly, this research proposes an integrated vehicle–road cooperative control framework, termed the CTS, which leverages the Soft Actor-Critic (SAC) algorithm to achieve the multi-objective optimization of traffic efficiency, emissions, and energy consumption in large-scale urban networks. The main innovations of the CTS include the following:

(1)

Collaborative Control Architecture: A joint control model integrating traffic signals and vehicle speeds is constructed to overcome the limitations of single-dimension control, mitigate congestion, and reduce both carbon emissions and fuel consumption. Ablation studies confirm that joint control outperforms signal-only control in overall performance.

(2)

Action Space Adaptation: The SAC algorithm is innovatively enhanced by employing a Beta distribution to address the high estimation bias of Gaussian policies in continuous and bounded action spaces within traffic scenarios.

(3)

Algorithm Generalization Verification: The approach demonstrates strong scalability by reducing average delays compared with traditional DRL methods across scenarios ranging from single intersections to large-scale networks.

2. Traffic Signal Controller System

This research proposes a cooperative control method integrating traffic signals and vehicle speeds. As a core system component, the Traffic Signal Controller (TSC) dynamically adjusts the phase sequence and duration of traffic lights to optimize vehicle flow efficiency in urban networks. This section systematically details the theoretical foundation, the physical model, and the adapted control algorithm underlying the proposed method.

2.1. Traffic Signal Model

Based on the theory of Markov Decision Processes (Markov property), this research establishes a state transition model for the traffic system. In the TSC, the traffic signal at each intersection is considered as an agent. The phase of traffic lights is influenced solely by the previous phase, and the transient changes in vehicle speeds are constrained by the current motion state. Both the traffic signal phase switching and vehicle acceleration/deceleration behaviors can be modeled as Markov processes as follows:

$$P\left(S_{t+1}|S_t\right)=\mathbb{P}\left(S_{t+1}|S_1,S_2,\cdots ,S_t\right)$$

(1)

where $P$ is the state transition probability function, and $\mathbb{P}$ represents the conditional probability. $S_t$ denotes the state space of the system at time $t$.

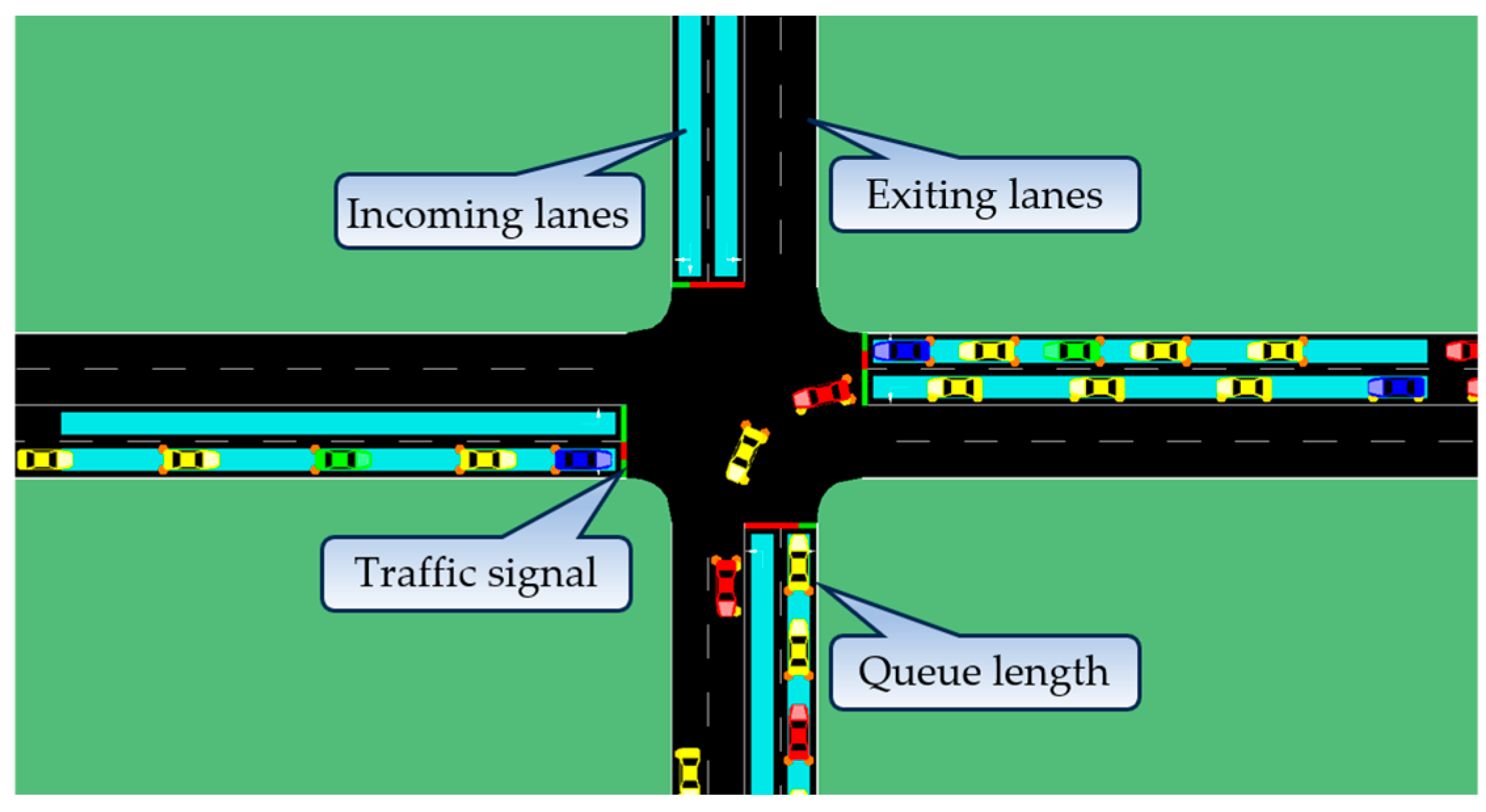
In the traffic systems, the state space of the TSC primarily comprises two components: the current traffic signal phases and the traffic flow state information within the networks. According to Laval’s research [1], the traffic congestion and vehicle density in the road network conform to a power-law distribution. Therefore, this research incorporates the vehicle density, queue length, and waiting time of stationary vehicles into the state space.

Table 1. Observation space of the Traffic Signal Controller.

Observation Space	Dimensions
Current phase of the traffic signal	$N_P$
Lane density [number of vehicles in lane]	$N_L$
Queue length per lane	$N_L$
Total waiting time of stopped vehicles per lane	$N_L$

summarizes the state space of the TSC, where $N_P$ is the number of signal phases at the intersection, and $N_L$ is the number of incoming lanes connected to the traffic signals in the networks. Figure 1 further illustrates the state space of the TSC. In Figure 1, the blue segments indicate incoming lanes.

The Markov Reward Process (MRP) is an extension of the Markov process by adding a reward function $R$ and a discount factor $\gamma$, typically represented by the quadruple $<S,P,R,\gamma >$, which determine how the agent evaluates and optimizes its policy to achieve its goal. $G_t$ represents the total reward the agent receives starting from time $t$, and the formula is

$$G_t=R_t+\gamma \cdot R_{t+1}+{\gamma }^2\cdot R_{t+2}+\cdots$$

(2)

The state value function is proposed to evaluate the expected value that an agent can obtain when taking actions based on the current policy at a given state. According to the Bellman Equation, the state value function is expressed as

$$V\left(s\right)=R\left(s\right)+\gamma \sum _{s^{\prime }\in S}P\left(s^{\prime }|s\right)V\left(s^{\prime }\right)$$

(3)

where $s$ denotes the current state at time $t$, and $s^{\prime }$ represents a possible state at the next time step. The value function consists of two parts: the expected immediate reward $R\left(s\right)$ and the expected value of the next state, which is the discounted sum of future expected rewards.

The Markov Decision Process (MDP) extends the Markov Reward Process by introducing an action $A$, forming the tuple $<S,A,P,R,\gamma >$. In traffic systems, changing the signal phase or adjusting the vehicle speed is regarded as taking an action $A$. Here, both the state transition function $P$ and the reward function $R$ are related to the specific action $A$. The state transition function $P$ in a Markov Decision Process is

$$P\left(s^{\prime }|s,a\right)=\mathbb{P}\left[S_{t+1}=s^{\prime }|S_t=s,A_t=a\right]$$

(4)

where $S_t$ and $A_t$ are random variables representing possible states and actions, respectively. The reward function $R$ is

$$R(s,a)=\mathbb{E}[R_t\mid S_t=s,A_t=a]$$

(5)

The action space of the TSC is discrete and bounded. Specifically, within the TSC, the phase sequence and duration of traffic signals constitute the actions of the agents. This research employs a binary-encoded action space for the TSC, where each discrete element corresponds to a specific signal phase. In this binary coding scheme, “0” represents a red light and “1” represents a green light, with a mandatory 2 s yellow light phase inserted between red–green transitions. The TSC executes control decisions at fixed 5 s intervals, establishing a minimum allowable duration of 5 s for both red and green signal phases.

For dense urban networks, MARL is more appropriate and is generally modeled using a Markov Game. In this research, the Markov Game is represented by a six-tuple $<N,S,A,P,R,\gamma >$, where N: $N=\left\{\mathrm{1,2},\cdots ,n\right\}$ denotes the set of $n$ agents in the system, and $R_t^i$ represents the reward obtained by agent $i$ at time $t$. The discounted return is

$$G_t^i=R_t^i+\gamma \cdot R_{t+1}^i+{\gamma }^2\cdot R_{t+2}^i+\cdots$$

(6)

The reward of the TSC primarily concerns traffic flow information in the network, including the queue length [26], waiting time [27], and traffic pressure [28]. The reward function mainly depends on the optimization objectives of the experiment. There are numerous factors influencing traffic congestion, including the maximum road throughput and traffic flow density. These factors are often not easily accessible directly; therefore, this research selects the traveling time of vehicles—closely related to congestion—as the primary optimization objective for the TSC. The reward function for a single intersection is defined as follows:

$$r_i=-\sum _{\forall l\in L_i} \sum _{\nu eh\in {Veh}_l} T\left(\nu eh,l\right)$$

(7)

where $L_i$ denotes the set of incoming lanes at intersection $i$, and ${Veh}_l$ represents the set of all vehicles currently in lane $l$; $T\left(\nu eh,l\right)$ is the travel time of vehicle $\nu eh$ in lane $l$.

To directly guide the agent decision-making and policy optimization, the state-action value function $Q_{\pi }(s,a)$ serves as the core evaluation metric in Reinforcement Learning (RL), quantifying the expected cumulative future rewards from action $a_t$ at time $t$ under policy $\pi$:

$$Q_{\pi }^i\left(s_t,a_t\right)={\mathbb{E}}_{\pi }\left[G_t^i\mid S_t=s_t,A_t=a_t\right]$$

(8)

The goal of RL is to discover the optimal policy at each state in the environment to maximize the expected reward, while the single agent optimizes the objective function J through individual policy networks.

$$\underset{\pi }{max} J\left(\pi \right)={\mathbb{E}}_s\left[V_{\pi }\left(S\right)\right]$$

(9)

2.2. Traffic Signal Controller Design

The objective of the TSC is to enhance the overall traffic efficiency within urban networks and achieve a global optimum. Achieving global optimality and multi-agent collaboration entails addressing several challenges, such as competitive and cooperative interactions among agents and the curse of dimensionality [29,30]. Currently, mainstream MARL approaches share the state space among neighboring agents, strengthening interactions and no longer treating traffic signals in isolation, which facilitates global optimization and better reflects real-world conditions. However, sharing the state space inevitably increases communication costs and computational burdens, which tends to cause the system to fall into the curse of dimensionality. To address these issues, this research designs a dynamic reward mechanism that integrates a global reward signal with individual contribution assessments, maintaining agent autonomy while enabling system-level cooperation. The cooperative reward function is

$$\begin{array}{c}{r}_i^{Tsc}=r_i+\alpha \cdot {\displaystyle \sum _{i\in N}} r_i\end{array}$$

(10)

The discount factor α balances the individual reward and the global reward. As α approaches 0, agents prioritize local traffic optimization, potentially exacerbating network-wide congestion. Higher α values promote cooperative behavior, benefiting system-level efficiency.

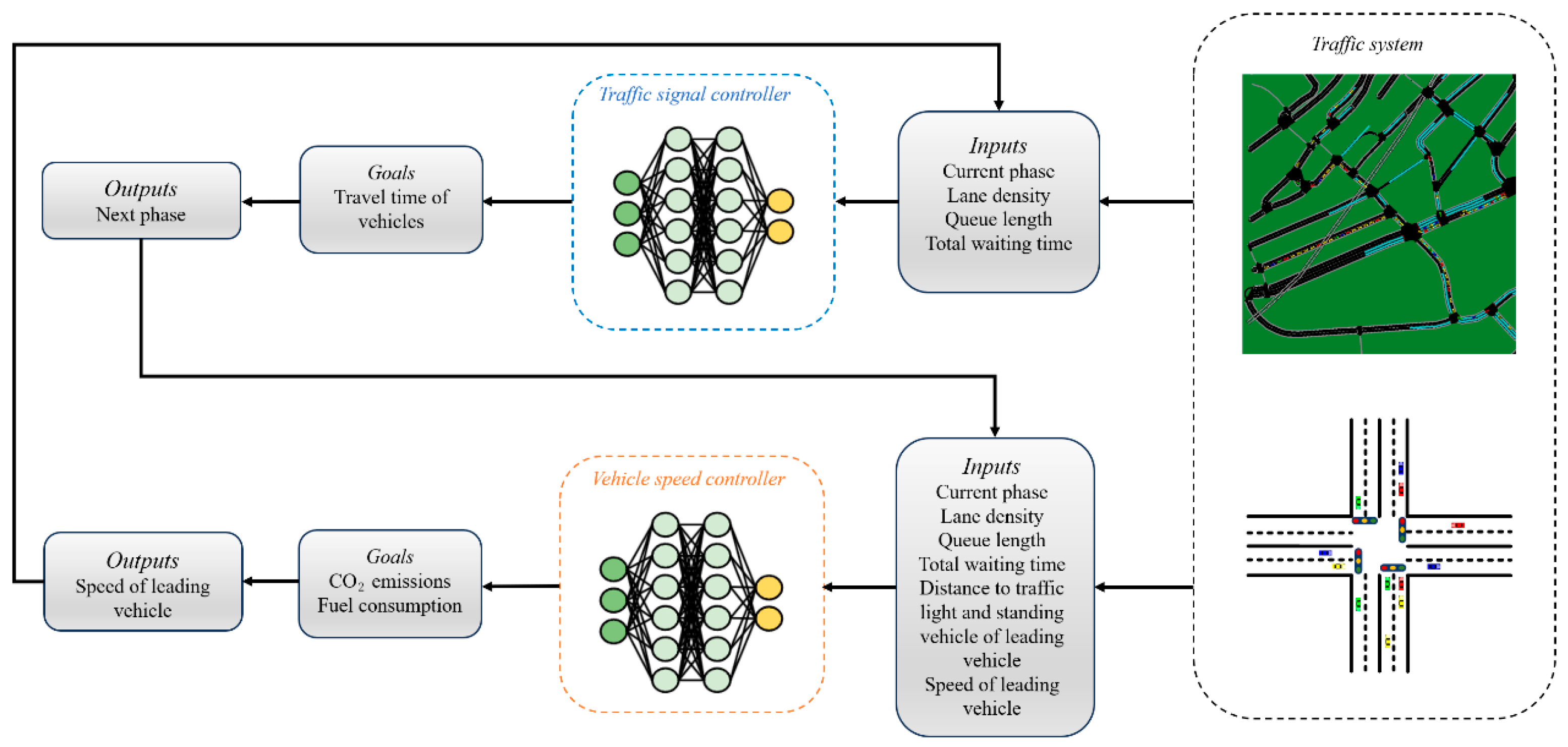
Each intersection (agent) shares a unified global reward function aimed at minimizing the total vehicle travel time, while retaining decentralized decision-making based on real-time local conditions. Compared with state-sharing approaches, our cooperative reward mechanism achieves global optimization with reduced communication costs and computational overhead. The system architecture is illustrated in Figure 2.

2.3. SAC for Traffic Signal Controller

For general DRL algorithms, the learning objective is straightforward: to learn a policy π that maximizes the expected cumulative reward:

$$\pi =\mathit{arg}\underset{\pi }{max} {\mathbb{E}}_{\left(s,a\right)}\left[\sum _t R\left(s,a\right)\right]$$

(11)

The primary objective of applying deep reinforcement learning (DRL) in intelligent transportation systems is to optimize spatiotemporal resource allocation through reward functions. Nevertheless, the effectiveness of the reward design is critical to algorithmic performance. For example, an excessive emphasis on traffic efficiency may inadvertently increase energy consumption, whereas a narrow focus on environmental metrics could undermine the overall network capacity.

The SAC algorithm is an off-policy algorithm developed for Maximum Entropy Reinforcement Learning [31]. Compared with DDPG, which is also based on the Actor-Critic architecture, the SAC algorithm enhances the exploration capability by maximizing policy entropy (Equation (12)), effectively addressing the multi-objective optimization challenges in traffic control.

$$\pi =\mathit{arg}\underset{\pi }{max} {\mathbb{E}}_{\left(s,a\right)}\left[\sum _t R\left(s,a\right)+\lambda H_{\pi }\left(s\right)\right]$$

(12)

where $\lambda$ is a hyperparameter that can automatically adjust the weight between the policy entropy and reward, and $H_{\pi }\left(s\right)={\mathbb{E}}_{a\sim \pi (\cdot |s)}\left[-\mathrm{l}\mathrm{n}\pi \left(a\right|s)\right]$ represents the entropy of the agent’s action $a$. Entropy is used to quantify the uncertainty of the outcomes of random variables. In a traffic environment, the larger the entropy of a signal phase, the lower and more random the predictability of the traffic condition under that phase.

The conventional objective of policy learning is to maximize the expected state value function, as shown in Equation (9). The difference is that SAC adds the expected entropy of the action, ${\mathbb{E}}_S\left[H_{\pi }\left(S\right)\right]$, as a regularization term to the objective function:

$$\underset{\pi }{max}J\left(\pi \right)\triangleq {\mathbb{E}}_S\left[V_{\pi }\left(S\right)\right]+\lambda \cdot {\mathbb{E}}_S\left[H_{\pi }\left(S\right)\right]={\mathbb{E}}_S\left[V_{\pi }\left(S\right)+\lambda \cdot H_{\pi }\left(S\right)\right]$$

(13)

In time-varying traffic scenarios, there often exists a considerable interval between peak and off-peak periods. If the traffic signal control policy converges prematurely within either phase, it may fail to adapt to subsequent variations in traffic flow. However, by leveraging its entropy-driven exploration mechanism, the SAC enables the control system to actively sustain a dynamic balance within the policy space, thereby mitigating the adaptation degradation caused by the premature convergence.

To achieve continuous control, the SAC reparametrizes the policy network, typically using the Squashed Gaussian policy as the policy function:

$$\mathrm{R}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{z}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{T}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{k} a=\mathit{tanh}\left(\mu \left(s;{\theta }^{\mu }\right)+\sigma \left(s;{\theta }^{\sigma }\right)\odot ϵ\right),\hspace{1em}\hspace{1em}ϵ\sim \mathcal{N}\left(\mathrm{0,1}\right)$$

(14)

where for an n-dimensional continuous action space, the outputs of the neural networks $\mu \left(s;{\theta }^{\mu }\right)$ and $\sigma \left(s;{\theta }^{\sigma }\right)$ are both n-dimensional vectors; $\theta =\left({\theta }^{\mu },{\theta }^{\sigma }\right)$ are the parameters of the neural networks. Each component of the n-dimensional vector $ϵ$ follows a standard normal distribution, i.e., $ϵ\sim \mathcal{N}\left(\mathrm{0,1}\right)$; $\odot$ denotes the Hadamard product, meaning element-wise multiplication. The SAC network architecture proposed in this paper for traffic systems is shown in Figure 3.

3. Cooperative Traffic Controller System

This chapter will first introduce the Vehicle Speed Controller (VSC) in the Cooperative Traffic Controller System (CTS), explain the interaction between the TSC and the VSC, and finally introduce the CTS proposed in this research.

3.1. Vehicle Speed Controller

The VSC is formulated as an MDP within the traffic environment and employs DRL methods for policy optimization. Studies have shown that the average vehicle speed is a crucial indicator for measuring congestion and traffic flow, and both the average vehicle speed and the factors it reflects (congestion and traffic flow) follow a power-law distribution [2]. By constraining vehicle speeds within a reasonable range, the VSC effectively reduces frequent acceleration and deceleration events, thereby achieving the objectives of energy conservation and emission reduction [32]. 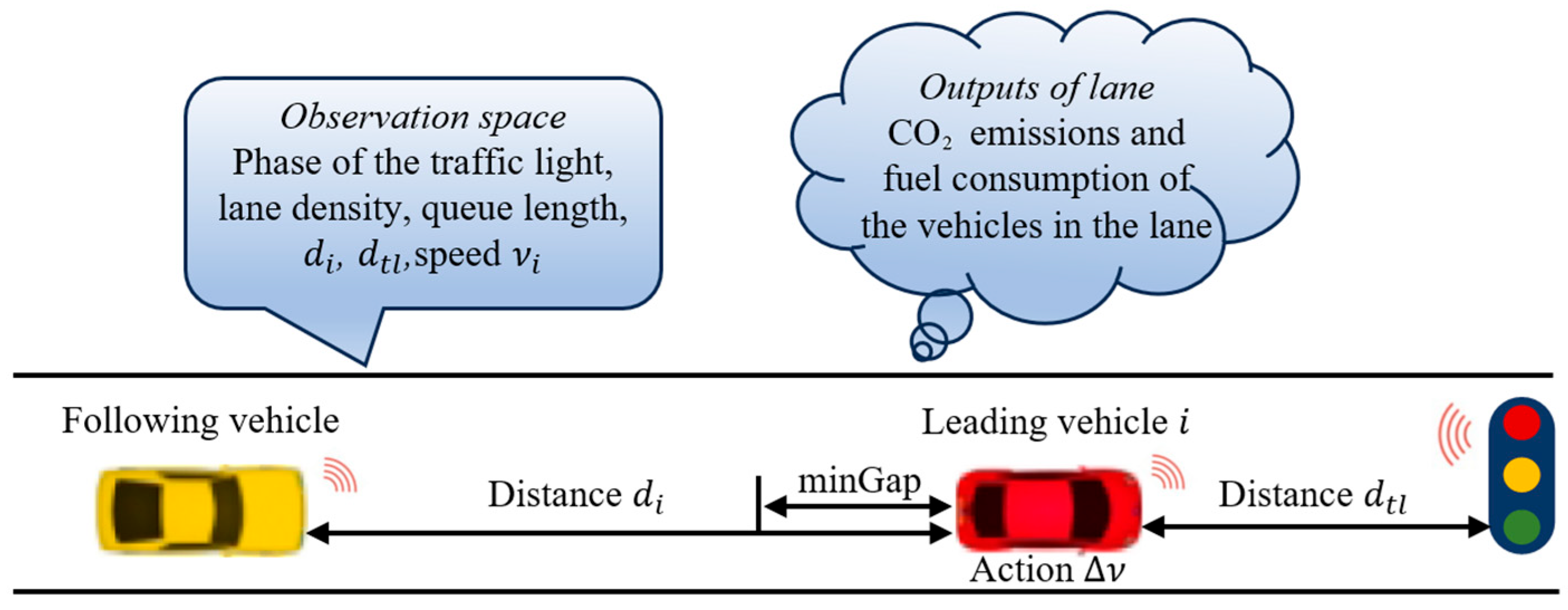Following the setting in [25], this research considers the leading vehicle in each lane as the control target. The detailed design of the state space, action space, and reward function for the VSC is presented as follows:

The state space of the VSC includes not only traffic signal phases and vehicle information but also focuses on the leader vehicle in the lanes. The state space of the VSC is shown in

Table 2. Observation space of the Vehicle Speed Controller.

Observation Space	Dimensions
Current phase of the traffic light	$N_P$
Lane density [number of vehicles in lane]	$N_L$
Queue length per lane	$N_L$
Total waiting time of stopped vehicles per lane	$N_L$
Distance to traffic light of leader vehicle	$N_L$
Distance to following vehicle of leader vehicle	$N_L$
Speed of leader vehicle	$N_L$

. In Table 2, the lane density, queue length, and total waiting time are used to evaluate the congestion level, while the information of the leader vehicle serves as the input for the VSC.

Similarly to the TSC, the VSC takes an action every 5 s of simulation time to change the speed of the leader vehicle. This action limits the speed of the leader vehicle within a continuous range, thereby controlling the speed of all vehicles. From a safety perspective, this research limits the speed within $[{\nu }_{lead}-\mathrm{\Delta }\nu ,{\nu }_{max}]$, where ${\nu }_{lead}$ is the current leader vehicle’s speed, ${\nu }_{max}$ is the maximum speed limit for the current lane, and $\mathrm{\Delta }\nu$ is set to 10% of the ${\nu }_{lead}$ in the experiment.

Since vehicle CO₂ emissions and fuel consumption are strongly influenced by the speed and travel time [8], the primary objective of the VSC in this study is to minimize the CO₂ emissions and fuel consumption. For safety considerations, the risk of vehicle collisions during travel is evaluated by imposing a minimum safety gap (minGap), as illustrated in Figure 4. If the distance between two consecutive vehicles falls below this threshold, a substantial penalty is applied in the reward function. Furthermore, vehicles in the lane are encouraged to maintain a steady and relatively high speed, which not only contributes to energy conservation and emission reductions but also helps sustain a high level of traffic efficiency. Therefore, the reward function for VSC is

$$\begin{array}{c}{r}_1=-{\displaystyle \sum _{i\in V}} E(i)+F(i)\hfill \\ r_2=\left\{\begin{array}{cc}100{\displaystyle \sum _{i\in V}}\left(d_i-minGap\right) & d_i<minGap\\ 0 & d_i\ge minGap\end{array}\right.,\hfill \\ r_3=-{\displaystyle \frac{{\displaystyle \sum _{i\in V}} \left({\nu }_{max}-{\nu }_i\right)}{{\nu }_{max}\times \left|V\right|}},{\nu }_i\le {\nu }_{max},\hfill \\ r^{Vsc}=r_1+r_2+r_3\hfill \end{array}$$

(15)

where V is the set of vehicles in the lane; $E\left(i\right)$ and $F\left(i\right)$ are the CO₂ emissions and fuel consumption of vehicle $i$ in the lane, respectively; $d_i$ is the distance between two adjacent vehicles; and ${\nu }_i$ is the current speed of vehicle $i$. $r_1$ in Equation (15) maximizes the environmental and economic benefits of the vehicle. $r_2$ measures the safety of the vehicle during travel. The smaller the distance between two adjacent vehicles, the greater the penalty. In this experiment, the minGap is set to 2.5 m, and $r_3$ encourages vehicles to travel at a higher speed, reducing the travel time.

The flowchart of the VSC framework is presented in Figure S1 of the Supporting Information. The process begins by traversing all vehicles in the current lane and selecting the leading vehicle as the control target. Based on the current state space, the controller then determines the appropriate action and immediately verifies its feasibility. This verification step is designed to prevent abrupt changes in the vehicle speed within a short time horizon, which could otherwise increase the risk of traffic accidents.

3.2. SAC with Beta Policy for CTS Design

Figure 5 illustrates the structure of the CTS, which integrates both the TSC and VSC. Within this framework, the traffic light phase serves as the output of the Traffic Signal Controller and simultaneously as the input to the VSC. The output of the VSC, in turn, determines the vehicle queue length and traffic density on the road, thereby influencing the subsequent input to the TSC. Through this mutual interaction, the two controllers form a closed-loop control system.

The standard SAC algorithm uses the Gaussian policy as the policy function, which is a policy based on the Gaussian distribution used for handling continuous action spaces, as shown in Equation (16). The probability density function of the Gaussian distribution is

$$f\left(x\right)={\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}\mathit{exp}\left(-{\displaystyle \frac{(x-\mu {)}^2}{2{\sigma }^2}}\right)$$

(16)

where $\mu$ and $\sigma$ are the mean and standard deviation of the Gaussian distribution, respectively. Since the Gaussian distribution is an unbounded probability distribution, the Gaussian policy is more suitable for environments with unbounded action spaces. However, the action space of the traffic light is a binary set. Clearly, simply using the Gaussian policy to output the action will inevitably cause a bias.

To address the aforementioned problem, one possible solution is to adopt the Squashed Gaussian policy as the policy function, as defined in Equation (14). This approach integrates a squashing function with the Gaussian policy to produce continuous yet bounded actions. Nevertheless, when the optimal action approaches an extreme value, the gradient of the tanh function becomes nearly zero. This can readily result in vanishing gradients, a reduction in policy entropy, and constrained exploration. In high-dimensional settings, where each action dimension undergoes nonlinear compression, the issue of gradient saturation is further exacerbated.

Another approach is to introduce the Beta policy based on the Beta distribution as the policy function. The Beta distribution is represented as follows:

$$f(x;\alpha ,\beta )={\displaystyle \frac{\Gamma (\alpha +\beta )}{\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}}{x}^{\alpha -1}{(1-x)}^{\beta -1}$$

(17)

where $\alpha$ and $\beta$ are the shape parameters of the Beta distribution, and $\Gamma \left(n\right)=(n-1)!$ is the Gamma function, which extends the factorial to real numbers. The Beta policy, as a policy function, can map actions to other intervals through a linear transformation, such as [$a_{min},a_{max}$]. Thus, Equation (14) will be modified as follows:

$$a=(a_{max}-a_{min})\cdot \tilde{a}+a_{min},\hspace{1em}\hspace{1em}\tilde{a}\sim Beta\left(\alpha \left(s;{\theta }^{\alpha }\right),\beta \left(s;{\theta }^{\beta }\right)\right)$$

(18)

where $\tilde{a}\in {\left(\mathrm{0,1}\right)}^n$ is an action sampled from the Beta distribution, and ${\theta }^{\alpha }$ and ${\theta }^{\beta }$ are the network parameters used to generate $\alpha$ and $\beta$. The Beta distribution is bounded, and for data within a finite range, it usually provides a more accurate fit. Moreover, the bounded nature and inherent skewness of the Beta distribution facilitate a convergence in high-dimensional action tasks. In traffic environments, the vehicle speed constitutes a continuous and bounded action space. As vehicles approach intersections, the policy often needs to select actions near zero or the maximum speed. The Beta distribution naturally accommodates such skewed action distributions, enabling a more precise representation of boundary actions. Even when boundary actions are taken, it preserves relatively high entropy and balanced exploration, thereby accelerating the policy convergence and improving the final performance. Therefore, the Beta policy is more suitable as the policy function for the SAC algorithm in this research.

4. Experimental Methodology

4.1. Experimental Scenarios

To adequately evaluate the performance of each algorithm, the experimental scenarios should meet the following conditions: realistic and representative. Therefore, in this experiment, five urban networks that meet both conditions, as shown in Figure 6, were selected from previous studies: (a) single signal: a single intersection with 2015 vehicles passing per hour, and the main roads are dual-lane; (b) Ingolstadt corridor: a corridor from the Ingolstadt region in Germany, with 7 main intersections on the main road as the research subject, with 3030 vehicles passing per hour [33]; (c) Cologne region: a city road network from Cologne, Germany, with 8 main intersections as the research subject, with 2046 vehicles entering the region per hour; (d) Ingolstadt region: an expanded version of the (b) area, forming a complex urban road network, with 21 major intersections as the research subject and 4280 vehicles entering the region per hour; and (e) 4 × 4 grid: a 4 × 4 synthetic traffic grid, with each road being a three-lane major road and 1472 vehicles passing per hour [34]. The experimental scenarios are implemented in the simulation platform SUMO, which includes the traffic network construction, traffic flow configuration, and simulation experiments.

4.2. Parameters Details of Algorithms

To verify the performance of the proposed algorithms, this experiment compares it with the following algorithms: PPO (Proximal Policy Optimization), A3C (Asynchronous Advantage Actor-Critic), and DQN (Deep Q-Network). DQN and A3C are classic algorithms in MARL, and their variant algorithms are widely applied in the field of traffic signal control. PPO performs excellently both in traffic signal control (which involves discrete action spaces) and in vehicle speed control (which involves continuous action spaces). For the detailed configuration of SAC and other algorithms, please refer to Tables S1–S5 in the Supporting Information.

5. Experimental Results

This section presents the three main experimental results, highlighting the excellent performance of the proposed CTS. First, an ablation study was conducted to validate the effectiveness of the CTS, demonstrating that the SAC outperforms other MARL algorithms in this domain. Second, further comparisons confirmed the superior performance of the SAC over alternative MARL approaches in the given context. Finally, experiments analyzed the performance differences between the Gaussian and Beta policies, as well as the specific effectiveness of the CTS across different intersections in large-scale networks. In the experiment, both the CO₂ emissions and fuel consumption model for vehicles adopt the default emissions model of SUMO.

5.1. Validity of Cooperative Traffic Controller System

Figure 7 compares traffic conditions under the CTS and TSC. (1) Trip Delay (Figure 7a,b): The CTS consistently achieves a shorter trip delay than the TSC in both the Cologne region and 4 × 4 grid scenarios, regardless of the algorithm (SAC or PPO). While the difference is marginal in the smaller Cologne network (fewer intersections), the CTS demonstrates a significantly better performance in the larger 4 × 4 grid (more intersections). (2) Average CO₂ Emissions (Figure 7c,d): The CTS outperforms the TSC in both the Ingolstadt corridor and region. The performance gap is more pronounced in the larger Ingolstadt region (21 intersections) than in the corridor (7 intersections). Under PPO, emissions from the CTS and TSC initially converge but diverge sharply after approximately 200 training episodes. In the regional network, this divergence eventually stabilizes at a gap of about 50,000 mg, which is considerably larger than the gap observed in the corridor. This pronounced disparity arises in part from the CTS’s explicit inclusion of CO₂ emissions in its reward function, as well as the larger scale and greater complexity of the regional network. Figure 7 illustrates the consistently superior performance of the CTS over the TSC across most scenarios, with the extent of the improvement contingent on the scale and complexity of the networks.

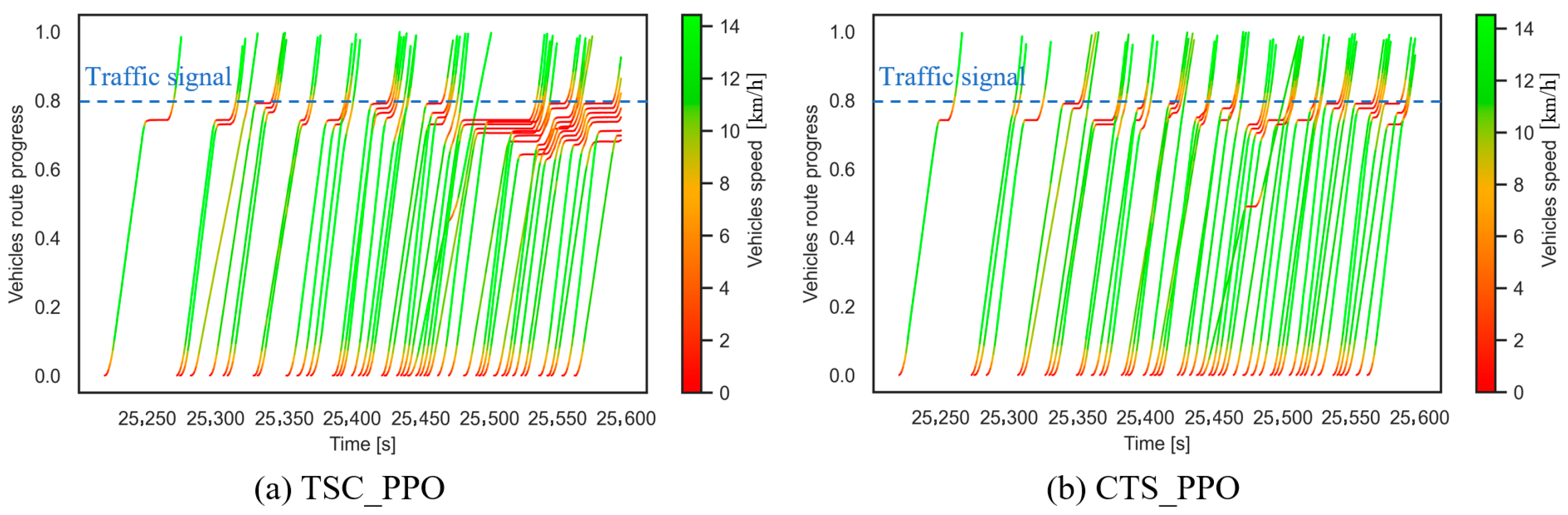
Figure 8a,b depict the speed profiles of traffic flows in the TSC and CTS, respectively, traversing the single intersection shown in Figure 8a. The left vertical axis represents the normalized vehicle progress through the intersection, where zero indicates an entry into the speed-controlled section, and one denotes the passage through the signalized intersection into another lane. Vehicles within the [0, 1] interval are under speed control, with 1 marking the endpoint to account for potential intersection congestion. Each curve represents an individual vehicle’s speed trajectory, color-coded by speed (green: faster, red: slower). The line slope indicates traffic efficiency: steeper slopes denote higher efficiency. A horizontal dark-red segment signifies vehicle congestion. While the slopes in Figure 8a,b are initially comparable, congestion levels diverge in the latter traffic flow phase. The CTS exhibits only minor congestion, with average vehicle waiting times remaining below 10 s. In contrast, the TSC leads to substantially more severe congestion, with waiting times approaching 50 s.

5.2. An Analysis of the Proposed Algorithm

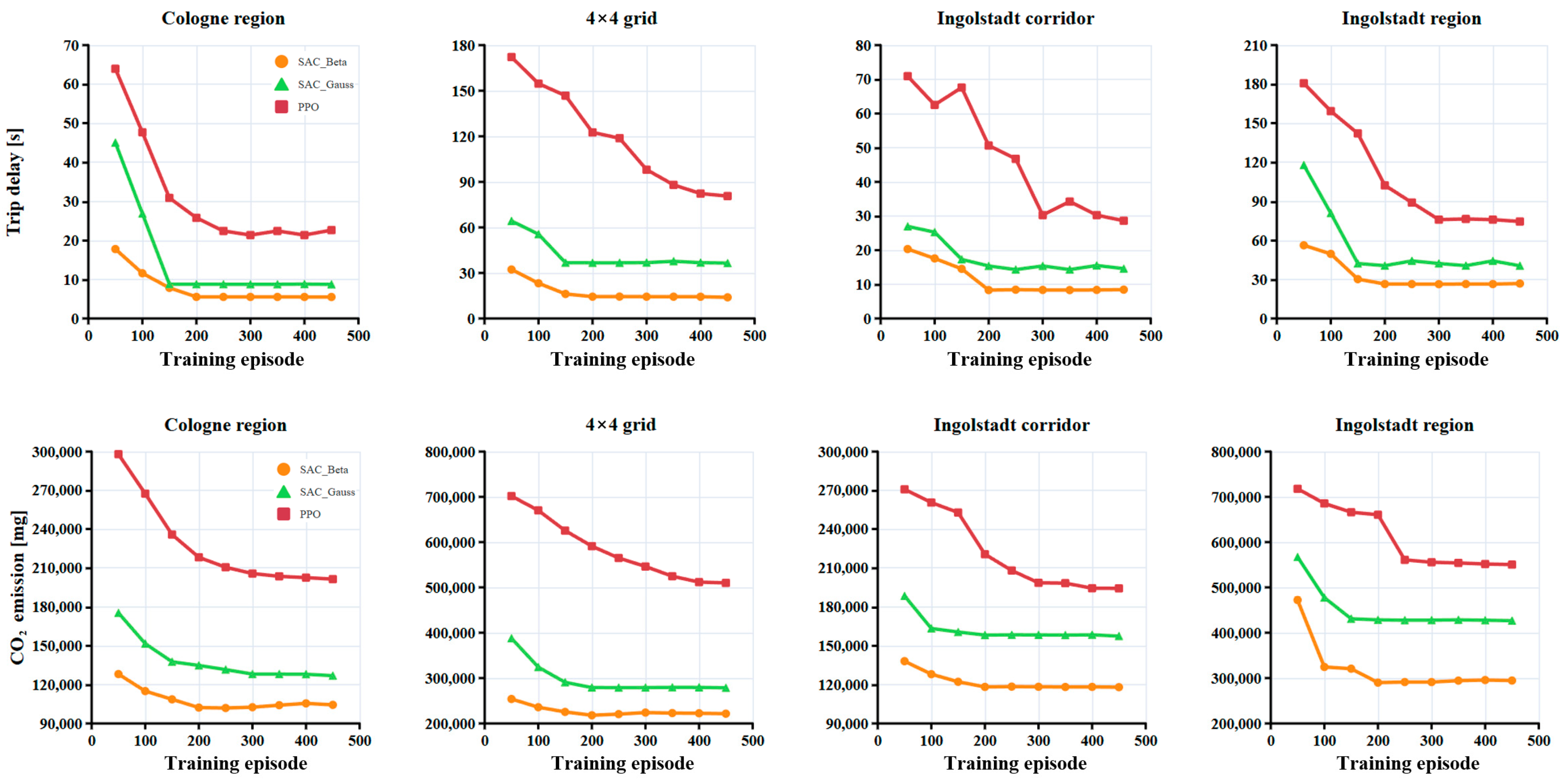
Figure 9 compares the performance of the standard SAC, SAC with Beta policy, and PPO applied to the CTS across diverse scenarios, with each point representing the average value per 50 training cycles. As illustrated, SAC-Beta consistently outperforms the other methods. In smaller-scale networks (Cologne region and Ingolstadt corridor), it achieves vehicle delay times of approximately 10 s and CO₂ emissions below 12,000 g.

Conversely, PPO performs less effectively, particularly in larger networks with higher traffic volumes. Its relatively weak exploration mechanism depends heavily on environmental randomness or external exploration strategies, thereby requiring more time to identify optimal actions as the network size increases. For example, in the largest network (Ingolstadt region), SAC-Beta sustains delays below 30 s, saving nearly a minute compared with PPO. Correspondingly, the CO₂ emissions of PPO in Ingolstadt are nearly double those of SAC-Beta. A reduced delay directly translates into shorter waiting times and fewer stop–start events. Since frequent acceleration significantly increases CO₂ emissions compared to steady driving, the vehicle delay serves as a key determinant of emissions. Figure 9 demonstrates that the SAC outperforms PPO in the CTS, and the Beta policy is better suited than the Gaussian policy for traffic signals and vehicle speed control. In continuous-action tasks, such as vehicle speed control, SAC-Gauss requires the compression and mapping of the action space. If the optimal action lies near the boundary (e.g., the vehicle reaches its maximum speed), the exploratory capability of the Gaussian distribution may be affected.

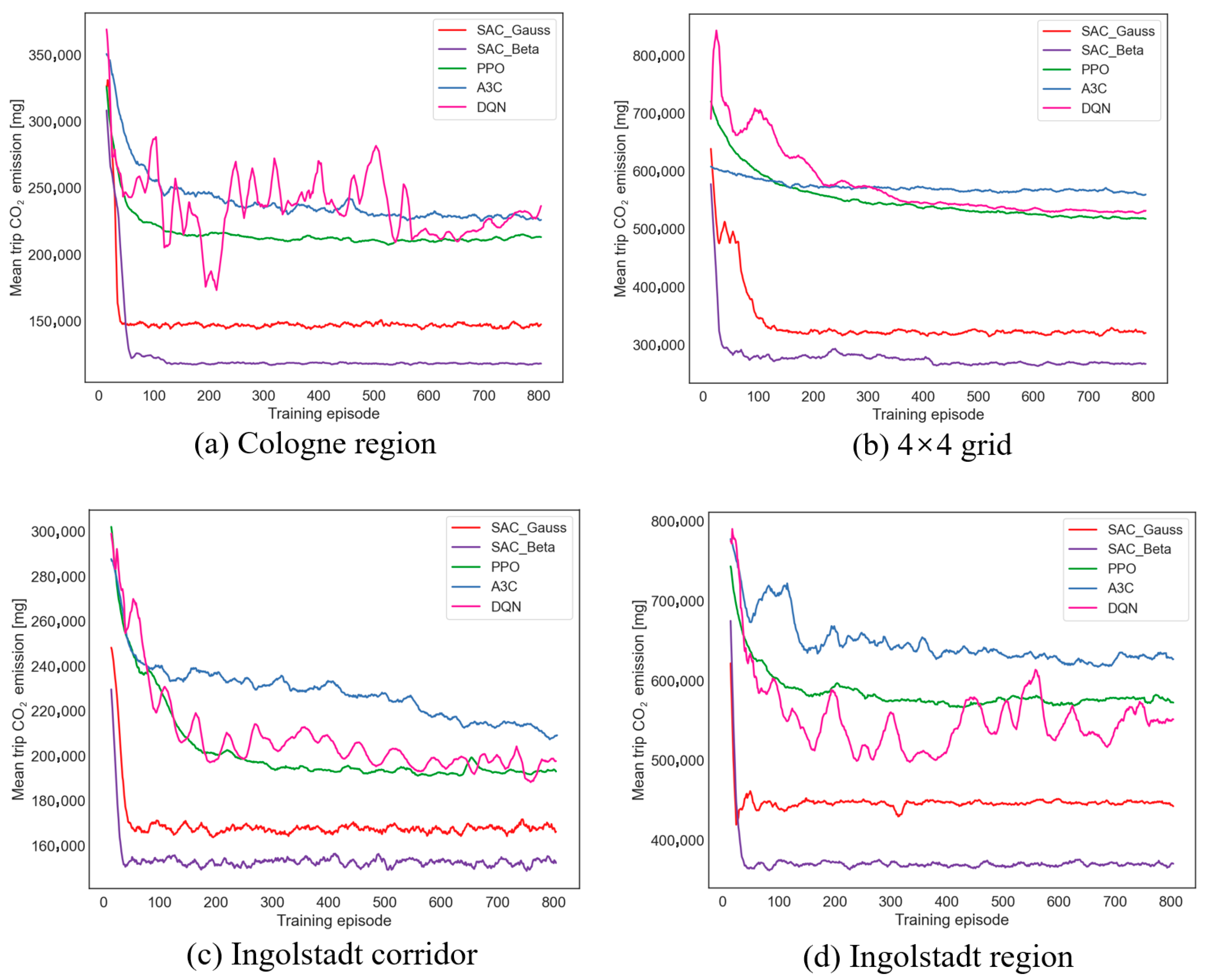
Figure 10 compares CO₂ emissions across traffic scenarios for five MARL algorithms in the TSC. Both SAC algorithms substantially outperform the other methods. The SAC achieves the fastest convergence, around 50 training cycles. Owing to entropy regularization, the SAC preserves the training stability and converges more rapidly than traditional Q-learning. PPO ranks second, converging at approximately 200 cycles, consistent with the results in Figure 9. The SAC is an off-policy algorithm that can leverage a replay buffer to repeatedly train on historical interaction data. Learning based on historical traffic flow data is likely the main reason for the rapid convergence of the SAC. In contrast, PPO is an on-policy algorithm, and each policy update relies solely on new data collected under the current policy.

After convergence, the SAC achieves substantially lower CO₂ emissions than other algorithms, which display only marginal differences among themselves. The performance gaps are most evident in the largest-scale network, the Ingolstadt region. The DQN fails to converge even after 800 training cycles. A3C yields the highest CO₂ emissions, followed by the PPO. The Beta policy converges the fastest and reduces CO₂ emissions by at least 20% versus the Gaussian policy.

Table 3. Fuel consumption [mg] of algorithms under CTS in different scenarios.

	Cologne Intersection and Region		Ingolstadt Corridor and Region		4 × 4 Grid
SAC-Beta	27,509.9	32,657.4	37,757.1	87,355.9	69,520.2
SAC-Gauss	28,152.1 (+2.3%)	40,793.2 (+24.9%)	50,418.7 (+33.5%)	136,575.1 (+56.3%)	89,124.1 (+28.2%)
PPO	44,967.2 (+63.5%)	63,869.8 (+95.6%)	60,074.9 (+59.1%)	168,534.4 (+92.9%)	145,900.9 (+109.9%)

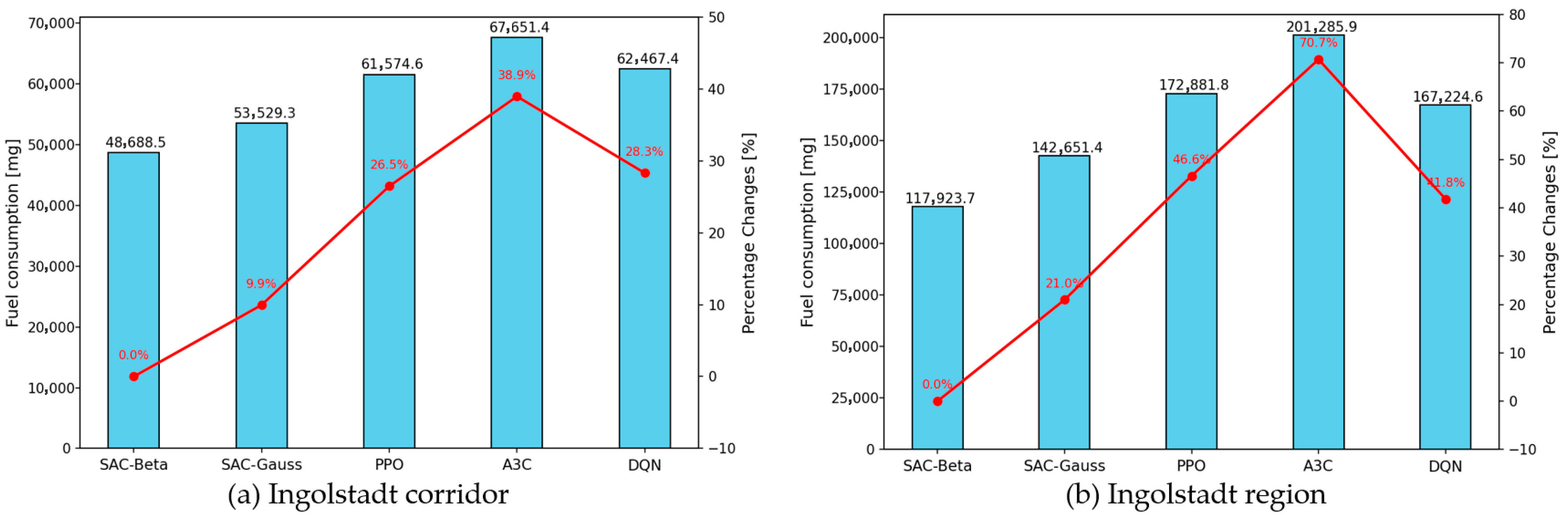
Notes: Data represents averages from the final 100 post-convergence training cycles. The best measurements are in bold. Percentage changes shown in parentheses are compared to the best measurements.

summarizes the fuel consumption under the CTS across various scenarios. SAC-Beta consistently exhibits the lowest fuel consumption in the CTS, outperforming SAC-Gaussian. At a single intersection, the performance gap between SAC-Beta and SAC-Gaussian is minimal, with differences below 10% under both systems. This gap widens significantly with the increased network scale and traffic flow, reaching approximately 56%. Figure 11 presents the fuel consumption results of different algorithms after the convergence under the TSC. The red polyline in Figure 11 depicts the percentage increase of other algorithms compared to SAC-Beta in fuel consumption. In Ingolstadt networks, SAC-Beta achieves the best performance, followed by SAC-Gaussian. PPO ranks third, whereas A3C and DQN demonstrate the poorest fuel efficiency.

The consistency with Figure 9 and Figure 10 confirms that algorithm performance rankings for the trip delay, CO₂ emissions, and fuel consumption are aligned. This alignment is expected, as the CO₂ emissions and fuel consumption scale proportionally with the trip delay. The vehicle stop–start frequency and delay time constitute key determinants of both metrics. This observed real-world correlation enhances the reliability of the experimental results. Furthermore, the advantage of SAC-Beta amplifies with increasing network complexity. This advantage arises from the Beta distribution being inherently bounded with the nonzero density at the boundaries. Particularly for continuous bounded action spaces that require precise control—such as vehicle speed—SAC-Beta does not require action mapping, unlike other algorithms.

5.3. Performance Analysis of CTS Under Intersections

Balancing local and global objectives constitutes a significant challenge in MARL. To further evaluate the performance of the SAC-Beta, SAC-Gaussian, and PPO policies within the CTS with respect to this balance, six key intersections in the Ingolstadt region were selected for observation (see Figure S2 in the Supporting Information). These intersections feature diverse geometries (crossroads and T-junctions) and road configurations (single-, double-, and three-lane roads).

Figure 12 and Figure 13 compare the traffic efficiency of the Beta and Gaussian policies at Intersections A and D, respectively. Figure 14 illustrates the speed variation for SAC-Beta and PPO at Intersection F. Traffic efficiency comparisons for the remaining three intersections (B, C, and E) are presented in Figures S3–S5. Collectively, these results demonstrate that the Beta policy significantly outperforms both the Gaussian policy and PPO in traffic efficiency across all six intersections.

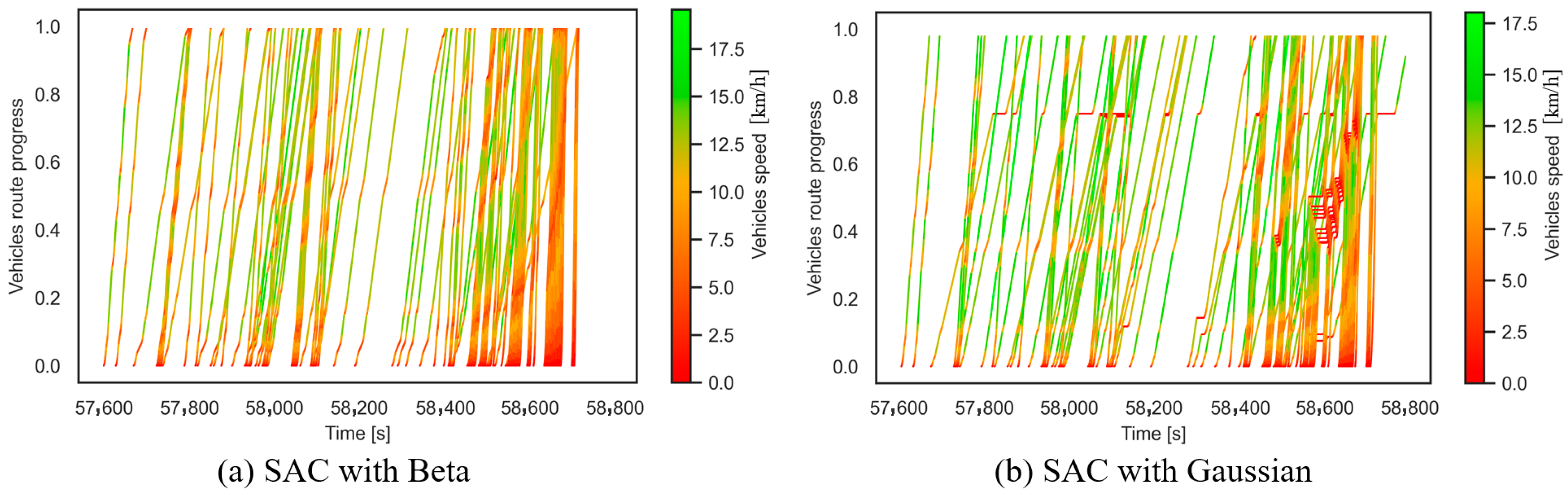
Figure 12 illustrates the performance of the Beta and Gaussian policies at Intersection A. The Beta policy predominantly exhibits a smooth green curve, indicating that vehicle speeds remain above 15 km/h while traversing the intersection. In contrast, the Gaussian policy displays fragmented dark-red curves, reflecting frequent vehicle stoppages with delays of up to approximately 100 s.

At Intersection D with heavy traffic flow (Figure 13), both policies predominantly produce red curves, with vehicle speeds frequently dropping below 10 km/h. Nevertheless, SAC-Beta maintains relatively smooth trajectories and avoids congestion despite the low speeds.

Table 4. Traffic conditions at Intersection D under the Beta and the Gaussian polices.

Method	Number of Vehicles	Queue Length	Traveling Time [s]	Vehicles Speed [km/h]
SAC-Beta	97	10	79	6.6
SAC-Gauss	101	18	103	6.4

Notes: (The queue length is defined as the number of consecutive vehicles traveling at speeds below 3 km/h. The traveling time refers to the average time a vehicle takes to travel from entering the VSC-controlled road section to exiting the intersection. The vehicle speed represents the average speed of all vehicles within the intersection).

offers a more detailed interpretation of the traffic conditions illustrated in Figure 13.

At Intersection F (Figure 14), the combination of heavy traffic flow and geometric constraints leads to relatively shallow curve slopes for both the Beta policy and PPO, indicating reduced traffic efficiency. Notably, PPO frequently produces deep-red curves indicative of congestion, whereas the Beta policy largely sustains a congestion-free operation.

Table 5. Traffic conditions at Intersection F under SAC-Beta and PPO.

Method	Number of Vehicles	Queue Length	Traveling Time [s]	Vehicles Speed [km/h]
SAC-Beta	77	4	93	10.4
PPO	68	11	122	8.1

offers a more detailed interpretation of the traffic conditions illustrated in Figure 14.

Overall, SAC-Beta demonstrates relatively excellent adaptability, delivering a substantially superior performance compared with the Gaussian policy and PPO across all six intersections. The efficacy of SAC-Beta at the intersection level enables the joint control system to achieve a high throughput, reduced emissions, and improved energy efficiency across large-scale networks.

6. Conclusions

This research proposes an eco-network control system based on MARL to alleviate urban congestion and environmental pollution. The framework synergistically integrates adaptive signal timing optimization with dynamic speed guidance control, overcoming traditional single-signal control limitations through dual-module coordination. By incorporating Beta distribution-enhanced SAC algorithms, our CTS demonstrates superior performance in traffic efficiency and ecological benefits compared to conventional approaches.

Future research directions include establishing a multi-power vehicle energy consumption model (covering fuel, electric, and hybrid vehicles) and implementing a nonlinear reward allocation strategy to optimize system practicality. In future work, we plan to incorporate vehicles with different emission levels into the networks, including light cars, buses, and heavy-duty trucks, and assign weights according to their emission levels in the reward function. Moreover, since it is difficult to ensure stable V2V and V2X communication for vehicles under different CAV penetrations, we will verify the practicality of the CTS in mixed CAV traffic flows.