Influence of Water Level Change on Vibration Response and Isolation of Saturated Soil Under Moving Loads
Abstract
1. Introduction
2. Basic Equation
3. Analysis of Soil Vibration Response
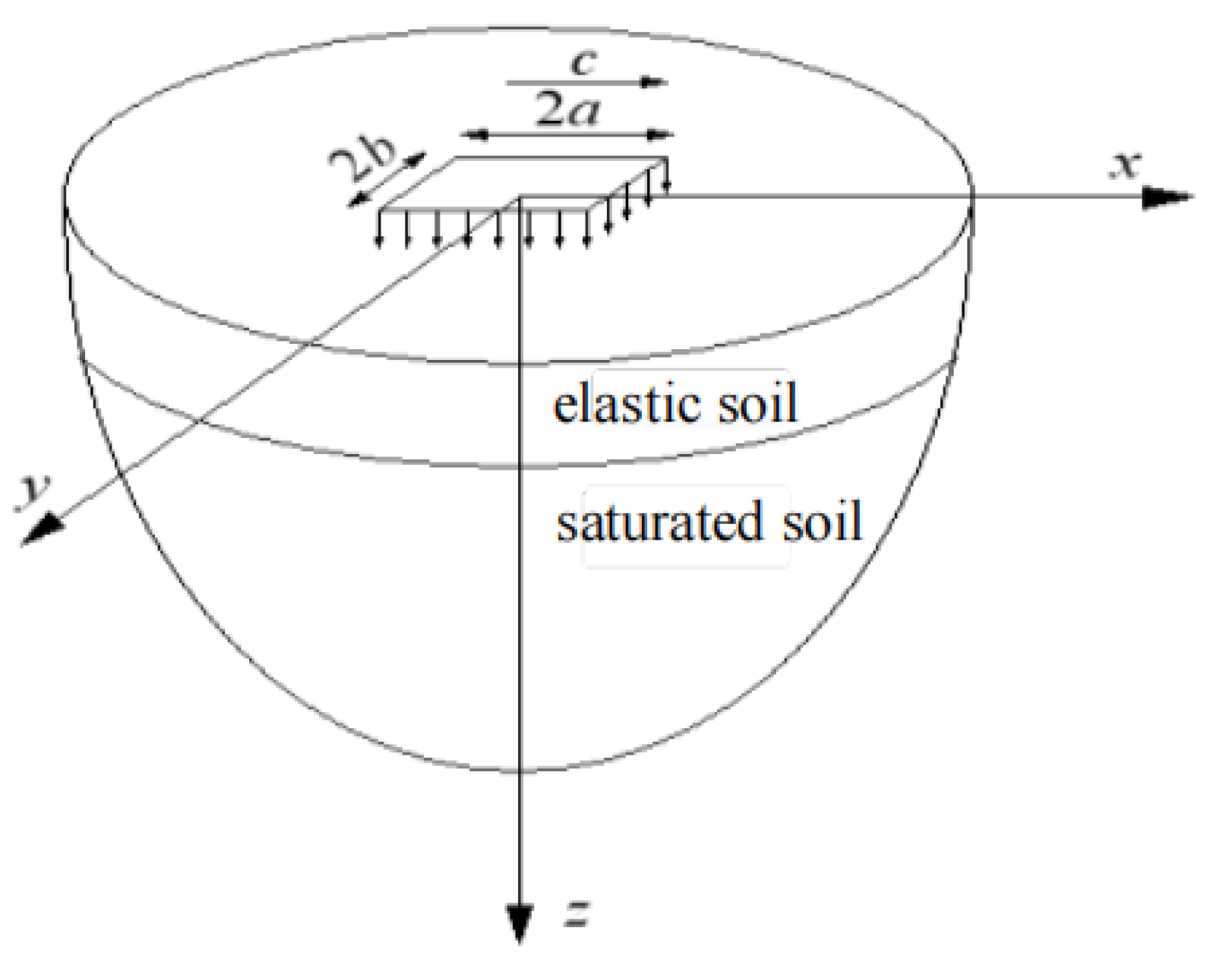
3.1. Vibration Response Model
3.2. Analysis of Vibration Calculation Results
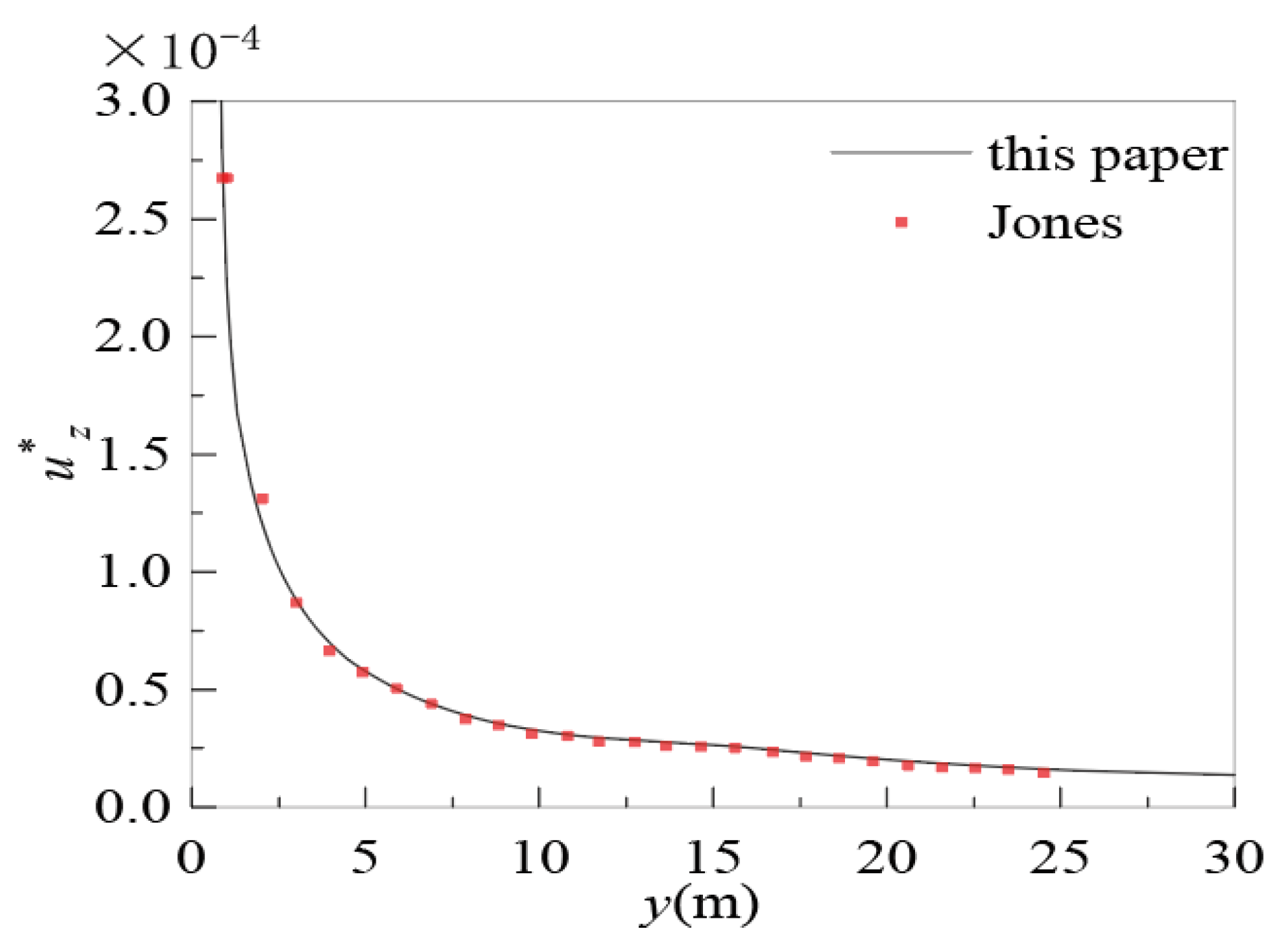
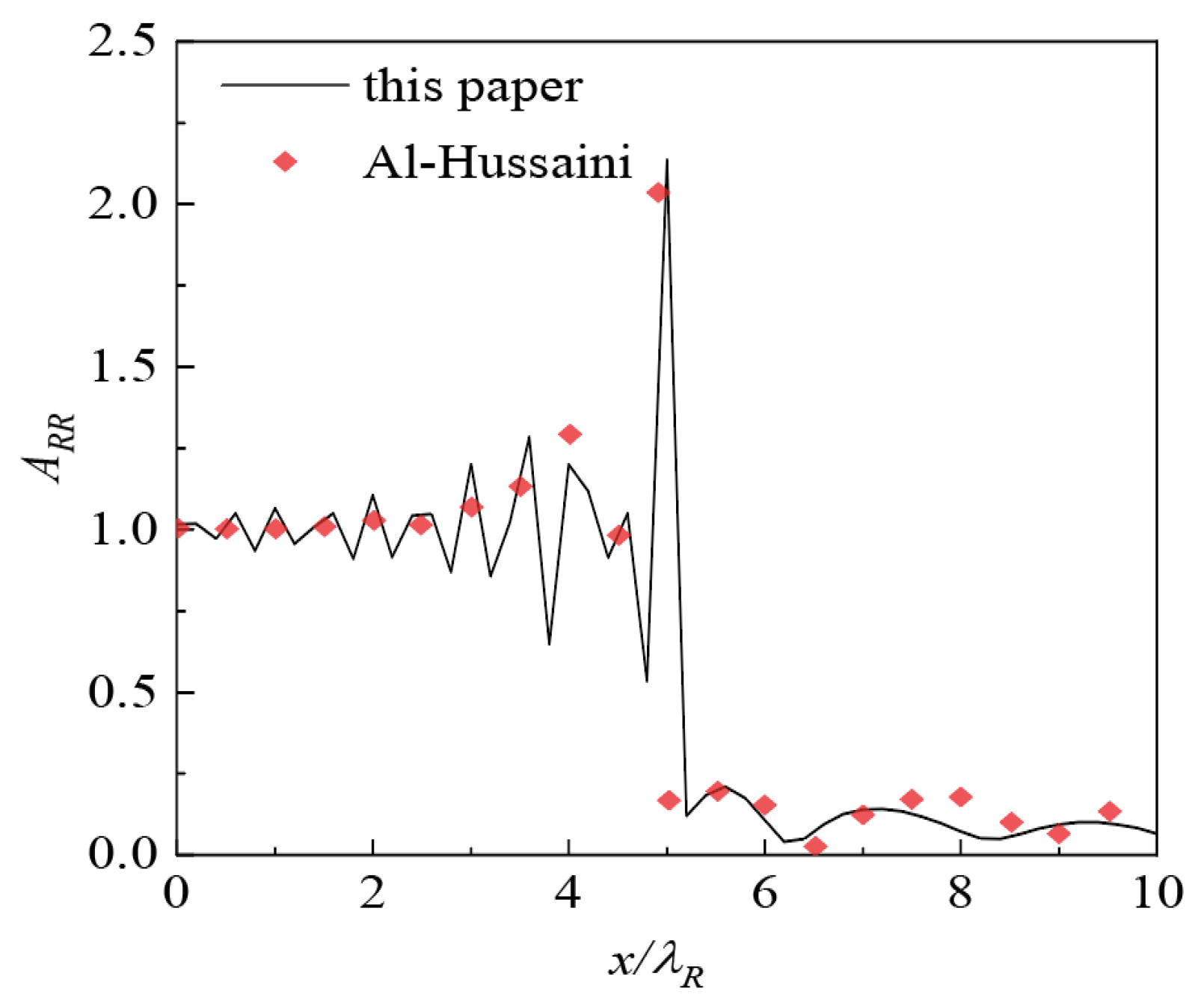
3.2.1. Model Verification
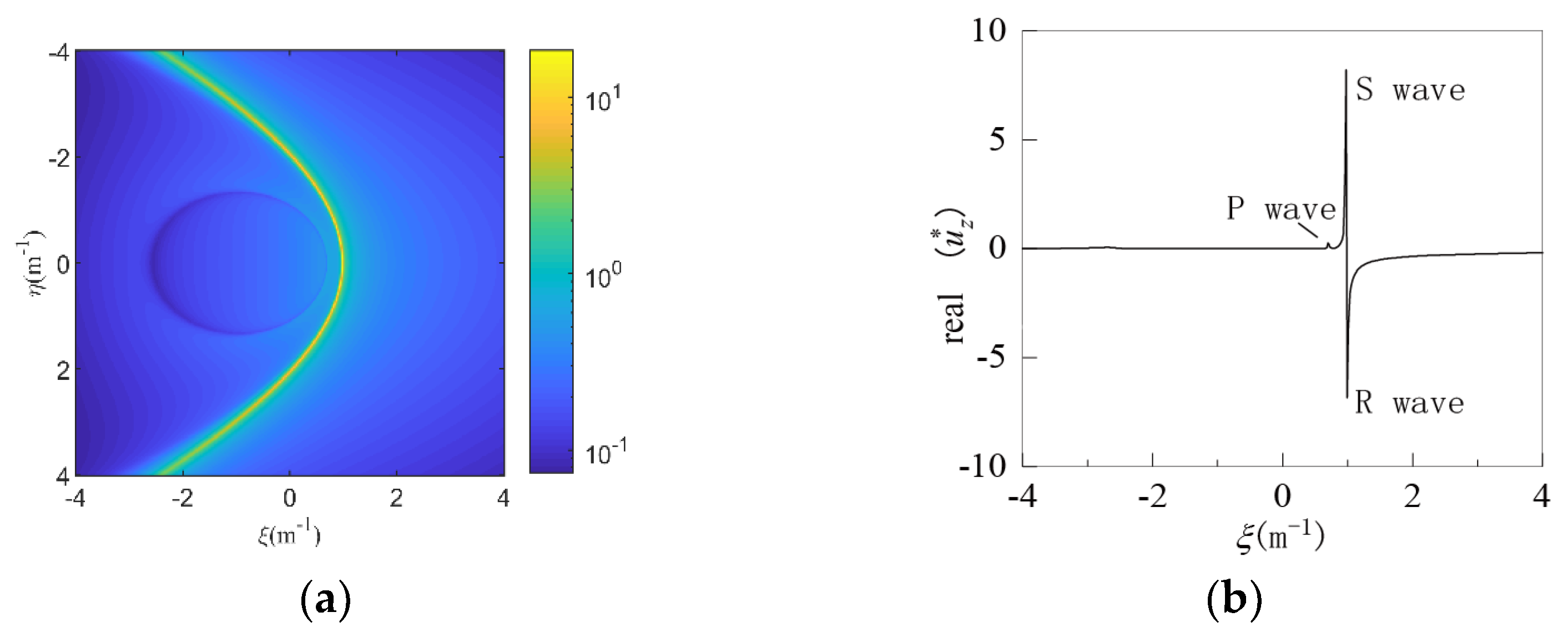
3.2.2. Analysis in Wave Number Domain
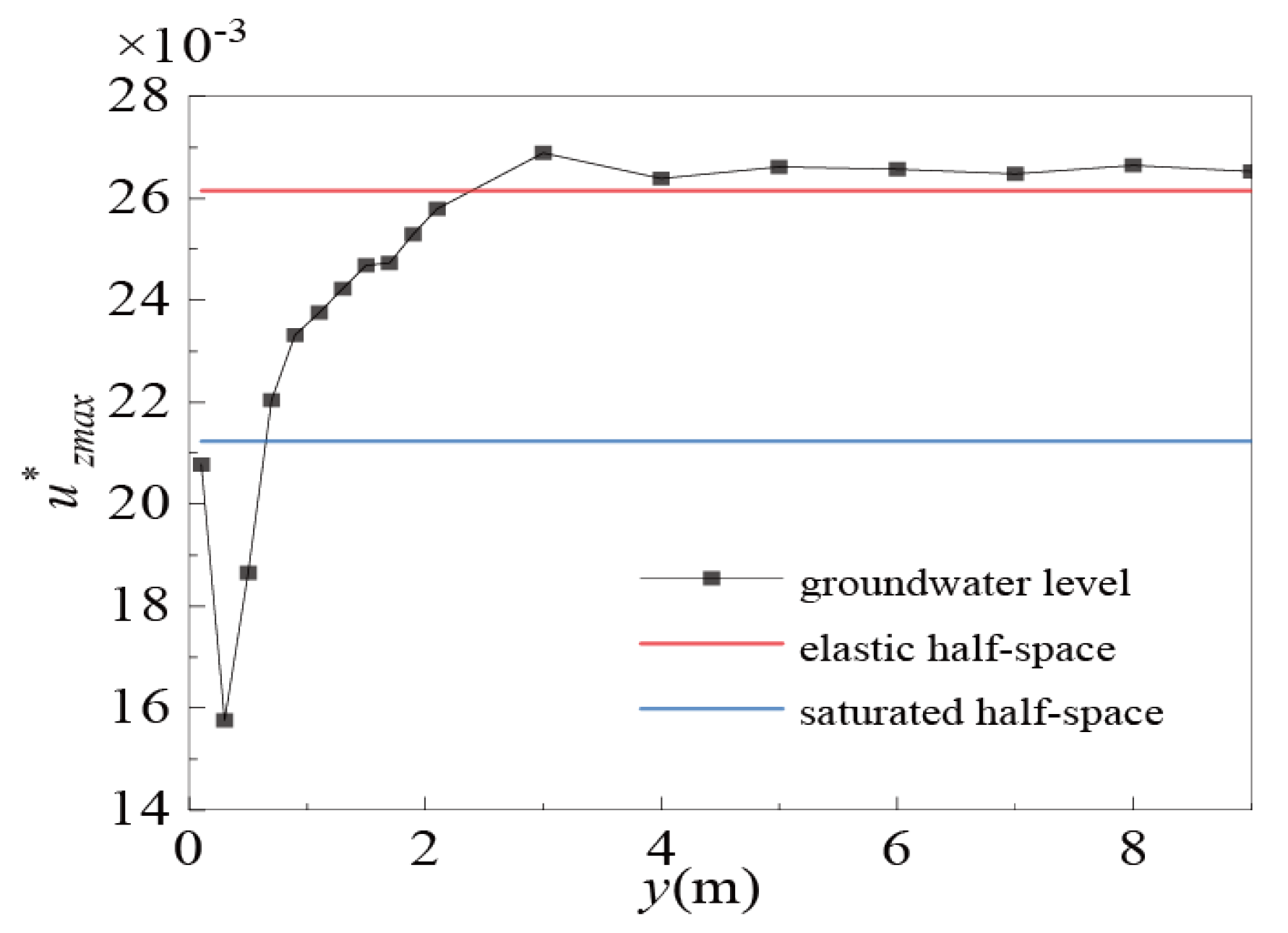
3.2.3. Analysis in Space Domain
4. Research on Natural Isolation Effect of Soil Mass
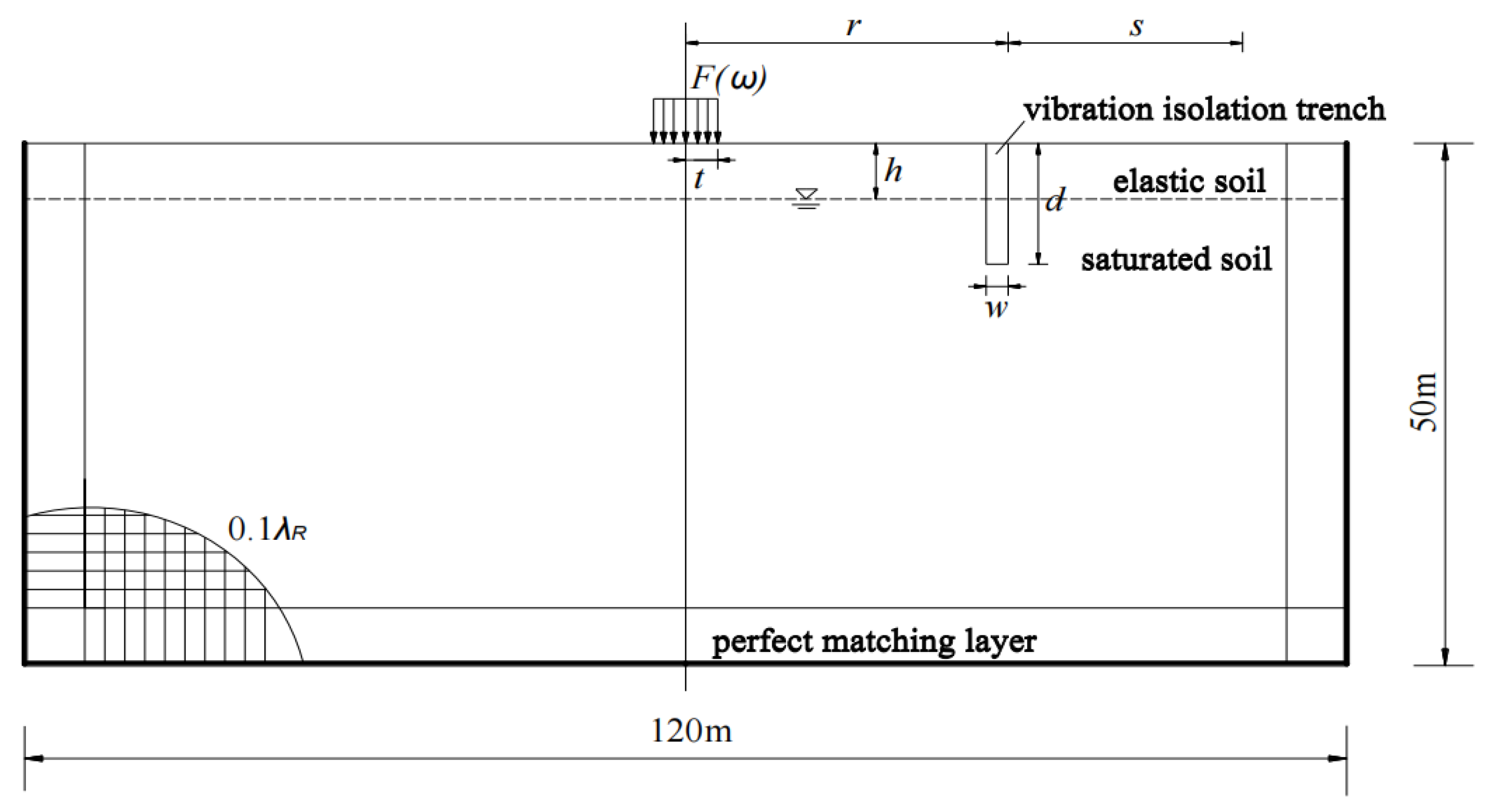
4.1. Establishment of Vibration Isolation Model
4.1.1. Model Assumptions
4.1.2. Model Size and Mesh Division
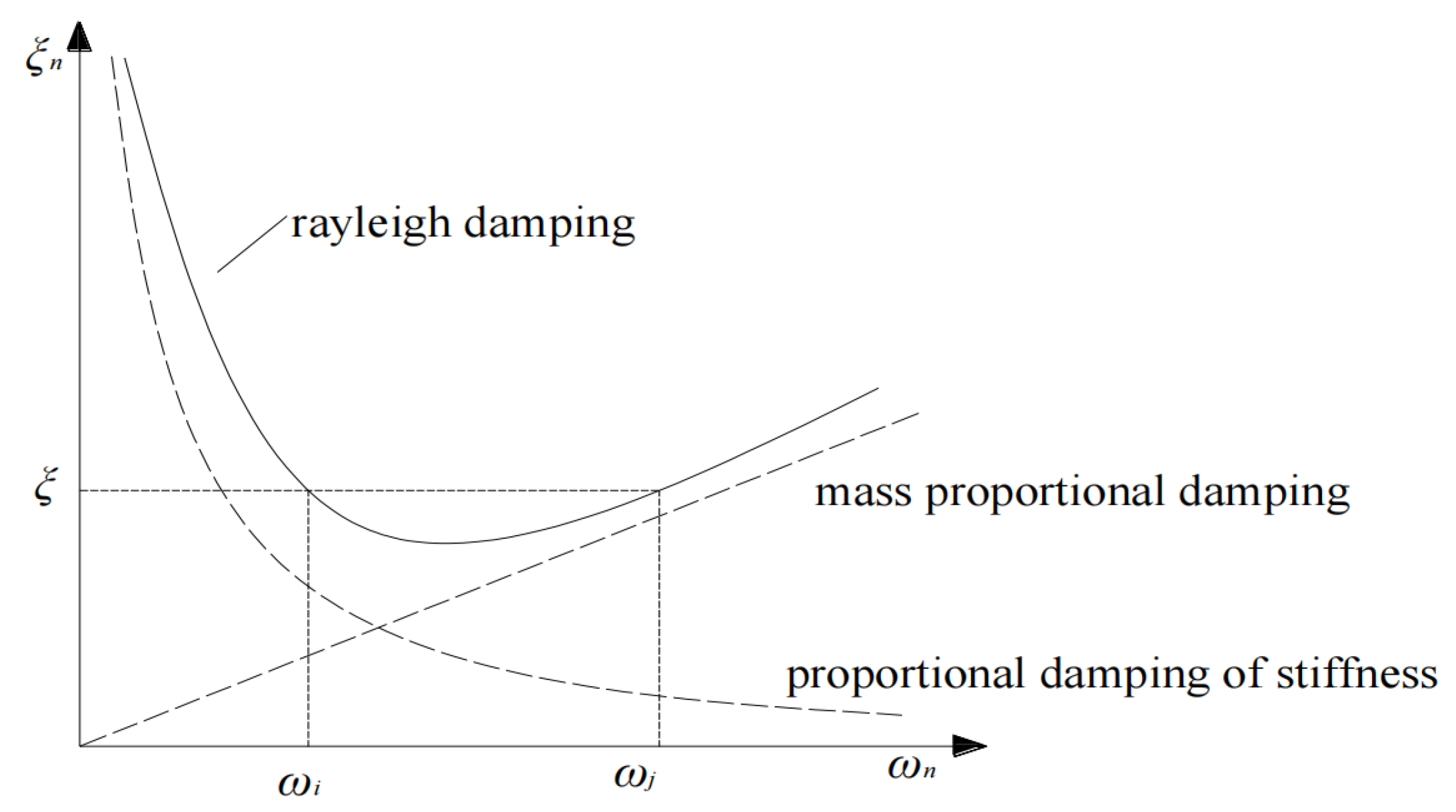
4.1.3. Damping Settings
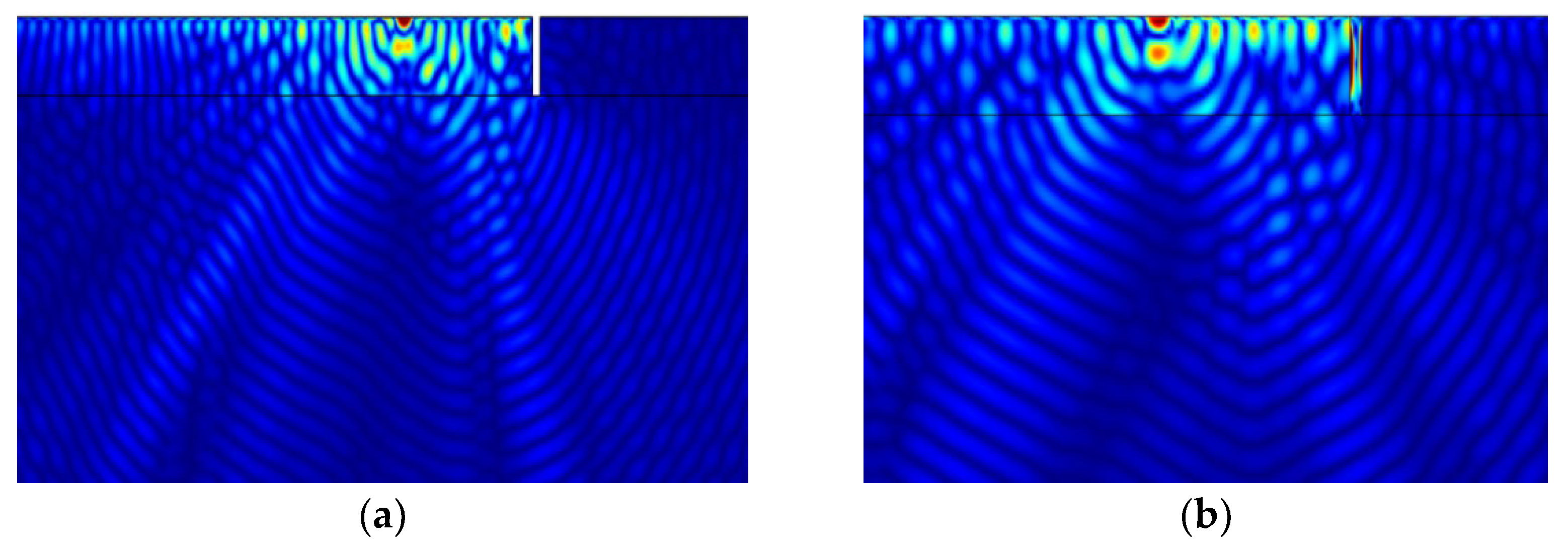
4.2. Model Verification
4.3. Parameter Analysis
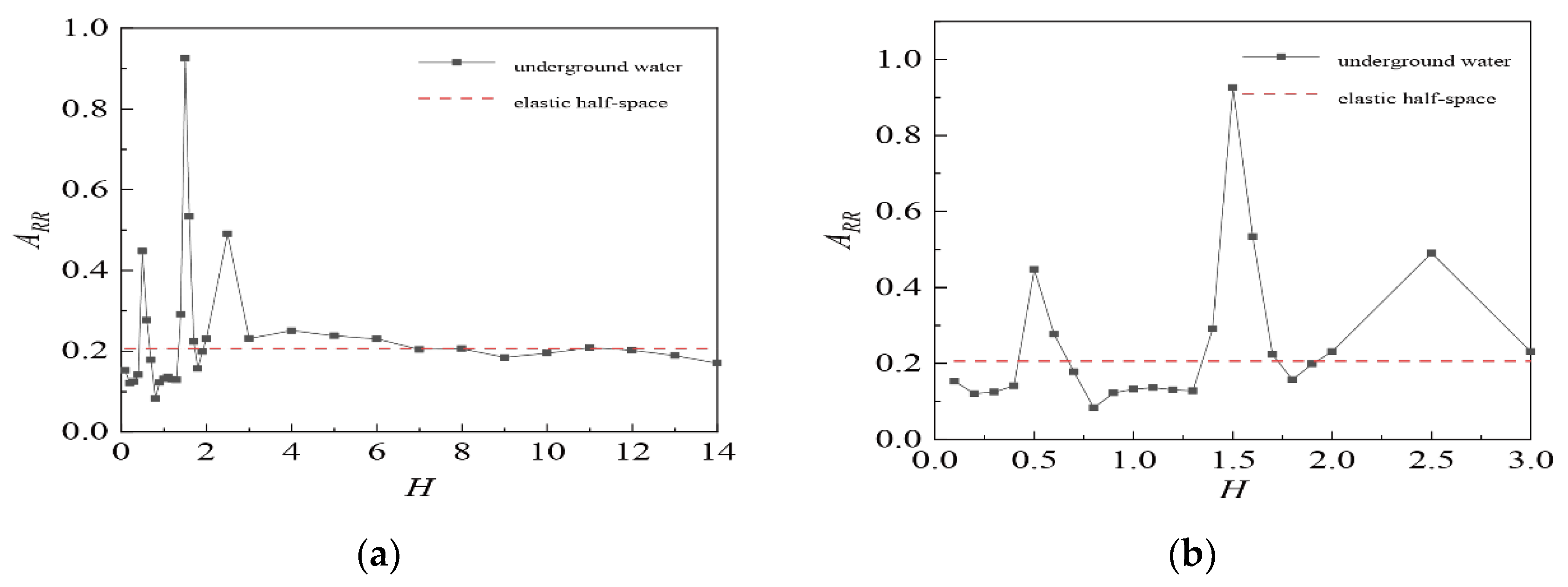
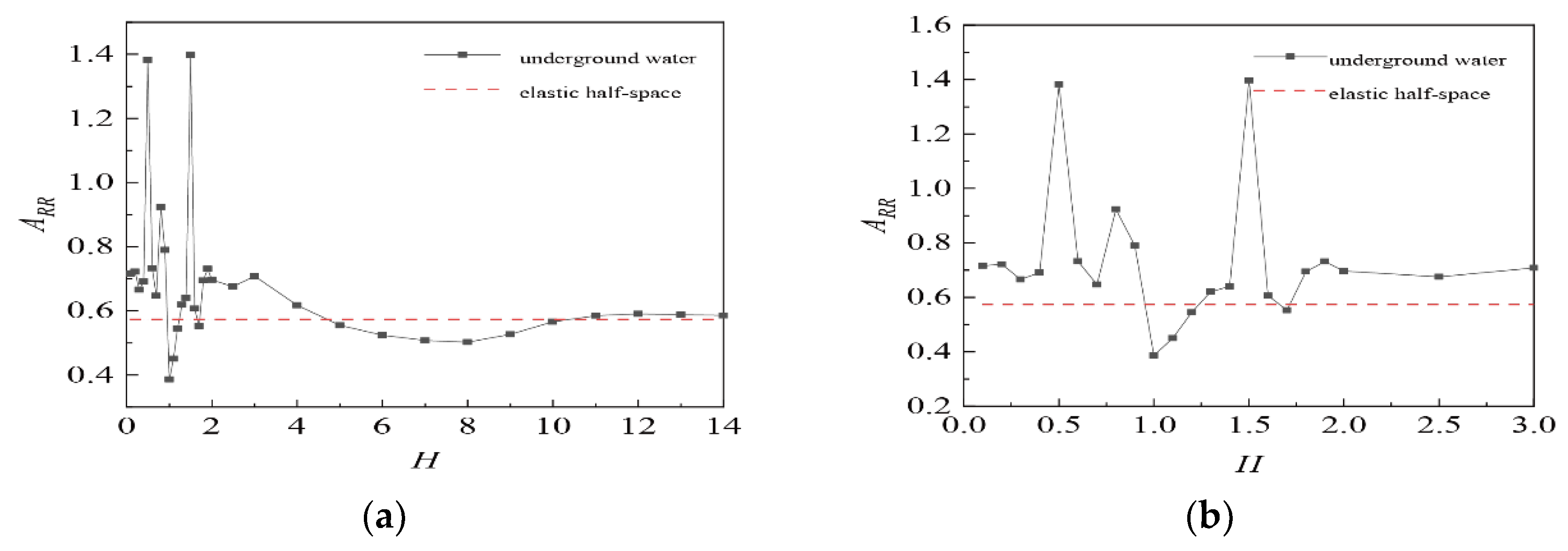
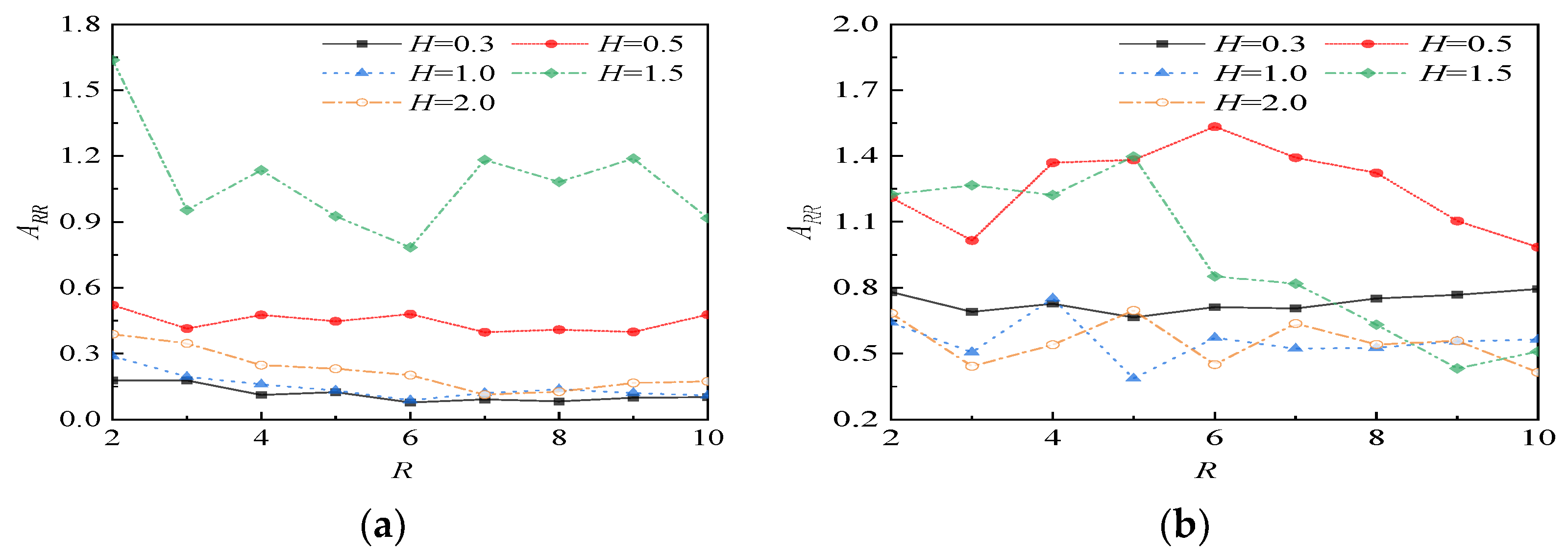
4.3.1. Influence of Water Level on Vibration Isolation Ditch
- (1)
- When the water level H ≤ 3, the water level change has a greater impact on the vibration isolation trench, and when the water level continues to decrease, the vibration isolation effect of the water level change is small. The water level is in the range of 0–3, the ARR in most positions of the empty trench is smaller than that in the elastic half-space, the ARR in the concrete in-filled trench is larger, and the vibration isolation effect of the empty trench is obviously better than that of the in-filled trench.
- (2)
- When the water level is near 0.5, 1.5, and 2.5 in the empty trench and 0.5 and 1.5 in the in-filled trench, ARR suddenly increases, and even exceeds 1 in the in-filled trench, because the elastic layer above these water levels resonates, consistent with the findings of Schevenels [29] (When n = 1, the thickness of the resonant elastic layer is 1.41 m, and the normalized water level height is H = 0.47; when n = 2, H = 1.41; when n = 3, H is 2.35, which basically corresponds to the resonance position in the figure).
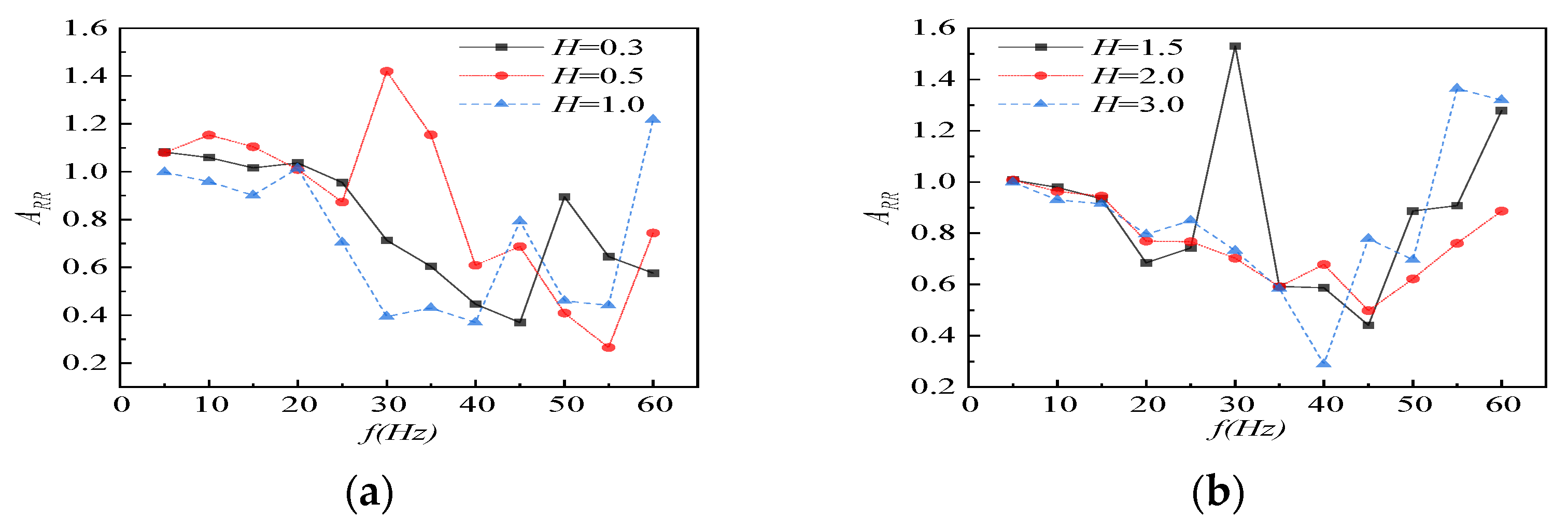
4.3.2. Influence of Load Frequency on Vibration Isolation Trench
- (1)
- The results show that vibration isolation effectiveness is not monotonic but highly frequency-dependent. These two types of trenches are most effective in the medium frequency range of approximately 20–50 Hertz. However, at very high frequencies, if they exceed 50 Hertz, it is consistent with the established principles of wave barrier design. This aligns with the work of Yang et al. [22]
- (2)
- The R wave, which is the main influence on far-field vibration isolation, is isolated, and the component of the P wave becomes larger. The influence on the vibration isolation effect in the overlying elastic soil layer is mainly the P wave. In the figures, at different water levels, ARR > 1 exists, indicating that both vibration isolation trenches have certain amplification frequencies that match the resonance frequency of the P wave, which is even more unfavorable for the vibration isolation effect. Both types of vibration isolation trenches have the phenomenon of vibration isolation failure caused by resonance at the same water level.
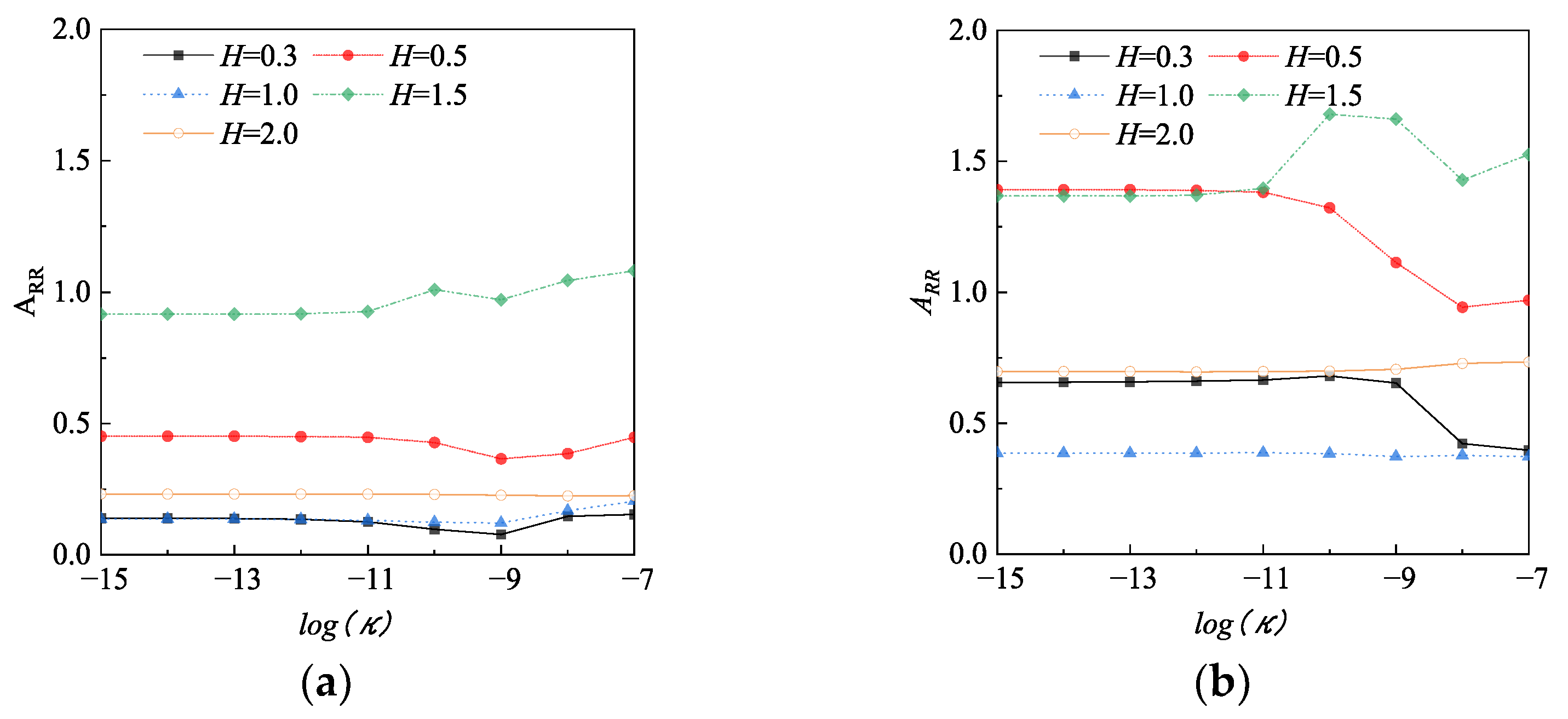
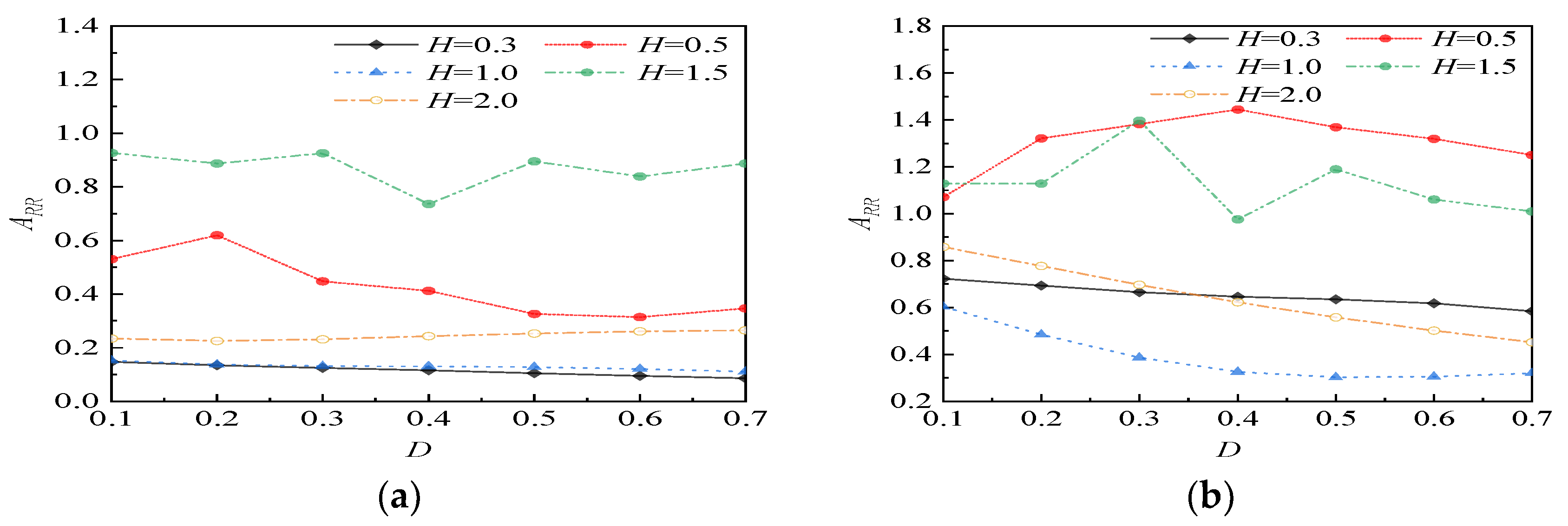
4.3.3. Influence of Water Permeability Coefficient on Vibration Isolation Effect
4.3.4. Influence of Barrier Depth on Vibration Isolation Effect
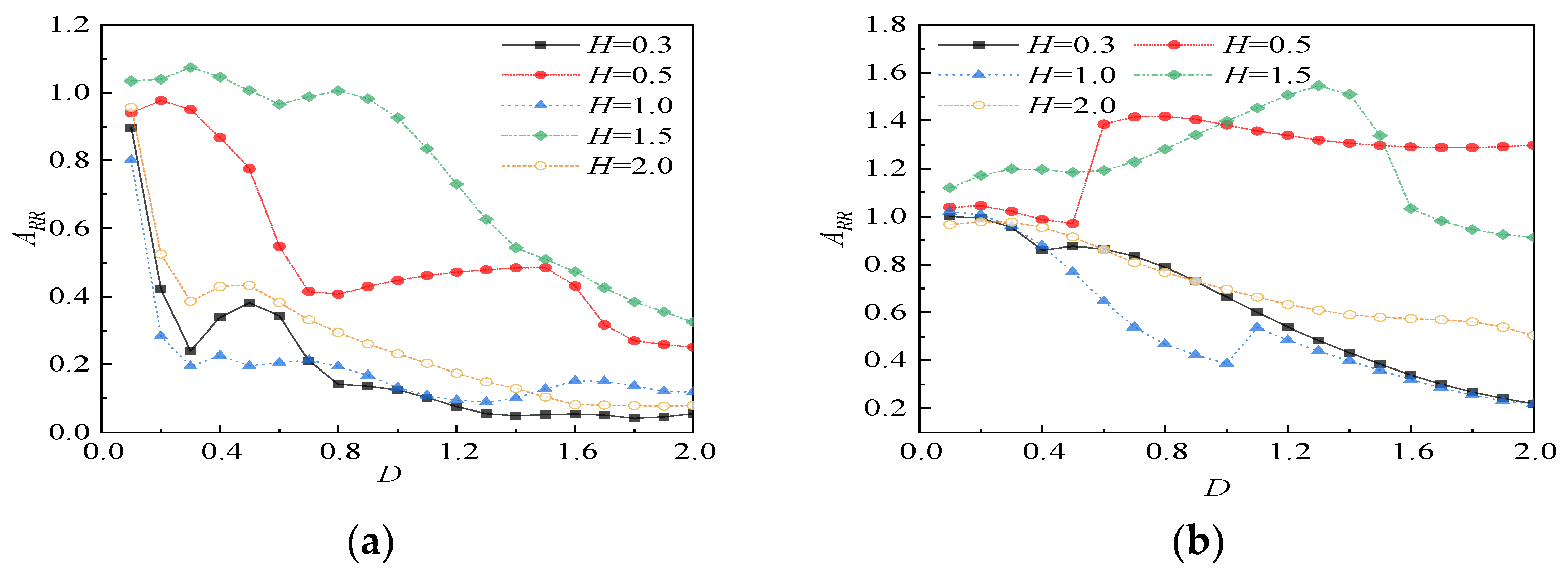
4.3.5. Influence of Barrier Distance on Vibration Isolation Effect
- (1)
- In the empty trench, except for the resonance water level, continuously decreases and then becomes stable as the barrier distance increases; The impact on the low water level is greater than that on the high water level. The empty trench’s performance is governed primarily by geometric diffraction, which is most effective in a homogeneous medium and benefits from distance until natural attenuation dominates.
- (2)
- In the in-filled trench, the change in barrier distance has an obvious influence on the vibration isolation effect, but the trend shows a certain fluctuation. At the resonance water level, when the distance is relatively large, the increase in barrier distance will enhance the vibration isolation effect. The in-filled trench’s performance is a result of complex wave transmission and interference, making it highly sensitive to placement and capable of counterintuitive behavior, particularly under resonant conditions.
4.3.6. Influence of Barrier Width on Vibration Isolation Effect
- (1)
- With the increase in empty trench width, ARR shows a decreasing trend, but the influence is limited; The effect of empty trench width on a high water level is greater than that of a low water level; For in-filled trenches, increased barrier width can effectively reduce the vibration behind the trenches.
- (2)
- The waves in the in-filled trench can be propagated to the vibration isolation area through the filling medium, and the transmitted energy of the waves through the filling medium can be reduced by increasing the width. The isolation of the empty trench is mainly through the distance change in the wave diffraction, so the increase in the barrier width is more conducive to enhancing the isolation effect of the in-filled trench.
5. Conclusions
- (1)
- Groundwater-induced stratification significantly alters the dynamic response of the soil foundation. The interface between the elastic layer and the saturated zone causes wave reflection and refraction, which amplifies or attenuates surface vibrations depending on the water table depth. When the water table is shallow, the response resembles that of a fully saturated half-space. As the water table lowers, the influence of reflections diminishes, and the behavior progressively approaches that of an elastic half-space.
- (2)
- The influence of water level depth on the isolation trench is limited to above a certain water level, and the isolation effect tends to be in the elastic medium when it is below this water level; The difference in water level height will cause P-wave resonance in elastic dry soil layer, which is not conducive to vibration isolation.
- (3)
- There will be different resonance water levels at different frequencies, so that the barrier loses the effect of vibration isolation but magnifies the vibration at some positions behind the ditch; The resonance of different types of waves has different effects on the isolation effect of empty trench and in-filled trench.
- (4)
- When the permeability coefficient of saturated soil is high, it will affect the vibration isolation effect, and when the permeability coefficient is relatively low, it will hardly affect the vibration isolation effect. The increase in the depth of the isolation ditch is generally conducive to vibration isolation; the relationship between the in-filled trench and the water level will also affect the isolation effect, and the depth of the in-filled trench below the water level will be worse than the isolation effect when the water level is higher.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xia, H.; Wu, X.; Yu, D.M. Environment vibration induced by urban rail transit system. J. North. Jiaotong Univ. 1999, 23, 1–7. [Google Scholar]
- Eason, G. The stresses produced in a semi-infinite solid by a moving surface force. Int. J. Eng. Sci. 1965, 2, 581–609. [Google Scholar] [CrossRef]
- Lefeuve-Mesgouez, G.; Houedec, D.L.; Peplow, A.T. Ground vibration in the vicinity of a high-speed moving harmonic strip load. J. Sound Vib. 2000, 231, 1289–1309. [Google Scholar] [CrossRef]
- Andersen, L.; Nielsen, S.R.K. Boundary element analysis of the steady-state response of an elastic half-space to a moving force on its surface. Eng. Anal. Bound. Elem. 2003, 27, 23–38. [Google Scholar] [CrossRef]
- Galvin, P.; Dominguez, J. Analysis of ground motion due to moving surface loads induced by high-speed trains- Science Direct. Eng. Anal. Bound. Elem. 2007, 31, 931–941. [Google Scholar] [CrossRef]
- Coelho, B.Z.; Nuttall, J.; Noordam, A.; Dijkstra, J. The impact of soil variability on uncertainty in predictions of induced vibrations. Soil Dyn. Earthq. Eng. 2023, 169, 107855. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, X.; Qiu, L.; Dong, J.; Zhou, Z.; Ji, Z.; Liang, L. Characteristics of Elastic Wave Propagation in Fluid-Saturated Porous Media Based on the Model of Soil Mechanics. Pure Appl. Geophys. 2023, 180, 2309–2326. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low frequency range. J. Acoust. Soc. Am. 1955, 28, 168–191. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid: II. Higher frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Theodorakopoulos, D.D.; Chassiakos, A.P.; Beskos, D.E. Dynamic effects of moving load on a poroelastic soil medium by an approximate method. Int. J. Solids Struct. 2004, 41, 1801–1822. [Google Scholar] [CrossRef]
- Lu, J.F.; Jeng, D.S. A half-space saturated poro-elastic medium subjected to a moving point load. Int. J. Solids Struct. 2007, 44, 573–586. [Google Scholar] [CrossRef]
- Gao, G.Y.; Li, N.; He, J.F.; Gao, M. Analysis of ground vibration generated by train moving loads on saturated soil. J. Vib. Shock 2011, 30, 86–92. [Google Scholar]
- Gao, G.Y.; Chen, Q.S.; He, J.F.; Liu, F. Investigation of Ground Vibration Due to Trains Moving on Saturated Multi-Layered Ground by 2.5D Finite Element Method. Soil Dyn. Earthq. Eng. 2012, 40, 87–98. [Google Scholar] [CrossRef]
- Anthony, E.; Vedanti, N. Simulation of seismic wave propagation in poroelastic media using vectorized Biot’s equations: An application to a CO2 sequestration monitoring case. Acta Geophys. 2020, 68, 435–444. [Google Scholar] [CrossRef]
- Alamo, G.M.; Bordón, J.D.; Aznarez, J.J.; Lombaert, G. The effectiveness of a pile barrier for vibration transmission in a soil stratum over a rigid bedrock. Comput. Geotech. 2019, 110, 274–286. [Google Scholar] [CrossRef]
- Yuan, Z.; Cao, Z.; Boström, A.; Cai, Y. The influence of pore-fluid in the soil on ground vibrations from a tunnel embedded in a layered half-space. J. Sound Vib. 2018, 419, 227–248. [Google Scholar] [CrossRef]
- He, C.; Zhou, S.; Guo, P. Train-Induced Vibrations from a Tunnel in a Layered Half-Space with Varied Groundwater Table. Int. J. Geomech. 2020, 20, 04020174. [Google Scholar] [CrossRef]
- Feng, S.-J.; Li, J.-P.; Zhang, X.-L.; Chen, Z.-L.; Li, Y.-C. Effects of water table on ground-borne vibration screening effectiveness by using open trenches. Soil Dyn. Earthq. Eng. 2020, 131, 10603. [Google Scholar] [CrossRef]
- Johnson, D.L.; Koplik, J.; Dashen, R. Theory of dynamic permeability and tortuosity in fluid-saturated porous-media. J. Fluid Mech. 1987, 176, 379–402. [Google Scholar] [CrossRef]
- Jones, D.V.; Houedec, D.L.; Petyt, M. Ground vibrations due to a rectangular harmonic load. J. Sound Vib. 1998, 212, 61–74. [Google Scholar] [CrossRef]
- Bo, Q.; Ali, L.; Irini, D.M. Numerical study of wave barrier and its optimization design. Finite Elem. Anal. Des. 2014, 84, 1–13. [Google Scholar] [CrossRef]
- Yang, Y.B.; Hung, H.H. A parametric study of wave barriers for reduction of train-induced vibrations. Int. J. Numer. Methods Eng. 2007, 40, 3729–3747. [Google Scholar] [CrossRef]
- Bérenger, J.P. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Woods, R.D. Screening of surface wave in soils. J. Soil Mech. Found. Div. 1968, 94, 951–979. [Google Scholar] [CrossRef]
- Ahmad, S.; Al-Hussaini, T.M. Simplified design for vibration screening by open and in-filled trenches. J. Geotech. Eng. (ASCE) 1991, 117, 67–88. [Google Scholar] [CrossRef]
- Lambe, T.W.; Whitman, R.V. Soil Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1969. [Google Scholar]
- Biot, M.A. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Wang, H.F. Theory of Linear Poroelasticity with Applications to Geomechanics and Hydrogeology; Princeton University Press: Princeton, NJ, USA, 2017. [Google Scholar]
- Schevenels, M.; Degrandec, G.; Lombaert, G. The influence of the depth of the ground water table on free field road traffic-induced vibrations. Int. J. Numer. Anal. Methods Geomech. 2004, 28, 395–419. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Chan, A.H.C.; Pastor, M.; Schrefler, B.A.; Shiomi, T. Computational Geomechanics with Special Reference to Earthquake Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]







| Parameter Names | Numerical Value |
| Shear modulus of saturated soil, μ | 2 × 107 N/m2 |
| Lame constant, λ | 2 × 107 N/m2 |
| Soil particle density, ρs | 2000 kg/m3 |
| Pore water density, ρf | 1000 kg/m3 |
| Porosity, n | 0.3 |
| Damping ratio, β | 0.02 |
| Permeability coefficient, k | 1 × 1011 m2 |
| Pore fluid bulk modulus, | 2.19 × 109 pa |
| Hydrodynamic viscosity, η | 1 × 10−3 Pa |
| Soil particle compression constant, α | 1 |
| Bending coefficient of porous media, a∞ | 1 |
| Parameter Names | Numerical Value |
| Modulus of elasticity, E | 3 × 1010 Pa |
| Poisson’s ratio, | 0.2 |
| Damping coefficient, | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, J.; Chen, Y.; Dong, L. Influence of Water Level Change on Vibration Response and Isolation of Saturated Soil Under Moving Loads. Appl. Sci. 2025, 15, 10461. https://doi.org/10.3390/app151910461
Yao J, Chen Y, Dong L. Influence of Water Level Change on Vibration Response and Isolation of Saturated Soil Under Moving Loads. Applied Sciences. 2025; 15(19):10461. https://doi.org/10.3390/app151910461
Chicago/Turabian StyleYao, Jinbao, Yueyue Chen, and Longhua Dong. 2025. "Influence of Water Level Change on Vibration Response and Isolation of Saturated Soil Under Moving Loads" Applied Sciences 15, no. 19: 10461. https://doi.org/10.3390/app151910461
APA StyleYao, J., Chen, Y., & Dong, L. (2025). Influence of Water Level Change on Vibration Response and Isolation of Saturated Soil Under Moving Loads. Applied Sciences, 15(19), 10461. https://doi.org/10.3390/app151910461






