A Hybrid Approach to Investigating Factors Associated with Crash Injury Severity: Integrating Interpretable Machine Learning with Logit Model
Abstract
1. Introduction
2. Literature Review
2.1. Traditional Statistical Modeling Approaches
- Unordered categorical models
- Ordered categorical models
2.2. Machine Learning Approaches
3. Data Source
4. Methodology
4.1. Framework
4.2. Random Forest
4.3. Shapely Additive Explanations
4.4. Statistical Models
4.5. Evaluation Metrics
5. Results and Discussion
5.1. Model Results
5.1.1. Validation of Injury Severity Category Merging
5.1.2. Model Results from Random Forest
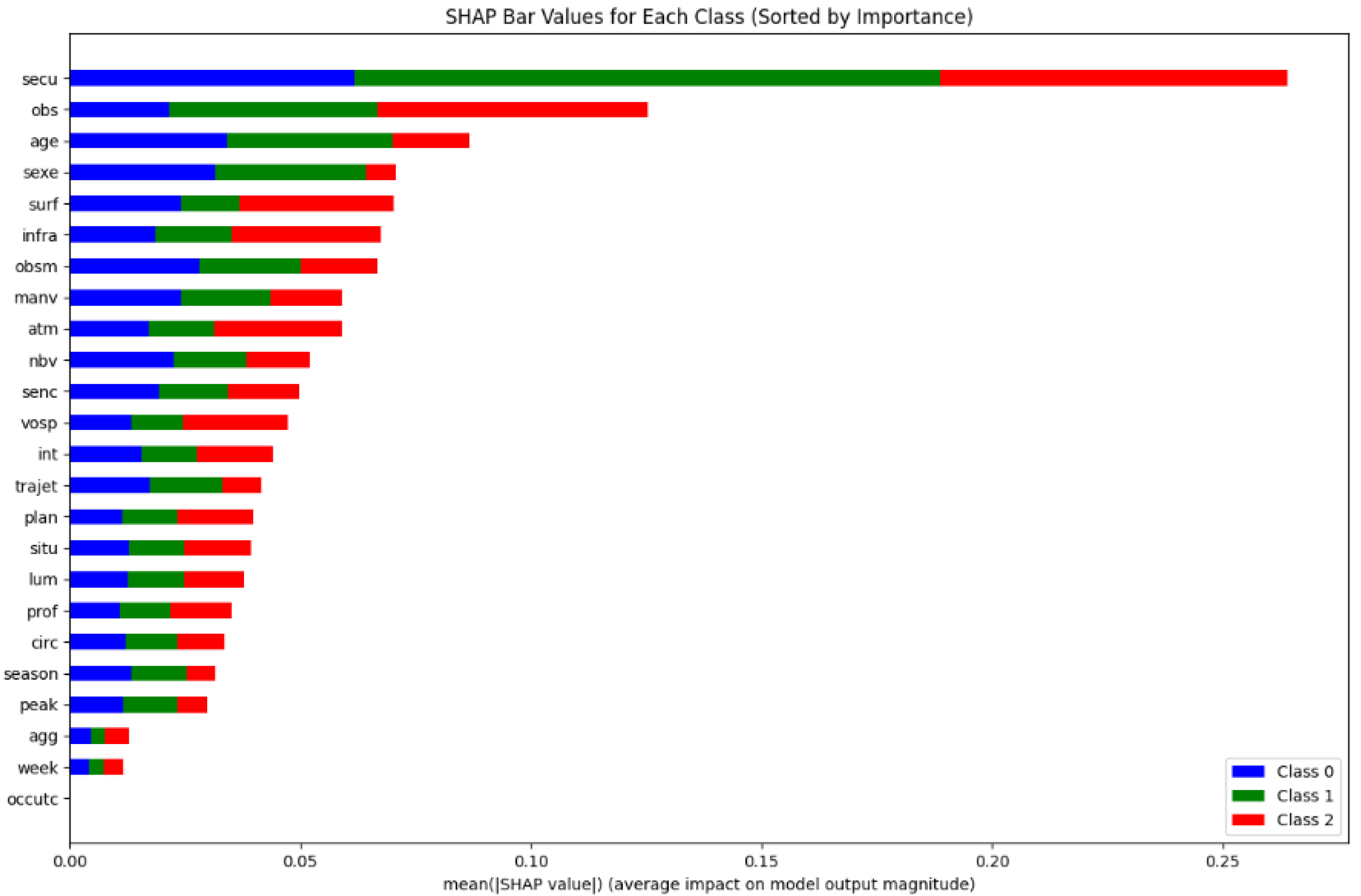
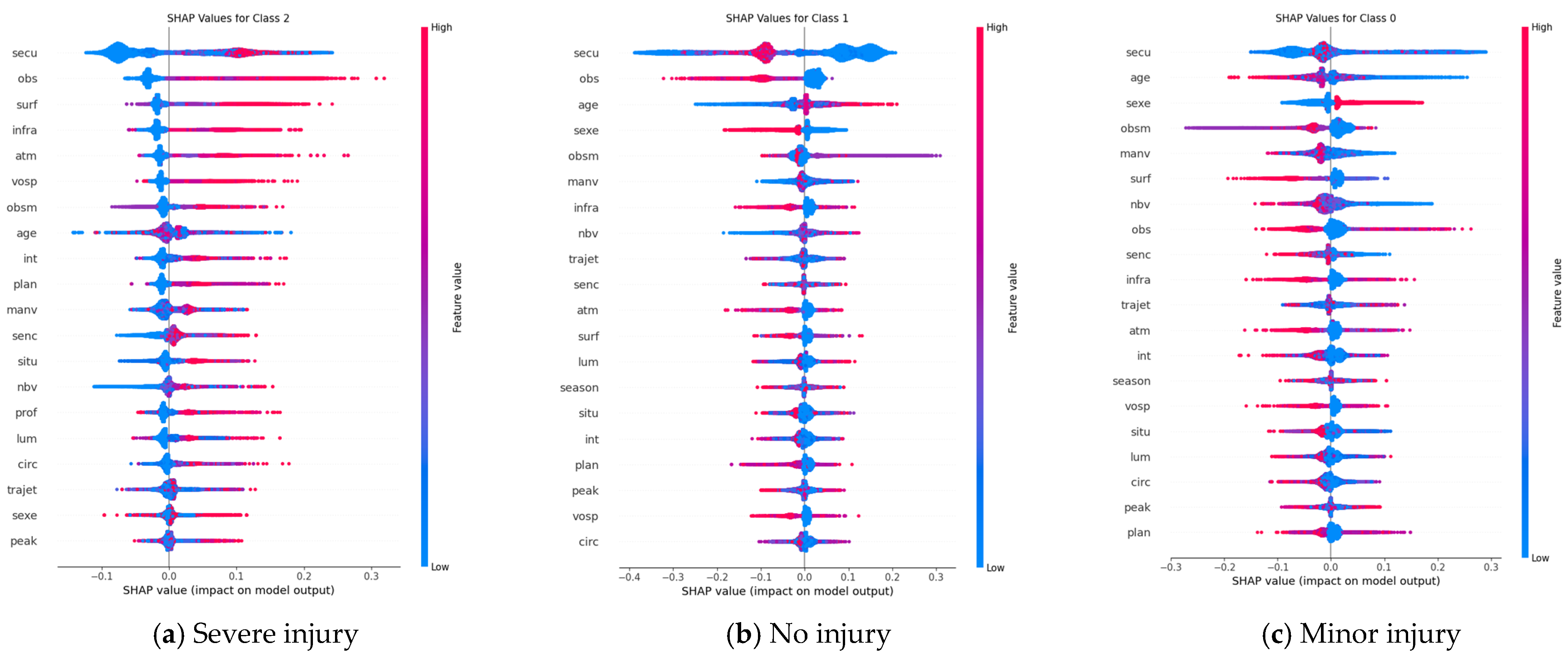
5.2. Model Interpretation by SHAP
5.3. Model Interpretation by Logit Models
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AUC | Area Under the Curve |
| MLAs | Machine Learning Algorithms |
| SHAP | Shapley Additive Explanations |
| TreeSHAP | Tree-based Shapley Additive Explanations |
| MNLogit | Multinomial Logit Model |
| ROC | Receiver Operating Characteristic |
| DT | Decision Tree |
| SVM | Support Vector Machine |
| GBM | Gradient Boosting Machine |
| XGBoost | eXtreme Gradient Boosting |
| OLR | Ordered Logit Regression |
| GOL | Generalized Ordered Logit |
| WHO | World Health Organization |
| POA | Proportional Odds Assumption |
| ONISR | Observatoire National Interministériel de la Sécurité Routière |
| PPO | Partial Proportional Odds (model) |
| AME | Average Marginal Effect(s) |
| OvR | One-vs-Rest |
| AIC | Akaike Information Criterion |
| BIC | Bayesian Information Criterion |
| CI | Confidence Interval |
| IIA | Independence of Irrelevant Alternatives |
| PR-AUC | Precision–Recall Curve |
| RF | Random Forest |
References
- World Health Organization Road Traffic Injuries. Available online: https://www.who.int/health-topics/road-safety (accessed on 23 July 2025).
- Observatoire National Interministériel de la Sécurité Routière Le Savez Vous? Available online: https://www.onisr.securite-routiere.gouv.fr/ (accessed on 23 July 2025).
- Ling, J.; Qian, X.; Gkritza, K. Electric Vehicles vs. Internal Combustion Engine Vehicles: A Comparative Study of Crashes Involving Vulnerable Road Users. Int. J. Transp. Sci. Technol. 2025, in press. [Google Scholar] [CrossRef]
- Lee, D.; Guldmann, J.-M.; von Rabenau, B. Impact of Driver’s Age and Gender, Built Environment, and Road Conditions on Crash Severity: A Logit Modeling Approach. Int. J. Environ. Res. Public Health 2023, 20, 2338. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Fan, W. A Multinomial Logit Model of Pedestrian-Vehicle Crash Severity in North Carolina. Int. J. Transp. Sci. Technol. 2019, 8, 43–52. [Google Scholar] [CrossRef]
- Karabulut, N.C.; Ozen, M. Exploring Driver Injury Severity Using Latent Class Ordered Probit Model: A Case Study of Turkey. KSCE J. Civ. Eng. 2023, 27, 1312–1322. [Google Scholar] [CrossRef]
- Keramati, A.; Lu, P.; Iranitalab, A.; Pan, D.; Huang, Y. A Crash Severity Analysis at Highway-Rail Grade Crossings: The Random Survival Forest Method. Accid. Anal. Prev. 2020, 144, 105683. [Google Scholar] [CrossRef] [PubMed]
- Parsa, A.B.; Movahedi, A.; Taghipour, H.; Derrible, S.; Mohammadian, A. Toward Safer Highways, Application of XGBoost and SHAP for Real-Time Accident Detection and Feature Analysis. Accid. Anal. Prev. 2020, 136, 105405. [Google Scholar] [CrossRef] [PubMed]
- Shaffiee Haghshenas, S.; Guido, G.; Shaffiee Haghshenas, S.; Astarita, V. Predicting the Level of Road Crash Severity: A Comparative Analysis of Logit Model and Machine Learning Models. Transp. Eng. 2025, 20, 100323. [Google Scholar] [CrossRef]
- Razi-Ardakani, H.; Mahmoudzadeh, A.; Kermanshah, M. A Nested Logit Analysis of the Influence of Distraction on Types of Vehicle Crashes. Eur. Transp. Res. Rev. 2018, 10, 44. [Google Scholar] [CrossRef]
- Ma, C.; Zhou, J.; Yang, D. Causation Analysis of Hazardous Material Road Transportation Accidents Based on the Ordered Logit Regression Model. Int. J. Environ. Res. Public Health 2020, 17, 1259. [Google Scholar] [CrossRef]
- Song, L.; Fan, W. Combined Latent Class and Partial Proportional Odds Model Approach to Exploring the Heterogeneities in Truck-Involved Severities at Cross and T-Intersections. Accid. Anal. Prev. 2020, 144, 105638. [Google Scholar] [CrossRef]
- Iranmanesh, M.; Seyedabrishami, S.; Moridpour, S. Identifying High Crash Risk Segments in Rural Roads Using Ensemble Decision Tree-Based Models. Sci. Rep. 2022, 12, 20024. [Google Scholar] [CrossRef] [PubMed]
- Sum, S.; Se, C.; Champahom, T.; Jomnonkwao, S.; Sinha, S.; Ratanavaraha, V. A Random Forest and SHAP-Based Analysis of Motorcycle Crash Severity in Thailand: Urban-Rural and Day-Night Perspectives. Transp. Eng. 2025, 21, 100369. [Google Scholar] [CrossRef]
- Dimitrijevic, B.; Asadi, R.; Spasovic, L. Application of Hybrid Support Vector Machine Models in Analysis of Work Zone Crash Injury Severity. Transp. Res. Interdiscip. Perspect. 2023, 19, 100801. [Google Scholar] [CrossRef]
- Mokhtarimousavi, S.; Anderson, J.C.; Azizinamini, A.; Hadi, M. Improved Support Vector Machine Models for Work Zone Crash Injury Severity Prediction and Analysis. Transp. Res. Rec. 2019, 2673, 680–692. [Google Scholar] [CrossRef]
- Champahom, T.; Se, C.; Watcharamaisakul, F.; Jomnonkwao, S.; Karoonsoontawong, A.; Ratanavaraha, V. Tree-Based Approaches to Understanding Factors Influencing Crash Severity across Roadway Classes: A Thailand Case Study. IATSS Res. 2024, 48, 464–476. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, D.; Gu, X.; Abdel-Aty, M.; Xing, Y.; Wang, J.; Lu, H.; Chen, Y. A Hybrid Approach of Random Forest and Random Parameters Logit Model of Injury Severity Modeling of Vulnerable Road Users Involved Crashes. Accid. Anal. Prev. 2023, 192, 107235. [Google Scholar] [CrossRef] [PubMed]
- Hasan, A.S.; Jalayer, M.; Das, S.; Asif Bin Kabir, M. Application of Machine Learning Models and SHAP to Examine Crashes Involving Young Drivers in New Jersey. Int. J. Transp. Sci. Technol. 2024, 14, 156–170. [Google Scholar] [CrossRef]
- Samerei, S.A.; Aghabayk, K. Analyzing the Transition from Two-Vehicle Collisions to Chain Reaction Crashes: A Hybrid Approach Using Random Parameters Logit Model, Interpretable Machine Learning, and Clustering. Accid. Anal. Prev. 2024, 202, 107603. [Google Scholar] [CrossRef] [PubMed]
- Jafari, M.; Persaud, B. Investigating the Influence of Socioeconomic Factors on the Relationships between Road Characteristics and Traffic Crash Frequency and Severity—A Hybrid Structural Equation Modelling–Artificial Neural Networks Approach. Accid. Anal. Prev. 2025, 218, 108076. [Google Scholar] [CrossRef]
- data.gouv.fr, Annual Databases of Road Traffic Injury Accidents—Years 2005 to 2023. Available online: https://www.data.gouv.fr/datasets/bases-de-donnees-annuelles-des-accidents-corporels-de-la-circulation-routiere-annees-de-2005-a-2022/ (accessed on 8 October 2024).

| Variables | Category | Severe Injury | No Injury | Minor Injury | ||||
|---|---|---|---|---|---|---|---|---|
| No. | % | No. | % | No. | % | |||
| sexe | Gender | 1: Male | 14,533 | 62.6 | 16,321 | 70.3 | 13,187 | 56.8 |
| 2: Female | 8683 | 37.4 | 6895 | 29.7 | 10,029 | 43.2 | ||
| obs | Fixed Obstacles | 0: No fixed obstacle | 19,525 | 84.1 | 22,334 | 96.2 | 20,987 | 90.4 |
| 1: Fixed obstacle | 813 | 3.5 | 348 | 1.5 | 650 | 2.8 | ||
| secu | The safety equipment | 0: No safety equipment | 8938 | 38.5 | 5084 | 21.9 | 7522 | 32.4 |
| 1: Seatbelt | 14,046 | 60.5 | 18,085 | 77.9 | 15,601 | 67.2 | ||
| 2: Child Seat | 0 | 0.0 | 0 | 0.0 | 0 | 0.0 | ||
| 3: Others | 232 | 1.0 | 46 | 0.2 | 93 | 0.4 | ||
| obsm | The mobile obstacle | 0: No mobile obstacle | 2739 | 11.8 | 813 | 3.5 | 1579 | 6.8 |
| 1: Mobile obstacle | 1230 | 5.3 | 2670 | 11.5 | 1416 | 6.1 | ||
| lum | Lighting condition | 1: Daylight | 14,185 | 61.1 | 16,414 | 70.7 | 15,578 | 67.1 |
| 2: Dusk or dawn | 952 | 4.1 | 1184 | 5.1 | 1393 | 6.0 | ||
| 3: Night without street lighting | 720 | 3.1 | 302 | 1.3 | 163 | 0.7 | ||
| 4: Night with street lighting not lit | 93 | 0.4 | 163 | 0.7 | 139 | 0.6 | ||
| 5: Night with street lighting lit | 7267 | 31.3 | 5154 | 22.2 | 5920 | 25.5 | ||
| plan | Road alignment | 1: Straight | 19,943 | 85.9 | 20,732 | 89.3 | 20,128 | 86.7 |
| 0: Curved | 1602 | 6.9 | 1323 | 5.7 | 1486 | 6.4 | ||
| prof | Road longitudinal profile | 0: Sloped | 511 | 2.2 | 116 | 0.5 | 70 | 0.3 |
| 1: Flat | 16,924 | 72.9 | 17,621 | 75.9 | 17,342 | 74.7 | ||
| atm | The weather condition | 1: Normal | 20,500 | 88.3 | 21,034 | 90.6 | 20,314 | 87.5 |
| 2: Rainy or snowy | 1602 | 6.9 | 1207 | 5.2 | 1695 | 7.3 | ||
| Severity | Mean | Std | Min | 25% | 50% | 75% | Max | |
|---|---|---|---|---|---|---|---|---|
| nbv | No injury | 2.69 | 1.93 | 0.0 | 1.0 | 3.0 | 3.0 | 11.0 |
| Minor injury | 2.7 | 2.0 | 0.0 | 1.0 | 3.0 | 3.0 | 11.0 | |
| Severe injury | 3.02 | 1.55 | 0.0 | 3.0 | 3.0 | 3.0 | 9.0 | |
| age | No injury | 43.9 | 17.43 | 3.0 | 30.0 | 41.0 | 56.0 | 100.0 |
| Minor injury | 39.77 | 16.74 | 2.0 | 27.0 | 36.0 | 50.0 | 101.0 | |
| Severe injury | 40.08 | 16.42 | 8.0 | 28.0 | 36.0 | 50.0 | 96.0 |
| Metric | Formula |
|---|---|
| Accuracy | |
| Precision (per class) | |
| Recall (per class) | |
| F1-score (per class) | |
| Macro-F1 | |
| Micro-F1 | |
| Weighted-F1 | |
| Balanced Accuracy | |
| ROC-AUC (OvR, Macro, Micro, Class-wise) | |
| PR-AUC (OvR, Class-wise) | |
| Confusion Matrix |
| Not Merged | Merged | |
|---|---|---|
| Balanced accuracy | 0.414 ± 0.018 | 0.501 ± 0.019 |
| Macro F1 | 0.450 ± 0.029 | 0.502 ± 0.022 |
| ROC-AUC (macro) | 0.792 ± 0.011 | 0.819 ± 0.015 |
| PR-AUC (macro) | 0.535 ± 0.024 | 0.668 ± 0.035 |
| Classification Report | ||||
|---|---|---|---|---|
| Precision | Recall | F1-Score | Support | |
| No injury | 0.83 | 0.86 | 0.85 | 2386 |
| Minor injury | 0.80 | 0.79 | 0.79 | 1788 |
| Severe injury | 0.70 | 0.64 | 0.67 | 311 |
| accuracy | 0.81 | 4485 | ||
| macro avg | 0.78 | 0.76 | 0.77 | 4485 |
| weighted avg | 0.81 | 0.81 | 0.81 | 4485 |
| Metric | Value |
|---|---|
| Accuracy | 0.8137 ± 0.0046 |
| Balanced Accuracy | 0.7607 ± 0.0046 |
| Macro-F1 | 0.7697 ± 0.0041 |
| Micro-F1 | 0.8137 ± 0.0021 |
| Weighted-F1 | 0.8129 ± 0.0058 |
| ROC-AUC (macro) | 0.9017 ± 0.0039 |
| ROC-AUC (micro) | 0.9270 ± 0.0021 |
| PR-AUC (macro) | 0.7908 ± 0.0027 |
| PR-AUC (micro) | 0.8565 ± 0.0061 |
| PR-AUC (per class) | No injury: 0.8819 ± 0.0023 |
| Minor injury: 0.8488 ± 0.0018 | |
| Severe injury: 0.6393 ± 0.0031 |
| Variable | Chi2 | p-Value | Violation (Yes/No) |
|---|---|---|---|
| age | 5.27 | 0.020 | Yes |
| secu1 | 2.11 | 0.150 | No |
| secu2 | 1.28 | 0.203 | No |
| secu3 | 1.74 | 0.180 | No |
| nbv | 8.53 | 0.000 | Yes |
| sexe2 | 12.43 | 0.000 | Yes |
| obs1 | 3.87 | 0.050 | Yes |
| obsm1 | 0.00 | 1.000 | No |
| lum2 | 1.93 | 0.160 | No |
| lum3 | 17.45 | 0.000 | Yes |
| lum4 | 0.06 | 0.800 | No |
| lum5 | 0.06 | 0.810 | No |
| plan0 | 0.45 | 0.500 | No |
| prof0 | 0.31 | 0.590 | No |
| atm0 | 4.26 | 0.040 | Yes |
| Model | Log-Likelihood | AIC | BIC |
|---|---|---|---|
| Ordered Logit | −6201.8 | 12,435.6 | nan |
| PPO Model | −6182.75 | 12,409.5 | 13,052.429399574658 |
| Variable | Panel I | Panel II | |
|---|---|---|---|
| Coefficient | Coefficient | ||
| obs = 1 (ref = 0) | Fixed obstacle vs. None | −0.990 *** | −0.990 *** |
| obsm = 1 (ref = 0) | Moving obstacle vs. None | 0.223 * | 0.223 * |
| plan = 0 (ref = 1) | Not straight vs. Straight | −0.107 | −0.107 |
| prof = 0 (ref = 1) | Not flat vs. Flat | −0.041 | −0.041 |
| atm = 0 (ref = 1) | Bad vs. Normal weather | −0.184 * | −0.184 * |
| secu = 1 (ref = 0) | Seatbelt vs. No equipment | 1.738 *** | 1.738 *** |
| secu = 2 (ref = 0) | Child seat vs. No equipment | 0.029 | 0.029 |
| secu = 3 (ref = 0) | Others vs. No equipment | 0.102 | 0.102 |
| age | Age | −0.003 * | −0.011 *** |
| nbv | The number of lanes | 0.091 ** | 0.019 |
| sexe = 2 (ref = 1) | Female vs. Male | 0.343 *** | 0.672 *** |
| lum = 2 (ref = 1) | Lum: Dawn/Dusk vs. Daylight | −0.344 | 0.072 |
| lum = 3 (ref = 1) | Lum: Night no streetlights vs. Daylight | 0.724 ** | −0.278 |
| lum = 4 (ref = 1) | Lum: Night without streetlights vs. Daylight | −0.263 | −0.128 |
| lum = 5 (ref = 1) | Lum: Night with streetlights vs. Daylight | 0.234 * | 0.260 *** |
| Variable | Severe | Minor | No Injury |
|---|---|---|---|
| age | −0.0004 (−0.0005, −0.0003) | −0.0019 (−0.0025, −0.0013) | 0.0024 (0.0017, 0.0030) |
| nbv | 0.0012 (0.0002, 0.0022) | 0.0096 (0.0091, 0.0098) | −0.0066 (−0.0120, −0.0012) |
| sexe2 | 0.0365 (0.0289, 0.0451) | 0.1194 (0.1029, 0.1367) | −0.1559 (−0.1806, −0.1320) |
| obs1 | 0.0678 (0.0480, 0.0902) | 0.1719 (0.1412, 0.1978) | −0.2936 (−0.2845, −0.1889) |
| obsm1 | −0.0084 (−0.0156, −0.0008) | −0.0427 (−0.0832, −0.0038) | 0.0511 (0.0046, 0.0985) |
| lum2 | 0.0012 (−0.0075, 0.0112) | 0.0045 (−0.0364, 0.0472) | −0.0058 (−0.0585, 0.0436) |
| lum3 | −0.0032 (−0.0169, 0.0152) | 0.0189 (−0.0938, 0.0581) | −0.0221 (−0.0738, 0.1106) |
| lum4 | −0.0040 (−0.0210, 0.0194) | −0.0241 (−0.1171, 0.0732) | 0.0280 (−0.0922, 0.1379) |
| lum5 | 0.0124 (0.0069, 0.0185) | 0.0497 (0.0290, 0.0701) | −0.0620 (−0.0877, −0.0354) |
| plan0 | 0.0053 (−0.0015, 0.0115) | −0.0225 (−0.0700, 0.0475) | −0.0278 (−0.0586, 0.0086) |
| prof0 | 0.0021 (−0.0024, 0.0071) | 0.0093 (−0.0111, 0.0297) | −0.0114 (−0.0369, 0.0135) |
| atm0 | 0.0087 (0.0022, 0.0171) | 0.0357 (0.0100, 0.0650) | −0.0444 (−0.0812, −0.0124) |
| secu1 | −0.0370 (−0.0423, −0.0324) | −0.2591 (−0.2891, −0.2257) | 0.2961 (0.2582, 0.3311) |
| secu2 | −0.0010 (−0.0104, 0.0102) | −0.0059 (−0.0525, 0.0424) | 0.0069 (−0.0528, 0.0626) |
| secu3 | −0.0041 (−0.0125, 0.0064) | −0.0203 (−0.0621, 0.0277) | 0.0244 (−0.0343, 0.0746) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Serre, T. A Hybrid Approach to Investigating Factors Associated with Crash Injury Severity: Integrating Interpretable Machine Learning with Logit Model. Appl. Sci. 2025, 15, 10417. https://doi.org/10.3390/app151910417
Wang C, Serre T. A Hybrid Approach to Investigating Factors Associated with Crash Injury Severity: Integrating Interpretable Machine Learning with Logit Model. Applied Sciences. 2025; 15(19):10417. https://doi.org/10.3390/app151910417
Chicago/Turabian StyleWang, Chenxi, and Thierry Serre. 2025. "A Hybrid Approach to Investigating Factors Associated with Crash Injury Severity: Integrating Interpretable Machine Learning with Logit Model" Applied Sciences 15, no. 19: 10417. https://doi.org/10.3390/app151910417
APA StyleWang, C., & Serre, T. (2025). A Hybrid Approach to Investigating Factors Associated with Crash Injury Severity: Integrating Interpretable Machine Learning with Logit Model. Applied Sciences, 15(19), 10417. https://doi.org/10.3390/app151910417






